Автоматика и телемеханика, № 10, 2019
© 2019 г. Б.М. МИЛЛЕР, д-р.физ.-мат.наук (bmiller@iitp.ru)
(Институт проблем передачи информации им. А.А. Харкевича РАН, Москва;
Университет Монаш, Мельбурн, Виктория, Австралия),
Е.Я. РУБИНОВИЧ, д-р. техн. наук (rubinvch@ipu.rssi.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ЧИСЛЕННЫЙ АНАЛИЗ УДАРНЫХ ВЗАИМОДЕЙСТВИЙ
НА ПРИМЕРЕ ПАРАДОКСА ПЕНЛЕВЕ
ПРИ “КОСОМ” ПАДЕНИИ СТЕРЖНЯ1
Рассматривается система, относящаяся к известным проблемам Пенле-
ве (Painlevé), для решения которой используется предложенный авторами
метод вскрытия пространственно-временных сингулярностей. Этот ме-
тод позволяет однозначно решить проблему определения скоростей тела
после удара о поверхность с сухим трением, т.е. разрешить ситуацию,
в которой традиционные подходы либо дают неоднозначный ответ, либо
приводят к неразрешимой системе соотношений (парадокс Пенлеве).
Ключевые слова: ударные взаимодействия при сухом трении, проблема
Пенлеве.
DOI: 10.1134/S0005231019100052
1. Введение
Систематическое изучение систем автоматического управления с им-
пульсными воздействиями связано с работами Я.З. Цыпкина, выполненными
в 40-60 гг. XX в. [1-3]. В действительности, такие системы возникли еще на
заре становления теории автоматического регулирования как прерывистые и
релейные регуляторы паровых машин, однако развитие адекватной теории
таких систем началось с 1948 г., когда Я.З. Цыпкин начал разрабатывать
единый подход к описанию дискретных систем на основе дискретного пре-
образования Лапласа (Z-преобразования), что позволило создать цельный
математический аппарат, подобный операторному методу описания непре-
рывных систем. Таким образом, для дискретных систем появились стандарт-
ные понятия передаточной функции, частотной характеристики и им по-
добные, и удалось обобщить классические критерии устойчивости Найкви-
ста и Михайлова на случай дискретных систем. Полученные на этом этапе
результаты были подытожены в монографии Я.З. Цыпкина [1], вышедшей
в 1951 г. [4].
Дальнейшее развитие теории импульсных систем шло по пути разработ-
ки частотных методов исследования и постепенного понимания необходимо-
сти описания импульсных воздействий в терминах теории обобщенных функ-
ций [5]. Еще более сложные проблемы были связаны с управлением дина-
мическими системами, где импульсные воздействия возникали в результате
1 Работа выполнена при частичной финансовой поддержке Российского фонда фунда-
ментальных исследований (проекты №№ 16-08-01285 и 16-08-01076).
100
применения управлений, вызывающих кратковременное изменение состоя-
ния, причем такие системы имели широкие области приложений, включая
робототехнику, космические аппараты, экономику и распределение природ-
ных ресурсов [6]. Оказалось, что описание импульсного воздействия в нели-
нейной динамической системе является далеко не тривиальным, поскольку
использование, казалось бы, естественного описания в терминах обобщен-
ных функций требует определенной осторожности, так как приводит к от-
сутствию оптимального управления [7] и невозможности описания оптималь-
ного решения в обычных терминах [8-10]. Эта проблема была решена с по-
мощью так называемого метода разрывной замены времени [11], идея ко-
торого следовала из метода разделения движений, описанного В.И. Гурма-
ном в [12, 13]. Плодотворность этого метода подтверждается многочислен-
ными последующими публикациями, в которых развивались методы оптими-
зации систем с управлениями-мерами, позволившие установить существова-
ние решений [14, 15] и получить условия оптимальности [16, 17] в различных
задачах экономики и квантовой механики с фазовыми ограничениями [18]
и необходимые условия оптимальности, полученные аналогичным методом
введения пространственно-временного управления [19, 20]. Таким образом,
в теории импульсного управления, особенно в публикациях последних лет,
проблема описания импульсного воздействия разрешается методом вскры-
тия сингулярности, основанным на разрывной замене времени [8, 9], когда
быстрое (практически мгновенное) изменение части фазовых координат рас-
тягивается в конечный промежуток времени и динамика системы на этом
промежутке описывается вспомогательной системой “медленного” движения.
Эта ситуация выглядит, с первого взгляда, аналогичной механическому уда-
ру, при котором скорости тел изменяются практически мгновенно, по срав-
нению с движениями до и после удара. При этом сам удар часто описывают
в терминах закона восстановления, связывающего скорости до и после уда-
ра, что при описании динамики движения “в целом” аналогично введению
δ-функций в правую часть системы дифференциальных уравнений, описы-
вающих динамику системы [21]. Именно поэтому аккуратное описание уда-
ра требует отдельного представления непосредственной фазы контакта [22]
с учетом закона взаимодействия и свойств контактирующих тел [23]. Фор-
мально это выглядит как растяжение момента удара в некоторый отрезок,
на котором динамика системы описывается другими уравнениями “быстро-
го движения” аналогично описанию импульсных воздействий. Однако непо-
средственное применение техники замены времени к анализу систем с уда-
рами затруднительно, так как при ударе часть фазовых координат, ответ-
ственных за величину реакции опоры, остается практически неизменной, по-
скольку деформации, отвечающие за реакцию системы на удар, весьма малы,
в то время как скорости изменяются значительно. В большинстве случаев,
известных еще из школьной физики, для определения скоростей тел после
удара достаточно воспользоваться одной из традиционных моделей удара:
упругий или полностью неупругий и далее применить законы сохранения
энергии, импульса или момента импульса. Развитие техники разрывной за-
мены времени было предложено в [24, 25], где было показано, что в этом слу-
чае разрывная динамика может быть описана с помощью пространственно-
101
временной сингулярной замены переменных, что особенно важно для опи-
сания динамики управляемого удара [26]. Необходимо отметить, что одно-
временная сингулярная замена пространственных и временных переменных,
хотя и родственна методу разделения движений [27], широко применяемо-
му в задачах с ударами, но позволяет рассматривать более общие случаи,
связанные с различными условиями окончания ударной (сингулярной) фа-
зы движения. Общий подход, предложенный в [24], гораздо ближе к мето-
дам, основанным на генетической теории удара или методологии штрафных
функций (penalization) [28], когда модель абсолютно твердого тела сначала
заменяется моделью деформируемого тела, но с большим коэффициентом
жесткости, который затем устремляется к бесконечности, чтобы в пределе
снова вернуться к модели абсолютно твердого тела. Этот подход, как выяс-
нилось, позволяет преодолеть проблемы неоднозначности и невозможности
определения решения, возникающие при использовании модели абсолютно
жесткого тела при наличии сухого трения [29, 30]. Родственный подход —
это специальные схемы численного анализа (time-stepping), в которых для
преодоления проблем сингулярности движения в окрестности точек удара
применяется переменный шаг интегрирования уравнений динамики [31, 32].
Тем не менее общая проблема описания движения систем с ударами весьма
сложна и общие теоремы существования и единственности решений были по-
лучены лишь в последние годы [33]. Применение метода пенализации к задаче
о падающем стержне было впервые предпринято в публикации [34], которая
была ориентирована на получение явных результатов и поэтому ограничива-
лась случаем абсолютно упругого удара и случаем, когда в процессе удара
не происходит остановки скольжения стержня. С точки зрения исследования
парадоксальных ситуаций (задача Пенлеве) этот случай не очень интересен,
так как полностью описывается классическими подходами. Более интерес-
ные результаты отмечены в публикации [35], в которой динамика стержня в
режиме контакта с поверхностью описывается с помощью методологии ком-
плиментарного подхода (linear complementary problem (LCP)) и теории си-
стем с разрывной правой частью и где показано, что с помощью этого под-
хода можно всегда решить задачу определения скоростей после удара при
коэффициенте трения, меньшем 4/3 ≈ 1,33, а при некоторых углах падения
стержня область √именимости комплиментарного подхода можно немного
расширить до 8/(3
3) ≈ 1,53. Интересный и вполне завершенный анализ этой
задачи дан в монографии [36], где указывается на необходимость изменения
модели для получения результатов при всех значениях коэффициента тре-
ния. В [37, 38] данная проблема была решена с помощью метода сингуляр-
ных пространственно-временных преобразований в частном случае “прямо-
го” падения стержня без бокового вращения и отсутствия поперечных скоро-
стей. Было доказано, что предельное движение, при коэффициенте жестко-
сти, стремящемся к бесконечности, полностью описывается вспомогательной
системой “быстрого движения”, которая является предельной для движений
с конечным, но достаточно большим коэффициентом жесткости. Были по-
казаны эффекты резонансного поглощения кинетической энергии стержня
и подскока без удара.
102
В данной статье, используя методы теории управления для систем с им-
пульсными воздействиями и ударами, развивается метод решения задачи
на случай “косого” падения стержня, для которого также известны слу-
чаи возникновения парадокса Пенлеве [39]. Применение метода сингулярных
пространственно-временных преобразований позволяет однозначно решить
проблему определения скоростей после удара при произвольных значениях
коэффициента трения и углах падения.
2. Геометрия проблемы Пенлеве для стержня,
падающего на шероховатую поверхность
Применение сингулярной пространственно-временной замены переменных
иллюстрируется на модифицированном примере из [39] в предположении, что
закон взаимодействия с препятствием описывается вязко-упругой моделью и
момент прекращения сингулярной фазы определяется из физического усло-
вия разрыва контакта, т.е. обращения реакции опоры в ноль.
Рассматривается задача об определении скоростей жесткого стержня еди-
ничной массы, длины 2l при ударе о вязко-упругую поверхность [39]. Геомет-
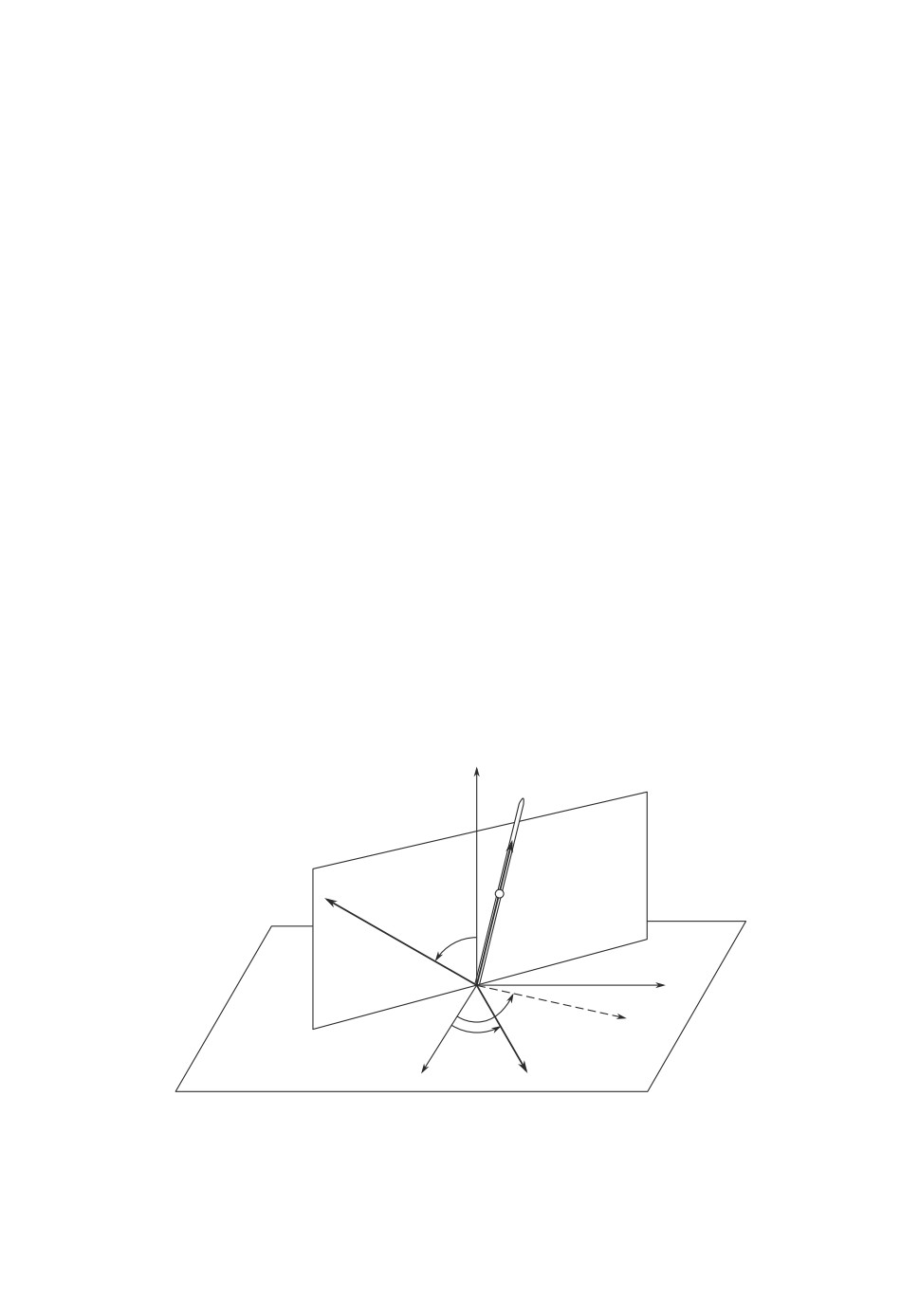
рия задачи показана на рис. 1.
В [39] приводятся условия возникновения и/или отсутствия парадоксаль-
ной ситуации. Во многих работах, начиная с классической книги Пенлеве [29],
отмечается что ее возникновение обусловлено не физикой задачей, а выбран-
ной математической моделью абсолютно жесткого тела, которая приводит
к так называемым условиям комплементарности, не совместным при боль-
ших значениях коэффициента трения (k ≥ 4/3), поэтому одним из способов
устранения парадокса является отказ от модели абсолютно жесткого тела и
i3
[x10, x20, x30]
i2
Направление
скольжения
i1
Рис. 1. Геометрия падающего стержня: 2l - длина, m = 1 - масса;
(x10, x20, x30) - координаты центра масс в неподвижной прямоугольной
системе координат с ортами i1, i2, i3, где i3 - нормаль к поверхности;
ψ, θ - углы наклона стержня; сила притяжения направлена вниз вдоль
оси i3.
103
допущение его податливости. Таким образом, например, в [39] принимается
полиномиальная зависимость силы реакции опоры от глубины проникнове-
ния [27]. Однако определение параметров этой модели представляет собой
отдельную проблему. В [38] используется модель вязко-упругой силы, при-
чем предполагается, что модель абсолютно жесткого тела получается при
переходе к пределу по коэффициенту жесткости, стремящемуся к бесконеч-
ности. Отметим, что вывод условий восстановления, т.е. определения связи
скоростей до и после удара, в общем виде не представляется возможным, так
как скорости в момент разрыва контакта можно определить лишь численно
как решения дифференциального уравнения “быстрого” движения. В данной
статье используется аналогичный подход, но для случая “косого” удара.
2.1. Уравнения движения в обобщенных координатах
В качестве обобщенных координат выбираем координаты центра масс
стержня, два угла наклона и их производные (рис. 1)
Xp = [x10,x20,x30,ψ,θ]⊤,
(1)
Xv =Xp = [ x10, x20, x30,ψ
θ]⊤.
Положим
Xv = [v1,v2,v3,ψ
θ]⊤,
тогда уравнения динамики стержня имеют вид
⎡
⎤
-
ψ2 sin ψ cos3 θ - l˙2 sin ψ cos θ
⎢
⎥
⎢
⎥
ψ2 cos ψ cos3 θ + lθ2 cosψ cos θ
⎡
⎤
⎢
⎥
F1
⎢
⎥
⎢
⎥
⎦+
⎢
L ψ2 sinθ + l θ2sinθ - g
⎥
(2)
Xv = Q⎣ F2
,
⎢
⎥
⎢
⎥
F3
2 ψ θsinθ
⎢
⎥
⎢
⎥
⎣
cos θ
⎦
− ψ2 sinθcosθ
матрица Q равна:
⎡
⎤
1+3cos2 ψ+3sin2 ψ sin2 θ
3 sinψ cosψ cos2 θ
3 sinψ sinθ cosθ
⎢
⎥
⎢
⎥
3 sinψ cosψ cos2 θ
1+3sin2 ψ+3cos2 ψ sin2 θ -3cosψ sinθcosθ
⎢
⎥
⎢
⎥
⎢
⎥
3 sinψ sinθ cosθ
-3 cosψ sinθ cosθ
1 + 3cos2 θ
⎢
⎥
(3) Q =⎢
⎥
⎢
3 cosψ
3 sinψ
⎥
⎢
⎥
0
⎢
⎥
l cosθ
l cosθ
⎢
⎥
⎣
⎦
3
3
3
-
sinψ sinθ
cosψ sinθ
-
cosθ
l
l
l
104
В уравнениях (2) и (3) зависимость от времени t опущена, F1,F2 - компо-
ненты силы трения, F3 - нормальная реакция опоры. Таким образом,
⎧
(
)
(
)
⎪
F1
1
v1
⎨
= -kF3√
, если v21 + v22 = 0,
F2
v2
v21 + v22
(4)
Fтр =
⎪
⎩ ≤ k|F3|,
если v21 + v22 = 0.
Заметим, что сила трения не может быть определена из соотношений (4)
при v21 + v22 = 0, т.е. при “стопорении” нижнего конца стержня. Далее, в под-
разделе 3.3 показано, как сила трения определяется из условия равновесия
стержня с помощью численного решения.
Сила нормальной реакции
(5)
F3 = -μx30 - 2μ1/2δ x30,
где μ - коэффициент жесткости, а δ ∈ [0, 1] - коэффициент вязкости.
Замечание 1. Для получения модели абсолютно жесткого тела коэф-
фициент μ устремляется к бесконечности. Цель - описать предельное движе-
ние при μ → ∞, что соответствует модели абсолютно твердого тела. Отличие
от традиционного комплементарного подхода - допущение о деформируемо-
сти поверхности.
2.2. Замена переменных: сингулярное
пространственно-временное преобразование
Из анализа уравнений движения следует, что глубина проникновения
стержня внутрь запрещенной области и время его пребывания там имеют
порядок μ-1/2, поэтому следующая замена переменных растягивает времен-
ной интервал и область взаимодействия в масштаб порядка единицы:
1
tμ(s) = τ +
√μs,s≥0,
(6)
Yμp(s) = Xp(τ) +
√μ [Xp(tμ(s)) - Xp(τ)],
Yμv(s) = Xv(tμ(s)),
где τ - момент начала сингулярной фазы движения (попадания на границу
одностороннего ограничения).
Предложение 1. На интервале s ∈ [0,S∗], где S∗ - момент выхода из
“запрещенной области”, существуют пределы:
(7)
lim
Yμp(s) =Yp(s), lim
Yμv(s) =Yv
(s),
μ↑∞
μ↑∞
удовлетворяющие системе уравнений “быстрого движения”.
Идея доказательства повторяет результат из [24] и состоит из следую-
щих этапов: проверяется репульсивный характер ограничения и устанав-
ливается равномерная по μ ↑ ∞ сходимость последовательности решений
(Yp(s), Yv(s)) на интервале s ∈ [0, S∗], откуда следует требуемый результат.
105
2.3. Уравнения “быстрого движения”
Предложение 2. Система уравнений “быстрого движения” имеет
вид:
¯
Y
p(s) =Yv(s),
⎛
⎞
Y1
v
√
⎜
⎟
⎜
(Y1v)2 + (Y2v)2
⎟
(8)
⎜
⎟
¯
⎜
⎟
Y
v(s) = -Q(Yp(0))⎜
⎟(-Y3p - 2δ Y3v)I{s ≤ S∗},
Y2
⎜
v
⎟
⎜
√
⎟
⎝
⎠
(Y1v)2 + (Y2v)2
1
где
{
}
S∗ = inf s :Y3p(s) + 2δ Y3v(s) < 0 ,
Yp(0) = Xp(τ),
Yv(0) = Xv(τ).
Доказательство этого факта для случая плоского удара приведено в [37, 38],
для “косого” удара доказательство проводится аналогично.
Замечание 2. Система уравнений (8) имеет единственное решение и
описывает фазу сингулярного движения при больших μ, что подтверждается
следующими соотношениями:
Yp(√μ(t - τ)) - Xp(τ)
Xp(t) ≈ Xp(τ) +
,
√μ
Xv(t) ≈Yv(√μ(t - τ)).
Другими словами, “быстрое” решение позволяет приближенно описать все
решения системы (2) при достаточно больших μ.
2.4. Уравнения для “скачка” скорости
Значения координат, линейных и угловых скоростей стержня после удара
описываются соотношениями:
¯
(9)
lim
Xp(τ) = Xp(τ-), lim
Xv(τ) =
Y
v(S∗),
μ↑∞
μ↑∞
гдеYv(s) - решение системы уравнений “быстрого” движения.
Доказательство. Идея доказательства повторяет в основном плоский
случай [37, 38]:
• Совокупность решений системы имеет равномерно ограниченную по μ ва-
риацию. Поэтому существует подпоследовательность, сходящаяся пото-
чечно к пределу, удовлетворяющему системе (8);
106
• Правая часть системы (8) обладает свойством
v
v
〉≤0
для любыхY′v, Y′′v. Это свойство позволяет заменить традиционное усло-
вие Липшица, которое используется для оценки квадрата разности скоро-
стей двух предполагаемых решений.
Таким образом, на интервале s ∈ [0, S∗] последовательность решений
(Yp(s), Yv(s)) сходится к решению системы уравнений “быстрого” движения,
которое можно определить численно и тем самым охарактеризовать поведе-
ние предельного движения, соответствующего модели абсолютно жесткого
тела. Никаких ограничений на значение коэффициента трения данный под-
ход не накладывает, и поэтому не возникает и “парадокса”.
3. Результаты численного моделирования
Особенность “косого” удара состоит в том, что при движении нижнего
конца стержня может происходить его остановка, при этом вращение сохра-
няется. В модели деформируемой поверхности при соударении нижний конец
стержня углубляется, происходит сжатие, которое затем разряжается путем
выталкивания стержня. Момент завершения взаимодействия соответствует
моменту обращения в нуль реакции опоры, после которого движение стерж-
ня происходит по инерции и уже под действием силы тяжести. Скорости
стержня в момент размыкания контакта и определяют закон восстановления.
При моделировании на первом этапе определяется профиль реакции опоры
и момент обращения его в нуль. Это время различно для различных значе-
ний коэффициента трения. Кроме того, при численном решении уравнений
“быстрого” движения (8) при “стопорении” нижнего конца, т.е. при обраще-
нии в нуль переменныхY1v, Y2v, правая часть системы (8) не определена, хотя
при численном решении эти переменные отличны от нуля, но происходит ча-
стое переключение знака силы, которое выглядит как “скользящий” режим,
известный в теории автоматического управления [40]. Значение силы трения
при “стопорении” стержня можно определить методом эквивалентного управ-
ления, приравняв в системе уравнений (8) производные переменныхY1v, Y2v
нулю.
3.1. Начальные условия
В момент начала удара принимаем
Yp = [0,0,0,0,π/3],
Yv = [0,05;-0,05;-0,04;4,0;4,0].
Численный анализ производим для двух значений коэффициента трения:
“малый” k = 0,5 и “большой” k = 1,7.
107
3.2. Малый коэффициент трения
Вычисление профиля силы реакции опоры показано на рис. 2.
Таким образом, время контакта равно S∗ = 1,865. Профили скоростей (см.
рис. 3) показывают, что “стопорения” не происходит, стержень просто тормо-
зится.
Аналогично уменьшается угловая скорость вращения по углу θ (рис. 4).
0,025
0,020
0,015
0,010
0,005
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
Время S
Рис. 2. Реакция опоры (обращается в нуль при S∗ = 1,865).
0,06
0,04
0,02
0
0,02
0,04
0,06
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
Время S
Рис. 3. Профиль скоростей по осям i1, i2.
108
4,000
3,998
3,996
3,994
3,992
3,990
3,988
3,986
3,984
3,982
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
Время S
Рис. 4. Профиль угловой скорости вращения по θ.
0,045
0,040
0,035
0,030
0,025
0,020
0,015
0,010
0,005
0
0,005
0
0,5
1,0
1,5
2,0
2,5
3,0
Время S
Рис. 5. Профиль реакции опоры (обращается в нуль при S∗ = 2,53). В момент
S = 0,5 происходит “стопорение” стержня, это можно увидеть по результатам
численной процедуры, что проявляется в виде небольших зубцов на графике.
3.3. Большой коэффициент трения
Вычисление профиля силы реакции опоры показано на рис. 5.
Таким образом, время контакта равно S∗ = 2,53. Профили скоростей (см.
рис. 6), показывают, что момент “стопорения” равен S = 0,5.
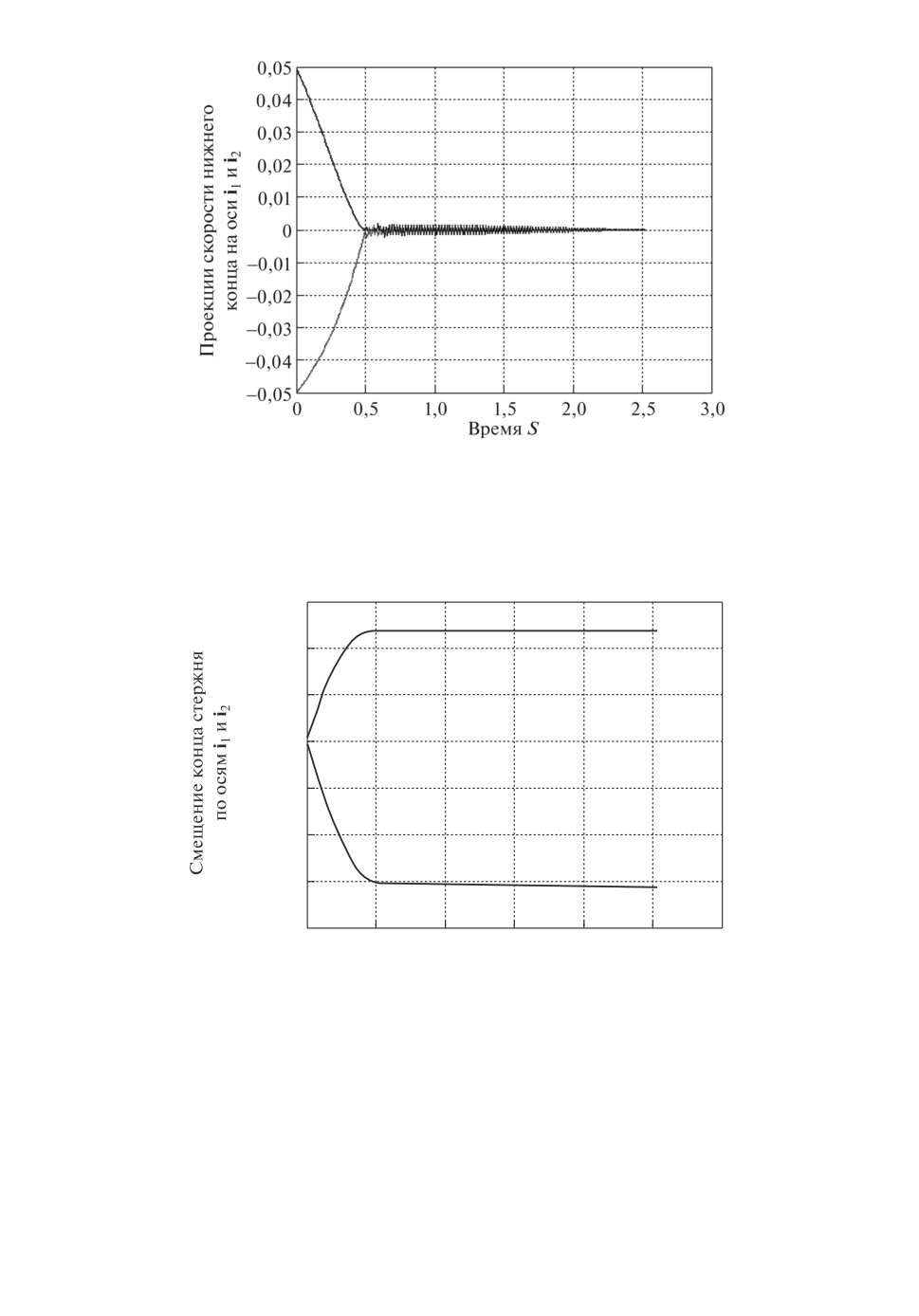
На графике рис. 7 показано смещение нижнего конца стержня, некоторая
асимметрия возникает из-за начального вращения по углу ϕ.
109
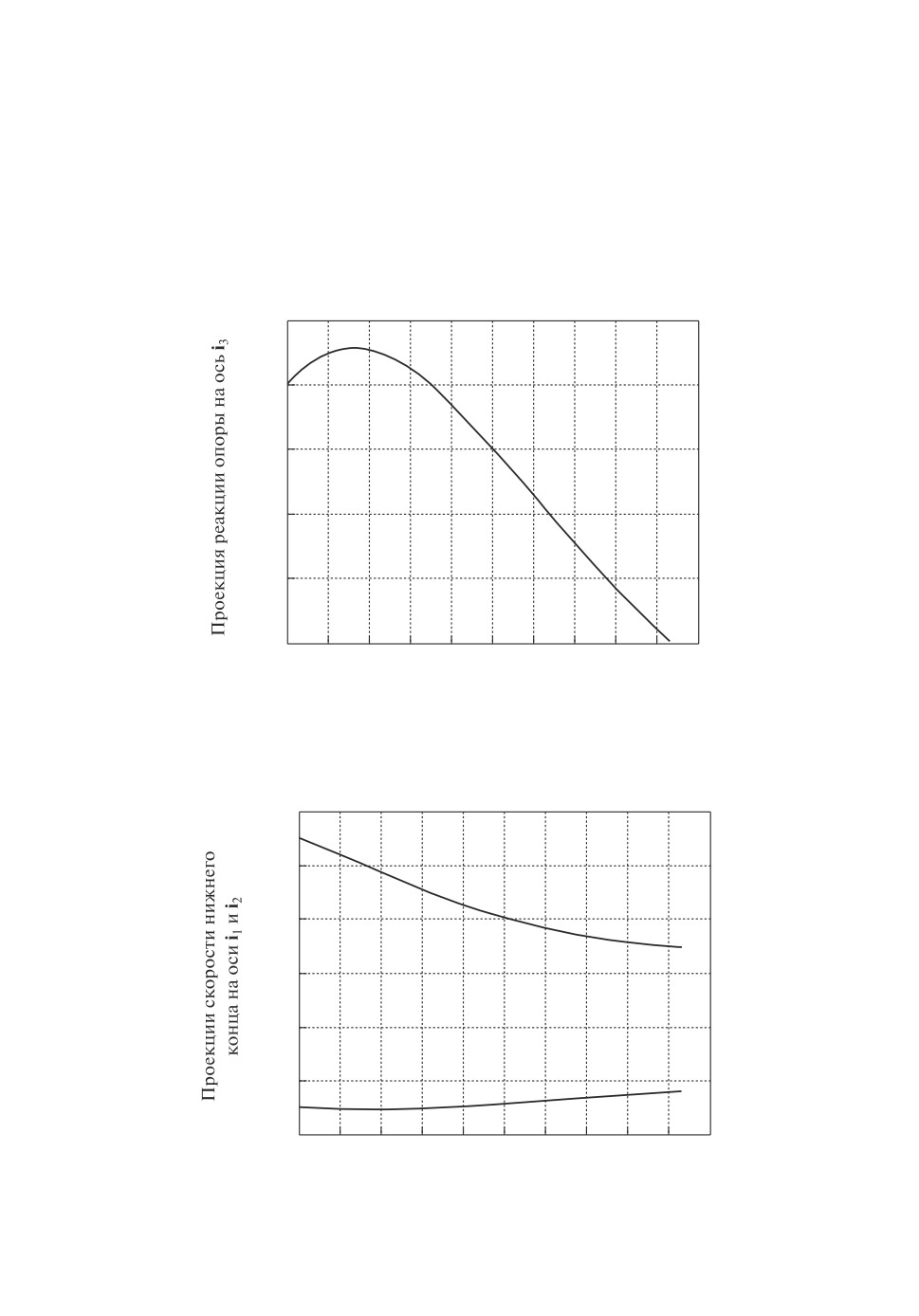
Рис. 6. Профили скоростей по осям i1, i2. После момента
“стопорения” численная процедура показывает наличие
“скользящего” режима.
0,015
0,010
0,005
0
0,005
0,010
0,015
0,020
0
0,5
1,0
1,5
2,0
2,5
3,0
Время S
Рис. 7. Смещение нижнего конца стержня по осям i1, i2.
Угловая скорость вращения по углу θ обнаруживает наличие “стопорения”
резким изменением знака углового ускорения в момент S = 0,5.
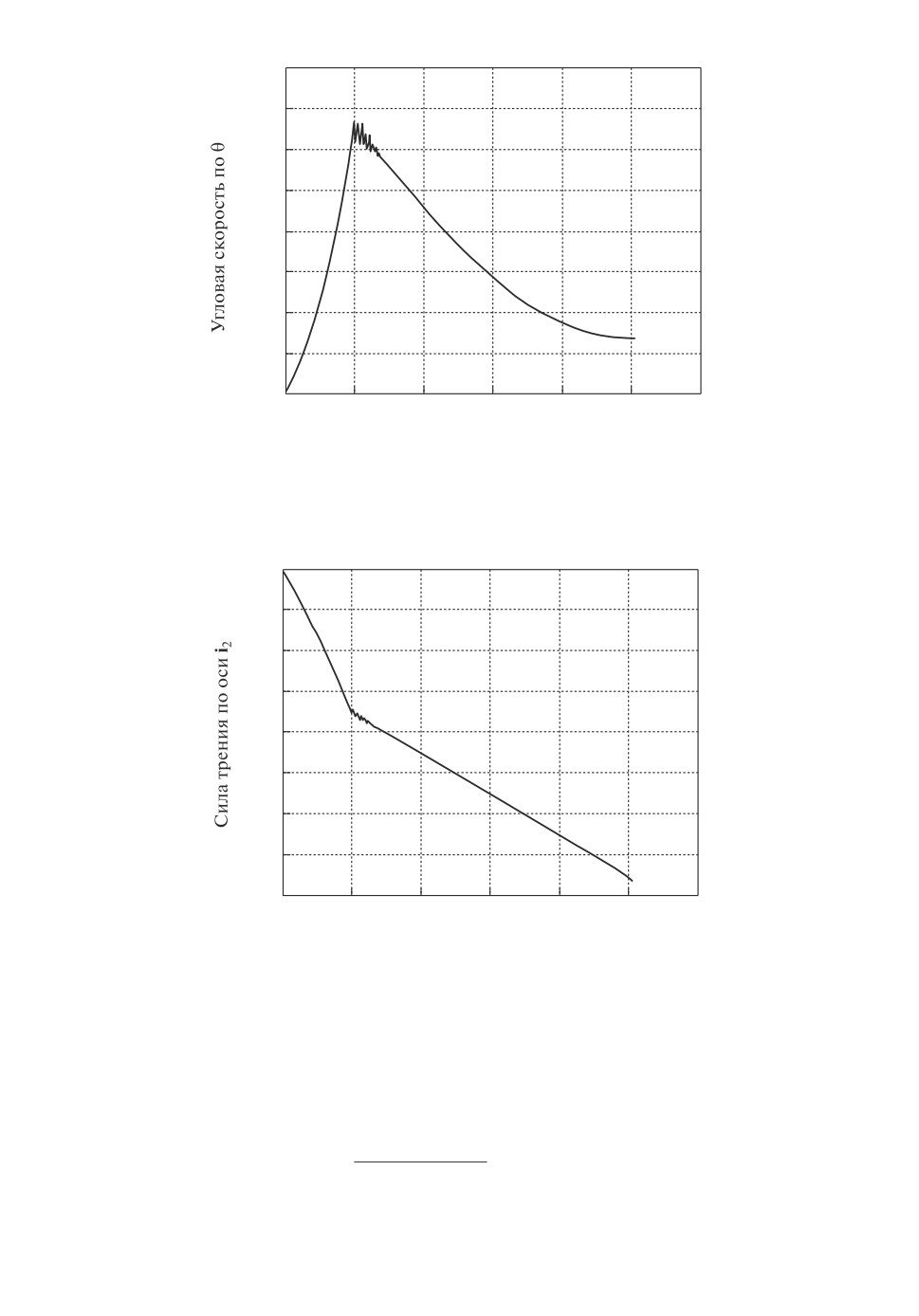
Этот эффект хорошо просматривается на рис. 8 в момент “стопорения”
S = 0,5. Также можно сравнить теоретическое и найденное из численного
решения значение силы трения. Для этого вычисляется интеграл от силы
трения по оси i2, соответствующий график представлен на рис. 9.
110
4,040
4,035
4,030
4,025
4,020
4,015
4,010
4,005
4,000
0
0,5
1,0
1,5
2,0
2,5
3,0
Время S
Рис. 8. Профиль угловой скорости вращения по θ
при “большом” коэффициенте трения.
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
0
0,5
1,0
1,5
2,0
2,5
3,0
Время S
Рис. 9. Профиль интеграла силы трения по оси i2.
Из графика находим наклон второй половины, соответствующей режиму
¯
2
“стопорения”, равный ≈ - 0,42, теоретическое значение из условия
Y
=0
v
дает значение наклона графика
3sin θ cos θ
-
≈ -0,437,
k(1 + 3 cos2 θ)
что можно считать неплохим соответствием.
111
4. Заключение
В данной статье показано, что импульсные воздействия, возникаю-
щие вследствие ударов в механических системах, требуют весьма акку-
ратных моделей для описания результатов такого взаимодействия. Метод
пространственно-временных сингулярных преобразований позволяет “вскры-
вать” такие сингулярности, но часто требует применения численных мето-
дов. Многие авторы [27] считали, что для определения импульсной силы,
возникающей при ударе, нужен закон взаимодействия и точное знание ко-
эффициентов жесткости и вязкости. Однако предложенный подход, который
гарантирует существование единственного решения при достаточно больших
значениях жесткости и сходимость к единственному решению при стремле-
нии жесткости к бесконечности, позволяет однозначно определить скорости
после удара и согласуется с экспериментальными результатами, демонстри-
рующими зависимость закона восстановления от угла падения стержня [38].
Отметим, что в публикациях, использующих другое описание взаимодействия
стержня с поверхностью, например с точки зрения гибридных систем [35]
закон Герца или полиномиальную зависимость [27, 39], парадокс Пенлеве не
устраняется при больших коэффициентах трения, в то время как предложен-
ный подход свободен от этого недостатка и позволяет определить скорости
после удара при любом коэффициенте трения.
СПИСОК ЛИТЕРАТУРЫ
1. Цыпкин Я.З. Переходные и установившиеся процессы в импульсных системах.
М.: Госэнергоиздат, 1951.
2. Цыпкин Я.З. Теория импульсных систем. М.: Физматгиз, 1958.
3. Цыпкин Я.З. Теория линейных импульсных систем. М.: Физматгиз, 1963.
4. Поляк Б.Т. Развитие теории автоматического управления // Проблемы управ-
ления. 2009. Спец. выпуск. № 3.1. С. 13-18.
5. Халанай А., Векслер Д. Качественная теория импульсных систем / Пер. с ру-
мын. М.: Мир, 1971.
6. Цыпкин Я.З., Попков Ю.С. Теория нелинейных импульсных систем. М.: Наука,
1973.
7. Rishel R.W. An Extended Pontriagin Principle for Control Systems whose Control
Laws Contain Measures // J. SIAM. Ser. A. Control. 1965. V. 3. No. 2. P. 191-205.
8. Miller B.M., Rubinovich E.Ya. Impusive Control in Continuous and Discrete-
Continuous Systems. N.Y.: Kluwer Acad./Plenum Publishres, 2003.
9. Миллер Б.М., Рубинович Е.Я. Оптимизация динамических систем с импульс-
ными управлениями. М.: Наука, 2005.
10. Миллер Б.М., Рубинович Е.Я. Оптимизация динамических систем с импульс-
ными управлениями и ударными воздействиями. М.: ЛЕНАНД/URSS, 2019.
11. Миллер Б.М. Метод разрывной замены времени в задачах оптимального управ-
ления импульсными и дискретно-непрерывными системами // АиТ. 1993. № 12.
С. 3-32.
Miller B.M. Method of Discontinuous Time Change in Problems of Control for
Impulse and Discrete-Continuous Systems // Autom. Remote Control. 1993. V. 54.
No. 12. P. 1727-1750.
112
12.
Гурман В.И. Об оптимальных процессах с неограниченными производными //
АиТ. 1972. № 12. С. 14-21.
Gurman V.I. On Optimal Processes With Unbounded Derivatives // Autom. Remote
Control. 1972. V. 33. No. 12. P. 1924-1930.
13.
Миллер Б.М., Рубинович Е.Я. Динамические системы с разрывными решения-
ми и задачи с неограниченными производными // Изв. Иркут. гос. ун-та. Сер.
Математика. 2017. Т. 19. С. 136-149.
14.
Завалищин С.Т., Сесекин А.Н. Импульсные процессы: Модели и приложения.
М.: Наука, 1991.
15.
Zavalishchin S.T., Sesekin A.N. Dynamic Impulse Systems. Theory and
Applications. The Netherlands, Dordrecht: Kluwer Acad. Publishers, 1997.
16.
Миллер Б.М. Условие оптимальности в задаче управления системой, описывае-
мой дифференциальным уравнением с мерой // АиТ. 1982. № 6. С. 60-72.
Miller B.M. An Optimality Condition in Control of a System which is Described
by a Differential Equation with a Measure // Autom. Remote Control. 1982. V. 43.
No. 6. P. 752-761.
17.
Миллер Б.М. Условия оптимальности в задачах обобщенного управления. I, II //
АиТ. 1992. № 3. С. 362-370; 1992. № 4. С. 505-513.
Miller B.M. Conditions for Optimality in Generalized Control Problems. I. Necessary
Conditions for Optimality // Autom. Remote Control. 1992. V. 53. No. 3. P. 362-370.
Miller B.M. Optimality Conditions in Generalized Control Problems. II. Sufficient
Conditions of Optimality // Autom. Remote Control. 1992. V. 53. No. 4. P. 505-513.
18.
Дыхта В.А., Самсонюк О.Н. Оптимальное импульсное управление с приложе-
ниями. М.: Физматлит, 2000.
19.
Bressan A., Rampazzo F. On Differential Systems with Quadratic Impulses and
Their Applications to Lagrangian Mechanics // SIAM J. Control Optim. 1993. V. 31.
P. 1206-1220.
20.
Bressan A., Rampazzo F. Impulsive Control Systems without Commutativity
Assumptions // J. Optim. Theory Appl. 1994. V. 81. No. 3. P. 435-457.
21.
Пановко Я.Г. Введение в теорию механического удара. М.: Наука, 1977.
22.
Козлов В., Трешев Д. Биллиарды. (Генетическое введение в динамику систем с
ударами). М.: Изд-во МГУ, 1991.
23.
Иванов А.П. Динамика систем с механическими соударениями. М.: Междунар.
программа образования, 1997.
24.
Bentsman J., Miller B.M. Dynamical Systems with Active Singularities of Elastic
Type: A Modeling and Controller Synthesis Framework // IEEE Trans. Autom.
Control. 2007. V. 52. No. 1. P. 39-55.
25.
Миллер Б.М. Управляемые системы с ударными воздействиями // Соврем. мат.
Фундамент. направл. 2011. Т. 42. С. 166-178.
26.
Миллер Б.М., Рубинович Е.Я. Разрывные решения в задачах оптимально-
го управления и их представление с помощью сингулярной пространственно-
временной замены // АиТ. 2013. № 12. С. 56-103.
Miller B.M., Rubinovich E.Ya. Discontinuous Solutions in the Optimal Control
Problems and their Representation by Singular Space-Time Transformations //
Autom. Remote Control. 2013. V. 74. No. 12. P. 1969-2006.
27.
Stronge W.J. Rigid Body Collisions with Friction // Proc. Roy. Soc. London. Ser.
A. 1990. V. 431. P. 168-181.
113
28.
Paoli L., Schatzman M. Mouvement à un nombre fini de degrés de liberté avec
contraintes unilatérales: cas avec perte d’énergie // Math. Modelling and Numerical
Analysis. 1993. No. 27. P. 673-717.
29.
Painlevé P. Leçons sur le Frottement. Paris: Hermann, 1895. / Пер. Пенлеве П.
Лекции о трении. М.: ГиТТЛ, 1954.
30.
Самсонов В.А. Динамика тормозного башмака и “удар, вызванный трением” //
Прикл. математика и механика. 2005. Т. 69. № 6. С. 912-921.
31.
Stewart D.E. Convergence of a Time-Stepping Scheme for Rigid-Body Dynamics
and Resolution of Painleve’s Problem // Arch. Rational Mech. Anal. 1998. V. 145.
P. 215-260.
32.
Stewart D.E. Rigid-Body Dynamics with Friction and Impact // SIAM Rev. 2000.
V. 42. No. 1. P. 3-39.
33.
Ballard P., Basseville S. Existence and Uniqueness for Dynamical Unilateral Contact
with Coulomb Friction: a Model Problem // Math. Model. Numer. Anal. 2005. V. 39.
No. 1. P. 59-77.
34.
Schatzman M. Penalty Approximation of Painlevé Problem // Adv. Mech. Math.
Nonsmooth mechanics and analysis. N.Y.: Springer, 2006. V. 12. P. 129-143.
35.
Génot F., Brogliato B. New Results on Painlevé Paradoxes // Eur. J. Mech. A/Solids.
1999. V. 18. No. 18. P. 653-678.
36.
Pfeifer F., Glocker C. Multi-Body Dynamics with Unilateral Constraints. N.Y.:
Wiley, 1996.
37.
Miller B.M., Rubinovich E.Ya., Bentsman J. Spatiotemporal Singular
Transformation in Dynamical Systems with Impacts and its Use in Obtaning
Generalized Solution of Painlevé Problem // Preprints 18th IFAC World Congr.
Milano (Italy). August 28-September 2. 2011. P. 3463-3473.
38.
Miller B.M., Rubinovich E.Ya., Bentsman J. Singular Space-time Transformations.
Toward one Method for Solving the Painlevé Problem // J. Math. Sci. 2016. V. 219.
No. 2. P. 208-219.
39.
Zhao ea. Z. The Painlevé Paradox Studied at a 3D Slender Rod // Multibody Syst.
Dyn. 2008. V. 19. P. 323-343.
40.
Уткин В.И. Скользящие режимы и их применение в системах с переменной
структурой. М.: Наука, 1974.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 19.07.2018
После доработки 11.10.2018
Принята к публикации 08.11.2018
114