Автоматика и телемеханика, № 10, 2019

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СИНТЕЗ МНОГОМЕРНЫХ СИСТЕМ ПО ИНЖЕНЕРНЫМ

КРИТЕРИЯМ КАЧЕСТВА НА ОСНОВЕ H_∞-ОПТИМИЗАЦИИ¹

Решается задача синтеза регуляторов по выходу многомерных систем,

гарантирующих заданные либо достижимые: ошибки регулирования, ра-

диус запасов устойчивости и время регулирования при действии полигар-

монических внешних возмущений с неизвестными амплитудами (с огра-

ничением их суммы), частотами и неограниченным числом гармоник.

Подход к решению опирается на специальным образом сконструирован-

ную стандартную задачу H_∞-оптимизации и новое правило выбора весо-

вой матрицы по заданной точности. Впервые дана физическая интерпре-

тация радиуса запасов устойчивости многомерных систем на языке годо-

графов Найквиста отдельных контуров, разомкнутых на выходе объекта.

Доказана связь свойства абсолютной устойчивости замкнутой системы и

радиуса запасов устойчивости. Рассмотрен пример синтеза для взаимо-

связанного электропривода.

Ключевые слова: ограниченные внешние возмущения, ошибки регулиро-

вания, время регулирования, радиус запасов устойчивости, абсолютная

устойчивость.

DOI: 10.1134/S0005231019100076

1. Введение

В реальных условиях работы автоматических систем всегда присутству-

ют нелинейности, неизбежны отклонения параметров объекта от расчетных,

имеется немоделируемая динамика и действуют ограниченные внешние воз-

мущения. Классическая теория управления одномерными (SISO) объекта-

ми [1], в основу которой положены инженерные требования к точности, запа-

сам устойчивости (по модулю и фазе) и времени регулирования, на физически

ясном языке частотных характеристик разомкнутой системы (знаменитый

метод ЛАЧХ) показала свою удивительную практическую эффективность

на протяжении последних 70 лет. В многомерном (MIMO) случае подобный

подход к синтезу регуляторов еще находится в стадии формирования, хо-

тя его начало пришлось на ранние 60-е гг. 20-го в., сразу после создания

теории LQ-оптимизации, которая гарантированно обеспечивает асимптоти-

ческую устойчивость замкнутой многомерной системы.

Для MIMO систем известен общий поход к анализу на основе сингуляр-

ных значений частотных передаточных матриц [2] (см. также [3-6]), который

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 18-08-01067). Посвящается памяти безвременно ушедшего друга

Ю.В. Садомцева.

132

в рамках рассматриваемой в статье задачи имеет чисто качественный харак-

тер. В настоящее время в теории управления прочное место заняли такие

техники, как H₂, H_∞, l₁ и μ-синтез [3-7]. Эти подходы весьма косвенно учи-

тывают инженерные требования, напрямую преобладавшие в классической

теории автоматического управления [1]. Помимо этого, в [8] на SISO примерах

продемонстрировано, что регуляторы по выходу, построенные на основе этих

современных техник, могут привести к системам с малыми запасами устой-

чивости по фазе и модулю, что недопустимо на практике. В настоящей статье

для определения близости замкнутой системы к неустойчивости используется

понятие радиуса запасов устойчивости [9], которое прямо указывает на бли-

зость годографа Найквиста к критической точке (-1, j0), нежели запасы по

фазе и модулю, а именно: система имеет радиус запасов устойчивости r, если

годограф Найквиста разомкнутой системы не пересекает круга максимально-

го радиуса r с центром в критической точке (-1, j0). Чем меньше r, тем ближе

замкнутая система к неустойчивости. Более подробно это понятие обсужда-

лось в SISO и MIMO случаях в [10-12] (см. также раздел 4 настоящей статьи).

Надо сказать, что радиус запасов устойчивости — более адекватная характе-

ристика близости системы к неустойчивости, нежели запасы устойчивости по

фазе и модулю. Действительно, умозрительно можно изобразить множество

годографов Найквиста, обладающих превосходными запасами устойчивости

по фазе и модулю, однако сколь угодно близко подходящих к критической

точке (-1, j0), т.е. имеющих сколь угодно малый радиус запасов устойчиво-

сти. Реальный пример такой ситуации в системе с наблюдателем состояния

приведен в [13]. Необходимо отметить, что в методе ЛАЧХ, упоминавшимся

ранее как эталон классического метода синтеза, такая ситуация просто невоз-

можна по внутренней сути метода (в окрестности критической точки (-1, j0)

всегда есть конечная область в виде криволинейной трапеции, определяемая

запасами по фазе и модулю, которую годограф Найквиста не пересекает [1]).

Практика автоматического управления на протяжении более семи десятиле-

тий показала эффективность такой оценки робастности замкнутой системы

по отношению к конечным отклонениям коэффициентов передаточной функ-

ции разомкнутой системы от номинальных.

В мировых научных публикациях, насколько известно автору, приоритет в

постановке (в рамках теории LQ- и H_∞-оптимизации) и решении отдельных

задач этой весьма непростой проблемы принадлежит А.Г. Александрову [14]

и его ученикам. В частности, Ю.В. Садомцев в [15] впервые в мире рас-

смотрел фундаментальный вопрос теории управления о принципиальной

регулируемости заданного выхода системы при подавлении ступенчатых и

стохастических внешних возмущений, а также задачу обеспечения радиуса

запасов устойчивости регулятором пониженного порядка на основе LQG-

оптимизации в непрерывном и дискретном случаях. Отметим также публи-

кации [13-17] в качестве сильно мотивирующих на исследования подобного

рода.

Первой публикацией в рамках H_∞-теории, посвященной задаче обеспе-

чения заданной точности при полигармонических внешних возмущениях с

конечным и известным числом гармоник, была совместная статья автора,

с, увы, ушедшим учителем А.Г. Александровым [18]. В публикациях автора

133

[11, 12] строились H_∞-регуляторы, где требования к радиусу запасов устойчи-

вости выражались обеспечением необходимой H_∞-нормы матрицы чувстви-

тельности по физическому выходу/входу объекта. H_∞-регуляторы, постро-

енные исходя из требований к точности и радиусу запасов устойчивости,

получены в [19], а того же типа, но обеспечивающие радиус запасов устой-

чивости и заданную степень устойчивости предложены в [20]. Публикация

автора [21] посвящена построению H_∞-регуляторов по заданной точности

и степени устойчивости. Таким образом, разработана теория синтеза H_∞-

регуляторов одновременно только по двум из трех инженерных требований

к качеству — при полигармонических внешних возмущениях с конечным и

известным числом гармоник. Поэтому цель настоящей статьи — объединить

эти инженерные показатели (ошибки регулирования, время регулирования и

радиус запасов устойчивости) в едином методе синтеза (при действии поли-

гармонических внешних возмущений с неизвестными амплитудами (с ограни-

чением их суммы), частотами и уже неограниченным числом гармоник), что

частично и определяет научную новизну статьи. Надо сказать, что техника

H_∞-теории оказалась очень естественным и удобным инструментом при ре-

шении таких задач: а именно регуляторы, построенные в [11, 12, 21] без учета

требований к времени регулирования (степени устойчивости), имеют необ-

ходимый и достаточный характер при обеспечении соответственно радиуса

запасов устойчивости и требуемой точности. Причем требования к точности

выражены аналитическими соотношениями для выбора весовых коэффици-

ентов критерия оптимизации.

Поскольку сам факт возможной реализации регулятора на практике во

многом определяется значением радиуса запасов устойчивости, который он

гарантирует, требования к радиусу обязательно должны включаться в пере-

чень показателей качества замкнутой системы. Отсутствие такого требования

в показателях качества зачастую ведет к практической неработоспособности

регуляторов, построенных на основе современных техник, что ярко проде-

монстрировала публикация [8]. В этой связи чрезвычайно поучителен при-

мер синтеза из [21], где регулятор строился только на основе требований к

точности. Непосредственная проверка показывает, что радиус запасов устой-

чивости при размыкании замкнутой системы по входам и выходам объекта

весьма мал (r ≈ 0,016), за исключением главной регулируемой переменной

(где r ≈ 0,818), по которой (по остальным аналогично) и получился эталон-

ный монотонный переходный процесс при ступенчатом изменении внешнего

возмущения (нагрузки), хотя найденный регулятор непригоден к практиче-

ской реализации. Таким образом, по переходным процессам, вообще говоря,

нельзя судить о степени робастности замкнутой MIMO системы.

Это делает весьма актуальным в научном и практическом смыслах раз-

работку процедур синтеза регуляторов (при ограниченных внешних возму-

щениях), в которых бы обеспечивались заданные либо достижимые: ошибки

регулирования, время регулирования и радиус запасов устойчивости. Необ-

ходимо отметить противоречивость этих требований [19-29], известную еще в

классической теории и практике управления SISO объектами, а также потен-

циальную неединственность регулятора. Например, в SISO случае в [26, 27]

для этой цели используется модальное управление, а в [18-23] в MIMO слу-

134

чае применяется H_∞-подход. Некоторые результаты представленной работы

анонсировались ранее в публикациях [22-24], где, однако, не было соответ-

ствующих доказательств.

В отличие от публикаций [18, 19, 21-23], где рассматриваются внешние

возмущения, ограниченные по мощности, с известным числом гармоник, в

представленной статье исследуется случай векторного внешнего возмущения

(в отличие от [25-27], где возмущение — скаляр) с бесконечным числом гармо-

ник, каждая компонента которого — абсолютно сходящийся ряд. Последнее

позволило получить результаты по гарантированной точности, не зависящие

от числа гармоник ограниченного полигармонического внешнего возмуще-

ния. Главное отличие (при изменении характера ограниченности внешнего

возмущения при решении проблемы точности) настоящей статьи от упомя-

нутых публикаций состоит в новом математически строгом правиле выбора

весовых коэффициентов диагональной матрицы, взвешивающей компоненты

вектора физически регулируемых переменных объекта в задаче H_∞-опти-

мизации, к которой и сводится синтез регулятора по измеряемому выходу.

Нельзя не отметить, что метод инвариантных эллипсоидов [17], снявший се-

рьезнейшую проблему реализуемости и высокого порядка L₁ (l₁)-регулято-

ров, обеспечивающих наименьшие ошибки регулирования, не гарантирует,

вообще говоря, наличия у системы приемлемого в практических приложени-

ях радиуса запасов устойчивости как, впрочем, и L₁ (l₁)-подход. В настоящей

статье обеспечивается только заданная точность (а не максимально возмож-

ная), что не приводит к неоправданному росту коэффициентов регулятора

(что часто и ведет к весьма малому радиусу запасов устойчивости).

Помимо этого, новизна статьи состоит в том, что впервые дана физиче-

ская интерпретация радиуса запасов устойчивости MIMO систем на языке

годографов Найквиста отдельных контуров, разомкнутых на выходе объекта,

и установлено свойство абсолютной устойчивости замкнутых систем с неста-

ционарными секторными нелинейностями на выходе объекта, границы секто-

ра которых определяются полученным при синтезе радиусом запасов устой-

чивости. Последнее крайне важно для любого метода синтеза регуляторов,

претендующего на практическое применение [13-17, 25-29].

Показано, что поставленная задача сводится к специальным образом

сконструированной проблеме H_∞-оптимизации [3-7]. Численно такую зада-

чу удобно решать на основе метода линейных матричных неравенств (LMI)

[30, 31], например, в MATLAB-пакете Robust Control Toolbox [32]. Рассмотрен

пример синтеза при управлении взаимосвязанным электроприводом [19, 21].

2. Постановка задачи

Рассмотрим полностью управляемый и наблюдаемый объект управления:

(2.1)

x = Ax + B₁w + B₂

u, y = Cx,

где x ∈ Rⁿ — вектор состояния объекта; u ∈ R^m — вектор управляющих воз-

действий; y ∈ Rm2 — вектор измеряемых и одновременно регулируемых пере-

менных объекта (вход регулятора); w ∈ Rm3 — вектор неизмеряемых внешних

возмущений. Матрицы объекта A, B₁, B₂, C заданы.

135

Пусть объект (2.1) замкнут стабилизирующим динамическим регулятором

по выходу:

(2.2)

x_c = A_cx_c + B_cy, u = C_cx_c + D_c

где x_c ∈ Rⁿ- вектор состояния регулятора размерности n; A_c, B_c, B_c, C_c —

матрицы чисел.

Компоненты вектора внешних возмущений — полигармонические функ-

ции:

∑

(2.3)

w_i(t) =

w_ik sin(ω_kt + ψ_ik), i = 1,m₃.

k=1

Причем амплитуды w_ik ≥ 0, начальные фазы ψ_ik (i = 1, m₃, k = 1, ∞), а

также частоты ω_k (k = 1, ∞) сигналов неизвестны. Число гармоник не огра-

ничено.

Предполагается, что внешнее возмущение ограничено в следующем смыс-

ле:

∑

(2.4)

w_ik ≤ w^∗i, i = 1,m₃,

k=1

где w^∗i > 0 (i = 1, m₃) - заданные числа.

Ошибки по регулируемым переменным определим соотношениями [26]:

(2.5)

y_i,st = sup |y_i(t)|, i = 1,m₂,

t≥tp

где t_p - время регулирования.

Обычно на практике требуют, чтобы выполнялись неравенства

(2.6)

y_i,st ≤ y^∗i, i = 1,m₂,

где y^∗i (i = 1, m₂) - заданные положительные числа (желаемые ошибки регу-

лирования).

Время регулирования в замкнутой системе (2.1), (2.2) можно оценить как

[1, 33, 34]

(2.7)

t_p

≈ 3/β,

где β - степень устойчивости замкнутой системы - минимальное расстояние

от мнимой оси до ближайшего собственного значения матрицы замкнутой

системы (2.1), (2.2) A_cl:

[

]

A+B

2DcC B2Cc

A_cl =

B_cC

A_c

136

Известно, что такой подход к оценке времени регулирования справедлив,

если среди собственных значений матрицы A_cl нет кратных, ближайших к

мнимой оси. Несмотря на весьма приближенный характер формулы (2.7), она

хорошо себя зарекомендовала в инженерной практике для начальной оценки

времени регулирования.

Наличие радиуса r запасов устойчивости на физическом выходе объекта

гарантирует выполнение кругового частотного неравенства [11, 19, 20]

(2.8)

[I + W^y(-jω)]^T[I + W^y(jω)] ≥ r²

I, ω ∈ [0,∞),

где

0 < r ≤ 1, W^y(s) = -W(s) · K(s)

— передаточная матрица систе-

мы (2.1),

(2.2), разомкнутой по физическому выходу объекта. Здесь

W (s) = C(sI - A)-1B₂ — передаточная матрица объекта по управлению;

K(s) = C_c(sI - A_c)-1B_c + D_c — передаточная матрица регулятора.

Отметим, что требования к точности (2.6) не всегда могут быть выпол-

нены, что в равной степени относится и к условиям (2.7), (2.8). Если объ-

ект (2.1) неминимально-фазовый, то для чисел в левой части соотношений

(2.6), (2.7) существуют нижние, а для чисел правой части соотношения (2.8)

(если объект дополнительно неустойчив) верхние предельные значения, ко-

торые только и могут быть достижимы линейным регулятором (2.2).

Задача. Найти стабилизирующий регулятор (2.2) такой, чтобы:

1) выполнялись требования к точности

(2.9)

y_i,st ≤ γy^∗i, i = 1,m₂,

где γ > 0 — заданное или достижимое число;

2) выполнялось неравенство (2.8), где r — заданное или достижимое чис-

ло;

3) собственные значения матрицы A_cl замкнутой системы удовлетворя-

ли условию

(2.10)

Reλ_i(A_cl

) ≤ -β, i = 1,2n,

где β ≥ 0 - заданное или достижимое число.

Замечание 1. Модель внешнего возмущения (2.3), (2.4) описывает зна-

чительную часть встречающихся на практике сигналов, которые являются

непрерывными кусочно-дифференцируемыми функциями времени и, следо-

вательно, разложимыми в абсолютно сходящийся ряд Фурье [35, 36] (частный

случай (2.3) с кратными частотами).

3. Решение задачи на основе процедуры H_∞-оптимизации

Переходя к преобразованию Лапласа при нулевых начальных условиях и

исключая векторы состояния объекта и регулятора, представим уравнения

(2.1), (2.2) как

y = W(s)u + W₁(s)w, u = K(s)(y + w₁) = K(s)z₁, z₂ = Q1/2y,

137

W₁(s)

W (s)

z₂

Q^1/2

объект

w₁

К (s)

z₁

регулятор

Рис. 1. Структурная схема замкнутой системы.

где W₁(s) = C(sI - A)-1B₁ — передаточная матрица объекта (2.1) по возму-

щению; w₁ ∈ Rm2 помеха измерения (фиктивный вход) на входе регулятора

(2.2), z₁ ∈ Rm2 - вектор фиктивных регулируемых переменных (w₁ и z₁ свя-

заны между собой матрицей чувствительности по выходу объекта Tz1w₁ (s) =

= (I + W^y(s))-1, которая необходима для обеспечения требования (2.8)). Но-

вый вектор регулируемых переменных z₂ ∈ Rm2 — вектор y, взвешенный с

помощью диагональной матрицы Q = diag[q₁, q₂, . . . , qm2 ] с положительными

элементами q_i > 0 (i = 1, m₂), которые выбираются далее для обеспечения

заданной точности по физически регулируемым переменным (2.9). Этим по-

следним уравнениям соответствует структурная схема на рис. 1 (см. подроб-

нее [11, 19, 21]).

[

]

Введем расширенный вектор внешних возмущений w^T =

wT1

w^T

и рас-

[

]

ширенный вектор регулируемых переменных z^T =

zT1

zT2

и обозначим че-

рез T_zw(s) передаточную матрицу замкнутой системы, которая связывает эти

векторы. Она будет иметь следующую структуру:

[

]

[

]

[

]

z₁

Tz1w₁

Tz1w

w₁

(3.1)

=T_zw · w=

z₂

Q1/2Tyw1

Q1/2T_yw

где Tz1w₁ , Tz₁w, Tyw₁ , Tyw — передаточные матрицы замкнутой системы от w1

к z₁, от w к z₁, от w₁ к y и от w к y соответственно.

Переходя к доказательству главного результата этого раздела статьи, сна-

чала учтем желаемое время регулирования. Собственные значения матри-

цы A_cl замкнутой системы (2.1), (2.2) должны удовлетворять неравенству

(2.10).

Заменив матрицу A объекта на смещенну

A = A + βI, найдем смещен-

ный регулятор, обеспечивающий устойчивость смещенной замкнутой систе-

мы [20, 21]:

[

]

A+B₂D_cC B₂C_c

(3.2)

Reλ_i

A_cl) = Reλ_i

< 0, i = 1, 2n,

B_cC

A_c

где

A_c,B_c,C_c,D_c — матрицы смещенного регулятора.

138

Искомый же регулятор имеет матрицы [20, 21]:

(3.3)

A_c

A_c - βI, B_c, C_c, D_c.

Действительно, собственные значения матрицы A_cl

A_cl с таким регулято-

ром связаны очевидным соотношением Re λ_i

A_cl) = Re λ_i(A_cl)+β < 0, откуда

следует (2.10).

Пусть регулятор с матрицам

A_c,B_c,C_c,D_c разрешает задачу минимиза-

ции H_∞-нормы смещенной передаточной матрицы замкнутой системы (где A

заменена н

A = A + βI):

(3.4)

∥T_zw(-β + jω)∥_∞

≤ γ,

где γ — заданное или минимизируемое число.

Тогда [5] каждый блок этой матрицы удовлетворяет аналогичному (3.4)

условию, в частности:



(3.5)

∥Tz1w₁ (-β + jω)∥_∞ ≤ γ,

Q1/2T_yw(-β + jω)

≤ γ.

∞

Замечание 2. Если решена смещенная проблема (3.4), то регулятор

(2.2), (3.3) будет обеспечивать выполнение соответствующих частотных нера-

венств и для несмещенных передаточных матриц разомкнутой и замкнутой

системы [20, 21].

Таким образом, разрешая смещенную задачу (3.4), имеем:

(3.6)

∥T_zw(jω)∥_∞

≤ γ,



(3.7)

∥Tz1w₁ (jω)∥_∞ ≤ γ,

Q1/2T_yw(jω)

≤ γ.

∞

Первое из неравенств (3.7) может быть представлено в эквивалентном виде

[11, 19, 20]:

(3.8)

[I + W^y(-jω)]^T[I + W^y(jω)] ≥ γ-2

I, ω ∈ [0,∞).

А это - целевое неравенство (2.8), в котором r = γ-1. Второе неравенство

(3.7) имеет следующую эквивалентную частотную форму [21]:

(3.9)

TTyw(-jω)QT_yw (jω) ≤ γ²

I, ω ∈ [0,∞).

Имеет место утверждение, впервые сформулированное в [24] и доказанное в

Приложении.

Лемма (о рабочем процессе). Пусть выполнено частотное неравен-

ство (3.9). Тогда ошибки по регулируемым переменным устойчивой систе-

мы (2.1), (2.2) при действии входного сигнала из класса (2.3), (2.4) удовле-

творяют неравенствам

⎛

⎞₂

∑

(3.10)

q_iy2i,st ≤ γ² ⎝

w^∗⎠ , i = 1,m2,

j=1

139

где w^∗j - границы компонент внешних возмущений из правых частей нера-

венств (2.4).

Если элементы диагональной весовой матрицы Q выбирать из равенств

)

(∑_m

w^∗

j=1

(3.11)

q_i =

i = 1,m₂,

(y^∗i)2

то из соотношения (3.10) придем к целевому неравенству (2.9) поставленной

задачи.

Суммируя изложенное, придем к следующему утверждению.

Теорема 1. Регулятор (2.2), (3.3) разрешает задачу, если весовые ко-

эффициенты матрицы Q в смещенной H_∞-проблеме (3.4) выбраны из ра-

венств (3.11). При этом радиус запасов устойчивости r = 1/γ, где γ — ре-

ализовавшееся значение при решении задачи (3.4).

Заметим, что переход от неравенства (3.4) к (3.5), а затем к (3.6), (3.7)

придает достаточный характер представленному результату.

4. Физическая интерпретация радиуса запасов устойчивости

Прежде всего покажем, что матричное частотное неравенство (2.8) имеет

важное следствие, если размыкание осуществлять не по всем выходам, а по

любому i-му. Это соответствует инженерной практике, поскольку допускает

экспериментальную проверку на основе реального физического эксперимен-

та [1, 26]. Обозначим такую передаточную функцию разомкнутой системы

как w_i(s), а передаточную функцию, связывающую i-ю компоненту векто-

ра w₁ с i-й компонентой вектора z₁ (когда все остальные входы на структур-

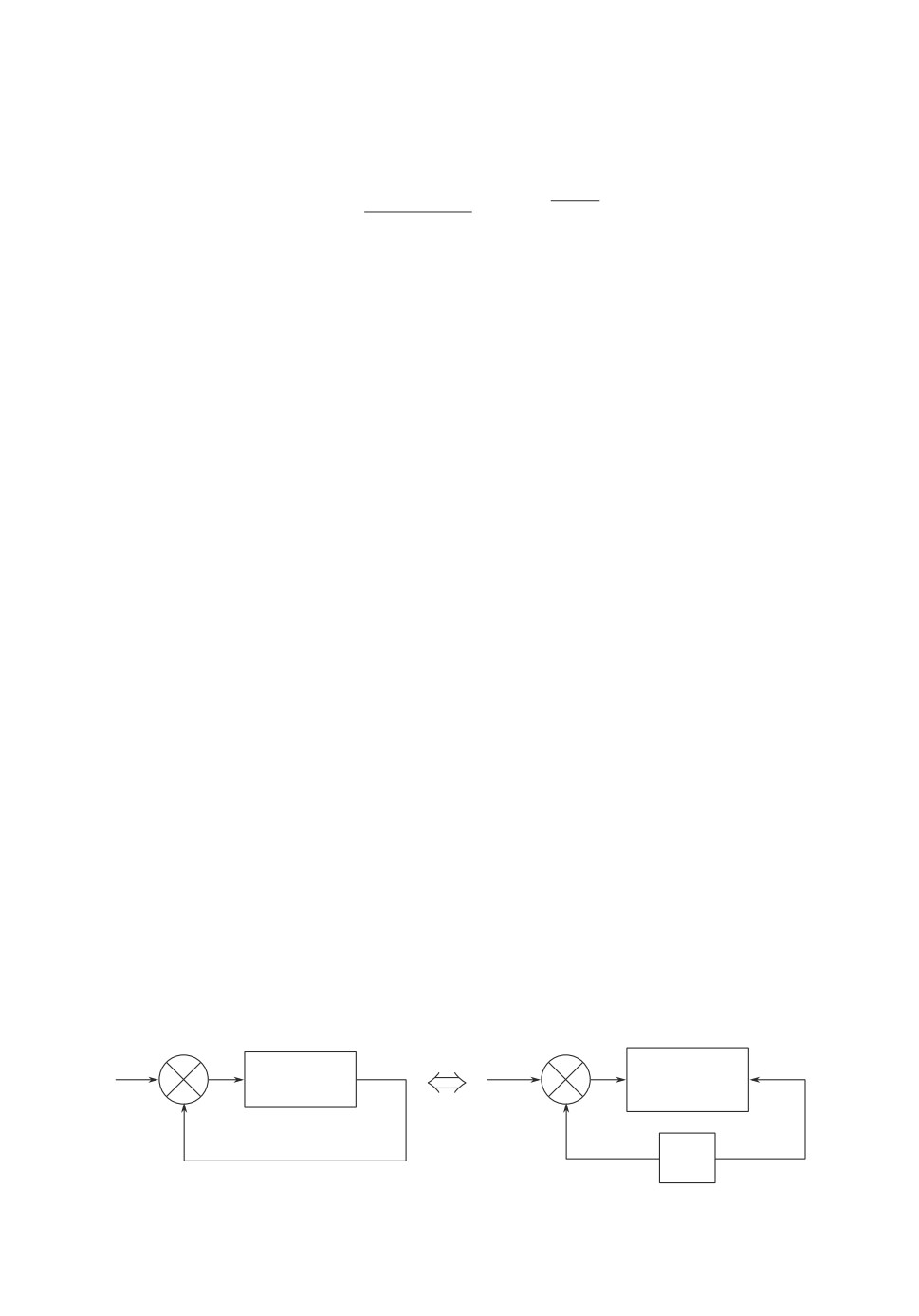
ной схеме рис. 1 нулевые) как t_i(s). Этому соответствует структурная схема

левой части рис. 2, где w(s) представляет передаточную функцию, получен-

ную путем замыкания всех обратных связей на рис. 1, кроме i-й. Правая часть

рис. 2 представлена в эквивалентном виде, где очевидно, что w_i(s) = - w(s).

Таким образом, передаточные функции t_i(s) и w_i(s) связаны известным со-

отношением

(4.1)

t_i(s) = 1/(1 + w_i

(s)),

которое является аналогом классической передаточной функции замкнутой

системы по ошибке [1]. С другой стороны, функция (4.1) является i-м диаго-

w1i

y_i

w1i

y_i

~(s)

w_i(s)

Рис. 2. Замкнутая система с i-й обратной связью.

140

нальным элементом передаточной матрицы Tz1w₁ . Матрица Tz₁w₁ удовлетво-

ряет первому неравенству (3.7), откуда для ее i-го диагонального элемента [5]

можно записать, что |t_i(jω)| ≤ γ или t_i(-jω)t_i(jω) ≤ γ², что при обозначении

r = 1/γ и с учетом равенства (4.1) окончательно приводит к скалярному ана-

логу (2.8):

(4.2)

[1 + w_i(-jω)] [1 + w_i(jω)] ≥ r²

ω ∈ [0,∞).

Геометрическая интерпретация этого условия [9-11, 28] приводит к следую-

щему утверждению.

Теорема 2. Пусть выполнено матричное частотное неравенство (2.8),

тогда годограф Найквиста системы (2.1), (2.2), разомкнутой по i-му выхо-

ду объекта, не пересекает круга радиуса r с центром в критической точке

(-1, j0).

Таким образом, теорема 2 гарантирует, что устойчивость контура не нару-

шается, если передаточная функция w_i(s) рис. 2 возмущается устойчивой ад-

дитивной добавкой Δ(s), удовлетворяющей неравенству ∥Δ∥_∞ < r [7]. В [10]

установлено важнейшее свойство: если w_i(s) заменить на w_i(s)·ke^jψ, то устой-

чивость контура рис. 2 не нарушится для любой пары (k, ψ), одновременно

удовлетворяющей неравенствам:

<k<

;

1+r

1-r

(

)

r²

⁽r⁾

|ψ| < arccos

= 2arcsin

Эти соотношения, в частности, выражают связь радиуса r и гарантируемых

запасов устойчивости по коэффициенту усиления и фазе соответственно, ес-

ли пара (k, ψ) изменяется не одновременно, а именно как (k, 0) или (1, ψ) в

указанных выше пределах.

Подчеркнем, что радиус запасов устойчивости всегда допускает экспери-

ментальное определение на основе реального физического эксперимента. Это

крайне важно для практических приложений. Если разомкнутая система

на рис. 2 устойчива, то можно непосредственно строить годограф Найкви-

ста w_i(jω). В противном случае снимаются частотные характеристики си-

стемы рис. 2 в замкнутом состоянии, а именно t_i(jω). В этом случае радиус

запасов устойчивости r = 1/ ∥t_i∥_∞, т.е. равен величине, обратной максимуму

модуля функции чувствительности t_i(jω) контура рис. 2 [6, 29].

Из теоремы 2 ясно, что годограф w_i(jω) не пересекает и отрезка веще-

ственной оси с граничными точками (-(1 + r), j0) и (-(1 - r), j0), а это в

силу кругового критерия абсолютной устойчивости [37] значит, что система

(2.1), (2.2) не потеряет устойчивости, если по i-му выходу объекта ввести

нестационарную нелинейность, принадлежащую гурвицевому углу (сектору)

(1/(1 + r), 1/(1 - r)). В частности, это может быть нестационарный коэффи-

циент усиления l_i(t), изменяющийся в интервале (1/(1 + r), 1/(1 - r)). Мно-

гомерный круговой критерий позволяет усилить этот результат, когда нели-

нейности вводятся по каждому физическому выходу объекта. С этой целью

141

запишем уравнения замкнутого контура в виде

(4.3)

y = -W^y

(s)ξ, ξ = y.

Эта система асимптотически устойчива по построению регулятора (2.2), (3.3),

следовательно, требование минимальной устойчивости кругового критерия

выполнено. Кроме того, предположим, что ни объект, ни регулятор не имеют

чисто мнимых полюсов (это требование можно ослабить). Заменим второе

линейное уравнение (4.3) на векторную нелинейность

(4.4)

ξ = φ(t,y),

где каждая компонента нестационарной вектор-функции ξ ∈ Rm2 принадле-

жит сектору

(4.5)

α ≤ φ_i(t,y_i)/y_i ≤ β, φ_i(t,0) = 0, i = 1,m₂,

где α < 1 и β > 1 — соответственно нижняя и верхняя границы секторной

нелинейности. В соответствии с круговым критерием для абсолютной устой-

чивости системы (4.3)-(4.5) должно выполняться частотное неравенство [37]

{

}

[I + αW^y(-jω)]^Tτ[I + βW^y(jω)]

> 0, ω ∈ (-∞, ∞) ,

[

]∕

где ReY =

Y^T(-jω) + Y (jω)

2 — эрмитова часть комплексной матрицы Y .

Здесь τ — диагональная положительно определенная матрица. Рассмотрим

это неравенство при α = 1/(1 + r), β = 1/(1 - r) и τ = (1 + r)(1 - r)I, что да-

ет выражение

{

}

[I + rI + W^y(-jω)]^T[I - rI + W^y(jω)]

> 0, ω ∈ (-∞, ∞) .

Последнее условие ведет к неравенству

{

}

[I + W^y(-jω)]^T [I + W^y(jω)] - r²I + V (jω)

> 0, ω ∈ (-∞, ∞) ,

[

]

где косоэрмитова матрица V (jω) = r

W^y(jω) - WyT(-jω)

удовлетворяет

условию ReV (jω) = 0. Таким образом, последнее неравенство сводится к

неравенству (2.8), которое должно быть строгим (>). Следовательно, име-

ет место теорема 3.

Теорема 3. Пусть выполнено строгое матричное частотное неравен-

ство (2.8). Тогда система (2.1), (2.2), (3.3) с нелинейностями из класса (4.4),

(4.5) (где α = 1/(1 + r), β = 1/(1 - r)), вводимыми по каждому физическому

выходу объекта (2.1) (при w = 0), будет абсолютно устойчива.

В частном случае нелинейности (4.4) могут быть нестационарными коэф-

фициентами усиления l_i(t): ξ_i = l_i(t)y_i, i = 1, m₂ с границами (4.5), где α =

= 1/(1 + r) и β = 1/(1 - r). При этом они могут меняться независимо друг

от друга с произвольной скоростью. Если эти коэффициенты стационарны,

то границы (4.5) совпадают с полученными в [38], где неравенства для коэф-

фициентов строгие. Подчеркнем, что даже строгие границы (4.5) для неста-

ционарных l_i(t) принципиально не могут быть получены подходом из [38].

142

5. Процедура синтеза

Поскольку вектор регулируемых переменных в системе (3.1) не содержит

управлений, то задача (3.4) вырождена и численно может быть решена (см.

[11, 21]) LMI-техникой MATLAB-пакета [32], как представлено далее. Заме-

тим, что чрезмерное увеличение степени устойчивости β ведет к резкому па-

дению радиуса запасов устойчивости и, как следствие, большим выбросам

в переходной функции замкнутой системы [13, 20, 39]. Это аналог эффекта

всплеска из [17] с регулятором по выходу. Поэтому в алгоритме синтеза ис-

пользуется принцип постепенного увеличения быстродействия или β.

1. Заменим матрицу A объекта н

A = A + βI, полагая сначала β = 0.

2. Выбираем весовую матрицу Q из равенств (3.11) и строим матрицы

уравнений состояния A_об, B_об, C_об, D_об обобщенного объекта A_об

A, B_об =

[

]

B₁

B₂

⎡

⎤

C₂

[

]

D₁₁

D₁₂

⎢

⎥

C_об =

⎣ Q1/2C₂

⎦, Dоб =

D₂₁

D₂₂

C₂

[

]

[

]

D₁₁ =

D₁₂ = 0, D₂₁ =

D₂₂ = 0,

где размеры матриц должны быть согласованы. Следует отметить, что в [19],

матрица D₁₁ ошибочно приведена без второй блочной строки.

3. Формируем системную матрицу обобщенного объекта с помощью ко-

манды

P = ltisys(A_об,B_об,C_об,D_об).

4. Находим оптимальное γ₀ = hinflmi (P, [m₂, m]) в задаче (3.4), где m₂

и m - число входов и выходов регулятора соответственно.

5. Выбираем γ > γ₀ и строим системную матрицу регулятора K, разре-

шающего задачу (3.4), с помощью процедуры [γ, K] = hinflmi(P, [m₂, m], γ, ε),

где ε - точность вычисления γ.

6. Из системной матрицы K извлекаем матрицы уравнений состояния сме-

щенного регулятора процедурой

A_c,B_c,C_c,D_c] = ltiss(K).

7. Находим матрицы A_c

A_c - βI, B_c, C_c, D_c искомого регулятора (2.2).

8. Строим переходный процесс в замкнутой системе при действии внешних

возмущений из класса (2.3), (2.4), находим ошибки и время регулирования,

а также радиус запасов устойчивости. Если требования к точности (2.6) и

радиусу запасов устойчивости (2.8) не выполнены, то задача неразрешима

данным подходом. Иначе, переходим к п. 9.

9. Если требования к быстродействию не выполняются, то увеличиваем

параметр β и переходим к п. 1, иначе задача решена.

143

При первом проходе алгоритма естественно использовать γ = γ₀. Если тре-

бования (2.6) и/или (2.8) не выполнены, то целесообразно решить отдельные

задачи синтеза по радиусу запасов устойчивости [11] и/или заданной точно-

сти [21] (с весовыми коэффициентами из (3.11)), которые имеют необходимый

и достаточный характер, что позволяет определить значения γ₀, определяю-

щие достижимые значения точности (2.9), либо значения радиуса r₀ = γ-10

при решении этих отдельных задач.

6. Задача синтеза для взаимосвязанного электропривода

Рассмотрим взаимосвязанный электропривод, модель которого приведена

в [19, 21, 40]. Структурная схема модели приведена в [41]. В [42] такая модель

отнесена к классу параллельных систем.

Компоненты вектора состояния x ∈ R⁵ имеют следующий смысл: x₁, x₂ -

отклонения выходных напряжений тиристорных преобразователей от номи-

нальных, x₃ = i₁, x₄ = i₂ - отклонения якорных токов двигателей от номи-

нальных, x₅ = ω - отклонение угловой скорости двигателей от номинальной

(двигатели работают на общую нагрузку и жестко связаны, т.е. имеют одина-

ковую угловую скорость). В [42], помимо требований к подержанию угловой

скорости двигателей в заданных границах, большое значение придается обес-

печению требования равнонагруженности двигателей, т.е. близости их якор-

ных токов. Стандартные настройки ПИ-регуляторов в ряде случаев приводят

к перегрузке одного из двигателей [42].

Вектор управления u имеет две компоненты u₁ и u₂ - отклонения управ-

ляющих напряжений от номинальных на входах тиристорных преобразова-

телей. Внешнее возмущение w = M_c - отклонение момента сопротивления

(нагрузки) от номинального, не превышающее величины 600 Нм. Регулируе-

мые и измеряемые переменные для этого объекта совпадают и связаны с фи-

зическими переменными соотношениями y₁ = x₃, y₂ = x₄, y₃ = x₅; внешние

возмущения и управляющие воздействия приложены в разных точках.

Матрицы объекта:

⎡

⎤

-100

⎢

-83,333

⎥

⎢

⎥

A=^⎢

137,811

-11,287

-1123,155

^⎥,

⎢

⎥

⎣

132,459

-11,065

-1101,133

⎦

0,2487

0,254

⎡

⎤

⎡

⎤

16120

⎡

⎤

⎢

⎥

⎢

13702

⎥

⎢

⎥

⎢

⎥

⎢

⎦_.

B₁ =^⎢

B₂ =

^⎥, C =⎣ 0

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦

−0,031

Требования к системе:

• ошибки по угловой скорости и токам: |y₃| ≤ y∗3 = 1 рад/c, y₁ ≤ 375 А,

y₂ ≤ 375 А;

144

Амплитуда

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

10⁰

10¹

10²

10³

10⁴

Частота, рад/с

Рис. 3. Амплитудно-частотная характеристика замкнутой системы.

• запасы устойчивости обеспечиваются по выходу объекта: переменным

y₁, y₂, y₃;

• время регулирования t_p = 0,25 c.

Желаемую степень устойчивости выберем из соотношения (2.7):

β = 3/t_p = 3/0,25 = 12.

Весовую диагональную матрицу Q сформируем из равенств (3.11):

q1/21 = q1/22 = 1,6; q1/23 = 600.

Алгоритм синтеза из раздела 5, реализованный на базе [32], приводит к ре-

гулятору:

⎡

⎤

1019,1

-352,41

-12033

17853

32780

⎢

−174,04

-741,28

-7498,6

-32956

-56967

⎥

⎢

⎥

A_c =^⎢

93,347

60,638

494,16

85,83

74,78

^⎥,

⎢

⎥

⎦

⎣ -9,606

17,318

0,204

-22,099

25,108

−45,578

81,196

-1,066

3033,4

-1203,9

⎡

⎤

-0,005

0,015

-0,001

⎢

−0,005

0,004

0,002

⎥

⎢

⎥

B_c =^⎢

−1,342

1,378

0,002

^⎥,

⎢

⎥

⎣-3,927

⎦

-3,861

0,014

281,69

271,61

-10,208

[

]

[

]

0,025

0,045

0,64

1,728

2,951

C_c =

D_c =

−0,064

-0,014

-0,723

1,842

3,354

145

Рис. 4. Переходные процессы по регулируемым переменным.

Реализовавшееся при решении H_∞-проблемы (3.4) значение γ при расчете

регулятора составило 14,58 (оптимальное же значение γ₀ = 12,86).

На рис. 3 построена амплитудно-частотная характеристика замкнутой си-

стемы от возмущения (момента нагрузки) к главной регулируемой перемен-

ной y₃ (угловой скорости двигателей). Эта характеристика промасштабирова-

на границей внешнего возмущения w^∗ = 600. Из этой монотонно убывающей

характеристики очевидно, что наихудшее внешнее возмущение из класса по-

лигармонических функций (2.3), (2.4) — ступенчатое.

На рис. 4,а и 4,б приведены графики переходных процессов по токам двига-

телей и угловой скорости соответственно при ступенчатом изменении момен-

та нагрузки w = 600. Из графиков монотонных переходных процессов видно,

что требования к точности выполнены, в частности (рис. 4,б) по угловой ско-

рости (главной регулируемой переменной) |y₃| ≤ y∗3 = 1 рад/с, а время регу-

лирования меньше заданного 0,25 с. Также из рис. 4,а следует, что двигатели

равнонагруженные (их якорные токи близки).

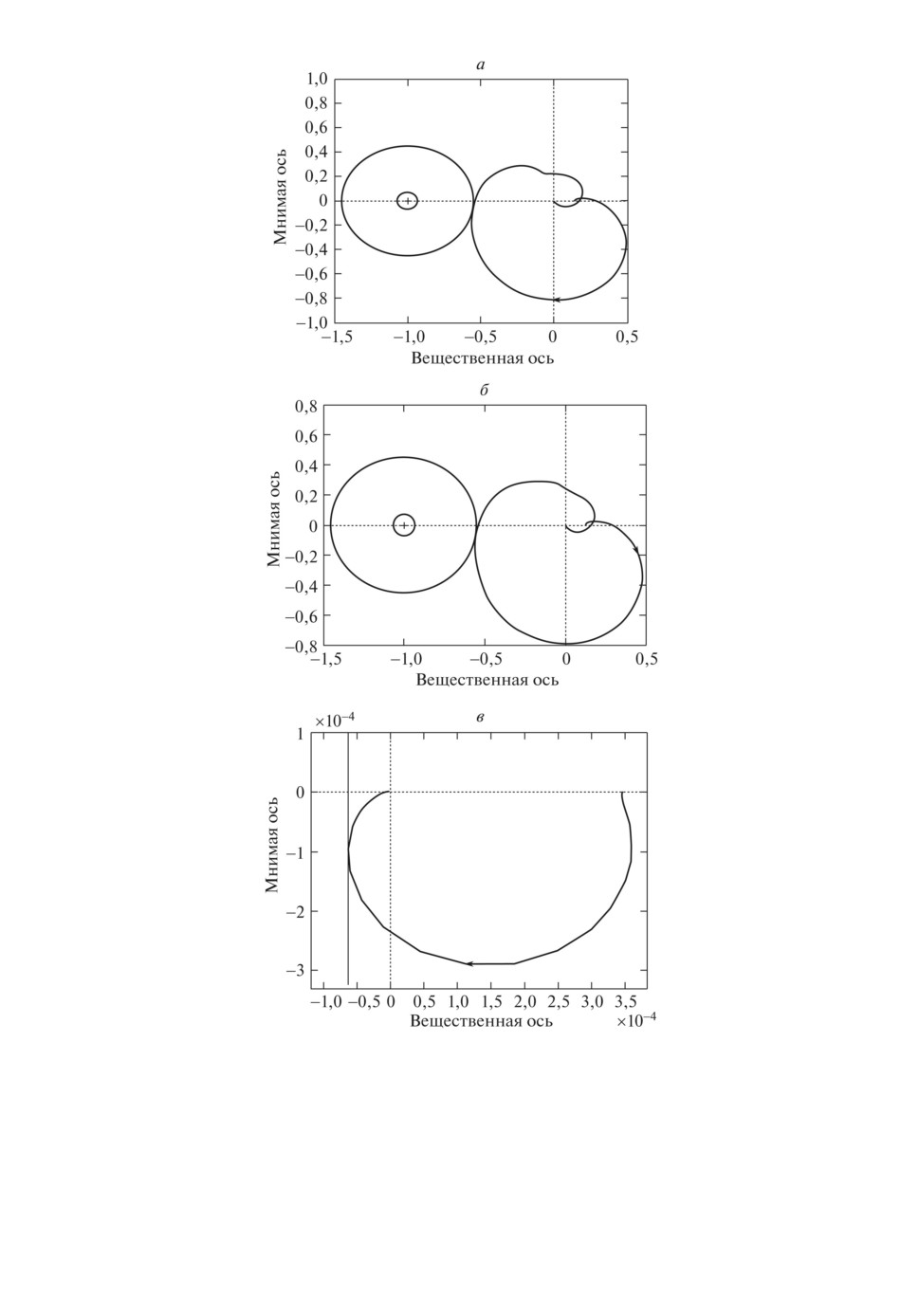
На рис. 5 приведены годографы Найквиста при размыкании замкнутой си-

стемы по выходам объекта: а — по первому выходу (якорному току первого

двигателя); б — по второму выходу (якорному току второго двигателя); в — по

третьему выходу (угловой скорости двигателей). На рис. 5 окружность мень-

шего радиуса r = 1/γ с центром в критической точке (-1, j0) соответствует

гарантируемому радиусу запасов устойчивости, а окружность большего ра-

диуса — его истинному значению.

При сравнительно малом гарантируемом радиусе запасов устойчивости

на выходе объекта (r = 1/γ = 0,069) истинные радиусы вполне приемле-

мые: по первому выходу 0,449 (рис. 5,а), по второму выходу 0,452 (рис. 5,б ),

по третьему выходу — главной регулируемой переменной объекта: 0,99994

(рис. 5,в). Проверка запасов устойчивости на входе объекта также дала при-

емлемые значения: радиус составил величину 0,45.

146

(сумма которых ограничена), частотами и их числом, который обеспечивает

заданные либо достижимые: ошибки регулирования, время регулирования и

радиус запасов устойчивости.

Подход к решению такой задачи базируется на специальным образом скон-

струированной стандартной проблеме H_∞-оптимизации и носит достаточный

характер.

Дана физическая интерпретация радиуса запасов устойчивости многомер-

ных систем на языке годографов Найквиста отдельных контуров, разомкну-

тых на выходе объекта. Доказана абсолютная устойчивость замкнутой си-

стемы с полученным регулятором при наличии на выходе объекта секторных

нестационарных нелинейностей, границы сектора которых определяются ве-

личиной радиуса запасов устойчивости. Порядок получаемого динамического

регулятора по выходу не превышает порядка исходного физического объекта,

что важно для практических приложений. Приведена процедура синтеза ре-

гуляторов в MATLAB-пакете Robust Control Toolbox [32], численная эффек-

тивность которой продемонстрирована на примере взаимосвязанного элек-

тропривода. Аналоги теорем 1-3, очевидно, справедливы и при размыкании

системы по физическому входу объекта.

ПРИЛОЖЕНИЕ

Доказательство леммы. Согласно [26], когда текущее время t пре-

вышает время регулирования t_p, на выходе всякой устойчивой системы возни-

кает процесс, названный рабочим. Его отличие от установившегося процесса

заключается в наличии экспоненциально убывающих функций e_i(t), которые

при t = t_p составляют не более 5% от установившегося. Поэтому далее вы-

нужденные колебания на выходе замкнутой системы (2.1), (2.2) опишем без

этого экспоненциально убывающего слагаемого

∑

(Π.1)

y_i(t) =

a_i(ω_k)sin(ω_kt + φ_i(ω_k)), i = 1,m₂,

k=1

где a_i(ω_k) ≥ 0 и φ_i(ω_k)— амплитуды и фазы выходных колебаний, вызванных

k-й гармоникой входного сигнала w вида (2.3).

Амплитуды колебаний по каждой координате вектора y из (П.1) с частотой

являются модулями соответствующих компонент следующих комплексно-

сопряженных векторов T_yw(jω_k)w(k)+ и T_yw(-jω_k)w(k)-, где

[

w(k)+ =

w1kejϕ1k ,w2kejϕ2k ,... ,wm3kejϕm3k

]^T ,

[

]_T

w(k)- =

w1ke-jϕ1k ,w2ke-jϕ2k ,... ,wm3ke-jϕm3k

Действительно, легко проверить, что k-я гармоника входного вектора w с

компонентами из (2.3) может быть представлена в виде

(

)∕

w(k)+ejwkt - w(k)-e-jwkt

(2j).

148

Тогда, определив частные решения уравнений замкнутой системы (2.1),

(2.2) при w = w(k)+e^jωk^t и w = w(k)-e^-jωk^t и обозначив соответствующие им зна-

чения вектора выхода y₊ и y_-, в силу принципа суперпозиции для k-й гар-

моники выходного вектора y с компонентами из (П.1) можно записать, что

(

)

(y₊ - y_-)/(2j) = T_yw(jω_k)w(k)+ejωkt - T_yw(-jω_k)w(k)-e-jωkt

/(2j).

Очевидно, что a2i(ω_k) = y_-iy+i, где y_-i и y+i — i-е компоненты векторов y_-

и y₊ соответственно. Теперь, принимая во внимание диагональную структуру

∑

матрицы Q, получим q_ia2i(ω_k) = yT-Qy₊ = w(k)T-TTyw(-jω_k)QT_yw(jω_k)w(k)+,

i=1

i = 1,m₂.

Учитывая диагональную структуру матрицы правой части (3.9) и само

∑

это неравенство, получим, что

q_ia2i(ω_k) ≤ γ²w(k)T-w(k)+ = γ²

^∑w2jk.

i=1

j=1

∑

Отсюда следует очевидное неравенство q_ia2i(ω_k) ≤ γ²w(k)T-w(k)+ = γ² w2jk,

j=1

i = 1,m₂.

Извлекая квадратный корень из обеих частей последнего неравенства, по-

лучим

:⎛

⎞₂

:∑

∑

√q_ia_i(ω_k) ≤ γ√

w2jk ≤ γ√⎝

w_jk⎠ , i = 1,m₂.

j=1

∑

И, следовательно,

√q_ia_i(ω_k) ≤ γ

w_jk, i = 1,m₂.

j=1

√

∑

Суммируя по всем частотам, будем иметь

q_i

a_i(ω_k) ≤ γ

w_jk,

k=1

j=1 k=1

i = 1,m₂.

∑

Учитывая, что y_i,st ≤

a_i(ω_k), i = 1,m₂, и принимая во внимание (2.4),

k=1

получим, что

∑∑

∑

√q_iy_i,st ≤ γ

w_jk ≤ γ w^∗j, i = 1,m₂.

j=1 k=1

j=1

Из последнего неравенства и следует доказываемое соотношение (3.10).

СПИСОК ЛИТЕРАТУРЫ

1. Воронов А.А. Основы теории автоматического управления. Линейные системы

регулирования одной величины. М.-Л.: Энергия, 1965.

149

Doyle J.C., Stein G. Multivariable Feedback Design: Concepts for a Classical / Mod-

ern Synthesis // IEEE Trans. Autom. Control. 1981. V. 26. No. 1. P. 4-16.

Zhou K., Doyle J.C., Glover K. Robust and Optimal Control. N.J.: Prentice-Hall,

1996.

Zhou K., Doyle J.C. Essentials of Robust Control. N.J.: Prentice-Hall, 1998.

The Control Handbook / Ed. W.S. Levine. IEEE Press, 1996.

Skogestad S., Postlethwaite I. Multivariable feedback control. Analysis and design.

N.Y.: John Wiley and Sons, 2006.

Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2002.

Keel L.H., Bhattacharyya S.P. Robust, Fragile, or Optimal? // IEEE Trans. Autom.

Control. 1997. V. 42. No. 8. P. 1098-1105.

Александров А.Г. Критерии грубости нестационарных систем автоматического

регулирования // Аналитические методы синтеза регуляторов. Межвуз. науч.

сб. Саратов: Сарат. политехн. ин-т, 1980. С. 3-14.

10.

Li Ya., Lee B. Stability Robustness Characterization and Related Issues for Control

Systems Design // Automatica. 1993. V. 29. No. 2. P. 479-484.

11.

Честнов В.Н. Синтез регуляторов многомерных систем по заданному радиусу

запасов устойчивости на базе процедуры H_∞-оптимизации // АиТ. 1999. № 7.

С. 100-109.

Chestnov V.N. Design of Controllers of Multidimensional Systems with a Given

Radius of Stability Margins Based on the H_∞-optimization Procedure // Autom.

Remote Control. 1999. V. 60. No. 7. P. 986-993.

12.

Честнов В.Н. Синтез дискретных H_∞-регуляторов по заданному радиусу запа-

сов устойчивости и времени регулирования // АиТ. 2014. № 9. С. 65-82.

Chestnov V.N. Synthesis of Discrete H_∞-controllers with Given Stability Margin

Radius and Settling Time // Autom. Remote Control. 2014. V. 75. No. 9. P. 1593-

1607.

13.

Astrom K.J., Murray R.M. Feedback systems: an introduction for scientists and

engineers. N.J.: Princeton University Press, 2008.

14.

Александров А.Г. Синтез регуляторов многомерных систем. М.: Машиностр.,

1986.

15.

Садомцев Ю.В. Конструирование систем управления с обратной связью по кри-

териям точности и грубости. Саратов: СГТУ, 2003.

16.

Anderson B.D.O., Moore J.B. Optimal Control. Linear Quadratic Methods. N.Y.:

Prentice Hall, 1990.

17.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях. Техника линейных матричных неравенств. М.:

ЛЕНАНД, 2014.

18.

Александров А.Г., Честнов В.Н. Синтез многомерных систем заданной точно-

сти. II. Применение процедур H_∞-оптимизации // АиТ. 1998. № 8. С. 124-138.

Aleksandrov A.G., Chestnov V.N. Synthesis of Multidimensional Systems of Given

Accuracy. II. Application of H_∞-optimization Procedures // Autom. Remote

Control. 1998. V. 59. No. 8. P. 1153-1164.

19.

Агафонов П.А., Честнов В.Н. Синтез регуляторов по заданному радиусу запа-

сов устойчивости с учетом внешних возмущений на основе H_∞-подхода // АиТ.

2004. № 10. С. 101-108.

150

Agafonov P.A., Chestnov V.N. Controllers of a Given Radius of Stability Margin:

Their Design by the H_∞-approach with Regard for External Disturbances // Autom.

Remote Control. 2004. V. 65. No. 10. P. 1611-1617.

20.

Честнов В.Н. Синтез робастных H_∞-регуляторов многомерных систем по за-

данной степени устойчивости // АиТ. 2007. № 3. C. 199-205.

Chestnov V.N. Design of Robust H_∞-controllers of Multivariable Systems Based on

the Given Stability Degree // Autom. Remote Control. 2007. V. 68. No. 3. P. 557-563.

21.

Честнов В.Н. Синтез H_∞-регуляторов многомерных систем заданной точности

и степени устойчивости // АиТ. 2011. № 10. С. 170-185.

Chestnov V.N. Synthesizing H_∞-controllers for Multidimensional Systems with

Given Accuracy and Degree of Stability // Autom. Remote Control. 2011. V. 72.

No. 10. P. 2161-2175.

22.

Честнов В.Н., Зацепилова Ж.В. Синтез регуляторов многомерных систем по

инженерным показателям точности, времени регулирования и запасов устойчи-

вости // Сб. тр. Межд. конф. “Проблемы управления, передачи и обработки

информации (АТМ-ТКИ-50)” 2009. Саратов: СГТУ, С. 41-45.

23.

Честнов В.Н. Синтез многомерных систем заданной точности, времени регу-

лирования и радиуса запасов устойчивости // Дифф. уравнения. 2014. № 8.

С. 1138-1139.

24.

Александров А.Г., Честнов В.Н. Обеспечение заданной точности на основе LQ-

и H_∞-оптимизации // Матер. Межд. конф. “Управление в технических, эрга-

тических, организационных и сетевых системах”. СПб.: ЦНИИ Электроприбор,

2012. С. 33-36.

25.

Александров А.Г. К аналитическому синтезу регуляторов // АиТ. 2010. № 6.

С. 3-19.

Aleksandrov A.G. On Analytical Design of Controllers // Autom. Remote Control.

2010. V. 71. No. 6. P. 977-992.

26.

Александров А.Г. Синтез регуляторов по показателям точности и быстродей-

ствию. I. Минимально-фазовые одномерные объекты // АиТ. 2015. № 5. С. 27-42.

Aleksandrov A.G. Controller Design in Precision and Speed. I. Minimal Phase One-

Dimensional Plants // Autom. Remote Control. 2015. V. 76. No. 5. P. 749-761.

27.

Александров А.Г. Синтез регуляторов по показателям точности и быстродей-

ствию. II. Неминимально-фазовые одномерные объекты // АиТ. 2017. № 6.

С. 3-17.

Aleksandrov A.G. Design of Controllers by Indices of Precision and Speed. II.

Nonminimal-Phase Plants // Autom. Remote Control. 2017. V. 78. No. 6. P. 961-973.

28.

Александров А.Г. Запасы устойчивости и робастная устойчивость // Известия

РАН. Теория и системы управления. 2010. № 6. С. 32-41.

29.

Doyle J.C., Francis B.A., Tannenbaum A.R. Feedback Control Theory. N.Y.:

Macmillan, 1992.

30.

Gahinet P., Apkarian P. A Linear Matrix Inequality Approach to H_∞ Control //

Int. J. Robust and Nonlinear Control. 1994. V. 4. P. 421-448.

31.

Iwasaki T., Skelton R. All Solutions for the General H_∞ Control Problem: LMI

Existence Conditions and State-Space Formulas // Automatica. 1994. V. 30. No. 8.

P. 1307-1317.

32.

Balas G.J., Chiang R.Y., Packard A., Safonov M.G. Robust Control Toolbox 3.

User’s guide/Natick (Mass.). The MathWorks, Inc., 2010.

33.

Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир,

1977.

151

34. Мирошник И.В. Теория автоматического управления. Линейные системы. СПб.:

Питер, 2005.

35. Бари Н.К. Тригонометрические ряды. М.: Госуд. издат. физ.-мат. лит., 1961.

36. Толстов Г.П. Ряды Фурье. М.: Наука, 1980.

37. Якубович В.А. Методы теории абсолютной устойчивости / Методы исследова-

ния нелинейных систем автоматического управления (под ред. Р.А. Нелепина).

М.: Наука, 1975. С. 74-180.

38. Lehtomaki N.A., Sandell N.R., Athans M. Robustness Results in Linear-Quadratic

Gaussian Based Multivariable Control Designs // IEEE Trans. Autom. Control. 1981.

V. 26. No. 1. P. 75-92.

39. Честнов В.Н., Шатов Д.В. Синтез одномерных регуляторов по заданному по-

казателю колебательности: модальный и H_∞-подходы // Пробл. управления.

2019. № 2. С. 2-8.

40. Chestnov V.N., Shatov D.V. Multivariable Systems Design of Desired Accuracy

Based on LQ and H_∞ Optimization Procedures / Proc. Eur. Control Conf.

(ECC-2018). Cyprus, Limassol, IFAC Publication, 2018. P. 2511-2516.

41. Агафонов П.А., Честнов В.Н. Одновременное обеспечение запасов устойчивости

на входе и выходе многомерного объекта на основе H_∞ подхода // АиТ. 2004.

№ 9. С. 110-119.

Agafonov P.A., Chestnov V.N. H_∞-Control for Guaranteed Simultaneous Input and

Output Stability Margins for a Multivariate System // Autom. Remote Control.

2004. V. 65. No. 9. P. 1452-1460.

42. Astrom K.J., Нagglund Т. Аdvanced PID Control. ISA, 2006.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 19.07.2018

После доработки 14.08.2018

Принята к публикации 08.11.2018

152