Автоматика и телемеханика, № 10, 2019

(anatoli.juditsky@univ-grenoble-alpes.fr)

(LJK, Университет Гренобль-Альпы, Гренобль, Франция),

А.С. НЕМИРОВСКИЙ, д-р физ.-мат. наук (nemirovs@isye.gatech.edu)

(ISyE, Технологический институт Джорджии, Атланта, США)

ВОССТАНОВЛЕНИЕ СИГНАЛОВ С ПОМОЩЬЮ

СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ¹

Рассматривается подход к восстановлению сигналов в обобщенных ли-

нейных моделях, при котором задача оценивания сигналов сводится к ре-

шению стохастических монотонных вариационных неравенств (ВН). Ре-

шения таких ВН могут быть получены с помощью эффективно вычисли-

тельных процедур, а в случае сильно монотонных ВН допускают верхнюю

границу на конечном времени для ожидаемой ошибки ∥ · ∥²², сходящуюся

к нулю со скоростью O(1/K) с ростом числа K наблюдений. Принятые

структурные предположения существенно слабее тех, которые необходи-

мы для обеспечения выпуклости оптимизационной задачи, возникающей

при применении метода максимального правдоподобия. Прослеживается

связь предлагаемого подхода с идеями, лежащими в основе алгоритма

персептрона Розенблата.

Ключевые слова: обобщенные линейные модели, задача статистического

оценивания, стохастическая оптимизация, вариационные неравенства.

DOI: 10.1134/S0005231019100088

1. Введение

Задачи статистического оценивания составляют одну из важнейших при-

кладных областей стохастической оптимизации. Типичная постановка задачи

выглядит следующим образом (например, см. [1] и обширную библиографию,

приведенную в этой книге). Допустим, что имеются независимые одинаково

распределенные наблюдения ω^K = (ω₁, . . . , ω_K ), ω_k = (η_k, y_k), где η_k ∈ R^n×m,

yk ∈ Rm — реализации регрессоров (независимые переменные) и отклики

(метки) соответственно. Предполагаем, что наблюдения описываются обоб-

щенной линейной моделью (ОЛМ) [2, 3], т.е. условное (по η) математическое

ожидание y равно f(η^Tx), гдe верхний индекс^T — знак транспонирования,

f (·) : R^m → R^m — известная функция связи, а x ∈ R^m — неизвестный “сиг-

нал”, т.е. вектор параметров модели. Цель состоит в “подгонке модели”, т.е. в

восстановлении вектора x по наблюдениям ω^K . При стандартном подходе к

решению задачи оценивания выбирают функцию потерь ℓ(y, θ) : R^m × R^m →

→ R и в качестве оценки x принимают оптимальное решение оптимизацион-

¹ Работа первого автора поддержана грантом 2016-2032H, PGMO. Работа первого и вто-

рого авторов финансировалась грантом CCF-1523768, NSF.

153

ной задачи

{

}

(1)

minEω∼Px

ℓ(y, f(η^Tu))

u∈X

где P_x — функция распределения наблюдений ω = (η, y), отвечающая “истин-

ному сигналу x”, а X — априори известное множество сигналов. Иными сло-

вами, задача статистического оценивания сводится к задаче стохастической

оптимизации (1), которая должна решаться приближенно, исходя из имею-

щихся наблюдений ω^K . Это может быть сделано или напрямую (“пакетно”)

путем минимизации по u ∈ X аппроксимации выборочного среднего (ВСА)

∑

(2)

ℓ(y_k, f(ηTk

u))

k=1

для математического ожидания в

(1) (например, см. [4]) или путем приме-

нения итеративных алгоритмов стохастической оптимизации типа стохасти-

ческой аппроксимации (СА) [5, 6].

Пусть функция условного по η распределения P^x|η величины y, индуциро-

ванная распределением P_x, принадлежит известному параметрическому се-

мейству P = {P^θ : θ ∈ Θ ⊂ R^m}, а именно, P^x|η = Pf(ηTx⁾; тогда стандартный

выбор функции потерь дается методом максимального правдоподобия (МП).

Иными словами, считая, что распределения P^θ имеют плотности p_θ относи-

тельно некоторой меры Π, полагают

ℓ(y, θ) = - ln(p_θ(y)).

Например, в классической логистической регрессии имеем m = 1, f(s) =

= (1 + e^-s)-1, Θ = (0, 1), а P^θ, θ ∈ Θ, — распределение Бернулли, т.е. y при-

нимает значение единица с вероятностью q = (1 + exp{-η^Tx})-1 и нуль с ве-

роятностью 1 - q, что приводит к

(

)

(3)

ℓ(y, f(η^Tu)) = ln

1 + exp{η^Tu}

- yη^T

В этом случае задача (1) становится оптимизационной задачей вида

{

}

(4)

minE(η,y)∼Px

ln(1 + exp{η^Tu}) - y η^Tu

u∈X

и соответствующая задача ВСА записывается как

∑[

]

(5)

min

ln(1 + exp{ηTku}) - y_kηTku

u∈X K

k=1

а ее оптимальное решение x_ML(ω^K ) и есть МП-оценка сигнала x. При пред-

положении о выпуклости множества X сигналов обе эти задачи выпуклы и,

следовательно, глобальный оптимум в задаче ВСА может быть эффективно

вычислен, а для алгоритмов СА для

(4) могут быть получены гарантиро-

ванные скорости сходимости.

154

В более общем случае, когда распределения наблюдений образуют семей-

ство условных экспоненциальных распределений [7, 8], функция правдоподо-

бия имеет вид

ℓ(y, η^Tu) = F (η^Tu) - yη^Tu

с выпуклой кумулянтной функцией F , а соответствующая задача (1) мини-

мизации риска записывается как

{

}

(6)

minE(η,y)∼Px

F (η^Tu) - yη^Tu

u∈X

В этом случае, так же как и при логистической регрессии, для получения

МП-оценок параметров модели можно применять ВСА или СА.

Заметим, однако, что предположение о принадлежности распределений

экспоненциальному семейству довольно ограничительно. С другой стороны,

для распределений, которые не удовлетворяют этому предположению, вы-

пуклость оптимизационной задачи, получающейся при выборе функции по-

терь ℓ(·) по методу максимального правдоподобия, является скорее исключе-

нием, чем правилом. Например, рассмотрим нелинейную схему наименьших

квадратов, в которой величина y получается из f(η^Tx) добавлением центри-

рованного гауссовского шума, не зависящего от регрессоров:

y = f(η^Tx) + ξ, ξ ∼ N(0,σ²I_m).

В этом случае задача (1) и ее ВС-аппроксимация при выборе ℓ(·) по методу

максимального правдоподобия приобретают вид

{

}

minEη∼Q ∥f(ηTx) - f(ηTu)∥2

u∈X

{

}

∑

(7)

min

∥y_k - f(ηTku)∥²

u∈X K

k=1

где Q — распределение регрессоров (они предполагаются независимыми от

сигнала). Если функция f нелинейна, то обе эти задачи обычно невыпук-

лы, и их численное решение затруднено. Аналогично, в задаче “неэкспонен-

циальной логистической регрессии”, в которой сигмоидная функция f(s) =

= (1 + exp{-s})-1 заменена на общего вида неубывающую функцию свя-

зи f(s) : R → (0, 1) (например, так называемая пробит-функция или допол-

няющая log - log функция), МП-выбор функции потерь, как правило, влечет

невыпуклость задачи (1) и ее ВС-аппроксимации.

Цель последующего изложения — предложить альтернативу решению за-

дачи настройки модели, основанному на решении оптимизационной зада-

чи (1) с МП-выбором функции потерь при оценивании сигнала по наблюдени-

ям в ОЛМ. Идеи, лежащие в основе подхода, предлагаемого в настоящей ста-

тье, восходят к итеративному алroритму персептрона Розенблата [9, 10] и его

“пакетной” версии [11]. В этом случае структурные требования, предъявляе-

мые к модели, оказываются существенно слабее тех, которые приводят к вы-

155

пуклости задач (1) с МП-выбором функции потерь и их ВС-аппроксимаций².

При этих предположениях вместо того, чтобы использовать классический

подход с формированием задачи стохастической оптимизации

(1) и функ-

ции потерь [12-16], задача оценивания сводится к другой задаче с выпук-

лой структурой — сильно монотонному вариационному неравенству (ВН),

представимому в виде стохастического оракула. Полученное вариационное

неравенство может быть эквивалентно задаче выпуклой минимизации (на-

пример, при m = 1 такое ВН эквивалентно задаче выпуклой оптимизации,

аналогичной

(6)); но даже и в этом случае получающаяся задача, как пра-

вило, отличается от МП-версии задачи (1). Решение такого ВН может быть

получено в результате эффективной численной процедуры, и оно оказывает-

ся “хорошей” оценкой “истинного” сигнала по имеющимся наблюдениям. Для

этой оценки здесь доказываются верхние границы на ожидаемую квадратич-

ную ошибку в норме ∥ · ∥²², сходящуюся к нулю со скоростью O(1/K) при

K →∞³.

2. Постановка задачи

Рассматривается обобщенная линейная модель наблюдений, характери-

зующаяся следующими предположениями.

Наблюдения зависят от неизвестного сигнала x, принадлежащего задан-

ному выпуклому компактному множеству X ⊂ Rⁿ, и представлены в виде

(8)

ω^K = {ω_k = (η_k,y_k

), 1 ≤ k ≤ K},

где ω_k, 1 ≤ k ≤ K, — независимые одинаково распределенные реализации

случайной пары (η, y) с распределением P_x таким, что

• регрессор η является случайной (n × m)-матрицей с некоторым вероят-

ностным распределением Q, не зависящим от x;

• отклик (“метка”) y является m-мерным случайным вектором таким, что

его условное по η распределение, индуцированное распределением P_x, имеет

математическое ожидание f(η^Tx):

(9)

E^x|η{y} = f(η^T

x),

где E^x|η — условное по η математическое ожидание метки y, задаваемое рас-

пределением P_x величины ω = (η, y), а f(·) : R^m → R^m — заданное отобра-

жение.

Ниже будут сформулированы предположения о параметрах обобщенной

линейной модели (а именно, условия на f(·) и на распределение P_x, x ∈ X

пары (η, y)), необходимые для обоснования предлагаемого подхода.

² Например, в нелинейной схеме наименьших квадратов с m = 1 и в неэкспоненциаль-

ной логистической регрессии от функции f требовалась лишь непрерывная дифференци-

руемость и положительность производной, а от множества X сигналов — выпуклость.

³ Несмотря на простоту приводимых ниже выкладок, авторам не удалось найти упоми-

нание о предлагаемом подходе в статистической литературе.

156

2.1. Предварительные сведения: монотонные векторные поля

Монотонное векторное поле на R^m — это однозначное всюду определенное

отображение g(·) : R^m → R^m, обладающее свойством монотонности:

[g(z) - g(z^′)]^T[z - z^′] ≥ 0

∀z, z^′ ∈ R^m.

Скажем, что такое поле монотонно с модулем κ ≥ 0 на замкнутом выпуклом

множестве Z ⊂ R^m, если

[g(z) - g(z^′)]^T[z - z^′] ≥ κ∥z - z^′∥²²

∀z, z^′ ∈ Z;

назовем g сильно монотонным на Z, если модуль монотонности κ поля g

на Z положителен. Очевидно, что для монотонного векторного поля f, непре-

рывно дифференцируемого на замкнутом выпуклом множестве Z с непустой

внутренностью, условие

(10)

d^Tf^′(z)d ≥ κd^Td

∀(d ∈ Rⁿ

,z∈Z)

является необходимым и достаточным условием монотонности с модулем κ.

Стандартными примерами монотонных векторных полей являются

• градиентные поля

∇φ(x) непрерывно дифференцируемых выпуклых

функций m переменных, а также векторные поля [∇_xφ(x, y); -∇_yφ(x, y)],

порожденные непрерывно дифференцируемыми функциями φ(x, y), вы-

пуклыми по x и вогнутыми по y;

• “диагональные” векторные поля f(x) = [f₁(x₁); . . . ; f_m(x_m)] с монотонно

неубывающими компонентами f_i(·) — функциями одного аргумента. Ес-

ли, кроме того, f_i(·) непрерывно дифференцируемы с положительными

производными, то соответствующее поле f сильно монотонно на любом

компактном выпуклом подмножестве в R^m с модулем монотонности, за-

висящим от подмножества.

Монотонные векторные поля на Rⁿ допускают выполнение простых опе-

раций, включающих, например, следующие:

I. [аффинная подстановка аргумента]: Если f(·) — монотонное векторное по-

ле на R^m и A есть (n × m)-матрица, то векторное поле

g(x) = Af(A^Tx + a)

также монотонно на Rⁿ; если, кроме того, поле f монотонно с модулем

κ ≥ 0 на замкнутом выпуклом множестве Z ⊂ R^m, а множество X ⊂ Rⁿ

замкнуто, выпукло и обладает свойством A^Tx + a ∈ Z для всех x ∈ X, то

поле g монотонно с модулем σ²κ на X, где σ — минимальное сингулярное

значение матрицы A.

II. [суммирование]: Пусть S — польское пространство, f(x, s) : Rm × S →

→ R^m — борелевская векторнозначная функция, монотонная по x при

каждом s ∈ S, а μ(ds) — борелевская вероятностная мера на S такая, что

векторное поле

∫

F (x) = f(x, s)μ(ds)

157

определено для всех x; тогда F (·) монотонно. Если, кроме того, X — за-

мкнутое выпуклое множество в R^m, а f(·, s) монотонно на X с борелев-

∫ким по s модулем κ(s) для всякого s ∈ S, то F монотонно на X с модулем

κ(s)μ(ds).

2.2. Предположения

В дальнейшем потребуются следующие предположения об основных ком-

понентах задачи оценивания, описанной во введении.

A.1. Векторное поле f(·) непрерывно и монотонно, а векторное поле

{

}

F (z) = E_η∼Q

ηf(η^Tz)

корректно определено (следовательно, монотонно, как и поле f, см. I, II).

A.2. Множество X сигналов непусто, выпукло и компактно, а векторное

поле F монотонно с положительным модулем κ на X .

A.3. Для соответствующим образом выбранного M < ∞ и всякого x ∈ X

верно

{

}

(11)

E(η,y)∼Px

∥ηy∥²²

≤M².

Простое достаточное условие выполнения предположений A.1-A.3 с соответ-

ствующим образом выбранным M < ∞ и κ > 0 заключается в следующем:

• распределение Q регрессора η имеет конечные моменты всех порядков и

E_η∼Q{ηη^T} ≻ 0;

• функция f непрерывно дифференцируема, и d^Tf^′(z)d > 0 для всех d = 0

и всех z. Кроме того, f имеет полиномиальный рост, т.е. для некоторых

констант C ≥ 0 и p ≥ 0 и всех z выполнено ∥f(z)∥₂ ≤ C(1 + ∥z∥p2).

Проверка достаточности осуществляется непосредственно.

3. Построения и основной результат

Сформулируем ключевое наблюдение, лежащее в основе представляемых

ниже конструкций.

Предложение 1. Пусть выполнены предположения A.1-A.3. Сопоста-

вим паре (η, y) ∈ R^n×m × R^m векторное поле

(12)

G(η,y)(z) = ηf(η^Tz) - ηy : Rⁿ → Rⁿ.

Тогда для любого x ∈ X имеем

{

}

(a)

E(η,y)∼Px

= F(z) - F(x)

∀z ∈ Rⁿ

G(η,y)(z)

(13)

(b)

∥F (z)∥₂ ≤ M

∀z ∈ X

{

}

∥G(η,y)(z)∥²²

≤ 4M²

∀z ∈ X.

158

Доказательство. Пусть x ∈ X. Тогда, пользуясь соотношением (9) и

определением поля F , имеем

{

}

{

}

E(η,y)∼Px {ηy} = E_η∼Q E^x|η{ηy}

=E_η

ηf(η^Tx)

= F(x).

Отсюда получаем

{

}

{

}

E(η,y)∼Px

G(η,y)(z)

=E(η,y)∼Px

ηf(η^Tz) - ηy

{

}

=E(η,y)∼Px

ηf(η^Tz)

- F(x) =

{

}

=E_η∼Q

ηf(η^Tz)

- F(x) = F(z) - F(x);

последнее неравенство следует из (13.a). Кроме того, для x, z ∈ X обозначим

через P^z|η условное по η распределение величины z, индуцированное распре-

делением P_z величины (η, y) = η^Ty. С учетом того, что маргинальное распре-

деление величины η, индуцированное распределением P_z, есть не что иное

как Q, приходим к

{

}

{

}

E(η,y)∼Px

∥ηf(η^Tz)∥²²

=E_η∼Q

∥ηf(η^Tz)∥²²

{

}

=E_η∼Q

∥E_y∼P z

{ηy}∥²

≤

[поскольку E_y∼P z {y} = f(η^Tz)]

|η

{

}}

≤E_η∼Q E_y∼Pz

∥ηy∥²²

[по неравенству Йенсена]

|η

{

}

=E⃗η,y)∼Pz

∥ηy∥²²

≤M²

[по A.3, поскольку z ∈ X ].

В совокупности с соотношением E(η,y)∼Px {∥ηy∥²²} ≤ M², справедливым в

соответствии с A.3 (поскольку x ∈ X ), это влечет выполнение (13.b) и (13.c).

3.1. Основной результат

Напомним, что целью статьи является восстановление сигнала x ∈ X по

наблюдениям (8). В предположениях A.1-A.3 точка x есть корень монотон-

ного векторного поля

{

}

(14)

G(z) = F (z) - F (x), F (z) = E_η∼Q

ηf(η^Tz)

;

причем известно, что этот корень принадлежит множеству X и он единствен,

поскольку поле G(·) сильно монотонно на X , равно как и поле F (·). Известно,

что для заданного выпуклого компактного множества X задача отыскания

такого корня эффективно разрешима при наличии “оракула”, который, имея

на входе точку z ∈ X , выдает значение G(z) поля в этой точке. Это не совсем

та ситуация, которая здесь описана, поскольку поле G есть математическое

ожидание случайного поля:

{

}

G(z) = E(η,y)∼Px

ηf(η^Tz) - ηy

и заранее не известно, каково то распределение, по которому берется ожида-

ние. Однако выборка из этого распределения доступна, причем выборочные

159

значения в точности и есть наблюдения (8); эти выборочные значения мо-

гут использоваться для аппроксимации поля G тем или иным способом с

последующим применением этой аппроксимации для восстановления сигна-

ла x. Два стандартных пути реализации этой простой идеи суть ВСА и СА,

упоминавшиеся выше. Обсудим эти два метода применительно к ситуации, в

которой находимся.

3.1.1. Оценивание: аппроксимация выборочным средним. Идея, лежащая

в основе аппроксимации по выборочному среднему (ВСА), совершенно про-

зрачна: имея наблюдения (8), будем аппроксимировать неизвестное поле G

его эмпирическим аналогом

∑[

]

η_kf(ηTkz) - η_ky_k

GωK (z) =

k=1

По закону больших чисел при K → ∞ эмпирическое поле G_ωK сходится к ин-

тересующему нас полю G, поэтому при некоторых необременительных усло-

виях регулярности с большой вероятностью поле G_ωK будет равномерно на X

близко к полю G для достаточно больших значений K. Вследствие сильной

монотонности G отсюда следует, что множество “почти нулей” поля G_ωK на X

будет близко к нулю x поля G, т.е. к сигналу, который и подлежит восстанов-

лению. Вопрос теперь заключается в том, как правильно определить понятие

“почти нуля” поля G_ωK на X⁴. В данной ситуации это удобно сделать исходя

из понятия слабого решения вариационного неравенства (ВН) с монотонным

оператором, определяемого (в данном конкретном случае) следующим обра-

зом.

Пусть X ⊂ Rⁿ — непустое выпуклое компактное множество и пусть H(z):

X →Rⁿ — монотонное векторное поле (т.е. [H(z)-H(z^′)]^T[z-z^′]≥0 для

всех z, z^′ ∈ X ). Вектор z_∗ ∈ X называется слабым решением вариацион-

ного неравенства, связанного с H, X , если

H(z)^T(z - z_∗) ≥ 0

∀z ∈ X.

Пусть X ⊂ Rⁿ — непустое выпуклое компактное множество и пусть H

монотонно на X . Хорошо известно, что

• ВН, связанное с H, X (обозначим его через VI(H, X )), всегда имеет слабое

решение. Ясно, что если z ∈ X — корень H, то z — слабое решение для

VI(H, X ).⁵

• Если поле H непрерывно на X , то любое слабое решение z неравенства

VI(H, X ) также является и сильным решением в том смысле, что

(15)

H^T

(z)(z - z) ≥ 0 ∀z ∈ X .

⁴ Заметим, что “почти нуль” поля G_ωK на X не может быть определен как корень G_ωK

на этом множестве. Если у G действительно имеется корень, принадлежащий множеству X,

то у G_ωK такого корня может и не быть.

⁵ Если z∈ X и H(z) = 0, то монотонность H влечет H(z)^T[z - z] = [H(z) - H(z)]^T[z - z] ≥

≥0 для всех z ∈ X, т.е. z — слабое решение для VI(H,X).

160

Действительно, соотношение (15) очевидным образом выполнено для z =

= z. При z = z, положив z_t = z + t(z - z), 0 < t ≤ 1, имеем H^T(z_t)(z_t -

- z) ≥ 0 (так как z является слабым решением), откуда H^T(z_t)(z - z) ≥ 0

(поскольку z - z кратно z_t - z с положительным множителем). Перехо-

дя к пределу при t → +0 и вспоминая про непрерывность H, получаем

желаемое H^T(z)(z - z) ≥ 0.

• Если H — градиентное поле непрерывно дифференцируемой выпуклой

на X функции (такое поле монотонно), слабые (или сильные, что в случае

непрерывного H одно и то же) решения неравенства VI(H, X ) являются

точками минимума функции на X .

Заметим еще, что сильное решение неравенства VI(H, X ) с монотонным

H всегда является и слабым решением: если z ∈ X удовлетворяет условию

H^T(z)(z - z) ≥ 0 при всех z ∈ X, то и H(z)^T(z - z) ≥ 0 при всех z ∈ X,

поскольку вследствие монотонности имеем H(z)^T(z - z) ≥ H^T(z)(z - z).

В дальнейшем будем существенно использовать следующий простой и хо-

рошо известный факт.

Лемма 1. Пусть X — выпуклое компактное множество и пусть H —

монотонное векторное поле на X с модулем монотонности κ > 0, т.е.

[H(z) - H(z^′)]^T[z - z^′] ≥ κ∥z - z^′∥²²

∀z,z^′ ∈ X.

Пусть также z — слабое решение неравенства VI(H, X ). Тогда слабое ре-

шение VI(H,X) единственно. Кроме того,

(16)

H^T(z)[z - z] ≥ κ∥z - z∥²².

Доказательство. В условиях леммы положим z ∈ X, и пусть z есть

слабое решение неравенства VI(H, X ) (помним, что оно существует!). Поло-

жив z_t = z + t(z - z) при t ∈ (0, 1), получаем цепочку неравенств

H^T(z)[z - z_t] ≥ H^T(z_t)[z - z_t] + κ∥z - z_t∥² ≥ κ∥z - z_t∥²,

первое из которых справедливо в силу сильной монотонности H, а второе

следует из того, что величина H^T(z_t)[z - z_t] кратна H^T(z_t)[z_t - z] с поло-

жительным коэффициентом. Последняя величина неотрицательна, посколь-

ку z является слабым решением исследуемого ВН. Таким образом, име-

ем H^T(z)(z - z_t) ≥ κ∥z - z_t∥²² и, переходя к пределу при t → +0, приходим

к (16).

Для доказательства единственности слабого решения предположим, что

помимо слабого решения z имеется отличное от него слабое решение z, и

положим z^′ =¹² [z + z]. Поскольку и z, и z — слабые решения, то обе величины

H^T(z^′)[z^′ - z] и H^T(z^′)[z^′ - z] должны быть неотрицательны, а поскольку в

сумме они равны нулю, то каждое из них равно нулю. Поэтому, применяя (16)

к z = z^′, получаем z^′ = z, откуда также и z = z.

Вернемся теперь к исходной задаче оценивания. Пусть предположения

A.1-A.3 выполнены, так что векторные поля G(ηk ,y_k)(z), определенные в (12),

161

а следовательно, и векторное поле G_ωK (z) непрерывны и монотонны. При ис-

пользовании ВСА было найдено слабое решение x(ω^K ) вариационного нера-

венства VI(G_ωK , X ) и принято в качестве ВСА-оценки сигнала x по наблюде-

ниям (8). Поскольку векторное поле G_ωK (·) монотонно и его значения эффек-

тивно вычислимы — при условии, что таковым является f, — задача вычисле-

ния слабого решения ВН VI(G_ωK , X ) (точнее, очень хорошего приближения

к нему) также является эффективно разрешимой (например, см. [17]). Хотя

авторы не ставили перед собой такой задачи в настоящей работе, исполь-

зуя методологию из [16, 18-20] и дополняя предположения A.1-A.3 необреме-

нительными условиями регулярности, можно доказать неасимптотическую

верхнюю границу, например, для ожидаемой ошибки ∥ · ∥²² ВСА-оценки как

функцию размера выборки K и найти скорость, с которой эта верхняя гра-

ница сходится к нулю с ростом K → ∞.

Рассмотрим ВСА-оценки в схеме логистической регрессии. Имеем f(u) =

= (1 + e^-u)-1 и

[

]

exp{ηTkz}

G(η_k ,y_k)(z) =

-y_k η_k,

1 + exp{ηTk z}

[

]

∑

exp{ηTkz}

GωK (z) =

-y_k η_k =

1 + exp{ηTkz}

k=1

]

[∑(

(

)

∇_z

1 + exp{ηTk z}

-y_kηTkz

Иначе говоря, G_ωK (z) является градиентным полем отрицательного логариф-

ма эмпирического МП ℓ(z, ω^K ), см. (5). В результате слабые решения ВН

VI(G_ωK , X ) дают в точности оптимальные решения задаче (5), т.е. в схеме

логистической регрессии ВСА-оценки есть оценки максимального правдопо-

добия x_ML(ω^K)⁶. С другой стороны, в примере для нелинейной схемы наи-

⁶ Заметим, что это явление специфично для модели логистической регрессии. То, что в

этом случае ВСА-оценки совпадают с МП-оценками, объясняется тем, что логистическая

сигмоида f(s) = exp{s}/(1 + exp{s}) удовлетворяет тождеству f^′(s) = f(s)(1 - f(s)). При

ее замене на f(s) = φ(s)/(1 + φ(s)) с дифференцируемой монотонно неубывающей положи-

тельной φ(·) ВСА-оценка доствляет слабое решение вариационному неравенству VI(Φ, X ) с

[

]

∑

φ(ηTkz)

Φ(z) =

-y_k η_k.

1 + φ(ηTkz)

С другой стороны, градиентное поле отрицательного логарифма МП

∑[

]

y_k ln(f(ηTkz)) + (1 - y_k) ln(1 - f(ηTkz))

которое должно минимизироваться при отыскании МП-оценок, имеет вид

[

]

∑

φ^′(ηTkz)

φ(ηTkz)

Ψ(z) =

-y_k η_k.

φ(ηTkz)

1 + φ(ηTkz)

При k > 1 и неэкспоненциальной φ поля Φ и Ψ “существенно различны”; соответственно,

ВСА-оценка, как правило, отлична от МП-оценки.

162

меньших квадратов, приведенном во введении, с монотонной (для простоты

скалярной) функцией f(·) векторное поле G_ωK (·) имеет вид

∑[

]

f (ηTkz) - y_k

η_k,

GωK (z) =

k=1

“существенно отличный” (при условии нелинейности f) от градиентного поля

∑

[

]

Ψ(z) =

f^′(ηTkz)

f (ηTkz) - y_k

η_k

k=1

для МП (7). В результате в этом случае МП-оценка (7), вообще говоря, от-

личается от ВСА-оценки, но в отличие от МП-оценки ВСА-оценка гораздо

проще с вычислительной точки зрения.

3.1.2. Оценивание: стохастическая аппроксимация. Оценки метода стоха-

стической аппроксимации (СА) генерируются простым алгоритмом субгра-

диентного спуска решения вариационного неравенства VI(G,X). Если бы

значения векторного поля G(·) были доступны, можно было бы аппрокси-

мировать корень x ∈ X этого ВН, пользуясь рекурсией

z_k = Proj_X [zk-1 - γ_kG(zk-1)], k = 1,... ,K,

где

• Proj_X [z] — метрическая проекция Rⁿ на X:

Proj_X [z] = argmin ∥z - u∥₂;

u∈X

• γ_k > 0 — заданная длина шага;

• начальное приближение z₀ — произвольная точка из X .

Хорошо известно, что в предположениях A.1-A.3 такая рекуррентная проце-

дура с надлежащим выбором длины шага и начальной точкой из X позволяет

аппроксимировать корень поля G (на самом деле, также и любое слабое реше-

ние VI(G, X )) с произвольно высокой точностью, если K достаточно велико.

Здесь, однако, имеем ситуацию, когда истинные значения поля G недоступ-

ны; стандартный способ преодоления этой трудности заключается в замене

“ненаблюдаемых” значений G(zk-1) поля G, присутствующих в рекуррентной

процедуре, их несмещенными случайными оценками G(ηk ,y_k)(zk-1). Такая мо-

дификация приводит к процедуре стохастической аппроксимации (восходя-

щей к [21]) — рекурсии вида

(17)

z_k = Proj_X [zk-1 - γ_kG(ηk,y_k)(zk-1

)],

1 ≤ k ≤ K,

где z₀ — раз и навсегда выбранная точка из X , а γ_k > 0 — детерминированные

скалярные множители.

Анализ сходимости. Приводимый ниже результат очень хорошо известен;

для полноты изложения приводим стандартное доказательство этого утвер-

ждения в Приложении.

163

Предложение 2. В предположениях A.1-A.3 при выборе длины шага

(18)

γ_k = [κ(k + 1)]-1

k = 1,2,...

для последовательности оценок x_k(ω^k) = z_k любого сигнала x ∈ X , даваемой

процедурой СА (17) с ω^k = (η_k,y_k), определенными в (8) для любого k, выпол-

няется следующая оценка:

{

}

4M²

(19)

∥x_k(ω^k) - x∥²

≤

k = 0,1,...,

E_ωk∼Pkx

κ²(k + 1)

где P_x — распределение пары (η, y), обусловленное сигналом x.

3.2. Численный пример

Для иллюстрации изложенных выше построений приведем результаты

некоторых численных экспериментов. Для наглядности рассматриваем про-

стейшие ситуации, а именно:

• X = {x ∈ Rⁿ : ∥x∥₂ ≤ R};

• распределение Q регрессора η есть N (0, I_n);

• f — монотонное векторное поле на R, задаваемое одним из следующих

четырех способов:

A. f(s) = exp{s}/(1 + exp{s});

B. f(s) = s;

C. f(s) = max[s, 0];

D. f(s) = min[1, max[s, 0]].

• условное по η распределение y, индуцированное распределением P_x, есть

— распределение Бернулли с вероятностью f(η^Tx) исхода единица в слу-

чае A (т.е. этот случай соответствует логистической модели),

— гауссовское распределение N (f(η^Tx), I_n) в случаях B-D.

Обратим внимание, что в рассматриваемом примере поле F (z) легко вычис-

ляется. Действительно, для всех z ∈ Rⁿ имеем

(

)

zz^T

η=

η+ I_n -

∥z∥²²

∥z∥²

η_⊥

и в силу независимости η^Tz и η_⊥ получаем

}

^{zz^Tη

F (z) = Eη∼N(0,I){ηf(η^Tz)} = Eη∼N(0,I)

f (η^Tz)

∥z∥²

Eζ∼N(0,1){ζf(∥z∥₂ζ)},

∥z∥₂

т.е. F (z) пропорционально z/∥z∥₂ с коэффициентом

h(∥z∥₂) = Eζ∼N(0,1){ζf(∥z∥₂ζ)}.

164

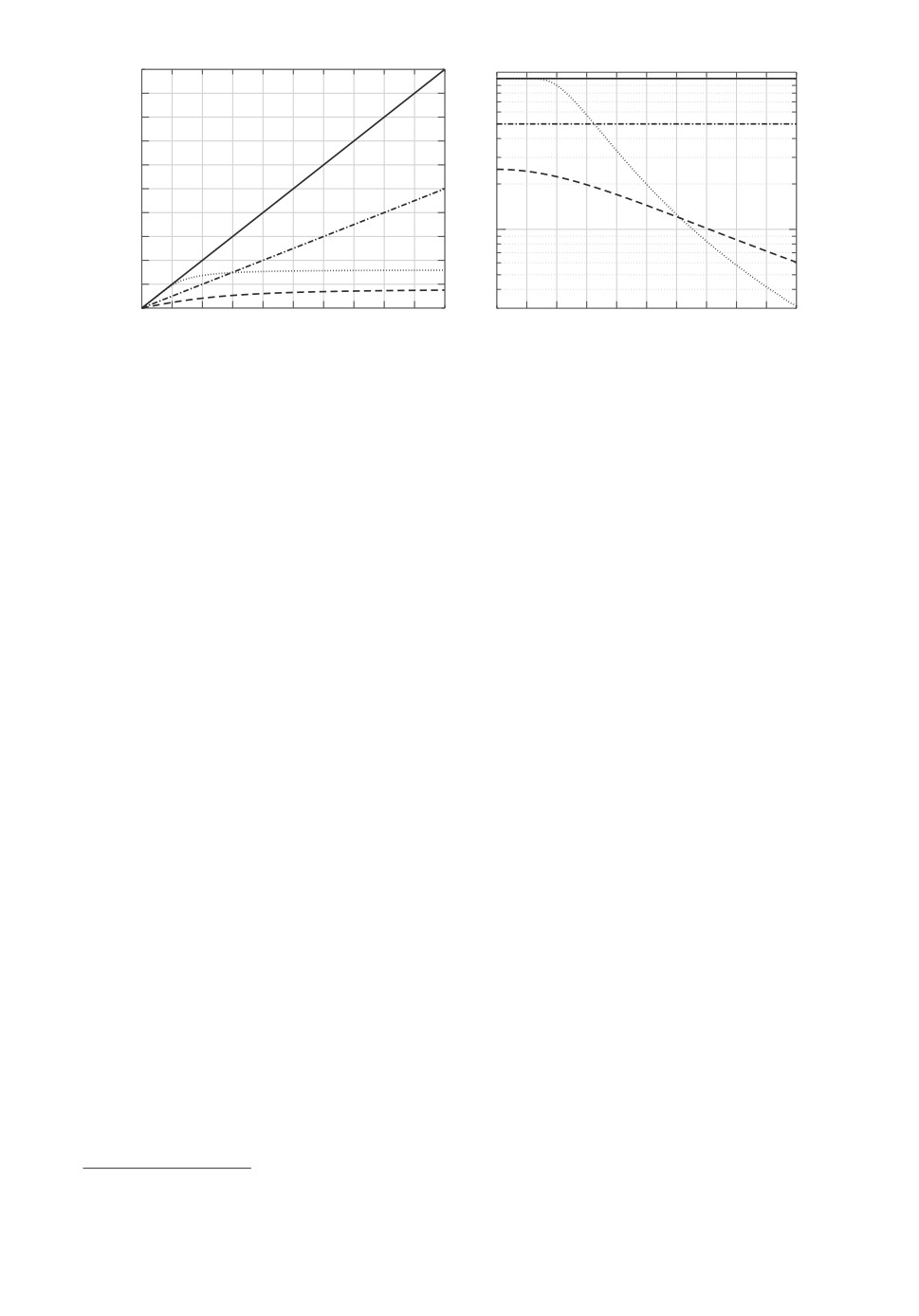
5,0

4,5

4,0

3,5

3,0

2,5

2,0

10¹

1,5

1,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

5,0

0,2

0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0

Рис. 1. Слева: функции h; справа: модули сильной монотонности операторов

F (·) на X = {z : ∥z∥₂ ≤ R} как функции R. Пунктирные линии — случай A,

сплошные линии — случай B, штрих-пунктирные линии — случай C, точечные

линии — случай D.

На рис. 1 представлены графики функции h(t) для случаев A-D, а также за-

висимости модулей сильной монотонности соответствующих отображений F

на шаре X от радиуса R шара. Размерность n во всех экспериментах пола-

галась равной 100, а количество K наблюдений полагалось 400, 10³, 4·10³,

10⁴ и 4 · 10⁴. Для каждой комбинации параметров проводилось 10 модели-

рований сигнала x, порождающего наблюдения (8), генерируемого случайно

равномерно на единичной сфере (границе множества X ).

В каждом эксперименте вычислялись ВСА-оценки и СА-оценки (заметим,

что в случаях A и B оценки, даваемые ВСА, совпадают с МП-оценками).

Длина γ_k шага в СА выбиралась в соответствии с (18) при “эмпирическом”

выборе величины κ⁷. Точнее, полученные наблюдения ω_k = (η_k, y_k), k ≤ K

(8) использовались для построения СА-оценок в два этапа:

— на этапе настройки генерировался случайный “обучающий сигнал” x^′ ∈ X ,

после чего генерировались метки y^′k так, как если бы x^′ являлся истинным

сигналом. Например, в случае A метке y^′k придавалось значение единица с

вероятностью q = f(ηTkx^′) и нуль с вероятностью 1 - q. После того как сге-

нерированы “обучающий сигнал” и соответствующие метки, к полученным

искусственным наблюдениям применялась схема СА с различными значения-

ми κ, вычислялась точность полученных оценок и выбиралось то значение κ,

которое приводит к наилучшему восстановлению сигнала;

— на этапе исполнения алгоритм СА прогонялся на фактических данных с

шагом (18), определяемым тем значением κ, которое было найдено на этапе

настройки.

Результаты некоторых численных экспериментов представлены на рис. 2.

Подчеркнем, что время вычислений включает в себя оба этапа. Вывод из

результатов экспериментов таков: будучи лишь немногим лучше СА по ка-

⁷ Для величины модуля сильной монотонности векторных полей F(·) могут быть ана-

литически получены нижние границы, однако это требует немалых усилий, а границы

оказываются консервативными.

165

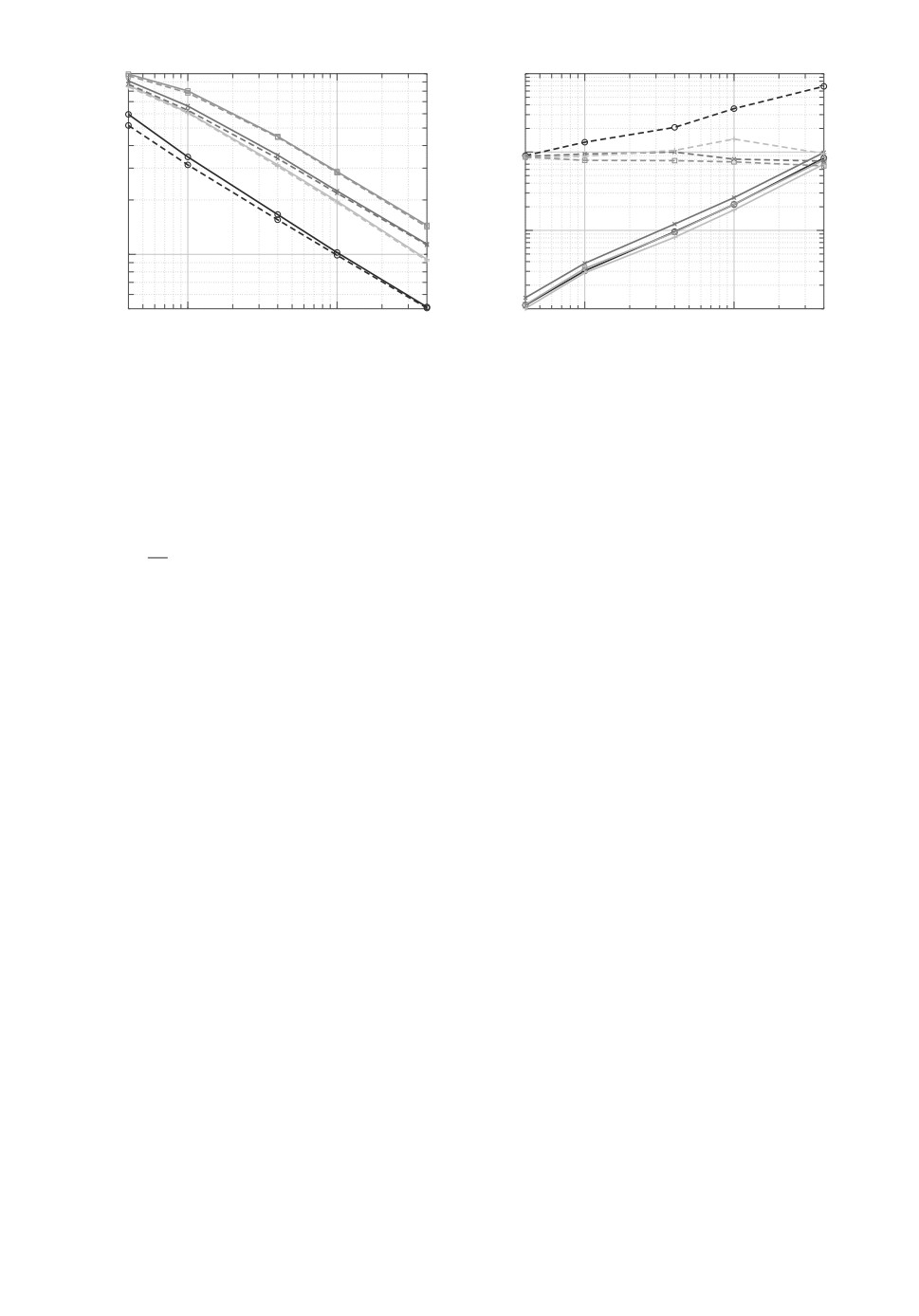
10⁰

10²

10¹

10⁰

10¹

10³

10⁴

10³

10⁴

Cредняя ошибка оценивания

Время вычислений

k(^k) x 2

Рис. 2. Численные результаты: средние ошибки и время вычислений для

СА-оценок (сплошная линия) и ВСА-оценок (пунктирная линия). o — слу-

чай A, × — случай B, + — случай C, □ — случай D.

честву оценивания, ВСА значительно проигрывает ему по времени исполне-

ния. Заметим также, что наблюдаемая в экспериментах зависимость ошибок

восст√новления от размера K выборки соответствует скорости сходимости

O(1/

K), установленной в предложении 2.

4. Случай “одного наблюдения”

Исследуем один специальный случай задачи оценивания, в котором по-

следовательность η₁, . . . , η_K регрессоров в (8) детерминированная. На пер-

вый взгляд, такая формулировка не укладывается в рамки рассматриваемой

здесь общей постановки, в которой регрессоры предполагаются случайны-

ми независимыми, одинаково распределенными, выбираемыми из некоторого

распределения Q. Однако имеется возможность обойти это “противоречие”,

считая, что находимся в ситуации с одним наблюдением, где регрессором яв-

ляется матрица [η₁, . . . , η_K ], а Q — вырожденное одноточечное распределение.

Конкретно, пусть имеем наблюдение

(20)

ω = (η,y) ∈ R^n×mK × R^mK

(m, n, K — известные натуральные числа), а распределение P_x наблюдений,

порожденных сигналом x ∈ Rⁿ, имеет следующую форму:

• η — заданная детерминированная матрица, не зависящая от x;

• метка y случайна, и распределение y, индуцированное распределением P_x,

имеет среднее φ(η^Tx), где φ : R^mK → R^mK — некоторое заданное отобра-

жение.

В качестве информативного примера, связывающего рассматриваемую по-

становку с предыдущей, приведем конструкцию, в которой η = [η₁, . . . , η_K ]

с n × m детерминированными “индивидуальными регрессорами” η_k, y =

= [y₁; . . . ; y_K ], имеющими “индивидуальные метки” y_k ∈ R^m, которые условно

(при данном x) независимы по k и такими, что математические ожидания y_k,

166

индуцированные сигналом x, имеют вид f(ηTkx) для некоторой f : R^m → R^m.

Положим φ([u₁; . . . ; u_K ]) = [f(u₁); . . . ; f(u_K )]. Полученная модель “одного на-

блюдения” представляет собой естественный аналог модели K наблюдений,

которая и рассматривалась до сих пор. Единственная разница состоит в том,

что индивидуальные регрессоры теперь образуют детерминированную после-

довательность, не являясь выборкой некоторой случайной матрицы.

Как и повсюду, в настоящей работе цель — использовать наблюдения (20)

для восстановления неизвестного сигнала x, порождающего, как объяснено

выше, распределение наблюдения. Формально находимся в ситуации K = 1

в исходной задаче восстановления, в которой носителем распределения Q яв-

ляется точка {η}, поэтому можем пользоваться всеми предложенными ранее

конструкциями. Конкретно:

• векторное поле F (z), соответствующее задаче, имеет вид

F (z) = ηφ(η^Tz)

(ранее было E_η∼Q{ηf(η^Tz)}), а векторное поле G(z) = F (z) - F (x), где x —

сигнал, породивший наблюдение (20), имеет вид

G(z) = E(η,y)∼Px {F (z) - ηy}

(ср. с (14)). Как и ранее, восстанавливаемый сигнал является нулем это-

го поля G(·). Обратим внимание на то, что теперь векторное поле F (z)

наблюдаемо, а векторное поле G по-прежнему является математическим

ожиданием (по P_x) наблюдаемого векторного поля:

G(z) = E(η,y)∼Px {ηφ(η^Tz) - ηy},

Gy (z)

ср. с леммой 1.

• предположения A.1-A.2 теперь принимают следующий вид.

A.1^′. Векторное поле φ(·) : R^mK → R^mK непрерывно и монотонно, так

что F (·) также непрерывно и монотонно.

A.2^′. Множество X непусто, компактно и выпукло, а поле F сильно моно-

тонно на X с модулем κ > 0.

Простым достаточным условием выполнения приведенных выше условий

монотонности является положительная определенность матрицы ηη^T в сово-

купности с сильной монотонностью φ на любом ограниченном множестве.

• Предположение A.3 удобно переписать в следующей эквивалентной фор-

ме:

A.3^′. Для надлежащим образом выбранного σ ≥ 0 и всякого x ∈ X спра-

ведливо

{

}

E(η,y)∼Px

∥η[y - φ(η^Tx)]∥²²

≤σ².

167

Теперь в новой постановке ВСА-оценка x(y) является единственным сла-

бым решением ВН VI(G_y, X ), а качество этой оценки дается следующим

утверждением.

Предложение 3. Пусть в рассматриваемой ситуации выполнены

предположения A.1^′-A3^′. Тогда для всякого x ∈ X и любой реализации со-

ответствующих наблюдений (η,y) (20) справедливо

(21)

∥x(y) - x∥₂ ≤ κ-1∥ η[y - φ(η^Tx)]∥2,

Δ(x,y)

откуда также следует

(22)

E(η,y)∼Px {∥x(y) - x∥²²} ≤ σ²/κ².

Доказательство. Пусть x ∈ X — сигнал, породивший наблюдения (20)

и пусть G(z) = F (z) - F (x) — соответствующее векторное поле G. Имеем

Gy(z) = F (z) - ηy = F (z) - F (x) + [F (x) - ηy] =

= G(z) - η[y - φ(η^Tx)] = G(z) - Δ(x, y).

При фиксированном y точка z = x(y) является слабым, а, следовательно, и

сильным (так как G_y(·) непрерывно) решением ВН VI(G_y , X ), что в силу

x ∈ X, влечет

0 ≤ GTy (z)[x - z] = G^T(z)[x - z] - Δ^T(x,y)[x - z],

откуда

-G^T(z)[x - z] ≤ -Δ^T(x,y)[x - z].

Кроме того, G(x) = 0, откуда G^T(x)[x - z] = 0, так что приходим к

[G(x) - G(z)]^T[x - z] ≤ -Δ^T(x, y)[x - z],

откуда также следует

κ∥x - z∥²² ≤ -Δ^T(x, y)[x - z],

поскольку наряду с F поле G сильно монотонно на X с модулем κ, а x, z ∈ X .

Применяя неравенство Коши, приходим к (21).

Пример 1. Пусть m = 1, φ сильно монотонна на всем R^K с модулем

κ_φ > 0, а η в (20) выбирается случайно из “гауссовского ансамбля”, т.е. столб-

цы η_k матрицы η размера n × K — независимые случайные векторы с рас-

пределением N (0, I_n). Пусть шум в наблюдениях также гауссовский:

y = φ(η^Tx) + λξ, ξ ∼ N(0,I_K).

Хорошо известно, что при K/n → ∞ минимальное сингулярное значение

(n × n)-матрицы ηη^T с большой вероятностью имеет порядок по крайней

168

10⁰

10¹

10²

10³

10⁴

10³

10⁴

Cредняя ошибка оценивания

k(^k) x 2

Время вычисления, сек

Рис. 3. Средние ошибки и время вычисления для стандартного уклонения

λ = 1 (пунктир) и λ = 0,1 (сплошная линия).

мере O(1)K, откуда следует, что при K/n ≫ 1 для величины модуля силь-

ной монотонности поля F (·), “как правило”, верно κ ≥ O(1)Kκ_φ. Более того,

в ситуации при K/n → ∞ фробениусова норма матрицы η с большой веро-

√

ятностью имеет порядок не более O(1)

nK. Иными словами, для больших

значений K/n задача восстановления по описанному выше ансамблю, “как

правило”, удовлетворяет предположению 3 с κ = O(1)Kκ_φ и σ² = O(λ²nK).

В результате (22) дает

{

}

λ²n

E(η,y)∼Px

∥x(y) - x∥²²

≤ O(1)

[K ≫ n].

κ2φK

Известно, что для стандартного случая линейной регрессии, где φ(x) = κ_φx,

получающаяся граница почти оптимальна при условии, что X достаточно

велико.

Численная иллюстрация. В условиях рассмотренного выше примера поло-

жим m = 1, n = 100 и примем

φ(u) = arctan[u] := [arctan(u₁); . . . ; arctan(u_K )] : R^K → R^K .

Множество X — единичный шар {x ∈ Rⁿ : ∥x∥₂ ≤ 1}. В конкретном экспери-

менте η выбиралась случайно из гауссовского ансамбля, как описано выше,

сигнал x ∈ X , порождающий наблюдения (20), выбирался случайно, помеха

y-φ(η^Tx) в наблюдении имеет распределение N(0,λ²I_K). Результаты 10 экс-

периментов для каждой комбинации размера выборки и дисперсии λ² шума

представлены на рис. 3.

5. Заключение

Рассмотрен подход к восстановлению сигналов в обобщенных линейных

моделях, основанный на сведении к решению стохастических вариационных

169

неравенств. Рассмотрены условия, при которых соответствующие ВН силь-

но монотонны. Показано, что в этом случае полученные оценки допускают

верхнюю границу на конечном времени для ожидаемой ошибки в ℓ₂-норме,

сходящуюся к нулю со скоростью O(1/K) с ростом числа K наблюдений.

ПРИЛОЖЕНИЕ

Доказательство предложения

Во-первых, заметим, что z_k

являются детерминированными функциями z_k = Z_k(ω^k) “начальных фраг-

ментов” ω^k = {ω_t, 1 ≤ t ≤ k} ∼ P_x × . . . × P_x

последовательности наблюдений

P^kx

ω^K = {ω_k = (η_k,y_k),1 ≤ k ≤ K}. Введем

D_k(ω^k) =

∥Z_k(ω^k) - x∥²² =

∥z_k - x∥²², d_k = E_ωk_∼P k{Dk(ωk)},

где x ∈ X — сигнал, породивший наблюдения (8). Напомним, что метриче-

ская проекция на замкнутое выпуклое множество X является сжимающим

отображением:

∀(z ∈ Rⁿ, u ∈ X ) : ∥Proj_X [z] - u∥₂ ≤ ∥z - u∥₂.

Соответственно, при 1 ≤ k ≤ K имеем

D_k(ω^k) =

∥Proj_X [zk-1 - γ_kGωk (zk-1) - x]∥²² ≤

≤

∥zk-1 - γ_kGωk (zk-1) - x∥²² =

∥zk-1 - x∥²² - γ_kGTω

(zk-1)(zk-1 - x) +

γ2k∥G_ω

(zk-1)∥²².

Беря математическое ожидание относительно ω^k ∼ P^kx от обеих частей полу-

ченного неравенства и учитывая соотношения (13) вместе с тем фактом, что

zk-1 ∈ X, получаем

{

}

(Π.1)

G(zk-1)^T(zk-1 - x)

+ 2γ2kM².

d_k ≤ dk-1 - γ_kEωk-1∼Pk-1x

Поскольку в данном случае поле G сильно монотонно на X с модулем κ > 0,

x является слабым решением ВН VI(G, X ), а zk-1 принимает значения в X ,

то, привлекая (16), получаем, что величина математического ожидания в

(Π.1) равна по крайней мере 2κd_k, и приходим к соотношению

(Π.2)

d_k ≤ (1 - 2κγ_k)dk-1 + 2γ2kM².

Положим

κS

S =

γ_k =

;

κ²

4M²(k + 1)

κ(k + 1)

170

заметим, что γ_k есть в точности длины шагов в (18). Проверим по индукции

по k, что соотношение

d_k ≤ (k + 1)-1S

(∗_k)

выполнено для k = 0, 1, . . . , K.

Основание индукции k = 0. Через D обозначим ∥·∥₂-диаметр множества X ,

и пусть z_± ∈ Z таково, что ∥z₊ -z_-∥₂ = D. Согласно (13) имеем ∥F (z)∥₂ ≤ M

для всех z ∈ X , а сильная монотонность поля G(·) на X влечет

[G(z₊) - G(z_-)]^T[z₊ - z_-] = [F (z₊) - F (z_-)][z₊ - z_-] ≥ κ∥z₊ - z_-∥²² = κD².

По неравенству Коши левая часть последнего неравенства не превосходит

2MD, поэтому

D≤

откуда S ≥ D²/2. С другой стороны, по определению d₀ имеем d₀ ≤ D²/2.

Таким образом, (∗₀) выполнено.

Шаг индукции (∗k-1) ⇒ (∗_k). Предположим теперь, что (∗k-1) выполнено

при некотором k, 1 ≤ k ≤ K, и докажем, что (∗_k) также выполнено. Посколь-

ку κγ_k = (k + 1)-1 ≤ 1/2, то

d_k ≤ dk-1(1 - 2κγ_k) + 2γ2kM² ≤

[по (Π.2)]

≤

(1 - 2κγ_k) + 2γ2kM² =

[по (∗k-1) и вследствие κγ_k ≤ 1/2]

(

)

⁽k-1

≤

k+1

(k + 1)²

k+1

поэтому (∗_k) справедливо. Индукция закончена. Остается заметить, что по

определению величины d_k имеем d_k =¹² E{∥x_k - x∥²²}.

СПИСОК ЛИТЕРАТУРЫ

1. Devroye L., Györfi L., Lugosi G. A Probabilistic Theory of Pattern Recognition

(Stochastic Modelling and Applied Probability No. 31). N.Y.: Springer Sci. &

Business Media, 2013.

2. Nelder J.A., Wedderburn R.W.M. Generalized Linear Models // J. Royal Statist.

Soc., Ser. A (General). 1972. V. 135. No. 3. P. 370-384.

3. McCullagh P., Nelder J.A. Generalized Linear Models. Boca Raton: CRC Press,

1989.

4. Shapiro A., Dentcheva D., Ruszczynski A. Lectures on Stochastic Programming:

Modeling and Theory. 2nd ed. Philadelphia: SIAM, 2014.

5. Robbins H., Monro S. A Stochastic Approximation Method // Ann. Math. Statist.

1951. V. 22. No. 3. P. 400-407.

6. Wolfowitz J. On the Stochastic Approximation Method of Robbins and Monro //

Ann. Math. Statist. 1952. V. 23. No. 3. P. 457-461.

171

Barndorff-Nielsen O. Information and Exponential Families in Statistical Theory.

N.Y.: Wiley, 1978.

Feigin P.D. Conditional Exponential Families and a Representation Theorem for

Asympotic Inference // Ann. Statist. 1981. V. 9. No. 3. P. 597-603.

Rosenblatt F. The Perceptron: A Probabilistic Model for Information Storage and

Organization in the Brain // Psychol. Rev. 1958. V. 65. No. 6. P. 386-408.

10.

Block H.-D. The perceptron: A model for brain functioning. I // Rev. Modern Phys.

1962. V. 134. No. 1. P. 123.

11.

Helmbold D.P., Warmuth M.K. On Weak Learning // J. Comput. Syst. Sci. 1995.

V. 50. No. 3. P. 551-573.

12.

Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Теоретические основы метода

потенциальных функций в задаче об обучении автоматов разделению входных

ситуаций на классы // АиТ. 1964. Т. 25. № 6. С. 917-936.

Aizerman M.A., Braverman E.M., Rozonoer L.I. Theoretical Foundations of the

Potential Function Method in Pattern Recognition Learning // Autom. Remote

Control. 1964. V. 25. No. 6. P. 821-837.

13.

Девятериков И.П., Пропой А.И., Цыпкин Я.З. О рекуррентных алгоритмах

обучения распознаванию образов // АиТ. 1967. № 1. С. 122-132.

Devyaterikov I.P., Propoi A.I., Tsypkin Ya.Z. Iterative Learning Algorithms for

Pattern Recognition // Autom. Remote Control. 1967. V. 28. No. 1. P. 108-117.

14.

Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций

в теории обучения машин. М.: Наука, 1970.

15.

Bousquet O., Boucheron S., Lugosi G. Introduction to Statistical Learning Theory /

Bousquet O., von Luxburg U., Rätsch G. (eds) Advanced Lectures on Machine

Learning. ML 2003. Lecture Notes in Computer Science, vol 3176. Springer, Berlin,

Heidelberg. P. 169-207.

16.

Sridharan K., Shalev-Shwartz S., Srebro N. Fast Rates for Regularized Objectives //

Advances in Neural Information Proc. Syst. No. 21. 2009. P. 1545-1552.

17.

Nemirovski A., Onn S., Rothblum U. Accuracy Ccertificates for Computational

Problems with Convex Structure // Math. Oper. Res. 2010. V. 35. No. 1. P. 52-78.

18.

Bousquet O., Elisseeff A. Stability and Generalization // J. Machine Learning Res.

2002. V. 2. P. 499-526.

19.

Rakhlin A., Mukherjee S., Poggio T. Stability Results in Learning Theory // Anal.

Appl. 2005. V. 3. No. 4. P. 397-417.

20.

Shalev-Shwartz S., Shamir O., Srebro N., Sridharan K. Stochastic Convex

Optimization // Conf. Learning Theory. 2009.

21.

Kiefer J., Wolfowitz J. Stochastic Estimation of the Maximum of a Regression

Function // Ann. Mat. Statist. 1952. V. 23. No. 3. P. 462-466.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 19.07.2018

После доработки 12.09.2018

Принята к публикации 08.11.2019

172