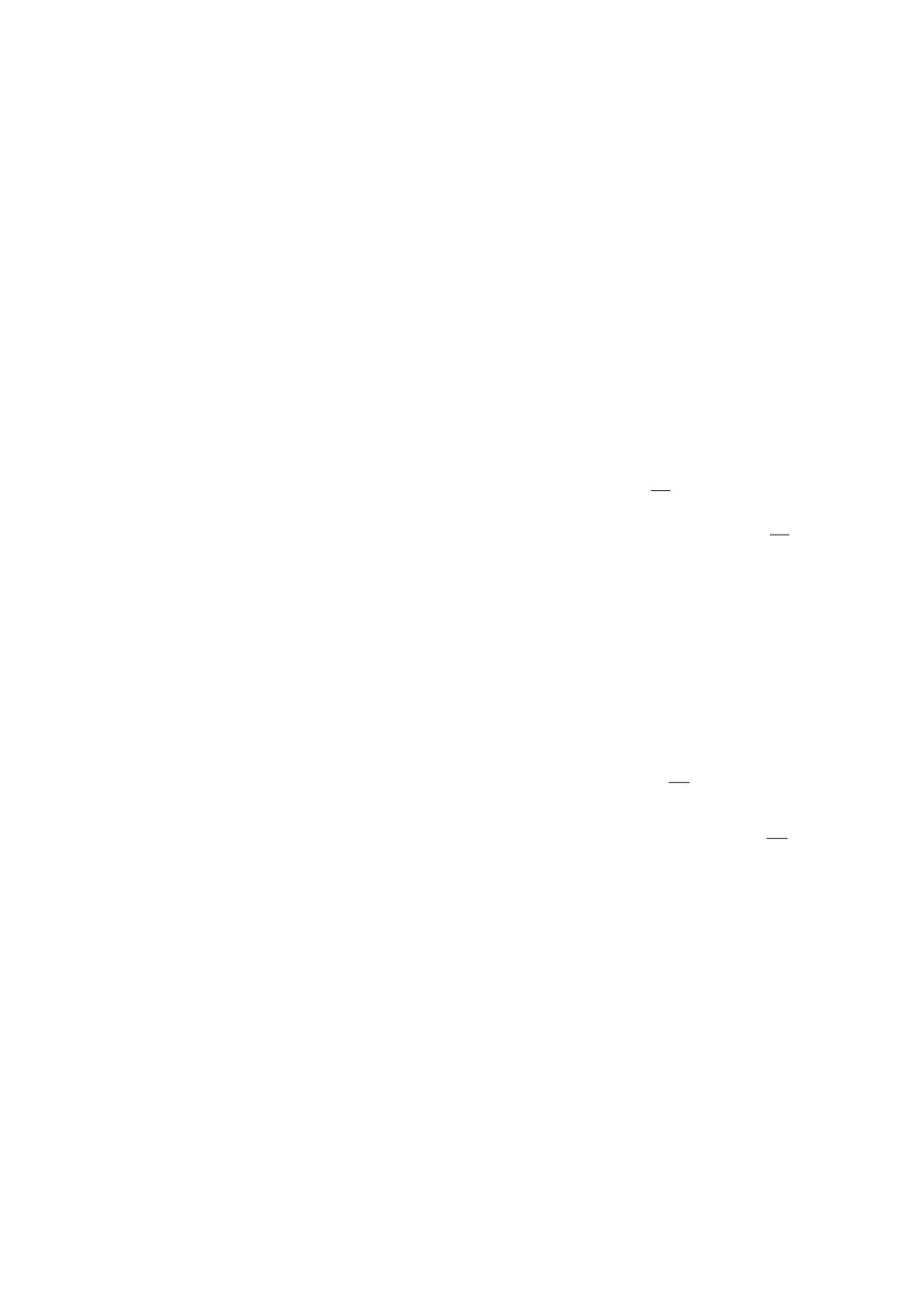Автоматика и телемеханика, № 11, 2019
Нелинейные системы
© 2019 г. А.И. МАЛИКОВ, д-р физ.-мат. наук (a_i_malikov@mail.ru)
(Казанский национальный исследовательский технический
университет им. А.Н. Туполева - КАИ,
Институт механики и машиностроения - обособленное структурное
подразделение ФИЦ “Казанский научный центр” РАН)
ОЦЕНИВАНИЕ СОСТОЯНИЯ И СТАБИЛИЗАЦИЯ
ДИСКРЕТНЫХ СИСТЕМ С НЕОПРЕДЕЛЕННЫМИ
НЕЛИНЕЙНОСТЯМИ И ВОЗМУЩЕНИЯМИ1
Рассматриваются неавтономные дискретные системы управления с
неопределенными нелинейностями, подверженные воздействию ограни-
ченных внешних возмущений. На основе метода матричных систем срав-
нения и техники разностных линейных матричных неравенств развивает-
ся подход к задачам оценивания состояния, ограниченности относитель-
но заданных множеств, подавления начальных отклонений и неопреде-
ленных возмущений с помощью линейной обратной связи по состоянию.
Предлагается способ синтеза управления с переменными коэффициента-
ми, обеспечивающий гарантированный переход из одного заданного эл-
липсоида в другой при любых возмущениях, ограниченных по L∞ норме.
Ключевые слова: неавтономные дискретные системы с липшицевыми
нелинейностями, неопределенные возмущения, оценивание состояния,
ограниченность на конечном интервале, синтез управления.
DOI: 10.1134/S0005231019110035
1. Введение
Для оценивания вектора фазового состояния динамических систем широко
используются развитые в [1-6] методы эллипсоидов, которые дают локально-
оптимальные или минимаксные гарантированные эллипсоидальные оценки
множества процессов с учетом неопределенных начальных отклонений, внеш-
них возмущений и параметрических изменений. Эти методы позволяют най-
ти внешние или внутренние аппроксимирующие эллипсоиды, которые яв-
ляются оптимальными относительно некоторого заданного критерия (след,
объем, диаметр и т.д.). Применение этих методов позволяет решать задачи
синтеза управления, обеспечивающего подавление произвольных ограничен-
ных внешних возмущений, с использованием техники линейных матричных
1 Работа выполнена при частичной поддержке Российского фонда фундаментальных
исследований (проект 18-08-01045a) (разделы 2-4) и Программы фундаментальных иссле-
дований РАН № 7 “Новые разработки в перспективных направлениях энергетики, механики
и робототехники” (раздел 5, 6).
59
неравенств (ЛМН) [7]. Методом инвариантных эллипсоидов [7-9] синтез оп-
тимального (или субоптимального) регулятора сводится к поиску наимень-
шего инвариантного эллипсоида замкнутой системы. Эти методы наиболее
эффективны для линейных стационарных систем управления. В [10, 11] тех-
ника ЛМН использовалась уже в целях робастной стабилизации систем с
неопределенной нелинейностью, однако без учета воздействия внешних воз-
мущений. В [12, 13] этот подход применен для нахождения инвариантных
эллипсоидов и синтеза линейных регуляторов (в том числе робастных) по
состоянию для одного класса нелинейных автономных систем (с липшицевы-
ми и квази-липшицевыми нелинейностями) при учете неопределенных огра-
ниченных внешних возмущений. В [14-18] метод матричных систем сравне-
ния (МСС), предложенный в [19] для анализа устойчивости регулируемых
систем типа Лурье, развит для анализа динамики и оценивания состояния
нелинейных регулируемых систем с неопределенными возмущениями, пара-
метрическими и структурными изменениями. В [20] дано обоснование мето-
да матричных систем сравнения для оценивания состояния дискретных мо-
делей систем управления, доказывается теорема о матричных разностных
неравенствах. Изучаются свойства матричных разностных уравнений с пра-
вой частью, монотонной относительно конуса неотрицательно определенных
матриц. Предлагаются способы построения разностных матричных систем
сравнения и процедуры получения эллипсоидальных оценок множества дис-
кретных процессов.
Дискретные системы, представленные разностными уравнениями, не яв-
ляются аналогами непрерывных систем и имеют свои особенности, которые
вносят специфику в методы анализа и синтеза. Эти особенности отмечались
рядом авторов. В частности, в [21] отмечено, что существование дискретно-
го процесса в прямом времени не означает существование процесса в обрат-
ном времени, а определение сопряженной системы должно быть несколько
модифицировано по сравнению с непрерывным случаем, чтобы установить
дуальную связь между управляемостью и наблюдаемостью. В [22] говорится,
что сразу же после открытия и доказательства принципа максимума Понт-
рягина были сделаны попытки нахождения “дискретной” версии принципа
максимума по аналогии с непрерывным, которые, как оказалось, не давали в
общем случае ни необходимых, ни достаточных условий оптимальности. В ре-
зультате потребовалось уточнять и доказывать принцип максимума, а также
обосновывать метод динамического программирования непосредственно для
дискретных систем. Поэтому неудивительно, что несмотря на имеющиеся ана-
логии в публикациях разработка и обоснование методов анализа, оценивания
состояния и синтеза управления, производятся как для непрерывных, так и
для дискретных систем.
Для стабилизации неавтономных дискретных систем обычно используют-
ся законы управления с изменяющимися во времени коэффициентами. В пуб-
ликациях имеются примеры использования законов управления с зависимы-
ми от времени коэффициентами для линейных автономных систем, например
линейный квадратичный регулятор на конечном интервале времени [23, 24].
Для определения коэффициентов регулятора на основе метода динамическо-
го программирования требуется численное решение матричного разностного
60
уравнения Риккати в обратном времени [23], что представляет определенные
трудности, в частности предполагает наличие информации о параметрах мо-
дели в будущем времени. Предпринимались попытки найти способы синте-
за регуляторов, коэффициенты которого определяются на основе численного
решения матричного уравнения в прямом времени. В [25] был предложен
метод эвристического динамического программирования на основе последо-
вательного приближения функции Беллмана для решения задачи оптималь-
ного управления дискретных систем в прямом времени. В дальнейшем в ряде
публикаций [26-28 и др.] для аппроксимации функции Беллмана использова-
лись нейронные сети с итерационным обучением и улучшением управления
в реальном времени даже без использования математической модели. В то
же время в последние годы для линейных неавтономных систем активно раз-
виваются методы анализа ограниченности на конечном интервале времени и
синтеза управления, основанные на технике разностных линейных матрич-
ных уравнений и неравенств [29].
В данной статье на основе метода матричных систем сравнения [14-18, 20]
и техники разностных линейных матричных неравенств (РЛМН) [29] пред-
лагаются способы оценивания состояния, анализа устойчивости и ограничен-
ности относительно заданных множеств на конечном интервале времени, на-
хождения инвариантных эллипсоидов и синтеза управления в виде обрат-
ной связи по состоянию (с зависимыми от времени коэффициентами) как
для автономных, так и неавтономных нелинейных дискретных систем. По-
лучены разностное матричное уравнение (РМУ) и РЛМН, решения которых
определяют эволюционирующие во времени инвариантные эллипсоиды для
процессов исходной системы при любых нелинейностях, удовлетворяющих
заданному ограничению, и любых внешних возмущениях, ограниченных по
норме. Условия устойчивости и ограниченности относительно заданных мно-
жеств, определяющих качество функционирования исходной системы, пред-
ставляются в виде ограничений на частные решения РМУ или РЛМН на
всем рассматриваемом интервале времени. Задача синтеза сводится к чис-
ленному решению РЛМН с оптимизацией в каждый момент времени следа
матрицы инвариантного эллипсоида, ограничивающего состояния или выход.
Отметим, что аналогичные задачи для непрерывных неавтономных систем с
липшицевыми нелинейностями и неопределенными возмущениями были рас-
смотрены в [30].
В автономном случае оценки предельного множества в виде инвариантно-
го эллипсоида могут быть получены на основе численного решения РЛМН,
численного итерирования РМУ или численного решения алгебраических мат-
ричных уравнений, являющихся уравнениями равновесия для РМУ. При этом
от РЛМН можно перейти к алгебраическим ЛМН, которые оказываются ана-
логичными ЛМН, полученным для автономного случая методом инвариант-
ных эллипсоидов [12]. На простом примере демонстрируются возможности и
эффективность предлагаемого подхода для решения указанных задач.
Отметим, что задачи нахождения эллипсоида, ограничивающего при
t → ∞ состояния или выход автономной системы с липшицевыми и квази-
липшицевыми нелинейностями и неопределенными возмущениями, были ре-
шены в [12, 13], где также предложены способы синтеза управления с посто-
61
янными коэффициентами из условия минимальности по критерию следа пре-
дельного (при t → ∞) инвариантного эллипсоида. Однако эти методы имеют
существенный недостаток, поскольку не могут обеспечить требуемое огра-
ничение на управление при начальных отклонениях, выходящих за границу
полученного предельного инвариантного эллипсоида.
Развиваемый в статье подход будет использовать квадратичную функцию
Ляпунова с переменными параметрами, которая представляет в простран-
стве состояний последовательность эллипсоидов. В случае обратной связи
по состоянию эти эллипсоиды также будут связаны с состоянием системы.
Для каждого такого эллипсоида определяются коэффициенты усиления с
учетом ограничения на управление. При любом состоянии системы из это-
го эллипсоида управление с коэффициентами усиления, определенными для
этого эллипсоида, будет удовлетворять заданному ограничению. В результа-
те появляется возможность планировать изменение коэффициентов усиления
для обеспечения лучшего качества управления. Именно в этом и заключает-
ся особенность представляемого в статье подхода. При больших отклонениях
вектора состояния требуются меньшие коэффициенты усиления управления,
а при малых отклонениях можно использовать более высокие коэффициенты
усиления. Следовательно, выбор коэффициента усиления будет зависеть от
текущего состояния системы. Для этого из имеющейся последовательности
определяется минимальный эллипсоид, содержащий вектор состояния систе-
мы, и будет выбираться управление, соответствующее этому эллипсоиду.
2. Системы с неопределенными нелинейностями
и ограниченными возмущениями
Рассматривается динамическая система с дискретным временем, представ-
ленная следующей моделью в пространстве состояний:
x(t + 1) = A(t)x(t) + D(t)w(t) + Φ(t)ϕ(t, x(t)),
(1)
z(t) = C(t)x(t),
где t ∈ T - время, x ∈ Rn - вектор состояния, w(t) ∈ W ⊂ Rr - внешнее воз-
мущение, z ∈ Rl - вектор управляемого выхода, A(t) ∈ Rn×n, D(t) ∈ Rn×r,
Φ(t) ∈ Rn×q, C(t) ∈ Rq×n - известные матрицы с ограниченными элементами
при всех t ∈ T . Интервал времени T может быть конечным T = [t0, t0 + 1,
...,t1], t1 - заданная константа, или бесконечным T = [t0,t0 + 1,...,∞).
Нелинейная векторная функция ϕ(t, x) удовлетворяет ограничению, за-
данному в виде
(2)
∥ϕ(t, x)∥2 ≤ μ0 + μ1 ∥Cf (t)x∥2 ∀t ∈ T, x ∈ Rn,
где Cf (t) ∈ Rq×n - известная матрица с ограниченными элементами при всех
t ∈ T. Здесь и далее ∥·∥ означает евклидову норму вектора, μ0, μ1 ≥ 0 - за-
данные константы.
Предположим, что неопределенные возмущения являются ограниченными
в каждый момент времени:
{
}
(3)
W = w(t) ∈ Rr : ∥w(t)∥2 ≤ 1
∀t ∈ T
62
Отметим, что автономные системы вида (1) с неопределенными огра-
ниченными возмущениями и нелинейностями, удовлетворяющими ограни-
чению (2), при Cf = I были рассмотрены в [12], где было сказано, что
при μ0 = 0 ограничение (2) охватывает секторные нелинейности и локально-
липшицевые, заданные так, что они равны нулю в начале координат.
3. Задача оценивания состояния
Пусть в начальный момент времени t0 состояние x(t0) = x0 системы явля-
ется неопределенным и известно, что оно принадлежит эллипсоиду
{
}
(4)
E(Q0) =
x∈Rn :xTQ-10x≤1
,
где Q0 - заданная положительно определенная матрица.
Предполагается, что матрица C(t) является матрицей полного ранга
строк.
Требуется на заданном интервале времени T получить эллипсоидальную
оценку множества состояний для процессов системы (1), начинающихся из
заданного эллипсоида E(Q0) (4), при нелинейностях, удовлетворяющих (2),
и неопределенных возмущениях из (3).
Оценка вектора состояния будет находиться в виде эволюционирующего
эллипсоида, инвариантного для процессов системы (1).
Напомним, что инвариантным эллипсоидом для динамической системы
называется эллипсоид
{
}
(5)
E(Q(t)) =
x ∈ Rn : xTQ-1(t)x ≤ 1
,
Q(t) > 0,
обладающий следующим свойством: любая траектория системы x(t, t0, x0),
исходящая из точки x(t0) = x0 ∈ E(Q(t0) = Q0), в любой момент времени
t ∈ T принадлежит этому эллипсоиду, т.е. x(t,t0,x0) ∈ E(Q(t)).
Здесь положительно определенная матричная функция Q(t) определяет
последовательность эллипсоидов для моментов времени t ∈ T , которая в со-
вокупности и представляет эволюционирующий эллипсоид.
Теорема 1. Эллипсоид E(Q(t)), где Q(t) = Q(t,t0,Q0) есть положи-
тельно определенное решение разностного матричного уравнения
[
]-1
μ1
Q(t + 1) = A(t)Q(t) αQ(t) -
Q(t)CTf(t)Cf (t)Q(t)
Q(t)AT(t) +
β
(6)
1
+
D(t)DT(t) + βΦ(t)ΦT(t)
1-α-μ0
β
63
или разностного линейного матричного неравенства
⎡
⎤
Q(t + 1) - βΦ(t)ΦT(t) A(t)Q(t)
D(t)
0
0
⎢
⎥
⎢
Q(t)AT(t)
αQ(t)
0
Q(t)CTf(t)
0
⎥
⎢
⎥
⎢
⎥
⎢
DT(t)
0
(1 - α)I
0
I
⎥
⎢
⎥
(7)
≥ 0,
⎢
⎥
⎢
β
⎥
⎢
0
Cf (t)Q(t)
0
I
0
⎥
⎢
μ1
⎥
⎣
⎦
β
0
0
I
0
I
μ0
является инвариантным для траекторий системы (1), стартующих из на-
чального эллипсоида E(Q0).
Доказательство теоремы 1 дано в Приложении 1.
Из теоремы 1 следует, что положительно определенное решение Q(t) =
= Q(t,t0,Q0), если оно существует при некоторых β > 0 и 0 < α < 1, будет
определять инвариантный эллипсоид E(Q(t)), ограничивающий состояния
исходной системы (1). Каждый такой эллипсоид будет являться приближе-
нием внешней оценки множества достижимости, т.е множества, содержаще-
го все траектории x(t, t0, x0) системы (1) в момент времени t ∈ T при всех
x0 ∈ E(Q0), неопределенных внешних возмущениях w ∈ W и нелинейностях
из (2). Как замечено в [3], более точным приближением внешней оценки мно-
жества достижимости будет являться пересечение совокупности эллипсои-
дов, полученных при различных значениях α и β.
Из доказательства теоремы 1 следует, что если при некоторых α и β най-
дется положительно определенное решение Q(t) = Q(t, t0, Q0) уравнения (6),
то оно также будет являться решением РЛМН (7) при тех же α и β. Суще-
ствование в (6) обратной матрицы на каждой итерации можно обеспечить
подходящим выбором значения параметра β.
Следует отметить, что в автономной линейной системе инвариантный эл-
липсоид с постоянной матрицей Q∗, определяемой на основе решения алгеб-
раического уравнения Ляпунова (или разрешимости ЛМН) будет являться
притягивающим, т.е. множеством, к которому будут стремиться все реше-
ния с любыми начальными данными и при внешних возмущениях, удовлет-
воряющих (3). В нелинейной автономной системе инвариантный эллипсоид
будет притягивающим только для решений с начальными данными, принад-
лежащими области притяжения некоторого предельного множества, которое
в свою очередь будет принадлежать указанному инвариантному эллипсоиду.
Для нахождения оценок множества состояний исходной нелинейной систе-
мы в текущие моменты времени для траекторий, стартующих из начального
эллипсоида, и для построения оценок области притяжения в автономном слу-
чае будем использовать РМУ (6) и РЛМН (7).
Теорема 2. Пусть Q(t) = Q(t,t0,Q0)
- решение при Q(t0) = Q0 > 0
РМУ (6) (или РЛМН (7)) на интервале T . Тогда для решений исходной
системы (1) с начальными данными x(t0) = x0 ∈ E(Q0), нелинейностями
64
из (2) и неопределенными возмущениями из (3) имеют место оценки при
всех t ∈ T :
1) x(t, t0, x0) ∈ E(Q(t));
2) x(t, t0, x0)xT(t, t0, x0) ≤ Q(t, t0, Q0) (неравенство относительно конуса
неотрицательно определенных матриц);
3) xT(t, t0, x0)x(t, t0, x0) ≤ trace(Q(t, t0, Q0));
4) x2i(t, t0, x0) ≤ Qii(t, t0, Q0), i = 1, . . . , n;
5) zT(t)z(t) ≤ trace(CTQ(t, t0, Q0)C).
Доказательство теоремы 2 приведено в Приложении.
Определение 1. Матричная функция F(t,Q) называется неубываю-
щей относительно Q, если для любых Q1, Q2 ∈ Rn×n, таких что Q2 - Q1 ≥
≥ 0, следует, что F (t, Q2) - F (t, Q1) ≥ 0 (или аналогично из условия
yT(Q2 - Q1)y ≥ 0 следует yT[F(t,Q2) - F(t,Q1)]y ≥ 0 для всех y ∈ Rn и
t ∈ T).
Лемма 1. Система разностных уравнений (6) является матричной си-
стемой сравнения для системы (1).
Доказательство леммы 1 дано в Приложении.
В [21] доказана теорема о матричных разностных неравенствах и уста-
новлены следующие свойства матричных разностных уравнений с монотон-
но неубывающей правой частью: существование неотрицательно определен-
ных решений, монотонность решений по начальным данным, инвариант-
ность некоторых множеств. Для получения оценок множества решений в виде
невырожденного эволюционирующего эллипсоида интерес представляет су-
ществование положительно определенного решения МСС (6).
Лемма 2. Предположим, что матрица A является неособой или мат-
1
рица
D(t)DT(t) + βΦ(t)ΦT(t) - положительно определенная, и для
1-α-μ0/β
любой положительно определенной матрицы Q, удовлетворяющей неравен-
ству 0 < Q < αI, где α > 0 - заданное число, найдется число β > 0, такое
Cf ≤1αI. Тогда если существует ре-
что имеет место неравенствоμ1β
f
шение МСС (6) с начальным условием 0 < Q(t0) = Q0 < αI на некотором
интервале T, то для него будет выполнено неравенство Q(t,t0,Q0) > 0 для
всех t ∈ T .
Доказательство леммы 2 дано в Приложении.
В дальнейшем будем находить минимальные (в некотором смысле) инва-
риантные эллипсоиды, содержащие траектории или выход z(t) рассматривае-
мой системы.
На основе теоремы 1 задача получения верхней оценки множества траек-
торий системы (1), стартующих из начального эллипсоида, сводится к сле-
дующей задаче оптимизации trace(Q(t1)) → min при ограничениях Q(t) > 0,
Q(t0) ≥ Q0, β > 0,
0 < α < 1 и (7), записанных при t0 + 1,t0 + 2,...,t1.
При фиксированном α данная задача относительно совокупности матриц
Q(t0 + 1), Q(t0 + 2), . . . , Q(t1) и параметра β(t) относится к классу задач по-
луопределенного программирования, для которых имеются эффективные ре-
шатели.
65
Для автономной системы может быть получена верхняя оценка предель-
ного множества в виде минимального инвариантного эллипсоида путем ре-
шения задачи оптимизации trace(Q) → min при ограничениях Q > 0, β > 0,
0 < α < 1 и (7) относительно матрицы Q (Q = Q(t) = Q(t + 1), что соответ-
ствует случаю, рассмотренному в теореме 3 из [12]).
Также может быть получена внутренняя оценка области начальных дан-
ных, из которой траектории системы (1) будут стремиться к заданному эл-
липсоиду E(QT ), где QT > 0 - известная матрица. Для этого следует решить
задачу trace(Q(t0)) → max при ограничениях Q(t1) ≤ QT , β > 0, 0 < α < 1
и неравенствах (7), записанных при t0 + 1, t0 + 2, . . . , t1. При фиксирован-
ном α данная задача относительно совокупности матриц Q(t0), Q(t0 + 1),
Q(t0 + 2), . . . , Q(t1) и параметра β(t) также относится к классу задач полу-
определенного программирования.
Для оценки области начальных данных в виде эллипсоида с максималь-
ным расстоянием до его границы по заданному направлению в фазовом про-
странстве выбирается направление, определяемое вектором c единичной дли-
ны, и решается задача γ → max при тех же ограничениях, как в предыдущей
задаче, и дополнительно обеспечивая принадлежность точки γc начальному
эллипсоиду:
(
)
1
γcT
≥ 0.
γc Q(t0)
4. Задача об ограниченности (устойчивости)
относительно заданных множеств
Пусть заданы в виде эллипсоидов E(R0) = {x ∈ Rn : xTR-10x ≤ 1}, E(R(t)) =
= {x ∈ Rn : xTR-1(t)x ≤ 1}, (R0, R(t) - известные симметрические положи-
тельно определенные матрицы) - соответственно множество начальных со-
стояний и множество допустимых состояний в моменты времени t ∈ T .
Определение 2. Будем говорить, что система (1) обладает на T свой-
ством ограниченности относительно заданных множеств [E(R0),E(R(t))]
(при отсутствии неопределенных внешних возмущений
— свойством
устойчивости относительно заданных множеств [E(R0),E(R(t))]), если
для всех x0 ∈ E(R0) существуют на T решения x(t) = x(t, t0, x0) систе-
мы (1) с начальными данными x(t0) = x0, для которых имеет место
x(t, t0, x0) ∈ E(R(t)) при всех t ∈ T , всех нелинейностях из (2) и возмущени-
ях из (3) (соответственно x(t, t0, x0) ∈ E(R(t)) при всех t ∈ T и всех нели-
нейностях из (2), где μ0 = 0).
Отметим, что в данном здесь определении, в отличие от общепринятых
определений абсолютной устойчивости и ограниченности, указываются кон-
кретные множества начальных данных и множества, которым должны при-
надлежать траектории системы с этими начальными данными. В этом от-
ношении определения аналогичны определениям устойчивости и ограничен-
ности на конечном интервале времени, активно изучаемые в последние го-
ды [21]. В рассматриваемом случае интервал времени может быть как конеч-
ным, так и бесконечным.
66
Теорема 3. Система (1) обладает на T свойством ограниченности
относительно заданных множеств
[E(R0), E(R(t))] (при отсутствии
внешних возмущений и μ0 = 0 — свойством устойчивости относительно
[E(R0), E(R(t))]) если существует решение Q(t) = Q(t, t0, Q0) РМУ (6) (или
РЛМН (7)) с начальными данными Q0 ≥ R0, удовлетворяющее неравенству
Q(t) ≤ R(t) для всех t ∈ T .
Доказательство теоремы 3 представлено в Приложении.
5. Задача синтеза управления
Рассмотрим дискретную систему с управлением:
x(t + 1) = A(t)x + B(t)u + D(t)w + Φ(t)ϕ(t, x, u), x(t0) = x0,
(8)
z = C(t)x,
где x ∈ Rn - вектор состояния, w(t) ∈ W - внешнее возмущение, удовлетво-
ряющее ограничению (3), u ∈ Rm - управление, z ∈ Rl - вектор управляемого
выхода. Нелинейная векторная функция ϕ(t, x, u) ∈ Rq удовлетворяет огра-
ничению
(9)
∥ϕ(t, x, u)∥2 ≤ μ0 + μ1 ∥Cf (t)x(t) + Bf (t)u(t)∥2 ∀t ∈ T, x ∈ Rn, u ∈ Rm,
где A(t) ∈ Rn×n, B(t) ∈ Rn×m, D(t) ∈ Rn×r, Φ(t) ∈ Rn×q, C(t) ∈ Rl×n, Cf (t) ∈
∈ Rq×n, Bf(t) ∈ Rq×m - известные матрицы с ограниченными элементами при
всех t ∈ T . Предполагается, что пара (A, B) управляема, пара (A, C) наблю-
даема, а управление должно удовлетворять ограничению
{
}
(10)
u(t) ∈
u : uTZ-1(t)u ≤ 1
,
t∈T,
где Z(t) - заданная симметрическая положительно определенная (m × m)-
матрица.
Задача состоит в нахождении управления в виде обратной связи по состоя-
нию
(11)
u = K(t)x :
1) стабилизирующего замкнутую систему и подавляющего воздействие на-
чальных отклонений и внешних возмущений в смысле минимальности огра-
ничивающего эллипсоида для выхода z;
2) обеспечивающего ограниченность замкнутой системы.
Задача синтеза сводится к оптимизации критерия при ограничениях в виде
разностных линейных матричных неравенств. В качестве критерия берется
след матрицы, определяющий размер инвариантного ограничивающего со-
стояния или выход эллипсоида [12].
Теорема 4. Решение Q∗(t) = Q∗(t,t0,Q0) > 0, Y ∗(t) задачи
trace[CQCT] → min
67
при ограничениях
⎡
⎤
Q(t + 1) - βΦΦT
AQ(t) + BY
D
0
0
⎢
⎥
⎢Q(t)AT + YTBT
αQ(t)
0
Q(t)CTf + YTBTf
0
⎥
⎢
⎥
⎢
⎥
⎢
DT
0
(1 - α)I
0
I
⎥
(12)
⎢
⎥≥ 0,
⎢
⎥
⎢
β
⎥
⎢
0
CfQ(t)+BfY
0
I
0
⎥
⎢
μ1
⎥
⎣
β
⎦
0
0
I
0
I
μ0
[
]
Z Y
(13)
≥ 0,
YT Q
где минимизация проводится по матричным переменным Q(t) =
= QT(t) ∈ Rn×n, Y (t) ∈ Rm×n, скалярной переменной β > 0 и скалярно-
му параметру 0 < α < 1, определяет при каждом t ∈ T матрицу Q∗(t)
ограничивающего эллипсоида для вектора состояния x(t), матрицу CQ∗CT
ограничивающего эллипсоида для вектора выхода z(t) системы (8) и за-
висимую от времени матрицу коэффициентов регулятора по состоянию
K∗(t) = Y∗(t)Q∗-1(t). Если, кроме того, матрица Q∗(t) удовлетворяет
дополнительно ограничениям Q∗(t0) ≥ R0 и Q∗(t) ≤ R(t) для всех t ∈ T, где
R0 и R(t) - заданные положительно определенные симметрические матри-
цы, то искомое управление (11) обеспечивает ограниченность замкнутой
системы относительно множеств [E(R0),E(R(t))].
Доказательство теоремы 4 представлено в Приложении.
Замечание 1. В случае автономной системы в задаче оптимизации с
ограничениями (12), (13) все матрицы могут быть постоянными, что соответ-
ствует применению метода инвариантных эллипсоидов (см. теорему 4 из [12]).
Замечание 2. Также к задаче оптимизации с ЛМН может быть сведен
синтез управления из условия получения максимальной по критерию следа
матрицы эллипсоида допустимых начальных отклонений или максимального
по заданному направлению расстояния до его границы.
Численное решение задачи оптимизации на всем рассматриваемом интер-
вале может производиться итерационно на каждом шаге. В результате ре-
шения задачи оптимизации на первом шаге находятся матрицы Q(t0) ≥ R0,
Q(t0 + 1) > 0 и Y (t0), удовлетворяющие ограничениям (12), (13). Данная
задача при каждом фиксированном α относится к классу задач полу-
определенного программирования и может быть эффективно решена суще-
ствующими методами. Решая последовательность задач оптимизации при
варьировании параметра 0 < α < 1, выбирается значение α, при котором
trace[CQ(t0 + 1)CT] будет наименьшим. В качестве решения на первой итера-
ции принимаются матрицы Q0 = Q(t0) и K0 = Y (t0)Q-10. Аналогичным обра-
зом на второй итерации находятся матрицы Q1 ≥ Q(t0 + 1), K1 = Y (t1)Q-11 и
матрица Q(t0 + 2) > 0 с минимальным trace[CQ(t0 + 2)CT]. Итерации завер-
шаются на шаге t1.
68
С целью определения коэффициентов регуляторов, обеспечивающих более
эффективное подавление начальных отклонений и неопределенностей, следу-
ет при численном решении задачи оптимизации на всем интервале использо-
вать многошаговые итерации.
В частности, на k-й двухшаговой итерации решается следующая задача
оптимизации: trace(Q(t0 + 2k)) → min при ограничениях Q(t0 + 2k - 1) > 0,
Q(t0 + 2k) > 0, βk > 0, 0 < αk < 1 и ЛМН (12), (13), записанных при tk =
= t0 + 2k - 2 и tk1 = tk + 1 = t0 + 2k - 1 (k = 1,2,... ,t1/2):
trace[CQ(tk + 2)CT] → min при ограничениях
Qk ≥ Q(tk), Q(tk + 1) > 0, Q(tk + 2) > 0,
⎡
⎤
Q(tk +1)-βkΦ(tk)ΦT(tk) A(tk)Qk +B(tk)Y (tk) D(tk)
0
0
⎢
⎥
⎢
QkAT(tk)+YT(tk)BT(tk)
αkQk
0
QkCTf(tk)+YT(tk)BTf(tk)
0
⎥
⎢
⎥
⎢
⎥
⎢
DT(tk)
0
(1-αk)I
0
I
⎥
⎢
⎥
≥ 0,
⎢
⎥
⎢
⎥
0
Cf (tk)Qk +Bf (tk)Y (tk)
0
βk I
0
⎢
⎥
μ1
⎣
⎦
0
0
I
0
βk I
μ0
⎡
⎤
Q(tk + 2)-
A(tk1)Q(tk1)+
D(tk1)
0
0
⎢
−βkΦ(tk1)ΦT(tk1)
+B(tk1)Y (tk1)
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
Q(tk1)AT(tk1)+
Q(tk1)CTf(tk1)+
⎥
⎢
αkQ(tk1)
0
0
⎥
+YT(tk1)BT(tk1)
+YT(tk1)BTf(tk1)
⎢
⎥
⎢
⎥
⎢
⎥
≥ 0,
⎢
DT(tk1)
0
(1 - αk)I
0
I
⎥
⎢
⎥
⎢
⎥
⎢
βk
⎥
⎢
0
Cf (tk1)Q(tk1)+Bf(tk1)Y (tk1)
0
I
0
⎥
⎢
⎥
μ1
⎢
⎥
⎣
⎦
0
0
I
0
βk I
μ0
[
]
[
]
Z(tk) Y (tk)
Z(tk1) Y (tk1)
≥ 0,
≥ 0.
YT(tk) Q(tk)
YT(tk1) Q(tk1)
6. Обеспечение гарантированного перехода
из заданной области начальных данных в другую
Применение метода инвариантных эллипсоидов [12] позволяет синтези-
ровать регулятор из условия получения минимального предельного инвари-
антного эллипсоида, ограничивающего состояние или выход при t → ∞, или
регулятор из условия получения максимального инвариантного эллипсоида,
ограничивающего область начальных данных, из которой процессы будут
сходиться к некоторому предельному множеству, принадлежащему этому эл-
липсоиду. При учете нелинейностей и ограничений на управление (10) коэф-
фициенты усиления этих регуляторов будут различными. При этом первый
69
регулятор сможет обеспечить оптимальное подавление неопределенностей из
области начальных данных, меньшей, чем второй регулятор. В то же время
минимальный предельный инвариантный эллипсоид системы со вторым ре-
гулятором может оказаться значительно большим, чем у системы с первым
регулятором. Дополнительный учет ограничения на область начальных дан-
ных при синтезе приводит к получению третьего регулятора с промежуточ-
ным между первым и вторым регулятором качеством. Таким образом, что-
бы обеспечить (например, как с помощью первого регулятора) наибольшее
подавление начальных отклонений и неопределенных возмущений из макси-
мально возможной области начальных данных (как с помощью второго регу-
лятора) потребуется организовать изменение коэффициентов регулятора для
рассматриваемой автономной системы. Для этого будем использовать способ
синтеза регулятора из теоремы 4.
Итак, пусть заданы в виде эллипсоидов E(R0) = {x ∈ Rn : xTR-10x ≤ 1},
E(RT ) = {x ∈ Rn : xTR-1Tx ≤ 1} - область начальных данных и допустимая
область для состояний в заданный момент времени t = t1. Предполагается,
что E(RT ) ⊆ E(R0). Требуется синтезировать регулятор с переменными ко-
эффициентами усиления, который бы обеспечил гарантированный переход из
начального множества E(R0) в заданное конечное множество E(RT ).
Если найдется на интервале T решение Q∗(t) > 0, Y∗(t) задачи оптимиза-
ции trace[Q(t1)] → min при ограничениях (12), (13) с граничными условиями
Q(t0) ≥ R0, Q(t1) ≤ RT , то согласно теореме 4 регулятор (11) с переменными
коэффициентами усиления K∗(t) = Y∗(t)Q∗-1(t) обеспечит гарантированный
переход состояния системы (8) из начального множества E(R0) в заданное
конечное множество E(RT ) при любых допустимых возмущениях из (2) и
нелинейностях из (9). При этом переключение коэффициентов усиления сле-
дует производить в моменты, когда состояние системы переходит в эллипсоид
E(Q(t)) = {x : xTQ∗-1(t)x ≤ 1} с наименьшим значением trace[Q(t)].
7. Пример
В качестве примера рассмотрим систему (1) с нелинейностью ϕ(x), удовле-
творяющей ограничениям (2) с μ0 = 0 и μ1 = 20. В качестве выхода системы
выберем вектор z = (x1, x2)T. Чтобы избежать больших значений управле-
ния, учитывается ограничение u2 ≤ Z, где Z = 50, и неопределенность в на-
чальном состоянии системы, задаваемая матрицей Q0. При этом для данной
системы определим матрицы в (1) следующим образом:
[
]
[
]
[
]
[
]
1,6487
0,1494
0
0
0
A=
,
Φ=
,
B=
,
D=
,
0
1,35
-0,25
1
1
[
]
[
]
[
]
1
0
0
0,34
-3
C =
,
Cf =
,
Bf = [0] , Q0 =
0
1
1
-3
27
Так как коэффициенты системы не зависят от времени, то при применении
теоремы 4 все матрицы берутся постоянными, что соответствует рассмотрен-
ному в [12] случаю автономных систем. Численное решение задач оптими-
зации с ЛМН проводилось в пакете Matlab с использованием программного
70
обеспечения CVX. Для исходной системы с учетом ограничения на управле-
ние при α = 0,51, β = 4,2073 была найдена матрица
[
]
0,1016
-1,1116
QP1 =
−1,1116
14,4634
минимального инвариантного эллипса и соответствующий регулятор с по-
стоянными коэффициентами K1 = [ -18,0355
-2,9845 ], а при α = 0,51,
β = 6,6171 получена матрица максимального по критерию следа инвариант-
ного эллипса
[
]
0,1492
-1,5778
QD11 =
−1,5778
19,2332
При α = 0,39 и β = 8,4506 была найдена матрица
[
]
0,1536
-1,6504
QD12 =
−1,6504
19,9506
максимального по критерию следа инвариантного эллипса. Этот эллипс пред-
ставляет внутреннюю оценку множества начальных данных, из которой тра-
ектории исходной системы с регулятором K1 гарантированно будут стремить-
ся к предельному множеству, внешней оценкой которого является инвариант-
ный эллипс с матрицей QP1. При этом будет выполняться заданное ограни-
чение на управление. Отметим, что так как заданный начальный эллипс с
матрицей Q0 не является вложенным в эллипсы QD11, QD12, то для него не
гарантируется выполнение ограничения на управление с K1.
Также в результате решения задачи trace(Q) → max с ЛМН ограничения-
ми при α = 0,68 и β = 32,4318 получен регулятор с постоянными коэффици-
ентами K2 = [ -11,692
-2,312 ], гарантирующий оценку области начальных
данных в виде инвариантного эллипса с матрицей
[
]
0,4829
-3,7667
QD2 =
−3,7667
35,1005
Для системы с регулятором K2 при α = 0,68 и β = 38,4023 получена мат-
рица минимального по критерию следа инвариантного эллипса
[
]
0,4708
-3,6157
QP21 =
,
−3,6157
33,8214
a при α = 0,75 и β = 34,308 получена матрица минимального по критерию
следа инвариантного эллипса
[
]
0,4259
-3,2171
QP22 =
−3,2171
30,8997
На рис. 1 показаны инвариантные эллипсы с матрицами QP1, QD11, QD12,
QD2, QP21, QP22.
71
6
4
2
0
2
4
6
0,8
0,4
0
0,4
0,8
x1
Рис. 1. Инвариантные эллипсы с матрицами QP1, QD11, QD12 (показаны
сплошной, сплошной с маркером + и сплошной с маркером × линиями соот-
ветственно) для системы с регулятором K1 и инвариантные эллипсы с матри-
цами QD2, QP21, QP22 (изображены штриховой, точечной и штрихпунктирной
линиями соответственно) для системы с регулятором K2.
6
4
2
0
2
4
6 0,8
0,4
0
0,4
0,8
x1
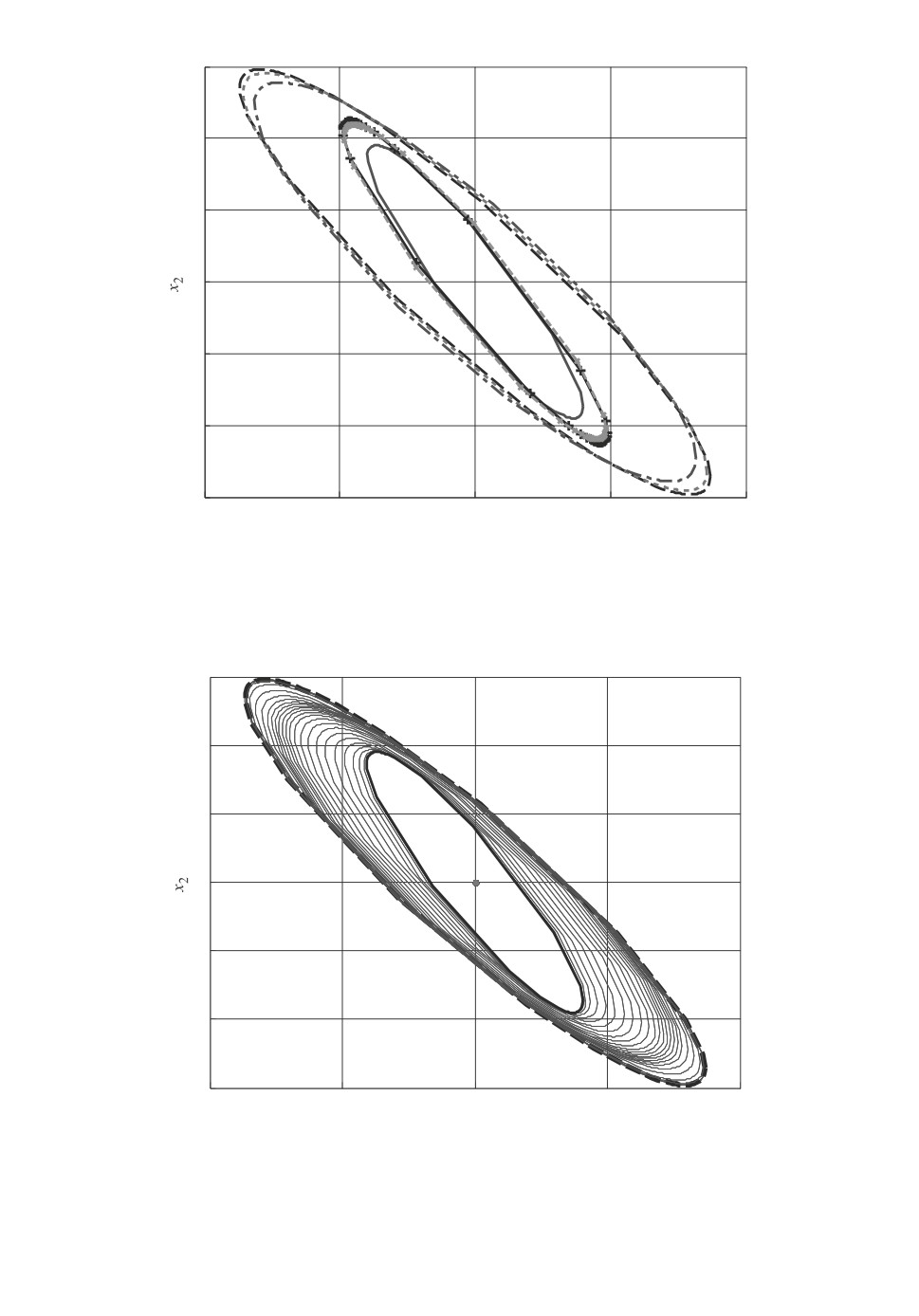
Рис. 2. Обеспечение перехода из эллипса начальных данных QD2 (штриховая
линия) в минимальный инвариантный эллипсоид с матрицей QP1 (сплошная
полужирная линия) для системы с регулятором с переменными коэффици-
ентами, определяемых из решения задач оптимизации с РМН двухшаговыми
итерациями.
72
40
30
20
10
0
10
20
0
5
10
15
20
25
t
Рис. 3. Изменение параметра β(t) (штриховая линия) и коэффициентов уси-
ления регулятора K3(t) = (K31(t) K32(t)) (сплошная и точечная линии соот-
ветственно).
6
4
2
0
2
4
6
0,8
0,4
0
0,4
0,8
x1
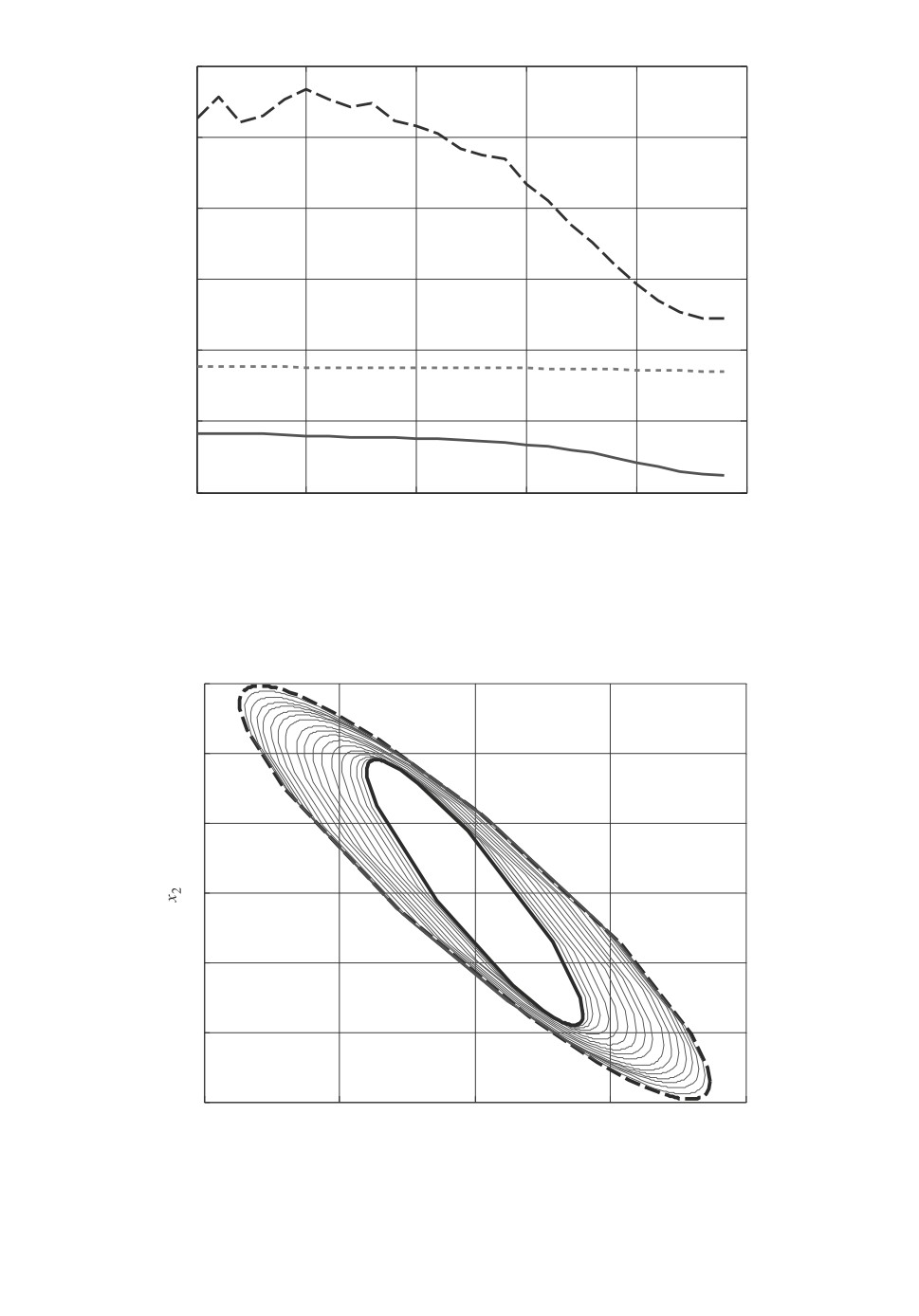
Рис. 4. Эллипсы, полученные в результате решения задачи оптимизации
trace[Q(16)] → min при ограничениях (12), (13) с граничными условиями
Q(0) ≥ QD2, Q(16) ≤ QP1.
73
40
30
20
10
0
10
20
4
8
12
16
t
Рис. 5. Изменение параметров β(t) (штриховая линия), α(t) (штрихпунктир-
ная линия) и коэффициентов усиления регулятора K4(t) = (K41(t) K42(t))
(сплошная и точечная линии соответственно).
6
4
2
0
2
4
6
0,8
0,4
0
0,4
0,8
x1
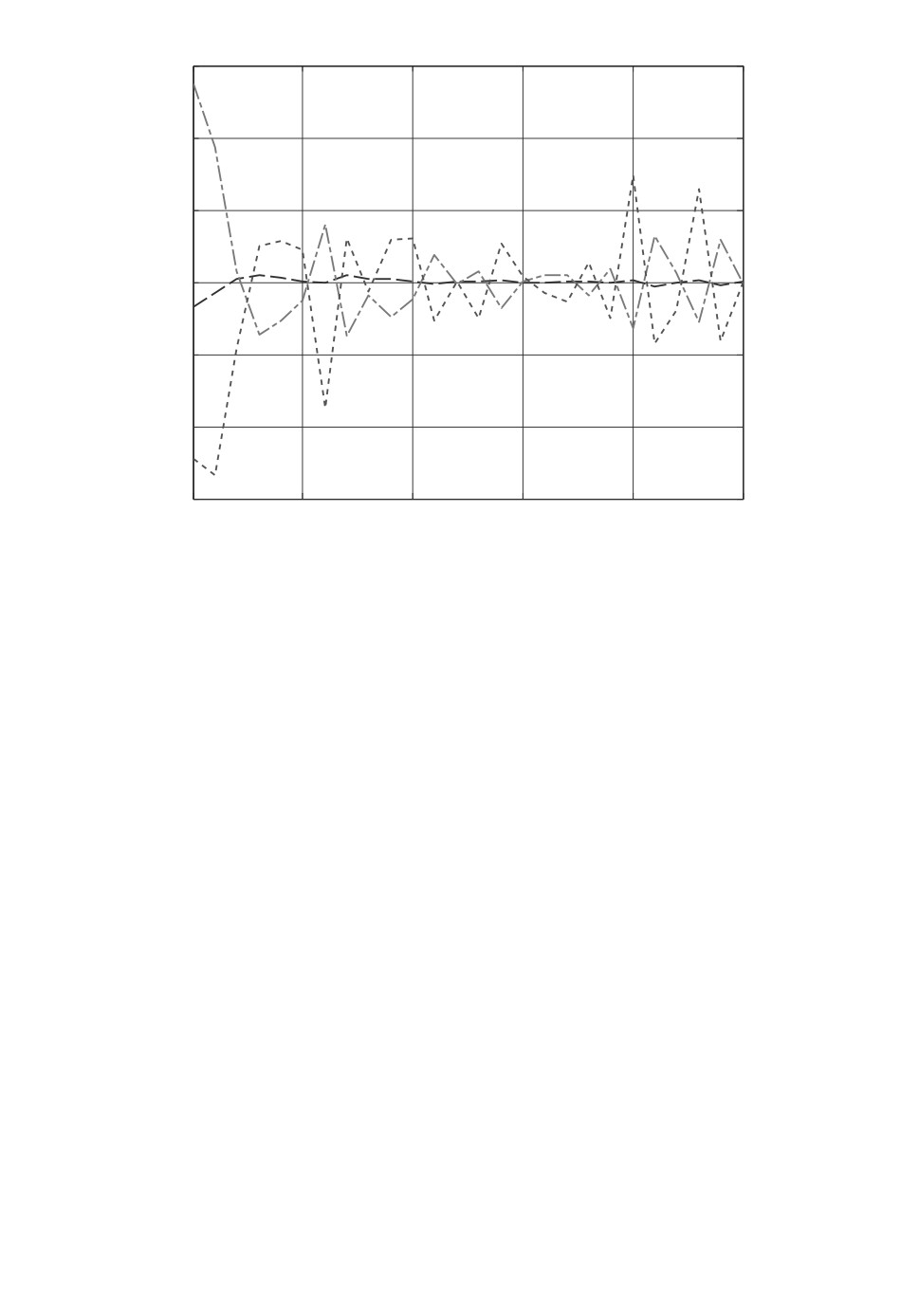
Рис. 6. Инвариантные эллипсы, полученные при численном решении МСС (6)
для исходной системы с регулятором с переменными коэффициентами усиле-
ния, и траектория системы с начальными данными x0 = (-0,67 5,5)T.
74
6
4
2
0
2
4
6
0
5
10
15
20
25
t
Рис. 7. Изменение координат состояния x1(t), x2(t) (показаны штриховой и
штрихпунктирной линиями соответственно) и управляющего воздействия u(t)
(показано точечной линией) в системе с регулятором K4(t) = (K41(t) K42(t)).
Теперь эллипс с матрицей Q0 принадлежит эллипсу с матрицей QD2 (так
как QD2 - Q0 > 0), поэтому для него гарантируется выполнение ограничения
на управление с K2. Однако при этом управлении получены предельные ин-
вариантные эллипсы QP21, QP22, значительно большими, чем при управлении
сK1.
Из рис. 1 следует, что регулятор с коэффициентами K1 обеспечивает более
сильное подавление неопределенностей, чем регулятор с коэффициентами K2,
при котором, однако, обеспечивается наибольшая оценка области начальных
отклонений. Таким образом, чтобы обеспечить (например, как с помощью
регулятора K1) наибольшее подавление начальных отклонений и неопреде-
ленных возмущений из максимально возможной области начальных данных
(как с регулятором K2), требуется организовать изменение коэффициентов
регулятора для рассматриваемой автономной системы.
В результате решения на интервале [0, 24] задачи оптимизации двухшаго-
выми итерациями получен регулятор с переменными коэффициентами, ко-
торый обеспечивает переход из заданного матрицей QD2 эллипса (показан
штриховой линией на рис. 2) в минимальный инвариантный эллипс, задан-
ный матрицей QP1 (показан сплошной полужирной линией). Тонкими сплош-
ными линиями показаны эллипсы, полученные на промежуточных итераци-
ях. Матрица каждого такого эллипса определяет, какие коэффициенты уси-
ления должен иметь регулятор при попадании в него траектории системы,
чтобы затем перейти в следующий вложенный в него эллипс. На рис. 3 пока-
75
заны графики изменения параметра β и коэффициентов усиления регулятора
K3(t) = (K31(t) K32(t)).
Кроме того, на интервале [0, 16] было найдено решение Q∗(t) > 0, Y∗(t),
(t = 0, 1, . . . , 16) задачи оптимизации trace[Q(16)] → min при ограничени-
ях (12), (13) с граничными условиями Q(0) ≥ QD2 и Q(16) ≤ QP1. На рис. 4
представлены эллипсы с матрицами Q(0) = QD2 (показан штриховой ли-
нией), Q∗(1), Q∗(2), . . . , Q∗(15) (отмечены тонкими сплошными линями)
и Q∗(16) (полужирная сплошная линия). На рис. 5 представлены графи-
ки изменения параметров β(t), α(t) и коэффициентов усиления регулятора
K4(t) = (K41(t) K42(t)). Аналогичные эллипсы получены при численном ре-
шении МСС (6) для исходной системы, замкнутой регулятором с переменны-
ми коэффициентами усиления. Они представлены на рис. 6, где штриховой
линией показан начальный эллипс и сплошной линией - эллипс, получен-
ный при t = 16. Штрихпунктирной линией выделена траектория системы с
полученным регулятором с начальными данными x0 = (-0,67
5,5)T, нели-
нейностью ϕ(x) = 20 sin(x2) и возмущением w(t) = 2a sin(3t - 1) cos(t/2), где
амплитуда a задавалась из диапазона [-0,5 0,5] с помощью датчика случай-
ных чисел. Изменения координат состояния системы с регулятором с пере-
менными коэффициентами показаны на рис. 7.
Таким образом, полученный регулятор обеспечивает эффективное подав-
ление внешних ограниченных возмущений и гарантированный переход из об-
ласти начальных отклонений в виде эллипса с матрицей Q(0) = QD2 ≥ Q0
в заданную эллипсом с матрицей QP1 область. Отметим, что управление с
постоянными коэффициентами усиления, полученными методом инвариант-
ных или притягивающих эллипсоидов из [12, 13] при учете ограничения на
управление, может быть использовано только для начальных отклонений из
области, принадлежащей предельному инвариантному эллипсоиду.
8. Заключение
Методы матричных систем сравнения и матричных разностных нера-
венств применяются для решения задач оценивания состояния, анализа
устойчивости и ограниченности относительно заданных множеств начальных
данных и множества, ограничивающего состояния или выход, и задачи по-
давления начальных отклонений и внешних возмущений для одного класса
нелинейных неавтономных дискретных систем с ограниченными внешними
возмущениями. Задачи оценивания состояния и анализа ограниченности от-
носительно заданных множеств сведены к численному решению разностного
матричного уравнения или разностных линейных матричных неравенств и
проверки условий, представленных линейными матричными неравенствами.
Синтез регуляторов в виде линейной обратной связи по состоянию сведен к
задачам поиска решений разностных линейных матричных неравенств или
к задачам полуопределенного программирования. Предлагаемый подход рас-
пространяет на неавтономные системы подход, основанный на методе инва-
риантных эллипсоидов и технике линейных матричных неравенств, приме-
нительно к нелинейным системам с ограниченными внешними возмущения-
ми. В частности, рассмотрена задача подавления начальных отклонений и
76
внешних возмущений с помощью переменной по времени, линейной обрат-
ной связи по состоянию, минимизирующей размер инвариантных (или огра-
ничивающих) эллипсоидов динамической системы. По сравнению с методом
инвариантных и притягивающих эллипсоидов [12, 13] предложенный способ
синтеза управления позволяет решать задачу гарантированного перехода из
одной области начальных данных в заданную область путем последователь-
ного изменения коэффициентов усиления в зависимости от текущего состоя-
ния системы. Эффективность предлагаемого подхода для решения указанных
задач продемонстрирована на примере дискретной системы второго порядка.
Полученные результаты могут быть применены для решения аналогичных
задач в робастной постановке, связанных с оцениванием состояния, анализом
ограниченности и синтезом управления, обеспечивающего гарантированный
переход из одного заданного множества в другое при неопределенных внеш-
них возмущениях и параметрических изменениях.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Доказательство во многом аналогично
доказательству теоремы 3 из [12]. Определим функцию v(t, x) = xTQ-1(t)x,
Q(t) = QT(t) > 0, Q(t0) = Q0. Для любого x0 ∈ E(Q0) имеет место
v(t0, x0) = xT0Q-10x0 ≤ 1. Для того чтобы траектории x(t) = x(t, t0, x0)
исходной системы не покидали эллипсоид E(Q(t)) = {x ∈ Rn : v(t, x) ≤ 1},
достаточно потребовать, чтобы при v(t, x) = 1 при всех допустимых внешних
возмущениях из (3) и при нелинейностях ϕ(t, x) из (2) выполнялось
(Π.1)
v(t + 1, x(t + 1), w, ϕ) ≤ 1.
Опуская зависимость от t, вычислим
v(t + 1, x(t + 1), w, ϕ) = xT(t + 1)Q-1(t + 1)x(t + 1) =
= [Ax + Dw + Φϕ(t, x)]TQ-1(t + 1)[Ax + Dw + Φϕ(t, x)] =
⎡
⎡
⎤T
⎤⎡
⎤
(Π.2)
ATQ-1(t + 1)A ATQ-1(t + 1)D ATQ-1(t + 1)Φ
x
x
⎥
=⎣w⎦ ⎣DTQ-1(t+1)ADTQ-1(t+1)DDTQ-1(t+1)Φ⎦⎣
w⎦.
ϕ ΦTQ-1(t + 1)A ΦTQ-1(t + 1)D ΦTQ-1(t + 1)Φϕ
С использованием S-процедуры в части достаточности для (П.1) с учетом
(П.2), предположения v(t, x) = 1, ограничений на внешние возмущения (3) и
нелинейности ϕ(t, x) (2) получаем: существуют α, δ, γ ≥ 0 такие, что
⎡
⎡
⎤T
⎤⎡
⎤
x
ATQ-1(t + 1)A ATQ-1(t + 1)D ATQ-1(t + 1)Φ
x
⎥
⎣w⎦ ⎣DTQ-1(t+1)ADTQ-1(t+1)DDTQ-1(t+1)Φ
⎦+
⎦⎣
w
(Π.3)
ϕ ΦTQ-1(t + 1)A ΦTQ-1(t + 1)D ΦTQ-1(t + 1)Φϕ
+ α(1 - xTQ-1(t)x) + δ(1 - wTw) + γ(μ0 + μ1xTCTf Cf x - ϕTϕ) - 1 ≤ 0.
77
Перепишем (П.3) в виде
⎡
⎤
⎡
⎤T
ATQ-1(t+1)A+γμ1CfCf -αQ-1(t) ATQ-1(t + 1)D
ATQ-1(t + 1)Φ
x
⎥
⎣w⎦ ⎣
DTQ-1(t + 1)A
DTQ-1(t+1)D-δI DTQ-1(t + 1)Φ
⎦×
ϕ
ΦTQ-1(t + 1)A
ΦTQ-1(t + 1)D ΦTQ-1(t + 1)Φ- γI
⎡
⎤
x
×⎣ w
⎦+α+δ+γμ0 - 1 ≤ 0.
ϕ
Таким образом, чтобы выполнялось (П.1) при учете указанных ограничений
достаточно, чтобы существовали α, δ, γ ≥ 0, такие что α + δ + γμ0 ≤ 1, и име-
ло место матричное неравенство
⎡
⎤
ATQ-1(t+1)A+γμ1CfCf -αQ-1(t) ATQ-1(t + 1)D ATQ-1(t + 1)Φ
⎢
⎥
(Π.4)
⎣
DTQ-1(t + 1)A
DTQ-1(t+1)D-δI DTQ-1(t + 1)Φ
⎦≤0.
ΦTQ-1(t + 1)A
ΦTQ-1(t + 1)D ΦTQ-1(t + 1)Φ- γI
Неравенство (П.4) представимо в виде
⎡
⎤
⎡
⎤
αQ-1(t) - γμ1CTfCf
0
0
AT
[
]
⎣
⎦≥ ⎣DT
⎦Q-1(t+1)
0
δI
0
A D Φ
,
0
0
γI
ΦT
откуда по лемме дополнения Шура получаем:
⎡
⎤
Q(t + 1)
A
D Φ
⎢
AT αQ-1(t) - γμ1CTfCf
0
0
⎥
⎢
⎥
0.
⎣
⎦≥
DT
0
δI
0
ΦT
0
0
γI
Дважды применив лемму дополнения Шура, имеем:
⎡
⎤
1
1
Q(t + 1) -
ΦΦT -
DDT
A
⎣
γ
δ
⎦≥0.
AT
αQ-1(t) - γμ1CTfCf
Далее, умножая слева и справа на матрицу diag{I Q(t)}, полагая δ = δmax =
= 1 - α - γμ0 и обозначив β = 1/γ, приходим к матричному неравенству:
⎡
⎤
1
Q(t + 1) - βΦΦT -
DDT
AQ(t)
⎣
1 - α - μ0/β
⎦
(Π.5)
≥ 0.
Q(t)AT
αQ(t) - Q(t)CTfCf Q(t)μ1/β
Неравенство (П.5) будет выполнено, если определять матрицу Q(t + 1) при
каждом t ∈ T из уравнения (6), где выбором значения параметра β можно
обеспечить на каждой итерации существование обратной матрицы.
78
С другой стороны, по лемме дополнения Шура неравенство (П.5) эквива-
лентно неравенству
⎡
⎤
Q(t + 1) - βΦΦT
AQ(t)
D
⎢
⎥
⎣
Q(t)AT
αQ(t) - Q(t)CTfCf Q(t)μ1/β
0
⎦ ≥ 0,
DT
0
(1 - α - μ0/β)I
и, еще дважды применяя к нему лемму дополнения Шура, приходим к
РЛМН (7). Теорема 1 доказана.
Доказательство теоремы 2. Пусть для заданной матрицы Q0 > 0
на интервале T существует положительно определенное решение Q(t) =
= Q(t,t0,Q0) РМУ (6) или РЛМН (7). Согласно теореме 1 это решение опре-
деляет в каждый момент времени невырожденный эллипсоид E(Q(t)), яв-
ляющийся инвариантным для решений исходной системы (1) с начальными
данными x(t0) = x0 ∈ E(Q0). Поэтому справедлива оценка п. 1.
Пусть справедлива оценка п. 1. Тогда для решений x(t) = x(t, t0, x0) име-
ет место неравенство 0 ≤ 1 - xT(t)Q-1(t)x(t). По лемме дополнения Шура
данное неравенство эквивалентно матричному неравенству для всех t ∈ T
[
]
1
xT(t)
≥ 0.
x(t) Q(t)
Отсюда следует, что Q(t) - x(t)xT(t) ≥ 0 для всех t ∈ T . Поэтому оценка п. 2
имеет место.
Оценки пп. 3-5 непосредственно следуют из оценки п. 2. Теорема 2 дока-
зана.
Доказательство леммы
1. Из теоремы
2
следует, что част-
ное решение Q(t) = Q(t, t0, Q0) системы (6) мажорирует поведение матрич-
ной функции сравнения V (t, x(t)) = x(t)xT(t) на решениях исходной систе-
мы (1). Кроме того, правая часть уравнения (6) является монотонной мат-
ричной функцией относительно Q. Действительно, пусть даны матрицы
Q′0,Q′′0, такие что Q′′0 ≥ Q′0 > 0, и существует β такое, что матрицы (Q′′0)-1-
Cf - не особые. Так как матрицы Q′0, Q′′0 по-
-μ1β
f
Cf и (Q′0)-1 -μ1β
f
ложительно определенные и упорядоченные, то имеет место неравенство
Cf . При обращении левой и правой части
(Q′′0)-1 -μ1β
f
Cf ≤ (Q′0)-1 -μ1β
f
Cf]-1,
отсюда получаем неравенство [(Q′′0)-1 -μ1β
f
Cf]-1 ≥ [(Q′0)-1 -μ1β
f
которое при имеющихся предположениях эквивалентно неравенству
(
)-1
(
)-1
μ1
μ1
Q′′0
Q′′0 -
Q′′0CTfCfQ′′
Q′′0 ≥ Q′
Q′0 -
Q′0CTfCf Q′
Q′0.
0
0
0
β
β
Поскольку другие члены правой части РМУ (6) не зависят от Q, то послед-
нее неравенство и доказывает монотонность правой части РМУ (6). Соглас-
но лемме 3 из [21] РМУ(6) является матричной системой сравнения для (1).
Лемма 1 доказана.
Доказательство леммы 2. Из неравенства 0 < Q0 < αI следует
Cf ≤1αI, получа-
неравенство 0 <1α I < Q-10. Учитывая предположениеμ1β
f
Cf > 0. Тогда существует обратная матрица, ко-
ем, что матрица Q-10 -μ1β
f
79
торая также является положительно определенной. Далее с учетом сделанно-
го предположения правая часть МСС (6) будет положительно определенной
матрицей, что и доказывает Q(t0 + 1) > 0. По индукции аналогичными рас-
суждениями доказывается положительная определенность Q(t0 + k, t0, Q0)
для любых k, при которых решение существует. Лемма 2 доказана.
Доказательство теоремы 3. Пусть Q(t) = Q(t,t0,Q0) > 0 - реше-
ние РМУ (6) (или РЛМН (7)) с начальными данными Q0 ≥ R0 > 0. Так как
Q0 ≥ R0, то E(R0) ⊆ E(Q0), т.е. эллипсоид E(R0) содержится в эллипсои-
де E(Q0). Кроме того, так как Q(t) ≤ R(t), то E(Q(t)) ⊆ E(R(t)), т.е. эл-
липсоид E(Q(t)) принадлежит эллипсоиду E(R(t)). По теореме 1 эллипсо-
ид E(Q(t)) содержит при t ∈ T все решения исходной системы, начинающие-
ся из заданного эллипсоида E(Q0). Поэтому выполнены все условия опре-
деления 2 и имеет место свойство ограниченности относительно заданных
множеств [E(R0), E(R(t))].
При отсутствии внешних возмущений и μ0 = 0 в ограничении (2) РМУ (6)
принимает вид
[
]-1
μ1
(Π.6)
Q(t + 1) = AQ(t) Q(t) -
Q(t)CTfCf Q(t) Q(t)AT + βΦΦT.
β
Если Q(t) = Q(t, t0, Q0) - решение (П.6), удовлетворяющее условиям теоре-
мы 3, то будут выполнены все условия определения 2 и имеет место свойство
устойчивости относительно заданных множеств [E(R0), E(R(t))]. Теорема 3
доказана.
Доказательство теоремы 4. Подставим (11) в (8). Применим тео-
рему 1 для поиска инвариантного эллипсоида E(Q(t)) с матрицей Q(t), удов-
летворяющей РЛМН (7), принимающему для замкнутой системы вид:
⎡
⎤
Q(t + 1) - βΦΦT
AQ(t)+BKQ(t)
D
0
0
⎢
⎥
Q(t)AT +Q(t)KTBT
αQ(t)
0
Q(t)CTf +Q(t)KTBTf
0
⎢
⎥
⎢
⎥
⎢
DT
0
(1-α)I
0
I
⎥
(Π.7)
⎢
⎥
≥0
⎢
β
⎥
⎢
0
Cf Q(t)+Bf KQ(t)
0
I
0
⎥
⎣
μ1
⎦
β
0
0
I
0
I
μ0
при всех t ∈ T и некоторых β > 0,
0 < α < 1.
В (П.7) переменные Q и K входят нелинейным образом. Введем матрич-
ную переменную Y = KQ, Y ∈ Rm×n. Тогда неравенство (П.7) примет ли-
нейный (по P и Y ) вид (12). Далее, с учетом введенной переменной Y поиск
минимального по критерию следа, ограничивающего выход z(t) эллипсоида,
приводит к задаче
trace[CQCT] → min
при ограничении (12) и t ∈ T . Ограничение на управление (10) после под-
становки (11) принимает вид xTKTZ-1Kx ≤ 1. По лемме дополнения Шура
оно эквивалентно матричному неравенству KxxTKT ≤ Z. Учитывая оцен-
ку п. 2 из теоремы 2, последнее неравенство будет иметь место при условии
80
KQKT ≤ Z. Это неравенство с учетом замены Y = KQ представляется в ви-
де Z - Y Q-1YT ≥ 0, а по лемме дополнения Шура записывается в виде (13).
Пусть матрицы Q∗(t), Y∗(t) - решение рассматриваемой задачи оптимиза-
ции с РЛМН (12) и ЛМН (13) при t ∈ T . Тогда матрица коэффициентов уси-
ления регулятора определится как K∗(t) = Y∗(t)Q∗-1(t). Если матрица Q∗(t)
удовлетворяет дополнительно ограничениям Q∗(t0) ≥ R0 и Q∗(t) ≤ R(t) для
всех t ∈ T , где R0 и R(t) - заданные положительно определенные симметри-
ческие матрицы, то согласно теореме 3 управление (11) обеспечивает огра-
ниченность замкнутой системы относительно множеств [E(R0), E(R(t))], что
завершает доказательство теоремы 4.
СПИСОК ЛИТЕРАТУРЫ
1.
Schweppe F.C. Uncertain Dynamic Systems. N.J.: Prentice Hall, 1973.
2.
Черноусько Ф.Л. Оценивание фазового состояния динамических систем. Метод
эллипсоидов. М.: Наука, 1988.
3.
Kurzhanskii А.В., Valyi I. Ellipsoidal Calculus for Estimation and Control. Boston:
Birkhauser, 1997.
4.
Pronzato L., Walter E. Minimal volume ellipsoids // Int. J Adaptat. Control Signal
Process. 1994. V. 8 (1). P. 15-30.
5.
Bounding Approaches to System Identification / Eds Milanese M., Norton J., Piet-
Lahanier H., Walter E. N.Y.: Springer Science+Business Media, 1994.
6.
Durieu C., Walter E., Polyak B. Multi-Input Multi-Output Ellipsoidal State
Bounding // J. Optim. Theory Appl. 2001. V. 111. No. 2. P. 273-303.
7.
Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in
System and Control Theory. Philadelphia: SIAM, 1994.
8.
Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных
матричных неравенств. М.: Физматлит, 2007.
9.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными системами
при внешних возмущениях. М.: ЛЕНАНД, 2014.
10.
Siljak D.D., Stipanović D.M. Robust Stabilization of Nonlinear Systems: the LMI
Approach // Math. Probl. Engineer. 2000. V. 6. P. 461-493.
11.
Zečević A.I.,
Siljak D.D. Control of Complex Systems. Structural Constraints and
Uncertainty. Ser. Communications and Control Engineering / Eds Sontag E.D.,
Thoma M., Isidori A., van Schuppen J.H. N.Y: Springer Science+Business Media,
LLC 2010.
12.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Нелинейные системы с ограничен-
ными или мультипликативными возмущениями // Проблемы устойчивости и
управления. Сб. науч. статей, посв. 80-летию акад. В.М. Матросова. М.: Физ-
матлит, 2013. С. 270-299.
13.
Poznyak A., Polyakov A., Azhmyakov V. Attractive Ellipsoids in Robust Control.
Switzerland: Springer Int. Publishing, 2014.
14.
Маликов А.И., Благов А.Е. Динамический анализ систем автоматического
управления с помощью матричных систем сравнения // Вестн. КГТУ им.
А.Н. Туполева. 1996. № 4. С. 71-75.
15.
Маликов А.И., Благов А.Е. Анализ динамики многосвязных систем автоматиче-
ского регулирования с помощью матричных систем сравнения // Вестн. КГТУ
им. А.Н. Туполева. 1998. № 2. С. 37-43.
81
16.
Маликов А.И. Матричные системы сравнения в анализе динамики систем управ-
ления со структурными изменениями // Изв. РАН. ТиСУ. 1999. № 3. С. 11-21.
17.
Маликов А.И. Матричные системы дифференциальных уравнений с условием
квазимонотонности // Изв. ВУЗов. Математика. 2000. № 8. С. 35-45.
18.
Маликов А.И. Метод матричных систем сравнения в анализе и синтезе систем
управления с неопределенностями // Аналитическая механика, устойчивость и
управление: Тр. X Междунар. Четаевской конф. Т. 2. Секц. 2. Устойчивость. Ка-
зань, 12-16 июня 2012 г. Казань: Изд-во Казан. гос. техн. ун-та, 2012. С. 360-370.
19.
Постников Н.С., Сабаев Е.Ф. Матричные системы сравнения и их приложения
к задачам автоматического регулирования // АиТ. 1980. № 4. С. 24-34.
Postnikov N.S., Sabaev E.F. Matrix Comparison Systems and Their Applications to
Automatic Control Problems // Autom. Remote Control. 1980. No. 4. P. 455-465.
20.
Маликов А.И. Эллипсоидальное оценивание состояния дискретных систем
управления с помощью матричных систем сравнения // Изв. ВУЗов. Матема-
тика. 2004. № 1. С. 53-69.
21.
Куо Б. Теория и проектирование цифровых систем управления. М.: Машино-
строение, 1986.
Kuo B.C. Digital Control Systems. Oxford Univ. Press, 1995.
22.
Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука,
1973.
23.
Lewis F.L., Vrabie D.L., Syrmos V. Optimal Control. 2nd ed. N.Y.: Wiley, 1995.
24.
Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир,
1977.
25.
Werbos P.J. Approximate Dynamic Programming for Real-Time Control and
Neural Modeling // Handbook of Intelligent Control: Neural, Fuzzy, and Adaptive
Approaches. V. 15. N.Y.: Nostrand, 1992. P. 493-525.
26.
Al-Tamimi A., Lewis F.L., Abu-Khalaf M. Discrete-Time Nonlinear HJB Solution
Using Approximate Dynamic Programming: Convergence Proof // IEEE Trans.
Syst., Man Cyb. 2008. V. 38. No. 4. P. 943-949.
27.
Yu H., Jiang Z-P. Robust Adaptive Dynamic Programming. N.J.: Wiley-IEEE Press,
2017.
28.
Kamalapurkar R., Walters P., Rosenfeld J., Dixon W. Reinforcement Learning for
Optimal Feedback Control. A Lyapunov-Based Approach. Springer, 2018.
29.
Amato F., Ambrosino R., Ariola M., Cosentino C., De Tommasi G. Finite Time
Stability and Control. Lecture Notes in Control and Information Science. London:
Springer-Verlag, 2014.
30.
Маликов А.И. Оценивание состояния и стабилизация непрерывных систем с
неопределенными нелинейностями и возмущениями // АиТ. 2016. № 5. С. 19-36.
Malikov A.I. State Estimation and Stabilization of Continuous Systems with
Uncertain Nonlinearities and Disturbances // Autom. Remote Control. 2016. V. 77.
No. 5. P. 764-778.
Статья представлена к публикации членом редколлегии М.В. Хлебниковым.
Поступила в редакцию 05.10.2018
После доработки 02.03.2019
Принята к публикации 25.04.2019
82