Автоматика и телемеханика, № 11, 2019
Робастное, адаптивное и сетевое
управление
© 2019 г. Р.П. АГАЕВ, д-р физ.-мат. наук (agaraf3@gmail.com)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
О РОЛИ СОБСТВЕННОГО ПРОЕКТОРА ЛАПЛАСОВСКОЙ
МАТРИЦЫ В ЗАДАЧЕ ДОСТИЖЕНИЯ КОНСЕНСУСА
В МНОГОАГЕНТНЫХ СИСТЕМАХ ВТОРОГО ПОРЯДКА1
Рассматривается проблема консенсуса в многоагентных системах вто-
рого порядка при отсутствии остовного исходящего дерева в орграфе за-
висимостей. Доказана теорема, согласно которой, асимптотическое пове-
дение системы однозначно определяется собственным проектором лапла-
совской матрицы орграфа зависимостей. Обобщены результаты, ранее по-
лученные автором, а также результаты, полученные в работах В. Рена и
Э. Аткинс. Предложен метод регуляризации для случая, когда орграф
зависимостей не содержит остовного исходящего дерева.
Ключевые слова: многоагентные системы второго порядка, консенсус, ре-
гуляризация, собственный проектор, лапласовская матрица орграфа.
DOI: 10.1134/S0005231019110072
1. Введение
Известно, что в многоагентных системах первого порядка с информацион-
ной связью консенсус достигается тогда и только тогда, когда ноль является
простым собственным значением соответствующей лапласовской матрицы.
Это условие эквивалентно наличию остовного исходящего дерева в оргра-
фе зависимостей. Поскольку при нарушении данного условия консенсус не
достигается, алгебраические свойства таких орграфов (в том числе соответ-
ствующие лапласовские матрицы) мало изучены. Изучение асимптотического
свойства системы с орграфом зависимостей, не содержащим остовного дере-
ва, с помощью собственного проектора лапласовской матрицы или ее спектра
позволяет “сопоставить системе некий наиболее естественный консенсус, до-
стигаемый при минимально возможном изменении” [1]. За последние годы
была опубликована серия работ (см., например, [1-3]), где изучаются асимп-
тотические свойства многоагентных систем с орграфами зависимостей, не со-
держащими остовного дерева. В этих работах наряду с алгебраическими свой-
ствами системы также изучается подпространство начальных характеристик,
1 Исследование асимптотики модели консенсуса второго порядка проведено при под-
держке гранта Российского научного фонда
№ 19-19-00673, предоставленного ИПУ
им. В.А. Трапезникова РАН. Выражение для динамики регуляризованной модели второго
порядка получено при частичной поддержке программы президиума РАН №30 “Теория и
технологии многоуровневого децентрализованного группового управления в условиях кон-
фликта и кооперации”.
127
векторы которого приводят к консенсусу. В [1] доказано, что асимптотические
свойства системы однозначно определяются собственным проектором лапла-
совской матрицы орграфа зависимостей. Собственные проекторы лапласов-
ских матриц можно вычислить как итеративно за конечное число шагов мень-
ше порядка самой матрицы, так и с помощью предела некоторых выражений.
На сегодня задачи достижения консенсуса в многоагентных системах с ор-
графами зависимостей, не содержащими остовного дерева, в основном ис-
следованы в работах автора данной статьи и его соавтора П.Ю. Чеботарева.
Задача регуляризации для дискретных моделей достижения консенсуса тес-
но связана с задачей PageRank. Безусловно, итеративную регуляризацию для
произвольной стохастической матрицы [4] также можно отнести к аналогич-
ным задачам. Добавление “фоновых связей” не обязательно приводит к пол-
ному изменению исходной структуры. Также в задаче PageRank изменение
исходной стохастической матрицы за счет добавления стохастической мат-
рицы с одинаковыми весами физически не приводит к новым связям между
хостами в Интернете, а всего лишь проводится на алгоритмическом уровне.
Конечно, при этом в моделях достижения консенсуса добавление “фоновых
связей” производится только для достижения консенсуса, которого до этого
не было.
Заметим, что в задачах достижения консенсуса в многоагентной системе
с неориентированным графом консенсус достигается тогда и только тогда,
когда граф связный. Напомним, что граф называется связным, если любая
пара его вершин соединена маршрутом. Система с несвязным графом раз-
деляется на две непересекающиеся части. Например, для системы с графом
зависимостей с множествами вершин {a, b, c, d} и ребер {{a, b}, {c, d}} го-
ворить о каком-либо консенсусе довольно трудно. Иначе обстоит дело для
случая орграфа, который не содержит остовного дерева, но между любыми
двумя вершинами всегда существует полупуть, т.е. маршрут без учета на-
правления дуг, в котором все вершины различны.
В настоящей работе рассматриваются многоагентные системы второго по-
рядка, которые впервые были изучены в [5, 6]. В таких системах единствен-
ность нулевого собственного значения лапласовской матрицы является необ-
ходимым, но не достаточным условием для консенсуса. Тем не менее в этих
моделях при определенном ограничении на параметр γ (коэффициент пере-
счета (scaling factor)), входящий в протокол системы, консенсус также опреде-
ляется единственным нормированным левым собственным вектором лапла-
совской матрицы. Здесь будем изучать более общий случай, когда ограни-
чение на параметр γ удовлетворяет определенному условию, но кратность
нулевого собственного значения лапласовской матрицы больше единицы. Вы-
ведено явное выражение, к которому асимптотически стремятся характери-
стики агентов. Полученный результат является обобщением леммы 4.1 из [5]
и теоремы о лесах и консенсусе [3].
В [1] было рассмотрено несколько протоколов консенсуса в многоагентных
системах с орграфом зависимостей, не содержащим остовного дерева. Эти
протоколы позволяют регуляризировать модель таким образом, что при лю-
бом векторе начальных значений в системе может быть достигнут консенсус.
В настоящей работе один из таких протоколов применим для многоагентной
128
системы второго порядка и для достаточно большого значения времени t вы-
ведем выражение для асимптотического консенсуса. Согласно предложенно-
му протоколу к исходному орграфу зависимостей добавляется полный граф с
весами δ/n, а консенсус определяется пределом при δ, стремящимся к нулю.
Структура работы. В разделе 2 введены необходимые понятия и рассмот-
рены вспомогательные результаты. В частности, приведено предложение о
регуляризации с помощью “фоновых связей” для систем первого порядка.
Основные результаты изложены в разделе 3, где доказана теорема 1 об асимп-
тотическом поведении системы второго порядка. Здесь также доказана теоре-
ма 2, обобщающая регуляризацию с помощью “фоновых связей” для системы
второго порядка.
2. Необходимые понятия и вспомогательные результаты
Введем некоторые понятия из теории графов. Орграф называется силь-
носвязным или сильным, если любые две его вершины взаимно достижимы.
Любой максимальный по включению сильный подграф данного орграфа на-
зывается его сильной компонентой или бикомпонентой. Базовой бикомпонен-
той называют такую бикомпоненту орграфа, в которую не входят дуги извне.
Подграф ориентированного графа называют остовным, если множества вер-
шин графа и подграфа совпадают. Исходящее дерево - это ориентированное
корневое дерево, содержащее направленные пути из корня во все другие вер-
шины. Легко показать, что из множества вершин всех базовых бикомпонент
имеются пути во все вершины орграфа и что орграф содержит остовное де-
рево тогда и только тогда, когда он содержит единственную базовую биком-
поненту.
Рассмотрим дифференциальную модель первого порядка поиска консен-
суса, описываемую системой уравнений
∑
(1)
xi(t) = -
aij (xi(t) - xj
(t)) , i = 1, . . . , n,
j=1
где xi(t) - характеристика i-го агента. A = (aij ) - матрица влияния j-го аген-
та на i-го. Приняв A за матрицу смежности орграфа зависимостей (влияний),
последний можно назвать орграфом зависимостей многоагентной системы с
лапласовской матрицей
L = diag(A1) - A,
где 1 = (1, . . . , 1)T.
Заметим, что систему (1) можно представить в матричном виде как
(2)
x(t) = -L x(t),
где x(t) = (x1(t), . . . , xn(t))T.
Пусть A ∈ Rn×n - произвольная квадратная матрица, R(A) и N (A) - соот-
ветственно образ и ядро A. Пусть ν = ind A - индекс A, то есть наименьшее
k ∈ {0,...n}, при котором rankAk+1 = rankAk (A0 ≡ I, где I - единичная
матрица порядка n).
129
Собственным проектором матрицы A, соответствующим собственному
значению 0, (или просто собственным проектором A) называют такой про-
ектор (идемпотентную матрицу) A⊢, что R(A⊢) = N (Aν ) и N (A⊢) = R(Aν ).
Асимптотическое поведение системы (2) при орграфе зависимостей, не со-
держащем остовного дерева описывается следующим предложением.
Предложение 1. Если x(t) - решение системы (2), то
lim
x(t) = lim e-Ltx(0) = L⊢ x(0).
t→∞
t→∞
Отметим, что первое равенство следует из представления решения систе-
мы дифференциальных уравнений, а доказательство второго равенства непо-
средственно следует из теоремы о лесах и консенсусе (теорема 1 в [3]).
Рассмотрим протокол поиска консенсуса для непрерывной модели первого
порядка, согласно которому к исходному орграфу зависимостей добавляется
полный взвешенный орграф “фоновых связей” с весамиδn :
(3)
x(t) = -(L + δK) x(t),
где K = I - E
- лапласовская матрица полного графа с весами
1/n,
E = 1n(1...1)T(1...1) - матрица порядка n с элементами 1/n.
Следующее утверждение следует из теоремы 3 в [1]:
Предложение 2. Если x(t) - решение системы (3), то
lim
lim x(t) = EL⊢x(0).
δ→0+
t→∞
Согласно предложению 2 при добавлении слабых “фоновых связей” и
устремлении силы связей к нулю консенсус всегда достигается и его значе-
ние определяется произведением EL⊢. Формально для получения консенсу-
са нужно вычислить скалярное произведение вектора начальных значений с
вектором средних значений столбцов собственного проектора лапласовской
матрицы, которая совпадает с нормированной матрицей максимальных ис-
ходящих лесов (более подробно, см. лемму 1 в [1]).
3. Модели второго порядка
Рассмотрим дифференциальную модель второго порядка [5]
˙
ξ
i = ζi,
˙
ζ
i = ui,
где ξi и ζi - состояние и скорость i-го агента, а ui - управление, определяемое
протоколом
∑
ui = - aij[(ξi - ξj) + γ(ζi - ζj)],
j=1
γ - коэффициент пересчета (scaling factor).
130
В матричной форме данный протокол имеет следующее представление:
[
]
[
]
ξ
ξ
(4)
=Γ
,
ζ
ζ
где
[
]
0n×n In
Γ=
-L
-γL
Цель протокола (4) - при t → ∞ обеспечить |ξi - ξj| → 0 и |ζi - ζj| → 0.
Доказательство следующей вспомогательной леммы приведено в [7] (см.
предложение 7).
Лемма 1. Если L⊢ - собственный проектор матрицы L, то линейная
оболочка столбцов матрицы L⊢ совпадает с ядром матрицы L, а линей-
ная оболочка строк L⊢ - с левым собственным подпространством нулевого
значения матрицы L.
Предположим, что γ удовлетворяет условию
1
Im2(μi)
(5)
γ2 > max
,
μi=0 Re(μi) Im2(μi) + Re2(μi)
где μi - ненулевое собственное значение соответствующей лапласовской мат-
рицы L.
Условие (5) в той или иной форме приведено в некоторых работах (на-
пример, [8, 9]) и является необходимым и достаточным условием достижения
консенсуса при равенстве единице кратности нулевого собственного значения
лапласовской матрицы.
Теорема 1. Пусть для γ выполняется условие (5), а кратность нулево-
го собственного значения лапласовской матрицы L равна m. Если [ξT,ζT]T -
решение системы (4), то для достаточно большого значения t имеет место
[
]
[
]
[
]
ξ(t)
1
t
ξ(0)
(6)
≈
⊗L⊢
,
ζ(t)
0
1
ζ(0)
где L⊢ - собственный проектор для L, ⊗ - знак произведения Кронекера.
Доказательство приведено в Приложении.
Теорема была доказана конструктивно и заодно было установлено, что
геометрическая кратность нулевого собственного значения матрицы Γ равна
алгебраической кратности нулевого собственного значения лапласовской мат-
рицы L. Поскольку число нулевых собственных значений Γ равно 2m (см. (8)
в [5]), а каждой паре нулевых собственных значений матрицы Γ соответствует
жордановая клетка размерности не меньше двух, очевидно, что у матрицы Γ
нет нулевого блока размерности больше двух (иначе кратность нуля для Γ
была бы больше 2m). Таким образом, из доказанной теоремы, в частности,
следует, что индекс матрицы Γ равен 2.
131
Согласно лемме 4.1 из [5] асимптотический консенсус не достигается для
любого вектора начальных значений x(0), если кратность нуля матрицы Γ
больше 2. Проведем регуляризацию [1], добавив к исходному орграфу зави-
симостей полный граф “фоновых связей” с весами δ/n.
Важно отметить, что в отличие от моделей первого порядка матрица
limt→∞ etΓ не является собственным проектором для Γ. Однако собственный
проектор для матрицы Γ согласно теореме 3.1 из [10] можно определить как
(I - tΓ2)-1 для достаточно большого значения t и можно доказать (например,
непосредственной проверкой определения собственного проектора для Γ2),
что собственный проектор Γ⊢ для Γ равен
[
]
L⊢
0n×n
Γ⊢ =
0n×n L⊢
Многоагентную систему второго порядка с добавленными фоновыми свя-
зями представим как
[
]
[
]
ξ
ξ
(7)
=ΓK
,
ζ
ζ
где
[
]
0
n×n
In
ΓK =
-(L + δK) -γ(L + δK)
Теорема 2. Пусть для γ выполняется условие (5), а кратность нулево-
го собственного значения лапласовской матрицы L равна m. Если [ξT,ζT]T -
решение системы (7), то для достаточно большого значения t и δ → 0 име-
ет место
[
]
[
]
[
]
ξ(t)
1
t
ξ(0)
(8)
≈
⊗ EL⊢
ζ(t)
0
1
ζ(0)
Выражение (8) можно считать обобщением системы (2), полученной для
многоагентной системы первого порядка.
Замечание. Лемма 4.1 из [5] является частным случаем теоремы 1. Со-
гласно этой лемме в многоагентной системе второго порядка с протоколом (4)
асимптотический консенсус достигается тогда и только тогда, когда крат-
ность нулевого собственного значения матрицы Γ равна двум, а действитель-
ные части остальных собственных значений отрицательны.
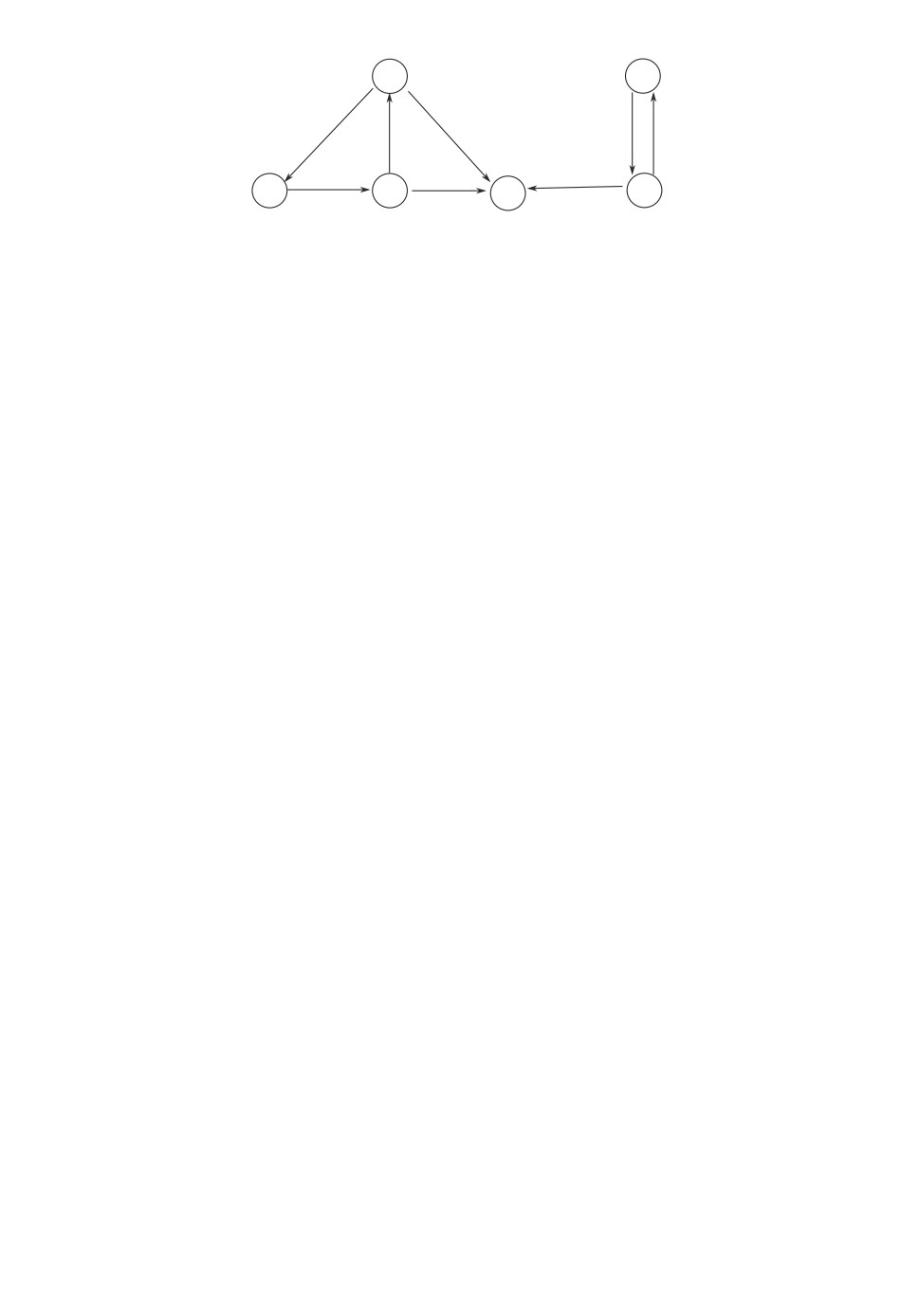
Пример. Рассмотрим систему из шести агентов с орграфом зависимо-
стей, представленным на рис. 1, с двумя базовыми бикомпонентами {1, 2, 3}
и {4, 5}.
132
1
4
1
3
1
1
2
2
2
1
2
3
6
5
Рис. 1. Орграф зависимостей.
Данному орграфу соответствуют лапласовская матрица L и матрица Γ:
⎡
⎤
3
0
-3
0
0
0
⎢
−1
1
0
0
0
0
⎥
⎢
⎥
[
]
⎢
0
-2
2
0
0
0
⎥
0n×n In
L=
⎢
⎥,
Γ=
⎢
0
0
0
2
-2 0
⎥
-L
-γL
⎣
⎦
0
0
0
-1
1
0
−1
0
-2
0
-1 4
По спектру матрицы L с условием (5) определяем пороговое значение γ,
обеспечивающее отрицательность действительных частей ненулевых соб-
ственных значений матрицы Γ: γ > 0,2462.
Определим собственный проектор матрицы L:
⎡
⎤
0,1818
0,5455
0,2727
0
0
0
⎢
0,1818
0,5455
0,2727
0
0
0
⎥
⎢
⎥
0,1818
0,5455
0,2727
0
0
0
⎥
L⊢ =⎢
⎥.
⎢
0
0
0
0,3333
0,6667
0
⎥
⎣
⎦
0
0
0
0,3333
0,6667
0
0,1364
0,4091
0,2045
0,0833
0,1667
0
Согласно теореме 1 определяем правые собственные и присоединенные век-
торы нулевого собственного значения матрицы Γ:
w1 = [1, 1, 1, 0, 0, 0,75, 0, 0, 0, 0, 0, 0]T;
w2 = [0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0,75]T;
w3 = [0, 0, 0, 1, 1, 0,25, 0, 0, 0, 0, 0, 0]T;
w4 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0,25]T.
Аналогичным образом определяем левые собственные v2, v4 и присоеди-
ненные векторы v1, v3 нулевого собственного значения матрицы Γ:
v1 = [0,1818, 0,5455, 0,2727, 0, 0, 0, 0, 0, 0, 0, 0, 0]T;
v2 = [0, 0, 0, 0, 0, 0, 0,1818, 0,5455, 0,2727, 0, 0, 0]T;
v3 = [0, 0, 0, 0,3333, 0,6667, 0, 0, 0, 0, 0, 0, 0]T;
v4 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0,3333, 0,6667, 0]T.
133
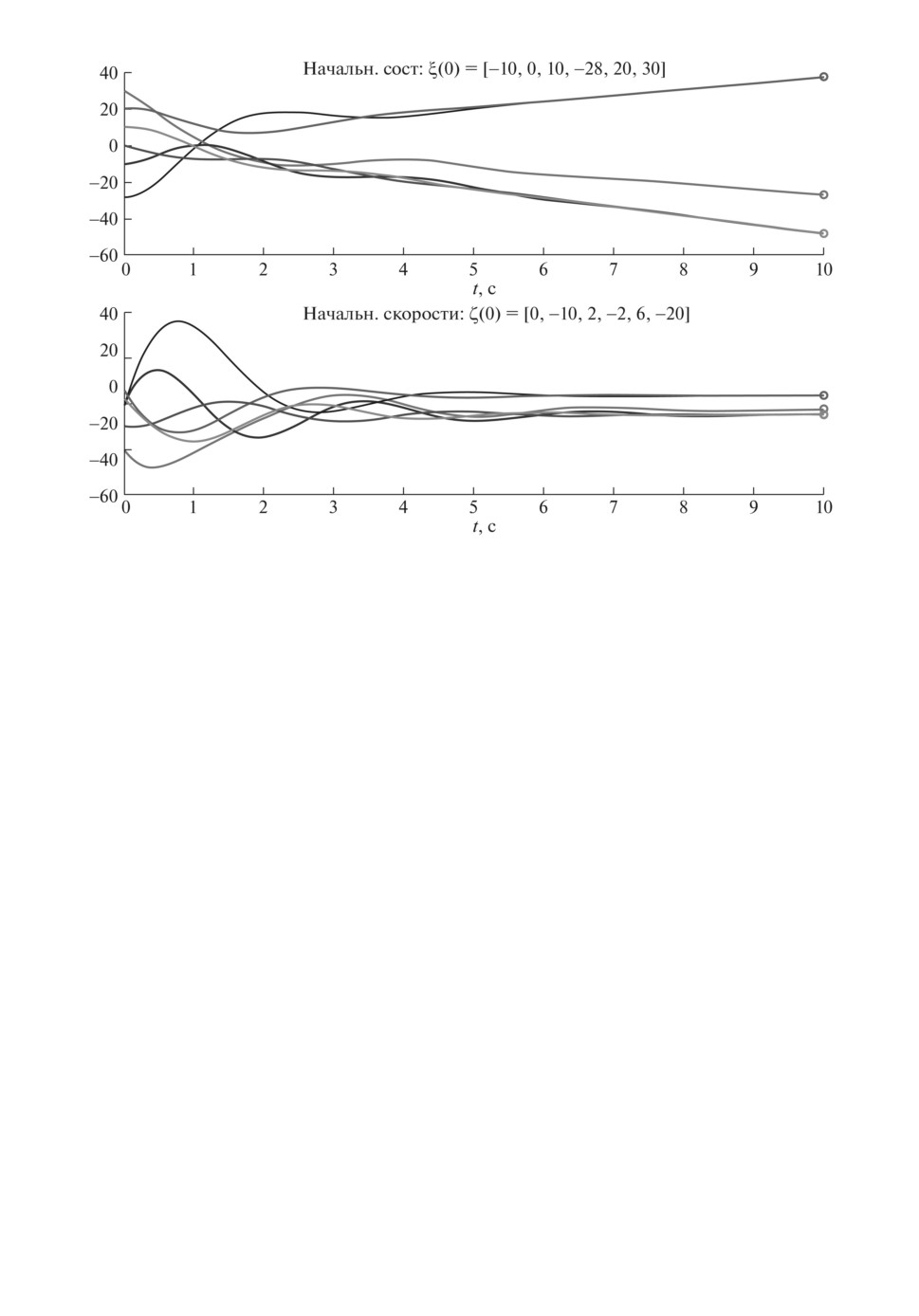
Рис. 2. Состояния и скорости агентов до добавления фоновых связей: γ = 0,5;
T = 10 c.
Согласно условию (Π.2) матрица eΓt для t = 100 определяется выражением
⎡
⎤
vT1
⎡
⎤
1
100
0
0
⎢
⎥
⎢
⎥
vT2
1
0
0
⎥⎢
⎥
e100Γ ≈ [w1,w2,w3,w4]⎣0
⎦⎢
⎥=
0
0
1
100
⎢
T
⎥
⎣ v
3
⎦
0
0
0
1
vT
4
⎡
⎤
0,1818
0,5455
0,2727
0
0
0
18,182
54,545
27,273
0
0
0
⎢
⎥
0,1818
0,5455
0,2727
0
0
0
18,182
54,545
27,273
0
0
0
⎢
⎥
⎢
⎥
⎢
0,1818
0,5455
0,2727
0
0
0
18,182
54,545
27,273
0
0
0
⎥
⎢
⎥
⎢
⎥
0
0
0
0,3333
0,6667
0
0
0
0
33,333
66,667
0
⎢
⎥
⎢
⎥
⎢
0
0
0
0,3333
0,6667
0
0
0
0
33,333
66,667
0
⎥
⎢
⎥
⎢
0,1364
0,4091
0,2046
0,0833
0,1667
0
13,636
40,909
20,455
8,333
16,667
0
⎥
=⎢
⎥
⎢
⎥
0
0
0
0
0
0
0,1818
0,5455
0,2727
0
0
0
⎢
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0,1818
0,5455
0,2727
0
0
0
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0,1818
0,5455
0,2727
0
0
0
⎥
⎢
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0
0
0
0,3333
0,6667
0
⎥
⎢
⎥
⎣
0
0
0
0
0
0
0
0
0
0,3333
0,6667
0
⎦
0
0
0
0
0
0
0,1364
0,4091
0,2045
0,0833
0,1667
0
134
Рис. 3. Состояния и скорости агентов после добавления фоновых связей:
δ/6 = 0,01; γ = 0,5; T = 50 c.
На рис. 2 приведены состояния и скорости системы, орграф зависимостей
которой приведен на рис. 1. Заметим, что до добавления “фоновых связей”
при начальном состоянии ξ(t) = [-10, 0, 10, -28, 20, 30]T, начальной скоро-
сти ζ(t) = [0, -10, 2, -2, 6, -20]T и γ = 0,5 в системе консенсус не дости-
гается.
Для t = 200 значения состояний и скоростей агентов сильно отличаются:
[ξ(t)T, ζ(t)T]T =
= [-981, -981, -981, 671, 671, -568, -4,9, -4,9, -4,9, 3,3, 3,3, -2,8]T.
Аналогичные зависимости после добавления “фоновых связей”, обеспе-
чивающих достижение консенсуса, приведены на рис. 3 для t = 50, γ = 0,5,
δ = 6/100.
Для t = 200, δ = 6/100 (итоговый вес 0,01) приближенный консенсус зада-
ется следующим вектором:
[ξ(t)T, ζ(t)T]T =
= [-362, -362, -362, -363, -363, -362, -1,9, -1,9, -1,9, -1,7, -1,7, -1,8, ]T.
4. Заключение
В многоагентных системах, как обычно, под достижением консенсуса име-
ется в виду асимптотическое совпадение характеристик для любого вектора
начальных значений. Однако если усилить это условие, т.е. потребовать, что-
бы консенсус достигался для векторов начальных значений только из опре-
135
деленной области, то наличие остовного дерева не будет необходимым усло-
вием для согласия. Такая задача может быть решена только с помощью соб-
ственного проектора лапласовской матрицы. С другой стороны, если дости-
жение консенсуса подразумевает сходимость при любом векторе начальных
значений, то “фоновая связь” может быть вложена в протокол системы: ес-
ли орграф зависимостей содержит дерево, то добавление “фоновых связей”
ничего не меняет и консенсус однозначно определится собственным проекто-
ром; а при отсутствии остовного дерева консенсус определится произведени-
ем EL⊢.
В работе доказано, что в многоагентных системах второго порядка асимп-
тотическое поведение системы при некотором ограничении на параметр γ
однозначно определяется собственным проектором лапласовской матрицы и
вектором начальных характеристик. Полученный результат, во-первых, обоб-
щает ранее полученный результат В. Рена и Э. Аткинс; во-вторых, позво-
ляет применить методы регуляризации, разработанные для многоагентных
систем первого порядка с орграфом зависимостей, не содержащим остовного
дерева.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Согласно лемме 1 линейно независи-
мые столбцы p1, . . . , pm матрицы L⊢ составляют базис ядра матрицы L. По-
этому каждый вектор w2i-1 = [pTi, 01×n]T, i = 1,... ,m, является собствен-
ным вектором нулевого собственного значения для матрицы Γ.
С другой стороны, из
[
]2
[
]
0
n
-L
-γL
Γ2 =n×n I
=
−L
-γL
γL2 -L + γ2L2
следует, что w2i = ( 01×n, pTi)T, i = 1, . . . , m, является присоединенным век-
тором для данного нулевого собственного значения матрицы Γ, т.е. Γw2i =
=w2i-1.
Векторы w1, w2, . . . , w2n нормируем так, чтобы их компоненты, соответ-
ствующие базовым бикомпонентам, были равными единице. Напомним, что
базовая бикомпонента орграфа - это максимальный по включению сильный
подграф, в который не входят дуги извне.
Аналогичным образом составляем левые собственные vT2, vT4, . . . , vT2m и
присоединенные vT1, vT3, . . . , vT2m-1 векторы нулевого собственного значения
матрицы Γ. Пусть q1, . . . , qm — линейно независимые строки матрицы L⊢.
Согласно лемме 1 эти векторы составляют базис ядра L как левые собствен-
ные векторы. Тогда каждый вектор v2i = (01×n, qTi)T, i = 1, . . . , m, будет ле-
вым собственным вектором, а векторы v2i-1 = (qTi, 01×n)T, i = 1, . . . , m, —
присоединенными для матрицы Γ.
Предположим, что определены все собственные и присоединенные векторы
(w1, w2, . . . , w2n) и (v1, v2, . . . , v2n) для матрицы Γ. Тогда матрицу Γ можно
136
представить через ее жорданову форму следующим образом:
Γ = [w1,w2,...,w2n] ×
⎡
⎤
0
1
0
0
01×(2n-2m)
⎢
0
0
0
0
01×(2n-2m)
⎥
⎢
⎥
⎢
⎥
×⎢
⎥
⎢
⎥×
⎢
0
0
0
1
01×(2n-2m)
⎥
⎣
⎦
0
0
0
0
01×(2n-2m)
0(2n-2m)×1
0(2n-2m)×1 ...
0(2n-2m)×1
0(2n-2m)×1
C
⎡
⎤
T
v
1
⎢
⎥
⎢
vT2
⎥
×⎢
⎥,
⎢
⎥
⎣
⎦
vT
2n
где матрица C - жордановые блоки для ненулевых собственных значений
матрицы Γ.
Как следует из решения 1, асимптотическое поведение системы однозначно
определяется
[
]
[
]
ξ(t)
ξ(0)
lim
= lim
eΓt
t→∞ ζ(t)
t→∞
ζ(0)
С другой стороны, согласно условию теоремы действительные части всех
собственных значений матрицы C (ее диагональные элементы) отрицатель-
ны. Поэтому при t → ∞ имеет место eCt → 0(2n-2m)×(2n-2m) и для достаточно
большого значения t можно положить eCt ≈ 0(2n-2m)×(2n-2m). Итак, для до-
статочно большого значения t получим
(Π.1)
eΓt ≈ [w1,w2,... ,w2n
]×
⎡
⎤
1
t
0
0
01×(2n-2m)
⎢
0
1
0
0
01×(2n-2m)
⎥
⎢
⎥
⎢
⎥
⎢
⎥
×
⎢
⎥×
⎢
0
0
1
t
01×(2n-2m)
⎥
⎣
⎦
0
0
0
1
01×(2n-2m)
0(2n-2m)×1
0(2n-2m)×1 ...
0(2n-2m)×1
0(2n-2m)×1
0(2n-2m)×(2n-2m)
⎡
⎤
T
v
1
⎢
⎥
⎢
vT2
⎥
⎢
⎥.
⎢
⎥
⎣
⎦
vT
2n
137
Заметим, что последнее выражение не зависит от векторов w2m+1, . . . , w2n и
v2m+1,... ,v2n. Поэтому (Π.1) можно записать как
⎡
⎤
⎡
⎤
1
t ...
0
0
vT1
⎢
0
1
0
0
⎥
⎢
⎥
⎢
⎥
vT2
⎢
⎥
⎥
(Π.2)
eΓt ≈ [w1,w2,... ,w2m]⎢⎢
⎢
⎥
⎥
⎣
⎦
⎣
⎦
0
0
1
t
vT
0
0
0
1
2m
Из определений векторов wi и vi, i = 1, . . . , m, для достаточного большого t
получаем
[
]
L⊢ L⊢t
eΓt ≈
0n×n L⊢
Следующая эквивалентная запись полученной формулы завершает дока-
зательство теоремы:
[
]
[
]
L⊢ L⊢t
1
t
=
⊗L⊢.
0n×n L⊢
0
1
Доказательство теоремы 2. В утверждении теоремы предполага-
ется выполнение условия (5) для матрицы L. Однако если это условие выпол-
няется для L, то оно выполнится и для матрицы L + δK при любом δ ≥ 0.
Действительно, пусть μ - собственное значение матрицы L, а x - соответ-
ствующий ему собственный вектор. Очевидно, что Lx = L(x + c) = μx, где
c - вектор с одинаковыми компонентами. Тогда
(L + δK)x = (L + δI - δE)x = Lx + δx - δEx = μx + δx - x =
(Π.3)
= (μ + δ)x + x = (μ + δ)(x + xo) = (L + δK)(x + xo),
1
где xo = x
- вектор с одинаковыми компонентами.
μ+δ
Из (Π.3) непосредственно следует, что (μ + δ) - собственное значение мат-
рицы L + δK. Поэтому если условие (5) выполняется для матрицы L, то для
достаточно маленького значения δ это же условие будет выполняться для
L+δK.
Доказательство (8) следует из теоремы 1 и предложения 2. Действительно,
[
]
[
]
EL⊢ EL⊢t
1
t
=
⊗ EL⊢.
0n×n EL⊢
0
1
СПИСОК ЛИТЕРАТУРЫ
1. Агаев Р.П., Чеботарев П.Ю. Модели латентного консенсуса // АиТ. 2017. № 1.
С. 106-120.
Agaev R.P., Chebotarev P.Yu. Models of Latent Consensus // Autom. Remote
Control. 2017. V. 78. No. 1. P. 88-99.
138
2.
Агаев Р.П., Чеботарев П.Ю. О методе проекции для непрерывной модели кон-
сенсуса // АиТ. 2015. № 8. С. 140-152.
Agaev R.P., Chebotarev P.Yu. The Projection Method for Continuous-time
Consensus Seeking // Autom. Remote Control. 2015. V. 76. No. 8. P. 1436-1445.
3.
Chebotarev P., Agaev R. The Forest Consensus Theorem // IEEE Transact. Autom.
Control. 2014. V. 59. No. 9. P. 2475-2479.
4.
Поляк Б.Т., Тремба А.А. Решение задачи PageRank для больших матриц с по-
мощью регуляризации // АиТ. 2012. № 11. C. 144-166.
Polyak B.T., Tremba A.A. Regularization-based Solution of the PageRank Problem
for Large Matrices // Autom. Remote Control. 2012. V. 73. No. 11. P. 1877-1894.
5.
Ren W., Atkins E. Distributed multi-vehicle coordinated control via local information
exchange // Int. J. Robust Nonlinear Control. 2007. V. 17. No. 10-11. P. 1002-1033.
6.
Olfati-Saber R. Flocking for multi-agent dynamic systems: Algorithms and theory //
IEEE Transactions on Automatic Control. 2006. V. 51. No. 3. P. 401-420.
7.
Чеботарев П.Ю., Агаев Р.П. Согласование характеристик в многоагентных си-
стемах и спектры лапласовских матриц орграфов // АиТ. 2009. № 3. С. 136-151.
Chebotarev P.Yu., Agaev R.P. Coordination in Multiagent Systems and Laplacian
Spectra of Digraphs // Autom. Remote Control. 2009. V. 70. No. 3. P. 469-483.
8.
Yu W., Chen G., Cao M. Some Necessary and Sufficient Conditions for Second-
order Consensus in Multi-agent Dynamical Systems // Automatica. 2010. V. 46.
No. 6. P. 1089-1095.
9.
Liu H., Xie G., Wang L. Necessary and Sufficient Conditions for Solving Consensus
Problems of Double-integrator Dynamics via Sampled Control //Int. J. Robust
Nonlinear Control. 2010. V. 20. No. 15. P. 1706-1722.
10.
Meyer C.D. Limits and the Index of a Square Matrix // SIAM J. App. Math. 1974.
V. 26. P. 469-478.
Статья представлена к публикации членом редколлегии А.Л. Фрадковым.
Поступила в редакцию 27.07.2018
После доработки 16.04.2019
Принята к публикации 18.07.2019
139