Автоматика и телемеханика, № 11, 2019

Оптимизация, системный анализ

и исследование операций

(Национальный исследовательский университет

«Высшая школа экономики», Москва),

М.В. УЛЬЯНОВ, д-р техн. наук (muljanov@mail.ru)

(Институт проблем управления РАН им. В.А. Трапезникова, Москва

ВМК МГУ им. Ломоносова),

М.И. ФОМИЧЕВ (michan94@yandex.ru)

(Национальный исследовательский университет

«Высшая школа экономики», Москва)

КОМБИНИРОВАННЫЙ ТОЧНЫЙ АЛГОРИТМ

ДЛЯ АСИММЕТРИЧНОЙ ЗАДАЧИ КОММИВОЯЖЕРА:

ПОСТРОЕНИЕ И СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ

ВРЕМЕННОЙ ЭФФЕКТИВНОСТИ¹

Приведены результаты сравнительного статистического анализа вре-

мени решения несимметричной задачи коммивояжера (NTSP) методом

ветвей и границ (без предвычисления тура) и комбинированным мето-

дом. Комбинированный метод состоит из приближенного алгоритма Lin-

Kernighan-Helsgaun, используемого для вычисления начального тура, и

метода ветвей и границ. Показано, что использование приближенного ре-

шения, найденного с помощью алгоритма Lin-Kernighan-Helsgaun, поз-

воляет существенно уменьшить время поиска точного решения задачи

коммивояжера методом ветвей и границ для задач из некоторого клас-

са. Построен прогноз времени поиска точного решения методом ветвей и

границ и комбинированным алгоритмом. Вычислительный эксперимент

показал, что доля задач, которые комбинированным алгоритмом были

решены быстрее,чем методом ветвей и границ, растет с ростом размерно-

сти задачи.

Ключевые слова: задача коммивояжера, метод ветвей и границ, аппрок-

симация вероятностного распределения, квантиль вероятностного распре-

деления, вероятностный прогноз времени.

DOI: 10.1134/S0005231019110096

1. Введение

Задача коммивояжера заключается в поиске гамильтонова цикла с мини-

мальной суммой весов ребер в полном (ориентированном в случае несиммет-

ричной задачи) графе. Уже при относительно небольшом (порядка десятков)

¹ Исследование выполнено за счет гранта Российского научного фонда (проект № 17-

19-01665).

155

порядке матрицы, описывающей задачу, для осуществления полного перебо-

ра всевозможных гамильтоновых циклов требуется слишком много времени,

поэтому были предприняты многочисленные попытки усовершенствовать пе-

ребор. Одним из наиболее известных и широко применяемых алгоритмов оп-

тимизированного перебора является метод ветвей и границ (англ. Branch and

Bound Method, сокращенно B&B) [1-8].

В рамках проведенного исследования использовалась классическая реали-

зация метода ветвей и границ [1], которая предполагает следующие особен-

ности:

• дуга ветвления (k, l) выбирается так, чтобы получить большую по вели-

чине нижнюю границу подмножества множества допустимых решений, ко-

торые не содержат дугу (k, l);

• приведенная матрица стоимостей хранится только в корне дерева, в узлах

поискового дерева решений матрицы не хранятся, матрица стоимостей усе-

кается при необходимости для каждого из узлов дерева решений;

• для хранения листьев поискового дерева решений используется упорядо-

ченный список;

• процедура удаления вершин поискового дерева решений осуществляется

каждый раз при нахождении нового кандидата на оптимальное решение.

Метод ветвей и границ пытались улучшить, например в [9], в том чис-

ле за счет использования в качестве начального тура гамильтонова цикла,

найденного другим (например, жадным) алгоритмом [10-14]. Такой способ

позволяет исключить из рассмотрения вершины дерева решений с нижней

оценкой, не меньшей суммы весов дуг этого тура. Однако показано [15], что

только в случае рекорда, очень близкого к оптимальному туру (т.е. со стоимо-

стью, превышающей не более чем на 5% стоимость оптимального решения),

значительное число вершин может быть исключено. Предвычисленные ту-

ры со стоимостью, значительно большей стоимости оптимального тура, не

ускоряют работу метода ветвей и границ.

Ранее [16] авторами статьи исследовалась такая характеристика индиви-

дуальной задачи коммивояжера, как сложность [17], равная числу вершин

поискового дерева, построенного при решении задачи методом ветвей и гра-

ниц.

Поскольку число вершин дерева решений зависит от того, использовался

ли предвычисленный тур, и от качества этого тура, то будем далее называть

сложностью индивидуальной задачи коммивояжера число вершин, постро-

енных классическим методом ветвей и границ (без предвычислений). Число

вершин, порожденных методом ветвей и границ с использованием предвы-

численого тура, будем называть сложностью индивидуальной задачи при ис-

пользовании предвычисленного тура, полученного некоторым эвристическим

алгоритмом.

Отметим, что сложность индивидуальной задачи коммивояжера при ис-

пользовании предвычисленного тура не будет значительно меньше сложности

индивидуальной задачи коммивояжера (без предвычислений), если стоимость

предвычисленного тура значительно больше стоимости оптимального тура.

156

2. Постановка задачи

Объектом исследования в данной статье является несимметричная задача

коммивояжера. Решаются индивидуальные несимметричные задачи комми-

вояжера с матрицей стоимостей, элементы которой — псевдослучайные числа

с равномерным распределением.

Предмет исследования — временная эффективность программной реали-

зации комбинированного точного алгоритма, включающего в себя эвристи-

ческий алгоритм для поиска начального тура и метод ветвей и границ для

получения точного решения задачи коммивояжера.

Авторы ставят перед собой в рамках данной статьи следующие задачи:

Выбор эвристического алгоритма для получения первоначального псевдо-

оптимального тура, обеспечивающего начиная с некоторой размерности

асимметричной задачи коммивояжера сокращение среднего значения вре-

мени получения точного решения. В комбинированном алгоритме (далее

E + B&B) время получения точного решения представляет собой сумму

времени работы эвристического алгоритма E и метода ветвей и границ

(далее B&B ) с предвычисленным туром, т.е. надо найти такой эвристи-

ческий алгоритм E и такую размерность задачи n₀, что

(1)

∀n > n₀

tE+B&B(n) < tB&B

(n).

Статистическое исследование экспериментально полученных значений

времени работы программных реализаций алгоритмов B&B и E + B&B

с целью сравнения быстродействия алгоритмов. Построение аппрокси-

мирующих семейств распределений времени работы алгоритмов B&B и

E + B&B. Прогнозирование среднего и квантилей времени работы алго-

ритма E + B&B при помощи линейных функций, зависящих от размерно-

сти ATSP.

Оценка качества прогноза путем сравнения прогнозируемых значений

среднего времени работы алгоритма E + B&B, а также квантилей аппрок-

симирующего распределения с соответствующими значениями контроль-

ной выборки.

Определение характерных особенностей индивидуальных задач, для кото-

рых комбинированный алгоритм E + B&B обеспечивает ощутимое сокра-

щение времени расчета:

(2)

tE+B&B(A) < tB&B

(A).

Исследование зависимости времени решения задачи коммивояжера от

сложности.

Формулировка рекомендаций по применению комбинированного алгорит-

ма.

3. Выбор эвристического алгоритма

Классический метод ветвей и границ не предполагает наличие какого-либо

тура в момент начального запуска, поэтому сначала многократно проводит-

ся процедура ветвления, порождаются вершины поискового дерева, а исклю-

чение вершин из рассмотрения не ведется. В зависимости от особенностей

157

индивидуальной задачи число вершин дерева решений может быть довольно

большим к моменту, когда будет найден первый тур. Использование тура,

найденного заранее каким-либо приближенным методом, позволяет начать

исключение вершин из рассмотрения раньше, в результате будет порождено

меньшее число вершин дерева решений, что уменьшит сложность задачи и

время поиска оптимального тура.

С другой стороны, на получение начального тура придется тратить время,

так что общее время расчетов будет складываться из времени, затраченного

на поиск начального тура, и времени работы метода ветвей и границ с най-

денным туром (будем называть его далее предвычисленным туром). В связи

с этим будем искать настолько быстрый алгоритм поиска начального тура,

чтобы суммарное время работы алгоритма для нахождения предвычисленно-

го тура и алгоритма метода ветвей и границ с найденным предвычисленным

туром было не больше времени работы классического метода ветвей и границ.

Из экспериментального исследования, проведенного одним из авторов ста-

тьи [15], следует:

• если предвычисленный тур является оптимальным, то сложность инди-

видуальной задачи при использовании предвычисленного тура меньше в

среднем приблизительно на 35-40% ;

• если стоимость предвычисленного тура на 5% больше, чем оптимального,

то сложность индивидуальной задачи при использовании предвычисленно-

го тура не будет заметно меньше, чем сложность при решении этой задачи

классическим B&B.

Обозначим через ε точность предвычисленного тура:

p_E(A) - pB&B(A)

(3)

ε=

pB&B(A)

где pB&B(A) и p_E(A) — соответственно стоимость оптимального тура зада-

чи коммивояжера с матрицей стоимостей A и стоимость тура, найденного

приближенным алгоритмом E. Пусть γ — отношение сложности при исполь-

зовании предвычисленного тура к сложности индивидуальной задачи комми-

вояжера:

cB&B(A) - cE+B&B(A)

(4)

γ=

cB&B(A)

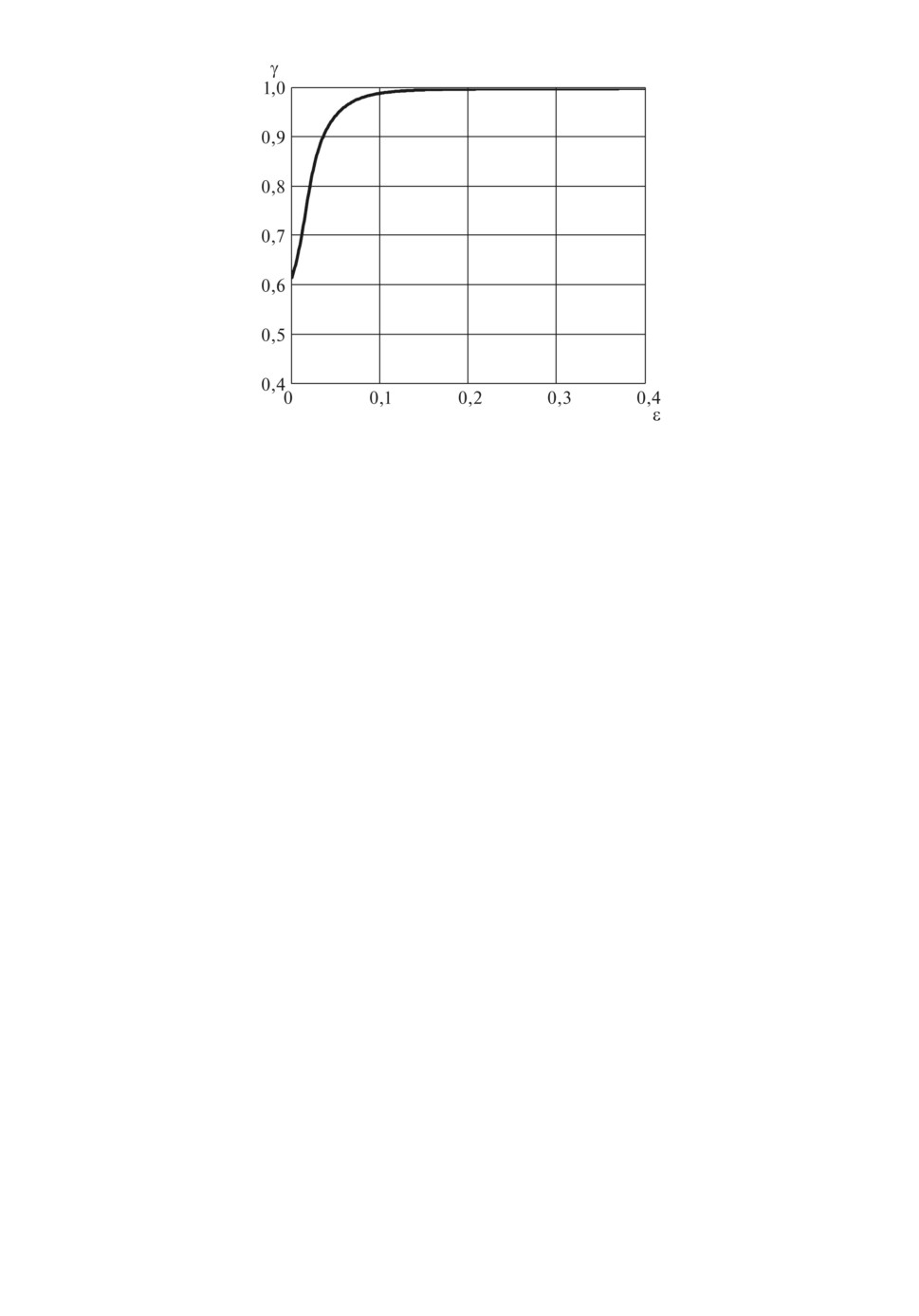
На рисунке представлена зависимость γ от точности ε предвычисленного

тура для n = 45 [15], для других размерностей график аналогичный.

Зависимость получена для несимметричных задач коммивояжера с эле-

ментами матрицы стоимостей, полученными генератором псевдослучайных

чисел с равномерным распределением.

Таким образом, для поиска начального тура для метода ветвей и границ

необходим приближенный алгоритм, быстро находящий решение, очень близ-

кое к оптимальному. Будем искать подходящий алгоритм в классе эвристи-

ческих алгоритмов.

158

Зависимость γ от ε.

На основе предварительного анализа литературных источников [15, 18-28]

было решено для получения предвычисленного тура использовать эвристиче-

ские алгоритмы, улучшающие решения. В 1971 г. S. Lin и B.W. Kernighan [29]

предложили эффективный эвристический алгоритм, основанный на итера-

ционном улучшении случайно полученного тура. Позднее, в 2000 г. Keld

Helsgaun представил в [30] модифицированную реализацию алгоритма Lin-

Kernighan. Алгоритм Lin-Kernighan-Helsgaun (далее LKH) находит допусти-

мое решение, затем строит два множества дуг таких, что если все дуги пер-

вого множества удалить из найденного тура и заменить их дугами из второго

множества, то результатом будет тур с меньшей суммой весов дуг. Процесс

замены дуг повторяется до тех пор, пока невозможно сформировать два под-

ходящих множества дуг. Все ограничения на множества дуг и особенности их

выбора подробно описаны в [30].

Этот алгоритм достаточно часто находит не только субоптимальные, но и

оптимальные решения за приемлемое время даже для задач большой размер-

ности (порядка 10⁴). Именно благодаря этому свойству, алгоритм LKH был

выбран в качестве эвристического алгоритма для получения предвычислен-

ного тура. В предлагаемом исследовании алгоритм LKH запускается только

один раз, аналогично [31].

4. Статистическое исследование времени работы B&B и E + B&B

Сравнение времени работы B&B без предвычисленного тура и комби-

нированного алгоритма вначале проведем на основе выборочных средних

(табл. 1), затем сравним выборочные квантили распределений времени ра-

боты этих алгоритмов и доли задач в выборке и ее частях, которые были

решены комбинированным алгоритмом быстрее, чем B&B.

Вычислительный эксперимент проводился на стационарном компьютере

со следующими характеристиками:

• процессор Intel i7 8700K 4700 MHz;

159

Таблица 1. Минимальное, максимальное и среднее время работы B&B и

E + B&B, мс.

min min

max

среднее среднее

СКО СКО

n B&B комб. B&B

комб.

B&B комб. B&B комб.

227

2764

588975

589430

24070

31457

30747

30655

324

5287

2010030

1967021

78111

87304

108205

106739

445

5723

15011713

12654423

263125

270031

467713

439801

2144

8307

68240602

49713361

875652

848704

210841

1708932

4013

10533

1464202466

441979575

3046440

2634915

21328841

7631699

• оперативная память Corsair Vengeance LPX CMK32GX4M2B3466C16R

DDR4 3466MHz 32 ГБ;

• материнская плата ASRock Fatal1ty Z370 Gaming K6;

• операционная система Arch with kernel version 4.14.13-1-ARCH.

Для минимизации шумов операционной системы фоновые процессы, кото-

рые не нужны для исследования, были отключены, а также отсутствует гра-

фический пользовательский интерфейс, а управление операционной системой

осуществлялось посредством командной строки. Алгоритмы реализованы на

языке С++ и скомпилированы в исполняемый файл с помощью компилятора

gcc 7.2.1 20171224.

На данной аппаратной конфигурации был проведен вычислительный экс-

перимент по решению задач коммивояжера с матрицами стоимостей, имею-

щими порядок от 30 до 50. Для каждого значения порядка матрицы стоимо-

стей было рассмотрено 10⁴ задач коммивояжера, каждая задача была решена

методом ветвей и границ и комбинированным методом. Все выборочные ха-

рактеристики были вычислены при объеме выборки 10⁴.

Как видно из табл. 1, среднее время работы комбинированного алгоритма

больше для задач размерностей до 40, а для размерностей более 45 комбини-

рованный алгоритм работает несколько быстрее в среднем. Кроме того, сред-

неквадратическое отклонение времени работы комбинированного алгоритма

меньше, чем у B&B, причем с ростом размерности задач до 50 среднеквад-

ратическое отклонение (СКО) времени работы комбинированного алгоритма

становится меньше почти в 3 раза по сравнению с B&B.

Также можно заметить, что максимальное время работы комбинирован-

ного алгоритма растет медленнее с ростом размерности, чем в случае B&B,

так что для n = 45 максимальное значение времени работы комбинированно-

го алгоритма на 27% меньше, а для n = 50 — на 70% меньше.

В табл. 1 n — число вершин графа в задаче коммивояжера (равное порядку

матрицы стоимостей), время здесь и далее в статье измеряется в миллисекун-

дах.

Для построения прогноза квантилей и среднего времени работы алгорит-

мов построим аппроксимирующее семейство распределений для натурально-

го логарифма времени работы алгоритмов. Для определения типа распреде-

ления воспользуемся квантильными коэффициентами асимметрии и эксцесса

[32, 33] аналогично тому, как это было сделано для сложности индивидуаль-

ных задач коммивояжера в [16, 34].

160

Для выборок времени работы B&B по 10000 задач для каждой раз-

мерности были получены значения квантильного коэффициента асимметрии

от -0,037 до 0,018 и квантильного коэффициента эксцесса от 1,206 до 1,262.

Для комбинированного алгоритма соответственно имеем квантильный коэф-

фициент асимметрии от -0,022 до 0,079 и квантильный коэффициент эксцес-

са от 1,194 до 1,297. Для нормального распределения независимо от значе-

ний параметров квантильный коэффициент асимметрии равен 0, а квантиль-

ный коэффициент эксцесса — примерно 1,23, поэтому будем далее использо-

вать нормальное распределение в качестве аппроксимирующего распределе-

ния для натурального логарифма времени работы B&B и комбинированного

алгоритма.

Параметры аппроксимирующего нормального распределения будем под-

бирать, строя линейную зависимость выборочных средних и выборочных

среднеквадратических отклонений от размерности задач. Для диапазона раз-

мерностей от 30 до 50 с шагом 1 были получены выборки по 10000 матриц

стоимостей для каждой размерности. Распределение элементов матриц было

выбрано равномерным непрерывным на интервале [0, 1]. Каждая задача бы-

ла решена B&B, затем те же самые задачи в том же порядке были решены

комбинированным алгоритмом. При решении задачи коммивояжера комби-

нированным алгоритмом приближенный алгоритм LKH запускался один раз,

затем полученный псевдооптимальный тур использовался в качестве предвы-

численного тура в B&B.

По полученным выборкам были вычислены значения выборочных средних

натурального логарифма времени работы обоих алгоритмов, а также сред-

неквадратические отклонения. Далее методом наименьших квадратов были

вычислены коэффициенты сдвига и масштаба линейных функций, наилуч-

шим образом приближающих зависимость выборочных средних и средне-

квадратического отклонения от размерности задачи (для комбинированно-

го алгоритма и B&B). Полученные линейные функции были использованы

для аппроксимации и экстраполяции зависимости от размерности задачи па-

раметров нормального распределения, приближающего распределение нату-

рального логарифма времени работы каждого алгоритма.

Обозначим μB&B(n), σB&B(n), μE+B&B(n), σE+B&B(n), найденные линей-

ные зависимости выборочных средних и среднеквадратических отклонений

времени работы B&B и комбинированного алгоритма соответственно:

(5)

μB&B

(n) = 0,217n + 3,06,

(6)

σB&B

(n) = 0,015n + 0,59,

(7)

μE+B&B

(n) = 0,219n + 2,96,

(8)

σE+B&B

(n) = 0,0135n + 0,65.

Отклонения выборочных средних (вычисленных по выборкам объема 10000

для каждой размерности задач от 30 до 50) от соответствующих значений,

найденных по формулам (5)-(8), составляют менее 0,5%, для среднеквадра-

тических отклонений — менее 2%.

Далее для размерностей задач от 30 до 50 были вычислены квантили нор-

мальных распределений с параметрами, найденными по формулам (5)-(8).

161

Качество аппроксимации натурального логарифма времени работы каждого

алгоритма нормальным распределением с параметрами (5)-(8) оценим, срав-

нивая вычисленные квантили нормального распределения с выборочными

квантилями натуральных логарифмов времени работы алгоритмов. Исполь-

зуем данные о времени работы B&B и комбинированного алгоритма при

решении одного набора по 10000 задач коммивояжера для каждой размер-

ности от 30 до 50. Выборочные квантили натурального логарифма времени

работы B&B уровня 25, 50 и 75% отличаются от квантилей нормального рас-

пределения с параметрами, вычисленными по (5)-(8), на 0,1-0,5%. Различие

между выборочными квантилями и квантилями соответствующего нормаль-

ного распределения монотонно уменьшается с ростом размерности задач для

квантилей уровня от 10 до 90%.

Ввиду того, что логарифмическая функция монотонно возрастает (исполь-

зуется натуральный логарифм), квантили времени работы B&B (а также

комбинированного алгоритма) можно найти, потенцируя соответствующие

квантили натурального логарифма времени. Выборочные квантили времени

работы B&B уровня 25, 50% отличаются от экспонент квантилей нормаль-

ного распределения (или, что то же самое, квантилей логнормального рас-

пределения) с параметрами, вычисленными по (5)-(8) менее, чем на 7%, для

квантилей уровня 75% отличие менее 4%. С ростом размерности задач до

50 отличия квантилей времени уровней 5-99% от аппроксимирующих значе-

ний уменьшаются до 1-2%.

Выборочные квантили времени работы комбинированного алгоритма при

небольших значениях уровня отличаются от аппроксимирующих значений

сильнее, чем у B&B, особенно для небольших (до 40) размерностей задач.

Так, отличие квантилей уровня 5% уменьшается от 66 до 7% с ростом раз-

мерности задачи от 30 до 50. Отличие квантилей уровней 50 и 75% от аппрок-

симирующих значений уменьшается соответственно от 40 и 25 до 1%. В то

же время квантили уровня 90% и больше отличаются в меньшей степени от

аппроксимирующих значений, в основном на 1-5% даже для размерностей

от 35.

Различное поведение квантилей низких порядков у времени работы B&B

и комбинированного алгоритма объясняется влиянием времени, затраченного

приближенным алгоритмом LKH на вычисление тура. Это время не пропор-

ционально времени, затраченному B&B на решение этой задачи, оно мало

по сравнению со средним временем решения задачи этой же размерности, но

от близкого к минимальному наблюдаемому времени решения задачи может

отличаться несильно.

5. Построение прогноза и оценка его качества

Используем аппроксимацию натурального логарифма времени решения

задачи коммивояжера нормальным распределением для построения прогно-

за среднего и среднеквадратического отклонения натурального логарифма

времени работы B&B и алгоритма как функций размерности.

Далее будем использовать связь нормального и логнормального распреде-

лений: если случайная величина X имеет логнормальное распределение, то

162

Таблица 2. Сравнение прогнозируемых квантилей с выборочными

ω₂₅

ω₅₀

ω₇₀

ω₉₀

n B&B E + B&B B&B E + B&B B&B E + B&B B&B E + B&B

-4

-2

-8

-6

-9

-8

-9

-2

-4

-12

-14

-11

-17

-13

-22

-28

-21

-26

-11

-27

случайная величина ln X распределена нормально с теми же параметрами

μ и σ. Для удобства приведем формулы плотностей соответствующих друг

другу нормального (9) и логнормального (9) распределений [35]:

-(x-μ)

(9)

f (x) =

√ e 2σ²

2π

-(ln x-μ)

(10)

f (x) =

√ e

2σ²

xσ

2π

Прогноз квантилей времени решения задачи коммивояжера B&B и ком-

бинированного алгоритма можно получить по формулам

(11)

q_p = eqpорм,

где qpорм — квантили нормального распределения с параметрами, вычислен-

ными по (5)-(8).

Сравним прогнозируемые (по результатам статистической обработки вы-

борок объема 10000 задач размерности от 30 до 50) значения квантилей вре-

мени работы B&B и E + B&B с соответствующими значениями контрольной

выборки объема 1000 размерностей 55, 60 и 65. В табл. 2 представлены отно-

сительные отличия (в %) прогнозируемых и наблюдаемых квантилей уровня

25, 50, 70 и 90, вычисленные по формуле

qpыборочн - qpорм

(12)

ω_p = 100

qpыборочн

Для прогноза среднего значения натурального логарифма времени рабо-

ты алгоритмов можно воспользоваться зависимостями (5) и (7), используе-

мыми в качестве аппроксимации параметра μ нормального распределения,

приближенно описывающего распределение натурального логарифма време-

ни работы алгоритмов. Прогноз среднего времени работы алгоритмов можно

получить по формулам, связывающим математическое ожидание и диспер-

сию логнормально распределенной случайной величины X с параметрами μ

и σ соответствующей нормальной случайной величины:

(13)

EX = eμ+σ2/²,

(14)

DX = (eσ2 - 1)e2μ+σ2 ,

√

(15)

DX = EX eσ2

− 1.

163

Таблица 3. Среднее относительное ускорение и доля ускоренных задач

среднее, среднее, отн. откл.,

СКО,

отн. откл.,

n прогноз выборка

прогноз

выборка

натуральные логарифмы времени B&B

14,99

14,95

-0,24

1,41

0,24

16,07

16,06

-0,08

1,48

1,53

2,88

17,16

17,08

-0,48

1,56

1,75

10,88

натуральные логарифмы времени комбинированного алгоритма

15,0

14,96

-0,29

1,39

1,35

-2,65

16,1

16,02

-0,47

1,46

1,42

-2,16

17,19

16,97

-1,29

1,52

1,57

3,1

время B&B

8851632

18426169

22402702,86

289538698,43

29210827

57601429

83689156,34

686238735,54

96940941

197362756

315309546,87

1534229312,24

время комбинированного алгоритма

8662623

9622779

21134291

53524540

28510984

27846776

-2

77706642

87834992

94265716

87403339

-7

287648920

325819590

натуральные логарифмы времени B&B, без максимумов

14,99

14,94

-0,33

1,41

1,38

-2,06

16,07

16,05

-0,12

1,48

1,51

1,68

17,16

17,07

-0,53

1,56

1,74

10,11

натуральные логарифмы времени комбинированного алгоритма, без максимумов

15,0

14,95

-0,36

1,39

1,33

-4,33

16,1

16,01

-0,5

1,46

1,41

-2,85

17,19

16,96

-1,32

1,52

1,56

2,46

время B&B, без максимумов

8851632

8579177

-3,17

22402702,86

20893391,09

-7,22

29210827

36285516

19,49

83689156,34

130486873,56

35,86

96940941

152130922

36,27

315309546,87

557043066,24

43,39

время комбинированного алгоритма, без максимумов

8662623

7649809

-13

21134291

15181657

-39

28510984

25822374

-10

77706642

60203855

-29

94265716

78828873

-19

287648920

180950805

-58

Для контроля качества построенного прогноза среднего времени работы

алгоритмов и среднеквадратического отклонения используем контрольные

выборки объема 1000 задач размерности 55, 60 и 65. В табл. 3 приведены

прогнозируемые значения среднего натурального логарифма времени (во вто-

ром столбце) и его среднеквадратического отклонения (в пятом столбце) для

обоих алгоритмов, а также прогнозируемое и наблюдаемое среднее время

и его среднеквадратическое отклонение. В третьем и шестом столбцах таб-

лицы даны средние значения и среднеквадратические отклонения выборок,

в четвертом и седьмом столбцах — относительные отклонения выборочных

значений от прогнозируемых, вычисленные по формулам:

Z^∗

ω=

· 100,

Z^∗

164

где Z^∗ — прогнозируемое значение величины Z,

Z — выборочное значение Z.

В четвертом столбце приведены относительные отклонения выборочных зна-

чений от прогнозируемых для среднего, в седьмом — для среднеквадратиче-

ского отклонения.

Под двойной чертой в этой таблице представлены результаты таких же

расчетов, проведенных по тем же выборкам, но из каждой выборки было

удалено максимальное значение времени. Как видно, среднее время не может

служить надежной характеристикой временной эффективности алгоритма,

поскольку оно очень сильно меняется под влиянием единичных задач, на

решение которых понадобилось значительно больше времени, чем в среднем

на остальные.

С одной стороны, чем больше объем выборки, тем более точно матема-

тическое ожидание наблюдаемой случайной величины может быть оценено

выборочным средним. С другой — чем больше выборка, тем больше вероят-

ность встретить в ней задачу, которая будет решаться очень долго и серьезно

повлияет на величину выборочного среднего.

Резюмируя сказанное выше, отметим, что более предпочтительными ха-

рактеристиками временной эффективности кажутся квантили распределения

времени работы алгоритма, они гораздо менее чувствительны к отдельным

выделяющимся значениям.

Полученные результаты свидетельствуют о том, что построенная аппрок-

симация может быть использована для грубой оценки времени решения за-

дачи коммивояжера при размерностях больше 50. Большие отличия выбо-

рочных и теоретических квантилей при размерности 65 по сравнению с раз-

мерностями 55 и 60 могут означать, что используемый вычислительный ком-

плекс работает на пределе своих возможностей. В этом случае для решения

большого числа задач большей размерности следует использовать более про-

изводительную вычислительную систему.

6. Определение характерных особенностей индивидуальных задач

Анализируя данные об относительном ускорении решения задачи комми-

вояжера, вычисленном по формуле

tB&B - tE+B&B

(16)

ν = 100

tB&B

можно заметить, что некоторые задачи решаются комбинированным алго-

ритмом медленнее, чем B&B, но в основном это задачи, решаемые обоими

алгоритмами быстро. В этом случае ускорение расчетов благодаря наличию

тура незначительно, в то время как приближенный алгоритм тратит на поиск

тура хоть и небольшое время, но сравнимое со временем работы B&B, так что

сумма времени работы приближенного алгоритма и B&B с предвычисленным

туром оказывается больше времени работы B&B без предвычислений. С дру-

гой стороны, для задач, требующих много времени на нахождение точного

решения, ускорение за счет использования предвычисленного тура может до-

стигать 50%, т.е. комбинированный алгоритм работает в 2 раза быстрее на

некоторых задачах.

165

Таблица 4. Среднее относительное ускорение и доля ускоренных задач, eμ+kσ

e^μ,

eμ+σ,

eμ+2σ,

eμ+3σ,

n сред. уск., доля сред. уск., доля сред. уск., доля сред. уск., доля

-28,24

6,44

-10,16

11,99

-3,53

17,8

0,87

36,36

-11,28

7,67

-4,11

12,83

-0,38

42,71

2,39

100,0

-3,58

13,62

-0,22

40,33

2,69

94,01

9,17

100,0

0,17

46,7

2,59

94,14

7,67

100,0

21,28

100,0

2,17

75,49

5,89

98,57

15,09

100,0

33,37

100,0

Для более детального анализа из выборок объема 10000 для каждой раз-

мерности задач комивояжера от 30 до 50 были извлечены подмножества за-

дач, для которых время решения B&B было больше, чем

(17)

eμ+kσ

k = 0,1,2,3,

где μ и σ — параметры нормального распределения, аппроксимирующего рас-

пределение логарифма времени решения задач коммивояжера. Эти парамет-

ры немного отличаются у B&B и комбинированного алгоритма.

Таким образом, для каждой размерности задачи коммивояжера было по-

лучено 4 подмножества задач из выборки объема 10000. Для каждого тако-

го подмножества было вычислено относительное ускорение каждой задачи

комбинированным алгоритмом по формуле (16), а также среднее в этом под-

множестве ускорение и доля задач, для которых ускорение было больше 0.

Результаты анализа приведены в табл. 4.

Как видно из таблицы, доля задач, решаемых быстрее комбинированным

алгоритмом, растет с ростом времени работы B&B. Среднее относительное

ускорение варьируется от -28% до 33%. Несмотря на сравнительную малость

среднего относительного ускорения, оно значительно влияет на величину

среднего времени расчета в выборке из 10000 задач. Так, ускорение 0,2%

наиболее долго решаемых задач размерности 50 в среднем на 33% в сово-

купности со значительно меньшим ускорением остальных задач приводит к

уменьшению среднего времени решения для всей выборки почти на 1% по

сравнению с B&B без предвычислений.

Аналогичный расчет был проведен на основе квантилей логнормального

распределения с параметрами, соответствующими параметрам нормального

распределения, аппроксимирующего логарифм времени работы B&B. При

фиксированной размерности задач коммивояжера параметры μ и σ логнор-

мального распределения времени работы каждого алгоритма соответствуют

параметрам μ и σ нормального распределения, аппроксимирующего нату-

ральный логарифм времени работы.

Из выборок объема 10000 для каждой размерности задач коммивояжера

от 30 до 50 были извлечены подмножества задач, для которых время решения

B&B было больше, чем квантиль уровня p = 50,60,70 и 80 логнормального

распределения с параметрами, вычисленными по формулам (5) и (6). Для

каждой размерности задачи коммивояжера опять было получено 4 подмно-

жества задач из выборки объема 10000. Среднее относительное ускорение и

доля задач, для которых ускорение было больше 0, приведены в табл. 5.

166

Таблица 5. Среднее относительное ускорение и доля ускоренных задач, q_p

q₅₀,

q₆₀,

q₇₀,

q₈₀,

n сред. уск., доля сред. уск., доля сред. уск., доля сред. уск., доля

-12,36

10,63

-28,24

6,44

-22,51

7,64

-17,51

8,91

-4,96

11,53

-11,28

7,67

-9,06

8,23

-7,06

9,32

-0,72

31,75

-3,58

13,62

-2,54

16,7

-1,6

21,87

2,16

89,43

0,17

46,7

0,73

57,76

1,34

72,98

5,01

97,79

2,17

75,49

2,81

86,86

3,67

94,75

Заметим, что среднее относительное ускорение для задач размерности не

более 40 отрицательное, это значит, что большой вклад в эту величину вносят

задачи, которые решаются B&B быстрее, чем комбинированным алгорит-

мом. При больших размерностях на решение задачи коммивояжера тратится

больше времени и применение комбинированного алгоритма приводит чаще

к сокращению времени поиска оптимального решения, кроме того, величина

относительного сокращения у задач, решаемых наиболее долго, становится

больше.

7. Зависимость эффективности комбинированного алгоритма

от сложности индивидуальных задач ATSP

При вычислении сложности индивидуальной задачи учитываются верши-

ны дерева решений с нижней оценкой менее стоимости уже найденного тура.

В случае классической реализации B&B (без предвычислений) до тех пор,

пока не найден какой-то тур, учитываются все порожденные вершины дерева

решений, а после того, как тур получен, только те, у которых нижняя оценка

ниже стоимости этого тура.

Значения сложности индивидуальных задач коммивояжера фиксирован-

ной размерности (от 20 до 50) различаются на порядки, что серьезно затруд-

няет исследование временной эффективности алгоритмов. Так, в выборке из

100000 задач размерности 40 встретились задачи со сложностями 77 и 598 893,

причем выборочная средняя сложность составила 8145.

Поскольку задачи с небольшим значением сложности решаются программ-

ной реализацией B&B достаточно быстро, то использование предвычислен-

ного тура не приведет к заметному уменьшению времени работы алгорит-

ма. Более того, сумма времени, затраченного на поиск рекорда даже таким

быстрым алгоритмом, как метод LKH, и времени работы B&B с полученным

предвычисленным туром будет больше времени работы B&B без предвычис-

ленного тура.

С другой стороны, задачи с большой сложностью требуют много времени

на получение решения с помощью B&B, и в этом случае достаточно быстро

найденное приближенное решение LKH приводит к такому уменьшению вре-

мени работы B&B, что сумма времени получения тура LKH и поиска точного

решения B&B уже будет меньше времени работы B&B без предвычисленно-

го тура.

В связи с этим каждая выборка 10000 матриц фиксированной размерности

(от 35 до 45) была упорядочена по убыванию сложности, затем в упорядо-

ченной выборке был найден номер задачи N(C_max) такой, что для всех задач

167

с меньшими номерами время работы комбинированного алгоритма меньше,

чем классического B&B. N(C_max) почти монотонно возрастает от 11 до 292

с ростом размерности задачи от 35 до 45. Также для каждой размерности

от 35 до 45 были найдены значения сложности C_крит, такие что все зада-

чи большей сложности из выборки решаются комбинированным алгоритмом

быстрее, чем классическим B&B. C_крит растет от 40000 до 100000 с ростом

размерности задачи от 35 до 45.

Кроме того, эти же выборки, содержащие по 10000 матриц для каждой

размерности от 35 до 45, были упорядочены по убыванию времени работы

классического B&B. Число задач с наибольшим временем решения алгорит-

мом B&B, которые были решены комбинированным алгоритмом быстрее,

увеличивается от 11 до 171. Обозначим через t время работы классического

B&B, такое что все задачи, решаемые B&B за время, большее t, решаются

комбинированным алгоритмом быстрее, чем классическим B&B. Это время t

растет от 1100000 мс до 6400000 мс с ростом размерности задачи от 35 до 45.

Таким образом, применение комбинированного алгоритма сокращает вре-

мя решения задачи коммивояжера в основном в случае задач с большим зна-

чением сложности. Эти задачи решаются классическим B&B дольше задач

с небольшим значением сложности, поэтому закономерность «более слож-

ная задача решается быстрее комбинированным алгоритмом» сохраняется в

виде «задача, которая решается классическим B&B дольше, решится комби-

нированным алгоритмом быстрее». В отличие от этого в упорядоченной по

времени работы LKH выборке не наблюдается аналогичной закономерности.

8. Формулировка рекомендаций по применению

комбинированного алгоритма

Ввиду того, что задачи небольших размерностей (до 40-45) решаются ме-

тодом ветвей и границ относительно быстро, не рекомендуется использовать

комбинированный алгоритм в таких случаях. Причина в том, что уменьше-

ние суммарного времени вычислений за счет использования предвычисленно-

го тура будет настолько мало, что окажется меньше времени, требующегося

на поиск начального тура даже таким быстрым приближенным алгоритмом,

как LKH. В результате комбинированный алгоритм будет работать дольше,

чем классический метод ветвей и границ.

В случае решения задач размерности больше 45 разумно использовать

комбинированный алгоритм для решения большой серии задач коммивояже-

ра, поскольку среднее время решения будет несколько меньше, так что общее

время расчетов сократится.

Комбинированным алгоритмом стоит решать задачи с большим значением

сложности, именно для таких задач ускорение расчетов за счет использова-

ния предвычисленного тура максимально.

9. Заключение

В статье на основании проведенных исследований, экспериментов с про-

граммными реализациями алгоритмов и статистического исследования полу-

168

ченных времен решения индивидуальных несимметричных задач коммивоя-

жера показано что:

• алгоритм Lin-Kernighan-Helsgaun быстро находит достаточно близкий к

оптимальному решению тур, позволяющий в некоторых случаях суще-

ственно уменьшить время поиска точного решения задачи коммивояжера

методом ветвей и границ;

• комбинированный метод, в котором на первом этапе используется эври-

стический алгоритм для нахождения предвычисленного тура, а на втором

этапе применяется программная реализация метода ветвей и границ с по-

лученным туром в качестве начального, может быть построен с использо-

ванием эвристического алгоритма Lin-Kernighan-Helsgaun;

• программная реализация предложенного комбинированного алгоритма на-

чиная с размерностей задачи больших, чем 45, показывает лучшие времена

решений по оценке в среднем, чем классический метод ветвей и границ,

несмотря на то, что доля задач, которые решаются быстрее, составляет

менее половины;

• логнормальное распределение является удовлетворительным приближени-

ем распределения времен решения индивидуальных задач как для про-

граммных реализаций классического метода ветвей и границ, так и для

предложенного комбинированного метода в диапазоне размерностей от 30

до 50;

• результаты вероятностного квантильного прогнозирования времен на ос-

нове полученного семейства логнормальных распределений достаточно хо-

рошо совпадают с полученными экспериментальными данными для раз-

мерностей 55, 60 и 65, что позволяет использовать полученные результаты

для вероятностного прогнозирования времен.

Параметры аппроксимирующего распределения были оценены по выбор-

кам задач коммивояжера (объема 10000 для каждой размерности задачи от

30 до 50), затем методом наименьших квадратов была построена линейная

зависимость этих параметров от размерности задачи. Сравнение квантилей

аппроксимирующего распределения с выборочными квантилями натураль-

ного логарифма времени решения контрольных выборок объема 1000 задач

коммивояжера размерностей 55, 60 и 65 показало, что прогноз удовлетвори-

тельный.

Также исследована зависимость эффективности применения комбиниро-

ванного алгоритма от сложности задачи коммивояжера. Для этого было про-

ведено дополнительное статистическое исследование выборки тех индивиду-

альных задач, для которых сокращение времени расчета комбинированным

алгоритмом значительно. В результате показано, что в основном это такие ин-

дивидуальные задачи, сложность которых велика для классического метода

ветвей и границ. На основе проведенных исследований авторы рекомендуют

использовать комбинированный метод для индивидуальных несимметричных

задач коммивояжера начиная с размерности порядка 45 и для индивидуаль-

ных задач меньшей размерности, для которых известно, что их сложность

велика. Авторы видят дальнейшее развитие исследования в поиске таких ха-

рактеристических функционалов исходных матриц индивидуальных задач,

которые позволили бы определить за полиномиальное время принадлежность

169

задачи к классу сложных (имеющих большое значение сложности, т.е. много

вершин в поисковом дереве, построенном B&B) .

СПИСОК ЛИТЕРАТУРЫ

Little J.D.C., Murty K.G., Sweeney D.W., Karel C. An Algorithm for the Traveling

Salesman Problem // Oper. Res. 1963. No. 11. P. 972-989.

Land A.H., Doig A.G. An automatic method of solving discrete programming

problems // Econometrica. 1960. V. 28 No. 3. P. 497-520.

Гудман С., Хидетниеми С. Ведение в разработку и анализ алгоритмов. М.: Мир,

1981.

Korte B., Vygen J. Combinatorial Optimization: Theory and Algorithms, Springer

Publishing Company, Inc., 2007.

Matai R., Mittal M.L., Singh S. Travelling salesman problem: An overview of

applications, formulations and solution approaches/Davendra, D. (ed.) Chapter 1

in Travelling Salesman Problem: Theory and Applications. Intech Open Access

Publisher, Rijeka, 2010. P. 1-24.

Slominski L. Probabilistic analysis of combinatorial algorithms: a bibliography with

selected annotations // Computing. 1982. V. 28. P. 257-267.

Колесников А.В., Кириков И.А., Листопад С.В. и др. Решение сложных за-

дач коммивояжера методами функциональных гибридных интеллектуальных

систем / Под ред. А.В. Колесникова. М.: ИПИ РАН, 2011.

Ульянов М.В. Ресурсно-эффективные компьютерные алгоритмы. Разработка и

анализ. М.: ФИЗМАТЛИТ, 2008.

Сергеев С.И. Задача коммивояжера. Использование нелинейных разрешающих

функций// АиТ. 2013 № 6. С. 101-120.

Sergeev S. Nonlinear Resolving Functions for the Travelling Salesman Problem//

Autom. Remote Control. 2013. V. 74. No. 6. P. 978-994.

10.

Oliver I., Smith D., Holland J. A Study of Permutation Crossover Operators on

the Traveling Salesman Problem. J. Grefenstette (Ed.)// Proc. 2 Int. Conf. Genet.

Algorithm, Lawrence Erlbaum Associat., Hillsdale N.J., 1987. P. 224-230.

11.

Cotta C., Aldana J., Nebro A., Troya J. Hybridizing Genetic Algorithms with

Branch and Bound Techniques for the Resolution of the TSP/ D. Pearson, N. Steele,

R. Albrecht (Eds.), Artificial Neural Nets and Genetic Algorithm 2. Wien N.Y.:

Springer-Verlag, 1995. P. 277-280.

12.

Goldberg D., Lingle R.J. Alleles, Loci, and the Travelling Salesman Problem J.

Grefenstette (Ed.)// Proc. 1st Int. Conf. Genet. Algorithms, Lawrence Erlbaum

Associat., Hillsdale N.J., 1985. P. 154-159.

13.

Toriello A. Optimal Toll Design: a Lower Bound Framework for the Asymmetric

Traveling Salesman Problem // Math. Programm. 2014. V. 144. No. 1/2. P. 247-

264.

14.

Cornuéjols G., Karamanov M., Li Y. Early Estimates of the Size of Branch-and-

Bound Trees // INFORMS J. Comput. 2006. V. 18. No. 1. P. 86-96.

15.

Фомичёв М.И. Сравнительный анализ метаэвристических алгоритмов решения

несимметричной задачи коммивояжера // Системы управления и информаци-

онные технологии 2017. № 3 (69). С. 88-92.

16.

Головешкин В.А., Жукова Г.Н., Ульянов М.В., Фомичев М.И. Распределение ло-

гарифма сложности индивидуальных задач коммивояжера при фиксированной

длине входа // Современ. информ. технологии и ИТ-образование. 2016. Т. 12.

№ 3. Ч. 2. C. 131-137.

170

17.

Knuth D.E. Estimating the Efficiency of Backtracking Programs // Math. Comput.

1975. V. 29. P. 121-136.

18.

Пантелеев А.В. Метаэвристические алгоритмы поиска глобального экстрему-

ма. М.: Изд-во МАИ-ПРИНТ, 2009.

19.

Applegate D.L., Bixby R.E., Chavatal V. and Cook W.J.K. The Traveling Salesman

Problem, Princeton, N.J.: PUP, 2006.

20.

Colorni A., Dorigo M., Maniezzo V. Distributed Optimization by Ant Colonies.

Proc. First Eur. Conf. on Artificial Life, Paris, France, F. Varela and P. Bourgine

(Eds.), Elsevier Publishing, 1991. P. 134-142.

21.

Dorigo M., Gambardella L. M. Ant colony system: a cooperative learning approach

to the traveling salesman problem//IEEE Trans. Evol. Comput. Apr. 1997. V. 1.

No. 1. P. 53-66.

22.

Bonavear E., Dorigo M. Swarm Intelligence: from Natural to Artificial Systems,

Oxford, the UK: OUP, 1999.

23.

Gamboa D., Rego C., Glover F. Data Structures and Ejection Chains for Solving

Large Scale Traveling Salesman Problems//Eur. J. Oper. Res. 2005. V. 160 (1).

P. 154-171.

24.

Kaplan H., Lewenstein M., Shafrir N., Sviridenko M. Approximation algorithms for

asymmetric TSP by decomposing directed regular multigraphs//J. ACM (JACM).

2005. V. 52. No. 4. P. 602-626.

25.

Mömke T., Svensson O. Removing and Adding Edges for the Traveling Salesman

Problem// J. ACM (JACM). 2016. V. 63. No. 1. P. 1-28.

26.

Бородин В.В., Ловецкий С.Е., Меламед И.И., Плотинский Ю.М. Эксперимен-

тальное исследование эффективности эвристических алгоритмов решения зада-

чи коммивояжера // АиТ. 1980. № 11. С. 76-84.

Borodin V.V., Lovetskij S.E., Melamed I.I., Plotinskij Yu.M. Experimental Study

of the Efficiency of Heuristic Algorithms for Solution of the Traveling Salesman

Problem // Autom. Remote Control. 1980. V. 41. No. 11. P. 1543-1550.

27.

Cormen T.H., Leiserson C.E., Rivest R.L., Stein C. Introduction to Algorithm, 3rd

ed. Cambridge. MA: MIT Press, 2009.

28.

Stutzle T., Hoos H.H. Max-Min ant system// Future Generat. Comput. Syst. 2000.

V. 16. P. 889-914.

29.

Lin S., Kernighan B.W. An Effective Heuristic Algorithm for the Traveling-Salesman

Problem // Oper. Res. 1973. V. 21. P. 498-516.

30.

Helsgaun K. An effective implementation of the Lin-Kernighan traveling salesman

heuristic // Eur. J. Oper. Res. Elsevier. 2000. V. 126(1). P. 106-130.

31.

Жукова Г.Н., Ульянов М.В., Фомичев М.И. Эффективный по времени точный

комбинированный алгоритм для асимметричной задачи коммивояжера. Бизнес-

информатика. 2018. № 3 (45). С. 20-28.

32.

Moors J.J.A. A Quantile Alternative for Kurtosis// The Statist. 1988. V. 37.

P. 25-32.

33.

Moors J.J.A., Wagemakers R.Th.A., Coenen V.M.J., et al. Characterizing Systems

of Distributions by Quantile Measures// Statist. Neerlandica. 1996. V. 50. No. 3.

P. 417-430.

34.

Головешкин В.А., Жукова Г.Н., Ульянов М.В., Фомичев М.И. Вероятностный

прогноз сложности индивидуальных задач коммивояжера на основе идентифи-

кации распределения сложности по экспериментальным данным // АиТ. 2018.

№ 7. С. 149-166.

171