Автоматика и телемеханика, № 12, 2019

Линейные системы

(Нижегородский государственный университет им. Н.И. Лобачевского),

Р.С. БИРЮКОВ, канд. физ.-мат. наук (biryukovrs@gmail.com),

М.М. КОГАН, д-р физ.-мат. наук (mkogan@nngasu.ru)

(Нижегородский государственный архитектурно-строительный университет)

МИНИМАКСНОЕ УПРАВЛЕНИЕ УКЛОНЕНИЯМИ ВЫХОДОВ

ЛИНЕЙНОЙ ДИСКРЕТНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ¹

Показано, как можно синтезировать оптимальные на конечном го-

ризонте цифровые регуляторы для линейных нестационарных объектов

при неопределенных начальных условиях, находящихся под воздействи-

ем внешних возмущений. Квадрат оптимизируемого критерия, назван-

ного максимальным уклонением выхода, представляет собою точное га-

рантированное максимальное по времени значение квадрата евклидовой

нормы выхода системы, нормированное суммой квадратов евклидовых

норм возмущений и квадратичной формы начального состояния системы.

Максимальные уклонения выхода и приводящие к ним наихудшие возму-

щения и/или начальные условия, а также минимаксные управления, в

том числе и многокритериальные, минимизирущие максимальные укло-

нения нескольких выходов, находятся как решения задачи полуопреде-

ленного программирования. Получены необходимые и достаточные усло-

вия устойчивости и ограниченности системы на конечном интервале, поз-

воляющие синтезировать соответствующие законы управления.

Ключевые слова: линейная нестационарная дискретная система, макси-

мальное отклонение выхода, оптимальное управление, многокритериаль-

ная задача, оптимальная виброизоляция.

DOI: 10.1134/S0005231019120018

1. Введение

Анализ и синтез систем управления, функционирующих на конечном вре-

менном интервале, давно привлекает внимание специалистов. Особый инте-

рес здесь вызывают задачи, связанные с оптимизацией максимальных откло-

нений выходов системы и самого управления от их номинальных значений.

Обзор различных работ этого направления и соответствующие ссылки мож-

но найти в статьях [1, 2], в которых синтезируются управления максималь-

ными отклонениями выходов линейных нестационарных систем в непрерыв-

ном времени на конечном горизонте. Что касается изучения максимальных

отклонений в дискретных системах, то в [3] были получены условия устой-

чивости и стабилизации линейной обратной связью на конечном горизонте,

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проекты №№ 18-41-520002, 19-01-00289).

в [4, 5] - условия ограниченности при действии возмущения, генерируемо-

го заданной системой, в [6] осуществляется синтез обратных связей по вы-

ходу, обеспечивающих устойчивость на конечном горизонте, в [7] получены

достаточные условия устойчивости и ограниченности на конечном горизонте

неопределенных дискретных систем. В [8] для дискретных систем с нулевы-

ми начальными условиями был получен оптимальный регулятор по выходу,

минимизирующий максимальное по времени значение евклидовой нормы вы-

хода при действии возмущения из класса l₂ на бесконечном горизонте, реа-

лизация которого требует решения уравнения Риккати и задачи выпуклого

программирования, а в [9, 10] для дискретных систем были синтезированы

законы управления, минимизирующие верхние оценки всплесков, вызванных

неизвестным начальным возмущением. Таким образом, несмотря на многооб-

разие работ по этой теме, здесь отсутствуют точные характеристики макси-

мальных отклонений выхода при наличии обоих факторов: неопределенных

начальных условий и внешнего возмущения.

Данная работа идейно следует [1, 2], однако использует другой матема-

тический аппарат. Введены понятия максимальных уклонений выходов ли-

нейных дискретных нестационарных систем при внешнем и/или начальном

возмущениях и получены их характеризации в терминах решений нестацио-

нарных уравнений Ляпунова или в терминах решений задач полуопределен-

ного программирования. Установлено соответствие между понятиями устой-

чивости и ограниченности линейной нестационарной системы на конечном

интервале и максимальными уклонениями ее определенного выхода. Введе-

ны альтернативные понятия устойчивости и ограниченности системы на ко-

нечном интервале и получены соответствующие необходимые и достаточные

условия. Для стационарных систем при нулевых начальных условиях макси-

мальное уклонение выхода на конечном интервале, вызванное внешним огра-

ниченным в классе l₂ возмущением, оказывается монотонно возрастающей и

ограниченной сверху функцией длины интервала, что позволяет определить

в этом случае максимальное уклонение на бесконечном горизонте и характе-

ризовать его в терминах решения алгебраического уравнения Ляпунова. По-

лученные характеризации максимальных уклонений выражаются в терминах

линейных матричных неравенств, что позволяет синтезировать оптимальные

законы управления, в том числе и многокритериальные.

2. Максимальные уклонения на конечном горизонте

при начальном и/или внешнем возмущениях

Рассмотрим линейную дискретную нестационарную систему

xt+1 = A_tx_t + B_tv_t,

(2.1)

z_t = C_t x_t, t = t₀,t₀ + 1,... ,t₀ + N₀, N₀ ≥ 1,

где x_t - состояние, z_t - выход, v_t - внешнее возмущение. Определим макси-

мальное уклонение выхода при начальном и внешнем возмущениях на вре-

менном горизонте [t₀, t₀ + N₀] как

max

|z_t|

t=t₀,..., t₀+N₀

(2.2)

J0,v =

max

(

)1/2 ,

x^t0^,vt0^,...,vt0+N0-1

∑

xTt

R-1xt0

|v_i|²

i=t₀

где R = R^T > 0 - весовая матрица и знаменатель не обращается в ноль. Так

как

|z_t|

J0,v =

max

(

)1/2 ,

t=t₀,..., t₀+N₀

x^t0^,vt0^,...,vt0+N0-1

∑

xTt

R-1xt0

|v_i|²

i=t₀

а выход z_t определяется только возмущениями vt0 , . . . , vt-1, то

|zt0+N |

(2.3)

J0,v = max

max

(

)1/2 ,

N=0,..., N₀

x^t0^,vt0^,...,vt0+N0-1

∑

xTt

R-1xt0

|v_i|²

i=t₀

т.е. максимальное уклонение на горизонте [t₀, t₀ + N₀] равно максимуму из

максимальных относительных значений модуля выхода на концах горизонтов

[t₀, t₀ + N] по всем N = 0, . . . , N₀.

Для нахождения этой величины запишем решение уравнения (2.1) в виде

∑

x_t = Φ(t,t₀)xt0 +

Φ(t, i + 1)B_iv_i, t ≥ t₀ + 1,

i=t₀

где переходная матрица

{

At-1At-2 ··· At0 , t ≥ t₀ + 1,

Φ(t, t₀) =

I, t=t₀

является решением разностного уравнения

(2.4)

Φ(t + 1, t₀) = A_tΦ(t, t₀), t ≥ t₀.

Выход может быть представлен как

∑

z_t = C_tΦ(t,t₀)xt0 +

G(t, i)v_i,

i=t₀

где G(t, i) = C_tΦ(t, i + 1)B_i, i = t₀, . . . , t - 1 - матричная импульсная переход-

ная функция системы.

Теорема 2.1. Максимальное уклонение выхода при начальном и внеш-

нем возмущениях в системе (2.1) на заданном горизонте [t₀, t₀ + N₀] нахо-

дится как

(2.5)

J0,v =

max λ1/2max(C_tP_tCTt),

t=t₀,..., t₀+N₀

где λ_max(·) обозначает максимальное собственное значение соответствую-

щей матрицы, P_t = PTt ≥ 0 - решение уравнения

(2.6)

Pt+1 = A_tP_tATt + B_tBTt

с начальным условием Pt0 = R. Если максимальное значение J0,v = γ_∗ до-

стигается при t = t_∗, то наихудшие начальное состояние и внешнее возму-

щение определяются как

x^∗t

= γ-1∗R1/2Φ^T(t_∗,t₀)CTte∗, e∗ = emax(Ct∗ Pt∗ CTt

∗

(2.7)

v^∗t = γ-1∗BTtΦ^T(t_∗,t + 1)CTte∗, t = t0,... ,t∗ - 1,

∗

где e_max(·) обозначает нормированный собственный вектор, отвечающий

максимальному собственному значению соответствующей матрицы.

Доказательства этого и последующих утверждений содержатся в Прило-

жении. Заметим, что внешнее возмущение на интервале [t_∗, t₀ + N₀] не влияет

на максимальное уклонение на всем интервале [t₀, t₀ + N₀]: большие значения

внешнего возмущения на интервале [t_∗, t₀ + N₀], конечно, вызовут большие

значения выхода, но максимальное уклонение выхода, определенное в (2.2),

не превысит величину γ_∗.

Теорема 2.2. Максимальное уклонение выхода при начальном и внеш-

нем возмущениях на горизонте [t₀, t₀ + N₀] находится в результате реше-

ния задачи полуопределенного программирования

J20,v = min γ² :

⎛

⎞

Y_t

∗

(

)

Y_t

∗

⎜

⎟

⎝ AtYt Yt+1 ∗

⎠ ≥ 0,

≥ 0, Yt0 ≥ R,

(2.8)

C_tY_t γ²I

BTt I

(

)

t₀+N₀

∗

t = t₀,...,t₀ + N₀ - 1,

≥0

Ct0+N₀ Yt₀+N₀

γ²I

относительно неизвестных Yt0+1,... ,Yt₀+N₀ .

Заметим, что минимум в задаче (2.8) достигается не обязательно при

Y_t = P_t, t = t₀ + 1,... ,t₀ + N₀, но в любом случае он равен соответствующему

максимальному уклонению выхода.

В частном случае, когда начальное состояние нулевое, максимальное укло-

нение выхода при внешнем возмущении определяется как

max

|z_t|

t=t₀,..., t₀+N₀

J_v =

max

(

)1/2 =

v^t0^,...,vt0+N0-1 t₀+∑-1

|v_i|²

i=t₀

(2.9)

|zt0+N |

= max

max

(

)1/2 .

N=1,..., N₀

v^t0^,...,vt0+N-1 t0 ∑-1

|v_i|²

i=t₀

Так как в этом случае xt0 = 0, то

∑

G(t, i)v_i,

)

|v_t|²,

zt0+N =

|zt0+N |² ≤ λmax(Ct₀+N Pt₀+N

t₀+N

i=t₀

t=t₀

где матрица

∑

Pt0+N =

Φ(t₀ + N, i + 1)B_iBTiΦ^T(t₀ + N, i + 1)

i=t₀

является решением разностного уравнения

(2.10)

Pt+1 = A_tP_tATt + B_tBTt, Pt0

= 0.

Таким образом, максимальное уклонение и наихудшее внешнее возмущение

при нулевых начальных условиях определяются как в (2.5) и (2.7) при Pt0 = 0

и находятся согласно процедуре (2.8) при Yt0 ≥ 0.

В другом частном случае, когда внешнее возмущение отсутствует, а на-

чальное состояние неизвестно, задачу нахождения максимального уклонения

выхода принято называть задачей о всплеске. Максимальное уклонение при

начальном возмущении определяется как

max

|z_t|

t=t₀,..., t₀+N₀

|zt0+N |

(2.11)

J₀ = max

= max

max

N=0,..., N₀

x^t0⁼⁰ (xt0 R-1xt0 )1/2

В этом случае

zt0+N = Ct₀+NΦ(t0 + N,t0)xt₀ ,

)xTt

R-1xt0 ,

|zt0+N|² ≤ λmax(Ct₀+NPt₀+N

t₀+N

где матрица

Pt0+N = Φ(t0 + N,t0)RΦ^T(t0 + N,t0)

является решением разностного уравнения

(2.12)

Pt+1 = A_tP_tATt, Pt0 = R, t = t₀,... ,t₀

+ N - 1.

Таким образом, максимальный всплеск на горизонте [t₀, t₀ +N₀] определяется

как

J₀ = max λ1/2max(Ct0+NPt₀+N

t₀+N

N=0,..., N₀

где Pt0+N =

≥ 0 - решение уравнения (2.12), и находится согласно про-

t₀+N

цедуре (2.8), в которой следует положить B_t ≡ 0. Если максимальное значение

J₀ = γ_∗ достигается при t = t_∗, то наихудшие начальное состояние определя-

ется как

(2.13)

x^∗t

= γ-1∗RΦ^T(t_∗,t₀)CTte∗, e∗ = emax(Ct∗Pt∗ CTt).

∗

Максимальное уклонение выхода может пониматься не только как макси-

мальное по времени относительное значение нормы вектора выхода, но и в бо-

лее широком смысле как максимум из максимальных по времени относитель-

ных значений норм векторов, составляющих в совокупности вектор выхода.

Это позволяет рассматривать функционалы, характеризующие максималь-

ные значения из максимальных отклонений нескольких векторных выходов

(см. пример в разделе 6). А именно, рассмотрим систему

xt+1 = A_tx_t + B_tv_t,

(2.14)

z_t = col (z(1)t,... ,z(m)t), z(i)t = C(i)tx_t, i = 1,... ,m,

комбинированный выход которой состоит из m векторов z(i)t ∈ Rni . Макси-

мальное уклонение выхода этой системы определим как

max

|z(i)t|

t=t₀,..., t₀+N₀

i=1,..., m

(2.15)

J0,v =

max

(

)1/2 .

x^t0^,vt0^,...,vt0+N0-1

∑

xTt

R-1xt0

|v_i|²

i=t₀

Ясно, что при m = 1 это определение переходит в (2.2). Нетрудно также ви-

деть, что для комбинированного выхода

J0,v = max

J(i)0,v,

i=1,..., m

где J(i)0,v - максимальное уклонение выхода z(i)t, определенное в (2.2). Из тео-

ремы 2.1 непосредственно следует, что в случае комбинированного выхода

(

)

(2.16)

J0,v = max

max λ1/2max C(i)tP_tC(i)T

i=1,..., m

t=t₀,..., t₀+N₀

где матрица P_t есть решение уравнения (2.6). В частном случае z_i могут быть

компонентами вектора z и тогда

(

)

J0,v = max

max d1/2max C(i)tP_tC(i)T

i=1,..., m

t=t₀,..., t₀+N₀

где d_max(·) обозначает максимальный диагональный элемент соответствую-

щей матрицы.

3. Максимальное уклонение выхода стационарной системы при внешнем

возмущении на конечном и бесконечном горизонтах

Покажем, что для стационарной системы (2.1) с нулевыми начальными

условиями при

∑

A_t ≡ A, B_t ≡ B, C_t ≡ C, t₀ = 0, z_t = G_t-iv_i,

i=0

{

CAk-1B, k > 0,

Gk =

0, k ≤ 0

можно определить и вычислить максимальное уклонение при внешнем воз-

мущении на бесконечном горизонте. Действительно, в этом случае решение

матричного уравнения (2.10), имеющее вид

∑

P_t = At-1-iBB^T(At-1-i)^T,

i=0

монотонно не убывает, т.е. Pt+1 ≥ P_t. Следовательно,

max λ1/2max(CP_N C^T) = λ1/2max(CPN0 C^T),

N=1,..., N₀

т.е. для стационарных систем максимальное уклонение на конечном горизон-

те при внешнем возмущении и нулевом начальном состоянии всегда достига-

ется на конце горизонта при N = N₀.

Теорема 3.1. Максимальное уклонение выхода при внешнем возмуще-

нии в стационарной системе на горизонте [0,N₀] определяется формулой

J_v = λ^m

ax(CN₀ PN₀ CN0 ), где PN₀ - решение уравнения (2.10), и вычисляется

как

J2v = min γ² :

⎛

⎞

Y_t

∗

(

)

(3.1)

⎜

⎟

YN0

∗

⎝AYt Yt+1 ∗⎠≥0, Y0≥0, t=0,...,N0-1,

≥ 0.

CN0YN0

γ²I

B^T I

Определим максимальное уклонение выхода устойчивой стационарной си-

стемы при внешнем возмущении на бесконечном горизонте

sup|zt|

t≥0

(3.2)

J(∞)v = max

(

)1/2 .

{vt}

^∑ |v_i|2

i=0

Теорема 3.2. Максимальное уклонение выхода при внешнем возмуще-

нии в устойчивой стационарной системе (2.1) на бесконечном горизонте

равно

J(∞)v = λ_max(CP_∗C^T),

где P_∗ = PT∗ ≥ 0 - грамиан управляемости, являющийся решением уравнения

(3.3)

P = APA^T + BB^T.

Следствие 3.1. Максимальное уклонение при внешнем возмущении на

бесконечном горизонте находится как решение задачи полуопределенного

программирования:

J(∞)v = min γ² :

⎛

⎞

∗

(

)

(3.4)

∗

⎝_AYY

∗

⎠≥0,

≥ 0.

CY γ²I

B^T I

Отметим, что максимальное уклонение выхода устойчивой стационарной

системы при нулевом начальном состоянии и внешнем возмущении на бес-

конечном горизонте является, по существу, одним из вариантов обобщен-

ной H₂-нормы, введенной в [11] для непрерывных систем, а понятие мак-

симального уклонения комбинированного выхода в этом случае совпадает с

понятием обобщенной H₂-нормы, данным в [12, 13]. Из доказательства тео-

ремы 3.2, которое использует методы оценки соответствующей операторной

нормы из [14], следует, что наихудшее возмущение на бесконечном горизонте

является “предельным” для наихудших возмущений на горизонте длины N,

когда N неограниченно возрастает.

4. Синтез законов управления максимальными уклонениями

4.1. Оптимальное управление максимальным уклонением

Перейдем к синтезу оптимальных законов управления, которые обеспе-

чивают минимальное значение максимальному уклонению целевого выхо-

да системы. Вначале заметим, что соответствующая вариационная задача

управления является вырожденной даже в случае, когда управление непо-

средственно включено в целевой выход, и имеет бесконечно много решений.

Покажем, что синтез оптимального управления в виде линейной нестацио-

нарной обратной связи по состоянию может быть осуществлен на основе ха-

рактеризации максимального уклонения, данной в теореме 2.2 в терминах

линейных матричных неравенств.

Для объекта управления

xt+1 = A_tx_t + B_tv_t + B_u,tu_t,

(4.1)

z_t = C_t x_t + D_t u_t, t = t₀,t₀ + 1,... ,t₀ + N₀

при законе управления вида u_t = Θ_tx_t максимальное уклонение выхода при

начальном и внешнем возмущениях согласно теореме 2.2 находится при ре-

шении задачи (2.8), в которой вместо матрицы A_t должна стоять матрица

замкнутой системы A_t + B_u,tΘ_t, а вместо C_t - матрица C_t + D_tΘ_t. Вводя но-

вые переменные Z_t = Θ_tY_t, приходим к следующему результату.

Теорема 4.1. Матрицы Θ_t закона управления, минимизирующего мак-

симальное уклонение выхода при внешнем и начальном возмущениях в за-

мкнутой системе на горизонте [t₀,t₀ + N₀], находятся как Θ_t = Z_tY-1t при

решении следующей задачи полуопределенного программирования:

min γ² :

⎛

⎞

Y_t

∗

(

)

⎜

⎟

Y_t

∗

⎝AtYt + Bu, tZt Yt+1 ∗

⎠≥0,

≥ 0, Yt0 ≥ R,

(4.2)

C_tY_t + D_tZ_t γ²I

BTt I

(

)

t₀+N₀

∗

t = t₀,...,t₀ + N₀ - 1,

≥ 0.

Ct0+N₀ Yt₀+N₀ + Dt₀+N₀ Zt₀+N₀ γ²I

Аналогичным образом синтезируются законы управления, обеспечиваю-

щие минимальное значение максимальному уклонению при внешнем возму-

щении или всплеску при начальном возмущении.

4.2. Оптимальные по Парето управления максимальными уклонениями

нескольких выходов

Рассмотрим теперь многокритериальную задачу управления максималь-

ными уклонениями нескольких целевых выходов системы

xt+1 = A_tx_t + B_tv_t + B_u,tu_t, t = t₀,... ,t₀ + N₀,

(4.3)

z(i)t = C(i)t x_t + D(i)tu_t, i = 1,... ,m,

где z(i)t, i = 1, . . . , m - целевые выходы. Пусть J(i)0,v(Θt0+N0 ) - максимальное_t

уклонение i-го целевого выхода при внешнем и начальном возмущении для

этой системы, замкнутой обратной связью u_t = Θ_tx_t, t = t₀, . . . , t₀ + N₀, где

Θt0+N0t₀ обозначает набор матриц Θt0 ,... ,Θt0+N0 . Поставим задачу нахожде-

ния оптимальных по Парето параметров Θt0+N0 в многокритериальной зада-_t

че

{

}

Θt0+N0_=argmin

(4.4)

J(i)0,v(Θt0+N0 ), i = 1,... ,m

t₀

Θt0+N0

^t0

Множество P = {Θt0+N0 } является оптимальным по Парето, если неравен-_t

ства J(i)0,v(Θt0+N0t₀ ) ≤

(Θt0+N0), i = 1,... ,m, в которых по меньшей мере_t

0, v

одно является строгим, не выполняются для любого набора матриц Θt0+N0 ._t

Одним из методов решения этой задачи является выбор скалярной целевой

функции

(4.5)

J_α(Θt0+N0t₀ ) = max

J(i)0,v(Θt0+N0t₀ )/αi,

i=1,..., m

где α = (α₁, . . . , α_m), α_i > 0, i = 1, . . . , m, известной как свертка Гермейера

[15]. Необходимые условия оптимальности по Парето формулируются сле-

дующим образом.

Теорема 4.2 ([12]). Пусть (γ₁,...,γ_m) - оптимальная по Парето точ-

ка в пространстве критериев и минимум целевой функции J_α(Θt0+N0)_t

при α_i = γ_i/maxk=1,...,m γ_k достигается в Θt0+N0t₀ (α). Тогда Θt0+N0(α) ∈ P и₀

J(i)0,v(Θt0+N0t₀(α)) = γi, i = 1,... ,m.

Согласно (4.5) и теореме 2.1 свертка Гермейера в рассматриваемой много-

критериальной задаче имеет вид

max λ1/2max(C(i)tP_tC(i)Tt)/α_i,

(4.6)

J_α(Θt0+N0t₀ ) = max

i=1,..., m

t₀,..., t₀+N₀

где P_t = PTt ≥ 0 - решение уравнения (2.6) для замкнутой системы. Обраща-

ясь к (2.16), нетрудно видеть, что свертка Гермейера (4.6) является макси-

мальным уклонением комбинированного выхода замкнутой системы

xt+1 = (A_t + B_u,tΘ_t)x_t + B_tv_t, t = t₀,... ,t₀ + N₀,

(4.7)

z_t = col(z(1)t,... ,z(m)t), z(i)t = α-1i(C(i)t + D(i)tΘ_t)x_t, i = 1,... ,m.

Это непосредственно приводит к следующему результату.

Теорема 4.3. Оптимальные по Парето управления в многокритериаль-

ной задаче (4.4) минимизации максимальных уклонений выходов систе-

мы (4.3) суть оптимальные управления по отношению к максимальному

уклонению комбинированного выхода системы (4.7), состоящего из пара-

метризованных выходов системы (4.3) при всех α_i, i = 1,... ,m.

Заметим, что, вообще говоря, не всякое оптимальное управление по отно-

шению к максимальному уклонению комбинированного выхода системы бу-

дет оптимальным по Парето. Матрицы параметров оптимальных по Парето

регуляторов могут быть найдены, если вычисление свертки Гермейера осу-

ществлять с помощью задачи полуопределенного программирования подобно

тому, как это было сделано выше для вычисления максимального уклонения

выхода при внешнем и начальном возмущениях. А именно, из (4.6) следует,

что матрицы параметров оптимальных по Парето регуляторов находятся как

Θ_t = Z_tY-1y при решении задачи

min γ² :

⎛

⎞

Y_t

∗

(

)

Y_t

∗

⎜

⎟

⎝AtYt + Bu, tZt Yt+1 ∗

⎠≥0,

≥ 0, Yt0 ≥ R,

C(i)tT_t + D(i)tZ_t γ²α2iI

BTt I

(4.8)

i = 1,...,m, t = t₀,...,t₀ + N₀ - 1,

(

)

Yt0+N₀

∗

≥ 0, i = 1, . . . , m.

C(i)t

Zt0+N₀

γ²α2iI

0+N0

Yt0+N₀ + D(i)t0+N₀

Аналогичным образом решаются и многокритериальные задачи управления

максимальными уклонениями при внешнем возмущении и нулевых началь-

ных условиях и при неизвестном начальном состоянии невозмущенной систе-

мы. Для стационарных систем на бесконечном горизонте имеет место сле-

дующее утверждение.

Теорема 4.4. Оптимальные по Парето стационарные законы управле-

ния в многокритериальной задаче минимизации максимальных уклонений

стационарной системы (4.3) при нулевом начальном состоянии и внешнем

возмущении на бесконечном горизонте имеют параметры Θ_α = Z_αY-1α, где

Y_α = YTα и Z_α - решения задачи полуопределенного программирования:

J(∞)v = min γ² :

⎛

⎞

∗

(

)

(4.9)

∗

⎜

⎟

⎝AY + BuZ Y

∗⎠≥0,

≥ 0, i = 1, . . . , m.

C(i)Y +D(i)Z γ²α2iI

B^T I

Заметим, что в многокритериальных задачах одним из целевых выходов

целесообразно выбирать управление, чтобы обеспечить компромисс между

максимальными уклонениями некоторых выходов и максимальным уклоне-

нием самого управления.

5. Необходимые и достаточные условия устойчивости и ограниченности

на конечном горизонте

По аналогии с непрерывными системами назовем дискретную систему

(5.1)

xt+1 = A_tx_t + B_tv_t, t = t₀,t₀ + 1,... ,t₀ + N₀, N₀

≥1

ограниченной на конечном интервале [t₀, t₀ + N₀] при ненулевых начальных

условиях и внешнем возмущении из класса l₂ для заданных положительных

параметров c₁, c₂, d (c₁ < c₂) и положительно определенной матричной функ-

ции Γ_t = ΓTt, если верна импликация

(5.2)

xTtΓt0 xt0 ≤ c1 ⇒ xTtΓtxt < c2

∀t ∈ [t₀,t₀ + N₀],

∀v : ∥v∥²²

≤ d.

Ограниченность дискретной системы при внешнем возмущении, порождае-

мом заданной линейной экзогенной системой, была определена и изучена в

[4, 5]. Выясним условия ограниченности системы в смысле определения (5.2).

Если для максимального уклонения выхода z_t = Γ1/2tx_t при выборе R-1 =

= Γt0 справедливо неравенство

max x

Γ_tx_t

t=t₀,..., t₀+N₀

c₂

(5.3)

J20,v =

max

x^t0^,vt0^,...,vt0+N0-1

∑

c₁ + d

xTtΓt0 xt0 +

|v_i|²

i=t₀

то система (5.1) ограничена для заданных c₁, c₂, d и Γ_t. С учетом тео-

рем 2.1 или 2.2 условие (5.3) формулируется в терминах решений разност-

ных матричных уравнений или неравенств. Однако выполнение неравен-

ства (5.3) не является необходимым для ограниченности системы, так как

из J20,v ≥ c₂/(c₁ + d) при xTtΓt0 xt0 ≤ c1 и ∥v∥22 ≤ d не следует, вообще гово-

ря, неравенство xTtΓ_tx_t ≥ c₂, т.е. система может оставаться ограниченной в

смысле определения (5.2).

Модифицируем определение (5.2) и скажем, что система (5.1) ограничена

на конечном интервале времени для заданных положительных параметров

s₁, s₂ (s₁ ≤ s₂) и положительно определенной матричной функции Γ_t, если

верна импликация

(5.4)

xTtΓt0 xt0 + ∥v∥22 ≤ s1 ⇒ xTtΓtxt ≤ s2

∀t ∈ [t₀,t₀ + N₀

Необходимые и достаточные условия ограниченности системы на конечном

интервале в смысле определения (5.4) формулируются следующим образом.

Теорема 5.1. Следующие утверждения являются эквивалентными.

(a) Система (5.1) является ограниченной в смысле определения (5.4) на

конечном интервале [t₀,t₀ + N₀] для заданных s₁, s₂ (s₁ ≤ s₂) и Γ_t > 0.

(b) Максимальное уклонение выхода z_t = Γ1/2tx_t при R-1 = Γt0 удовлетво-

ряет неравенству J20,v ≤ s₂/s₁.

(

)

(5.5)

λ_max Γ1/2tP_tΓ1/2

≤ s₂/s₁

∀t ∈ [t₀,t₀ + N₀

(d) Линейные матричные неравенства

⎛

⎞

Y_t

∗

⎜

⎟

⎝ AtYt Yt+1 ∗

⎠ ≥ 0, t = t0,...,t0 + N0 - 1, Yt₀ ≥ Γŧ1,₀

(5.6)

BTt I

Y_t ≤ (s₂/s₁)Γ-1,

t = t₀ + 1,... ,t₀ + N₀

являются разрешимыми.

Согласно [3, 6] система (5.1) при отсутствии внешнего возмущения называ-

ется устойчивой на конечном интервале для заданных ε иR > 0, если верна

импликация

(5.7)

xTt

Rxt0 ≤ 1 ⇒ xTt Rx_t < ε²

∀t ∈ [t₀,t₀ + N₀

Достаточные условия устойчивости системы на конечном интервале, полу-

ченные там же, состоят в выполнении следующих неравенств:

ATtXt+1A_t - X_t < 0, X_t ≥R, t = t₀,... ,t₀ + N₀ - 1,

(5.8)

Xt0+N₀ ≥R, Xt₀ < ε² R.

Модифицируем данное определение с целью получения неконсервативных

условий. Систему (5.1) при отсутствии внешнего возмущения назовем устой-

чивой на конечном интервале для заданных ε и^R, если верна импликация

(5.9)

xTt

Rxt0 ≤ 1 ⇒ xTt Rx_t ≤ ε²

∀t ∈ [t₀,t₀ + N₀

Разница между этими определениями состоит в замене строгого неравенства

в одном на нестрогое неравенство в другом. Согласно теореме 5.1 при B_t ≡ 0,

s₁ = 1, s₂ = ε², Γ_t ≡R необходимые и достаточные условия устойчивости си-

стемы на конечном интервале в смысле определения (5.9) состоят в выпол-

нении неравенств

A_tY_tATt - Yt+1 ≤ 0, Y_t ≤ ε² R-1, t = t₀,... ,t₀ + N₀ - 1,

(5.10)

Yt0+N₀ ≤ ε² R-1, Yt₀ ≥R-1.

Умножая первое неравенство в (5.10) слева и справа на Y-1t+1, обозначая X_t =

= ε²Y -1t и применяя лемму Шура, приходим к неравенствам

ATtXt+1A_t - X_t ≤ 0, X_t ≥R, t = t₀,... ,t₀ + N₀ - 1,

(5.11)

Xt0+N₀ ≥R, Xt₀ ≤ ε² R,

которые также, как (5.10), выражают необходимые и достаточные условия

устойчивости системы на конечном интервале в предложенной модифика-

ции. Сравнение (5.11) и (5.8) выявляет лишь “небольшое” отличие: в (5.11)

все неравенства являются нестрогими, тогда как в (5.8) два из них строгие.

Таким образом, переход от строгого неравенства к нестрогому в определении

устойчивости на конечном интервале позволяет сформулировать конструк-

тивные необходимые и достаточные условия.

Замечание 1. Если импликация (5.4) верна при xt0 = 0, то система (5.1)

при нулевом начальном состоянии называется устойчивой по входу и выходу

на конечном интервале для заданных s₁, s₂ и Γ_t > 0. Из теоремы 5.1 следует,

что необходимые и достаточные условия того, что система обладает данным

свойством, выражаются неравенствами (5.5) при Pt0 = 0 или неравенства-

ми (5.6), из которых исключено неравенство Yt0 ≥ Γ-1._t

Условия ограниченности системы на конечном интервале, сформулирован-

ные в теореме 5.1, п. (d), позволяют синтезировать законы управления, обес-

печивающие устойчивость, устойчивость по входу и выходу и ограниченность

системы на конечном интервале при заданных значениях параметров s₁, s₂

и матричной функции Γ_t.

6. Синтез оптимального виброизолятора

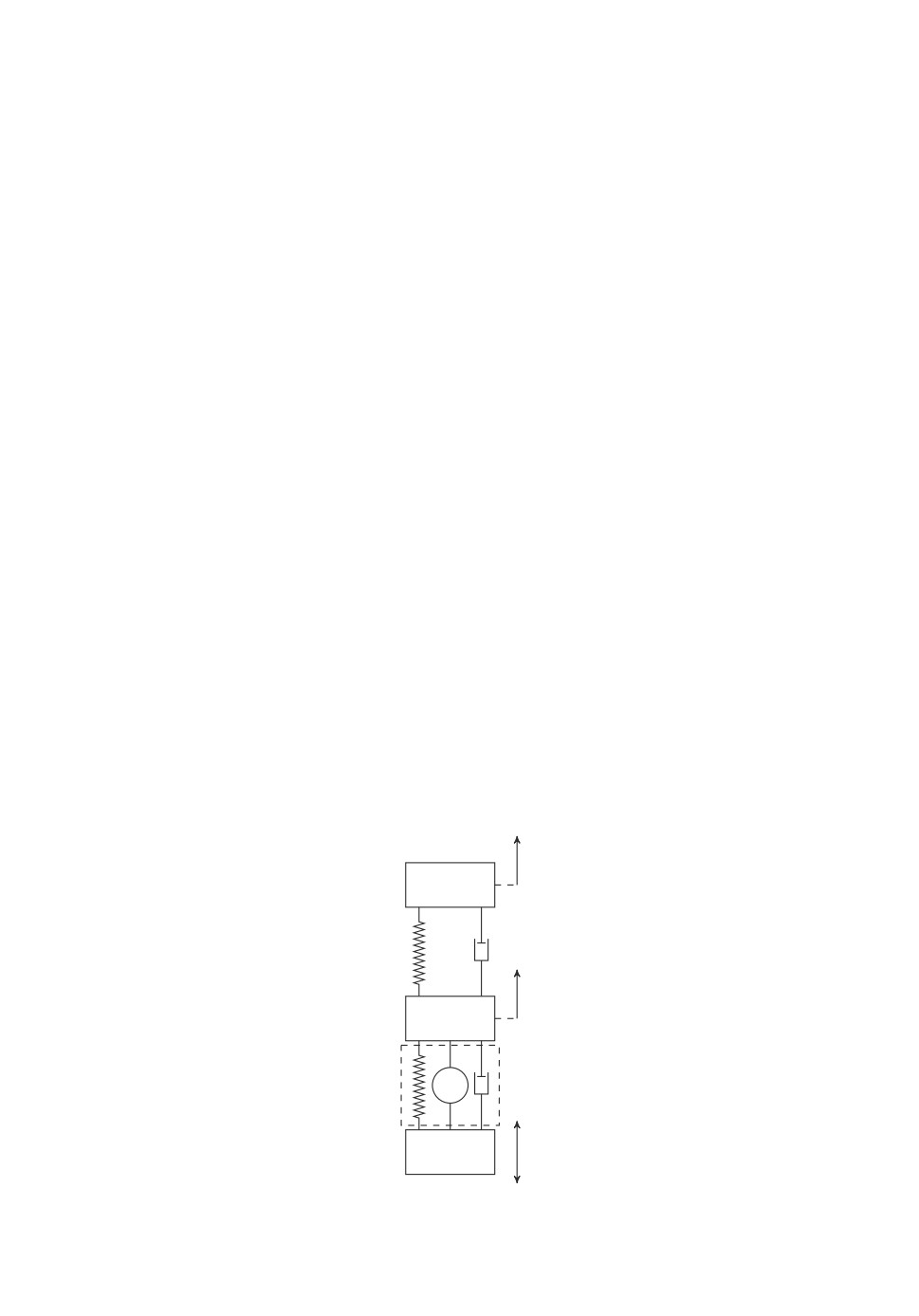
Рассмотрим механическую систему с двумя степенями свободы, показан-

ную на рис. 1 и представляющую собой упругий объект, который модели-

руется двумя материальными точками 2 и 3, связанными между собой ли-

нейными упругим и диссипативным элементами; этот упругий объект связан

такими же линейными упругим и диссипативным элементами и управляемым

элементом (называемым далее виброизолятором) с другим телом 1, который

моделирует подвижное основание. Динамика данной механической системы

(в безразмерных переменных и параметрах) описывается дифференциальны-

ми уравнениями

x₁ = -2x₁ + x₂ - 2β x₁ + β x₂ + u + v,

x₂ = x₁ - x₂ + β x₁ - β x₂ + v,

(6.1)

x₁(0) = x₁₀, x₂(0) = x₂₀,

x₁(0) = x₃₀,

x₂(0) = x₄₀,

где x₁ и x₂ - координаты материальных точек 2 и 3 относительно подвижно-

го основания, u - усилие, создаваемое виброизолятором при его деформации

(т.е. при смещении точки 2 относительно точки 1), v - с точностью до знака

ускорение основания (материальной точки 1), β - заданный положительный

параметр демпфирования. Задача виброизоляции состоит в поиске управле-

ния u = θ₁(t)x₁ + θ₂(t)x₂ + θ₃(t) x₁ + θ₄(t) x₂, определяющего характеристику

x₂

x₁

Рис. 1. Схематическое изображение системы активной виброзащиты.

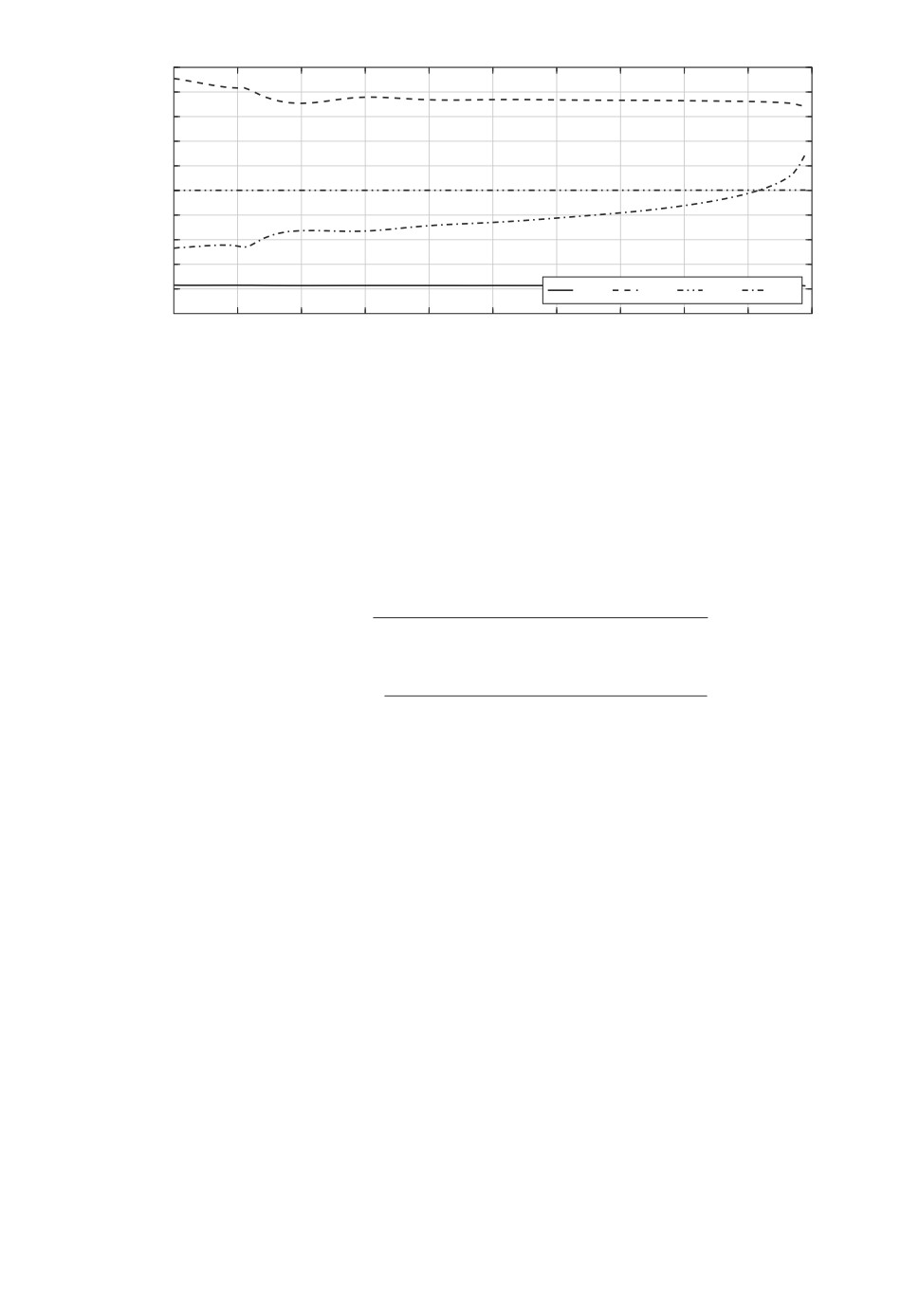
Рис. 2. Графики зависимостей от времени оптимальных по критерию J₁ ко-

эффициентов обратной связи.

виброизолятора и обеспечивающего требуемое качество переходных процес-

сов в данной механической системе.

Для количественной оценки переходных процессов на конечном интервале

времени [0, T ] введем два показателя

(t)|}

supt∈[0,T] max{|x₁(t)|,|x₂(t)-x₁

J₁[Θ(t)]= sup

x₀, v∈L₂

(x^T0R-1x₀ + ∥v∥²²)1/2

supt∈[0,T] | - x₁(t) - β x₁(t) + u(t)|

J₂[Θ(t)] = sup

x₀, v∈L₂

(x^T0R-1x₀ + ∥v∥²²)1/2

где x₀ = (x₁₀ x₂₀ x₃₀ x₄₀)^T, Θ(t) = (θ₁(t) θ₂(t)θ₃(t) θ₄(t))^T, R - заданная по-

ложительно определенная матрица,

∫T

∥v∥²² =

|v(t)|²dt.

Первый показатель характеризует максимальную деформацию механической

системы, а второй - максимальную силу, противодействующую смещению

упругого объекта относительно основания. Желательно, чтобы оба эти пока-

зателя были как можно меньше.

Проведем далее на отрезке [0, T ] дискретизацию данной системы и ука-

занных показателей J₁ и J₂ с шагом дискретизации h и получим дискрет-

ную систему 4-го порядка вида (2.14) с показателями в форме максимальных

уклонений вида (2.15). Зададим следующие числовые значения параметров:

h = 0,2, T = 20, β = 0,1, R = blockdiag(0,1I₂,I₂). Сначала рассмотрим задачу

оптимального управления, в которой минимизируется показатель J₁. В ре-

зультате применения изложенной выше теории получены оптимальные коэф-

фициенты θ₁(t), θ₂(t), θ₃(t), θ₄(t), графики которых представлены на рис. 2,

J₂

4,0

3,5

3,0

2,5

2,0

1,5

1,0

3,5

3,0

2,5

2,0

0,5

1,5

1,0

4,0

J₁

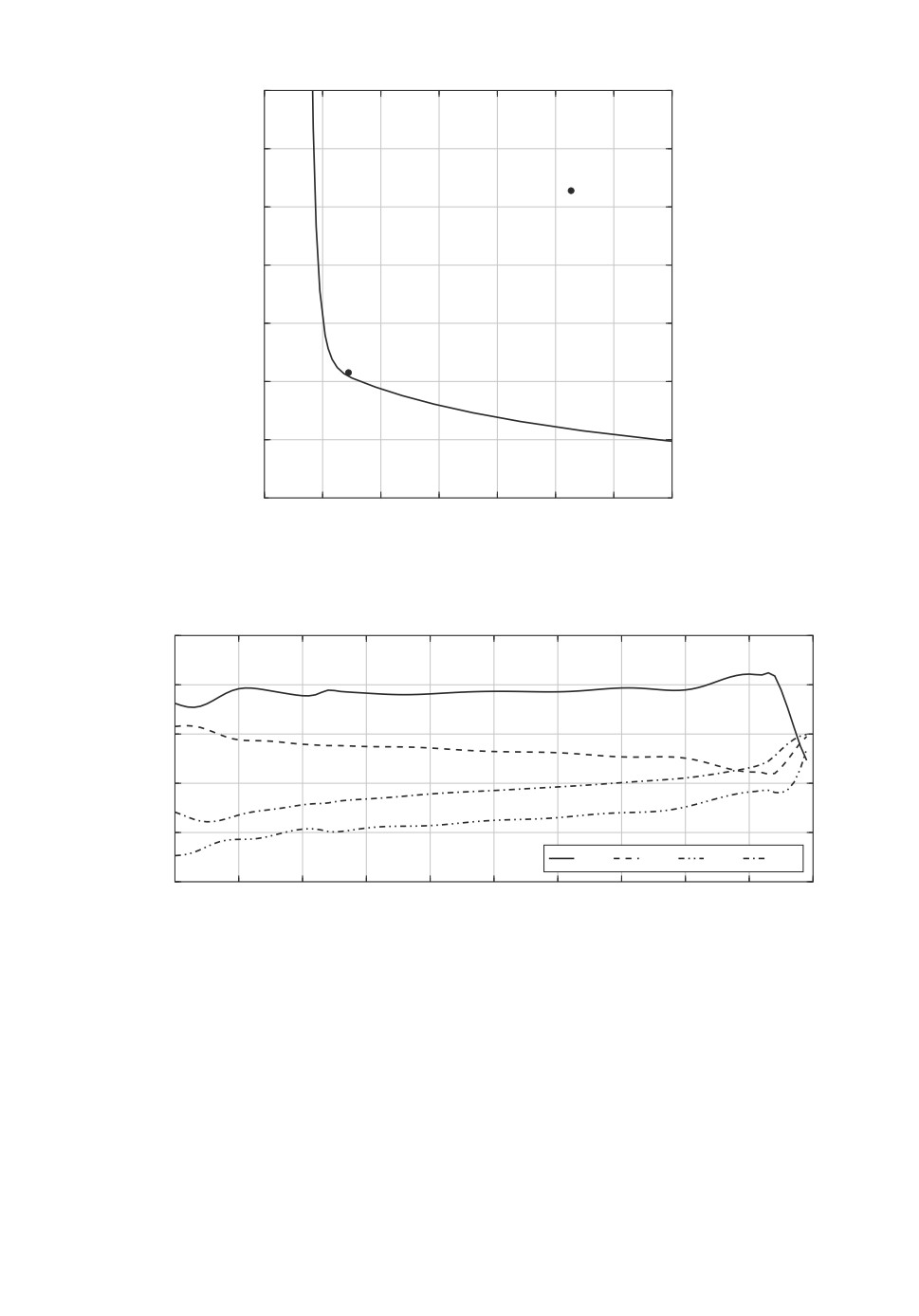
Рис. 3. Парето оптимальный фронт.

1,0

⁴ 0,5

0,5

1,0

1,5

Рис. 4. Графики зависимостей от времени оптимальных по Парето коэффи-

циентов обратной связи.

при этом J₁ = 0,847, а J₂ = 152,56. Таким образом, минимизация только од-

ного показателя (J₁) приводит к очень большому значению другого (J₂), по-

этому целесообразно рассмотреть далее двухкритериальную задачу. Резуль-

таты решения двухкритериальной задачи представлены на рис. 3 в виде кри-

вой (Парето оптимальный фронт) на плоскости (J₁, J₂). На этом же рисунке

указана точка A, которая соответствует случаю отсутствия управления (т.е.

u = 0). Точке с координатами (1,183;

1,568), принадлежащей указанной кри-

вой, на рис. 3 соответствуют оптимальные нестационарные параметры Θ(t),

графики которых представлены на рис. 4. Если усреднить значения этих ко-

эффициентов обратной связи по времени, то получатся постоянные коэффи-

циенты Θ = (0,428; -0,168; -0,868; -0,564), которым на рис. 3 соответствует

точка B с координатами (1,222;

1,576). Таким образом, выбор стационар-

ного регулятора (виброизолятора) с указанными параметрами обеспечивает

приемлемый компромисс между выбранными показателями.

7. Заключение

В статье показано, что максимальные уклонения выхода линейной неста-

ционарной динамической системы на конечном временном горизонте при

внешнем и/или начальном возмущениях можно характеризовать в терминах

решений линейных матричных неравенств. Это позволяет синтезировать оп-

тимальные по максимальным уклонениям нестационарные законы управле-

ния, в том числе и многокритериальные. Получены необходимые и достаточ-

ные условия устойчивости и ограниченности системы на конечном интервале,

позволяющие синтезировать соответствующие законы управления. Установ-

лено, что максимальное уклонение выхода стационарной системы при нуле-

вом начальном состоянии и внешнем возмущении на бесконечном горизонте

и оптимальное по этому критерию управление могут быть найдены как ре-

шения линейных матричных неравенств. Приводятся результаты численных

экспериментов в задаче виброзащиты, которые показывают эффективность

предлагаемого подхода и, в частности, возможность синтеза субоптимального

управления в виде линейной стационарной обратной связи.

ПРИЛОЖЕНИЕ

Сначала приведем вспомогательное утверждение.

Лемма П.1. Нормированные собственные векторы матриц S^TS и SS^T,

отвечающие максимальным собственным значениям, связаны соотношени-

ем

(Π.1)

e_max(S^TS) = λ-1/2max(SS^T)S^Te_max(SS^T

где λ_max(SS^T) = λ_max(S^TS).

Доказательство леммы П.1. Так как

SS^Te_max(SS^T) = λ_max(SS^T)e_max(SS^T),

то, умножая обе части этого равенства слева на S^T и нормируя вектор

S^Te_max(SS^T), получим (Π.1).

Доказательство теоремы 2.1. Запишем выход системы (2.1) в виде

zt0+N = SNwN,

где

S_N = (Ct0+NΦ(t0 + N,t0)R1/2 G(t0 +N,t0)··· G(t0 +N,t0 +N -1)),

⎛

⎞

R-1/2xt0

(Π.2)

⎜

⎟

vt0

⎜

⎟

w_N =

⎝

···

⎠^.

vt0+N-1

С учетом того, что λ_max(STNS_N) = λ_max(S_NSTN) и S_NSTN = Ct0+NPt₀+N

t₀+N

получим

(

)

∑

) xTt

R-1xt0 +

|v_t|2

|zt0+N |² ≤ λmax(Ct₀+N Pt₀+N

t₀+N

t=t₀

где равенство достигается и

Pt0+N = Φ(t0 + N,t0)RΦ^T(t0 + N,t0) +

∑

Φ(t₀ + N, i + 1)B_iBTiΦ^T(t₀ + N, i + 1).

i=t₀

В силу (2.4) матрица Pt0+N является решением разностного уравнения (2.6).

Таким образом, учитывая (2.3), приходим к (2.5).

Пусть максимальное уклонение выхода происходит в момент t_∗ = t₀ + N_∗.

Тогда zt0+N∗ = SN∗ wN∗ , где SN∗ и wN∗ определены в (Π.2) при N = N∗, а

wN∗ = e_max(STN∗SN∗). С уче-

max{|zt0+N∗ |² : |wN∗ | = 1} = γ^∗ достигается при

том леммы П.1 получим

wN∗ = γ-1∗STN

e_max(SN∗STN

)=γ-1∗STN

e_max(Ct∗ Pt∗ CTt

∗

что непосредственно приводит к (2.7).

Доказательство теоремы 2.2. Пусть в задаче (2.8) min γ2 = γ2∗.

Тогда матрицы Y_t = YTt, t = t₀, · · · , t₀ + N₀ удовлетворяют неравенствам

(Π.3)

Yt+1 ≥ A_tY_tATt + B_tBTt, C_tY_tCTt ≤ γ²I, Yt0

≥ R.

Из (Π.3) следует, что соотношения

Yt+1 = A_tY_tATt + B_tBTt + Q_t, Yt0 ≥ R

выполняются при некоторых матрицах Q_t = QTt ≥ 0. Тогда с учетом (2.6)

имеем

Yt+1 - Pt+1 = A_t(Y_t - P_t)ATt + Q_t, Yt0 - Pt0 ≥ 0.

Отсюда получим, что для всех t = t₀, . . . , t₀ + N₀

∑

Y_t - P_t = Φ(t,t₀)(Yt0 - Pt0 )Φ^T(t,t₀) +

Φ(i, t₀)Q_iΦ^T(i, t₀) ≥ 0.

i=t₀

Следовательно,

J20,v =

max

λ_max(C_tP_tCTt) ≤

max λ_max(C_tY_tCTt) ≤ γ2∗.

t=t₀,..., t₀+N₀

Если предположить, что J20,v = γ²⁰ < γ2∗, то задача (2.8) при Y_t = P_t, t = t₀ +

+1, . . . , t₀+N₀ имеет решение γ²⁰ < γ2∗, что противоречит условию min γ² = γ2∗.

Доказательство теоремы

3.2. При неограниченном увеличении

длины горизонта, т.е. когда N₀ → ∞, решение разностного уравнения

(Π.4)

Pt+1 = AP_tA^T + BB^T, P₀

= 0,

∑_∞

монотонно стремится к граммиану управляемости P_∗ =

AⁱBB^TAiT -

i∑

t-1

решению алгебраического уравнения

(3.3). Так как z_t =

Gt-ivi и

i=0

λ_max(SS^T) = λ_max(S^TS), то верны следующие неравенства:

(

)

(

)

∑

|z_t|² ≤ λ_max

GiGⁱ

|v_i|²

≤λ_max

GiGⁱ

|v_i|²,

i=0

∑

GiGⁱ = CP∗C^T.

i=0

∑_∞

Отсюда следует, что supt≥0 |z_t| ≤ λ∗/2(

|v_i|²)1/2, где λ_∗ = λ_max(CP_∗C^T).

i=0

Осталось показать, что здесь имеет место равенство. Выбирая некоторое N,

определим возмущение

∑

vi = λ∗1/2G^N-ie, e = emax(CP∗C^T),

|e| = 1,

|v_i|² ≤ 1.

i=0

При этом возмущении имеем

∑

|z_t| = max z^Tz_t ≥ e^Tz_t = λ∗1/2e^T

Gt-iG^N-ie,

|z|=1

i=0

и, значит, для любого N найдется возмущение, при котором

∑

sup|zt| ≥ λ∗1/2 sup eT

Gt-iG^N-ie = λ∗1/2

e^T

GiGⁱe.

t≥0

i=0

Отсюда следует, что

∑

sup|zt| ≥ λ∗1/2 sup eT

GiGⁱe = λ∗1/2

e^T

GiGⁱe = λ∗/2,

t≥0

N>0

i=0

что и требовалось доказать.

Доказательство теоремы 5.1. Утверждение (a) → (b) докажем от

противного: пусть при выполнении (5.4) имеем J20,v > s₂/s₁. Так как

J20,v = s-11 max

max

xTtΓ_tx_t > s₂/s₁,

x^t0^,v∈l2

t∈[t₀,t₀+N₀]

где max берется по всем xTt

Γt0 xt0 + ∥v∥²² = s₁, то maxt∈[t0,t₀+N₀] x^tΓtxt > s2,

что противоречит (5.4). Утверждение (b) → (a) следует непосредственно из

неравенства

max

xTtΓ_tx_t ≤ J20,v(xTtΓt0 xt0 + ∥v∥2) ≤ s2.

Утверждение (b) ↔ (c) следует из теоремы 2.1. Утверждение (c) ↔ (d) сле-

дует из теоремы 2.2.

СПИСОК ЛИТЕРАТУРЫ

Balandin D.V., Biryukov R.S., Kogan M.M. Finite-Horizon Multi-Objective

Generalized H₂ Control with Transients // Automatica. 2019. V. 106. No. 8. P. 27-34.

Баландин Д.В., Бирюков Р.С., Коган М.М. Оптимальное управление макси-

мальными уклонениями выходов линейной нестационарной системы на конеч-

ном интервале времени // АиТ. 2019. № 10. C. 37-61.

Balandin D.V., Biryukov R.S., Kogan M.M. Optimal Control of Maximum Output

Deviations of a Linear Time-Varying System on a Finite Horizon // Autom. Remote

Control. 2019. V. 80. No. 10. P. 1783-1802.

Amato F., Carbone M., Ariola M., Cosentino C. Finite-Time Stability of Discrete-

Time Systems // Proc. Amer. Control Conf. Boston, USA. 2004. P. 1440-1444.

Amato F., Ariola M. Finite-Time Control of Discrete-Time Linear Systems // IEEE

Trans. Autom. Control. 2005. V. 50. No. 5. P. 724-729.

Ichihara H., Katayama H. Necessary and Sufficient Conditions for Finite-Time

Boundedness of Linear Discrete-Time Systems // Proc. Joint 48th IEEE CDC

28th Chinese Control Conf., Shanghai, P.R. China. 2009. P. 3226-3231.

Amato F., Ariola M., Cosentino C. Finite-time control of discrete-time linear

systems: Analysis and design conditions // Automatica. 2010. V. 46. P. 919-924.

Kussaba H.T.M., Ishihara J.Y., Borges R.A. Finite time boundedness and stability

analysis of discrete time uncertain systems // Proc. 54th CDC Osaka, Japan. 2015.

P. 5972-5977.

Wilson D.A., Nekoui M.A., Halikias G.D. An LQR weight selection approach to

the discrete generalized H₂ control problem // Int. J. Control. 1998. V. 71. No. 1.

P. 93-101.

Коган М.М., Кривдина Л.Н. Синтез многоцелевых линейных законов управ-

ления дискретными объектами при интегральных и фазовых ограничениях //

АиТ. 2011. № 7. С. 83-95.

Kogan M.M., Krivdina L.N. Synthesis of Multipurpose Linear Control Laws of

Discrete Objects under Integral and Phase Constraints // Autom. Remote Control.

2011. V. 72. No. 7. P. 1427-1439.

10.

Агиевич В.Н., Парсегов С.Э., Щербаков П.С. Верхние оценки всплеска в линей-

ных дискретных системах // АиТ. 2018. № 11. С. 32-46.

Ahiyevich U.M., Parsegov S.E., Shcherbakov P.S. Upper Bounds on Peaks in

Discrete-Time Linear Systems // Autom. Remote Control. 2018. V. 79. No. 11.

P. 1976-1988.

11. Wilson D.A. Convolution and Hankel Operator Norms for Linear Systems // IEEE

Trans. Autom. Control. 1989. V. 34. P. 94-97.

12. Баландин Д.В., Коган М.М. Оптимальное по Парето обобщенное H₂-управление

и задачи виброзащиты // АиТ. 2017. № 8. С. 76-90.

Balandin D.V., Kogan M.M. Pareto Optimal Generalized H₂-control and Vibro-

protection Problems // Autom. Remote Control. 2017. V. 78. No. 8. P. 1417-1429.

13. Balandin D.V., Kogan M.M. Multi-objective generalized H₂ control // Automatica.

2019. V. 99. No. 1. P. 317-322.

14. Chellaboina V., Haddad W.M., Bernstein D.S., Wilson D.A. Induced Convolution

Operator Norms of Linear Dynamical Systems // Proc. Amer. Control Conf., San

Diego. 1999. P. 3805-3809.

15. Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.

Статья представлена к публикации членом редколлегии А.П. Крищенко.

Поступила в редакцию 06.02.2019

После доработки 02.04.2019

Принята к публикации 25.04.2019