Автоматика и телемеханика, № 12, 2019

Стохастические системы

(Институт радиотехники и электроники им. В.А. Котельникова РАН, Москва)

СТОХАСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПЕЛЕНГА

В АДАПТИВНЫХ АНТЕННЫХ РЕШЕТКАХ С ГРУБЫМИ

ПРОСТРАНСТВЕННО-ВРЕМЕННЫМИ СТАТИСТИКАМИ

Анализируется построение системы обработки пространственно-вре-

менных сигналов в радиотехнической системе, учитывающей техниче-

ские ограничения при измерении пеленга. Заданная эффективность мо-

жет быть достигнута применением упрощенных процедур обработки

с использованием стохастической управляемой интерполяции пеленга.

Для реализации применяется обработка на базе усеченных (малоэле-

ментных) управляемых апертур антенных решеток и грубых («бинарно-

знаковых») робастных статистик сигнала. Предлагается нетрадиционный

подход, предполагающий в процессе цифровой обработки применять ме-

тод Монте-Карло с обратной связью: осуществлять рандомизацию и по-

этапное стохастическое управление положением фазового центра путем

последовательной активизации малого числа элементов при накоплении и

усреднении грубых отсчетов входного сигнала. Приводятся количествен-

ные результаты снижения инструментальных погрешностей измерения

пеленга.

Ключевые слова: стохастическая линеаризация, многоэтапное усреднение,

рандомизация, стохастическая радиолокация, метод Монте-Карло, схема

Бернулли, квазислучайные точки, инструментальные ошибки.

DOI: 10.1134/S0005231019120067

1. Введение

Системы адаптивной пространственно-временной (ПВ) обработки сигна-

лов находят широкое применение в информационной измерительной технике,

радиосвязи и радиолокации. Гибкость структуры обработки и формирования

сигналов обеспечивается применением цифровой ПВ обработки сигналов, фа-

зированных антенных решеток (ФАР) и цифровых сигнальных процессоров

(DSP).

Сложность построения системы в значительной степени определяется раз-

рядностью обрабатываемых сигналов. При параллельной обработке в ре-

альном времени (на регистровом и топологическом уровнях, в интерфей-

сах) разрядность напрямую определяет сложность построения аппаратуры

(АЦП аналого-цифровых преобразователей, фазовращателей, умножителей,

арифметико-логических устройств и т.п.). При последовательной обработке

с применением DSP техническая реализация упрощается, однако увеличива-

ется время обработки, снижается быстродействие системы.

103

В цифровых ФАР разрядность РЛ (радиолокационных данных), частоты

дискретизации, размеры ПВ окон должны быть минимальными, однако это

становится несовместимым с требованием высокой эффективности: растут

шумы квантования, боковые лепестки, проявляются стробоскопический и ин-

терференционные эффекты, нелинейности типа «зона нечувствительности»,

«люфт», «жесткое ограничение» и др. Компромисс между грубым квантова-

нием и необходимым усреднением (объемом усредняющей выборки) предла-

гается искать в применении метода Монте-Карло, основанном на вероятност-

ном моделировании с использованием грубых статистик [1].

В [2-4] исследованы вопросы анализа и синтеза адаптивных ФАР, осу-

ществляющих дискретизацию пространства, однако специальные разделы,

относящиеся к электронному управлению ФАР, повышению инструменталь-

ной точности измерения пеленга при использовании грубых статистик ни-

кем не исследовались. Несовершенства инструмента ограничивают потенци-

альную точность, а экстенсивный путь приводит к увеличению разрядно-

сти АЦП.

В последние годы развивается направление стохастической радиолокации

[5-8], где введено понятие «грубые статистики» (ГС), связанное с понятием

«грубые отсчеты» (ГО) так: «ГО + Р = ГС», где Р — рандомизация (зашум-

ление).

Технический прием Р — это искусственное введение случайности (стоха-

стичности, хаоса).

В развитие направления в [9] предложено повышать инструментальную

точность измерения пеленга применением Р-стохастической интерполяции

ГО. Измерение пеленга указанным способом (методом Монте-Карло) сводит

измерение пеленга к задаче оценки интерполирующей добавки Δ_x (дробной

части грубой шкалы) через измерение вероятности p = Δ_x/Δ, где Δ — эле-

мент грубой дискретности. Процедура измерения пеленга при Р близка к

известным процедурам стохастической аппроксимации (СА). Примером СА

является рекуррентная форма усреднения

∑

i-1

m_i

(1)

Δ∗x(i) =

m_ℓ =

Δ∗x(i-1) +

Δ,

l=1

где μ_i = 1/0 — статистика исходов вероятности p = Δ_x/Δ; Δx(i) — ее i-я оцен-

ка на i-й итерации.

Расходимость гармонического ряда 1/i в известных процедурах СА [10, 11]

обеспечивает гарантированное движение к экстремуму целевой функции (min

среднеквадратической ошибки) при его поиске.

1.1. Постановка задачи

В рассматриваемой задаче пеленг θ = θ(α, β) для направления на источ-

ник излучения с азимута α и угла места β является постоянным. В плоско-

волновом приближении волна λ (длина), падающая на апертуру под углом

(пеленгом) θ от оси антенны, формирует поле, описываемое пространствен-

104

ными частотами:

2π

(2)

Ω_α =

tg α cos θ;

2π

(3)

Ω_β =

tg β cos θ.

Для получения оценки Δ_x методом Монте-Карло в качестве исходной в [9]

использована бинарно-знаковая статистика отсчетов квадратурных состав-

ляющих сигнала, сохраняющих доплеровскую и угловую информацию. Для

рандомизированной обработки осуществлена модуляция положения фазово-

го центра путем последовательной активизации малого числа слабонаправ-

ленных элементов и усреднении ГО. В отличие от известного метода СА для

учета инженерных ограничений на каждой итерации будет использована гру-

бая статистика, а Р применена целенаправленно, что является особенностью

для направления стохастической радиолокации (Ст. РЛ) [14].

2. Стохастическая радиолокация: интерполяция пеленга

Обобщение работ по анализируемому направлению Ст. РЛ представлено

структурной схемой Ст. РЛ в [8], где дан соответствующий обзор. Здесь умест-

но указать такие имена ученых: В.Г. Гайсов, А.К. Микельсон, Р.Ф. Немиров-

ский, И.Я. Билинский, Э.И. Вологдин, Г.П. Вихров, В.С. Гладкий, В.Г. Стру-

гач, Ю.Г. Полляк, О.Н. Граничин, В.И. Фомин и ряд других, широко извест-

ных в кругу специалистов направлений, близких к Ст. РЛ. Следует отметить

также Ю.Б. Черняка, который применительно к обычной РЛ в 1970-х гг. ис-

следовал операцию «жесткого широкополосного ограничения — фильтрации»

и доказал ее линейные свойства — по существу, метода «бинарно-знаковой»

обработки сигналов в СВЧ приемнике, что не является парадоксом, а, ско-

рее, подтверждает существование некоторой закономерности, оформленной

в теорию Ст. РЛ.

Прототипом исследований возьмем работу [9], где рассмотрен подход адап-

тивного измерения пеленга θ, эквивалентный последовательной хаотической

модуляции положения фазового центра путем активизации малоэлементных

сегментов ФАР. В качестве элементарной ячейки использована схема двух-

точечного пространственного дискретного преобразования Фурье (ДПФ) —

схема «бабочка», реализующая на своих выходах «сумму — разность». На

каждую угловую координату α (2) и β (3) задействовано две схемы — один

сегмент включает четыре элемента ФАР («крест»). Состоятельность гру-

бых измерений пеленга θ сохраняет в пределе и трехэлементный сегмент —

«треугольник». Положение трех- и четырeхэлементного сегмента на апертуре

ФАР задается хаотично.

Синтезирование направленных (узких) лучей осуществляется последова-

тельно — когерентным суммированием отсчетов поля в пространстве на пе-

редачу и суммированием отсчетов на прием. В основе предложения лежит

идея многопозиционной радиолокации [12] и ее частного случая — много-

канальных РЛС (так называемые MIMO (multiple input — multiple output —

105

«много входов — много выходов») РЛС. В отличие от аналога — французской

РЛС RIAS (1984 г.), где все элементы передающей решетки излучали одно-

временно взаимноортогональные сигналы, смещенные по частоте, и поэтому,

как и в обычных ФАР, требовалась большая суммарная пиковая мощность

передатчика, в рассматриваемой системе сигнал формируется последователь-

но, в результате чего при сохранении энергии пиковая мощность передатчи-

ка уменьшается. Уменьшение энергии сигнала компенсируется увеличением

времени наблюдения.

В задаче измерения пеленга θ полный ресурс обрабатываемых ПВ отсче-

тов определяется размером выборки, равным N × K × M, где N — размер

временной выборки; K — число сегментов ФАР по оси x (для α), а M —

число сегментов ФАР по оси y (для β), K × M — размер результирующей

пространственной выборки полномасштабной решетки Рэйли. Прореженная

решетка в виде креста Миллса при M = K имеет размер 2K(M).

Сигналы РЛС на отдельных посылках, сформированные сегментом, соот-

ветствуют одному испытанию в методе Монте-Карло. Закон распределения

точек положения фазового центра устройством управления выбирается та-

ким, что распределение ошибок квантования пеленга будет равномерным, а

испытания независимы (схема Бернулли).

Применительно к задаче измерения пеленга в [9] приведена схема форми-

рования квадратурных составляющих сигнала. Аддитивная смесь x = s + c

полезного сигнала s и коррелированной по пространству активной помехи c

по каждой квадратуре на аналоговых выходах ФАР подвергается квантова-

нию с помощью идеально симметричного ограничителя, на выходе которого

по каждому i-му отсчету имеем знаковую статистику x_i = sign{x_i}Δ = μ_iΔ,

причем μ_i = 1 при x_i > 0 и μ_i = -1 при x_i ≤ 0 (Δ — масштабный коэффи-

циент).

С целью стохастической линеаризации нелинейной характеристики огра-

ничителя во входную смесь добавляется искусственный шум ξ, в результате

на выходе АЦП имеем СВ

{

1, с вероятностью p = 2-1 + x_i(2Δ)¹;

(4)

μ_i =

-1, с вероятностью q = 1 - p.

Моменты СВ μ_i:

(5)

а) M_i{μ_i} = x_i/Δ; б) M_i{μ2i} = 1; в) M₁{μ_iμ_j} = x_ix_j/Δ².

Из (5),а) следует, что M₁ x_i = x_i, т.е. операция M{·} линеаризует нелиней-

ность sign{·} (эффект «стохастической линеаризации»). Условие (5),б) экви-

валентно равенству M₁ x2i = Δ², объясняющему робастность — эффект «нор-

мирования мощности» за счет амплитудной характеристики симметричного

ограничителя.

В [9] оценен прирост коэффициента направленного действия и динамиче-

ского диапазона ФАР. Сходимость инструментальных СКО измерения пелен-

га в этом случае составила ∼ K-1/2.

106

3. Ускорение сходимости в схеме с многоэтапным измерением

В [13] рассмотрены методы испытаний, приводящих к сокращению их чис-

ла за счет введения некоторого числа неслучайных точек в алгоритмы Монте-

Карло. Возможность использования, связанных цепью Маркова, и групповых

зависимых испытаний по Лемеру ранее рассматривалась в [14]. В настоящей

статье на основании публикаций [20, 21] сделаем обобщения применительно

к задаче многоэтапного измерения пеленга.

3.1. Теоретико-вероятностное содержание вопроса

Задача измерения интерполирующей добавки Δ_x при измерении пеленга

методом Монте-Карло сводится к измерению вероятности. На каждом этапе

образуется статистика

∑

(6)

m= μ_i,

i=1

где μ_i — элемент вектора выборки μ = (μ₁, . . . , μ_N ) из совокупности с ку-

мулятивной функцией распределения F (μ, p), p — неизвестная вероятность,

подлежащая оценке.

В терминологии [15] это задача нахождения условных оценок. В терми-

нологии [16] это задача параметрического статистического оценивания. При

известном априорном распределении измеряемого параметра вырабатывает-

ся байесова оценка. Статистика (6) имеет биномиальное при независимых

и полиномиальное при зависимых испытаниях распределение. Для выборок

большого размера используется асимптотика Муавра-Лапласа [17].

3.2. Байесова и максимально правдоподобные оценки

вероятности по частоте

При независимых испытаниях и равномерном распределении имеем байе-

сову

m+1

(7)

p∗опт =

N+2

и м аксимально правдоподобную

(8)

p∗мп =

оценки вероятности (7) и (8).

Оценка максимального правдоподобия (8) является состоятельной и эф-

фективной, а ее нижняя граница дисперсии согласно неравенству Рао-

Крамера [18] равна

p(1 - p)

(9)

σ²(p∗мп) =

107

M{(p* p)²/p}

10³

p* = p_m

n = 16

p* = p_опт

n = 64

0,2

0,4

0,6

0,8

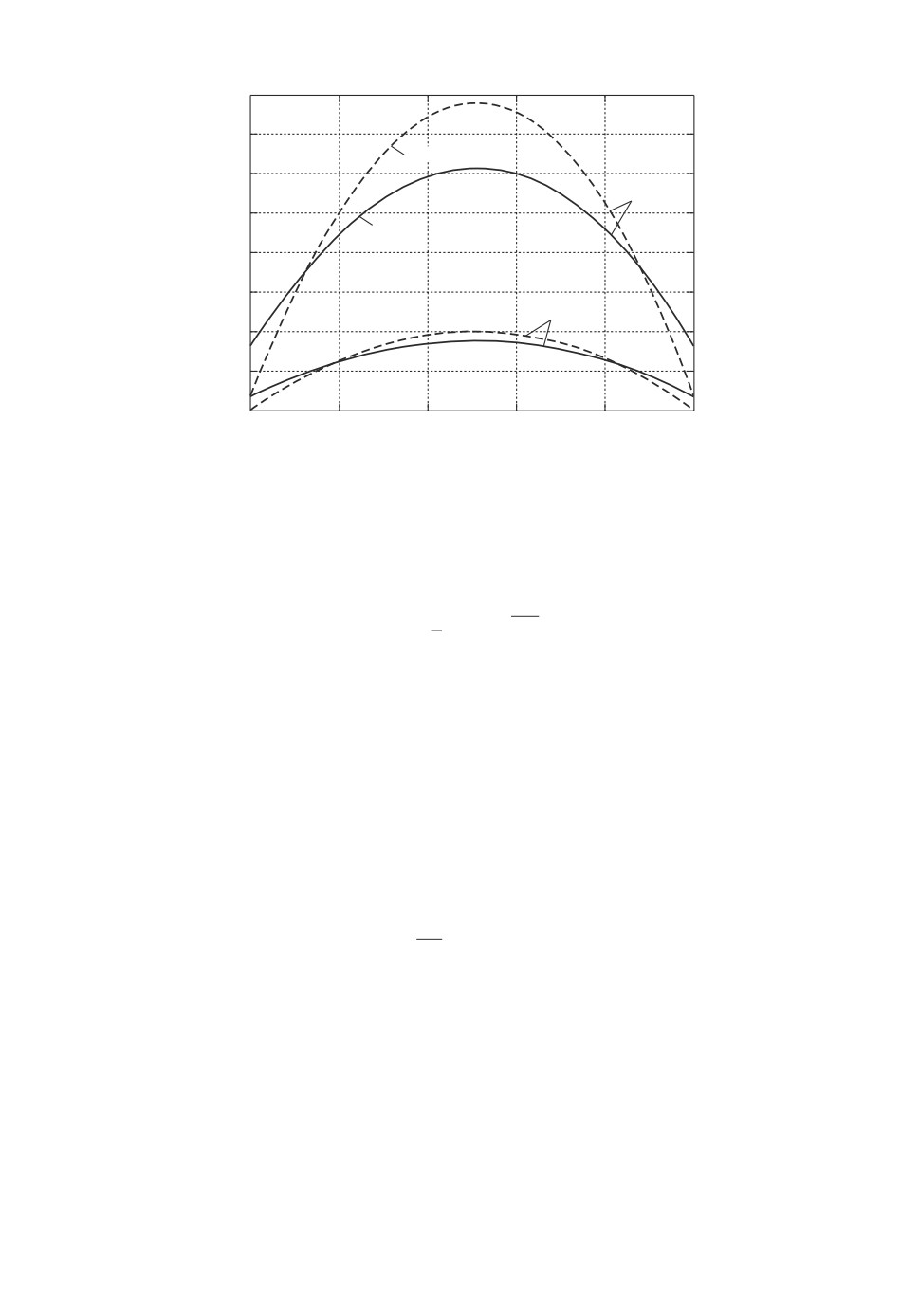
Рис. 1. СКО измерения вероятности p для байесовой (сплошная линия) и

максимально-правдоподобной (штрих-пунктирная линия) оценок.

Сравнивая СКО для оценок (7) и (8), можно найти точки пересечения

кривых (рис. 1)

√

(10)

p1,2 ≈

(1 ±

0,5),

где видно, что при p < 0,15 и p > 0,85 следует пользоваться оценкой макси-

мального правдоподобия, в остальном диапазоне p лучше байесова оценка.

3.3. Организация обратной связи в методе Монте-Карло

Для повышения инструментальной точности измерения вероятности после

использования априорных сведений используем подход, основанный на изме-

нении условий проведения измерений, что не предусмотрено в [18]. Прежде

покажем, что использование для этой цели лишь разбиение N на этапы не

дает результата. Действительно, если на каждом этапе взять оценку

m_i

(11)

p∗мп(m_i) =

i = 1,2,...,L,

N_i

где L — число этапов измерения; i — номер этапа; N_i — размеры каждого

этапа, то по результатам L этапов можно сформировать оценку

∑

(12)

p_Σ∗ =

η_ip∗мп(m_i

i=1

где η_i — весовые коэффициенты, удовлетворяющие условию нормировки

∑

(13)

η_i

= 1.

i=1

108

Оптимизируя весовые коэффициенты методом неопределенных множите-

лей Лагранжа получим

N_i

(14)

ηiопт =

∑

N_i

i=1

Подставляя (14) в (12), имеем

^L m_i

(15)

p_Σ∗ =i=1

∑

N_i

i=1

Таким образом, суммарная оценка p_Σ∗ (15) совпадает с оценкой макси-

мального правдоподобия одноэтапной процедуры с числом испытаний N =

∑

= N_i.

i=1

Далее в методе Монте-Карло организуем обратную связь: будем рекурсив-

но изменять условия проведения измерений от этапа к этапу.

Весь объем испытаний N по аналогии с [20, 21] разобьем на два и более

этапов. Первый этап объемом N₁ представляет собой классическую схему

Бернулли. На первом этапе выработаем оценку p∗1 исходной вероятности p.

Далее по оценке p∗1 вырабатывается корректирующая эталонная добавка δ.

На втором этапе объемом n₂ проведем промежуточные измерения на новой

величине p₂ = p₁ + δ, сводящей измерения к точкам (10). При введении δ в

измерителях дальности [21] использовалась коммутируемая линия задерж-

ки с отводами. При измерении пеленга θ управляемые добавки вводятся в

квадратурные каналы сигнала [9, 22].

Результаты анализа двухэтапной оценки вероятности показали, что при

организации обратной связи в схеме Бернулли незначительно снижаются

СКО измерения [20].

Резервы повышения точности целесообразно искать в разбиении всего

объема N испытаний на L этапов и организации рекуррентной зависимости

испытаний. Здесь отметим, что известная последовательная оценка вероят-

ности по частоте [19] не фиксирует число испытаний, а основополагающие

работы Вальда и последующие работы глубоко и всеобъемлюще разрешают

эту проблему, однако возникают трудности вычислительного плана. Одна из

трудностей [19] состоит в следующем. Для построения оптимальной процеду-

ры по методу последовательного анализа, нужно решить систему рекуррент-

ных уравнений. Во многих подобных ситуациях решение уравнений удается

получить для небольшого числа шагов.

Алгоритм формирования оценок p^∗i, i = 1, . . . , L, вероятности p следую-

щий. После первого этапа формируется оценка p∗1 вероятности p. По этой

оценке вырабатывается корректирующая добавка δ₁ = 1 - p∗1, сводящая из-

мерения на втором этапе к узлам СКО (10).

109

p₁

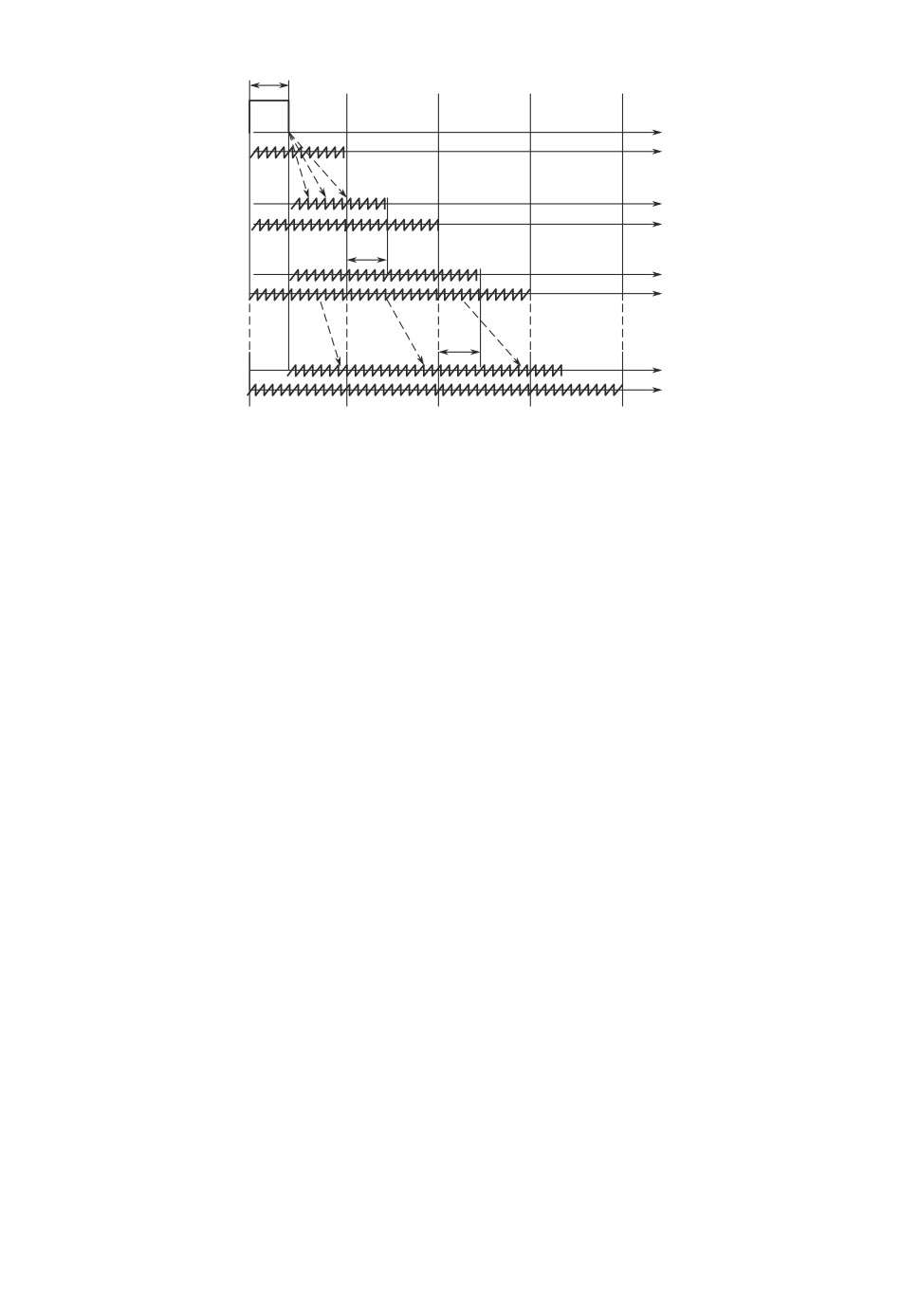
Рис. 2. Области изменения параметров θ_i и их оценок θ^∗i.

На втором этапе измеряется параметр θ₂ = p + δ₁ и формируется оценка

исходной вероятности по формуле p∗2 = θ∗2 - δ₁, где θ∗2 = m₂/N₂ — оценка θ₂.

Далее вырабатывается корректирующая добавка δ₂ = 1 - p∗2 для измерения

параметра θ₃ = p + δ₂ на третьем этапе и т.д.

В общем виде оценку p^∗L вероятности p₁ = p на L-м этапе можно предста-

вить в виде

(16)

p^∗L = θ^∗L - δL-1,

где θ^∗L = m_L/N_L — результат измерения параметра θ_L = p_L + δL-1 на L-м эта-

пе (11); m_L — число совпадений; N_L — число испытаний; δL-1 = 1 - p∗L-1 —

корректирующая добавка на L-м этапе, определяемая через оценку p∗L-1 на

(L - 1)-м этапе; p∗L-1 = θ∗L-1 - δL-2 и т.д.

По результатам измерений (16) после L этапов формируется результирую-

щая оценка

∑

p_Σ∗ =

η_ip^∗i,

i=1

где η_i — весовые коэффициенты, удовлетворяющие условию (13).

Из анализа [21] следует, что дисперсия D{p^∗L} оценки зависит от дис-

персии оценки параметра θ^∗L = m_L/N_L и дисперсии эталонной добавки δL-1:

D{p^∗L} = D{θ^∗L} + D{δL-1}.

Для определения D{θ^∗L} обратимся к рис. 2, на котором для фиксирован-

ного значения p₁ показаны области изменения (аттракторы) параметров θ_i,

их оценок θ^∗i, а также реализации отдельных случайных траекторий их из-

менения.

Результаты анализа рекурсивной многоэтапной оценки вероятности пока-

зывают, что организация обратной связи в схеме Бернулли может дать боль-

110

шие выигрыши в снижении инструментальных погрешностей, если одновре-

менно повышать число измерений на этапах.

3.4. Асимптотика Муавра-Лапласа и оценка предельных возможностей

Применение асимптотики Муавра-Лапласа [17] позволяет конкретизиро-

вать распределение параметров θ_i и через функциональное преобразование

дробной части p_i = R{θ_i} определить качество результирующей оценки p^∗L.

Исходя из принципа формирования эталонных добавок, заключающегося

в сведении измерений к узлу θ_i = 1 с использованием несмещенных оценок

θ^∗i = m_i/N_i, можно показать, что все математические ожидания M{θ_i} пара-

метров θ_i равны 1 за исключением θ₁ = p₁. Поэтому, аппроксимируя распре-

деление W {θ_L} нормальным распределением со средним значением a = 1 и

дисперсией DL-1 = σ2L-1, а также учитывая свойства функции дробной до-

ли R{·}, можно определить значения первого и второго моментов вероятно-

сти p_L.

В результате вычислений при σL-1 ≪ 1 получим [21]

√

p_L - p²

2/π - σL-1

2/π

(17)

σ2L =

=σL-1

⁼σL-1

N_L

√

Учитывая, что σ₁ =

(p₁q₁)/N₁, q₁ = 1 - p₁, нетрудно видеть в (17), что

при увеличении L кривая СКО становится все более плоской в окрестности

точки p₁ = 1/2, поэтому для получения усредненного по p₁ значения σ2L доста-

точно выполнить вычисления в точке p₁ = 1/2. Подставляя p₁ = 1/2 и находя

∑_l

экстремум (минимум) при фиксированном N =

N_i, получим следующее

i=1

оптимальное соотношение между этапами:

(18)

N_L/NL-1 = NL-1/NL-2 = ... = N₂/N₁

= 2.

Используя соотношение (18), дисперсия будет

)

)₍₂L-1-1)/2L-1(L-1∏

∕∏

⁽2

σ2L =

2(i+1)/2i

N1/2i

i=0

Тогда

√

σ_L = lim σ2L =

2/π(2²/N),

∑

∑ i+1

так как lim

= 2, а lim

=2⁴.

L→∞ i=0 2ⁱ

l→∞ i=0

В предельном случае, как это следует из формулы (23), измерения на

L-м этапе будут обеспечивать скорость уменьшения среднеквадратической

ошибки как 1/N. Уменьшение числа этапов L, а также учет других об-

стоятельств, связанных с формированием эталонных псевдослучайных тра-

екторий, приводит к уменьшению достигаемого предела вплоть до значе-

ний 1/N3/4 для L = 2 и 1/N в предельном случае. Таким образом, ско-

рость сходимости предельная ∼ K-3/4 ÷ K-1, K = 1, 2, 3, . . ., т.е. более высо-

кая, чем в классической схеме Бернулли. Эталонные добавки при измерении

111

пеленга физически трактуются как учитываемые фазовые вставки, коррек-

тирующие измеряемые положения фазового фронта поля в апертуре ФАР

(это эквивалентно хаотической случайной перестройке положения фазового

центра при последовательной аппроксимации пеленга «грубыми статистика-

ми») [22]. Предельное инструментальное разрешение и точность измерения

пеленга метода усреднения ГО возрастает как ряд ∼ (K1/2 - K), где K —

размер пространственной апертуры ФАР.

3.5. Возможности предлагаемого подхода

Стохастическое управление фазовым центром реализует скорости увели-

чения инструментальной точности и разрешающей способности, эквивалент-

ные ряду ∼ K1/2 ÷ K, где K — размер пространственной апертуры ФАР. Для

оценки вероятности в методе используется «грубая» бинарная статистика μ_i,

равная 1 или 0. В этом состоит достоинство подхода, когда текущие грубые

отсчеты получить сложно (или невозможно) либо это делается искусственно

с целью учета ограниченности аппаратурных или вычислительных ресурсов

аппаратуры пеленгатора. В данном случае обратная связь в методе Монте-

Карло отчасти использует ресурс зависимых испытаний. Известны [13] по-

казательные и расчетные примеры ускорения сходимости метода, когда при

оценке вероятности, связанной с числом π в опыте подбрасывания связан-

ной пары игл (засчитываемых за два испытания), точность измерения ве-

роятности по частоте возрастала по сравнению с опытом последовательного

проведения двух независимых испытаний и подсчете числа пересечений игла-

ми начерченных на плоскости параллельных линий. Чем-то это напоминает

«урновую схему» Пойя (см. [23]), когда в урну добавлялось не только из-

вестное количество шаров (здесь это эталонные добавки δ), но и менялся их

цвет. Статистика измерения вероятности по частоте в данном случае — ли-

нейная статистика. Однако, оставляя текущую статистику «грубой» (μ_i = 1

или μ_i = 0), в варианте использования нелинейной статистики для оценки

вероятности можно упомянуть процедуру последовательного деления отрез-

ка пополам, т.е. процедуру Больцано. Эта процедура также является поис-

ковой, а скорость увеличения инструментальной (не потенциальной) точно-

сти в идеальном случае возрастет как два в степени K = 1, 2, . . . Поэтому

можно считать, что это есть достоинство предлагаемого подхода, когда при

уверенном отношении сигнал/шум (в условиях отсутствия шума, т.е. модели

пеленга — не как математическое ожидание, а как детерминированная кон-

станта) можно существенно уменьшить инструментальную погрешность, но

это обстоятельство не совсем верное. На самом деле, учет шума приводит

к процедурам стохастической аппроксимации, процедурам Роббинса-Монро,

Кифера-Вольфовица и др. в вариантах использования как линейных, так и

нелинейных оценок, что является предметом исследований других статей.

4. Заключение

Предлагается метод построения информационной системы, осуще-

ствляющей измерение пеленга за счет интерполяции грубых («бинарно-

знаковых») ПВ отсчетов входного сигнала на базе усеченных (малоэлемент-

112

ных) апертур со слабонаправленными приeмопередающими элементами ан-

тенной решетки. Задача измерения пеленга сводится к оценке вероятности

методом Монте-Карло с обратной связью. Для различных алгоритмов при-

водятся результаты расчета инструментальных погрешностей измерения пе-

ленга. Оценка резервов уменьшения инструментальной СКО оценки пеленга

при использовании многоэтапной процедуры в методе Монте-Карло составля-

ет ∼ K-3/4 ∼ K-1, K = 1, 2, 3, . . . Инструментальная точность метода может

быть приведена в соответствие с потенциальной точностью и увеличиваться

с ростом K как ряд K1/2 ÷ K, где K — размер пространственной апертуры

(выборки).

СПИСОК ЛИТЕРАТУРЫ

Metropolis N., Ulam S. The Monte Carlo Metod // J. Amer. Statist. Assoc. 1949.

V. 44.

Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию:

Пер. с англ. М.: Радио и связь, 1986.

Klemm R. Space-Time Detection Theory // The material in this publication was

assembled to support a lecture series under the sponsorship of the sensor and

lectronics Technology Panel (SET) and the Consultant and Exchange Programmer

of RTO presented on 23-24 september 2002 in Moscow, Russia.

Воскресенский Д.И. Антенны с обработкой сигнала: Уч. пос. для вузов. М.:

САЙНС — ПРЕСС, 2002.

Горбунов Ю.Н. Цифровая обработка радиолокационных сигналов в условиях ис-

пользования грубого (малоразрядного) квантования: монография / Федераль-

ное космическое агентство, ФГУП «ЦНИРТИ им. акад. А. И. Берга». М., 2007.

Горбунов Ю.Н., Лобанов Б.С., Куликов Г.В. Введение в стохастическую радио-

локацию. Уч. пос. для вузов. М.: Горячая линия — Телеком, 2015.

Горбунов Ю.Н. Рандомизированная обработка сигналов в радиолокации и связи.

ISBN 978-3-659-37797-6, Изд-во «LAP LAMBERT Academic Publishing», 66121,

Saarbrücken, Germany, 2015.

Горбунов Ю.Н. Стохастическая радиолокация: условия решения задач

обнаружения, оценивания и фильтрации

// Электрон. издание

«Жур-

нал радиоэлектроники», ISSN

1684-1719. М.: ИРЭ им. В.А. Котельни-

кова РАН,

2014.

№ 11. http://jre.cplire.ru/jre/nov14/3/text.html; http://

jre.cplire.ru/jre/nov14/3/text.pdf

Горбунов Ю.Н. Стохастическая интерполяция пеленга в адаптивных антенных

решетках с последовательным диаграммо-образованием на базе усечённых (ма-

лоэлементных) апертур и робастных статистик сигнала на входе / Изд-во «Ра-

диотехника». журн. «Антенны». 2015. № 6. С. 18-26.

10.

Первозванский А.А. Поиск. М.: Наука, 1970.

11.

Цыпкин Я. З. Адаптация и обучение в автоматических системах. М.: Наука,

1968.

12.

Черняк В.С. О новых и старых идеях в радиолокации: МIМО РЛС // Успехи

современной радиоэлектроники. 2011. Вып. 2. С. 5-20.

13.

Соболь И.М. Численные методы Монте-Карло. М.: Наука, 1973.

14.

Горбунов Ю.Н., Бондарев А.В. Алгоритмы и устройства цифровой стохастиче-

ской обработки сигналов в радиолокации. Уч. пос. М.: НИЦЭВТ, ИПК МРП,

1990.

113

15. Левин Б.Р. Теоретические основы статистической радиотехники. Кн. 3. М.: Сов.

радио, 1976.

16. Уилкс С. Математическая статистика. М.: Наука, 1967.

17. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1965.

18. Крамер Г. Математические методы статистики. М.: Мир, 1975.

19. Вальд А. Последовательный анализ. М.: Физматгиз, 1960.

20. Гайсов В.Г., Горбунов Ю.Н. Двухэтапная процедура измерения временных ин-

тервалов методом статистических испытаний с обратной связью // Автометрия.

Сиб. отделение АН СССР. 1982. № 2. С. 54-60.

21. Горбунов Ю.Н. Многоэтапная процедура измерения параметров повторяющего-

ся сигнала методом стохастического усреднения цифровых отсчетов // Авто-

метрия. Сиб. отделение АН СССР. 1985. № 3. С. 96-99.

22. Горбунов Ю.Н. Неслучайные траектории стохастической аппроксимации пелен-

га в адаптивных антенных решетках с грубыми пространственно-временными

статистиками // IX Всерос. Научн.-техн. конф. «Радиолокация и радиосвязь»,

ИРЭ им. В.А. Котельникова РАН. М.: 23-25 ноября 2015. С. 57-60.

23. Феллер В. Введение в теорию вероятностей и ее приложения. T. II. М: Мир,

1967.

Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.

Поступила в редакцию 08.07.2016

После доработки 17.12.2018

Принята к публикации 18.07.2019

114