Автоматика и телемеханика, № 12, 2019

Управление в технических системах

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

Л.А. ШАЛБИ (lina.khamis@gmail.com)

(Московский физико-технический институт)

СТАБИЛИЗАЦИЯ КОСМИЧЕСКОГО АППАРАТА В ТОЧКАХ

ЛАГРАНЖА С МИНИМАЛЬНЫМ РАСХОДОМ ТОПЛИВА¹

Рассматривается движение космического аппарата (КА), описываемое

дифференциальными уравнениями задачи трех тел для системы Земля —

Луна. Цель состоит в том, чтобы стабилизировать его в окрестности кол-

линеарных лагранжевых точках, которые являются неустойчивыми точ-

ками равновесия, с помощью управления с минимальным расходом топ-

лива. Используемый метод — это l₁-оптимизация для линеаризованных

и дискретизированных уравнений с терминальными условиями, равными

точке назначения. Таким образом, задача преобразуется в задачу линей-

ного программирования, и ее решение определяет импульсные управле-

ния для исходных уравнений трех тел. После этого КА на некоторое время

остается в неконтролируемом полете, пока его отклонение от лагранжевой

точки не превысит некоторого порога. Затем коррекция повторяется, тем

самым КА удерживается в небольшой окрестности неустойчивой точки

равновесия.

Ключевые слова: ограниченная задача трех тел, лагранжевы точки, ме-

тод l₁-минимизации, оптимальное управление, стабилизация, неустойчи-

вая точка равновесия.

DOI: 10.1134/S0005231019120109

1. Введение

Ограниченная задача трех тел описывает движение тела малой массы,

притягиваемого двумя массивными телами, вращающимися вокруг своего

центра масс (барицентра) по круговым орбитам под действием их взаимного

гравитационного притяжения. Ее изучение восходит к Пуанкаре; трудность

задачи заключается в том, что аналитического решения в общем случае не

существует, а частные решения бывают необычайно сложными и носят хаоти-

ческий характер [1]. В дальнейшем проблема подвергалась многочисленным

исследованиям, отметим среди них [2-8].

Хорошо известно, что в этой проблеме имеется пять точек равновесия си-

стемы, они называются лагранжевы точки или точки либрации. Три из них

являются коллинеарными, лежащими на оси x, а две другие точки образуют

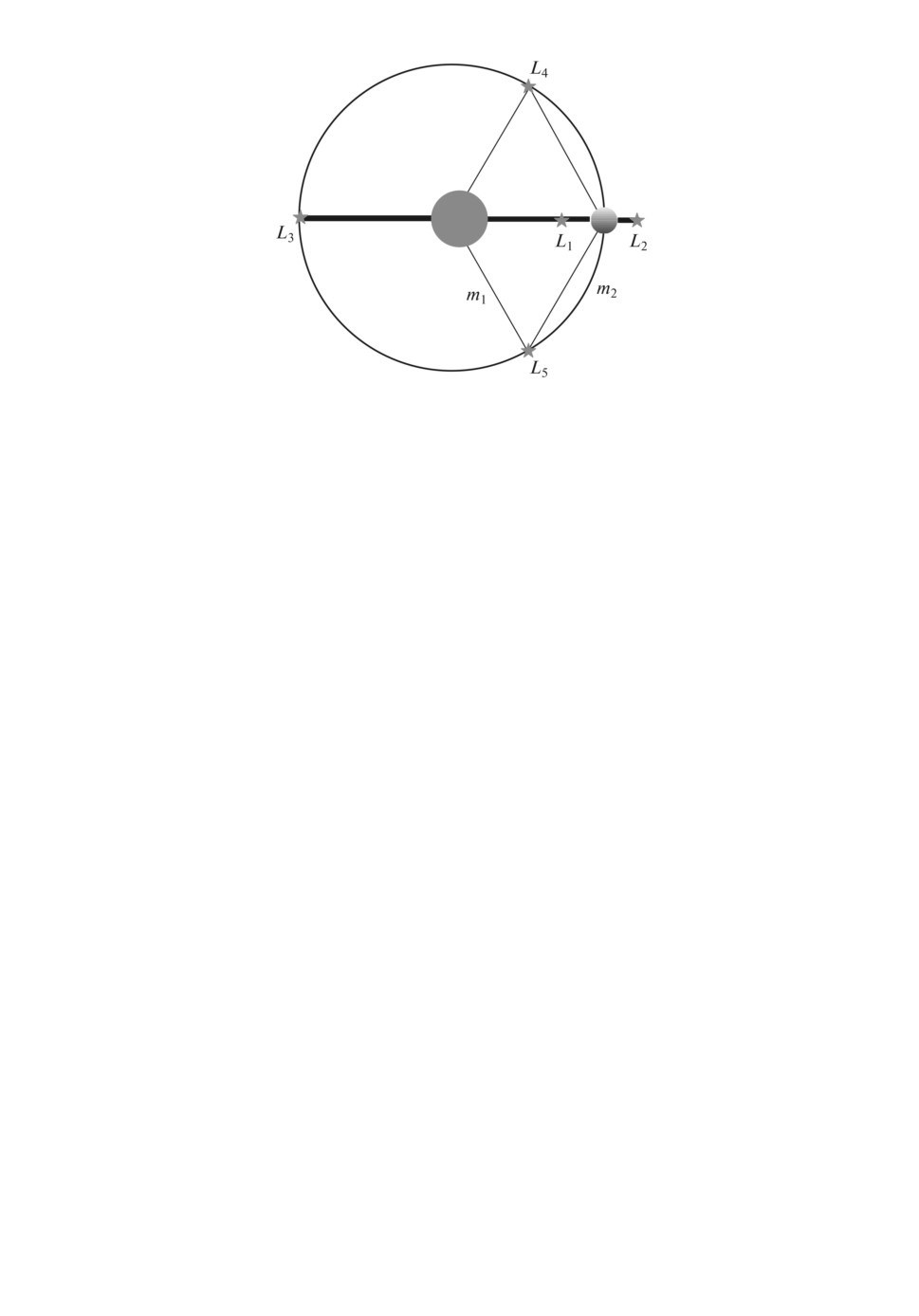
равносторонний треугольник с двумя телами m₁ и m₂ (m₁ > m₂). Рисунок 1

показывает точки Лагранжа по отношению к m₁ и m₂.

¹ Работа первого автора выполнена при финансовой поддержке Российского научного

фонда (грант 16-11-10015).

160

Рис. 1. Расположение лагранжевых точек.

Все эти точки равновесия являются неустойчивыми, между тем, во многих

случаях полезно помещать космический аппарат (КА) в одну из этих точек

для целей наблюдения и связи. Так, совсем недавно (в 2019 г.) китайские

исследователи разместили КА в точке L₄ системы Земля - Луна для наблю-

дения за посадкой и движением лунохода, высаженного на обратной стороне

Луны.

Настоящая работа посвящена методу стабилизации КА в точках Лагран-

жа системы Земля - Луна (хотя используемый подход применим и к дру-

гим задачам такого типа). При отклонении аппарата от точки равновесия

на некоторую величину решается задача оптимального управления для его

возвращения в эту точку при минимальном расходе топлива. Численное ре-

шение находится путем линеаризации и дискретизации уравнений движения

с функционалом типа l₁, отвечающим минимальному расходу топлива. Тем

самым приходится решать задачу линейного программирования. Полученное

импульсное управление применяется для исходной задачи; оно перемещает

КА в точку, близкую к желаемой. После этого начинается неуправляемый

полет КА, при возникновении существенного отклонения вновь включается

коррекция. Таким образом, КА остается все время в небольшой окрестности

точки равновесия ценой малого расхода топлива.

По сравнению с классическими численными методами для оптимального

управления [9-12] используемый в работе метод учитывает специфическую

форму негладкого минимизируемого функционала (l₁-оптимизация). Ранее

подобные методы применялись для расчета космических перелетов с мини-

мальным расходом топлива [13-15], но не для стабилизации КА в точке рав-

новесия.

2. Уравнения движения и лагранжевы точки

В данном исследовании рассматривается движение КА в системе Зем-

ля - Луна. Движение происходит за счет гравитационных сил Земли и Лу-

ны и реактивных двигателей КА. В безразмерных координатах (координа-

161

тах x, y) уравнения движения будут представлять собой автономные нели-

нейные дифференциальные уравнения. Для безразмерной системы положим,

(0 ≤ μ ≤¹² ), а тре-

+m₂

тье тело (КА) имеет пренебрежимо малую массу. Центром масс является

начало координат, ось x соединяет точки m₁ и m₂, а ось y перпендикулярна

к ней, так что позиции m₁ и m₂ находятся в (-μ, 0, 0) и (1 - μ, 0, 0) соответ-

ственно. Масса Земли составляет m₁ = 5,972 × 10²⁴ кг и масса Луны состав-

ляет m₂ = 7,34767 × 10²² кг, так что μ = 0,012155, расстояние между Землей

и Луной составляет 384400 км, а единица времени — 1 ч. При отсутствии

тяги КА дифференциальные уравнения, описывающие его движение, хоро-

шо известны (ограниченная задача трех тел) и в безразмерных координатах

имеют вид

x = u,

y=v,

x+μ

x+μ-1

u = 2v + x - (1 - μ)

-μ

(1)

r³¹

r³

(

)

1-μ

v = -2u +

r³¹

r³

где x, y — координаты КА, u, v — его горизонтальная и вертикальная скоро-

сти, а

√

r₁ =

(x + μ)² + y², r₂ =

(x + μ - 1)² + y²

— его расстояния до Земли и Луны. В краткой записи уравнения движения

имеют вид

(2)

= f(X),

где X = [x, y, u, v]^T .

Полная энергия системы (1) имеет следующий вид (см. [7, 10]):

(

)

(

)

1-μ

x² + y²

μ.

r₁

r₂

При нулевом значении кинетической энергии оставшаяся часть E₀ полной

энергии и константа Якоби C задаются формулой

(

)

1-μ

(3)

E₀ = -

x² + y²

r₁

r₂

Контур и поверхность 3D-графика E₀ представлены на рис. 2,а и 2,b соот-

ветственно.

Точки равновесия для уравнений (1) являются лагранжевыми точками.

В них все силы уравновешивают друг друга: u = v = u = v = 0. Первые три

коллинеарные точки Лагранжа L₁, L₂ и L₃ определяются из этих уравнений

162

Таблица 1. Координаты лагранжевых точек и собственные

значения якобианов

Лагранжевы точки

Собственные значения

λ1,2 = ±2,33441j

L₁ = (0,83689, 0)

λ3,4 = ±2,93209

λ1,2 = ±1,86282j

L₂ = (1,15569, 0)

λ3,4 = ±2,15864

λ1,2 = ±1,01042j

L₃ = (-1,00506, 0)

λ3,4 = ±0,17790

√

λ1,2 = ±0,95448j

L4,5 = (0,48784, ±

)

λ3,4 = ±0,29825j

а L4,5 соответствуют y = 0, так что 1 - 1-μ

- μ

= 0 и r₁ = r₂ = 1, поэто-

r³¹

r³

√

(

√

)

му x^∗ = 0,5 - μ и y^∗ = ±

, т.е. L4,5 =

0,5 - μ, ±

. В каждой из этих

точек можно вычислить собственные значения соответствующих якобианов

⎞

^⎛ 0

⎜

1⎟

⎝

⎠, где выражения для ux, uy, vx и vy могут быть упрощены:

u_x

u_y

v_x

v_y

-2 0

2μ

(1-μ)

• при y^∗ = 0, u_x = 1 +2(1-μ)

u_y = 0 и v_x = 0, v_y = 1 -

|x^∗+μ|³

|x^∗+μ-1|³

|x^∗+μ|³

− μ

для первых трех точек L₁, L₂ и L₃;

|x^∗+μ-1|³

√

• при x^∗ = 0,5 - μ и y^∗ = ±

получаем u_x =³⁴ , u_y = ±³

(1 - 2μ) и v_x =

√

=±³

(1 - 2μ), v_y =⁹⁴ для L4,5. В этих точках якобианы имеют равные

собственные значения и могут быть записаны в терминах μ в виде

√

√√

λ1,2 = ±√

27μ² - 27μ + 1 - 1, λ3,4 = ±√

27μ² - 27μ + 1 - 1.

Для системы Земля - Луна лагранжевы точки и их собственные значения

представлены в табл. 1, здесь j =

√-1.

Из табл. 1 видно, что все точки Лагранжа неустойчивы. Численная про-

верка подтверждает это. Система решается численно методом Рунге-Кутты

при условии, что КА начинает двигаться с нулевой начальной скоростью

из начальной точки, близкой к L₁. Оказывается, что КА будет удаляться

от точки равновесия — он будет вращаться либо вокруг Земли, либо во-

круг Луны. Например, на рис. 3 показаны две траектории: для начально-

го положения (x^∗

- 0,001, 0,001) это будет движение вокруг Земли, а для

L₁

(x^∗

+ 0,001, 0,001) — вокруг Луны. Рисунок 4,а — это более подробно по-

L₁

казанная траектория космического аппарата, вращающегося вокруг Луны из

начального положения (x^∗

+ 0,001, 0,001). Видно, что траектории хаотич-

L₁

ны, т.е. они сильно зависят от начальных условий и трудно предсказуемы.

С другой стороны, КА, который находится в позиции, близкой к L₂, будет

вращаться вокруг Земли и Луны, как на рис. 4,a и рис. 4,b, а из точки близкой

к L₃ он будет двигаться как на рис. 4,c.

164

3. Оптимальное управление движением

Поскольку лагранжевы точки неустойчивы, для стабилизации КА в этих

точках надо применять управление. Будем предполагать, что он оснащен

реактивным двигателем с возможным изменением направления силы тяги.

Горизонтальную направляющую силы тяги обозначим через U¹, а вертикаль-

ную составляющую — через U², тогда уравнения движения принимают вид

x = u,

y=v,

x+μ

x+μ-1

u = 2v + x - (1 - μ)

-μ

+U¹,

(5)

r³¹

r³

(

)

1-μ

v = -2u +

y+U².

r³¹

r³

Цель - из заданного начального условия вблизи точки равновесия (для

конкретности L₁) вернуться к точке равновесия за фиксированное время T .

Расход топлива за время управления пропорционален интегралу

∫T

(6)

J =

(|U¹| + |U²

|)dt.

Таким образом, приходим к задаче оптимального управления — минимизи-

ровать функционал (6) на решениях дифференциального уравнения (5) при

заданном начальном условии (вблизи L₁) и заданном терминальном усло-

вии (попадание в точку равновесия). Специфический негладкий вид функ-

ционала (6) приводит к тому, что оптимальным управлением в такого рода

задачах являются импульсные управления (см. [16]). Это ограничивает воз-

можности применения стандартных численных методов оптимального управ-

ления [9, 12]. Разрабатываемый здесь подход будет основываться на лине-

аризации и дискретизации уравнения и замене интеграла суммой модулей

дискретизированных управлений. Тем самым численное решение сводится к

задаче линейного программирования. Полученное кусочно-постоянное управ-

ление используется в исходной нелинейной системе (5).

Более подробно, схема алгоритма решения имеет следующий вид.

1. Заменим переменные, чтобы задать начало координат в точке Лагран-

жа.

2. Линеаризуем уравнения в окрестности начала координат.

3. Дискретизируем линейную систему по времени.

4. Установим начальное условие (близкое положение к началу коор-

динат, например Y₀ =

^[0,01 0,01

0]T ) и терминальное условие (YN =

^[0

0]T ).

∑N-1 ∑₂

5. Запишем целевую функцию в виде J =

|U^kn|.

n=0

k=1

6. Возникающую задачу сведем к задаче линейного программирования;

решим ее и найдем оптимальное решение U_n, n = 1, . . . , N.

166

7. Применим полученное управление как импульсное в исходной нелиней-

ной системе (интегрируя ее более точным методом типа Рунге-Кутта), при

этом получим близкое к нулю терминальное положение, и рассчитаем истин-

ный расход топлива.

8. Продолжаем траекторию движения КА без управления начиная с полу-

ченного терминального значения и проверяем величину отклонения от точ-

ки L₁. Если оно превышает значение r, переходим к п. 3.

Теперь опишем некоторые подробности. Вводим y₁ = x - L₁, y₂ = y, y₃ =

= u, y₄ = v. Тогда система (5) записывается как

(7)

= f (Y ) + BU,

где Y = [y₁ y₂ y₃ y₄]^T . Система (7) после линеаризации принимает вид

(8)

= AY + BU,

где A — якобиева матрица системы (7) в начале координат. Затем линеари-

зованная система (8) дискретизируется с помощью прямого метода Эйлера с

шагом δ и становится дискретной:

(9)

Yn+1 - Y_n = δ(AY_n + BU_n).

Пусть C = I + δA, тогда

∑

Yn+1 = CY_n + δBU_n = Cn+1Y₀ + δ CⁱBU_n-i.

i=0

Конечномерная аппроксимация оптимизируемой функции J выглядит сле-

дующим образом:

∑

(10)

J =

|U^kn

| → min.

n=0 k=1

Уравнение (9) вместе с граничными условиями записывается в виде

∑

Y_N - C^NY₀

(11)

CN-i-1BU_i =

i=0

Введем обозначения

Y_N - C^NY₀

D = [B CB ... CN-1B],

U= [U₀

U₁

... UN-1]^T, E=

где D ∈ R4×2(N-1),U ∈ R2×(N-1) и E ∈ R⁴, тогда уравнение (11) может быть

записано явно в виде

(12)

= E.

Таким образом, получается задача минимизации функции (10) при ограни-

чении типа равенств (12). Стандартные приемы (замена модуля разностью

неотрицательных переменных) позволяют свести ее к задаче линейного про-

граммирования. Тем самым можно применить эффективный алгоритм LP в

MatLab. Аналогичные методы для задач оптимального управления применя-

лись в [14].

167

Рис. 5. Сравнение управляемой и неуправляемой траекторий.

При вычислениях бралось T = 1 и N = 500, δ = 1/500 (т.е. Y₅₀₀ =

]_T

^[0

0]T ). Начальное условие было взято Y0 =[0, 01 0, 01

(на-

поминаем, что эти значения — в новых координатах, т.е. в отклонениях от

лагранжевой точки и с нулевой начальной скоростью). Управление U имеет

две компоненты U¹ и U², в результате вычислений оказалось, что каждая из

них имеет два ненулевых элемента:

U¹⁰ = -13,85764, U¹⁴⁹⁸ = 3,02778, U²⁰ = -5,89732, U²⁴⁰¹ = 4,73736

(все остальные равны нулю). Это согласуется с тем, что оптимальное решение

должно иметь четыре ненулевых импульса (имеется четыре терминальных

условия).

Теперь полученное управление U_n с ненулевыми импульсами в моменты

n = 0,401,498 подставляется в исходную непрерывную систему, которая ин-

тегрируется методом Рунге-Кутта. При этом затраты топлива оказываются

равными 27,520867. На рис. 5 сравниваются управляемые и неуправляемые

траектории на плоскости x, y, которые стартуют из одной начальной позиции

близкой к L₁. Видно, что неуправляемая траектория удаляется далеко от L₁,

а управляемая траектория возвращается к L₁.

После того как скорректируем траекторию и попадаем в точку, очень

близкую к L₁ с малым расходом топлива, КА продолжит свое движение без

управления. В результате он удаляется от точки равновесия. Когда это уда-

ление превосходит некоторый порог (конкретно бралось значение r = 0,01),

коррекция повторяется, применяется управление таким же образом, чтобы

держать КА в окрестности L₁. Для трехкратного цикла коррекций в табл. 2

представлены значения начальных и конечных условий, импульсные значе-

ния управления U_n и расход топлива. Тактом обозначен интервал времени,

равный 0,002 (цикл управления — 500 тактов).

На рис. 6 и 7 видно поведение корректируемых и неуправляемых участков

траектории для шести коррекций. После второй коррекции траектория имеет

повторяющуюся форму с очень небольшими отличиями.

168

0,850

0,845

0,840

0,835

0,830

0,825

0,010

0,005

0,010

Рис. 6. Изменение x и y во времени на [0, 10].

В размерных величинах точка L₁ находится на расстоянии 321703 км от

барицентра. Исходное положение x = 325547 км и y = 3844 км. После пер-

вой коррекции космический аппарат оказывается на расстояние 321491 км от

барицентра (около 212 км) от L₁.

Аналогичные вычисления были проделаны для стабилизации КА в точ-

ках L₂ и к L₃ за время [0, 10]. Рисунки 8 и 9 показывают коррекцию траек-

Таблица 2. Начальные и конечные условия, управления и расход топлива для трех

коррекций траектории

Расход

Y₀

Y_N

топлива

⎡

⎤ ⎡

⎤

0,84689

0,835539

Первая

⎢

0,01

⎥

⎢-0,00007⎥

U⁽¹⁾⁰ = -13,85764 U⁽²⁾⁰ = -5,89732

⎣

⎦

⎣

⎦

27,52086

коррекция

-0,00417

U⁽¹⁾⁴⁹⁸ = 3,02778

U⁽²⁾⁴⁰¹ = 4,73736

0,00227

Неуправляемый полет 333 тактов

⎡

⎤⎡

⎤

0,82786

0,83917

Вторая

⎢

0,00436

⎥⎢-0,00077⎥

U⁽¹⁾⁰ = 28,13806 U⁽²⁾⁰ = 5,82087

⎣

⎦⎣

⎦

36,53279

коррекция

-0,02523

0,00676

U⁽¹⁾⁴⁹⁸ = 0,145938 U⁽²⁾⁴⁰¹ = 2,43383

0,01373

-0,00327

Неуправляемый полет 237 тактов

⎡

⎤⎡

⎤

0,84607

0,83762

U⁽²⁾³⁴⁰ = -1,78599

Третья

⎢-0,00407⎥⎢

0,00001

⎥

U⁽¹⁾⁰ = -29,60898

⎣

⎦⎣

⎦

U⁽²⁾³⁴¹ = -6,22046 37,64523

коррекция

0,02734

0,00196

U⁽¹⁾⁴⁹⁹ = -0,01489

−0,01263

-0,00124

U⁽²⁾⁴⁹⁹ = -0,01489

Неуправляемый полет 446 тактов

169

Рис. 7. Траектория на плоскости x, y.

Рис. 8. Начальное положение близко к L₂: a - изменение x во времени; b -

изменение y во времени; c - траектория на плоскости x, y для четырех кор-

рекций.

торией с начальными условиями (L₂ + 0,01, 0,01, 0, 0) и (L₃ + 0,01, 0,01, 0, 0)

соответственно. В близкой позиции к L₂ управление является более точным,

чем для L₁ и L₃. За то же время t ∈ [0, 10] достаточно всего четырех коррек-

ций, чтобы держаться ближе к L₂ и L₃. Управление в окрестности L₃ имеет

необычную форму, затем оно повторяется, как показано на рис. 9,c.

170

Рис. 9. Начальное положение близко к L₃: a - изменение x во времени; b - из-

менение y во времени; c - траектория на плоскости x, y для шести коррекций.

Расход топлива для первых шести коррекций, нужных чтобы удержать

КА в небольшой окрестности L₂ составляет {23,84050, 29,79414, 29,34968,

29,31751,

29,25641,

29,28363} и

{18,68749,

16,85702,

16,42808,

19,67782,

14,68712, 16,88330} для L₃. Видно, что стабилизация в L₁ более затратна, чем

в L₂ и L₃, эта разница обусловлена преодолением сил, действующих на КА.

В окрестности L₁ сильнее сказывается эффект гравитации Земли и Луны,

а гравитационные силы меньше в L₂ и еще меньше в L₃. Поэтому в L₃ —

наименьший необходимый расход топлива для стабилизации.

Расход топлива при принятой стратегии коррекции сравнивался с другой

∑N-1 ∑₂

стратегией, когда вместо l₁ критерия J =

|U^kn| применялся более

n=0

k=1

∑N-1 ∑₂

привычный l₂ критерий J =

|U^kn|². При этом решение оказыва-

n=0

k=1

лось неимпульсного вида (реактивный двигатель все время включен на этапе

коррекции), а расход топлива оказывался на 15-20% выше.

4. Вывод

В работе для стабилизации космического аппарата в точках либрации

предлагается стратегия управления, основанная на чередовании этапов кор-

рекции и неуправляемого полета. При этом для коррекции с минимальным

расходом топлива используется метод l₁-минимизации. Решение соответст-

вующей задачи оптимального управления основывается на ее линеаризации

171

и дискретизации с последующим сведением к задаче линейного программиро-

вания. Проведенные вычисления для системы Земля - Луна и трех лагран-

жевых точек L₁, L₂ и L₃ показали высокую эффективность предлагаемой

методики и малый суммарный расход топлива на стабилизацию.

СПИСОК ЛИТЕРАТУРЫ

Poincaré H. The Three-Body Problem and the Equations of Dynamics / Poincare’s

Foundational Work on Dynamical Systems Theory. N.Y.: Springer, 2017.

Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука,

1978.

Маршал К. Задача трeх тел. Ижевск: РХД, 2004.

Пуанкаре А. Лекции по небесной механике. М.: Наука, 1965.

Broucke R. A. Periodic orbits in the restricted three body problem with earth-moon

masses. NASA, Technical Report 82-1168, 1968.

Murray C. D. Dynamical effects of drag in the circular restricted three-body problem:

I. Location and stability of Lagrangian equilibrium points // Icarus. 1994. V. 112.

No. 2. P. 465-484.

Szebehely V. Theory of Orbit: The Restricted Problem of Three Bodies. Elsevier,

2012.

Valtonen M., Karttunen H. The Three-Body Problem. Cambridge University Press,

2006.

Федоренко Р.П. Приближенное решение задач оптимального управления. М.:

Наука, 1978.

10.

Pini G., Seidelmann K.P. Celestial Mechanics and Astrodynamics: Theory and

Practice. Berlin: Springer, 2016.

11.

Miele A. Flight mechanics. V.1: Theory of Flight Paths; V. 2: Theory of Optimal

Flight Paths. Addison-Wesley, 1962.

12.

Мухарлямов Р.Г. Моделирование процессов управления, устойчивость и стаби-

лизация систем с программными связями // Изв. РАН. Теория и системы управ-

ления. 2015. № 1. С. 15-28.

13.

Alesova I., Babadzanjanz K., Pototskaya I., et al. Fuel optimal control of non-linear

oscillations of a satellite on elliptical orbit // Stability and Oscillations of Nonlinear

Control Systems (Pyatnitskiy’s Conf.), Int. Conf. IEEE, 2016.

14.

Tabak D., Kuo B.C. Optimal Control by Mathematical Programming. SRL

Publishing Company, 1971.

15.

Serra R., Arzelier D., Brehard M., et al. Fuel-optimal impulsive fixed-

time trajectories in the linearized circular restricted 3-body-problem // IAF

Astrodynamics Symposium in 69th Int. Astronautical Congr., 2018. P. 1-9.

16.

Миллер Б.М., Рубинович Е.Я. Оптимизация динамических систем с импульс-

ными управлениями. М.: Наука, 2005.

Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.

Поступила в редакцию 06.03.2019

После доработки 24.06.2019

Принята к публикации 18.07.2019

172