Автоматика и телемеханика, № 2, 2019
Линейные системы
© 2019 г. И.Б. ФУРТАТ, д-р техн. наук (cainenash@mail.ru)
(Институт проблем машиноведения РАН, Санкт-Петербург,
Университет ИТМО, Санкт-Петербург),
П.А. ГУЩИН, канд техн. наук (guschin.p@mail.ru)
(Институт проблем машиноведения РАН, Санкт-Петербург,
Российский государственный университет нефти и газа
(национальный исследовательский университет) имени И.М. Губкина, Москва)
АЛГОРИТМ УПРАВЛЕНИЯ ОБЪЕКТАМИ С ЗАПАЗДЫВАЮЩИМ
ВХОДНЫМ СИГНАЛОМ НА БАЗЕ СУБПРЕДИКТОРОВ
РЕГУЛИРУЕМОЙ ВЕЛИЧИНЫ И ВОЗМУЩЕНИЯ1
Предложен алгоритм управления линейными объектами с запазды-
вающим входным сигналом при наличии внешних возмущений. Сначала
для синтеза алгоритма используются предиктор регулируемой величины
и предиктор возмущения. Предиктор регулируемой величины осуществ-
ляет асимптотический прогноз вектора состояния объекта, а уравнение
замкнутой системы на базе данного предиктора содержит запаздывание
по состоянию. Вследствие этого существует некоторое предельное значе-
ние запаздывания в объекте, для которого алгоритм остается работоспо-
собным. Предиктор возмущения строится в предположении существова-
ния ограниченных производных от возмущения. Далее строятся субпре-
дикторы регулируемой величины и возмущения в виде последовательного
соединения соответствующих предикторов, осуществляющих многошаго-
вое прогнозирование. Получены достаточные условия устойчивости замк-
нутой системы в виде разрешимости линейных матричных неравенств.
Приведены результаты моделирования, иллюстрирующие эффективность
предложенной схемы по сравнению с некоторыми существующими. Чис-
ленные примеры показывают, что полученные достаточные условия га-
рантируют устойчивость регулятора, основанного на субпредикторах, при
больших значениях запаздывания по сравнению с регулятором на базе
предикторов.
Ключевые слова: объект с запаздыванием по управлению, предиктор,
компенсация возмущений, линейное матричное неравенство.
DOI: 10.1134/S0005231019020016
1. Введение
Управление в условиях возмущений является одной из главных проблем
в теории автоматического управления. Данная проблема усложняется нали-
чием запаздывания во входном сигнале. Такие задачи являются типичными
1 Исследование выполнено за счет гранта Российского научного фонда (проект № 18-
79-10104) в Институте проблем машиноведения РАН.
3
при дистанционном управлении, управлении в химической промышленности,
управлении через цифровые каналы связи и т.д.
Впервые решение задачи управления в условии запаздывания предложено
О. Смитом в [1] для устойчивых объектов без возмущения. Для неустойчи-
вых объектов А. Манитиус и А. Олброт в [2] предложили статический закон
управления с использованием пропорционально-интегрального предиктора,
построенного на базе решения уравнения объекта. В [3, 4] рассмотрено ис-
пользование схемы [2] для подавления ограниченных возмущений за счет со-
ответствующего распределения собственных чисел замкнутой системы. Од-
нако в [5-8] было показано, что численная реализация предиктора [2] позво-
ляет стабилизировать только определенный класс неустойчивых объектов с
запаздыванием. Следовательно, принцип подавления возмущений [3, 4] не
всегда гарантирует уменьшение влияния возмущений на качество переход-
ных процессов. В [9] для повышения качества переходных процессов пред-
полагалось, что возмущение описывается конечной суммой синусоидальных
сигналов. Однако структура алгоритма [9] и расчет настраиваемых парамет-
ров зависели от количества синусоидальных слагаемых в возмущении, ка-
чество переходных процессов зависело от наличия несинусоидальной состав-
ляющей, а также использовался интегральный алгоритм [2] без его численной
реализации.
В [10] предложен метод компенсации возмущений (ограниченных вместе с
заданным количеством производных) для неустойчивых объектов с запазды-
ванием по управлению без использования численной реализации схемы [2].
Таким образом, в отличие от [9] в [10] рассматривались возмущения, кото-
рые раскладываются в ряд Фурье с бесконечным числом слагаемых. Однако
в [10] для прогноза возмущения использовались наблюдатели, что усложня-
ло реализацию схемы и повышало ее чувствительность к помехам измерения.
В [11] независимо от [10] (статьи [10, 11] были поданы в журналы одновремен-
но) предложена схема компенсации ограниченных вместе с заданным коли-
чеством производных возмущений на базе схемы [2]. В отличие от [10] в [11]
рассмотрена численная реализация [2] и получены достаточные условия схо-
димости решений замкнутой системы. Дополнительно в [11] для прогноза воз-
мущения применялась теорема Лагранжа о среднем, что позволило избежать
использования наблюдателей производных возмущения в отличие от [10], где
для прогноза возмущения применялся ряд Тэйлора. В [11] также показано,
что метод компенсации возмущений позволяет эффективно управлять объ-
ектами с запаздывающим входным сигналом в отличие от метода подавле-
ния возмущений [2-4]. Это связано с тем, что значение сигнала компенсации
возмущений противоположно значению возмущений и сигнал компенсации
возмущений не влияет на собственные числа замкнутой системы. Однако ал-
горитм [11] слишком трудоемкий в связи с численной реализацией интеграль-
ной составляющей предиктора [2].
В [12] предложен новый предиктор, позволяющий проектировать алгорит-
мы управления неустойчивыми объектами. По сравнению с [2], предиктор [12]
не требует численной реализации и, как следствие, гораздо проще в техниче-
ской реализации и расчете параметров. В [13] на базе предиктора [12] предло-
жен субпредиктор, осуществляющий многошаговое прогнозирование регули-
4
руемой переменной. Численные примеры показали, что применение субпре-
дикторного алгоритма позволяет управлять объектами с большим временем
запаздывания, чем при использовании алгоритма на базе предиктора [12].
Однако результаты [12, 13] слишком чувствительны к возмущениям.
В данной статье будет предложено обобщение результатов [12, 13] на объ-
екты с возмущениями. Дополнительно в отличие от [11] будет предложен
многошаговый прогноз возмущения в виде соответствующего субпредикто-
ра. Также в отличие от [10] будут предложены достаточные условия устой-
чивости замкнутой системы, представленные разрешимостью линейных мат-
ричных неравенств (ЛМН), размерность которых существенно меньше, чем
в [11].
В статье, как и в публикациях [2-4, 10-13], будет рассмотрен линейный
объект с возмущением и запаздыванием по управлению. Доступен измерению
вектор состояния. В разделе 3 будет предложена схема управления с исполь-
зованием предикторов регулируемой переменной и возмущений. В разделе 5
будет рассмотрено обобщение предложенной схемы управления с использо-
ванием субпредикторов регулируемой величины и возмущения. Достаточные
условия устойчивости замкнутой системы в зависимости от параметров си-
стемы управления и запаздывания представлены в разделах 4 и 5 в виде
разрешимости ЛМН. В разделе 6 будут приведены результаты расчетов, мо-
делирования и сравнительный анализ предложенных схем управления с неко-
торыми существующими.
2. Постановка задачи
Рассмотрим объект с запаздыванием в канале управления, который опи-
сывается уравнением
(2.1)
x(t) = Ax(t) + Bu(t - h) + Bf(t), t ≥ 0, u(s) = 0, s < 0,
где x(t) ∈ Rn — измеряемый вектор состояния, u(t) ∈ Rm — сигнал управле-
ния, f(t) ∈ Rm — внешнее возмущение с ограниченными r + 3 производны-
ми, r ≥ 0 — параметр, который будет использоваться при синтезе алгорит-
ма управления, h > 0 — известное время запаздывания, A и B — известные
матрицы соответствующих размеров, пара (A, B) управляема и выполнено
условие B+B = Im, B+ — псевдообратная матрица для матрицы B и Im —
единичная матрица порядка m. Отметим, что объект управления (2.1) с при-
веденными допущениями рассматривался в [3, 4, 10-13].
Алгоритмы [1-4, 5-8, 12, 13] обеспечивают устойчивость (2.1) по вход-
состоянию (input-to-state stability) и выполнение условия
(2.2)
lim
|x(t)| ≤ δ,
t→∞
(
)
O(χ)
где δ = O
limt→∞ |f(t)|
, O(χ) для χ ∈ R означает, что limt→∞
= const,
χ
| · | — евклидова норма соответствующего вектора, т.е. точность регулирова-
ния в установившемся режиме в [1-4, 5-8], [12, 13] зависит от сигнала возму-
щения.
5
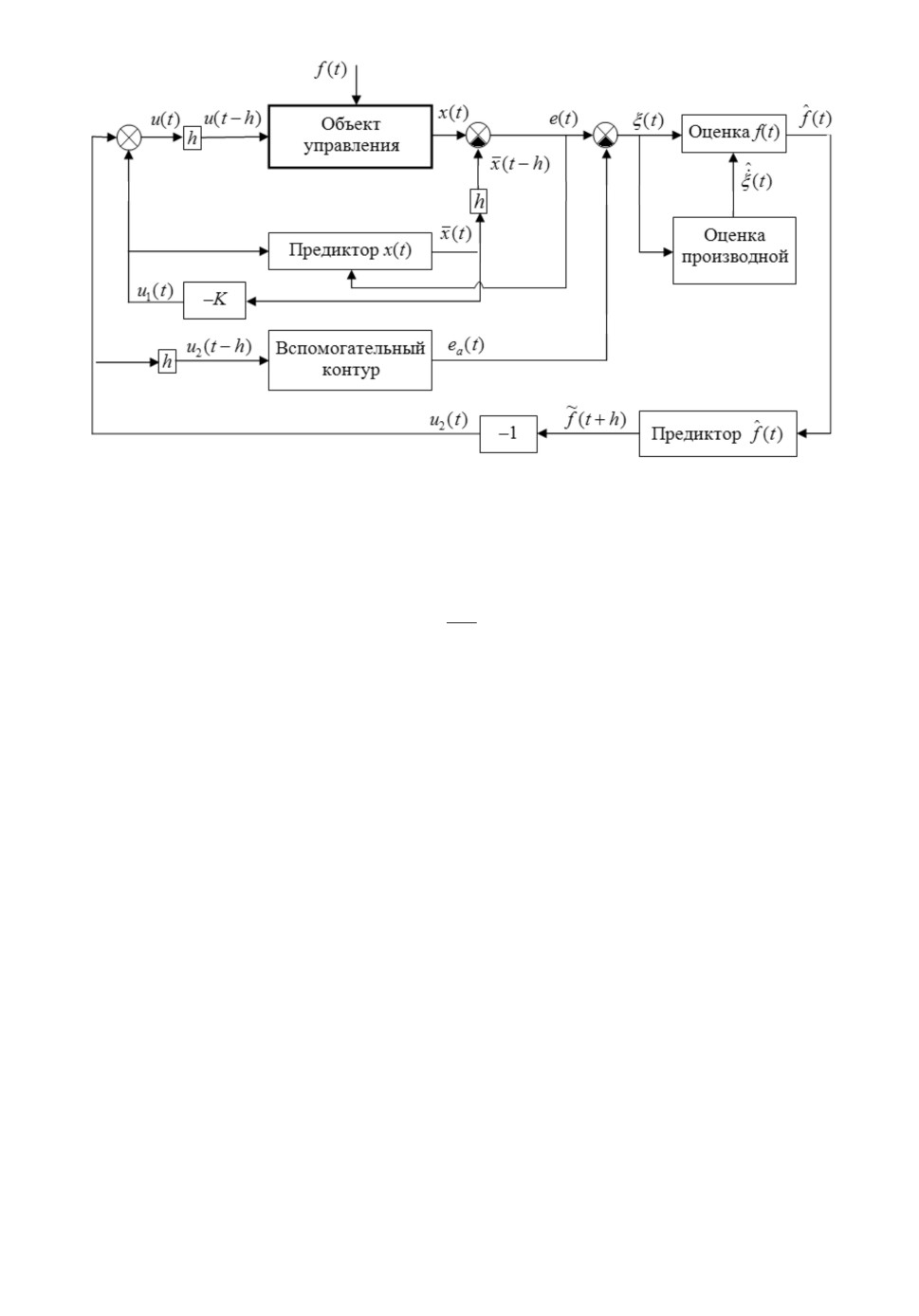
Рис. 1. Структурная схема системы управления.
В данной статье цель управления состоит в разработке алгоритма управ-
ления, который обеспечит
(
)
δ = O hr+1 lim
f(r+1)(t)
,
t→∞
т.е. в отличие от [1-4, 5-8, 12, 13] предложенный алгоритм позволит компен-
сировать большие по амплитуде возмущения. Достаточное условие для обес-
печения поставленной цели управления будет приведено в утверждении 1.
Опишем кратко схему синтеза алгоритма управления. Сигнал u предста-
вим в виде
(2.3)
u(t) = u1(t) + u2
(t).
С помощью сигнала u1 будем обеспечивать устойчивость замкнутой системы,
а с помощью сигнала u2 — компенсацию возмущения f. В разделе 3 форми-
руется предиктор регулируемой величины для синтеза u1 (“Предиктор x(t)”
на рис. 1). Затем формируется оценка возмущени
f с использованием вспо-
могательного контура и алгоритма оценки производной. Для прогноза оцен-
ки возмущени
f используется предиктор возмущения (“Предикто
f (t)” на
рис. 1). После формируется сигнал компенсации возмущения u2.
В разделе 5 будет предложено обобщение результатов раздела 4 для управ-
ления объектами с большим временем запаздывания. Также новый алгоритм
позволит существенно сократить время прогноза возмущения. Для решения
данной задачи будут синтезированы субпредикторы регулируемой величины
и возмущения. Структурная схема такой системы управления подобна схе-
ме, представленной на рис. 1, где вместо предикторов будут использоваться
соответствующие субпредикторы.
6
3. Синтез предиктора регулируемой величины и предиктора возмущения
Сначала синтезируем закон управления u1. Для этого потребуется про-
гноз регулируемой величины на время запаздывания h. С этой целью введем
предиктор
(3.1)
x(t)=Ax(t)+D(x(t)-x(t-h))+Bu1(t),
где матрица D выбирается так, чтобы решения уравнения
(3.2)
κ(t) = Aκ(t) - Dκ(t - h), κ(t) ∈ Rn,
были предельно ограниченными. В утверждении 1 будет сформулировано ко-
личественное условие для выбора матрицы D в виде разрешимости ЛМН.
Зададим закон управления u1 в виде
(3.3)
u1
(t) = -K x(t),
где матрица K выбирается из условия гурвицевости матрицы A - BK.
Введем ошибку прогноза e(t) = x(t) - x(t - h). С учетом (2.3) продиффе-
ренцируем e(t) вдоль решений уравнений (2.1) и (3.1):
(3.4)
ė(t) = Ae(t) - De(t - h) + Bu2
(t - h) + Bf(t).
Из (3.4) следует, что выполнить условие limt→∞ e(t) = 0 при наличии внеш-
него возмущения f невозможно, но величину limt→∞ |e(t)| можно уменьшить
путем соответствующего выбора закона управления u2, который обеспечит
частичную компенсацию возмущения f. Поэтому далее синтезируем алго-
ритм компенсации возмущений.
Получим сначала информацию о возмущении f. С этой целью введем вспо-
могательный контур
(3.5)
ėa(t) = Aea(t) - Dea(t - h) + Bu2
(t - h),
где ea(t) ∈ Rn. Найдем производную по времени от функции ξ(t) = e(t) - ea(t)
вдоль траекторий уравнений (3.3) и (3.5):
˙
(3.6)
ξ
(t) = Aξ(t) - Dξ(t - h) + Bf(t).
Следуя структуре уравнения (3.6), зададим оценку возмущения в виде
(
)
˙
(3.7)
f (t) = B+
ξ
(t) - Aξ(t) + Dξ(t - h)
,
˙
где сигнал
ξ
(t) определяется согласно алгоритму
p
˙
(3.8)
ξ
i(t) =
ξi
(t), i = 1, . . . , n.
μp + 1
Здесь μ > 0 - достаточно малое число, p = d/dt - оператор дифференциро-
вания.
7
Для частичной компенсации возмущения f закон управления u2 требуется
задать в виде u2(t) =
f (t + h). Для построения прогноза оценки возмущения
воспользуемся теоремой Лагранжа о среднем [14], согласно которой функцию
f (t + h) можно записать в виде
∑
(3.9)
f (t + h) =
(-1)j-1Cjr+1f
(t - h(j - 1)) + R(t),
j=1
где Cjr+1 =(r+1)!(r+1-j)!j! , R(t) = hr+1fˆ(r+1) (t - [(r + 1)θ - 1] h) - остаток разло-
жения, 0 < θ < 1. Поскольку остаток R(t) недоступен измерению, то предик-
тор возмущения и закон частичной компенсации возмущения определим в
виде:
∑
(3.10)
f (t + h) =
(-1)j-1Cjr+1f
(t - h(j - 1)),
j=1
(3.11)
u2(t) = -f
(t + h).
Для дискретного времени алгоритм (3.10) рассмотрен в [15], для непрерыв-
ного времени - в [16]. Из (3.10) следует, что для прогноза оценки возмущения
требуется время rh.
В результате сформирован алгоритм управления, состоящий из предикто-
ра регулируемой величины (3.1), вспомогательного контура (3.5), предиктора
возмущения (3.10) и закона управления (2.3), состоящего из (3.3) для обеспе-
чения устойчивости замкнутой системы и (3.11) для компенсации возмуще-
ния. Для формулировки основного результата раздела 3 необходимо сформи-
ровать уравнение замкнутой системы.
4. Уравнение замкнутой системы и основной результат
Введем новую переменную x1 = x - e и продифференцируем ее вдоль ре-
шений (2.1) и (3.4):
(4.1)
x1(t) = (A - BK)x1
(t) + De(t - h).
Рассмотрим ошибку оценки производной η
ξ-
ξ. Принимая во внимание
(3.7), (3.8) и обозначив z
ξ, запишем выражения:
1
η(t) = -
η(t) + z(t),
(4.2)
μ
Ż(t) = Az(t) - Dz(t - h) +
f (t).
Поскольку сигнал
f (t) ограниченный и матрица D выбирается из условия
обеспечения предельной ограниченности решений (3.2), то сигнал η(t) пре-
дельно ограниченный.
8
Введем новые переменные w(t) = η(r+1)(t) и g(t) = ξ(r+3)(t). Принимая во
внимание (4.2), продифференцируем η и z по времени r + 1 раз и результат
запишем в виде:
1
w(t) = -
w(t) + g(t),
(4.3)
μ
ġ(t) = Ag(t) - Dg(t - h) + Bf(r+3)(t).
Так как сигнал f(r+3)(t) - ограниченный, то сигнал w(t) - предельно ограни-
ченный.
Перепишем (3.6) как Bf(t)
=˙ξ(t) - Aξ(t) + Dξ(t - h). С учетом (3.7) и
(3.9)-(3.11), составим соотношения
λ(t) = u2(t - h) + f(t)
f (t)
f (t) + f(t)
f (t) =
(4.4)
= R(t - h) + B+η(t) = hr+1fˆ(r+1) (t - (r + 1)θh) + B+η(t) =
[
]
=hr+1 f(r+1) (t - (r + 1)θh) - B+w (t - (r + 1)θh) + B+η(t).
Из ограниченности f(r+1)(t), w(t) и η(t) следует ограниченность λ(t). Подста-
вив (4.4) в (3.4), получим
(4.5)
ė(t) = Ae(t) - De(t - h) + Bλ(t).
В результате, замкнутая система представлена уравнениями (4.1)-(4.3)
и (4.5). Поскольку решения уравнений (4.2) и (4.3) - предельно ограниченные,
то для исследования устойчивости замкнутой системы достаточно рассмот-
реть только уравнения (4.1) и (4.5).
Введем вектор и матрицы
[
]
A-BK On×n
xp = col{x1,e}, Ap =
,
On×n
A
[
]
[
]
On×n D
On×n
Dp =
,
Bp =
,
On×n
-D
B
где On×m - нулевая матрица размеров n × m. Перепишем уравнения (4.1)
и (4.5) в виде
xp(t) = Apxp(t) + Dpxp(t - h) + Bpλ(t)
или, используя формулу Ньютона-Лейбница, как
∫t
(4.6)
xp(t) = (Ap + Dp) xp(t) - Dp
xp(s)ds + Bp
λ(t).
t-h
9
Утверждение 1. Рассмотрим систему управления, состоящую из
объекта (2.1), предиктора регулируемой величины (3.1), вспомогательно-
го контура (3.5), предиктора возмущения (3.10) и закона управления (2.3),
(3.3), (3.11). Пусть для заданного числа α > 0 и матриц K и D существуют
коэффициент β > 0 и матрицы P > 0, P2 > 0, P3 > 0, Q > 0, S > 0 такие,
что выполнено ЛМН
⎡
⎤
Ψ11
P -PT2+(Ap+Dp)TP3 O4n×4n
-hPT2Dp PT2Bp
⎢
⎥
⎢
⎥
∗
-P3 - PT3 + hS
O4n×4n
-hPT3Dp PT3Bp
⎢
⎥
⎢
⎥
(4.7)
Ψ :=⎢
∗
∗
-e-2αhQ O4n×4n O4n×(2m+n)
⎥< 0,
⎢
⎥
⎢
⎥
⎢
⎥
∗
∗
-hS O4n×(2m+n)
⎣ ∗
⎦
∗
∗
∗
∗
-βI2m+n
где
(4.8)
Ψ11 = PT2 (Ap + Dp) + (Ap + Dp)T P2
+ 2αP + Q.
Тогда решения замкнутой системы (4.1)-(4.3), (4.5) предельно ограничены.
Причем
(
)
δ = O hr+1 supf(r+1)(t)
в целевом условии (2.2) при достаточно малом μ.
Доказательство. Для исследования устойчивости (4.6) рассмотрим
функционал Ляпунова-Красовского в виде
(4.9)
V =V1 +V2 +V3,
где
V1 = xTpPxp,
∫t
V2 = e2α(σ-t)xTp(σ)Qxp(σ)dσ,
t-h
∫0
∫
t
V3 =
e2α(σ-t) xTp(σ)S xp(σ)dσdζ.
-h t+ζ
Отметим, что составляющая V3 позволяет получить условие устойчивости
замкнутой системы, которое в явном виде будет зависеть от запаздывания
(delay depended condition [17]). Принимая во внимание (4.6), составим выра-
10
жения:
[
]
V1 + 2αV1 = xTpP xp + 2αxTpPxp + 2
xTpPT2 + xTpPT3
×
⎡
⎤
t
∫
×⎣(Ap + Dp)xp(t) - D
xp(s)ds + Bpλ(t) - xp(t)⎦ ,
t-h
(4.10)
V2 + 2αV2 = xTp(t)Qxp(t) - e-2αhxTp(t - h)Qxp(t - h),
∫t
V3 + 2αV3 = h xTpS xp - e2α(σ-t) xTp(σ)S xp(σ)dσ.
t-h
При составлении первого выражения в (4.10) использовался дескрипторный
метод [17]. Воспользовавшись неравенством Йенсена (Jensen’s inequality [17]),
оценим последнее выражение в (4.10) в виде
∫
t
∫
t
-2αh
(4.11)
V3 + 2αV3 ≤ h xTpS xp -e
xTp(σ)dσ S
xp
(σ)dσ.
h
t-h
t-h
Введем вектор
⎧
⎫
t
⎨
∫
⎬
1
y(t) = col
xp(t), xp(t),xp(t - h),
xp(σ)dσ,λ(t)
⎩
h
⎭
t-h
и запишем выражениеV + 2αV - βλTλ ≤ yTΨy. Очевидно, что yTΨy ≤ 0, ес-
ли выполнено условие (4.7).
Теперь покажем, что в замкнутой системе обеспечивается (2.2) с δ =
(
)
=O
hr+1 sup
f(r+1)(t)
. Принимая во внимание
(2.3) и
(4.4), перепи-
шем (2.1) в виде x(t) = Ax(t) + Bu1(t - h) + Bλ(t). Обозначим
Δ(μ) = lim |λ(t)|.
t→∞
Тогда из (4.2), (4.3) и (4.4) следует, что
lim
Δ(μ) = hr+1 lim
f(r+1)(t).
μ→0
t→∞
Таким образом, предложенный алгоритм обеспечивает (2.2) с точностью
(
)
δ=O
hr+1 limt→∞
f(r+1)(t)
, в то время как существующие алгоритмы [1-4,
(
)
6-9, 12, 13] обеспечивают δ = O
limt→∞ |f(t)|
. Утверждение 1 доказано.
Замечание. Покажем ограниченность всех сигналов в замкнутой систе-
ме. Так как вектор y - предельно ограниченный, то сигнал xp - предельно
ограниченный. Из предельной ограниченности xp следует предельная огра-
ниченность x1 и e. Из выражения x1 = x - e следует предельная ограничен-
ность x. Из предельной ограниченности e, x и e(t) = x(t) - x(t - h) следует
11
предельная ограниченность x. Значит, из (3.4) следует предельная ограни-
ченность u1.
Продифференцируем (3.6):
ξ(t) =
ξ(t) -
ξ(t - h) +
f (t). Из ограни-
˙
˙
ченности
f
следует предельная ограниченность
ξ
. Перепишем (3.8) в виде
ˆ
ξ=-1μξ+1μξ˙. Из предельной ограниченности˙ξ следует предельная ограни-
ченностьξ. Из предельной ограниченностиξ и ξ следует предельная огра-
ниченност
f. Сигнал u2 ограничен из (3.10) и (3.11). Значит, сигнал u пре-
дельно ограничен из (2.3). В результате все сигналы ограничены в замкнутой
системе. Замечание доказано.
5. Синтез субпредиктора регулируемой величины
и субпредиктора возмущения
На базе результатов разделов 3 и 4 рассмотрим синтез субпредикторов,
которые осуществляют многошаговое прогнозирование вектора состояния и
возмущения. Как будет показано на численных примерах в разделе 6, субпре-
дикторный алгоритм может сократить время прогноза возмущения и обеспе-
чить устойчивость замкнутой системы по отношению к большему запазды-
ванию в канале управления в (2.1), чем при использовании предикторов из
раздела 4.
Для прогноза регулируемой величины введем систему уравнений:
(
)
xi(t) =Axi(t) + Di
xi+1(t) - xi(t -h)
+ Bu1(t - (i - 1)h),
(5.1)
i = 1,...,M - 1,
(
)
xM (t) =AxM (t) + DM
x(t) - xM (t -h)
+ Bu1(t - (M - 1)h),
где
xi(t) ∈ Rn,
h=h
M
Число M задается разработчиком, а матрицы Di выбираются из условия
обеспечения предельной ограниченности решений следующей системы урав-
нений:
κi(t) = Aκi(t) - Diκi(t -h) + Di+1κi+1(t -h), i = 1,... ,M - 1,
(5.2)
κM (t) = AκM (t) - DM κM (t -h),
где κi ∈ Rn, i = 1, . . . , M. В утверждении 2 будет сформулировано количе-
ственное условие для выбора матриц Di в виде разрешимости ЛМН. Систе-
му (5.1) будем называть субпредиктором регулируемой величины, поскольку
каждое уравнение системы (5.1) обеспечивает прогноз регулируемой величи-
ны на время запаздыванияhM .
Введем ошибки прогноза:
ei(t) = xi+1(t - (M - i)h) - xi(t - (M - i + 1)h), i = 1,... ,M - 1,
(5.3)
eM (t) = x(t) - xM (t -h).
12
При ei(t) → 0, i = 1, . . . , M, следует, что x1(t - h) → x(t) или x1(t) → x(t + h).
С учетом (2.3) продифференцируем (5.3) вдоль решений уравнений (2.1)
и (5.1):
ėi(t) = Aei(t) - Diei(t -h) + Di+1ei+1(t -h), i = 1,... ,M - 1,
(5.4)
ėM (t) = AeM (t) - DM eM (t -h) + Bu2(t - h) + Bf(t).
Если положить u2(t) ≡ 0 и f(t) ≡ 0 и выбрать Di, i = 1, . . . , M, таки-
ми, что система (5.2) асимптотически устойчива, то из (5.3) следует, что
limt→∞ x(t + h) = limt→∞ x1(t). Следовательно, зададим закон управления u1
в виде
(5.5)
u1(t) = -Kx1
(t),
где матрица K задается из условия гурвицевости матрицы A - BK.
Однако f = 0 по условию задачи. Поэтому далее синтезируем алгоритм
компенсации возмущений u2 с целью уменьшения влияния возмущения f на
значение ошибок прогноза ei, i = 1, . . . , M. Введем вспомогательный контур
(5.6)
ėa(t) = Aea(t) - DM ea(t -h) + Bu2
(t - h),
где ea(t) ∈ Rn. Найдем производную по времени от функции
ξ(t) = eM (t) - ea(t)
вдоль траекторий M-го уравнения в системе (5.4) и уравнения (5.6):
(5.7)
˙ξ(t) = Aξ(t) - DM ξ(t -h)
+ Bf(t).
Следуя структуре (5.7), зададим оценку возмущения в виде
(
)
(5.8)
f (t) = B+
˙ξ(t) - Aξ(t) + DM ξ(t -h) ,
˙
где сигнал
ξ
(t) получен с помощью алгоритма (3.8).
Теперь сформируем алгоритм прогноза оценки возмущени
f (t). Для этого
запишем выражение дл
f (t +ĥ) в виде
∑
(5.9)
f (t +ĥ) =
(-1)j-1Cjr+1fˆ(t -ĥ(j - 1)) +R(t),
j=1
ĥ= h
где
, число N > 0 выбирается разработчиком,
R(t) =ĥr+1fˆ(r+1)×
(
N
)
× t - [(r + 1)θ - 1]ĥ
- остаток разложения.
Очевидно, что значени
f (t +ĥ) недостаточно для компенсации возмуще-
ний. Следовательно, сдвинем вправо аргумент функции
f (t +ĥ) в (5.9) на
13
величинуĥ последовательно N раз. Следуя данной процедуре, прогноз воз-
мущения на величину h можно сформировать в виде:
∑
f (t +ĥ) =
(-1)j-1Cjr+1fˆ(t -ĥ(j - 1)),
j=1
∑
∑
f (t + lĥ)=
(-1)j-1Cjr+1f˜(t -ĥ(j - l))+
(-1)j-1Cjr+1fˆ(t -ĥ(j - l)),
j=1
j=l
(5.10)
l = 2,...,r + 1 (или l = 2,...,N, если N < r + 2),
∑
f (t+kĥ)=
(-1)j-1Cjr+1f˜(t -ĥ(j - k)),
j=1
k = r + 2,...,N (если N ≥ r + 2).
Систему (5.10) будем называть субпредиктором возмущений. Отметим,
что при N < r + 2 субпредиктор возмущения состоит только из первых двух
выражений (5.10). При N ≥ r + 2 субпредиктор возмущения включает в себя
все уравнения (5.10). Также из (5.10) видно, что время прогноза возмущения
составляетĥr =hrN , т.е. по сравнению с (3.10) алгоритмы (5.10) позволяют
уменьшить время прогноза возмущения в N раз.
Сформируем закон частичной компенсации возмущения в виде
(5.11)
u2(t) = -f
(t + h).
В итоге сформирован алгоритм управления, состоящий из субпредиктора
регулируемой величины (5.1), вспомогательного контура (5.6), субпредиктора
возмущения (5.10) и закона управления (2.3), в состав которого входят сиг-
нал (5.5) для обеспечения устойчивости замкнутой системы и сигнал (5.11)
для компенсации возмущения.
Перед формулировкой основного результата настоящего раздела предва-
рительно сформируем уравнение замкнутой системы. С учетом (5.9)-(5.10)
составим ошибки прогноза εl(t)
f (t + lĥ)
f (t + lĥ), l = 1, . . . , N, в виде
ε1(t) =R(t),
∑
εl(t) =
(-1)j-1Cjr+1εl-j (t) + ε1(t + (l - 1)ĥ),
j=1
(5.12)
l = 2,...,r + 2 (или l = 2,...,N, если N ≤ r + 2),
∑
εv(t) =
(-1)j-1Cjr+1εv-j (t) + ε1(t + (v - 1)ĥ),
j=1
v = r + 3,...,N (если N > r + 2).
14
Рассмотрим выражение
λ1(t) = u2(t - h) + f(t) =
f (t) + f(t) =
(5.13)
=
f (t)
f (t) + f(t)
f (t) = εN (t - h) + B+η(t).
Введем новую переменную
∑
x1 = x - ei.
i=1
С учетом (5.13) продифференцируем x1 по времени вдоль решений (2.1) и
(5.4):
(5.14)
x1(t) = (A - BK)x1(t) + D1e1(t -h
).
Составим ошибку оценки производной η
ξ-
ξ в виде (4.2). Обозначив
z
ξ, найдем производную от z с учетом (5.7):
(5.15)
Ż(t) = Az(t) - DM z(t -h) + Bf
(t).
Введем новые переменные w(t) = η(r+1)(t) и g(t) = ξ(r+3)(t). Принимая во
внимание (4.2) и (5.15), продифференцируем η и z по времени r + 1 раз и
результат запишем в виде:
1
w(t) = -
w(t) + g(t),
μ
(5.16)
ġ(t) = Ag(t) - DM g(t -h) + Bf(r+3)(t).
С учетом (5.13) перепишем (5.4) как
ėi(t) = Aei(t) - Diei(t -h) + Di+1ei+1(t), i = 1,... ,M - 1,
(5.17)
ėM (t) = AeM (t) - DM eM (t -h) + Bλ1(t).
Покажем ограниченность λ1(t). Поскольку сигналы f(t)
f (t) и f(r+3)(t)
ограниченные, то из подобия струткур (5.15), второго уравнения (5.16) и
последнего уравнения (5.2) следует предельная ограниченность ξ(t) и η(t).
Продифференцируем (5.7)
ξ(t) =
ξ(t) - DMξ˙(t - h) +
f (t). Из ограничен-
˙
ности
f
следует предельная ограниченность
ξ. Перепишем (3.8) в виде
ˆ
˙
ξ=-1μ˙ξ + 1μξ˙. Из предельной ограниченностиξ
следует предельная огра-
˙
ниченностьξ
. Из предельной ограниченностиξ, ξ и (5.8) следует ограни-
ченность
f. Из (5.10) следует ограниченность
f. Сигнал εN(t) ограничен
из (5.12). В результате λ1(t) ограничен из (5.13).
15
Поскольку решения (5.15) и (5.16) предельно ограниченные, то для ис-
следования устойчивости замкнутой системы достаточно рассмотреть только
уравнения (5.14) и (5.17).
Введем вектор и матрицы:
⎡
⎤
A-BK On×n ... On×n O
n×n
⎢
⎥
On×n
A ... On×n On×n
⎢
⎥
⎢
⎥
xp = col {x1,e1,e2,... ,eM } , Ap =
⎢
⎥
⎢
On×n On×n
⎥,
⎢
⎥
⎣ On×n On×n ... A On×n
⎦
On×n On×n ... On×n A
⎡
⎤
On×n D1 On×n On×n ... On×n
⎢
⎥
⎡
⎤
⎢
On×n
-D1
D2
On×n ... On×n
⎥
On×m
⎢
⎥
⎢
On×n On×n
-D2
D3
.... On×n
⎥
⎢
⎥
⎢
⎥
⎢
⎥
Dp =
⎢
⎥,
Bp =
⎢
⎥
On×n On×n On×n
-D3
On×n
⎢
⎥
⎣ On×m
⎦
⎢
⎥
⎢
⎥
B
⎣
⎦
On×n On×n On×n On×n ...
-DM
Перепишем уравнения (5.14) и (5.17) в виде
xp(t) = Apxp(t) + Dpxp(t -h) + Bpλ1(t)
или
∫t
(5.18)
xp(t) = (Ap + Dp) xp(t) - Dp
xp(s)ds + Bpλ1
(t).
t-h
Отметим, что в разделе 4 уравнение замкнутой системы (4.6) содержа-
ло запаздывание h. Использование субпредиктора (5.1) позволило получить
новое уравнение замкнутой системы (5.18) с уменьшенным в M раз запазды-
ваниемh.
Утверждение 2. Рассмотрим систему управления, состоящую из
объекта (2.1), субпредиктора регулируемой величины (5.1), вспомогатель-
ного контура (5.6), субпредиктора возмущения (5.10) и закона управления
(2.3), (5.5), (5.11). Пусть для заданного числа α > 0 и матриц K, D суще-
ствуют коэффициент β > 0 и матрицы P > 0, P2 > 0, P3 > 0, Q > 0, S > 0
такие, что выполнено ЛМН
⎡
⎤
Ψ11
P -PT2+AT0 P3 O(3+M)n×(3+M)n
-hPT2Dp
PT2B
p
⎢
⎥
⎢
∗
+hS O(3+M)n×(3+M)n
⎥
⎢
-P3 -
3
-hPT3Dp
PT3Bp
⎥
⎢
⎥
(5.19)
Ψ :=⎢
⎥< 0,
⎢
∗
∗
-e-2αhQ
O(3+M)n×(3+M)n O(3+M)n×(n+m)
⎥
⎢
⎥
⎢
⎥
⎣ ∗
∗
∗
-hS
O(3+M)n×(n+m)
⎦
∗
∗
∗
∗
-βIn+m
16
где Ψ11 имеет вид (4.8). Тогда решения замкнутой системы (2.1), (2.3),
(5.1), (5.5), (5.6), (5.10), (5.11) предельно ограничены и выполнено целевое
(
)
условие (2.2), где δ = O
limt→∞ |εN (h, t)|
при достаточно малом μ. Допол-
нительно: все сигналы ограничены в замкнутой системе.
Доказательство. Для доказательства утверждения
2
рассмотрим
функционал Ляпунова-Красовского (4.9), где только V2 и V3 сформируем
с учетом нового запаздывания h в (5.18):
∫t
V2 = e2α(σ-t)xTp(σ)Qxp(σ)dσ,
t-h
∫0
∫
t
V3 =
e2α(σ-t) xTp(σ)S xp(σ)dσdζ.
-h t+ζ
В силу подобия структур систем (4.6) и (5.18) вывод условия
V
+ 2αV - βλT1 λ1 ≤ yTΨy ≤ 0
аналогичен выводу в утверждении 1.
Так как yTΨy ≤ 0, то сигнал xp - предельно ограниченный. Из предельной
ограниченности xp следует предельная ограниченность x1, ei, i = 1, . . . , M,
η и z. Доказательство ограниченности остальных сигналов в замкнутой си-
стеме аналогично доказательству в замечании.
Принимая во внимание (2.3) и (4.4), перепишем (2.1) в виде
x(t) = Ax(t) + Bu1(t - h) + Bλ1(t).
Обозначив
Δ1(μ) = lim
|λ1(t)| ,
t→∞
имеем
lim
Δ1(μ) = lim
|εN (h, t)|.
μ→0
t→∞
Таким образом, предложенный алгоритм управления обеспечивает (2.2) с
(
)
точностью δ = O
limt→∞ |εN (h, t)|
в (2.2). Утверждение 2 доказано.
6. Примеры
Рассмотрим модель объекта управления (2.1) с параметрами [18, 19]:
⎡
⎤
⎡
⎤
0
1
0
0
0
⎢
0
0
a1
0
⎥
⎢
b1
⎥
⎢
⎥
⎢
⎥
A=
B=
a1 = -1, a2 = 10/3,
⎣0
0
0
1
⎦,
⎣0
⎦,
0
0
a2
0
b2
b1 = 0,1, b2 = -1/30 и x(0) = [0,98
0
0,2
0]T.
17
В [18] показано, что данная модель может описывать перевернутый маят-
ник на подвижной тележке, где x = [x1 x2 x3 x4]T, x1 — позиция тележ-
ки, x2 — скорость тележки, x3 — угол маятника относительно вертикальной
оси, x4 — угловая скорость маятника, a1 = -mpg/Mc, a2 = g/l, b1 = 1/Mc,
b2 = -1/(Mcl), Mc = 10 — масса тележки, mp = 1 — масса маятника, l = 3 —
длина маятника и g = 10 — ускорение свободного падения. Положим, что
(
π)
100
( d(t))
f (t) = 1 + sin(0,2t) + cos t + sin
1,5t +
+
sat
,
4
(5p + 1)7
10
sat(·) — функция насыщения, d(t) — сигнал, моделируемый в Matlab Simulink
с помощью блока “Band-Limited White Noise” с мощность шума (noise
power) 0,1 и периодом (sample time) 0,1.
В [18, 19] для стабилизации данного объекта использовался закон управ-
ления u = -Kx, где K = [2 12 378 210]. Далее во всех алгоритмах будем
использовать одно и то же значение K. Максимальное значение запаздыва-
ния, для которого можно стабилизировать объект в [19], равно hmax = 0,2.
При этом система управления [19] очень чувствительна к возмущениям.
1. Синтез алгоритма на базе предикторов.
⎡
⎤
0
0
0
0
⎢1,5
2,5
0
0
⎥
Выберем D =
⎣
⎦ в предикторе регулируемой перемен-
0
0
0
0
0
0
5
2,5
ной (3.1). В алгоритме оценки производной (3.8) зададим μ = 0,01. ЛМН (4.7)
разрешимо при hLMImax = 0,38. Моделирование в Matlab Simulink показало, что
система устойчива при hMSmax = 0,41, т.е. решение ЛМН имеет небольшое от-
клонение (7,3 %) от значения, полученного в Matlab Simulink, причем схема
управления на базе предиктора позволяет стабилизировать объект при боль-
шем в 2 раза времени запаздывания в канале управления по сравнению с [19].
Теперь сравним качество переходных процессов для предложенной схемы
и алгоритмов [4, 12]. Пусть h = 0,35. На рис. 2 приведены результаты пере-
ходных процессов для разработанного алгоритма при r = 3 и r = 4 в (3.10).
На рис. 3 изображены графики переходных процессов при использовании ал-
горитмов [4, 12]. Отметим, что разработанный алгоритм и алгоритмы [4, 12]
сохраняют устойчивость при максимальном запаздывании h = 0,41.
Дополнительный анализ результатов моделирования для алгоритмов [4, 12]
показал, что изменение параметров K с целью подавления, а не компенсации,
возмущений ведет к потере устойчивости замкнутой системы. Однако разра-
ботанный алгоритм обеспечивает компенсацию возмущений для любых зна-
чений K, при которых замкнутая система остается устойчивой, так как кон-
тур компенсации возмущений не зависит от контура стабилизации замкнутой
системы.
2. Синтез алгоритма на базе субпредикторов.
Выберем M = 2 и D1 = D2 = D в (5.1), т.е. каждый субпредиктор пред-
ставляет собой предиктор с такими же параметрами, но с уменьшенным
18
10
5
0
-5
0
20
40
60
80
100
10
5
0
-5
0
20
40
60
80
100
10
5
0
-5
0
20
40
60
80
100
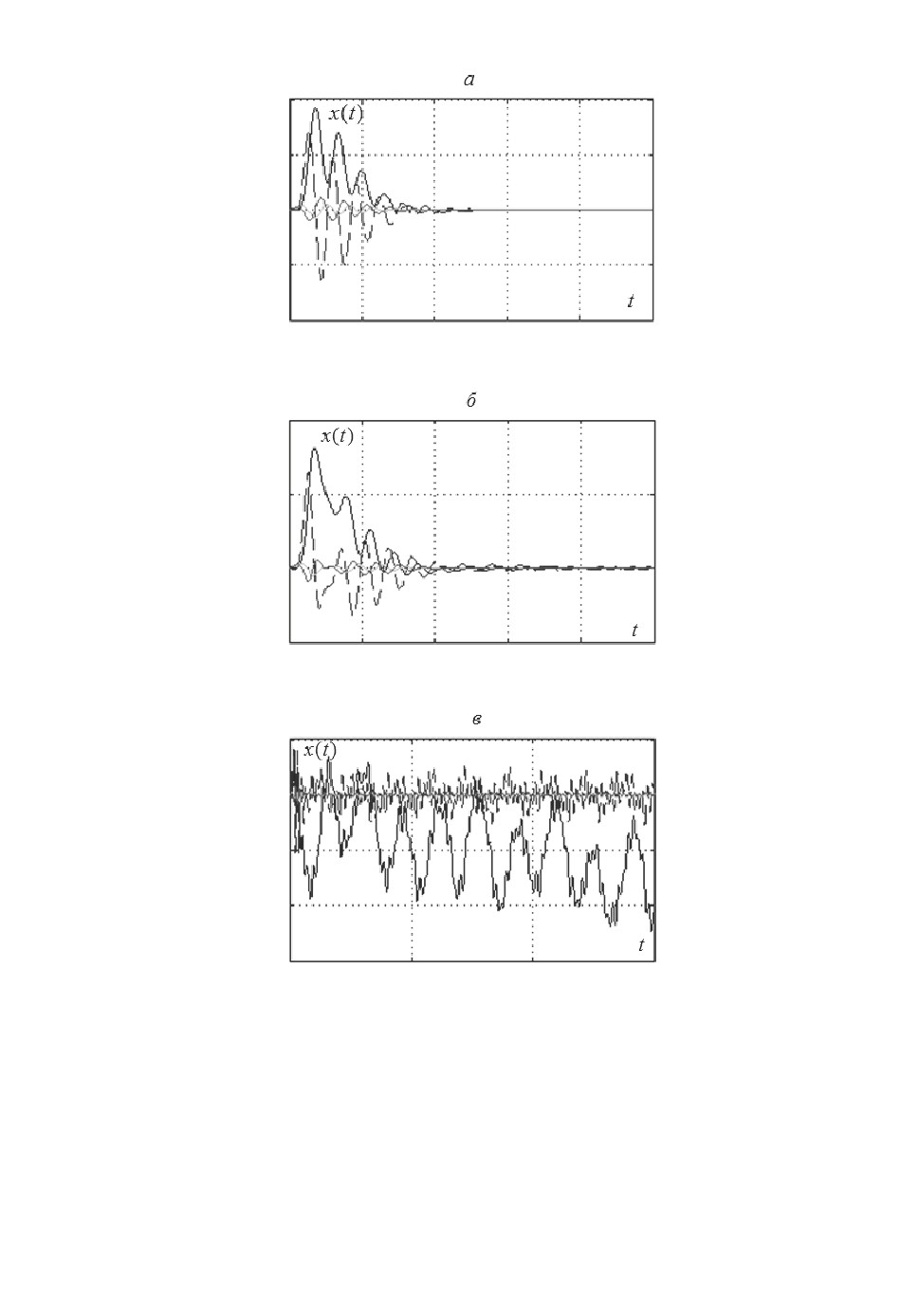
Рис. 2. Переходные процессы по x(t): при r = 3 и f = 0 (а), при r = 3 (б ) и
r = 4 (в) в условиях f = 0.
в два раза временем запаздывания. Пусть N = 4 и r = 4 в (5.10), т.е. со-
кратим время прогноза возмущения в 4 раза. ЛМН (5.19) разрешимо при
hLMImax = 0,75. Моделирование в Matlab Simulink показало, что система устой-
чива при hMSmax = 0,8, т.е. консервативность при использовании ЛМН составля-
ет 6,3 %. Таким образом, схема управления на базе субпредикторов позволяет
19
2
0
-2
-4
-6
0
100
200
300
5
0
-5
-10
0
20
40
60
80
100
Рис. 3. Переходные процессы по x(t) при использовании алгоритма [4] (а) и
алгоритма [12] (б ).
стабилизировать объект при большем времени запаздывания в канале управ-
ления в 4 раза по сравнению с [19] и в 2 раза по сравнению с разработанным
алгоритмом на базе предикторов и алгоритма [4]. Результаты переходных
процессов при h = 0,7 для разработанного алгоритма на базе субпредикто-
ров и алгоритма [13] приведены на рис. 4.
7. Заключение
Синтезированы алгоритмы управления линейными объектами с запазды-
вающим входным сигналом при наличии внешних возмущений. Первый ал-
горитм основан на использовании предикторов регулируемой величины и
возмущения. Второй алгоритм базируется на использовании субпредикторов
регулируемой величины и возмущения. Показано, что использование прин-
ципа компенсации возмущений позволяет существенно уменьшить влияние
возмущений на качество переходных процессов по сравнению с методами по-
давления возмущений [3, 4]. Получены достаточные условия устойчивости
замкнутой системы в виде разрешимости линейных матричных неравенств.
20
20
10
0
-10
-20
0
10
20
30
40
50
20
10
0
-10
0
10
20
30
40
50
20
0
-20
-40
-60
0
100
200
300
Рис. 4. Переходные процессы по x(t) при использовании разработанного ал-
горитма на базе субпредикторов (при f = 0 (а) и f = 0 (б )) и алгоритма [13]
при f = 0 (в).
Моделирование разработанных алгоритмов показало их эффективность по
сравнению со схемами [4, 12, 13, 19]. Результаты моделирования также пока-
зали, что отсутствие возмущения заметно не влияет на величину предельного
запаздывания, которое получено с помощью ЛМН или с помощью моделиро-
вания исследуемых алгоритмов в Matlab Simulink.
21
СПИСОК ЛИТЕРАТУРЫ
1.
Smith J.M. Closer Control of Loops with Dead Time // Chem. Eng. Prog. 1959.
No. 53. P. 2217-2219.
2.
Manitius A.Z., Olbrot A.W. Finite Spectrum Assignment Problem for Systems with
Delays // IEEE Trans. Autom. Control. 1979. V. AC-24. No. 4. P. 541-553.
3.
Kristic M. Delay Compensation for Nonlinear, Adaptive, and PDE Systems.
Birkhauser, 2009.
4.
Mazenc F., Niculesqu S.-I., Krstić M. Lyapunov-Krasovskii Functionals and
Application to Input Delay Compensation for Linear Time-Invariant Systems //
Automatica. 2012. V. 48. P 1317-1323.
5.
Van Assche V., Dambrine M., Lafay J.F., Richard J.P. Some Problems Arising in
the Implementation of Distributed-Delay Control Laws // Proc. 38th IEEE Conf. on
Decision and Control, Phoenix, 1999.
6.
Engelborghs K., Dambrine M., Rose D. Limitations of a Class of Stabilization
Methods for Delay Systems // IEEE Trans. Autom. Control. 2001. V. AC-46. No. 2.
P. 336-339.
7.
Mondié S., Dambrine M., Santos O. Approximation of Control Laws with
Distributed Delays: a Necessary Condition for Stability // Kybernetika. 2002. V. 38.
No. 5. P. 541-551.
8.
Mondié S., Michiels W. Finite Spectrum Assignment of Unstable Time-Delay
Systems With a Safe Implementation // IEEE Trans. Autom. Control. 2003. V. 48.
No. 12. P. 2207-2212.
9.
Ван Ц., Арановский С.В., Бобцов А.А., Пыркин А.А. Компенсация мультисину-
соидального возмущения на основе параметризации Юлы-Кучеры // АиТ. 2017.
№ 9. С. 19-33.
Wang J., Aranovskiy S.V., Bobtsov A.A., Pyrkin A.A. Compensating for a
Multisinusoidal Disturbance Based on Youla-Kucera Parametrization // Autom.
Remote Control. 2017. V. 78. No. 9. P. 1559-1571.
10.
Sanz R., Garcia P., Albertos P. Enhanced Disturbance Rejection for a Predictor-
Based Control of LTI Systems with Input Delay // Automatica. 2016. V. 72.
P. 205-208.
11.
Furtat I., Fridman E., Fradkov A. Disturbance Compensation with Finite Spectrum
Assignment for Plants with Input Delay // IEEE Trans. Autom. Control. 2018. V. 63.
No. 1. P. 298-305.
12.
Dugard L., Verriet E. Stability and Control of Time-delay Systems, London:
Springer, 1997.
13.
Najafi M., Hosseinnia S., Sheikholeslam F., Karimadini M. Closed-Loop Control of
Dead Time Systems via Sequential Sub-predictors // Int. J. Control. 2013. V. 86.
No. 4. P. 599-609.
14.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1.
М.: Физматлит, 2003.
15.
Цыпкин Я.З. Скользящая аппроксимация и принцип поглощения // Докл. РАН.
1997. Т. 357. № 6. С. 750-751.
Tsypkin Ya.Z. Moving Approximation and the Absorption Principle // Dokl.
Mathematics. 1997. V. 56. No. 3. P. 976-977.
16.
Фуртат И.Б. Алгоритмы скользящей аппроксимации // Мехатроника, автома-
тизация, управление. 2017. Т. 18. № 3. С. 147-158.
17.
Fridman E. Introduction to Time-Delay Systems. Analysis and Control. Birkhauser,
2014.
22
18. Wang X., Lemmon M.D. Self-triggered Feedback Control Systems with Finite-Gain
L2 Stability // IEEE Trans. Autom. Control. 2009. V. 54. No. 3. P. 452-467.
19. Selivanov A., Fridman E. Observer-Based Input-to-State Stabilization of Networked
Control Systems with Large Uncertain Delays // Automatica. 2016. V. 74. P. 63-70.
Статья представлена к публикации членом редколлегии А.Л. Фрадковым.
Поступила в редакцию 15.09.2018
После доработки 20.08.2018
Принята к публикации 08.11.2018
23