Автоматика и телемеханика, № 2, 2019

Нелинейные системы

А.Е. ШУМСКИЙ, д-р техн. наук (a.e.shumsky@yandex.com)

(Дальневосточный федеральный университет, Владивосток,

Институт проблем морских технологий ДВО РАН, Владивосток)

НЕПАРАМЕТРИЧЕСКИЙ МЕТОД ДИАГНОСТИРОВАНИЯ

НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ¹

Рассматривается задача функционального диагностирования нелиней-

ных динамических систем непараметрическим методом, особенность ко-

торого состоит в том, что значения некоторых параметров диагностируе-

мой системы могут быть неизвестными. Предлагается подход, позволяю-

щий производить локализацию дефектов. Устанавливаются необходимые

и достаточные условия возможности преобразования системы к канони-

ческому виду, необходимому для применения непараметрического метода

при диагностировании заданной нелинейной системы.

Ключевые слова: нелинейные системы, диагностирование, поиск дефек-

тов, непараметрический метод.

DOI: 10.1134/S0005231019020028

1. Введение и постановка задачи

Настоящая статья является логическим продолжением работы [1], где рас-

сматривалась задача диагностирования технических систем, описываемых

динамическими линейными моделями, на основе непараметрического мето-

да, особенность которого состоит том, что знание значений постоянных па-

раметров системы не является обязательным для реализации процедуры ди-

агностирования, в линейном случае достаточно знать только размерности

векторов входа, состояния и выхода и места вхождения этих параметров в

описание системы [2-6].

В настоящей работе рассматриваются системы, описываемые нелинейны-

ми динамическими моделями. Напомним, что для применения непараметри-

ческого метода исходная система должна быть представлена в виде вход-

выходных соотношений, что всегда можно сделать для линейных моделей.

В отличие от этого далеко не всякая нелинейная система может быть пред-

ставлена в таком виде, поэтому основное внимание в работе уделяется разра-

ботке условий такого представления и процедур его получения.

Для формулирования этих условий и процедур используется специальный

математический аппарат - алгебра функций, разработанная в [7] для решения

¹ Работа выполнена при финансовой поддержке Российского научного фонда (проект

№ 16-19-00046).

задач анализа нелинейных динамических систем и позволяющая рассмат-

ривать системы с негладкими нелинейностями, к числу которых относятся

такие типичные нелинейности, как сухое трение, люфт, гистерезис, насыще-

ние. Кроме этого, для решения задачи используется логико-динамический

подход [8], позволяющий при ограничении на класс используемых преобра-

зований исходной системы применять для решения задачи только методы

линейной алгебры.

Рассматривается класс систем, описываемых нелинейной динамической

моделью

(1.1)

x(t + 1) = f(x(t), u(t), γ), y(t) = h(x(t)).

Здесь x ∈ X ⊆ Rⁿ, u ∈ R^m, y ∈ R^l - векторы состояния, управления и выхо-

да; γ = (γ₁, . . . , γ_s)^T - вектор параметров, i-й дефект ρ_i в системе проявляет-

ся в виде недопустимого отклонения i-го параметра γ_i от его номинального

значения, f и h - нелинейные функции, при этом функция f может быть

недифференцируемой.

Для решения задачи диагностирования непараметрическим методом тре-

буется произвести преобразование векторов состояния и выхода

(1.2)

x_∗i(t) = ϕ(i)(x(t)), i = 1,... ,N, y_∗

(t) = ψ(y(t))

с помощью некоторых функций ϕ⁽¹⁾, . . . , ϕ(N) и ψ такое, что в новых коорди-

натах преобразованная система описывается моделью без обратных связей:

x∗1(t + 1) =

∗ (x∗2(t), . . . , x∗N (t), y(t), u(t)),

x_∗i(t + 1) =

∗ (x∗i+1(t), . . . , x∗N (t), y(t), u(t)), i = 2, . . . , N - 1,

(1.3)

x_∗N(t + 1) =

∗ (y(t), u(t)),

y_∗(t) = h_∗(x∗1(t))

для некоторых функций

∗

,...,

∗

, h_∗; для упрощения будем опускать

вектор γ там, где это возможно. Отметим, что в нелинейном случае некоторые

переменные x_∗i могут быть векторными.

В ряде случаев исходная модель может быть приведена к более простому

виду, нежели (1.3):

x∗1(t + 1) =

∗ (x∗2(t), y(t), u(t)),

x_∗i(t + 1) =

∗ (x∗i+1(t), y(t), u(t)), i = 2, . . . , N - 1,

(1.4)

x_∗N(t + 1) =

∗ (y(t), u(t)),

y_∗(t) = h_∗(x∗1(t)).

Условия и способы приведения модели (1.1) к виду (1.3) или (1.4) рассмот-

рены в разделах 3 и 4. Остановимся вначале на использовании полученных

моделей для целей диагностирования.

2. Основные конструкции непараметрического метода

2.1. Преобразование построенной модели

Для применения непараметрического метода произведем в представлени-

ях (1.3) и (1.4) ряд временных сдвигов и подстановок, для конкретности рас-

смотрим только (1.4):

x∗1(t + 2) =

∗ (x∗2(t + 1), y(t + 1), u(t + 1)) =

∗ (

∗ (x∗3(t), y(t), u(t)), y(t + 1), u(t + 1)),

x∗1(t+3) =

∗ (

∗ (x∗4(t), y(t), u(t)), y(t + 1), u(t + 1)), y(t + 2), u(t + 2)),

x∗1(t + N) = F_∗(y(t),u(t),y(t + 1),u(t + 1),... ,y(t + N - 1),u(t + N - 1))

для некоторой функции F_∗. В результате с учетом y_∗ = h_∗(x∗1) получаем

(

(2.1) y_∗(t + N) = F_∗∗ y(t), u(t), y(t + 1), u(t + 1), . . .

)

...,y(t + N - 1),u(t + N - 1) ,

где F_∗∗ = h_∗(F_∗).

Будем полагать, что функция F_∗∗ представляет собой сумму нелинейных

членов вида

∑

F∗∗ =

Γ_i(γ)P_i(y(t),u(t),y(t + 1),u(t + 1),... ,y(t + N - 1),u(t + N - 1)),

i=1

где Γ_i(γ) - алгебраическое выражение, представляющее собой функцию эле-

ментов вектора параметров γ, значения которых могут быть неизвестными,

функция P_i(∗) может содержать только такие элементы вектора γ, значения

которых известны, i = 1, . . . , p, p - число слагаемых. Отметим, что искомое

представление всегда может быть получено для полиномиальных функций.

Если функция P_i(∗) содержит параметр, значение которого может быть неиз-

вестно, то для возможности применения непараметрического метода ее сле-

дует представить степенным рядом, коэффициенты которого будут зависеть

от этого параметра.

Из сказанного следует, что равенство (2.1) может быть записано в виде

y_∗(t + N) = F_∗∗(y(t),u(t),... ,y(t + N - 1),u(t + N - 1)) =

⎛

⎞

P₁(t,... ,t + N - 1)

⎜

⎟

P₂(t,... ,t + N - 1)

⎜

⎟

= (Γ₁(γ) Γ₂(γ) . . . Γ_p(γ))

⎝

⎠^,

P_p(t,... ,t + N - 1)

где

P_i(t,... ,t + N - 1) := P_i(y(t),u(t),... ,y(t + N - 1),u(t + N - 1)).

Имея последнее представление в виду, запишем, как и в линейном случае [1],

выражение для значения величины y_∗ для T моментов времени:

(2.2)

Y_T (t) = (y_∗(t) y_∗(t-1) ... y_∗(t-T +1)) = (Γ₁(γ) Γ₂(γ) ... Γ_p(γ))P_T

(t),

⎛

⎞

P1(t - 1, . . . , t - N) P1(t - 2, . . . , t - N - 1) . . . P1(t - T, . . . , t - N - T + 1)

⎜

P2(t - 1, . . . , t - N) P2(t - 2, . . . , t - N - 1) . . . P2(t - T, . . . , t - N - T + 1)

⎟

P_T (t) =⎝

⎠.

Pp(t - 1, . . . , t - N) Pp(t - 2, . . . , t - N - 1) . . . Pp(t - T, . . . , t - N - T + 1)

Характерной особенностью полученного выражения является то, что па-

раметры, значения которых могут быть неизвестны, находятся в строке

(Γ₁(γ) Γ₂(γ) . . . Γ_p(γ)), строка Y_T (t) и матрица P_T (t) зависят только от

измеряемых значений векторов управления и выхода и элементов вектора γ,

значения которых известны. Последнее позволяет осуществлять диагности-

рование с использованием строки Y_T (t) и матрицы P_T (t), т.е. без знания зна-

чений ряда или всех параметров системы.

2.2. Генерация невязки

Для генерации невязки, на основе которой принимается решение о возник-

ших дефектах, используется несколько методов [1], остановимся на методе,

основанном на анализе ядра матрицы P_T (t). В [2, 5] размер временного окна T

выбирается минимальным, при котором rank (P_T (t)) = rank (PT-1(t)). Отсю-

да следует, что последний столбец матрицы P_T (t) линейно выражается через

предыдущие столбцы, т.е. существует ненулевой вектор v(T ), для которого

P_T (t)v(T) = 0; это означает, что матрица P_T (t) имеет непустое ядро. Из (2.2)

тогда следует Y_T (t)v(T ) = 0, которое является соотношением избыточности.

Из сказанного следует, что правило генерации невязки

(2.3)

r_T (t) = Y_T (t)v(T), v(T) ∈ ker(P_T

(t)),

рассмотренное для непрерывных систем в [2, 5], является робастным в том

смысле, что оно строится без знания значений некоторых параметров систе-

мы. Вычисление элементов соотношения (2.3), однако должно производиться

непосредственно в процессе диагностирования в реальном масштабе време-

ни. Этим правило (2.3) отличается от известных методов генерации невязки,

опирающихся на полное описание системы, что дает возможность выполнить

ряд вычислений предварительно - перед проведением процесса диагностиро-

вания. Отметим, что невязка r_T (t) генерируется для каждого момента t, т.е.

временное окно является скользящим.

Недостатком рассмотренного подхода является то, что при наличии по-

грешностей в результатах измерений равенство невязки r_T (t) нулю не будет

выполняться даже при отсутствии дефектов. Этот недостаток можно устра-

нить за счет использования пороговой логики принятия решений путем срав-

нения невязки с неким адаптивным порогом, некоторые правила построения

которого приведены в [8].

Ясно, что операции определения T , при котором rank (P_T (t)) =

= rank(PT-1(t)), требуют определенных ресурсов времени и не всегда мо-

гут быть реализованы в реальном масштабе времени. Кроме того, вычисле-

ние рангов матриц, сформированных на основе экспериментальных данных,

является плохой обусловленной задачей. Для устранения этих недостатков

можно выбирать T заранее так, чтобы число столбцов матрицы P_T (t) бы-

ло больше числа ее строк, так будет при T ≥ p + 1; в этом случае заведомо

выполняется равенство rank (P_T (t)) = rank (PT-1(t)).

2.3. Поиск дефектов

При решении задачи поиска дефектов необходимо построить банк преоб-

разованных моделей, каждая из которых будет чувствительна к одной груп-

пе дефектов и нечувствительна к остальным. Детальный анализ дефектов

с этой точки зрения содержится в [8], не останавливаясь на нем, уточним,

что модель, нечувствительная к дефекту ρ_i, строится на основе результатов

рассматриваемой ниже теоремы 2.

Отметим, что модель, нечувствительная к дефекту ρ_i, может оказаться

нечувствительной и к некоторым другим дефектам, это можно выяснить по

виду системы уравнений (1.3) или (1.4): если в ее описание не входят па-

раметры γ_i, γ_j , . . . , γ_k, то модель нечувствительна к дефектам ρ_i, ρ_j , . . . , ρ_k и

чувствительна к остальным. Для отражения этих особенностей и принятия

решения о возникшем дефекте используется матрица синдромов S. Для па-

раметра γ_i строится вектор-синдром S_i по следующему правилу: если этот

параметр входит в описание k-й модели, полагаем S_ki = 1, в противном слу-

чае S_ki = 0 (см. пример).

Совпадение синдромов S_i и S_j для некоторых параметров γ_i и γ_j означает,

что дефекты ρ_i и ρ_j в рамках рассматриваемого подхода неразличимы. В этом

случае параметры γ_i и γ_j помещаются в одно множество K_d для некоторо-

го d. Параметры, имеющие индивидуальные синдромы, образуют множества,

включающие в себя только один параметр. В результате компоненты вектора

параметров (γ₁, γ₂, . . . , γ_s)^T раскладываются в семейство непересекающихся

множеств K = {K₁, K₂, . . . , K_w}. Матрица синдромов S строится из множе-

ства векторов-синдромов, соответствующих элементам множества K, как из

столбцов.

3. Преобразование исходной модели

Условия и способы приведения исходной системы к виду (1.3) или (1.4),

рассматриваемые ниже, опираются на математический аппарат алгебры

функций, который детально изложен в [7]. Основные конструкции этого ап-

парата - отношение частичного порядка на множестве функций ≤, бинарные

операции × и ⊕, бинарное отношение Δ, а также операторы M и m - кратко

описаны в Приложении.

3.1. Общий результат

Теорема 1. Система (1.1) преобразуема к виду (1.3) или (1.4) тогда и

только тогда, когда

(3.1)

m(h × (m(h × . . . × m(h) . . .))) ⊕ h = 1

(оператор m используется N раз).

Доказательство. Необходимость. Пусть ϕ⁽¹⁾,...,ϕ(N) и ψ - функ-

ции с необходимыми свойствами, т.е. преобразованные координаты (1.2) под-

чиняются уравнениям (1.3) (для конкретности рассмотрим только эти урав-

нения). Заменим в последнем из них переменную x_∗N (t + 1) на ϕ(N)(x(t + 1))

и y(t) на h(x(t)):

ϕ(N)(x(t + 1)) = ϕ(N)(f(x(t), y(t))) =

∗ (h(x(t)), u(t)).

По определению отношения Δ и оператора m отсюда следует включение

(h, ϕ(N)) ∈ Δ и неравенство ϕ(N) ≥ m(h). По аналогии из второго уравнения

в (1.3) следует неравенство

(

)

(3.2)

ϕ(i) ≥ m h × ϕ(i+1) × . . . × ϕ(N)

i = N - 1,...,2.

C учетом свойств операции × и оператора m получаем

при i = N - 1

(

)

ϕ(N-1) ≥ m h × ϕ(N)

≥ m(h × m(h));

при i = N - 2

(

)

ϕ(N-2) ≥ m h × ϕ(N-1) × ϕ(N)

≥ m(h × m(h) × m(h × m(h))).

Так как

h ≥ h × m(h),

то

m(h) ≥ m(h × m(h)),

а тогда

m(h) × m(h × m(h))= m(h × m(h)),

что в итоге дает

ϕ(N-2) ≥ m(h × m(h × m(h))).

Продолжая аналогично, получим в итоге из (3.2)

ϕ(1) ≥ m(h × (m(h × . . . × m(h) . . .)))

(оператор m используется N раз). Запишем равенство y_∗ = ψ(y) при

y_∗ = h_∗(x∗1) = h_∗(ϕ⁽¹⁾(x)) и y = h(x) в виде h_∗(ϕ⁽¹⁾) = ψ(h). Поскольку h_∗ и

ψ - нетривиальные функции, то из последнего равенства имеем ϕ⁽¹⁾ ⊕ h = 1,

откуда с учетом полученного выше выражения для функции ϕ⁽¹⁾ следует

неравенство (3.1).

Достаточность. На основе неравенства (3.1) можно задать различные

функции ϕ⁽¹⁾, . . . , ϕ(N) и, следовательно, получить различные модели без об-

ратных связей. Для простоты рассмотрим случай приведения исходной мо-

дели к (1.4). Положим

ϕ(N) = m(h), x_∗N = ϕ(N)(x),

ϕ(i) = m(h × ϕ(i+1)), x_∗i = ϕ(i)(x), i = N - 1, . . . , 1.

Заметим, что если при некотором i функция m(h × ϕ(i+1)) является вектор-

ной, то для уменьшения размерности строящейся модели в качестве ϕ(i)

можно выбрать скалярную функцию такую, что ϕ(i) ≥ m(h × ϕ(i+1)); ска-

занное относится и к выбору функции ϕ(N). Отметим, что такой выбор не

всегда приводит к требуемому результату, в этом случае необходимо выби-

рать векторную функцию m(h × ϕ(i+1)). По определению оператора m имеем

(α, m(α)) ∈ Δ для произвольной функции α, поэтому

(

)

(h, m(h)) ∈ Δ и h × ϕ(i+1), m(h × ϕ(i+1))

∈ Δ,

что после подстановки дает

(

)

(

)

h, m(ϕ(N))

∈Δ и h×ϕ(i+1),ϕ(i)

∈ Δ, i = N - 1,... ,1.

По определению отношения Δ это означает, что для некоторых функций

∗

,...,

∗

справедливы уравнения (1.4). Из определения функций ϕ⁽¹⁾, . . .

...,ϕ(N) получаем

ϕ(1) = m(h × (m(h × . . . × m(h) . . .)))

(оператор m используется N раз). Отсюда и из неравенства (3.3) следует

существование функций h_∗ и ψ таких, что

h_∗(ϕ⁽¹⁾) = ψ(h) = ϕ⁽¹⁾ ⊕ h = 1,

или

y_∗ = h_∗(ϕ⁽¹⁾(x)) = ψ(y).

Отметим, что теорема справедлива и для систем с непрерывным временем,

это следует из результатов [7].

Пример 1. Рассмотрим дискретную систему

x₁(t + 1) = (x₂(t)(x₃(t) + x₅(t)) + x₄(t))x₄(t)u(t)),

x₂(t + 1) = x₁(t)/x₄(t),

x₃(t + 1) = x₁(t)x₅(t)/x₄(t) - |x₃(t) + x₅(t)| - u(t),

x₄(t + 1) = x₂(t)(x₃(t) + x₅(t)) + x₄(t),

x₅(t + 1) = |x₃(t) + x₅(t)| + u(t),

y₁(t) = x₅(t), y₂(t) = x₄(t).

Проверим выполнение условия (3.1) для h(x) = (x₅, x₄)^T : так как

(h × u) ⊕ f = x₄ = f₁/f₄,

то

m(h) = x₁/x₄.

Аналогичные вычисления дают следующее:

m(h × m(h)) = (x₁/x₄, x₂, x₃ + x₅)^T,

m(h × m(h × m(h))) = (x₁/x₄, x₂, x₃ + x₅, x₄, x₅)^T.

Нетрудно видеть, что при N = 3 условие (3.1) выполняется, при этом

m(h × m(h × m(h))) ≤ h.

Положим

ϕ(3)(x) = m(h) = x₁/x₄.

Так как

m(h × x₁/x₄) = (x₁/x₄, x₂, x₃ + x₅)^T,

примем

ϕ(2)(x) = (x₂, x₃ + x₅)^T,

а поскольку

m(h × ϕ⁽²⁾) = (x₁/x₄, x₂, x₃ + x₅, x₄, x₅)^T,

положим

ϕ(1)(x) = (x₄, x₅)^T.

Отметим, что выбор в качестве ϕ(i) скалярных функций приводит к невоз-

можности построения преобразованной модели, о чем было сказано в дока-

зательстве достаточности.

Положим x∗5 = x₁/x₄, x∗4 = x₂, x∗3 = x₃ + x₅, x∗2 = x₅, x∗1 = x₄. В резуль-

тате преобразованная модель принимает вид

x∗1(t + 1) = x∗3(t)x∗4(t) + y₂(t),

x∗2(t + 1) = |x∗3(t)| + u(t),

x∗3(t + 1) = x∗5(t)y₁(t),

x∗4(t + 1) = x∗5(t),

x∗5(t + 1) = y₂(t)u(t),

y₁(t) = x∗2(t), y₂(t) = x∗1(t).

Проведя серию временных сдвигов и подстановок на основе полученной

модели, нетрудно получить ее вход-выходное описание:

y₁(t + 3) = |y₁(t + 1)y₂(t)u(t)| + u(t + 2),

y₂(t + 3) = y₂(t + 2) + y₁(t + 1)(y₂(t)u(t))².

Отметим, что получение аналогичного вход-выходного описания путем вре-

менных сдвигов и подстановок на основе исходной модели - нетривиальная

задача из-за громоздкости получаемых выражений и необходимости их де-

тального анализа. Так, например, заменяя x₅(t) на y₁(t) и x₄(t) на y₂(t), по-

лучаем

y₂(t + 1) = x₂(t)(x₃(t) + y₁(t)) + y₂(t),

)

x₁(t)

⁽x₁(t)y₁(t)

y₂(t + 2) =

- |x₃(t) + y₁(t)| - u(t) + y₁(t + 1)

+ y₂(t + 1);

y₂(t)

ясно, что только сложный анализ последнего выражения даст нужный ре-

зультат.

3.2. Преобразование к модели, свободной от параметра

Для решения задачи локализации дефектов введем для i-й компоненты

вектора параметров γ векторную функцию α(i) с максимальным числом ком-

понент такую, что композиция α(i)(f(x, u, γ)) не содержит параметр γ_i. Если

функция f дифференцируема по этому параметру, сформулированное усло-

вие может быть записано в виде

∂

α(i)(f(x,u,γ)) = 0, i = 1,... ,s.

∂γ_i

Известно [8], что модель, заданная в новых координатах с помощью преоб-

разования ϕ = ϕ⁽¹⁾ × ϕ⁽²⁾ × . . . × ϕ(N), не будет зависеть от i-й компоненты

вектора параметров, т.е. будет нечувствительной к i-му дефекту, если вы-

полняется следующее условие:

(3.3)

α(i)

≤ ϕ.

Условия построения модели, заданной в новых координатах и не зависящей

от i-й компоненты вектора параметров, даются следующей теоремой.

Теорема 2. Система (1.1) преобразуема к модели (1.4) c тождествен-

ной функцией h_∗, не зависящей от i-й компоненты вектора параметров,

тогда и только тогда, когда выполняются следующие условия:

(3.4)

α(i)

⊕ m(h) = 1,

(

)

)))

(

)

(3.5)

m h × α(i) ⊕ m h × ... × α(i) ⊕ m(h) ...

⊕ α(i) ⊕h

(оператор m используется N раз).

Доказательство. Необходимость. Пусть система (1.1) преобра-

зуема к модели (1.4), не зависящей от i-й компоненты вектора парамет-

ров. Это означает, что существуют функции ϕ⁽¹⁾, ϕ⁽²⁾, . . . , ϕ(N), ψ, реализую-

щие преобразования (1.2), при этом α(i) ≤ ϕ = ϕ⁽¹⁾ × ϕ⁽²⁾ × . . . × ϕ(N). Из по-

следнего условия получаем α(i) ≤ ϕ(j) для всех j. Из теоремы 1 следует

(h × ϕ(j+1), ϕ(j))) ∈ Δ, j = 1, . . . , N - 1, (h, ϕ(N)) ∈ Δ, что с учетом свойств

оператора m и неравенства α(i) ≤ ϕ(j) дает ϕ(j) ≥ α(i) ⊕ m(h × ϕ(j+1)) и

ϕ(N) ≥ α(i) ⊕ m(h) соответственно. Из последнего неравенства следует усло-

вие (3.4). Рассмотрим для простоты случай N = 3, тогда

(

)

(

))

ϕ(2) ≥ α(i) ⊕ m h × ϕ⁽³⁾

≥ α(i) ⊕ m h × α(i) ⊕ m(h)

(

)

(

))))

(3.6)

ϕ(1) ≥ α(i) ⊕ m h × ϕ⁽²⁾

≥α(i) ⊕m h× α(i)⊕m h× α(i) ⊕m(h)

Так как y_∗ = h_∗(x∗1) и y_∗ = φ(y), то (φ(h))(x) = (h_∗(ϕ⁽¹⁾))(x). Это означает,

что h ⊕ ϕ⁽¹⁾ = 1, а тогда с учетом (3.6) получаем условие (3.5).

Достаточность. Из (3.5) следует существование функций γ₁, γ₂ и ϕ⁽¹⁾

таких, что

(

)

))))

ϕ(1) = γ₁ m h × α(i) ⊕ m h × . . . × α(i) ⊕ m(h) . . .

(

)

=γ₂

α(i) ⊕ h

= 1.

Из равенства ϕ⁽¹⁾ = γ₂(α(i) ⊕ h) следует ϕ⁽¹⁾ ≥ h и ϕ⁽¹⁾ ≥ α(i). Из определения

функции ϕ⁽¹⁾, условия (3.5) и свойств операторов m и M получаем

(

)

))

(

)

h × α(i) ⊕ m h × ... × α(i) ⊕ m(h) ...

≤M ϕ⁽¹⁾

Выберем в качестве ϕ⁽²⁾ максимальную функцию, удовлетворяющую усло-

виям h × ϕ⁽²⁾ ≤ M(ϕ⁽¹⁾) и

(

)

α(i) ⊕ m h × ... × α(i) ⊕ m(h) ...

≤ϕ⁽²⁾

(оператор m используется N - 1 раз), тогда справедливо включение

(h × ϕ⁽²⁾, ϕ⁽¹⁾) ∈ Δ. Из предыдущего следует, что это можно сделать всегда,

положив

(

)

ϕ(2) = α(i) ⊕ m h × . . . × α(i) ⊕ m(h)

Тогда

(

)

ϕ(2) ≥ m h × . . . × α(i) ⊕ m(h) . . . и ϕ⁽²⁾ ≥ α(i).

По аналогии строятся функции ϕ⁽³⁾, . . . , ϕ(N-1), для которых справедливы

включение (h × ϕ(j+1), ϕ(j)) ∈ Δ и неравенство ϕ(j) ≥ α(i), j = 3, . . . , N - 1.

Используя оператор M N - 1 раз, получим из (3.5) нетривиальную (в си-

лу условия (3.4)) функцию ϕ(N) = α(i) ⊕ m(h), откуда следует ϕ(N) ≥ m(h)

и ϕ(N) ≥ α(i), т.е. справедливо включение (h,ϕ(N)) ∈ Δ. Так как ϕ = ϕ⁽¹⁾×

×ϕ⁽²⁾ × ... × ϕ(N) и ϕ(j) ≥ α(i) для всех j, то ϕ ≥ α(i), т.е. справедливо усло-

вие (3.3). Из всего сказанного и определения отношения Δ следует, что для

некоторых функций

∗

,...,

∗

справедливы уравнения (1.4). Из неравен-

ства ϕ⁽¹⁾ ≥ h следует существование функции ψ такой, что ϕ⁽¹⁾ = ψ(h), отку-

да y_∗ = ψ(y) = ψ(h(x)) = ϕ⁽¹⁾(x), т.е. h_∗ - тождественная функция.

Пример 2. Рассмотрим дискретную систему

x₁(t + 1) = γ₂x₂(t) + x₃(t) - x₂(t),

x₂(t + 1) = u(t)|x₁(t)|,

x₃(t + 1) = u(t)|x₁(t)| + x₁(t)x₄(t),

x₄(t + 1) = γ₁x₅(t)(x₃(t) - x₂(t)),

x₅(t + 1) = u(t)x₁(t),

y₁(t) = x₁(t), y₂(t) = x₃(t) - x₂(t).

Проверим выполнение условий теоремы 2 для первого дефекта, которо-

му соответствует функция α⁽¹⁾ = (x₁, x₂, x₃, x₅)^T. Так как m(h) = (x₂, x₅)^T,

то α⁽¹⁾ ⊕ m(h) = (x₁, x₂, x₃, x₅)^T ⊕ (x₂, x₅)^T = (x₂, x₅)^T = 1, т.е. выполняется

условие (3.4). Далее

(

)

h × α⁽¹⁾ ⊕ m(h)

= (x₁, x₂, x₃, x₅)^T

(

)

m h × (α⁽¹⁾ ⊕ m(h))

= (x₁, x₂, x₄, x₅)^T,

а так как α⁽¹⁾ ⊕ h = (x₁, x₃ - x₂)^T, то выполняется условие (3.5).

Положим ϕ⁽¹⁾(x) = (x₁, x₂, x₄, x₅)^T ⊕ (x₁, x₃ - x₂)^T = x₁; так как ϕ⁽²⁾

должно удовлетворять условию

ϕ(2) ≥ α⁽¹⁾ ⊕ m(h) = (x₁, x₂, x₃, x₅)^T ⊕ (x₂, x₅)^T = (x₂, x₅)^T,

примем ϕ⁽²⁾(x) = x₂.

Положим x∗1 = x₁, x∗2 = x₂; преобразованная модель, нечувствительная к

первому дефекту, имеет вид

x∗1(t + 1) = γ₂x∗2(t) + y₂(t),

x∗2(t + 1) = u(t)|y₁(t)|,

y₁(t) = x∗1(t).

Для второго дефекта, которому соответствует функция

α⁽²⁾(x) = (x₂,x₃,x₄,x₅)^T,

аналогичным образом можно показать, что x∗1 = x₂, x∗2 = x₃, x∗3 = x₄,

x∗4 = x₅; модель, нечувствительная к этому дефекту, принимает вид

x∗1(t + 1) = u(t)|y₁(t)|,

x∗2(t + 1) = u(t)|y₁(t)| + y₁(t)x∗3(t),

x∗3(t + 1) = γ₁x∗4(t)y₂(t),

x∗4(t + 1) = u(t)y₁(t),

y₂(t) = x∗2(t) - x∗1(t).

На основе этих моделей нетрудно получить вход-выходное описание системы.

4. Решение на основе логико-динамического подхода

Теоремы 1 и 2 дают исчерпывающий ответ на вопрос о возможности пред-

ставления исходной системы в виде, необходимом для применения непара-

метрического метода. Они дают общее решение задачи, когда преобразова-

ние (1.2) исходной системы к форме (1.3) или (1.4) может быть нелинейным,

и требуют применения сложного математического аппарата алгебры функ-

ций. В случае ограничения класса преобразований линейными функциями

решение может быть получено методами линейной алгебры на основе логико-

динамического подхода [8]. Для возможности его применения исходная систе-

ма должна быть представлена в виде

⎛

⎞

ψ₁(A₁x(t),u(t))

∑

x(t + 1) = F x(t) + Gu(t) + C^⎝

⎠+Did_i(t),

(4.1)

ψ_q(A_qx(t),u(t))

i=1

y(t) = Hx(t),

где x ∈ Rⁿ, u ∈ R^m, y ∈ Rl - векторы состояния, управления и выхода;

F, G и C - матрицы при номинальных значениях параметров, F и G описы-

вают линейную динамику; H, D₁, . . . , D_s - известные постоянные матрицы,

d₁(t),... ,d_s(t) - скалярные функции, описывающие дефекты: если i-й па-

раметр имеет номинальное значение, то d_i(t) = 0, в противном случае d_i(t)

становится неизвестной функцией времени, i = 1, . . . , s; ψ₁, . . . , ψ_q - произ-

вольные нелинейности, A₁, . . . , A_q - матрицы-строки. Модель (4.1) всегда мо-

жет быть получена из нелинейной модели (1.1) путем ряда эквивалентных

преобразований, детально описанных в [8].

Известно [8], что логико-динамический подход реализуется в три этапа,

на первом из которых из модели (4.1) удаляется нелинейная составляющая,

на втором рассматриваемая задача решается для линейной системы с до-

полнительным ограничением линейного же характера, на третьем к полу-

ченному линейному решению добавляется преобразованная нелинейная со-

ставляющая. Коротко опишем решение на втором этапе, в основе которого

лежит процедура синтеза модели, представленной в канонической форме [8],

на основе которой нетрудно получить вход-выходные соотношения, лежащие

в основе непараметрического метода.

Приведем описание преобразованной модели:

x_∗i(t + 1) = x∗i+1(t) + J_iy(t) + G_∗iu(t), i = 1,... ,k - 1,

(4.2)

x_∗k(t + 1) = J_ky(t) + G_∗ku(t),

y_∗(t) = x∗1(t),

где x_∗ ∈ R^k - вектор состояния модели, x_∗ = Φx, y_∗ = Ry. Известно, что мат-

рицы, описывающие исходную систему и эту модель, в также матрицы Φ и R

удовлетворяют следующим уравнениям [8]:

(4.3)

RH = Φ₁, Φ_iF = Φi+1 + J_iH, i = 1,... ,k - 1, Φ_kF = J_k

где Φ_i и J_i - i-е строки матриц Φ и J, i = 1, . . . , k, k - размерность модели.

Дополнительное ограничение на матрицу Φ имеет вид

(

)

(4.4)

A=A_∗

для некоторой матрицы A_∗, где

(

AT1 ... ATq

)^T.

Равенство (4.4) эквивалентно условию [8]

(

)

(

)

(4.5)

rank

Φ^T H^T

= rank

Φ^T H^T A^T

Известно, что уравнения (4.3) можно свернуть в одно:

(4.6)

RHF^k = J₁HFk-1 + J₂HFk-2 + ... + J_k

Решение этого уравнения дает минимальную размерность k и матрицы R и J.

Для построения модели, не содержащей i-й компоненты вектора парамет-

ров, напомним, что соответствующее условие имеет вид ΦD_i = 0 [8]. Учет

этого условия приводит к уравнению [1]

(4.7)

-J₁

-J₂

-J_k) (U(k) B(k)

) = 0,

где

⎛

⎞

HF^k

⎜

⎟

⎜

HFk-1

⎟

U(k) =^⎜

⎟,

⎜

HFk-2

⎟

⎝

⎠

(4.8)

⎛

⎞

HD_i HFD_i HF²D_i ... HFk-1D

⎜

⎟

⎜

HD_i HFD_i ... HFk-2D_i

⎟

B(k) =^⎜

⎟.

⎜

HD_i ... HFk-3D_i

⎟

⎝

⎠

Минимальное значение размерности k, при котором это уравнение имеет

нетривиальные решения, определяется условием

(4.9)

rank (U(k) B(k)

) < l(k + 1).

При его выполнении найдется вектор-строка (R

-J₁

-J₂

-J_k) , удо-

влетворяющая уравнению (4.7). Далее по формулам (4.3) определяются стро-

ки матрицы Φ и проверяется условие (4.5), при его выполнении рассчитыва-

ется матрица G_∗ = ΦG и строится модель в форме (4.2). Если условие (4.5) не

выполняется, рекомендуется найти другое решение уравнения (4.7) или уве-

личить размерность k; невыполнение этого условия при всех k < n означает,

что модели, не содержащей i-й компоненты вектора параметров, не существу-

ет. Далее будем полагать, что условие (4.5) выполняется, т.е. уравнение (4.4)

имеет решение.

Для построения нелинейной составляющей заметим, что она описывается

выражением

⎛

⎞

ψ₁(A∗1z(t),u(t))

(4.10)

C_∗ ⎝

⎠_,

ψ_q(A_∗qz(t),u(t))

(

)

(

)

x_∗

где z =

, строка A∗1 определяется из уравнения A_i = A_∗i

i = 1,...,q, соответствующего (4.4), C_∗ = ΦC. Если выражение (4.10) имеет

вид, соответствующий правым частям моделей (1.3) или (1.4), т.е. не содер-

жит обратных связей, составляющая (4.10) добавляется к ранее построенной

линейной части. В противном случае следует найти другое решение уравне-

ния (4.7) при прежней или увеличенной размерности.

Отметим, что если все строки матрицы A линейно выражаются через стро-

ки матрицы H, то выражение (4.10) заведомо имеет требуемый вид. Если это

условие не выполняется, добиться его выполнения можно путем расширения

вектора выхода исходной системы. Детальное рассмотрение этого вопроса,

однако, выходит за рамки настоящей работы.

Дальнейшие действия с полученной моделью не отличаются от тех, кото-

рые были описаны в разделе 2.

В некоторых случаях система не может быть преобразована к виду (1.3)

или (1.4), однако с помощью эвристических приемов она может быть приве-

дена к виду (2.1), рассмотрим это на примере.

Пример 3. Пусть преобразованная модель описывается системой урав-

нений

x∗1(t + 1) = x∗2(t) + η₁(x∗1(t)) + J₁y(t),

x∗2(t + 1) = x∗3(t) + η₂(x∗2(t)) + J₂y(t),

x∗3(t + 1) = η₃(x∗3(t)) + J₃y(t),

y_∗(t) = x∗1(t),

где η₁ ÷ η₃ — произвольные нелинейные функции, вектор управления для

простоты опущен, элементы матриц-строк J₁, J₂ и J₃ зависят от парамет-

ров исходной системы. Особенность модели состоит в том, что правая часть

уравнения для каждой переменной содержит нелинейную функцию той же

переменной. Рассмотрим ряд временных сдвигов и подстановок для перемен-

ной y_∗:

y_∗(t+2) = x∗1(t + 2) = x∗2(t + 1) + η₁(x∗1(t + 1)) + J₁y(t + 1) =

= η₁(y_∗(t + 1)) + J₁y(t + 1) + x∗3(t) + η₂(x∗2(t)) + J₂y(t),

y_∗(t+3) = η₁(y_∗(t+2))+J₁y(t+2)+x∗3(t+1)+η₂(x∗2(t+1))+J₂y(t+1) =

= η₁(y_∗(t + 2)) + J₁y(t + 2) + J₂y(t + 1)+

+ η₂(x∗3(t) + η₂(x∗2(t)) + J₂y(t)) + η₃(x∗3(t)) + J₃y(t).

Из выражения для y_∗(t + 2) найдем сумму x∗3(t) + η₂(x∗2(t)) + J₂y(t):

x∗3(t) + η₂(x∗2(t)) + J₂y(t) = y_∗(t + 2) - η₁(y_∗(t + 1)) - J₁y(t + 1)

и подставим ее в уравнение для y_∗(t + 3) вместо аргумента функции η₂:

y_∗(t + 3) = η₁(y_∗(t + 2)) + J₁y(t + 2) + J₂y(t + 1)+

+ η₂(y_∗(t + 2) - η₁(y_∗(t + 1)) - J₁y(t + 1)) + η₃(x∗3(t)) + J₃y(t).

Если далее из последнего соотношения выразить сумму η₃(x∗3(t)) + J₃y(t),

найти выражение для y_∗(t + 4) и подставить эту сумму вместо аргумента

функции η₃, то итоговое выражение для y_∗(t + 4) будет содержать только

временные сдвиги векторов y_∗ и y, что и требуется для применения непара-

метрического подхода.

5. Практический пример

Рассмотрим модель электропривода при отсутствии внешнего нагрузочно-

го момента и без учета вязкого трения:

x₁ =

¹x₂,

i_p

K_M

x₂ =

x₃ -

K_d sign(x₂),

J_H

K_ω

K_U

x₃ = -

x₂ -

x₃ +

где x₁ - угол поворота выходного вала редуктора, x₂ - угловая скорость вра-

щения вала электродвигателя, x₃ - ток электродвигателя, i_p - передаточное

отношение редуктора, J_H - момент инерции ротора двигателя и вращающих-

ся частей редуктора, приведенный к ротору, K_M - моментный коэффициент

электродвигателя, K_ω - коэффициент противо-э.д.с., K_d - момент сухого тре-

ния в двигателе, R - активное сопротивление обмотки якоря электродвига-

теля, L - индуктивность якорной обмотки электродвигателя, K_U - коэффи-

циент усиления усилителя мощности.

Дискретизированную модель представим в виде

x⁺¹ = γ₁x₂ + x₁,

(5.1)

x⁺² = γ₂x₃ + γ₃sign(x₂) + x₂,

x⁺³ = γ₄x₂ + γ₅x₃ + γ₆u,

где для простоты используются обозначения x⁺ = x(t + 1), x = x(t), u = u(t),

коэффициенты γ₁ ÷ γ₆ представляют описанные выше параметры и интервал

дискретизации.

Из уравнений (5.1) ясно, что коэффициенты γ₂, γ₃, а также γ₄ ÷ γ₆ одина-

ковым образом влияют на переменные x₂ и x₃ соответственно, поэтому можно

говорить о трех дефектах. Полагая, что измеряемыми являются переменные

x₁ и x₃, рассматриваемую модель опишем следующими матрицами:

⎛

⎞

⎛

⎞

(

)

γ₁

F =^⎝ 0

γ₂

⎠,G= ⎝₀

⎠,H=

γ₄

γ₅

γ₆

⎛

⎞

ϕ(x, u) = sign(Ax), A = (0 1 0), C =^⎝ γ₃

⎠_,

⎛

⎞

⎛

⎞

⎛

⎞

D₁ =^⎝ 0

⎠,D2 = ⎝ 1

⎠,D3 = ⎝ 0

⎠_.

Следуя логико-динамическому подходу, удалим нелинейный член из мо-

дели и рассмотрим ее линейную часть. Непосредственные вычисления для

первого дефекта дают следующее:

(

)

HD₁ =HFD₁ =

⎞

^⎛1

2γ₁

γ₁γ₂

⎜

⎟

⎜0

γ₄(1 + γ₅) γ₂γ₄ + γ²⁴

0⎟

⎜

⎟

⎜1

γ₁

1⎟

⎜

⎟

(U⁽²⁾, B⁽²⁾) =

⎜

⎟

γ₄

γ₅

⎜

⎟

⎜

⎟

⎝1

0⎠

Ясно, что rank (U⁽²⁾, B⁽²⁾) < 2(2 + 1) = 6, поэтому уравнение (4.7) имеет ре-

шение, приведем его в виде

-J₁

-J₂) = (0

-(1 + γ₅)

-(γ₂γ₄ - γ₅)) .

Тогда

(

)

γ₆

Φ₁ = (0 0 1), Φ₂ = (0 γ₄

- 1), G_∗ =

-γ₆

Нетрудно проверить, что условие (4.5) выполняется и матрицу A_∗ можно

принять в виде A_∗ = (0 1/γ₄ 0 1), кроме того,

(

)

C_∗ = ΦC =

γ₃γ₄

В результате нелинейная преобразованная модель описывается уравне-

ниями

x+∗1 = x∗2 + (1 + γ₅)y₂ + γ₆u,

x+∗2 = (γ₂γ₄ - γ₅)y₂ - γ₆u + γ₃γ₄sign((y₂ + x∗2)/γ₄),

y∗1 = x∗1 = y₂,

где

x∗1 = x₃, x∗2 = γ₂x₂ - x₃.

Временные сдвиги дают следующее:

y₂(t + 1) = x∗2(t) + (1 + γ₅)y₂(t) + γ₆u(t),

y₂(t + 2) = (γ₂γ₄ - γ₅)y₂(t) - γ₆u(t) + γ₃γ₄sign((y₂(t) + x∗2(t))/γ₄) +

+ (1 + γ₅)y₂(t + 1) + γ₆u(t + 1).

Из выражения для y₂(t + 2) следует, что сумма первых трех его слагаемых

из правой части может быть представлена как

y₂(t + 2) - (1 + γ₅)y₂(t + 1) - γ₆u(t + 1).

Имея это в виду, приведем выражение для y₂(t + 3):

y₂(t + 3) = (γ₂γ₄ - γ₅)y₂(t + 1) - γ₆u(t + 1) + (1 + γ₅)y₂(t + 2) + γ₆u(t + 2) +

+ γ₃γ₄sign((y₂(t + 1) + y₂(t + 2) - (1 + γ₅)y₂(t + 1) - γ₆u(t + 1))/γ₄).

Поскольку функция sign содержит параметры γ₄, γ₅ и γ₆, то для применения

непараметрического метода их значения должны быть известны.

Выражения для остальных сдвигов могут быть получены по аналогии. Так

как последнее выражение содержит 5 слагаемых, то T = 6. Обозначим функ-

цию sign(∗) в последнем выражении через z(t) и запишем его в виде (3.2),

приняв y_∗ = Ry = y₂ :

Y₆(t) = (y₂(t) y₂(t - 1) y₂(t - 2) y₂(t - 3) y₂(t - 4) y₂(t - 5)) =

= (γ₂γ₄ - γ₅

-γ₆

1+γ₅

γ₆

γ₃γ₄) P₆(t),

где

⎛

⎞

y₂(t - 2) y₂(t - 3) y₂(t - 4) y₂(t - 5) y₂(t - 6) y₂(t - 7)

⎜

⎟

u(t - 2) u(t - 3) u(t - 4) u(t - 5) u(t - 6) u(t - 7)

⎜

⎟

⎜

⎟

P₆(t) =

⎜

y₂(t - 1) y₂(t - 2) y₂(t - 3) y₂(t - 4) y₂(t - 5) y₂(t - 6)

⎟.

⎜

⎟

⎝ u(t - 1) u(t - 2) u(t - 3) u(t - 4) u(t - 5) u(t - 6)

⎠

z(t - 3) z(t - 4) z(t - 5) z(t - 6) z(t - 7) z(t - 8)

Невязка формируется в виде r⁽¹⁾⁶(t) = Y⁽¹⁾⁶(t)v(6), где v(6) ∈ ker(P⁽¹⁾⁶(t)).

Можно показать, что уравнение (4.7) для второго дефекта не имеет реше-

ний. Выполняя требуемые действия для третьего дефекта, получаем следую-

щую преобразованную модель:

x+∗1 = x∗2 + 2y₁,

x+∗2 = -y₁ + γ₁γ₂y₂ + γ₁γ₃sign((y₁ + x∗2)/γ₁),

y∗1 = x∗1 = y₁,

где x∗1 = x₁, x∗2 = γ₁x₂ - x₁. Произведя временные сдвиги, можно заметить,

что в результирующем выражении функция sign содержит параметр γ₁, по-

этому для применения непараметрического метода его значение должно быть

известно. Невязка r⁽²⁾ формируется по аналогии с r⁽¹⁾⁶.

Нетрудно видеть, что матрица синдромов в рассматриваемом примере

имеет вид

⁽ 0 1 1⁾

где строки соответствуют невязкам r⁽¹⁾⁶ и r⁽²⁾, столбцы - множествам

K₁ = {γ₁}, K₂ = {γ₂,γ₂}, K₃ = {γ₄,γ₅,γ₆}.

Для моделирования примем k₁ = k₂ = k₆ = 1, k₃ = k₄ = k₅ = -1, u(t) =

= 2sin(t/10). На рис. 1 представлены результаты моделирования в случае

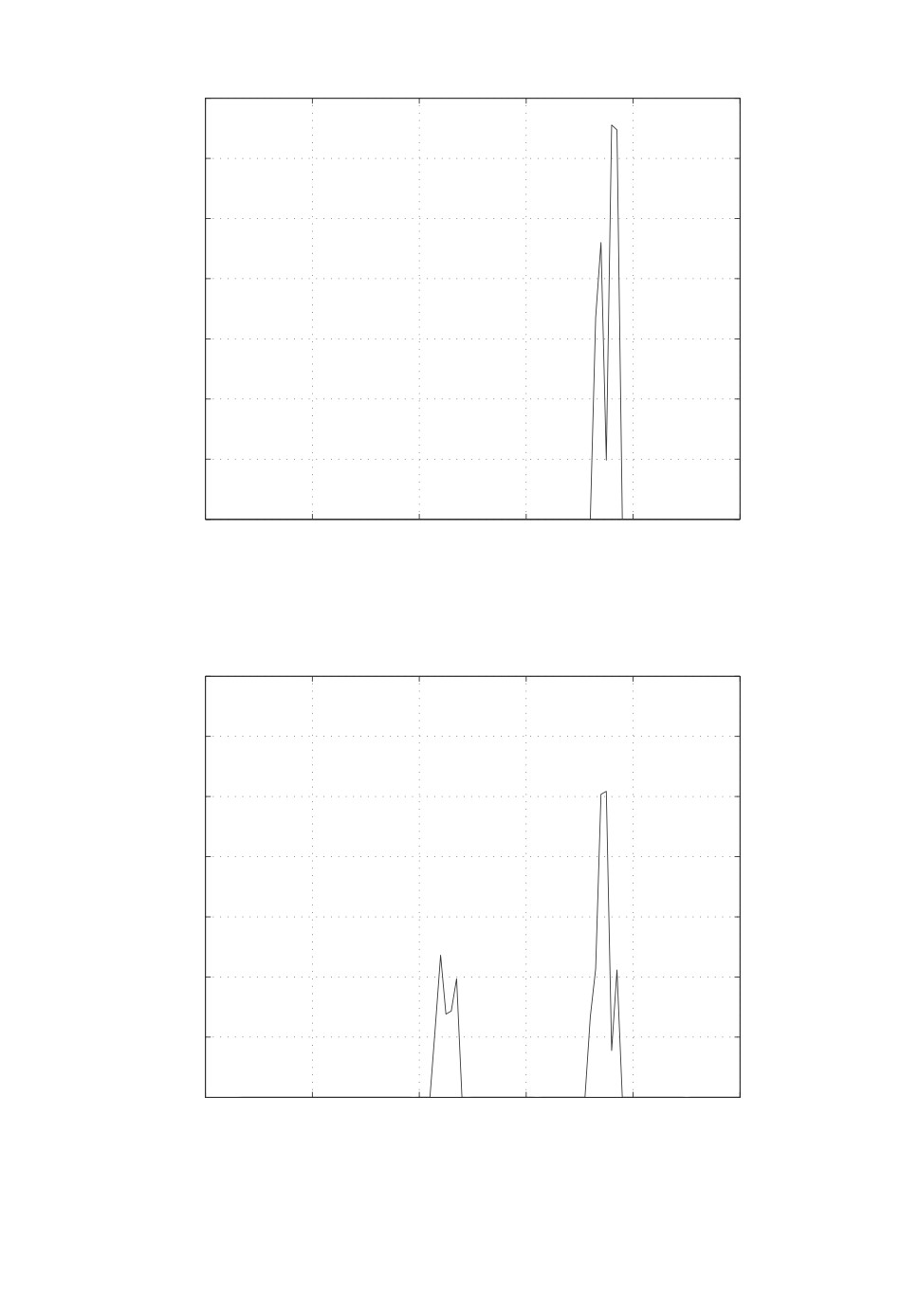
k₁ = 1,2 в момент t = 40 и k₂ = 1,2 в момент t = 70; видно, что невязка r⁽¹⁾⁶

нечувствительна к изменению первого параметра и чувствительна ко второ-

му. На рис. 2 представлены результаты моделирования в случае k₃ = -1, 2 в

момент t = 40 и k₄ = -1, 2 в момент t = 70; видно, что невязка чувствительна

к изменению обоих параметров.

6. Заключение

В работе рассмотрен подход к решению задачи диагностирования техни-

ческих систем, описываемых нелинейными моделями, путем проверки соот-

ношений, существующих между входами и выходами системы, измеряемыми

на конечном интервале времени. Получены критерии возможности построе-

ния таких соотношений для заданной нелинейной системы. Для проверки

используется правило, реализуемое на основе непараметрического метода.

Теоретические результаты иллюстированы примером диагностирования ре-

альной технической системы.

ПРИЛОЖЕНИЕ

Используемый в работе математический аппарат (алгебра функций) со-

держит четыре основные конструкции: 1) отношение частичного предпоряд-

ка, обозначаемое как ≤, 2) две бинарные операции × и ⊕, 3) бинарное от-

ношение Δ, 4) операторы m и M. Первые два элемента определены на мно-

жестве V_W произвольных векторных функций с некоторой областью опре-

деления W , в то время как два последних - на множестве V_X векторных

функций с областью определения в пространстве состояний X. Рассмотрим

эти элементы более подробно.

1. Отношение частичного предпорядка. Для произвольных функций

α, β ∈ V_W записывается α ≤ β, если существует функция γ такая, что

β(w) = γ(α(w))

∀w ∈ W. Определение означает, что каждая компонента

функции β может быть выражена через компоненты функции α. Если α ≤ β

и β ≤ α, то функции α и β называются эквивалентными, что обозначается

как α⁼ β.

Отметим, что= является отношением эквивалентности. Оно разбива-

ет множество V_W на классы эквивалентности, содержащие эквивалентные

функции. Обозначим через V_E множество классов эквивалентности, тогда от-

ношение ≤ является частичным порядком на этом множестве и пара (V_E , ≤)

представляет собой решетку [9]. Существуют две специальные функции 0

и 1 такие, что для произвольной функции α выполняется условие 0 ≤ α ≤ 1.

Функция 0 эквивалентна тождественной функции, 1 - постоянной функции.

2. Бинарные операции. Поскольку пара (V_E , ≤) представляет собой решет-

ку, то для произвольных функций α, β ∈ V_W существуют две бинарные опе-

рации × and ⊕, определяемые следующим образом [9]:

α × β = inf(α,β), α ⊕ β = sup(α,β).

Указанные операции определяют функции с точностью до эквивалентности.

Правило вычисления операции × выглядит просто:

(

)

α(w)

(α × β)(w) =

β(w)

Операция ⊕ может быть вычислена с использованием средств дифференци-

альной геометрии [7]. В простейших случаях может быть использовано опре-

деление операции α ⊕ β как наименьшей верхней грани функций α и β.

Рассмотрим пример вычисления функций α × β и α ⊕ β. Пусть W = R³,

)

⁽w₁ +w₂

⁽w₁w₃)

α(w) =

β(w) =

w₃

w₂w₃

Тогда (α × β)(w)= (w₁ + w₂, w₃, w₁w₃)^T, (α ⊕ β)(w) = w₃(w₁ + w₂).

3. Бинарное отношение Δ. Для заданных функций α, β ∈ V_X

(α, β) ∈ Δ ⇐⇒ α(f(x, u, γ)) = f_∗(β(x), u, γ)

для всех (x, u) ∈ X × U и некоторой функции f_∗. Бинарное отношение Δ са-

мостоятельного значения не имеет и используется для определения операто-

ров.

4. Операторы m и M. Для произвольных функций α, β ∈ V_X определяются

операторы m и M следующим образом.

Оператор m задает функцию m(α) ∈ S_X , которая удовлетворяет усло-

виям: (i) (α, m(α)) ∈ Δ, (ii) если (α, β) ∈ Δ, то m(α) ≤ β.

Оператор M задает функцию M(β) ∈ S_X , которая удовлетворяет усло-

виям: (i) (M(β), β) ∈ Δ, (ii) если (α, β) ∈ Δ, то α ≤ M(β).

Из последних определений следует, что для произвольной α выраже-

ние m(α) представляет собой минимальную функцию, формирующую пару

с α, и для произвольной β выражение M(β) представляет собой максималь-

ную функцию, формирующую пару с β.

Оператор m может быть вычислен следующим образом. Пусть функция γ

удовлетворяет условию (α × u) ⊕ f⁼ γ(f). Тогда m(α)= γ. Можно пока-

зать, что функция γ всегда существует. Правило вычисления оператора M

не приводится, поскольку в работе оно не используется.

Операторы m и M обладают рядом свойств, которые детально описаны

в [7].

Отметим, что стандартные математические пакеты программ нельзя ис-

пользовать для вычисления операций и операторов алгебры функций. По-

этому на основе пакета Mathematica была разработана вычислительная сре-

да, доступная на сайте [10] и позволяющая организовать облачные вычисле-

ния для нахождения упомянутых операций и операторов, а также проверки

условий теорем 1 и 2. Характерной особенностью таких вычислений является

возможность их выполнения без наличия пакета Mathematica у пользователя

сайта.

СПИСОК ЛИТЕРАТУРЫ

1. Жирабок А.Н., Шумский А.Е., Павлов С.В. Диагностирование линейных дина-

мических систем непараметрическим методом // АиТ. 2017. № 7. С. 3-21.

Zhirabok A.N., Shumsky A.E., Pavlov S.V. Diagnosis of Linear Dynamic Systems

by the Nonparametric Method // Autom. Remote Control. 2017. V. 78. No. 7.

P. 1173-1188.

2. Ding S. Data-driven Design of Fault Diagnosis and Fault-tolerant Control Systems.

London: Springer-Verlag, 2014.

3. Lindner B., Auret L. Data-driven fault getection with process topology for fault

identification // Proc. 19th World IFAC Congr. 2014. P. 8903-8908.

4. Haghani A., Krueger M., Jeinsch T., Ding S., Engel P. Data-driven multimode

fault detection for wind energy conversion systems // Proc. 9th IFAC Sympos.

Safeprocesses’2015. P. 633-6385.

5. Шумский А. Функциональное диагностирование нелинейных динамических си-

стем с запаздыванием // АиТ. 2009. № 3. С. 172-184.

Shumskii A.E. Functional Diagnosis of Nonlinear Dynamic Delay Systems // Autom.

Remote Control. 2009. V. 70. No. 3. P. 502-512.

6. Shumsky A., Zhirabok A. Redundancy relations for fault diagnosis in hybrid

systems // Proc. 8th IFAC Sympos. Safeprocesses’2012. P. 1226-1231.