Автоматика и телемеханика, № 2, 2019
© 2019 г. М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ОПТИМИЗАЦИЯ БИЛИНЕЙНОЙ СИСТЕМЫ УПРАВЛЕНИЯ
ПРИ ВНЕШНИХ ВОЗМУЩЕНИЯХ:
I. ЗАДАЧА АНАЛИЗА1
Рассмотрены результаты, связанные с задачей анализа для билинейной
системы при произвольных ограниченных внешних возмущениях. Постав-
лены и решены задачи конструктивного построения эллипсоида стаби-
лизируемости и области стабилизируемости квадратичной динамической
системы в непрерывном и дискретном времени. Главным инструментом
при этом является техника линейных матричных неравенств.
Простой и универсальный подход имеет большой потенциал и возмож-
ности для обобщений; в частности, он распространим на разнообразные
робастные постановки задачи.
Ключевые слова: билинейная система, внешние возмущения, квадратич-
ная функция Ляпунова, линейная обратная связь, эллипсоид стабилизи-
руемости, область стабилизируемости, линейные матричные неравенства.
DOI: 10.1134/S000523101902003X
1. Введение
Задачам, связанным с вопросами устойчивости, стабилизации и синтеза
управления для билинейных систем, традиционно уделяется достаточно боль-
шое внимание в публикациях, начиная с появления монографии [1]; при этом
предлагаются как самые различные постановки задач, так и подходы к их
решению, см. [2-15] и др.; в частности, в некоторых публикациях [6] пред-
принимаются попытки эллипсоидального подхода к рассматриваемой пробле-
матике.
В [16, 17] был предложен подход к описанию области стабилизируемости
билинейной системы. На основе техники линейных матричных неравенств и
квадратичных функций Ляпунова конструктивно строился так называемый
эллипсоид стабилизируемости такой, что траектории замкнутой системы, на-
чинаясь внутри эллипсоида, асимптотически стремятся к нулю. Это позво-
лило эффективно строить невыпуклые аппроксимации областей стабилизи-
руемости билинейных систем управления. Среди наиболее идейно близких
публикаций отметим [18, 19], которые также посвящены построению квадра-
тичных функций Ляпунова для задач стабилизации билинейных систем при
помощи аппарата линейных матричных неравенств.
1 Исследование выполнено при частичной поддержке Российского фонда фундамен-
тальных исследований (проект № 18-08-00140).
46
Однако настоящая статья существенно отличается от всех указанных пуб-
ликаций: в ней рассматривается билинейная система, подверженная воздей-
ствию внешних возмущений. Эта тематика (применительно к линейным си-
стемам) восходит к работам Б.В. Булгакова, см. [20-22], который занимал-
ся так называемой проблемой о накоплении возмущений. В статье решает-
ся задача конструктивного построения эллипсоида стабилизируемости нели-
нейной (квадратичной) динамической системы, подверженной воздействию
внешних возмущений; кроме того, в ней ставится и решается новая задача
построения области стабилизируемости системы.
Статья организована следующим образом: в разделе 2 изложен важный
вспомогательный технический результат, являющийся обобщением так назы-
ваемой леммы Питерсена; раздел 3 посвящен построению эллипсоида стаби-
лизируемости, в разделе 4 рассматривается построение области стабилизи-
руемости квадратичной системы, подверженной воздействию внешних воз-
мущений; в разделе 5 полученные результаты распространяются на системы
в дискретном времени; раздел 7 содержит заключительные комментарии.
Несмотря на то что в статье рассматриваются системы со скалярным
управлением, предложенный подход в полной мере распространим и на систе-
мы с многомерным управлением. При этом выкладки становятся несколько
более громоздкими, в то время как идейная сторона меняется мало.
Всюду далее ∥ · ∥ — евклидова норма вектора и спектральная норма матри-
цы,⊤ — символ транспонирования, I — единичная матрица соответствующих
размеров, а все матричные неравенства понимаются в смысле знакоопреде-
ленности матриц.
2. Вспомогательный результат: лемма Питерсена
Так называемая лемма Питерсена [23] эффективно применяется в разно-
образных робастных постановках задач стабилизации и управления. Приве-
дем ее в следующей формулировке.
Лемма 1 (Питерсен). Пусть G = G⊤ ∈ Rn×n, а M ∈ Rn×p и N ∈ Rq×n —
ненулевые матрицы. Неравенство
G + MΔN + N⊤Δ⊤M⊤ ≼ 0
справедливо для всех Δ ∈ Rp×q : ∥Δ∥ ≤ 1 тогда и только тогда, когда суще-
ствует число ε такое, что
(G + εMM⊤ N⊤ )
≼ 0.
N
-εI
Модификация леммы Питерсена, представленная в следующей лемме 2,
охватывает случай векторной неопределенности, удовлетворяющей эллипсо-
идальному ограничению.
Лемма 2. Пусть G = G⊤ ∈ Rn×n, 0 ≺ P = P⊤ ∈ Rq×q, а M ∈ Rn×q и
N ∈ R1×n — ненулевые матрицы. Матричное неравенство
G+MδN +N⊤δ⊤M⊤ ≼0
47
справедливо для всех δ ∈ Rq : δ⊤P-1δ ≤ 1 тогда и только тогда, когда суще-
ствует число ε такое, что
1
G + εMPM⊤ +
N⊤N ≼ 0,
ε
или, эквивалентно,
⎛
⎞
G MP N⊤
⎜
⎟
⎜PM⊤ -εP
0
⎟
0.
⎝
⎠≼
1
N
0
-
I
ε
В дальнейшем изложении этот результат будет использоваться самым су-
щественным образом.
3. Эллипсоид стабилизируемости
Рассмотрим билинейную систему управления
(1)
x = Ax + Bxu + bu + Dw, x(0) = x0,
где A, B ∈ Rn×n, D ∈ Rn×m, b ∈ Rn, с фазовым состоянием x ∈ Rn, скаляр-
ным управлением u ∈ R и внешним возмущением w ∈ Rm, измеримым по t и
ограниченным в каждый момент времени:
(2)
∥w(t)∥ ≤ γ при всех t ≥ 0.
Замкнув билинейную систему (1), (2) статической линейной обратной свя-
зью
u = k⊤x, k ∈ Rn,
приходим к квадратичной динамической системе
(
)
x= Ac
+ Bxk⊤ x + Dw,
где Ac = A + bk⊤. Динамические системы такого вида и исследуются в на-
стоящей статье.
Итак, рассмотрим квадратичную динамическую систему вида
(
)
(3)
x = A + Bxh⊤
x+Dw,
где A, B ∈ Rn×n, D ∈ Rn×m, h ∈ Rn, с фазовым состоянием x ∈ Rn и внеш-
ним возмущением (2). Отметим, что никаких других ограничений на возму-
щение w(t) не накладывается; так, оно не предполагается ни случайным, ни
гармоническим.
Таким образом, рассматриваются L∞-ограниченные внешние возмущения.
Класс таких возмущений будем называть допустимым.
48
Будем полагать, что матрица A гурвицева (действительные части ее соб-
ственных значений отрицательны).
Система (3) при отсутствии внешних возмущений (D = 0) исследовалась
в [16, 17], где на основании техники линейных матричных неравенств и квад-
ратичных функций Ляпунова был предложен регулярный подход к построе-
нию так называемого эллипсоида стабилизируемости билинейной системы —
эллипсоида, обладающего следующим свойством: траектории системы, начи-
наясь внутри эллипсоида, асимптотически стремятся к нулю.
Цель данного раздела — построение эллипсоида стабилизируемости систе-
мы (3) при внешних возмущениях (2). В отличие от системы без возмущений
теперь поведение траекторий системы будет иным — траектории системы бу-
дут входить в множество достижимости системы (либо будут стремиться к
точке на его границе). Общим же является то, что траектория системы (3), ис-
ходящая из любой точки x0 внутри эллипсоида стабилизируемости, остается
в этом эллипсоиде — теперь уже при всех допустимых внешних возмущени-
ях (2).
Следующая теорема 1 устанавливает достаточное условие, при котором
эллипсоид
{
}
(4)
E = x∈Rn: x⊤P-1x≤1
,
P ≻ 0,
является эллипсоидом стабилизируемости для рассматриваемой системы.
Теорема 1. Эллипсоид (4) является эллипсоидом стабилизируемости
для системы (3), (2), если его матрица P удовлетворяет матричным нера-
венствам
⎛
⎞
AP + P A⊤ + αP + εBP B⊤ P h γD
⎜
⎟
(5)
⎝
h⊤P
-ε
0
⎠
≼ 0,
P ≻ 0,
γD⊤
0
-αI
при некоторых α и ε.
Доказательства этого и последующих утверждений помещены в Приложе-
ние.
Понятно, что не при любом размахе внешних возмущений γ эллипсоид
стабилизируемости для системы (3), (2) будет существовать. Ответ на вопрос
о максимально допустимом размахе γ дается следующим утверждением.
Теорема 2. Максимальный размах γ внешних возмущений (2) в систе-
ме (3), при котором эллипсоид стабилизируемости существует, дается ре-
шением задачи
max γ
при ограничениях
⎛
⎞
AP + P A⊤ + αP + εBP B⊤ P h γD
⎜
⎟
⎝
h⊤P
-ε
0
⎠ ≼ 0,
P ≻ 0,
γD⊤
0
-αI
49
где оптимизация проводится относительно матричной переменной P =
= P⊤ ∈ Rn×n, скалярной переменной γ и скалярных параметров α и ε.
Далее, для γ ≤ γ естественно стремиться максимизировать эллипсоид ста-
билизируемости по некоторому критерию; в частности, максимизируя объем
эллипсоида, получаем следствие теоремы 1.
Следствие 1. Пуст
P — решение задачи выпуклой оптимизации
max log det P
при ограничениях
⎛
⎞
AP + P A⊤ + αP + εBP B⊤ P h γD
⎜
⎟
⎝
h⊤P
-ε
0
⎠ ≼ 0,
P ≻ 0,
γD⊤
0
-αI
относительно матричной переменной P = P⊤ ∈ Rn×n и скалярных пара-
метров ε и α.
Тогда
{
}
E = x∈Rn: x
P-1x ≤ 1
является эллипсоидом стабилизируемости для системы (3), (2).
Обратим внимание, что и теорема 2, и следствие 1 предполагают осуществ-
ление процедуры двумерной оптимизации по α и по ε, поскольку каждый из
этих параметров нелинейно входит в соответствующие ограничения.
Замечание. В рассматриваемых далее примерах (для упрощения вы-
числений) будем предполагать, что матрица B — единичная; это позволит
избежать необходимости проведения оптимизации на двумерной сетке. Дей-
ствительно, в этом случае первое из матричных неравенств (5) примет вид
⎛
⎞
AP + P A⊤ + αP + εP P h γD
⎜
⎟
⎝
h⊤P
-ε
0
⎠ ≼ 0.
γD⊤
0
-αI
Вводя новую скалярную переменную
μ=α+ε
и тем самым исключая ε, получаем матричное неравенство
⎛
⎞
AP + P A⊤ + μP P h γD
⎜
⎟
⎝
h⊤P
α-μ
0
⎠ ≼ 0,
γD⊤
0
-αI
линейное относительно матричной переменной P = P⊤ ∈ Rn×n и скалярной
переменной α с одним скалярным параметром μ.
50
4. Область стабилизируемости
В разделе 3 был найден максимальный (по критерию объема) эллипсоид
стабилизируемости E для системы (3), (2). Понятно, что существуют и иные
эллипсоиды стабилизируемости, в том числе максимальные по тому или ино-
му критерию. Рассмотрим множество, образованное объединением эллипсои-
дов стабилизируемости; будем называть его областью стабилизируемости
системы (3), (2). Очевидно, что по построению область стабилизируемости
будет обладать тем же свойством, что и каждый образующий ее эллипсо-
ид стабилизируемости — траектория системы, исходящая из любой точки x0
внутри этой области, остается в ней при всех допустимых внешних возмуще-
ниях (2).
Нетрудно видеть, что в рамках техники линейных матричных неравенств
по произвольному вектору c можно эффективно построить точку, лежащую
на границе области стабилизируемости системы по направлению c; более того,
нахождение соответствующей точки сводится к решению задачи полуопреде-
ленного программирования.
Действительно, выберем направление, определяемое вектором c единич-
ной длины, и будем требовать принадлежности точки γc эллипсоиду стаби-
лизируемости, максимизируя параметр γ. Заметив, что условие принадлеж-
ности точки γc эллипсоиду стабилизируемости с матрицей P представимо по
лемме Шура в линейном относительно P и γ виде
)
(1
γc⊤
≽ 0,
γc P
приходим к следующему результату, устанавливающему простую характе-
ризацию области стабилизируемости квадратичной динамической системы,
подверженной воздействию внешних возмущений.
Теорема 3. Пусть c — заданный вектор и пусть γ — решение задачи
полуопределенного программирования
max γ
при ограничениях
⎛
⎞
AP + P A⊤ + αP + εBP B⊤ P h γD
⎜
⎟
⎝
h⊤P
-ε
0
⎠ ≼ 0,
γD⊤
0
-αI
(
)
1
γc
≽ 0,
γc⊤ P
где оптимизация проводится по матричной переменной P = P⊤ ∈ Rn×n,
скалярной переменной γ и скалярным параметрам α и ε.
Тогда точка γc лежит на границе области стабилизируемости систе-
мы (3), (2) по направлению c.
51
5. Системы в дискретном времени
Рассмотрим билинейную систему управления в дискретном времени
(6)
xℓ+1 = Axℓ + Bxℓuℓ + buℓ + Dwℓ,
где A, B ∈ Rn×n, D ∈ Rn×m, b ∈ Rn, с начальным состоянием x0, фазовым
состоянием xℓ ∈ Rn, скалярным управлением uℓ ∈ R и внешним возмущением
wℓ ∈ Rm, удовлетворяющим ограничению
(7)
∥wℓ
∥ ≤ γ при всех ℓ = 0,1,2,...
Замкнув билинейную систему (6), (7) статической линейной обратной
связью
uℓ = k⊤xℓ, k ∈ Rn,
приходим к дискретной квадратичной динамической системе
(
)
xℓ+1 = Ac + Bxℓk⊤ xℓ + Dwℓ,
где Ac = A + bk⊤.
Итак, рассмотрим квадратичную динамическую систему вида
(
)
(8)
xℓ+1 = A + Bxℓh⊤ xℓ + Dwℓ,
где A, B ∈ Rn×n, D ∈ Rn×m, h ∈ Rn, с фазовым состоянием x ∈ Rn и внешним
возмущением (7). Как и в непрерывном случае, никаких других ограниче-
ний на возмущение wℓ не накладывается; таким образом, рассматриваются
l∞-ограниченные внешние возмущения. Класс таких возмущений будем на-
зывать допустимым.
Будем полагать, что матрица A — шуровская (ее собственные значения
лежат внутри единичного круга).
Цель данного раздела — построение эллипсоида стабилизируемости систе-
мы (8) при внешних возмущениях (7). Следующая теорема 4, являющаяся
дискретным аналогом теоремы 1, устанавливает достаточное условие, при
котором эллипсоид
{
}
(9)
E = x∈Rn: x⊤P-1x≤1
,
P ≻ 0,
является эллипсоидом стабилизируемости для рассматриваемой системы.
Теорема 4. Эллипсоид (9) является эллипсоидом стабилизируемости
для системы (8), (7), если его матрица P удовлетворяет матричным нера-
венствам
⎛
⎞
-αP
0
0
0
Ph PA⊤
⎜
⎟
0
-P
0
BP
0
0
⎜
⎟
⎜
⎟
⎜
0
0
-(1 - α)I
0
0
γD⊤⎟
⎜
⎟
≼ 0,
P ≻ 0,
⎜
⎟
⎜
0
PB⊤
0
-εP
0
PB⊤⎟
⎜
⎟
⎝h⊤P
0
0
0
-1εI
0
⎠
AP
0
γD
BP
0
-P
при некоторых α и ε.
52
Как и ранее, эллипсоид стабилизируемости для системы (8), (7) существу-
ет не при любом размахе внешних возмущений γ. Ответ на вопрос о мак-
симально допустимом размахе γ дается следующим дискретным аналогом
теоремы 2.
Теорема 5. Максимальный размах γ внешних возмущений (7) в систе-
ме (8), при котором эллипсоид стабилизируемости существует, дается ре-
шением задачи
max γ
при ограничениях
⎛
⎞
-αP
0
0
0
Ph PA⊤
⎜
⎟
⎜
0
-P
0
BP
0
0
⎟
⎜
⎟
⎜
0
0
-(1 - α)I
0
0
γD⊤⎟
⎜
⎟
≼ 0,
P ≻ 0,
⎜
⎟
⎜
0
PB⊤
0
-εP
0
PB⊤⎟
⎜
⎟
⎝h⊤P
0
0
0
-1εI
0
⎠
AP
0
γD
BP
0
-P
где оптимизация проводится относительно матричной переменной P =
= P⊤ ∈ Rn×n, скалярной переменной γ и скалярных параметров α и ε.
Максимизируя (для допустимого γ ≤ γ) эллипсоид стабилизируемости по
критерию объема, получаем следующий результат.
Следствие 2. Пуст
P — решение задачи выпуклой оптимизации
max log det P
при ограничениях
⎛
⎞
-αP
0
0
0
Ph PA⊤
⎜
⎟
⎜
0
-P
0
BP
0
0
⎟
⎜
⎟
⎜
0
0
-(1 - α)I
0
0
γD⊤⎟
⎜
⎟
≼ 0,
P ≻ 0,
⎜
⎟
⎜
0
PB⊤
0
-εP
0
PB⊤⎟
⎜
⎟
⎝h⊤P
0
0
0
-1εI
0
⎠
AP
0
γD
BP
0
-P
относительно матричной переменной P = P⊤ ∈ Rn×n и скалярных пара-
метров ε и α.
Тогда
{
}
E = x∈Rn: x
P-1x ≤ 1
является эллипсоидом стабилизируемости для системы (8), (7).
Наконец, следующий дискретный аналог теоремы 3 устанавливает про-
стую характеризацию области стабилизируемости рассматриваемой системы.
53
Теорема 6. Пусть c — заданный вектор и пусть γ — решение задачи
полуопределенного программирования
max γ
при ограничениях
⎛
⎞
-αP
0
0
0
Ph PA⊤
⎜
⎟
⎜
0
-P
0
BP
0
0
⎟
⎜
⎟
⎜
0
0
-(1 - α)I
0
0
γD⊤⎟
⎜
⎟
≼ 0,
⎜
⎟
⎜
0
PB⊤
0
-εP
0
PB⊤⎟
⎜
⎟
⎝h⊤P
0
0
0
-1εI
0
⎠
AP
0
γD
BP
0
-P
(
)
1
γc
≽ 0,
γc⊤ P
где оптимизация проводится по матричной переменной P = P⊤ ∈ Rn×n,
скалярной переменной γ и скалярным параметрам α и ε.
Тогда точка γc лежит на границе области стабилизируемости систе-
мы (8), (7) по направлению c.
6. Примеры
Ограничимся рассмотрением демонстрационных примеров; продолжение
статьи, посвященное вопросам синтеза управления, будет сопровождаться
примерами, проистекающими из реальных задач.
Пример 1. Рассмотрим систему вида (3) с матрицами
(
)
(
)
0
1
(1)
1
(10)
A=
,
B=I,
D=
,
h=
−1 -3
0
-1
Воспользовавшись теоремой 2 (с учетом замечания), находим максимально
допустимый размах внешних возмущений:
γ = 0,0232.
Теорема 1 для γ = 0,95γ дает матрицу
(
)
0,0943
-0,2271
P
0,95 =
-0,2271
0,7150
эллипса стабилизируемости, для γ = 0,75γ матрица эллипса стабилизируе-
мости имеет вид
(
)
0,1236
-0,2928
P
0,75 =
,
-0,2928
0,9447
54
1,5
1
0,5
0
-0,5
-1
-1,5
-0,4
-0,3
-0,2
-0,1
0
0,1
0,2
0,3
0,4
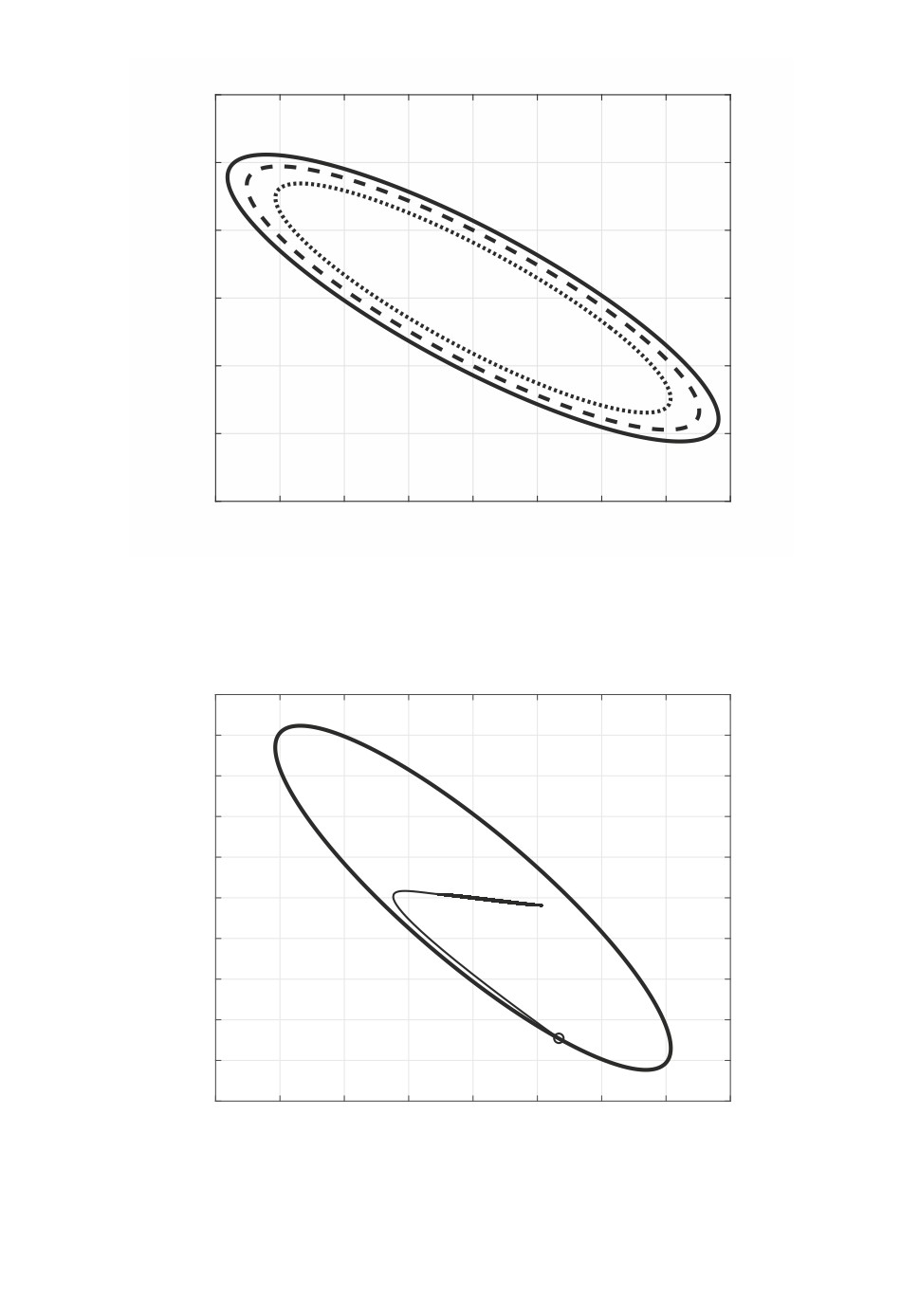
Рис. 1. Эллипсы стабилизируемости для разных уровней внешних возмущений
из примера 1: сплошная линия — γ = 0,5γ; штриховая линия — γ = 0,75γ;
точечная линия — γ = 0,95γ.
1
0,8
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
-0,8
-1
-0,4
-0,3
-0,2
-0,1
0
0,1
0,2
0,3
0,4
Рис. 2. Эллипс стабилизируемости и траектория системы из примера 1.
55
1,5
1
0,5
0
-0,5
-1
-1,5
-0,4
-0,3
-0,2
-0,1
0
0,1
0,2
0,3
0,4
Рис. 3. Область стабилизируемости и эллипс стабилизируемости из примера 2.
а для γ = 0,5γ имеем
(
)
0,1456
-0,3402
P0,5 =
−0,3402
1,1201
На рис. 1 показаны найденные эллипсы стабилизируемости для системы (10).
На рис. 2 показана траектория системы (10) при некотором допусти-
мом внешнем возмущении и соответствующий эллипс стабилизируемости при
γ = 0,95γ.
Эти и последующие вычисления проводились в среде MATLAB с исполь-
зованием программного пакета cvx [24].
Пример 2. Вновь обратившись к системе из примера 1 и воспользо-
вавшись теоремой 3, находим область стабилизируемости системы (для γ =
= 0,75γ).
На рис. 3 сплошной линией показана найденная область стабилизируе-
мости; для сравнения точечной линией показан найденный выше эллипс ста-
билизируемости, максимальный по критерию объема.
7. Заключение
В статье введены понятия эллипсоида стабилизируемости и области ста-
билизируемости квадратичной динамической системы с внешними возмуще-
ниями и предложен легко реализуемый с вычислительной точки зрения под-
ход к их конструктивному построению. Полученные результаты обобщены на
56
системы в дискретном времени. Дальнейшим естественным развитием полу-
ченных результатов будет служить их распространение на решение задачи
синтеза управления билинейной системой, подверженной воздействию про-
извольных ограниченных внешних возмущений.
Более того, полученные результаты могут быть распространены на си-
стемы с многомерным управлением, а также на разнообразные робастные
постановки задачи; в частности — со структурированной матричной неопре-
деленностью в матрицах системы.
Автор признателен Б.Т. Поляку за интерес к работе, плодотворные обсуж-
дения и полезные предложения.
ПРИЛОЖЕНИЕ
Лемма П.1. Пусть A ∈ Rn×n, D ∈ Rn×m — заданные матрицы, P ∈
∈ Rn×n, L(·) — матричнозначная функция матричного аргумента, α,β ∈ R.
Тогда множества
{
}
1
Ω1 = (P,α): L(P) + αP +
DD⊤ ≼ 0, α > 0
α
и
{
}
1
Ω2 = (P,α): L(P) + αP +
DD⊤ ≼ 0
при некотором
0<β≤α
β
совпадают.
Доказательство леммы П.1. Нетрудно видеть, что Ω1 ⊂ Ω2; пока-
жем обратное включение.
Пусть (P, α) ∈ Ω2, тогда существует 0 < β ≤ α такое, что
1
L(P ) + αP +
DD⊤ ≼ 0.
β
При этом
)
1
1
(1
1
L(P ) + αP +
DD⊤ = L(P) + αP +
DD⊤ +
-
DD⊤ ≼ 0,
α
β
α
β
(
)*
+
≤0
т.е. (P, α) ∈ Ω1. Лемма П.1 доказана.
Доказательство теоремы 1. Введем в рассмотрение квадратичную
форму
V (x) = x⊤Qx, Q ≻ 0.
Для того чтобы траектории x(t) системы (3) не выходили за границу эллип-
соида
E = {x ∈ Rn: V (x) ≤ 1},
57
достаточно потребовать выполнения следующего условия:
V (x) ≤ 0 при V (x, w) ≥ 1 и всех допустимых ∥w∥ ≤ γ.
C учетом того, что производная функции V (x) в силу системы (3) имеет
вид
V (x) = x⊤Qx + x⊤Q x =
(
)⊤
(
)
= Ax + Bxh⊤x + Dw
Qx + x⊤Q Ax + Bxh⊤x + Dw
=
(
)
= x⊤ A⊤Q + QA + QBxh⊤ + hx⊤B⊤Q x + w⊤D⊤Qx + x⊤QDw,
это условие запишем как
(
)
x⊤ A⊤Q + QA + QBxh⊤ + hx⊤B⊤Q x + w⊤D⊤Qx + x⊤QDw ≤ 0
при x⊤Qx ≥ 1 и w⊤w ≤ γ2
или, введя составной вектор
)
(x
s=
∈Rn+m,
w
в виде
(
)
A⊤Q + QA + QBxh⊤ + hx⊤B⊤Q QD
s⊤
s≤0
D⊤Q
0
)
)
(Q 0
(0
0
при s⊤
s≥1
и s⊤
s ≤ 1.
0
0
0
γ-2I
Воспользовавшись S-процедурой в ее достаточной части, приходим к усло-
вию
(
)
)
A⊤Q + QA + QBxh⊤ + hx⊤B⊤Q QD
(Q 0)
(0
0
+α
-β
≼0
D⊤Q
0
0
0
0
γ-2I
при некоторых α ≥ β ≥ 0, т.е.
(
)
A⊤Q + QA + αQ + QBxh⊤ + hx⊤B⊤Q QD
≼ 0.
D⊤Q
-βγ-2I
Воспользовавшись леммой Шура и домножив получившееся соотношение
слева и справа на матрицу P = Q-1 ≻ 0, получим
1
(Π.1)
AP + P A⊤ + αP + Bxh⊤P + P hx⊤B⊤ +
γ2DD⊤
≼ 0.
β
58
Потребуем, чтобы матричное неравенство (Π.1) выполнялось при всех x
из эллипсоида
{
}
E = {x ∈ Rn: V (x) ≤ 1} = x ∈ Rn: x⊤P-1x ≤ 1
Воспользовавшись леммой 2, приходим к эквивалентному матричному
неравенству
1
1
AP + P A⊤ + αP +
γ2DD⊤ + εBPB⊤ +
P hh⊤P ≼ 0,
β
ε
в котором фигурируют два числовых параметра 0 ≤ β ≤ α. Однако от одного
них можно избавиться с помощью леммы П.1, положив β = α (см. подроб-
нее [25, 26]).
Дважды воспользовавшись леммой Шура, окончательно получаем соот-
ношение (5). Теорема 1 доказана.
Доказательство теоремы 4. Введем в рассмотрение квадратичную
форму
V (x) = x⊤Qx, Q ≻ 0.
Для того чтобы траектории x(t) системы (8) не выходили за границу эллип-
соида
E = {x ∈ Rn: V (x) ≤ 1},
достаточно потребовать выполнения следующего условия:
V (xℓ+1) ≤ 1 при V (xℓ) ≤ 1 и всех допустимых ∥wℓ∥ ≤ γ.
C учетом того, что
V (xℓ+1) = x⊤ℓ+1Qxℓ+1 =
(
)⊤ (
)
= Axℓ + Bxℓh⊤xℓ + Dwℓ
Q Axℓ + Bxℓh⊤xℓ + Dwℓ
=
= x⊤ℓ A⊤QAxℓ + x⊤ℓ hx⊤ℓ B⊤QAxℓ + w⊤ℓ D⊤QAxℓ + x⊤ℓ A⊤QBxℓh⊤xℓ +
+ x⊤ℓ hx⊤ℓ B⊤QBxℓh⊤xℓ + w⊤ℓ D⊤QBxℓh⊤xℓ + x⊤ℓ A⊤QDwℓ +
+ x⊤ℓ hx⊤ℓ B⊤QDwℓ + w⊤ℓ D⊤QDwℓ =
(
)
= x⊤ℓ A⊤QA + A⊤QBxℓh⊤ + hx⊤ℓ B⊤QA + hx⊤ℓ B⊤QBxℓh⊤ xℓ +
(
)
+ w⊤ℓ D⊤QA + D⊤QBxℓh⊤ xℓ +
(
)
+ x⊤ℓ A⊤QD + hx⊤ℓ B⊤QD wℓ + w⊤ℓ D⊤QDwℓ,
это условие запишем как
(
)
x⊤ℓ A⊤QA + A⊤QBxℓh⊤ + hx⊤ℓB⊤QA + hx⊤ℓB⊤QBxℓh⊤ xℓ +
(
)
(
)
+ w⊤ℓ D⊤QA + D⊤QBxℓh⊤ xℓ + x⊤
A⊤QD + hx⊤ℓB⊤QD wℓ +
ℓ
+ w⊤ℓ D⊤QDwℓ ≤ 1 при x⊤ℓ Qxℓ ≤ 1 и w⊤ℓ wℓ ≤ γ2
59
или, введя составной вектор
)
(xℓ
sℓ =
∈Rn+m,
wℓ
в виде
)
(A⊤QA + A⊤QBxℓh⊤ + hx⊤ℓB⊤QA + hx⊤ℓB⊤QBxℓh⊤ A⊤QD + hx⊤ℓB⊤QD
s⊤
s≤1
D⊤QA+D⊤QBxℓh⊤
D⊤QD
)
)
(Q 0
(0
0
при s⊤
s≤1
и s⊤
s ≤ 1.
0
0
0
γ-2I
Воспользовавшись S-процедурой в ее достаточной части, приходим к усло-
вию
(
)
A⊤QA+ A⊤QBxℓh⊤ + hx⊤ℓB⊤QA+ hx⊤ℓB⊤QBxℓh⊤ A⊤QD + hx⊤ℓB⊤QD
-
D⊤QA+ D⊤QBxℓh⊤
D⊤QD
(
)
)
Q 0
(0
0
-α
-β
≼0
0
0
0
γ-2I
или
(
)
A⊤QA- αQ +A⊤QBxℓh⊤+ hx⊤ℓB⊤QA+hx⊤ℓB⊤QBxℓh⊤ A⊤QD +hx⊤ℓB⊤QD
≼0
D⊤QA + D⊤QBxℓh⊤
D⊤QD - βγ-2I
при некоторых α, β ≥ 0 таких, что α + β ≤ 0.
Полученное условие представим в виде
⎞
⎛A⊤QA - αQ + A⊤QBxℓh⊤ + hx⊤ℓB⊤QA hx⊤ℓB⊤Q A⊤QD + hx⊤ℓB⊤QD
⎜
⎟
⎝
QBxℓh⊤
-Q
0
⎠≼0
D⊤QA + D⊤QBxℓh⊤
0
D⊤QD - βγ-2I
или
⎛
⎞
A⊤QA - αQ
0
A⊤QD
⎜
⎟
⎝
0
-Q
0
⎠+
D⊤QA
0
D⊤QD - βγ-2I
(Π.2)
⎛
⎞
⎛
⎞
A⊤QB
h
(
)
(
)
⎜
⎟
⎜
⎟
+⎝ QB
⎠xℓ
h⊤
0
0
+
⎝0⎠xℓ
B⊤QA B⊤Q B⊤QD
≼ 0.
D⊤QB
0
Потребуем, чтобы матричное неравенство (Π.2) выполнялось при всех xℓ
из эллипсоида
{
}
E = {xℓ ∈ Rn: V (xℓ) ≤ 1} = xℓ ∈ Rn: x⊤ℓ Qxℓ ≤ 1
60
Воспользовавшись леммой 2 и леммой Шура [27], приходим к эквивалент-
ному матричному неравенству
⎛
⎞
A⊤QA - αQ
0
A⊤QD
A⊤QB h
⎜
⎟
⎜
0
-Q
0
QB
0
⎟
⎜
⎟
⎜
⎟
⎜
D⊤QA
0
D⊤QD - βγ-2I D⊤QB
0
⎟
⎜
⎟
≼
0,
⎜
⎟
⎜
B⊤QA B⊤Q
B⊤QD
-εQ
0
⎟
⎜
⎟
⎝
⎠
1
h⊤
0
0
0
-
I
ε
представимому в виде
⎛
⎞
⎛
⎞
-αQ
0
0
0
h
A⊤
⎜
⎟
⎜
⎟
⎜
0
-Q
0
QB
0
⎟
⎜
0
⎟
⎜
⎟
⎜
⎟
)
⎜
0
0
-βγ-2I
0
0
⎟
+
⎜D⊤⎟
(A 0 D B
0
≼ 0,
⎜
⎟
⎜
⎟Q
⎜
⎟
⎜
⎟
⎝ 0
B⊤Q
0
-εQ
0
⎠
⎝B⊤⎠
h⊤
0
0
0
-1εI
0
откуда по лемме Шура имеем, что
⎛
⎞
-αQ
0
0
0
h A⊤
⎜
⎟
⎜
0
-Q
0
QB
0
0
⎟
⎜
⎟
⎜
0
0
-βγ-2I
0
0
D⊤
⎟
⎜
⎟
≼ 0.
⎜
⎟
⎜
0
B⊤Q
0
-εQ
0
B⊤
⎟
⎜
⎟
⎝ h⊤
0
0
0
-1εI
0
⎠
A
0
D
B
0
-Q-1
Обозначив P = Q-1 и умножив полученное матричное неравенство слева
и справа на матрицу
⎞
⎛P
0
0
0
0
0
⎜
⎟
⎜0
P
0
0
0
0⎟
⎜
⎟
⎜0
0
γI
0
0
0⎟
⎜
⎟
,
⎜
⎟
0
0
0
P
0
0
⎜
⎟
⎜
⎟
⎝0
0
0
0
I
0⎠
0
0
0
0
0
I
приходим к соотношению
⎛
⎞
-αP
0
0
0
Ph PA⊤
⎜
⎟
0
-P
0
BP
0
0
⎜
⎟
⎜
⎟
⎜
0
0
-βI
0
0
γD⊤⎟
⎜
⎟
≼ 0.
⎜
⎟
⎜
0
PB⊤
0
-εP
0
PB⊤⎟
⎜
⎟
⎝h⊤P
0
0
0
-1εI
0
⎠
AP
0
γD BP
0
-P
61
Остается заметить, что аналогично непрерывному случаю (см. также [26])
можем положить β = βmax = 1 - α. Теорема 4 доказана.
СПИСОК ЛИТЕРАТУРЫ
1.
Mohler R.R. Bilinear Control Processes. N.Y.: Academic Press, 1973.
2.
Ryan E., Buckingham N. On Asymptotically Stabilizing Feedback Control of Bilinear
Systems // IEEE Trans. Automatic Control. 1983. V. 28. No. 8. P. 863-864.
3.
Chen L.K., Yang X., Mohler R.R. Stability Analysis of Bilinear Systems // IEEE
Trans. Automatic Control. 1991. V. 36. No. 11. P. 1310-1315.
4.
Čelikovský S. On the Global Linearization of Bilinear Systems // Syst. Control Lett.
1990. V. 15. No. 5. P. 433-439.
5.
Čelikovský S. On the Stabilization of the Homogeneous Bilinear Systems // Syst.
Control Lett. 1993. V. 21. No. 6. P. 503-510.
6.
Tibken B., Hofer E.P., Sigmund A. The Ellipsoid Method for Systematic Bilinear
Observer Design // Proc. 13th IFAC World Congress. San Francisco, USA, June
30-July 5, 1996. P. 377-382.
7.
Коровин С.К., Фомичев В.В. Асимптотические наблюдатели для некоторых
классов билинейных систем с линейным входом // ДАН. Теория управления.
2004. Т. 398. № 1. С. 38-43.
8.
Belozyorov V.Y. Design of Linear Feedback for Bilinear Control Systems // Int. J.
Appl. Math. Comput. Sci. 2002. V. 11. No. 2. P. 493-511.
9.
Belozyorov V.Y. On Stability Cones for Quadratic Systems of Differential
Equations // J. Dyn. Control Syst. 2005. V. 11. No. 3. P. 329-351.
10.
Andrieu V., Tarbouriech S. Global Asymptotic Stabilization for a Class of Bilinear
Systems by Hybrid Output Feedback // IEEE Trans. Automatic Control. 2013. V. 58.
No. 6. P. 1602-1608.
11.
Coutinho D., de Souza C.E. Nonlinear State Feedback Design with a Guaranteed
Stability Domain for Locally Stabilizable Unstable Quadratic Systems // IEEE
Trans. Circuits Syst. I. Regular Papers. 2012. V. 59. No. 2. P. 360-370.
12.
Omran H., Hetel L., Richard J.-P., et al. Stability Analysis of Bilinear Systems under
Aperiodic Sampled-Data Control // Automatica. 2014. V. 50. No. 4. P. 1288-1295.
13.
Kung C.-C., Chen T.-H., Chen W.-C., et al. Quasi-Sliding Mode Control for a
Class of Multivariable Discrete Time Bilinear Systems // Proc. IEEE Int. Conf. on
Systems, Man, and Cybernetics (SMC). Seoul, Korea. October 2012. P. 1878-1883.
14.
Athanasopoulos N., Bitsoris G. Constrained Stabilization of Bilinear Discrete-Time
Systems Using Polyhedral Lyapunov Functions // Proc. 17th IFAC World Congress.
Seoul, Korea, July 6-11, 2008. P. 2502-2507.
15.
Athanasopoulos N., Bitsoris G. Stability Analysis and Control of Bilinear Discrete-
Time Systems: A Dual Approach // Proc. 18th IFAC World Congress. Milano, Italy,
August 28-September 2, 2011. P. 6443-6448.
16.
Khlebnikov M.V. Quadratic Stabilization of Bilinear Control Systems // 14th
European Control Conf. (ECC’15). Linz, Austria, July 15-17, 2015. IEEE Catalog
Number(USB): CFP1590U-USB. P. 160-164.
17.
Хлебников М.В. Квадратичная стабилизация билинейной системы управле-
ния // АиТ. 2016. № 6. С. 47-60.
Khlebnikov M.V. Quadratic Stabilization of Bilinear Control Systems // Autom.
Remote Control. 2016. V. 77. No. 6. P. 980-991.
62
18. Tarbouriech S., Queinnec I., Calliero T.R., et al. Control Design for Bilinear Systems
with a Guaranteed Region of Stability: An LMI-Based Approach // Proc. 17th
Mediterranean Conf. on Control & Automation (MED’09). Thessaloniki, Greece.
June 2009.
19. Amato F., Cosentino C., Merola A. Stabilization of Bilinear Systems via Linear State
Feedback Control // IEEE Trans. Circuits Syst. II. Express Briefs. 2009. V. 56. No. 1.
P. 76-80.
20. Булгаков Б.В. О накоплении возмущений в линейных колебательных системах
с постоянными параметрами // ДАН СССР. 1946. Т. 5. Вып. 5. С. 339-342.
21. Гноенский Л.С. Задача Булгакова о накоплении возмущений / Задача Булгакова
о максимальном отклонении и ее применение. Под ред. В.В. Александрова. М.:
Изд-во МГУ им. М.В. Ломоносова, 1993.
22. Жермоленко В.Н. Максимальное отклонение колебательной системы второго
порядка с внешним и параметрическим возмущениями // Изв. РАН. ТиСУ. 2007.
№ 3. С. 75-80.
23. Petersen I.R. A Stabilization Algorithm for a Class of Uncertain Linear Systems //
Syst. Control Lett. 1987. V. 8. P. 351-357.
24. Grant M., Boyd S. CVX: Matlab software for disciplined convex programming,
25. Boyd S., El Ghaoui L., Feron E., et al. Linear Matrix Inequalities in System and
Control Theory. Philadelphia: SIAM, 1994.
26. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-
ми при внешних возмущениях: Техника линейных матричных неравенств. М.:
ЛЕНАНД, 2014.
27. Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
Статья представлена к публикации членом редколлегии Б.Т. Поляком.
Поступила в редакцию 07.08.2018
После доработки 27.09.2018
Принята к публикации 08.11.2018
63