Автоматика и телемеханика, № 3, 2019

Нелинейные системы

(Институт динамики систем и теории управления

им. В.М. Матросова СО РАН, Иркутск),

М.В. КОЗЛОВ (kozlov.mvl@yandex.ru)

(Национальный исследовательский Мордовский государственный

университет им. Н.П. Огарева, Саранск)

ОБ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ ОДНОРОДНЫХ

СИНГУЛЯРНЫХ СИСТЕМ С ПЕРЕКЛЮЧЕНИЯМИ¹

Рассматривается задача об устойчивости сингулярных переключаемых

систем с однородными функциями в правых частях. На основе деком-

позиции на изолированные подсистемы быстрых и медленных движений

получены условия устойчивости полной системы при произвольном режи-

ме переключений. Предложен способ выбора стабилизирующей обратной

связи в случае, когда измерению доступны только быстрые переменные.

Ключевые слова: устойчивость, сингулярные системы, системы с пере-

ключениями, однородные функции, общие функции Ляпунова.

DOI: 10.1134/S0005231019030036

1. Введение

Изучение динамики сингулярных систем, моделируемых дифференциаль-

ными уравнениями с малым параметром при старшей производной, было на-

чато А.Н. Тихоновым [1]. Эти системы играют важную роль в современной

теории управления и интенсивно изучаются (см., например, обзор [2], где ци-

тируется более 500 работ по этой тематике). Начиная с основополагающей

статьи [3] для анализа устойчивости сингулярных систем разрабатывается

подход, основанный на декомпозиции исходной системы на две изолирован-

ные подсистемы для “быстрых” и “медленных” переменных, каждая из ко-

торых существенно меньшей размерности, чем исходная, и изучении их в

отдельности. Аналогичный подход применяется и для решения задачи стаби-

лизации, т.е. синтеза такого закона управления, который гарантирует нуж-

ные свойства устойчивости замкнутой системе [4]. При этом управляющие

обратные связи могут формироваться не по всем координатам, а только по

некоторым, например “быстрым” переменным [5].

В теории управления активно изучаются гибридные системы, описывае-

мые уравнениями с переключениями правых частей в ходе процесса управле-

ния [6-8]. Наличие переключений существенно затрудняет решение задач ана-

лиза динамики и синтеза стабилизирующих управлений, поэтому актуальной

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 17-31-50034).

задачей является развитие теории управления для такого рода гибридных

систем [9]. Основным, а часто и единственным строгим методом исследова-

ния динамики гибридных систем обычно выступает метод функций Ляпунова

(см., например, [10-14]). Как следует из обзоров [6-8], наиболее изучены во-

просы устойчивости, стабилизации, построения общих квадратичных функ-

ций Ляпунова для линейных систем. Нелинейные системы с переключениями

в этом плане значительно менее изучены. Как отмечается в [9, с. 206], необхо-

димо прежде всего исследовать отдельные специальные классы нелинейных

систем с переключениями, такие как однородные системы или системы с об-

ратными связями. Устойчивость для класса нелинейных сингулярных систем

с переключениями ранее практически не изучалась в литературе, например,

в подробном обзоре [2] в разделе об устойчивости нелинейные системы с пе-

реключениями не упоминаются.

Основная цель данной статьи состоит в получении условий асимптотиче-

ской устойчивости сингулярной системы с переключениями и однородными

функциями в правых частях в терминах аналогичных свойств отдельных изо-

лированных подсистем быстрых и медленных движений. Переход к изолиро-

ванным подсистемам существенно снижает размерность задачи и упрощает

построение общей функции Ляпунова для конечного семейства дифферен-

циальных уравнений. Рассмотрены два случая: один, когда в правых частях

присутствуют однородные первого порядка функции, удовлетворяющие ло-

кальному условию Липшица, и второй, когда присутствуют однородные поли-

номы нечетной степени от медленных переменных. Доступными измерению

считаются только быстрые переменные, и именно по ним строится стабили-

зирующая обратная связь. При этом матричные коэффициенты выбираются

в отдельности для двух изолированных подсистем. Тем самым исходная за-

дача декомпозируется на две аналогичных, только меньшей размерности, что

существенно упрощает решение.

2. Устойчивость сингулярных однородных первого порядка систем

с переключениями

Рассмотрим семейство сингулярно возмущенных систем

x = f(k)(x) + A(k)12 y,

(1)

εy = g(x) + A₂₂y.

Здесь k ∈ S = {1, . . . , N}, x ∈ Rnx , y ∈ Rny ; ε — малый положительный пара-

метр, A(k)12 и A₂₂ — матрицы соответствующих размерностей; g(x) и f(k)(x) —

однородные первого порядка функции, удовлетворяющие локальному усло-

вию Липшица. Семейство (1) порождает систему с переключениями

x = f(σ(t))(x) + A(σ(t))12y,

(2)

εy = g(x) + A₂₂y.

Здесь σ : [0, +∞) → S — кусочно-постоянная правосторонне непрерывная

функция, имеющая в каждом конечном отрезке лишь конечное число то-

чек разрыва. Функция σ(t) называется законом или режимом переключения

и показывает, какая система из семейства (1) функционирует в каждый мо-

мент времени. Задача состоит в том, чтобы получить условия устойчивости

нулевого решения системы (2) при произвольном режиме переключений.

Используя второе уравнение, выпишем линейную систему

(3)

y=A₂₂y

и выражение y через x

(4)

y = -A-122

g(x).

Подставляя (4) в первое уравнение (1), придем к семейству уравнений с од-

нородными правыми частями

(5)

x = f(k)(x) - A(k)12 A-122

g(x).

Теорема 1. Если линейная система (3) асимптотически устойчива, а

для семейства однородных систем (5) построена однородная порядка η > 1

общая функция Ляпунова V₁(x), удовлетворяющая оценкам

(6)

a₁||x||^η ≤ V₁(x) ≤ a₂||x||^η,

||grad_xV₁(x)|| ≤ a₃||x||η-1,



V₁

≤ -a₄||x||^η, a_i > 0,

(5)

то существует ε₀ > 0 такое, что при всех 0 < ε < ε₀ нулевое решение си-

стемы (2) асимптотически устойчиво при произвольных переключениях.



V₁

Здесь через

обозначена производная от функции V₁(x) в силу систе-

(5)

мы (5) и всюду далее аналогичным образом обозначаются производные в

силу соответствующих систем.

Доказательство приведено в Приложении. Данная теорема декомпозирует

и упрощает процесс исследования устойчивости гибридной системы (2). По-

строение общей функции Ляпунова проводится не для полного семейства (1),

а для семейства однородных систем (5) меньшей размерности. При этом мо-

гут использоваться частные функции Ляпунова для отдельных систем семей-

ства (5) и теорема 1 из [12].

Теперь рассмотрим вопрос об условиях неустойчивости.

Теорема 2. Если линейная система (3) асимптотически устойчива, а

для семейства однородных систем (5) построена однородная порядка η > 1

общая функция Ляпунова V₁(x), удовлетворяющая условиям:

1) V₁(0) = 0, сколь угодно близко к точке x = 0 есть точки x, в которых

V₁(x) < 0;

2) ||grad_xV₁(x)|| ≤ a₃||x||η-1;



V₁



≤ -a₄||x||^η, a_i > 0,

(5)

то существует ε₀ > 0 такое, что при всех 0 < ε < ε₀ нулевое решение си-

стемы (2) неустойчиво при произвольных переключениях.

Доказательство теоремы приведено в Приложении.

3. Стабилизация сингулярных переключаемых систем

с однородными полиномами

Рассмотрим задачу стабилизации до асимптотической устойчивости нуле-

вого решения сингулярной системы с однородными полиномами относительно

“медленных” переменных в правых частях при наличии переключений. До-

ступными измерению при этом считаются только “быстрые” переменные, и

именно по ним строится стабилизирующая обратная связь.

Пусть μ > 1 - некоторое нечетное число, x ∈ Rnx . Через x^{μ} = col(xμ1, xμ2,

...,xnx) ∈ Rnx будем обозначать вектор, составленный из μ степеней ком-

поне

(

)

= col xμ1, xμ-11x₂, . . . , xⁿ

∈ RNx, составленный из всех расположенных в

лексикографическом порядке мономов μ-й степени.

Рассмотрим семейство управляемых систем

x=A(i)11x[μ] +A(i)12y+U₁,

(7)

εy=A₂₁x[μ] +A₂₂y+U₂,

i ∈ S = {1,...,N}.

Здесь x ∈ Rnx , y ∈ Rny , A₂₁, A₂₂, A(i)11, A(i)12 — постоянные матрицы соответ-

ствующих размерностей, ε > 0 — малый положительный параметр. Управ-

ляющие воздействия U₁, U₂ строятся по принципу обратной связи по “быст-

рым” переменным y, так как только они предполагаются доступными непо-

средственному измерению.

Семейство (7) порождает гибридную систему с переключениями

x=A(σ(t))11x[μ] +A(σ(t))12y+U₁,

(8)

εy=A₂₁x[μ] +A₂₂y+U₂.

Здесь σ : [0, +∞) → S — кусочно-постоянная правосторонне непрерывная

функция с конечным числом точек разрыва в каждом конечном отрезке.

Управления выберем линейными

(9)

U₁ = K₁ y, U₂ = K₂

где K₁ и K₂ — соответственно постоянные прямоугольная n_x × n_y и квад-

ратная n_x × n_x матрицы. Задача стабилизации состоит в том, чтобы выбрать

матрицы K₁ и K₂ так, чтобы нулевое решение системы (8), замкнутой управ-

лением (9), было асимптотически устойчиво при любом режиме переключе-

ний σ(t). Положим

(10)

K₂ = -E - A₂₂.

Здесь E — единичная матрица. Подставляя (10) во второе уравнение (8) и

приравнивая правую часть к нулю, получим

(11)

y=A₂₁x[μ].

Заменяя теперь в правой части первого уравнения (8) y выражением (11),

приходим к системе с однородной правой частью

[

]

(12)

x= A(σ(t))11 +A(σ(t))A21 + K1A21 x[μ].

Теорема 3. Если матрица K₂ выбрана в соответствии с (10), а мат-

рица K₁ выбрана так, что для системы (12) существует общая функция

Ляпунова V₁(x), удовлетворяющая оценкам

a₁||x||^η ≤ V₁(x) ≤ a₂||x||^η,

||grad_xV₁(x)|| ≤ a₃||x||η-1,



V₁



≤ -a₄||x||η-1+μ, η > 1, a_i > 0, i = 1,4,

(12)

то существует ε₀ > 0 такое, что при всех 0 < ε < ε₀ нулевое решение си-

стемы (8), замкнутой указанными управлениями, асимптотически устой-

чиво при произвольном режиме переключений.

Доказательство теоремы приведено в Приложении. Укажем теперь два

случая, в которых можно выбрать стабилизирующую матрицу K₁ так, чтобы

были выполнены условия теоремы 3.

В случае, когда N_x = dim x[μ] = dim y = n_y и квадратная матрица A₂₁ яв-

ляется невырожденной, за счет выбора матрицы K₁ можно сделать матри-

цу K₁A₂₁ произвольной. Выбирая K₁ так, чтобы было K₁A₂₁x[μ] = -hEx^{μ},

где h > 0 — достаточно большое число, получаем, что все условия теоремы 3

будут выполняться для функции V₁(x) =¹² ||x||². В случае, когда в системе (8)

вместо x[μ] присутствует только x^{μ} и rank A₂₁ = n_x, матрица A^T21A₂₁ явля-

ется симметричной положительно определенной. Управление U₁ с матрицей

K₁ = -hA^T21, h > 0 стабилизирует систему (12), принимающую вид

[

]

x = A(σ(t))11 + A(σ(t))12A₂₁ - hA^T

A21 x{μ},

при достаточно больших h > 0. При этом в качестве функции V₁(x), удовле-

∑

творяющей условиям теоремы 3, можно взять V₁(x) =

xμ+1i.

μ+1

i=1

4. Примеры

Пример 1. Материальная точка малой массы εm движется в трехмерном

пространстве под действием кубической пружины с переменным коэффици-

ентом жесткости и сил сопротивления. Уравнения движения имеют вид

εm x_i + b x_i + a(x) x3i = 0, i = 1, 2, 3,

a₀

a(x) =

a₀ > 0, b > 0.

||x||²

x²¹ + x²² + x²

Не ограничивая общности, массу можем считать единичной m = 1. Позици-

онные силы F_i(x) = -a(x) x3i являются возвращающими (всегда направлены

к равновесию x = 0), но не являются потенциальными, так как ∂Fi(x)∂x

= ∂Fj(x),_∂x

поэтому третья теорема Томсона-Тэта-Четаева [15] не применима.

-1

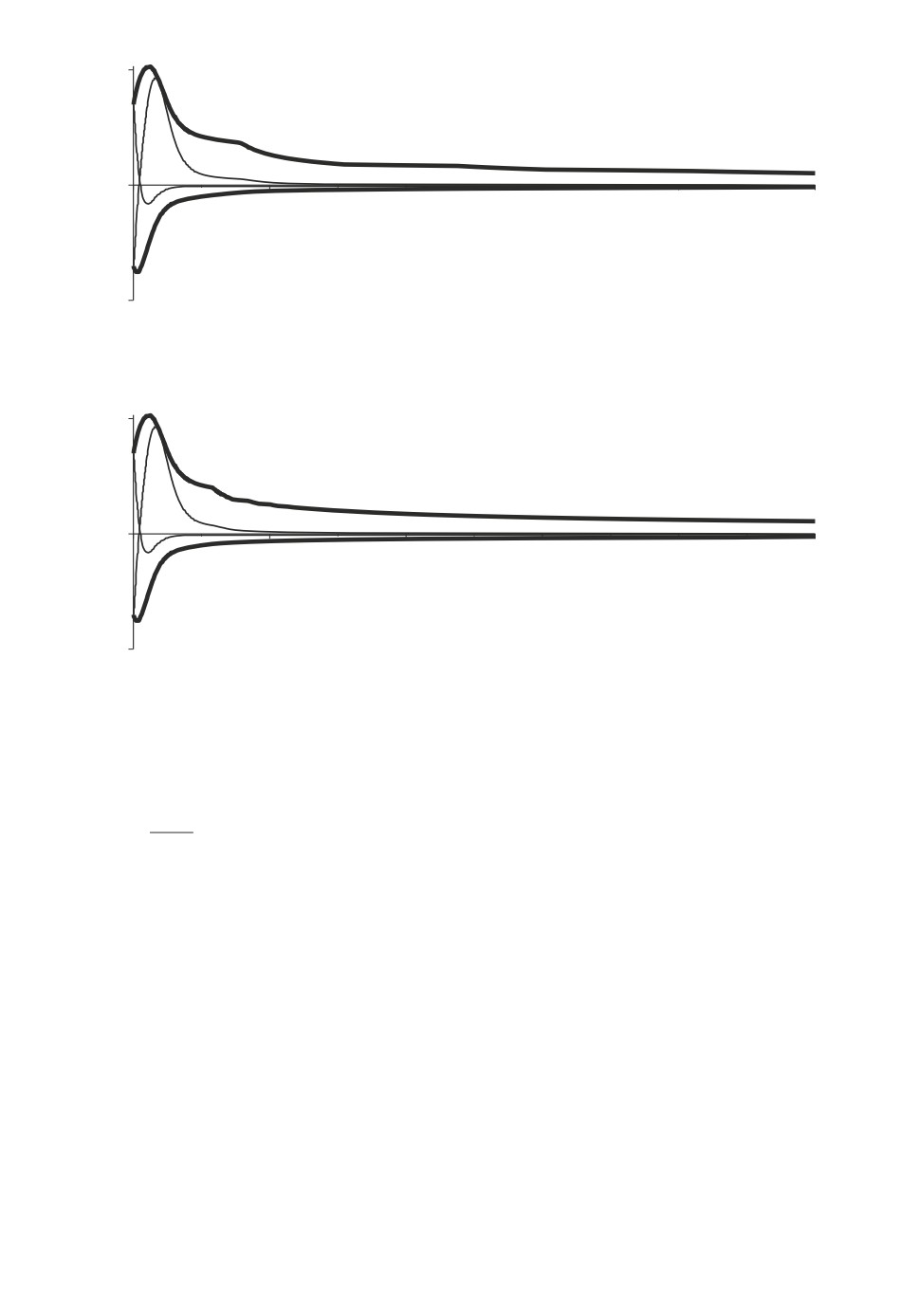
Рис. 1. Решение системы с переключениями из примера 2 при законе пере-

ключения σ(t) = 1 при sin 2t ≥ 0, и σ(t) = 2 при sin 2t < 0.

-1

Рис. 2. Решение системы с переключениями из примера 2 при законе пере-

ключения σ(t) = 1 при sin 2t³ ≥ 0, и σ(t) = 2 при sin 2t³ < 0.

В данном примере линейная система

(3) принимает вид

y_i = -by_i,

i = 1,2,3, а однородная система

(5) записывается следующим образом:

x_i = -a0

x3i, i = 1,2,3. Применяя теорему 1, устанавливаем, что положение

b||x||²

равновесия x = 0 асимптотически устойчиво при достаточно малых ε > 0.

Если же позиционные силы являются отталкивающими, т.е a₀ < 0, то из

теоремы 2 следует неустойчивость равновесия при достаточно малых ε > 0.

Пример 2. Рассмотрим сингулярную систему

x₁ = a(σ(t))1x³¹ + x³² + u₁,

x₂ = x³¹ + a(σ(t))2x³² + u₂,

εy₁ =x³¹ -y₁, εy₂ =x³² -y₂.

Здесь σ : [0, +∞) → S, a(j)i > R, i = 1, 2, j ∈ S. Из теоремы 3 следует, что при

управлении u₁ = k₁y₁, u₂ = k₂y₂ при всех достаточно малых ε > 0 нулевое ре-

шение замкнутой системы будет асимптотически устойчивым при произволь-

ных переключениях, если только коэффициенты обратной связи выбраны в

соответствии с условиями k_i < -1 - max

a(j)i, i = 1,2.

j∈S

Приведем для иллюстрации графики решений системы с переключениями

при следующих значениях параметров: ε = 0,1, S = {1, 2}, a⁽¹⁾¹ = 3, a⁽²⁾¹ = -3,

a⁽¹⁾² = -1, a⁽²⁾² = 3, коэффициентах, стабилизирующих обратных связей по

быстрым переменным k₁ = k₂ = -4,1, и начальных условиях x₁(0) = 0,25,

x₂(0) = -0,25, y₁(0) = -0,25, y₂(0) = 0,25 для двух различных законов пе-

реключения σ(t). Изменение медленных переменных x₁(t), x₂(t) показано

жирной линией, изменение быстрых переменных y₁(t), y₂(t) показано тонкой

линией. Каждая из четырех компонент вектора решения однозначно иденти-

фицируется по начальному условию. Точки излома на кривых соответствуют

моментам переключений.

Пример 3. Уравнения системы непрямого управления имеют вид [16,

с. 93]

(13)

σ=c^T

y - ρf(σ),

y = Ay + bf(σ).

Здесь y ∈ Rⁿ, σ ∈ R, ρ > 0, c и b — постоянные n-мерные векторы, A — посто-

янная n × n матрица, все собственные числа которой имеют отрицательные

вещественные части, нелинейная характеристика f(σ) удовлетворяет усло-

вию σf(σ) > 0 при σ = 0. Первое уравнение системы (13) скалярное и описы-

вает регулятор, второе уравнение векторное и описывает объект управления.

Пусть для объекта управления характерна быстрая динамика, т.е. в урав-

нениях объекта присутствует малый параметр ε при y, нелинейная характе-

ристика является степенной f(σ) = kσ^μ с нечетной степенью μ > 1 и k > 0,

регулятор может переключаться на несколько режимов с номерами j ∈ S (на-

пример, с основного режима j = 1 на резервный j = 2 и обратно вследствие

возможных отказов и восстановлений). Тогда после переобозначения σ = x,

f (σ) = kx^μ = kx[μ] уравнения (13) принимают вид

(14)

x = cTj y - ρ_jkx[μ], j ∈ S, εy = Ay + bkx[μ],

где ρ_j , c_j ∈ R, j ∈ S — переключаемые параметры регулятора. Уравнения (14)

являются частным случаем для (7).

Применяя теорему 3 к системе (14) как к системе (7) с уже заданными

обратными связями по координатам объекта y(t), приходим к следующему

результату. Если выполнены неравенства

(15)

ρ_j + cTjA-1

b > 0, j ∈ S,

то нулевое решение σ = 0, y = 0 гибридной системы, порождаемой семей-

ством уравнений (14), асимптотически устойчиво при всех достаточно ма-

лых ε > 0 при произвольном режиме переключений. Выполнение нера-

венств (15) является необходимым условием устойчивости для каждой из

систем семейства (14), рассматриваемых изолированно, т.е. при фиксирован-

ном j [16, с. 97].

В заключение отметим, что аналогичным образом рассматриваются слу-

чаи, когда матрица A имеет нулевые собственные значения [16, с. 98], а также

когда в системе присутствует не одна, а несколько степенных нелинейностей.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Из асимптотической устойчивости си-

стемы (3) следует, что существует квадратичная форма V₂(z), удовлетворяю-

щая условиям



V₂

(Π.1)

b₁||z||² ≤ V₂(z) ≤ b₂||z||²,

||gradV₂(z)|| ≤ b₃||z||,



≤ -b₄||z||².

(3)

Введем новую переменную по формуле z = y + A-122g(x). Тогда систему (2)

можно переписать в виде

x = f(σ(t))(x) - A(σ(t))12A-122 g(x) + A(σ(t))12z,

(Π.2)

Ż=ε-1A₂₂z+A-1

g(x(t)).

²² dt

Здесь с учетом локальной липшицевости g(x)

g(x(t)) = lim

[g(x(t + h)) - g(x(t))] .

h→+0 h

C учетом свойств функций, входящих в правые части (1), будут иметь место

оценки



f(k)(x) - A⁽

A-122g(x) ≤ k1||x||,

A⁽

z ≤ k2||z||,



−1



g(x(t))

k₃ (k₁||x|| + k₂||z||) .

A

≤

²² dt

Здесь k₁, k₂, k₃ — некоторые положительные числа. В качестве общей функ-

ции Ляпунова для системы (Π.2) возьмем V (x, z) = V₁(x) + V₂(z). Для ее про-

изводной получим оценку



≤ -a₄||x||^η - ε-1b₄||z||² + b₃||z||k₃ (k₁||x|| + k₂||z||) +

(Π2)

(Π.3)



σ(t))



+ a₃||x||η-1

A⁽

 ||z||.

Без ограничения общности порядок однородности η функции V₁(x) можно

считать равным двум. Тогда в правой части (Π.3) имеем квадратичную фор-

му, которая при достаточно больших ε-1 будет определенно отрицательной.

Тем самым теорема 1 доказана.

Доказательство теоремы 2. Вновь рассмотрим в качестве функции

Ляпунова V (x, z) = V₁(x) + V₂(z) и для производной в силу системы (Π.2) по-

лучим ту же самую оценку, что и при доказательстве теоремы 1. Эта произ-

водная будет отрицательно определенной при любых переключениях. Однако

сама функция V (x, z) теперь может принимать отрицательные значения при

x = x, z = 0. Поэтому для V (x,z) выполнены все условия первой теоремы

Ляпунова о неустойчивости, ссылка на которую завершает доказательство.

Доказательство теоремы

Введем новые переменные

z = y - A₂₁x[μ], тогда при управлении (10) система

(8) перепишется в

виде

[

]

[

]

(Π.4)

x= A(σ(t))11 +A(σ(t))A21 + K1A21 x[μ] + A(σ(t))

+K₁

[μ]

[(

)

(

) ]

∂x

Ż = -ε-1z-A21

A(σ(t))11 +A(σ(t))A21 +K1A21 x[μ] + A(σ(t))

+K₁ z .

∂x

Для входящих в правые части системы (Π.4) функций имеют место оценки

(

)



σ(t))



 A(

+A(σ(t))

A₂₁ + K₁A₂₁ x[μ]

 ≤ c1||x||μ,

(

)



σ(t))



 A(

+K₁ z ≤ c2||z||, ci > 0.

В качестве общей функции Ляпунова для системы (Π.4) возьмем V (x, z) =

= V₁(x) + ¹²||z||². Для ее производной получим оценку



(Π.5)



≤ -a₄||x||η-1+μ + a₃||x||η-1c₂||z|| - ε-1||z||²+

(Π4)

+||A₂₁|| ||z|| ||x||μ-1 [c₁||x||^μ + c₂||z||] .

Без ограничения общности можно считать порядок однородности η функ-

ции V₁(x) сколь угодно большим. Правая часть (Π.5) будет определенно от-

рицательной в некоторой окрестности нулевого решения x = 0, z = 0 при вы-

полнении неравенства [17]

η-1

> 1.

η-1+μ

Это неравенство сводится к η > μ + 1 и выполняется при достаточно боль-

шом η. Ссылка на теорему Ляпунова об асимптотической устойчивости за-

вершает доказательство теоремы 3.

СПИСОК ЛИТЕРАТУРЫ

1. Тихонов А.Н. О зависимости решений дифференциальных уравнений от малого

параметра // Мат. сборник. 1948. Т. 22 (64). № 2. С. 193-204.

2. Yan Zhang, D. Subbaram Naidu, Chenxiao Cai, Yun Zou. Singular Perturbations

and Time Scales in Control Theories and Applications: an overview 2002-2012 //

Int. J. Inform. Syst. Sci. 2014. V. 9. No. 1. P. 1-36.

3. Климушев А.И., Красовский Н.Н. Равномерная асимптотическая устойчивость

систем дифференциальных уравнений с малым параметром при производных //

Прикл. мат. и механика. 1961. Т. 25. Вып. 4. С. 680-690.

4. Yang C., Zhang Q., Zhou L. Stability Analysis and Design for Nonlinear Singular

Systems / Lecture Notes in Control and Information Sciences. Berlin-Heidelberg:

Springer-Verlag, 2013.

5. Lobry C., Sari T. Singular Perturbation Methods in Control Theory / Control

lineaire appl. Travaux en cours 64, Hermann, Paris. 2005. P. 151-177.

Shorten R., Wirth F., Mason O., Wulf K., King C. Stability Criteria for Switched

and Hybrid Systems // SIAM Rev. 2007. V. 49. No. 4. P. 545-592.

Шпилевая О.Я., Котов К.Ю. Переключаемые системы: устойчивость и проек-

тирование (Обзор) // Автометрия. 2008. Т. 44. № 5. С. 71-87.

Hai Lin, Antsaklis P.J. Stability and Stabilizability of Switched Linear Systems: a

Survey of Recent Results // IEEE Trans. Automat. Control. 2009. V. 54. No. 2.

P. 308-322.

Unsolved Problems in Mathematical Systems and Control Theory / Edited by

V.D. Blondel & A. Megretski. Princeton, Oxford: Princeton Univer. Press, 2004.

10.

Liberzon D. Switching in Systems and Control. Boston, MA: Birkhauser, 2003.

11.

Пакшин П.В., Поздяев В.В. Критерий существования общей квадратичной

функции Ляпунова множества линейных систем второго порядка // Изв. РАН.

Теория и системы управления. 2005. № 4. С. 22-27.

12.

Васильев С.Н., Косов А.А. Анализ динамики гибридных систем с помощью об-

щих функций Ляпунова и множественных гомоморфизмов // АиТ. 2011. № 6.

C. 27-46.

Vassilyev S.N., Kosov A.A. Analysis of Hybrid Systems Dynamics Using the

Common Lyapunov Functions and Multiple Homomorphisms // Autom. Remote

Control. 2011. V. 72. No. 6. P. 1163-1183.

13.

Александров А.Ю., Косов А.А., Чэнь Я. Об устойчивости и стабилизации меха-

нических систем с переключениями // АиТ. 2011. № 6. С. 5-17.

Aleksandrov A.Yu., Kosov A.A., Chen Yangzhou. Stability and Stabilization of

Mechanical Systems with Switching // Autom. Remote Control. 2011. V. 72. No. 6.

P. 1143-1154.

14.

Aleksandrov A.Yu., Kosov A.A., Platonov A.V. On the Asymptotic Stability of

Switched Homogeneous Systems // Syst. Control Lett. 2012. V. 61. No. 1. P. 127-133.

15.

Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука, 1987.

16.

Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970.

17.

Александров А.Ю. Устойчивость движений неавтономных динамических систем.

СПб.: Изд-во СПбГУ. 2004.

Статья представлена к публикации членом редколлегии А.А. Бобцовым.

Поступила в редакцию 15.07.2018

После доработки 19.09.2018

Принята к публикации 08.11.2018