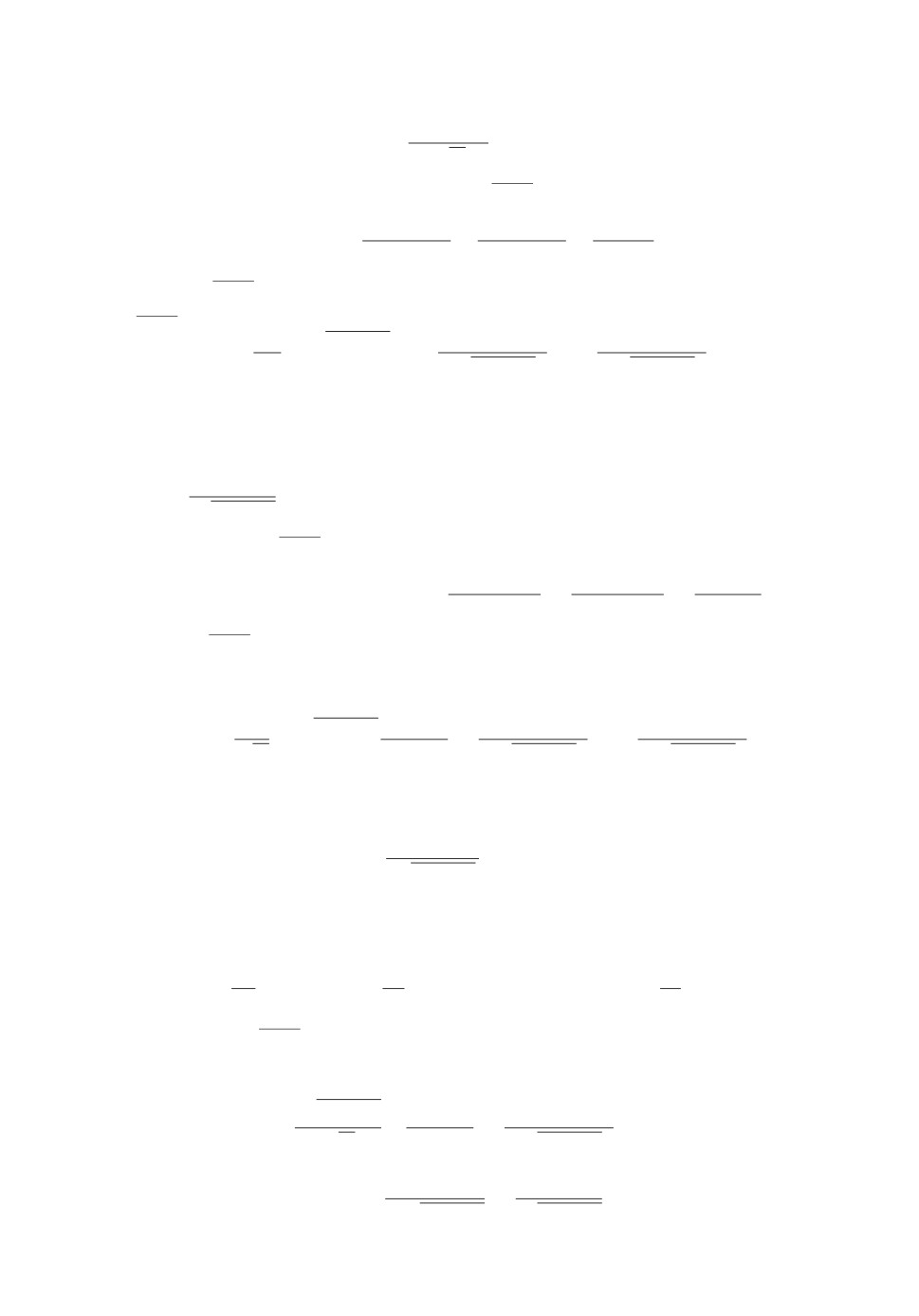Автоматика и телемеханика, № 3, 2019
© 2019 г. С.Л. СЕМАКОВ, д-р физ.-мат. наук (slsemakov@yandex.ru)
(Московский физико-технический институт;
Московский авиационный институт),
И.С. СЕМАКОВ (champione7@yandex.ru)
(Московский авиационный институт)
ВЕРОЯТНОСТЬ ПЕРВОГО ДОСТИЖЕНИЯ УРОВНЯ
СЛУЧАЙНЫМ ПРОЦЕССОМ НА ЗАДАННОМ ПРОМЕЖУТКЕ
Оценивается вероятность события, состоящего в том, что первое дости-
жение заданного уровня непрерывным случайным процессом происходит
на заданном промежутке изменения независимой переменной. Результаты
конкретизируются для гауссовского процесса. Приводится пример чис-
ленных оценок.
Ключевые слова: случайный процесс, вероятность достижения уровня,
момент первого достижения уровня.
DOI: 10.1134/S0005231019030061
1. Введение
При исследовании стохастических систем нередко возникает вопрос: “С ка-
кой вероятностью в течение заданного промежутка времени процесс функ-
ционирования системы не выйдет из некоторых заранее оговоренных рамок?”
В более узкой и математически формализованной постановке этот вопрос
можно сформулировать, в частности, так: “С какой вероятностью исследуе-
мый случайный процесс, имеющий непрерывные реализации, первый раз до-
стигнет интересующего исследователя уровня на заданном промежутке из-
менения независимой переменной?” В данной постановке задача была сфор-
мулирована в [1], хотя в близкой более общей постановке ее можно найти
в [2]. Необходимость в оценке вероятностей событий такого типа возникает
при решении задач из различных предметных областей, например в задачах
обеспечения точности и безопасности посадки самолета [3, 4].
Для диффузионных марковских процессов нахождение указанной вероят-
ности может быть сведено к решению краевой задачи для уравнения в част-
ных производных, что было показано еще в [2]. Примеры точного вычисления
этой вероятности как решения соответствующей краевой задачи приведены
в [3, 5].
Для непрерывных немарковских процессов оценки искомой вероятности
получены в [1] и затем усилены в [6]. Все другие известные авторам резуль-
таты, связанные с вычислением вероятности достижения уровня такими про-
цессами, носят очень частный характер. В качестве примеров можно привести
результаты из [7-9]. В [7] для стационарного гауссовского процесса получены
оценки вероятности
P {ξ(x) ≤ kx + a для любого x ∈ [0, x∗]}
83
невыхода такого процесса за наклонный уровень в предположении, что для
корреляционной функции указанного процесса справедливо определенное
асимптотическое представление. В [8] для стационарного гауссовского про-
цесса найдена асимптотика вероятности пересечения барьера u + f(x) при
u → +∞, где f(x) - детерминированная непрерывная функция, удовлетво-
ряющая некоторым дополнительным условиям. В [9] найдено точное выра-
жение для вероятности
P {ξ(x) ≥ 0 для любого x ∈ [0, x∗]},
где процесс ξ(x) определяется равенством ξ(x) = U + V cos(xβ + W ), в кото-
ром U, V, W - независимые случайные величины, причем U и V распреде-
лены нормально с нулевыми математическими ожиданиями и дисперсиями
1 - β2 и β2 соответственно, а W имеет равномерное распределение на отрез-
ке [0, 2π].
Настоящая статья является продолжением публикации [10], в которой об-
щие результаты, полученные в [1, 6] для непрерывных процессов, конкрети-
зируются для гауссовского процесса.
2. Постановка задачи
Рассмотрим случайный процесс ξ(x) c непрерывными реализациями,
определенный на отрезке [x0, x′′], x0 > -∞, или на полуинтервале (x0, x′′],
x0 ≥ -∞. Пусть задана произвольная точка x′ из интервала (x0,x′′) и неко-
торое число h. Будем предполагать, что выполнено равенство
(1)
P {ξ(x0
) > h} = 1,
если x изменяется на отрезке [x0, x′′], или выполнено равенство
(2)
lim
P {ξ(x) > h} = 1,
x→x0
если x изменяется на полуинтервале (x0, x′′]. Физический смысл равенств (1)
или (2) состоит в том, что изучаемая числовая характеристика, поведение
которой описывается процессом ξ(x), в начальный момент удовлетворяет из-
вестному условию. В данном случае это условие означает, что в момент на-
чала изучения исследуемая характеристика заведомо больше числа h.
Следуя [11], обозначим чеpез Gh(x0, x′′) множество непpеpывных на пpо-
межутке от x0 до x′′ - [x0, x′′] или (x0, x′′] (в зависимости от pассматpивае-
мого множества значений пеpеменной x) - скаляpных функций, котоpые не
совпадают тождественно с h ни в одном из интеpвалов этого пpомежутка.
Будем использовать понятия “вход под уровень”, “выход за уровень”, “пере-
сечение уровня” и “касание уровня” непрерывной функцией в соответствии с
естественными определениями этих понятий, данными в [11], а именно: функ-
ция f(x) из множества Gh(x0, x′′) в точке x∗ ∈ (x′, x′′) имеет:
а) вход под уровень h, если существует ϵ > 0 такое, что
f (x) ≥ h ∀x ∈ (x∗ - ϵ, x∗), f(x) ≤ h ∀x ∈ (x∗, x∗ + ϵ);
84
б) выход за уровень h, если существует ϵ > 0 такое, что
f (x) ≤ h ∀x ∈ (x∗ - ϵ, x∗), f(x) ≥ h ∀x ∈ (x∗, x∗ + ϵ);
в) пересечение уровня h, если для любого ϵ > 0 cуществуют x и x из про-
межутка (x∗ - ϵ, x∗ + ϵ) такие, что
(f(x) - h)(f(x) - h) < 0;
г) касание уровня h, если f(x∗) = h и существует ϵ > 0 такое, что разность
f (x) - h не меняет знака в интервале (x∗ - ϵ, x∗ + ϵ).
Обозначим чеpез N(x1, x2), N-(x1, x2) и N+(x1, x2) cpедние1 числа пере-
сечений уровня h, входов под уровень h и выходов за уровень h пpоцесса ξ(x)
на пpомежутке (x1, x2), если эти средние существуют. Введем в рассмотрение
событие
}
{ существует x∗ ∈ (x′, x′′) такое, что для любого x < x∗ ξ(x) > h
Z =
,
и при этом ξ(x∗) = h
смысл которого заключается в том, что первое достижение уровня h процес-
сом ξ(x) происходит на интервале (x′, x′′). В [1] получены следующие оценки
для вероятности P {Z}.
Теорема 1. Пусть 1) с веpоятностью 1 реализации процесса ξ(x) пpи-
надлежат множеству Gh(x0, x′′) и не имеют касаний уpовня h на пpоме-
жутке (x0, x′′), N(x0, x′′) < ∞; 2) P {ξ(x′) = h} = 0; 3) выполнено условие (1),
если x изменяется на отрезке [x0, x′′], или выполнено условие (2), если x из-
меняется на полуинтервале (x0,x′′]. Тогда
(3)
N-(x′,x′′) - N+(x0,x′′) ≤ P{Z} ≤ N-(x′,x′′
).
Затем оценки (3) были усилены в [6].
Теорема 2. Пусть выполнены условия теоремы 1. Тогда при любом раз-
биении промежутка (x0,x′′) точками x1,... ,xn-1, n ≥ 2, где
x0 < x1 < ... < xn-1 < xn = x′′
и для любого i = 1,... ,n - 1 P{ξ(xi) = h} = 0, справедливы неравенства
(4)
N-(x′,x′′) - N+(x0,x′′) + Δ ≤ P{Z} ≤ N-(x′,x′′
),
где
⎧
⎡
⎤⎫
∑
⎨(
)
⋂ (
)
⎬
⎦
Δ = Δ(x1,...,xn) =
∩⎣
ξ(xj ) > h
P⎩ξ(xi)<h
⎭
i=1
j=i+1
Причем если к имеющимся точкам разбиения xi, i = 1, . . . , n - 1, добавить
новые точки xk, для которых P {ξ(xk) = h} = 0, то величина Δ может от
этого разве лишь возрасти и, как следствие, нижняя из оценок (4) - может
только лишь улучшиться.
1 Под средним здесь и далее понимается математическое ожидание соответствующей
случайной величины.
85
Достаточные условия выполнения предположения 1) теоремы 1 хорошо
изучены и подробно описаны, например, в [11]. Числа N- и N+ для диффе-
ренцируемых процессов вычисляются по известным формулам Райса:
∫x′′
∫
0
N-(x′,x′′) = - dx
vρx(h,v)dv,
x′
-∞
∞
∫x′′
∫
N+(x0,x′′) = dx vρx(h,v)dv,
x0
0
полученным в [12]. Здесь ρx(u, v) - плотность совместного распределения зна-
чений процесса ξ(x) и его производнойdξ(x)dx в среднеквадратичном в один и
тот же момент x.
Что касается точности полученных оценок, т.е. разности между верхней
и нижней оценками искомой вероятности P {Z}, то она зависит от “склонно-
сти” реализаций ξ(x) пеpесекать уpовень h снизу ввеpх на интеpвале (x0, x′′)
и во многом опpеделяется величиной числа N+(x0, x′′). Иллюстрирующие
пpимеpы пpиведены в [3], где помимо прочего показано, насколько эффек-
тивными оказались оценки (3) в авиационных приложениях при их исполь-
зовании для вычисления вероятности успешного приземления реальных са-
молетов, в частности самолетов корабельного базирования при их посадке
на реальный2 авианесущий крейсер с учетом и возможной качки корабля.
В этом случае в роли ξ(x) выступает случайный процесс изменения высоты
полета самолета в системе координат, связанной с посадочной поверхностью,
уровень h = 0, а независимой переменной x является дальность полета. Со-
бытие Z при этом означает, что начальное касание самолетом посадочной
поверхности происходит на заданном участке.
В настоящей статье исследуется вопрос, состоящий в том, как сильно мож-
но улучшить оценки (3) за счет подсчета величины Δ(x1, . . . , xn) с целью
последующего использования более точных оценок (4). При фиксированном
числе n - 1 точек x1, . . . , xn-1, n ≥ 2, разбиения интервала (x0, x′′) величи-
на Δ(x1, . . . , xn) не фиксирована: она может меняться в зависимости от рас-
положения точек x1, . . . , xn-1. Желаемый выбор точек x1, . . . , xn-1 — такой,
при котором Δ(x1, . . . , xn) принимает наибольшее значение, в результате чего
получается наилучшая нижняя оценка для P {Z}. Другими словами, задача
выбора точек x1, . . . , xn-1 — это задача отыскания точки максимума функции
(n - 1)-й переменной. В [10] эта задача решена в случае n = 2 для гауссов-
ского процесса. В настоящей статье рассматривается случай n = 3, т.е. когда
при подсчете величины Δ берется не одна (как в [10]), а две точки разбиения
интервала (x0, x′′), что позволяет улучшить оценки искомой вероятности по
сравнению со случаем n = 2, рассмотренным в [10].
2 Речь идет о самолетах МиГ-29К при посадке на авианесущий крейсер “Адмирал Куз-
нецов”.
86
3. Конкретизация для гауссовского процесса
Пусть процесс ξ(x) имеет вид
ξ(x) = -a1x + a0 + ζ(x), x ∈ (-∞, x′′],
где a1 > 0 и a0 - постоянные, ζ(x) - стационарный центрированный гауссов-
ский процесс с непрерывными реализациями и нормированной корреляцион-
ной функцией
M{ζ(x)ζ(x + y)}
r(y) =
,
σ2
σ2 - дисперсия процессов ξ(x) и ζ(x), символ M означает операцию взятия
математического ожидания. Будем считать, что существует конечная вторая
производная r′′(0). Тогда (см., например, [11]) для процесса ξ(x) условия тео-
рем 1 и 2 выполнены.
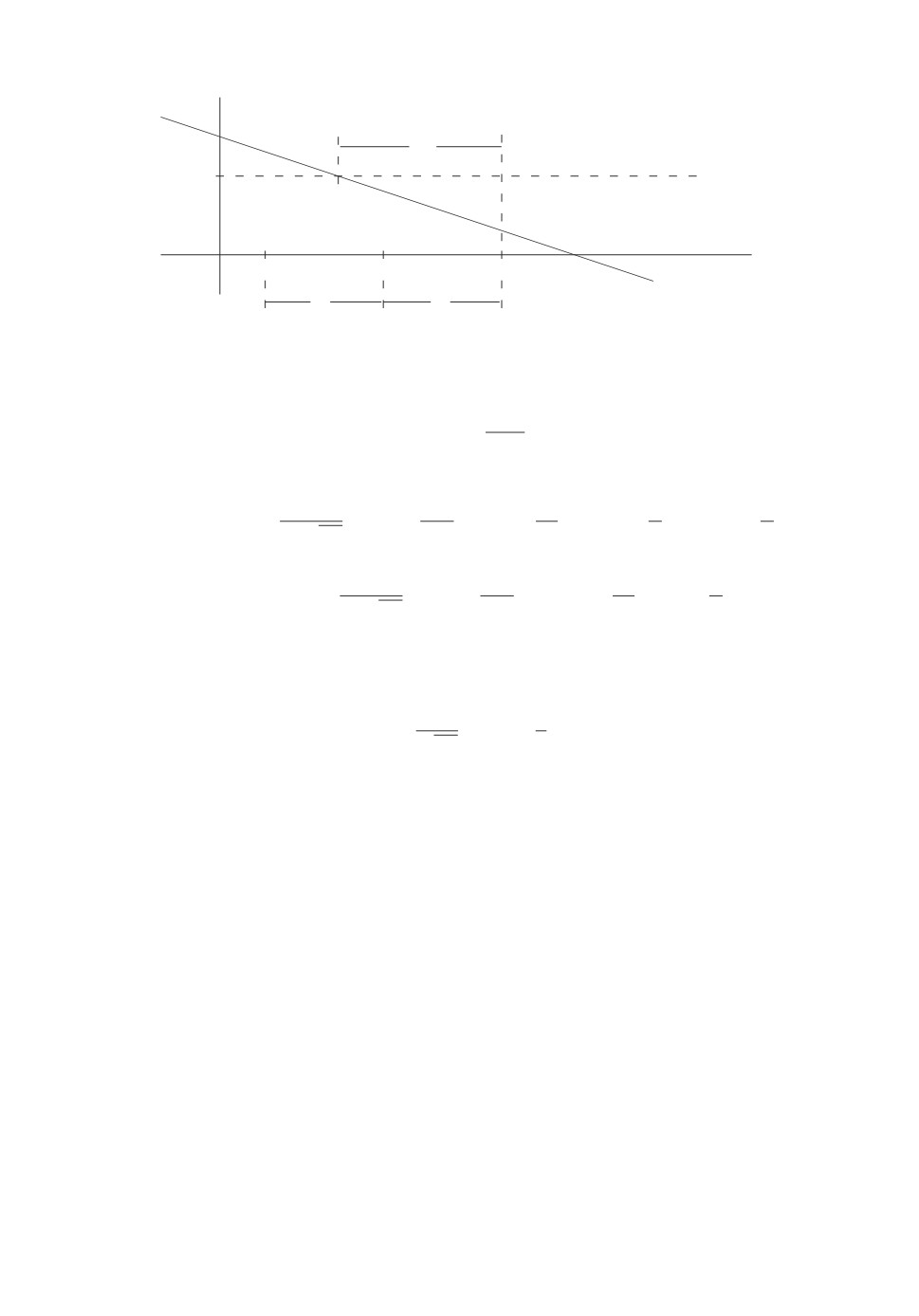
Пусть для определенности точки x′ и x′′ расположены симметрично от-
носительно абсциссы точки пересечения уровня h прямой y = -a1x + a0 (см.
рис. 1). В этом случае разности (-a1x′ + a0) - h и h - (-a1x′′ + a0) положи-
тельны и одинаковы; обозначим их через b (см. рис. 1): (-a1x′ + a0) - h =
= h - (-a1x′′ + a0) = b > 0.
y
h
b
x
x′
x′′
y = -a1x + a0
τ0
τ0
Рис. 1.
В силу существования r′′(0) процесс ζ(x) дифференцируем в среднеквад-
ратичном, так что для подсчета средних N-(x′, x′′) и N+(-∞, x′′) можно
воспользоваться формулами Райса. Плотность ρx(u, v) совместного распреде-
ления значений процесса ξ(x) и его производнойdξ(x)dx в среднеквадратичном
в один и тот же момент x в данном случае имеет вид
{
}
1
(u - (-a1x + a0))2
(v - (-a1))2
ρx(u,v) =
exp
-
-
,
2πσσ1
2σ2
2σ2
1
87
y
τ0
h
x
x1
x2
x′′ = x3
y = -a1x + a0
t
τ
Рис. 2.
где σ21 = -σ2r′′(0) - дисперсия процессаdξ(x)dx . Подстановка этой плотности в
формулы Райса дает следующие результаты для N-(x′, x′′) и N+(-∞, x′′):
(
{
}
))(
))
σ1
a21
(a1
(b)(
b
(5) N-(x′, x′′) =
√
exp
-
+Φ
Φ
-Φ -
,
a1
2π
2σ21
σ1
σ
σ
(
{
}
(
))
σ1
a21
a1
(b)
(6)
N+(-∞,x′′) =
√
exp
-
-Φ -
Φ
,
a1
2π
2σ21
σ1
σ
где введено обозначение
∫α
{
}
1
1
Φ(α) =
√
exp
-
z2
dz.
2π
2
−∞
Теперь займемся исследованием величины Δ. Выпишем выражение для
Δ(x1, . . . , xn) при n = 3:
⎧
⎡
⎤⎫
∑
⎨(
)
⋂ (
)
⎬
⎦
Δ(x1, x2, x3) =
∩⎣
ξ(xj ) > h
=
P⎩ξ(xi)<h
⎭
i=1
j=i+1
(7)
{(
)
(
)
(
)}
= P ξ(x1) < h
∩ ξ(x2) > h
∩ ξ(x3) > h
+
{(
)
(
)}
+ P ξ(x2) < h
∩ ξ(x3) > h
Введем переменные t и τ следующим образом (см. рис. 2):
t=x2 -x1, τ =x′′ -x2.
Поскольку при n = 3 будет x′′ = x3, то при фиксированном значении x′′ ве-
личина Δ(x1, x2, x3) однозначно определяется значениями t и τ. При этом
88
заметим, что t и τ могут принимать только положительные значения. Зада-
ча состоит в отыскании таких положительных t и τ, при которых величи-
на Δ(x1, x2, x3) принимает наибольшее значение.
В дальнейшем для краткости первое слагаемое в правой части (7) будем
обозначать через p(τ, t) (это слагаемое зависит и от τ, и от t), а второе сла-
гаемое — через q(τ) (это слагаемое зависит от τ и не зависит от t):
{(
)
(
)
(
)}
p(τ, t) = P ξ(x1) < h
∩ ξ(x2) > h
∩ ξ(x3) > h
,
{(
)
(
)}
q(τ) = P ξ(x2) < h
∩ ξ(x3) > h
,
так что
Δ(x1, x2, x3) = p(τ, t) + q(τ).
Положим по определению V = ξ(x2), U = ξ(x3) и W = ξ(x1). Тогда слу-
чайные величины V, U, W имеют одинаковые дисперсии σ2 и совместное
нормальное распределение. Обозначим через ρVU (v, u) плотность совместного
распределения случайных величин V и U. Поскольку
M{V } = -a1x2 + a0, M{U} = -a1x3 + a0,
а коэффициент корреляции случайных величин V и U дается значением
r = r(τ), то
{
1
1
( (v - (-a1x2 + a0))2
ρVU (v,u) =
√
exp
-
+
2πσ2
1 - r2(τ)
2(1 - r2(τ))
σ2
)}
2
(u - (-a1x3 + a0))
(v - (-a1x2 + a0))(u - (-a1x3 + a0))
+
- 2r(τ)
σ2
σ2
и
∫
∞
∫
h
{(
)
(
)}
q(τ) = P ξ(x2) < h
∩ ξ(x3) > h
= du ρVU (v, u)dv.
h
-∞
Нетрудно показать, что вычислительную формулу для вероятности q(τ) мож-
но привести к виду
∫∞
{
} (
)
))
1
1
1
(b(τ
(8)
q(τ) =
√
exp
-
y2
Φ -√
-1
+r(τ)y
dy,
2π
2
1-r2(τ) σ τ0
b/σ
где введено обозначение τ0 = b/a1 (см. рис. 1 и 2).
Теперь займемся вычислением вероятности
{(
)
(
)
(
)}
p(τ, t) = P ξ(x1) < h
∩ ξ(x2) < h
∩ ξ(x3) > h
89
Введем обозначения:
m1 = M{ξ(x1)}, m2 = M{ξ(x2)}, m3 = M{ξ(x3)},
M{(ξ(x1) - m1)(ξ(x2) - m2)}
r12 =
,
r21 = r12,
σ2
M{(ξ(x1) - m1)(ξ(x3) - m3)}
r13 =
,
r31 = r13,
σ2
M{(ξ(x2) - m2)(ξ(x3) - m3)}
r23 =
,
r32 = r23,
σ2
r11 = r22 = r33 = 1.
Заметим, что r12 = r(t), r23 = r(τ), r13 = r(t + τ), где r(y) - ранее введенная
нормированная корреляционная функция процесса ζ(x). Положим по опре-
делению
r11
r12
r13
R = R(τ,t) =
r21
r22
r23
= 1 + 2r12r13r23 - r212 - r213 - r223;
r31
r32
r33
Rij - алгебраическое дополнение элемента rij определителя R. Тогда
⎧
⎫
∫
h
∫
∞
∫
∞
-3/2
⎨
⎬
(2π)
1
∑ (zi- mi)(zj - mj)
(9) p(τ, t) =
√
dz1
dz2
exp
-
Rij
dz3.
σ3
R
⎩
2R
σ2
⎭
i,j=1
−∞ h
h
В Приложении 1 показано, что вычислительную формулу для p(τ, t) можно
привести к виду
∫
∞
{
}
1
1
p(τ, t) =
exp
-
u2
F (u, τ, t)du,
2π
2
b/σ
где функция F(u, τ, t) выписана в явном виде в Приложении 1.
Поставим задачу нахождения точки абсолютного максимума функции
Δ(τ, t) ≡ p(τ, t) + q(τ)
в области τ > 0, t > 0. Из вероятностных соображений и гауссовости рассмат-
риваемых распределений очевидно, что при непрерывной корреляционной
функции r(y) функция Δ(τ, t) непрерывна и ограничена в указанной области.
Кроме того, для рассматриваемого процесса ξ(x) из определения вероятно-
стей p(τ, t) и q(τ) следует, что
lim
q(τ) = 0, lim
p(τ, t) = 0
∀t > 0, lim p(τ,t) = 0
∀τ > 0,
τ→0
τ→0
t→0
lim
q(τ) = 0, lim
p(τ, t) = 0
∀t > 0, lim p(τ,t) = 0
∀τ > 0,
τ→∞
τ→∞
t→∞
90
т.е. при приближении к границам области функция Δ(τ, t) стремится к ну-
лю. В этой ситуации, приняв во внимание положительность, ограниченность
и непрерывность функции Δ(τ, t) в области {(τ, t) : τ > 0, t > 0} для рассмат-
риваемого процесса ξ(x), можно утверждать, что точка абсолютного мак-
симума существует и этот максимум достигается по крайней мере в одной
точке (τ∗, t∗) области τ > 0, t > 0.
Будем предполагать функцию r(y) дифференцируемой. Тогда из получен-
ных явных выражений для p(τ, t) и q(τ) следует, что функция Δ(τ, t) диф-
ференцируема по каждой из переменных τ и t, так что точка (τ∗, t∗) должна
удовлетворять следующим необходимым условиям максимума:
∂Δ
∂Δ
= 0,
= 0,
∂τ
∂t
τ=τ∗,t=t∗
τ=τ∗,t=t∗
т.е. для нахождения значений τ∗ и t∗ требуется в области {(τ, t) : τ > 0, t > 0}
решить систему двух уравнений:
∂p(τ,t)
dq(τ)
∂p(τ,t)
(10)
+
= 0,
= 0.
∂τ
dτ
∂t
Нетрудно убедиться, что
{
}
)2
dq(τ)
1
1
(b)2(
τ
(11)
=
exp
-
-1
×
dτ
2π
2
σ
τ0
(
)
{
}
√
2
r′(τ)
d
2πb
×
-
√
exp
-
-
Φ(-d)
,
1 - r2(τ)
2
στ0
где
(
)
b
1 - r(τ)
τ
d = d(τ) =
√
1-
σ
1 - r2(τ)
τ0
В Приложении 2 показано, что
(
)
∂p(τ,t)
1
(12)
=
α(τ, t) + β(τ, t) + γ(τ, t) и
∂τ
2π
)
∂p(τ,t)
1 (
=
α(τ, t)
β(τ, t)
,
∂t
2π
где α(τ, t), β(τ, t), γ(τ, t), α(τ, t)
β(τ, t) - функции переменных τ и t, выпи-
санные в явном виде в Приложении 2.
С учетом результатов (11) и (12) первое из уравнений (10) принимает вид
α(τ, t) + β(τ, t) + γ(τ, t) =
{
}(
)
)2
{
}
√
(13)
2
1
(b)2(τ
r′(τ)
d
2πb
= exp
-
-1
√
exp
-
+
Φ(-d)
,
2
σ
τ0
1-r2(τ)
2
στ0
91
а второе -
(14)
α(τ, t) +β
(τ, t) = 0.
Система уравнений (13), (14) может быть решена каким-либо численным ме-
тодом. Если решений будет несколько, нужно взять то решение, которому
будет соответствовать наибольшее значение функции Δ(τ, t).
4. Пример численных оценок
Для рассматриваемого процесса ξ(x) оценки (3) для вероятности P {Z}
имеют вид
(15)
N-(x′,x′′) - N+(-∞,x′′) ≤ P{Z} ≤ N-(x′,x′′
),
где числа N-(x′, x′′) и N+(-∞, x′′) вычисляются по формулам (5) и (6). Более
точные оценки для P {Z}, следующие из общего результата (4) при n = 2, в
данном случае выглядят так:
(16)
N-(x′,x′′) - N+(-∞,x′′) + q(τmax) ≤ P{Z} ≤ N-(x′,x′′
),
где τmax - значение τ, при котором функция q(τ), τ > 0, вычисляемая
по (8), достигает наибольшего значения. Наконец, еще более точные оцен-
ки для P {Z}, следующие из (4) при n = 3, имеют вид
(17)
N-(x′,x′′) - N+(-∞,x′′) + Δ(τ∗,t∗) ≤ P{Z} ≤ N-(x′,x′′
),
где (τ∗, t∗) - точка абсолютного максимума функции Δ(τ, t) в области τ > 0
и t > 0.
Для подсчета чисел N-(x′, x′′) и N+(-∞, x′′) по формулам (5) и (6) до-
статочно задать значения дробей b/σ и a1/σ1. Чтобы найти τmax, τ∗ и t∗ и
подсчитать q(τmax) и Δ(τ∗, t∗), нужно дополнительно задать функцию r(τ).
При этом заметим, что параметр τ0 после задания дробей b/σ, a1/σ1 и функ-
ции r(τ) также определяется:
b
b/σ σ
b/σ
σ
b/σ
1
(18)
τ0 =
=
=
√
=
√
a1
a1/σ1 σ1
a1/σ1 σ
-r′′(0)
a1/σ1
−r′′(0)
Пример. Пусть
b
a1
= 1,
= 1, r(τ) = exp{-τ2}.
σ
σ1
Тогда3
√
N-(x′,x′′) = 0,739, N+(-∞,x′′) = 0,070, τ0 = 1/
2, τmax = 0,972,
q(τmax) = 0,024, τ∗ = 0,730, t∗ = 0,614, Δ(τ∗, t∗) = 0,030.
3 Приводимые далее численные значения N-(x′, x′′), N+(-∞,x′′), τmax, q(τmax), τ∗, t∗
и Δ(τ∗, t∗) даются с округлением до тысячных долей единицы.
92
Оценки (15), (16) и (17) приводят к результатам
0,669 ≤ P {Z} ≤ 0,739,
0,693 ≤ P {Z} ≤ 0,739 и
0,699 ≤ P {Z} ≤ 0,739
соответственно, или, используя эквивалентную форму записи, к результатам
P {Z} = 0,704 ± 0,035, P {Z} = 0,716 ± 0,023 и P {Z} = 0,719 ± 0,020.
Как видно из этого примера (и как уже отмечалось в [10]), исполь-
зование неравенств (4) вместо неравенств (3) позволяет заметно точнее
оценить искомую вероятность P {Z} уже при n = 2, т.е. когда для под-
счета величины Δ(x1, . . . , xn) берется лишь одна точка разбиения ин-
тервала (x0, x′′). Так, в данном примере в случае использования нера-
венств (15) относительная погрешность определения вероятности составля-
ет (0,035/0,704) · 100 % = 4,97 %, а в случае использования неравенств (16) -
(0,023/0,716) · 100 % = 3,21 %.
При переходе к использованию неравенств (17), т.е. при n = 3, когда
для подсчета величины Δ(x1, . . . , xn) берутся две точки разбиения интерва-
ла (x0, x′′), относительная погрешность в рассматриваемом примере умень-
шается до значения (0,020/0,719) · 100 % = 2,78 %. Спрашивается, существен-
но ли такое улучшение оценок? Ответ на этот вопрос зависит от конкретной
практической задачи, которая приводит к необходимости подсчета изучаемой
вероятности. Если речь идет об оценке вероятности успешного приземления
самолета, то такое улучшение существенно.
5. Заключение
Таким образом, в настоящей работе для гауссовского процесса конкре-
тизированы ранее полученные для непрерывных процессов общие резуль-
таты, касающиеся оценок вероятности события, состоящего в том, что пер-
вое достижение заданного уровня исследуемым случайным процессом проис-
ходит на заданном промежутке изменения независимой переменной. Пред-
лагаемые оценки (3) для искомой вероятности основаны на использова-
нии известных результатов Райса для среднего числа пересечений, а уси-
ление оценок (3) оценками (4) дополнительно предполагает подсчет величи-
ны Δ(x1, . . . , xn), n ≥ 2, фигурирующей в теореме 2. Показано, что исполь-
зование неравенств (4) вместо (3) позволяет существенно улучшить оцен-
ки искомой вероятности уже в случае n = 2. Использование неравенств (4)
с Δ(x1,... ,xn) при n = 3 приводит к дальнейшему, вполне заметному улучше-
нию оценок, хотя и не столь значительному, как при переходе от использова-
ния неравенств (3) к использованию неравенств (4) с Δ(x1, . . . , xn) при n = 2.
ПРИЛОЖЕНИЕ 1
Упростим правую часть равенства (9). Замена переменных
z1 - m1
z2 - m2
z3 - m3
z1 =
,
z2 =
,
z3 =
σ
σ
σ
93
позволяет привести интеграл (9) к виду
∞
∫
-3/2
(2π)
p(τ, t) =
√
dz2
×
R
h-m2
σ
∫∞
{
}
z22
z23
r23
×
dz3 exp
-
-
+
z2z3
×
2
2(1 - r223)
2(1 - r223)
1-r
23
h-m3
σ
h-m1
⎧
)2⎫
∫
σ
⎨
(√
⎬
1
r13r23 - r12
r12r23 - r13
×
exp
-
1-r223z1 +
√
z2 +
√
z3
dz1,
⎩
2R
1-r223
1-r223
⎭
-∞
откуда, вычисляя внутренний интеграл по z1, получим
∞
∫
-1
(2π)
p(τ, t) =
√
dz
3×
1-r2
23h-m
3
σ
∫∞
{
}
z22
z23
r23z2z3
×
Φ(g(z2, z3)) exp
-
-
+
dz2,
2
2(1 - r223)
2(1 - r223)
1-r
23
h-m2
σ
где введено обозначение
)
(√
1
h-m1
r13r23 - r12
r12r23 - r13
g(z2, z3) =
√
1-r2
+
√
z2 +
√
z3
23
R
σ
1-r223
1-r2
23
Сделав в получившемся двойном интеграле для p(τ, t) замену переменных
z2 - r23z3
v=
√
,
u=z3,
1-r2
23
приведем его к виду
⎧
⎫
∫
∞
{
}
⎨ ∫∞
{
}
⎬
1
u2
v2
p(τ, t) =
exp
-
Φ (g(v, u)) exp
-
dv du,
2π
2
⎩
2
⎭
h-m3
f (u)
σ
где
√
(
)
1-r223
h-m1
r13r23 - r12
g(v, u) =
√
+
√
v-r13u
,
R
σ
1-r
2
23
h-m2
r23u
f (u) =
√
-
√
σ
1-r223
1-r2
23
94
Если теперь учесть, что (см. рис. 1 и 2)
m3 = -a1x3 + a0, m2 = -a1(x3 - τ) + a0, m1 = -a1(x3 - τ - t) + a0,
h - m3 = b, a1 = b/τ0,
то
(
)
(
)
h-m3
b
h-m2
b
τ
h-m1
b
τ+t
=
,
=
1-
,
=
1-
;
σ
σ
σ
σ
τ0
σ
σ
τ0
кроме того, r23 = r(τ), r12 = r(t), r13 = r(τ + t), R = R(τ, t), так что функ-
ция f(u) зависит еще и от τ, а функция g(v, u) — еще и от τ и t. Окончательно
можем записать
∫
∞
{
}
1
1
(Π.1.1)
p(τ, t) =
exp
-
u2
F (u, τ, t)du,
2π
2
b/σ
где
∫∞
{
}
1
F (u, τ, t) =
exp
-
v2
Φ (g(v, u, τ, t)) dv,
2
f (u,τ)
b(1 - τ/τ0)
ur(τ)
f (u, τ) =
√
-
√
,
σ
1 - r2(τ)
1 - r2(τ)
(
)
√
(
)
1-r2(τ)
b
τ+t
r(t + τ)r(τ) - r(t)
g(v, u, τ, t) =
√
1-
+v
√
- ur(t + τ)
R(τ, t)
σ
τ0
1 - r2(τ)
ПРИЛОЖЕНИЕ 2
Найдем частную производную∂p(τ,t)∂τ . В соответствии с (П.1.1) получим4,
что
∫
∞
{
}
∂p(τ,t)
1
1
(Π.2.1)
=
exp
-
u2
×
∂τ
2π
2
b/σ
⎧
⎫
⎨
∫
∞
{
}
⎬
1
∂Φ (g(v,u,τ,t))
×
exp
-
v2
dv du -
⎩
2
∂τ
⎭
f (u,τ)
∫
∞
{
}
1
∂f(u,τ)
f2(u,τ) + u2
−
exp
-
Φ(g(f(u,τ),u,τ,t)) du.
2π
∂τ
2
b/σ
4 Здесь и далее все аналитические преобразования и вычисления представлены настоль-
ко подробно, насколько это позволяет сделать ограничение на объем статьи.
95
Нетрудно показать, что
∂f(u,τ)
= A - Bu, g(f(u,τ),u,τ,t) = C - Du,
∂τ
где обозначено:
(
)
]
1
b
[r(τ)r′(τ)
τ
1
A = A(τ) =
√
1-
-
,
1 - r2(τ) σ
1 - r2(τ)
τ0
τ0
r′(τ)
B = B(τ) =
,
(1 - r2(τ))3/2
r(τ + t) - r(t)r(τ)
D = D(τ,t) =
√
√
,
1 - r2(τ)
R(τ, t)
√
[(
)
(
)]
1 - r2(τ)
b
τ+t
r(τ + t)r(τ) - r(t)
τ
C = C(τ,t) =
√
1-
+
1-
R(τ, t) σ
τ0
1 - r2(τ)
τ0
C учетом этого равенство (П.2.1) принимает вид
∫
∞
{
}
∂p(τ,t)
1
1
(Π.2.2)
=
exp
-
u2
×
∂τ
2π
2
b/σ
⎧
⎫
⎨
∫
∞
{
}
⎬
1
∂Φ (g(v,u,τ,t))
×
exp
-
v2
dv du -
⎩
2
∂τ
⎭
f (u,τ)
⎧
[
(
)]2⎫
∫
∞
⎨
⎬
u - r(τ)b
1-τ
K
σ
τ0
−
(A - Bu) exp
-
Φ(C - Du)du,
2π
⎩
2(1 - r2(τ))
⎭
b/σ
где
{
}
)
2
1
(b)2(
τ
K = K(τ) = exp
-
1-
2
σ
τ0
96
Вычислим внутренний интеграл в первом слагаемом правой части равен-
ства (П.2.2). Если ввести обозначения:
√
(
)
1 - r2(τ)
b
τ+t
E = E(τ,t) =
√
1-
,
R(τ, t) σ
τ0
r(t + τ)r(τ) - r(t)
F = F(τ,t) =
√
,
R(τ, t)
√
1 - r2(τ)
G = G(τ,t) = -r(t + τ)
√
,
R(τ, t)
E= E(τ,t)=∂E(τ,t)
,
∂τ
∂F(τ,t)
F
F (τ, t) =
,
∂τ
G= G(τ,t)=∂G(τ,t)
,
∂τ
то
∂g(v,u,τ,t)
g(v, u, τ, t) = E + F v + Gu,
= E
Fv + Gu,
∂τ
и для искомого внутреннего интеграла получим
∫
∞
{
1
} ∂Φ (g(v,u,τ,t))
exp
-
v2
dv =
2
∂τ
f (u,τ)
{
}
F
H2
(E + Gu)2
=
√
exp
-
-
+
2π(1 + F2)
2
2(1 + F2)
{
}
2
(E +Gu)(1 + F2) - (E + Gu)FF
(E + Gu)
+
exp
-
Φ(-H),
(1 + F2)3/2
2(1 + F2)
где
√
(E + Gu)F
H = H(u,τ,t) =
1 + F2f(u,τ) +
√
1+F2
97
С учетом этого равенство (П.2.2) принимает вид
∫
∞
{
}
∂p(τ,t)
1
F
H2
(E + Gu)2
u2
(Π.2.3)
=
√
exp
-
-
-
du +
∂τ
2π
2π(1 + F2)
2
2(1 + F2)
2
b/σ
∫
∞
{
}
1
E+Gu)(1 + F2) - (E + Gu)FF
(E + Gu)2
u2
+
exp
-
-
Φ(-H)du +
2π
(1 + F2)3/2
2(1 + F2)
2
b/σ
⎧
⎫
[
(
)]2
∫
∞
⎨
⎬
u - r(τ)b
1-τ
1
σ
τ0
+
(-K)(A - Bu) exp
-
Φ(C - Du)du.
2π
⎩
2(1 - r2(τ))
⎭
b/σ
Интеграл в первом слагаемом правой части равенства (П.2.3) вычисляется:
∫
∞
{
}
F
H2
(E + Gu)2
u2
√
exp
-
-
-
du =
2π(1 + F2)
2
2(1 + F2)
2
b/σ
√
R(τ, t)
F
(Π.2.4)
=
×
1 - r2(t) (1 - r2(τ))(1 - r2(t + τ))
(
√
√
)
{
}
R(τ, t)T2
T2
b
1 - r2(t)
1
R(τ, t)
1
× exp
-
Φ
-
-
T1
,
8(1 - r2(t))
2
σ R(τ,t)
2
1 - r2(t)
где
[(
)
2
b
τ+t
T1 = T1(τ,t) =
-1
(r(t + τ) - r(τ)r(t)) +
R(τ, t) σ
τ0
(
)
]
τ
+
-1
(r(τ) - r(t + τ)r(t)) ,
τ0
)2 [
(
)2
1
(b
(
)
τ
T2 = T2(τ,t) =
1 - r2(t + τ)
-1
+
R(τ, t) σ
τ0
)2
)(
)]
(
)
(τ+t
(τ
τ+t
+
1 - r2(τ)
-1
+ 2(r(t + τ)r(τ) - r(t))
-1
-1
τ0
τ0
τ0
98
Интеграл во втором слагаемом правой части (П.2.3) приводится к виду
∫
∞
{
}
E + Gu)(1 + F2) - (E + Gu)FF
(E + Gu)2
u2
exp
-
-
Φ(-H)du =
(1 + F2)3/2
2(1 + F2)
2
b/σ
{
}
)
2
1
(b)2(
t+τ
(Π.2.5)
= exp
-
1-
×
2
σ
τ0
⎡
∫
∞
{
}
{
}
1
1
×⎣B∗ exp
-
w2
Φ(C∗w - D∗)dw + A∗ exp
-
s2
Φ(L3)+
2
2
s
⎤
{
}
r(τ) - r(t + τ)r(t)
D∗2
+A∗√
√
exp
-
Φ(L4)⎦ ,
1 - r2(t)
1 - r2(t + τ)
2(1 + C∗2)
где
G+GF2 - G
F
A∗ = A∗(τ,t) =
√
,
(1 + F2)
1+F2 +G2
E+ EF2-EFF˜
(G +GF2 - G
F )EG
B∗ = B∗(τ,t) =
-
,
(1 + F2)3/2
(1 + F2)3/2(1 + F2 + G2)
r(τ) - r(t + τ)r(t)
C∗ = C∗(τ,t) =
√
,
R(τ, t)
[
(
)]
b/σ
t+τ
s = s(τ,t) =
√
1 - r(t + τ)
1-
,
1 - r2(t + τ)
τ0
√
[
(
)]
b
1 - r2(t + τ)
τ
t+τ
D∗ = D∗(τ,t) =
√
1-
- r(t)
1-
,
σ
R(τ, t)
τ0
τ0
√
b
1 - r2(t + τ)
L3 = L3(τ,t) =
√
×
σ
R(τ, t)
(
)
(
)]
[r(τ) - r(t + τ)r(t)
r(t) - r(t + τ)r(τ)
t+τ
τ
×
+
1-
- 1-
,
1 - r2(t + τ)
1 - r2(t + τ)
τ0
τ0
√
b
1 - r2(t)
L4 = L4(τ,t) =
√
×
σ
R(τ, t)
(
)
(
)
]
[r(t + τ) - r(τ)r(t)
t+τ
r(τ) - r(t + τ)r(t)
τ
×
1-
+
1-
-1 .
1 - r2(t)
τ0
1 - r2(t)
τ0
99
Интеграл в третьем слагаемом правой части (П.2.3) приводится к виду
⎧
⎫
[
(
)]2
∫
∞
⎨
⎬
u - r(τ)b
1-τ
σ
τ0
(-K)(A - Bu) exp
-
Φ(C - Du)du =
⎩
2(1 - r2(τ))
⎭
b/σ
⎡
{
}
)2
1
(b)2(
τ
⎢
b/σ
= exp
-
1-
×
2
σ
τ0
⎣τ0√1 - r2(τ)
∫∞
{
} (
√
)
1
(Π.2.6)
× exp
-
w2
Φ L5 -D
1 - r2(τ)w
dw +
2
d
⎧
(
(
))2⎫
⎨
⎬
√
1 - r(τ)
1-τ
(b)2
τ0
+B
1 - r2(τ) · exp
-
Φ(L1) +
⎩
σ
2(1 - r2(τ))
⎭
⎧
(
(
))2⎫
⎤
⎨
⎬
1-τ+tτ
- r(t)
1-τ
r(t)r(τ) - r(t + τ)
(b)2
0
τ0
⎥
+B
√
exp
-
Φ(L2)⎦,
1 - r2(t)
⎩
σ
2(1 - r2(t))
⎭
где
L1 = L1(τ,t) =
[
(
)
(
)]
τ
r(t)r(τ) - r(t + τ) + (r(t + τ)r(τ) - r(t))
1-τ
+ (1 - r2(τ))
1-t+τ
b
0
τ0
=
√
√
,
σ
1 - r2(τ)
R(τ, t)
L2 = L2(τ,t) =
[
(
)
(
)
]
t+τ
(r(t + τ) - r(t)r(τ))
1-
+ (r(τ) - r(t)r(t + τ))
1-τ
+r2(t)-1
b
τ0
τ0
=
√
√
,
σ
1 - r2(t)
R(τ, t)
√
[
(
)]
b
1 - r2(τ)
τ +t
τ
L5 = L5(τ,t) =
√
1-
- r(t)
1-
,
σ
R(τ, t)
τ0
τ0
[
(
)]
τ
1 - r(τ)
1-
b
τ0
d = d(τ) =
√
σ
1 - r2(τ)
C учетом равенств (П.2.4), (П.2.5) и (П.2.6) равенство (П.2.3) можно пе-
реписать в виде
∂p(τ,t)
1
=
(α(τ, t) + β(τ, t) + γ(τ, t)),
∂τ
2π
где через α(τ, t) обозначена правая часть равенства (П.2.4), через β(τ, t) - пра-
вая часть равенства (П.2.5) и через γ(τ, t) - правая часть равенства (П.2.6).
100
Найдем производную∂p(τ,t)∂t . В соответствии с (П.1.1) получим, что
⎧
⎫
∫
∞
{
}⎨
∫
∞
{
}
⎬
∂p(τ,t)
1
1
1
∂Φ (g(v,u,τ,t))
=
exp
-
u2
exp
-
v2
dv du.
∂t
2π
2
⎩
2
∂t
⎭
b/σ
f (u,τ)
Отсюда совершенно аналогично тому, как было получено равенство (П.2.3)
из (П.2.1), найдем, что
∫
∞
{
}
∂p(τ,t)
1
F
H2
(E + Gu)2
u2
(Π.2.7)
=
√
exp
-
-
-
du +
∂t
2π
2π(1 + F2)
2
2(1 + F2)
2
b/σ
∫
∞
{
}
1
E+Ĝu)(1 + F2) - (E + Gu)FF
(E + Gu)2
u2
+
exp
-
-
Φ(-H)du.
2π
(1 + F2)3/2
2(1 + F2)
2
b/σ
где
∂F(τ,t)
Ê= Ê(τ,t)=∂E(τ,t)
Ĝ= Ĝ(τ,t)=∂G(τ,t)
,
F
F (τ, t) =
,
∂t
∂t
∂t
Если теперь ввести обозначения:
Ĝ+ĜF2 - G
F
A∗∗ = A∗∗(τ,t) =
√
,
(1 + F2)
1+F2 +G2
Ê+ ÊF2-EF
F
(Ĝ +ĜF2 - G
F )EG
B∗∗ = B∗∗(τ,t) =
-
,
(1 + F2)3/2
(1 + F2)3/2(1 + F2 + G2)
которые отличаются от введенных выше обозначений A∗ и B∗ лишь тем, что
вместоE
F иGпишутсяÊ
F иĜ соответственно, то из (П.2.7) получим, что
∂p(τ,t)
1
=
(α(τ,t)
β(τ, t)),
∂t
2π
где функция α(τ, t) отличается от ранее введенной функции α(τ, t) лишь тем,
что вместо
F пишетс
F, а функци
β(τ, t) отличается от ранее введенной
функции β(τ, t) лишь тем, что вместо A∗ и B∗ пишутся A∗∗ и B∗∗ соответ-
ственно.
СПИСОК ЛИТЕРАТУРЫ
1. Семаков С.Л. Первое достижение границ случайным процессом // АиТ. 1988.
№ 6. С. 87-95.
Semakov S.L. First Arrival of a Random Process on the Boundary // Autom. Remote
Control. 1988. V. 49. No. 6. P. 757-764.
2. Понтpягин Л.С., Андpонов А.А., Витт А.А. О статистическом pассмотpении
динамических систем // Жуpн. экспеpимент. и теоp. физики. 1933. Т. 3. № 3.
С. 165-180.
101
3.
Семаков С.Л. Выбросы случайных процессов: приложения в авиации. М.: Наука,
2005.
4.
Семаков С.Л. Применение известного решения одной задачи о достижении гра-
ниц немарковским процессом к оценке вероятности успешного приземления са-
молета // Изв. РАН. ТиСУ. 1996. № 2. С. 139-145.
5.
Семаков С.Л. Первый выход случайного процесса на границу области // АиТ.
2015. № 4. С. 80-96.
Semakov S.L. Estimating the Probability That a Multidimensional Random Process
Reaches the Boundary of a Region // Autom. Remote Control. 2015. V. 76. No. 4.
P. 613-626.
6.
Семаков С.Л. Вероятность первого достижения уровня компонентом многомер-
ного процесса на заданном промежутке с соблюдением ограничений на его дру-
гие компоненты // Теория вероятн. и ее примен. 1989. Т. 34. № 2. С. 402-406.
7.
Мирошин Р.Н. Пересечения кривых гауссовскими процессами. Ленинград: ЛГУ,
1981.
8.
Berman S. Excursions of Stationary Gaussian Processes Above High Moving
Barriers // Ann. Probab. 1973. V. 1. No. 3. P. 365-387.
9.
Slepian D. The One-Sided Barrier Problem for Gaussian Noise // Bell Syst. Techn.
J. 1962. V. 41. No. 2. P. 463-501.
10.
Семаков С.Л., Семаков И.С. Оценка вероятности одного события, связанного с
моментом первого достижения уровня случайным процессом // АиТ. 2018. № 4.
С. 65-74.
Semakov S.L., Semakov I.S. Estimating the Probability of an Event Related to the
Moment When a Random Process First Reaches a Given Level // Autom. Remote
Control. 2018. V. 79. No. 4. P. 632-640.
11.
Крамер Г., Лидбеттер М. Стационарные случайные процессы. М.: Мир, 1969.
12.
Rice S.O. Mathematical Analysis of Random Noise // Bell Syst. Techn. J. 1945.
V. 24. No. 1. P. 46-156.
Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.
Поступила в редакцию 23.02.2018
После доработки 25.06.2018
Принята к публикации 08.11.2018
102