Автоматика и телемеханика, № 3, 2019

(Московский авиационный институт)

ДВУСТОРОННЯЯ ВЕРОЯТНОСТНАЯ ГРАНИЦА

ДЛЯ СИММЕТРИЧНОЙ УНИМОДАЛЬНОЙ

СЛУЧАЙНОЙ ВЕЛИЧИНЫ¹

Для симметричной унимодальной случайной величины с известными

модой и дисперсией построена неулучшаемая верхняя граница вероятно-

сти попадания вне произвольно заданного интервала. Описано распреде-

ление, на котором достигается полученная граница. В частном случае,

когда расстояние между модой и серединой интервала меньше 29 % его

радиуса, найденная граница определяется неравенством Гаусса. Получен-

ный результат применен к построению робастных доверительных интер-

валов.

Ключевые слова: унимодальное (одновершинное) распределение, неравен-

ство Гаусса, вероятностная граница, наихудшее распределение, робаст-

ный доверительный интервал.

DOI: 10.1134/S0005231019030073

1. Введение

Понятие унимодальности (или одновершинности) распределения отражает

естественное требование монотонного убывания плотности случайной вели-

чины от ее наиболее вероятного значения [1]. При соблюдении этого условия

вероятность отклонения случайной величины от своей моды можно оценить

сверху с помощью неравенства Гаусса [2]. Если мода совпадает с математиче-

ским ожиданием, то это неравенство описывает верхнюю границу, в 9/4 раз

меньшую того, что дает неравенство Чебышёва. Если же мода неизвестна, то

вероятность отклонения унимодальной величины от своего среднего оцени-

вается с помощью неравенства Высочанского — Петунина [3]. По форме оно

совпадает с н√авенством Гаусса при условии, что порог отклонения составля-

ет не меньше

8/3 средних квадратичных отклонений. В результате правило

“трех сигм” при наихудшем выборе унимодального распределения выполня-

ется с надежностью 77/81 ≈ 0,9506. В этом случае доверительный интервал,

основанный на знании первых двух моментов и предположении об унимо-

дальности, оказывается лишь в полтора раза шире интервала, построенного

согласно гипотезе о нормальном распределении [4].

Благодаря этому факту стохастические модели с неопределенным унимо-

дальным распределением находят свое применение в различных прикладных

задачах, таких как: анализ импульсной активности нейронов [5]; определение

границ ошибок при обработке геологических данных [6]; оценка надежности

при неопределенной интенсивности отказов [7]; определение технологическо-

го допуска с заданной вероятностью [8]. Кроме того, описание неопределен-

ности с помощью различных классов унимодальных распределений встре-

чается и в теоретических работах. В [9-11] доказано, что для случайного

¹ Работа выполнена при поддержке Российского научного фонда (проект № 16-11-00063).

103

вектора с ограниченным носителем равномерное распределение доставляет

минимум вероятности попадания в выпуклое множество. В [12] рассмотре-

ны задачи оптимизации при наличии вероятностных ограничений, которые

должны соблюдаться при произвольном выборе распределения альфа-унимо-

дального вектора с фиксированными математическим ожиданием и ковариа-

ционной матрицей. В [13] для проблем моментов Маркова, рассматриваемых

на классе многомерных унимодальных распределений, разработан метод их

преобразования к задачам полуопределенного программирования.

Помимо [3] нахождением неравенств для вероятности выхода унимодаль-

ной величины из заданного интервала занимались многие авторы: в [14] зада-

ча максимизации указанной вероятности решена для фиксированных значе-

ний моды, среднего и дисперсии; в [15] решение этой задачи определено для

односторонней вероятности (т.е. вероятности превышения случайной величи-

ной заданного порога); в [16] получено обобщение неравенства Высочанско-

го — Петунина с использованием (вместо дисперсии) центрального момента

любого положительного порядка; в [17] максимизация односторонней веро-

ятности для симметричной величины с известными моментами сведена к эк-

вивалентной задаче полуопределенного программирования; в [18] определен

минимум вероятности попадания положительной величины в интервал с цен-

тром в моде, совпадающим с математическим ожиданием.

Таким образом, за рамками изучения осталась задача нахождения верхней

границы двусторонней вероятности при условии, что унимодальная случай-

ная величина является симметричной относительно известной моды, не сов-

падающей с центром интервала. Решение данной задачи планируется при-

менить к построению менее консервативных минимаксных оценок ограни-

ченных параметров в линейных регрессионных моделях при использовании

вероятностных критериев качества [19, 20]. Кроме того, результаты статьи

могут найти свое применение при разработке робастных методов принятия

решений в задачах проверки статистических гипотез, планирования экспери-

мента и доверительного оценивания.

Точная формулировка рассматриваемой задачи дана в разделе 2, вид ис-

комой вероятностной границы описан в разделе 3, численный анализ харак-

теристик доверительных интервалов, построенных на основе полученного ре-

шения, представлен в разделе 4.

2. Постановка задачи

Условие унимодальности случайной величины ξ, имеющей нулевую моду,

означает, что функция распределения F (x) = P{ξ ≤ x} является выпуклой

на (-∞, 0) и вогнутой на (0, ∞). Это равносильно тому, что вероятность по-

падания в любое борелевское множество B можно записать в виде

∫

(1)

P{ξ ∈ B} = (1 - q)δ₀(B) + q

f (x) dx,

где q — число из отрезка [0, 1], δ₀ — мера Дирака, сосредоточенная в нуле,

f (x) — плотность вероятности, монотонно невозрастающая справа от нуля и

монотонно неубывающая слева от нуля.

104

Предположение о том, что ξ имеет унимодальное распределение, симмет-

ричное относительно нуля, означает, что имеет место представление (1),

в котором функция f(x) может быть выбрана четной. Если дополнительнo

известна дисперсия Dξ = d, то указанное предположение о величине ξ будем

записывать в виде ξ ∼ U(d), а также ξ ∼ U при d = 1.

Важным представителем класса U(d) является смесь двух распределений:

вырожденного δ₀ и равномерного R(-u, u). Смесь двух распределений P₀ и P₁

будем обозначать (1 - q)P₀ + qP₁.

Цель работы — определить точную верхнюю грань вероятности того, что

симметричная унимодальная величина с фиксированными модой и диспер-

сией находится вне заданного интервала. Такую границу принято называть

двусторонней, поскольку в ее определении участвуют вероятности попадания

величины справа и слева от интервала. Данное событие обычно восприни-

мается как нежелательное, поэтому распределение, на котором достигается

искомая граница, называется наихудшим.

Если считать, что мода равна нулю, а дисперсия равна единице, то эту

задачу можно сформулировать следующим образом.

Задача. Для любых h > 0 и m ∈ R определить вероятностную границу

(2)

u_h(m) = sup

P{|ξ - m| ≥ h}

ξ∼U

и описать распределение, на котором достигается данный супремум.

Отметим, что граница (2) представляет собой функцию двух переменных:

середины m и радиуса h промежутка (m - h, m + h). Указанные переменные

удобно называть сдвигом и порогом, поскольку (2) — это наихудшее значение

вероятности превышения случайной величиной порога h с учетом сдвига m.

Если сдвиг нулевой, т.е. m = 0, то искомая граница совпадает с правой частью

неравенства Гаусса [2]:

⎧

√

⎪

√ , h ≤ 2/

⎨

(3)

P{|ξ| ≥ h} ≤ g_h =

⎪

√

⎩⁴

h ≥ 2/

9h²

Если же m = 0, то промежуток (m - h, m + h) расположен несимметрично

относительно моды, и в этом случае задача (2) не имеет известного решения.

Отметим, что помимо (3) известно неравенство Высочанского — Петунина

[3, 4]:

(4) P{|ξ - m| ≥ h} ≤ v_h(m) =

⎧

√

⎪1,

h≤

m² + 1,

⎪

⎨

√

4(m² + 1)

m² + 1 ≤ h ≤

8(m² + 1)/3,

⁼⎪⎪

3h²

⎪

(m² + 1)

√

⎩⁴

h≥

8(m² + 1)/3,

9h²

105

которое справедливо для любой унимодальной величины ξ без требования

симметричности распределения и без ограничения на моду, но при тех же

условиях на моментные характеристики Eξ = 0 и Dξ = 1.

3. Решение задачи

Сначала опишем элементарные свойства вероятности, которая подлежит

максимизации в задаче (2).

Лемма. Если ξ ∼ U(d) и h > 0, то вероятность

π_h(m) = P{|ξ - m| ≥ h},

как функция параметра m ∈ R: четна; выпукла на отрезке [-h, h]; монотон-

но не убывает на [0,∞) и не возрастает на (-∞,0]; принимает наимень-

шее значение в нуле; непрерывна всюду кроме, быть может, точек ±h, но

π_h(m) → π_h(h) при m ↓ h или m ↑ -h.

Из леммы следует, что искомая функция u_h(m) тоже обладает свойством

симметрии: u_h(m) = u_h(-m). Поэтому не ограничивая общности, можно счи-

тать, что m ≥ 0, т.е. середина интервала смещена вправо от моды.

Решение поставленной задачи приведено в следующей теореме.

Теорема. Для h > 0 и m ≥ 0 граница (2) имеет вид

⎧

(

)

⎪

√

m≤ 1-

√

h≤

√ , (i)

⎪

-′′ - ′′ - ′′-

h≥

√ , (ii)

⎪

9h²

⎪

(

)

⎪

⎪1-

√

h ≤ m < h, q₁ ≥ 1, (iii)

⎪

⎨

{

}

(

)₃

u_h(m) =

a-2

⎪

-′′ - ′′ - ′′-

q₁ ≤ 1 ≤ q₂, (iv)

⎪

a-1

9h²

a-1

⎪

{

}

⎪

⎪1

h-m

⎪

√

-′′ - ′′ - ′′-

q₂ ≤ 1 ≤ q₃, (v)

⎪2

⎪

-′′ - ′′ - ′′-

q₃ ≤ 1, (vi)

⎪

⎪9(h - m)2

⎪

^⎩1,

m ≥ h,

(vii)

106

где обозначено

(

)2/3

h-m

(

)₂

q₁ =

3h²

a-1

q₂ =

3(h - m)²(a - 1)²

q₃ =

3(h - m)²

причем указанные параметры удовлетворяют условиям

⎧

(

)

⎪

⎨a > 2,

<q₁ <q₂ <q₃,

если

√

h < m < h,

3h²

(

)

⎪

^⎩a = 2, q₁ =

<q₂ =q₃ =

если m =

√

3h²

В зависимости от выбора случая из (i)-(vi) граница (2) будет достигать-

ся на одном из следующих распределений:

√

(i), (iii), (v) R(-

3);

(

)

(ii)

(1 - q)δ₀ + qR

при q =

;

3h²

(iv)

(1 - q)R(-u₀, u₀) + qR(-u₁, u₁), где

3h(a - 1)

aq₁ - 1

u₀ =

<u₁ =

и q=

;

a3/2

a-1

(

3(h - m)

3(h - m)⁾

(vi)

(1 - q)δ₀ + qR -

при q = q₃.

В случае (vii) граница (2) достигается на последовательности распреде-

(

√

)

лений (1 - q_n)δ₀ + q_nR

3/q_n,

3/q_n

, где q_n ↓ 0.

Доказательство теоремы дано в Приложении.

Для сдвига произвольного знака во всех приведенных формулах необхо-

димо заменить m на модуль |m|.

Важнейшим следствием сформулированной теоремы является тот факт,

что граница g_h из неравенства Гаусса (3) остается в силе для сравнительно

малых значений сдвига.

Следствие 1. Неравенство Гаусса

⎧

⎪

⎨1-

√

h≤

√ ,

(5)

P{|ξ - m| ≥ h} ≤ g_h =

⎪

⎩

h≥

√ ,

9h²

107

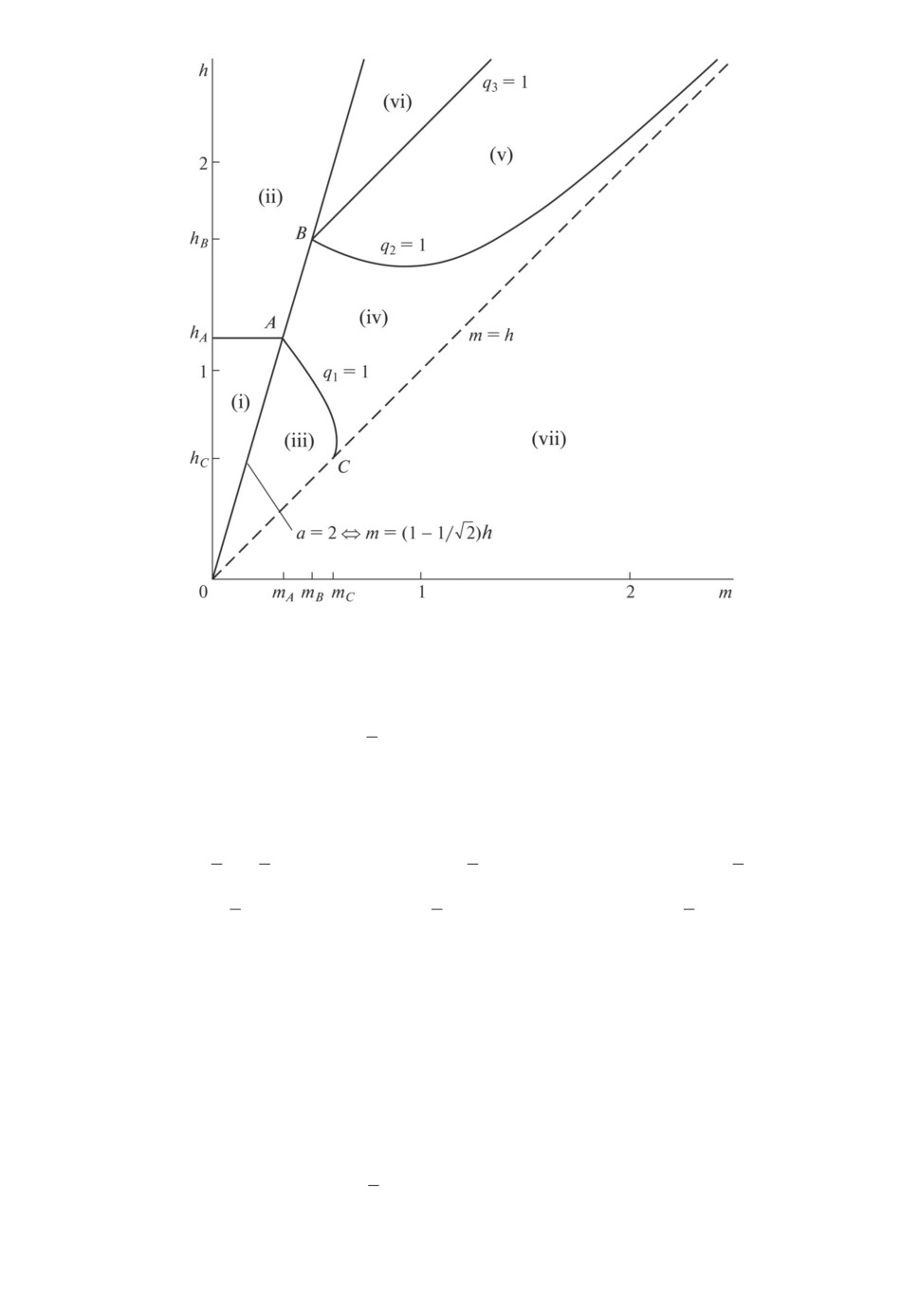
Рис. 1. Области (i)-(vii).

описывает неулучшаемую верхнюю границу вероятности выхода случайной

величины ξ ∼ U за пределы√нтервала, смещение которого m относительно

моды не превышает 1 - 1/

2 ≈ 0,2928 доли радиуса h.

Каждый из случаев (i)-(vii) соответствует своей области, изображенной

на рис. 1. Точки пересечения границ нескольких областей имеют следующие

координаты:

√

m_A = (2 -

2)/

3 ≈ 0,3382, m_B =

2m_A ≈ 0,4783, m_C = 1/

3 ≈ 0,5774,

√

h_A = 2/

3 ≈ 1,1547, h_B =

2h_A ≈ 1,6330, h_C = 1/

3 ≈ 0,5774.

На границе между любой из двух областей (i)-(vi) описанные наихудшие

распределения совпадают, кроме двух пар: (ii), (iv) и (ii), (vi). Это означа-

ет, что на указанных границах в качестве наихудшего распределения можно

взять смесь распределений, соответствующих внутренностям двух областей.

Поэтому искомое распределение на общей границе имеет вид:

(1 - ε)(1 - q)δ₀ + 2ε(1 - q)R(-u₀, u₀) + (q - ε(1 - q))R(-u₁, u₁) для (ii) и (iv),

(1 - q - εq)δ₀ + 2εqR(-u₀, u₀) + (1 - ε)qR(-u₁, u₁) для (ii) и (vi),

√

где q = 4/(3h²), u₀ = 3h/(2

2), u₁ = 3h/2, а ε — произвольное число из от-

резка [0, 1].

108

= 1/36

= 1/18

= 1/12

= 1/9

h_B

h_A

= 1/6

h_C

= 1/3

= 1/2

= 2/3

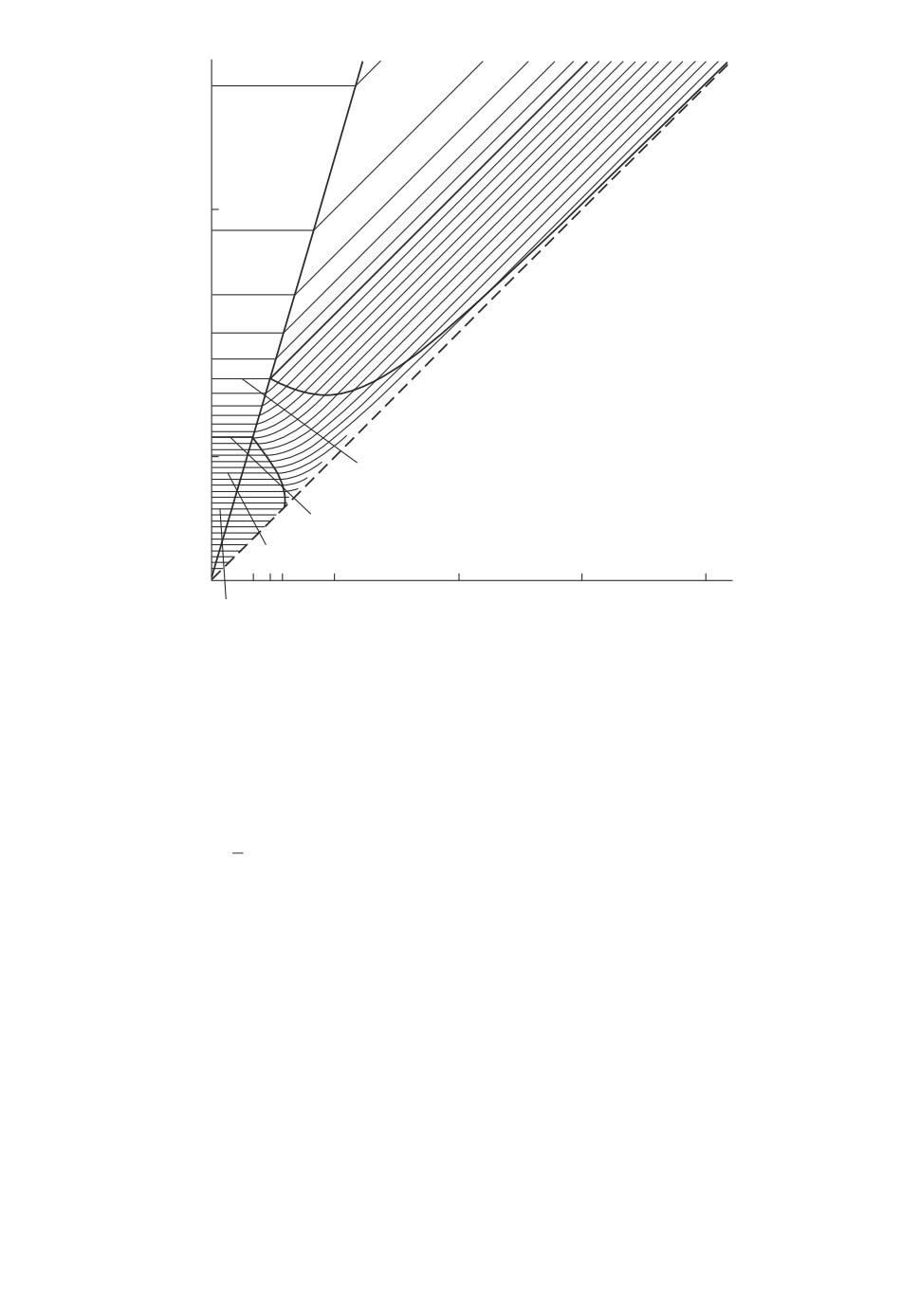
Рис. 2. Линии уровня u_h(m) = α для α = k/36 при k = 1, . . . , 35.

При доказательстве теоремы был использован метод преобразования за-

дачи (2) к проблеме моментов Маркова, т.е. к задаче оптимизации на клас-

се неотрицательных мер без требований унимодальности, но при специаль-

ных моментных ограничениях. Анализ этой задачи показывает, что ее ре-

шение определено единственным образом при любом сочетании парамет-

ров m и h, взятых из области |m| < h за исключением двух полупрямых:

√

m = ±(1 - 1/

2)h, h > h_A. При положительных m это соответствует грани-

цам областей (ii), (iv) и (ii), (vi) кроме точки A (см. рис. 1).

Вид линий уровня функции u_h(m), рассматриваемой на плоскости пере-

менных (m, h), представлен на рис. 2.

Из теоремы следует, что для нахождения границы u_h(m) достаточно рас-

сматривать только распределения, представляющие собой смесь двух рав-

номерных. Чтобы получить явные соотношения, следующие из этого фак-

та, определим вероятность выхода величины ξ ∼ R(-u, u) из интервала

(m - h, m + h) при 0 ≤ m < h:

⎧

⎪0,

u ≤ h - m,

⎨

{

}

(6)

P{|ξ - m| ≥ h} =

1 - (h - m)/u

/2, h - m ≤ u ≤ h + m,

⎪

⎩

1 - h/u,

u ≥ h + m.

109

Если три выражения в (6) обозначить как ρ_k(m, h; u), k = 0, 1, 2, заменив

всюду m на |m|, то равенство (6) при |m| < h можно записать в виде

P{|ξ - m| ≥ h} = max

ρ_k(m,h; u).

k=0,1,2

Теперь сформулируем полученное утверждение.

Следствие 2. В определении границы (2) класс U можно заменить на

семейство распределений вида (1 - q)R(-u₀, u₀) + qR(-u₁, u₁), где парамет-

ры подчиняются ограничениям

(7)

q ∈ [0,1], u₀ > 0, u₁ > 0 и

(1 - q)u²⁰ + qu²¹

= 3.

Граница u_h(m) представляет собой непрерывную выпуклую функцию па-

ры переменных (m,h), таких что |m| < h, и может быть записана в виде

(8)

u_h(m) = sup{(1 - q)ρ_k(m,h; u₀) + qρ_k(m,h; u₁

)},

где супремум берется по всевозможным наборам (k,q,u₀,u₁), в которых

k = 0,1,2, а q,u₀,u₁ удовлетворяют (7). Но на диагоналях m = ±h имеет

место разрыв:

⎧

⎪

√

h≤

√ ,

⎪

lim

u_h(m) =

lim u_h(m) = 1.

|m|↑h

⎪

(

)

|m|↓h

⎪1

⎩

h≥

√ ,

9h²

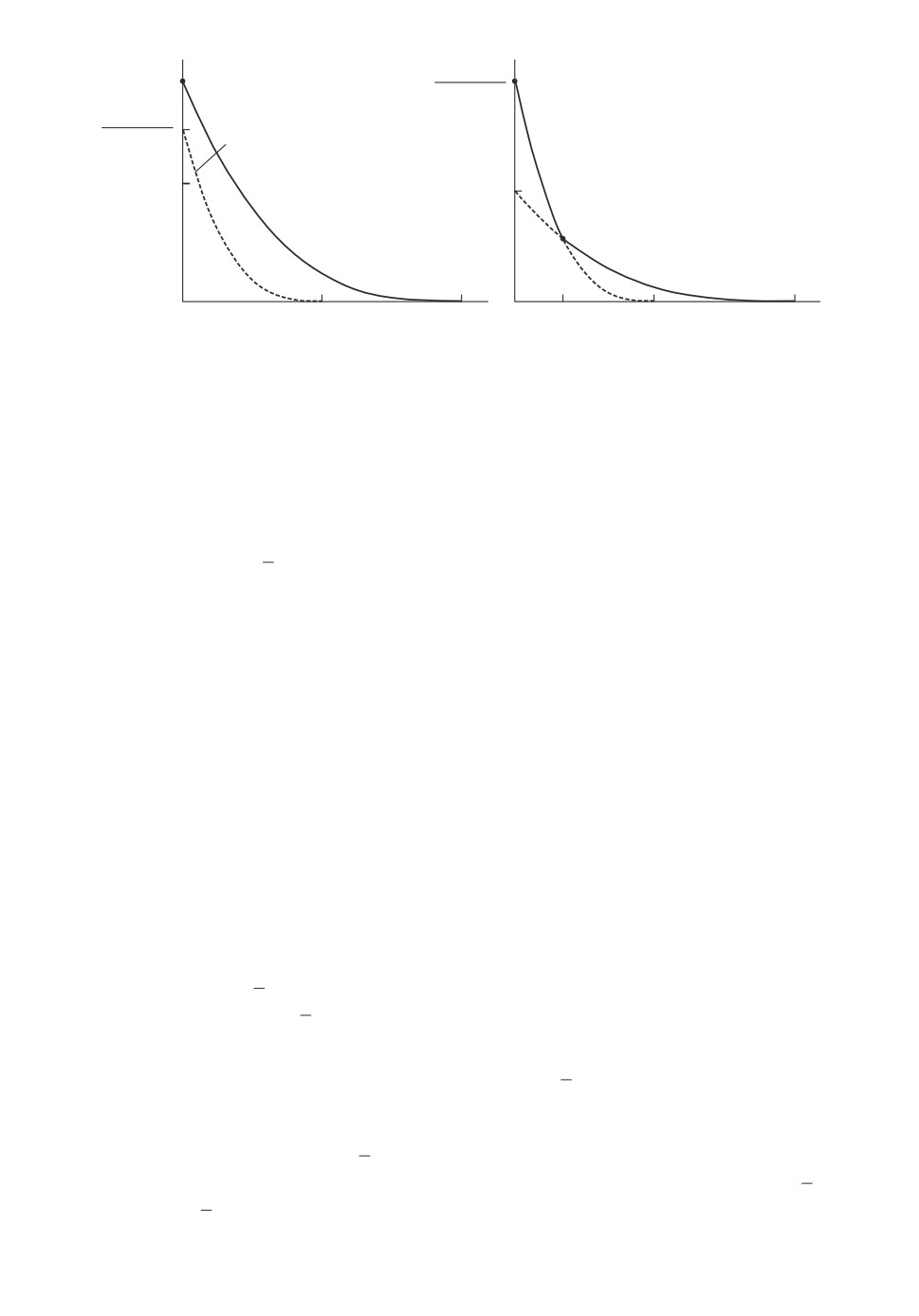
Теперь перейдем к рассмотрению найденной границы как функции одной

переменной.

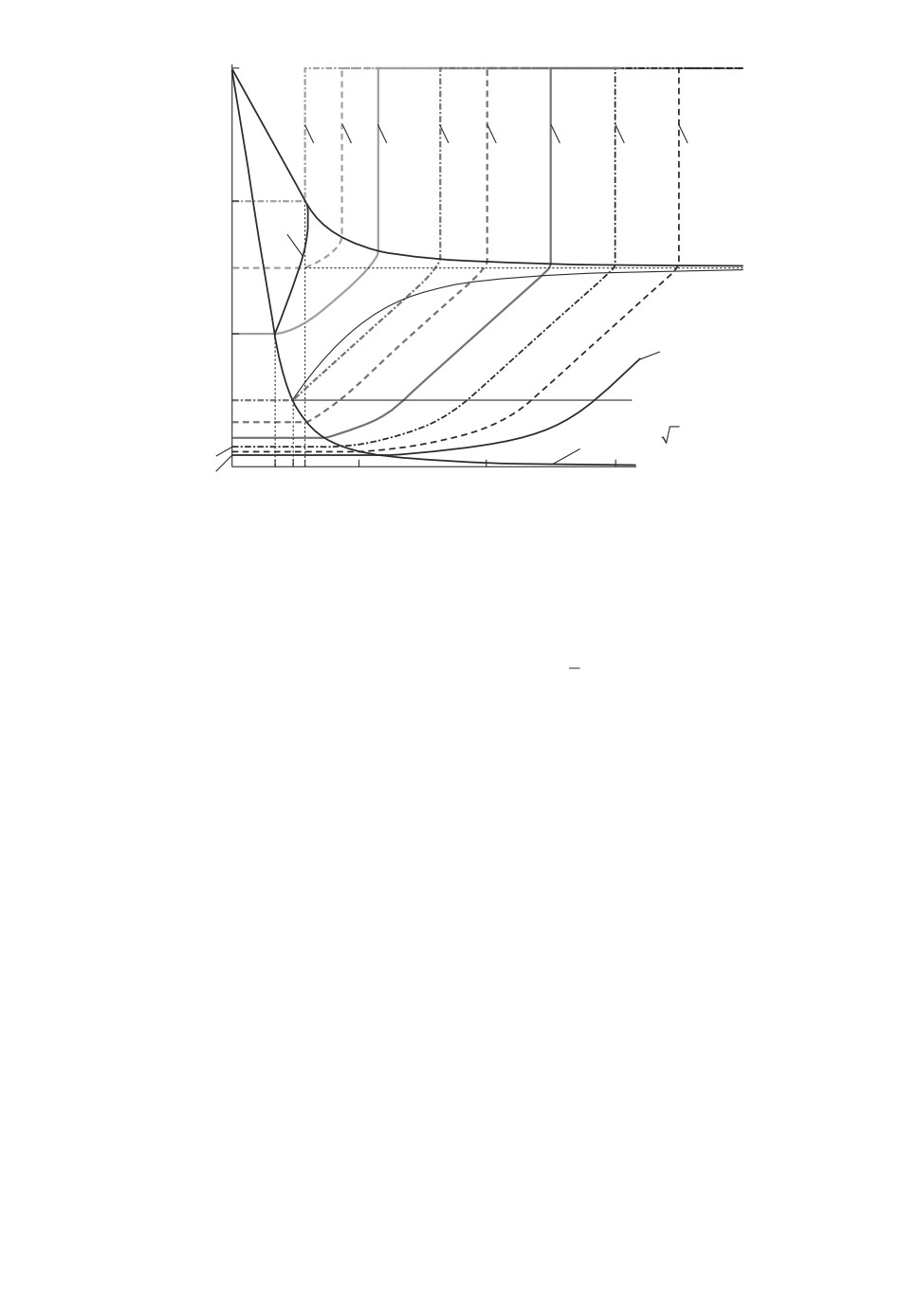
На рис. 3 изображена зависимость вероятности α = u_h(m) от сдвига m ≥ 0

для нескольких значений порога h > 0. Полученные функции монотонно не

убывают, выпуклы на промежутке [0, h], терпят разрыв в точке m = h и

√

постоянны при m ≤ (1 - 1/

2)h ≈ 0,2928h. Поэтому при относительно ма-

лых значениях сдвига неравенство Гаусса остается в силе. Например, при

m = 1 и h = 3 неравенство Гаусса дает 4/81, что лишь на 11 % меньше истин-

ной границы u_h(m) = 1/18. Если же h = 2, то при том же значении сдвига

отличие между двумя границами становится существенным: 1/9 ≈ 0,1111 и

√

(1 - 1/

3)/2 ≈ 0,2113 соответственно.

На рис. 3 представлены также границы областей (i)-(vii), описанных в тео-

реме (см. также рис. 1 и 2). Общая граница для областей (i) и (ii) опущена,

так как она представляет собой отрезок, совпавший с частью графика функ-

ции u (m)._h

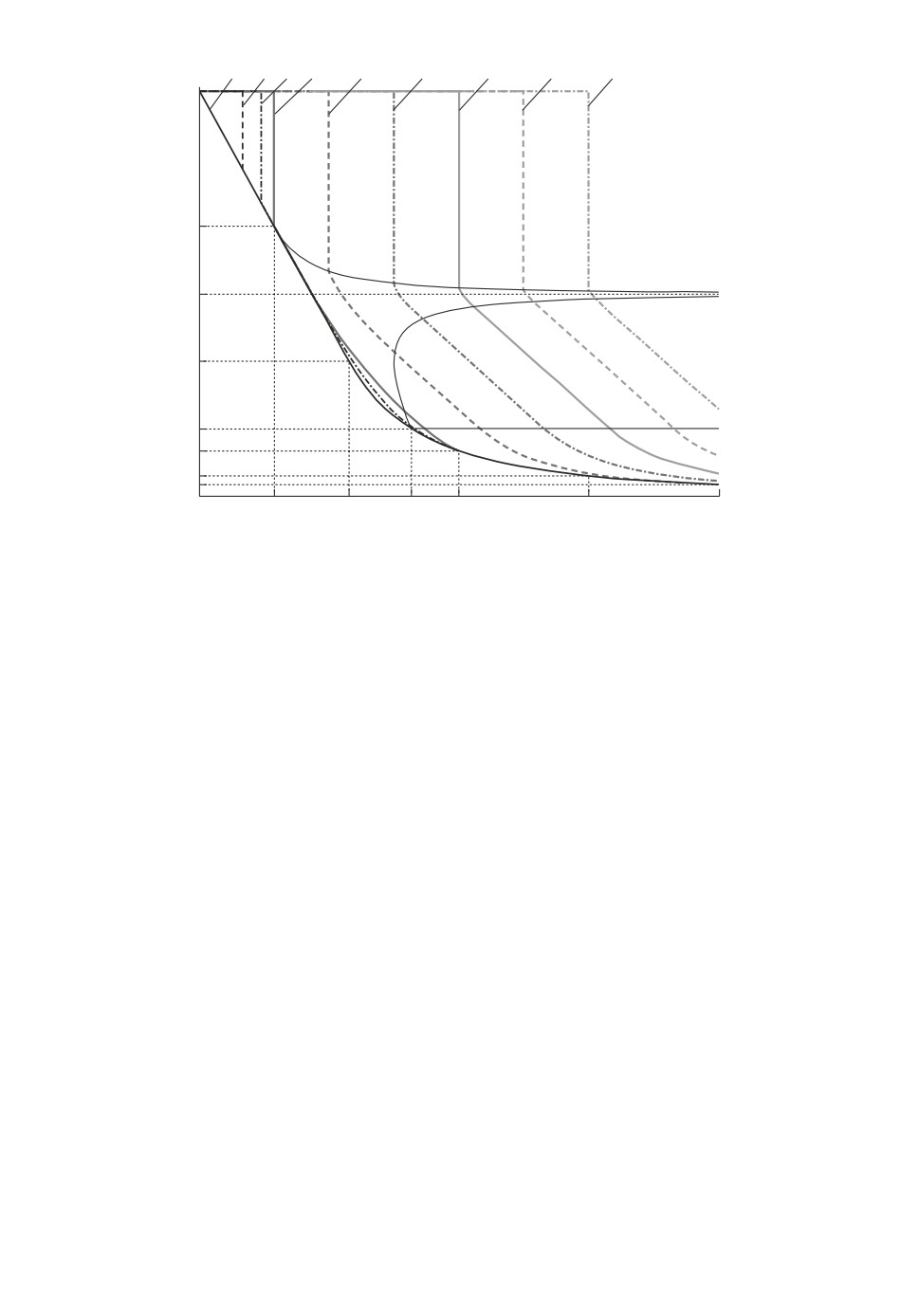
Зависимость вероятностной границы α = u_h(m) от величины порога h ≥ 0

для нескольких значений m представлена на рис. 4. Полученные функции мо-

нотонно не возрастают, равны единице при h ≤ m, имеют разрыв при h = m

и выпуклы при h ≥ m. Случай m = 0 соответствует правой части неравен-

ства Гаусса, т.е. u_h(0) = g_h. График этой функции оказывается самой ниж-

ней кривой, на которую ложатся все графики α = u_h(m), соответствующие

110

2/3

q₁ = 1

m = h

1/2

q₂ = 1

1/3

1/6

q₃ = 1

1/9

m = (1

2)h

4/81

1/36

m_A

m_B

m_C

Рис. 3. Графики зависимости α = u_h(m) от m для нескольких значений h

(толстые кривые 1-9: 1 — h = h_C ; 2 — h = 1,5h_C ; 3 — h = h_A; 4 — h = h_B;

5 — h = 2; 6 — h = 2,5; 7 — h = 3; 8 — h = 3,5; 9 — h = 4) и границы областей

(тонкие сплошные кривые).

значениям параметра m ≤ m_A и рассматривае√ е при h > m. С указанной

кривой совпадает проекция прямой m = (1 - 1/

2)h, которая служит грани-

цей нескольким областям (см. рис. 1). Часть этой кривой при α ∈ [1/3, 2/3]

представляет собой проекцию общей границы областей (iii) и (iv). Граница

между (i) и (ii) при проектировании на плоскость переменных (h, α) превра-

тилась в точку (h_A, 1/3).

Отсутствие непрерывности u_h(m) на всей плоскости параметров (m, h)

объясняется тем, что класс распределений U не образует множества, компакт-

ного в слабой топологии. Если же носитель распределений P_ξ считать рав-

номерно ограниченным, то аналогичная вероятностная граница будет непре-

рывной при любом соотношении между переменными m и h. Однако полное

решение соответствующей задачи выходит за рамки данной статьи.

4. Сравнительный анализ

Найденную вероятностную границу можно использовать для анализа на-

дежности доверительных интервалов и повышения их робастности.

Допустим, что для неизвестного параметра θ ∈ R используется точечная

оценка^θ, которая имеет фиксированную дисперсию D^θ = 1, неизвестное, но

ограниченное смещение m ∈ [-r, r] и неопределенное симметричное унимо-

дальное распределение. Тогда (θ- h,θ+ h) называется доверительным ин-

тервалом гарантированной надежности 1 - α, если

(9)

P{θ ∈ (θ- h,θ

+ h)} ≥ 1 - α.

111

2/3

m = h

1/2

q₂ = 1

1/3

1/6

q₃ = 1

1/9

4/81

1/36

h_C

h_A

h_B

Рис. 4. Графики зависимости α = u_h(m) от h для нескольких значений m

(толстые кривые 1-9: 1 — m = 0; 2 — m = m_A; 3 — m = m_B; 4 — m = m_C ; 5 —

m = 1; 6 — m = 1,5; 7 — m = 2; 8 — m = 2,5; 9 — m = 3) и границы областей

(тонкие сплошные кривые).

Определение числа 1 - α как неулучшаемой границы в этом неравенстве

равносильно решению поставленной задачи. Чтобы в этом убедиться, введем

в рассмотрение центрированную ошибку ξ = Δθ- m и запишем неравенство

для противоположной вероятности P{|ξ + m| ≥ h} ≤ α. Тогда для нахожде-

ния α необходимо вычислить точную верхнюю грань левой части по всем

ξ ∼ U и |m| ≤ r. В силу леммы указанная вероятность монотонно зависит

от |m|, поэтому достаточно взять m = r. Теперь искомый уровень значимо-

сти α будет определяться как вероятностная граница (2):

(10)

u_h

(r) = α.

Если выполнено (10), то будем говорить, что построен робастный довери-

тельный интервал (θ- h,θ+ h) на уровне значимости α.

При этом интервал (θ- h,θ+ h) будет наименьшим среди интервалов вида

(θ- h₁,θ+ h₂), для которых условие P{θ ∈ (θ- h₁,θ+ h₂)} ≥ 1 - α выполне-

но при произвольном выборе ограниченного смещения m ∈ [-r, r] и распре-

деления центрированной ошибки из класса U.

Описанные предположения возникают при использовании линейных сме-

щенных оценок^θ = 〈ℓ, Y 〉 параметрической функции θ = 〈b, υ〉 в модели ли-

нейной регрессии Y = Aυ + η в присутствии ограниченного вектора неизвест-

ных параметров υ и центрированной помехи η с неопределенным распределе-

нием симметричного и унимодального вида. Чтобы определить гарантирован-

112

ную надежность 1 - α соответствующей интервальной оценки (θ- h,θ+ h)

необходимо положить α = u_h/σ(r/σ), где σ² — дисперсия оценки^θ, а r — наи-

большее значение смещения 〈A^∗ℓ - b, υ〉 с учетом априорных ограничений на

вектор υ.

Важность изучения смещенных оценок объясняется тем, что отказ от

несмещенности позволяет снизить среднеквадратическую ошибку оценива-

ния за счет использования априорных ограничений на неизвестные парамет-

ры. Более того, в моделях с большим числом факторов и в мультиколлинеар-

ных регрессиях построение несмещенных оценок наталкивается на серьезные

численные проблемы, связанные с точным соблюдением равенства A^∗ℓ = b.

Сравним характеристики интервальных оценок для нескольких гипотез

о распределении центрированной ошибки ξ:

1) ξ — нормальная случайная величина, т.е. ξ ∼ N(0, 1);

2) ξ имеет распределение Тьюки T = (1 - ε)N(0, σ²⁰) + εN(0, σ²¹), где доля

выбросов ε равна 10 %, а соотношение между номинальными значениями и

выбросами задается дробью σ₁/σ₀ = 5 c учетом Dξ = (1 - ε)σ²⁰ + εσ²¹ = 1;

3) ξ определяет решение задачи (2), т.е. P_ξ — наихудший представитель

класса симметричных унимодальных распределений U;

4) P_ξ — распределение, на котором достигается граница v_h(m) из неравен-

ства Высочанского — Петунина (4).

Во всех четырех случаях речь идет об унимодальной величине с едины-

ми моментными характеристиками: Eξ = 0 и Dξ = 1. Первые три распределе-

ния симметричны относительно нуля, который одновременно выполняет роль

единственной моды. Четвертое распределение имеет неопределенную моду и

может быть несимметричным.

Теперь для каждого из четырех вариантов рассмотрим вероятность

{

}

(11)

P θ ∈ (θ- h, θ+ h)

= P{|ξ + m| ≥ h}.

При ξ ∼ N(0, 1) указанная вероятность равна

ν_h(m) = Ψ(h - m) + Ψ(h + m),

где

∫∞

e-t2/²

Ψ(x) =

√ dt.

2π

Для случая ξ ∼ T вероятность (11) принимает вид

[

)

⁽h-m

⁽h+m)]+

τ_h(m) = (1 - ε) Ψ

+Ψ

σ₀

[

)

⁽h-m

⁽h+m)].

+ε Ψ

+Ψ

σ₁

113

Таблица 1. Надежность доверительного интервала

m h

1 - ν_h(m)

1 - τ_h(m)

1 - u_h(m)

1 - v_h(m)

0,866

0,6135

0,8258

0,5

1,282

0,8

0,9200

0,7294

0,5215

1,633

0,8975

0,9430

0,8333

0,9545

0,9537

0,8889

0,9973

0,9731

0,9506

0,9999

0,9860

0,9722

0,5

1,282

0,7453

0,8680

0,7074

0,3185

0,5

0,9270

0,9506

0,8889

0,8611

0,5

0,9936

0,9723

0,9506

0,9383

0,5

0,9998

0,9853

0,9722

0,9653

0,8400

0,9216

0,7887

0,6667

0,9772

0,9699

0,9444

0,9012

0,9986

0,9833

0,9722

0,9444

0,8413

0,9318

0,7887

0,5926

0,9772

0,9755

0,9444

0,8611

0,8413

0,9346

0,7887

0,5

Для третьего и четвертого вариантов распределений вероятность (11) сов-

падает со своим наихудшим значением: u_h(m) и v_h(m) соответственно (см.

теорему и неравенство (4)). В отличие от первых двух случаев здесь распре-

деление не является фиксированным и само зависит от параметров m и h.

В табл. 1 для каждой из четырех гипотез приведены данные о надежности

доверительного интервала в зависимости от его радиуса h и величины сме-

щения m. Первые три значения h выбраны из следующих соображений: во-

первых, при h = 1,5h_A ≈ 0,866 неравенство Гаусса дает g_h =√5; во-вторых,

h ≈ 1,282 — решение уравнения Ψ(h) = 0,1; в третьих, h_B =

8/3 ≈ 1,633 —

наименьшее значение порога h, при котором границы Гаусса и Высочанско-

го — Петунина совпадают, т.е. g_h = v_h(0).

В целом, можно отметить, что граница u_h(m) остается приемлемой при

значительном смещении. Например, если пользоваться правилом “трех сигм”,

то при наличии смещения в “одну сигму” надежность доверительного интер-

вала будет: примерно 0,98 в гауссовском случае; почти 0,97 в модели Тьюки;

не меньше 0,94 в случае симметричного унимодального распределения; около

0,9 при наихудшем выборе моды.

Теперь найдем радиус h робастного доверительного интервала (θ- h,

^θ+ h), построенного на уровне значимости α. Для этого необходимо опре-

делить наибольшую вероятность события {|ξ + m| ≥ h} с учетом ограничен-

ности смещения m и априорной информации о распределении центрирован-

ной ошибки ξ. Максимум по m ∈ [-r, r] будет достигаться при m = ±r в си-

лу симметричной и монотонной зависимости от m (см. лемму и выражения

для границ u_h(m) и v_h(m)). Следовательно, искомый радиус h находится из

уравнения, в одной части которого стоит α, а в другой — одна из четырех

вероятностей: ν_h(r), τ_h(r), u_h(r) или v_h(r).

114

Таблица 2. Радиус робастного доверительного интервала

α r h: ν_h(r) = α h: τ_h(r) = α h: u_h(r) = α h: v_h(r) = α

0,2

1,282

0,806

1,491

1,581

0,2

0,5

1,439

1,078

1,542

1,768

0,1

1,645

1,137

2,108

0,1

0,5

1,839

1,427

2,108

2,357

0,1

2,284

1,874

2,491

2,981

0,05

1,960

1,853

2,981

0,05

0,5

2,181

1,984

2,981

3,333

0,05

2,646

2,303

3,108

4,216

0,05

1,5

3,145

2,715

3,608

5,375

0,025

2,241

3,119

4,216

0,025

0,5

2,485

3,172

4,216

4,714

0,025

2,961

3,332

4,216

5,963

0,025

1,5

3,460

3,599

4,481

7,601

0,025

3,960

3,962

4,981

9,428

В табл. 2 для каждой из четырех гипотез указаны значения радиуса h ро-

бастного доверительного интервала в зависимости от уровня значимости α и

границы смещения r. Стоит отметить, что использование границы Высочан-

ского — Петунина в ситуации большого смещения приводит к неоправданно

широким интервалам. Вместе с тем граница u_h(r) в этой ситуации дает воз-

можность построить робастный доверительный интервал приемлемой дли-

ны. Например, при наличии смещения в “одну сигму” такой интервал лишь

на четверть длиннее интервала, построенного для объединенной гипотезы:

N(0, 1) или T.

Итак, при использовании симметричных унимодальных статистик с не-

определенным распределением и ограниченным смещением новая вероят-

ностная граница u_h(m) позволяет получать робастные статистические ре-

шения, существенно менее консервативные, чем известные ранее.

5. Заключение

В статье найдена точная верхняя грань вероятности попадания вне конеч-

ного интервала для случайной величины с неопределенным симметричным

унимодальным распределением и фиксированными модой и дисперсией. Спе-

цифика этой задачи состоит в том, что мода смещена относительно середины

интервала. Однако если смещение составляет меньше 29 % радиуса интерва-

ла, то найденная вероятностная граница определяется неравенством Гаусса,

т.е. оказывается такой же, как в случае нулевого смещения. Полученный ре-

зультат позволил построить робастные версии интервальных оценок, которые

сохраняют приемлемую точность даже при наличии неизвестного ограничен-

ного смещения центральной статистики. Решенная в статье задача расши-

ряет инструментарий робастных методов анализа данных и идентификации

систем.

115

ПРИЛОЖЕНИЕ

Доказательство леммы. Вероятность π_h(m) можно записать через

функцию распределения F (x) с учетом симметрии распределения:

π_h(m) = P{ξ ≤ m - h} + P{ξ ≥ m + h} = F(m - h) + F(-m - h).

Ясно, что π_h(m) = π_h(-m). Выпуклость по m ∈ [-h, h] следует из того,

что F (x) выпукла при x ≤ 0. Если m ↓ h, то π_h(m) → π_h(h) в силу того, что

F (x) непрерывна справа в точке x = 0 и непрерывна при x < 0. Величина

скачка π_h(m) в точке m = h равна неотрицательной величине 1 - q. Других

точек разрыва у этой функции, рассматриваемой при m ≥ 0, нет. Поэтому

для проверки монотонност( по m ≥ 0 остается пр)верить знак производной.

Ее можно записать в виде q

f (m - h) - f(-m - h)

в силу (1). Если m ≤ h, то

производная неотрицательна в сил(у того, что f(x) не уб)вает при x ≤ 0. Если

же m ≥ h, то производная равна q

f (m - h) - f(m + h)

в силу f(x) = f(-x)

и неотрицательна благодаря тому, что f(x) не возрастает при x ≥ 0. Тем са-

мым лемма доказана.

При доказательстве основного результата понадобится утверждение, поз-

воляющее преобразовать задачу оптимизации на классе унимодальных рас-

пределений к проблеме моментов Маркова.

Лемма П.1. Пусть M - класс неотрицательных счетно-аддитивных

мер μ, заданных на борелевских подмножествах открытого интерва-

ла (0, ∞).

Существует взаимно однозначное соответствие между распределения-

ми P_ξ из класса U(d) и мерами μ ∈ M, которые подчиняются ограничениям

∫

∞

∫

∞

y³

(Π.1)

y μ(dy) ≤ 1 и

μ(dy) = d.

Указанное соответствие определено равенством

⎧

⎫

∫∞

∫

∞

⎨∫y

⎬

(Π.2)

g(x) P_ξ (dx) =

g(x) dx

μ(dy),

⎩

⎭

где g(x)

— произвольная борелевская функция, такая что g(0) = 0 и

E|g(ξ)| < ∞.

Доказательство леммы П.1. Для каждого P_ξ ∈ U(d) зададим меру

Лебега — Стилтьеса μ:

(

)

μ((a, b]) = 2q

f (a) - f(b)

0 < a < b < ∞,

где число q и функция f(x) взяты из представления (1), причем f(x) выбрана

непрерывной справа при x > 0. Из теоремы Каратеодори в силу монотонно-

сти f(x) следует μ ∈ M. Запишем интеграл в левой части (Π.2) с помощью

116

равенства 2qf(x) = μ((x, ∞)):

⎧

⎫

∫

∞

∫

∞

∫

⎬

g(x)μ((x, ∞)) dx = g(x)

I{y > x} μ(dy)

dx.

⎩

⎭

Меняя местами интегралы, приходим к правой части равенства (Π.2).

Построенное соответствие взаимно однозначно, так как

∫∞

∫

∞

f (x) = μ((x, ∞))/q, q = P{ξ = 0} = 2 I{x > 0} P_ξ (dx) = y μ(dy).

Остается проверить соотношения (Π.1). Первое из них вытекает из условия

нормировки, доказанного равенства (Π.2) и условия q ≤ 1:

∫∞

∫

∞

1=1-q+2

I{x > 0} P_ξ (dx) = 1 - q + y μ(dy).

Второе соотношение (Π.1) следует из предположения Eξ² = d и равен-

ства (Π.2), в котором g(x) = x². Лемма П.1 доказана.

Доказательство теоремы. Начнем с проверки случая (vii): m ≥ h.

В этом случае интервал (m - h, m + h) не содержит нуля, поэтому вероят-

ность попадания в него случайной величины

(

√

)

ξ_n ∼ (1 - q_n)δ₀ + q_nR

3/q_n,

3/q_n

√

равна q_n h

q_n/3 для всех достаточно малых q_n > 0. Если q_n ↓ 0, то противопо-

ложная вероятность сходится к единице, что с учетом ξ_n ∼ U дает u_h(m) = 1.

Пусть теперь и далее 0 ≤ m < h. В силу симметрии распределения имеем

∫∞

π_h(m) = P{ξ ≥ h - m} + P{ξ ≥ h + m} = g(x)P_ξ(dx),

где g(x) = I{x ≥ h - m} + I{x ≥ h + m}. Первообразная этой функции имеет

вид

∫

{

}

G(y) = g(x) dx = max

0, y - (h - m), 2(y - h)

Если в определении искомой границы (2) расширить класс распределений до_⋃

U(d), то благодаря лемме П.1 получится неравенство

d≤1

⎧

⎫

∫

∞

∫

∞

∫

∞

⎨

⎬

y³

u_h(m) ≤

sup

G(y) μ(dy):

y μ(dy) ≤ 1,

μ(dy) ≤ 1

μ∈M

⎩

⎭

Нахождение супремума в правой части составляет проблему моментов

Маркова. Для ее решения введем множители λ₁, λ₂, функцию H_λ(y) = λ₁ y +

117

9h²

9(h m)²

= h₁(₁)

2 = h1( 1)

9(h m)²

9h²

= h₂(₁)

2 = h2( 1)

Рис. 5. Зависимости λ₂ = h₁(λ₁), λ₂ = h₂(λ₁) и граница множества Λ (сплош-

ная кривая); точки и участки сплошной кривой соответствуют областям (i)-

(vi); слева изображен случай h₁(0) < h₂(0), справа — случай h₁(0) > h₂(0).

+λ₂y³/3 и воспользуемся стандартным переходом к двойственной задаче

(см., например, [2]):

(Π.3)

u_h(m) ≤

inf {λ₁ + λ₂ : G(y) ≤ H_λ(y) ∀ y > 0, λ₁ ≥ 0, λ₂

≥ 0}.

λ₁,λ₂

Выполнение неравенства G ≤ H_λ справа от нуля равносильно тому, что

график z = H_λ(y) лежит не ниже двух прямых: z = y - (h - m) и z =

= 2(y - h). Достаточно рассмотреть только те множители λ₁, λ₂, при кото-

рых график z = H_λ(y) касается хотя бы одной из двух прямых. Для пер-

вой прямой условие касания означает, что равенства H_λ(y) = y - (h - m)

и H^′λ(y) = 1 выполнены для некоторого y > 0. Для второй прямой анало-

гично: H_λ(y) = 2(y - h) и H^′λ(y) = 2. После несложных выкладок указан-

ные условия преобразуются в два уравнения: λ₂ = 4(1 - λ₁)³/(9(h - m)²) при

λ₁ ∈ [0,1] и λ₂ = (2 - λ₁)³/(9h²) при λ₁ ∈ [0,2]. Обозначим эти зависимости

как λ₂ = h₁(λ₁) и λ₂ = h₂(λ₁) соответственно. Тогда множество, образованное

множителями λ₁, λ₂ из (Π.3), можно записать в виде

Λ = {(λ₁,λ₂): λ₂ ≥ h₁(λ₁), λ₂ ≥ h₂(λ₁), λ₁ ≥ 0, λ₂ ≥ 0}.

Вид этого множества зависит от соотношения между числами h₁(0) =

= 4/(9(h - m)²) и h₂(0) = 8/(9h²) (см. рис. 5). Если выполнено h₁(0) ≤ h₂(0),

√

т.е. m ≤ (1 - 1/

2)h, то график второй функции лежит выше графика пер-

√

вой. Если же (1 - 1/

2)h ≤ m, то графики пересекаются в точке λ₁ = λ∗1, где

(

)2/3

λ∗1 = (a - 2)/(a - 1), a =

2h/(h - m)

, причем 0 ≤ λ∗1 ≤ 1 и a ≥ 2.

√

Для решения (Π.3) в случае m ≤ (1 - 1/

2)h достаточно определить

минимум функции λ₁ + h₂(λ₁) по λ₁ ∈ [0, 2]. Так как производная равна

1 - (2 - λ₁)²/(3h²), то минимум на бесконечном промежутке (-∞,2] дости-

√

гается в точке λ′′1 = 2 - h

3. В зависимости от знака (λ′′1 ≥ 0 или λ′′1 ≤ 0)

√

получаем случаи, описанные в формулировке теоремы: (i) h ≤ 2/

√

(ii) h ≥ 2/

3 соответственно. В случае (i) подстановка λ₁ = λ′′1, λ₂ = h₂(λ′′1)

118

Таблица 3

(iii)

(iv)

(v)

(vi)

1≤q₁

q₁ ≤ 1 ≤ q₂ q₂ ≤ 1 ≤ q₃ q₃ ≤ 1

λ∗1 ≤ λ′′1 λ′′1 ≤ λ∗1 ≤ λ′1

0≤λ′1 ≤λ∗1 λ′1 ≤0

√

в выражение (λ₁ + λ₂)/2 дает 1 - h/

3, а в случае (ii) минимум достигается

при λ₁ = 0, откуда λ₂ = h₂(0) и (λ₁ + λ₂)/2 = 4/(9h²).

√

Теперь предположим, что выполнено (1 - 1/

2)h ≤ m < h. В этом слу-

чае точную нижнюю грань в (Π.3) можно найти как минимум выражения,

определяемого двумя функциями: λ₁ + h₁(λ₁) при λ₁ ∈ [0, λ∗1] и λ₁ + h₂(λ₁)

при λ₁ ∈ [λ∗1, 2]. Для этого понадобятся точки λ′1 и λ′′1, в которых эти функ-

ции достигают минимума на промежутках (-∞, 1] и (-∞, 2] соответственно.

√

Точка λ′′1 указана выше, а точка λ′1 = 1 - (h - m)

3/2 находится из равен-

ства нулю производной 1 - 4(1 - λ₁)²/(3(h - m)²). Нетрудно проверить, что

следующие пары неравенств эквивалентны: λ′1 ≤ 0 и q₃ ≤ 1; λ′1 ≤ λ∗1 и q₂ ≤ 1;

λ′′1 ≤ λ∗1 и q₁ ≤ 1, причем q₁ ≤ q₂ ≤ q₃. В зависимости от того, как расположена

единица относительно чисел q₁, q₂, q₃, получаются четыре варианта взаимно-

го расположения точек 0, λ′1, λ′′1, λ∗1. Эти варианты (см. табл. 3) соответствуют

случаям (iii)-(vi), перечисленным в формулировке теоремы.

В случае (iii) минимум в (Π.3) достигается при λ₁ = λ′′1, λ₂ = h₂(λ′′1). Это

√

идентично случаю (i): (λ₁ + λ₂)/2 = 1 - h/

В случае (iv) точкой минимума будет (λ∗1, λ∗2), где

(

)₃

λ∗2 = h₂(λ∗1) =

9h²

a-1

откуда следует, что

{

}

(

)₃

λ∗1 + λ∗2

a-2

a-1

9h²

a-1

√

В случае (v) минимум достигается при λ₁ = λ′1, λ₂ = h₁(λ′1) = (h-m)

3/6,

√

поэтому (λ₁ + λ₂)/2 = (1 - (h - m)/

3)/2.

Наконец, в случае (vi) точка минимума определяется через λ₁ = 0 и

λ₂ = h₁(0). Тогда (λ₁ + λ₂)/2 = 2/(9(h - m)²).

Итак, доказано неравенство: искомая граница u_h(m) не превосходит вы-

ражений, представленных в теореме для каждого из случаев (i)-(vi). Чтобы

установить равенство, остается предъявить распределение, на котором полу-

ченная верхняя оценка достигается.

√

Возьмем ξ ∼ R(-

3) и воспользуемся представлением (6). Тогда име-

√

ет место равенство P{|ξ - m| ≥ h} = 1 - h/

3 для всех точек (m, h), лежа-

√

щих ниже прямой h + m =

3. Судя по рис. 1, области (i) и (iii) лежат ниже

указанной прямой. Поэтому утверждение теоремы доказано для случаев (i)

и (iii).

√

Теперь возьмем точку (m, h) между прямыми h + m =

3 и h-m=

(

√

)

Тогда в силу (6) справедливо P{|ξ - m| ≥ h} =

1 - (h - m)/

/2. Так как

119

область (v) лежит между указанными прямыми, то утверждение теоремы

доказано для случая (v).

Предположим, что ξ ∼ (1 - q)δ₀ + qR(-u, u), где u = 3h/2 и q = 4/(3h²).

Из (6) следует P{|ξ - m| ≥ h} = q(1 - h/u) = 4/(9h²), если u ≥ h + m. По-

следнее неравенство означает, что точка (m, h) лежит выше прямой h = 2m.

Это заведомо так для точек области (ii). Поэтому утверждение теоремы уста-

новлено для случая (ii).

Проверим, что в случае (iv) справедливы неравенства

(Π.4)

h-m<u₀ <h+m<u₁,

где u₀ = 3h(a - 1)/a3/2, u₁ = 3h(a - 1)/a и a3/2 = 2h/(h - m). Запишем по-

следнее равенство как m/h = 1 - 2/a3/2 и подставим его в (Π.4):

2/a3/2 < 3(a - 1)/a3/2 < 2 - 2/a3/2 < 3(a - 1)/a.

Первое неравенство равносильно условию a > 5/3, которое заведомо выполне-

но, так как a ≥ 2 в случае (iv). Если во втором неравенстве обозначить x = a,

а в третьем положить x = 1/a, то оба неравенства превращаются в одно и то

же соотношение 2x3/2 - 3x + 1 > 0, где x ∈ (0, 1/2] ∪ [2, ∞). Это соотношение

верно, так как при x > 0 минимум этой функции равен нулю и достигается

в единственной точке x = 1.

Теперь рассмотрим

ξ ∼ (1 - q)R(-u₀,u₀) + qR(-u₁,u₁),

(

)

где q = (aq₁ - 1)/(a - 1), q₁ = a²/

3h²(a - 1)²

. В силу (Π.4) с помощью (6)

получаем

)

(

)

⁽1

h-m

P{|ξ - m| ≥ h} = (1 - q)

2u₀

u₁

Если обозначить p = (a/(a - 1))³/(3h²), то веса можно записать как q = p -

- 1/(a - 1) и 1 - q = a/(a - 1) - p. Тогда искомая вероятность принимает

вид

(

)

(

)(

)

⁾⁽1

-p

+ p-

a-1

3(a - 1)

a-1

3(a - 1)

)

(

)

⁽1

1-a

a-2

-1

3(a - 1)

a-1

2(a - 1)

что совпадает с выражением, указанным в теореме для случая (iv).

Остается рассмотреть только случай (vi). Пусть величина ξ распределена

по закону (1 - q)δ₀ + qR(-u, u), где u = 3(h - m)/2, q = 4/(3(h - m)²). Чтобы

применить формулу (6), проверим два неравенства h - m < u < h + m. Пер-

вое из них очевидно, а второе можно записать в виде со√тношения m > 0,2h,

которое выполнено на области (vi),(ак как m ≥ (1)- 1/

2)h > 0,29h. Теперь

вероятность P{|ξ - m| ≥ h} равна q

1 - (h - m)/u

/2 = q/6 = 2/(9(h - m)²),

что и требовалось.

Итак, теорема полностью доказана.

120

СПИСОК ЛИТЕРАТУРЫ

Dharmadhikari S., Joag-Dev K. Unimodality, Convexity, and Applications. San

Diego: Academic, 1988.

Карлин С., Стадден В. Чебышевские системы и их применение в анализе и

статистике. М.: Наука, 1976.

Высочанский Д.Ф., Петунин Ю.И. Об одном неравенстве Гаусса для одно-

вершинных распределений // Теория вероятн. и ее примен. 1982. Т. 27. № 2.

С. 339-341.

Vysochanskii D.F., Petunin Yu.I. On a Gauss Inequality for Unimodal

Distributions // Theory Probab. Appl. 1983. V. 27. No. 2. P. 359-361.

Pukelsheim F. The Three Sigma Rule // The American Statistician. 1994. V. 48.

P. 88-91.

Петунин Ю.И. Приложение теории случайных процессов в биологии и меди-

цине. Киев: Наук. думка, 1981.

Chiles J.-P., Delfiner P. Geostatistics. Modeling Spatial Uncertainty. N.Y.: J. Wiley

& Sons, 1999.

Barlow Р., Proschan F. Mathematical Theory of Reliability. Philadelphia: SIAM,

1996.

Чернышев К.Р. Вероятностные неравенства чебышевского типа в одной задаче

робастного управления // Информационно-управляющие системы. 2010. № 3.

С. 9-12.

Barmish B.R., Lagoa C.M. The Uniform Distribution: A Rigorous Justification for

Its Use in Robustness Analysis // Math. Control Signal. Syst. 1997. V. 10. P. 203-222.

10.

Кибзун А.И. О наихудшем распределении в задачах стохастической оптимиза-

ции с функцией вероятности // АиТ. 1998. № 11. С. 104-116.

Kibzun A.I. On the Worst-Case Distribution in Stochastic Optimization Problems

with Probability Function // Autom. Remote Control. 1998. V. 59. No. 11. P. 1587-

1597.

11.

Кан Ю.С. Об обосновании принципа равномерности в задаче оптимизации ве-

роятностного показателя качества // АиТ. 2000. № 1. С. 54-70.

Kan Yu.S. On the Justification of the Uniformity Principle in the Optimization of

a Probability Performance Index // Autom. Remote Control. 2000. V. 61. No. 1.

P. 50-64.

12.

Stellato B. Data-Driven Chance Constrained Optimization: Master thesis / Swiss

Federal Institute of Technology (ETH) Zürich. Zürich, 2014.

https://doi.org/10.3929/ethz-a-010266857

13.

Van Parys B.P.G., Goulart P.J., Kuhn D. Generalized Gauss Inequalities via

Semidefinite Programming // Math. Program. 2016. V. 156. P. 271-302.

14.

Ulin B. An Extremal Problem in Mathematical Statistics

// Scandinavian

Actuarial J. 1953. No. 1. P. 158-167.

15.

Clarkson E., Denny J.L., Shepp L. ROC and the Bounds on Tail Probabilities

via Theorems of Dubins and F. Riesz // Ann. Appl. Probab. 2009. V. 19. No. 1.

P. 467-476.

16.

Dharmadhikari S.W., Joag-Dev K. The Gauss—Tchebyshev Inequality for Unimodal

Distributions // Теория вероятн. и ее примен. 1985. Т. 30. № 4. С. 817-820.

Dharmadhikari S.W., Joag-Dev K. The Gauss—Tchebyshev Inequality for Unimodal

Distributions // Theor. Probab. Appl. 1986. V. 30. No. 4. P. 867-871.

121

17. Popescu I. A Semidefinite Programming Approach to Optimal Moment Bounds for

Convex Classes of Distributions // Math. Oper. Res. 2005. V. 30. No. 3. P. 632-657.

18. Стойкова Л.С. Наибольшая точная нижняя граница вероятности отказа систе-

мы в специальном интервале времени при неполной информации о функции

распределения времени до отказа системы // Кибернетика и системный анализ.

2017. Т. 53. № 2. С. 65-73.

Stoikova L.S. Greatest Lower Bound of System Failure Probability on a Special Time

Interval under Incomplete Information about the Distribution Function of the Time

to Failure of the System // Cybern. Syst. Anal. 2017. V. 53. No. 2. P. 217-224.

19. Панков А.Р., Семенихин К.В. О минимаксном оценивании по вероятностному

критерию // АиТ. 2007. № 3. С. 66-82.

Pankov A.R., Semenikhin K.V. Minimax Estimation by Probabilistic Criterion //

Autom. Remote Control. 2007. V. 68. No. 3. P. 430-445.

20. Семенихин К.В. Минимаксность линейных оценок неопределенно-стохастиче-

ского вектора по обобщенным вероятностным критериям // АиТ. 2007. № 11.

С. 88-104.

Semenikhin K.V. Minimax Nature of the Linear Estimates of the Indefinite

Stochastic Vector from the Generalized Probabilistic Criteria // Autom. Remote

Control. 2007. V. 68. No. 11. P. 1970-1985.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 05.09.2018

После доработки 05.10.2018

Принята к публикации 08.11.2018

122