Автоматика и телемеханика, № 3, 2019

Интеллектуальные системы управления,

анализ данных

(Институт системного анализа Федерального исследовательского центра

“Информатика и управление” РАН, Москва;

Национальный исследовательский университет

“Высшая школа экономики”, Москва;

Московский физико-технический институт

(Государственный университет))

ЭНТРОПИЙНОЕ ОЦЕНИВАНИЕ В ЗАДАЧАХ КЛАССИФИКАЦИИ¹

Рассматривается задача бинарной классификации, предлагается алго-

ритм ее решения, базирующийся на методе энтропийного оценивания па-

раметров решающего правила. Приведено подробное описание энтропий-

ного метода оценивания и алгоритма классификации, описаны преиму-

щества и недостатки такого подхода, приведены результаты численных

экспериментов и сравнения с классическим методом опорных векторов

по точности классификации и степени зависимости от объема обучающей

выборки.

Ключевые слова: машинное обучение, классификация, метод максимума

энтропии.

DOI: 10.1134/S0005231019030097

1. Введение

Задача бинарной классификации является одной из основополагающих в

теории машинного обучения и одной из самых распространенных задач при-

кладного анализа данных [1]. Существует множество алгоритмов решения

задачи классификации, различающихся способами работы с обучающей вы-

боркой, моделями решающего правила и методами решения задачи оптими-

зации. В качестве наиболее распространенных и универсальных алгоритмов

можно выделить решающие деревья (Decision tree) [2], наивный байесовский

классификатор (NB) [3] и логистическую регрессию (Logistic regression) [4].

Среди метрических классификаторов наиболее распространенными являют-

ся метод ближайших соседей (kNN) [5] и машина опорных векторов (SVM),

в том числе ядровые модификации (Kernel SVM) для линейно нераздели-

мых классов [6]. Еще две отдельные группы образуют методы, основанные на

построении нейронных сетей и различные композиционные алгоритмы обу-

чения, такие как стекинг и бустинг [7]. В данной статье будет представлен

альтернативный метод классификации, основанный на рандомизации модели

решающего правила и принципе максимума энтропии [8].

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 17-29-02115).

138

Принцип максимума энтропии уже применяется в различных методах ма-

шинного обучения, например для выбора разделяющего правила в решающих

деревьях или при отборе информативных признаков [9]. Кроме того, суще-

ствует группа методов, основанных на оценке вероятностей принадлежности

объектов к разным классам. К ним относятся широко распространенный ме-

тод под названием maxEnt [10] и обобщение логистической регрессии на слу-

чай нескольких классов (multinomial logistic regression) [11]. Подчеркнем, что

в данных методах принцип максимума энтропии применяется в отношении

вероятностей принадлежности классам, т.е. ответам классификатора, а не к

параметрам математических моделей, описывающих решающее правило.

Под энтропийным оцениванием параметров решающего правила понима-

ют применение классического метода максимума энтропии (General Maximum

Entropy) [12], который был разработан преимущественно для задачи регрес-

сии в случаях, когда классический подход, основанный на методе наименьших

квадратов, оказывается неэффективным. В [13], например, продемонстриро-

вана эффективность энтропийного оценивания для линейной регрессии при

наличии несимметричных и негауссовских шумов, а также в условиях малой

обучающей выборки.

Основная идея метода энтропийного оценивания заключается в представ-

лении параметров модели случайными величинами и подборе для них таких

функций распределения вероятности, которые обладали бы наибольшей эн-

тропией, но и согласовывались бы с данными обучающей выборки. Такой

подход позволяет получить наиболее робастное решение в условиях наиболь-

шей неопределенности [14].

2. Классический линейный классификатор

Линейным классификатором называют алгоритм классификации, осно-

ванный на построении линейной разделяющей поверхности в пространстве

признаков. Для бинарной классификации двумерных объектов разделяющей

поверхностью будет прямая, для трехмерных — плоскость, а в общем слу-

чае — гиперплоскость [1].

Пусть объекты из множества X описываются числовыми признаками

f_j : X → R, j = 1,... ,d, в пространстве R^d. Пусть Y — множество меток клас-

сов, для случая бинарной классификации Y = {-1, 1}. Тогда линейный клас-

сификатор определяется так:

⎛

⎞

∑

(2.1)

a(x, w) = sign^⎝ w_jf_j(x) - w₀⎠

= sign 〈x,w〉 ,

j=1

где 〈x,w〉 - скалярное произведение признакового описания объекта на

вектор параметров w = (w₀, w₁, . . . , w_d). Далее в качестве признакового

описания объектов будут использоваться компоненты матрицы X = {x_ij ,

i = 1,n, j = 0,d}, дополненной единичным столбцом.

Основной задачей машинного обучения в данном случае является

“настройка” вектора весов, т.е. по заданной обучающей выборке Xⁿ =

139

= {(x₁, y₁), . . . , (x_n, y_n)} построить алгоритм указанного вида, минимизирую-

щий функционал эмпирического риска, т.е. число неправильно классифици-

рованных объектов:

∑

(2.2)

Q(w) =

[a(x_i, w) = y_i] → min .

i=1

Для решения оптимизационной задачи (2.2) вводится понятие отступа

(margin)

(2.3)

M (x_i) = y_i 〈x_i

,w〉 .

Отступ представляет собой числовое значение, характеризующее степень по-

гружения объекта в соответствующий класс. Чем меньше значение M(x_i),

тем ближе объект x_i находится к разделяющей поверхности между класса-

ми и тем выше становится вероятность ошибки классификации. Поскольку

величина отступа M(x_i) становится отрицательной лишь для тех примеров,

на которых алгоритм ошибается, то функционал эмпирического риска можно

переписать в виде

∑

(2.4)

Q(w) =

[M(x_i

) < 0].

i=1

Поскольку в таком виде функционал эмпирического риска является

недифференцируемой функцией от вектора параметров w, то градиентные

методы оптимизации оказываются неприменимыми. Существует несколько

подходов для численного решения данной задачи. Так, в методе опорных

векторов (SVM) задача минимизации эмпирического риска заменяется зада-

чей построения оптимальной разделяющей гиперплоскости. Еще одним под-

ходом для численного решения задачи оптимизации является замена поро-

говой функции потерь некоторыми непрерывными аппроксимациями, после

чего минимизируется не сам функционал эмпирического риска, а его верхняя

оценка:

∑

(2.5)

Q(w) ≤^Q(w) = L (M(x_i)) → min .

i=1

Наиболее распространенными аппроксимациями функции потерь являют-

ся: квадратичная (дискриминант Фишера), сигмоидная (однослойный пер-

цептрон), логарифмическая, экспоненциальная и кусочно-линейная с L₂-ре-

гуляризацией [15].

3. Линейный классификатор с энтропийным оцениванием параметров

От классических методов машинного обучения энтропийное оценивание

отличается другой интерпретацией модели решающего правила. Вектор па-

раметров w, определяющий разделяющую поверхность, полагается многомер-

ной случайной величиной, реализации которой будут описывать не одну раз-

деляющую поверхность, а ансамбль возможных поверхностей. Задачей энтро-

пийного оценивания является вычисление энтропийно-оптимальной функции

140

плотности распределения вероятности для параметров решающего правила.

Такой подход был предложен в [14, 16], однако в настоящей статье рассмот-

рена его модификация, основанная на использовании дискретных случайных

величин вместо непрерывных, что существенно снижает вычислительные за-

траты и ускоряет работу алгоритма.

Итак, пусть дискретные случайные величины w_j , j = 0, d, определены на

множествах значений W_j = {wj1, wj2, . . . , w_jk} и имеют дискретные функции

распределения p(j) = {pj1, pj2, . . . , p_jk}. Задачей оценивания является восста-

новление значений вероятностей для всех возможных исходов случайных ве-

личин p_jl, j = 0, d, l = 1, k, обладающих наибольшей энтропией:

∑∑

(3.1)

H(p) = -

p_jl ln p_jl → max.

j=0 l=1

Нетрудно видеть, что максимальной энтропией обладают равномерно рас-

пределенные случайные величины, поэтому дополнительно накладываются

ограничения на значения функций распределения

∑

(3.2)

p_jl

= 1, j = 0, d,

l=1

и балансовые ограничения на средние значения случайных величин

(3.3)

E^w [M(x_i

)] > 0, i = 1, n.

Ограничение (3.3) является аналогом условия неотрицательности отсту-

пов (2.3) для рандомизированных параметров w и обеспечивает согласован-

ность с обучающей выборкой. Распишем более подробно выражение (3.3):

⎡

⎤

∑

E^w [M(x_i)] = E^w [y_i 〈x_i,w〉] = E^w

⎣ y_ix_ijw_j⎦ =

j=0

(3.4)

∑

∑∑

= y_ix_ijE^w [w_j] =

y_ix_ijw_jlp_jl > 0.

j=0

j=0 l=1

Задача поиска условного экстремума (3.1) с ограничениями равенства-

ми (3.2) и ограничениями неравенствами (3.4) удовлетворяет всем услови-

ям теоремы Куна-Таккера и решается методом неопределенных множителей

Лагранжа. Функция Лагранжа имеет вид

(

)

∑∑

∑

L(μ,λ) =

p_jl ln p_jl +

μ_j

p_jl - 1

j=0 l=1

j=0

l=1

(3.5)

⎛

⎞

∑

∑∑

− λ_i⎝

y_ix_ijw_jlp_jl⎠,

i=1

j=0 l=1

141

тогда в стационарной точке ее частные производные обращаются в 0:

∑

∂L(μ,λ)

(3.6)

= ln p_jl + 1 + μ_j -

λ_iy_ix_ijw_jl

= 0.

∂p

i=1

Следовательно, решение для p_jl имеет вид:

(

)

∑

(3.7)

p_jl = exp

-1 - μ_j + λ_iy_ix_ijw_jl

i=1

Подставляя это выражение в ограничения равенства (3.2), получим:

(

)

∑

exp

λ_iy_ix_ijw_jl

i=1

(3.8)

p_jl

(

j = 0,d, l = 1,k.

∑

exp

λ_iy_ix_ijw_jl

l=1

i=1

Выражение (3.8) определяет вид энтропийно-оптимальных функций рас-

пределения, параметризованных множителями Лагранжа λ₁, . . . , λ_n, которые

восстанавливаются из условий неотрицательности (λ_i ≥ 0) и дополнительной

нежесткости:

∑∑

(3.9)

λ_iE^w [M(x_i)] =

λ_iy_ix_ijw_jlp_jl

= 0, i = 1, n.

j=0 l=1

Система уравнений (3.9) решается численными методами, например, посред-

ством минимизации квадратичной функции невязки с использованием гра-

диентных методов оптимизации.

Таким образом, были вычислены значения функций распределения для

параметров модели линейного классификатора (2.1). В качестве точечной

оценки параметров используется среднее значение по полученным согласно

выражению (3.8) распределениям вероятности, т.е.:

∑

(3.10)

w^∗j = E^w [w_j] =

w_jlp_jl

j = 0,d.

l=1

Параметры (3.10) задают разделяющую поверхность между точками разных

классов аналогично с классическим линейным классификатором. С другой

стороны, полученные распределения вероятностей открывают более широкие

возможности для дальнейшей настройки и тестирования классификатора.

4. Алгоритм рандомизированной классификации

Рандомизированная классификация базируется на идее семплирования по-

лученных в результате энтропийного оценивания распределений случайных

142

величин. В таком случае каждый семпл параметров будет определять неко-

торую отдельную разделяющую поверхность, а весь набор случайных вели-

чин — ансамбль линейных классификаторов.

В отличие от использования точечной оценки семплирование случайных

величин позволяет получить некоторую выборку значений и применить аппа-

рат математической статистики; например, в задаче регрессии это позволит

рассчитать дисперсию для оценки параметров модели и построить довери-

тельные интервалы. Преимуществом такого подхода в задаче классификации

является возможность определения вероятностей принадлежности объектов

к различным классам, даже для методов, предполагающих только бинарную,

но не вероятностную классификацию. Например, описанный алгоритм линей-

ной классификации аналогично методу опорных векторов позволяет опре-

делить лишь класс объекта, но не вероятность принадлежности к данному

классу, в отличие, например, от метода логистической регрессии для задачи

классификации.

Приведем один из возможных алгоритмов использования ансамбля слу-

чайных величин для решения задачи бинарной классификации.

• Генерируется выборка значений w(s) = {w(s)0, . . . , w(s)d}, s = 1, m, объе-

мом m. Тогда каждый набор параметров w(s) определяет линейный клас-

сификатор вида

⎛

⎞

∑

(4.1)

a(x, w(s)) = sign x, w(s)

= sign^⎝ x_jw(s)j⎠.

j=0

• Для каждого объекта из обучающей коллекции вычисляется ансамбль от-

ветов:

(4.2)

a(x, w(s)) : x_i → y(s)i

i = 1,n, s = 1,m.

• Вычисляются эмпирические вероятности принадлежности объектов к раз-

ным классам, равные доле ответов соответствующего класса среди всего

ансамбля классификаторов:

∑[

]

p(i)1 =

y(s)i = -1

s=1

(4.3)

i = 1,n.

∑[

]

p(i)2 =

y(s)i = 1

s=1

Эмпирические вероятности (4.3) могут использоваться в качестве ответов

в задачах, в которых требуется определить лишь вероятность принадлежно-

сти к классам, а для задач с требованием четкого определения класса для

каждого нового объекта эмпирические вероятности должны быть преобразо-

ваны в метки классов, например посредством выбора некоторого порогового

143

значения t ∈ (0, 1):

⎧

⎨-1,p(i)

≥ t,

(4.4)

y_i =

^⎩1, p(i)1 < t.

Пороговое значение t определяет уровень достоверной классификации и

является гиперпараметром алгоритма. Как и другие гиперпараметры алго-

ритмов классификации, оптимальное пороговое значение может быть опреде-

лено в результате серий экспериментов над обучающей выборкой. В данной

статье использовался метод перекрестной проверки по пяти блокам (5-fold).

Другим известным подходом к подбору гиперпараметров является ROC-ана-

лиз, основанный на построении ROC-кривых (ROC-curve) [17].

5. Случай линейной неразделимости классов

Несмотря на широкую распространенность линейных классификаторов,

большинство практических примеров обучающих коллекций являются ли-

нейно неразделимыми. В таких случаях применяют ядровые модификации,

основанные на использовании нелинейных функций похожести точек обучаю-

щей выборки [1, 6]. Приведем аналог ядровой модификации для линейного

классификатора с энтропийным оцениванием параметров.

Предположим, что исходное признаковое пространство проецируется в

пространство большей размерности с помощью отображения φ : R^d → Rⁿ, в

котором также определено скалярное произведение между образами точек

〈φ(x_i), φ(x_j )〉. Запишем решающее правило линейного классификатора в но-

вом пространстве аналогично (2.1):

a(x_i, w) = sgn (s(x_i, w)) = sgn (〈φ(x_i), φ(w)〉) ,

∑

(5.1)

где φ(w) =

w_jy_jφ(x_j).

j=1

Тогда

∑

(5.2)

s(x_i, w) =

w_jy_j 〈φ(x_i),φ(x_j

)〉 , i = 1, n.

j=1

Прием, получивший в публикациях название “Kernel trick”, позволяет в ка-

честве скалярного произведения между образами точек использовать функ-

цию ядра, обладающую свойствами симметричности и неотрицательной опре-

деленности. Например, гауссовское ядро выглядит так:

(

)

(5.3)

K(x_i, x_j ) = exp

-||x_i - x_j||²

i, j = 1, n.

Таким образом, решающее правило линейного классификатора принимает

вид

∑

(5.4)

s(x_i, w) =

w_jy_jK(x_i,x_j

i = 1,n.

j=1

144

Теперь сформулируем задачу энтропийного оценивания для вычисления

параметров w_j, j = 1, n. В данном случае оценивается вектор параметров зна-

чительно большей размерности (n > d), однако общий подход, изложенный в

разделе 3, остается неизменным:

∑∑

(5.5)

H(p) = -

p_jl ln p_jl → max

j=1 l=1

при ограничениях

∑

(5.6)

p_jl

= 1, j = 1, n,

l=1

(5.7)

E^w [M(x_i

)] > 0, i = 1, n.

С учетом определения отступа M(x_i) согласно (2.3) и решающего прави-

ла (5.4) ограничение (5.7) примет вид

E^w [M(x_i)] = E^w [y_is(x_i,w)] =

(5.8)

∑∑

y_iy_jK(x_i,x_j)w_jlp_jl > 0, i = 1,n.

j=1 l=1

Дальнейшая процедура восстановления энтропийно-оптимального распреде-

ления вероятностей аналогична разделу 3 с тем отличием, что в данном слу-

чае потребуется дополнительно O(n²) памяти для хранения значений функ-

ции ядра, следовательно, увеличиваются необходимые вычислительные ре-

сурсы и время работы алгоритма.

6. Результаты экспериментов

Приведем результаты тестирования алгоритма классификации с исполь-

зованием энтропийного оценивания (GME) по сравнению с методом опорных

векторов как для линейной разделяющей поверхности, так и для гауссовской

функции ядра.

6.1. Данные для тестирования

Для экспериментов использовались наборы из открытого репозитория

данных для задач машинного обучения лаборатории KEEL (Knowledge

Extraction based on Evolutionary Learning) [18]. Все датасеты включают при-

меры двух классов в различных пропорциях p₁ и p₂, а все признаки являют-

ся числовыми. Общее число признаков d и объем коллекции n приведены в

табл. 1.

Очевидно, что все приведенные наборы данных имеют свои особенности

и свою уникальную структуру, поэтому построение наилучшего классифи-

катора для каждого из них является отдельной задачей. Целью же данных

145

Таблица 1. Параметры датасетов для тестирования

Название

p₁, %

p₂, %

hepatitis

0,162

0,838

appendicitis

106

0,802

0,198

sonar

208

0,466

0,534

spectfheart

267

0,206

0,794

heart

270

0,444

0,556

haberman

306

0,735

0,265

ionosphere

351

0,359

0,641

wdbc

569

0,372

0,628

wisconsin

683

0,650

0,350

mammographic

830

0,514

0,486

экспериментов является не получение наибольшей точности классификации

для рассмотренных датасетов, а начальная апробация предложенных алго-

ритмов энтропийной и рандомизированной классификации и демонстрация

их работоспособности.

6.2. Сравнение точности классификаторов

Для первого эксперимента были выбраны датасеты, показывающие вы-

сокую точность при классификации линейным алгоритмом. Сравниваются

методы оценивания SVM и GME, а также основанный на GME алгоритм

рандомизированной классификации (Randomized GME), изложенный в раз-

деле 4. В качестве решения для алгоритма SVM используется базовая реа-

лизация из пакета MATLAB R2017a (fitcsvm) с значениями гиперпараметров

по умолчанию, в то время как алгоритмы GME и RGME реализованы при

использовании инструментов оптимизации (Optimization Toolbox).

При реализации энтропийного оценивания использовалось линейное раз-

биение области допустимых значений параметров решающего правила для

выбора допустимых дискретных значений, т.е. весь отрезок от -1 до 1 де-

лится на k = 5 равных интервалов, границы которых образуют множество

возможных значений дискретной случайной величины. Отметим, что энтро-

пийное оценивание для непрерывных случайных величин является более точ-

ным, но и более вычислительно затратным по сравнению с дискретным при-

ближением. Причем количество интервалов k и схема дискретизации также

являются гиперпараметрами алгоритма, а их дополнительная настройка с це-

лью получения наилучшей точности классификации в данных экспериментах

не проводилась.

Точность классификации вычисляется методом кроссвалидации по пяти

блокам (5-fold) и усредняется по результату 100 различных разбиений, что

обеспечивает стабильность и воспроизводимость результатов.

Результаты первой серии экспериментов представлены в табл. 2. Как вид-

но, энтропийное оценивание параметров модели линейного классификатора

показывает конкурентоспособный результат по сравнению с методом SVM, а

для некоторых датасетов, таких как “hepatitis”, “sonar”, “heart” и “haberman”,

превосходит SVM по точности классификации. Для остальных примеров ли-

бо разница в точности невелика, либо энтропийное оценивание существенно

146

Таблица 2. Сравнение методов оценивания для линейного классификатора

Название

SVM

GME

RGME RGME vs GME

hepatitis

83,28 ± 2,73

84,08 ± 2,44

85,42 ± 2,69

•

appendicitis

87,43 ± 1,33

85,89 ± 1,72

86,68 ± 1,55

•

sonar

74,87 ± 1,98

78,92 ± 1,91

79,23 ± 1,28

◦

spectfheart

78,76 ± 1,59

68,63 ± 2,82

75,61 ± 3,76

•

heart

83,81 ± 0,95

84,13 ± 1,08

84,56 ± 0,87

•

haberman

72,82 ± 0,57

74,97 ± 2,45

75,44 ± 1,41

•

ionosphere

87,84 ± 1,10

87,35 ± 1,01

87,29 ± 0,74

◦

wdbc

97,04 ± 0,51

96,87 ± 0,72

95,94 ± 0,69

◦

wisconsin

96,72 ± 0,22

96,69 ± 0,15

96,91 ± 0,15

•

mammographic

82,46 ± 0,69

81,24 ± 0,55

81,61 ± 0,77

•

Таблица 3. Сравнение методов оценивания при использовании функции ядра

Название

SVM

GME

RGME

RGME vs GME

hepatitis

83,75 ± 1,07

86,37 ± 1,55

86,51 ± 1,41

◦

appendicitis

87,14 ± 0,91

86,12 ± 1,83

86,40 ± 1,17

•

spectfheart

79,40 ± 0,67

71,35 ± 1,24

71,32 ± 1,42

◦

haberman

73,26 ± 0,92

73,65 ± 1,17

73,71 ± 1,24

◦

wisconsin

95,34 ± 0,26

94,43 ± 0,59

94,56 ± 0,62

◦

уступает, например для данных “appendicitis” и “spectfheart”, что может быть

связано с особенной структурой признаков или несимметричностью распре-

деления по классам.

В последнем столбце табл. 2 приведены результаты проверки гипотезы о

статистической значимости улучшения точности классификации при исполь-

зовании семплирования (RGME vs GME), где согласно 95-процентному уров-

ню значимости по критерию Стьюдента незакрашенный индикатор (◦) озна-

чает выполнение нулевой гипотезы (H₀ : μ_RGME = μ_GME), а закрашенный (•)

соответствует выполнению альтернативной гипотезы (H₁ : μ_RGME > μ_GME).

В результате экспериментов для большинства рассмотренных датасетов пе-

реход к рандомизированной классификации, основанной на семплировании

энтропийно-оптимальных распределений вероятностей, позволяет повысить

точность линейного энтропийного классификатора, что особенно заметно при

малом объеме обучающей выборки до 250 - 300 объектов. Однако для вы-

борок более 300 объектов энтропийное оценивание становится не столь эф-

фективным и уступает по точности методу SVM. Кроме того, независимо от

объема выборки энтропийное оценивание значительно уступает методу SVM

по времени исполнения.

Следующая серия экспериментов посвящена сравнению методов оценива-

ния при использовании в классификаторе функции гауссовского ядра (5.3).

Для сравнения выбраны наборы данных из табл. 1, показывающие высокую

точность при классификации с использованием функции ядра. Результаты

сравнения представлены в табл. 3, где все обозначения аналогичны описан-

ным выше.

Как видно из данных табл. 3, эффективность энтропийного оценивания

также распространяется и на ядровые модификации линейного классифика-

147

тора. Однако в отличие от линейной разделяющей поверхности в этом слу-

чае для большинства примеров использование ансамбля классификаторов не

приводит к статистически значимому повышению точности, что может объяс-

няться высокой размерностью задачи оптимизации (5.5) по сравнению с за-

дачей (3.1).

Кроме того, в данных сериях экспериментов не проводилась настройка

гиперпараметров алгоритмов GME и RGME, таких как количество значений

для дискретных случайных величин (k в выражениях (3.1) и далее) и объем

ансамбля при семплировании (m в выражении (4.2)). Поэтому подбор опти-

мальных значений гиперпараметров для каждого набора данных позволит

дополнительно повысить точность классификации.

6.3. Влияние объема обучающей выборки

Приведем результаты исследования зависимости точности классификато-

ров SVM, GME и RGME от объема данных в обучающей коллекции. Для

этого эксперимента используется метод кросс-валидации с заданным процен-

том объектов для тестирования (holdout). Например, при значении h = 0,2

для обучения будет использоваться 80 % выборки, а остальные 20 % — для

тестирования, что соответствует одной из пяти итераций по методу 5-fold.

Таким образом, при увеличении значения h от 0 до 1 для обучения модели

будет использоваться все меньше объектов.

Зависимость обычного линейного классификатора протестирована на при-

мере данных “appendicitis”, а классификатора с использованием функции яд-

ра — на примере данных “hepatitis”. Результаты сравнения, усредненные по

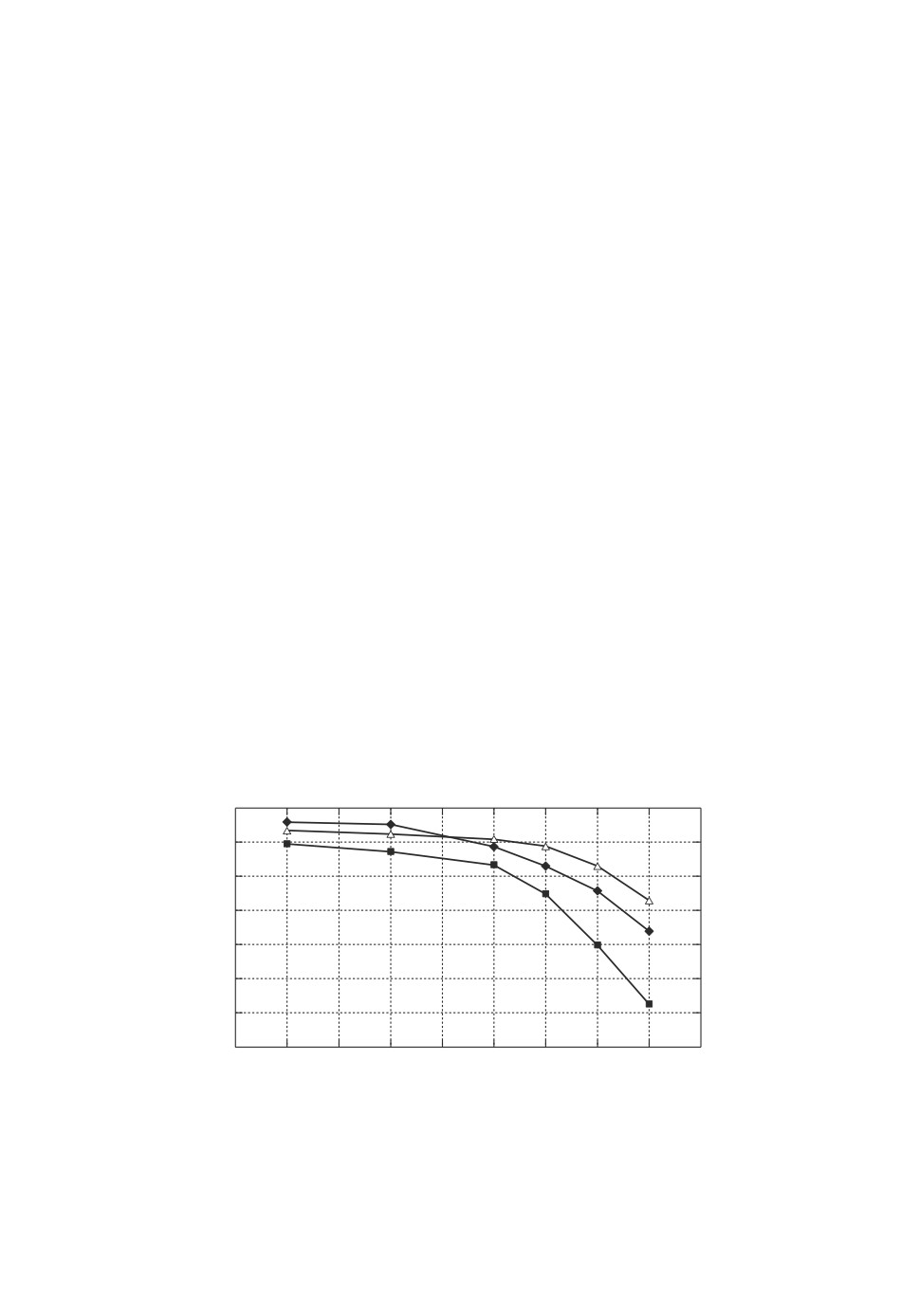
1000 различных разбиений, представлены в виде графиков на рис. 1 и 2 со-

ответственно.

Точность кросс-валидации (holdout CV),%

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Коэффициент использования обучающей

выборки для тестирования

Рис. 1. Зависимость точности линейного классификатора от объема обучаю-

щей выборки на примере датасета “appendicitis” (ромбами отмечены точки

графика для метода SVM, квадратами и треугольниками — для GME и RGME

соответственно).

148

Точность кросс-валидации (holdout CV),%

87,0

86,5

86,0

85,5

85,0

84,5

84,0

83,5

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Коэффициент использования обучающей

выборки для тестирования

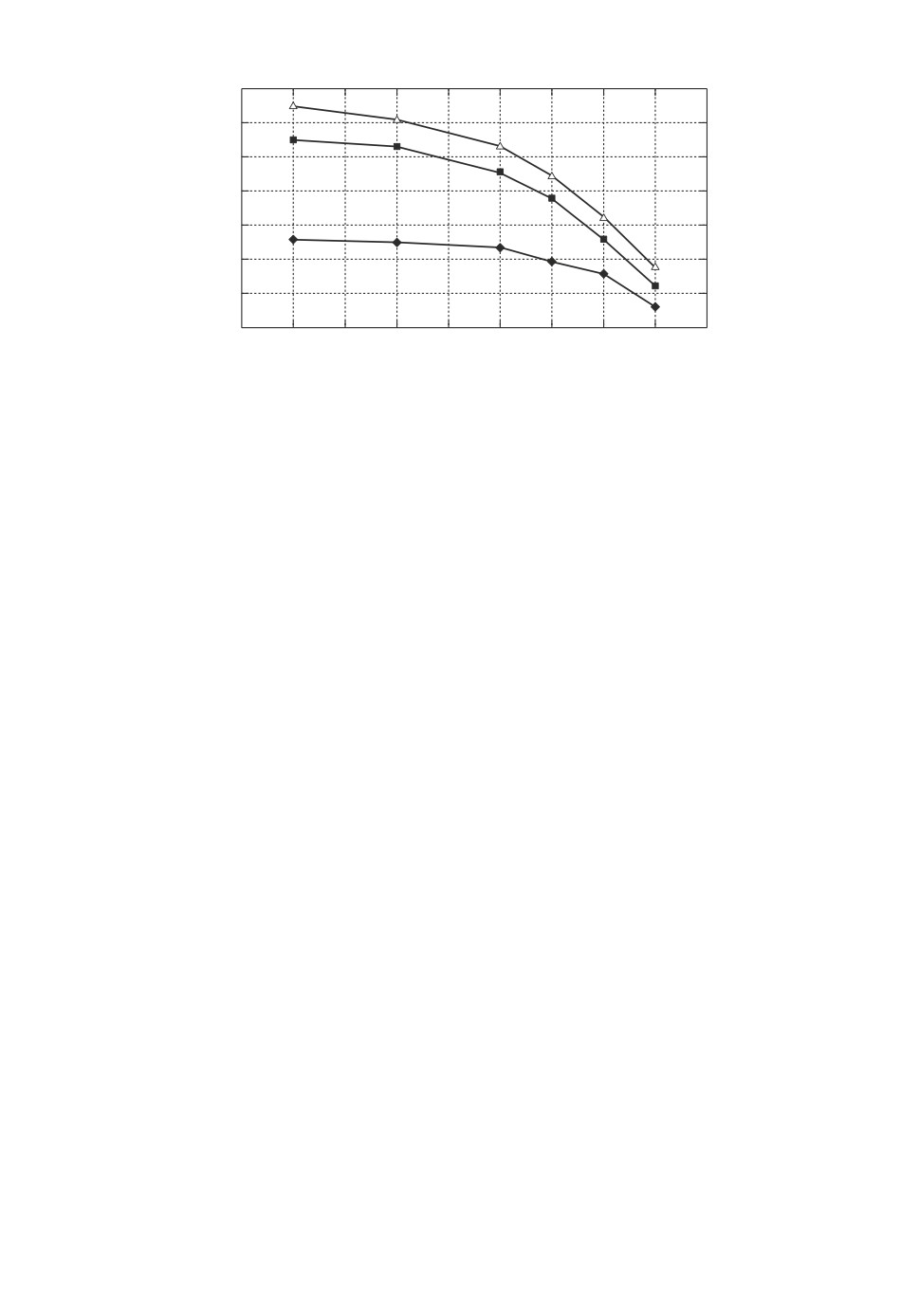
Рис. 2. Зависимость точности классификатора с гауссовским ядром от объема

обучающей выборки на примере датасета “hepatitis” (ромбами отмечены точки

графика для метода SVM, квадратами и треугольниками — для GME и RGME

соответственно).

Результаты исследования показывают, что точность линейного классифи-

катора (рис. 1), основанного на энтропийном оценивании параметров, под-

вержена влиянию объема обучающей выборки и подобно методу SVM пада-

ет при сокращении данных для обучения. С другой стороны, использование

семплирования совместно с энтропийным оцениванием в алгоритме RGME

позволяет уменьшить падение точности более чем в два раза для рассмот-

ренного датасета. Так, согласно графику на рис. 1 при использовании 40 %

и менее данных для обучения рандомизированная классификация позволя-

ет получить точность, превосходящую точность алгоритмов SVM и GME,

несмотря на то, что изначально наилучшую точность показывал алгоритм

SVM.

С другой стороны, для ядровых модификаций (рис. 1) падение точности

классификации при уменьшении объема обучающей выборки оказывается

менее существенным, что связано, в первую очередь, с размерностью зада-

чи оптимизации. Если в обычном линейном классификаторе необходимо для

d-мерного признакового пространства восстановить d параметров независи-

мо от объема обучающей выборки, то в ядровой модификации происходит

переход в n-мерное пространство, где n соответствует объему выборки для

обучения. Падение же точности для всех рассматриваемых алгоритмов на

рис. 2 меньше, чем на рис. 1, однако именно алгоритм рандомизированной

классификации оказывается, хотя и незначительно, но точнее остальных при

малом объеме данных для обучения.

7. Заключение

В статье продемонстрирован новый подход к построению линейного клас-

сификатора, базирующийся на энтропийном оценивании его параметров. Под

энтропийным оцениванием понимается восстановление распределений веро-

149

ятности для параметров модели, обладающих наибольшей информационной

энтропией и согласующихся с обучающей выборкой в терминах балансовых

ограничений. В свою очередь, восстановленные таким образом вероятности

могут использоваться как для получения точечной оценки параметров моде-

ли, так и для получения ансамбля классификаторов посредством семплиро-

вания.

Представленный алгоритм классификации был апробирован на примере

нескольких датасетов из открытых источников. Результаты экспериментов

показывают высокую, сравнимую с методом опорных векторов, точность

классификации. Дополнительно были исследованы статистическая значи-

мость повышения точности при переходе к рандомизированной классифи-

кации и влияние объема обучающей выборки данных. В результате исследо-

ваний была продемонстрирована эффективность энтропийного оценивания и

рандомизированной классификации, особенно при малых объемах обучаю-

щих выборок.

СПИСОК ЛИТЕРАТУРЫ

Bishop C. Pattern Recognition and Machine Learning (Information Science and

Statistics). Springer, 2006.

Breiman Leo, Friedman J.H., Olshen R.A., Stone C.J. Classification and Regression

Trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software, 1984.

Domingos P, Pazzani M. On the Optimality of the Simple Bayesian Classifier under

Zero-One Loss // Mach. Learn. 1997. No. 29. P. 103-130.

Hosmer D.W., Lemeshow S. Applied Logistic Regression, 2nd ed. N.Y.: Chichester,

Wiley, 2002.

Belur V. Dasarathy (ed.), Nearest Neighbor (NN) Norms: NN Pattern Classification

Techniques. 1991.

Cristianini N., Shawe-Taylor J. An Introduction to Support Vector Machines and

Other Kernel-Based Learning Methods. Cambridge University Press, 2000.

Bühlmann P., Hothorn T. Boosting Algorithms: Regularization, Prediction and

Model Fiting // Stat. Sci. 2007. P. 477-505.

Cover T.M., Thomas J.A. Elements of Information Theory. N.Y.: John Wiley and

Sons Ltd, 1991.

Abellán J., Castellano J.G. Improving the Naive Bayes Classifier via a Quick Variable

Selection Method Using Maximum of Entropy // Entropy. 2017. V. 19. Iss. 6. No. 247.

10.

Phillips Steven J. A Brief Tutorial on Maxent. Network of Conservation Educators

and Practitioners, Center for Biodiversity and Conservation, American Museum of

Natural History // Lessons in Conservation. 2009. V. 3. P. 108-135.

11.

Yu Hsiang-Fu, Huang Fang-Lan, Lin Chih-Jen. Dual Coordinate Descent Methods

for Logistic Regression and Maximum Entropy Models // Mach. Lear. 2011. V. 85.

P. 41-75.

12.

Golan Amos, Judge George G., Miller Douglas. Maximum Entropy Econometrics:

Robust Estimation with Limited Data. Chichester, U.K.: John Wiley and Sons Ltd.,

1996.

13.

Eruygur H. Ozan. Generalized Maximum Entropy (GME) Estimator: Formulation

and a Monte Carlo Study // VII National Sympos. on Econometrics and Statistics,

Istanbul, Turkey. 2005. May 26-27.

150

14. Popkov Yu.S., Dubnov Yu.A., Popkov A.Yu. Randomized Machine Learning:

Statement, Solution, Applications // Proc. 2016 IEEE 8-th Int. Conf. on Intelligent

Systems (IS16). September 4-6, 2016. Hotel Hemus, Sofia, Bulgaria. P. 27-39.

15. Langford J. Tutorial on Practical Prediction Theory for Classification // J. Mach.

Learn. Research. 2005. V. 6. P. 273-306.

16. Popkov Yuri S., Volkovich Zeev, Dubnov Yuri A., Avros Renata, Ravve Elena.

Entropy ‘2’-Soft Classification of Objects // Entropy. 2017. V. 19. Iss. 4. No. 178.

17. Fawcett T. An Introduction to ROC Analysis // Pattern Recogn. Lett. 2006. No. 27.

P. 861-874.

18. Alcalá-Fdez J., Fernandez A., Luengo J., Derrac J., Garcia S., Sánchez L.,

Herrera F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of

Algorithms and Experimental Analysis Framework // J. Multiple-Valued Logic and

Soft Computing. 2011. V. 17. No. 2-3. P. 255-287.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 19.07.2018

После доработки 06.11.2018

Принята к публикации 08.11.2018

151