Автоматика и телемеханика, № 4, 2019

Стохастические системы

Ю.С. КАН, д-р. физ.-мат. наук (yu_kan@mail.ru)

(Московский авиационный институт)

УСИЛЕННАЯ ОЦЕНКА ФУНКЦИИ БЕЛЛМАНА В ЗАДАЧАХ

СТОХАСТИЧЕСКОГО ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

С ВЕРОЯТНОСТНЫМ КРИТЕРИЕМ КАЧЕСТВА¹

Рассматривается задача оптимального управления дискретной стоха-

стической системой с вероятностным терминальным критерием обще-

го вида. С использованием метода динамического программирования и

свойств функции Беллмана для этой функции строятся новые двусторон-

ние границы, уточняющие известные ранее. С использованием указанных

оценок приводится обоснование применения модифицированной страте-

гии, оптимальной в двухшаговой задаче управления портфелем ценных

бумаг с учетом риска, для решения аналогичной многошаговой задачи.

На примере демонстрируются преимущества такой стратегии перед дру-

гими известными стратегиями.

Ключевые слова: дискретные системы, стохастическое оптимальное

управление, вероятностный критерий, метод динамического программи-

рования, функция Беллмана, управление портфелем ценных бумаг.

DOI: 10.1134/S0005231019040032

1. Введение

Задачи оптимального управления стохастическими марковскими система-

ми с дискретным временем и терминальным вероятностным критерием ис-

следуются с середины XX в. Интерес к исследованию данного класса задач

мотивирован аэрокосмическими [1-5], экономическими [6-13] и робототехни-

ческими [14-16] приложениями. В аэрокосмических приложениях вероятност-

ный критерий исследовался, например, в [1, 5] в рамках задачи оптимальной

импульсной коррекции траектории движения искусственного спутника Зем-

ли в окрестности геостационарной орбиты. В [1] были сформулированы до-

статочные условия оптимальности для задач оптимального управления дис-

кретными стохастическими системами с вероятностным критерием в форме

рекуррентных соотношений динамического управления. Публикации [6-13]

посвящены задачам оптимального управления портфелем ценных бумаг с

учетом риска. В модели [6-13] система управления характеризует изменение

капитала во времени, за управление принимаются доли капитала, вклады-

ваемые в безрисковый актив, имеющий детерминированную доходность, и

¹ Результаты работы получены в рамках выполнения государственного задания Мин-

обрнауки № 2.2461.2017/ 4.6.

рисковые активы, имеющие случайную доходность с известным распределе-

нием. Вероятностный критерий моделирует вероятность достижения капита-

лом к заданному моменту времени некоторого уровня. В ходе исследования

указанных задач был разработан численный алгоритм решения [7]. Интерес

к моделям оптимального управления портфелем ценных бумаг в схожих по-

становках проявляется и в настоящее время, см., например, [17, 18].

Метод динамического программирования (МДП) является основным [1]

инструментом решения задач синтеза оптимального управления дискретны-

ми стохастическими системами с вероятностным критерием качества. Сре-

ди недавних публикаций, посвященных данной проблематике, можно выде-

лить [5, 6, 14-16]. Для ряда случаев АДП позволяет найти оптимальную стра-

тегию в классе измеримых ограниченных функций [7]. Однако в связи с “про-

клятьем размерности” по сей день нет эффективных численных методов ре-

шения уравнения динамического программирования (уравнения Беллмана).

Тем не менее в ряде случаев оптимальное управление может быть найде-

но аналитически с использованием свойств и двусторонних оценок функции

Беллмана [5, 6]. Например, в [5] было найдено аналитическое решение задачи

оптимального управления билинейной системой со скалярным ограниченным

управлением и вероятностным терминальным критерием. Такая модель ис-

пользуется в задачах импульсной коррекции орбиты геостационарного спут-

ника (см., например, [1]). Техника нахождения двусторонних оценок функции

Беллмана для синтеза оптимальных и субоптимальных управлений исполь-

зовалась, например, в [19] для других (не вероятностных) критериев.

Отдельно отметим публикации [14-16], где выделен широкий класс задач

оптимального управления с вероятностным критерием, для которого разра-

ботаны численные алгоритмы поиска оптимального управления. Указанный

класс характеризуется тем, что функция системы (функция перехода), об-

ратная связь по состоянию и точностной функционал являются полинома-

ми, система управления стационарна, а носитель распределения случайных

возмущений ограничен. Постулирование полиномиальной обратной связи по

состоянию позволило свести бесконечномерную оптимизационную задачу к

конечномерной задаче стохастического программирования большой размер-

ности.

Настоящая статья является продолжением [6], где для задач оптимального

управления дискретными стохастическими системами с вероятностным тер-

минальным критерием на основе метода динамического программирования и

свойств функции Беллмана, исследованных в [5], была найдена двусторонняя

оценка для функции Беллмана. В [5] показано, что нижняя и верхняя оценки

функции Беллмана как функции состояния определяются в результате реше-

ния соответствующих задач стохастического программирования с целевыми

функциями в форме функций вероятности. Для задачи оптимального управ-

ления портфелем ценных бумаг двусторонняя оценка была найдена в явном

виде [6], где, в частности, установлено, что управление, найденное из реше-

ний задач стохастического программирования для нижней оценки, является

асимптотически оптимальным при стремлении горизонта управления к бес-

конечности. В настоящей статье находятся усиленные оценки для функции

Беллмана, которые уточняют полученные раннее двусторонние оценки. На

примере задач оптимального управления портфелем ценных бумаг показано,

что полученная оценка является лучше, а стратегия, полученная в результате

решения соответствующих задач стохастического программирования, обеспе-

чивает лучшее значение вероятностного критерия по сравнению с известными

стратегиями управления в указанной задаче.

2. Постановка задачи

Рассмотрим стохастическую систему управления с дискретным временем

{

xk+1 = f_k (x_k,u_k,ξ_k) ,

(1)

k = 0,N,

x₀ = X,

x_k ∈ Rⁿ - вектор состояния. Начальное состояние X предполагается случай-

ным с известным распределением, u_k ∈ R^m - вектор управления, ξ_k ∈ R^s -

случайный вектор с известным распределением, f_k : Rⁿ × R^m × R^s → Rⁿ -

непрерывная для всех k = 0, N функция, N ∈ N - горизонт управления, при-

чем N ≥ 2.

Пусть ξ^k = (ξ₀, . . . , ξ_k)^T. Предположим, что ξ^N не зависит от X, а ξk+1

не зависит от ξ^k. Обозначим через U_k множество борелевских функций

u_k = u_k (x), значения которых удовлетворяют ограничениям u_k (x) ∈ U_k, где

U_k ⊂ R^m - компактные множества.

На траекториях системы (1) задан функционал вероятности

P_ϕ (u(·)) = P(Φ (xN+1 (u(·) ,ζ)) ≤ ϕ) ,

где P - вероятность, Φ : Rⁿ → R - ограниченная снизу непрерывная функ-

(

)_T

ция, ϕ ∈ R - известный скаляр, u (·) =

uT0 (·) ,... ,uTN (·)

- управление,

(

ζ =

X^T,ξT0,... ,ξTN

)^T.

Задача стохастического оптимального управления с вероятностным тер-

минальным критерием имеет вид

(2)

P_ϕ (u(·)) → max ,

u(·)∈U

где U = U₀ × . . . × U_N .

Введем в рассмотрение функцию Беллмана B_k : Rⁿ → [0, 1], которая по

определению [1] является точной верхней гранью функционала вероятности

при фиксированном текущем состоянии x_k = x, т.е.

B_k (x) =

(



)



sup

P Φ(xN+1 (x_k,uk (·),...,u_N (·),ξ_k,...,ξ_N))≤ϕxk = x .

u_k(·)∈U_k,...,u_N (·)∈U_N

В [1] установлено, что если существует стратегия u^ϕ (·) ∈ U, удовлетворяю-

щая следующим рекуррентным соотношениям динамического программиро-

вания:

[



]

u^ϕk (x) = arg max M

Bk+1 (f_k (x_k,u_k,ξ_k))xk = x

u_k∈U_k

[



]

B_k (x) = max M

Bk+1 (f_k (x_k,u_k,ξ_k))xk = x

k = 0,N,

u_k∈U_k

BN+1 (x) = I(-∞,ϕ] (Φ (x)),

то она оптимальна в задаче (2). Здесь M - оператор математического ожи-

дания по распределению P, I_A (x) - индикаторная функция множества A.

В [5] с использованием поверхностей уровней 1 и 0 функции Беллмана,

называемых изобеллами, удалось получить модификацию соотношений ди-

намического программирования, на основе которой было получено аналити-

ческое решение некоторых аэрокосмических задач. В разделе 3 приводятся

вспомогательные утверждения из [5], составляющие методологическую осно-

ву для приводимых далее результатов по уточнению оценок для функции

Беллмана.

3. Определение изобелл и модификация уравнения Беллмана

Основной идеей, заложенной в [5], является рассмотрение уравнения Белл-

мана в разных областях пространства состояний, а именно в таких, в которых

функция Беллмана равна единице, нулю и не равна ни единице, ни нулю. Пер-

вые две области, а точнее множества, названы в [5] изобеллами уровней 1 и 0.

Они определяются следующими соотношениями [5]:

{

}

{

( )

}

I_k = x ∈ Rⁿ : B_k (x) = 1 , O_k = x ∈ Rⁿ

B_k x

= 0 , k = 0,N.

Рассмотрим также множество, где функция Беллмана не равна ни 1, ни 0,

B_k = Rⁿ \ {I_k ∪ O_k} .

Отметим, что из определения множеств I_k, B_k, O_k следует, что

⎧

⎨Bk (x) = 1,

x∈I_k,

I_k ∪ B_k ∪ O_k = Rⁿ,

B_k (x) ∈ (0,1) ,

x∈B_k,

⎩

B_k (x) = 0,

x∈O_k.

В статьях [5, 6] исследованы важные свойства изобелл уровней 1 и 0, с по-

мощью которых установлены новые свойства функции Беллмана. Указанные

свойства объединены в одну лемму 1.

Лемма 1. Справедливы следующие утверждения:

1. Множества I_k удовлетворяют реккурентным соотношениям в обрат-

ном времени k = 0, N :

{

}

I_k = x ∈ Rⁿ :

∃u_k ∈ U_k : P(f_k (x,u_k,ξ_k) ∈ Ik+1) = 1 ,

{

}

IN+1 = x ∈ Rⁿ : Φ (x) ≤ ϕ ;

2. Множества O_k удовлетворяют реккурентным соотношениям в об-

ратном времени k = 0, N :

{

}

O_k = x ∈ Rⁿ :

∀u_k ∈ U_k : P(f_k (x,u_k,ξ_k) ∈ Ok+1) = 1 ,

{

}

ON+1 = x ∈ Rⁿ : Φ (x) > ϕ ;

3. Для x_k ∈ I_k оптимальным управлением на шаге k является любой

элемент из множества U^Ik (x_k):

{

}

U^Ik (x_k) = u ∈ U_k : P(f_k (x_k,u,ξ_k) ∈ Ik+1) = 1

4. Для x_k ∈ O_k оптимальным управлением на шаге k является любой

элемент из множества U_k;

5. Уравнение Беллмана в области x ∈ B_k допускает представление

{

(3) B_k (x) = max P (f_k (x, u_k, ξ_k) ∈ Ik+1) + P (f_k (x, u_k, ξ_k) ∈ Bk+1) ×

u_k∈U_k

[



]}



× M Bk+1 (fk (x,u_k,ξ_k))fk (x, uk, ξk) ∈ Bk+1

;

6. Для x ∈ B_k и u_k ∈ U_k справедлива система неравенств

{

M [Bk+1 (f_k (x, u_k, ξ_k))] ≥ P (f_k (x, u_k, ξ_k) ∈ Ik+1) ,

(4)

M [Bk+1 (f_k (x, u_k, ξ_k))] ≤ 1 - P (f_k (x, u_k, ξ_k) ∈ Ok+1) ;

7. Для x ∈ B_k функция Беллмана удовлетворяет двустороннему неравен-

ству

(5)

B_k (x) ≤ B_k (x) ≤ B_k

(x) ,

где B_k (x) - нижняя, а B_k (x) - верхняя оценки функции Беллмана

B_k (x) = sup P(f_k (x,u_k,ξ_k) ∈ Ik+1) ,

u_k∈U_k

B_k (x) = sup {1 - P(f_k (x,u_k,ξ_k) ∈ Ok+1)} ,

u_k∈U_k

причем B_N (x) = B_N (x) = B_N (x).

Пункты 1 и 2 леммы 1 устанавливают рекуррентную формулу для вычис-

ления изобелл, достоинством которой является ее “независимость” от функ-

ции Беллмана. П. 3 позволяет найти оптимальное управление при x ∈ I_k,

избегая решения сложных оптимизационных задач, путем решения вероят-

ностного уравнения. П. 4 закрывает вопрос об оптимальном управлении

при x ∈ O_k. П. 5 отражает “модифицированное” уравнение Беллмана в обла-

сти B_k, которое по сути является следствием применения формулы полного

математического ожидания в правой части классического уравнения Беллма-

на. П. 6 является следствием п. 5 и представляет собой двустороннюю оценку

для функции правой части уравнения Беллмана, из которой получается дву-

сторонняя оценка для самой функции Беллмана п. 7 (см. [6]).

Отметим, что п. 1-4 леммы 1 позволяют в ряде случаев аналитически

найти изобеллы, оптимальное управление при x ∈ I_k и x ∈ O_k и соответ-

ствующие решения задач стохастического программирования для нижней и

верхней оценок функции Беллмана [5, 6]. В некоторых частных случаях с

использованием оценок п. 5 удается найти также и оптимальное управление

при x ∈ B_k [5]. Тем не менее даже в задачах с достаточно простой струк-

турой (см., например, задачу оптимального управления портфелем ценных

бумаг [20]) с одномерным пространством состояний вопрос об оптимальном

управлении при x ∈ B_k является нерешенным. Таким образом, к настоящему

времени не найдено аналитическое решение указанной задачи для случая за-

данного горизонта управления (только для случая N = 1 [12]). Тем не менее

в [6] с использованием результата п. 6 было найдено управление, обеспечи-

вающее асимптотическую оптимальность (N → ∞).

В разделе 2 приводится обобщение результата п. 6, а именно усиленная

оценка функции Беллмана. Как будет показано далее, она позволяет найти

субоптимальную стратегию в задаче управления портфелем ценных бумаг

с заданным горизонтом управления, которая оказывается лучше известных

стратегий в смысле функционала вероятности.

4. Основной результат

Поскольку вопрос об оптимальном управлении для областей пространства

состояний I_k, O_k считается закрытым (см. п. 1-4 леммы 1), исследуем новые

свойства функции Беллмана для x ∈ B_k.

Рассмотрим рекуррентные соотношения в дискретном времени l = 0, k для

функции B^kl : Rⁿ → [0, 1]

⎧

[



]



⎨Bkl (x) = sup M Bkl+1 (fk (xk,uk,ξk))xk = x , l = 0, k,

(6)

u_k∈U_k

⎩

Bkk+1 (x) = I_I

(x)

k+1

и функции B^kl : Rⁿ → [0, 1]

⎧

[



]



⎨Bkl (x) = sup M Bkl+1 (fk (xk,uk,ξk))xk = x , l = 0, k,

(7)

u_k∈U_k

⎩

Bkk+1 (x) = I_I

k+1∪Bk+1 (x).

Граничное условие для указанных последовательностей задано в момент вре-

мени k. Нетрудно видеть, что выполнены B^kk (x) = B_k (x) и B^kk (x) = B_k (x).

Следующая теорема устанавливает усиленную двустороннюю оценку для

функции Беллмана и является основным результатом настоящей статьи.

Теорема. Для x ∈ B_k функция Беллмана удовлетворяет двусторонне-

му неравенству

(8)

max

B^lk (x) ≤ B_k (x) ≤ min B^lk

(x),

l=k,N

где функции B^lk (x) и B^lk (x) удовлетворяют рекуррентным соотношени-

ям (6), (7).

Доказательство теоремы приведено в Приложении.

Отметим важные свойства функций в левой и правой частях неравен-

ства (8)

⎧

⎪Bkl (x) = Bkl (x) = 1,

x∈I_k,

⎨

Bkl (x) = 1, B

(x) = 0, x ∈ B_k,

∀l = 0,k,

∀k = 0,N.

⎪

⎩

Bkl (x) = B^kl (x) = 0,

x∈O_k,

Задачи (6), (7) по сути являются уравнениями метода динамического про-

граммирования (МДП) для 2N - 2 задач стохастического оптимального

управления с вероятностным терминальным критерием.

Воспользуемся результатами раздела 4 при решении задачи управления

портфелем ценных бумаг.

5. Управление портфелем ценных бумаг

Рассмотрим задачу управления портфелем ценных бумаг с вероятност-

ным терминальным критерием [9-12]. Пусть X - размер стартового капитала,

x_k - размер капитала на начало k-го года, u1k - доля x_k капитала, вклады-

ваемого в безрисковый инструмент (например, в надежный банк), имеющий

доходность b, u2k - доля капитала x_k, вкладываемая в рисковый актив, харак-

теризующийся случайной доходностью ξ_k ∼ R [-1, a], имеющей равномерное

распределение на отрезке [-1, a], где -1 < b < a. Динамику капитала будем

описывать конечно-разностным соотношением [9-12]

{

(

)

xk+1 = x_k

1+u1kb+u2kξ_k

(9)

k = 0,N.

x₀ = X,

Множество U_k имеет вид

{

}

U_k = U = u ∈ R² : u¹ + u² = 1, uⁱ ≥ 0, i = 1,2 , k = 0,N.

Первое ограничение на компоненты вектора u_k моделирует тот факт, что в

каждом k-м году осуществляется вложение всего капитала x_k. Второе ограни-

чение на компоненты вектора u_k характеризует запрет операции “short sales”

(взятие средств в долг). В отличие от исходных предположений в данном

примере начальное состояние x₀ = X является детерминированной величи-

ной.

Рассматривается задача

(10)

P(-xN+1 ≤ ϕ) → max ,

u(·)∈U

где ϕ < 0 - фиксированный скаляр. Задача (10) заключается в максимизации

вероятности того, что уровень капитала к началу (N + 1)-го года окажется

не меньше фиксированного уровня (-ϕ).

Система (9) рассматривалась в [10-12] для случая N = 1 (двухшаговая

постановка). При этом в [10] рассмотрен случай усеченного нормального,

а в [11, 12] - равномерного распределения случайной величины ξ_k. Настоя-

щая модель соответствует модели из [11, 12], обобщенной на случай заданного

горизонта управления N.

Отметим, что в [10] было найдено аналитическое решение задачи (10) для

случая N = 1, при этом для k = N оптимальное управление и функция Белл-

мана определяются выражениями:

⎧

(

]

⎪

⎨(0, 1)T , x ∈

-∞,-

1+b

(11)

u^ϕN (x) = v₁ (x,ϕ) =

[

)

⎪

⎩(1, 0)^T , x ∈ -

,+∞

1+b

⎧

(

]

⎪

⎪0,

x∈

-∞,-

⎪

1+a

⎨

(

)

(12)

B_N (x) = J₁ (x,ϕ) =

x∈

⎪

x(1 + a)

1+a

1+b

⎪

[

)

⎪

⎩1,

x∈

,+∞

1+b

а для k = N - 1 оптимальное управление и функция Беллмана имеют вид:

⎧

(

]

⎪

⎪(0, 1)T , x ∈

-∞,-

⎪

(1 + b)²

⎪

⎪(

)_T

⎪

(1 + a) (1 + b)

⎨

⎛

(

)

⎞

1+a

(13) uϕN-1 (x) = v₂ (x, ϕ) =

1 + ln

1+b

⎪

⎠_,

x ∈ ^⎝-ϕ

,-ϕ

⎪

(1 + b)²

(1 + b)(1 + a)

⎪

⎡

(

)

⎞

⎪

1+a

⎪

1 + ln

1+b

⎪

1, 0)^T , x ∈ ⎣-ϕ

,+∞^⎠,

⎩⁽

(1 + b) (1 + a)

(14) BN-1 (x) = J₂ (x, ϕ) =

⎧

(

]

⎪

⎪0,

x∈

-∞,-

⎪

(1 + a)²

⎪

(

))

⎪

(

]

⎪

ϕ 1 + ln

-x(1+a)2

⎪

⎪1+

x∈

⎪

x (1 + a)

(1 + a)²

(1 + a) (1 + b)

⎪

(

))

(

))

⎛

⎤

⎪

1+a

⎨

ϕ 1+ln

1+b

x∈^⎝-

⎦_,

⁼⎪⎪

x (1 + a)

(1 + a)(1 + b)

⎪

(

))

⎛

(

))

⎞

⎪

1+a

ϕ(1 + b) ln

ϕ 1+ln

⎪

1+b

⎪1+

x∈^⎝-

⎠_,

⎪

(ϕ + x(1 + a)(1 + b))(1 + a)

(1 + a) (1 + b)

(1 + b)²

⎪

[

)

⎪

x∈

,+∞

⎩¹

(1 + b)

В [6] найдены изобеллы уровней 1 и 0 для функции Беллмана в задаче (10):

[

)

I_k =

ϕIk , +∞

ϕIk = -ϕ (1 + b)k-N-1 ,

(

]

O_k =

-∞,ϕ^Ok

ϕOk = -ϕ (1 + a)k-N-1 .

Из этих соотношений, используя п. 7 леммы 1, получаем верхнюю и нижнюю

оценки для функции Беллмана.

Утверждение 1. Справедливы утверждения:

1. Решение задач стохастического программирования (6) для k = 0, N - 1

и l = k имеет вид

[



]



u^kk (x) = arg max M B^kk (f_k (x_k,u_k,ξ_k))xk = x

u_k∈U_k

(

)

(

)

(

)

= arg max

P x

1+u1kb+u2kξ_k

≥ϕ^I

= v₁ x,-ϕ^I

k+1

u_k∈U

а оптимальное значение целевой функции равно

[



]



B^kk (x) = max M B^kk (f_k (x_k,u_k,ξ_k))xk = x

u_k∈U_k

(

)

(

)

(

)

= max

P x

1+u1kb+u2kξ_k

≥ϕ^I

= J₁ x,-ϕ^I

;

k+1

u_k∈U

2. Решение задач стохастического программирования (7) для k = 0, N - 1

и l = k имеет вид

[



]



u^kk (x) = arg max M B^kk (f_k (x_k,u_k,ξ_k))xk = x

u_k∈U_k

(

)

(

)

(

)

= arg max

P x

1+u1kb+u2kξ_k

≥ϕ^O

k+1

= v₁ x,-ϕ^O

k+1

u_k∈U

а оптимальное значение целевой функции равно

[



]



B^kk (x) = max M B^kk (f_k (x_k,u_k,ξ_k))xk = x

u_k∈U_k

(

)

(

)

= max

1+u1kb+u2kξ_k

≥ϕOk+1

=J₁

x,-ϕOk+1

u_k∈U

где функции v₁ : R × R → R² и J₁ : R × R → [0, 1] определяются выражения-

ми (11) и (12) соответственно.

Доказательство утверждения 1 заключается в подстановке пара-

метров (-ϕIk+1) и (-ϕOk+1) вместо параметра ϕ в выражения для оптималь-

ного управления и функции Беллмана при k = N (12).

Как видно из приведенных выражений, верхняя B^kk (x) и нижняя B^kk (x)

оценки функции Беллмана совпадают с функцией Беллмана при k = N с

точностью до параметров ϕ, -ϕIk+1 и -ϕOk+1. Отсюда с учетом рекуррент-

ных соотношений (6) и (7) делаем вывод, что функции BN-1 (x), Bk+1k (x)

и Bk+1k(x) тоже совпадают с точностью до тех же параметров. Приведем ре-

шение задач стохастического программирования (6) и (7).

Утверждение 2. Справедливы утверждения:

1. Решение задач стохастического программирования (6) для k = 0, N - 2

и l = k + 1 имеет вид

[



]

(

)



uk+1k (x) = arg max M Bk+1k+1 (f_k (x_k,u_k,ξ_k))xk = x

= v₂ x,-ϕ^I

k+2

u_k∈U_k

а оптимальное значение целевой функции равно

[



]

(

)



Bk+1k (x) = max M Bk+1k+1 (f_k (x_k,u_k,ξ_k))xk = x

= J₂ x,-ϕ^I

;

k+2

u_k∈U_k

2. Решение задач стохастического программирования (7) для k = 0, N - 2

и l = k + 1 имеет вид

[



]

(

)



uk+1k (x) = arg max M Bk+1k+1 (f_k (x_k,u_k,ξ_k))xk = x

= v₂ x,-ϕ^O

k+2

u_k∈U_k

а оптимальное значение целевой функции равно

[



]

(

)



Bk+1k (x) = max M Bk+1k+1 (f_k (x_k,u_k,ξ_k))xk = x

= J₂ x,-ϕ^O

k+2

u_k∈U_k

где функции v₂ : R × R → R² и J₂ : R × R → [0, 1] определяются выражения-

ми (13) и (14) соответственно.

Доказательство утверждения 2 заключается в подстановке пара-

метров (-ϕIk+2) и (-ϕOk+2) вместо параметра ϕ в выражения для оптималь-

ного управления и функции Беллмана при k = N - 1 (14).

На рис. 1 изображены двусторонние оценки для функции Беллмана для

следующих значений параметров: N = 2, k = 0, ϕ = -1,2, a = 1,2, b = 0,05.

1,00

0,75

0,50

0,25

0,50

0,75

1,00

Рис. 1. Двусторонние оценки функции Беллмана. Жирная

k+1

линия - B

(x), штрихпунктирная - B

(x), пунктирная -

Bk+1k (x), точечная - B^kk (x).

1,00

0,75

0,50

0,25

1,00

0,75

0,50

0,25

0,5

1,0

1,5

2,0

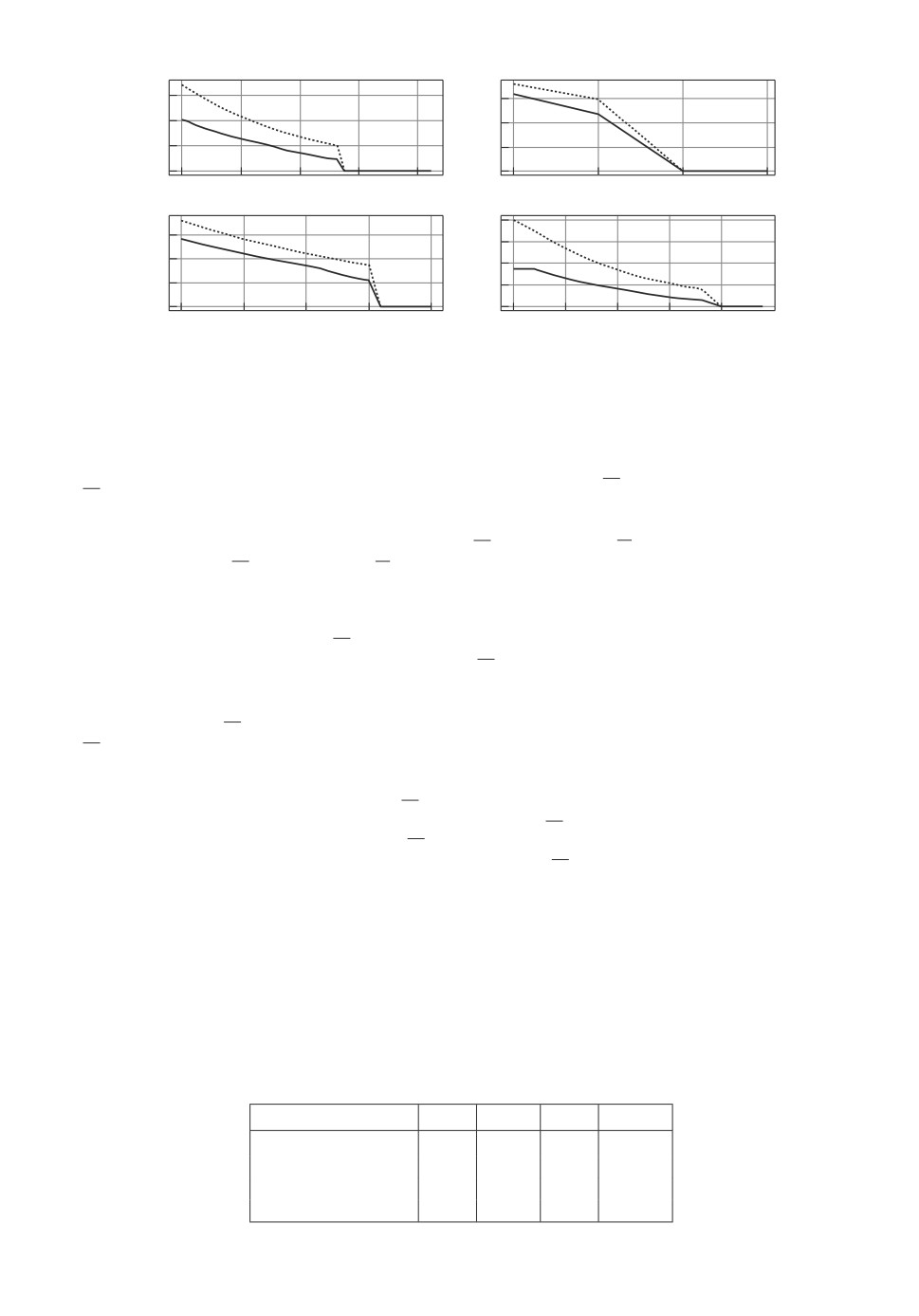
Рис. 2. Двусторонние оценки функции Беллмана.

Из графика видно, что нижняя и верхняя оценки (8) для функции Беллма-

на при l = k + 1 существенно точнее оценок при k = l, т.е. найденных в [5].

Другими словами, выполнены B^kk (x) > Bk+1k (x) и B^kk (x) < Bk+1k (x). Проведем

еще несколько экспериментов при других значениях параметров, занесенных

в табл. 1. Графики оценок функции Беллмана для случаев а-г приведены на

рис. 2.

Из графиков рис. 2 видно, что в некоторых случаях нижние, а в неко-

торых - верхние оценки функции Беллмана практически совпадают. Тем не

менее во всех случаях двусторонняя оценка (8) при l = k + 1 оказывается

точнее оценки при l = k.

Исследуем теперь усиленную оценку для функции оптимального значе-

ния вероятностного критерия. Отметим, что стратегии u^kk (x) и uk+1k (x) яв-

ляются субоптимальными в исходной задаче, поскольку максимизирует ниж-

ние границы (см. (6) при l = k и l = k + 1) функции Беллмана. Причем

в [6] доказано, что стратегия u^kk (x) при определенных условиях является

Таблица 1. Значение вероятностного критерия

№ эксперимента N

-4

3,2

0,05

-10

1,12

0,2

-3

3,5

0,05

-15

0,5

0,2

0,75

0,6

0,50

0,4

0,25

0,2

1,00

0,75

0,50

0,25

2,5

5,0

7,5

10,0

12,5

Рис. 3. Функции ΔF⁰ (точечная линия) и ΔF¹ (жирная линия)

в зависимости от N.

асимптотически оптимальной (N → ∞) и совпадает с так называемой “рис-

ковой стратегией”. Введем в рассмотрение функции F^l : R × R × N → [0, 1] и

F^l : R × R × N → [0,1]:

F^l (ϕ,X,N) = Bl0 (X) , F^l (ϕ,X,N) = Bl0 (X) .

В [6] было доказано, что

[

]

(15)

lim F⁰ (ϕ, X, N) - F⁰ (ϕ, X, N)

= 0.

N→∞

Используя утверждения

2, можно получить явный вид функций

F^l (ϕ,X,N) и F^l (ϕ,X,N) при l = 0 и l = 1.

Проведем сравнение функций

ΔF⁰ (ϕ,X,N) = F⁰ (ϕ,X,N) - F⁰ (ϕ,X,N) и

ΔF¹ (ϕ,X,N) = F¹ (ϕ,X,N) - F¹ (ϕ,X,N) ,

как функций аргумента N, т.е. горизонта управления. Рассмотрим 4 экспе-

римента, входные данные которых занесены в табл. 2. Отметим, что входные

параметры подбирались так, чтобы для всех N > 2 верхние границы функ-

ции оптимального значения вероятностного критерия не были равны нулю

(в противном случае оптимальное значение критерия равно нулю). На рис. 3

изображены их графики функций ΔF⁰ и ΔF¹ от аргумента N для случа-

ев а-г.

Таблица 2. Значение вероятностного критерия

№ эксперимента X

1,01

-4

3,2

0,05

1,01

-2,2

1,12

0,2

1,01

-2,5

1,5

0,05

1,01

-10

5,5

0,2

Таблица 3. Значения вероятностного критерия

Стратегия a = 1,12 a = 1,2 a = 1,3 a = 1,9

uk+1k

0,611

0,645

0,669

0,783

u^kk

0,594

0,623

0,664

0,769

u^Lk

0,501

0,548

0,592

Из рис. 3 видно, что оценка функции Беллмана при l = k + 1 “сходится”

быстрее оценки функции Беллмана при l = k.

Аналитическое исследование свойств найденных стратегий затруднено их

нетривиальной структурой, в частности нелинейностью по состоянию. Про-

ведем сравнение известных стратегий управления портфелем ценных бумаг

(см. раздел 5) со стратегией uk+1k (x) (п. 1 утверждения 2). Рассматриваются

рисковая стратегия [21] (п. 1 утверждения 1)

{

(1, 0)^T , x ≥ -ϕ (1 + b)k-N-1 ,

u^kk (x) = u^Rk (x) =

(0, 1)^T , x < -ϕ (1 + b)k-N-1 ,

k = 0,N,

и логарифмическая стратегия Келли [20]

[

(

)]

(16) u^Lk = arg max

M ln

1+u1kb+u2kξ_k

u_k∈U

[

(

)

(

)

1+b

1+u2k

+ au2k

= arg max

1+b

1+u2k

+ au2k

u_k∈U (1 + a)u2k

(

))]

(

))

u¹

1+u²

u1k + b

1+u2k

k = 0,N.

Оптимизационную задачу (16) можно свести [20] к задаче выпуклого про-

граммирования со скалярной стратегией

[

⁽1+b(1+ ũ_k)+aũ_k )

(17)

ũ^Lk = arg max

(1 + b (1 + ũ_k) + aũ_k) ln

0≤ũ_k≤1 (1 + a)ũ_k

)]

⁽1 - ũ_k + b(1 + ũ_k)

- (1 - ũ_k + b (1 + ũ_k)) ln

k = 0,N,

(

)_T

при этом u^Lk =

1-ũ^Lk, ũ^Lk

Зададим следующие числовые значения параметров [12]: N = 3, X = 1,

b = 0,05, ϕ = -1,2. Параметр a будем варьировать. Для численного построе-

ния оценок вероятностного критерия P_ϕ (u (·)) используется метод Монте

Карло по выборке из 2000 реализаций, а для численного поиска логариф-

мической стратегии (задача (17)) используется метод дихотомии. Результаты

вычислений сведены в табл. 3.

Из табл. 3 видно, что стратегия uk+1k превосходит известные стратегии по

значению вероятностного критерия.

6. Заключение

На основе метода динамического программирования и изобелл для за-

дач оптимального управления дискретными стохастическими системами с

вероятностным терминальным критерием получена усиленная двусторонняя

оценка для функции Беллмана. Показано, что данная оценка является точнее

оценки [6], полученной с использованием изобелл уровней 1 и 0. По аналогии

с [6] с использованием усиленной двусторонней оценки выведены соотноше-

ния для поиска субоптимальной стратегии, эфективность которой проверена

на задаче оптимального управления портфелем ценных бумаг с вероятност-

ным критерием в многошаговой постановке. В данной задаче субоптималь-

ная стратегия найдена в явном виде. Результаты численного эксперимента

показали, что полученная стратегия является лучше известных стратегий в

смысле значений функционала вероятности.

ПРИЛОЖЕНИЕ

Доказательство теоремы. Рассмотрим шаг k = N метода динами-

ческого программирования. C учетом п. 7 леммы 1 получаем, что неравенства

для функции Беллмана превращаются в равенства B_N (x) = B_N (x) = B_N (x).

Перейдем к шагу k = N - 1 метода динамического программирования. Ис-

пользуя п. 7 леммы 1 получаем оценку

BN-1 (x) ≤ BN-1 (x) ≤ BN-1 (x).

Легко видеть, что функции левых частей соотношений (6) и (7) в силу гранич-

ных условий совпадают с нижей и верхней оценками для функции Беллмана

(п. 7 леммы 1).

Пусть теперь k = N - 2. Выполнив подстановку

x = xN-1 = fN-2(xN-2,uN-2,ξN-2),

с учетом свойств математического ожидания получим

{

[

]

M[BN-1 (fN-2 (x,uN-2,ξN-2))] ≥ M

BN-1(fN-2(x,uN-2^,ξN-2⁾⁾

[

]

M[B_N (fN-2 (x,uN-2,ξN-2))] ≤ M

BN-1 (fN-2 (x,uN-2,ξN-2))

откуда, взяв супремум по uN-2 ∈ UN-2 в обеих частях неравенств, получаем

⎧

[

]

⎨BN-2 (x) ≥ sup M

BN-1 (fN-2 (x,uN-2,ξN-2))

= BN-1N-2 (x),

uN-2∈UN-2

[

]

⎩BN-2 (x) ≤ sup M

BN-1 (fN-2 (x,uN-2,ξN-2))

= BN-1N-2 (x),

uN-2∈UN-2

откуда с учетом неравенства п. 7 леммы 1, а также равенств B^kk (x) = B_k (x)

и Bkk (x) = Bk (x) для всех k = 0,N имеем, что

(Π.1)

max

BlN-2 (x) ≤ BN-2 (x) ≤ max BlN-2

(x) .

l=N-2,N

Теперь рассмотрим произвольный шаг k + 1, где k ≤ N - 2. Предположим,

что с учетом (П.1) выполнено неравенство

(Π.2)

max

Blk+1 (x) ≤ Bk+1 (x) ≤ min Blk+1

(x) ,

l=k+1,N

тогда получаем эквивалентную систему неравенств

Blk+1 (x) ≤ Bk+1 (x) ≤ Blk+1 (x) , l = k + 1,N.

Выполнив подстановку x = xk+1 = f_k (x_k, u_k, ξ_k), с учетом свойств математи-

ческого ожидания получим систему неравенств для всех l = k + 1, N

⎧

[



]

[



]



⎨M Bk+1 (f_k (x_k,u_k,ξ_k))xk = x

≥ M Blk+1 (fk (x_k,u_k,ξ_k))xk = x ,

[



]

[



]



⎩M Bk+1 (f_k (x_k,u_k,ξ_k))xk = x

≤ M Blk+1 (fk (x_k,u_k,ξ_k))xk = x ,

откуда, взяв супремум по u_k ∈ U_k в обеих частях неравенств, получаем

⎧

[



]



⎨Bk (x) ≥ sup M Blk+1 (f_k (x_k,u_k,ξ_k))xk = x

= Blk (x),

u_k∈U_k

[



]

l = k + 1,N,



⎩B_k (x) ≤ sup M Blk+1 (f_k (x_k,u_k,ξ_k))xk = x

= Blk (x),

u_k∈U_k

откуда имеем

Blk (x) ≤ B_k (x) ≤ B^lk (x) , l = k + 1, N.

С учетом равенств B^kk (x) = B_k (x), B^kk (x) = B_k (x) и неравенства п. 7 леммы 1

получаем

Blk (x) ≤ B_k (x) ≤ B^lk (x) , l = k, N,

откуда окончательно имеем, что

(Π.3)

max

B^lk (x) ≤ B_k (x) ≤ min B^lk

(x).

l=k,N

В результате доказано, что из (П.2) следует (П.3) для всех k, поэтому с учетом

математической индукции из (П.1) следует и (П.3).

Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления лета-

тельными аппаратами. М.: Машиностроение, 1987.

2. Красильщиков М.Н., Малышев В.В., Федоров А.В. Автономная реализация

динамических операций на геостационарной орбите. I. Формализация задачи

управления // Изв. РАН. ТиСУ. 2015. № 6. С. 82-95.

Малышев В.В., Старков А.В., Федоров А.В. Cинтез оптимального управления

при решении задачи удержания космического аппарата в орбитальной группи-

ровке // Космонавтика и ракетостроение. 2012. № 4. С 150-158.

Малышев В.В., Старков А.В., Федоров А.В. Совмещение задач удержания и

уклонения в окрестности опорной геостационарной орбиты // Вестн. Москов-

ского городского педагогич. ун-та. Сер. Экономика. 2013. № 1. С 68-74.

Азанов В.М., Кан Ю.С. Синтез оптимальных стратегий в задачах управле-

ния стохастическими дискретными системами по критерию вероятности // АиТ.

2017. № 6. С. 57-83.

Azanov V.M., Kan Yu.S. Design of Optimal Strategies in the Problems of Discrete

System Control by the Probabilistic Criterion // Autom. Remote Control. 2017.

V. 78. No. 6. P. 1006-1027.

Азанов В.М., Кан Ю.С. Двухсторонняя оценка функции Беллмана в задачах

стохастического оптимального управления дискретными системами с вероят-

ностным критерием // АиТ. 2018. № 2. С. 3-18.

Azanov V.M., Kan Yu.S. Bilateral Estimation of the Bellman Function in the

Problems of Optimal Stochastic Control of Discrete Systems by the Probabilistic

Performance Criterion // Autom. Remote Control. 2018. V. 79. No. 2. P. 203-215.

Кибзун А.И., Игнатов А.Н. О существовании оптимальных стратегий в задаче

управления стохастической системой с дискретным временем по вероятностному

критерию // АиТ. 2017. № 10. С. 139-154.

Kibzun A.I., Ignatov A.N. On the Existence of Optimal Strategies in the Control

Problem for a Stochastic Discrete Time System with Respect to the Probability

Criterion // Autom. Remote Control. 2017. V. 78. No. 10. P. 1845-1856.

Кибзун А.И., Игнатов А.Н. Сведение двухшаговой задачи стохастического оп-

тимального управления с билинейной моделью к задаче смешанного целочис-

ленного линейного программирования // АиТ. 2016. № 12. С. 89-111.

Kibzun A.I., Ignatov A.N. Reduction of the Two-Step Problem of Stochastic Optimal

Control with Bilinear Model to the Problem of Mixed Integer Linear Programming //

Autom. Remote Control. 2016. V. 77. No. 12. P. 2175-2192.

Кибзун А.И., Игнатов А.Н. Двухшаговая задача формирования портфеля цен-

ных бумаг из двух рисковых активов по вероятностному критерию // АиТ. 2015.

№ 7. С. 78-100.

Kibzun A.I., Ignatov A.N. The Two-Step Problem of Investment Portfolio Selection

from two Risk Assets via the Probability Criterion // Autom. Remote Control. 2015.

V. 76. No. 7. P. 1201-1220.

10.

Кибзун А.И., Кузнецов Е.А. Оптимальное управление портфелем ценных бу-

маг // АиТ. 2001. № 9. С. 101-113.

Kibzun A.I., Kuznetsov E.A. Optimal Control of the Portfolio // Autom. Remote

Control. 2001. V. 62. No. 9. P. 1489-1501.

11.

Бунто Т.В., Кан Ю.С. Оптимальное управление по квантильному критерию

портфелем ценных бумаг с ненулевой вероятностью разорения // АиТ. 2013.

№ 5. С. 114-136.

Bunto T.V., Kan Yu.S. Quantile Criterion-based Control of the Securities Portfolio

with a Nonzero Ruin Probability // Autom. Remote Control. 2013. V. 74. No. 5.

P. 811-828.

12.

Григорьев П.В., Кан Ю.С. Оптимальное управление по квантильному критерию

портфелем ценных бумаг // АиТ. 2004. № 2. С. 179-197.

Grigor’ev P.V., Kan Yu.S. Optimal Control of the Investment Portfolio with Respect

to the Quantile Criterion // Autom. Remote Control. 2004. V. 65. No. 2. P. 319-336.

13.

Вишняков Б.В., Кибзун А.И. Оптимизация двухшаговой модели изменения ка-

питала по различным статистическим критериям // АиТ. 2005. № 7. С. 126-143.

Vishnyakov B.V., Kibzun A.I. A Two-Step Capital Variation Model: Optimization

by Different Statistical Criteria // Autom. Remote Control. 2005. V. 66. No. 7.

P. 1137-1152.

14.

Jasour A.M., Aybat N.S., Lagoa C.M. Semidefinite Programming For Chance

Constrained Optimization Over Semialgebraic Sets // SIAM J. Optimization. 2015.

№ 25 (3). P. 1411-1440.

15.

Jasour A.M., Lagoa C.M. Convex Chance Constrained Model Predictive Control //

arXiv preprint arXiv:1603.07413, 2016.

16.

Jasour A.M., Lagoa C.M. Convex Relaxations of a Probabilistically Robust Control

Design Problem // 52nd IEEE Conf. on Decision and Control. 2013. P. 1892-1897.

17.

Hsieh Chung-Han, Barmish B. Ross On Drawdown-Modulated Feedback Control in

Stock Trading // IFAC Proc. July 2017. V. 50. No. 1. P. 952-958.

18.

Hsieh Chung-Han, Barmish B. Ross, Gubner J. At What Frequency Should the Kelly

Bettor Bet? // Proc. IEEE Amer. Control Conf. (ACC). Milwaukee. WI. January

2018.

19.

Норкин Б.В. О численном решении задачи стохастического оптимального управ-

ления дивидендной политикой страховой компании // Компьютерная матема-

тика. 2014. № 1. С. 131-140.

20.

Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероят-

ностными критериями. М.: Физматлит, 2009.

21.

Kibzun A.I., Kan Yu.S. Stochastic Programming Problems with Probability and

Quantile Functions. Chichester: Wiley, 1996.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 22.04.2018

После доработки 29.10.2018

Принята к публикации 08.11.2018