Автоматика и телемеханика, № 4, 2019
© 2019 г. А.И. ПЕСЧАНСКИЙ, д-р техн. наук (peschansky_sntu@mail.ru)
(Севастопольский государственный университет)
СТАЦИОНАРНЫЕ ХАРАКТЕРИСТИКИ НЕНАДЕЖНОЙ
МНОГОКАНАЛЬНОЙ СИСТЕМЫ ОБСЛУЖИВАНИЯ
С ПОТЕРЯМИ И ВРЕМЕННЫМ РЕЗЕРВОМ1
Рассматривается ненадежная восстанавливаемая многоканальная си-
стема обслуживания с потерями, в которой во время обслуживания зая-
вок могут происходить отказы каналов, но обслуживание будет продол-
жаться за счет случайного временного резерва. Входящий поток счита-
ется простейшим, а все остальные случайные величины, описывающие
систему, имеют распределения общего вида. Построена полумарковская
модель эволюции системы во времени и найдено стационарное распреде-
ление вложенной цепи Маркова. Получены выражения для определения
стационарных вероятностей и средних стационарных времен пребывания
системы в различных физических состояниях, которые позволяют оце-
нить влияние временного резерва на стационарные характеристики си-
стемы.
Ключевые слова: многоканальная система обслуживания, временной ре-
зерв, полумарковский процесс, стационарное распределение вложенной
цепи Маркова, стационарная вероятность состояний, среднее стационар-
ное время пребывания в состояниях.
DOI: 10.1134/S0005231019040044
1. Введение
Анализу систем массового обслуживания посвящены многочисленные пуб-
ликации. Обзор по ненадежным системам обслуживания можно найти, на-
пример, в [1-3]. Для улучшения показателей функционирования систем с от-
казами возможны различные методы. Так, в [4] исследованы модели с ре-
зервированным обслуживанием запросов разными узлами для кластера од-
ноканальных систем с индивидуальными очередями. Для многоканальных
систем с общей очередью модели систем с резервированным обслуживани-
ем запросов предложены в [5-7]. В [8-11] рассмотрены модели ненадежной
восстанавливаемой системы обслуживания с учетом проведения различных
стратегий технического обслуживания. Еще одним методом повышения на-
дежности технических систем является временное резервирование, когда для
устранения причины отказа система имеет запас времени, в течение которого
она выполняет свои функции (см., например, [12-14]).
Следует отметить, что наиболее полная теория построена для систем об-
служивания, эволюция которых описывается марковскими процессами. Для
1 Работа выполнена в рамках Государственного задания Минобрнауки Российской Фе-
дерации (№ 1.10513.2018/11.12), при финансовой поддержке Российского фонда фундамен-
тальных исследований (проект № 19-01-00704).
70
построения моделей таких систем необходимо, чтобы все случайные факто-
ры, влияющие на эволюцию системы во времени, обладали отсутствием по-
следействия, т.е. все случайные времена действия факторов имели бы по-
казательные распределения. Если же некоторые из времен действия факто-
ров имеют произвольные функции распределения, отличные от показатель-
ных, то построение и анализ систем обслуживания значительно усложняет-
ся. Для исследования таких систем, например, в [15, 16] применяется аппа-
рат теории полумарковских процессов с дискретно-непрерывным фазовым
пространством состояний. Этот аппарат используется и в данной статье, по-
скольку предполагается, что входящий в систему обслуживания поток заявок
является простейшим, а все остальные случайные величины, определяющие
эволюцию системы во времени, имеют распределения общего вида. Данная
статья является обобщением на случай многокомпонентной системы постро-
енной в [17] полумарковской модели однолинейной ненадежной восстанавли-
ваемой системы с временным резервом.
2. Постановка задачи
В ненадежную восстанавливаемую N-компонентную систему обслужива-
ния M/G/N/0 поступает простейший поток заявок с интенсивностью λ. Вре-
мя αk обслуживания заявки k-м каналом имеет произвольную функцию рас-
пределения (ФР) Fk(t) = P {αk ≤ t} с плотностью распределения (ПР) fk(t),
k = 1,N. Если в момент поступления заявки в систему свободно несколько
работоспособных каналов, то с равной вероятностью она начинает обслужи-
ваться любым из них. В момент обслуживания заявки канал может отказать.
Длительность промежутка времени с момента начала обслуживания заявки
до отказа канала — случайная величина (СВ) γk с ФР Φk(t) и ПР ϕk(t).
Отказ канала обнаруживается мгновенно и сразу начинается его восстанов-
ление, которое длится случайное время σk с ФР Ψk(t) и ПР ψk(t). После
отказа канала обслуживание заявки продолжается за счет временного резер-
ва с учетом времени уже проведенного обслуживания. Наличие временного
резерва для каждого канала может рассматриваться как существование еще
одного канала, который продолжает обслуживание заявки на период восста-
новления неисправного канала (расходуется резервное время) и простаивает
во время исправной работы канала (резервное время не расходуется). Вели-
чина временного резерва — СВ ξk с ФР Rk(t) и ПР rk(t).
Если во время обслуживания заявки за счет резерва происходит восстанов-
ление канала, то ему передается дообслуживание заявки с учетом уже прове-
денного времени обслуживания (в том числе и за счет временного резерва).
Через случайное время γk после восстановления канала во время обслужива-
ния все той же заявки вновь может произойти отказ канала. Обслуживание
заявки снова продолжается за счет случайного временного резерва ξk. Таким
образом, при обслуживании одной и той же заявки неоднократно может быть
использован временной резерв.
Если во время обслуживания заявки за счет резерва исчерпывается его
объем, то обслуживание заявки прерывается, она теряется и на дообслужи-
вание не возвращается. Следующую заявку на обслуживание канал может
принять после своего восстановления.
71
Предполагается, что все СВ, описывающие систему, независимы, имеют
конечные математические ожидания Eαk, Eγk, Eξk и Eσk и дисперсии.
Цель статьи — построить математическую модель функционирования си-
стемы, найти стационарные вероятности пребывания системы в различных
физических состояниях и средние стационарные времена пребывания в этих
состояниях, а также оценить влияние временного резерва на указанные ха-
рактеристики.
3. Полумарковская модель системы
Для построения математической модели используем аппарат теории по-
лумарковских процессов с дискретно-непрерывным множеством состояний
[15, 16]. Пусть (E, ζ) — измеримое пространство: E интерпретируется как
фазовое пространство состояний стохастической системы, ζ — булева ал-
гебра выделенных подмножеств из E, интерпретируемых как совокупность
наблюдаемых подмножеств состояний системы. Полумарковский процесс
(ПМП) S(t) определим с помощью процесса марковского восстановления
{Sn, Θn; n ≥ 0}, где {Sn; n ≥ 0} — вложенная цепь Маркова (ВЦМ), Θn —
времена пребывания полумарковского процесса в состояниях.
Определим фазовое пространство рассматриваемой системы обслужива-
ния и опишем ее физические состояния. Каждый канал может находиться в
следующих состояниях: 11 — канал в работоспособном состоянии обслужи-
вает заявку; 12 — канал восстанавливается, заявка обслуживается за счет
временного резерва; 2 — канал восстанавливается, заявка не обслуживает-
ся; 0 — канал в работоспособном состоянии ожидает заявку. Физические
состояния всей системы описываются N-мерным вектором d = (d1, . . . , dN ),
k-я компонента которого указывает на физическое состояние k-го канала,
т.е. dk = 0, 11, 12, 2; k = 1, N . Для того чтобы в моменты изменения физи-
ческих состояний системы она обладала марковским свойством, расширим
фазовое пространство состояний добавлением непрерывных составляющих и
перед вектором d укажем номер i канала, который изменил свое физическое
состояние посл{ним. В результ}е фазовое пространство состояний будет
иметь вид E =
id x z u, i = 1, N
, где x = (x1, . . . , xN ) — вектор, координа-
ты которого указывают на время, прошедшее с момента начала обслужи-
вания заявки соответствующим каналом. Очевидно, что xk = 0, если dk = 0
или dk = 2. Кроме того, xi = 0 в момент принятия к обслуживанию заявки
i-м каналом. Ненулевые координаты вектора z = (z1, . . . , zN ) указывают на
оставшееся время до отказа k-го канала, если dk = 11, либо на оставшееся
время резерва, если dk = 12; для остальных физических состояний каналов
соответствующие компоненты равны нулю. Кроме того, в моменты перехода
i-го канала в состояния 11 и 12 компонента zi = 0. Ненулевые компоненты
вектора u = (u1, . . . , uN ) — оставшиеся времена до восстановления соответ-
ствующих каналов в момент изменения физического состояния i-го канала.
Очевидно, что uk > 0, если dk = 12, 2, и uk = 0 для dk = 11, 0.
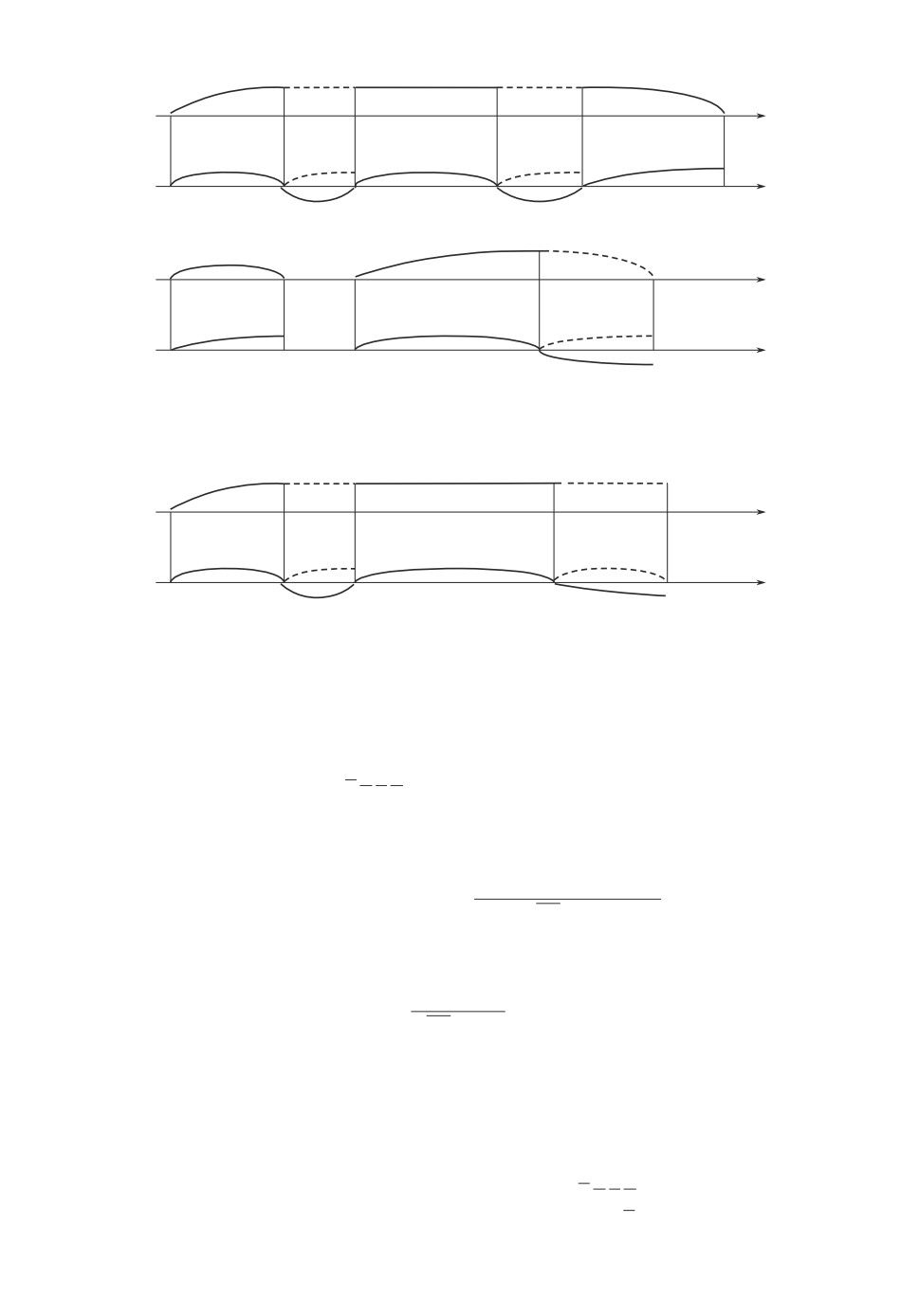
Временные диаграммы функционирования k-го канала системы представ-
лены на рис. 1 и 2. На рис. 1 рассмотрены случаи, когда при обслуживании
заявки резерв используется дважды, ни разу не используется и обслуживание
72
k
t
k
k
k
k
k
t
k
k
k
k
t
k
k
k
t
k
Рис. 1. Заявка обслужена.
k
t
k
k
k
k
t
k
k
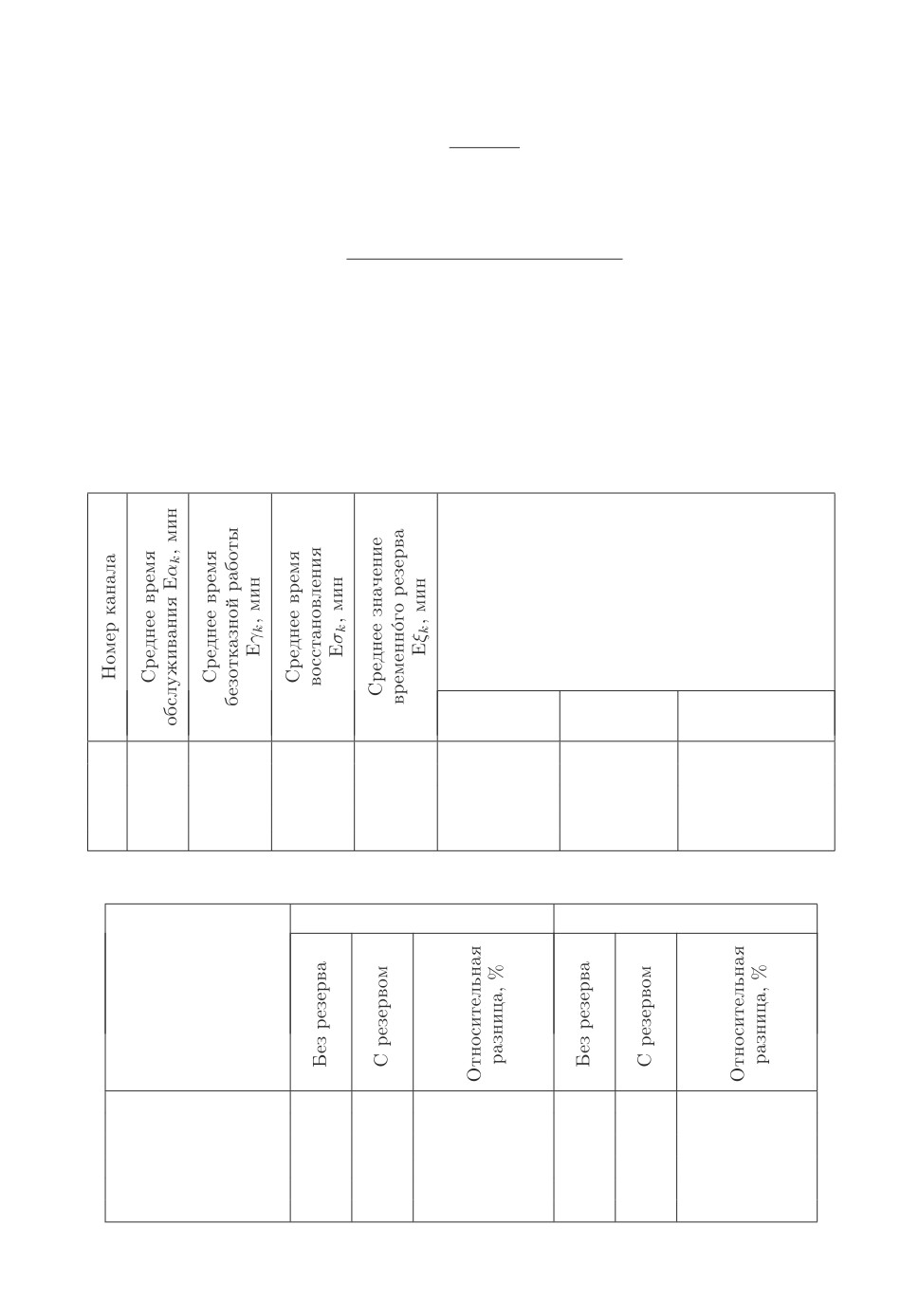
Рис. 2. Потеря заявки при обслуживании.
завершается за счет временного резерва. На рис. 2 представлен случай, когда
при втором использовании объем резерва исчерпывается и заявка теряется.
Определим времена пребывания системы в состояниях. Для этого введем
обозначения для вектора id x z u: [αk - xk]+ — остаточное время обслужива-
ния заявки k-м каналом при условии, что время обслуживания превысило
величину xk. Эта СВ имеет ФР
{
}
Fk(xk + t) - Fk(xk)
P
[αk - xk]+ ≤ t
=
Fk(xk)
и ПР
fk(xk + t)
Fk(xk)
В случае xk = 0 будем полагать, что [αk]+ есть αk;
(
)
(
)
ω=
∧
uk
∧
∧
zk
uk>0
zk>0
— минимум положительных компонент вектора id x z u (∧ — знак миниму-
ма); Ω11d,Ωd2 ,Ωd,Ωd —совокупностиномероввектораd,равных11,12,2и0
73
соответственно; Ω11,12d=Ωd1
⋃Ω12d ;d — число нулевых компонент вектора d
(число элементов множества Ω0d), т.е. число свободных работоспособных ка-
налов в системе.
С учетом ввееных обозначений время пребывания системы в состоянии
=0определяетсяформулой
id x z u в случае
d
⎧
β∧γi ∧
∧
[αk - xk]+ ∧ ω,
di = 11,
⎪
⎪
k∈Ω11,12
d
⎨
β∧σi ∧ξi ∧
∧
[αk - xk]+ ∧ ω, di = 12,
(1)
Θidxzu =
k∈Ω11,12
⎪
d
⎪
⎩
β∧
∧
[αk - xk]+ ∧ ω,
di = 0,2.
k∈Ω11,12
d
Если какое-либо из множеств Ωmd (m = 11, 12, 0, 2) пустое, то соответствую-
=0,в(1)
щая составляющая в (1) отсутствует. Так, в случае Ω0d = ∅, т.е.
d
будет отсутствовать СВ β - время между поступлениями заявок.
Стохастические соотношения (1) означают, что времена пребывания в со-
стояниях ПМП S(t) задаются минимумом СВ, а события переходов ВЦМ из
одного состояния в другие — событиями, которые определяются минимумом
этих величин. Опишем переходные вероятности ВЦМ {Sn; n ≥ 0}. Рассмот-
=0.Событияпереходов
рим, например, состояние id x z u в случае di = 11,
d
из этого состояния определяются минимумом β ∧ γi ∧
∧
[αk - xk]+ ∧ ω.
k∈Ω11,12d
Если Θidxzu = [αi - xi]+, то система переходит в состояние id′ x′ z′ u′ с
плотностью вероятности
{
}
∏
fi(xi + y)
Fk(xk + y)
p
id x z u → id′ x′ z′ u′
= e-λyΦi(y)
,
Fi(xi)
Fk(xk)
k∈Ω11,12d
k=i
где
Φi(y) = 1 - Φi(y), Fk(y) = 1 - Fk(y), d′i = 0, d′k = dk, k = i, y < ω;
{
11,12
xk + y, k ∈ Ω
, k = i,
d
x′k =
0,
k ∈ Ω11,12d,k = i,
{
11,12
zk - y, k ∈ Ω
, k = i,
d
z′k =
0,
k ∈ Ω11,12d,k = i,
{
12
uk - y, k ∈ Ω
⋃Ω2d,
d
u′k =
0,
⋃Ω2d.
k ∈ Ω12d
Если Θidxzu = γi, то
{
}
∏
Fk(xk + y)
p
id x z u → id′ x′ z′ u′
= e-λyϕi(y)
,
Fk(xk)
k∈Ω11,12
d
74
где
d′i = 12, d′k = dk, k = i, y < ω;
{
11,12
xk + y, k ∈ Ω
,
d
x′k =
0,
k ∈ Ω11,12d,
{
11,12
zk - y, k ∈ Ω
, k = i,
d
z′k =
0,
k ∈ Ω11,12d,k = i,
{
12
uk - y, k ∈ Ω
⋃Ω2d,
d
u′k =
0,
⋃Ω2d.
k ∈ Ω12d
В случае Θidxzu = β имеем
{
}
λ
∏
Fk(xk + y)
p
id x z u → jd′ x′ z′ u′
=
e-λyϕi(y + zi)
,
d
Fk(xk)
k∈Ω11,12
d
где
j ∈ Ω0d, d′j = 11, d′k = dk, k = j, y < ω,
zi > 0;
{
11,12
xk + y, k ∈ Ω
,
d
x′k =
0,
k ∈ Ω11,12d,
⎧
⎨
zk - y, k ∈ Ω11,12d,k=i,
z′k =
zi,
k = i,
⎩
0,
k ∈ Ω11,12d,
{
12
uk - y, k ∈ Ω
⋃Ω2d,
d
u′k =
0,
⋃Ω2d.
k ∈ Ω12d
Аналогично выписываются плотности вероятностей переходов в остав-
шиеся состояния.
Очевидно, что в случае пустого подмножества Ωmd (m = 11, 12, 0, 2) соот-
ветствующий множитель в выра ении для плотности вероятности перехода
=0отсутствуетмножительe-λy.
отсутствует. Например, в случае
d
4. Стационарное распределение вложенной цепи Маркова
Стационарное распределение ВЦМ {Sn, n ≥ 0} найдем из системы уравне-
ний
∫
(2)
ρ(B) =
ρ(dx)P (x, B),
E
где P (x, B) — вероятность перехода из состояния x в множество состояний B;
ρ(·) — стационарное распределение ВЦМ [15, 16].
75
Прежде чем сформулировать теорему о виде стационарного распределе-
ния, приведем некоторые сведения из теории процессов восстановления [18].
Функционирование k-го канала во время обслуживания заявки описывается
альтернирующим процессом восстановления. Этот процесс образован момен-
тами отказа канала (12-восстановлениями) и следующими за ними момен-
тами устранения неисправности (11-восстановлениями) при условии, что вре-
менной резерв канала не исчерпывается. Длительность времени между сосед-
ними 11-восстановлением и 12-восстановлением имеет распределение Φk(x), а
между∫12-восстановлением и 11-восстановлением — несобственное распреде-
x
ление
ψk(t)Rk(t)dt. Поток 11-восстановлений этого альтернирующего про-
0
цесса образует простой обрывающийся процесс восстановлени∫я с несобствен-
x
ным распределением, равным свертке распределений Φk(x) и
ψk(t)Rk(t)dt.
0
Обозначим через H(1)k(x) функцию восстановления этого потока, т.е. среднее
число восстановлений работоспособности k-го канала за время x. Плотность
h(1)k(x) =ddxH(1)k(x) функции восстановления представляется в виде
∑
h(1)k(x) =
(ϕk ∗ ψkRk)∗(n)(x),
n=1
∫x
где (ϕk ∗ψkRk)∗(n)(x) — n-кратная свертка функции
ϕk(x - s)ψk(s)Rk(s)ds.
0
Поток 12-восстановлений альтернирующего процесса образует обрываю-
щийся процесс восстановления с запаздыванием, который определяется
∫x
функциями Φk(x) и
Φk(x-s)ψk(s)Rk(s)ds. Обозначим через H(2)k(x) функ-
0
цию восстановления этого процесса, т.е. среднее число отказов k-го канала за
время x. Плотность h(2)k(x) этой функции представима в виде
∑[
]
h(2)k(x) =
ϕk ∗ (ϕk ∗ ψkRk)∗(n-1) (x).
n=1
С рассмотренным альтернирующим процессом восстановления связаны
следующие случайные величины. Прямое (остаточное) время восстановле-
ния (перескок) работоспособного канала (или остаточное время наработки на
отказ) определяется как время от момента x до ближайшего момента 12-вос-
становления альтернирующего процесса, т.е. до ближайшего отказа канала.
Если в момент x канал находится в работоспособном состоянии, эта СВ имеет
несобственное распределение с плотностью v(11)k(x, z):
∫x
v(11)k(x,z) = ϕk(x + z) + h(1)k(s)ϕk(x + z - s)ds,
0
∞
∫
v(11)k(x,z)dz = 1 + H(1)k(x) - H(2)k(x).
0
76
Если в момент x канал восстанавливается и обслуживает заявку за счет
резерва, то совместное несобственное распределение оставшегося времени до
конца резерва и конца восстановления канала имеет плотность v(12)k(x, u, z):
∫x
v(12)k(x,u,z) = h(2)k(s)ψk(x + u - s)rk(x + z - s)ds;
0
∫
∞
∫
∞
∫
x
dz v(12)k(x, u, z)du = H(2)k(x) - H(1)k(x) - H(2)k(x - s)Ψk(s)rk(s)ds.
0
0
0
Заметим, что
∫
∞
∫
∞
∫
∞
∫
x
v(11)k(x,z)dz + dz v(12)k(x,u,z)du = 1 - H(2)k(x - s)Ψk(s)rk(s)ds,
0
0
0
0
∫x
где
H(2)k(x - s)Ψk(s)rk(s)ds — вероятность обрыва альтернирующего про-
0
цесса, который не оборвался до момента x.
Теорема 1. Стационарное распределение ВЦМ {Sn,n ≥ 0} ПМП S(t)
определяется выражениями:
∏
(3)
ρ(id x z u) = ρa(xi, zi, ui)
Fk(xk)v(11)k(xk, zk
)×
k∈Ω11d
k=i
∏
∏
×
Fk(xk)v(12)k(xk, zk, uk)
V (2)k(uk),
k∈Ω12d
k∈Ω2d
k=i
k=i
⎧
1,
di = 0 или di = 11, xi = zi = 0,
⎪
⎪
⎨
Fi(xi)hi1)(xi), di = 11, xi > 0,
a(xi, zi, ui) =
⎪
Fi(xi)hi2)(xi), di = 12,
⎪
⎩
v(2)i(ui),
di = 2,
⎧
d!
⎪
⎨
ρ0
,
di = 0,
λ|d|
(
)
ρ0 = const,
ρ=⎪
d-1
!
⎪
⎩ ρ0
, di = 0,
λ|d|-1
77
∞
∫∞
∫
[
]
(2)
v
(u) = h(2)k(s)ds ψk(y + u)
fk(y + s)Rk(y) + Fk(y + s)rk(y)
dy,
k
0
0
∫∞
V (2)k(u) = v(2)k(t)dt =
u
∫∞
∫
∞
[
]
= h(2)k(s)ds Ψk(y + u)
fk(y + s)Rk(y) + Fk(y + s)rk(y)
dy.
0
0
Доказательство теоремы
1
приводится в Приложении. Заметим, что
v(2)k(u) — плотность несобственного распределения оставшегося времени до
конца восстановления k-го канала в момент завершения обслуживания заяв-
ки за счет резерва, либо в момент ее потери по причине расходования резерва.
Значение постоянной ρ0 находится из условия нормировки.
5. Стационарные вероятности состояний
Пусть фазовое пространство состояний E представлено в виде объедине-
⋃
ния непересекающихся подмножеств E = Ei, Ei
⋂Ej = ∅. Известно, что
i=1
в случае существования единственного распределения ВЦМ {Sn, n ≥ 0} ста-
ционарные вероятности p∗i пребывания системы в подмножествах состояний
определяются формулами из [15]
⎞-1
∫
⎛∫
p∗i = lim
P {S(t) ∈ Ei/S(0) = x} = m(x)ρ(dx)⎝ m(x)ρ(dx)⎠
,
(4)
t→∞
Ei
E
i = 1,n,
где m(x) — среднее время пребывания системы в состоянии x ∈ E, ρ(·) —
стационарное распределение вложенной цепи Маркова.
С помощью равенств (4) найдем стационарные вероятности пребывания
рассматриваемой системы обслуживания в различных физических состоя-
ниях. Обозначим через D множество всех физических векторов d, опи-
сываю {их состояния, а через }∗ — некоторое его подмножество. Пусть
ED∗ =
id x z u, i = 1, N, d ∈ D∗
— подмножество фазовых состояний си-
стемы, дис
∫
∑
∫
жение дляE
D∗
m(x)ρ(dx) =d∈D∗ Ed m(x)ρ(dx),гдеEd—подмножества
фазовых состояний E с фиксированным вектором состояний d. Заметим, что
это подмножество содержит состояния, в которых свое физическое состояние
последним изменил любой канал. Кроме этого, если некоторая компонента
вектора d равна 11, т.е. dk = 11, то Ed содержит как состояния, в которых
xk = 0, так и состояния, в которых xk > 0.
78
∫
При нахождении выражения для
m(x)ρ(dx) учтем, что среднее время
Ed
E[Θidxzu] пребывания системы в состоянии id x z u определяется формулами
⎧
ω
∫
⎪
∏
⎪
Fk(xk + t)
e-λtΦi(t)
dt,
⎪
i ∈ Ω11d ,
⎪
Fk(xk)
⎪
0
k∈Ω11,12
d
⎪
ω
∫
⎪
∏
⎨
Fk(xk + t)
e-λtΨi(t)Ri(t)
dt, i ∈ Ω12d,
(5)
E[Θidxzu] =
Fk(xk)
⎪
0
k∈Ω11,12d
⎪
⎪
k=i
⎪
∫
ω
⎪
∏
⎪
Fk(xk + t)
⎪
e-λt
dt,
i∈Ω0d
⋃Ω2d,
⎩
Fk(xk)
0
k∈Ω11,12
d
(
)
(
)
где ω =
∧
zk
∧
∧
uk
. Если какое-либо из подмножеств Ω11d,Ωd2 ,
zk>0
uk>0
Ω0d
⋃Ω2d — пустое, то соответствующее выражение под знаком интеграла в (5)
отсутствует.
В результате преобразований, учитывая вид стационарного распределения
ВЦМ (3) и (5), получаем (см. Приложение), что
∫
d!
∏
∏
∏
(6)
m(x)ρ(dx) = ρ0
T(11)
T(12)
T(2)k,
k
k
λ|d|
Ed
k∈Ω11
k∈Ω12d
k∈Ω2
d
d
где
∫∞
[
]
T(11)k = Eαk + Fk(x) H(1)k(x) - H(2)k(x) dx,
0
∫∞
∫
∞
T(12)k = h(2)k(s)ds Fk(y + s)Ψk(y)Rk(y)dy,
0
0
∫
∞
∫
∞
∫
∞
T(2)k = Eσk fk(t)H(2)k(t)dt - h(2)k(s)ds Fk(y + s)Ψk(y)Rk(y)dy.
0
0
0
Отметим вероятностный смысл выражений из (6): T(11)k, T(12)k, T(2)k —
средние времена пребывания k-го канала соответственно в состояниях 11,
12, 2 между двумя соседними моментами начала обслуживания заявок, а
∫∞
fk(t)H(2)k(t)dt — среднее число отказов этого канала за время обслужива-
0
ния заявки.
79
Таким образом, стационарная вероятность p∗(D∗) того, что по дискретной
компоненте d система находится в состояниях, принадлежащих подмноже-
ству физических состояний D∗, определяется формулой
p∗(D∗) = lim
P {S(t) ∈ ED∗ } =
t→∞
∑
d!
∏
∏
∏
T(11)
T(12)
T(2)k
k
k
|d|
λ
(7)
11
k∈Ω2
d∈D∗
k∈Ω
k∈Ω12d
d
d
=
∑
d!
∏
∏
∏
T(11)
T(12)
T(2)
k
k
k
|d|
λ
12
k∈Ω2
d∈D
k∈Ω11
d
k∈Ω
d
d
В результате преобразований сумм произведения средних формулу (7) можно
записать в виде
∑
d!
∏
∏
∏
T(11)
T(12)
T(2)k
k
k
|d|
λ
d∈D∗
k∈Ω
11
k∈Ω12d
k∈Ω2
d
d
(8)
p∗(D∗) =
,
∑
∑
∏(
)
(N - n) !
T(11)s
+T(12)s
+T(2)
N-n
i
i
si
λ
n=0
{s1,...,sn} i=1
где {s1, . . . , sn} — некоторое сочетание из {1, 2, . . . , N} по n;
∫
∞
[
]
T(11)s
+T(12)s
+T(2)s
= Eαsi + Fsi(x) H(1)s(x) - H(2)(x) dx +s
i
i
i
i
i
0
∫∞
+ Eσsi fsi(t)H(2)(t)dt.s
i
0
В частности, пусть n — число занятыхканалов в системе, тогда число
=N-n.ОбозначимчерезD∗
свободных работоспособных каналов равно
d
n
множество векторов, число ненулевых компонент которых равно n. Из (8)
вытекает, что стационарная вероятность того, что число занятых каналов в
системе равно n, имеет вид
∑
∏(
)
(N - n) !
T(11)s
+T(12)s
+T(2)
N-n
i
i
si
λ
{s1,...,sn} i=1
p∗n = P(D∗n) =
,
∑
∑
∏(
)
(9)
(N - n) !
T(11)s
+T(12)s
+T(2)
si
N-n
i
i
λ
n=0
{s1,...,sn} i=1
n = 0,N.
Отметим, что стационарные вероятности состояний ненадежной системы
обслуживания, в которой отсутствует временной резерв, также находятся
80
по (9), если полагать, что
∫∞
∫
∞
(10)
T(11)k = Fk(t)Φk(t)dt, T(12)k = 0, T(2)
= Eσk Fk(t)ϕk
(t)dt.
k
0
0
Для однородной системы обслуживания, в которой все каналы описыва-
ются одинаковыми случайными величинами, равенства (9) принимают вид
формул Эрланга
Λn/n!
p∗n =
,
∑
Λn/n!
n=0
где
[
]
Λ=λ T(11) +T(12) +T(2)
=
⎡
⎤
∞
∞
∫
[
]
∫
= λ⎣Eα + F(x) H(1)(x) - H(2)(x) dx + Eσ f(t)H(2)(t)dt⎦ .
0
0
В частном случае для однородной системы, когда T(11) = Eα и T(12) =
= T(2) = 0, (9) совпадают с известными стационарными вероятностями того,
что в системе M/G/N/0 с абсолютно надежными каналами обслуживанием
занято ровно n каналов [2].
Рассмотрим состояния системы, в которых указана причина занятости ка-
нала. Пусть D∗klm — подмножество физических состояний, когда в системе
k работоспособных каналов обслуживают заявки, l каналов восстанавлива-
ются и обслуживают заявки за счет резерва, m каналов восстанавливаются и
не обслуживают заявки, т.е. n = k + l + m. В случае однородной системы (9)
принимают вид
[
]k
[
[
]l
]m
λT(11)
λT(12)
λT(2)
l!
m!
p∗klm
= k![
]n .
∑λ
T(11) + T(12) + T(2)
n!
n=0
Определим вероятность того, что заявка, принятая к обслуживанию, не
будет потеряна при обслуживании по причине неисправности канала. Для
системы без временного резерва такая вероятность для k-го канала равна
∫∞
Pk = P {αk < γk} = fk(t)Φk(t)dt.
0
81
Наличие временного резерва увеличивает эту вероятность до значения
∞
∫∞
∫
(11)
Pk = h(2)k(s)ds rk(t)Ψk(t)Fk
(t + s)dt.
0
0
Вероятность того, что поступающая в систему с резервом заявка будет
обслужена, т.е. принята к обслуживанию и не потеряется при обслуживании,
находится по формуле полной вероятности
(12)
(
∑
∑
∑
∏
∑
(N-1)!
N
Pk +(N-n-1)!
si
+
si
+Ts2)
i
Pk
λ
λN-n
k=1
n=1
{s1,...,sn} i=1
k=1
k={s1,...,sn}
Pобс =
∑
∑ (N-n) !
N -n
∏ (T(11)si + T(12)si + T(2))
si
λ
n=0
{s1,...,sn} i=1
Вероятность Pпот потери поступающей в систему заявки равна Pпот = 1 -
-Pобс.
Чтобы оценить влияние наличия резерва на данные характеристики нуж-
но сравнить их с аналогичными, определяемыми по таким же формулам, в
которых следует полагать, что средние времена пребывания канала в различ-
ных состояниях между двумя соседними моментами начала обслуживания
заявок определяются равенствами (10), и заменить Pk н
Pk.
6. Среднее стационарное время пребывания в состояниях
Пусть множество физических состояний системы представимо в виде
D=D+
⋃D-, D+ ⋂D- = ∅. Обозначим через D′+ множество пограничных
физических состояний, т.е. множество таких векторов d ∈ D+, для кото-
рых изменение некоторой одной из компонент переводит вектор d в множе-
ство D-. Для вектора d ∈ D′+ обозначим через Gkm(d) множество номеров
его компонент, изменение значения каждой из которых с значения m на k
(m, k = 11, 12, 2, 0) переводит вектор в множество D-. Пространство состоя-
ний E разобьем на два непересекающихся подмножества E = ED+
⋃ED-, где
{
}
ED± =
id x z u, i = 1, N , d ∈ D±
. Для определения среднего стационарно-
го времени T (ED+ ) пребывания ПМП S(t) в подмножестве состояний ED+
используем равенство из [15]
⎡
⎤-1
∫
∫
⎢
⎥
T (ED+ ) =
m(x)ρ(dx)⎣ ρ(dx)P (x, ED- )⎦
ED+
ED+
82
Теорема 2. Среднее стационарное время пребывания системы в под-
множестве состояний ED+ определяется по формуле
(
)
∑
∏
∏
∏
1
d!
(13)
T
ED+
=
T(11)
T(12)
T(2)k,
k
k
A
λ|d|
d∈D+
k∈Ω11
k∈Ω12d
k∈Ω2
d
d
⎧
⎪
⎨(
)
∑
d-1
!
∑
∏
∏
∏
A=
T(11)
T(12)
T(2)k +
k
k
⎪
-1
λ|d|
d∈D′+
⎩
k∈Ω2
m∈G110 (d) k∈Ω11
d
k∈Ω12d
d
⎡
⎢
∑
∏
∏
∏
d
!
⎢
+
⎢
(tm)0
T(11)
T(12)
T(2)k +
2
k
k
⎣
λ|d|
m∈G02(d)
k∈Ω11
k∈Ω12d
k∈Ω2d
d
k=m
∑
∏
∏
∏
+
(tm)0
T(11)
T(12)
T(2)k +
(14)
1
1
k
k
m∈G01
(d)
k∈Ω11d
k∈Ω12d
k∈Ω2
1
d
k=m
∑
∏
∏
∏
+
(tm)12
T(11)
T(12)
T(2)k+
1
1
k
k
m∈G121(d)
k∈Ω11d
k∈Ω12d
k∈Ω2
d
1
k=m
⎤⎫
⎪
⎬
∑
∏
∏
∏
⎥
⎥
+
(tm)2
T(11)
T(12)
T(2)k⎥
,
11
k
k
⎦⎪
m∈G21
(d)
k∈Ω11
k∈Ω12d
k∈Ω2d
⎭
2
d
k=m
∫∞
[
]
(tm)02 = fm(x) H(2)m(x) - H(1)m(x) dx, (tm)01
=
1
0
∫∞
[
]
= 1 + fm(x) H(1)m (x) - H(2)m (x) dx,
0
∫∞
∫
∞
(tm)2
11
=
rm(s)Ψm(s)ds h(2)m(y)Fm(s + y)dy,(tm)11 =1
2
0
0
∫∞
= fm(x)H(1)m(x)dx.
0
83
В случае какого-либо пустого из множеств Gkm(d) соответствующие слагае-
мые в (14) следует опустить. Доказательство теоремы 2 приводится в При-
ложении.
Из (13) с учетом того, что (tm)02 + (tm)0
= 1, следует, что среднее время,
11
в течение которого заняты n каналов системы, определяется выражением
(15)
Tn = T(ED∗)=
n
∑
∏(
)
(N-n) !
T(11)s
+T(12)s
+T(2)
λN-n
i
i
si
{s1,...,sn} i=1
=
⎧
⎫
,
⎨
⎬
[
]
[
]
∑
∑
∏
∏
(N-n) !
sj
+
sj
+Ts2)
j
+(N-n)!
sj
+
sj
+Ts2)
j
λN-n-1
⎩λN-n
i=1 j=1
j=1
⎭
{s1,...,sn}
j=i
где n = 1, N - 1; {s1, . . . , sn} — некоторое сочетание из {1, 2, . . . , N} по n.
В частности, среднее время, в течение которого все каналы системы сво-
бодны, равно T0 = 1/λ, а когда все приборы заняты —
∏[
]
(2)
T(11)j + T(12)j + T
j
j=1
TN
=
∏
[
]
(2)
T(11)j + T(12)j + T
j
i=1 j=1
j=i
Для однородной системы формула (15) принимает вид
(2)
T(11) + T(12) + T
Tn =
n + λ[T(11) + T(12) + T(2)]
В качестве частного случая выпишем стационарные характеристики для
системы обслуживания, в которой все случайные величины, ее описываю-
щие, имеют показательные распределения. Пусть время обслуживания заяв-
ки k-м каналом имеет плотность распределения вероятностей fk(t) = μke-μk t;
время γk безотказной работы канала — плотность ϕk(t) = ηke-ηkt; время σk
восстановления канала — плотность ψk(t) = νke-νkt; резерв времени ξk —
плотность rk(t) = κke-κkt. Тогда в (9) и (15) для определения стационарных
вероятностей и средних стационарных времен пребывания в состояниях вы-
ражения (6) принимают вид
(μk + νk + κk)(νk + ηk)
T(11)k + T(12)k + T(2)k =
νk[μ2k + μk(νk + ηk + κk) + ηkκk]
Заметим, что в частном случае, когда в однородной системе отсутствует
временной резерв (κ → ∞), формулы для вычисления финальных вероятно-
стей совпадают с известными формулами из [19]. Для ненадежной системы
84
без временного резерва вероятность того, что принятая k-м каналом заявка
будет обслужена, равна
μk
Pk =
,
μk + ηk
а для системы с временным резервом эта же вероятность принимает значение
μ2k + μk(νk + ηk + κk)
Pk =
μ2k + μk(νk + ηk + κk) + ηkκk
7. Численный пример
Рассмотрим пятиканальную систему обслуживания, в которую поступает
простейший поток заявок с интенсивностью λ = 0,5 1/мин. Предполагается,
что времена обслуживания заявок, восстановления каналов и временной ре-
зерв имеют распределения Эрланга второго порядка, а времена безотказной
Таблица 1. Характеристики каналов обслуживания
Вероятность полного
обслуживания принятой заявки
Относительная
Без резерва С резервом
разница, %
1
4
9
1,111
0,909
0,821
0,9125
+11,17
2
5,714
7,5
1,25
0,8
0,636
0,772
+21,33
3
5
6
1,667
0,714
0,6
0,7133
+18,91
4
4,444
5,455
1,818
0,69
0,609
0,7163
+17,61
5
6,667
8,571
1,333
0,833
0,628
0,7072
+12,661
Таблица 2. Стационарные показатели системы
Стационарные вероятности Среднее время пребывания
Состояние
каналов
системы
Все свободны
0,115
0,101
-12,394
2
2
0
Четыре свободных
0,253
0,236
-6,669
1,374
1,401
+1,957
Три свободных
0,276
0,274
-0,69
1,044
1,075
+2,
Два свободных
0,2
0,212
+5,549
0,841
0,871
+3,547
Один свободен
0,109
0,122
+12,053
0,703
0,73
+3,912
Нет свободных
0,047
0,056
+18,83
0,863
0,915
+6,049
85
работы каналов — распределения Эрланга третьего порядка. Параметры этих
случайных величин и вероятности полного обслуживания заявки каналами
при наличии резерва и без него, приводятся в табл. 1.
Результаты расчетов в системе компьютерной математики Mathcad-15 ста-
ционарных характеристик по формулам (9) и (15) при наличии временного
резерва и без него и результаты сравнения этих характеристик помещены в
табл. 2.
Стационарная вероятность того, что поступающая в систему заявка будет
обслужена, вычисляется по формуле (12) и ее значение равно Pобс = 0,725.
Такая же вероятность для системы без временного резерва равн
Pобс = 0,63.
Таким образом, наличие временного резерва улучшает данную характеристи-
ку системы на 14,958%. Вероятности потери заявки, поступающей в систему
с резервом и без резерва, соответственно равны Pпот = 0,275
Pпот = 0,37.
8. Заключение
С помощью аппарата полумарковских процессов с дискретно-непрерыв-
ным фазовым пространством состояний построена модель эволюции во вре-
мени многоканальной системы массового обслуживания M/G/N/0, в которой
во время обслуживания заявок может произойти отказ канала, но обслужи-
вание некоторое случайное время продолжается за счет резерва. В результате
решения системы интегральных уравнений найдено стационарное распреде-
ление вложенной цепи Маркова, что позволило определить выражения для
расчета стационарных вероятностей пребывания системы в различных фи-
зических состояниях и среднего стационарного времени пребывания в этих
состояниях, а также оценить влияние резерва на вероятность полного об-
служивания заявки. В приведенном численном примере вычислены стацио-
нарные характеристики системы и количественно оценено влияние наличия
резерва на стационарную вероятность полного обслуживания поступающей в
систему заявки.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. В справедливости утверждения тео-
ремы убедимся непосредственной подстановкой выражений (3) в систему ин-
тегральных уравнений (2).
Предварительно введем обозначения: если z = (z1, . . . , zk, . . . , zN ), то век-
торы (z + t), (z + t)m, ((z + t), t)i определяются так:
{
zk + t, zk > 0,
[(z + t)]k =
0,
zk = 0,
{
zk + t, zk > 0, k = m,
[(z + t)m]k =
0,
zk = 0, k = m,
⎧
⎨
zk + t, zk > 0, k = i,
[((z + t), t)i]k =
0,
zk = 0, k = i,
⎩
t,
k = i.
86
Аналогично определяются векторы (x - t), (x - t)m, (u + t) и (u + t)m. Рас-
смотрим одно из уравнений системы (2):
∫
ρ(id x z u) =
e-λtϕi(t) ×
0
∏
[
]
Fj (xj )
×
ρ id′(x - t)(z + t)(u + t) dt +
Fj (xj - t)
j∈Ω11,12
d
∫
∑
+
e-λtϕm(zm + t) ×
m∈Ω11
0
d
∏
[
]
Fj (xj )
×
ρ md′(x - t)((z + t)m,t)i(u + t) dt +
Fj (xj - t)
j∈Ω11,12
d
∫
∑
+
e-λtψm(um + t)rm(zm + t) ×
m∈Ω12d
0
m=i
∏
[
]
Fj (xj )
×
ρ md′(x - t)((z + t)m,t)i(u + t)m dt +
Fj (xj - t)
j∈Ω11,12
d
∫
∑
∏
[
]
Fj (xj )
+
e-λt
ρ md′(x - t)((z + t),t)i(u + t) dt +
Fj (xj - t)
m∈Ω0d
⋃ Ω2
0
j∈Ω11,12
d
d
⎧
∏
⎪
Fj (xj )
⎪
ϕm(zm + xmin)e-λxmin
×
⎪
Fj (xj - xmin)
⎪
j∈Ω11,12
⎪
[
d
]
⎪
⎪
× ρ md′(x - xmin)((z + xmin)m,xmin)i(u + xmin) , xmin = xm, m ∈ Ω11d ,
⎨
∏
Fj (xj )
+⎪⎪
×
⎪
ϕi(xmin)e-λxmin
⎪
Fj (xj - xmin)
⎪
j∈Ω11,12d
[
]
⎪
⎪
ρ × id′(x - xmin)i(z + xmin)(u + xmin) , xmin = xi,
⎪
⎩
0, xmin = xm, m ∈ Ω12d,m=i,
где
di = 12, d′i = 11, d′k = dk, k = i;
xmin = Λ xk.
xk>0
87
Подставим выражения (3) для стационарного распределения в правую
часть уравнения и учтем тождества
∂
v(11)k(xk - t,t) = -h(1)k(xk - t)ϕk(t),
∂t
∂
v(11)k(xk - t,zk + t) = -h(1)k(xk - t)ϕk(zk + t),
∂t
∂
v(12)k(xk - t,zk + t,uk + t) = -h(2)k(xk - t)ψk(zk + t)rk(zk + t),
∂t
∂
V (2)k(uk + t) = -v(2)k(uk + t),v(11)k(xk,0) = h(2)k(xk),v(11)k(0,zk) =
∂t
= ϕk(zk),v(12)k(0,zk,uk) = 0.
В результате преобразований интегральные слагаемые в правой части
уравнения приводятся к виду
⎧
⎪
∫
min
⎨
d
∂
∏
−ρ0
Fi(xi)vi11)(xi - t, t)
Fk(xk)v(11)k(xk - t, zk + t)×
∂t⎪
λ|d|
0
⎩
k∈Ω11
d
⎫
⎪
⎬
∏
∏
×
Fk(xk)v(12)k(xk - t, zk + t, uk
+ t)e-λt
V (2)k(uk + t)
dt =
⎪
k∈Ω12d
k∈Ω2d
⎭
k=i
d!
∏
∏
=ρ0
Fi(xi)hi2)(xi)
Fk(xk)v(11)k(xk, zk)
Fk(xk)v(12)k(xk, zk, uk) ×
|
λ|d
k∈Ω11
k∈Ω
12
d
d
k=i
∏
d
!
×
V(2)
(uk) - ρ0
k
Fi(xi)vi11)(xi - xmin, xmin) ×
λ|d|
k∈Ω2
d
∏
×
Fk(xk)v(11)k(xk - xmin, zk + xmin) ×
k∈Ω11
d
∏
∏
×
Fk(xk)v(12)k(xk - xmin, zk + xmin, uk + xmin)e-λxmin
V (2)k(uk + xmin).
k∈Ω12d
k∈Ω2
d
k=i
Очевидно, что выражение в правой части уравнения совпадает с выраже-
нием стационарного распределения в левой части, задаваемого формулой (3).
Теорема 1 доказана.
∫
Вывод равенства (6). Преобразуем
m(x)ρ(dx) с учетом вида сред-
Ed
него времени пребывания системы в состояниях и стационарного распреде-
88
ления ВЦМ и тождеств
∞
∞
∞
∫
∫
∫
d
(11)
1)
-
Fi(xi + t)dxi vi (xi, zi)dzi = Fi(t)Φi(t) + Φi(t) fi(t + s)H(
(s)ds,
i
dt
0
t
0
∫
∞
∫
∞
∫
∞
∫
∞
d
(12)
-
Fi(xi + t)dxi dzi vi (xi, zi, ui)dui = Ψi(t)Ri(t) fi(t + s)Hi
2)(s)ds.
dt
0
t
t
0
Получаем
∫
∑∫∫∫
[
]
m(x)ρ(dx) =
ρ(id x z u)E
Θidxzu
dxdzdu =
i=1
Ed
RxRzRu
⎧
∫
∞
⎨
∫
∞
∫
∞
d
∏
!
d
= -ρ0
e-λt
Fk(xk + t)dxk v(11)k(xk, zk)dzk ×
dt ⎩
λ|d|
0
k∈Ω11
0
t
d
⎫
∞
∞
∞
∞
∫
∫
∫
∫
⎬
∏
∏
×
(xk, zk, uk)duk
V(2)
(uk)duk dt =
Fk(xk + t)dxk dzk v(12)
k
k
⎪
k∈Ω12
0
t
t
k∈Ω2
d t
d
∞
∞
∫
∫
∏
d!
=ρ0
Fk(xk)v(11)k(xk, zk)dxkdzk ×
λ|d|
k∈Ω11
0
0
d
∫
∞
∫
∞
∫
∞
∫
∞
∏
∏
×
(xk, zk, uk)dxkdzkduk
V (2)k(uk)duk =
Fk(xk)v(12)
k
k∈Ω12
0
0
0
k∈Ω2
d 0
d
d!
∏
∏
∏
=ρ0
T(11)
T(12)
T(2)k.
k
k
λ|d|
12
k∈Ω2
k∈Ω11
d
k∈Ω
d
d
Здесь
∫∫∫
dxdzdu =
RxRzRu
∫∞
∫
∞
∫
∞
∫
∞
∫
∞
∫
∞
= ... dxs1 ...dxsm
dzs1 . . . dzsk
dus1 . . . dusl
0
0
0
0
0
0
5
67
85
67
85
67
8
xs1>0...xsm>0
zs1>0...zsk>0
us1>0...usl>0
89
Равенство (6) доказано.
Доказа∫ельство теоремы
2.
Преобразуем сумму интегралов в
выраженииE
ρ(dx)P (x, ED- ), содержащих ρ(id x z u), i = 1, N , с фикси-
D+
рованным вектором d ∈ D′+ из пограничного слоя, для которого изменение
m-й компоненты с dm = 11 на d′m = 0 переводит вектор d в множество D-,
т.е. m ∈ G011 (d). Из состояния id x z u система переходит в подмножество E-,
если минимум времен пребывания в этом состоянии достигается на СВ αm
(если xm = 0), т.е. Θidxzu = αm или Θidxzu = [αm - xm]+ (если xm > 0). Ве-
роятности этих переходов соответственно равны
ω
∫
∏
Fk(xk + t)
e-λtfm(t)Φm(t)
dt
Fk(xk)
0
k∈Ω11,12d
k=m
и
ω
∫
∏
fm(xm + t)
Fk(xk + t)
e-λt
Φm(t)
dt.
Fm(xm)
Fk(xk)
0
k∈Ω11,12d
k=m
В результате преобразований, аналогичным преобразованиям, которые ис-
пользовались при выводе (6), получаем, что
∑ ∫∫∫
ρ(id x z u)P (id x z u, E-)dxdzdu =
i=1
RxRzRu
⎧
⎪
∞
∞
∞
∫
⎨
∫
∫
d!
d
= -ρ0
e-λt
fm(xm + t)dxm v(11)m(xm,zm)dzm ×
dt ⎪
λ|d|
⎩
0
0
t
∞
∞
∫
∫
∏
×
Fk(xk + t)dxk v(11)k(xk, zk)dzk ×
k∈Ω11d
0
t
k=m
⎫
⎪
∫
∞
∫
∞
∫
∞
∫
∞
⎬
∏
∏
×
(xk, zk, uk)duk
V(2)
(uk)duk
dt =
Fk(xk + t)dxk dzk v(12)
k
k
⎪
k∈Ω12
0
t
t
k∈Ω2
d t
⎭
d
d!
∏
∏
∏
=ρ0
(tm)0
T(11)
T(12)
T(2)k.
11
k
k
λ|d|
k∈Ω11d
k∈Ω12d
k∈Ω2
d
k=m
90
Таким образом, в правую часть (14) входит сумма слагаемых для всех но-
меров m ∈ G0 (d). Аналогичные выкладки проводятся для других компонент1
1
векторов из пограничного слоя. Теорема 2 доказана.
СПИСОК ЛИТЕРАТУРЫ
1.
Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания.
М.: Наука, 1987.
2.
Бочаров П.П., Печинкин А.В. Теория массового обслуживания. М.: Изд-во
РУДН, 1995.
3.
Рыков В.В. Управляемые системы массового обслуживания // Итоги науки и
техн. Сер. вероят., мат. стат., теор. кибернет. 1975. Т. 12. С. 43-153.
4.
Богатырев В.А., Богатырев А.В. Оптимизация резервированного распределе-
ния запросов в кластерных системах реального времени // Информационные
технологии. 2015. Т. 21. № 7. С. 495-502.
5.
Дудин А.Н., Сунь Б. Ненадежная многолинейная система обслуживания
с управляемым широковещательным обслуживанием // АиТ. 2009. № 12.
С. 147-160.
Dudin A.N., Sung V. Unreliable Multi-Server System with Controllable Broadcasting
Service // Autom. Remote Control. 2009. V. 70. No. 12. P. 2073-2084.
6.
Kim C.S., Lee M.H., Dudin A.N., Klimenok V.I. Multi-server Queuing Systems with
Cooperation of the Servers // Ann. Oper. Res. 2008. V. 162. No. 1. P. 57-68.
7.
Богатырев В.А., Сластихин И.А. Эффективность резервированного выполне-
ния запросов в многоканальных системах обслуживания // Науч.-технич. вестн.
информационных технологий, механики и оптики. 2016. Т. 16. № 2. С. 311-317.
8.
Гришунина Ю.Б. Исследование полумарковской модели технического обслу-
живания с целью оптимального выбора вида ремонта // Надежность. 2010.
№ 2 (33). С. 44-53.
9.
Peschansky A.I., Kovalenko A.I. Semi-Markov Model of a Single-Server Queue with
Losses and Maintenance of an Unreliable Server // Cybern. Syst. Anal. 2015. V. 51.
No. 4. P. 632-643.
10.
Песчанский А.И., Коваленко А.И. Полумарковская модель ненадежной одноли-
нейной системы обслуживания с потерями и различными типами восстановле-
ния // АиТ. 2016. № 11. С. 112-126.
Peschansky A.I., Kovalenko A.I. A Semi-Markov Model for an Unreliable Single-Line
Queueing System with Losses and Different Restoration Types // Autom. Remote
Control. 2016. V. 77. No. 12. P. 2192-2204.
11.
Peschansky A.I., Kovalenko A.I. On a Strategy for the Maintenance of an Unreliable
Channel of a One-Server Loss Queue // Automatic Control and Computer Sciences.
2016. V. 50. No. 6. P. 397-407.
12.
Черкесов Г.Н. Надежность аппаратно-программных комплексов. СПб.: Питер,
2005.
13.
Ushakov I.A. Probabilistic Reliability Models. Wiley, 2012.
14.
Копп В.Я., Обжерин Ю.Е., Песчанский А.И. Стохастические модели автомати-
зированных производственных систем с временным резервированием. Севасто-
поль: Изд-во СевНТУ, 2001.
15.
Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах
надежности систем. К.: Наук. думка, 1982.
91
16. Корлат А.Н., Кузнецов В.Н., Новиков М.И. и др. Полумарковские модели вос-
станавливаемых систем и систем массового обслуживания. Кишинев: Штиинца,
1991.
17. Песчанский А.И. Полумарковская модель ненадежной восстанавливаемой ре-
зервированной одноканальной системы обслуживания с потерями // Вестн. Са-
мар. гос. техн. ун-та. Сер. Техн. науки. 2017. № 1 (53). С. 31-41.
18. Beichelt F., Franken P. Zuverlässigkeit und Instanphaltung, Mathematische
Methoden. Berlin: VEB Verlag Technik, 1983.
19. Якушев Ю.Ф. Об одной задаче обслуживания потока вызовов ненадежными
приборами // Пробл. передачи информации. 1969. Т. 5. Вып. 4. С. 84-88.
Статья представлена к публикации членом редколлегии В.М. Вишневским.
Поступила в редакцию 01.03.2018
После доработки 13.10.2018
Принята к публикации 08.11.2018
92