Автоматика и телемеханика, № 4, 2019
Робастное, адаптивное и сетевое
управление
© 2019 г. В.Б. ГОРЯИНОВ, д-р физ.-мат. наук (vb-goryainov@bmstu.ru)
(Московский государственный технический университет им. Н.Э. Баумана),
Е.Р. ГОРЯИНОВА, канд. физ.-мат. наук (el-goryainova@mail.ru)
(Национальный исследовательский университет
“Высшая школа экономики”, Москва)
СРАВНИТЕЛЬНЫЙ АНАЛИЗ РОБАСТНЫХ И КЛАССИЧЕСКИХ
МЕТОДОВ ОЦЕНИВАНИЯ ПАРАМЕТРОВ УРАВНЕНИЯ
ПОРОГОВОЙ АВТОРЕГРЕССИИ
При помощи компьютерного моделирования и исследования асимпто-
тического распределения изучается относительная эффективность М-оце-
нок коэффициентов порогового авторегрессионного уравнения по отноше-
нию к оценкам наименьших квадратов и наименьших модулей. Предпола-
гается, что обновляющая последовательность авторегрессионного уравне-
ния может иметь распределения Стьюдента, логистическое, двойное экс-
поненциальное, нормальное и загрязненное нормальное. Доказана асимп-
тотическая нормальность М-оценок с выпуклой функцией потерь.
Ключевые слова: пороговая авторегрессионная модель, оценка наимень-
ших квадратов, М-оценка, асимптотическая относительная эффектив-
ность, распределение Тьюки.
DOI: 10.1134/S0005231019040056
1. Введение
Среди нелинейных моделей временных рядов широко распространены по-
роговые модели, описываемые кусочно-линейными уравнениями в зависи-
мости от величины пороговой переменной [1]. Пороговые модели применя-
ются во многих областях науки и техники, например в биологии и меди-
цине [2-5], психологии [6], экономике и финансах [2, 7], гидрологии [2, 8],
океанологии [2, 9], астрономии [2], радиотехнике и обработке сигналов [2, 10],
при изучении качки корабля и для управления сервоприводом и паровой ма-
шиной [2].
Когда каждый линейный режим описывается авторегрессионным уравне-
нием, пороговая модель называется пороговой авторегрессионной моделью.
Если пороговой переменной является функция прошлых наблюдений этого
же временного ряда, то пороговая модель называется самовозбуждающейся.
Примеры, приведенные в [11], показывают, что пороговые модели обеспе-
чивают лучшее описание реальных временных рядов, чем линейные модели.
В частности, этими моделями может быть описан целый ряд нелинейных эф-
фектов, например предельные циклы и резонансные скачки [11].
93
Одной из важнейших задач при исследовании пороговой авторегресси-
онной модели является оценивание ее параметров — коэффициентов соот-
ветствующего порогового уравнения. В линейных стохастических моделях
наиболее известными оценками являются оценки наименьших квадратов и
наименьших модулей. Однако известно, что в этих моделях оценки наимень-
ших квадратов являются наилучшими лишь в гауссовском случае и резко
теряют эффективность даже при небольшом нарушении предположения о
гауссовости наблюдений, а эффективность оценок наименьших модулей для
основных вероятностных распределений наблюдений невысока [12]. Хорошим
компромиссом в этом случае являются робастные оценки [12-16], в частности
М-оценки.
В настоящей статье М-оценки предлагается использовать для оценивания
параметров порогового авторегрессионного уравнения. Проводится сравни-
тельный анализ перечисленных оценок при наиболее распространенных ве-
роятностных распределениях обновляющего процесса порогового уравнения.
Исследование проводится как при помощи изучения асимптотического рас-
пределения оценок, так и с помощью компьютерного статистического экс-
перимента. При этом доказана асимптотическая нормальность М-оценок с
выпуклой целевой функцией.
2. Постановка задачи
Рассмотрим случайный процесс Xt, описываемый кусочно-разностным
уравнением [17, с. 77]
{ a11Xt-1 + a21Xt-2 + ··· + ap1Xt-p + εt, Ut ≥ r,
(1)
Xt =
a12Xt-1 + a22Xt-2 + ··· + ap2Xt-p + εt, Ut < r,
с переключением в некоторой известной точке r ∈ R, называемой порогом.
Переключающая переменная Ut может иметь как внешнее (экзогенное) про-
исхождение, так и может определяться самой моделью. В данной статье рас-
сматривается самовозбуждающаяся модель, где переключение в момент t яв-
ляется измеримой функцией предыдущих наблюдений Ut = U(X1, . . . , Xt-1).
Авторегрессионные коэффициенты aij представляют собой действительные
числа, являются параметрами авторегрессионной пороговой модели и счи-
таются неизвестными. Далее всюду предполагается, что обновляющий про-
цесс εt — последовательность независимых одинаково распределенных непре-
рывных случайных величин с плотностью распределения вероятности f, ну-
левым математическим ожиданием Eεt = 0 и конечной дисперсией Dεt = σ2.
Будем также считать, что процесс Xt является стационарным и эргодиче-
ским. В случае p = 1, Ut = Xt-1 и r = 0 для этого достаточно одновременное
выполнение условий a11 < 1, a12 < 1 и a11a12 < 1 [18]. В более общих случаях
эти условия являются громоздкими (см. [19]).
Рассмотрим задачу оценивания по наблюдениям X1, X2, . . . , Xn про-
цесса Xt параметров модели
(1)
— вектора коэффициентов a = (a11, . . .
...,ap1,a12,...,ap2)⊤. Обозначим через Fk σ-алгебру, порожденную величи-
нами X1, X2, . . . , Xk, а через E[Xt|Ft-1] — условное математическое ожида-
ние Xt относительно σ-алгебры Ft-1. M-оценку â вектора a по наблюдениям
94
X1,X2,... ,Xn определим как точку минимума функции
∑
(2)
L(a) = ρ(Xt - E[Xt|Ft-1
]),
t=2
где ρ — некоторая неотрицательная четная функция. При построении M-оце-
нок ρ-функция обычно выбирается возрастающей при x > 0, удовлетворяет
условию ρ(0) = 0 и растет на бесконечности медленнее, чем x2 (см. [12, с. 31]).
M-оценки образуют целое семейство, зависящее от вида функции ρ. Свое на-
звание M-оценка получила из-за того, что если ρ(x) = - ln f(x), то она совпа-
дает с оценкой максимального правдоподобия. Оценки наименьших квадра-
тов ã и наименьших модулей a∗ являются частными случаями M-оценок при
ρ(x) = x2 и ρ(x) = |x| соответственно.
Необходимость в появлении M-оценок была обусловлена недостатками оце-
нок наименьших квадратов и наименьших модулей. Основной недостаток ме-
тода наименьших квадратов заключается в его сильной чувствительности
к большим значениям невязок εt = Xt - E[Xt|Fn-1], поскольку они влияют
на минимизируемую функцию (2) квадратичным образом. Вследствие этого
точность оценки наименьших квадратов достаточно сильно ухудшается при
росте вероятности экстремальных значений εt, что происходит, если плот-
ность распределения вероятности f случайных величин εt медленно убывает
на бесконечности.
Этого недостатка лишен метод наименьших модулей, в котором влияние
невязок на минимизируемую функцию (2) линейно. Однако в методе наи-
меньших модулей недостаточно внимания уделяется небольшим значениям
невязок, которые также искажают функцию (2). Например, в случае нор-
мального распределения εt, плотность которого f(x) с ростом |x| стремится
к нулю достаточно быстро, асимптотическая относительная эффективность
оценки наименьших квадратов по отношению к оценке наименьших модулей
равна π/2 (см., [12, 16, 20]), т.е. методу наименьших модулей требуется в пол-
тора раза больше наблюдений для достижения точности метода наименьших
квадратов.
В этом смысле M-оценки являются значительным обобщением, позволяю-
щим использовать преимущества и оценки наименьших квадратов и оценки
наименьших модулей. M-оценки, как и оценку наименьших модулей, целесо-
образно использовать при отклонении распределения εt от нормального, но
в отличие от оценки наименьших модулей M-оценки почти не теряют эффек-
тивность и в случае нормального распределения εt. Механизм такого пове-
дения M-оценок хорошо виден на примере M-оценки с наиболее распростра-
ненной ρ-функцией, называемой ρ-функцией Хьюбера [16], которая совпадает
с x2 в окрестности (-k,k) начала координат и ведет себя линейно вне этой
окрестности. Семейство ρ-функций Хьюбера имеет вид
{
x2,
если |x| ≤ k,
(3)
ρH(x) =
2k|x| - k2,
если |x| > k,
где k — параметр, принимающий положительные значения.
95
В М-методе с ρ-функцией Хьюбера ρH(x) оптимальный выбор параметра k
приводит к тому, что слагаемые в (2) с небольшими невязками становятся
как и в методе наименьших квадратов еще меньше, а слагаемые с большими
невязками становятся как и в методе наименьших модулей не слишком боль-
шими. Таким образом, вклад в сумму (2) наблюдений Xt, сформировавшихся
под влиянием экстремальных значений εt, будет принижен по сравнению с
вкладом остальных наблюдений.
Цель настоящей статьи — исследование свойств M-оценок вектора коэф-
фициентов a по наблюдениям X1, . . . , Xn случайного процесса (1) и сравнение
M-оценки с ρ-функцией (3) с оценками наименьших квадратов и наименьших
модулей при наиболее распространенных вероятностных распределениях об-
новляющего процесса εt.
3. Асимптотическое распределение оценок
Из двух оценок лучшей будем считать ту, которая меньше отклоняется
от оцениваемого параметра. Тогда точность несмещенной оценки скалярного
параметра будет определяться ее дисперсией — чем меньше дисперсия, тем
точнее оценка. Обычно удается найти лишь асимптотические дисперсии оце-
нок и установить их асимптотическую несмещенность. В этом случае лучшей
из оценок следует считать оценку с наименьшей асимптотической диспер-
сией, а в качестве сравнительной характеристики их точности использовать
асимптотическую относительную эффективность, определяемую как обрат-
ное отношение их асимптотических дисперсий. А именно предположим, что
есть две последовательностиb1 иb2 оценок параметра b, построенные по n на-
блюдениям. Если последовательность
√n(bi - b) слабо сходится при n → ∞ к
нормальной случайной величине с нулевым средним и дисперсией di, i = 1, 2,
то асимптотическая относительная эффективность оценкиb2 относительноb1
равна d1/d2 (см., например, [21, 22]).
Асимптотическая относительная эффективность одной оценки по отноше-
нию к другой показывает, во сколько раз меньше наблюдений нужно первой
оценке для достижения точности второй оценки. Если оценки являются век-
торными, но их асимптотические ковариационные матрицы пропорциональ-
ны, то асимптотическая относительная эффективность определяется как об-
ратное отношение этих коэффициентов пропорциональности.
Положим
Yt = (Y11(t),... ,Yp1(t),Y12(t),... ,Yp2(t))⊤,
где
Yi1(t) = Xt-iI(Ut ≥ r), Yi2(t) = Xt-iI(Ut < r), i = 1,2,... ,p.
Обозначим через K ковариационную матрицу вектора Yt, через ã — оценку
наименьших квадратов, а через a∗ — оценку наименьших модулей парамет-
ра a порогового уравнения (1).
Известно
[19, 23], что случайные последовательности
√n(ã - a) и
√n(a∗ - a) асимптотически нормальны с нулевым средним и ковариацион-
ными матрицами σ2K-1 и (4f2(0)K)-1 соответственно. Таким образом, для
96
сравнения M-оценки â с оценками наименьших квадратов и наименьших мо-
дулей нужно знать ее асимптотическое распределение.
Имеет место следующая теорема.
Теорема. Пусть â- M-оценка параметра a=(a11,...,ap1,a12,...,ap2)⊤
уравнения (1), определяемая как точка минимума функции (2). Пусть про-
цесс Xt, описываемый уравнением (1), является стационарным и эргоди-
ческим, ρ(x) в (2) — выпуклая функция, ρ′′(x) непрерывна почти всюду и
ограничена на R, плотность f(x) независимых одинаково распределенных
случайных величин εt в (1) удовлетворяет условиям Eεt = 0, E(ρ′(εt)2) < ∞,
Eρ′(εt) = 0, 0 < Eρ′′(εt) < ∞ и σ2 = Dεt < ∞.
Тогда при n → ∞ случайный вектор
√n(â - a) является асимптотиче-
ски нормальным с нулевым математическим ожиданием и ковариационной
матрицей B = K-1E[ρ′(ε1)2]
(E[ρ′′(ε1)])2
Доказательство теоремы приведено в Приложении. Отметим, что из вы-
пуклости ρ(x) вытекает выпуклость функции (2), поэтому M-оценка всегда
существует.
Согласно теореме относительная асимптотическая эффективность
M-оценки по отношению к оценкам наименьших квадратов и наименьших
модулей равна e(α, α) =σ2(E[ρ′′(ε1)])2
и e(α, α∗) =(E[ρ′′(ε1)])2
соответствен-
E[ρ′(ε1)2]
4f2(0)E[ρ′(ε1)2]
но. Отметим, что асимптотическая относительная эффективность оценки
наименьших квадратов по отношению к оценке наименьших модулей равна
1
e(α, α∗) =
4σ2f2(0)
4. Сравнение оценок
В приложениях обычно считается, что εt — нормальные случа
(
)
1
личины с нулевым математическим ожиданием, т.е. f(x) =
√
exp
-x2
2πσ
2σ2
Это допущение обосновывается центральной предельной теоремой.
С другой стороны, согласно центральной предельной теореме предполо-
жение о нормальности выполняется лишь приближенно. Общепринятой мо-
делью приближенного нормального распределения является смесь распреде-
лений [24] с плотностью
2
1
(4)
f (x) = (1 - γ)√
e-x2
+ γgfγ
(x),
τ > 1,
0 < γ < 1,
2π
где fγ(x) — плотность распределения, моделирующего отклонение от нор-
мального. Другими словами, среди εt с вероятностью 1 - γ встречаются стан-
дартные (с нулевым математическим ожиданием и единичной дисперсией)
нормальные величины, а с вероятностью γ — случайные величины с плотно-
2
1
стью fγ(x). Будем полагать, что fγ(x) =
√
e
2τ2 , т.е. среди стандартных
2πτ
нормальных случайных величин εt с вероятностью γ встречаются нормаль-
ные величины с дисперсией τ2 > 1. Чем больше γ и τ, тем сильнее смесь
гауссовских распределений (4), называемая в этом случае загрязненным или
засоренным нормальным распределением, отклоняется от нормального.
97
Однако не только нормальное распределение возникает естественным об-
разом при описании возмущений εt. Во многих случаях разумно полагать, что
распределение случайных величин εt является нормальным, но со случай-
ной дисперсией η (точнее, нормальным является условное распределение εt
при условии, что случайная дисперсия η приняла какое-то конкретное зна-
чение y). Если о дисперсии η дополнительно не делается никаких предпо-
ложений, кроме существования средней дисперсии Eη, то, считая положение
дисперсии η на числовой оси максимально неопределенным, методами тео-
рии информации можно получить [25], что безусловное распределение εt бу-
дет двусторонним экспоненциальным распределением, или распределением
√
2|x|
1
Лапласа с плотностью f(x) =
√
e-
σ
2σ
Вследствие изложенного было проведено сравнение оценок для перечис-
ленных распределений. Кроме того, в качестве тестовых распределений рас-
сматривались логистическое распределение с плотностью f (x) =e-x
и
(1+e-x)2
распределение Стьюдента с числом степеней свободы n = 3 и n = 30 с плот-
n+1
(
)-(n+1)/2
)
2
ностью f(x) =√Γ(
1 + x2/n
, где Γ — гамма-функция.
nπΓ(n2 )
Результаты вычислений асимптотической относительной эффективности
M-оценки с ρ-функцией Хьюбера по отношению к оценкам наименьших квад-
ратов и наименьших модулей при различных распределениях εt приведены в
пятом и шестом столбцах таблицы. Постоянная k в (3) обычно выбирается та-
ким образом (см., например, [12]), чтобы e(α, α) = 0,95, если εt — нормальные
случайные величины. Согласно этим рекомендациям k = 1,345.
Сравнение оценок посредством вычисления асимптотической относитель-
ной эффективности носит асимптотический характер. Чтобы понять, на-
сколько надежно пользоваться асимптотическими результатами, величи-
на e(α, α) сопоставлялась с относительной эффективностью en(α, α) оценок α
и α, построенных по n наблюдениям X1,... ,Xn для n, равного 50, 100 и 500.
Для простоты рассматривалась модель (1) с p = 1, Ut = Ut-1, r = 0, полага-
лось a11 = -0,3, a12 = 0,5, Dεt = 1. Величины εt моделировались при помощи
датчиков псевдослучайных чисел из MatLab. Минимум функции (2) нахо-
дился итерационным методом наименьших квадратов с весами, веса опре-
делялись функцией (3), описание метода и доказательство его сходимости
приведено, например, в [12, § 9.1]. Так как параметр a векторный, то для
определенности величина en(α, α) определялась как обратное отношение дис-
персий оценок координаты a11. Величина en(α, α) оценивалась при помощи
компьютерного моделирования. Для n = 50, n = 100 и n = 500 эксперимент
проводился по N = 103 раз, реализации X1, . . . , Xn длины n процесса Xt мо-
делировались при помощи датчиков псевдослучайных чисел для вероятност-
ных распределений из левого столбца таблицы. Для каждого i = 1, . . . , N вы-
числялись оценки αi и αi координаты a11, затем величина en(α, α) оценива-
∑N
∑N
,
(αi-α)2
i=1
∑N
∑N
где α = N-1
αi, α=N-1
αi. Оценки величин e50(α, α), e100(α, α)
i=1
i=1
и e500(α, α), полученные по N = 103 компьютерным реализациям, приведены
во втором, третьем и четвертом столбцах таблицы. Видно, что результаты
98
0,5
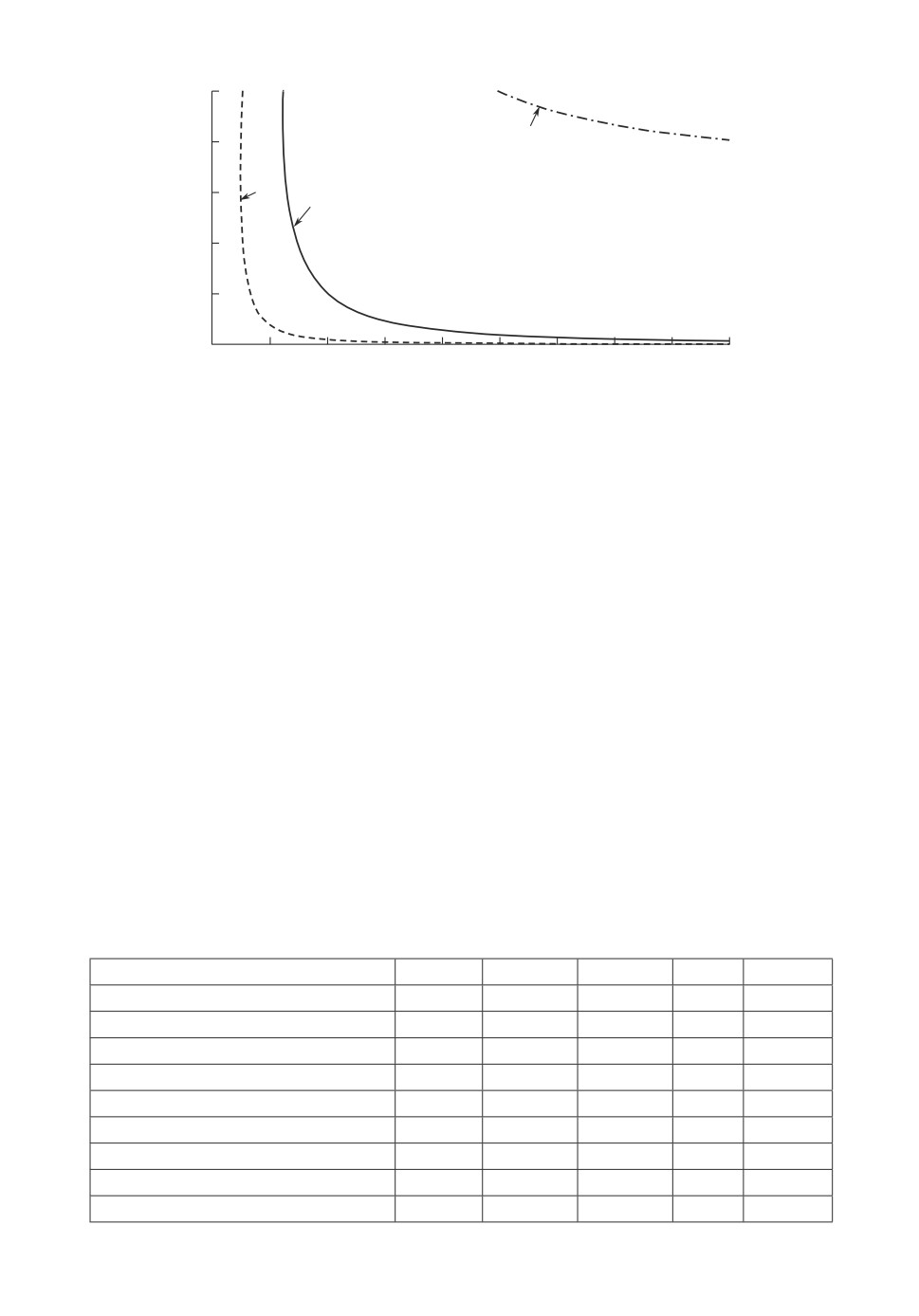
M4
3
0,4
1
M3
0,3
2
0,2
M2
0,1
M1
01
2
3
4
5
6
7
8
9
10
1 — кривая e(α, α) = 1; 2 — кривая e(α,α∗) = 1; 3 — кривая e(α,α∗) = 1;
e(α, α) < 1 на множестве M1, e(α, α∗) < 1 на множестве M4, e(α, α∗) > 1 на
множестве M1 ∪ M2.
моделирования достаточно хорошо согласуются с асимптотическими показа-
телями.
Анализ таблицы показывает, что метод наименьших квадратов предпочти-
телен только если распределение εt является нормальным или практически
не отличается от него, как в случае распределения Стьюдента с большим
числом степеней свободы, причем даже в этих случаях потеря эффективно-
сти M-оценок по отношению к оценке наименьших квадратов невелика. Для
логистического распределения, которое статистический критерий хи-квадрат
К. Пирсона иногда путает с нормальным, M-оценка лучше оценки наимень-
ших квадратов. Также M-оценка становится лучше оценки наименьших квад-
ратов, если в последовательности нормальных случайных величин εt в сред-
нем у каждого сотого члена в три раза увеличить среднеквадратическое от-
клонение. Таким образом, чем медленнее убывает f на бесконечности (чем
“толще” у нее “хвосты”), тем эффективнее M-оценка по отношению к оцен-
ке наименьших квадратов. И наконец, M-оценка практически всегда лучше
Асимптотическая эффективность M-оценок по отношению к оценкам квадратов и
наименьших модулей
Распределение εt
e50(α, α) e100(α, α) e500(α, α) e(α, α) e(α, α∗)
Нормальное
0,950
1,492
1,492
0,950
1,492
Логистическое
1,041
1,092
1,085
1,065
1,295
Тьюки (γ = 0,01, τ = 3)
1,007
1,003
1,003
1,005
1,481
Тьюки (γ = 0,01, τ = 10)
1,358
1,515
1,623
1,833
1,473
Тьюки (γ = 0,10, τ = 3)
1,218
1,279
1,355
1,386
1,388
Тьюки (γ = 0,10, τ = 10)
4,219
5,452
6,965
7,595
1,322
Стьюдента, 30 степеней свободы
1,202
1,124
1,077
0,976
1,455
Стьюдента, 3 степени свободы
1,267
1,589
1,703
1,927
1,189
Лапласа
1,190
1,286
1,368
1,406
0,703
99
оценки наименьших модулей, уступая ей лишь в случае экстремальных вы-
бросов загрязненного нормального распределения (см. рисунок) и в случае
распределения Лапласа.
Теперь предположим, что εt имеют загрязненное нормальное распределе-
ние и рассмотрим величины e(α, α) и e(α, α∗) как функции от (τ, γ). В этом
случае наглядное сравнение оценок позволяет получить рисунок, на кото-
ром в координатной плоскости (τ, γ) изображены линии уровня единич-
ной асимптотической относительной эффективности, т.е. кривые e(α, α) = 1
и e(α, α∗) = 1. Для сравнения на этом же рисунке приведена линия уровня
e(α∗, α) = 1 асимптотической относительной эффективности оценки наимень-
ших модулей по отношению к оценке наименьших квадратов.
Эти линии представляют собой множество точек (τ, γ) равной эффектив-
ности соответствующих оценок и разбивают плоскость (τ, γ) на четыре мно-
жества Mi, i = 1, 2, 3, 4, в каждом из которых одна из двух сравниваемых
оценок всегда предпочтительнее конкурирующей. Оценка наименьших квад-
ратов α на множестве M1 лучше M-оценки α, а на множестве M1 ∪ M2 лучше
оценки наименьших модулей α∗. Другими словами, оценка α лучше оцен-
ки α, если точка (τ, γ) лежит левее кривой e(α, α) = 1 и лучше оценки α∗,
если точка (τ, γ) лежит левее кривой e(α, α∗) = 1. M-оценка α лучше оцен-
ки наименьших квадратов α на множестве M2 ∪ M3 ∪ M4 и лучше оценки
наименьших модулей α∗ на множестве M1 ∪ M2 ∪ M3. Оценка наименьших
модулей α∗ лучше оценки наименьших квадратов α на множестве M3 ∪ M4 и
лучше M-оценки α на множестве M4.
В [20, § 1.2] обсуждается вопрос о том, насколько часто встречаются боль-
шие ошибки в данных. Под большими ошибками подразумеваются “ошибки,
которые редко, но с большой мощностью порождаются источником отклоне-
ний”, например ошибки в перфорации данных или в неправильном размеще-
нии десятичных точек, способных менять значения величин на порядок. Как
пишут авторы в [20, § 1.2], “сделать общее заключение о том, насколько часто
встречаются большие ошибки, по-видимому, нельзя, и в этом ничего удиви-
тельного нет, так как слишком многое зависит от конкретных обстоятельств”.
Тем не менее из приведенного в [2(] обзора литерат)ры можно сделать вывод
о том, что 1 %-10 % загрязнений
т.е. γ ∈ (0,01; 0,1)
уровня τ ∈ (3, 10) явля-
ются нередким на практике. Из рисунка видно, что при этих значениях γ и τ
M-оценка практически всегда эффективнее и оценки наименьших квадратов,
и оценки наименьших модулей. Таким образом, на практике при оценивании
параметров модели пороговой авторегрессии M-оценку, по-видимому, следу-
ет предпочесть как оценке наименьших квадратов, так и оценке наименьших
модулей.
ПРИЛОЖЕНИЕ
Доказательство теоремы. Основная идея доказательства состоит в
том, чтобы аппроксимировать (2) квадратичной функцией, чей минимум име-
ет асимптотически нормальное распределение, и затем показать, что M-оцен-
ка â близка к этому минимуму настолько, что имеет то же асимптотическое
распределение.
100
Заметим, что вектор â минимизирует (2) тогда и только тогда, когда век-
тор α =
√n(â - a) является точкой минимума функции
∑( (
)
)
L(α) =
ρ εt -α⊤Ytn-1/2
- ρ(εt)
t=2
Установим асимптотическую нормальность α, откуда будет вытекать утвер-
ждение теоремы. Раскладывая ρ в точке εt по формуле Тейлора до второй
производной включительно, получим
L(α) = -A⊤nα + 2-1α⊤Bnα + βn(α),
где вектор An, матрица Bn и остаточный член βn(α) имеют соответственно
вид:
∑
∑
An = n-1/2 ρ′(εt)Yt,
Bn
=n-1
ρ′′(εt)YtY⊤t,
t=2
t=2
∑( (
)
)
βn(α) = (2n)-1
ρ′′ εt - τα⊤Ytn-1/2
- ρ′′(εt) α⊤YtY ⊤tα,
0 < τ < 1.
t=2
Оценим E|βn(α)|. Из стационарности εt следует, что стационарным будет
и Yt. Поэтому
[
(
)
]
E|βn(α)| ≤ (2)-1E
ρ′′ ε1 - τα⊤Y1n-1/2
- ρ′′(ε1)α⊤Y1Y⊤1α .
Так как σ2 < ∞ влечет E|Y1|2 < ∞ [26], ρ′′ непрерывна почти всюду и огра-
ничена, а случайная величина ε1 непрерывна, то E|βn(α)| → 0 при n → ∞ по
теореме Лебега о мажорируемой сходимости [27, c. 204]. Следовательно из
неравенства Чебышёва вытекает, что βn(α) → 0 при n → ∞ по вероятности.
Последовательности ρ′(εt), Yt, YtY⊤t и ρ′′(εt)YtY⊤t являются стационарны-
ми и эргодическими как преобразования белого шума εt (см. [28, с. 170 и 182]).
Поэтому по закону больших чисел для эргодических последовательностей
(см. [28, с. 181]) существуют пределы по вероятности:
∑
lim n-1
YtY⊤t = K,
lim
Bn = KE[ρ′′(ε1)].
n→∞
n→∞
t=2
Обозначим через α минимум функции -A⊤nα + 2-1α⊤KEρ′′(ε1)α, явля-
ющейся квадратичной аппроксимацией функции L(α). Очевидно, что α =
= (KE[ρ′′(ε1)])-1An.
Найдем асимптотическое распределение α. Заметим, что вектор Yt изме-
рим относительно σ-алгебры Ft, а εt независима от Ft. Отсюда, а также из
Eρ′(εt) = 0 и свойств условных математических ожиданий (см. [27, §7.4])
следует, что Eρ′(εt)Yt = 0. Поэтому по центральной предельной теореме для
мартингалов (см., напрмер, [29, § 23] и [30, § 5.5]) случайный вектор An явля-
ется асимптотически нормальным с нулевым математическим ожиданием и
101
ковариационной матрицей KE[ρ′(ε1)2]. Следовательно (см. [31, § 6a.2]), слу-
чайная величина α асимптотически нормальна с нулевым математическим
ожиданием и ковариационной матрицей K-1E[ρ′(ε1)2]
(E[ρ′′(ε1)])2
Докажем теперь, что α - α → 0 по вероятности, откуда будет вытекать
утверждение теоремы. Из изложенного следует, что
L(α) = -A⊤nα + 2-1E[ρ′′(ε1)]α⊤Kα + γn(α),
где γn(α) → 0 по вероятности при n → ∞. Другими словами, последователь-
ность выпуклых случайных функций L(α) + A⊤nα стремится по вероятности
в каждой точке α к выпуклой функции 2-1E[ρ′′(ε1)]α⊤Kα. Поэтому (см. [32])
sup|γn(α)| → 0 по вероятности для любого компакта K.
α∈K
Возьмем шар B произвольного радиуса δ с центром α. Так как α сходится
по распределению, то α стохастически ограничена и, следовательно, суще-
ствует компакт K, содержащий B с вероятностью сколь угодно близкой к
единице. Поэтому Δ = sup |γn(α)|→0 по вероятности.
α∈B
Рассмотрим поведение L(α) вне B. Пусть α = α + te, где e — единичный
вектор произвольного направления, t > δ. Обозначим α∗ = α + δe. Так как
L(α) выпукла, то
(
)
L(α∗) ≤ δt-1L(α) +
1-δt-1
L(α).
Следовательно,
(
)
L(α) ≥ tδ-1L(α∗) - tδ-1
1-δt-1
L(α) = tδ-1 (L(α∗) - L(α)) + L(α).
Так как
L(α∗) = L(α) + δ2E[ρ′′(ε1)]eT Ke + γn(α∗) - γn(α),
то
(
)
inf
L(α) = L(α) + inf
tδ-1 (L(α∗) - L(α))
≥ L(α) + δ2E[ρ′′(ε1)]eT Ke - 2Δ.
α∈B
t>δ
Так как K положительно определена, то δ2E[ρ′′(ε1)]eT Ke > 0 в силу
0 < Eρ′′(εt) < ∞. Поэтому с вероятностью, стремящейся к 1, точка миниму-
ма L(α) не может быть вне B. Таким образом, P{|α - α| > δ} → 0 для лю-
бого δ > 0 и, следовательно, асимптотическое распределение α совпадает с
асимптотическим распределением α, т.е. α асимптотически нормальна с ну-
E[ρ′(ε11)2]
левым средним и ковариационной матрицей K-1
. Теорема дока-
(E[ρ′′(ε11)])2
зана.
СПИСОК ЛИТЕРАТУРЫ
1. De Gooijer J.G. Elements of Nonlinear Time Series Analysis and Forecasting. Cham:
Springer, 2017.
102
2.
Tong H. Threshold Models in Non-linear Time Series Analysis. N.Y.: Springer, 1983.
3.
Ozaki T. Time series modeling of neuroscience data. N.Y.: CRC Press, 2012.
4.
Chavas J.-P. Modeling Population Dynamics: a Quantile Approach // Math. Biosci.
2015. V. 262. P. 138-146.
5.
Yang K., Wang D., Li H. Threshold Autoregression Analysis for Finite-Range Time
Series of Counts with an Application on Measles Data // J. Stat. Comput. Simulat.
2018. V. 88. No. 3. P. 597-614.
6.
Hamaker E.L., Zhang Z, van der Maas H.L.J. Using Threshold Autoregressive
Models to Study Dyadic Interactions // Psychometrika. 2009. V. 74. No. 4. P. 727-
745.
7.
Hansen B.E. Threshold Autoregression in Economics // Statistics and its interface.
2011. V. 73. No. 8. P. 563-573.
8.
Bertone E., O’ Halloran K., Stewart R.A., de Oliveira G.F. Medium-term Storage
Volume Prediction for Optimum Reservoir Management: A Hybrid Data-Driven
Approach // J. Clean. Prod. 2017. V. 154. No. 15. P. 353-365.
9.
Pu Shuzhen, Yu Huiling. Threshold Autoregression Models for Forecasting El Nino
Events // Acta Oceanologica Sinica. 1990. V. 9. No. 1. P. 61-67.
10.
Kabiri S., Lotfollahzadeh T., Shayesteh M.G., Kalbkhani H. Modelling and
Forecasting of Signal-to-Interference Plus Noise Ratio in Femtocellular Networks
Using Logistic Smooth Threshold Autoregressive Model // IET Signal Process. 2015.
V. 9. No. 1. P. 48-59.
11.
Howell Tong’s contributions to statistics / ed. Kung-sik Chan, London: World
Scientific, 2009.
12.
Maronna R.A., Martin D., Yohai V. Robust Statistics: Theory and Methods.
Chichester: Wiley, 2006.
13.
Поляк Б.Т., Хлебников М.В. Метод главных компонент: робастные версии //
АиТ. 2017. № 3. P. 130-148.
Polyak B.T., Khlebnikov M.V. The Method of Principal Components: Robust
Versions // Autom. Remote Control. 2017. V. 78. No. 3. P. 490-596.
14.
Poljak B.T., Tsypkin Ja.Z. Robust Identification // Automatica. 1980. V. 16. No. 1.
P. 53-63.
15.
Поляк Б.Т., Цыпкин Я.З. Робастные псевдоградиентные алгоритмы адапта-
ции // АиТ. 1980. № 10. P. 91-97.
Polyak B.T., Tsypkin Ya.Z. Robust Pseudogradient Adaptation Algorithms //
Autom. Remote Control. V. 41. No. 10. Part 1. P. 1404-1409.
16.
Huber P., Ronchetti E.M. Robust statistics. Hoboken: Wiley, 2009.
17.
Douc R., Moulines E., Stoffer D. Nonlinear Time Series: Theory, Methods and
Applications with R Examples. Boca Raton: CRC Press, 2014.
18.
Petruccelli J.D., Woolford S.W. A threshold AR(1) Model // J. Appl. Probab. 1984.
V. 21. No. 2. P. 270-286.
19.
Li D., Ling S. On the Least Squares Estimation of Multiple-Regime Threshold
Autoregressive Models // J. Econometrics. 2012. V. 167. No. 1. P. 240-253.
20.
Робастность в статистике. Подход на основе функций влияния / Пер. с англ.
Хампель Ф., Рончетти Э., Рауссеу П., Штаэль В. М.: Мир, 1989.
21.
Леман Э. Теория точечного оценивания. М.: Наука, 1991.
22.
Hettmansperger T.P., McKean J.W. Robust nonparametric statistical methods.
Boca Raton: CRC Press, 2011.
103
23. Wang L., Wang J. The Limiting Behavior of Least Absolute Deviation Estimators
for Threshold Autoregressive Models
// J. Multivariate Anal. 2004. V. 89. No. 2.
P. 243-260.
24. Королев В.Ю. Вероятностно-статистический анализ хаотических процессов с по-
мощью смешанных гауссовских моделей. М.: Изд-во МГУ, 2008.
25. Мудров В.И., Кушко В.Л. Метод наименьших модулей. М.: Знание, 1971.
26. Qian L. On Maximum Likelihood Estimators for a Threshold Autoregression //
J. Statist. Plann. Inference. 1998. V. 75. No. 1. P. 21-46.
27. Ширяев А.Н. Вероятность. М.: Наука, 2011.
28. Stout W.F. Almost Sure Convergence. N.Y.: Acad. Press, 1974.
29. Биллингсли П. Сходимость вероятностных мер. М.: Наука, 1977.
30. Липцер Р.Ш., Ширяев А.Н. Теория мартингалов. М.: Наука, 1986.
31. Рао С.Р. Линейные статистические методы и их применения. М.: Наука, 1968.
32. Andersen P.K., Gill R.D. Cox’s Regression Model for Counting Processes: a Large
Sample Study // Ann. Statist. 1982. V. 10. No. 4. P. 1100-1120.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 14.03.2018
После доработки 26.10.2018
Принята к публикации 08.11.2018
104