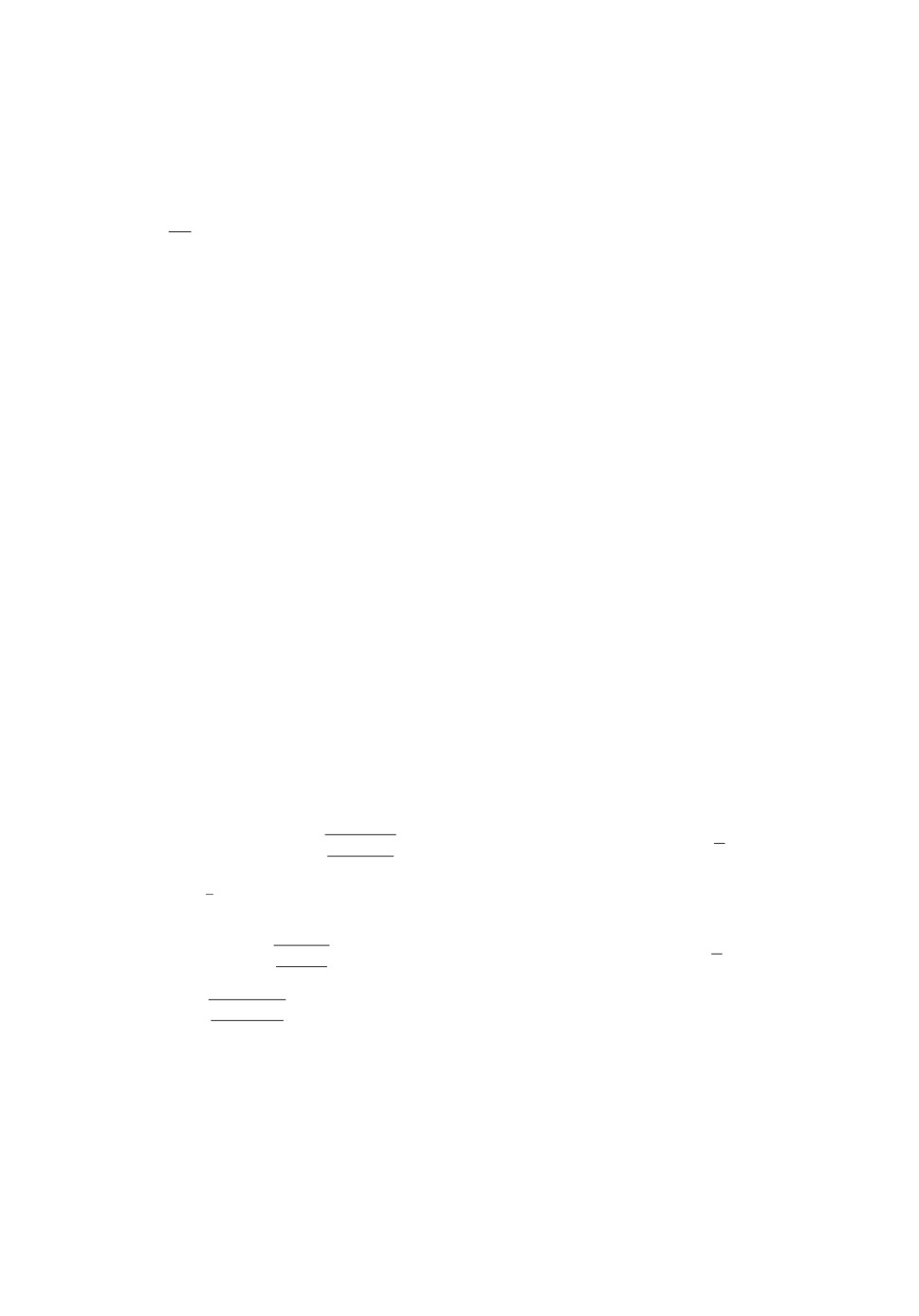Автоматика и телемеханика, № 4, 2019
Оптимизация, системный анализ
и исследование операций
© 2019 г. Е.А. ВОРОНЦОВА, канд. физ.-мат. наук (vorontsovaea@gmail.com)
(Дальневосточный федеральный университет, Владивосток),
А.В. ГАСНИКОВ, д-р физ.-мат. наук (gasnikov@yandex.ru),
Э.А. ГОРБУНОВ (ed-gorbunov@yandex.ru)
(Московский физико-технический институт)
УСКОРЕННЫЙ СПУСК ПО СЛУЧАЙНОМУ НАПРАВЛЕНИЮ
С НЕЕВКЛИДОВОЙ ПРОКС-СТРУКТУРОЙ1
Рассматриваются задачи гладкой выпуклой оптимизации, для числен-
ного решения которых полный градиент недоступен. В 2011 г. Ю.Е. Несте-
ровым были предложены ускоренные безградиентные методы решения
таких задач. Поскольку рассматривались только задачи безусловной оп-
тимизации, то использовалась евклидова прокс-структура. Однако если
заранее знать, например, что решение задачи разреженно, а точнее, что
расстояние от точки старта до решения в 1-норме и в 2-норме близки,
то более выгодно выбирать не евклидову прокс-структуру, связанную с
2-нормой, а прокс-структуру, связанную с 1-нормой. Полное обоснование
этого утверждения проводится в статье. Предлагается ускоренный метод
спуска по случайному направлению с неевклидовой прокс-структурой для
решения задачи безусловной оптимизации (в дальнейшем подход пред-
полагается расширить на ускоренный безградиентный метод). Получены
оценки скорости сходимости метода. Показаны сложности переноса опи-
санного подхода на задачи условной оптимизации.
Ключевые слова: ускоренные методы первого порядка, выпуклая опти-
мизация, метод линейного каплинга, концентрация равномерной меры на
единичной евклидовой сфере, неевклидова прокс-структура.
DOI: 10.1134/S000523101904007X
1. Введение
В [1] были предложены ускоренные оракульные2 методы нулевого поряд-
ка (безградиентные методы) решения задач гладкой выпуклой безусловной
оптимизации.
1 Работа А.В. Гасникова по разделам 3 и 4 поддержана Российским фондом фунда-
ментальных исследований (проект № 18-31-20005 мол_а_вед). Работа Э.А. Горбунова и
Е.А. Воронцовой поддержана грантом Президента РФ МД-1320.2018.1. Работа А.В. Гасни-
кова и Е.А. Воронцовой поддержана Российским фондом фундаментальных исследований
(проект № 18-29-03071 мк).
2 Здесь и далее под оракулом понимается подпрограмма расчета значений целевой
функции и/или градиента (его части), а оптимальность метода на классе задач понимает-
ся в смысле Бахвалова-Немировского [2] как число обращений (по ходу работы метода) к
оракулу для достижения заданной точности (по функции).
126
В рассуждениях [1] существенным образом использовалось то, что была
выбрана евклидова прокс-структура (выпуклая гладкая функция, порождаю-
щая расстояние, и 1-сильно выпуклая относительно какой-то нормы (стро-
гое определение см. в разделе 4)). Такой выбор прокс-структуры для за-
дач безусловной оптимизации является вполне естественным (см., напри-
мер, [3]). Однако в ряде задач имеется дополнительная информация, которая,
например, позволяет рассчитывать на разреженность решения (в решении
большая часть компонент нулевые). В таких случаях использование других
прокс-структур бывает более выгодным. Для негладких задач стохастической
условной оптимизации с оракулом нулевого порядка недавно было показано
(см. [4, 5]), что в определенных ситуациях ускорение метода за счет перехода
от евклидовой прокс-структуры, связанной с 2-нормой, к прокс-структурам,
связанным с 1-нормой, может давать ускорение методу, по порядку равное
размерности пространства, в котором происходит оптимизация. К сожале-
нию, техника, использованная в [4, 5] существенным образом использовала
неускоренную природу оптимальных методов для негладких задач. Другими
словами, из [4, 5] непонятно, как получать аналогичные оценки для гладких
задач. В настоящей статье на базе специального варианта быстрого (уско-
ренного) градиентного метода [6] строится ускоренный метод спуска по слу-
чайному направлению. Особенностью метода из [6] является представление
быстрого градиентного метода как специальной выпуклой комбинации гради-
ентного спуска и зеркального спуска. В [6], как и во всех известных авторам
вариантах быстрого градиентного метода с двумя и более
“проекциями”,
обе проекции осуществлялись в одной норме/прокс-структуре. Главной иде-
ей настоящей статьи является использование разных норм/прокс-структур
в этих проекциях, а именно: в градиентном шаге всегда используется обыч-
ная евклидова проекция, а вот в зеркальном шаге выбор прокс-структуры
обусловлен априорной информацией о свойствах решения.
В настоящей статье на базе описанной конструкции для детерминирован-
ных задач безусловной гладкой выпуклой оптимизации строится ускоренный
метод спуска по случайному направлению3 (раздел 4).
В классе детерминированных спусков по направлению (к ним можно от-
нести и циклический координатный спуск) для получения лучших оценок
необходимо вводить рандомизацию (доказательство см. в. [8]), поэтому рас-
сматриваются сразу спуски по случайному направлению.
Показано, какие возникают сложности при попытке перенесения описан-
ного подхода на задачи оптимизации на множествах простой структуры (раз-
дел 4).
2. Постановка задачи
Рассматривается задача гладкой выпуклой оптимизации
(1)
f (x) → min,
x∈Q
3 Подробно о разнице в подходах в случае детерминированной постановки, но с введе-
нием рандомизации и в случае задач стохастической оптимизации см. в [7].
127
где функция f (x), заданная на выпуклом замкнутом множестве Q ⊆ Rn, име-
ет липшицев градиент с константой L2 (т.е. f(x) — L2-гладкая функция)
∥∇f (y) - ∇f (x)∥2 ≤ L2 ∥y - x∥2
и является μ-сильно выпуклой в p-норме (1 ≤ p ≤ 2) функцией (далее будем
использовать и обозначение μp), при этом в точке минимума x∗ выполнено
равенство ∇f (x∗) = 0, а итерационный процесс стартует с точки x0.
В данной статье для решения задачи (1) вместо обычного градиента ис-
пользуется его стохастическая аппроксимация, построенная на базе произ-
водной по случайно выбранному направлению [9]
= n〈∇f (x), e〉e,
где e — случайный вектор, равномерно распределенный на Sn2 (1) — единич-
ной сфере в 2-норме в пространстве Rn (e ∼ RSn2 (1); под этой записью бу-
дем понимать, что случайный вектор e имеет равномерное распределение на
n-мерной единичной евклидовой сфере), а угловые скобки 〈·, ·〉 обозначают
скалярное произведение4.
Имеет место следующая лемма (доказательство см. в [10]), являющаяся
следствием явления концентрации равномерной меры на сфере вокруг эква-
тора (см. также [11]; северный полюс задается градиентом ∇f (x)).
Лемма 1. Пусть e ∼ RSn2(1), n ≥ 8, s ∈ Rn, тогда
[
]
2
1
(2)
E ∥e∥2
≤ min {q - 1, 16 ln n - 8} nq -
,
2 ≤ q ≤ ∞,
q
[
]
√
(3)
E 〈s, e〉2 ∥e∥2
≤
3||s||22 min {2q - 1, 32 ln n - 8} nq -2
,
2 ≤ q ≤ ∞,
q
где под знаком || · ||q понимается векторная q-норма (норма Гельдера с по-
казателем q).
Из (3) (см. также [4]) вытекает следующий факт.
Утверждение. Пусть e ∼ RSn2 (1) и g (x, e) = n〈∇f (x), e〉e, тогда
[
]
√
2
Ee ∥g (x, e)∥2
≤
3min{2q - 1, 32ln n - 8}nq ∥∇f (x)∥22.
q
Используя данное утверждение, можно в сильно выпуклом случае при
условии ∇f (x∗) = 0 получить оценку необходимого числа обращений к ора-
кулу за производной по направлению для достижения по функции точности ε
в среднем [12]:
(
2
L2
(Δf0 ))
N (ε) = O nq ln n
ln
,
μp
ε
где Δf0 = f(x0) - f(x∗).
1
4 Отметим, что Ee[g(x,e)] = ∇f(x), что следует из факта: Ee[|ei|2] =
n
, где ei — i-я
компонента вектора e.
128
Имеется гипотеза (см., например, [3]), что, используя специальные уско-
ренные методы (типа Катюши (Katusha) из [13]), можно получить оценку
(
√
1
1
L2
(Δf0 ))
N (ε) = O nq +2 ln n
ln
μ
ε
Насколько известно авторам, эта гипотеза на данный момент не доказана и
не опровергнута.
В разделе 4 данной статьи для случая Q = Rn доказывается оценка
2
2
(4)
E[f (xN )] - f(x∗) ≤ Cn
q
+1 ln nL2R
N2
Эта оценка получается из приведенной выше оценки с помощью регуляриза-
ции μp = ε/R2 [7], где (с точностью до корня из логарифмического по n мно-
жителя) R — расстояние в p-норме от точки старта до решения.
3. Задача А.С. Немировского
Рассмотрим задачу (1) минимизации гладкого выпуклого функциона-
ла f (x) с константой Липшица градиента L2 в 2-норме на множестве
Q = Bn1 (R) (шар в пространстве Rn радиуса R в 1-норме). Тогда на рас-
сматриваемом классе функции для любого итерационного метода, на каждой
итерации которого только один раз можно обратиться к оракулу за градиен-
том функции, можно так подобрать функцию f(x) из этого класса, что имеет
место оценка скорости сходимости [14] в виде
2
C1L2R
(5)
f (xN) - f(x∗) ≥
,
N3
где
C1 — некоторая числовая константа5, x∗ — ближайшая к x0 точка ми-
нимума функции f(x). Поскольку f (xN ) - f(x∗) должно быть меньше или
равно ε, из (5) можно получить оценку на N(ε).
С другой стороны, если использовать обычный быстрый градиентный ме-
тод с KL-прокс-структурой для этой же задачи, то [15]:
C2L1R2 ln n
f (xN) - f(x∗) ≤
,
N2
где константа Липшица градиента L1 в 1-норме удовлетворяет условию:
L2/n ≤ L1 ≤ L26.
Отсюда нельзя сделать вывод, что нижняя оценка достигается. Достигается
ли эта нижняя оценка и если достигается, то на каком методе? Насколько
5 Как и
C2 далее. Здесь и далее все числовые константы не зависят от N и n.
6 Здесь под L1 понимается такое положительное число, что ||∇f(x) - ∇f(y)||∞ ≤
≤ L1||x - y||1.
129
авторам известно, это пока открытый вопрос, поставленный А.С. Немиров-
ским в 2015 г. (см. также [14]). Однако если оценивать не число итераций, а
общее число арифметических операций и если ограничиться рассмотрением
класса функций, для которых “стоимость” расчета производной по направ-
лению примерно в n раз меньше “стоимости” расчета полного градиента7,
то при N ≤ n (точнее даже при N ≃ n) выписанная оценка (4) (в варианте
для общего числа арифметических операций, необходимых для достижения
заданной точности в среднем) с точностью до логарифмического множителя
будет соответствовать нижней оценке (5), если последнюю понимать как
2
C1L2R
f (xN) - f(x∗) ≥
,
nN2
т.е.
(√
)
2
L2R
N (ε) = O
εn
Действительно (q = ∞), общее число арифметических операций равно
(
√
)
(√
)
L2R
2
(
)
L2R2
O (n) · O n2 ln n
≈O
n2
·O
ε
εn
5
67
8
число итераций
4. Обоснование формулы (4) в случае Q = Rn
Введем дивергенцию Брэгмана
[17] Vz (y), связанную с p-нормой
(1 ≤ p ≤ 2)
= d(y) - d(z) - 〈∇d(z), y - z〉,
где функция d(x) является непрерывно дифференцируемой и сильно выпук-
лой с константой сильной выпуклости, равной единице. Например, для p = 1
функцию d(x) можно выбрать так:
1
d(x) =
||x||2a,
2(a - 1)
где
2 log n
a=
2 log n - 1
7 Из-за быстрого автоматического дифференцирования [16] это предположение доволь-
но обременительное; но если функция задана моделью черного ящика, выдающего только
значение функции, а градиент восстанавливается при n + 1 таком обращении, то сделанное
предположение кажется вполне естественным.
130
Функцию d(x) будем называть прокс-функцией (или прокс-структурой), свя-
занной с p-нормой. Кроме того, пусть q — такое число, что1p +1q = 1. Да-
лее будем следовать обозначениям из [12]. Пусть случайный вектор e рав-
номерно распределен на поверхности евклидовой сферы единичного радиуса
(e ∼ RSn2 (1)). Положим, что
1
= x-
〈∇f (x) , e〉e,
L
= argmin {α 〈n 〈∇f (x) , e〉 e, y - z〉 + Vz (y)} ,
y∈Rn
где L — константа Липшица градиента функции f(x) в 2-норме (индекс 2 не
пишем, так как везде далее интересуемся константой Липшица в 2-норме).
Опишем ускоренный неевклидов спуск (английское название метода —
Accelerated by Coupling Directional Search, ACDS), построенный на базе спе-
циальной комбинации спусков по направлению в форме градиентного спуска
(Grad) и метода зеркального спуска (Mirr).
Алгоритм 1. Ускоренный неевклидов спуск (ACDS)
Вход: f — выпуклая дифференцируемая функция на Rn с липшицевым
градиентом с константой L по отношению к 2-норме; x0 — некоторая
стартовая точка; N — количество итераций.
Выход: точка yN , для которой выполняется Ee1,e2,...,eN [f(yN )] - f(x∗) ≤
2
1: y0 ← x0, z0 ← x0
2: for k = 0, . . . , N - 1 do
1
3:
αk+1 ←k+22LC
, τk ←
=2k+2
n,q
αk+1LCn,q
4:
Генерируется ek+1 ∼ RSn2 (1) независимо от предыдущих итераций
5:
xk+1 ← τkzk + (1 - τk)yk
6:
yk+1 ← Gradek+1(xk+1)
7:
zk+1 ← Mirrek+1(xk+1, zk, αk+1)
8: end for
9: return yN
Теорема. Пусть f(x)
— выпуклая дифференцируемая функция на
Q = Rn с константой Липшица для градиента, равной L в 2-норме, d(x) —
1-сильно выпуклая в p-норме функция на Q, N - число итераций метода,
x∗ — точка минимума функции f(x). Тогда ускоренный неевклидов спуск
(ACDS) на выходе даст точку yN , удовлетворяющую неравенству
4ΘLCn,q
Ee1,e2,...,eN [f(yN)] - f(x∗) ≤
,
N2
где
√
2
1
1
q
=
3 min{2q - 1, 32ln n - 8}n
+1,
+
= 1.
q
p
131
Сформулируем две ключевые леммы, которые понадобятся для доказа-
тельства теоремы (доказательства приведены в Приложении).
1
Лемма 2. Если τk =
, то для всех u ∈ Q = Rn верны неравен-
αk+1LCn,q
ства
αk+1〈∇f(xk+1),zk - u〉 ≤
Cn,q
≤α2k+1 ·
||∇f(xk+1)||22 + Vz
(u) -
k
2n
(6)
- Eek+1[Vzk+1(u) | e1, e2, ..., ek] ≤
≤ α2k+1LCn,q · (f(xk+1) - Ee
[f(yk+1) | e1, e2, . . . , ek]) +
k+1
+Vzk(u) - Eek+1[Vzk+1(u) | e1, e2, ..., ek].
Лемма 3. Для всех u ∈ Q = Rn выполнено неравенство
α2k+1LCnEe
[f(yk+1) | e1, . . . , ek] - (α2k+1LCn - αk+1)f(yk) +
k+1
(7)
+ Eek+1[Vzk+1(u) | e1,...,ek] - Vzk(u) ≤ αk+1f(u).
Сложности возникают при попытке перенесения этого результата на слу-
чай Q = Rn. Ограничимся рассмотрением случая p = q = 2, так как даже для
него не удается обобщить рассуждения из [6]. Введем обозначение
{
}
L
= -min
〈s, y - x〉 +
∥y - x∥2
2
y∈Q
2
Заметим, что вторая часть леммы 1 в евклидовом случае упрощается, а имен-
но
||s||22
Ee[〈s,e〉2] =
,
n
где e ∼ RSn2 (см. лемму B.10 из [18]; формулировка данной леммы из [18]
есть в Приложении — см. лемму (П.1)). Отсюда следует, что Cn,q = n2. Если
положить
{
}
L
= argmin
〈〈∇f(x), e〉e, x - y〉 -
∥y - x∥2
2
y∈Q
2
и
= argmin {α 〈n 〈∇f (x) , e〉 e, y - z〉 + Vz (y)} ,
y∈Q
то чтобы обобщить приведенные рассуждения на условный случай, нужно
оценить подходящим образом Progn〈∇f(x),e〉e(xk+1) (точнее, его математиче-
ское ожидание по ek+1), т.е., исходя из техники, используемой в [6], хотелось
бы доказать оценку
[
]
(8)
Eek+1
(xk+1)
≤ n2 (f(xk+1) - E[f (yk+1)]) ,
Progn〈∇f(xk+1), ek+1〉 ek+1
132
чтобы получить оценку скорости сходимости, как и в случае безусловной ми-
нимизации. К сожалению, существует пример (будет приведен далее) выпук-
лой L-гладкой функции и замкнутого выпуклого множества, для которых (8)
не выполняется.
Сначала рассмотрим более детально Progξ(x):
}
2
{L
Progξ(x) = -min
y - x + 〈ξ, y - x〉
=
y∈Q
2
2
}
2
2
2
{L
1
1
= -min
y - x
+ 〈ξ, y - x〉 +
ξ
+
ξ
=
y∈Q
2
2
2L
2
2L
2
√
√
}
{
2
2
1
L
L
1
= -min
√
ξ+
·y-
·x
+
ξ
=
y∈Q
2L
2
2
2
2L
2
(
}
{
)2
2
L
1
1
=-
min
y - x -
ξ
+
ξ
,
2
y∈Q
L
2
2L
2
т.е. точка, в которой достигается этот минимум8,
(
)
1
ŷ=πQ x-
ξ
L
Тогда
(
)
1
1
yk+1 = πQ x -
sk+1
,
= 〈∇f(xk+1), ek+1〉 ek+1 =
g(xk+1, ek+1).
L
n
Кроме того, обозначим через yk+1 точку множества Q, в которой достигается
минимум в формуле для Progn〈∇f(xk+1), ek+1〉 ek+1 (xk+1). Тогда
(
)
n
yk+1 = πQ x -
sk+1
L
Также для удобства рассмотрим следующие представления для yk+1 и yk+1:
1
yk+1 = xk+1 -
sk+1 + rk+1,
L
(9)
n
yk+1 = xk+1 -
sk+1 + rk+1,
L
где rk+1 и rk+1 будем называть векторами невязок.
Рассмотрим функцию
2
L
(10)
f (y) = f(xk+1) + 〈∇f(xk+1), y - xk+1〉 +
y - xk+1
2
2
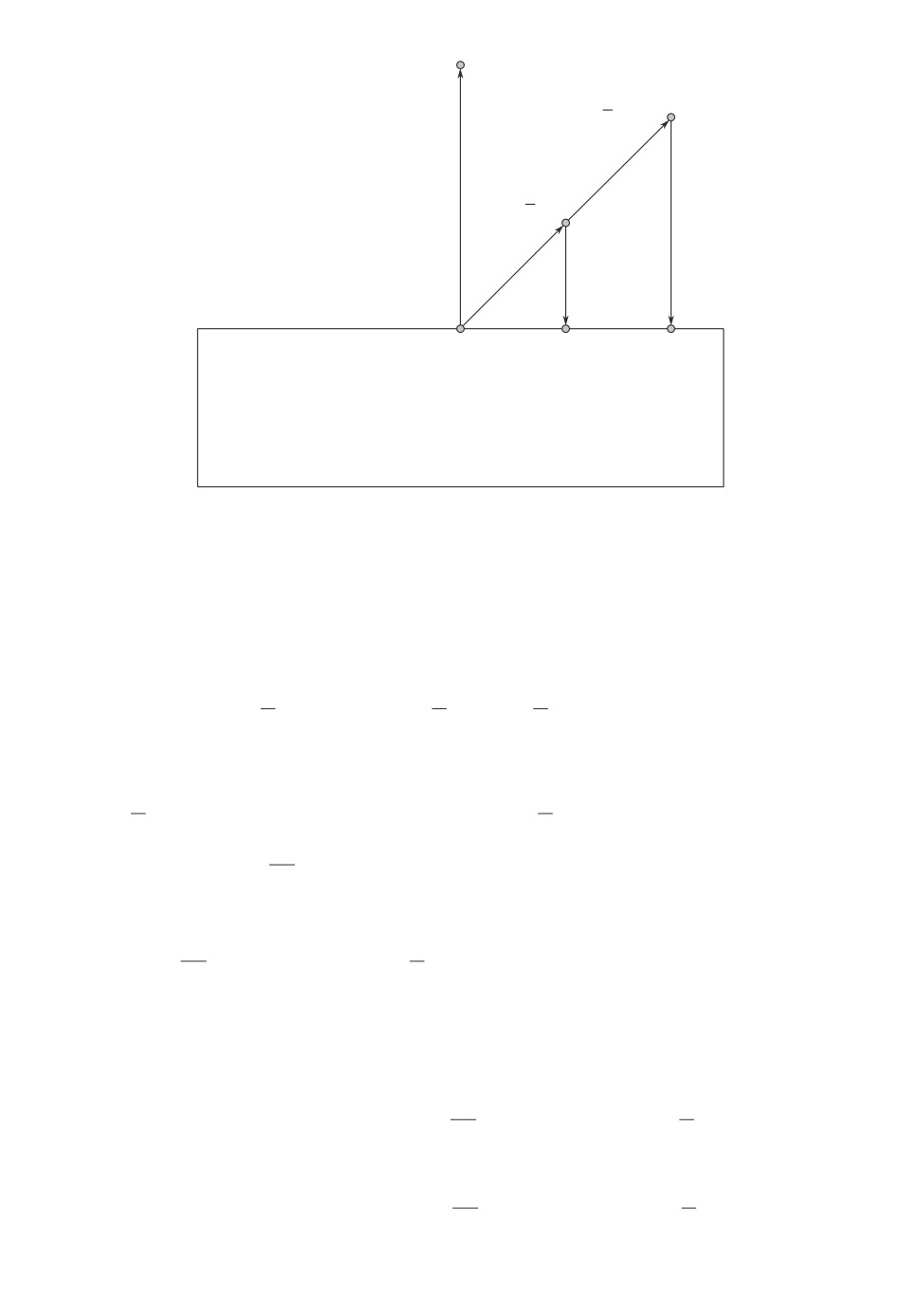
и множество, изображенное на рис. 1 (в качестве ∇f(xk+1) можно выбрать
любой ненулевой вектор, а в качестве Q — прямоугольный параллелепипед
8 См. [7].
133
xk + 1
f(xk + 1)
n
xk + 1
sk + 1
L
1
xk + 1
sk + 1
L
r
k + 1
rk + 1
y
xk + 1
yk + 1
k + 1
Q
Рис. 1. Пример ситуации, когда ключевое неравенство не выполнено.
с достаточно длинными сторонами, в центре одной из гиперграней которого
размещена точка xk+1).
Подставим в (10) значение y = yk+1 и воспользуемся представлением yk+1
из (9):
=
>
2
1
L
1
- ∇f(xk+1), -
sk+1 + rk+1
-
rk+1 -
sk+1
= f(xk+1) - f(yk+1).
L
2
L
2
Далее воспользуемся тем, что sk+1 = 〈∇f(xk+1), ek+1〉 ek+1:
2
1
L
〈∇f(xk+1), ek+1〉2 - 〈∇f(xk+1), rk+1〉 -
rk+1
+ 〈rk+1, sk+1〉 -
L
2
2
1
−
〈∇f(xk+1), ek+1〉2 = f(xk+1) - f(yk+1),
2L
или в более компактной форме
2
1
L
〈∇f(xk+1), ek+1〉2 -
rk+1
+ 〈rk+1, sk+1 - ∇f(xk+1)〉 =
(11)
2L
2
2
= f(xk+1) - f(yk+1).
При таком выборе функции и множества получаем, что n2 · ||rk+1||22 =
= ||rk+1||22 для всех единичных e. Действительно, если
2
1
L
〈∇f(xk+1), ek+1〉2 -
rk+1
Prog〈∇f(xk+1), ek+1〉 ek+1 (xk+1) =
2L
2
2
и
2
2
n
L
Progn〈∇f(xk+1), ek+1〉 ek+1 (xk+1) =
〈∇f(xk+1), ek+1〉2 -
rk+1
,
2L
2
2
134
то
Progn〈∇f(xk+1), ek+1〉 ek+1 (xk+1) = n2 Prog〈∇f(xk+1), ek+1〉 ek+1 (xk+1).
Отсюда и из (11) следует, что
1
Progn〈∇f(xk+1), ek+1〉 ek+1 (xk+1) + 〈rk+1, sk+1 - ∇f(xk+1)〉 =
n2
= f(xk+1) - f(yk+1).
Заметим, что вектор sk+1 всегда короче (точнее, не длиннее) вектора
∇f(xk+1) и направлен “вниз” (т.е. в то же полупространство, образованное
гранью Q, на которой лежит точка xk+1), как и ∇f(xk+1). Значит, раз-
ность sk+1 - ∇f(xk+1) будет направлена в противоположную часть простран-
ства. А вектор rk+1 тоже направлен вниз. Следовательно, всегда выполняет-
ся 〈rk+1, sk+1 - ∇f(xk+1)〉 ≤ 0, причем с ненулевой вероятностью выполнено
строгое неравенство. Это означает, что
Eek+1 [〈rk+1, sk+1 - ∇f(xk+1)〉] < 0.
Поэтому
[
]
Eek+1
(xk+1)
=
Progn〈∇f(xk+1), ek+1〉 ek+1
= n2(f(xk+1) - Ee
[f(yk+1)]) - Eek+1 [〈rk+1, sk+1 - ∇f(xk+1)〉] >
k+1
(
)
>n2
f (xk+1) - Eek+1 [f(yk+1)]
Представленный контр-пример показывает трудности в перенесении
предлагаемого в статье метода на задачи условной оптимизации. Теорема
утверждает, что ускоренный неевклидов спуск (алгоритм ACDS) через N ите-
раций выдаст точку yN , удовлетворяющую неравенству E[f(yN )] - f(x∗) ≤ ε,
(√
)
√
ΘL2Cn,q
ε > 0, если N = O
. По определению Cn,q =
3min{2q - 1,
ε
2
q
32 ln n - 8}n
+1, а в случае p = q = 2 можно взять Cn,q = n2, что видно из
леммы 1 и леммы B.10 из [18] (приведена в Приложении как лемма (П.1)),(
√
)
√
поэтому N = OΘL2n2
. Если же p = 1 и q = ∞, то Cn,q = n
3 (32 ln n - 8)
ε
(√
)
ln n
иN =OΘL2n
ε
5. Численные эксперименты
Для практического применения предложенный ускоренный неевклидов
спуск по случайному направлению ACDS был реализован на языке програм-
мирования Python. Код метода и демонстрация вычислительных свойств ме-
тода с построением графиков сходимости доступны как Jupyter Notebook и
выложены в свободном доступе на Github [19].
135
0,16
0,14
0,12
0,10
0,08
0,06
0,04
2
0,02
1
0
0
100
200
300
400
500
600
700
Число итераций, N
Рис. 2. Сходимость ускоренного неевклидового спуска ACDS для функ-
ции (12), размерность n = 10. Показана практическая зависимость точности
нахождения минимума f(xN ) - f(x∗) от числа итераций N алгоритма (гра-
(
)
4ΘLCn,q
фик 1) и теоретическая оценка O
(график 2).
N2
Рассмотрим следующую з а д а ч у. Пусть A — матрица размеров n × n
со случайными независимыми элементами, равномерно распределенными на
отрезке [0, 1], а матрица B =A⊤A
, где λmax(A⊤A) — максимальное
λmax(A⊤A)
собственное значение матрицы A⊤A.
Необходимо минимизировать функцию
1
(12)
f =
〈x - x∗, B(x - x∗)〉 , x ∈ Rn,
2
где x∗ = (1, 0, 0, . . . , 0)⊤. Решение этой задачи известно и равно x∗, f(x∗) = 0.
Начальная точка x0 для всех экспериментов выбиралась как (0, 0, 0, . . . , 1)⊤.
Константа Липшица градиента целевой функции L = 1.
Следует отметить важность достаточно точного решения вспомогательной
задачи минимизации для нахождения zk+1 на шаге 7 алгоритма 1 (зеркаль-
ный спуск). В рассматриваемом случае эту задачу с помощью метода множи-
телей Лагранжа можно свести к задаче одномерной минимизации, подробно-
сти с формулами см. в [19]. В реализации метода одномерная минимизация
выполняется с помощью обычной дихотомии с точностью, на один порядок
превышающей заданную.
Для различных n и заданной точности ε были рассчитаны теоретиче-
ски требуемые значения числа итераций по теореме и проведена провер-
ка сходимости на практике. Для данной задачи во всех случаях практи-
ческая скорость сходимости по функции была выше. Так, например, для
n = 10 и ε = 10-3 заданная точность была достигнута за 729 итераций (см.
136
104
3,0
4
2,5
3
2
2,0
1,5
1
1,0
0
20 000
40 000
60 000
80 000 100 000 120 000 140 000
Число итераций, N
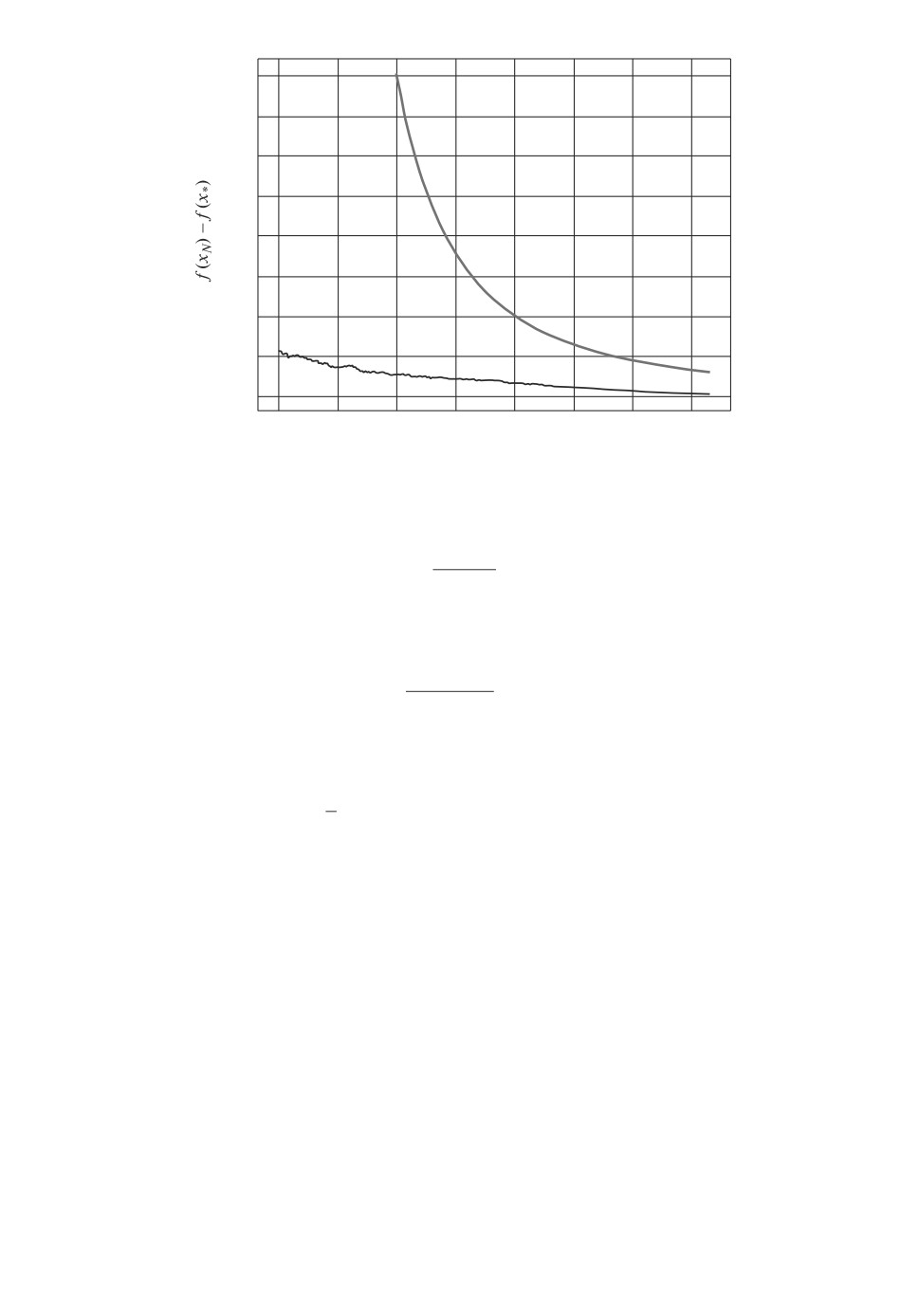
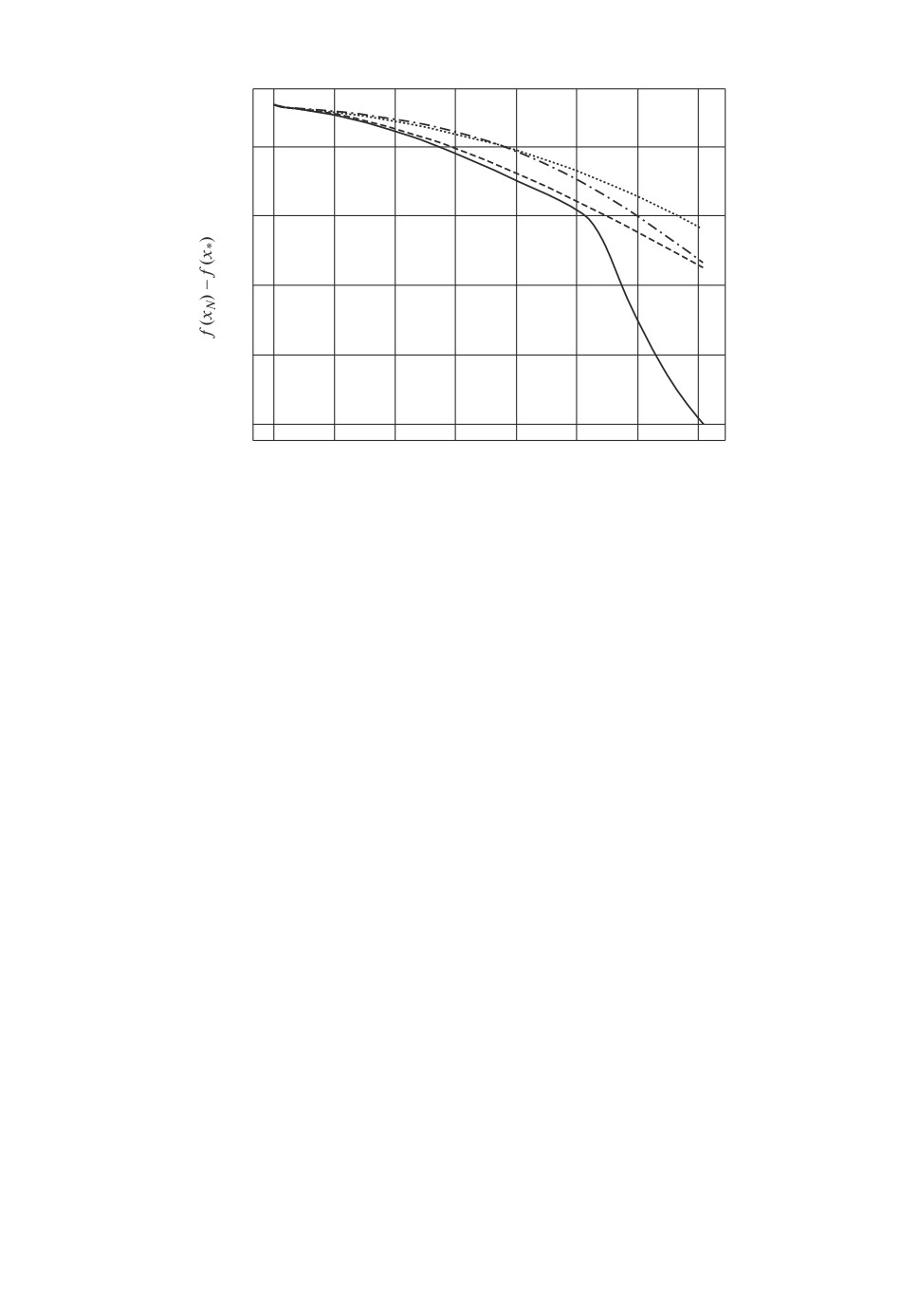
Рис. 3. Сходимость ускоренного неевклидового спуска ACDS для функ-
ции (12), размерность n = 103. Показана практическая зависимость точности
нахождения минимума f(xN ) - f(x∗) от числа итераций N алгоритма (сплош-
ная линия — график 1). Также для сравнения приведены результаты работы
метода при других p (евклидова норма — график 2; p = 1,8 — график 3;
p = 1,9 — график 4) при тех же генерируемых векторах e и точке старта x0.
рис. 2), а теоретическая оценка числа итераций дает 2537 итераций. Далее,
для n = 103 и ε = 10-4 теоретическая оценка числа итераций дает не более
чем 255972 итерации. По факту алгоритм завершил работу за 141643 ите-
рации (см. рис. 3). Медленный спуск в начале работы метода объясняется
близостью начального значения целевой функции к оптимальному именно в
данном примере (f(x0) = 0,00032983).
При проведении численных экспериментов было обнаружено, что преиму-
щество выбора прокс-структуры, связанной с 1-нормой, возникает только в
пространствах от средней размерности (от n = 1000). Будет ли иметь преи-
мущество предложенный метод, можно определить, сравнив теоретические
оценки числа итераций предложенного метода для разных p. На рис. 3 пока-
зан именно случай, когда ускоренный спуск по направлению с неевклидовой
прокс-структурой оказывается оптимальнее спуска по направлению с евкли-
довой прокс-структурой.
В целом, численные эксперименты с ускоренным спуском по случайному
направлению подтверждают теоретические результаты.
6. Заключение
В статье предложен ускоренный неевклидов спуск по направлению для
решения задачи выпуклой безусловной оптимизации. В отличие от извест-
ных вариантов методов спуска по направлению (см., например [1]) в данной
статье рассматривается ускоренный спуск по направлению с неевклидовой
137
прокс-структурой. В случае когда 1-норма решения близка к 2-норме реше-
ния (это имеет место, например, если решение задачи разрежено — имеет
много нулевых компонент), предлагаемый подход улучшает оценку на необ-
ходимое число итераций, полученную оптимальным методом из [1], прибли-
зительно в
√n раз, где n - размерность пространства, в котором происходит
оптимизация.
Данная статья открывает цикл работ, в которых планируется привести
полные доказательства утверждений, полученных авторами в 2014-2016 гг.
и приведенных (без доказательств) в [20]. В частности, далее планируется
распространить приведенные в настоящей статье результаты на безградиент-
ные методы, на задачи стохастической оптимизации и распространить все эти
результаты на случай сильно выпуклой функции.
Открытой проблемой остается распространение полученных здесь резуль-
татов на случай задач оптимизации на множествах простой структуры. На-
помним, что в статье существенным образом использовалось то, что оптими-
зация происходит на всем пространстве. Тем не менее в будущем планируется
показать, что приведенные здесь результаты распространяются на задачи оп-
тимизации на множествах простой структуры в случае, если градиент функ-
ционала в точке решения равен нулю (принцип Ферма).
Авторы выражают благодарность Павлу Двуреченскому и Александру
Тюрину за помощь в работе.
ПРИЛОЖЕНИЕ
Доказательство леммы 2. Докажем сначала первую часть нера-
венства:
αk+1〈n〈∇f(xk+1), ek+1〉ek+1, zk - u〉 =
= 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 +
○
+ 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk+1 - u〉
≤
○
(Π.1)
=
○
○
= 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 + Vzk (u) - Vzk+1 (u) - Vzk (zk+1)
≤
(
)
○
1
≤
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -
||zk - zk+1||2
+
p
2
+Vzk(u) - Vzk+1(u),
где ○ выполнено в силу того, что
zk+1 = argmin{Vzk (z) + αk+1〈n〈∇f(xk+1), ek+1〉ek+1, z〉} ,
z∈Rn
откуда следует, что 〈∇Vzk (zk+1) + αk+1n〈∇f(xk+1), ek+1〉 ek+1, u - zk+1〉 ≥ 0
для всех u ∈ Q = Rn, ○ выполнено в силу равенства треугольника для дивер-
138
генции Брэгмана9, ○ выполнено, так как Vx(y) ≥12 ||x - y||2p в силу сильной
выпуклости прокс-функции d(x).
Теперь покажем, что
1
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -
||zk - zk+1||2p ≤
2
α2k+1n2
≤
|〈∇f(xk+1), ek+1〉|2 · ||ek+1||2q.
2
Действительно, в силу неравенства Гельдера
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 ≤
≤ αk+1n||〈∇f(xk+1), ek+1〉ek+1||q · ||zk - zk+1||p =
= αk+1n|〈∇f(xk+1), ek+1〉| · ||ek+1||q · ||zk - zk+1||p,
откуда
1
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -
||zk - zk+1||2p ≤
2
(Π.2)
1
≤ αk+1n|〈∇f(xk+1), ek+1〉| · ||ek+1||q · ||zk - zk+1||p -
||zk - zk+1||2p.
2
Положим t = ||zk - zk+1||p, a =12 и b = αk+1n|〈∇f(xk+1), ek+1〉| · ||ek+1||q, то-
гда правая часть в (Π.2) имеет вид
bt - at2.
Если рассматривать полученное выражение как функцию от t ∈ R, то ее мак-
симум при t ∈ R равен (а значит, при t ∈ R+ не превосходит)b24a.Отсюда
и из (Π.2) следует неравенство
1
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -
||zk - zk+1||2p ≤
2
(Π.3)
α2k+1n2
≤
|〈∇f(xk+1), ek+1〉|2 · ||ek+1||2q.
2
Итак, учитывая (Π.1) и (Π.3), получаем, что
αk+1〈n〈∇f(xk+1), ek+1〉ek+1, zk - u〉 ≤
α2k+1n2
≤
|〈∇f(xk+1), ek+1〉|2 · ||ek+1||2q + Vz
(u) - Vzk+1 (u).
k
2
9 Действительно,
∀x, y ∈ Rn
〈-∇Vx(y), y - u〉 = 〈∇d(x) - ∇d(y), y - u〉 = (d(u) - d(x) - 〈∇d(x), u - x〉)-
- (d(u) - d(y) - 〈∇d(y), u - y〉) - (d(y) - d(x) - 〈∇d(x), y - x〉) = Vx(u) - Vy(u) - Vx(y).
139
Беря условное математическое ожидание Eek+1 [ · | e1, e2, . . . , ek] от левой и
правой частей последнего неравенства и пользуясь вторым неравенством из
леммы 1, получаем, что
αk+1〈∇f(xk+1), zk - u〉 ≤
Cn,q
≤α2k+1 ·
||∇f(xk+1)||22 + Vz
(u) - Eek+1 [Vzk+1 (u) | e1, e2, . . . , ek],
k
2n
√
2
где Cn,q =
3min{2q - 1, 32ln n - 8}nq +1. Чтобы доказать вторую часть
неравенства (6), покажем, что
(
)
(Π.4)
||∇f(xk+1)||22 ≤ 2nL
f (xk+1) - Eek+1 [f(yk+1) | e1, e2, . . . , ek]
Во-первых, для всех x, y ∈ R
∫1
f (y) - f(x) =
〈∇f(x + τ(y - x)), y - x〉dτ =
0
∫1
= 〈∇f(x), y - x〉 +
〈∇f(x + τ(y - x)) - ∇f(x), y - x〉dτ ≤
0
∫1
≤ 〈∇f(x), y - x〉 +
||∇f(x + τ(y - x)) - ∇f(x)||2 · ||y - x||2dτ ≤
0
∫1
≤ 〈∇f(x), y - x〉 + τL||y - x||2 · ||y - x||2dτ =
0
L
= 〈∇f(x), y - x〉 +
||y - x||22,
2
т.е.
L
-〈∇f(x), y - x〉 -
||y - x||22 ≤ f(x) - f(y).
2
Беря в последнем неравенстве x = xk+1, y = Gradek+1 (xk+1) = xk+1 -
-1L〈∇f(xk+1), ek+1〉ek+1, получим, что
1
1
f (xk+1) - f(yk+1) ≥
〈∇f(xk+1), ek+1〉2 -
〈∇f(xk+1), ek+1〉2 · ||ek+1||22 =
L
2L
1
=
〈∇f(xk+1), ek+1〉2.
2L
Возьмем от этого неравенства условное математическое ожидание Eek+1 [ · |
e1,e2,... ,ek], используя лемму B.10 из [18] (см. лемму (П.1)), и получим нера-
венство (Π.4). Лемма 2 доказана.
140
Доказательство леммы 3. Доказательство состоит в выписывании
цепочки неравенств:
αk+1(f(xk+1) - f(u)) ≤
≤ αk+1〈∇f(xk+1), xk+1 - u〉 =
=
○
○
(1 - τk)αk+1
=
〈∇f(xk+1), yk - xk+1〉 + αk+1〈∇f(xk+1), zk - u〉
≤
τk
○
(1 - τk)αk+1
○
≤
(f(yk) - f(xk+1)) + αk+1〈∇f(xk+1), zk - u〉
≤
τk
○
(1 - τk)αk+1
≤
(f(yk) - f(xk+1)) +
τk
+α2k+1LCn,q · (f(xk+1) - Ee
[f(yk+1) | e1, e2, . . . , ek]) +
k+1
=
○
= (α2
LCn,q - αk+1)f(yk) - α2k+1LCn,qEe
[f(yk+1) | e1, e2, . . . , ek] +
k+1
k+1
+αk+1f(xk+1) + Vzk(u) - Eek+1[Vzk+1(u) | e1, e2, ... , ek].
=τkzk +(1-τk)yk⇔τk(xk+1-zk) =
= (1 - τk)(yk - xk+1), ○ следует из выпуклости f(·) и неравенства 1 - τk ≥ 0,
1
○ справедливо в силу леммы 2 и в ○ используется равенство τk =
αk+1LCn,q
Лемма 3 доказана.
Доказательство теоремы. Заметим, что при αk+1 =k+2 выпол-2LC
n,q
нено равенство
1
α2kLCn,q = α2k+1LCn,q - αk+1 +
4LCn,q
Возьмем для k = 0, 1, . . . , N - 1 от каждого неравенства (7) леммы 3 матема-
тическое ожидание по e1, e2, . . . , eN , просуммируем полученные неравенства
и получим
∑
∑
1
α2NLCn,qE[f(yN)] +
E[f(yk)] + E[VzN (u)] - Vz0 (u) ≤
αkf(u),
4LCn,q
k=1
k=1
∑
где E[·] = Ee1, e2, ..., eN [·]. Положим u = x∗. Так как
αk =N(N+3)4LC
, E[f(yk)] ≥
n,q
k=1
≥ f(x∗), VzN(u) ≥ 0 и Vz0(x∗) = Vx0(x∗) ≤ Θ, то выполняется неравенство
)
(N + 1)2
(N(N + 3)
N -1
E[f(yN )] ≤
-
f (x∗) + Θ,
4LCn,q
4LCn,q
4LCn,q
. Теорема доказана.
+1)2
141
Приводим формулировку леммы B.10 из [18]. Отметим, что в доказатель-
стве нигде не использовалось, что второй вектор в скалярном произведении
(помимо e) есть градиент функции f(x) (поэтому утверждение леммы (П.1)
остается верным для произвольного вектора s ∈ Rn вместо ∇f(x)).
Лемма П.1. Пусть e ∼ RSn2(1) и вектор s ∈ Rn — некоторый вектор.
Тогда
||s||22
Ee[〈s, e〉2] =
n
СПИСОК ЛИТЕРАТУРЫ
1.
Nesterov Yu. Random gradient-free minimization of convex functions // CORE
Discussion Paper 2011/1. 2011.
2.
Немировский А.С., Юдин Д.Б. Сложность задач и эффективность методов оп-
тимизации. М.: Наука, 1979.
3.
Гасников А.В., Двуреченский П.Е., Нестеров Ю.Е. Стохастические градиент-
ные методы с неточным оракулом // Тр. МФТИ. 2016. Т. 8. № 1. С. 41-91. arXiv
preprint arXiv:1411.4218.
4.
Гасников А.В., Лагуновская А.А., Усманова И.Н., Федоренко Ф.А. Безградиент-
ные прокс-методы с неточным оракулом для негладких задач выпуклой стоха-
стической оптимизации на симплексе // АиТ. 2016. № 10. С. 57-77.
Gasnikov A.V., Lagunovskaya A.A., Usmanova I.N., Fedorenko F.A. Gradient-
Free Proximal Methods with Inexact Oracle for Convex Stochastic Nonsmooth
Optimization Problems on the Simplex // Autom. Remote Control. 2016. V. 77.
No. 11. P. 2018-2034.
5.
Гасников А.В., Крымова Е.А., Лагуновская А.А., Усманова И.Н., Федорен-
ко Ф.А. Стохастическая онлайн оптимизация. Одноточечные и двухточечные
нелинейные многорукие бандиты. Выпуклый и сильно выпуклый случаи // АиТ.
2017. № 2. C. 36-49.
Gasnikov A.V., Krymova E.A., Lagunovskaya A.A., Usmanova I.N., Fedorenko F.A.
Stochastic Online Optimization. Single-Point and Multi-Point Non-Linear Multi-
Armed Bandits. Convex and Strongly-Convex Case // Autom. Remote Control. 2017.
V. 78. No. 2. P. 224-234.
6.
Allen-Zhu Z., Orecchia L. Linear coupling: An ultimate unification of gradient and
mirror descent // arXiv preprint arXiv:1407.1537.
7.
Гасников А.В. Современные численные методы оптимизации. Универсальный
градиентный спуск. Уч. пос. М.: МФТИ, 2018.
8.
Nesterov Yu. Efficiency of Coordinate Descent Methods on Huge-Scale Optimization
Problems // SIAM J. Optim. 2012. № 22 (2). P. 341-362.
9.
Dvurechensky P., Gasnikov A., Tiurin A. Randomized Similar Triangles Method:
A Unifying Framework for Accelerated Randomized Optimization Methods
(Coordinate Descent, Directional Search, Derivative-Free Method) // arXiv preprint
arXiv:1707.08486.
10.
Горбунов Э.А., Воронцова Е.А., Гасников А.В. О верхней оценке математическо-
го ожидания нормы равномерно распределенного на сфере вектора и явлении
концентрации равномерной меры на сфере // arXiv preprint arXiv:1804.03722.
142
11.
Баяндина А.С., Гасников А.В., Лагуновская А.А. Безградиентные двухточечные
методы решения задач стохастической негладкой выпуклой оптимизации при
наличии малых шумов не случайной природы // АиТ. 2018. № 8. С. 38-49.
Bayandina A.S., Gasnikov A.V., Lagunovskaya A.A. Gradient-Free Two-Point
Methods for Solving Stochastic Nonsmooth Convex Optimization Problems with
Small Non-Random Noises // Autom. Remote Control. 2018. V. 79. No.
8.
P. 1399-1408.
12.
Гасников А.В., Двуреченский П.Е., Усманова И.Н. О нетривиальности быст-
рых (ускоренных) рандомизированных методов // Тр. МФТИ. 2016. Т. 8. № 2.
С. 67-100. arXiv preprint arXiv:1508.02182.
13.
Allen-Zhu Z. Katyusha: The First Direct Acceleration of Stochastic Gradient
Methods // arXiv preprint arXiv:1603.05953.
14.
Guzman C., Nemirovski A. On Lower Complexity Bounds for Large-Scale Smooth
Convex Optimization // J. Complexity. February 2015. V. 31. Iss. 1. P. 1-14.
15.
Гасников А.В., Нестеров Ю.Е. Универсальный метод для задач стохастической
композитной оптимизации // ЖВМ и МФ. 2018. Т. 58. № 1. C. 52-69. arXiv
preprint arXiv:1604.05275.
16.
Baydin A.G., Pearlmutter B.A., Radul A.A., Siskand J.M. Automatic Differentiation
in Machine Learning: a Survey // arXiv preprint arXiv:1502.05767.
17.
Брэгман Л.М. Релаксационный метод нахождения общей точки выпуклых мно-
жеств и его применение для решения задач выпуклого программирования //
ЖВМ и МФ. 1967. Т. 7. № 3. С. 200-217.
18.
Bogolubsky L., Dvurechensky P., Gasnikov A., Gusev G., Raigorodskii A.,
Tikhonov A., Zhukovskii M. Learning Supervised PageRank with Gradient-Based
and Gradient-Free Optimization Methods
//
13th Annual Conf. on Neural
Information Processing Systems (NIPS). 2016. arXiv preprint arXiv:1603.00717.
19.
20.
Гасников А.В. Эффективные численные методы поиска равновесий в больших
транспортных сетях. Дисс. на соискание уч. степ. д.ф.-м.н. по специальности
05.13.18 - Математическое моделирование, численные методы, комплексы про-
грамм. М.: МФТИ, 2016. arXiv preprint arXiv:1607.03142.
Статья представлена к публикации членом редколлегии Б.М. Миллером.
Поступила в редакцию 14.10.2017
После доработки 04.07.2018
Принята к публикации 08.11.2018
143