Автоматика и телемеханика, № 4, 2019
© 2019 г. С.Н. МЕДВЕДЕВ, канд. физ.-мат. наук (s_n_medvedev@mail.ru),
О.А. МЕДВЕДЕВА, канд. физ.-мат. наук (medvedeva@amm.vsu.ru)
(Воронежский государственный университет)
АДАПТИВНЫЙ АЛГОРИТМ РЕШЕНИЯ
АКСИАЛЬНОЙ ТРЕХИНДЕКСНОЙ
ЗАДАЧИ О НАЗНАЧЕНИЯХ
Предлагается вероятностная модификация алгоритма поиска мини-
мального элемента для решения аксиальной трехиндексной задачи о на-
значениях. Общая идея связана с расширением базовых алгоритмических
схем “жадного” типа посредством перехода к вероятностной постановке на
основе рандомизации переменных. Задача минимизации целевой функции
заменяется задачей минимизации ее математического ожидания. Для по-
строения алгоритма реализованы три этапа. На первом задается движе-
ние во множестве случайных величин. На втором решается неравенство —
условие локального улучшения. На третьем происходит пересчет вероят-
ностей, т.е. происходит процесс “адаптации”. Второй этап выявляет одну
из особенностей алгоритма: на формирование решения влияют не только
“качества” самого элемента, но и возможные потери при его выборе.
Ключевые слова: аксиальная трехиндексная задача о назначениях, дис-
кретная оптимизация, адаптивный алгоритм решения, вероятностная по-
становка задачи, условие локального улучшения.
DOI: 10.1134/S0005231019040093
1. Введение
Аксиальная задача о назначениях во многих отношениях напоминает клас-
сическую задачу о назначениях (ЗОН), однако в отличие от нее является
NP-трудной [1].
Для решения аксиальной трехиндексной ЗОН Гансом и Кауфманом [2]
был предложен прямо-двойственный алгоритм, который является аналогом
венгерского метода решения классической ЗОН. Ставится задача отыскания
максимального паросочетания гиперграфа, которая является NP-трудной.
Аналогично классическому методу вместо данной задачи можно рассмотреть
проблему отыскания минимального вершинного покрытия гиперграфа. Од-
нако для аксиальной трехиндексной ЗОН теорема Кенига не выполняется:
минимальное число вершин в минимальном покрытии может быть строго
больше, чем мощность любого (максимального) паросочетания. Дальнейшая
работа алгоритма [2], основанного на методе ветвей и границ, сводится к по-
иску соответствующих паросочетания и вершинного покрытия мощности n.
Как было сказано выше, получение оптимального результата аксиальной
трехиндексной ЗОН есть задача NP-трудная, поэтому было разработано боль-
шое количество приближенных методов решения. Первый эвристический ал-
горитм был предложен в 1967 г. [3]. В дальнейших исследованиях предла-
156
гались различные варианты изменений точных методов решения задач дис-
кретной оптимизации, примененных к аксиальной ЗОН. В 2005 г. был раз-
работан “жадный” алгоритм с перекомпановкой [4], который показал хоро-
шие результаты по времени работы на основе компьютерных вычислений.
Хуанг и Лим [5] предложили гибридный генетический алгоритм решения ак-
сиальной ЗОН. В [6] представлен метод, названный авторами “редукцион-
ным”. В разное время было разработано несколько эвристических алгорит-
мов для задач с декомпозицией целевых коэффициентов. В [7] исследована
задача, в которой целевые коэффициенты представимы в виде произведения
трех неотрицательных вещественных чисел. В [8] предложена постановка,
которая обобщает предложенный подход, в ней разложение коэффициентов
происходит на два числа. В ходе вычислительного эксперимента в [9] была
найдена экстремальная нижняя оценка для трехиндексной аксиальной за-
дачи о назначениях с 1,2-декомпозиционной матрицей стоимостей в случае,
когда количество значений индексов не превосходит трех.
Отдельные исследования посвящены так называемому многограннику
ограничений аксиальной трехиндексной ЗОН, т.е. выпуклой оболочке всех
допустимых решений. В [10, 11] исследовались различные классы вершин.
Причем стоит заметить, что авторы рассматривают как трех-, так и много-
индексные аксиальные ЗОН [12].
В [13-16] авторами был рассмотрен подход, связанный с вероятностной мо-
дификацией “жадных” алгоритмов комбинаторной оптимизации посредством
перехода к вероятностной постановке задачи. В данной статье предлагается
детальное рассмотрение такого подхода для решения трехиндексной аксиаль-
ной ЗОН, а также результаты обширного вычислительного эксперимента.
2. Постановка задачи
Аксиальная трехиндексная задача о назначениях, которая является обоб-
щением классической ЗОН, формулируется следующим образом: пусть зада-
ны n3 коэффициентов ckij , i, j, k = 1, n. Требуется найти две перестановки ϕ
и ψ такие, что
∑
ciϕ(i)ψ(i) → min
,
n
ϕ,ψ∈S
i=1
где Sn - множество всех перестановок чисел {1, . . . , n}.
Можно представить данную задачу как задачу целочисленного линейного
программирования. Ее математическая модель выглядит следующим обра-
зом:
∑
∑
(1)
L(X) =
ckijxkij
→ min,
i=1 j=1 k=1
∑
(2)
xkij
= 1, i = 1, n,
j=1 k=1
157
∑
(3)
xkij
= 1, j = 1, n,
i=1 k=1
∑
(4)
xkij
= 1, k = 1, n,
i=1 j=1
(5)
xkij
= {0, 1}, i, j, k = 1, n.
Ограничения (2)-(5) задают допустимое множество Ω, а (1) является це-
левой функцией.
В [1] показано, что аксиальная трехиндексная задача является NP-труд-
ной.
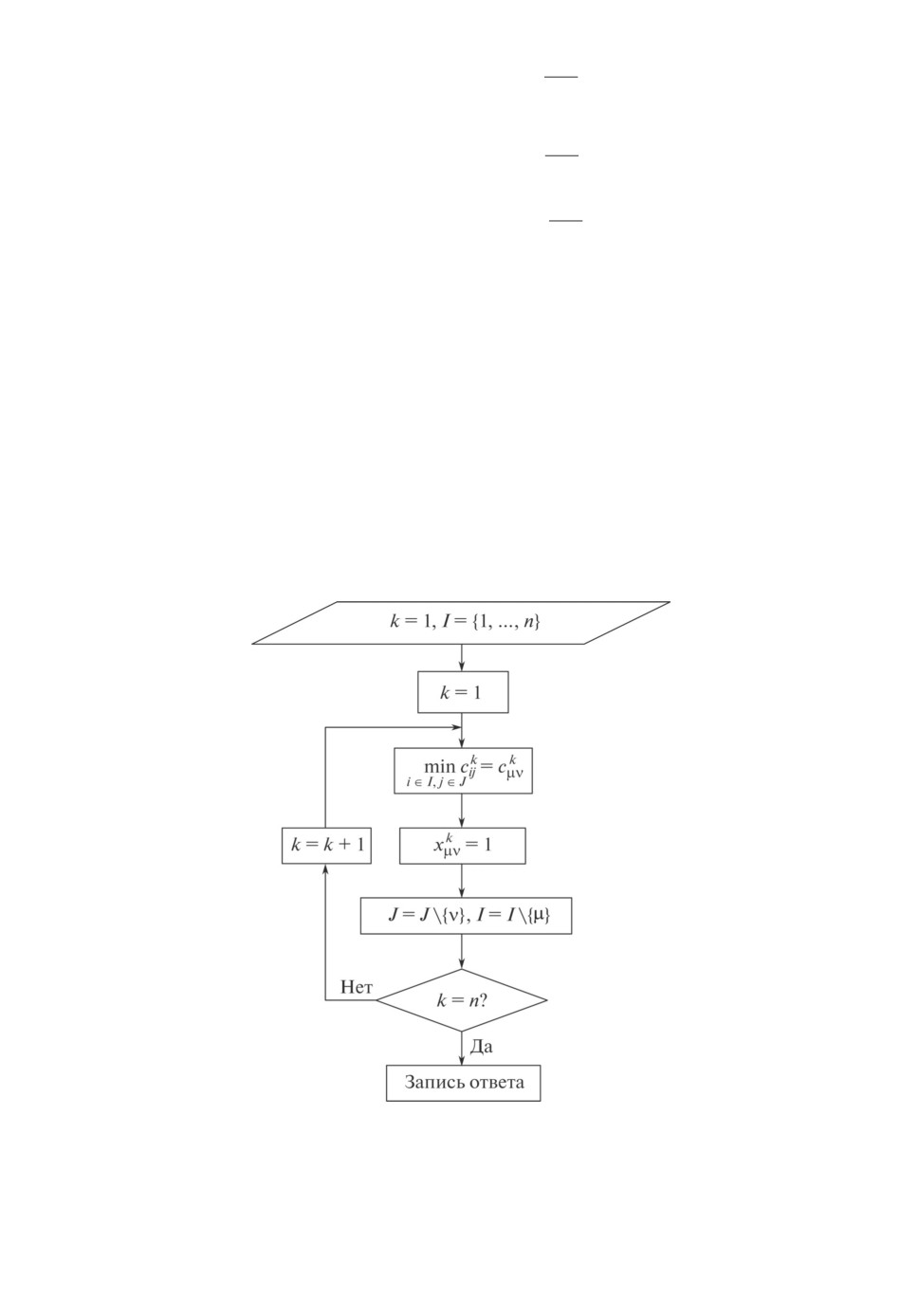
3. “Жадный” алгоритм решения
Для аксиальной задачи известен “жадный” алгоритм решения [17], осно-
ванный на поиске минимального элемента в плоских матрицах при фиксиро-
вании одного из индексов. Пример общей схемы одного из таких алгоритмов
представлен на рис. 1.
Рис. 1. Блок-схема алгоритма поиска минимального элемента для трехиндекс-
ной аксиальной задачи о назначениях.
Заметим, что вычислительная сложность данного алгоритма равна O(n3).
158
4. Адаптивный алгоритм решения
Для построения адаптивного аналога (далее адаптивного алгоритма) дан-
ного базового алгоритма осуществляется переход к вероятностной постановке
задачи на основе рандомизации переменных [13].
Задача
L(X) → min
X∈Ω
заменяется задачей вида
M (L(X)) → min
,
{X}:X∈Ω
где {X} - множество случайных величин X с реализациями X из множе-
ства Ω.
Здесь
X = [X1,...,Xn], Xk = [Xk1,...,Xkn]T, Xki = (Xki1,...,Xkin),
где Xk - матрица случайных величин размера n × n, Xki - строка матрицы Xk,
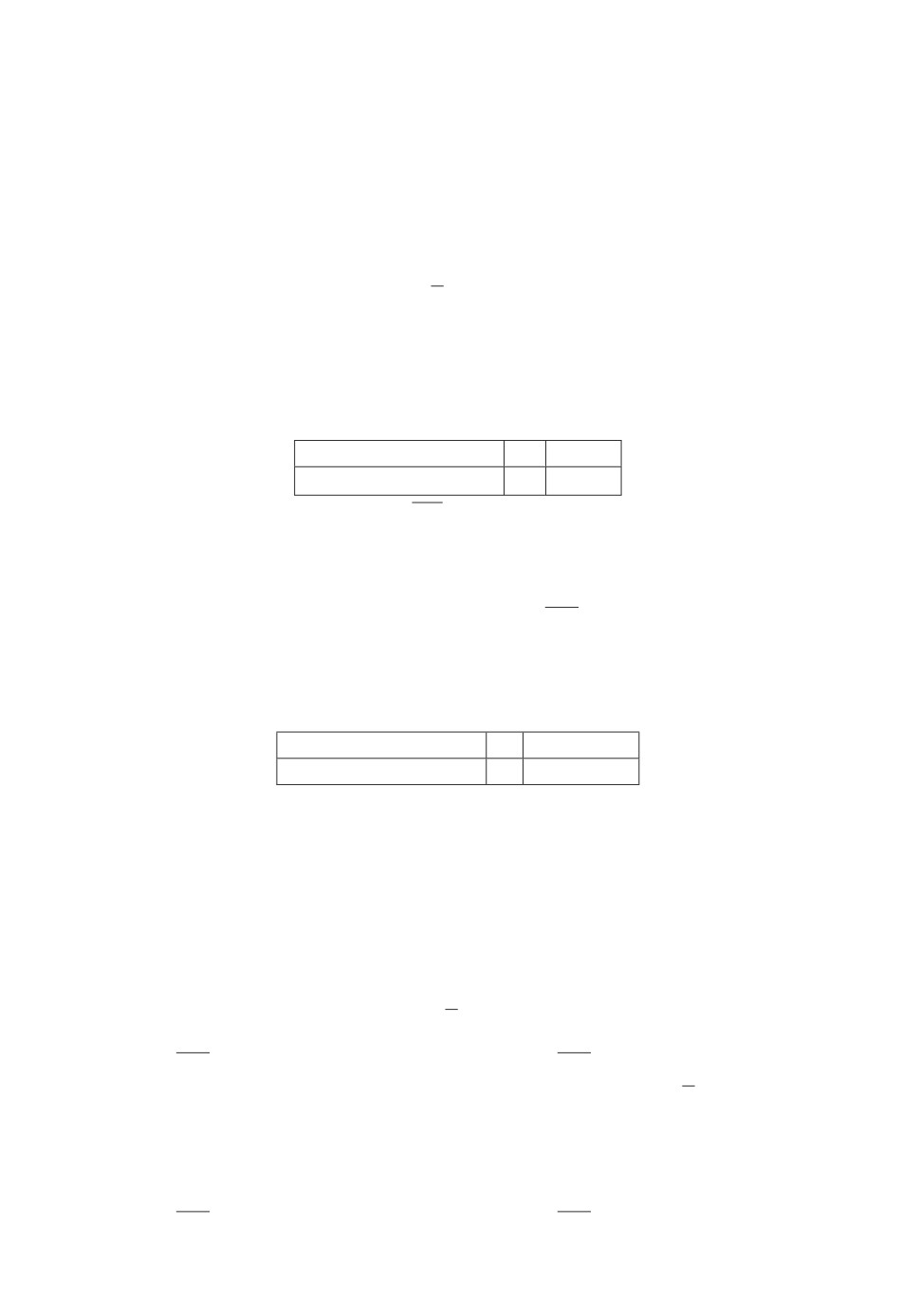
Xkij - случайная величина с рядом распределения, представленным в табл. 1.
Таблица 1. Ряд распределения Xkij
Возможные значения
1
0
Вероятность p
pkij
qkij = 1 - pkij
∗где i, j, k = 1, n.
Для каждого k = 1, n вводятся полные группы событий Akij , где Akij - со-
бытие, заключающееся в том, что xkij примет значение 1, т.е.
∑
pkij = 1, k = 1,n.
i=1 j=1
В основе алгоритма лежат этапы I-III:
I. задание движения во множестве случайных величин Xkij;
II. решение неравенства — условия локального улучшения (УЛУ)
(
(
(
(
)
(
))
(
))
(
))
M L
XN+1
-L
XN
=M L
XN+1
-M L
XN
=
(
(
(
)
(
)))
(6)
= MXN+1 MXN
L
XN+1
-L
XN
≤ 0,
где MXN - математическое ожидание случайных величин, зависящих от XN ;
III. пересчет вероятностей pkij, i,j,k = 1,n в соответствии с результатом
УЛУ.
159
Заметим, что УЛУ (6) означает, что случайная величина XN+1 должна вы-
бираться так, чтобы значение целевой функции в ней было лучше (меньше),
чем значение целевой функции в предыдущей точке, или таким же. Так как
случайные величины в данной задаче принимают значения только 1 или 0,
то на математическое ожидание влияют только значения вероятностей. Их
необходимый пересчет происходит на этапе III.
Опишем подробнее каждый из этапов.
I. Формула движения выбирается следующим образом:
(7)
XN+1 = uXN + uYN+1,
где YN+1 - неизвестная случайная величина, определяющая направление
движения на (N + 1)-м шаге, такая что YN+1 ∈ {X} и Ykij имеет ряд рас-
пределения, представленный в табл. 2.
Таблица 2. Ряд распределения Ykij
Возможные значения
1
0
Вероятность p
πkij
1-πkij
∗где i, j, k = 1, n.
Будем также считать, что
∑
πkij = 1, k = 1,n,
i=1 j=1
u - случайная величина с рядом распределения, представленным в табл. 3.
Таблица 3. Ряд распределения u
Возможные значения
1
0
Вероятность p
pu qu = 1 - pu
Лемма 1. Если движение задано формулой (7), то УЛУ можно запи-
сать в виде неравенства
(
(
(
)
(
)))
(8)
MX MY
L
YN+1
-L
XN
≤ 0.
Перепишем формулу движения в покоординатной форме и возьмем мате-
матическое ожидание от обеих частей:
((
)N+1 )
( (
)N
(
)N+1 )
M Xkij
=M u Xkij
+u Ykij
,
где i, j = 1, n для каждого фиксированного k = 1, n.
С учетом того, что случайные величины u и YN+1, а также u и XN вводятся
как независимые, формула пересчета вероятностей адаптивного алгоритма
будет выглядеть следующим образом:
(pkij)N+1 = qu(pkij)N + pu(πkij )N+1,
где i, j = 1, n для каждого фиксированного k = 1, n.
160
Вероятности πkij находятся из условия локального улучшения (8), пара-
метр pu задается некоторым числом от 0 до 1 (рекомендации по его выбору
представлены в вычислительном эксперименте).
II. Условие локального улучшения (УЛУ)
Теорема 1. УЛУ (8) для вероятностной постановки задачи представи-
мо в виде
⎛
⎞
∑
∑
∑
∑
clrs - ⎝
ckrj(pkrj)N +
ckis(pkis
)N ⎠ -
k=l+1 j∈J
k=l+1 i∈I
(9)
⎛
⎛
⎞⎞
∑
∑
∑
∑
-⎝clqh - ⎝
ckqj(pkqj)N +
ckih(pkih
)N ⎠⎠ ≤ 0
k=l+1 j∈J
k=l+1 i∈I
для фиксированного l = 1, n и произвольных номеров r, s, q, h,
где I, J - множества допустимых номеров i и j соответственно.
Пусть реализация случайной величины Xl зафиксирована (например, на
предыдущей итерации алгоритма), т.е. Xl = Eqh, где Eqh - матрица с одной
единицей на пересечении q-й строки и h-го столбца и остальными нулевыми
элементами. Тогда для выполнения УЛУ по теореме 1 необходимо, чтобы
выполнилось неравенство (9). Для этого номера r и s, Yl = Ers, необходимо((
))
∑
∑
∑
выбрать так, чтобы величина clrs -
ckrj(pkrj)N
+
∑ ckis(pkis
)N
k=l+1 j∈J
k=l+1 i∈I
была минимальной.
В результате решение YN+1 = [(Y1)N+1 . . . (Yn)N+1] находится следующим
образом:
(Ylμν )N+1 : πlμν = 1, если
⎛
⎛
⎞⎞
∑
∑
∑
∑
⎝cl
min
rs
-⎝
ckrj(pkrj)N +
ckis(pkis
)N ⎠⎠ =
r,s
k=l+1 j∈J
k=l+1 i∈I
⎛
⎞
∑
∑
∑
∑
=clμν -⎝
ckμj(pkμj)N +
ckiν(pkiν
)N ⎠,
k=l+1 j∈J
k=l+1 i∈I
(Ylij)N+1 : πlij = 0, i, j = 1, n, j = ν, i = μ,
(Yk)N+1 = (Xk)N , k = l + 1, n.
161
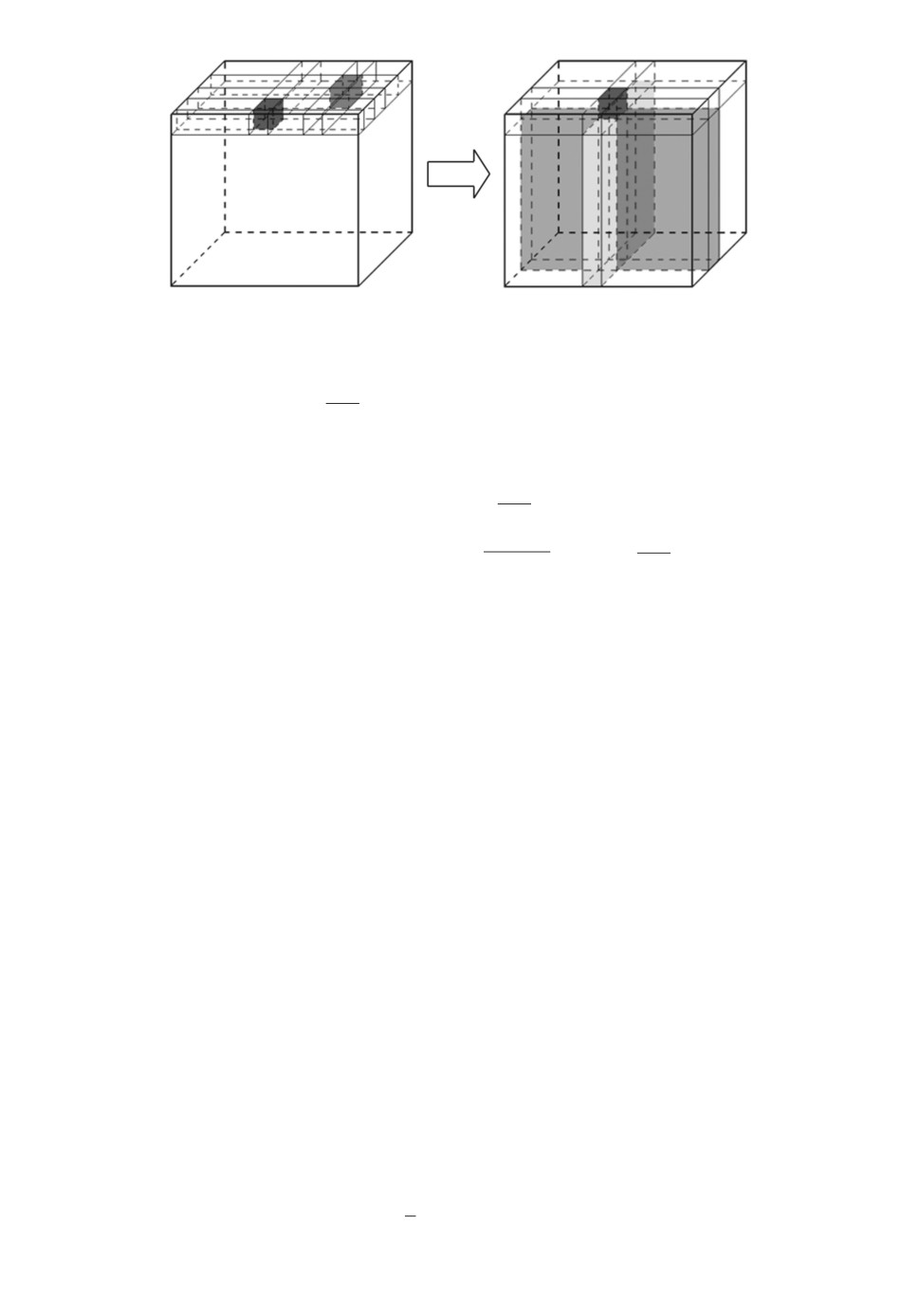
Рис. 2. Изменение “жадного” алгоритма.
Пересчет вероятностей при этом на этапе III с учетом того, что πlμν = 1, а
остальные πlij = 0, i, j = 1, n, j = ν, i = μ, происходит по формулам
(10)
(plμν )N+1 = (plμν )N qu + pu,
(11)
(plij )N+1 = (plij)N qu
,
i, j = 1, n, j = ν, i = μ,
(12)
(pkij)N+1 = (pkij )N
,
k = l + 1,n, i,j = 1,n.
Данный этап отвечает за “адаптацию” вероятностей и дает общее название
всему алгоритму, поскольку на каждой итерации производится подстройка
вероятностей на основе предыдущих шагов для получения лучшего решения.
Таким образом, УЛУ позволяет модифицировать соответствующий шаг
“жадного” алгоритма следующим образом:
при фиксированном k вместо
min
ckij = ckμν
i∈I,j∈J
вычислить
⎛
⎛
⎞⎞
∑
∑
∑
∑
min
⎝ckij - ⎝
clij(plij)N +
clij(plij
)N⎠⎠ =
i∈I,j∈J
l=k+1 j∈J
l=k+1 i∈I
⎛
⎞
∑
∑
∑
∑
=ckμν -⎝
clμj(plμj)N +
cliν(pliν
)N ⎠,
l=k+1 j∈J
l=k+1 i∈I
где J - множество номеров j, I - множество номеров i,
зафиксировать xkμν = 1 (для получения рекордов).
На рис. 2 наглядно изображена модификация “жадного” алгоритма.
Замечание 1. В указанных формулах участвуют условные вероятности.
На основании предположения о том, что все гипотезы распределены равно-
мерно, безусловные вероятности pN+1 пересчитываются через условные pN+1
162
по формуле
(
)
N
1
(13)
pN+1 =
pN +
pN+1
N+1
N
5. Алгоритм 1. Адаптивный алгоритм решения
аксиальной трехиндексной ЗОН
1. Задать начальное распределение вероятностей для каждого k = 1, n
1
(pkij )1 =
,
i, j = 1, n.
n2
Задать максимальное количество итераций Nmax. Положить N = 1.
2. Задать множества J = {1 . . . n}, I = {1 . . . n}, положить k = 1.
3. Вычислить
⎛
⎛
⎞⎞
∑
∑
∑
∑
min
⎝ckij - ⎝
clij(plij)N +
clij(plij
)N⎠⎠ =
i∈I,j∈J
l=k+1 j∈J
l=k+1 i∈I
⎛
⎞
∑
∑
∑
∑
=ckμν -⎝
clμj(plμj)N +
cliν(pliν
)N⎠ ,
l=k+1 j∈J
l=k+1 i∈I
зафиксировать соответствующее назначение
(xkμν )N = 1.
4. Пересчитать вероятности по формулам (10)-(12)
(pkμν )N+1 = (pkμν )N qu + pu,
(pkij )N+1 = (pkij)N qu, i, j = 1, n, j = ν, i = μ,
(plij)N+1 = (plij )N , l = k + 1, n, i, j = 1, n.
5. Пересчитать безусловные вероятности по формуле (13).
6. Изменить множества I, J : I = I \ {μ}, J = J \ {ν}.
7. Проверить: k = n? Если нет, то положить k = k + 1 и перейти к шагу 3,
если да, то переход к шагу 8.
8. Возможная смена рекорда (X)N , (L(X))N , (P )N .
9. Проверить: N = Nmax? Если нет, то положить N = N + 1 и перейти к
шагу 2, если да, то ОСТАНОВ. В качестве ответа записывается последний
рекорд.
Замечание 2. На шаге 3 алгоритма 1 для каждого элемента слоя осу-
ществляется проход по двум “плоским” матрицам (сложность O(n2)). Всего
элементов на слое n2, таким образом, сложность шага равна O(n4). Данный
шаг повторяется для каждого k = 1, n, в результате чего сложность одной
итерации алгоритма 1 составляет O(n5), что превышает сложность базового
“жадного” алгоритма.
163
Разработан специальный метод построения дополнительной кубической
матриц
C, при использовании которого вычислительная сложность данного
адаптивного алгоритма на каждой итерации будет равна O(n3).
6. Алгоритм 2. Построение дополнительной матриц
C
1. Задать i = 1, j = 1.
2. Задать cnij = 0.
3. Задать k = n - 1.
4. Вычислить ckij = ck+1ij + ck+1ijpk+1ij.
5. Проверить: k = 1?
Если нет, то задать k = k - 1 и перейти к шагу 4.
Если да, то задать j = j + 1 и перейти к шагу 6.
6. Проверить: j = n + 1?
Если нет, то перейти к шагу 2
Если да, то задать j = 1 и i = i + 1 и перейти к шагу 7.
7. Проверить: i = n + 1?
Если нет, то перейти к шагу 2.
Если да, то ОСТАНОВ, матриц
C получена.
Данный алгоритм использует один проход по кубической матрице, таким
образом, его вычислительная сложность равна O(n3).
Далее необходимо для каждого слоя матриц
C реализовать стандартную
процедуру подсчета суммы по строкам и по столбцам. Ее вычислительная
сложность на слое равна O(n2), на всей кубической матрице - O(n3).
Обозначим сумму в j-м столбце на k-м слое через Sum_stolbj, а сумму в
i-й строке на k-м слое через Sum_stri, i, j, k = 1, n.
Заменим в матриц
C каждый элемент на выражение
(
)
(14)
ckij := ckij - Sum_stolbj + Sum_stri - ci
j
в соответствии с (9). При этом слагаемое ckij вычитается, поскольку оно два
раза учтено в подсчете сумм по строкам и столбцам.
В итоге шаг 3 алгоритма 1 заменяется следующей последовательностью
шагов:
3.1. Составить дополнительную матриц
C по алгоритму 2.
3.2. Посчитать сумму по строкам и столбцам на каждом слое кубической
матрицы.
3.3. Применить формулу (14).
3.4. Вычислить
min
ckij = ckμν ,
i∈I,j∈J
зафиксировать соответствующее назначение
xkμν = 1.
164
Таким образом, вместо прямого применения формулы (9) предлагается
последовательное построение дополнительной матрицы в 4 этапа. С учетом
того, что их вычислительные сложности равны O(n3), результирующая слож-
ность каждой итерации алгоритма будет равна O(n3).
7. Вычислительный эксперимент
Для тестирования и анализа предложенного алгоритма был разработан
программный комплекс в среде программирования Borland Delphi 7.0, содер-
жащий в себе адаптивный и базовый алгоритмы.
Цели вычислительного эксперимента:
1) оценка влияния параметра pu на работу алгоритма;
2) сравнение базового “жадного”, итеративного “жадного” и адаптивного
алгоритмов;
3) время работы адаптивного алгоритма.
Исходные данные вычислительного эксперимента:
— кубические матрицы трех размерностей: 10 × 10 × 10, 50 × 50 × 50,
100 × 100 × 100;
— три варианта заполнения матриц: равномерное распределение чисел от 1
до 10 (обозначим как R(10)), от 1 до 50 (R(50)), от 1 до 100 (R(100)), от 1 до
300 (R(300));
— различные значения вероятности pu.
Оценивались следующие параметры: значение целевой функции и время
работы алгоритмов.
Для каждого варианта исходных данных задавались 500 кубических мат-
риц и вычислялось среднее арифметическое значений целевых функций.
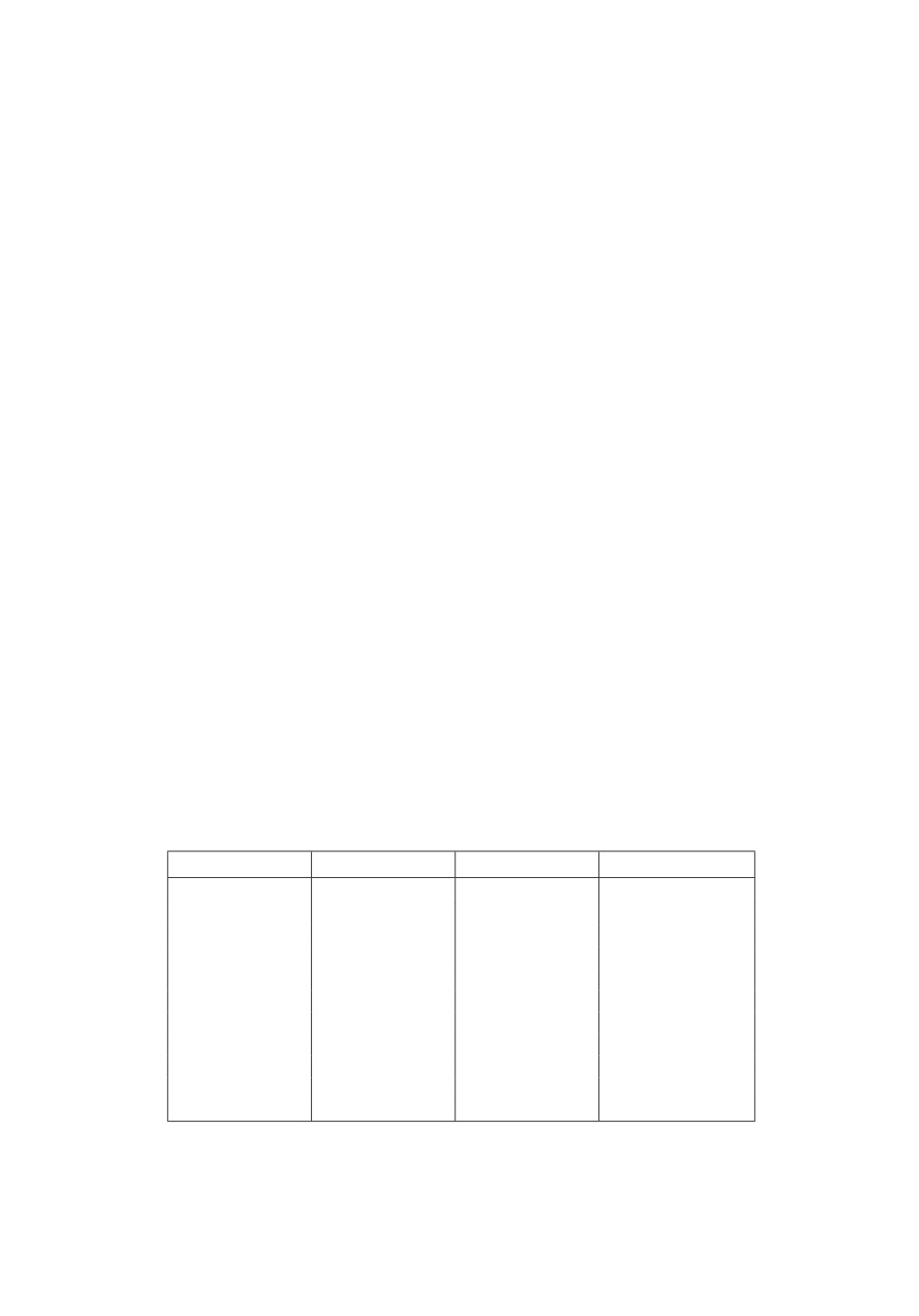
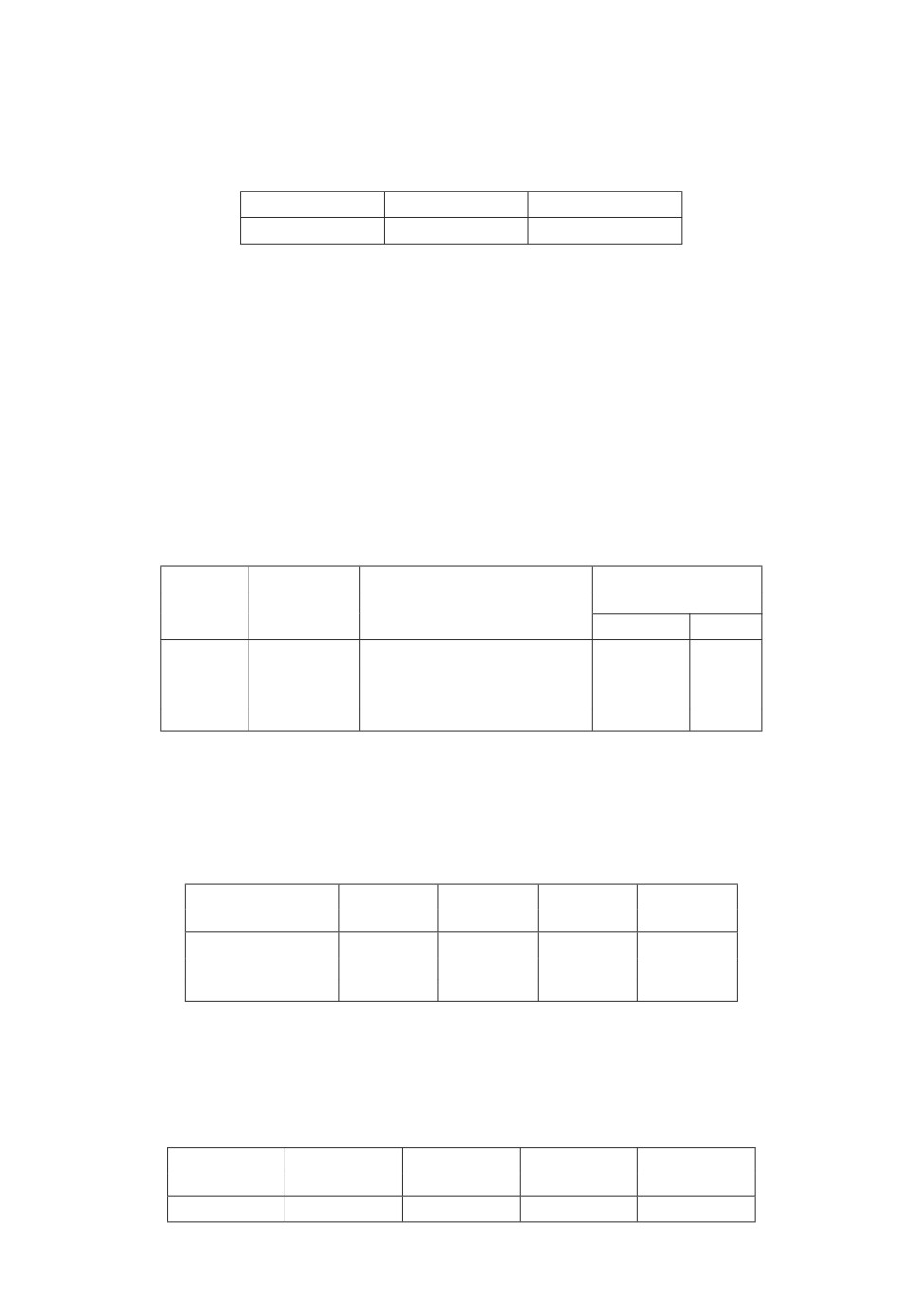
В табл. 4 для разных pu приведены результаты работы алгоритма для
задач размерности 100 × 100 × 100 при равномерном распределении чисел
от 1 до 100.
Таблица 4. Среднее арифметическое значений целевых функций
Значение pu
10 итераций
50 итераций
100 итераций
pu = 0,01
133,6
121,5
118,1
pu = 0,1
134,96
126,3
123,68
pu = 0,2
135,85
127,94
125,25
pu = 0,3
137,78
128,41
125,77
pu = 0,4
137,7
128,58
126,43
pu = 0,5
138,87
128,67
126,28
pu = 0,6
139,07
128,82
126,2
pu = 0,7
139,77
129,5
126,78
pu = 0,8
138,36
129,15
126,45
pu = 0,9
138,91
129,12
125,65
pu = 1
137,82
129,45
125,68
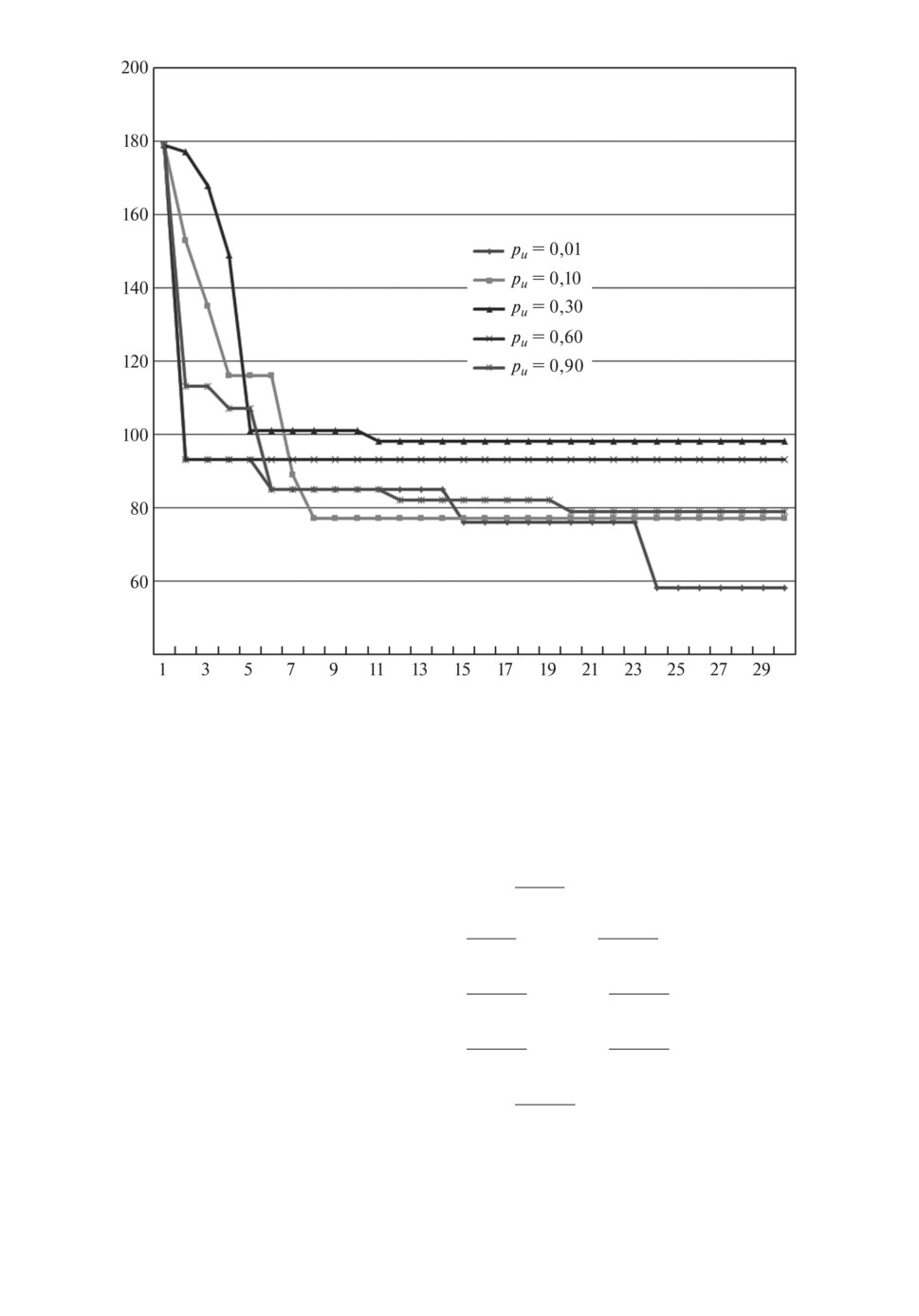
На рис. 3 представлены изменения значений целевой функции в процессе
работы алгоритма на первых 30 итерациях при различных значениях пара-
метра pu.
165
Рис. 3. Изменение значения целевой функции при разных pu.
Рассмотрим задание параметра pu в виде ступенчатой функции, зависящей
от количества итераций
⎧
Nmax
⎪
⎪0,01, если N ≤
;
⎪
5
⎪
Nmax
2Nmax
⎪
0,1,
если
<N ≤
;
⎪
⎪
5
5
⎨
2Nmax
3Nmax
(15)
pu(N) =
0,5,
если
<N ≤
;
⎪
5
5
⎪
⎪
3Nmax
4Nmax
⎪0,1,
если
<N ≤
;
⎪
5
5
⎪
⎪
Nmax
⎩0,01, если N >4
,
5
где N - номер текущей итерации, Nmax - максимальное количество итераций.
Такой подход позволит алгоритму избежать “застревания” в локальных
минимумах и, соответственно, улучшить решение.
166
В табл. 5 представлены результаты работы алгоритма для задач размер-
ности 100 × 100 × 100 при равномерном распределении чисел от 1 до 100 с
параметром pu, заданным в (15).
Таблица 5. Параметр pu, заданный формулой
10 итераций
50 итераций
100 итераций
132,42
121,0
117,51
Теперь рассмотрим сравнение адаптивного и базового “жадного” алгорит-
мов.
Так как предложенный адаптивный алгоритм является итеративным, то
целесообразно проводить его сравнение не только с “жадным” алгоритмом,
но и с его итеративной модификацией, заключающейся в изменении порядка
следования слоев на каждой итерации.
В табл. 6 представлены результаты работы алгоритмов для задач раз-
мерности 100 × 100 × 100. Для итеративных алгоритмов число итераций рав-
но 100.
Таблица 6. Среднее арифметическое значений целевых функций
Разброс
“Жадный” Итеративный “жадный” Адаптивный
алгоритм
алгоритм
алгоритм
pu = 0,01 pu(N)
R(10)
106,9
100,24
100,0
100,0
R(50)
146,1
108,74
106,16
105,62
R(100)
202,9
123,72
118,14
117,51
R(300)
396,66
186,68
178,68
175,92
В табл. 7 приведены средние значения времени работы алгоритма (в се-
кундах) для указанного числа итераций на задачах разных размерностей.
Таблица 7. Время работы алгоритма
Размерность
10
50
100
200
задачи
итераций итераций итераций итераций
10 × 10 × 10
0,0009
0,0024
0,006
0,0104
50 × 50 × 50
0,061
0,29
0,57
1,17
100 × 100 × 100
0,76
3,81
7,49
15,28
В табл. 8 приведены средние значения целевых функций при росте числа
итераций алгоритма.
Таблица 8. Средние значения целевых функций при pu = 0,1
10
50
100
200
1000
итераций итераций итераций итераций итераций
134,96
126,3
123,68
122,8
121,6
167
На основе проведенного вычислительного эксперимента можно сделать
следующие выводы.
1. Адаптивный алгоритм дает результаты лучше, чем
“жадный” (в
1,4-1,6 раз) и итеративный “жадный” алгоритмы (табл. 6).
2. Большое влияние на итоговый результат оказывает параметр pu. Экспе-
римент показал, что при малых значениях pu и в случае его функциональной
зависимости от числа итераций алгоритм работает эффективнее (табл. 4 и 5).
3. Увеличение количества итераций приводит к улучшению решения
(рис. 3). Однако большое число итераций приводит к незначительным улуч-
шениям ответа (табл. 8), поэтому их количество следует соотносить с време-
нем работы алгоритма (табл. 7).
4. В ряде случаев адаптивный алгоритм решает задачу точно! Например,
при размерности задачи 100×100×100 (табл. 6) и равномерном распределении
чисел от 1 до 10 по кубической матрице, т.е. при небольшом разбросе зна-
чений элементов матрицы относительно размерности задачи, алгоритм дает
оптимальное значение целевой функции, равное 100.
При размерности 50 × 50 × 50 и равномерном распределении чисел от 1
до 10 алгоритм дает оптимальное значение целевой функции, равное 50, в
среднем на 95 матрицах из 100 при 50 итерациях.
В ходе вычислительного эксперимента оказалось, что задание pu в виде
функциональной зависимости от количества итераций позволяет улучшить
результат работы алгоритма. В связи с этим дальнейшие исследования будут
направлены на изучение и анализ результатов работы адаптивного алгоритма
с изменяющимся в процессе работы параметром pu, а также на сравнение
данного метода с другими эвристическими алгоритмами.
8. Заключение
В статье предложен вероятностный аналог “жадного” алгоритма поиска
минимального элемента. Он назван адаптивным ввиду того, что на каж-
дой итерации происходит подстройка вероятностей с учетом результатов на
предыдущей итерации. Оригинальность метода заключается в том, что на
формирование решения влияют не только “качества” самого элемента, но
возможные потери при его выборе, что является несомненным преимуще-
ством и позволяет избежать перебора заведомо “плохих” решений. Также от-
личительной особенностью алгоритма является учет его предыдущих шагов
за счет “адаптации” матрицы вероятностей, которая позволяет организовать
направленный перебор допустимых решений.
В статье представлены результаты вычислительного эксперимента, на ос-
новании которых сделаны определенные выводы по работе алгоритма.
ПРИЛОЖЕНИЕ
Доказательство леммы 1. При выборе формулы движения (7) зна-
чение целевой функции в точке XN+1 будет равно
L(XN+1) = uL(XN ) + uL(YN+1).
168
Подставим данное выражение в УЛУ (6)
(
(
(
)
(
))
(
)
(
)
(
))
M L
XN+1
-L
XN
= M uL
XN
+ uL
YN+1
-L
XN
=
(
(
(
(
))
(
))
(
))
=quM L
XN
+puM L
YN+1
-M L
XN
=
(
(
(
))
(
))
= (qu - 1)M L
XN
+puM L
YN+1
=
(
(
(
))
(
(
)))
=pu M
L
YN+1
-M
L
XN
=
(
(
(
)
(
)))
=puMX MY
L
YN+1
-L
XN
≤ 0.
Так как pu > 0, то в итоге получается, что
(
(
(
)
(
)))
MX MY
L
YN+1
-L
XN
≤ 0.
Лемма 1 доказана.
Доказательство теоремы 1. Заметим, что неравенство (8) имеет
бесчисленное множество решений.
(
(
(
)
(
)))
MX MY
L
YN+1
-L
XN
=
⎛
⎛
⎞⎞
∑
∑
∑
∑
= MX ⎝MY ⎝
ckij(Ykij)N+1 -
ckij(Xkij
)N ⎠⎠ ≤ 0.
i=1 j=1 k=1
i=1 j=1 k=1
Воспользуемся идеей алгоритма покоординатного спуска. Решим неравен-
ство по неизвестной матрице Y1. Переменные Y2, . . . , Yn зафиксируем, т.е.
будем считать, что случайные величины (Ykij)N+1 и (Xkij)N имеют одинаковое
распределение, а именно (πkij )N+1 = (pkij )N при k = 2, n, i, j = 1, n.
Учитывая, что математическое ожидание от произведения независимых
случайных величин есть произведение их математических ожиданий, а так-
же используя формулу для условной вероятности, УЛУ можно переписать
следующим образом:
(
(
(
)
(
)))
MX MY
L
YN+1
-L
XN
=
(
(
(
)
(
)))
= MX1MX|X1 MY1MY|Y1
L
YN+1
-L
XN
≤ 0.
С учетом того, что
∑∑
∑
∑
L(X) =
c1ijX1ij +
ckijXkij,
i=1 j=1
i=1 j=1 k=2
∑∑
∑
∑
L(Y) =
c1ijY1ij +
ckijYkij,
i=1 j=1
i=1 j=1 k=2
169
УЛУ перепишется в виде
⎛
⎛
⎞⎞
∑∑
∑
MY1⎝
c1ij(Y1ij)N+1
+ MY|Y1 ⎝
ckij(Ykij
)N+1⎠⎠ -
i=1 j=1
i=1 j=1 k=2
⎛
⎛
⎞⎞
∑∑
∑
(Π.1)
- MX1 ⎝
c1ij(X1ij)N
+ MX|X1 ⎝
ckij(Xkij
)N ⎠⎠
≤0
i=1 j=1
i=1 j=1 k=2
или
⎛
⎞
∑∑
(
(
))
N+1
Y
⎠-
MY1⎝
c1ij(Y1ij)N+1
+ MY|Y1
L
i=1 j=1
⎛
⎞
∑∑
(
(
))
N
X
⎠
(Π.2)
-MX1⎝
c1ij(X1ij)N
+ MX|X1
L
≤ 0,
i=1 j=1
гдеY = [Y2 . . . Yn],X = [X2 . . . Xn].
∑
Учитывая, что
∑ p1ij = 1, зафиксируем реализацию случайной вели-
i=1 j=1
чины X1. Предположим, что x1qh = 1 (x1ij = 0, i = q, j = h соответственно).
(
(
))
∑
Выражение MX1
∑ c1ij(X1
)N + MX|X1 L(XN)
из формулы (П.2)
ij
i=1 j=1
(
)
примет вид c1qh + MX|X1
L(XN) . При фиксировании номеров q, h и с
=Eqh
учетом того, что {X} : X ∈ Ω, реализация условного математического ожи-
(
)
дания MX|X1
L(XN ) примет вид
=Eqh
(
)
c1qh + MX|X1
L(XN)
=
=Eqh
⎛
⎞
⎜∑
∑
∑∑∑
⎟
⎜
⎟
= c1qh + MX|X1=E
ckij(Xkij)N +
ckij(Xkij
)N
qh
⎝
⎠=
i=1
j=1 k=2
i=1 j=1
k=2
i=q
j=h
∑
∑
∑∑∑
=c1qh +
ckij(pkij)N +
ckij(pkij)N =
i=1
j=1 k=2
i=1 j=1
k=2
i=q
j=h
⎛
⎞
∑
∑
∑
∑∑
(Π.3)
=c1qh +
ckij(pkij)N - ⎝
ckqj(pkqj)N +
ckih(pkih
)N ⎠ .
i=1 j=1 k=2
k=2 j=1
k=2 i=1
Аналогично, при каждой реализации Y1 : V1 = Ers и с учетом того, что
YN+1 ∈ {X}: X ∈ Ω, а также, что (πkij)N+1 = (pkij)N при k = 2, n, i, j = 1, n,
170
(
(
))
∑
выражение M
∑ c1ij(Y1
)N+1 + MY|Y1 L(YN+1) примет вид
Y1
ij
i=1 j=1
⎛
⎞
∑
∑
∑
∑∑
(Π.4) c1rs +
ckij(pkij)N - ⎝
ckrj(pkrj)N +
ckis(pkis
)N ⎠.
i=1 j=1 k=2
k=2 j=1
k=2 i=1
УЛУ (П.1) с учетом (П.3) и (П.4) преобразуется следующим образом:
⎛
⎞
∑∑
(
)
MY1⎝
c1ij(Y1ij)N+1
+ MY|Y1
L(YN+1)
⎠-
i=1 j=1
⎛
⎞
∑∑
(
)
⎠=
- MX1 ⎝
c1ij(X1ij)N
+ MX|X1
L(XN)
i=1 j=1
⎛
⎞
∑
∑
∑
∑∑
=c1rs +
ckij(pkij)N - ⎝
ckrj(pkrj)N +
ckis(pkis
)N ⎠-
i=1 j=1 k=2
k=2 j=1
k=2 i=1
⎛
⎛
⎞⎞
∑
∑
∑
∑∑
-⎝c1qh +
ckij(pkij)N - ⎝
ckqj(pkqj)N +
ckih(pkih
)N ⎠⎠ =
i=1 j=1 k=2
k=2 j=1
k=2 i=1
⎛
⎞
∑∑
∑∑
=c1rs -⎝
ckrj(pkrj)N +
ckis(pkis
)N⎠ -
k=2 j=1
k=2 i=1
⎛
⎛
⎞⎞
∑∑
∑∑
(Π.5)
-⎝c1qh - ⎝
ckqj(pkqj)N +
ckih(pkih
)N⎠⎠
≤ 0.
k=2 j=1
k=2 i=1
Вышеизложенные рассуждения можно обобщить для неизвестной матри-
цы Yl, l = 1, n. В результате получим
⎛
⎞
∑
∑
∑
∑
clrs - ⎝
ckrj(pkrj)N +
ckis(pkis
)N⎠ -
k=l+1 j∈J
k=l+1 i∈I
⎛
⎛
⎞⎞
∑
∑
∑
∑
-⎝clqh - ⎝
ckqj(pkqj)N +
ckih(pkih
)N ⎠⎠ ≤ 0,
k=l+1 j∈J
k=l+1 i∈I
где I, J - множества допустимых номеров i и j соответственно.
Теорема 1 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Karp R.M. Reducibility Among Combinatorial Problems, in Complexity of Computer
Computations // N.Y.: Plenum Press, 1972. P. 85-103.
171
2.
Hansen P., Kaufman L. A Primal-Dual Algorithm for the Three-dimensional
Assignment Problem // Cahiers du GERO. 1973. V. 15. No. 3. P. 327-336.
3.
Pierskalla W.P. The Tri-substitution Method for the Three-dimensional Assignment
Problem // Canad. Oper. Res. Soc. J. 1967. V. 5. P. 71-81.
4.
Aiex R.M., Resende M.G.C., Pardalos P.M., Toraldo G. GRASP with Path
Relinking for Three-index Assignment // INFORMS J. Comput. 2005. V. 17.
P. 224-247.
5.
Huang G., Lim A. A Hybrid Genetic Algorithm for the Three-index Assignment
Problem // Eur. J. Oper. Res. 2006. V. 172. P. 249-257.
6.
Euler R. Odd Cycles and a Class of Facets of the Axial 3-index Assignment
Polytope // Appl. Math. (Zastowania Matematyki). 1987. V. 19. P. 375-386.
7.
Burkard R.E., Rudolf R., Woeginger G.J. Three-dimensional Axial Assignments
Problems with Decomposable Cost Coefficients // Discret Appl. Math. 1996. V. 65.
P. 123-139.
8.
Dell’Amico M., Lodi A., Martello S. Efficient Algorithms and Codes for the
k-cardinality Assignment Problem // Discret. Appl. Math. 2001. V. 110. P. 25-40.
9.
Афраймович Л.Г. Нижняя оценка для трехиндексной аксиальной задачи о на-
значениях с 1,2-декомпозиционной матрицей стоимостей // Вест. Волж. гос.
акад. водного транспорта. 2016. Вып. 49. С. 25-29.
10.
Кравцов В.М., Кравцов М.К. Характеризация типов максимально нецелочис-
ленных вершин релаксационного многогранника четырехиндексной аксиальной
задачи о назначениях // Журн. вычисл. мат. и мат. физики. 2013. Вып. 53. № 5.
С. 825.
11.
Кравцов М.К., Кравцов В.М. О типах максимально нецелочисленных вершин
релаксационного многогранника четырехиндексной аксиальной задачи о назна-
чениях // Изв. высш. уч. заведений. Математика. 2012. № 3. С. 9-16.
12.
Цидулко О.Ю. О разрешимости 8-индексной аксиальной задачи о назначениях
на одноциклических подстановках // Дискрет. анализ и исслед. операций. 2013.
Т. 20. № 5 (113). С. 66-83.
13.
Львович Я.Е., Каплинский А.И., Чернышова Г.Д., Черных О.И. Конструирова-
ние адаптивных схем перебора для решения дискретных задач оптимизации /
Актуальные проблемы фундаментальных наук. 1991. С. 44-46.
14.
Медведев С.Н. Адаптивные алгоритмы решения трехиндексных задач о назна-
чениях // Современные методы прикладной математики, теории управления и
компьютерных технологий: сб. трудов VI Междунар. конф. (Воронеж, 10-16 сен-
тября 2013 г.) 2013. С. 153-156.
15.
Медведев С.Н., Чернышова Г.Д. Использование адаптивных алгоритмов для ре-
шения трехиндексной задачи о назначениях // Вестн. факультета прикл. мат.,
информ. и механики, 2010. Вып. 8. С. 148-155.
16.
Медведева О.А., Медведев С.Н. Задача комплектования штатов // Актуальные
проблемы прикладной математики, информатики и механики : сб. трудов Меж-
дунар. конф. (Воронеж, 26-28 ноября 2012 г.) Ч. 2. 2012. С. 203-208.
17.
Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспорт-
ного типа. М.: Наука, 1969.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 31.07.2017
После доработки 05.06.2018
Принята к публикации 13.11.2018
172