Автоматика и телемеханика, № 6, 2019

Обзоры

(Институт проблем передачи информации им. А.А. Харкевича РАН, Москва),

Н.А. КУЗНЕЦОВ, академик РАН (kuznetsov@cplire.ru)

(Институт радиотехники и электроники им. В.А. Котельникова РАН, Москва,

Московский физико-технический институт (ГУ)),

П.Ю. ЧЕБОТАРЕВ, д-р физ.-мат. наук (pavel4e@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва,

Московский физико-технический институт (ГУ))

КОНСЕНСУС В АСИНХРОННЫХ МУЛЬТИАГЕНТНЫХ СИСТЕМАХ

III. КОНСТРУКТИВНАЯ УСТОЙЧИВОСТЬ

И СТАБИЛИЗИРУЕМОСТЬ¹

Описаны некоторые классы линейных асинхронных мультиагентных

систем с дискретным временем, для которых проблема устойчивости до-

пускает конструктивное решение. Описан также общий аналитический

подход к построению числовых характеристик, аналогичных обобщенно-

му спектральному радиусу в теории устойчивости, которые предостав-

ляли бы возможность анализировать стабилизируемость управляемых

мультиагентных систем. Работа завершает обзор авторов “Консенсус в

асинхронных мультиагентных системах”, первые две части которого опуб-

ликованы в [1, 2].

Ключевые слова: асинхронные мультиагентные системы, консенсус,

устойчивость, стабилизируемость, марковские системы, матричные про-

изведения, совместный спектральный радиус.

DOI: 10.1134/S0005231019060011

1. Введение

Как отмечалось в первых двух частях настоящего обзора [1, 2], многие

задачи устойчивости и консенсуса линейных мультиагентных систем с дис-

кретным временем могут быть сведены к задаче о сходимости произведений

матриц, описывающих поведение агентов в последовательные промежутки

времени, с сомножителями из некоторого множества матриц. Признанным

инструментом анализа сходимости такого рода матричных произведений в

настоящее время является метод совместного спектрального радиуса набора

матриц (см., например, библиографию [3]). При этом исследование сходимо-

сти соответствующих матричных произведений оказывается принципиально

более сложной задачей по сравнению с аналогичной задачей, возникающей

¹ Работа третьего автора поддержана грантом Российского научного фонда 19-19-00673,

предоставленным ИПУ им. В.А. Трапезникова РАН.

при анализе сходимости автономных линейных систем. В частности, как ока-

залось, в отличие от классической задачи сходимости решений автономных

линейных систем для линейных мультиагентных систем с дискретным вре-

менем общие аналитические критерии анализа устойчивости типа критериев

Рауса—Гурвица или Льенара—Шипара [4, 5] не могут существовать в прин-

ципе [6].

В этой ситуации особую роль приобретают методы численного анализа

устойчивости линейных мультиагентных систем с дискретным временем (схо-

димости матричных произведений). К сожалению, и эти методы оказываются

существенно более сложными и трудоемкими по сравнению с классическими

численными методами анализа устойчивости автономных линейных систем —

в общем случае они являются как минимум NP-сложными [7-11]. Тем не ме-

нее вполне работоспособные (для определенных классов систем) численные

методы в последние годы были разработаны, см., например, [12-28].

В связи с отмеченной выше как теоретической, так и вычислительной

сложностью анализа проблемы консенсуса и устойчивости линейных муль-

тиагентных систем с дискретным временем в общем случае особую важность

приобретает вопрос об описании отдельных классов систем, для которых со-

ответствующие вопросы допускали бы конструктивное решение. Именно это-

му кругу вопросов посвящена настоящая работа.

В разделе 2 описывается один из классов линейных переключающихся

систем, для которого вопросы устойчивости и стабилизируемости конструк-

тивно разрешимы. Предложенный в разделе подход выполнен в духе идеоло-

гии модульности конструирования систем управления — его можно сравнить

с созданием игрушек с помощью конструктора LEGO

. Напомним, что кон-

структор LEGO состоит из “кирпичиков с шипами”, соединяя которые прак-

тически в произвольном порядке (ориентированном за счет наличия шипов),

можно получать разнообразные конструкции. В изложении этого раздела бу-

дем следовать работе [29].

Как отмечалось во второй части настоящего обзора [2], для анализа устой-

чивости линейных мультиагентных систем с дискретным временем приходит-

ся прибегать к алгебраическим методам, наиболее распространенным из кото-

рых является метод совместного/обобщенного спектрального радиуса набора

матриц [3]. Однако использование методов совместного/обобщенного спект-

рального радиуса “в чистом виде” на практике не всегда возможно, поскольку

совместный/обобщенный спектральный радиус описывает асимптотическое

поведение мультиагентных систем только в классе всех (произвольных) “сра-

батываний” компонент (агентов). Поэтому в разделе 3 описывается подход,

позволяющий распространить методы совместного/обобщенного спектраль-

ного радиуса на более типичные в прикладных задачах ситуации, — когда

компоненты мультиагентных систем могут “срабатывать” не произвольным

образом, а в соответствии с некоторым марковским правилом. В частности,

в этом разделе показано, что для матричных произведений, описывающих

функционирование мультиагентных систем, в которых сомножители появля-

ются не в произвольном порядке, а подчиняются некоторому марковскому

правилу, также справедливы аналоги понятий совместного и обобщенного

спектрального радиуса. Данный подход позволил рассмотреть также ситуа-

цию, когда срабатывание отдельных агентов подчинено некоторым частот-

ным ограничениям — эта ситуация, естественная в практических постанов-

ках, как ни странно, долгое время не поддавалась математической формали-

зации.

Наконец, в разделе 4 описывается общий аналитический подход к построе-

нию числовых характеристик, аналогичных обобщенному спектральному ра-

диусу в теории устойчивости, которые предоставляли бы возможность ана-

лизировать стабилизируемость управляемых мультиагентных систем. С этой

целью в разделе вводятся несколько вариантов так называемых минимаксных

спектральных радиусов двух множеств матриц, один из которых описывает

функционирование агентов мультиагентной системы, а второй — допусти-

мых управлений соответствующей системы. Показывается, что в терминах

этих минимаксных радиусов можно дать необходимые и достаточные усло-

вия стабилизируемости управляемых мультиагентных систем.

2. Конструктивная устойчивость/стабилизируемость

мультиагентных систем

В абстрактной постановке линейной мультиагентной системой с дис-

кретным временем можно назвать любую систему, динамика которой (без

учета внешних возмущений) описывается уравнением

(1)

x(n + 1) = A(n)x(n), x(n) ∈ R^N ,

в котором (N × N)-матрицы A(n) при каждом значении n могут произволь-

ным образом принимать значения из некоторого множества (N × N)-мат-

риц A . При этом систему (1) называют (асимптотически) устойчивой, если

для каждой последовательности матриц A(n) ∈ A , n = 0, 1, . . . , соответст-

вующее решение x(n) стремится к нулю. Асимптотическая устойчивость си-

стемы (1) равносильна экспоненциальной сходимости к нулю каждой по-

следовательности {X(n)} матричных произведений X(n) = A(n) · · · A(1)A(0)

[30-37], что в свою очередь равносильно выполнению неравенства

(2)

ρ(A ) < 1,

в котором величина ρ(A ), называемая [38] совместным спектральным ра-

диусом множества матриц A , определяется равенством

(3)

ρ(A ) = lim sup

∥A_n · · · A₁∥1/n = inf sup ∥A_n · · · A₁∥1/n,

n→∞ A_i∈A

n≥1 A_i∈A

где ∥ · ∥ — произвольная матричная норма в M (N, N), порождаемая соответ-

ствующей векторной нормой в R^N .

Для систем (1), не обладающих свойством устойчивости, может быть по-

ставлен вопрос о существовании хотя бы одной последовательности матриц

A(n) ∈ A , n = 0, 1, . . . , для которой выполняется предельное соотношение

A(n) · · · A(1)A(0) → 0, т.е. о стабилизации системы. Система (1) допускает

стабилизацию, если выполнено неравенство

(4)

ρ(A ) < 1

(см. [11, 33, 39-41]), где величина ρ(A ), называемая нижним спектральным

радиусом (lower spectral radius) [33] множества матриц A , определяется ра-

венством

(5)

ρ(A ) = lim

inf

∥A_n · · · A₁∥1/n = inf

inf

∥A_n · · · A₁∥1/n.

n→∞

A_i∈A

n≥1

A_i∈A

Величина ρ(A ) (для произвольного, не обязательно ограниченного множе-

ства матриц) также может быть выражена равенством

ρ(A ) = lim

inf

ρ(A_n · · · A₁)1/n = inf

inf

ρ(A_n · · · A₁)1/n,

n→∞

A_i∈A

n≥1

A_i∈A

как было показано в [33, теорема B1] для конечных множеств A и в [39,

лемма 1.12; 41, теорема 1] для произвольных множеств A .

Неравенства (2) и (4), казалось бы, дают исчерпывающий ответ на вопрос

об устойчивости или стабилизируемости системы. С теоретической точки зре-

ния это действительно так, однако на практике воспользоваться этими крите-

риями затруднительно, поскольку вычислить пределы в формулах (3) и (5) в

явном виде достаточно сложно и, по-видимому, вообще невозможно, см., на-

пример, многочисленные отрицательные результаты в [6, 8, 43-46]. Это влечет

необходимость приближенного анализа величин (3) и (5) с привлечением чис-

ленных методов. При этом ситуация усугубляется тем, что априорные оценки

скорости сходимости в пределах (3) и (5) неизвестны, а объем необходимых

вычислений растет весьма быстро как с ростом n, так и с ростом размерности

системы.

В связи с этим отметим следующие задачи устойчивости и стабилизируе-

мости линейных переключающихся систем, не новых по сути, но остающихся

актуальными.

Задача 1. Описать классы асинхронных систем (классы множеств

матриц A ), для которых совместный спектральный радиус (3) допускал

бы эффективное вычисление.

Задача 2. Описать классы асинхронных систем (классы множеств

матриц A ), для которых нижний спектральный радиус (5) допускал бы

эффективное вычисление.

Исследование устойчивости и стабилизируемости систем (1) затрудняет-

ся еще одним обстоятельством, почти не упоминаемым в теории сходимости

матричных произведений, но критически важным в теории автоматического

управления. Дело в том, что в теории автоматического управления системы,

как правило, состоят не из одного блока, а из набора блоков, соединенных

определенным образом. В случае, когда эти блоки линейные и функциониру-

ют асинхронно, каждый из них описывается уравнением

(6)

x_out(n + 1) = A_i(n)x_in

(n),

!₁

x_in

x_out

!₃

!₄

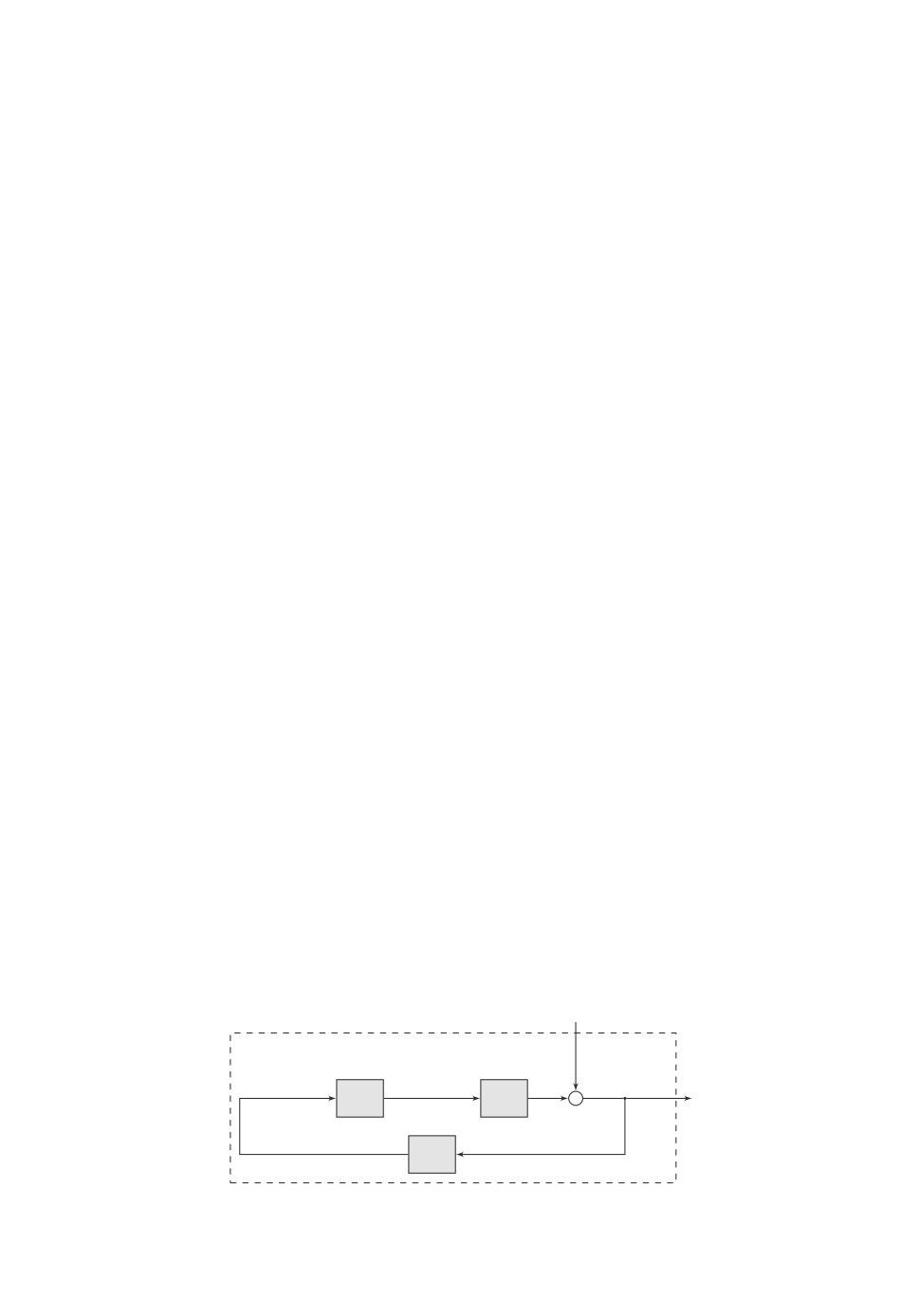
Рис. 1. Пример последовательно-параллельного соединения блоков системы.

где x_in(·) ∈ RNi , x_out(·) ∈ RMi , а (N_i × M_i)-матрицы A_i(n) при каждом зна-

чении n могут произвольным образом принимать значения из некоторого

множества (N_i × M_i)-матриц A_i, i = 1, . . . , Q, где Q — количество блоков в

системе.

В этом случае вопрос об устойчивости или стабилизируемости естествен-

но поставить не для отдельных блоков (6), а для системы в целом, в кото-

рой такого рода блоки могут соединяться параллельно или последовательно,

или более сложным образом, представляемым некоторым ориентированным

графом, с блоками вида (6), расположенными на ребрах графа, см. напри-

мер, рис. 1, на котором представлен пример последовательно-параллельного

соединения блоков системы: блоки A₁ и A₂ соединены параллельно; блок A₃

соединен последовательно с группой блоков A₁ и A₂; блок A₄ соединен парал-

лельно с группой блоков A₁, A₂ и A₃. К сожалению, при таком соединении

блоков классы матриц, описывающих переходные характеристики системы в

целом, оказываются весьма сложными и их свойства практически не изучены.

Как правило, даже в тех случаях, когда размерности входо-выходных векто-

ров отдельных блоков совпадают друг с другом и вопрос об устойчивости

или стабилизируемости для соответствующих блоков может быть каким-то

образом решен, после последовательно-параллельного соединения таких бло-

ков конструктивный ответ на вопросы устойчивости или стабилизируемости

получить уже не удается или, в лучшем случае, получить его крайне затруд-

нительно. Таким образом, актуальной является также следующая задача:

Задача 3. Описать классы асинхронных систем, для которых ответ

на вопрос об устойчивости или стабилизируемости мог бы быть конструк-

тивно получен не только для отдельного асинхронного блока (1) или (6), но

и для последовательно-параллельного соединения таких блоков.

Наконец, рассмотрим еще один аспект проблемы конструктивной устой-

чивости или стабилизации переключающихся систем.

Как совместный спектральный радиус (3), так и нижний спектральный ра-

диус (5) характеризуют лишь устойчивость или стабилизируемость системы

“в целом”. Они описывают предельное поведение “мультипликативно усред-

ненных” норм матричных произведений ∥A(n - 1) · · · A(0)∥1/n. В типичных

ситуациях (для так называемых неприводимых² классов матриц A ), если

² Набор матриц называется неприводимым, если его матрицы не имеют общих инвари-

антных подпространств за исключением нулевого и всего пространства.

говорим об устойчивости системы, то подразумеваем [31], что для каждой

последовательности матриц {A(n)} имеет место оценка

∥A(n - 1) · · · A(0)∥ ≤ Cρⁿ(A ).

Когда говорим о стабилизируемости системы, то подразумеваем, что в ти-

пичных ситуациях существует такая последовательность матриц {A(n)},

для которой имеет место оценка

∥A(n - 1) · · · A(0)∥

Cρⁿ(A ).

В то же время часто возникает необходимость найти такую последова-

тельность матриц, которая обеспечивала бы наиболее медленное или наибо-

лее быстрое “убывание” не норм произведений матриц ∥A(n - 1) · · · A(0)∥, а

(при заданном начальном условии x) векторов A(n - 1) · · · A(0)x. Более точ-

но, рассмотрим вещественную функцию ν(x) ≡ ν(x₁, . . . , x_N ), неубывающую

по каждой координате x_i вектора x = (x₁, . . . , x_N ) и определенную при всех

x₁,... ,x_N ≥ 0. Такую функцию будем называть покоординатно монотонной,

а в случае, когда она строго возрастает по каждой переменной x_i, — строго

покоординатно монотонной. Например, каждая из норм

∑

√∑

∥x∥₁ =

|x_i|,

∥x∥₂ =

|x_i|²,

∥x∥_∞ = max|xi|,

является покоординатно монотонной функцией. При этом нормы ∥x∥₁ и ∥x∥₂

являются строго покоординатно монотонными, а норма ∥x∥_∞ покоординатно

монотонна, но не строго покоординатно монотонна.

Если множество матриц A конечно и состоит из K элементов, то для

нахождения величины

max ν(Ax)

A∈A

в общем случае необходимо K раз вычислить значения функции ν(·) и найти

среди них максимальное. Аналогично, для нахождения величины

(7)

max

ν(Ain · · · Ai1

A_ij ∈A

в общем случае необходимо Kⁿ раз вычислить значения функции ν(·) и найти

среди этих значений максимальное, что с ростом n приводит к экспоненци-

альному росту количества вычислений. В связи с этим разумно поставить

следующую задачу.

Задача 4. Дана покоординатно монотонная функция ν(·) и вектор x=0.

Описать классы асинхронных систем (равносильно, классы множеств мат-

риц A ), для которых число вычислений функции ν(·), требуемых для на-

хождения величины (7), было бы меньше, чем Kⁿ. Желательно, чтобы оно

имело порядок Kn.

Для величины ν(Ain · · · Ai1 x) может быть поставлена аналогичная задача

минимизации. В связи с этим целью настоящего раздела является описание

одного класса асинхронных контроллеров (1), достаточно простых и есте-

ственных в приложениях, для которых удается получить приемлемые реше-

ния задач 1-3. Задача 4 рассматривается в [29].

2.1. Множества матриц с конструктивно вычислимыми

спектральными характеристиками

Одним из классов матричных множеств, для которых величины (3) и (5)

могут быть явно вычислены, является так называемый класс множеств по-

ложительных матриц с независимым изменением строк [47], описанный в [2,

раздел 4.1].

Отметим, что контроллеры, поведение которых описывается уравнения-

ми (1) или (6) с IRU-множествами матриц, — это достаточно типичные в тео-

рии автоматического управления асинхронные контроллеры, осуществляю-

щие независимую покоординатную коррекцию входов. Контроллеры, поведе-

ние которых описывается уравнениями (1) или (6) с линейно упорядоченными

множествами положительных матриц, — это своего рода усилители сигнала

с “матричным” коэффициентом усиления, меняющимся во времени.

Из [2, теоремы 7, 8 и замечание 2] вытекает следующее утверждение.

Теорема 1. Пусть имеется система (1), образованная рекурсивным

последовательно-параллельным соединением блоков (т.е. представимая

ориентированным графом, получаемым рекурсивными последовательными

или параллельными расширениями, стартующими из одной из вершин,

и с блоками, расположенными на ребрах графа

[48, 49]), описываемых

уравнениями (6), отвечающими H -множествам положительных мат-

риц A_i, i = 1,... ,Q. Тогда вопрос об устойчивости или стабилизируемос-

ти такой системы конструктивно решается путем нахождения матриц,

доставляющих максимум или минимум величин ρ_max(A ) = max_A∈A ρ(A) и

ρ_min(A ) = min_A∈A ρ(A) соответственно, где множество матриц A есть

полиномиальная сумма Минковского множеств матриц A_i, i = 1, . . . , Q,

отвечающая структуре соединения соответствующих блоков (см. необхо-

димые определения в [2, раздел 4.2]).

Пример 1. В системе A на рис. 1 вход и выход связаны соотношением

(

)

x_out(n + 1) =

A₃(n)(A₁(n) + A₂(n)) + A₄(n)

x_in(n),

где при каждом значении n матрицы A₁(n), . . . , A₄(n) произвольным обра-

зом выбираются из соответствующих множеств A₁, . . . , A₄. Соответственно,

в данном случае все возможные значения матрицы перехода системы A мо-

гут быть получены как элементы следующей полиномиальной суммы Мин-

ковского множеств матриц A₁, A₂, A₃, A₄:

P (A₁, A₂, A₃, A₄) = A₃(A₁ + A₂) + A₄.

2.2. Заключительные замечания

При проектировании систем управления с асинхронно срабатывающими

(переключающимися) компонентами одной из основных является проблема

оценки (вычислимости) совместного или нижнего спектральных радиусов по-

лучившейся системы, определяющих ее устойчивость или стабилизируемость

соответственно.

Предложенный в разделе подход к решению данной проблемы выполнен

в духе идеологии модульности конструирования систем управления — его

можно сравнить с созданием игрушек с помощью конструктора LEGO

Как показано в разделе, каждое H -множество матриц A также мож-

но интерпретировать как своего рода конструктор LEGO для создания

систем управления, элементами которого (кирпичиками в этом конструк-

торе) являются асинхронные блоки (контроллеры) с переходными харак-

теристиками, описываемыми множествами матриц A_i ∈ A . Тогда, как по-

казано выше, любое последовательно-параллельное рекурсивное соединение

блоков такого “конструктора” A приводит к образованию систем, совмест-

ный и нижний спектральные радиусы которых, определяющие их устойчи-

вость или стабилизируемость, всегда могут быть конструктивно вычислены,

см. [2, теоремы 6 и 8].

3. Марковские мультиагентные системы

Как видно из предыдущих разделов, см. также, библиографию [3], в насто-

ящее время математические методы анализа устойчивости линейных мульти-

агентных систем разработаны лишь для нескольких классов мультиагентных

систем — систем, рассинхронизованных по фазе, в меньшей степени для си-

стем, рассинхронизованных по частоте, и достаточно полно для систем, в

которых не накладывается никаких ограничений на “временной” характер

взаимодействия отдельных агентов (компонент).

Для анализа последнего случая в настоящее время принято использо-

вать достаточно полно разработанную в последние 30 лет теорию обобщенно-

го/совместного спектрального радиуса множеств матриц. Эта теория сводит

анализ вопросов устойчивости линейных мультиагентных систем с произволь-

ным функционированием агентов к анализу сходимости матричных произве-

дений. Одним из ключевых элементов этой теории является так называемая

формула Бергера—Ванга, устанавливающая равенство между совместным и

обобщенным спектральными радиусами семейств матриц. Для матричных

произведений, в которых сомножители появляются не в произвольном по-

рядке, а подчиняются некоторому марковскому правилу, также справедливы

аналоги понятий совместного и обобщенного спектрального радиуса. Одна-

ко известные доказательства формулы Бергера—Ванга на этот случай непо-

средственно не переносятся, поскольку они существенно используют факт

произвольности появления различных матриц в соответствующих матрич-

ных произведениях. Тем не менее формула Бергера—Ванга верна [50] и для

“марковских” аналогов совместного и обобщенного спектрального радиуса,

хотя доказательство в этом случае опирается на более изощренную технику

мультипликативной эргодической теории. Достаточно элементарное доказа-

тельство теоремы Дая было предложено в [51].

Изложение этого раздела базируется на [51, 52].

3.1. Марковский совместный спектральный радиус

Пусть A = {A₁, . . . , A_N } — конечный набор (d × d)-матриц с элементами

из поля K = R, C вещественных или комплексных чисел. Если в K^d×d задана

некоторая мультипликативная норма³ ∥ · ∥, то предел

(

)

(8)

ρ(A ) := lim

ρ_n(A )

= lim

ρ_n(A ) = inf

ρ_n(A )

n→∞

n≥1

где

{

}

ρ_n(A ) := sup

∥Ain · · · Ai1 ∥1/n : i_j ∈ {1, . . . , N}

называется совместным спектральным радиусом набора матриц A [38]. Этот

предел всегда существует, конечен и не зависит от выбора нормы ∥ · ∥. Если

A состоит из одной матрицы, то выражение (8) превращается в известную

формулу Гельфанда для спектрального радиуса линейного оператора. Поэто-

му иногда (8) называют обобщенной формулой Гельфанда [53].

Обобщенным спектральным радиусом набора матриц A называют вели-

чину, определяемую сходной с (8) формулой, в которой вместо нормы берется

спектральный радиус ρ(·) соответствующих матриц [54, 55]:

(

)

(9)

ρ(A ) := lim

ρn(A )

= sup ρ_n(A )

n→∞

n≥1

где

{

}

ρn(A ) := sup ρ(Ain · · · Ai1)1/n : ij ∈ {1, . . . , N}

Как впервые заметили М. Бергер и Я. Ванг [56], величины ρ(A ) и ρ(A )

для ограниченных семейств матриц A на самом деле совпадают:

(10)

ρ(A ) = ρ(A ).

Эта фундаментальная формула имеет многочисленные приложения в тео-

рии обобщенного/совместного спектрального радиуса. В частности, из нее

вытекает непрерывная зависимость обобщенного/совместного спектрально-

го радиуса от семейства матриц A . Другим важным следствием форму-

лы Бергера—Ванга (10) является тот факт, что величины ρ_n(A ) и ρ_n(A )

для любых n образуют нижние и верхние оценки соответственно обобщенно-

го/совместного спектрального радиуса семейства матриц A :

(11)

ρn(A ) ≤ ρ(A ) = ρ(A ) ≤ ρn(A ),

³ Норма ∥ · ∥ в пространстве линейных операторов называется мультипликативной

(sub-multiplicative), если ∥AB∥ ≤ ∥A∥ ∥B∥ для любой пары операторов A и B.

что может служить основой для оценки точности вычисления обобщенно-

го/совместного спектрального радиуса.

Отличительной чертой определений (8) и (9) является то обстоятельство,

что в них берутся матричные произведения Ain · · · Ai1 , отвечающие всем воз-

можным последовательностям индексов (i₁, . . . , i_n). Более сложной является

ситуация, когда на матричные произведения Ain · · · Ai1 в (8) и (9) накладыва-

ются какие-либо дополнительные ограничения, например, в них запрещены

определенные комбинации матриц. Опишем более детально ситуацию подоб-

ного рода.

Пусть задана (N × N)-матрица Ω = (ω_ij ) с элементами из множе-

ства {0, 1}. Конечную последовательность (i₁, . . . , i_n) с элементами из мно-

жества {1, . . . , N} будем называть Ω-допустимой, если ωij+1i_j = 1 при всех

1 ≤ j ≤ n - 1 и, кроме того, найдется такое i_∗ ∈ {1,... ,N}, что ωi∗in = 1.

Множество всех конечных Ω-допустимых последовательностей (i₁, . . . , i_n)

обозначим через W_N,Ω. Произведения матриц Ain · · · Ai1 , отвечающие Ω-до-

пустимым последовательностям (i₁, . . . , i_n), будем называть марковскими, по-

скольку такого рода произведения естественно возникают в теории матрич-

ных коциклов над топологическими цепями Маркова, см., например, [57, 58].

Определим теперь аналоги формул (8) и (9) для Ω-допустимых матричных

произведений. Предел

(12)

ρ(A , Ω) := lim

ρ_n

(A , Ω),

n→∞

где

{

}

ρ_n(A ,Ω) := sup

∥Ain · · · Ai1 ∥1/n

: (i₁, . . . , i_n) ∈ W_N,Ω

назовем марковским совместным спектральным радиусом набора матриц A ,

определяемым матрицей допустимых переходов Ω. Если при некотором n

множество Ω-допустимых последовательностей (i₁, . . . , i_n) пустое, то будем

полагать ρ_n(A , Ω) = 0. В этом случае при каждом k ≥ n множества Ω-до-

пустимых последовательностей (i₁, . . . , i_k) также будут пустыми и, следова-

тельно, ρ(A , Ω) = 0. Вопрос о существовании сколь угодно длинных Ω-до-

пустимых последовательностей решается алгоритмически за конечное число

шагов. Достаточным условием непустоты этого множества является наличие,

по крайней мере, одного ненулевого элемента в каждом столбце матрицы Ω.

Предел (12) всегда существует, конечен, не зависит от выбора нормы ∥ · ∥.

При этом, как и для (8), в силу леммы Фекете [59] (см. также [60, гл. 3, § 1])

из субмультипликативности по n величины ρⁿⁿ(A , Ω) вытекает существование

предела lim_n→∞ ρ_n(A , Ω) и инфимума infn≥1 ρ_n(A , Ω), а также их равенство

пределу (12):

ρ(A , Ω) := lim

ρ_n(A ,Ω) = lim

ρ_n(A ,Ω) = inf

ρ_n(A ,Ω).

n→∞

n≥1

Марковским обобщенным спектральным радиусом набора матриц A ,

определяемым матрицей допустимых переходов Ω, назовем величину

(13)

ρ(A , Ω) := lim

ρn

(A , Ω),

n→∞

где

{

}

: (i₁, . . . , i_n) ∈ W_N,Ω

ρn(A , Ω) := sup ρ(Ain · · · Ai1)1/n

Здесь, как и в предыдущем случае, будем полагать ρ_n(A , Ω) = 0, если мно-

жество Ω-допустимых последовательностей индексов (i₁, . . . , i_n) пустое. При

этом, как и для (9), предел (13) совпадает с величиной supn≥1 ρ_n(A , Ω).

Для марковских произведений матриц справедливы аналогичные (11)

неравенства

(14)

ρn(A , Ω) ≤ ρ(A , Ω) ≤ ρ(A , Ω) ≤ ρn(A , Ω),

однако вопрос о справедливости равенства

(15)

ρ(A , Ω) = ρ(A , Ω),

аналогичного равенству Бергера—Ванга (10), становится более сложным.

Причина этого заключается в том, что известные доказательства [53, 56,

61-63] классической формулы Бергера—Ванга (10) существенно использова-

ли тот факт, что в возникающих матричных произведениях матрицы могут

перемножаться в произвольном порядке. Невозможность произвольного про-

изведения матриц при переходе к “марковскому” случаю потребовала прин-

ципиально иного подхода. Возникшие трудности были преодолены C. Даем

в [50] с использованием аппарата мультипликативной эргодической теории;

для формулировки соответствующего утверждения понадобятся вспомога-

тельные определения.

Назовем Ω-допустимую (конечную) последовательность (i₁, . . . , i_n) перио-

дически продолжимой, если ωi1in = 1. Вообще говоря, не каждая Ω-допусти-

мая конечная последовательность периодически продолжима, но если суще-

ствуют сколь угодно длинные Ω-допустимые последовательности, то найдут-

ся и сколь угодно длинные Ω-допустимые периодически продолжимые после-

довательности. Через W(per)N,Ω будем обозначать множество всех Ω-допустимых

периодически продолжимых последовательностей.

Определим величины

{

}

ρ(per)n(A , Ω) := sup ρ(Ain · · · Ai1 )1/n : (i₁, . . . , i_n) ∈ W^(per)

N,Ω

и положим⁴

ρ(per)(A , Ω) := lim

ρ(per)n(A , Ω).

n→∞

Теорема 2

[50, 51]. Справедливо равенство: ρ^(per)(A , Ω) = ρ(A , Ω).

Поскольку W(per)N,Ω ⊆ W_N,Ω, то ρnper)(A , Ω) ≤ ρ_n(A , Ω) при каждом n ≥ 1,

а значит, ρ^(per)(A , Ω) ≤ ρ(A , Ω). Отсюда и из (14) в силу теоремы Дая тогда

вытекает “марковский” аналог (15) формулы Бергера—Ванга (10).

⁴ Как и при определении марковских совместного и обобщенного спектральных ради-

усов, полагаем ρnper)(A , Ω) = 0, если множество периодически продолжимых последова-

тельностей индексов длины n пусто.

3.2. Системы с ограничениями на частоты срабатывания агентов

В различных теоретических и прикладных задачах возникают матричные

произведения

(16)

Aν0 Aν1 ··· Aνn

n ≥ 0,

где Ai — (d × d)-матрицы из некоторого конечного набора матриц A =

= {A₁, . . . , A_r} c элементами из поля K = R, C вещественных или комплекс-

ных чисел, а ν = (ν_n) ∈ I^N — некоторая последовательность символов из

множества I = {1, . . . , r}, см., например, [3, 35, 50, 64-66] и библиографию в

них.

Вопрос о скорости роста произведений матриц (16) относительно просто

(по крайней мере, теоретически) решается в “крайних” случаях, например,

когда последовательность ν = (ν_n) периодическая или когда в (16) рассмат-

риваются все возможные последовательности с символами из множества I =

= {1, . . . , r}. В последнем случае вопрос о скорости роста всех возможных

произведений матриц (16) дается в терминах так называемых совместного

или обобщенного спектральных радиусов набора матриц A [38, 54-56].

В “промежуточных” ситуациях, когда последовательности ν = (ν_n) в (16)

достаточно сложны, но в то же время не абсолютно произвольные, вопрос о

скорости роста матричных произведений (16) становится весьма нетривиаль-

ным, а ответ на него существенно зависит от структуры индексных после-

довательностей. В частности, одной из ключевых характеристик последова-

тельности индексов ν = (ν_n) в (16) является “частота” p_i появления индекса i

в рассматриваемой последовательности.

Обычно частота p_i появления индекса i в последовательности определяет-

ся как предел относительных частот p_i,n появления символа i среди первых

n членов последовательности. Следует, однако, иметь в виду, что данное по-

нятие частоты с точки зрения математического формализма является доста-

точно “тонким” и “не очень конструктивным”. Уже в ситуации, когда имеешь

дело лишь с единственной последовательностью ν = (ν_n), данное определе-

ние зачастую оказывается недостаточно информативным, поскольку не от-

вечает на вопрос о том, “насколько часто” отдельный символ появляется на

промежуточных, не стремящихся к бесконечности конечных отрезках задан-

ной последовательности. Еще менее удовлетворительным данное определение

оказывается в ситуациях, когда приходится иметь дело не с единственной

последовательностью объектов, а с бесконечным набором таких последова-

тельностей. Одним из основных недостатков здесь оказывается то, что дан-

ное выше определение частоты “не выдерживает” предельного перехода, что

приводит к существенным теоретическим и понятийным трудностям.

Чтобы придать определению частоты “хорошие” свойства (с точки зрения

возможности применения математических методов), зачастую приходится

либо требовать какого-либо рода “равномерной” сходимости относительных

частот p_i,n к p_i, либо рассматривать появление соответствующих символов

в последовательности как реализацию некоторых случайных событий, или

как траектории некоторых детерминированных систем, обладающих эргоди-

ческими свойствами, и т.п. Наиболее часто для анализа поведения матричных

произведений (16) в последнем случае привлекается так называемая мульти-

пликативная эргодическая теорема (в вероятностной или теоретико-эргодиче-

ской постановке), см., например, [67, 68]. При этом на законы формирования

индексных последовательностей ν = (ν_n) приходится накладывать достаточ-

но сильные ограничения, зачастую трудно проверяемые и подтверждаемые

в приложениях. В результате получающиеся совокупности объектов хотя и

могут оказаться достаточно привлекательными с чисто математической точ-

ки зрения, но их описание становится все менее и менее конструктивным,

что приводит зачастую к появлению достаточно существенного “понятийно-

го зазора” или своего рода “натяжек” при использовании соответствующих

объектов и конструкций в приложениях.

В настоящее время существует обширная литература, в которой изучают-

ся частотные свойства различных классов символических последовательно-

стей, см., например, [58, 69-73] и их библиографию. Менее исследован воп-

рос о конструктивном определении классов символических последователь-

ностей с заданными частотными свойствами и соответствующих матричных

произведений. Лишь недавно в [50, 51] сфера применимости методов теории

совместного и обобщенного спектрального радиуса была существенно расши-

рена на уравнения (16), в которых индексные последовательности ν = (ν_n)

описываются топологическими цепями Маркова. В связи с этим одной из

целей работы является описание класса r-символьных последовательностей,

для которых возможно конструктивное определение “приближенных” отно-

сительных частот символов по каждому блоку из ℓ последовательно стоящих

символов (ℓ-блоку). Такое описание будет дано в терминах ℓ-кратных тополо-

гических цепей Маркова, что позволяет применить развитый в [50, 51] подход

для определения совместного/обобщенного спектрального радиуса для мат-

ричных произведений, в которых сомножители появляются не в произволь-

ном порядке, а подчиняются некоторым ограничениям по частоте.

3.3. Последовательности с ограничениями для блочных

относительных частот символов

В дальнейшем инструментом анализа будут последовательности ν = (ν_n),

определенные при⁵ n ∈ N := {0, 1, . . .} и принимающие значения из алфавита

(множества символов) I = {1, . . . , r}, см. [73]. Совокупность всех таких по-

следовательностей будем обозначать через I^N, а через I_l обозначим множе-

ство всех конечных последовательностей ν = (ν_n) длины l. Обозначим также

через I^∗ = ∪l≥1I_l множество всех конечных последовательностей символов

из I . Для каждой последовательности ν ∈ I^∗ через |ν| будем обозначать

количество ее членов, а через |ν|_i — количество символов i в этой последова-

в этом случае называется относительной частотой

или пропорцией вхождения символа i в последовательность ν.

Пусть имеется некоторый набор неотрицательных чисел p = (p_i, . . . , p_r),

∑_r

сумма которых равна 1, т.е.

p_i = 1, а также наборы нижних и верхних

i=1

⁵ В символической динамике, см., например, [58, 73, 74], часто рассматривают также

последовательности, определенные при всех целых значениях i, т.е. при i ∈ Z. В настоящем

разделе такого рода последовательности не понадобятся.

границ для p:

(17)

p^- = (p-1,... ,p^-r), p⁺ = (p⁺¹,... ,p+r

удовлетворяющих соотношениям

(18)

0≤p^-i <p_i <p+i

≤ 1, i = 1, . . . , r.

Зададимся некоторым натуральным числом ℓ и обозначим через I_ℓ(p^±)

множество всех конечных последовательностей ν ∈ I_ℓ, для которых относи-

тельные частоты вхождения символов удовлетворяют соотношениям

|ν|_i

(19)

p^-i ≤

≤p+i

i = 1,...,r.

|ν|

Переписав эти соотношения в виде p^-i|ν| ≤ |ν|_i ≤ p+i|ν|, где i = 1, . . . , r, мож-

но интерпретировать их как наличие неких ограничений на количество вхож-

дений различных символов в последовательности ν ∈ I_ℓ, т.е. в последова-

тельности ν длины ℓ.

Наконец, через INℓ(p^±) будем обозначать множество всех последователь-

ностей из I^N, каждая конечная подпоследовательность ν длины ℓ которых

удовлетворяет ограничениям (19) на количество вхождений различных сим-

волов.

Пример 2. Пусть r = 3, ℓ = 10 и p = (0,23, 0,33, 0,44). Определим набо-

ры (17) нижних и верхних границ для p, полагая p^-i = p_i - 0,1 и p+i = p_i + 0,1

при i = 1, 2, 3, т.е.

p^- = (0,13, 0,23, 0,34), p⁺ = (0,33, 0,43, 0,54).

Тогда множеству INℓ(p^±) принадлежат следующие последовательности:

ν₁ = (2, 1, 2, 3, 3, 3, 2, 3, 3, 1, 2, 1, 2, 3, 1, 3, 2, 3, 3, 3,2, 1, 2, 2, 1,3, 3, 1, 3, 3, 2, 2, 1, 2, . . .),

ν₂ = (3, 2, 2, 1, 3, 3, 3, 3, 2, 1, 2, 1, 2, 3, 3, 2, 3, 3, 2, 1,2, 1, 3, 1, 3,2, 3, 3, 2, 2, 1, 3, 2, 1, . . .),

ν₃ = (1, 1, 3, 3, 2, 2, 1, 2, 3, 3, 1, 3, 1, 3, 2, 2, 3, 2, 2, 3,1, 3, 1, 3, 2,1, 3, 2, 2, 3, 1, 3, 1, 3, . . .).

Замечание 1. Множество I_ℓ(p^±) может оказаться пустым даже в

том случае, когда выполнены неравенства (18). Но если I_ℓ(p^±) = ∅, то и

INℓ(p^±) = ∅. Чтобы убедиться в этом, достаточно взять произвольную после-

довательность ν = (ν₀, ν₁, . . . , νℓ-1) ∈ I_ℓ(p^±) и заметить, что ее продолжение

по периодичности вправо (с периодом ℓ) принадлежит INℓ(p^±).

Замечание 2. В общем случае частоты появления символов i = 1,...,r

в последовательностях из INℓ(p^±) не определены. Более точно это означа-

ет следующее. Обозначим через ν_n = (ν₀, ν₁, . . . , ν_n) начальный отрезок из

n символов для произвольной последовательности ν = (ν₀, ν₁, . . .) ∈ INℓ (p^±).

является относительной часто-

той появления символа i среди первых n членов последовательности ν. От-

оказываются “близкими” к соответствующим ве-

личинам p_i, однако в общем случае они могут не иметь пределов при n → ∞.

Следующая лемма дает ответ на вопрос о непустоте множества I_ℓ(p^±).

Напомним, что для вещественного числа x через ⌊x⌋ обозначается наиболь-

шее целое число, не превосходящее x, а через ⌈x⌉ — наименьшее целое, не

меньшее чем x.

Лемма 1. I_ℓ(p^±) = ∅ тогда и только тогда, когда ⌈p-i ℓ⌉ ≤ ⌊p+i ℓ⌋, i =

∑_r

= 1, . . . , r и, кроме того,

⌈p^-iℓ⌉ ≤ ℓ ≤

⌊p+iℓ⌋.

i=1

Пример 3. Пусть r = 3, ℓ = 10, а наборы (17) нижних и верхних гра-

ниц для p такие же, как в примере 3. Тогда ⌈p-1ℓ⌉ = 2, ⌈p-2ℓ⌉ = 3, ⌈p-3ℓ⌉ = 4,

∑_r

⌊p⁺¹ℓ⌋ = 3,

⌊p⁺²ℓ⌋ = 4,

⌊p⁺³ℓ⌋ = 5 и при этом

⌈p^-iℓ⌉ = 9 ≤ ℓ ≤ 12 =

∑_r

i=1

⌊p+iℓ⌋. Таким образом, оба условия леммы 1 выполнены.

i=1

Пусть снова p = (0,23, 0,33, 0,44), но наборы (17) нижних и верхних гра-

ниц для p теперь определены равенствами p^-i = p_i - 0,01 и p+i = p_i + 0,01 при

i = 1,2,3, т.е.

p^- = (0,22, 0,32, 0,43), p⁺ = (0,24, 0,34, 0,45).

В этом случае ⌈p-1 ℓ⌉ = 3, ⌈p-2 ℓ⌉ = 4, ⌈p-3 ℓ⌉ = 5, ⌊p+1 ℓ⌋ = 2, ⌊p+2 ℓ⌋ = 3, ⌊p+3 ℓ⌋ = 4

и первое условие леммы 1 не выполняется ни при одном i = 1, 2, 3.

Наконец, пусть снова p = (0,23, 0,33, 0,44), но наборы (17) нижних и

верхних границ для p на этот раз определены равенствами p^-i = p_i - 0,05

и p+i = p_i + 0,05 при i = 1,2,3, т.е.

p^- = (0,18, 0,28, 0,39), p⁺ = (0,28, 0,38, 0,49).

В этом случае ⌈p-1ℓ⌉ = 2, ⌈p-2ℓ⌉ = 3, ⌈p-3ℓ⌉ = 4, ⌊p⁺¹ℓ⌋ = 2, ⌊p⁺²ℓ⌋ = 3, ⌊p⁺³ℓ⌋ =

= 4 и первое условие леммы 1 выполняется при каждом i = 1,2,3, но второе

∑_r

условие леммы 1 не выполнено, поскольку

⌊p+iℓ⌋ = 9 < ℓ.

i=1

Из леммы 1 и примера 3 видно, что для непустоты множества I_ℓ(p^±) необ-

ходимо, чтобы “зазор” между соответствующими величинами p^-i и p+i был не

слишком мал. Это означает, что апериодическое поведение последователь-

ностей из INℓ(p^±) может наблюдаться только в том случае, когда “зазор”

между соответствующими величинами p^-i и p+i окажется настолько “велик”,

чтобы выполнялось первое условие леммы 1, а во втором условии леммы 1

оба неравенства оказались строгими.

Замечание 3. Обнаружить в литературе явное упоминание о символи-

ческих последовательностях с разрешенными ℓ-блоками типа I_ℓ(p^±) не уда-

лось. Тем не менее близкие символические последовательности возникают

во многих прикладных и теоретических исследованиях. Cимволические по-

следовательности с разрешенными ℓ-блоками типа I_ℓ(p^±) могут рассмат-

риваться как “последовательности с ограничениями”, возникающие в теории

бесшумных каналов передачи данных с ограничениями (constrained noiseless

channels) [69, гл. 17]. Вопрос о частотных свойствах таких последовательно-

стей с определенными разрешенными или запрещенными комбинациями сим-

волов изучался, например, в [70, 71, 75], причем в [70, 71] для этих целей была

привлечена теория совместного спектрального радиуса. Идейно близкими яв-

ляются также последовательности с (d, k)-ограничениями ((d, k)-constrained

sequences), возникающие в методе RLL-кодирования (RLL coding, runlength-

limited coding), используемом при кодировании информации на жестких дис-

ках, CD и DVD дисках и пр., см., например, [58, 72].

Символические последовательности с разрешенными ℓ-блоками ти-

па I_ℓ(p^±) сходны с так называемыми k-сбалансированными последователь-

ностями (k-balanced sequences) [58, 73], хотя и образуют более широкий класс.

Символические последовательности с разрешенными ℓ-блоками типа I_ℓ(p^±)

могут не иметь предельных частот отдельных символов, что отличает их от

символических последовательностей, относительные частоты символов в ко-

торых равномерно сходятся [76].

3.4. Кратные топологические цепи Маркова

Покажем, что множество бесконечных последовательностей INℓ(p^±) мо-

жет естественным образом трактоваться как так называемая ℓ-кратная то-

пологическая цепь Маркова (или сдвиг конечного типа). Напомним необхо-

димые определения, следуя [57, 73].

Как обычно, оператор σ : ν → ν^′, переводящий последовательность

ν = (ν_n)n∈N ∈ I ^N в последовательность ν^′ = (ν^′n)n∈N ∈ I ^N, определяемую

равенствами ν^′n = νn+1 при n ∈ N, будет называться левым сдвигом или про-

сто сдвигом на I^N. Пусть задана квадратная матрица ω = (ω_ij)ri,j=1 порядка

r с элементами из множества {0,1}. Положим

{

}

INω := ν = (ν_n) ∈ I^N : ωνnνn+1 = 1, n ∈ N

Другими словами, матрица ω определяет все допустимые переходы между

символами алфавита I = {1, . . . , r} в последовательностях из INω. В этом

случае ограничение отображения сдвига σ на INω называют топологической

цепью Маркова, определяемой матрицей допустимых переходов ω [57, 73].

Отображение σ называют также сдвигом конечного типа⁶.

Имеется естественный класс более общих символических систем, чем цепи

Маркова. Пусть задано отображение

Ω : Iℓ+1 → {0,1}

{

}

INΩ := ν = (ν_n) ∈ I^N : Ω(ν_n,... ,νn+ℓ) = 1, n ∈ N

Тогда ограничение отображения сдвига σ на INΩ называют ℓ-кратной тополо-

гической цепью Маркова, определяемой функцией допустимых переходов Ω.

С точки зрения динамики ℓ-кратные топологические цепи Маркова — это

то же самое, что и (обычные) топологические цепи Маркова, так как они

⁶ Иногда термины “топологическая цепь Маркова” или “сдвиг конечного типа” приме-

няют к самому множеству последовательностей INΩ.

могут быть описаны как топологические цепи Маркова с алфавитом I =

= {1, . . . , r}^ℓ и такой матрицей ω, что

ω(ν1,...,ν_ℓ),(ν′1,...,ν^′ℓ) = 1,

если ν^′k = νk+1 при k = 1, . . . , ℓ - 1 и Ω(ν₁, . . . , ν_ℓ, ν^′ℓ) = 1, см., например, [57,

раздел 1.9].

Теорема 3. Пусть для некоторых наборов чисел

p^- = (p-1,... ,p^-r), p⁺ = (p⁺¹,... ,p+r),

удовлетворяющих соотношениям (18), выполняются условия леммы 1. То-

гда сужение сдвига σ на множество INℓ(p^±) является ℓ-кратной тополо-

гической цепью Маркова.

Несмотря на очевидность, теорема 3 имеет принципиальное значение, по-

скольку позволяет трактовать символические последовательности с ограни-

чениями для блочных относительных частот символов как (кратные) цепи

Маркова.

3.5. Ограниченный совместный/обобщенный спектральный радиус

Пусть, как и в предыдущем разделе, A = {A₁, . . . , A_r} — некоторый ко-

нечный набор матриц c элементами из поля K = R, C вещественных или ком-

плексных чисел. Зададимся некоторым целым числом ℓ и наборами чисел

p_i, p^±i, i = 1,... ,r, удовлетворяющими ограничениям (18). Конечную после-

довательность ν = (ν₁, . . . , ν_n) с элементами из множества I будем назы-

вать I_ℓ(p^±)-допустимой, если ν ∈ I^∗ℓ(p^±), т.е. каждая ее подпоследователь-

ность (ν_j , . . . , νj+ℓ-1) длины ℓ принадлежит I_ℓ(p^±), а каждая из подпосле-

довательностей длины, меньшей ℓ, допускает дополнение справа до после-

довательностей из I_ℓ(p^±). Множество всех конечных I_ℓ(p^±)-допустимых

последовательностей ν = (ν₁, . . . , ν_n) обозначим через WIℓ(p±). Произведе-

ния матриц Aνn · · · Aν1 , отвечающие I_ℓ(p^±)-допустимым последовательно-

стям (ν₁, . . . , ν_n), будем называть I_ℓ(p^±)-допустимыми.

Теперь можно определить понятия совместного и обобщенного спектраль-

ных радиусов для I_ℓ(p^±)-допустимых произведений матриц из A , почти до-

словно повторяя соответствующие определения из предыдущего раздела.

Предел

(

)

(

)

(20)

A ,I_ℓ(p^±)

:= lim

ρ_n

A ,I_ℓ(p^±)

n→∞

где

{

}

ρ_n(A ,I_ℓ(p^±)) := sup

∥Aνn · · · Aν1 ∥1/n

: (ν₁, . . . , ν_n) ∈ WIℓ(p±)

назовем I_ℓ(p^±)-ограниченным совместным спектральным радиусом.

Предел (20) всегда существует, конечен и не зависит от нормы ∥ · ∥. При

этом множества I^∗ℓ(p^±) обладают свойством субаддитивности, а тогда вели-

чина ρⁿⁿ(A , I_ℓ(p^±)) субмультипликативна по n. Поэтому по лемме Фекете [59]

(см. также [60, гл. 3, § 1]) существует предел lim_n→∞ ρ_n(A , I_ℓ(p^±)), совпа-

дающий как с ρ(A , I_ℓ(p^±)), так и с инфимумом infn≥1 ρ_n(A , I_ℓ(p^±)), т.е.

I_ℓ(p^±)-ограниченный совместный спектральный радиус можно определить

любым из следующих равенств:

(

)

(

)

A ,I_ℓ(p^±)

:= lim

ρ_n

A ,I_ℓ(p^±)

n→∞

(

)

(

)

= lim

ρ_n

A ,I_ℓ(p^±)

= inf

ρ_n

A ,I_ℓ(p^±)

n→∞

n≥1

Аналогично естественно назвать I_ℓ(p^±)-ограниченным обобщенным спек-

тральным радиусом набора матриц A величину

(

)

(

)

A ,I_ℓ(p^±)

:= lim

ρn

A ,I_ℓ(p^±)

n→∞

где

{

}

(

)

ρn

A ,I_ℓ(p^±)

:= sup ρ(Aνn · · · Aν1 )1/n

: (ν₁, . . . , ν_n) ∈ WIℓ(p±)

Для I_ℓ(p^±)-допустимых произведений матриц выполняются неравенства

(

)

(

)

(

)

(

)

(21)

ρn

A ,I_ℓ(p^±)

≤ ρ

A ,I_ℓ(p^±)

≤ρ

A ,I_ℓ(p^±)

≤ρ_n

A ,I_ℓ(p^±)

аналогичные (11) или (14). В то же время вопрос о справедливости равенства

(

)

(22)

A ,I_ℓ(p^±)

= ρ(A , I_ℓ(p^±

)),

аналогичного равенству Бергера—Ванга (10), как и в случае марковских ана-

логов совместного и обобщенного спектральных радиусов, менее очевиден.

Назовем I_ℓ(p^±)-допустимую конечную последовательность (ν₀, . . . , νn-1) пе-

риодически продолжимой, если она может быть продолжена вправо до n-пе-

риодической последовательности из INℓ(p^±). Множество всех I_ℓ(p^±)-допус-

тимых периодически продолжимых последовательностей обозначим через

W^(per)

. Очевидно, это множество непусто, если непусто множество I_ℓ(p^±),

I_ℓ(p^±)

поскольку каждая последовательность из I_ℓ(p^±) допускает ℓ-периодическое

продолжение вправо.

Определим величины

{

}

(

)

ρ(per)n

A ,I_ℓ(p^±)

:= sup ρ(Aνn · · · Aν1 )1/n : (ν₁, . . . , ν_n) ∈ W^(per)

I_ℓ(p^±)

и положим

(

)

(

)

ρ(per)

A ,I_ℓ(p^±)

:= lim

ρ(per)n

A ,I_ℓ(p^±)

n→∞

В этом случае справедливо следующее обобщение формулы Бергера—Ван-

га на случай матричных произведений с ограничениями для блочных относи-

тельных частот сомножителей или, что то же, на случай I_ℓ(p^±)-допустимых

матричных произведений.

Теорема 4. Справедливо равенство: ρ^(per)(A ,I_ℓ(p^±)) = ρ(A ,I_ℓ(p^±)).

Поскольку W^(per)

⊆ WIℓ(p±), то ρnper)(A ,Iℓ(p^±)) ≤ ρn(A ,Iℓ(p^±)) при

I_ℓ(p^±)

каждом n ≥ 1, а значит, ρ^(per)(A , I_ℓ(p^±)) ≤ ρ(A , I_ℓ(p^±)). Отсюда и из (21)

в силу теоремы 4 тогда вытекает аналог (22) формулы Бергера—Ванга (10)

для матричных произведений с ограничениями на блочные относительные

частоты сомножителей.

Замечание 4. В настоящем разделе допустимые последовательности

были определены следующим образом: было задано множество P = I_ℓ(p^±)

последовательностей длины ℓ и допустимыми считались все конечные по-

следовательности длины, меньшей ℓ, допускающие дополнение справа до по-

следовательностей из P, а также последовательности длины, большей или

равной ℓ, каждая конечная подпоследовательность которых длины ℓ принад-

лежит P.

В данном определении конкретный вид множества P не принципиален.

Поэтому все конструкции данного раздела сохранят силу для произвольного

выбора множеств P и соответствующим образом определенных допустимых

последовательностей, ср. [75]. При этом, конечно, вопрос о непустоте множе-

ства допустимых последовательностей должен решаться отдельно.

4. Минимаксный совместный спектральный радиус и

стабилизируемость мультиагентных линейных систем

Изложение настоящего раздела основано на работе [77].

Разнообразные прикладные и теоретические задачи вычислительной ма-

тематики, теории управления, теории кодирования, комбинаторики и др.

приводят к необходимости знать скорость роста/убывания произведений

(N × N)-матриц A_n · · · A₁ с сомножителями из некоторого множества мат-

риц A , см., например, [11, 39], а также библиографию [3]. Для оценки скоро-

сти роста соответствующих матричных произведений принято использовать

такие числовые характеристики множества матриц A , как совместный спек-

тральный радиус [38]

{

}

(23)

ρ(A ) = lim sup

∥A_n · · · A₁∥ⁿ : A_i ∈ A

n→∞

и нижний спектральный радиус [33]

{

}

(24)

ρ(A ) = lim

inf

∥A_n · · · A₁∥ⁿ : A_i ∈ A

n→∞

называемый также совместным спектральным подрадиусом. Пределы в (23)

и (24) всегда существуют и не зависят от нормы ∥ · ∥ на пространстве мат-

риц размерности N × N; соответствующие доказательства с историческими

комментариями можно найти, например, в [11, 39].

Понятия совместного и нижнего спектральных радиусов возникли во вто-

рой половине XX в., и к настоящему моменту их исследованию посвящено

несколько сотен публикаций, см. например, [3, 11]. Одной из областей, в ко-

торых применение совместного и нижнего спектрального радиусов оказы-

вается наиболее естественным и продуктивным, является теория линейных

переключающихся систем с дискретным временем. В частности, неравенство

ρ(A ) < 1 оказывается критерием устойчивости линейной переключающейся

системы с дискретным временем [53, 78], а неравенство ρ(A ) < 1 — критерием

стабилизируемости.

Несмотря на то, что совместный и нижний спектральные радиусы опре-

деляются “почти одинаковыми” равенствами (23) и (24), их свойства суще-

ственно различаются. Достаточно упомянуть лишь тот факт, что совместный

спектральный радиус ρ(A ) в естественном смысле непрерывно зависит от

множества A , в то время как нижний спектральный радиус ρ(A ) в общем

случае не является непрерывной функцией множества A , строгие формули-

ровки см., например, в [41, 79]. Более того, ряд свойств совместного и нижнего

спектральных радиусов, которые в окончательной формулировке выглядят

одинаково, доказываются с помощью совершенно разных подходов.

Сказанное вызывает естественное, на взгляд авторов, желание ввести

некую характеристику матричных произведений, которая объединяла бы

понятия как совместного, так и нижнего спектральных радиусов. Для ре-

ализации этой идеи в разделе рассматриваются матричные произведения

A_nB_n ··· A₁B₁ с сомножителями A_i ∈ A , B_i ∈ B размерностей N × M и

M × N соответственно из двух различных множеств матриц A и B, для

которых определяются числовые величины

μ(A , B) = lim

max

min

∥A_nB_n · · · A₁B₁∥ⁿ ,

n→∞

A_i∈A

B_i∈B

η(A , B) = lim

min

max

∥A_nB_n · · · A₁B₁∥ⁿ ,

n→∞

B_i∈B

A_i∈A

называемые далее нижним и верхним минимаксными совместными спек-

тральными радиусами пары {A , B}. Обе величины μ(A , B) и η(A , B) харак-

теризуют максимальную скорость роста матричных произведений A_nB_n · · ·

···A₁B₁ по всем наборам матриц A_i ∈ A и минимальную скорость роста по

всем наборам матриц B_i ∈ B.

4.1. Устойчивость/стабилизируемость неуправляемых линейных систем

Напомним теоретико-управленческую мотивацию привлечения понятий

совместного и нижнего спектральных радиусов для анализа проблемы устой-

чивости и стабилизируемости линейных (неуправляемых) переключающихся

систем.

Рассмотрим изображенную на рис. 2 переключающуюся динамическую си-

стему A с дискретным временем, состоящую из объекта A , выход которого,

аддитивно возмущенный внешним воздействием f, замыкается на вход с по-

мощью задержки в обратной связи.

Будем считать, что при каждом значении времени n = 1, 2, . . . выход x_out

и вход x_in объекта A связаны линейным уравнением

(25)

x_out = A_nx_in,

x_in,x_out ∈ R^N,

f(n)

x(n

x(n)

z¹

Рис. 2. Линейная переключающаяся система с дискретным временем.

где A_n является матрицей размерности N × N, принимающей значения из

некоторого конечного множества матриц A .

Последовательность матриц {A_n} в зависимости от контекста может ли-

бо определяться внешними возмущениями, либо формироваться специаль-

ным образом с целью придания всей системе некоторых свойств. Вектор-

функция f(n) представляет аддитивные внешние воздействия на вектор со-

стояния системы x. Блок z-1 является элементом запаздывания на единицу

времени (на один такт). В этом случае динамика рассматриваемой системы

описывается неоднородным уравнением

x(n) = A_nx(n - 1) + f(n),

n = 1,2...,

в котором переменные x(n) и f(n) предполагаются вектор-столбцами размер-

ности N.

В том случае, когда аддитивные внешние воздействия f отсутствуют, т.е.

f (n) ≡ 0, динамика системы описывается однородным уравнением

(26)

x(n) = A_n

x(n - 1),

n = 1,2,...

Определение 1. Систему A с нулевым входом f, описываемую уравне-

нием (26), называют асимптотически устойчивой в классе всех матриц A ,

если

(27)

x(n) = A_n · · · A₁

x(0) → 0

при n → ∞

для любой последовательности матриц {A_n ∈ A } и любого начального усло-

вия x(0).

Как известно [32, 33, 50, 54, 56, 68, 80], сходимость к нулю каждого реше-

ния уравнения (26) в классе матриц A влечет более сильное свойство экспо-

ненциальной сходимости к нулю каждой последовательности {X_n} матрич-

ных произведений X_n = A_n · · · A₁, т.е. существование таких констант C > 0

и λ ∈ (0,1) (не зависящих от матричных сомножителей A₁,...,A_n), что

∥A_n · · · A₁∥ ≤ Cλⁿ, где ∥ · ∥ — некоторая норма на пространстве (N × N)-мат-

риц. Последнее свойство, в свою очередь, влечет выполнение неравенства

ρ(A ) < 1, где ρ(A ) — совместный спектральный радиус множества мат-

риц A , определяемый равенством (23). С другой стороны, выполнение нера-

венства ρ(A ) < 1 очевидным образом влечет сходимость к нулю каждой по-

следовательности матриц X_n = A_n · · · A₁ с сомножителями из A . Отсюда вы-

текает следующее утверждение.

Предложение 1. Система A с нулевым входом f, описываемая уравне-

нием (26), асимптотически устойчива в классе матриц A тогда и только

тогда, когда ρ(A ) < 1.

Определение 2. Систему A с нулевым входом f называют поточечно

стабилизируемой в классе всех матриц A , если для каждого начального

условия x(0) найдется такая последовательность матриц {A_n ∈ A }, для

которой имеет место сходимость (27).

Определение 3. Систему A с нулевым входом f назовем равномерно

стабилизируемой или просто стабилизируемой в классе всех матриц A ,

если найдется такая последовательность матриц {A_n ∈ A }, что сходи-

мость (27) имеет место для каждого начального условия x(0).

Очевидно, равномерная стабилизируемость системы A с нулевым вхо-

дом f равносильна условию существования такой последовательности матриц

{A_n ∈ A }, для которой матричные произведения A_n · · · A₁ сходятся к нулю

по норме:

∥A_n · · · A₁∥ → 0 при n → ∞.

В литературе для обозначения понятий, эквивалентных поточечной или

равномерной стабилизируемости, применяется различная терминология. На-

пример, в ряде работ вместо термина стабилизируемость используется бо-

лее широкий термин управляемость, восходящий к Р. Калману, см., напри-

мер, [36, 81, 82]. В [83] для понятий поточечной или равномерной стабили-

зируемости применяются термины поточечная или равномерная сходимости

матричных произведений с матрицами из A . Равномерная сходимость мат-

риц влечет их поточечную сходимость, в то время как обратное утверждение

неверно.

Пример 4

[83, 84]. Произведения матриц из множества

{[

]

]}

[ √3

A =

√

-¹

сходятся поточечно, но не являются сходящимися равномерно.

Для характеризации стабилизируемости удобно использовать нижний

спектральный радиус ρ(A ), определяемый равенством (24). В частности, име-

ет место следующее утверждение.

Предложение 2. Система A с нулевым входом f, описываемая урав-

нением (26), равномерно стабилизируема тогда и только тогда, когда

ρ(A )<1.

Достаточность условия ρ(A ) < 1 для стабилизируемости следует непо-

средственно из формулы (24). А как показано в [81, предложение 1; 82, тео-

рема 3.9; 83], стабилизируемость системы A, описываемой уравнением (26),

влечет неравенство ρ(A ) < 1.

Таким образом, предложения 1 и 2 показывают, что совместный и ниж-

ний спектральный радиусы являются удобным аналитическим средством при

анализе устойчивости и стабилизируемости (неуправляемых) линейных пе-

реключающихся систем. К сожалению, вычисление как совместного, так и

нижнего спектрального радиуса является сложной задачей, и лишь в исклю-

чительных случаях удается описать классы матриц, для которых эти харак-

теристики могут быть вычислены в явном “формульном” виде, см., например,

библиографию в [3, 11, 85, 86].

4.2. Стабилизируемость управляемых линейных систем

Обратимся к более реалистичной системе управления AB с дискретным

временем, которая включает в себя не только объект управления A , но и

контроллер B, см. рис. 3.

Относительно объекта A будут делаться те же предположения, что и в

предыдущем разделе, а именно, будем считать что при каждом n = 1, 2, . . .

выход x_out объекта A связан с его входом x_in линейным уравнением

x_out = A_nx_in,

x_in ∈ R^M , x_out ∈ R^N,

где A_n является матрицей размерности N × M, принимающей значения из

некоторого конечного множества матриц A . Отличие от предположений (25),

накладывавшихся на объект A в разделе 4.1, заключается в том, что в дан-

ном случае размерности входов и выходов объекта A не обязаны совпадать.

Контроллер B также будет предполагаться функционирующим при каж-

дом n = 1, 2, . . . в соответствии с линейным уравнением

u_out = B_nu_in,

u_out ∈ R^M, u_in ∈ R^N,

в котором матрица B_n размерности M × N может выбираться из некоторого

конечного множества матриц B. Множество B можно трактовать как мно-

жество всех доступных управлений.

В данном контексте последовательность матриц

{A_n} определяется

(неконтролируемыми) внешними возмущениями объекта управления, а по-

следовательность матриц {B_n} представляет управляющие воздействия кон-

троллера, с помощью которых можно пытаться придать те или иные свой-

ства рассматриваемой системе. Вектор-функция f(n) представляет аддитив-

ные входные воздействия на вектор состояния системы. Блок z-1, как и в

разделе 4.1, является элементом запаздывания на единицу времени (на один

f(n)

x(n

u(n

x(n)

z¹

Рис. 3. Cистема управления, состоящая из объекта A и контроллера B.

такт). В этом случае динамика рассматриваемой системы описывается урав-

нением

x(n) = A_nB_nx(n - 1) + f(n),

n = 1,2...,

где x(n) и f(n) являются вектор-столбцами размерности N.

Снова, чтобы не отвлекаться на несущественные детали, будем интере-

соваться только вопросами устойчивости и стабилизируемости нулевого ре-

шения системы, изображенной на рис. 3, в случае нулевого внешнего воздей-

ствия f, т.е. когда f(n)≡0. Динамика такой системы описывается уравнением

(28)

x(n) = A_nB_n

x(n - 1),

n = 1,2...

Для системы управления AB с нулевым входом f, описываемой уравне-

нием (28), могут быть поставлены вопросы об (асимптотической) устойчиво-

сти и стабилизируемости, аналогичные тем, которые были поставлены для

системы A.

Определение 4. Систему AB с нулевым входом f назовем асимпто-

тически устойчивой в классе всех возмущений A объекта A и управле-

ний B контроллера B, если

(29)

x(n) = A_nB_n · · · A₁B₁

x(0) → 0

при n → ∞

для любых последовательностей матриц {A_n ∈ A }, {B_n ∈ B} и любого на-

чального условия x(0).

Отметим, впрочем, что рассмотрение абсолютной устойчивости для си-

стемы AB не привносит ничего нового по сравнению с рассмотрением си-

стемы A. Очевидно, система AB с нулевым входом f, описываемая урав-

нением (28), асимптотически устойчива в классе всех возмущений A и

управлений B тогда и только тогда, когда система A с нулевым входом f

асимптотически устойчива в классе матриц

A B := {AB : A ∈ A , B ∈ B}.

Из этого замечания и предложения 1 вытекает следующая

Теорема 5. Система AB, описываемая уравнением (28), асимптоти-

чески устойчива в классе всех возмущений A и управлений B тогда и толь-

ко тогда, когда ρ(A B) < 1.

Менее очевиден вопрос о стабилизируемости системы AB. Ограничимся

рассмотрением двух вариантов стабилизируемости.

Определение 5. Скажем, что система AB, описываемая уравнени-

ем (28), потраекторно стабилизируема в классе всех возмущений A объек-

та A с помощью управлений B контроллера B, если для любой последова-

тельности матриц {A_n ∈ A } (возмущений объекта A ) найдется последо-

вательность матриц {B_n ∈ B} (управлений контроллера B), для которых

при каждом начальном условии x(0) имеет место сходимость (29).

Определение 6. Скажем, что система AB, описываемая уравнени-

ем (28), универсально периодически стабилизируема, если найдется та-

кая (универсальная) периодическая последовательность матриц {B_n ∈ B}

(управлений контроллера B), что для каждой последовательности матриц

{A_n ∈ A } (возмущений объекта A ) и при каждом начальном условии x(0)

имеет место сходимость (29).

Отметим, что по сути вопрос о стабилизируемости системы AB близок

к теоретико-игровым постановкам [87, 88], в которых имеются два игрока —

внешние воздействия и управляющий контроллер, которые поочередно воз-

действуют на систему, причем первый из них стремится сделать систему как

можно более неустойчивой, а второй пытается ее стабилизировать.

Ясно, что универсально периодически стабилизируемые системы являют-

ся потраекторно стабилизируемыми. Кроме того, в обоих определениях ста-

билизируемости системы AB условие, что сходимость (29) имеет место при

каждом начальном условии x(0), равносильно условию

∥A_nB_n · · · A₁B₁∥ → 0 при n → ∞.

Замечание 5. Можно было бы ввести поточечные аналоги понятий по-

траекторной и универсальной стабилизируемости, ср., например, [81], но это

не является целью настоящего раздела.

4.3. Минимаксные совместные спектральные радиусы

По аналогии с нижним спектральным радиусом, характеризующим рав-

номерную стабилизируемость неуправляемой системы A, описываемой урав-

нением (26), естественно возникает желание ввести некие числовые величи-

ны для характеризации универсальной и потраекторной стабилизируемости

управляемой системы AB, описываемой уравнением (28). В качестве канди-

датов на такие численные величины предложим соответственно величины

(30)

μ(A , B) = lim

μ_n(A ,B)ⁿ ,

η(A , B) = lim

η_n(A ,B)ⁿ ,

n→∞

где при каждом n = 1, 2, . . .

μ_n(A ,B) = max

min

∥A_nB_n · · · A₁B₁∥,

A_i∈A

B_i∈B

(31)

η_n(A ,B) = min

max

∥A_nB_n · · · A₁B₁∥

B_i∈B

A_i∈A

(здесь ∥ · ∥ — некоторая норма на пространстве матриц размерности N × N).

Так как максимин любой функции не превосходит ее минимакс, то μ(A , B) ≤

≤ η(A ,B), что оправдывает следующее определение.

Определение 7. Пусть {A ,B} — пара множеств матриц размерно-

сти N × M и M × N соответственно. Величину μ(A ,B) будем называть

нижним, а величину η(A ,B) — верхним минимаксным совместным спек-

тральным радиусом пары {A , B}.

Существование пределов в (30) вытекает из следующей леммы 2. Напом-

ним, что в линейной алгебре норма ∥ · ∥ в пространстве матриц размерности

N × N называется субмультипликативной, если ∥XY ∥ ≤ ∥X∥∥Y ∥ для лю-

бых матриц X и Y . В частности, матричная норма ∥·∥ субмультипликативна,

если она порождается некоторой векторной нормой, т.е. ее значение ∥A∥ на

∥Ax∥

матрице A определяется равенством ∥A∥ = supx=0

, где ∥x∥ и ∥Ax∥ —

∥x∥

нормы соответствующих векторов в R^N .

Лемма 2. Для любых конечных множеств матриц A и B пределы

в (30) существуют и не зависят от нормы ∥ · ∥. Более того, если норма ∥ · ∥

в (31) субмультипликативна, то

μ(A , B) = inf

μ_n(A ,B)ⁿ ,

η(A , B) = inf

η_n(A ,B)ⁿ .

n≥0

Естественно ожидать, что в общем случае μ(A , B) = η(A , B), что и под-

тверждается следующим примером.

Пример 5. Рассмотрим множества A = {A₁,A₂} и B = {B₁,B₂}, где

[

]

[

]

[

]

[

]

A₁ =

A₂ =

B₁ =

B₂ =

тогда μ(A , B) = 1 и η(A , B) > 1.

Следующие две теоремы являются основными в настоящем разделе. Они

подтверждают, что минимаксные совместные спектральные радиусы действи-

тельно могут выступать в качестве характеристик стабилизируемости систе-

мы AB.

Теорема 6. Система AB, описываемая уравнением (28), потраектор-

но стабилизируема в классе всех возмущений A и управлений B тогда и

только тогда, когда μ(A , B) < 1.

Теорема 7. Система AB, описываемая уравнением (28), универсально

периодически стабилизируема в классе всех возмущений A и управлений B

тогда и только тогда, когда η(A , B) < 1.

4.4. Другие минимаксные характеристики матричных произведений

Согласно [56] в определении (23) совместного спектрального радиуса ρ(A )

норма матрицы ∥ · ∥ может быть заменена на ее спектральный радиус ρ(·) (с

одновременной заменой предела на верхний предел):

{

}

(32)

ρ(A ) = lim

sup ρ(A_n ··· A₁)n : Ai ∈A

;

n→∞

соответствующее утверждение известно как теорема Бергера—Ванга [56].

Аналогично, если в определении (24) заменить норму ∥ · ∥ матрицы на ее

спектральный радиус ρ(·), а предел на нижний предел, то получим другую

формулу для нижнего спектрального радиуса

{

}

(33)

ρ(A ) = lim inf ρ(A_n · · · A₁)n : Ai ∈A

n→∞

Для конечных множеств A справедливость равенства (33) была установлена

в [33, теорема B1], а позднее для произвольных множеств A аналогичное

утверждение было доказано в [39, лемма 1.12] и [42, теорема 1].

По аналогии с (32) и (33) для совместного и нижнего спектральных ра-

диусов определим следующие минимаксные характеристики матричных про-

изведений:

(34)

μ(A , B) = lim

μ_n(A ,B)ⁿ ,

η(A , B) = lim η_n(A , B)ⁿ ,

n→∞

(35)

μ(A , B) = lim

μ_n(A ,B)ⁿ ,

η(A , B) = lim η_n(A , B)ⁿ ,

n→∞

где при каждом n = 1, 2, . . .

μ_n(A ,B) = max

min

ρ(A_nB_n · · · A₁B₁),

A_i∈A

B_i∈B

ηn(A , B) = min

max

ρ(A_nB_n · · · A₁B₁).

B_i∈B

A_i∈A

Очевидно, наряду с уже введенными нижним и верхним минимаксными

спектральными радиусами μ(A , B) и η(A , B) величины (34) и (35) также

могли бы претендовать на роль числовых характеристик, характеризующих

стабилизируемость управляемой системы AB, описываемой уравнением (28).

Так как спектральный радиус линейного оператора не превосходит его

нормы, а величины μ(A , B) и η(A , B), как отмечалось в лемме 2, от выбора

нормы не зависят, то

μ(A , B) ≥ μ(A , B) ≥ μ(A , B), η(A , B) ≥ η(A , B) ≥ η(A , B).

А так как максимин любой функции не превосходит ее минимакс, то

μ(A , B) ≤ η(A , B),

μ(A , B) ≤ η(A , B).

Из примера 5 следует, что в общем случае μ(A , B) = η(A , B). А посколь-

ку все матрицы в примере 5 диагональные, то их нормы совпадают с соот-

ветствующими спектральными радиусами. Отсюда следует, что в условиях

примера 5 выполняются также неравенства

μ(A , B) < η(A , B),

μ(A , B) < η(A , B).

В связи с этим возникает вопрос о существовании классов матриц A и B,

для которых выполнялись бы равенства

(36) μ(A , B) = η(A , B) и/или

μ(A , B) = η(A , B), μ(A , B) = η(A , B).

По крайней мере, один класс таких матриц, введенный в [87, 89, 90], описан

в следующей теореме.

Теорема 8. Пусть A ,B — компактные H -множества положитель-

ных матриц размерности N × M и M × N соответственно. Тогда

μ(A , B) = η(A , B) = μ(A , B) = η(A , B) = μ(A , B) = η(A , B).

4.5. Вопросы и комментарии

Пусть A — это множество квадратных матриц размерности N ×N, а I :=

:= {I} — одноэлементное множество матриц, состоящее из тождественной

матрицы размерности N × N. Тогда очевидны соотношения

ρ(A ) = μ(A , I ) = η(A , I ) = μ(A , I ) = η(A , I ),

(37)

ρ(A ) = μ(I , A ) = η(I , A ) = μ(I , A ) = η(I , A ).

Замечание 6. Совместный спектральный радиус ρ(·) является в есте-

ственном смысле непрерывной и даже локально липшицевой функцией свое-

го аргумента, см. детали и точные формулировки в [11, 91-93]. В то же время

нижний спектральный радиус ρ(·) в общем случае не является непрерывной

функцией [11, 41, 43]. Но в силу равенств (37) μ(I , A ) = η(I , A ) = ρ(A ), и

поэтому в общем случае ни μ(·, ·), ни η(·, ·) также не являются непрерывными

функциями своих аргументов.

В теории совместного/нижнего спектрального радиуса большую роль иг-

рает теорема Бергера—Ванга [33, 39, 42, 56], дающая возможность выразить

совместный и нижний спектральные радиусы с помощью равенств (32) и (33)

соответственно. В связи с этим возникают следующие вопросы.

Вопрос 1. Имеют ли место равенства

μ(A , B) = μ(A , B), η(A , B) = η(A , B),

(38)

μ(A , B) = μ(A , B), η(A , B) = η(A , B)

(если верны хоть какие-то), т.е. справедливы ли для соответствующих мини-

максных величин аналоги теоремы Бергера—Ванга?

Вопрос 2. Если ответ на вопрос 1 в общем случае отрицателен, то для

каких множеств матриц A и B выполняются все или некоторые из ра-

венств (38)?

Хотя теорема 8 и описывает один из случаев, в котором справедливы ра-

венства (36), тем не менее следующий вопрос остается актуальным.

Вопрос 3. Так как согласно примеру 5 в общем случае

μ(A , B) = η(A , B),

то для каких множеств матриц A и B выполняются все или некоторые из

равенств (36)?

Замечание 7. В теореме

вместо множеств A ∈ H (N,M) и

B ∈H (M,N) можно брать множества

B, удовлетворяющие включени-

ям

(39)

A ⊆ co(A ), B ⊆B

⊆ co(B),

где A ∈ H (N, M) и B ∈ H (M, N), а символ co(·) обозначает выпуклую обо-

лочку множества. Справедливость данного замечания вытекает из того фак-

та, что все утверждения, использовавшиеся при доказательстве теоремы 8,

доказаны в [90] именно для множеств

B, удовлетворяющих включени-

ям (39).

Замечание 8. В разделе 4.2 была предпринята попытка объяснить, по-

чему понятие потраекторной стабилизируемости естественно в теории управ-

ления: если имеется последовательность возмущений объекта {A_n}, то есте-

ственно знать, существует ли последовательность “управлений” {B_n}, кото-

рая стабилизирует матричные произведения A_nB_n · · · A₁B₁. Именно эта про-

блема изучалась в настоящем разделе.

В то же время немедленно возникает и другой вопрос: даже в том случае,

когда есть способы стабилизировать матричные произведения A_nB_n · · · A₁B₁

за счет выбора подходящих {B_n}, возможно ли на практике определить (при

каждом n) матрицу B_n, используя только информацию о предшествующих

матрицах A₁, . . . , An-1? Это действительно практически важный вопрос, ко-

торый однако в настоящем разделе не обсуждается. Дополнительное обсуж-

дение данной тематики см., например, в [81].

СПИСОК ЛИТЕРАТУРЫ

Козякин В.С., Кузнецов Н.А., Чеботарев П.Ю. Консенсус в асинхронных муль-

тиагентных системах. I // АиТ. 2019. № 4. C.3-40.

Козякин В.С., Кузнецов Н.А., Чеботарев П.Ю. Консенсус в асинхронных муль-

тиагентных системах. II // АиТ. 2019. № 5. C. 3-31.

Kozyakin V. An annotated bibliography on convergence of matrix products and the

theory of joint/generalized spectral radius: Preprint. M.: Instit. Inform. Transmiss.

Probl., 2013. December. DOI: 10.13140/RG.2.1.4257.5040/1

Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967.

Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.

Козякин В.С. Алгебраическая неразрешимость задачи об абсолютной устойчи-

вости рассинхронизованных систем // АиТ. 1990. № 6. С. 41-47. URL: http://

www.mathnet.ru/rus/at5386

Kozyakin V.S. Algebraic Unsolvability of Problem of Absolute Stability of

Desynchronized Systems // Autom. Remote Control. 1990. V. 51. No. 6. P. 754-759.

Blondel V.D., Tsitsiklis J.N. When is a Pair of Matrices Mortal? // Inform. Process.

Lett. 1997. V. 63. No. 5. P. 283-286. DOI: 10.1016/S0020-0190(97)00123-3

Tsitsiklis J.N., Blondel V.D. The Lyapunov Exponent and Joint Spectral Radius

of Pairs of Matrices Are Hard — When Not Impossible — to Compute and to

Approximate // Math. Control Signals Syst. 1997. V. 10. No. 1. P. 31-40. DOI:

10.1007/BF01219774

Tsitsiklis J.N., Blondel V.D. Lyapunov Exponents of Pairs of Matrices. A Correction:

“ The Lyapunov Exponent and Joint Spectral Radius of Pairs of Matrices Are Hard —

When Not Impossible — to Compute and to Approximate” // Math. Control Signals

Syst. 1997. V. 10. No. 4. P. 381. DOI: 10.1007/BF01211553

10.

Blondel V.D., Tsitsiklis J.N. The Boundedness of All Products of a Pair of Matrices

Is Undecidable // Syst. Control Lett. 2000. V. 41. No. 2. P. 135-140. DOI: 10.1016/

S0167-6911(00)00049-9

11.

Jungers R. The joint spectral radius. Berlin: Springer-Verlag, 2009. V. 385 of Lecture

Notes Control Inform. Sci. Theory and applications. DOI: 10.1007/978-3-540-95980-9

12.

Gripenberg G. Computing the Joint Spectral Radius // Linear Algebra Appl. 1996.

V. 234. P. 43-60. DOI: 10.1016/0024-3795(94)00082-4

13.

Maesumi M. Calculating the spectral radius of a set of matrices / Wavelet analysis

and multiresolution methods (Urbana-Champaign, IL, 1999). N.Y.: Dekker, 2000.

V. 212 of Lecture Notes Pure Appl. Math. P. 255-272.

14.

Blondel V.D., Nesterov Yu. Computationally Efficient Approximations of the Joint

Spectral Radius // SIAM J. Matrix Anal. Appl. 2005. V. 27. No. 1. P. 256-272

(electronic). DOI: 10.1137/040607009

15.

Parrilo P.A., Jadbabaie A. Approximation of the Joint Spectral Radius of a Set of

Matrices Using Sum of Squares / Hybrid systems: computation and control. Berlin:

Springer, 2007. V. 4416 of Lecture Notes Comput. Sci. P. 444-458. DOI: 10.1007/978-

3-540-71493-4_35

16.

Guglielmi N., Zennaro M. An Algorithm for Finding Extremal Polytope Norms of

Matrix Families // Linear Algebra Appl. 2008. V. 428. No. 10. P. 2265-2282. DOI:

10.1016/j.laa.2007.07.009

17.

Kozyakin V. Iterative Building of Barabanov Norms and Computation of the Joint

Spectral Radius for Matrix Sets // Discret. Contin. Dyn. Syst. Ser. B. 2010. V. 14.

No. 1. P. 143-158. DOI: 10.3934/dcdsb.2010.14.143

18.

Chang C.-T., Blondel V. Approximating the Joint Spectral Radius Using a Genetic

Algorithm Framework // Proc. 18 IFAC World Congr. / IFAC. 2011. V. 18. P. 1.

P. 8681-8686.

19.

Kozyakin V. A Relaxation Scheme for Computation of the Joint Spectral Radius of

Matrix Sets // J. Difference Equat. Appl. 2011. V. 17. No. 2. P. 185-201. DOI:

10.1080/10236198.2010.549008

20.

Vankeerberghen G., Hendrickx J., Jungers R. et al. The JSR Toolbox. MATLAB

Central. 2011. http://www.mathworks.com/matlabcentral/fileexchange/33202-the-

jsr-toolbox

21.

Cicone A., Protasov V.

Joint spectral radius computation.

MATLAB

Central.

2012.

http://www.mathworks.com/matlabcentral/fileexchange/36460-

joint-spectral-radius-computation

22.

Ahmadi A.A., Jungers R.M. Switched Stability of nonlinear systems via SOS-convex

Lyapunov Functions and Semidefinite Programming // Proc. 52. IEEE Ann. Conf.

Decision. Control (CDC). 2013. P. 727-732. DOI: 10.1109/CDC.2013.6759968

23.

Bajovic D., Xavier J., Moura J. M.F., Sinopoli B. Consensus and Products

of Random Stochastic Matrices: Exact Rate for Convergence in Probability //

IEEE Transact. Signal Proc.

2013. V.

61.

No. 10. P. 2557-2571. DOI:

10.1109/TSP.2013.2248003

24.

Chang C.-T., Blondel V.D. An Experimental Study of Approximation Algorithms

for the Joint Spectral Radius // Numer. Algorithms. 2013. V. 64. No. 1. P. 181-202.

DOI: 10.1007/s11075-012-9661-z

25.

Guglielmi N., Protasov V. Exact Computation of Joint Spectral Characteristics of

Linear Operators // Found. Comput. Math. 2013. V. 13. No. 1. P. 37-97. DOI:

10.1007/s10208-012-9121-0

26.

Vankeerberghen G., Hendrickx J., Jungers R.M. JSR: a toolbox to compute the joint

spectral radius // Proc. 17. Int. Conf. Hybrid Syst.: Comput. Control. HSCC’14.

N.Y.: ACM, 2014. P. 151-156. DOI: 10.1145/2562059.2562124

27.

Chevalier P.-Y., Hendrickx J.M., Jungers R.M. Efficient Algorithms for the

Consensus Decision Problem // SIAM J. Control Optim.

2015. V. 53. No. 5.

P. 3104-3119. DOI: 10.1137/140988024

28.

Protasov V.Yu. Spectral Simplex Method // Math. Program. 2016. V. 156. No. 1-2,

Ser. A. P. 485-511. DOI: 10.1007/s10107-015-0905-2

29.

Kozyakin V.S. Constructive Stability and Stabilizability of Positive Linear Discrete-

Time Switching Systems // J. Commun. Technol. Electron.

2017. V. 62. No. 6.

P. 686-693. DOI: 10.1134/S1064226917060110

30.

Клепцын А.Ф., Козякин В.С., Красносельский М.А., Кузнецов Н.А. Устойчи-

вость рассинхронизованных систем // Докл. АН СССР.

1984. Т. 274.

№ 5.

С. 1053-1056.

31.

Барабанов Н.Е. О показателе Ляпунова дискретных включений. I-III // АиТ.

1988. № 2. С. 40-46; № 3. C. 24-29; № 5. C. 17-24.

Barabanov N.E. The Lyapunov Indicator of Discrete Inclusions. I-III // Autom.

Remote Control. 1988. V. 49. No. 2. P. 152-157; No. 3. P. 283-287; No. 5. P. 558-565.

32.

Козякин В.С. Об абсолютной устойчивости систем с несинхронно работающими

импульсными элементами // АиТ. 1990. № 10. С. 56-63.

http://www.mathnet.ru/rus/at5981

Kozyakin V.S. Absolute Stability of Systems with Asynchronous Sampled-Data

Elements // Autom. Remote Control. 1990. V. 51. No. 10. P. 1349-1355.

33.

Gurvits L. Stability of Discrete Linear Inclusion // Linear Algebra Appl.

1995.

V. 231. P. 47-85. DOI: 10.1016/0024-3795(95)90006-3

34.

Kozyakin V. A Short Introduction to Asynchronous Systems // Proc. Sixth Int.

Conf. Difference Equat. Boca Raton, FL: CRC, 2004. P. 153-165.

35.

Shorten R., Wirth F., Mason O. et al. Stability Criteria for Switched and Hybrid

Systems // SIAM Rev. 2007. V. 49. No. 4. P. 545-592. DOI: 10.1137/05063516X

36.

Lin H., Antsaklis P.J. Stability and Stabilizability of Switched Linear Systems:

A Survey of Recent Results // IEEE Trans. Automat. Control. 2009. V. 54. No. 2.

P. 308-322. DOI: 10.1109/TAC.2008.2012009

37.

Fornasini E., Valcher M.E. Stability and Stabilizability Criteria for Discrete-Time

Positive Switched Systems // IEEE Trans. Automat. Control. 2012. V. 57. No. 5.

P. 1208-1221. DOI: 10.1109/TAC.2011.2173416

38.

Rota G.-C., Strang G. A Note on the Joint Spectral Radius // Nederl. Akad.

Wetensch. Proc. Ser. A 63 = Indag. Math. 1960. V. 22. P. 379-381.

39.

Theys J. Joint spectral radius: theory and approximations: Ph. D. thesis / Faculté

des sciences appliquées, Département d’ingénierie mathématique, Center for Systems

Engineering and Applied Mechanics. Université Catholique de Louvain, 2005. 189 p.

http://dial.academielouvain.be/vital/access/manager/Repository/boreal:5161

40.

Shen J., Hu J. Stability of Discrete-Time Switched Homogeneous Systems on Cones

and Conewise Homogeneous Inclusions // SIAM J. Control Optim.

2012. V. 50.

No. 4. P. 2216-2253. DOI: 10.1137/110845215

41.

Bochi J., Morris I.D. Continuity Properties of the Lower Spectral Radius // Proc.

Lond. Math. Soc. (3). 2015. V. 110. No. 2. P. 477-509. DOI: 10.1112/plms/pdu058

42.

Czornik A. On the Generalized Spectral Subradius // Linear Algebra Appl.

2005.

V. 407. P. 242-248. DOI: 10.1016/j.laa.2005.05.006

43.

Bousch T., Mairesse J. Asymptotic Height Optimization for Topical IFS, Tetris

Heaps, and the Finiteness Conjecture // J. Amer. Math. Soc. 2002. V. 15. No. 1.

P. 77-111 (electronic). DOI: 10.1090/S0894-0347-01-00378-2

44.

Blondel V.D., Theys J., Vladimirov A.A. Switched systems that are periodically

stable may be unstable // Proc. Sympos. MTNS. Notre-Dame, USA: 2002.

http://www3.nd.edu/~mtns/papers/10181.pdf

45.

Kozyakin V. A Dynamical Systems Construction of a Counterexample to the

Finiteness Conjecture // Proc. 44 IEEE Conf. Decision Control, 2005 and 2005 Eur.

Control Conf. CDC-ECC’05. 2005. P. 2338-2343. DOI: 10.1109/CDC.2005.1582511

46.

Czornik A., Jurgas P. Falseness of the Finiteness Property of the Spectral

Subradius // Int. J. Appl. Math. Comput. Sci. 2007. V. 17. No. 2. P. 173-178. DOI:

10.2478/v10006-007-0016-1

47.

Blondel V.D., Nesterov Yu. Polynomial-time Computation of the Joint Spectral

Radius for Some Sets of Nonnegative Matrices // SIAM J. Matrix Anal. Appl. 2009.

V. 31. No. 3. P. 865-876. DOI: 10.1137/080723764

48.

Duffin R.J. Topology of Series-Parallel Networks // J. Math. Anal. Appl.

1965.

V. 10. P. 303-318. DOI: 10.1016/0022-247X(65)90125-3

49.

Eppstein D. Parallel Recognition of Series-Parallel Graphs // Inform. Comput. 1992.

V. 98. No. 1. P. 41-55. DOI: 10.1016/0890-5401(92)90041-D

50.

Dai X. Robust Periodic Stability Implies Uniform Exponential Stability of Markovian

Jump Linear Systems and Random Linear Ordinary Differential Equations //

J. Franklin Inst. 2014. May. V. 351. No. 5. P. 2910-2937.

DOI: 10.1016/j.jfranklin.2014.01.010

51.

Kozyakin V. The Berger-Wang Formula for the Markovian Joint Spectral Radius //

Linear Algebra Appl. 2014. May. V. 448. P. 315-328. DOI: 10.1016/j.laa.2014.01.022

52.

Kozyakin V. Matrix Products with Constraints on the Sliding Block Relative

Frequencies of Different Factors // Linear Algebra Appl. 2014. September. V. 457.

P. 244-260. DOI: 10.1016/j.laa.2014.05.016

53.

Shih M.-H., Wu J.-W., Pang C.-T. Asymptotic Stability and Generalized Gelfand

Spectral Radius Formula // Linear Algebra Appl. 1997. V. 252. P. 61-70. DOI:

10.1016/0024-3795(95)00592-7

54.

Daubechies I., Lagarias J.C. Sets of Matrices All Infinite Products of Which

Converge // Linear Algebra Appl. 1992. V. 161. P. 227-263.

DOI: 10.1016/0024-3795(92)90012-Y

55.

Daubechies I., Lagarias J.C. Corrigendum/addendum to: “Sets of matrices all infinite

products of which converge” [Linear Algebra Appl. 161 (1992), 227-263; // Linear

Algebra Appl. 2001. V. 327. No. 1-3. P. 69-83. DOI: 10.1016/S0024-3795(00)00314-1

56.

Berger M.A., Wang Y. Bounded Semigroups of Matrices // Linear Algebra Appl.

1992. V. 166. P. 21-27. DOI: 10.1016/0024-3795(92)90267-E

57.

Каток А.Б., Хассельблат Б. Введение в современную теорию динамических

систем. М.: Факториал, 1999.

58.

Kitchens B.P. Symbolic dynamics. Universitext. Berlin: Springer-Verlag, 1998. DOI:

10.1007/978-3-642-58822-8

59.

Fekete M.

Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen

mit ganzzahligen Koeffizienten // Math. Z. 1923. Bd. 17. H. 1. S. 228-249. DOI:

10.1007/BF01504345

60.

Полиа Г., Сеге Г. Задачи и теоремы из анализа. I. М.: Наука, 1978.

61.

Elsner L. Proc. Workshop “Nonnegat. Matric., Appl. General.” and the Eighth Haifa

Matrix Theory Conf. (Haifa, 1993). 1995. V. 220. P. 151-159. DOI: 10.1016/0024-

3795(93)00320-Y

62.

Bochi J. Inequalities for Numerical Invariants of Sets of Matrices // Linear Algebra

Appl. 2003. V. 368. P. 71-81. DOI: 10.1016/S0024-3795(02)00658-4

63.

Dai X. Extremal and Barabanov Semi-Norms of a Semigroup Generated by a

Bounded Family of Matrices // J. Math. Anal. Appl. 2011. V. 379. No. 2. P. 827-833.

DOI: 10.1016/j.jmaa.2010.12.059

64.

Protasov V. Applications of the joint spectral radius to some problems of functional

analysis, probability and combinatorics // Proc. 44. IEEE Conf. Decision. Control

Eur. Control Conf. 2005, Seville, Spain, December 12-15. 2005. P. 3025-3030.

65.

Jungers R.M., Protasov V., Blondel V.D. Efficient Algorithms for Deciding the Type

of Growth of Products of Integer Matrices // Linear Algebra Appl. 2008. V. 428.

No. 10. P. 2296-2311. DOI: 10.1016/j.laa.2007.08.001

66.

Guglielmi N., Zennaro M. Stability of Linear Problems: Joint Spectral Radius of

Sets of Matrices // Current Challeng. Stabil. Issues Numer. Differ. Equat. Springer,

2014. Lecture Notes. Math. P. 265-313. DOI: 10.1007/978-3-319-01300-8_5

67.

Dai X., Huang Y., Xiao M. Almost Sure Stability of Discrete-Time Switched Linear

Systems: A Topological Point of View // SIAM J. Control Optim.

2008. V. 47.

No. 4. P. 2137-2156. DOI: 10.1137/070699676

68.

Dai X., Huang Y., Xiao M. Periodically Switched Stability Induces Exponential

Stability of Discrete-Time Linear Switched Systems in the Sense of Markovian

Probabilities // Automatica J. IFAC.

2011. V. 47. No. 7. P. 1512-1519. DOI:

10.1016/j.automatica.2011.02.034

69.

MacKay D. J.C. Information theory, inference and learning algorithms. N.Y.:

Cambridge Univer. Press, 2003.

URL: http://www.inference.phy.cam.ac.uk/itprnn/book.pdf.

70.

Moision B.E., Orlitsky A., Siegel P.H. Bounds on the Rate of Codes Which Forbid

Specified Difference Sequences // Global Telecom. Conf., 1999. GLOBECOM ’99.

V. 1b. Rio de Janeiro: 1999. P. 878-882.

71.

Moision B.E., Orlitsky A., Siegel P.H. On Codes That Avoid Specified Differences //

IEEE Trans. Inform. Theory. 2001. V. 47. No. 1. P. 433-442. DOI: 10.1109/18.904557

72.

Immink K. A.S. Codes for mass data storage systems. Second edition. Eindhoven,

The Netherlands: Shannon Foundation Publishers, 2004. URL:

http://www.exp-math.uni-essen.de/~immink/pdf/codes_for_mass_data2.pdf.

73.

Lind D., Marcus B. An introduction to symbolic dynamics and coding. Cambridge:

Cambridge Univer. Press, 1995. DOI: 10.1017/CBO9780511626302

74.

Katok A., Hasselblatt B. Introduction to the modern theory of dynamical systems.

Cambridge: Cambridge Univer. Press, 1995. V. 54 of Encyclop. Math. Appl.

75.

Choi Y., Szpankowski W. Pattern matching in constrained sequences // Pro. IEEE

Int. Sympos. Inform. Theory 2007 (ISIT), Nice, France, June 24-29. 2007. P. 2606-

2610. DOI: 10.1109/ISIT.2007.4557611

76.

Ferenczi S., Monteil T. Infinite words with uniform frequencies, and invariant

measures // Combinat., Automat. Number Theory. Cambridge: Cambridge Univ.

Press, 2010. V. 135. Encyclop. Math. Appl. P. 373-409.

URL: http://www.lirmm.fr/~monteil/papiers/fichiers/CANT-ch07.pdf

77.

Kozyakin V. Minimax Joint Spectral Radius and Stabilizability of Discrete-Time

Linear Switching Control Systems // Discrete Contin. Dyn. Syst. Ser. B.

2018.

V. 22. No. 1531-3492_2017_11_206. P. 20. DOI: 10.3934/dcdsb.2018277

78.

Dai X. A Gel’fand-Type Spectral-Radius Formula and Stability of Linear

Constrained Switching Systems // Linear Algebra Appl.

2012. V. 436. No. 5.

P. 1099-1113. DOI: 10.1016/j.laa.2011.07.029

79.

Jungers R.M. On Asymptotic Properties of Matrix Semigroups with an Invariant

Cone // Linear Algebra Appl.

2012. V. 437. No. 5. P. 1205-1214. DOI:

10.1016/j.laa.2012.04.006

80.

Dai X., Huang Y., Xiao M. Pointwise Stability of Descrete-Time Stationary Matrix-

Valued Markovian Processes // IEEE Trans. Automat. Control. 2015. V. 60. No. 7.

P. 1898-1903. DOI: 10.1109/TAC.2014.2361594

81.

Jungers R.M., Mason P. On Feedback Stabilization of Linear Switched Systems via

Switching Signal Control // SIAM J. Control Optim. 2017. V. 55. No. 2. P. 1179-

1198. DOI: 10.1137/15M1027802

82.

Sun Z., Ge S.S. Switched linear systems: control and design / Communications and

Control Engineering. London: Springer, 2005.

83.

Stanford D.P., Urbano J.M. Some Convergence Properties of Matrix Sets // SIAM

J. Matrix Anal. Appl. 1994. V. 15. No. 4. P. 1132-1140.

DOI: 10.1137/S0895479892228213

84.

Stanford D.P. Stability for a Multi-Rate Sampled-Data System // SIAM J. Control

Optim. 1979. V. 17. No. 3. P. 390-399. DOI: 10.1137/0317029

85.

Dai X., Huang Y., Liu J., Xiao M. The Finite-Step Realizability of the Joint Spectral

Radius of a Pair of d × d Matrices One of Which Being Rank-One // Linear Algebra

Appl. 2012. V. 437. No. 7. P. 1548-1561. DOI: 10.1016/j.laa.2012.04.053

86.

Dai X. Some Criteria for Spectral Finiteness of a Finite Subset of the Real Matrix

Space R^d×d // Linear Algebra Appl. 2013. V. 438. No. 6. P. 2717-2727. DOI:

10.1016/j.laa.2012.09.026

87.

Asarin E., Cervelle J., Degorre A. et al. Entropy games and matrix multiplication

games // 33rd Sympos. Theoret. Aspect. Comput. Sci., (STACS 2016) / Ed. by

N. Ollinger, H. Vollmer. V. 47 of LIPIcs. Leibniz Int. Proc. Inform. Dagstuhl,

Germany: Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2016. P. 11:1-11:14.

DOI: 10.4230/LIPIcs.STACS.2016.11

88.

Bouyer P., Markey N., Randour M. et al. Average-Energy Games // Acta Inform.

2016. Jul. P. 1-37. DOI: 10.1007/s00236-016-0274-1

89.

Козякин В.С. Конструктивная устойчивость и стабилизируемость положитель-

ных линейных переключающихся систем с дискретным временем // Информа-

ционные процессы. 2016. Т. 16. № 2. С. 194-206.

URL: http://www.jip.ru/2016/194-206-2016.pdf

90.

Kozyakin V. Minimax Theorem for the Spectral Radius of the Product of Non-

Negative Matrices // Linear Multilinear Algebra. 2017. V. 65. No. 11. P. 2356-2365.

DOI: 10.1080/03081087.2016.1273877