Автоматика и телемеханика, № 6, 2019

(Нижегородский государственный университет им. Н.И. Лобачевского)

О ПРИМЕНЕНИИ ФУНКЦИЙ ГАУССА

ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧ

ОПТИМАЛЬНОГО УПРАВЛЕНИЯ¹

Доказываются утверждения о возможности сколь угодно точной ап-

проксимации в пространстве непрерывных функций одного переменного

на любом фиксированном отрезке с помощью линейных комбинаций сдви-

гов и сжатий функции Гаусса. На примере задачи о мягкой посадке на Лу-

ну описывается методика численного решения задач оптимального управ-

ления, основанная на указанном способе аппроксимации управляющей

функции. В рамках этого же примера исследуются вопросы чувствитель-

ности функционалов ограничений к погрешности задания оптимальных

параметров для решения тремя способами: 1) по принципу максимума

Л.С. Понтрягина (численно и теоретически); 2) по методу параметриза-

ции управления в сочетании с методом подвижных узлов; 3) предлагае-

мым методом. Проводится соответствующее сравнение, подтверждающее

эффективность метода 3).

Ключевые слова: техника параметризации управления, сосредоточенная

задача оптимального управления, аппроксимация функциями Гаусса.

DOI: 10.1134/S0005231019060035

1. Введение

Как было отмечено в [1], при дискретизации задач оптимального управ-

ления традиционно используется кусочно-постоянная или кусочно-линейная

аппроксимация управляющей функции, что даже в случае подвижной (управ-

ляемой) сетки приводит к большой размерности аппроксимирующей задачи

математического программирования.

В рамках техники параметризации управления (см. [2-6] и приведенную

в них библиографию) за счет предположения об однозначной разрешимости

управляемой системы для каждого допустимого управления функционалы

задачи сводятся к функциям конечного числа переменных — параметров ин-

терполяции управляющей функции, а исходная бесконечномерная задача оп-

тимизации — к конечномерной (аппроксимирующей задаче). Поскольку спо-

собы интерполяции могут быть разными, в [1] была обозначена проблема вы-

бора такого класса Ω функций, аппроксимирующих неизвестное управление,

который обеспечивал бы качественную аппроксимацию для функций из до-

статочно обширного множества при сравнительно малом количестве парамет-

ров аппроксимации, позволяя кроме того получать близкие к оптимальным

¹ Работа поддержана Министерством образования и науки Российской Федерации

в рамках проектной части Государственного задания в сфере научной деятельности

в 2014-2016 гг. (проект № 1727).

гладкие и устойчивые режимы управления. Целью работы [1] было показать,

что перечисленным требованиям удовлетворяет класс

{



}



Ω = Φ = Φ_ν[α,β,γ] ∈ C^∞[a;b]

 (α, β, γ) ∈ R3ν , ν ∈ N

[

]

(1)

∑

(x - β_j)²

Φ_ν[α,β,γ](x) =

α_jϕ_j[β_j,γ_j](x), ϕ_j[β_j,γ_j](x) = exp

ε+γ²

j=1

где ε > 0 — некоторое достаточно малое число (нужное только для того, что-

бы избежать нуля в знаменателе). При использовании аппроксимации управ-

ления функциями из класса Ω значения искомого оптимального управления

в контрольных точках тому, кто в данный момент решает соответствующую

задачу оптимизации, неизвестны (и в этом состоит принципиальное отличие

от обычной задачи аппроксимации). В этом случае неизвестные параметры

аппроксимации определяются путем минимизации значения целевого функ-

ционала, вычисляемого на функциях из класса Ω, если они являются допу-

стимыми по смыслу задачи либо на допустимых суперпозициях, содержащих

функции класса Ω (например, в рамках метода синус-параметризации). Ука-

занное принципиальное отличие следует учитывать при сравнении различ-

ных подходов к аппроксимации. В рамках обычной задачи аппроксимации

(при заданном количестве параметров) на первый план выходят вопросы, свя-

занные с минимизацией расхода времени (и прочих ресурсов) при отыскании

неизвестных параметров аппроксимации. В рамках же численного решения

задач оптимального управления главное — это повышение точности аппрок-

симации в отношении произвольной функции (неизвестного управления) в

смысле нормы отклонения в том или ином функциональном пространстве

при заданном количестве параметров аппроксимации, уменьшение этого ко-

личества при сохранении приемлемой точности (по управлению или хотя бы

по функционалу) и т.п.

В [1] были представлены результаты численных экспериментов по аппрок-

симации линейными комбинациями квадратичных экспонент с переменными

параметрами для: 1) многочлена пятой степени; 2) ступенчатой функции;

3) элементарной функции, заданной сложной формулой; 4) четырехзвенной

ломаной. Эти результаты показали достаточно высокую точность такого спо-

соба аппроксимации в смысле максимума модуля отклонения на достаточно

плотной сетке. Кроме того, в [1] доказано несколько утверждений о дискретно

точном характере изучаемых аппроксимаций (в [1] см. библиографию по во-

просу использования квадратичных экспонент для аппроксимации функций

одного переменного на всей числовой оси). Тем не менее строгого теоретиче-

ского обоснования возможности сколь угодно точной аппроксимации указан-

ного вида на любом конечном отрезке в метрике какого-либо функциональ-

ного пространства в [1] не было представлено. Настоящая статья восполняет

этот пробел, а именно: доказывается теорема о возможности сколь угодно

точной аппроксимации в метрике пространства C[a; b] линейной комбинаци-

ей не более n + 1 квадратичных экспонент полиномов n-й степени. В качестве

следствия устанавливается всюду плотное вложение класса Ω в пространства

C[a; b] и L_p[a; b], p ≥ 1.

Помимо результатов по аппроксимации функциями Гаусса, в статье на

примере известной задачи о мягкой посадке на Луну описывается методика

применения Ω-аппроксимаций для численного решения методом параметри-

зации управления и представляются результаты соответствующих численных

экспериментов. Устанавливается, что предлагаемый метод решения позволя-

ет существенно снижать размерность аппроксимирующей задачи (по срав-

нению с методом кусочно-постоянной аппроксимации в сочетании с методом

подвижных узлов) и (по крайней мере для указанного примера) в значитель-

ной степени понижает чувствительность численного решения к погрешно-

сти вычислений. Для задачи о мягкой посадке строится теоретический спо-

соб вычисления оптимального момента переключения в рамках решения по

принципу максимума Л.С. Понтрягина и устанавливается жесткость систе-

мы условий мягкой посадки при использовании соответствующего режима

управления. Жесткость системы здесь понимается в смысле единственности

ее решения в пространстве параметров и быстрого роста невязки при малом

отклонении от решения.

2. Формулировка основных результатов

Теорема. Пусть [a;b]⊂R — произвольно фиксированный конечный от-

резок. Тогда любой полином степени n ≥ 0 можно сколь угодно точно в мет-

рике C[a;b] аппроксимировать некоторой функцией вида Φ_ν[α,β,γ] ∈ Ω при

ν ≤ n + 1.

Доказательство теоремы приведено в Приложении.

Замечание 1. Фактически при доказательстве теоремы устанавливает-

ся, что при любой заданной точности для данного полинома P_n(x) при всех

достаточно больших по модулю числах β = 0 и γ > 0 имеет место представ-

ление

∑

P_n(x) ≈ α₀ + α_jϕβ,γj (x),

(2)

j=1

√

[

]

γ_j = γ/

j, ϕ_β,γ(x) = exp

-(x - β)²/γ²

(здесь, очевидно, ϕβ,γj = ϕ^jβ,γ ). Отсюда ясно, что по сравнению с n + 1 пара-

метров, необходимых для описания полинома, количество параметров, необ-

ходимых для его разложения по квадратичным экспонентам, больше всего

лишь на два параметра β и γ, которые к тому же могут выбираться беско-

нечным количеством способов. Отметим, что константа α₀ может быть сколь

угодно точно аппроксимирована одной квадратичной экспонентой (см. далее

лемму П.1). Но, видимо, лучше включить в класс Ω тождественную еди-

ницу. Кроме того, из анализа доказательства теоремы становится понятно,

что представление в форме (2) — это не единственная возможность. Поэто-

му представление полиномов функциями из класса Ω обладает некоторой

избыточностью. Исходя из этого, можно ожидать, что реально необходимое

количество слагаемых ν может оказаться еще меньше. На эту возможность

указывает еще и то, что величины ϕ^jβ,γ (x) быстро убывают с ростом индек-

са j. Кроме того, при ограничении представления функций полиномами фак-

тически сужаются возможности их представления функциями из класса Ω

на форму (2). Поэтому естественно ожидать, что представление функциями

из класса Ω открывает больше возможностей по сравнению с представлени-

ем полиномами. В принципе, представление функциями из класса Ω имеет

ряд общих черт с представлением так называемыми фреймами [7, § 1.8]. Что

касается избыточности, то для инженерных приложений она бывает полез-

на [7, § 1.8].

Любая функция из C^∞[a; b] может быть сколь угодно точно в метрике про-

странства C[a; b] аппроксимирована своим многочленом Тейлора. Более того,

согласно аппроксимационной теореме Вейерштрасса (см., например, [8, гл. IV,

§ 1, теорема 1.3, с. 150]), всякую непрерывную функцию в метрике простран-

ства C[a; b] можно сколь угодно точно приблизить многочленом. Поэтому

справедливо следующее утверждение.

Следствие 1. Класс Ω является всюду плотным в C[a;b].

С другой стороны, всякую функцию из L_p[a; b], p ≥ 1, можно по соответ-

ствующей норме сколь угодно точно аппроксимировать непрерывной функ-

цией (см., например, [9, гл. 4, § 6]). Поэтому имеет место следствие 2.

Следствие 2. Класс Ω является всюду плотным в L_p[a;b], p ≥ 1.

Замечание 2. В качестве следствия теоремы можно п[олучи]ь, что ма-

теринский вейвлет “мексиканская шляпа” ψ(t) = (1-t²) exp

-t²/2

на любом

конечном отрезке может быть сколь угодно точно в метрике C[a; b] аппрок-

симирован функцией вида Φ_ν [α, β, γ] ∈ Ω при ν ≤ 3. Однако в [10] непосред-

ственным образом (т.е. без использования теоремы и ей подобных) доказано

более сильное утверждение о том, что здесь всегда можно считать ν = 2.

Этот факт важен в связи со следующими обстоятельствами. Вейвлеты² ши-

роко используются при обработке сигналов, в том числе для их аппроксима-

ции и сжатия информации о сигнале, см., например, [7, 11]. Любую функцию

из L₂(R) можно при выполнении определенных условий относительно мате-

ринского вейвлета сколь угодно точно в L₂(R) аппроксимировать разложени-

ем по системе порожденных им вейвлетов. Причем локально (в частности, на

фиксированном отрезке), как правило, достаточно ограничиться небольшим

количеством членов разложения, за счет присущего им (а также и квадратич-

ным экспонентам) свойства частотно-временной локализации. Материнский

вейвлет “мексиканская шляпа” указанным условиям удовлетворяет (подроб-

нее см. [11, гл. 3]). Отдельные вейвлеты представляют собой сдвиги и сжатия

материнского вейвлета. Сдвиги и сжатия квадратичной экспоненты — это

тоже квадратичные экспоненты. Таким образом, имея разложение данной

функции по системе вейвлетов и зная представление материнского вейвлета

линейной комбинацией квадратичных экспонент, легко получаем разложение

той же функции по квадратичным экспонентам.

² В последнее время в отечественной литературе вместо слова “вейвлет” активно ис-

пользуется термин “всплеск”, предложенный К.И. Осколковым и более точно отражающий

его смысл.

Факт, указанный в замечании 2, подтверждается тем, что при ν = 2 ми-

нимизация квадратичной невязки аппроксимации упомянутого вейвлета на

отрезке [-π; π] дает

α = (50,9715;-49,9715), β = (0,2130;0,2187) · 10-14, γ = (1,4003;-1,4283),

а достигнутая точность аппроксимации на достаточно мелкой сетке: Δ =

= 4,3262 · 10-5. Графики визуально полностью совпадают. Здесь, в частности,

подтверждается гипотеза об избыточности числа ν = n+1 для представления

полиномов n-й степени.

Основываясь на теореме, ее следствиях и замечании 2, а также на ре-

зультатах численных экспериментов, представленных в [1, 10], приходим к

выводу, что использование параметризации управления путем его представ-

ления функцией класса Ω с управляемыми параметрами (α, β, γ) ∈ R3ν поз-

воляет существенно снижать размерность соответствующей аппроксимирую-

щей задачи математического программирования. Фактически, речь идет о

сжатии информации об управлении. Отличие от обычной проблемы сжа-

тия информации заключается в том, что здесь информация, подлежащая

сжатию, тому, кто решает задачу оптимизации, неизвестна, поскольку опти-

мальное управление и требуется найти. Основная идея состоит в том, что

задача об отыскании оптимального управления заменяется задачей об отыс-

кании таких параметров его аппроксимации, которые обеспечивают мини-

мум целевому функционалу при условии выполнения тех или иных ограни-

чений с заданной точностью. На основании изложенного актуальной явля-

ется разработка методик, позволяющих адаптировать популярные алгорит-

мы сжатия информации к неизвестному оптимальному управлению. Отме-

тим в связи с этим публикацию [12], где описывается подобная адаптация

метода JPEG-кодирования по отношению к управляющим функциям двух

переменных.

Далее опишем применение метода параметризации управления с помощью

квадратичных экспонент и проведем сравнение с другими способами пара-

метризации на примере известной задачи о мягкой посадке на Луну. Говоря

о других способах параметризации, будем иметь в виду два подхода. Первый

основан на использовании информации о структуре аналитического решения

этой задачи, полученного с помощью принципа максимума Л.С. Понтрягина.

Второй основан на применении методики, описанной в [2] и опирающейся

на кусочно-постоянную аппроксимацию управления на подвижной (управ-

ляемой) сетке. Оказывается, что в рамках первого подхода система условий

мягкой посадки является жесткой в том смысле, что она имеет единствен-

ное решение в (двумерном) пространстве параметров, причем невязка быстро

возрастает при малом отклонении от решения. Поэтому оптимизация целе-

вого функционала теряет смысл, поскольку производится на одноточечном

множестве. При учете ограничений путем добавления к целевому функцио-

налу штрафа за их нарушение численная оптимизация штрафного функцио-

нала вследствие той же жесткости оказывается неудачной: условия мягкой

посадки грубейшим образом нарушаются при наличии погрешности вычис-

ления момента переключения в оптимальном режиме уже в десятом знаке

после запятой. Для повышения гибкости системы ограничений в простран-

стве параметров приходится увеличивать их количество. В частности, второй

подход оказывается успешным лишь при количестве параметров, равном два-

дцати. Наконец, подход, предлагаемый в данной статье, хорошо работает уже

при четырех параметрах.

3. Постановка задачи о посадке на Луну

Рассмотрим управляемую систему из задачи о мягкой посадке на Луну

(здесь h — высота, v — скорость, m — масса, u — расход топлива в единицу

времени):

(3)

h^′ = v, v^′ = -g + (k/m)u, m^′

= -u; h(0) = H, v(0) = V, m(0) = M;

(4)

h[u](T ) = v[u](T ) = 0 (условие мягкой посадки);

m[u](T ) → max (функционал цели).

Ограничение на значения управления: u(t) ∈ [0; σ_∗], t ∈ [0; T ]. Будем считать,

что заданы следующие значения параметров: k = 3000, σ_∗ = 7,08, g = 1,62,

H = 190000, V = -2650, M = 500. Чтобы обеспечить дифференцируемость

правой части по фазовым переменным, переобозначим переменные: x₁ = h,

x₂ = v, x₃ = 1/m. Здесь исходим из того, что для искомого оптимального

управления масса аппарата m(t) > 0, t ∈ [0; T ] (а с физической точки зрения,

m(t) ≥ M₀, где M₀ — сухая масса спускаемого аппарата). В итоге задача

переформулируется следующим образом:

{

x′1 = x₂, x′2 = -g+kx₃u, x′3 = (x₃)²u; x₁(0) = H, x₂(0) = V, x₃(0) = 1/M;

(5)

x₁[u](T) = x₂[u](T) = 0; x₃[u](T) → min .

Из аналитического решения задачи минимизации (5) с помощью принципа

максимума Л.С. Понтрягина известна структура оптимального управления:

{

}

u_∗(t) =

0, если t ∈ [0; τ]; σ_∗, если t ∈ (τ; T ]

Момент переключения τ и финальное время T , вообще говоря, неизвестны.

В соответствии с информацией о структуре оптимального управления

определим набор параметров α = (α₁, α₂) ∈ R² и произведем параметриза-

цию:

{

}

τ = α²¹, T = α²¹ + α²², u[α](t) =

0, t ∈ [0; τ); σ_∗, t ∈ [τ; T ]

В результате функционалы задачи преобразуются в функции двух перемен-

ных:

J₀[α] = x₃[u](T) → min, J_i[α]

J2i[α] = 0, i = 1,2;

J_i[α] = x_i[u](T), i = 1,2,

u = u[α], α ∈ R². Финальные ограничения будем учитывать с помощью

штрафа:

f (α) = J₀[α] + σ₁J₁[α] + σ₂J₂[α], α ∈ R².

Решение управляемой задачи Коши из (5) для каждого конкретного управ-

ления будем искать численно методом Эйлера. В итоге исходная задача сво-

дится к задаче безусловной минимизации: f(α) → min, α ∈ R². Эту задачу ав-

тор решал численно методом Хука-Дживса (написав соответствующий ком-

плекс программ в системе MATLAB). Был получен следующий результат:

α ≈ (6,7;6,7), h(T) = 292,4533, v(T) = 0,015, m(T) = 197,7173. Попытка реше-

ния оказалась неудачной. И это не случайно. Дело в том, что решение управ-

ляемой системы слишком чувствительно к малейшим отклонениям значений

параметров α. Так, например, если взять α = (6,753702689; 6,7), то получаем

финальные значения: h(T ) = -0,0651, v(T ) = -25,1076, m(T ) = 198,7744. Ес-

ли же изменить значение α₁ лишь в последнем знаке: α = (6,753702688; 6,7),

то получаем: h(T ) = 274,1060, v(T ) = 233,6999, m(T ) = 182,1186. Стало быть,

коэффициент k обусловленности значения высоты h погрешностью вычисле-

ния параметра α₁: |Δh| ≤ k|Δα₁| можно оценить как 2 · 10¹¹.

Примечательно, что в [13, гл. III, § 3, п. 3, с. 126] тоже есть, своего рода,

косвенное замечание на эту же тему: “Такое Π-управление на практике да-

ет плохие результаты. Пусть момент включения тормозного двигателя t_дв не

совпадает с t₁,. . . ” (в статье это τ) “. . . что в действительности всегда име-

ет место. Если t_дв < t₁, то космический аппарат остановится на некоторой

высоте над Луной, а затем улетит от нее. Если же t_дв > t₁, то скорость при

посадке не будет нулевой и мягкой посадки не произойдет”. В статье роль

возмущения, порождаемого отличием реального объекта от модели, прини-

мает погрешность вычислений. Поэтому ситуация наблюдается аналогичная.

В разделе 4 приведем строгий анализ, который объясняет, почему так проис-

ходит.

В данном случае увеличение количества степеней свободы управляюще-

го режима (т.е. введение дополнительных параметров в шаблон управления)

позволяет все-таки найти оптимальное управление, переводящее возмущен-

ную (вследствие погрешностей) управляемую систему в требуемое состояние.

А именно разрешим управлению принимать произвольные постоянные зна-

чения v₁, v₂ ∈ [0; σ_∗] на каждом из промежутков [0; τ] и [τ; T ], произведя их

параметризацию следующим образом:

{

}

v_i

S(αi+2) = (σ_∗/2)

1 + sin(αi+2)

αi+2 ∈ R, i = 1,2.

Тогда функционалы задачи обращаются в функции четырех переменных.

Дальше забудем про максимизацию массы остатка топлива и, выбрав в каче-

стве начальных значений уже найденные α₁, α₂, а также α₃, α₄ из условий

v₁ = 0, v₂ = σ_∗, минимизируем квадрат нормы невязки выполнения условий

мягкой посадки с помощью метода Хука-Дживса. Тогда за 56 итераций по-

лучаем (с точностью представления до четырех знаков после запятой):

α ≈ (6,7141;6,5941;-1,4807;1,7631),

τ ≈ 45,0789, T ≈ 88,5614,

v₁ ≈ 0,0144, v₂ ≈ 0,9908 · σ_∗;

h(T ) ≈ 6,167 · 10-5, v(T ) ≈ 6,52 · 10-6; m(T ) ≈ 197,6789.

В статье [14] описана методика, которая позволяет вычислить градиенты

функционалов по совокупности четырех параметров:

∇_αJ₀ = (0;0,0024;0,0004;-0,0008),

∇_αJ̃₁ = (-3,7516;0,0208;0,7707;-0,6725) · 10⁴,

∇_αJ̃₂ = (-0,0029;0,1383;0,0220;-0,0447) · 10⁴.

Отсюда ясно, что, например, коэффициент k обусловленности значения высо-

ты h погрешностью вычисления параметра α₁: |Δh| ≤ k|Δα₁| можно оценить

как 3,75 · 10⁴. На самом деле приведенные выше значения h(T ) и v(T ) получа-

ются, лишь если учитывать 16 знаков после запятой. Если же оставить лишь

4 знака, что соответствует погрешности 10-5, то получаем: h(T ) = 0,5786 и

v(T ) = -0,1151. Отсюда приходим к оценке коэффициента обусловленности

примерно того же порядка. Если запретить варьирование параметров v₁ и v₂,

то ситуация резко ухудшается: h(T ) = 1,1773 · 10⁵ и v(T ) = 5000, а значения

производных по параметрам увеличиваются на порядок.

Отметим, кроме того, следующий интересный факт. Если полученный

оптимальный набор параметров (α₃, α₄) подвергнуть последовательно пря-

мому и обратному (через арксинус в смысле главного значения) синус-

преобразовани

S(α_i), i = 3, 4 (что с математической точки зрения не должно

ничего изменить), то даже при учете всех четырех параметров с 16 знаками

после запятой получим совершенно другой результат: h(T ) = -4,5295 · 10⁴ и

v(T ) = -0,2524 · 10⁴. Такое изменение возникает, видимо, из-за погрешности

вычисления синуса и арксинуса, а также в силу упомянутой выше обуслов-

ленности. Подобное явление, когда математически эквивалентные преобразо-

вания за счет несогласованного влияния погрешностей при наличии высокой

чувствительности к ним приводят к неожиданным результатам, известно спе-

циалистам по вычислительной математике, см., например, [15].

4. Жесткость системы условий мягкой посадки при задании режима

управления двумя параметрами

Далее покажем, что система условий мягкой посадки

(6)

J_i(α₁,α₂

) = 0, i = 1,2,

при использовании двухпараметрического режима управления, определяе-

мого из принципа максимума, имеет единственное решение, и, более того,

найдем его (с учетом того, что α₁ и α₂ однозначно восстанавливаются по

значениям τ и T ). Единственность решения означает, что система (6) жестко

определяет набор параметров, а задача максимизации массы остатка топлива

по этим двум параметрам теряет смысл. Другими словами, в рамках данной

парадигмы объект является жестко управляемым в заданную конечную точ-

ку, определяемую условиями мягкой посадки. Именно эта жесткость и вызы-

вает проблемы при численном решении задачи оптимизации по двум пара-

метрам. Ясно, что увеличение количества параметров (т.е. степеней свободы)

управления повышает его гибкость, но, как уже было показано на резуль-

татах численных экспериментов, при малом количестве параметров высокая

чувствительность решения к погрешностям сохраняется. Более того, можно

предположить, что для возмущенной (погрешностями) управляемой системы

система ограничений (6) перестает иметь решение (задача имеет признаки

некорректности).

В качестве предварительного результата установим, что момент включе-

ния двигателя τ, обеспечивающий мягкую посадку к некоторому моменту

T > τ, существует не более чем один; далее покажем, что один такой мо-

мент существует, и найдем его. Более того, по каждому моменту переключе-

ния τ определяется лишь один момент времени T = T (τ), при котором высота

h = h(T) = 0 при условии, что v(T) = 0. Малейшее отклонение от оптималь-

ного момента переключения τ_∗ ≈ 45 приводит к тому, что величина v(T (τ))

становится либо отрицательной, либо положительной (причем эти измене-

ния происходят достаточно резко), т.е. условие мягкой посадки нарушается.

А это значит, что при данной структуре управления отсутствует устойчивость

существования решения двухточечной краевой задачи (3), (4) и, более того,

соответствующая неустойчивость является сильной (обычная неустойчивость

означает, что в любой окрестности данного управления существуют управле-

ния, которым не отвечает ни одно решение управляемой двухточечной крае-

вой задачи; сильная неустойчивость означает, что при любом отклонении от

данного управления управляемая задача не имеет решения). Прежде всего

найдем решение системы (3) на промежутке [0; τ] (т.е. при u ≡ 0):

m(t) ≡ M, v(t) = V - gt, h(t) = H + V t - (gt²/2), t ∈ [0; τ].

Отсюда, кстати, решая соответствующее квадратное уравнение, нетрудно

найти время свободного падения: T_c ≈ 70. Теперь найдем решение системы

дифференциальных уравнений на промежутке [τ; T ) (т.е. при u ≡ σ_∗):

∫t

m^′ = -σ_∗ ⇒ m(t) = M - σ_∗(t - τ); h^′ = v ⇒ h(t) = h(τ) + v(ξ)dξ;

(

)

kσ_∗

σ_∗

v^′ = -g +

⇒ v(t) = v(τ) - g(t - τ) - kln

(t - τ)

M-σ_∗(t - τ)

Вычислим интеграл по частям:

∫

[

{

}

]

dv = dξ ⇒ v = -(1/σ_∗)

M - σ_∗(ξ - τ)

v(ξ) dξ =

u = v(ξ) ⇒ du = v^′(ξ)dξ

∫

[

]

_t

v(ξ)



kσ_∗

{M - σ_∗(ξ - τ)}



-g +

[M - σ_∗(ξ - τ)] dξ =

σ_∗

M -σ_∗(ξ-τ)

1 {

[

]}

v(τ)M - v(t)

M - σ_∗(t - τ)

σ_∗

{

}

(t - τ)

-gM(t - τ) + gσ_∗

+ kσ_∗(t - τ)

σ_∗

(T( ))

5000

4000

3000

2000

1000

Рис. 1. График функции v = v(T (τ)).

Таким образом, для определения параметров τ и T , обеспечивающих мягкую

посадку, получаем систему: h(T ) = v(T ) = 0, где

{

}

{

}

h(t) = h(τ) + (M/σ_∗)

v(τ) - v(t)

k - (gM/σ_∗)

(t - τ) + (g/2) (t - τ)²,

[

]

v(t) = v(τ) - g(t - τ) - kln

1 - (σ_∗/M)(t - τ)

Поскольку должно быть v(T ) = 0, то выражение для высоты несколько упро-

щается:

{

}

h(T ) = h(τ) + (M/σ_∗)v(τ) +

k - (gM/σ_∗)

(T - τ) + (g/2)(T - τ)².

Положим: T - τ = ξ > 0, a = g/2, b = k - (gM/σ_∗), c = h(τ) + (M/σ_∗)v(τ).

Тогда при известном τ момент³ T = T (τ) определяется из решения квадрат-

ного уравнения:

√

-b ±

b² - 4ac

aξ² + bξ + c = 0

⇒ ξ=

ξ > 0.

Непосредственным вычислением устанавливается, что условие ξ > 0 выпол-

няется, только если в числителе дроби берется знак +. Таким образом, пара-

метр ξ = ξ(τ) (ясно, что τ ∈ [0; 71]) определяется однозначно. По нему опре-

деляется T = T (τ). График функции v = v(T (τ)) см. на рис. 1. Видно, что

эта функция обращается в 0 лишь в одной точке τ = τ_∗ ≈ 45. Минимизируя

квадрат v(T (τ))² по τ методом золотого сечения на отрезке [45; 46], за 48 ите-

раций получаем практически точное значение момента переключения для

точной (невозмущенной) системы:

τ = 45,621808458300308, T = T(τ) = 88,409233510388248,

³ Это не есть момент соприкосновения с поверхностью Луны космического аппарата

при произвольном τ, поскольку в выражении h(T) в целях его упрощения было приня-

то v(T ) = 0, что заведомо верно при выполнении условий мягкой посадки в момент вре-

мени T , но в противном случае является, вообще говоря, искажением этого выражения.

Однако величина T = T(τ), определяемая из соответствующего условия h(T) = 0, доста-

точно информативна, так как в случае v(T ) = 0 мягкой посадки в момент T не будет.

h(T ) = 0, v(T ) ≈ 2,5389 · 10-9, m(T ) ≈ 197,06. Разумеется, погрешности чис-

ленного решения управляемой системы могут привести к отклонениям от

этих оптимальных значений как в ту, так и в другую сторону. В частно-

сти, в разделе 3 m(T ) ≈ 197,68, т.е. относительная погрешность составляет

0,62/197 ≈ 0,003. По графику также видно, что значения v(T (τ)) в окрест-

ности оптимальной точки переключения меняются очень быстро. Учиты-

вая что при τ ∈ [35; 55] график почти прямолинеен, можно получить оцен-

ку коэффициента обусловленности v(T (τ)), оценив угловой коэффициент:

k ≈ 2000/20 = 100. Но подчеркнем еще раз, что v(T(τ)) это не есть скорость

в момент посадки, поскольку T (τ) было получено из условия равенства нулю

выражения для h(T ), в котором было принято v(T ) = 0. Поэтому величи-

на v(T (τ)) является скоростью в момент посадки, только когда она равна ну-

лю. Обусловленность скорости в момент посадки будет гораздо выше. Именно

это и порождает высокую обусловленность функционало

Ji, i = 1, 2.

В дополнение к изложенному, ясно, что всегда существует погрешность

математической модели как таковой. Поэтому с прикладной и численной то-

чек зрения интересно было бы найти такой способ параметризации управле-

ния, который позволил бы сохранять гибкость системы вида (6) даже при

малом количестве параметров, обеспечивая тем самым хорошее (приемле-

мое) приближение к точному решению по функционалу и в смысле выполне-

ния ограничений, нечувствительное к погрешностям вычисления параметров

параметризованного управления (т.е. слабо обусловленное погрешностями).

В разделе 5 будут представлены некоторые способы параметризации управле-

ния, которые по итогам численных экспериментов демонстрируют указанные

свойства.

Слово “гибкость” будем понимать в том смысле, что для произвольной

точки α из множества решений S системы ограничений

J_i(α₁,... ,α_ν) = 0,

i = 1,2, в пространстве параметров R^ν существует достаточное количество

путей перемещения из этой точки, не выводящих из S. А это позволяет осу-

ществлять последовательное перемещение вдоль S в сторону уменьшения

значения минимизируемого функционала. В частности, если S оказывается

гладким многообразием размерности больше единицы, то рассматриваемую

систему можно, видимо, считать достаточно гибкой.

5. Понижение обусловленности ограничений при

численном решении задачи о посадке на Луну

Сравним следующие способы параметризации управления.

1. Кусочно-постоянная параметризация на подвижной сетке. Использу-

ем методику численного решения задач оптимального управления со сво-

бодным временем, описанную в [2]. Этот способ, вообще говоря, никак не

использует информацию о структуре точного аналитического решения оп-

тимизационной задачи. По крайней мере в том смысле, что количество уз-

лов сетки берется существенно больше трех (как следовало бы брать в со-

ответствии с указанной информацией). Отметим, что автор пытался брать и

меньшее число узлов (ближе к трем), но это не давало достаточно хороше-

го результата — видимо, чувствительность численного решения управляемой

7,03

5,62

4,22

2,82

1,41

0,01

Рис. 2. Метод подвижных узлов.

системы к изменению параметров параметризованного управления остава-

лась все еще высокой. При увеличении количества узлов наблюдается сниже-

ние чувствительности вплоть до приемлемого уровня. Итак, будем использо-

вать набор параметров, состоящий из двух поднаборов α = (α₁, . . . , α_k) ∈ R^k

и β = (β₁,...,β_k) ∈ R^k. Параметризацию управления будем производить по

правилу:

∑

σ_∗

u(t) =

(1 + sin β_i), t ∈ [ti-1; t_i), t₀ = 0, t_i =

α2j, i = 1,k, T = t_k.

j=1

Для k = 10 были получены следующие результаты:

h(T ) = -2,1136 · 10-5, v(T ) = -0,0001, m(T ) = 197,6182, T = 88,9913

(см. рис. 2).

Таким образом, для успешного численного решения понадобилось исполь-

зовать 20 параметров.

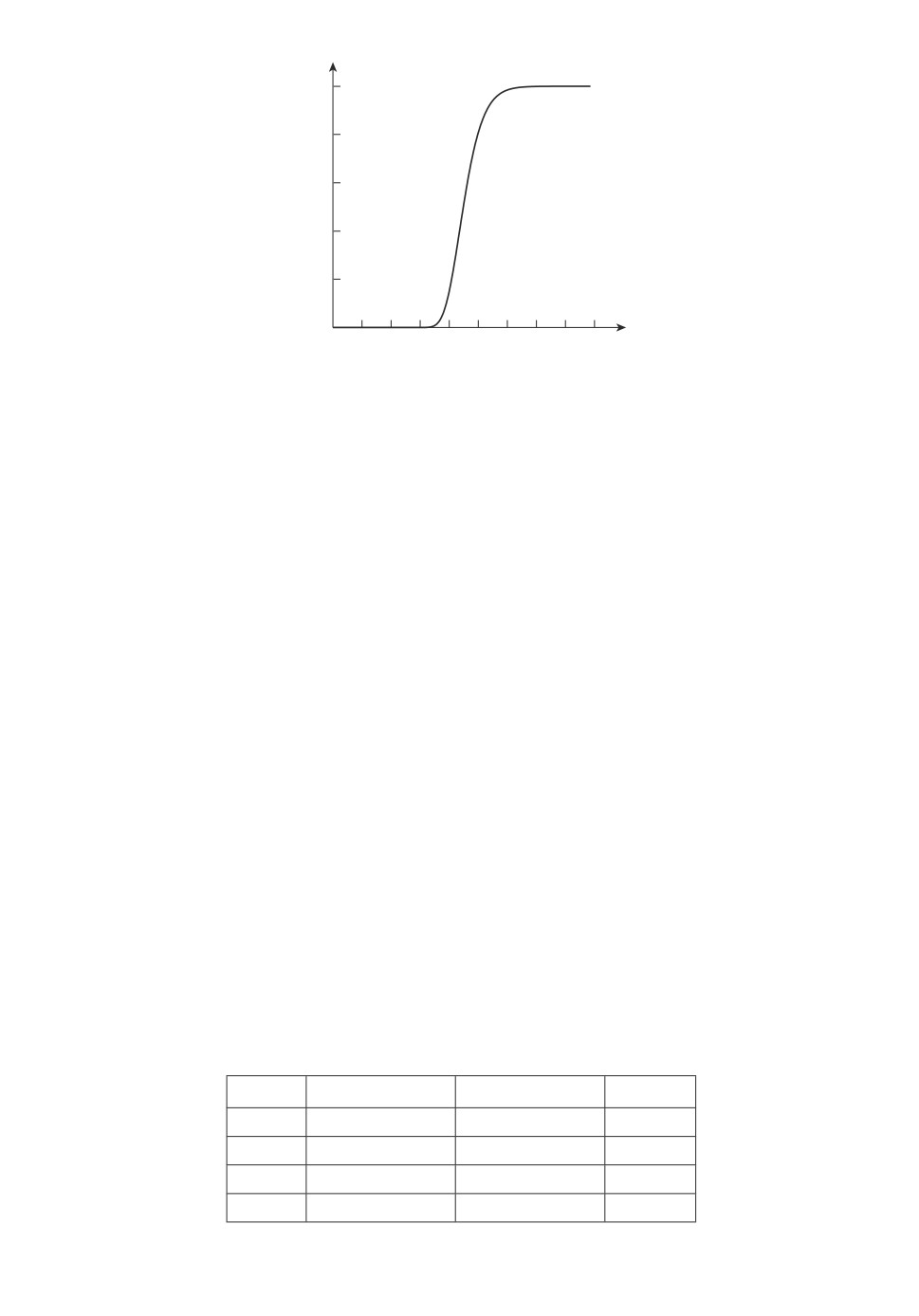
2. Использование суперпозиции функций Гаусса. Для того чтобы удовле-

творить ограничению на значения управления, автор использовал парамет-

ризацию вида

{

}

u(t) = σ_∗ exp -Φ2(t) ,

Φ = Φ_ν[α,β,γ], α,β,γ ∈ R^ν.

В качестве базового набора параметров выступает

(T, α, β, γ) ∈ R × R^ν × R^ν × R^ν .

В итоге при ν = 1 было получено приближенное решение:

T = 88,6066592856881950, α = 12,9396289585961490,

β = -5,5699194307950597, γ = 30,4427790686622010,

h(T ) = -7,4873 · 10-12, v(T ) = -9,3436 · 10-13, m(T ) = 197,6594

7,08

5,67

4,25

2,83

1,41

Рис. 3. Метод квадратичных экспонент.

При ν = 2 и ν = 3 результат получается примерно такой же.

В порядке исследования чувствительности рассмотрим таблицу. Здесь

представлена зависимость выходных параметров от количества значащих

цифр после запятой (запись e-005 означает умножение на 10-5). Видим, что

некоторая чувствительность выходных данных к точности задания управ-

ляемых параметров еще наблюдается, но она уже далеко не столь критич-

на, как при аналитически оптимальном управлении. Из таблицы можно оце-

нить коэффициенты обусловленности. Например, для высоты k ≈ 9 · 10³, т.е.

по сравнению с двухпараметрическим режимом управления, полученным из

принципа максимума, обусловленность понижается примерно в 2 · 10⁷ раз, а

по сравнению с методом подвижных узлов при четырех параметрах в рам-

ках решения задачи

J_i(α₁,... ,α₄) = 0, i = 1,2, — примерно в 5-6 раз (см.

раздел 3). Численные эксперименты позволяют сделать следующие выводы.

1. Подобно обычному методу параметризации управления, предлагаемый

в статье подход достаточно прост и позволяет разделить исходную задачу на

подзадачи (в частности, конечномерной оптимизации и решения управляемой

задачи Коши), для каждой из которых можно использовать как собственные

разработки, так и готовые программы, выбирая те, что наиболее эффектив-

ны или наиболее просты и доступны. При этом по сравнению с обычным

методом параметризации предлагаемый подход позволяет без существенных

потерь в смысле близости к оптимуму сокращать количество управляемых

параметров в разы (в частности, для задачи о мягкой посадке на Луну — в

пять раз (при ν = 1) по сравнению с методом кусочно-постоянной аппрокси-

Анализ чувствительности

Знаков

h(T )

v(T )

m(T )

-0,093413

0,00065807

197,6593

-1,122e - 005

2,3315e - 008

197,6594

9,2098e - 010

1,423e - 011

197,6594

-7,4873e - 012

-9,3436e - 013

197,6594

мации в сочетании с методом подвижных узлов при количестве параметров,

необходимом для обеспечения устойчивого численного решения).

2. Использование внешней параметризации (в частности, с помощью функ-

ции Гаусса) позволяет учитывать ограничения на значения управления, не

требуя включения их в число ограничений аппроксимирующей задачи, и в

сочетании с предлагаемым подходом оказывается работоспособным и эффек-

тивным.

3. Предлагаемый подход позволяет получать хорошее приближение (по

крайней мере, по значению функционала) к решению оптимизационной за-

дачи даже при достаточно малом количестве параметров аппроксимации.

4. Предлагаемый подход хорошо работает и в том случае, когда начальное

управление находится достаточно далеко от оптимального, причем для реше-

ния аппроксимирующей задачи используется метод Хука-Дживса (нулевого

порядка) в сочетании с методом штрафа в весьма простой и грубой форме, а

для решения управляемой системы при текущем управлении — простейший

метод Эйлера.

5. Значение целевого функционала и ограничения задачи оптимизации

оказываются мало чувствительными к малым изменениям полученного в ре-

зультате численного решения набора параметров аппроксимации.

6. Заключение

Поясним связь между установленной в начале статьи возможностью сколь

угодно точной аппроксимации функций одного переменного на любом фик-

сированном отрезке функциями класса Ω и особенностями использования

соответствующего способа аппроксимации управляющей функции при чис-

ленном решении задач оптимального управления со свободным временем на

примере задачи о мягкой посадке на Луну. На первый взгляд, может пока-

заться, что возможность сколь угодно точной аппроксимации не требуется,

поскольку чем ближе подходим к точному оптимальному управлению, тем

труднее будет происходить процесс численного решения. При детальном же

рассмотрении (см. разделы 3 и 4) оказалось, что причиной затруднений явля-

ется жесткость системы ограничений, которая наблюдается именно при двух

параметрах, а при увеличении их количества — снимается; в то же время

увеличение количества параметров как раз и повышает точность аппрокси-

мации. Вообще, какова бы ни была задача, всегда приходится стремиться

прийти к некому балансу между следующими двумя требованиями, проти-

воречащими друг другу. С одной стороны, размерность аппроксимирующей

задачи математического программирования должна быть не слишком вы-

сокой, чтобы ее не слишком сложно было решать. С другой стороны, ко-

личество ν используемых параметров должно быть достаточным для того,

чтобы система ограничений была достаточно гибкой в смысле ее разрешимо-

сти, и при этом наилучшее значение функционала на множестве аппрокси-

маций управления (за счет соответствующего расширения этого множества)

не слишком сильно отличалось бы от его наилучшего значения на множестве

допустимых управлений в исходной задаче. Использование функций Гаусса

позволяет удачным образом достигать компромисса между этими двумя тре-

бованиями. С одной стороны, как уже было сказано в разделе 1, такой способ

аппроксимации обеспечивает во многих случаях хорошую точность прибли-

жения при малом количестве параметров. С другой стороны, в силу того

же обстоятельства наилучшее значение функционала в аппроксимирующей

задаче не слишком сильно отличается от теоретически оптимального. При

этом гибкость системы ограничений, в данном случае систем

J_i(α,β,γ) = 0,

i = 1,2, обеспечивается за счет следующих обстоятельств. Во-первых, мно-

жество решений указанной системы (учитывая, что количество параметров

больше двух) оказывается гладким многообразием за счет гладкости левых

частей при их независимости. Дело в том, что функционалы аппроксимирую-

щей задачи при достаточной гладкости правой части системы и интегрантов

функционалов оказываются тоже гладкими (технику доказательства этого

факта можно вычленить из рассуждений [3, 4]) за счет того, что аппрокси-

мации зависят бесконечно дифференцируемым образом от параметров. Во-

вторых, возмущенная (за счет погрешностей) управляемая система, скорее

всего, имеет (см. рис. 2) оптимальный режим u ∈ L_∞[0; T ] не совсем такой

формы графика, как следует из принципа максимума, но это не мешает тому,

что найдется управление u, представимое с помощью функций из Ω, аппрок-

симирующее u сколь угодно точно в норме L_p[0; T ], p ∈ [1; ∞), а на участках

непрерывности — в норме C. А уже в рамках данного способа аппроксимации

(при заданном количестве параметров) соответствующая конечномерная ап-

проксимирующая задача оказывается, как уже сказано, достаточно гладкой,

вследствие чего сравнительно легко решается.

ПРИЛОЖЕНИЕ

Доказательство теоремы основано на следующих леммах.

Лемма П.1. Для любых [a;b] ⊂ R, ε > 0, а также для β ∈ R и γ > 0 та-

ких, что

{

}

√

(Π.1)

|β| + max(|a|, |b|)

/γ <

min(ε,1),



[

]



справедлива оценка: max

exp

-(x - β)²/γ²

-1 < ε.

x∈[a;b]

Доказательство. Раскладывая в ряд Маклорена, получаем:

∑

(-1)ⁿt2n

e-t2 - 1 =

∀t ∈ R.

n=1

Для каждого фиксированного t ∈ [-1; 1] справа стоит знакочередующий-

ся ряд с модулем общего члена, строго убывающим до нуля, т.е. ряд ти-

па Лейбница. Как известно, модуль суммы такого ряда (так же, как его



остатка) оценивается модулем своего первого члена. Тогда

^e-t2 - 1≤t2 при

все{t ∈ [-1;}]. Поэтому чтобы получить нужную оценку, достаточно, что-

бы

(x - β)²

/γ² < min(ε, 1). Выполнение этого неравенства обеспечивается

условием (Π.1). Лемма П.1 доказана.

Лемма П.2. Для любых [a;b] ⊂ R, a < b, C = 0 и ε > 0 найдутся пара-

метры α,β,d ∈ R и γ > 0 такие, что

Cx = αϕ_β,γ(x) + d + σ(x),

где



[

]

max

^σ(x)<ε,ϕβ,γ(x) = exp

-(x - β)²/γ²

x∈[a;b]

В качестве β = 0 и γ > 0 можно взять любые числа, удовлетворяющие нера-

венствам

2|C| max(|a|, |b|)(b - a)

|β| + max(|a|, |b|)}

(Π.2)

|β| >

и γ>

√

[

]

min(ε/

2|C|(b - a)

, 1)

Доказательство. Предварительно, считая параметры β ∈ R, β = 0 и

γ > 0 произвольными, положим α = Cγ²/(2β) и оценим разность



[

]



=|α|

≤

σ₁(x) =

^αϕ^′β,γ (x) - C

^-2 exp

-(x - β)²/γ²

(x - β)γ-2 - (C/α)



(



)

=|C|



≤ |2α| |x/γ²| + |C|ϕβ,γ(x) - 1

|x/β| +

ϕβ,γ(x) - 1

Обозначим ε₁ = ε/(b - a) и выберем β = 0 из условия |C| max(|a|, |b|)/|β| <

< ε₁/2. После этого выберем число γ > 0 из условия (Π.1) при замене ε на

ε₁/(2|C|). Тогда получим σ₁(x) < ε₁ для всех x ∈ [a;b]. Рассмотрим интеграл

∫

{

αϕ_β,γ (t) - Ct}′ dt = αϕβ,γ (x) + d - Cx ≡ -σ(x), x ∈ [a; b],

где d = Ca - αϕ_β,γ (a). Таким образом, получаем

∫



^σ(x)≤σ1(t)dt < ε1 (b - a) = ε

∀x ∈ [a;b].

Лемма П.2 доказана.

Доказательство теоремы. Рассмотрим на отрезке [a;b], a < b, про-

извольный полином степени n:

P_n(x) = K₀ + K₁x + ... + K_nxⁿ.

Если n = 0, то д√аточно просто сослаться на лемму П.1. Будем считать,

что n ≥ 1, C_m =^m

|K_m|, C = 1 + max C_m, s_m = sign K_m, m = 1, n. Тогда

m=1,n

∑

P_n(x) = K₀ +

s_m(C_mx)^m.

m=1

Зафиксируем произвольно число ε₁ ∈ (0; 1) и найдем числа β = 0 и γ > 0 из

условий (Π.2) при замене ε на ε₁. Согласно лемме П.2 найдутся числа d_m и

α_m ∈ R, m = 1,n, такие, что

∑

(

)_m

P_n(x) = K₀ +

s_m

α_mϕ_β,γ(x) + d_m + σ_m(x)

m=1



<ε1

^σ_m(x)

∀x ∈ [a;b],

m = 1,n. Пользуясь формулой бинома Ньютона, получаем, что

(

)_m

(

)_m

α_mϕ_β,γ(x) + d_m + σ_m(x)

α_mϕ_β,γ(x) + d_m

+ δ_m(x),

∑

(

δ_m(x) =

C^km

α_mϕ_β,γ(x) + d_m

)^m-kσ^km(x).

k=1

Заметим, что |σ_m(x)| < ε₁ < 1, и, таким образом,



∑



∑

(

)_m-k

≤ε1

^m-k

^δ_m(x)

C^kmCmx - σm(x)

≤ε₁

C^km

C|x| + 1

≤

k=1

∑

(

)_m-k

(

)_m

(

)_n

≤ε₁C^m C^km

|x| + 1

≤ε₁C^m

|x| + 2

≤ε₁Cⁿ

|x| + 2

k=1

Пользуясь теперь произволом в выборе ε₁, потребуем, чтобы выполнялось

условие

(

)_n

ε₁Cⁿ

max(|a|, |b|) + 2

< ε/(2n).

∑



Тогда для величины δ(x) =

s_mδ_m(x) получим:

^δ(x)< ε/2

для всех

m=1

x ∈ [a;b]. При этом по построению

∑

(

)_m

P_n(x) = K₀ +

s_m

α_mϕ_β,γ(x) + d_m

+ δ(x), x ∈ [a;b].

m=1

Опять же по формуле бинома Ньютона

(

)

∑

α_mϕ_β,γ(x) + d_m

^m = C^kmα^m-kmd^kmϕ^m-kβ,γ(x).

k=0

Значит, каждое слагаемое не содержит, по сути, ничего, кроме степеней функ-

ции ϕ_β,γ (x), максимально возможной из которых является n-я степень, до-

множенных на некоторые константы. Отсюда вытекает представление поли-

нома в виде

∑

P_n(x) = K₀ + f_jϕ^jβ,γ(x) + δ(x) =

j=0

∑

= C₀ + f_jϕ^jβ,γ(x) + δ(x), C₀ = K₀ + f₀.

j=1

Заметим, что ϕ^jβ,γ(x) = ϕ_β,γ

(x), γ_j = γ/√j. Пользуясь, наконец, леммой П.1,

∑

получаем представление P_n(x) = ϕβ0,γ₀ (x) + fjϕβ,γ_j (x) + σ(x) при некото-

j=1



<εдлявсехx∈[a;b].Теоремадоказана.

рых β₀ ∈ R, γ₀ > 0 и

^σ(x)

СПИСОК ЛИТЕРАТУРЫ

Чернов А.В. Об использовании квадратичных экспонент с варьируемыми пара-

метрами для аппроксимации функций одного переменного на конечном отрез-

ке // Вестн. Удмурт. ун-та. Математика. Механика. Компьютерные науки. 2017.

Т. 27. Вып. 2. С. 267-282.

Чернов А.В. О приближенном решении задач оптимального управления со сво-

бодным временем // Вестн. Нижегород. гос. ун-та им. Н.И. Лобачевского. 2012.

№ 6(1). С. 107-114.

Чернов А.В. О гладких конечномерных аппроксимациях распределенных опти-

мизационных задач с помощью дискретизации управления // Журн. вычисл.

матем. и матем. физ. 2013. Т. 53. № 12. С. 2029-2043.

Chernov A.V. Smooth Finite-Dimensional Approximations of Distributed

Optimization Problems via Control Discretization

// Comput. Math. Math.

Phys. 2013. V. 53. No. 12. P. 1839-1852.

Чернов А.В. О применимости техники параметризации управления к решению

распределенных задач оптимизации // Вестн. Удмурт. ун-та. Математика. Ме-

ханика. Компьют. науки. 2014. Т. 24. Вып. 1. С. 102-117.

Чернов А.В. О гладкости аппроксимированной задачи оптимизации системы

Гурса-Дарбу на варьируемой области // Тр. ИММ УрО РАН. 2014. Т. 20. № 1.

С. 305-321.

Чернов А.В. О кусочно постоянной аппроксимации в распределенных задачах

оптимизации // Тр. ИММ УрО РАН. 2015. Т. 21. № 1. С. 264-279.

Новиков И.Я., Протасов В.Ю., Скопина М.А. Теория всплесков. М.: Физматлит,

2006.

Гаевский Х., Грегер К., Захариас К. Нелинейные операторные уравнения и опе-

раторные дифференциальные уравнения. М.: Мир, 1978.

Gajewski H., Gröger K., Zacharias K. Nichtlineare Operatorgleichungen und Ope-

ratordifferentialgleichungen. Berlin: Akademie, 1974.

Федоров В.М. Курс функционального анализа. СПб.: Лань, 2005.

10.

Чернов А.В. О применении квадратичных экспонент для дискретизации за-

дач оптимального управления // Вестн. Удмурт. ун-та. Математика. Механика.

Компьют. науки. 2017. Т. 27. Вып. 4. С. 558-575.

11.

Добеши И. Десять лекций по вейвлетам. Ижевск: НИЦ РХД, 2001.

Daubechies I. Ten lectures on wavelets. Philadelphia: Society for Industrial and Appl.

Math., 1992.

12.

Чернов А.В. JPEG-подобный метод параметризации управления для численного

решения распределенных задач оптимизации // АиТ. 2017. № 8. С. 145-163.

Chernov A.V. JPEG-Like Method of Control Parametrization for Numerical Solution

of the Distributed Optimization Problems // Autom. Remote Control. 2017. V. 78.

No. 8. P. 1474-1488.

13.

Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория кон-

струирования систем управления. М.: Высш. шк., 2003.