Автоматика и телемеханика, № 6, 2019

(Московский государственный университет им. М. В. Ломоносова)

ПРОБЛЕМА НЕТРАНЗИТИВНОСТИ ДЛЯ ТРЕХ

НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Изучается проблема нетранзитивности отношения стохастического

предшествования для трех независимых случайных величин с распреде-

лениями из заданного класса непрерывных распределений. Первоначаль-

но этот вопрос был поставлен в связи с задачей из теории прочности.

В дальнейшем тема нетранзитивности стала популярной на примере так

называемых нетранзитивных (игральных) костей. Представлены крите-

рии, с помощью которых доказано, что нетранзитивности не может быть

для многих классических непрерывных распределений (равномерного, по-

казательного, нормального, логистического, Лапласа, Коши, Симпсона,

однопараметрического Вейбулла и др.). Отдельно рассмотрен случай рас-

пределений с полиномиальной плотностью на единичном отрезке. Опре-

делены интересные направления дальнейших исследований по тематике

работы.

Ключевые слова: нетранзитивность, нетранзитивные кости, стохастиче-

ское предшествование, непрерывные распределения.

DOI: 10.1134/S0005231019060059

1. Введение

Пусть заданы три независимые случайные величины X, Y и Z, такие что

(1)

P(X < Y ) >

(2)

P(Y < Z) >

Может показаться, что из (1) и (2) должно следовать

P(X < Z) >

однако существуют примеры, когда это не так, а напротив,

(3)

P(Z < X) >

Таким образом, отношение (1) между случайными величинами нетранзитив-

но и может идти по кругу, как в игре «камень, ножницы, бумага».

Далее для определенности под нетранзитивностью будем понимать ситуа-

цию, когда

p_XYZ = min{P(X < Y ),P(Y < Z),P(Z < X)} >

Первой попыткой изучения этого явления стало исследование С. Трыбу-

лы, начатое совместно с Г. Штейнгаузом [1, 2]. Было показано, что

√

5-1

max

p_XYZ =

≈ 0,618,

X,Y,Z

причем максимум достигается, например, на тройке случайных величин

{

1, с вероятностью p,

X =

4, с вероятностью 1 - p,

(4)

Y = 2,

{

0, с вероятностью 1 - p,

Z =

3, с вероятностью p,

где

√

5-1

тогда

√

5-1

P(X < Y ) = P(Y < Z) = P(Z < X) =

Далее в [3, 4] был рассмотрен случай n независимых случайных величин,

получены некоторые оценки максимума вероятностей, однако явное выраже-

ние было выведено лишь недавно в [5]. Оказалось, что

max min{P(X₁ < X₂), . . . , P(Xn-1 < X_n), P(X_n < X₁)} =

X₁,...,Xn

(5)

(

)-1

=1-

4 cos²

n ≥ 3.

n+2

В качестве возможного приложения в [2] речь идет о прочности материа-

лов. Пусть в лаборатории сравнивают попарно на прочность железные брус-

ки одинакового размера и формы, помещая их в одну рамку и прилагая к

ним одинаковую силу путем закручивания винта, пока один из брусков не

сломается. Предположим, что бруски производятся на трех разных заводах

(которые дают разное распределение прочности), и сравниваются бруски c

первого и второго, второго и третьего, первого и третьего заводов. Тогда тео-

ретически может сложиться парадоксальная ситуация, что бруски с первого

завода «хуже» (т.е. чаще ломаются раньше) брусков со второго завода, брус-

ки со второго «хуже» брусков с третьего, а бруски с третьего «хуже» брусков

с первого.

Понятно, что если сравнение производится с целью принять какое-то

управленческое решение, например продукцию с какого завода лучше поку-

пать, такой результат вызывает недоумение. Конкретно в приведенном при-

мере можно поступить иначе: не сравнивать прочности брусков друг с дру-

гом, а измерять их явно, численно, затем выбирать лучший завод по сред-

ней прочности брусков или другой числовой характеристике распределения.

Тогда парадокса нетранзитивности не возникает (может, правда, оказаться,

что характеристики в пределах точности равны и выбор опять-таки сделать

нельзя, но это уже другой вопрос).

Однако на практике бывают и ситуации, когда какая-то величина просто

не измеряется в явном виде и нет другого способа выявить ее соотношения,

кроме парных сравнений. В биологии речь может идти о парных взаимо-

действиях животных в борьбе за пищу, территорию, размножение или доми-

нирование в группе. Для людей речь может идти о сравнительных оценках

различных товаров и услуг, голосовании и др. Проблема нетранзитивности

предпочтений здесь была известна с XVIII в. (парадокс Кондорсе).

Общим вопросам нетранзитивности отношения превосходства в природе,

технике и обществе (главным образом, детерминированного, а не вероят-

ностно-статистического характера) посвящен ряд научных и научно-популяр-

ных статей А.Н. Поддьякова, в частности [6-9].

Проблема нетранзитивности возникает в теории кооперативных игр [10],

многокритериальных задачах индивидуального выбора [11], задачах вектор-

ной оптимизации [12], оптимизации бинарных опросников [13] и др.

Методам сравнения вероятностных распределений на основе статистиче-

ских данных (гистограмм) посвящена недавняя работа [14], где рассматрива-

лись различные стохастические порядки.

Отношение

(1) также называют стохастическим предшествованием

(stochastic precedence). В [15, 16] оно применялось в задачах статистического

анализа. В [17] оно использовалось в задачах ранжирования и называлось

доминированием по вероятности.

Появляются также работы, где проводятся различные обобщения поня-

тия транзитивности, и относительно этих более общих понятий стохастиче-

ское предшествование может быть «транзитивным» [18], однако практиче-

ский смысл таких обобщений не вполне ясен.

Тема нетранзитивности стохастического предшествования получила боль-

шую популярность на примере так называемых нетранзитивных костей

(nontransitive, intransitive dice). Имеются в виду наборы игральных костей, на

грани которых числа нанесены специальным образом, чтобы создать нетран-

зитивные отношения соответствующих случайных величин. Например, кости

Эфрона, изобретенные Б. Эфроном в 1960-е гг., представляют собой набор из

четырех костей A, B, C, D, которые имеют на своих гранях следующие числа:

A : 4, 4, 4, 4, 0, 0;

B : 3, 3, 3, 3, 3, 3;

C : 6, 6, 2, 2, 2, 2;

D : 5, 5, 5, 1, 1, 1.

Тогда результат броска каждой кости из набора больше результата бросания

следующей кости (по кругу) с вероятностью, большей 1/2:

P(A > B) = P(B > C) = P(C > D) = P(D > A) =

что соответствует максимуму (5) при n = 4.

Для n = 3 можно предложить кости [19, §1.13e]

A : 3, 3, 3, 3, 3, 6;

B : 2, 2, 2, 5, 5, 5;

C : 1, 4, 4, 4, 4, 4.

Тогда

P(A > B) = P(B > C) =

≈ 0,583, P(C > A) =

≈ 0,694.

В принципе, можно рассматривать кости с произвольным числом граней,

но максимум (5) достижим на них только при n = 4 [5].

Нетранзитивные кости были популяризованы М. Гарднером [20, 21], им

посвящена обширная (зарубежная) литература, например, [22-25]. К сожа-

лению, оборотной стороной популярности стало, во-первых, сужение темы

(до дискретных случайных величин, принимающих целочисленные значения

с равными или кратными вероятностями), во-вторых, не слишком серьезное

отношение со стороны ученых, зачастую относящих эту тему к игровой, раз-

влекательной математике (mathematical games, recreational math).

Между тем изначально С. Трыбулой была затронута вполне серьезная

проблема теории вероятностей с возможными приложениями на практике.

Прочность материалов, конечно, имеет непрерывное распределение, как и

многие другие характеристики объектов в природе, технике и обществе.

И при попарных сравнениях объектов из нескольких разных совокупностей

(категорий) теоретически может возникать нетранзитивность. Таким обра-

зом, вполне закономерно задаться вопросом, в каких классах непрерывных

распределений она бывает, а в каких нет. Также интересно, насколько вели-

ки в рамках класса могут быть максимумы вероятностей. Далее ограничимся

случаем n = 3 независимых случайных величин (X, Y и Z).

2. Когда нетранзитивности не может быть

Еще в [2, теорема 2] было показано, что если распределения случайных

величин X, Y и Z относятся к одному сдвиговому семейству, то нетранзи-

тивности быть не может. Понятно, что этот вывод также распространяется

на масштабные семейства распределений на положительной или отрицатель-

ной полупрямой (путем логарифмирования).

В частности, прочность материалов часто описывается распределением

Вейбулла

{

⁽x-a)α}

(6)

F (x) = 1 - exp

x ≥ a, a,b,α > 0,

предложенным еще в книге [26]. Таким образом, сразу можно сделать вывод,

что если случайные величины (прочности железных брусков с разных заво-

дов) имеют распределение Вейбулла с постоянными a и α и разными b или с

постоянными b и α и разными a, то нетранзитивность невозможна.

Обозначим общий класс распределений X, Y и Z через K.

Теорема. Пусть случайные величины X₁ и X₂ независимы и имеют

распределения F₁ и F₂ из K. Если существует такая характеристика рас-

пределения γ(F) для F ∈ K, что γ(F₁) < γ(F₂) верно тогда и только тогда,

когда P(X₁ < X₂) > 1/2, то нетранзитивности не может быть.

Будем обозначать хвост распределения F чере

F (x) = 1 - F (x). Введем

отношение (строгого) стохастического порядка распределений: F₁ ≺ F₂, если

F₁(x)

F₂(x) везде и

F₁(x)

F₂(x) на некотором интервале I = I(F₁,F₂).

Очевидно, это отношение транзитивно.

Назовем однопараметрическое семейство распределений {F_θ} стохасти-

чески возрастающим по параметру θ, если из θ₁ < θ₂ следует Fθ1 ≺ Fθ2 .

Следствие 1. Если K представляет собой однопараметрическое се-

мейство распределений, стохастически возрастающее по параметру, то

нетранзитивности не может быть.

Очевидно, аналогично можно определить однопараметрические семейства,

стохастически убывающие по параметру, и для них будет верно аналогичное

следствие.

Помимо ранее упомянутых случаев, к числу семейств, покрываемых

следствием 1, относятся, например, семейство степенных распределений

Fθ(x) = x^θ, x ∈ [0, 1], θ > 0, гамма-распределения с постоянным параметром

масштаба и др. Однако этим область действия теоремы не исчерпывается.

Утверждение 1. Пусть F_α(x) = 1 - exp{-x^α}, x ≥ 0, α > 0, тогда

нетранзитивности не может быть.

Это семейство (распределений Вейбулла с a = 0, b = 1) не является стоха-

стически возрастающим или убывающим по α, поскольку при α₁ < α₂ верно

Fα₁ (x)

Fα₂ (x) при 0 < x < 1, но

Fα₁ (x)

Fα₂ (x) при x > 1. Тем не менее

при этом

∫∞

P(X₁ < X₂) = exp{-xα2} d (1 - exp{-xα1 }) =

∫∞

{

}

= exp -uα2/α1 - u du > 1/2

и теорема выполняется.

Следовательно, для распределений Вейбулла с постоянными a и b и раз-

ными α нетранзитивность также невозможна.

Напомним понятие типа распределения. Распределения F₁ и F₂ называ-

ются относящимися к одному типу, если существуют такие a > 0 и b > 0, что

F₁(x) = F₂(a + bx). Тип удобно задавать одним его представителем — распре-

делением F₀, которое называют стандартным, а все остальные выражаются

через него, т.е. для любого F существуют такие a > 0 и b > 0, что

⁽x-a⁾

F (x) = F₀

Следствие 2. Если K состоит из одного или более типов распределе-

ний, в которых стандартные распределения симметричны относительно

нуля, то нетранзитивности не может быть.

Доказательства теоремы, утверждения 1 и следствий см. в Приложении.

Следствие 2 применимо к типам равномерного, нормального, логистиче-

ского распределения, распределений Лапласа, Коши, Симпсона и др.

Поскольку отношение нетранзитивности инвариантно относительно лю-

бого непрерывного строго возрастающего преобразования (применяемого ко

всем случайным величинам), то этот вывод можно также распространить на

логнормальные распределения.

К некоторым семействам распределений приходится применять специаль-

ные методы.

3. Распределения с полиномиальной плотностью на отрезке

Рассмотрим непрерывные распределения, заданные многочленами степени

N ≥ 2 на отрезке [0,1]:

∑

(7)

F (x) =

f_kx^k,

f_k

= 1, x ∈ [0, 1],

k=1

при этом на коэффициенты f_k, 1 ≤ k ≤ N, накладываются также ограниче-

ния, обусловленные неотрицательностью плотности распределения F .

Изучение подобных распределений имеет, например, тот смысл, что любое

непрерывное распределение на отрезке приближается многочленами. Однако

от степени приближения зависит не только погрешность в оценке функции,

но и то, насколько это приближение способно передать характерные свойства

отдельного распределения или их соотношений, в данном случае — свойство

нетранзитивности.

При N = 2 можно провести параметризацию

(8)

Fθ(x) = (1 - θ)x + θx²,

θ ∈ [-1,1],

семейство стохастически возрастает по θ, и по следствию 1 нетранзитивности

не может быть.

Утверждение 2. В случае N = 3 нетранзитивности не может быть.

Это утверждение требует уже нетривиального докaзательства (см. При-

ложение).

1,0

0,8

0,6

0,4

0,2

0,4

0,6

0,8

1,0

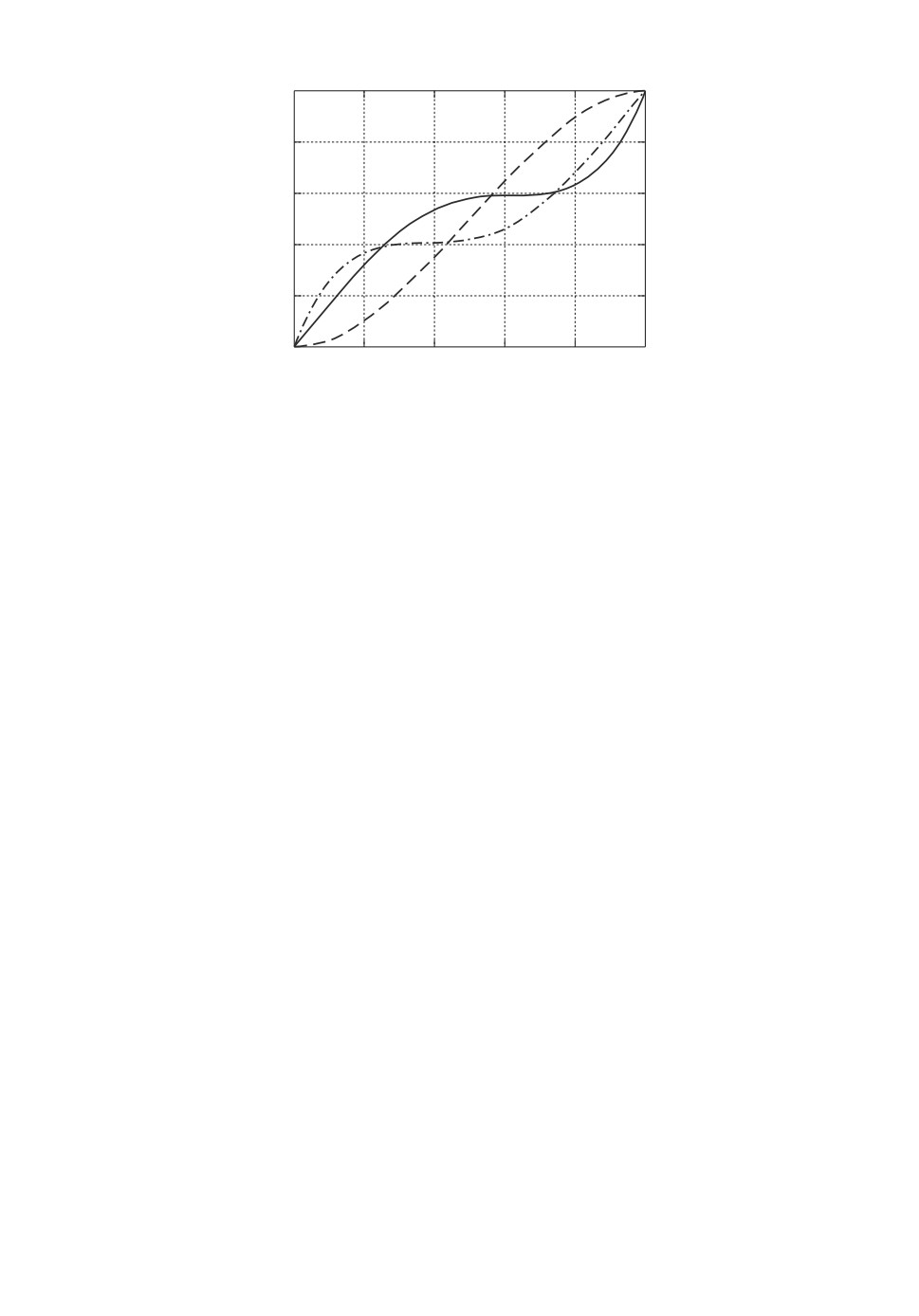
Рис. 1. Графики функций распределения к примеру (9).

При N = 4 нетранзитивность возможна. Это выяснилось только числен-

ным поиском в девятимерном пространстве коэффициентов с учетом огра-

ничений на неотрицательность плотности. Поскольку регулярный поиск был

затруднен, решено было использовать метод Монте-Карло и следующие эв-

ристические соображения.

Заметим, что в классической тройке (4) преобразование x → 4 - x сохра-

няет Y = 2 и переводит друг в друга X и Z (по распределению). Аналогом

такого преобразования на отрезке [0, 1] является x → 1 - x. Поэтому в каче-

стве полиномиального аналога распределения, сосредоточенного в точке 2,

логично взять распределение Y , симметричное на отрезке [0, 1], с максималь-

ным значением плотности в точке 1/2 и минимальным на остальном отрезке,

в том числе на его концах, где плотность может быть равна нулю, откуда по-

лучаем p_Y (x) = 6x(1 - x) и F_Y (x) = 3x² - 2x³. Для функций распределения

X и Z логично положить F_Z(x) = 1 - F_X(1 - x). Это сужает пространство

поиска до трехмерного пространства.

В качестве примера тройки распределений с заметно большим 1/2 значе-

нием p_XYZ ≈ 0,527 можно привести следующий:

FX (x) = 1,511x + 1,726x² - 7,470x³ + 5,233x⁴,

(9)

FY (x) = 3x² - 2x³,

FZ (x) = 3,486x - 10,716x² + 13,463x³ - 5,233x⁴.

На рис. 1 представлены графики функций распределения X (сплошная

линия), Y (пунктир) и Z (штрих-пунктир).

Отметим интересную топологическую особенность: значения функций рас-

пределения меняют свое взаимное расположение четыре раза, графики F_X

и F_Z имеют две точки пересечения, а график F_Y пересекается с каждым из

них по одному разу. Можно предположить, что такая картина характерна

при нетранзитивности.

3,0

2,5

2,0

1,5

1,0

0,5

0,2

0,4

0,6

0,8

1,0

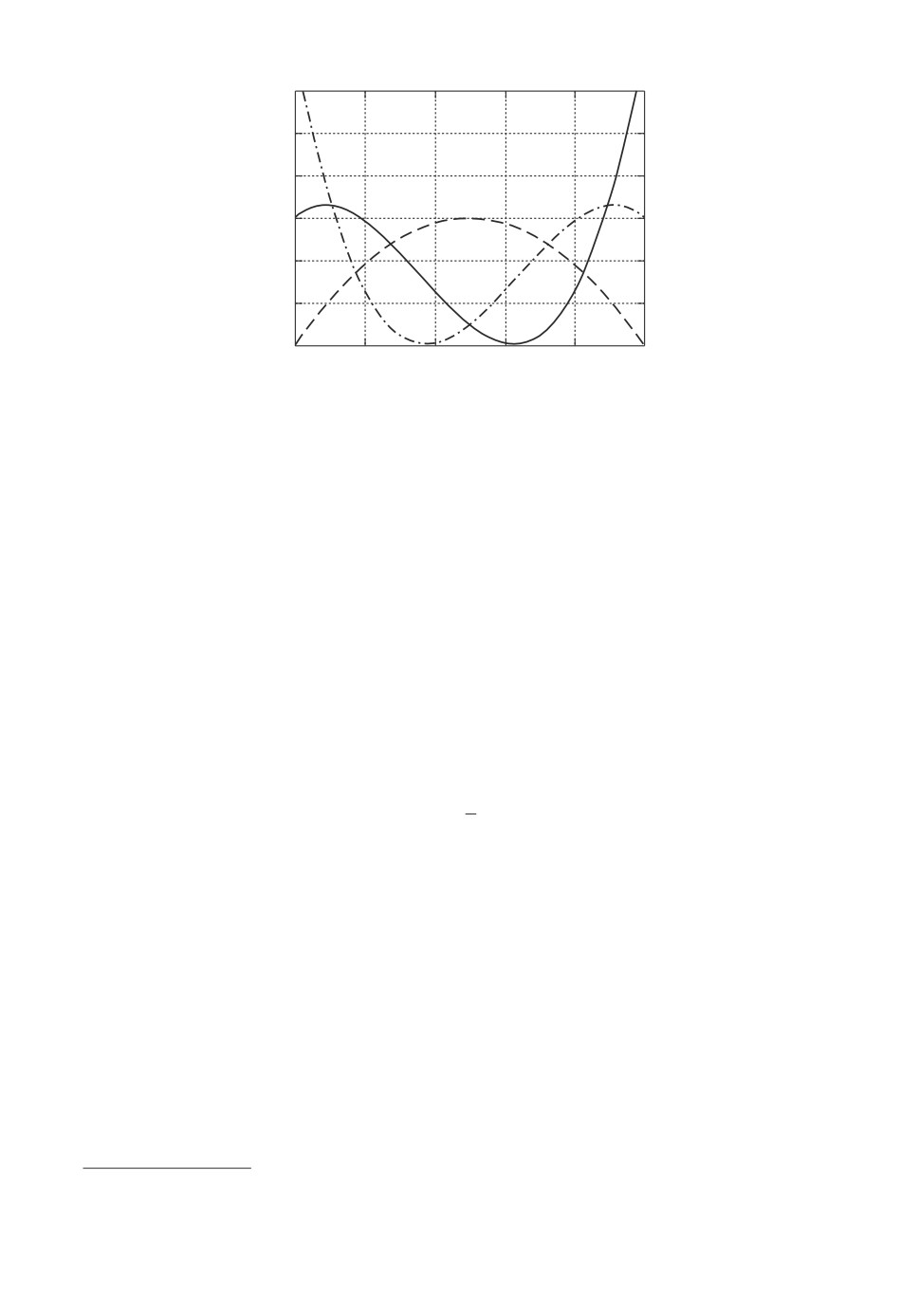
Рис. 2. Графики плотностей распределений к примеру (10).

Укажем также плотности, соответствующие функциям распределения (9):

p_X(x) = 1,511 + 3,452x - 22,410x² + 20,932x³,

(10)

p_Y (x) = 6x - 6x²,

p_Z(x) = 3,486 - 21,432x + 40,389x² - 20,932x³.

На рис. 2 представлены графики плотности распределения X (сплошная

линия), Y (пунктир) и Z (штрих-пунктир).

В настоящее время для данной модели продолжаются поиски оптималь-

ного набора (с максимальным значением p_XYZ ), и в любом случае хотелось

бы доказать его оптимальность аналитически.

Интересно также, как это максимальное значение растет с ростом N (при

√

N → ∞ оно, очевидно, стремится к (

5 - 1)/2 ≈ 0,618).

4. Заключение

В работе представлены критерии, с помощью которых доказано, что

для многих классических распределений нетранзитивности не может быть¹.

В случае распределений с полиномиальной плотностью на отрезке показано,

что нетранзитивность появляется начиная со степени N = 4.

Если рассматривать нетранзитивность как вредное явление, затрудняю-

щее принятие решения при сравнении каких-либо альтернатив, то практиче-

скую ценность имеет, во-первых, установление границ, в которых ее заведомо

не может быть, а значит, можно быть спокойным на этот счет, либо установ-

ление признаков, когда она может быть, и надо быть начеку, в том числе по

¹ Отдельно для равномерного, нормального, показательного и квадратичного (8) рас-

пределений это было ранее доказано студентом автора А.Ш. Изариповым в курсовой ра-

боте 2017/2018 учебного года.

возможности отказаться от использования отношения стохастического пред-

шествования и метода попарных сравнений либо дополнить их другими от-

ношениями и методами для большей уверенности.

Кроме того, на практике часто используются различные приближения ре-

альных распределений (которые могут просто никак не выражаться аналити-

чески), и важен вопрос, насколько хорошо эти приближения отражают харак-

терные свойства исходных распределений, в том числе, возможную нетран-

зитивность.

Отметим следующие интересные направления теоретических исследова-

ний по тематике работы.

1. Дальнейшее изучение возможности нетранзитивности в различных

классах непрерывных распределений. В частности, для распределений Вей-

булла с двумя или тремя произвольными параметрами в (6) вопрос остается

открытым. В случаях, когда нетранзитивность возможна, интересно также,

насколько могут быть велики максимумы типа (5) при различных ограниче-

ниях на распределения.

2. Помимо отношения стохастического порядка ≺, в теории вероятностей

и ее приложениях (в частности, в теории риска [27, гл. 2, 3]) рассматрива-

ются различные транзитивные отношения распределений. Если удастся най-

ти другие, возможно более слабые, транзитивные отношения, чем ≺, из ко-

торых следует стохастическое предшествование (1), это позволит обобщить

следствие 1. Интересно также, существует ли самое слабое транзитивное от-

ношение, из которого следует (1).

3. Отношение P(X<Y )>1/2 можно представить в виде E sign(Y -X)>0.

С другой стороны, отношение E(Y - X) > 0 транзитивно. Возникает вопрос,

при каких нечетных функциях f отношение Ef(Y - X) > 0 транзитивно, а

при каких нет. Подобные функции могут описывать нелинейные эффекты

взаимодействия объектов с характеристиками X и Y .

4. Можно далее рассмотреть случай n > 3 непрерывных случайных вели-

чин.

ПРИЛОЖЕНИЕ

Доказательство теоремы. Из (1) и (2) следует γ(F_X) < γ(FY ),

γ(F_Y ) < γ(F_Z ), откуда γ(F_X ) < γ(F_Z ), следовательно, P(X < Z) > 1/2, так

что имеет место транзитивность.

Доказательство следствия 1. Пусть случайные величины X₁ и X₂

независимы и имеют распределения Fθ1 и Fθ2 из K. Тогда из θ₁ < θ₂ следует

+^∞

∫

P(X₁ < X₂) =

Fθ₂ (x) dFθ₁ (x) >

Fθ₁ (x) dFθ₁ (x) = 1/2.

−∞

-∞

В обратную сторону, пусть P(X₁ < X₂) > 1/2. Если предположить,

что θ₁ > θ₂, то P(X₁ < X₂) < 1/2, а если предположить, что θ₁ = θ₂, то

P(X₁ < X₂) = 1/2, в обоих случаях приходим к противоречию, значит, из

P(X₁ < X₂) > 1/2 следует θ₁ < θ₂.

Таким образом, параметр θ здесь играет роль характеристики γ(F ).

Доказательство следствия 2. Случайные величины X₁ и X₂ можно

представить в виде:

X₁ = a₁ + b₁W₁, X₂ = a₂ + b₂W₂,

где W₁, W₂ — независимые случайные величины с некоторыми стандартными

распределениями F₀₁, F₀₂, симметричными относительно нуля. Обозначим

распределение b₁W₁ - b₂W₂ через G₁₂, оно тоже симметрично относительно

нуля. Тогда

P(X₁ < X₂) = P((a₁ + b₁W₁) - (a₂ + b₂W₂) < 0) = G₁₂(a₂ - a₁),

где правая часть больше 1/2 при a₂ - a₁ > 0 и меньше 1/2 при a₂ - a₁ < 0.

Таким образом, параметр сдвига a здесь играет роль характеристики γ(F ).

Доказательство утверждения 1. Достаточно показать, что

∫∞

I(α) = exp{-x^α - x} du > 1/2, α > 1.

Проблема в том, что подынтегральная функция возрастает по

α при

0 < x < 1 и убывает при x > 1.

Пусть α ≥ 2, тогда

∫¹

∫

I(α) > exp{-x^α - x} du ≥ exp{-x² - x} du =

(

√

)

(_√

))

√

πe1/4

-Φ

≈ 0,507 > 1/2.

Пусть 1 < α < 2, тогда функция xα-1, x > 0, является вогнутой и ее гра-

фик лежит ниже касательной в точке x = 1:

xα-1 ≤ (α - 1)x + (2 - α),

поэтому

x^α ≤ (α - 1)x² + (2 - α)x,

что используем для оценки интеграла:

∫∞

{

}

I(α) ≥ exp

-(α - 1)x² - (3 - α)x

dx =

(Π.1)

(

))

√

}(

^{ (3 - α)

3-α

exp

1-Φ

√

α-1

4(α - 1)

2(α - 1)

100

Оценка

0,55

0,54

0,53

0,52

0,51

0,50

1,0

1,2

1,4

1,6

1,8

2,0

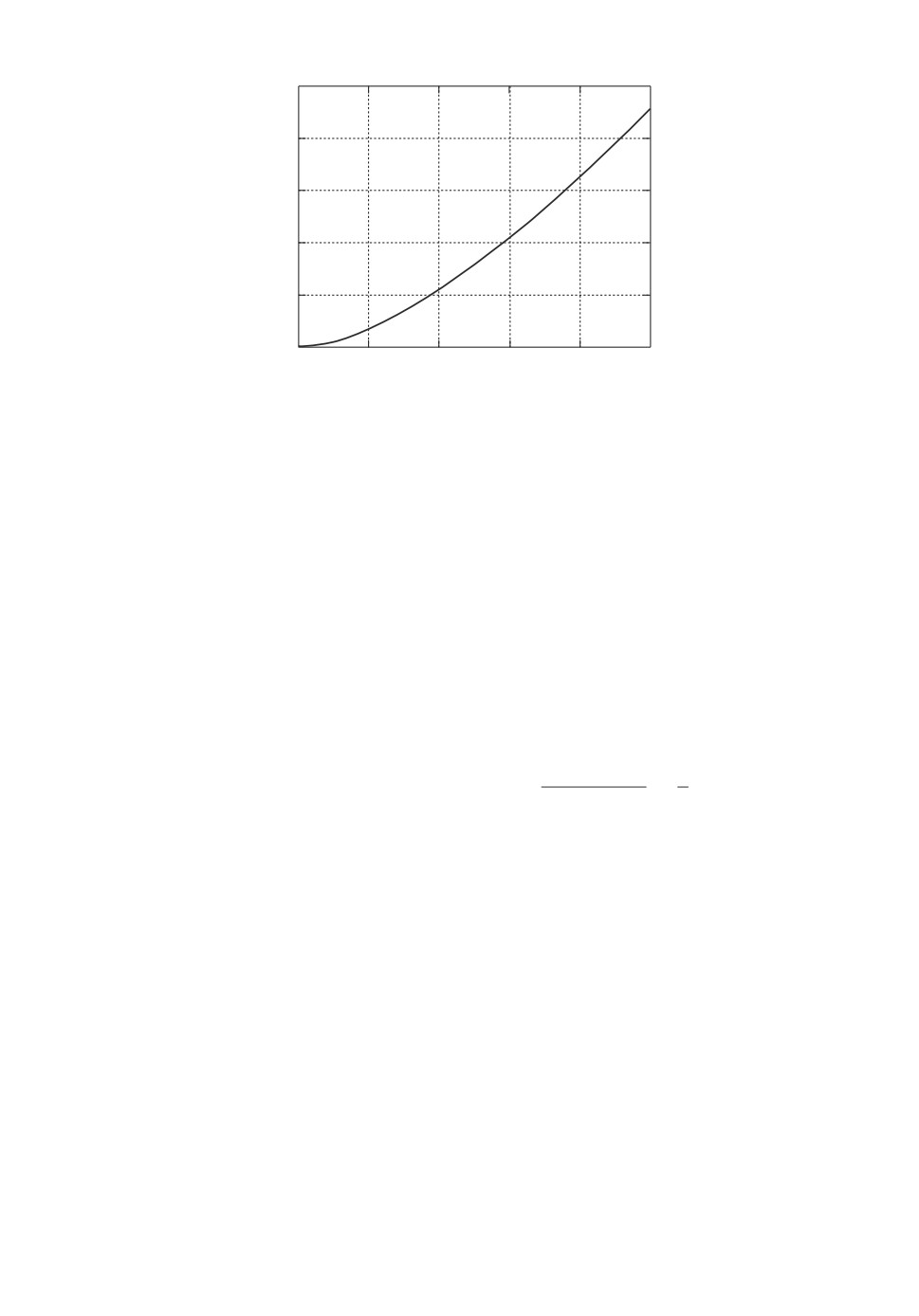
Рис. 3. График оценки (Π.1) к утверждению 1.

График правой части неравенства (Π.1) представлен на рис. 3. Видно,

что она больше 1/2. Отметим, что на концах отрезка [1, 2] это неравенство

обращается в равенство.

Доказательство утверждения 2. Обозначим:

FX (x) = a1x + a2x² + (1 - a1 - a2)x³,

FY (x) = b1x + b2x² + (1 - b1 - b2)x³,

FZ (x) = c1x + c2x² + (1 - c1 - c2)x³.

Тогда получаем

∫1

a₁b₂ - a₂b₁

P(X < Y ) = F_X (x) dF_Y (x) =

и таким образом, условие P(X < Y ) > 1/2 эквивалентно

(Π.2)

a₁b₂ - a₂b₁

> 0.

Введем полярные координаты:

a₁ = ρcos α, a₂ = ρsin α,

b₁ = ν cos β, b₂ = ν sin β,

тогда условие (Π.2) принимает вид

a₁b₂ - a₂b₁ = ρν(cos αsin β - sinα cos β) = ρν sin(β - α) > 0.

Скажем, что точка (b₁, b₂) следует за точкой (a₁, a₂), если угол против

часовой стрелки от радиус-вектора к точке (a₁, a₂) до радиус-вектора к точ-

ке (b₁, b₂) меньше 180^◦. Получается, что условие P(X < Y ) > 1/2 в точности

эквивалентно условию следования (b₁, b₂) за (a₁, a₂).

101

Выполнение условий нетранзитивности (1)-(3) эквивалентно существова-

нию точек (a₁, a₂), (b₁, b₂), (c₁, c₂), следующих друг за другом (по кругу).

Это возможно тогда и только тогда, когда начало координат O находится

внутри образованного ими треугольника, т.е. некоторая ε-окрестность O вхо-

дит в область допустимых коэффициентов (f₁, f₂) в (7). Однако это не так,

поскольку из неотрицательности плотности в нуле следует f₁ ≥ 0. Следова-

тельно, нетранзитивности здесь не может быть.

СПИСОК ЛИТЕРАТУРЫ

Steinhaus H., Trybula S. On a paradox in applied probabilities // Bull. de l’Acad.

Polon. Sci. 1959. V. 7. P. 67-69.

Trybula S. On the paradox of three random variables // Zastos. Matem. 1961. V. 5.

No. 4. P. 321-332.

Trybula S. On the paradox of n random variables // Zastos. Matem. (Appl. Math.)

1965. V. 8. No. 2. P. 143-156.

Usyskin Z. Max-min probabilities in the voting paradox // Ann. Math. Stat. 1964.

V. 35. No. 2. P. 857-862.

Богданов И.И. Нетранзитивные рулетки // Мат. просвещение. 2010. Сер. 3. Вып.

14. С. 240-255.

Поддьяков А.Н. Непереходность (нетранзитивность) отношений превосходства

и принятие решений // Психология. Журн. ВШЭ. 2006. № 3. С. 88-111.

Пермогорский М.С., Поддьяков А.Н. Отношение превосходства между объек-

тами и нетранзитивность их предпочтений человеком // Вопросы психологии.

2014. № 2. С. 3-14.

Поддьяков А.Н. Нетранзитивность — кладезь для изобретателей // Троицкий

вариант. № 242 от 21.11.2017.

Poddiakov A. Intransitive machines. Available at: https://arxiv.org/abs/1809.03869

(accessed September 8, 2018)

10.

Васильев В.А. О k-достижимости ядер T U-кооперативных игр // Мат. теория

игр и ее приложения. 2016. Т. 8. № 2. С. 3-27.

11.

Ларичев О.И. Свойства методов принятия решений в многокритериальных за-

дачах индивидуального выбора // АиТ. 2002. № 2. С. 146-158.

Larichev O.I. Properties of the Decision Methods in the Multicriteria Problems of

Individual Choice // Autom. Remote Control. 2002. V. 63. No. 2. P. 304-315.

12.

Гороховик В.В., Трофимович М.А. Условия оптимальности первого и второго

порядка в задачах векторной оптимизации с нетранзитивным отношением пред-

почтения // Тр. ИММ УрО РАН. 2014. Т. 20. № 4. С. 81-96.

13.

Аржененко А.Ю., Казакова О.Г., Чугаев Б.Н. Оптимизация бинарных опрос-

ников // АиТ. 1985. № 11. С. 138-144.

Arzhenenko A.Yu., Kazakova O.G., Chugaev B.N. Optimization of Binary

Questionnaries // Autom. Remote Control. 1985. V. 46. P. 1466-1472.

14.

Лепский А.Е. Стохастическое и нечеткое упорядочивание методом минималь-

ных преобразований // АиТ. 2017. № 1. С. 59-79.

Lepskiy A.E. Stochastic and Fuzzy Ordering with the Method of Minimal

Transformations // Autom. Remote Control. 2017. V. 78. No. 1. P. 50-66.

15.

Boland P.J., Singh H., Cukic B. The stochastic precedence ordering with applications

in sampling and testing // J. Appl. Probab. 2004. V. 41. No 1. P. 73-82.

102

16. Arcones M.A., Kvam P.H., Samaniego F.J. Nonparametric estimation of a

distribution subject to a stochastic precedence constraint // J. Amer. Stat. Assoc.

2002. V. 97. No. 457. P. 170-182.

17. Шахнов И.Ф. Задачи ранжирования интервальных величин при многокритери-

альном анализе сложных систем // Изв. РАН. ТиСУ. 2008. № 1. C. 37-44.

18. Martinetti D., Montes I., Diaz S., Montes S. A study on the transitivity of

probabilistic and fuzzy relations // Fuzzy Sets Syst. 2011. V. 184. P. 156-170.

19. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.-

Ижевск: Ин-т компьют. исслед. 2003.

20. Gardner M. The paradox of the nontransitive dice and the elusive principle of

indifference // Sci. Amer. 1970. V. 223. No. 6. P. 110-114.

21. Gardner M. On the paradoxical situations that arise from nontransitive relations //

Sci. Amer. 1974. V. 231. No. 6. P. 120-125.

22. Savage R. The paradox of nontransitive dice // Amer. Math. Montly. 1994. V. 101.

No. 5. P. 429-436.

23. Bozoki S. Nontransitive dice sets releazing the Paley tournament for solving Shütte’s

tournament problem // Miskolc Math. Notes. 2014. V. 15. No. 1. P. 39-50.

24. Conrey B., Gabbard J., Grant K., Liu A., Morrison K. E. Intransitive dice // Math.

Mag. 2016. V. 89. P. 133-143.

25. Buhler I., Graham R., Hales A. Maximally nontransitive dice // Amer. Math.

Montly, 2018. V. 125. No. 5. P. 387-399.

26. Weibull W. A statistical theory of the strength of materials. Stockholm:

Generalstabens litografiska anstalts förlag, 1939.

27. Булинская Е.В. Теория риска и перестрахование. М.: ООО «Мэйлер», 2008.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 05.10.2018

После доработки 18.01.2019

Принята к публикации 07.02.2019

103