Автоматика и телемеханика, № 6, 2019

Управление в социально-экономических

системах

(Санкт-Петербургский государственный университет),

К.С. КУЗНЕЦОВ (kostas.92@mail.ru)

(Санкт-Петербургский государственный университет)

СТОХАСТИЧЕСКАЯ МОДЕЛЬ УПРАВЛЕНИЯ СРЕДНЕВЗВЕШЕННОЙ

ЦЕНОЙ ПРОДАЖ ПРОИЗВОДИТЕЛЯ НА ТОВАРНЫХ БИРЖАХ

Предложен метод управления средневзвешенной ценой продаж произ-

водителя на товарных биржах. Актуальность поставленной задачи обу-

словлена необходимостью для производителя хеджировать свою прибыль

от резкого падения рыночных цен. Рассматриваются приложения пред-

ложенного управления к совершению торговых операций на реальных

товарных биржах с целью демонстрации его эффективности.

Ключевые слова: товарные биржи, случайные процессы, управление про-

дажами.

DOI: 10.1134/S0005231019060084

1. Введение

Нестабильность поведения цен на современных товарных рынках, включа-

ющих в себя торговлю нефтью, газом, древесиной и прочими широко востре-

бованными товарами общественного потребления, заставляет пересмотреть

ряд устоявшихся в течение длительного времени и ставших привычными

взаимоотношения между продавцами товара и его покупателями. Прежде

всего, это касается отказа от заключения долгосрочных контрактов, когда

покупатель, сознавая всю непредсказуемость будущего поведения рыночной

стоимости товара, предпочитает осуществлять его приобретение в рамках

специализированных бирж с обязательной поставкой купленного товара за

относительно короткий промежуток времени. Весьма убедительно описанная

тенденция проявляется, например, во взаимоотношениях производителей и

поставщиков российского природного газа и их европейских потребителей.

В настоящее время в Европе существует 13 хранилищ газа (хабов) и орга-

низованных при них 7 специализированных бирж, торгующих различными

объемами газа с его обязательной двухдневной поставкой начиная с момента

заключения сделки. Торговые операции при этом характеризуются высокой

ликвидностью и суммарным объемом, охватывающим значительную часть

мировой торговли газом. Разумеется, что подобный поворот событий требует

от продавца-производителя товара определенной реакции, связанной с по-

строением собственной стратегии управления продажами, обеспечивающей,

по крайней мере, хеджирование получаемой денежной выручки от резкого

142

«проседания» рыночной стоимости товара. Одной из таких стратегий может

служить построение управления, связанного с увеличением средневзвешен-

ной цены продаваемого данным производителем товара.

Разумеется, что подобная стратегия требует совершения продавцом това-

ра не только неравномерных по объему сделок, связанных с продажей товара,

но и так называемых «реверсов», отвечающих покупкам того же самого то-

вара, совершаемым в определенных объемах и в определенное время. Цель

настоящей работы заключается в описании одного из возможных способов

реализации указанной стратегии и демонстрации ее эффективности на при-

мере осуществления торгов в газовой отрасли на Европейской энергетической

бирже¹.

2. Формализация постановки задачи

Будем исходить из того, что на заданном промежутке времени [0, T ] цены

биржевых сделок x_t, t ∈ [0, T ] относительно единицы рассматриваемого това-

ра удовлетворяют следующему стохастическому дифференциальному урав-

нению:

(1)

dx_t = c (t, x_t) dt + σ_tx_tdW_t,

σ_t = σ(t,ω) - коэффициент волатильности, представляющий собой неизвест-

ную, вообще говоря случайную, функцию времени, не зависящую от x_t, W_t -

стандартный винеровский процесс [1]. Структура коэффициента сноса c(t, x_t)

в данной работе не требует отдельной спецификации, однако предполагается,

что реализации случайного процесса x_t не принимают отрицательных значе-

ний с вероятностью единица и, кроме того, задача Коши для уравнения (1)

имеет единственное сильное решение [2]. Вопрос об адекватности выбран-

ной модели ценообразования для рассматриваемой ниже задачи управления

обсуждается отдельно в Приложении 1. В дальнейшем соответствующими

буквами, но только с волной будем обозначать наблюдаемые реализации рас-

сматриваемых случайных процессов, как например x_t и x_t.

Под средневзвешенной ценой продаж производителя на промежутке вре-

мени [0, T ] будем понимать величину

V_T

x^avT =

ã_T

гд

V_T - вырученный на промежутке времени [0,T] объем денежных средств,

ã_T - количество проданных на том же промежутке времени единиц товара.

Под целью управления будем понимать такое количество продаваемого на

промежутке времени [0, t], где t ∈ [0, T ], единиц товара ã_t (ã₀ = 0, ã_t < 0, при

t > 0 и ã_t отвечает реализации цены x_t), которое бы обеспечило выполнение

условия

(2)

x^avT > max x_t,

t∈[0,T ]

¹ European Energy Exchange AG: [Электронный ресурс]. Лейпциг, 2017.

URL: https://www.eex.com (дата обращения: 15.05.2017).

143

при этом при построении управления ã_t в качестве обратной связи могут

быть использованы только цены совершаемых биржевых сделок на проме-

жутке времени [0, t]. Другими словами, исходим из того, что коэффициенты

в уравнении (1) не поддаются оценке, по крайней мере, с требуемой степенью

точности в режиме реального времени. Интуитивно понятно, что обеспечить

выполнение условия (2) можно только за счет наращивания некоторой спе-

кулятивной прибыли (точное определение будет дано ниже), возникающей

в результате постепенного реинвестирования в товар некоторой части вы-

свобождающихся в результате продаж наличных денег с последующей пере-

продажей товара, исходя из динамики биржевых сделок начиная с момента

начала управления. В следующем разделе будет построено одно из указан-

ных возможных управлений, которое при выполнении определенных условий

обеспечит справедливость неравенства (2).

3. Построение управления

Далее будем следовать непрерывной модели финансовых рынков [3] и,

в частности, подходу, связанному с построением управления альтернативно-

го стратегии самофинансирования, учитывающего процесс реинвестирования

денег в товар, первоначально предложенному в [4] и затем подробно изложен-

ному в [5] (см. также [6]), но только в отличие от упомянутой статьи [5] для

случая короткой позиции и применительно к операциям на товарной бирже.

Введем в рассмотрение случайную функцию, исходя из формулы

(3)

f_t = a_tx_t + m_t,

где a_t = a (t, ω) является измеримой случайной функцией, определяю-

щей количество единиц товара, проданного на промежутке времени [0, t];

m_t = m(t,ω) - измеримая случайная функция, явное выражение для которой

будет дано ниже. Будем исходить из управления функцией f_t, определяемого

на каждый момент времени соотношением

(4)

df_t = a_tdx_t + l (t, x_t

) dt,

где dx_t является правой частью уравнения (1). Второе слагаемое в (4) бу-

дем интерпретировать как вырученный в результате продаж и выведенный

из процесса управления за интервал времени [t, t + dt] объем наличных де-

нег. Зависимость l (t, x_t) в дальнейшем будет выступать в роли управляющей

функции. Применяя к левой и правой частям соотношения (3) процедуру

вычисления стохастического дифференциала, получим формулу

df_t = a_tdx_t + x_tda_t + da_tdx_t + dm_t.

Последнее соотношение с использованием зависимости (4) может быть пере-

писано в виде

dm_t = -xt+dtda_t + l (t, x_t) dt,

144

где xt+dt = x_t + dx_t, или в интегральной форме

∫t

∫

(5)

m_t = - xτ+dτ da_t + l (τ,x_τ

) dτ.

Определим понятие «спекулятивной прибыли», полученной в результате со-

вершенных на промежутке времени [0, t] торговых операций, следующим об-

разом:

∫t

(6)

p_t = a_tx_t - xτ+dτ da_t,

при этом здесь будет рассматриваться случай короткой позиции, когда a_t < 0

при t > 0.

С учетом (3)-(5) зависимость (6), как нетрудно проверить, эквивалентна

соотношению

∫t

(7)

p_t = f_t - l (τ,x_τ

) dτ.

Поясним понятие «спекулятивной прибыли» в данной конкретной ситуа-

ции более подробно. Предположим, что на фиксированные моменты времени

1, . . . , n по ценам x₁, . . . , x_n было продано или куплено b₁, . . . , b_n единиц това-

ра, при этом b_i < 0 отвечает продаже, b_i > 0 соответствует покупке указан-

ного его количества |b_i|. Будем исходить из того, что имеет место короткая

∑

позиция. Последнее означает выполнение неравенства

b_i < 0 для любого

i=1

j = 1,...,n. Тогда понятно, что сумма денежных средств, вырученная в ре-

∑

зультате указанных торговых операций, определится соотношением - x_ib_i.

i=1

∫

С другой стороны, интеграл - xτ+dτ da_τ представляет собой непрерывный

аналог указанного соотношения, при этом символ xτ+dτ означает, что при

представлении данного интеграла в виде предела соответствующих сумм

подынтегральная величина вычисляется на правом конце соответствующих

интервалов разбиения. Одновременно имеет место тождество

∫t

∫

− xτ+dτda_τ = a_tx_t - xτ+dτda_τ + |a_t|x_t,

т.е., другими словами, вырученная сумма денег на интервале времени [0, t]

состоит из «спекулятивной прибыли» и суммы денег, полученной от реали-

зации товара на момент времени t.

145

Цена

Границы

26-09-2014

04-10-2014

12-10-2014

Рис. 1. Выбор ценового коридора.

tg(z)

1,5

1,0

0,5

1,0

1,5

Рис. 2. Выбор корня трансцендентного уравнения.

Обратим внимание на то, что отличие модели (3), (4) от моделей управ-

ления с потреблением [7, 8] заключается в том, что величина m_t, как видно

из (5), отвечает процессу реинвестирования, когда денежные средства, вы-

ручаемые в процессе совершения спекулятивных операций, вкладываются в

покупку определенного количества единиц товара. Несмотря на то, что m_t

не входит явно в (7), ее отсутствие привело бы к тому, что в (7) величина f_t

равнялась бы a_tx_t. Это означало бы отсутствие указанного выше эффекта

реинвестирования и, как следствие, спекулятивной прибыли.

Введем в рассмотрение ценовой коридор [a, b], первоначально полагая, что

наблюдаемые значения стоимости единицы товара, т.е. реализация случай-

ного процесса x_t на всем промежутке времени t ∈ [0, T ], будут находиться

в указанном ценовом коридоре и, соответственно, x_t ∈ [a,b]. Ниже укажем

на способ расширения ценового коридора в процессе совершения торговых

операций при возникновении такой необходимости, т.е. в ситуации, когда на-

блюдаемое значение цены x_t пересечет одну из его границ. Кроме того, для

удобства вычислений нормируем цену единицы товара на величину верхней

границы ценового коридора и, соответственно, в процессе дальнейшего изло-

жения будем полагать, что x_t ∈ (β, 1), где β = a/b, как это показано на рис. 1.

146

0,8

0,6

0,4

0,2

0,70

0,75

0,80

0,85

0,90

0,95

1,00

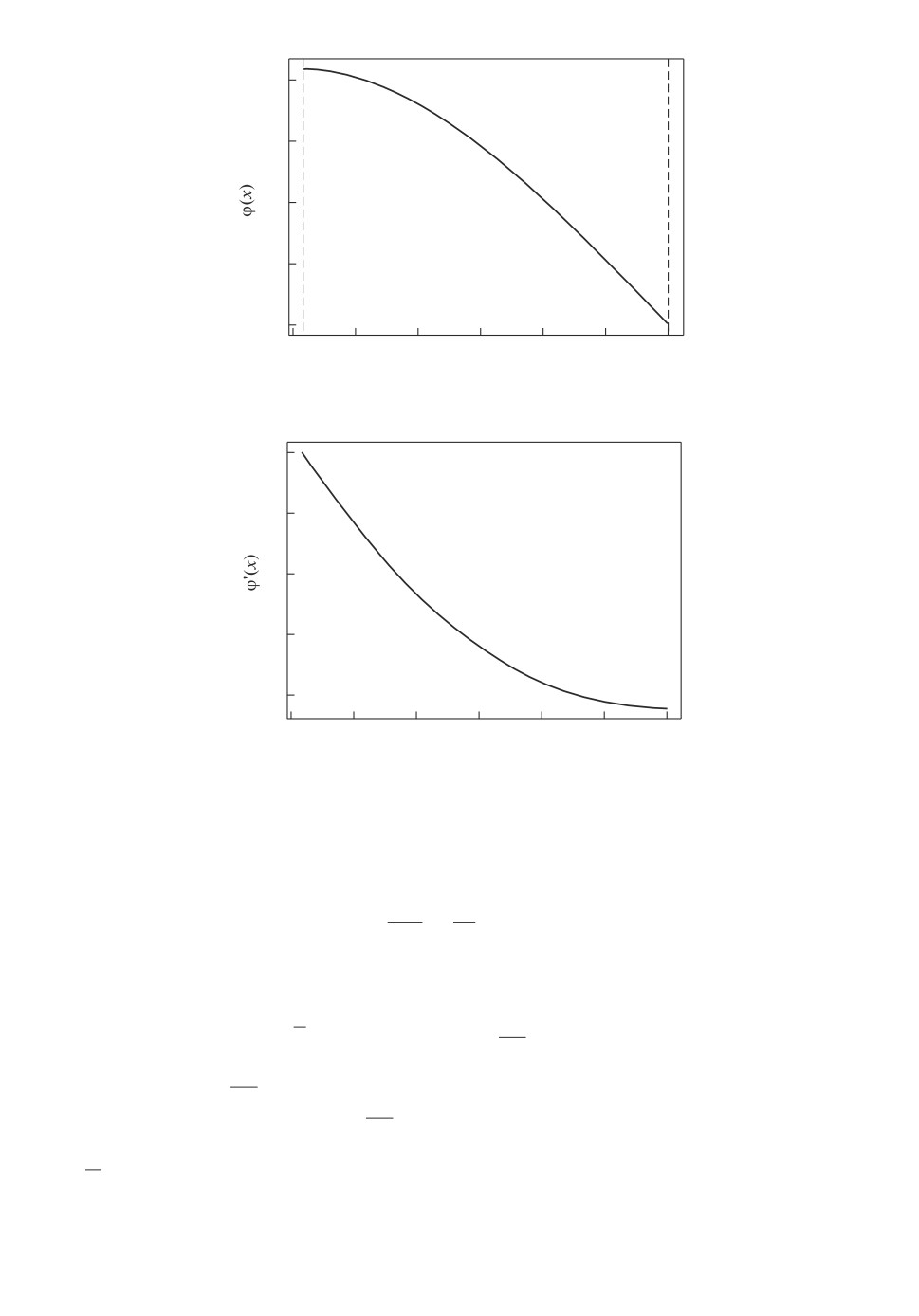
Рис. 3. ϕ(x) - решение задачи (8).

0,70

0,75

0,80

0,85

0,90

0,95

1,00

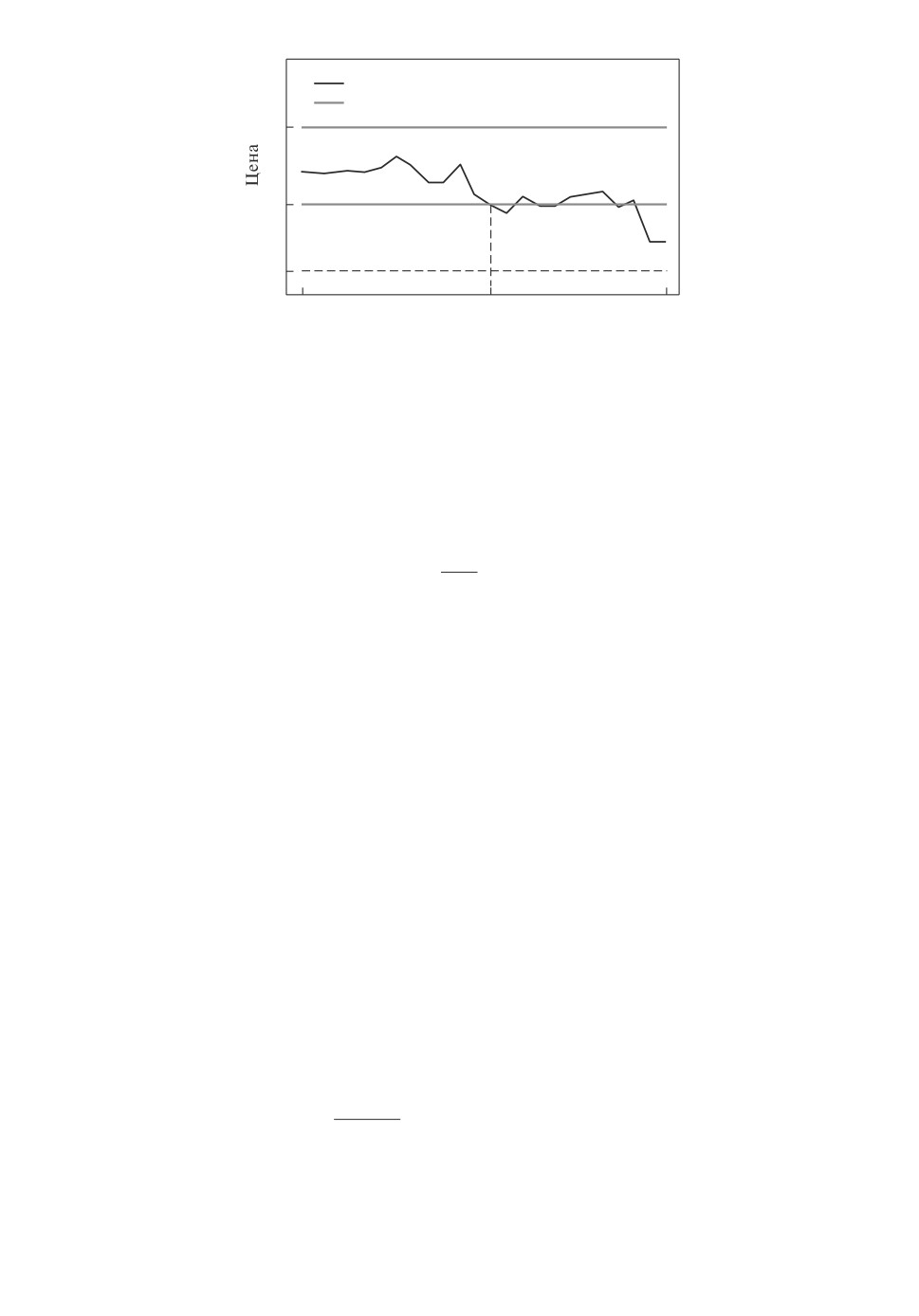
Рис. 4. ϕ^′(x) - производная от решения задачи (8).

Далее, введем в рассмотрение зависимость ϕ (x), отвечающую первой соб-

ственной функции задачи Штурма-Лиувилля

d²ϕ

λ²¹

(8)

ϕ = 0,

dx²

x²

ϕ(1) = ϕ^′ (β) = 0.

Нетрудно убедиться [9], что в качестве первой собственной функции мож-

но выбрать ϕ (x) =

√xsin (bln x), при b =n+lβ < 0, где z⁺ > 0 является мини-

мальным по модулю, строго положительным корнем трансцендентного урав-

нения tg z = -2zlnβ , как это показано на рис. 2, при этом, очевидно, должно

выполняться неравенство -2lnβ > 1, что требует выбора достаточно узкого

ценового коридора, а именно, величина β должна удовлетворять неравенству

< β < 1.

e²

Кроме того, на рис. 3 и 4 приведены соответственно графики функций

ϕ(x) и ϕ^′ (x).

147

Первое собственное число λ₁, отвечающее первой собственной функции

задачи (8), удовлетворяет зависимости λ²¹ = b² +¹⁴ , при этом заметим, что

ϕ′ (1) = b < 0. Зададим теперь динамику изменения количества единиц това-

ра a_t, проданного на интервале времени [0, t], следующим образом:

∫t

u₀ (τ)



(9)

ã_t =

dτ · ϕ^′ (x_t)

ϕ(x_τ)

xt=xt

где u₀ (τ) > 0 представляет собой произвольную кусочно-непрерывную функ-

цию.

Теорема. Пусть цена x_t следует стохастическому дифференциально-

му уравнению (1), при этом коэффициент волатильности σ_t = σ (t,ω) как

случайная функция не зависит от процесса x_t. Тогда если количество единиц

проданного товара во времени задается формулой (9), то «спекулятивная

прибыль» определяется соотношением

∫t

∫

λ²

σ2sds

u₀ (τ)

(10)

pt =

dτ · ϕ (x_t) - u₀ (τ) e

dτ,

ϕ(x_τ)

при этом зависимость

(11)

V_T = p_T + |ã_T | x_T

определяет общий объем вырученных на временном интервале [0,T] налич-

ных денег.

Доказательство теоремы приведено в Приложении 2.

Замечание. Отметим, что выбор именно первой собственной функции за-

дачи Штурма-Лиувилля (8) обеспечивает ее отличие от нуля внутри ценового

коридора (β, 1) и, как следствие, отсутствие сингулярностей в знаменателях

формул (9) и (10). Также заметим, что, как это было анонсировано ранее,

управление a_t, определяемое формулой (9), не содержит в явном виде коэф-

фициенты стохастического дифференциального уравнения (1).

Обратим внимание на то, что средневзвешенная цена реализованного то-

вара на интервале времени [0, T ] в количестве |a_T | может быть вычислена

исходя из соотношения

(12)

x^avT = x_T +

|ã_T |

Из (12) видно, что при одном и том же объеме проданного товара |ã_T | боль-

шая средневзвешенная цена отвечает большей спекулятивной прибыли. В то

же время анализ соотношения (10) показывает, что увеличению средневзве-

шенной цены способствуют два фактора. Первый фактор является времен-

ным и связан с увеличением средневзвешенной цены с ростом времени при

148

Цена

Границы

t *

Рис. 5. Расширение ценового коридора.

условии, что наблюдаемое значение цены x_t остается в одном и том же це-

новом коридоре. Второй фактор увеличения обусловлен влиянием коэффи-

циента волатильности, при котором второй интеграл в (10) экспоненциально

убывает при его росте. При этом выполнение неравенства

x^avT = x_T +

> max |x_t|

|ã_T |

t∈[0,T ]

обеспечивает достижение цели управления (2). Наконец заметим, что выбор

соответствующей функции ϕ(x) в формулировке теоремы обеспечивает же-

лаемый рост средневзвешенной цены при падении котировок, что следует

из (9), (10). Действительно, как видно из графиков функций ϕ(x) и ϕ^′(x),

изображенных соответственно на рис. 3, 4, падение котировок x_t приводит к

росту p_t и одновременно к уменьшению |ã_t|. Кроме того, обратим внимание

на тот факт, что рост котировок приводит к увеличению объема продаж.

Рассмотрим теперь вопрос о расширении ценового коридора в случае воз-

никновения такой необходимости. Предположим, что на момент времени t^∗

наблюдаемое значение цены x_t пересекает нижнюю границу ценового кори-

дора, как это показано на рис. 5. Вариант пересечения верхней границы ко-

ридора рассматривается аналогично.

В любом из этих двух случаев выбирается новый ценовой коридор, отве-

чающий интервалу (β₁, 1). Обозначим первую собственную функцию задачи

Штурма-Лиувилля (8) для нового ценового коридора через ϕ₁(x). Выберем

вместо u₀(τ) новую управляющую функцию u₁(τ) на временном интерва-

ле [0, t^∗] таким образом, чтобы выполнялось соотношение

∫

u₁ (τ)



dτ · ϕ′1 (x_t)

=ã^∗t

ϕ₁ (x_τ )

xt=xt

для всех t ∈ [0, t^∗], где зависимость ã^∗t отвечает уже совершенным на проме-

жутке времени [0, t^∗] торговым сделкам. Поставленная таким образом задача

149

сводится к рассмотрению уравнения Вольтерры первого рода

∫

K (t, τ) x (τ) dτ = f (t)

относительно неизвестной функции x (τ) = u₁ (τ). Здесь

ϕ′₁ (x_t) |xt=xt

K (t, τ) =

f (t) = ã^∗t.

ϕ(x_τ)

Последнее уравнение решается на основе стандартных методов теории некор-

ректных задач в пространстве L₂ на компактном множестве функций огра-

ниченной вариации [10]. Соответственно, при t > t^∗ функция управления

u₁(t) > 0 может, как и ранее, быть выбрана произвольным образом в классе

кусочно-непрерывных функций.

4. Пример реализации построенного управления

на реальных биржевых площадках

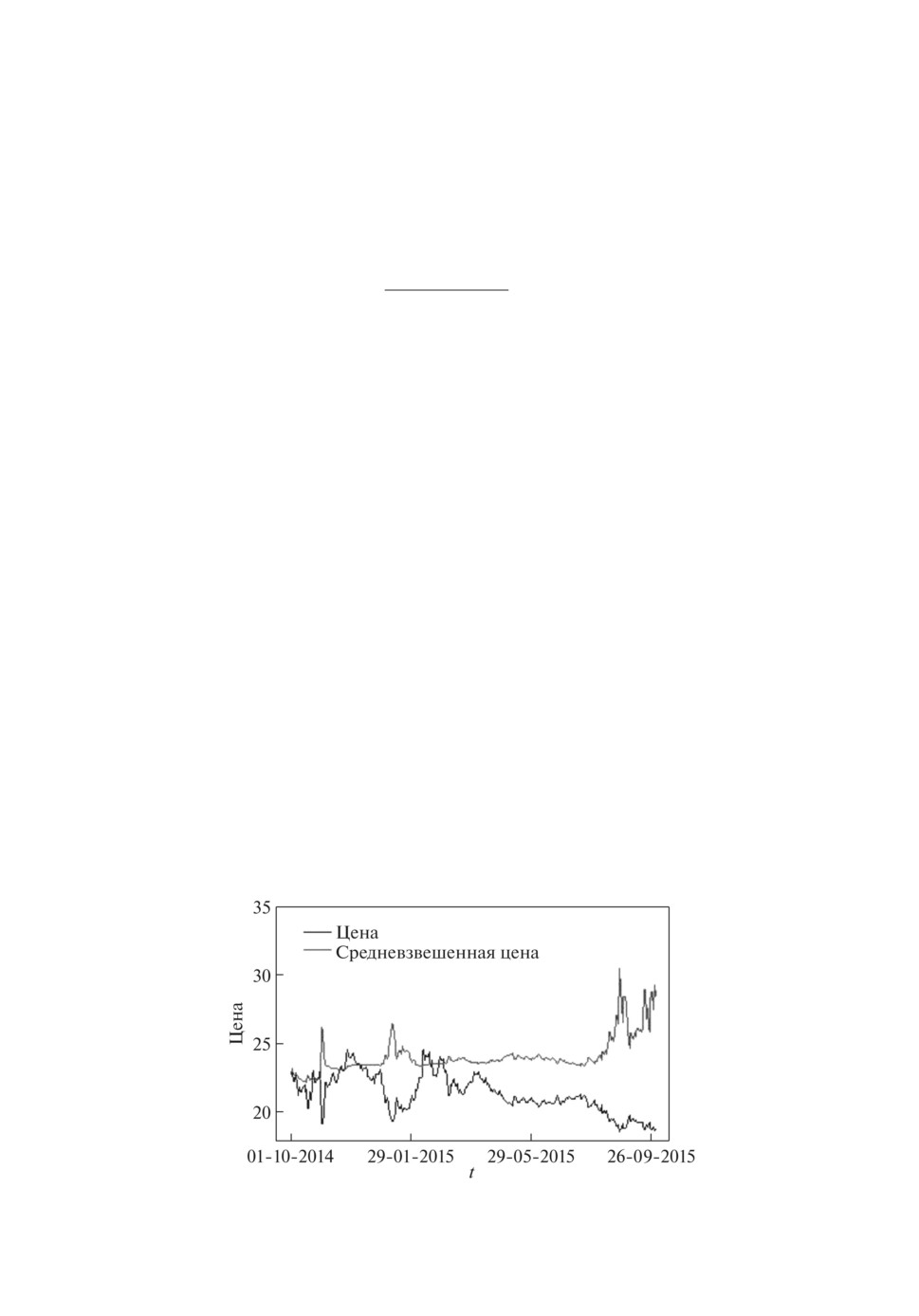
На рис. 6 приводится график цен биржевых сделок, отвечающих их усред-

ненным значениям за одну дневную торговую сессию в европейской валюте

на временном интервале с 1 октября 2014 г. по 30 сентября 2015 г. за 1 МВт·ч

торгуемой энергии. На этом же графике приведена и динамика средневзве-

шенной цены за одну единицу того же товара, полученной в результате по-

строенного выше управления (9). Здесь управляющая функция u₀ (τ) перво-

начально полагается всюду постоянной, при этом ценовой коридор выбира-

ется симметричным относительно первой совершенной системой управления

сделки и шириной, равной двум евро. В дальнейшем граница ценового ко-

ридора расширяется по мере необходимости на один евро в зависимости от

«пробития» ценой его верхней или нижней границы. При этом u₀ (τ) заме-

няется на управляющую функцию u₁ (τ) для определенных выше значений

Рис. 6. График средневзвешенной цены.

150

100

200

26-09-2014

04-10-2014

12-10-2014

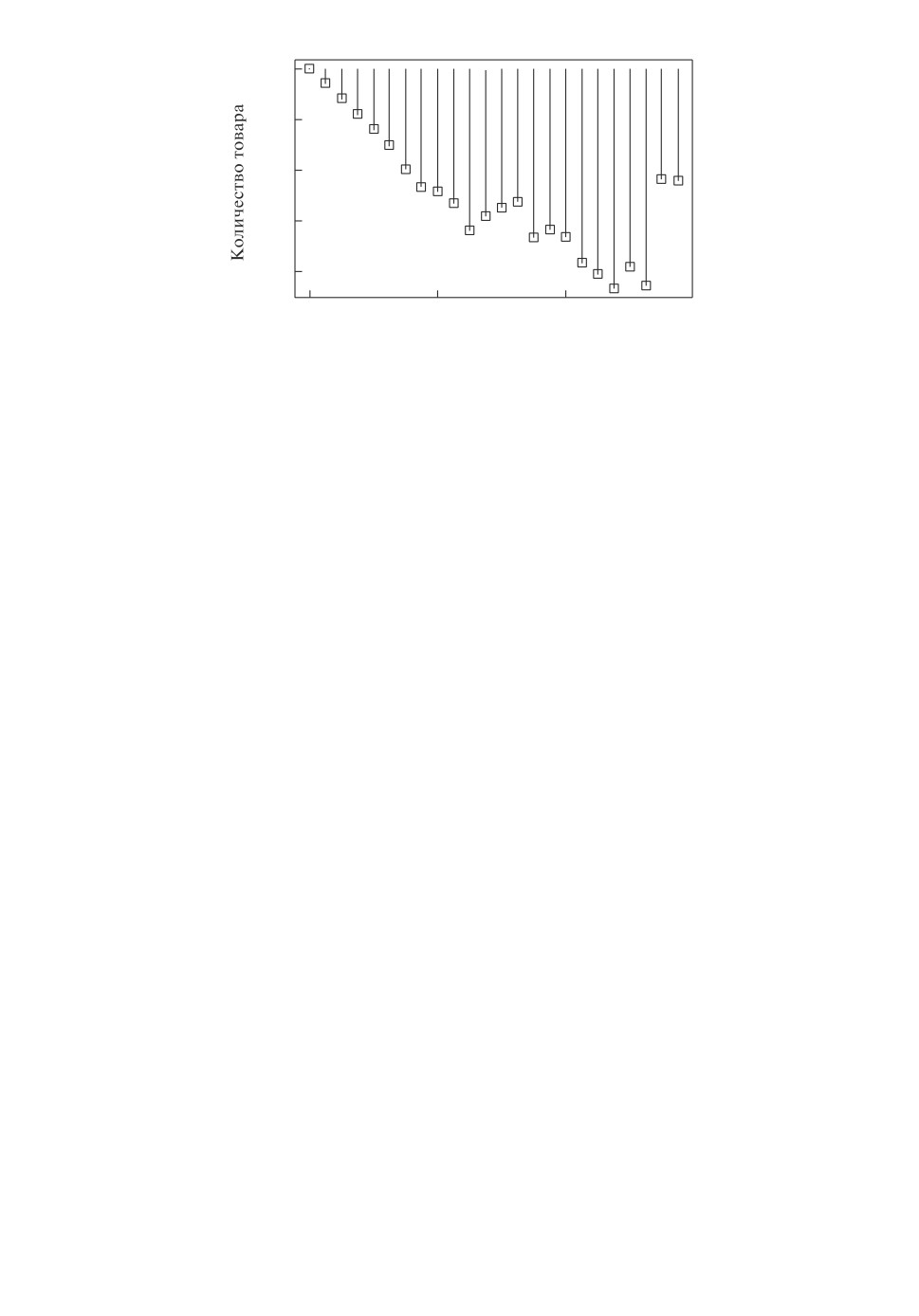
Рис. 7. Количество проданных единиц товара.

аргумента τ, принадлежащих промежутку [0, t^∗]. Кроме того на рис. 7 приве-

ден график изменения количества проданного товара, из которого ясно виден

процесс совершения соответствующих «реверсов».

5. Заключение

Анализ применения управления (9) на современных биржевых рынках тор-

говли газом демонстрирует эффективный метод повышения средневзвешен-

ной цены продаваемого товара в случае резкого уменьшения его рыночной це-

ны. Даже нарушение выполнения условия (2) на некотором достаточно малом

подмножестве временного интервала [0, T ] не делает построенное управление

менее эффективным поскольку априори «угадать», что именно соответствую-

щие цены будут максимально возможными по отношению к средневзвешен-

ной цене на момент времени T , не представляется возможным. Однако здесь

возникает проблема, связанная с планируемым объемом продаж газа на фик-

сированном промежутке времени. Приведенная конструкция указывает на то,

что проданное количество товара в результате проведения соответствующих

торговых операций становится случайным и вопросы, касающиеся конкрети-

зации выбора управляющей функции u₀ (τ), своевременного закрытия пози-

ций, а также планирования поставок товара, приобретают самостоятельный

характер.

ПРИЛОЖЕНИЕ 1

Вопрос об адекватности используемой в данной работе модели ценообра-

зования (1), по существу, сводится к вопросу об адекватности вычисления

спекулятивной прибыли по формуле (10) при изменении количества продан-

ного товара, определяемого соотношением (9). Заметим, что вычисление спе-

кулятивной прибыли по формуле (6) не использует конкретную модель це-

нообразования и осуществляется непосредственно исходя из изменения ко-

личества проданного товара ã_t и реестра биржевых сделок x_t. Поэтому без

потери общности полагаем в (9) u₀ (τ) ≡ 1 и вычисляем спекулятивную при-

быль по формуле (6) для заданной реализации цены x_t. С другой стороны

151

Рис. 8. Графики спекулятивной прибыли, вычисленные по формулам (6) и (7).

ту же самую величину находим с использованием формулы (10), которая по-

лучена на основе модели ценообразования (1), при этом интегральная вола-

тильность в (10) вычисляется на основе робастных алгоритмов оценивания,

описанных в [11, 12]. Существенно отметить, что относительная погрешность

вычисления искомой величины по формуле (10), как показывает анализ гра-

фиков на рис. 8, не превышает 7%. Здесь необходимо уточнить, что вычис-

ления проводились с учетом того, что из упомянутых внешних источников

были доступны и, соответственно, использовались лишь цены закрытия тор-

говых сессий, что, разумеется, существенно огрубляло точность сделанных

расчетов. В то же время для высоколиквидных активов, например акций из

категории “голубые фишки”, торгуемых как на российском, так и на аме-

риканском фондовом рынках, аналогичная величина, полученная на основе

полных “intraday” данных о котировках, составляет доли процента и меньше.

Кроме того заметим, что теорема будет оставаться справедливой и в случае

процесса диффузии со скачками, рассмотренного в [13], а также при исполь-

зовании модели Хестона [14], когда управляющие винеровские процессы в

указанной модели являются независимыми или когда используемый в ней

коэффициент “волатильность волатильности” равен нулю.

ПРИЛОЖЕНИЕ 2

Доказательство теоремы.

Будем искать неизвестную функцию f_t в виде f_t = f (t, x_t), где x_t удовле-

творяет уравнению (1). Применяя к функции f (t, x_t) формулу Ито и сравни-

вая ее с соотношением (4), получим зависимости

∂f

∂²f

(П.2.1)

σ2tx²

= l(t,x_t

);

∂t

^t ∂x²

∂f

(П.2.2)

a_t =

∂x_t

Управление l (t, x_t) будем искать в виде

(П.2.3)

l (t,x_t) = r (t) ϕ(x_t

152

где ϕ (x_t) представляет собой первую собственную функцию, отвечающую

первому собственному числу λ₁ задачи Штурма-Лиувилля (8). Структура

функции r (t) будет определена ниже. Зададим начальные и граничные усло-

вия:

(П.2.4)

f (0, x_t

) = 0,

∂f

(П.2.5)

→0

при x_t

→ β,

∂x_t

(П.2.6)

f (t, x_t) → 0 при x_t

→ 1.

С учетом соотношения (П.2.3) будем искать решение смешанной задачи

(П.2.4)-(П.2.6) для уравнения (П.2.1) методом разделения переменных (по-

скольку в силу условия теоремы σ_t не зависит от x_t) в виде

f (t, x_t) = K (t) ϕ (x_t) ,

где K (t) представляет собой неизвестную функцию. В результате несложных

преобразований получим соотношение

∫t

∫

λ²

σ2sds

(П.2.7)

f (t, x_t) = e²

r (τ) dτ · ϕ (x_t

Зависимости (П.2.2), (П.2.7) определяют количество проданного товара

исходя из формулы

)

∫

⁽ ∂f



λ²

σ2sds



(П.2.8)

ã_t =



= e²

r (τ)dτ · ϕ^′ (x_t)



xt=xt

∂x_t

xt=xt

Недостатком формулы (П.2.8) является то, что в нее в качестве обратной свя-

зи для вычисления ã_t входят не только цены совершаемых по данному товару

сделок, но и волатильность σ_t. Для устранения возникшей проблемы введем

в рассмотрение следующую процедуру. Разобьем отрезок [0; t] на n частей

следующим образом: 0 = t₀ < t₁ < . . . < t_n = t. Определим функцию r (τ) как

предел поточечно сходящейся к ней последовательности функций r_n (τ), за-

даваемых соотношением

∫

λ²

σ2sds

u_n (τ)

(П.2.9)

r_n (τ) =

ϕ(x_τ)

где τ ∈ (ti-1, t_i], u_n (τ)

- заданные функции, при этом последователь-

ность u_n (τ) при n → ∞ в условиях равномерного дробления отрезка [0; t]

предполагается поточечно сходящейся к некоторой функции u (τ) ≥ 0. Под-

ставляя в (П.2.8) вместо r (τ) последовательность (П.2.9), получим

∫

∑



u_n (τ)



ãtj =

dτ · ϕ^′ (x_t)

ϕ(x_τ)

xt=xt

i=1

ti-1

153

или

∫

u_n (τ)



ãtj =

dτ · ϕ^′ (x_t)

ϕ(x_τ)

xt=xtj

Осуществляя предельный переход при n → ∞ и исходя из условия равномер-

ного дробления отрезка [0; t], окончательно получим формулу, определяю-

щую непрерывное распределение количества проданного товара во времени

при наблюдаемом значении цены x_t:

∫t

u (τ)



(П.2.10)

ã_t =

dτ · ϕ^′ (x_t)



ϕ(x_τ)

xt=xt

Исходя, в свою очередь, из соотношений (7), (П.2.3), (П.2.7), (П.2.9) и рас-

суждая аналогичным образом, приходим к формуле для величины «спекуля-

тивной прибыли», отвечающей наблюдаемым значениям цены x_t на момент

времени t:

∫^t

∫

λ²

σ2sds

u (τ)

(П.2.11)

dτ · ϕ (x_t) - e

u(τ)dτ.

pt =

ϕ(x_τ)

СПИСОК ЛИТЕРАТУРЫ

Оксендаль Б. Стохастические дифференциальные уравнения. Введение в тео-

рию и приложения. М.: Мир, 2003.

Бородин А.Н. Случайные процессы. СПб.: Лань, 2013.

Ширяев А.Н. Основы стохастической финансовой математики. Т. 1, 2. М.: Фа-

зис, 1998.

Vavilov S.A. On the probability models to control the investor portfolio / Asymptotic

methods in probability and statistics with applications. Ed. by Balakrishnan N.,

Ibragimov I.A., Nevzorov V.B. Boston: Birkhauser, 2001. P. 535-547.

Vavilov S.A., Ermolenko K.Yu. On the new stochastic approach to control the

investment portfolio // IAENG I. J. A. M. 2008. V. 38. I. 1. P. 54-62.

(URL: http://www.iaeng.org/IJAM/issues_v38/issue_1/IJAM_38_1_09.pdf)

Вавилов С.А., Ермоленко К.Ю. Финансовая математика. Стохастический ана-

лиз. М.: Юрайт, 2016.

Флеминг У., Ришел Р. Оптимальное управление детерминированными и стоха-

стическими системами. М.: Мир, 1978.

Karatzas I., Lehoczky J.P., Shreve S.E. Optimal Portfolio and Consumption

Decisions for a “Small investor” on a Finite Horizon // SIAM J. Control Optim.

1987. V. 25. No. 6. P. 1557-1586.

Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.:

Наука, 1971.

10.

Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы

решения некорректных задач. М.: Наука, 1990.

154

11. Zhang L., Mykland A., Ait-Sahalia Y. A Tale of Two Time Scales: Determining

Integrated Volatility With Noisy High-Frequency Data // J. Amer. Stat. Ass. 2005.

V. 100. No. 472. P. 1394-1411.

12. Вавилов С.А., Ермоленко К.Ю. Об одном подходе к проблеме непараметрическо-

го оценивания в статистике случайных процессов на основе метода некорректной

задачи // Зап. научн. семинаров ПОМИ. 2007. Т. 351. С. 117-129.

13. Merton R. Option pricing when underlying stock returns are discontinuous //

J. Finan. Econom. 1976. V. 3. P. 125-144.

14. Heston S.L. A closed form solution for options with stochastic volatility with

applications to bond and currency option // Rev. Financ. Stud. 1993. V. 6. No.

2. P. 327-343.

Статья представлена к публикации членом редколлегии М.В. Губко.

Поступила в редакцию 08.12.2016

После доработки 09.01.2019

Принята к публикации 07.02.2019

155