Автоматика и телемеханика, № 7, 2019

Стохастические системы

(Институт проблем информатики Федерального исследовательского

центра “Информатика и управление” РАН, Москва;

Московский авиационный институт),

Г.Б. МИЛЛЕР, канд. физ.-мат. наук (gmiller@frccsc.ru)

(Институт проблем информатики Федерального исследовательского

центра “Информатика и управление” РАН, Москва)

УСЛОВНО-МИНИМАКСНЫЙ НЕЛИНЕЙНЫЙ ФИЛЬТР

И СИГМА-ТОЧЕЧНЫЕ ФИЛЬТРЫ:

ПРАКТИЧЕСКИЙ АНАЛИЗ И СРАВНЕНИЕ¹

Представлены результаты анализа и сравнения свойств двух концеп-

ций в задачах фильтрации состояний нелинейных стохастических дина-

мических систем наблюдения с дискретным временем — сигма-точечного

фильтра Калмана, основанного на дискретной аппроксимации непрерыв-

ных распределений, и условно-минимаксного нелинейного фильтра, реа-

лизующего метод условно-оптимальной фильтрации на основе имитаци-

онного моделирования. Краткое обсуждение структуры и свойств оценок

и обоснований соответствующих алгоритмов сопровождается значитель-

ным объемом модельных примеров, иллюстрирующих как положитель-

ные варианты применения, так и ограничения работоспособности проце-

дур оценивания. Простота и наглядность рассмотренных примеров (ска-

лярные автономные регрессии в уравнении состояния и линейные наблю-

дения) позволяют объективно охарактеризовать рассматриваемые мето-

дики оценивания. Предлагается новая модификация нелинейного филь-

тра, сочетающая идеи обоих рассмотренных направлений.

Ключевые слова: нелинейная стохастическая система наблюдения, сигма-

точечное преобразование, сигма-точечный фильтр, условно-оптимальная

фильтрация, условно-минимаксный нелинейный фильтр, имитационное

моделирование.

DOI: 10.1134/S000523101907002X

1. Введение

Стохастическая фильтрация, оценивание состояний и идентификация па-

раметров динамических систем наблюдения — важные и для множества при-

ложений, и для фундаментальной теории задачи, привлекающие значитель-

ный исследовательский интерес на протяжении многих лет. Самостоятельное

место в этих исследованиях занимают нелинейные модели и алгоритмы филь-

трации. В силу того что нелинейные системы крайне трудны для изучения

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 19-07-00187-а).

общими строгими методами, в этой области допускается определенная ма-

тематическая свобода, заключающаяся в возможности неформального обос-

нования предлагаемых решений соображениями разумности, инженерными

пояснениями и приближенными соотношениями. Полученные таким образом

результаты в целом определяются понятием “субоптимальная фильтрация”.

В отличие от фундаментальных результатов в области оптимальной стоха-

стической фильтрации субоптимальные фильтры имеют реальные перспек-

тивы практического применения, например обеспечивают возможность про-

ведения расчетов для сложных многомерных моделей. И хотя полученные

с их помощью оценки не обладают гарантированными свойствами, характе-

ризующими их качество, имеются примеры, подтверждающие практическую

применимость и полезность. Простой классический пример субоптимального

алгоритма — расширенный фильтр Калмана — успешно применяется в ряде

нелинейных задач, равно как и демонстрирует расходимость в других менее

“удачных” примерах. Детальный обзор субоптимальных алгоритмов филь-

трации не является задачей данной статьи, основное внимание будет уделено

лишь одному успешному и развитому направлению, получившему значитель-

ную популярность — сигма-точечной фильтрации.

Концепция данной модификации фильтра Калмана (unscented Kalman

Filter, сигма-точечный, или СТ-фильтр), впервые изложенная в публика-

ции [1], существенных изменений в дальнейшем не претерпела и успешно

эксплуатируется по настоящее время, превратившись в целое направление,

находящее применение в самых разных областях. Основная идея СТ-фильтра

состоит в аппроксимации непрерывных распределений параметров нелиней-

ной системы наблюдения дискретными с использованием специально под-

бираемого “базиса” — набора сигма-точек. Данная аппроксимация позволяет

приближенно рассчитывать моментные характеристики параметров, которые

используются в рекуррентных уравнениях фильтра калмановской структу-

ры. Хороший обзор приемов, методов и модификаций, касающихся сигма-

точечных алгоритмов фильтрации, можно найти в [2], где сделаны значи-

тельные усилия по систематизации результатов в данной области. Отдель-

ного упоминания заслуживает публикация [3], дополняющая исходную мето-

дику вариантом решения проблемы большой размерности (scaled unscented

transformation), а также [4, 5], исследующие свойства сигма-точечного филь-

тра Калмана для систем специального вида, подходы к робастификации

фильтра [6, 7], оптимизации параметров [8-10], повышению вычислительной

эффективности [11] и обобщению на непрерывное время [12]. Популярность

направления подтверждается большим числом публикаций практической на-

правленности, посвященных применению СТ-фильтра и его адаптации к но-

вым моделям [13-18].

Эвристический подход, характерный для направления субоптимальной

фильтрации, имеет альтернативы, с одной стороны, обеспечивающие стро-

гое математическое обоснование, а с другой — допускающие широкое при-

менение на практике из-за простоты реализации. Такой альтернативой яв-

ляется теория условно-оптимальной фильтрации Пугачева и ее развитие в

отношении динамических систем с дискретным временем — теория условно-

минимаксной нелинейной фильтрации (УМНФ) [19-22]. В настоящее время

эти результаты имеют менее широкую область применения по сравнению с

направлением СТ-фильтрации. Цель данной статьи — качественное сравне-

ние концепций, лежащих в основе двух практически значимых подходов, и

иллюстрация результатов этого анализа серией модельных экспериментов.

Отдельной задачей является развитие условно-минимаксного подхода на ос-

нове идей, заложенных в методе СТ-фильтрации.

2. Основная модель

Рассмотрим нелинейную систему наблюдения, описываемую следующими

разностными уравнениями:

x_t = ϕ(1)t (xt-1) + ϕ(2)t (xt-1) w_t, t = 1,2,... , x₀ = η,

(1)

y_t = ψ(1)t(x_t) + ψ(2)t(x_t)v_t.

Здесь x_t ∈ R^p — случайный процесс, определяющий состояние системы;

y_t ∈ R^q — косвенные наблюдения; w_t и v_t — дискретные белые шумы второ-

го порядка; случайный вектор начальных условий η также имеет конечный

второй момент; процессы w_t и v_t и вектор η независимы в совокупности.

Их математические ожидания и ковариации далее будем обозначать m_w (t) ,

D_w (t), m_v (t), D_v (t) , m_η, D_η соответственно.

Рассматривается задача оценивания состояния x_t по наблюдениям y_τ ,

τ = 1,...,t, критерий точности оценки x_t — среднеквадратический:

{

}

E ||x_t - x_t||2

Модель (1) — компромиссное описание системы наблюдения, подходящее

и для сигма-точечных, и для условно-минимаксных фильтров. Более то-

го, практически важным часто оказывается дополнительное предположе-

ние ψ(2)t(x) = 1 и/или требование существования всех моментов у процессов

w_t и v_t. Для целей данной статьи достаточно отметить, что при линейных

ограничениях на скорость роста функций на бесконечности и наличии вто-

рых моментов у всех возмущений процессы, описываемые (1), являются гиль-

бертовыми. Соответственно, в таких условиях рассматриваемая задача филь-

трации является корректной и можно, таким образом, говорить о ее решении

как об оптимальном — условном математическом ожидании x_t относительно

всех наблюдений, так и о каких-то вариантах аппроксимации решения.

3. Исследуемые концепции и методы

В основе обеих выбранных для исследования концепций синтеза алгорит-

мов нелинейной фильтрации лежат две простые статические задачи.

Сначала рассмотрим задачу, решение которой иллюстрирует суть мето-

да УМНФ. Пусть есть случайный вектор z = col (x, y), x ∈ R^p, y ∈ R^q с из-

вестным математическим ожиданием m_z = E {z} = col (m_x, m_y) и ковариаци-

(

)

D_x D_xy

ей D_z = cov (z, z) =

. Закон распределения F_z вектора z неиз-

D_yx D_y

вестен, предполагается, что F_z ∈ Φ(m_z, D_z) — классу всех вероятностных

распределений со средним m_z и ковариацией D_z. Требуется найти оценку

x = θ(y) ненаблюдаемого вектора x по наблюдениям y, исходя из среднеквад-

ратического критерия и заданного множества неопределенности Φ. Допусти-

мыми считаются любые оцениватели — измеримые по Борелю функции θ(y).

Точность оценивания, обеспечиваемую оценкой θ(y) при условии, что вектор z

имеет распределение F_z, обозначим через J(θ, F_z) = E{||x - x||²}.

Решение поставленной задачи дает седловая точка, определяемая неравен-

ствами J (θ^∗, F_z ) ≤ J (θ^∗, F^∗z) ≤ J (θ, F^∗z), где F^∗z — гауссовское распределение

с параметрами m_z, D_z, x^∗ = θ^∗ (y) = D_xyD+y y +(m_x -D_xyD+y m_y) - наилучшая

в среднем квадратическом линейная оценка x по наблюдению y [21, 22]. При

этом J (θ^∗, F^∗z) = D_x - D_xyD+yD_yx. Выше и далее обозначены: cov (x, y) —

ковариационная матрица случайных векторов x и y, E{x} — математическое

ожидание случайного вектора x, + — операция псевдообращения матрицы.

Из данного результата следует, что при формировании оценки в указанной

задаче оценивания x по наблюдению y минимаксно обоснованным является

линейный оцениватель, параметры которого определяются моментными ха-

рактеристиками совместного распределения. Этот результат лежит в основе

метода УМНФ, а именно: оценка фильтрации x_t состояния x_t получается в

результате решения следующих минимаксных задач для определения прогно-

за x_t и его коррекции:

{

}

(2)

x_t =θt (ξ_t) ,

θt = argminmax E

||x_t

θ_t (ξ_t) ||

, z = col(x_t,ξ_t

θ_t

{

}

x_t = x_t +θt(ζ_t),

θt = argmin maxE ||xt - xt

θ_t(ζ_t)||

, z = col(x_t - x_t,ζ_t).

θ_t

Здесь и далее ξ_t = ξ_t (x) и ζ_t = ζ_t (x, y) — некоторые структурные функции

фильтра, варианты выбора которых составляют практический багаж метода.

Далее собственно описание алгоритма УМНФ таково. Пусть имеется

xt-1 — оценка УМНФ состояния xt-1 по наблюдениям y_τ , τ = 1,... ,t - 1.

Прогноз x_t ищется в виде

(3)

x_t = F_tξ_t + f_t, ξ_t = ξ_t (xt-1) , ξ_t (x) = ϕ(1)t (x) + ϕ(2)t (x)m_w

(t) .

Структура прогноза “в силу системы” определяется структурной функ-

цией ξ_t (x) и коэффициентами F_t и f_t (матрица и вектор соответствующей

размерности), определяемыми в результате решения задачи (2), а именно

θt (ξt) = Ftξt + ft.

Оценка x_t состояния x_t ищется в виде

x_t = x_t + H_tζ_t + h_t, ζ_t = ζ_t (x_t, y_t) ,

(4)

ζ_t (x,y) = y - ψ(1)t (x) - ψ(2)t (x)m_v (t).

Структура коррекции в форме невязки определяется структурной функ-

цией ζ_t (x, y) (невязкой) и коэффициентами H_t и h_t (матрица и вектор соот-

ветствующей размерности), определяемыми в результате решения задачи (2),

а именно θt (ζ_t) = H_tζ_t + h_t.

Решения обеих задач в (2) при условии конечности необходимых вторых

моментов, очевидно, существуют, но могут быть не единственными. Един-

ственность обеспечивается дополнительным требованием о минимуме евкли-

довой нормы решения и, следовательно, использованием операции псевдооб-

ращения по Муру-Пенроузу. Таким образом, искомые коэффициенты зада-

ются в виде:

Ft = cov (xt, ξt) cov⁺ (ξt, ξt) , ft = E {xt} - FtE {ξt} ,

(5)

H_t = cov (x_t - x_t,ζ_t) cov⁺ (ζ_t,ζ_t) , h_t = -H_tE{ζ_t}.

Прогноз x_t и оценка фильтрации x_t при этом являются несмещенными и

обеспечивают следующее качество оценивания:

K_t = cov (x_t - x_t,x_t - x_t) = cov (x_t,x_t) - F_tcov (ξ_t,x_t),

(6)

K_t = cov (x_t - x_t,x_t - x_t) =Kt - H_tcov (ζ_t,x_t - x_t) ,

т.е. обеспечивается нерасходимость и “содержательность” оценок, подчерки-

вая словом “содержательность” гарантированное преимущество и прогноза,

и оценки по сравнению с тривиальной оценкой, поскольку F_tcov (ξ_t, x_t) ≥ 0,

H_tcov (ζ_t,x_t - x_t) ≥ 0.

Соотношения (3)-(5) определяют условно-оптимальный фильтр Пугаче-

ва, а концепция УМНФ дополняет их минимаксным обоснованием структу-

ры фильтра. Кроме того, непременным атрибутом УМНФ является способ

практического определения коэффициентов F_t, f_t, H_t и h_t методом Монте-

Карло, т.е. компьютерное имитационное моделирование. Сам фильтр полу-

чается заменой в (5) математических ожиданий и ковариаций их статистиче-

скими оценками, полученными в результате компьютерного моделирования.

По остальным вопросам, включая условия существования фильтров, можно

обратиться к публикации [23], в которой, кроме того, дан более подробный

обзор метода и направлений его развития. Отметим возможность гибкого

определения структурных функций фильтра — прогнозирующей ξ_t (x) и кор-

ректирующей ζ_t (x, y): представленный вариант прогноза “в силу системы” и

коррекции в форме невязки, конечно, является простейшим, и в зависимости

от свойств конкретной системы наблюдения ξ_t (x) и ζ_t (x, y) могут существен-

но изменяться.

Отметим еще, что УМНФ, в принципе, можно отнести к так называемым

нелинейным фильтрам Калмана или, как упоминалось в разделе 1, филь-

трам калмановской структуры. Поясним это, записав самый простой из таких

фильтров — расширенный фильтр Калмана (РФК). Здесь и далее не вводят-

ся дополнительные обозначения, а используются уже имеющиеся, например

x_t и x_t для обозначения прогноза и оценки фильтрации, ξ_t для прогноза “в си-

лу системы” и ζ_t для невязки. При этом из контекста понятно, какие именно

алгоритмы имеются в виду. Для РФК соотношения таковы:

x_t = ξ_t, ξ_t = ξ_t (xt-1) ,

ξ_t (x) = ϕ(1)t(x) + ϕ(2)t (x)m_w(t) ,



(1)



K_t = f_t Kt-1fTt + ϕ(2)tD_w (t)ϕ(2)tT, f_t =∂ϕt (x)

x= xt,

∂x



ϕ(2)t = ϕ(2)t (x_t) ,

x_t = x_t + H_tζ_t, ζ_t = y - ψ(1)t (x) - ψ(2)t (x) m_v (t),

(

)₊

(7)

H_t =KthTt h_t K_thTt + ψ(2)tD_v (t) ψ(2)tT



(1)



∂ψ_t

(x)

h_t =



x= x_t, ψ(2)t =ψ(2)t(x_t),

∂x



K_t =Kt - H_th_t K_t.

Другие повторно использованные обозначения также имеют смысл. Так,

f_t, h_t — некоторые оценки моментов, точнее, их аппроксимации, полученные

путем линеаризации, H_t имеет тот же смысл, что и в (5),

K_t и

K_t — кова-

риации ошибки прогноза и ошибки оценки, только здесь в отличие от (6) это

аппроксимации в силу элементарной линеаризации нелинейностей ϕ(1)t(x) и

ψ(1)t(x), а в УМНФ — точные значения или их статистические оценки.

Теперь обратимся к СТ-фильтрации. Калмановская структура фильтра в

этом методе сохраняется, а основная идея принципиально другая. Именно:

концептуальную основу СТ-фильтров составляет сигма-точечное преобразо-

вание (unscented transformation), состоящее в следующем. Пусть, как и вы-

ше, есть вектор z = col (x, y) ∈ Rp+q, такой что y = ϕ (x). Относительно рас-

пределения F_x вектора x предполагается, что F_x ∈ Φ (m_x, D_x), т.е. известны

два первых момента. Неформально относительно F_x можно сказать, что это

распределение предполагается непрерывным с формой, “близкой” к гауссов-

ской. Более того, во многих публикациях по данной тематике, следуя исход-

ным предложениям [1], обсуждение СТ-фильтрации иллюстрируется приме-

ром расчета именно с гауссовским вектором x. Отметим, что рассуждения

здесь, как и в публикациях, непосредственно посвященных данной тематике,

не претендуют на формальность и не предполагают математической строго-

сти условий и результатов. Как и в любых исследованиях по субоптимально-

му оцениванию, важна именно концептуальная составляющая — идея, обос-

нованная эмпирическими соображениями и подкрепленная модельными при-

мерами. Искомое преобразование состоит в представлении F_x его дискрет-

ным аналогом. Именно: вместо предположения о том, что x может прини-

мать любые значения, будем считать, что область значений x исчерпывается

конечным числом сигма-точек x⁰, x¹, . . . , x2p, с каждой из которых связана

соответствующая вероятность W⁰, W¹, . . . , W2p. Обратим внимание на связь

размерности p вектора x и числа сигма-точек 2p + 1. Это принципиальный

момент, подчеркивающий существенную ограниченность числа сигма-точек,

которых должно быть немного. В противном случае, выбирая неограниченно

много xⁱ и подбирая значения Wⁱ, можно, очевидно, добиться любой точ-

ности аппроксимации. Введенные обозначения дают простые приближенные

соотношения для моментов вектора y :

∑

m_y ≈ ŷ = Wⁱyⁱ, D_y ≈Dy = Wⁱ(yⁱ - ŷ)(yⁱ - ŷ)^T,

i=0

(8)

∑

(

)

D_xy ≈Dxy = Wⁱ(xⁱ - m_x)(yⁱ - ŷ)^T, yⁱ = ϕ

xⁱ

i=0

Близость моментов m_y и ŷ, D_y иDy, D_xy и D_xy в (8) и есть цель СТ-пре-

образования. И эта цель становится яснее с позиции следующего шага — оце-

нивания вектора x по наблюдениям y. Действительно, наилучшая линейная

оценка x по y имеет вид θ^∗ (y) = D_xyD+yy + (m_x - D_xyD+ym_y), СТ-преобра-

зование даст оценку x =Dxy D+yy + (m_x -Dxy D+y ŷ). При этом интуитивно

понятно, что чем точнее величинамиDxy,Dy, ŷ аппроксимируются моменты

D_xy,D_y,m_y, тем точнее будет и оценка x. Другое дело, что метод сигма-точек

не обременен какими-либо оптимизационными постановками в отношении

наилучшего выбора самих сигма-точек и весов, хотя и содержит изрядное

число разумных, физически обоснованных и практически проиллюстриро-

ванных вариантов их выбора (весьма полезен в этой части обзор [2]).

Заметим, что предложенная интерпретация СТ-преобразования нужна

только для иллюстрации. Обычно в публикациях по СТ-фильтрации не со-

общается о дискретном распределении, а речь идет только о сигма-точках и

“весах”, которые могут быть даже отрицательными. Выбор этих весов может

быть весьма разнообразным и неуниверсальным даже в рамках одной моде-

ли и различается в зависимости от цели преобразования. Один из вариантов,

который использовался в представленных далее расчетах, таков. Зададим па-

раметры преобразования α, β, γ (рекомендации по их выбору и физическая

интерпретация даны, например, в [24]). Определим “параметр масштаба” λ =

= α2 (p + γ) - p. Сигма-точки сформируются следующим образом:

(√

)

x⁰ = m_x, xⁱ

= m_x + (p + λ)D_x

i = 1,...,p,

(9)

(√

)

xⁱ = m_x -

(p + λ) D_x

i = p + 1,...,2p,

)

(√

√

где

(p + λ) D_x

— i-й столбец матрицы

(p + λ) D_x, под корнем от мат-

ричнозначного аргумента понимается результат разложения Холецкого. Веса

определяются так:

W⁰ =

для вычисления

ŷ,

p+λ

(10)

W⁰ =

+ 1 - α² + β для вычисления

D_y иDxy,

p+λ

Wⁱ =

i = 1,...,2p.

2(p + λ)

В примерах далее упомянутые рекомендации из [24] были использованы

для выбора базовых значений параметров α^∗, β^∗, γ^∗. Кроме того, в каждой за-

даче дополнительно выполнялась оптимизация, в которой базовые значения

выступали в роли начальных условий, расчеты многократно повторялись для

разных значений параметров и выбирались те, что обеспечивали СТ-фильтру

наибольшую точность. Реализовать такую операцию в рамках данной ста-

тьи удалось благодаря тому, что рассматривались только простые примеры

модельного характера, скалярные состояния и наблюдения, и не ограничи-

валось время, затрачиваемое на эксперименты. На практике, конечно, такая

оптимизация параметров не всегда окажется возможной.

Сделаем два важных замечания. Во-первых, представив оценку СТ-пре-

образования в виде x = m_x +Dxy D+y(y - ŷ), обратим внимание на сходство,

функциональную идентичность разности y - ŷ и невязки ζ_t, а также коэф-

фициентовDxy D+y и H_t в соотношениях (7) РФК. Это сходство и есть эм-

пирическое обоснование использования СТ-преобразования в соотношениях

нелинейного фильтра Калмана.

Второе замечание касается интерпретации моментов D_xy, D_y, m_y и со-

ответствующих аппроксимацийDxy,Dy, ŷ. Данное описание СТ-преобразо-

вания основано на статической модели оценивания, в которой эти парамет-

ры — просто моменты первого и второго порядков. Если же иметь в виду,

что роль вектора x будет играть состояние x_t динамической системы (1), а

предположение о его распределении будет изменяться в зависимости от на-

блюдений y_t, выполняющих роль y, то тогда F_x уместно характеризовать как

условное распределение x, форма которого неизвестна, но среднее значение

и ковариация — результаты оценивания, выполненного по ранее поступив-

шим наблюдениям. В этом смысле D_xy, D_y, m_y следует интерпретировать

как условные моменты.

Теперь изложение можно подытожить соотношениями СТ-фильтра для

системы (1). Эти соотношения приведены в соответствии с [24].

Пусть имеется xt-1 — оценка СТ-фильтра состояния xt-1 по наблюде-

ниям y_τ , τ = 1, . . . , t - 1, и

Kt-1 — оценка условной ковариационной мат-

рицы ошибки xt-1 - xt-1. Выберем сигма-точки xit-1 в соответствии с (9)

и веса Wⁱ согласно (10), используя D_x =Kt-1, и пересчитаем сигма-точки

(

)

(

)

x^it= ϕ1t

xit-1

+ϕ2t

xit-1

m_w (t), i = 0,... ,2p. Прогноз x_t ищется в виде

∑

x_t =

Wⁱx^it,

i=0

(11)

∑

(

)

(

)

(

))_T

K_t =

Wⁱ

x^it - x_t

(x^it -x_t)^T +ϕ2t

xit-1

D_w (t)

ϕ2t

xit-1

i=0

K_t

где

— СТ-оценка условной ковариационной матрицы ошибки прогноза

x_t - x_t. Далее пересчитываются следующие сигма-точки

(

)

(

)

y^it = ψ1t

x^it

+ψ2t

x^it

m_v (t).

Оценка x_t состояния x_t ищется в виде

∑

(

)

(

)

(

))_T

Wⁱy^it,

K^y

= Wⁱ

y^it - ŷ_t

(y^it - ŷ_t)^T + ψ2t

x^it

D_v (t)

ψ2t

x^it

ŷt =

i=0

∑

(

)

K^xy

(12)

= Wⁱ

x^it - x_t

(y^it - ŷ_t)^T,

i=0

H_t =Kxyt(Kyt)⁺,

x_t = x_t + H_tζ_t, ζ_t = y_t - ŷ_t,

K_t =Kt - H_t K^ytHTt.

Здесь отметим величиныKyt иKxyt, которые являются СТ-оценками услов-

ных ковариации невязки ζ_t и смешанной ковариации прогноза x_t и невяз-

ки ζ_t соответственно. Следует уточнить, что положения об условных момен-

тах выше опираются на специфическое услов

(

)

состояние xt-1 имеет распределение Fxt-1 ∈ Φ

xt-1,Kt-1 , т.е. вычисленные

на предыдущем шаге фильтрации величины xt-1 иKt-1 интерпретируются

как условное математическое ожидание и условная ковариация, по крайней

мере являются их аппроксимациями. Именно из-за этого соображения ранее

было сделано замечание в отношении интерпретации аппроксимаций

D_xy,

D_y, ŷ, получаемых в результате СТ-преобразования. На взгляд авторов, это

крайне важное замечание в отношении методологии СТ-фильтрации, объяс-

няющее практическую результативность алгоритмов фильтрации и высокую

точность оценок в конкретных экспериментах. При этом термин “условный”

здесь никак не связан с “действительно” условным распределением x_t отно-

сительно наблюдений y_τ , τ = 1, . . . , t, или какого-то иного набора случайных

величин. Но интуитивно содержание этого предложения понятно, а по форме

оно иллюстрируется строгими соотношениями линейного фильтра Калмана

и теоремой о нормальной корреляции [25].

Наконец, отметим, что использованные в (11) и (12) обозначения специ-

ально выбирались аналогичными обозначениям, использованным в соотно-

шениях (3)-(6) УМНФ и (7) РФК, для того чтобы подчеркнуть сходство и

даже идентичность в их интерпретации.

4. Модельные расчеты

4.1. Статическая регрессия и полярные координаты

Рассмотрим серию модельных примеров, позволяющих проиллюстри-

ровать наличие как “хороших”, так и “неудачных” условий применения

СТ-фильтров и проанализировать в таких же условиях поведение УМНФ.

Отметим, что, в целом, концепция СТ-оценивания представляется вполне

жизнеспособной и полезной и в ней имеются видимые достоинства и даже

перспективы, которые пока не реализованы. Но вместе с этим есть и ограни-

чения, систематическому изучению которых должного внимания со стороны

специалистов в этой области не уделялось. Одна из целей данной статьи —

выявить ограничения СТ-фильтров хотя бы на примерах академического ха-

рактера и убедиться, что в таких моделях возможность практической филь-

трации имеется (для этого привлекается УМНФ).

Рассмотрим простой статической пример, модель которого во многих пуб-

ликациях используется для иллюстрации результатов СТ-преобразования

(полностью такие рассуждения хорошо проиллюстрированы в [24]). Пусть

имеется гауссовский вектор col (x, y) , величины x, y интерпретируются как

декартовы координаты точки на плоскости. Будем считать эти координаты

независимыми, неизвестными и наблюдаемыми косвенно. Через ρ и φ обозна-

чим наблюдения соответствующих полярных координат x и y, зашумленных

гауссовским аддитивным шумом:

√

(13)

ρ=

x² + y² + v_ρ, φ = arctg(x/y) + v_φ,

где v_ρ, v_φ — независимые центрированные величины со среднеквадратически-

ми отклонениями σvρ = 30 м, σvφ = 5 град. Требуется по ρ и φ оценить x и y.

К оцениванию привлекаются следующие алгоритмы.

1. Наилучшая линейная оценка

θ^∗ (ρ,φ) = D_x,y,ρ,φD+ρ,φcol(ρ,φ) + (col(m_x,m_y) - D_x,y,ρ,φD+ρ,φcol(m_ρ,m_φ)),

(

)

⁽ cov(x, ρ) cov(x, φ)⁾

cov(ρ, ρ) cov(ρ, φ)

D_x,y,ρ,φ =

D_ρ,φ =

cov(y, ρ) cov(y, φ)

cov(φ, ρ) cov(φ, φ)

Все фигурирующие в этих соотношениях моментные характеристики вычис-

ляются методом Монте-Карло по выборке объема 10000.

2. Оценка СТ-фильтра. Вычисляется в точности по тем же формулам с

той лишь разницей, что моменты m_ρ, m_φ, D_x,y,ρ,φ, D_ρ,φ вычисляются по фор-

мулам СТ-фильтра (12) (прогноз (11) здесь не требуется в силу статичности

задачи), нужные для этого сигма-точки — по формулам (9), веса — по (10),

при этом параметры α, β, γ подвергаются дополнительной оптимизации, а

именно: выбираются наилучшие значения этих параметров с точки зрения

качества оценивания в рассматриваемой задаче.

Замечание. Здесь и далее, говоря об оптимизации параметров α, β и γ

СТ-фильтра, имеется в виду следующая вычислительная процедура. В соот-

ветствии с рекомендациями [24] в качестве базовых выбираются следующие

значения параметров: α^∗ = 0,5, β^∗ = 2,0, γ^∗ = 3 - p. Вокруг базовых значе-

ний формируется равномерная сетка возможных значений α, β, γ, из кото-

рых выбирается лучшая в смысле минимума второго момента ошибки оцен-

ки СТ-фильтра на последнем шаге фильтрации (единственном в статической

задаче пересчета полярных координат). В окрестности этой комбинации па-

раметров затем производится оптимизация методом Нелдера-Мида. В ито-

ге рассматривается порядка 10000-20000 комбинаций возможных значений

α, β, γ. Следует отметить, что в некоторых случаях вариация параметров

СТ-преобразования относительно базовых α^∗, β^∗, γ^∗ не приводит к видимым

изменениям качества оценивания. В таких случаях, а именно: когда разница

между минимальным и максимальным значениями второго момента ошибки

оценки на последнем шаге фильтрации не превышает 0,1 %, для оценивания

с помощью СТ-фильтра используются базовые значения.

Таблица

Сравнение для модели (13)

“Близко”

“Далеко”

D[x - x]

585

562

1. Линейная оценка

D[y - ŷ]

456

514

D[x - x]

614 (444)

562 (553)

2. Сигма-точечная оценка

D[y - ŷ]

467 (395)

514 (508)

D[x - x]

276

564

3. Оценка УМНФ

D[y - ŷ]

323

516

3. Оценка УМНФ. Заметим, во-первых, что наилучшая линейная оценка

в данной задаче также является и оценкой УМНФ, если считать, что струк-

турная функция (в данном статическом примере структурная функция толь-

ко одна) ζ = col(ρ, φ). Но в качестве “действительно” условно-минимаксной

оценки здесь будем использовать ζ = col (ζ_x, ζ_y), ζ_x = ρ cos φ, ζ_y = ρ sin φ, т.е.

соотношения перехода от полярных координат к декартовым, “обратные” в

смысле модели наблюдения (13). Это характерный пример подбора структу-

ры оценки УМНФ с использованием физического смысла модели.

Неопределенными в модели (13) остаются только условия на расположе-

(

)

D_x

ние исходной точки, т.е. параметры col (m_x, m_y) и

. Вторые момен-

D_y

ты принципиального разнообразия в эксперимент не внесут, поэтому всюду

полагаем D_x = D_y = 30². А вот значения m_x и m_y будут отражать понима-

ние физического свойства “близко-далеко”. В качестве “близко” полагалось

m_x = 30 и m_y = 40; “далеко” — m_x = 300, m_y = 400. Полученные результаты

представлены в таблице, где через D[x - x] и D[y - ŷ] обозначены диспер-

сии ошибок оценок координат x и y соответствующими алгоритмами. Для

СТ-фильтра дополнительно в скобках указывается оценка соответствующей

дисперсии, полученная усреднением величинKt из (12). Аналогичные “теоре-

тические” значения для линейной оценки и УМНФ не приводятся, так как они

близки к приведенным в таблице “статистическим” и становятся тем ближе,

чем больше экспериментов проводится в рамках метода Монте-Карло.

Для расчетов в модели “близко” были определены следующие параметры

СТ-преобразования: α = 1,06, β = 1,35, γ = 0,91. Эти параметры существен-

но улучшают точность оценивания по сравнению с базовыми, для которых

D[x - x] = 711, D[y - ŷ] = 477. Оптимизация в модели “далеко” не оказала

существенного влияния на качество оценивания, поэтому для СТ-преобразо-

вания были использованы базовые значения α^∗, β^∗ и γ^∗.

Первое, чем обращают на себя внимание приведенные результаты — это

идентичность свойств оценок в модели “далеко”, небольшой проигрыш УМНФ

в рамках статистической погрешности. Достаточно близки при этом и оценки

точности СТ-фильтра, что позволяет считать, что используемые в (12) оцен-

ки условных моментов также хорошо аппроксимируются с помощью сигма-

точек. Второе — это более чем двукратный проигрыш СТ-фильтра в модели

“близко”, сопровождаемый существенной погрешностью аппроксимации дис-

персии ошибки оценки. При этом чуть меньше, но также слишком велика

ошибка линейной оценки. УМНФ справляется с задачей существенно луч-

√

Рис. 1. Фрагменты поверхности ρ =

x² + y²: a - модель “далеко”; б - модель

“близко”.

ше и, что особо любопытно, значительно успешнее, чем в модели “далеко”.

Причина таких результатов, на взгляд авторов, довольна проста. Модель

“далеко” показывает поведение, “близкое к линейному”, модель “близко” —

существенно нелинейна. Подтверждает это рис. 1, на котором изображены

√

фрагменты поверхности ρ =

x² + y² для x ∈ [m_x - 2√Dx,mx + 2√Dx] и

√

y ∈ [m_y - 2

D_y,m_y + 2

D_y] и видно, что в модели “далеко” (рис. 1,а) этот

фрагмент визуально неотличим от плоскости, а в модели “близко” (рис. 1,б ) —

это совсем не плоскость, и эта нелинейность, как демонстрирует УМНФ, весь-

ма информативна.

Заметим, что такое поведение СТ-оценки не является неожиданным, на

него обращают внимание многие исследователи, обозначая условие эффек-

тивности СТ-преобразования “консервативностью” ковариации ошибки оцен-

ки, которая в данном примере обеспечивается линейным поведением модели

“далеко” и нарушается — нелинейным поведением модели “близко”.

4.2. Дробно-рациональная регрессия и кубический сенсор

Далее будем рассматривать примеры автономных скалярных динамиче-

ских систем. В таких примерах легко анализировать четко выраженные свой-

ства модели и их влияние, в конечном итоге, на точность оценок. Первая

модель в этом ряду такова:

xt-1

x_t =

+ w_t, t = 1,... ,T, T = 50, x₀ = η,

1+x²

(14)

t-1

y_t = x_t + x3t + v_t.

Шумы w_t и v_t будем предполагать стандартными гауссовскими, начальное

условие η тоже гауссовским с m_η = 0,1 и D_η = 1. Наблюдения в (14) хоро-

шо известны под названием “кубический сенсор”, они очень удобны (инфор-

мативны) для оценивания, так как при больших значениях x_t существенно

0,35

0,4

0,30

0,2

0,25

0,20

0,15

0,2

0,10

0,4

0,05

Рис. 2. Характеризация модели (14): a - функция регрессии; б - гистограмма

для x_T , E[x_T ] = 0, D[x_T ] = 1,16.

увеличивают отношение сигнал/шум, а при малых — близки к линейным.

Что касается динамики, то функция регрессии x/(1 + x²) хотя и нелинейная

(рис. 2,а), но демонстрирует довольно инертное поведение — обладает всего

двумя экстремумами, гладкими производными и асимптотически приближа-

ется к нулю на бесконечности.

Отметим также, что фазовый процесс x_t обладает одним полезным свой-

ством. Он, очевидно, является эргодическим (нетрудно показать это, сле-

дуя базовым результатам по нелинейной регрессии, изложенным, например,

в [26]), и при этом сходимость к предельному распределению практически

мгновенная: уже на втором шаге при начальных условиях, сильно отличаю-

щихся от предельных, получаются моменты, характерные для предельного

распределения E[x_T ] = 0, D[x_T ] = 1,16. (на рис. 2,б предельное распределение

иллюстрируется гистограммой x_T ). Таким образом, у системы (14) фактиче-

ски отсутствует переходной процесс, поэтому она представляется идеальной

как для СТ-фильтрации, так и для УМНФ.

Здесь и всюду далее СТ-фильтр реализован в соответствии с соотноше-

ниями (11), (12), дополненными упомянутой в первом примере оптимизацией

параметров α, β, γ. Структура УМНФ базовая: ξ_t (x) = x/(1 + x²), т.е. про-

гноз строится “в силу системы”, ζ_t (x, y) = y - x - x³ — коррекция в форме

невязки. Параметры УМНФ вычислялись методом Монте-Карло по пучку

10⁵ траекторий (его уместно называть обучающим), этот же пучок исполь-

зовался для оптимизации параметров СТ-фильтра. Качество оценок филь-

трации и моментные характеристики x_t оценивались по второму пучку из

10⁶ траекторий. Приведенные условия расчетов применялись и в следующих

примерах.

На рис. 3 показаны: примеры характерных траекторий (состояния, наблю-

дения — рис. 3,а), ошибок оценок СТ-фильтра и УМНФ — рис. 3,б , показа-

тели качества оценок — средние и дисперсии ошибок оценок и процесса пока-

1,2

1,0

0,8

0,6

0,4

0,2

Рис. 3. Примеры траекторий и показатели качества оценок в модели (14): a -

характерные траектории x_t (сплошная линия), y_t (точечная линия); б - траек-

тории ошибок фильтрации x_t -x_t УМНФ (черная линия), СТ-фильтра (серая

линия); в,г - показатели точности УМНФ и СТ-фильтра на фоне дисперсии

процесса D[x_t] (верхняя граница серой области): E[x_t - x_t] (сплошные линии),

D[x_t - x_t] (пунктирные линии),

K_t (точечные линии).

заны для УМНФ на рис. 3,в, для СТ-фильтра - на рис. 3,г. Выборочные мо-

менты предельных распределений ошибок оценивания равны E[x_T - x_T ] = 0,

D[x_T - x_T ] = 0,35 для УМНФ и E[x_T - x_T ] = 0, D[x_T - x_T ] = 0,34 для

СТ-фильтра. Дополнительно на рис. 3,в показана априорная оценка точно-

сти УМНФ, т.е. величина

K_t из (6), вычисленная методом Монте-Карло,

K_T = 0,35; на рис. 3,г показана “теоретическая” точность — усредненная ве-

личина

K_t из (12),

K_T = 0,11. Наилучшие найденные значения параметров

СТ-преобразования в данной модели α = 0,20, β = 1,99, γ = 1,23. Для базо-

вых значений параметров α^∗ = 0,5, β^∗ = 2,0, γ^∗ = 2,0 СТ-оценка оказалась

хуже тривиальной, обеспечивая точность D[x_T - x_T ] = 1,57 при D[x_T ] = 1,16.

Как видно, обе оценки демонстрируют близкие качества, обе несмещен-

ные и содержательные в том смысле, что дисперсия ошибки оценки меньше,

причем существенно меньше, дисперсии самогo процесса и дисперсии шума в

наблюдениях. Отметим также, что СТ-фильтр немного превосходит УМНФ,

но последний имеет самую простую структуру (прогноз “в силу системы”, кор-

рекция в форме невязки) и никаких вариантов ее улучшения не предприни-

малось, хотя они и легко просматриваются. Например, к улучшению качества

УМНФ приведет увеличение размерности базовой коррекции ζ_t (x, y) за счет

“дополнительных” наблюдений y2t, y3t. Также отметим, что “теоретическая”

точность СТ-фильтра далека от реальности, что не мешает ему справляться

с задачей.

4.3. Обратная регрессия

Перейдем теперь к моделям, представляющим не столь комфортные усло-

вия для нелинейного оценивания. При этом состояния, как и ранее, описы-

ваются скалярными автономными регрессиями с гауссовскими возмущения-

ми, обладающими эргодическим свойством. В данном подразделе рассмотрим

сразу две модели, использующих функцию обратной пропорциональности и

наблюдения — прямые линейные:

x_t =

√

+ 100w_t, t = 1, . . . , T, T = 50, x₀ = η,

xt-1

(15)

y_t = x_t + 100v_t,

(

)

x_t = min

10⁵,

+ 100w_t, t = 1, . . . , T, T = 50, x₀ = η,

(16)

x²

t-1

y_t = x_t + 100v_t.

Шумы w_t и v_t будем предполагать стандартными гауссовскими, началь-

ное условие η — тоже гауссовским с m_η = 3 и D_η = 1. Соотношения (15), (16)

необходимо для корректности дополнить равенством x_t = 10⁵, если xt-1 = 0.

В обеих моделях регрессионная функция одного класса 1/x^δ, δ =¹³ в (15),

δ = 2 в (16). Разница, легко видеть, в том, что степенью δ в (15) обеспечивает-

ся существование вторых моментов у x_t, а в (16) — напротив, нет даже перво-

го момента. Именно поэтому, чтобы сделать задачу фильтрации корректной,

в (16) добавлена верхняя граница 10⁵, которая обеспечивает существование

всех моментов. Предельные распределения процессов x_t в (15) и (16) характе-

ризуются типовыми унимодальными плотностями вероятности, предельные

выборочные средние значения E[x_T ] равны 0,18 и 6,06, дисперсии D[x_T ] равны

10314,41 и 361201,04 соответственно.

Оба процесса x_t имеют аналогичное поведение: близкое к нулевому ма-

тематическое ожидание и “много” реализаций около нуля, большая диспер-

сия, обеспечиваемая периодически появляющимися “большими” значениями,

когда реализации xt-1 ≈ 0. Заметим, что обе модели не попадают в сфе-

ру робастного оценивания, здесь нет “исчезнувших” или “ложных” наблю-

дений, выбросов и т.п. Робастификация в традиционном смысле не даст в

этой модели результата, так как редкие всплески требуется оценивать, по-

скольку они представляют фактическое состояние оцениваемого процесса и

не могут быть проигнорированы. Результаты проведенных расчетов иллю-

стрируются следующими рисунками. Для (15) приведены примеры харак-

терных траекторий (состояния, наблюдения — на рис. 4,а), ошибок оценок

СТ-фильтра и УМНФ — на рис. 4,б ), показатели качества оценок — сред-

ние и дисперсии ошибок оценок и процесса показаны для УМНФ на рис. 4,в,

200

400

100

200

100

200

10 000

8000

6000

4000

2000

Рис. 4. Примеры траекторий и показатели качества оценок в модели (15): a -

характерные траектории x_t (сплошная линия), y_t (точечная линия); б - траек-

тории ошибок фильтрации x_t -x_t УМНФ (черная линия), СТ-фильтра (серая

линия); в,г - показатели точности УМНФ и СТ-фильтра на фоне дисперсии

процесса D[x_t] (верхняя граница серой области): E[x_t - x_t] (сплошные линии),

D[x_t - x_t] (пунктирные линии),

K_t (точечные линии).

для СТ-фильтра — на рис. 4,г. Выборочные моменты предельных распре-

делений ошибок оценивания равны E[x_T - x_T ] = -1,87, D[x_T - x_T ] = 5107,98

для УМНФ и E[x_T - x_T ] = -1,62, D[x_T - x_T ] = 5109,28 для СТ-фильтра.

Дополнительно на рис. 4,в показана величина

K_t из (6),

K_T = 5000,11; на

рис. 4,г — усредненная величина

K_t из (12),

K_T = 5000,04. Для модели (16)

аналогичные результаты приведены на рис. 5. Выборочные моменты пре-

дельных распределений ошибок оценивания здесь равны E[x_T - x_T ] = -0,78,

D[x_T - x_T ] = 9667,38 для УМНФ и E[x_T - x_T ] = 2,51, D[x_T - x_T ] = 92521,33

для СТ-фильтра. Дополнительно на рис. 5,в показана величина

K_t из (6),

K_T = 9804,96; на рис. 5,г — усредненная величина

K_t из (12),

K_T = 5007,19.

В обеих моделях (15), (16) вариация базовых значений параметров СТ-пре-

образования α^∗, β^∗, γ^∗ не приводит к улучшению качества оценки.

Полученные результаты соответствуют ожиданиям: в комфортных услови-

ях модели (15) обе оценки ведут себя одинаково хорошо, в “неудобной” моде-

ли (16) работает только УМНФ, его точность хоть и ненамного, но выше точ-

ности прямых наблюдений. Причина этого не в плохой реализации СТ-филь-

17 500

8000

15 000

12 500

6000

10 000

4000

7500

5000

2000

2500

350 000

300 000

250 000

200 000

150 000

100 000

50 000

Рис. 5. Примеры траекторий и показатели качества оценок в модели (16): a -

характерные траектории x_t (сплошная линия), y_t (точечная линия); б - траек-

тории ошибок фильтрации x_t -x_t УМНФ (черная линия), СТ-фильтра (серая

линия); в,г - показатели точности УМНФ и СТ-фильтра на фоне дисперсии

процесса D[x_t] (верхняя граница серой области): E[x_t - x_t] (сплошные линии),

D[x_t - x_t] (пунктирные линии),

K_t (точечные линии).

тра, а в неприменимости в этой модели самой концепции сигма-точек, по-

скольку такую нелинейность, как в (16), охарактеризовать небольшим ко-

нечным набором образцов преобразований (сигма-точек), по-видимому, нель-

зя. Но самое неприятное, на взгляд авторов, для СТ-фильтра в этой моде-

ли следующее обстоятельство. В данном простом модельном примере зара-

нее предсказать его плохое поведение можно, просто визуально анализируя

характер нелинейности в уравнении состояния. На практике же такую осо-

бенность вряд ли удастся предсказать априорно, поскольку рассчитывать на

успешный визуальный анализ уравнений, чуть более сложных, чем представ-

ленная скалярная автономная регрессия, вряд ли возможно.

4.4. Логистическая модель

Следующей рассмотрим модель, основанную на дискретном аналоге хо-

рошо известной логистической модели (модели для численности популя-

ции) — логистическом отображении или отображении Фейгенбаума x_t =

= δxt-1(1 - xt-1) [27]. Добавив в данную модель аддитивное гауссовское воз-

200

400

200

400

600

800

1000

20 000

15 000

10 000

5000

Рис. 6. Примеры траекторий и показатели качества оценок в модели (17): a -

характерные траектории x_t (сплошная линия), y_t (точечная линия); б - траек-

тории ошибок фильтрации x_t -x_t УМНФ (черная линия), СТ-фильтра (серая

линия); в,г - показатели точности УМНФ и СТ-фильтра на фоне дисперсии

процесса D[x_t] (верхняя граница серой области): E[x_t - x_t] (сплошные линии),

D[x_t - x_t] (пунктирные линии),

K_t (точечные линии).

мущение, получим динамику системы наблюдения. Модель при этом полу-

чается неустойчивой и, как и ранее, ее приходится искусственно ограничить.

Причем при достижении границы процесс предлагается возвращать в исход-

ное состояние, чтобы взрывные явления повторялись раз за разом. Таким

образом, в этом разделе будем рассматривать следующую систему наблюде-

ния:

{

xt-1 (1 - xt-1) , если xt-1 (1 - xt-1) > -10³,

x_t =

+ w_t, t = 1,... ,50, x₀ = η,

0, иначе

(17)

y_t = x_t + 100v_t.

Здесь в основе динамики логистическое отображение с δ = 1, поэтому если

бы в (17) не фигурировала нижняя граница (-10³), то имел бы место “взрыв”

в отрицательную область: x_t → -∞. Но при этом, даже если убрать из (17)

границу (-10³), формально у состояния x_t есть все конечные моменты в лю-

бой момент времени, так что решение задачи фильтрации есть для любого t.

Другое дело, что рост моментов и абсолютных значений x_t характеризуется

степенной скоростью, поэтому при компьютерных расчетах за короткое время

любая траектория в модели без границы превысит компьютерный максимум.

Полученные результаты иллюстрирует рис. 6. Выборочные моменты пре-

дельных распределений ошибок оценивания равны

E[x_T - x_T ] = -0,83, D[x_T - x_T ] = 6208,12 для УМНФ

E[x_T - x_T ] = -17,07, D[x_T - x_T ] = 13527,82 для СТ-фильтра,

тогда как выборочная дисперсия процесса D[x_T ] = 16341,25. Дополнительно

на рис. 6,в показана величина

K_t из (6),

K_T = 6300,53; на рис. 6,г — усред-

ненная величина

K_t из (12),

K_T = 3068,76. В данной модели оптимизация

параметров СТ-преобразования также не дает результата, поэтому использу-

ются базовые α^∗, β^∗, γ^∗.

Данный пример представляется яркой иллюстрацией потенциальных

сложностей практического применения алгоритмов СТ-фильтрации. Он

представляет собой простую полиномиальную регрессию, обеспечивающую

формальное существование всех моментов, и информативные линейные на-

блюдения, но фазовый процесс при этом имеет “взрывной” характер, уследить

за которым сигма-точечным методом не удается. СТ-фильтр оказывается су-

щественно смещенным, точность оценки близка к тривиальной и не выдер-

живает сравнения с точностью УМНФ. Ошибка оценки УМНФ также велика,

но оценивание условно-минимаксным методом имеет смысл, поскольку дис-

персия ошибки определенно меньше дисперсии шума в наблюдениях.

4.5. Модель переключающихся каналов наблюдения

Эта модель основана на идее дополнительного внешнего влияния на харак-

теристики наблюдателя, впервые привлекшей внимание около 50 лет назад

(см., например, [28]) и в дальнейшем обобщенной в моделях систем случай-

ной структуры и скрытых марковских моделях. Здесь рассматривается один

из самых простых вариантов.

Пусть имеется не зависящий от состояния x_t белый шум δ_t, сечения-

ми которого являются дискретные случайные величины, принимающие зна-

чения δⁱ, i = 1, . . . , n, с известным распределением P {δ_t = δⁱ} = pⁱ. Для

удобства будем считать, что δⁱ — n-мерные единичные векторы, т.е. δⁱ =

= (0, . . . , 1, . . . 0)^T, где 1 стоит на i-м месте. Пусть d, σ ∈ Rⁿ. Выражение d^Tδ_t

дает i-ю координату вектора d = (d¹, . . . , dⁿ)^T. Будем считать, что состоя-

ние x_t в момент t может наблюдаться одним из n каналов линейных на-

блюдений y_t = dⁱx_t + σⁱv_t, реализация которых определяется величиной δ_t.

С помощью введенных обозначений такие наблюдения записываются в ви-

де y_t = d^Tδ_tx_t + σ^Tδ_tv_t. Состояние x_t опишем простой линейной регрессией,

получив, таким образом, следующую систему наблюдения:

x_t = axt-1 + b + cw_t, t = 1,... ,T, T = 50, x₀ = η,

(18)

y_t = d^Tδ_tx_t + σ^Tδ_tv_t,

где η, w_t, v_t — стандартные гауссовские.

Для проведения расчетов выберем n = 3, p¹ = p³ = 0,25, p² = 0,5, d^T =

= (4; 1; 0,5), σ^T = (1; 1; 3), a = 0,8, b = 0,2, c = 6,0. Предельное распределе-

ние x_t, легко видеть, является гауссовским со средним единица и дисперси-

ей 100.

В данном примере нельзя использовать ни соотношения

(11),

(12)

СТ-фильтра, ни соотношения (1)-(4) УМНФ из-за формального несоответ-

ствия моделей (18) и (1). Устраняется это несоответствие следующим обра-

зом. В дополнение к шуму w_t введем еще один независимый гауссовский бе-

лый шум {w^δt} и непересекающиеся интервалы Δⁱ: P {w^δt ∈ Δⁱ} = pⁱ, i = 1, 2, 3.

Далее дополним состояние x_t второй координатой

( (

)

(

)

(

))

x^δt = I w^δt

∈Δ1 ,I wδt

∈Δ2 ,I wδt

∈Δ³

(1, 2, 3)

^T,

т.е. номером реализации δ_t. В уравнении наблюдений вместо d^Tδ_t будем ис-

(

)

пользовать функцию ψ(1)t

x_t,x^δt

= dⁱx_t, если x^δt = i, i = 1,2,3, и аналогич-

но вместо σ^Tδ_t — функцию ψ(2)t(x_t, x^δt) = σⁱx_t, если x^δt = i. Эти обозначе-

ния формально сводят модель (18) к виду (1), состояние при этом стано-

вится двумерным, наблюдения остаются скалярными. Таким образом, в реа-

лизации СТ-фильтра будет использоваться пять сигма-точек в соответствии

с (9). Заметим, что дополнительных соображений в формировании структу-

ры СТ-фильтра рассматриваемая модель не дает. Иная ситуация с УМНФ.

Специфическая структура системы наблюдения требует учета в структуре

фильтра, в его корректирующем члене ζ_t (x, y). Действительно, сформировав

стандартный прогноз x_t “в силу системы” и определив его точность

K_t со-

гласно (3) и (6), шаг коррекции можно рассматривать как вспомогательную

задачу оценивания x_t по одному наблюдению y_t = d^Tδ_tx_t + σ^Tδ_tv_t, решение

которой при дополнительном предположении, что распределение x_t — гаус-

совское с параметрами x_t и

K_t, легко записать в виде взвешенной суммы

линейных оценок x_t по каждому возможному наблюдению y_t = dⁱx_t + σⁱv_t,

веса в которой образуют отношения правдоподобия. Этот подход дает сле-

дующую базовую коррекцию:

)

(

)(

(

)-1 (

)

pⁱN y; dⁱx_t, di2 K_t

+σi2

dⁱ K_t di2 K_t + σi2

y-dⁱx

ζ_t

(x, y) =i=1

)

∑ (

pⁱN y; dⁱx_t, di2 K_t

+σi2

i=1

(

)

где через N

y;m,σ²

обозначена гауссовская плотность с параметрами m, σ²,

вычисленная в точке y.

Комментируя это предложение, можно сказать, что выражения

(

)

pⁱN y_t;dⁱx_t,di2 K_t

+σi2

)

∑ (

pⁱN y_t;dⁱx_t,di2 K_t

+σi2

i=1

представляют оценку апостериорной вероятности события {δ_t = δⁱ}, величи-

(

)-1 (

)

ны dⁱ K_t di2 K_t + σi2

y-dⁱx_t

, по сути, являются корректирующими сла-

120

100

Рис. 7. Примеры траекторий и показатели качества оценок в модели (18): a -

характерные траектории x_t (сплошная линия), y_t (точечная линия); б - траек-

тории ошибок фильтрации x_t -x_t УМНФ (черная линия), СТ-фильтра (серая

линия); в,г - показатели точности УМНФ и СТ-фильтра на фоне дисперсии

процесса D[x_t] (верхняя граница серой области): E[x_t - x_t] (сплошные линии),

D[x_t - x_t] (пунктирные линии),

K_t (точечные линии).

гаемыми линейного фильтра Калмана при условии, что в момент t реализо-

вался i-й канал наблюдения.

В данной модели была дополнительно предпринята попытка оптимиза-

ции значений параметров СТ-преобразования отдельно на шагах прогнози-

рования и коррекции, т.е. дополнительного пересчета точек y^it в (12) в соот-

ветствии с (9). Наилучшие найденные значения таковы: α = 2,46, β = 3,82,

γ = 2,59 для шага прогнозирования и α = 0,52, β = 4,15, γ = 1,24 для шага

коррекции. При этом добиться серьезного улучшения точности СТ-фильтра

не удается: для базовых значений параметров α^∗, β^∗, γ^∗ точность оценивания

составляет D[x_T - x_T ] = 71,81.

Результаты расчетов иллюстрирует рис. 7. Выборочные моменты предель-

ных распределений ошибок оценивания равны

E[x_T - x_T ] = 0,18, D[x_T - x_T ] = 14,30 для УМНФ

E[x_T - x_T ] = 0,29, D[x_T - x_T ] = 70,18 для СТ-фильтра.

Дополнительно на рис. 7,в показана величина

K_t из (6),

K_T = 14,41; на

рис. 7,г — усредненная величинаKt из (12),KT = 45,27.

Результаты демонстрируют ожидаемый значительный проигрыш

СТ-фильтра по отношению к УМНФ. Ясно, что высокое качество оценки

УМНФ обеспечивается выбором коррекции ζ_t (x,y), отражающим специфи-

ку модели. Иллюстрация гибкости метода УМНФ в отношении структуры

фильтра - одна из целей данного примера и его отличие от всех предыдущих.

СТ-фильтр, наоборот, поставлен в заведомо проигрышные условия формаль-

ным сведением модели (18) к виду (1). В данном примере нетрудно увидеть

и реализовать гораздо более качественный СТ-фильтр, выбрав сигма-точки

с учетом дискретного характера распределения δ_t, а именно для каждой из

трех сигма-точек, выбранных отдел(но дл)я первой координаты xt, опреде-

лить три двумерных сигма-вектора

x^it,δ^j

, j = 1, 2, 3, сформировав таким

образом окончательный набор из девяти сигма-точек для состояния (x_t, δ_t).

Такой вариант не был реализован по следующим причинам. Во-первых, он

нарушает существенную часть концепции СТ-фильтрации — предположение

о небольшом по отношению к размерности задачи числе сигма-точек (в дву-

мерном случае стандартно рекомендуется пять сигма-точек). Во-вторых,

такой подход для СТ-фильтрации не будет универсальным. Он применим

в данной частной ситуации с тремя переключающимися каналами, так как

9 сигма-точек — не слишком большое число, но с ростом числа каналов

станет неприемлем. Наконец, слишком больших вычислительных ресурсов

требует используемая во всех примерах процедура оптимизации параметров

СТ-фильтрации α, β, γ из соотношений (9), (10).

5. Модифицированный УМНФ

Результаты выполненных экспериментов с СТ-фильтрами, их сравнение с

УМНФ в целом подтверждают эффективность обеих концепций. Тем не ме-

нее, СТ-фильтр в любой практической задаче — это всегда вызов с непредска-

зуемым результатом, и получение хороших результатов — это всегда ориги-

нальная манипуляция параметрами (сигма-точками). Условно-минимаксный

фильтр работает всегда, структура подбирается естественно и несложно, но

при этом оценка может оказаться слишком консервативной, что характер-

но для минимаксных задач. Перспективным представляется комбинирование

двух концепций. Возможный вариант в этом направлении — модификация

УМНФ за счет использования в структуре фильтра оценок условных момент-

ных характеристик, ковариаций, вычисляемых вместе с оценками состояния

на каждом шаге фильтрации по аналогии с тем, как это делается в СТ-филь-

тре. Но в отличие от СТ-фильтров для этого предлагается использовать не

сигма-точечное преобразование, а метод Монте-Карло, т.е. имитационное мо-

делирование.

Для описания алгоритма модифицированного УМНФ (МУМНФ) вернем-

ся к соотношениям (5), (6), в которых коэффициенты УМНФ выражаются

через математические ожидания и ковариации состояния x_t, базового про-

гноза ξ_t, ошибки прогноза x_t - x_t и базовой коррекции ζ_t. В реализациях

УМНФ операции E {·} и cov (·, ·) заменялись соответствующими статистиче-

скими оценками, рассчитанными априорно по смоделированному пучку тра-

екторий. Обозначим соответствующие операторы усреднения E {·} и cov (·, ·).

∑_N

Например, в (5) вместо E {x_t} используется E {x_t} =¹

x^it, в (6) вместо

N (i=1

∑_N

cov (ζ_t, x_t - x_t) используется cov (ζ_t, x_t - x_t) =

ζ^it

x^it - x^it

)^T, где N -

N i=1

число смоделированных траекторий, а x^it, x^it, ζ^it, i = 1, . . . , N, — реализации.

В модифицированном фильтре предлагается исключить априорное модели-

рование и выполнять оценивание параметров фильтра в процессе расчетов

для каждой траектории. Соответственно алгоритм МУМНФ таков.

Пусть в момент t имеется xt-1 — оценка МУМНФ состояния xt-1 по на-

блюдениям y_τ , τ = 1, . . . , t - 1,Kt-1 — оценка условной ковариации ошибки.

На шаге t выполняется моделирование выборок: {xit-1}^N

— из гауссовского

i=1

распределения со средним xt-1 и ковариацией

Kt-1, {w^it,v^it}Ni=1 — дискрет-

ных белых шумов в соответствии с моделью (1), и рассчитываются наборы

{x^it, y^it}Ni=1 по формулам (1). Прогноз МУМНФ x_t ищется в виде x_t = E {x_t} .

Заметим, что здесь не нужна функция базового прогноза ξ_t, коэффициент

Ft = 0, поскольку не моделируется выборка оценок xt-1, и расчет выпол-

няется также, как и на первом шаге УМНФ. Точность прогноза определя-

ется как

K_t = cov (x_t - x_t,x_t - x_t). Далее формируется набор {ζ^it}Ni=1 и вы-

числяются коэффициенты H_t = cov (x_t - x_t, ζ_t) cov⁺ (ζ_t, ζ_t), h_t = -H_tE {ζ_t},

(

)

ζ^it = ζ_t

x_t, y^it

и оценка точностиKt =Kt - H_tcov (ζ_t, x_t - x_t). Оценка x_t со-

стояния x_t, как и в УМНФ, ищется в виде x_t = x_t + H_tζ_t + h_t, ζ_t = ζ_t (x_t, y_t).

Таким образом, идея МУМНФ состоит в аппроксимации условного рас-

пределения xt-1 относительно y_τ , τ = 1, . . . , t - 1, гауссовским, а соответст-

вующих моментов — результатами фильтрации, и в вычислении параметров

фильтра через оценки математических ожиданий и ковариаций, полученных

имитационным моделированием. Заметим, что предположение о гауссовской

аппроксимации условного распределения можно считать таким же минимакс-

ным контекстом, что и в УМНФ. Также важно отметить, что размеры моде-

лируемых выборок в УМНФ и МУМНФ должны принципиально отличаться,

поскольку расчет коэффициентов УМНФ выполняется априорно и, таким

образом, ничем не ограничен, расчет коэффициентов МУМНФ выполняется

в процессе фильтрации, т.е. предполагает реализуемость в режиме реально-

го времени. По этой причине в экспериментах для УМНФ моделировались

пучки объемов 10⁵ и в отдельных примерах 10⁶ траекторий, далее в расчете

МУМНФ N полагается равным 10³.

Для проверки работоспособности МУМНФ и демонстрации продуктивно-

сти комбинирования концепций УМНФ и СТ-фильтрации рассмотрим мо-

дель регрессии с порогами. Из множества проведенных экспериментов это

самая простая модель, которая демонстрирует идентичное поведение УМНФ

и СТ-фильтра, с одной стороны, и преимущество МУМНФ — с другой. Осно-

вана эта модель на следующей идее. Пусть для скалярного x_t определены

n интервалов (xi-1, xⁱ], i = 1, . . . , n: -∞ = x⁰ < x¹ < . . . < xn-1< xⁿ = +∞.

Через e(x_t) обозначим n-мерный единичный вектор: e(x_t) = (0, . . . , 1, . . . 0)^T,

где единица стоит на i-м месте, если x_t ∈ (xi-1, xⁱ]. Пусть a, b, c ∈ Rⁿ. Вы-

0,16

0,14

0,12

0,10

0,08

0,06

0,04

0,02

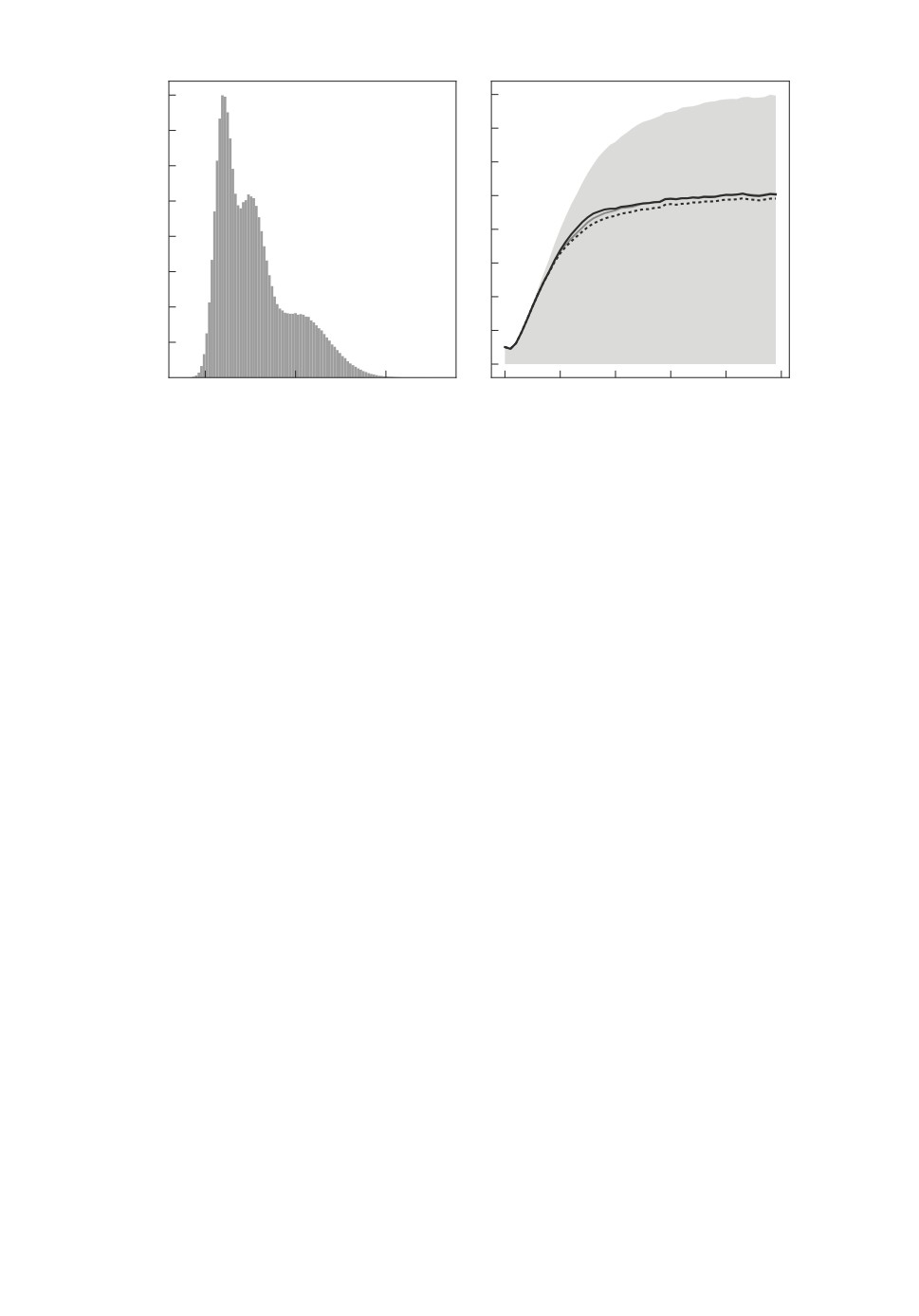
Рис. 8. Модель (19): a - гистограмма для x_T , E[x_t] = 5,56, D[x_T ] = 15,93;

б - дисперсия ошибки оценки СТ-фильтра (серая линия), УМНФ (черная

сплошная линия) и МУМНФ (черная точечная линия) на фоне дисперсии

процесса D[x_t] (верхняя граница серой области).

ражение a^Te(x_t) дает i-ю координату вектора a, номер которой определя-

ется принадлежностью x_t i-му отрезку. С помощью этого простого приема

легко записать, например, n линейных регрессий: i-я регрессия будет иметь

вид a_ix + b_i + c_iw_t. Окончательная модель имеет вид x_t = a^Te (xt-1) xt-1+

+b^Te(xt-1) + c^Te(xt-1) w_t, т.е. представляет собой комбинацию n авторегрес-

сий первого порядка. Дополнив приведенные соотношения простыми линей-

ными наблюдениями, получаем следующую систему наблюдения:

x_t = a^Te(xt-1) xt-1 + b^Te(xt-1) + c^Te(xt-1)w_t, t = 1,2,... , x₀ = η,

(19)

y_t = x_t + 10v_t,

где η, w_t, v_t — стандартные гауссовские.

Для проведения расчетов выберем n = 3, интервалы -∞ < 3 < 7 < +∞,

a^T = (0,3; 0,4; 0,7), b^T = (1,4; 3,0;3,0), c^T = (0,9; 1,5; 2,5). Как и во всех мо-

делях ранее, и здесь процесс x_t — эргодический, его предельное распределе-

ние проиллюстрировано рис. 8,а, а выборочные моменты равны E[x_T ] = 5,56,

D[x_T ] = 15,93.

У этого распределения легко видеть три “пика”, соответствующие трем

устойчивым авторегрессиям x_t = a_ixt-1 + b_i + c_iw_t. Предельное распределе-

ние каждой их регрессий, рассмотренной в отдельности от других, будет

гауссовским со средним m_i = b_i/(1 - a_i) и дисперсией σ2i = c2i/(1 - a2i). Об-

разуя вместе с заданными порогами процесс x_t в соответствии с (19), вы-

бранные параметры обеспечивают предельную плотность, показанную на

рис. 8,а, которой отвечают следующие вероятности p¹ = P (x_t ≤ 3,0) ≈ 0,33,

p² = P(3,0 < x_t ≤ 7,0) ≈ 0,37, p³ = P(x_t > 7,0) ≈ 0,3.

Кроме мультимодального предельного распределения модель (19) еще поз-

воляет продемонстрировать возможность гибкого формирования структуры

оценки УМНФ. Причем здесь, в отличие от модели с переключающимися ка-

налами наблюдения (18), структуру фильтра определяет прогноз. Используе-

мая, как и в большинстве примеров приведенных ранее, коррекция в форме

невязки естественна для линейных наблюдений. Прогнозирующую структур-

ную функцию ξ_t (x) определим по аналогии с коррекцией дл( модели)(18)

на основе отношений правдоподобия, используя обозначение N

x;m,σ²

для

гауссовской плотности:

(

)

pⁱN

x;m_i,σ2i

(a_ix + b_i)

ξ_t

(x) =i=1

^∑ piN ⁽x;m_i,σ2⁾

i=1

Комментируя такой базовый прогноз, можно сказать, что выражение

∑

pⁱN(x;m_i,σ2i)

i=1

следует рассматривать как элементарную оценку предельной плотности, по-

казанной на рис. 8,а, а отношение

∕∑3

pⁱN(x;m_i,σ2i)

i=1

- как оценку условной вероятности попадания xt-1 в i-й интервал.

Результаты расчетов иллюстрирует рис. 8,б . Все три исследуемых филь-

тра демонстрируют хорошее качество оценивания, МУМНФ с предельной

выборочной дисперсией ошибки оценки D[x_T - x_T ] = 9,82 имеет небольшое

преимущество порядка 2-3 %, СТ-фильтр c D[x_T - x_T ] = 10,11 совсем незна-

чительно проигрывает УМНФ c D[x_T - x_T ] = 10,06. При этом напомним, что

для СТ-фильтра используется предварительная оптимизация параметров,

УМНФ также требует выполнения значительного объема априорных рас-

четов, тогда как для МУМНФ нет необходимости в априорных вычислени-

ях, а значит, отсутствуют ограничения в отношении горизонта оценивания.

Наилучшие найденные значения параметров СТ-преобразования в данной

модели: α = 0,71, β = 1,45, γ = 2,56 для шага прогнозирования и α = 0,41,

β = 1,80, γ = 1,84 для шага коррекции, они позволяют улучшить точность

оценивания СТ-фильтра D[x_T - x_T ] = 11,77 для базовых значений α^∗, β^∗, γ^∗.

В заключение отметим, что подбор простой модели для иллюстрации ре-

зультатов МУМНФ оказался довольно затруднительным. Продемонстриро-

ванный результат обеспечен, по-видимому, характерным предельным распре-

делением (рис. 8,а). Большего эффекта удастся добиться, если отказаться от

скалярных уравнений.

6. Заключение

В целом, совокупность экспериментов, проведенных со всеми рассмотрен-

ными фильтрами, позволяет на качественном уровне дать характеристику

вычислительной трудоемкости и ресурсоемкости алгоритмов. Необходимость

априорного расчета и хранения коэффициентов УМНФ делает этот фильтр

самым ресурсоемким. При этом объем хранимых параметров определяется

задаваемым горизонтом фильтрации, а значительные затраты на априорное

моделирования компенсируются крайней простотой вычисления апостериор-

ных оценок и характеризуются той же вычислительной сложностью, что име-

ет классический фильтр Калмана в линейной задаче. “Оптимизированный”

СТ-фильтр в скалярном случае предполагает проведение такого же неболь-

шого объема вычислений, но этот объем растет с ростом размерности задачи,

т.е. с ростом числа 2p + 1 сигма-точек x^it ∈ R^p, усложняется в связи с необхо-

димостью выполнения вычисления матричнозначного корня на каждом шаге

оценивания. Кроме того, надо учитывать, что отсутствие априорных расче-

тов для СТ-фильтра не гарантирует даже “удачного” выбора его параметров,

а оптимизация, выполненная в рассмотренных экспериментах, требует тех

же ресурсов, что и моделирование параметров УМНФ в скалярных приме-

рах. Вычислительная сложность такой оптимизации экспоненциально растет

с ростом размерности, так что возможность оптимального подбора парамет-

ров α, β, γ СТ-фильтра в практически значимых задачах представляется

сомнительной. Отсутствие априорных расчетов и затрат на хранение пара-

метров — свойство и преимущество МУМНФ. Достигается оно за счет пе-

реноса шагов моделирования в апостериорный расчет. Объем моделирования

при этом меньше, чем для априорного расчета коэффициентов УМНФ (в при-

мерах 10³ против 10⁵ и 10⁶), но все равно значительный, и представляется

целесообразным только при наличии соответствующих вычислительных воз-

можностей, которыми обладают современные компьютерные системы.

СПИСОК ЛИТЕРАТУРЫ

1. Julier S.J., Uhlmann J.K., Durrant-Whyte H.F. A New Approach for Filtering

Nonlinear Systems // Proc. IEEE Amer. Control Conf. (ACC’95). 1995. P. 1628-

1632.

2. Menegaz H.M.T., Ishihara J.Y., Borges G.A., Vargas A.N. A Systematization of

the Unscented Kalman Filter Theory // IEEE Trans. Autom. Control. 2015. V. 60.

No. 10. P. 2583-2598.

3. Julier S.J. The Scaled Unscented Transformation // Proc. IEEE Amer. Control

Conf. (ACC’02). 2002. P. 4555-4559.

4. Xu L., Ma K., Fan H. Unscented Kalman Filtering for Nonlinear State Estimation

with Correlated Noises and Missing Measurements // Int. J. Control Autom. Syst.

2018. V. 16. No. 3. P. 1011-1020.

5. Li L., Xia Y. Stochastic Stability of the Unscented Kalman Filter with Intermittent

Observations // Automatica. 2012. V. 48. No. 5. P. 978-981.

6. Lee D., Vukovich G., Lee R. Robust Unscented Kalman Filter for Nanosat Attitude

Estimation // Int. J. Control Autom. Syst. 2017. V. 15. No. 53. P. 2161-2173.

7. Zhao Y., Gao S.-S., Zhang J., Sun Q.-N. Robust Predictive Augmented Unscented

Kalman Filter // Int. J. Control Autom. Syst. 2014. V. 12. No. 5. P. 996-1004.

8. Scardua L.A., da Cruz J.J. Complete Offline Tuning of the Unscented Kalman

Filter // Automatica. 2017. V. 80. P. 54-61.

Straka O., Dunik J., Simandl M. Unscented Kalman Filter with Advanced

Adaptation of Scaling Parameter // Automatica. 2014. V. 50. No. 10. P. 2657-

2664.

10.

Dunik J., Simandl M., Straka O. Unscented Kalman Filter: Aspects and Adaptive

Setting of Scaling Parameter // IEEE Trans. Autom. Control. 2012. V. 57. No. 9.

P. 2411-2416.

11.

Biswas S.K., Qiao L., Dempster A.G. A Novel a Priori State Computation Strategy

for the Unscented Kalman Filter to Improve Computational Efficiency // IEEE

Trans. Autom. Control. 2017. V. 62. No. 4. P. 1852-1864.

12.

Sarkka S. On Unscented Kalman Filtering for State Estimation of Continuous-Time

Nonlinear Systems // Trans. Autom. Control. 2007. V. 52. No. 9. P. 1631-1641.

13.

Li X., Liu A., Yu C., Su F. Widely Linear Quaternion Unscented Kalman Filter

for Quaternion-Valued Feedforward Neural Network // IEEE Signal Process. Lett.

2017. V. 24. No. 9. P. 1418-1422.

14.

Bhotto M.Z.A., Bajic I.V. Constant Modulus Blind Adaptive Beamforming Based

on Unscented Kalman Filtering // IEEE Signal Process. Lett. 2015. V. 22. No. 4.

P. 474-478.

15.

Li L., Xia Y. Unscented Kalman Filter over Unreliable Communication Networks

with Markovian Packet Dropouts // Trans. Autom. Control. 2013. V. 58. No. 12.

P. 3224-3230.

16.

Wu P., Li X., Bo Y. Iterated Square Root Unscented Kalman Filter for

Maneuvering Target Tracking Using TDOA Measurements // Int. J. Control

Autom. Syst. 2013. V. 11. No. 4. P. 761-767.

17.

Jochmann G., Kerner S., Tasse S., Urbann O. Efficient Multi-Hypotheses

Unscented Kalman Filtering for Robust Localization // Lect. Notes Comput. Sci.

(including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in

Bioinformatics) 7416 LNCS. 2012. P. 222-233.

18.

Leven W.F., Lanterman A.D. Unscented Kalman Filters for Multiple Target

Tracking with Symmetric Measurement Equations // Trans. Autom. Control. 2009.

V. 54. No. 2. P. 370-375.

19.

Пугачев В.С. Рекуррентное оценивание переменных и параметров в стохасти-

ческих системах, описываемых разностными уравнениями // ДАН СССР. 1978.

Т. 243. № 5. С. 1131-1133.

20.

Пугачев В.С. Оценивание переменных и параметров в дискретных нелинейных

системах // АиТ. 1979. № 6. С. 63-79.

Pugachev V.S. Estimation of Variables and Parameters in Discrete-Time Nonlinear

Systems // Autom. Remote Control. 1979. V. 40. No. 4. P. 39-50.

21.

Панков А.Р. Рекуррентная условно-минимаксная фильтрация процессов в раз-

ностных нелинейных стохастических системах // Изв. РАН. Теория и системы

управления. 1992. № 3. С. 63-70.

Pankov A.R. Recurrent Conditionally Minimax Filtering of Processes In Nonlinear

Difference Stochastic Systems // J. Comput. Syst. Sci. Int. 1993. V. 31. No. 4.

P. 54-60.

22.

Pankov A.R., Bosov A.V. Conditionally Minimax Algorithm for Nonlinear System

State Estimation // IEEE Trans. Autom. Control. 1994. V. 39. No. 8. P. 1617-1620.

23.

Борисов А.В., Босов А.В., Кибзун А.И., Миллер Г.Б., Семенихин К.В. Ме-

тод условно-оптимальной нелинейной фильтрации и современные подходы к

оцениванию состояний нелинейных стохастических систем // АиТ. 2018. № 1.

С. 3-17.