Автоматика и телемеханика, № 7, 2019

Н.Е. КИРИЛЕНКО (nikolai-kirilenko@mail.ru),

С.О. КРАСНИКОВ (krasnikov90@mail.ru)

(Южный федеральный университет, Ростов-на-Дону)

МЕТОД ПОИСКА НЕИЗВЕСТНЫХ ВЫСОКОЧАСТОТНЫХ

ОСЦИЛЛЯТОРОВ В СОСТАВЕ ЗАШУМЛЕННЫХ СИГНАЛОВ

НА ОСНОВЕ НЕПРЕРЫВНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

Предложен метод поиска априорно неопределенных структур неизвест-

ных временн ых флуктуаций частотных осцилляторов разной интенсивно-

сти в составе выходных сигналов синхронизированных динамических си-

стем. В отличие от традиционных подходов разработанный метод основан

на непрерывном вейвлет-преобразовании наблюдаемого сигнала и работо-

способен в случаях, когда частотные характеристики искомого паттерна

близки к характеристикам шумов выходного сигнала.

Ключевые слова: непрерывное вейвлет-преобразование, вейвлет-энтро-

пия, паттерн.

DOI: 10.1134/S0005231019070055

1. Введение

Задачи анализа, классификации и идентификации сигналов, продуцируе-

мых динамическими системами в различных условиях функционирования,

получили широкое практическое распространение. В биомедицинских при-

ложениях [1, 2], электроэнергетике [3] и в других областях науки и техники

особый интерес представляют синхронизированные динамические осцилля-

торные системы, неизвестные спонтанные активности которых находят от-

ражение в регистрируемых сигналах в виде паттернов с априорно неопреде-

ленными формами и характеристиками. Традиционно в перечисленных об-

ластях анализу подлежат нестационарные во времени или неоднородные в

пространстве сигналы с высокой зашумленностью, в составе которых случай-

ным образом возникают априорно неопределенные структуры неизвестных

временн ых флуктуаций некоторых частотных осцилляторов разной интен-

сивности [1-6]. Часто локализация во времени подобных паттернов и позво-

ляет выяснить принципы синхронизации исследуемой системы и качественно

выполнить процедуры классификации и идентификации.

Несмотря на то что методы анализа, классификации и идентификации

подобных систем в настоящее время достаточно хорошо изучены, проблемы

в некоторых частных случаях все же существуют. Так, шумы наблюдаемых

сигналов могут быть обусловлены не только, например, шумами электронных

трактов измерительной и регистрирующей аппаратуры, но и шумами, свя-

занными с принципиально неизвестными исследователю физическими про-

цессами функционирования динамической системы. В свою очередь непол-

нота, ограниченные возможности экспериментальных исследований и гетеро-

122

генность структур данных могут не позволить получить достаточную и по-

дробную статистическую информацию о механизмах синхронизации и функ-

ционирования исследуемой динамической системы. Подобные проблемы не

позволяют применять традиционные процедуры предварительной обработки

сигналов - фильтрации, взвешивания и им подобных, что обычно увеличива-

ет информативность данных. Это и приводит к существенной неопределен-

ности формализуемых математических моделей и к необходимости предва-

рительного исследования свойств регистрируемых сигналов. В основе такого

предварительного анализа лежат известные положения теории информации,

позволяющие выявить скрытые закономерности в составе сигналов и понять

природу наблюдаемой осцилляторной системы. Предложен метод энтропий-

ного анализа сигналов, эффективный в случаях, когда частотные характери-

стики искомого паттерна близки к характеристикам шумов выходного сигна-

ла и традиционные подходы неработоспособны.

2. Традиционные методы на основе дискретного вейвлет-преобразования

Основные положения традиционного подхода [4-6] могут быть кратко

сформулированы следующим образом. Некоторая выходная характеристи-

ка динамической системы f (t) посредством процедуры наблюдения (изме-

рения) с постоянным шагом по времени Δt представляется конечным од-

номерным рядом {x_k }N−1

объемом N чисел, где t_k = t₀ + kΔt: x_k = f (t_k);

k=0

k = 0,1,...,(N − 1); t₀ - начальный момент времени наблюдения. В составе

ряда {x_k}N−1

k=0 предполагаетсяналичиепаттерна,существующегонакоротком

временном интервале, существенно меньшем интервала времени измерений

[t₀; N Δt], положение которого по оси времени неизвестно. В ходе анализа

требуется найти тот временной интервал, где с максимальной вероятностью

может существовать паттерн. Без потери общности далее полагаем t₀ = 0;

Δt = 1; t_k = k.

Традиционные методы энтропийного анализа реализованы на основе кон-

цепции многоуровневого частотного разложения сигналов посредством дис-

кретного вейвлет-преобразования (ДВП). Временной ряд {x_k }N−1

при этом

k=0

представляется в виде суммы аппроксимирующей и детализирующих ком-

понент [7], полностью характеризующих его в частотно-временной области.

Исходя из очевидного условия о финитности энергии множества {x}, отра-

∑

жающего исследуемый сигнал f (t) с дискретностью Δt = 1, т.е.

k |xk| < ∞,

и на основе аналога теоремы Парсеваля о равенстве энергии сигнала f (t) и

энергии его непрерывного вейвлет-разложения

∫

∞

∫

∞

∫

∞

(1)

|f (t)|² dt = C−1

|W (a, b)|² dadb;

a, b ∈ R, a = 0,

a²

−∞

−∞ −∞

где C - нормирующий коэффициент;

∫∞

⁽t−b⁾

W (a, b) = |a|−1/2

f (t) ψ^∗

a dt

−∞

123

- интегральное вейвлет-преобразование функции f (t) ∈ L² (R); ψ - базисный

вейвлет (символом^∗ обозначена процедура комплексного сопряжения), в [4-6]

сформулирован вывод о допустимости аппроксимирующего равенства

∞

∫

∑

(2)

|f (t)|² dt⁼

|x_k |² ,

−∞

∑

где

k |xk|² =^E- полная энергия вейвлет-разложения сигнала xk. Так как

вейвлет-энергию сигнала E_j на уровне декомпозиции j = 1, 2, . . . , M находят

как суммарную энергию всех детализирующих коэффициентов этого уровня,

то полную вейвлет-энергию^E из равенства (2) находят как^E =∑M

j=1 Ej,где

M - количество итераций, которое определяется исходя из особенностей сиг-

нала и ограничено сверху числом∕N его дискретных значений [7]. Выполняя

процедуру нормализации p_j = E_j

^E, находят вероятности p_j распределения

вейвлет-энергии по уровням декомпозиции, причем∑M

j=1 pj =1,ивводятпо-

нятие вейвлет-энтропии (wavelet entropy , WE )

∑

(3)

H = − p_j log2 (p_j

j=1

{

}N−1

Для временной локализации паттернов исходный ряд

x_k

разби-

{

}n−1

вается на I > 1 временн ых выборок объемом n < N чисел

xi,˜

^k=0,где

= 0, 1, . . . , (n − 1), i = 1, 2, . . . , I - номер скользящего окна, для которых из-

менения статистических характеристик нестационарных процессов протека-

ют достаточно медленно, выполняется гипотеза о стационарности и процес-

сы можно рассматривать как псевдостационарные [2, 7, 8]. Так как вейвлет-

энтропии (3) последовательно вычисляются для каждого i-го временного ок-

на H = H (i), то можно говорить далее о переходе к временному анализу

энтропии и осуществлять поиск той i-й выборки, в которой с максимальной

вероятностью присутствует искомый паттерн.

При поиске исходят из того известного факта, что максимальные значе-

ния энтропии достигаются для сигнала, представляющего собой белый шум,

так как в этом случае спектральные составляющие равномерно распреде-

лены по всему диапазону задействованных частот и относительные энергии

практически равномерны на всех уровнях декомпозиции. Относительный же

энергетический вклад случайного паттерна концентрируется вокруг некото-

рого уровня разложения, спектральные составляющие распределяются по ча-

стотам неравномерно, энтропия на временном интервале существования это-

го паттерна принимает низкое значение и, следовательно, функция стоимо-

сти определяется из условия поиска минимума H (i). С целью повышения

качества сравнительного временного анализа также могут использоваться

дополнительные критериальные функции, например относительная вейвлет-

энтропия (relative wavelet entropy , RWE ) или иные [5], но, в целом, сути ме-

тода это не изменяет.

124

Основной недостаток изложенного подхода проявляется тогда, когда ха-

рактеристики искомого паттерна - частоты и интенсивности соответствую-

щих осцилляторов, близки к характеристикам шумовых составляющих сигна-

ла, а его локализация во времени априорно неизвестна. В подобных случаях

оказывается, что критериальные функции имеют низкую чувствительность

и часто не позволяют определить временную локализацию паттерна. Резуль-

таты численных исследований, подтверждающие этот вывод, представлены

далее.

3. Разработанный метод на основе непрерывного вейвлет-преобразования

Широкое практическое применение ДВП объясняется его эффективно-

стью с вычислительной точки зрения, так как коэффициенты частотного

масштабирования a и временного сдвига b принимают здесь лишь значения,

кратные степени двойки. В то же время известно [9, 10], что непрерывное

вейвлет-преобразование (НВП) в рассматриваемом классе задач иногда ока-

зывается более эффективным инструментарием. Во-первых, избыточность

НВП, связанная с непрерывным изменением параметров a и b, позволяет

более четко и полно представить и затем проанализировать содержащуюся

в сигнале информацию, четче выявить его структуру и осуществить поиск

паттернов. Во-вторых, как показано в [10], природа интегрального вейвлет-

преобразования W (a, b) такова, что имеет право на существование понятие

локальности его энергетического спектра. Так, одной из особенностей НВП

является возможность получения локализованных характеристик и изучения

локальных свойств процессов. Соответственно плотность спектра вейвлет-

энергии

(4)

E_W (a,b) = |W (a,b)|²

из равенства (1), называемая еще локальным спектром энергии и характе-

ризующая энергетические уровни функции f (t) в частотно-временном про-

странстве, может быть определена как для фиксированного масштаба a, так

и для конкретного коэффициента b [10]. Глобальным спектром энергии, отра-

жающим распределение энергии по масштабам на всем временном интервале,

называют величину

+^∞

E_W

(5)

(a) =

|W (a, b)|²

d b,

−∞

а полную энергию функции f (t) в этом случае находят из уравнения

∫

E_f

E_W

(6)

=C−1

(a)^da

a² .

Ясно, что при непрерывном изменении параметров a и b множество

вейвлет-функций ψ (t) оказывается избыточным, а большие вычислитель-

ные затраты - нецелесообразными. Поэтому при соблюдении естественно-

го условия о возможности последующего восстановления сигнала из его

125

трансформант проводится дискретизация параметров a = a_α, b = b_β , где

α = 0,1,...,(N_α − 1), β = 0,1,...,(N_β − 1), и вместо интегрального вейвлет-

преобразования W (a, b) используется его оценка

)

∑

⁽k−b_β

^W (a_α, b_β ) =

x_kψ^∗

;

w (a_α,b_β)

a_α

k=0

(

)

)₂

∑

w (a_α, b_β ) =

exp

−1(k−bβ

B a_α

k=0

вычисляемая на дискретном множестве значений аргументов a_α и b_β для

конечного временного ряда {x_k }N−1

k=0 ,гдеB-коэффициент,определяемый

типом базисного вейвлета ψ. Вопросы дискретизации параметров a_α, b_β и

выбора их диапазонов N_α, N_β подробно рассмотрены в [10].

Также воспользуемся дискретной оценкой локального спектра энергии

E_W (a,b) (4) - скалограммой



(7)

E_S (a_α,b_β) =

^W

(a_α, b_β )

²,

отражающей распределение энергии {x_k}N−1

теперь уже по дискретным па-

k=0

раметрам “масштаб - время” и скейлограммой

N_β−1∑

E_S

(8)

(a_α) =

E_S (a_α,b_β

β=0

представляющей собой оценку глобального спектра энергииEW (a) (5). В (8)

N_S - число точек, по которому осуществляется осреднение. Скейлограмма

E_S

(a_α) (8) отражает распределение вейвлет-энергии для масштаба a_α на всем

наборе N наблюдений сигнала x_k. Учитывая, что согласно (6) величина пол-

ной энергии сигнала E_f пропорциональна площади под кривой

E_W

(a) /a²

и равенство (2), оценку полной вейвлет-энергии {x_k }N−1

представим теперь

k=0

как

∑

(9)

E_x =

E_S

(a_α

α=0

Так как скалограмма E_S (a_α, b_β ) (7) выявляет локальное частотно-вре-

менное распределение энергии процесса, то по аналогии с изложенным вы-

ше традиционным подходом введем в рассмотрение вероятности распределе-

ния вейвлет-энергии сигнала по масштабам a_α, рассчитываемые для каждого

i-го временного окна,

∑

(10)

pα (i) =^ES (aα, i)∕Ex (i),

pα

= 1,

α=0

126

а уравнение вейвлет-энтропии теперь запишем в виде

∑

(11)

H_S (i) = −

pα (i) log2 (^pα

(i)) .

α=0

Необходимо еще раз отметить, что энтропия (11) отражает распределение

вейвлет-энергии сигнала во времени. Так, если в i-м окне в составе сигнала

присутствовала структурная особенность, какие-либо особенные флуктуации

частотных осцилляторов или что-либо, отличающее состояние динамической

системы на этом временном интервале наблюдений от всех иных состояний,

то энтропия H_S (i) принимает сравнительно низкое значение.

В силу упомянутой возможности использовать НВП для оценивания лока-

лизованных энергетических характеристик временного ряда будем проводить

анализ ряда {x_k }N−1

не в полном диапазоне α = 0, 1, . . . , (N_α − 1) масшта-

k=0

бов a_α (не во всем частотном диапазоне), а исследовать его в узком диапазоне,

интересующем с точки зрения проблемы поиска флуктуаций соответствую-

щих частотных осцилляторов. Тогда в (7) и (8) будем рассматривать лишь

диапазон масштабов [a_αmin ; a_αmax ], а (9)-(11) перепишем в виде:

∑

(12)

E_x (i) =

E_S

(a_α, i) ;

E_x (i),

= 1;

pα (i) =^ES (aα, i)^∕

pα

α=α^min

∑

H_S (i) = −

pα (i) log2 (^pα (i)).

α=α^min

Неясным при этом остается выбор минимального α^min и максимально-

го α^max граничных значений в случае поиска флуктуаций осцилляторов за-

ранее неизвестных частот. Необходимо отметить, что проведенные практиче-

ские исследования показали существенную зависимость и фактически - ра-

ботоспособность критериальной функции H_S (i) именно лишь при точном за-

дании этих значений. Однако же понятно, что, исходя из особенностей иссле-

дуемой осцилляторной системы, расширенные границы частотного спектра

искомого паттерна в каждом практическом случае априорно известны. По-

этому такие расширенные оценки граничных значений коэффициентов мас-

штабирования могут быть заданы из условий α^min < α^min, α^max > α^max. Для

окончательного разрешения проблемы предлагается ввести в рассмотрение

дополнительную функцию стоимости. Будем определять α^min, α^max из усло-

вия минимума вейвлет-энтропии

∑

(13)

h_S (α) = −

) = 1,

pi (aα) log2 (^pi (^aα));

pi (aα

i=1

рассчитываемой теперь отдельно для каждого масштаба a_α из расширен-

ного диапазона α = α^min, . . . , α^max на всем наборе N наблюдений сигна-

ла x_k , где p_i (a_α) =ES (a_α, i)^∕e_x (a_α) - вероятности распределений вейвлет-

127

энергий по временн ым окнам для каждого масштаба в отдельности; e_x (a_α) =

=∑Nβ−¹

E_S (a_α,b_β) - полная вейвлет-энергия на всем временном интервале

β=0

наблюдений {x_k }N−1

для каждого масштаба в отдельности.

k=0

В отличие от (11), (12), энтропия (13) отражает распределение вейвлет-

энергии по масштабам (частотам), т.е. в пределах масштабов, соответствую-

щих спектру частот искомого паттерна, если он присутствует в любой момент

времени наблюдений в составе сигнала x_k, то энтропия (13) будет принимать

сравнительно низкое значение. Далее представлены результаты практиче-

ских исследований, иллюстрирующие эффективность разработанного метода

в сравнении с традиционными, основанными на ДВП.

4. Результаты численных исследований

В ходе численных исследований воспользовались имеющимися записями

биомедицинских электрограмм (ЭГ), в составе которых выбирали участки,

соответствующие фоновой активности организма и характеризующиеся, та-

ким образом, отсутствием паттернов ответной биоэлектрической активно-

сти. В подобные дискретные выборки объемом N = 2048 отсчетов инкап-

сулировали различные аддитивные модельные паттерны, характерные для

{

}₂₀₄₇

биомедицинских приложений [8]. Подобные модельные ЭГ

x_k

k=0 делились

{

}₂₅₅

на I = 15 временн ых выборок по n = 256 отсчетов

xi,˜

^k=0 cперекрытием

Δn = 128 отсчетов, где i = 1,2,... ,15;^k = k − (i − 1) Δn. Следует отметить,

что при использовании непересекающихся временн ых окон искомый паттерн

может быть локализован в двух соседних выборках, что ухудшает точность

его поиска.

Результаты исследований показали, что традиционные критериальные

функции (3) и другие подобные имеют низкую чувствительность в случаях,

когда характеристики искомых паттернов близки к характеристикам шумо-

вых составляющих сигнала. Правильная локализация во времени периодиче-

ски наблюдалась лишь в тех случаях, когда в состав выборки фоновой ЭГ

инкапсулировали относительно низкочастотные паттерны. Нашел подтвер-

ждение и тот факт, что увеличение количества уровней декомпозиции ДВП

позволяет лишь более детально и подробно анализировать низкочастотные

составляющие сигнала и не увеличивает точность поиска осцилляторов вы-

сокой частоты.

Далее представлены результаты моделирования, когда в состав фоновых

ЭГ инкапсулировали паттерн длительностью 150 отсчетов, частотные харак-

теристики которого были близки к характеристикам шумовых составляю-

щих, задававшегося уравнением

y₀ = 0;

u_k = sin (2πk/1000) ;

{

(14)

k ∈ [1100;1250] : K (−0,4sin(5πu_k) + 0,6sin(15πu_k)),

yk+1 =

где константа K выбиралась из диапазона [3; 10] с целью исследования влия-

ния амплитуды модельного осциллятора на точность его поиска. Графики

128

y_k

Участки модельных ЭГ с аддитивными

паттернами при

К = 5 и

= 10

100

150

Модельные

ЭГ

Выборка

фоновой ЭГ

575

1149

1723

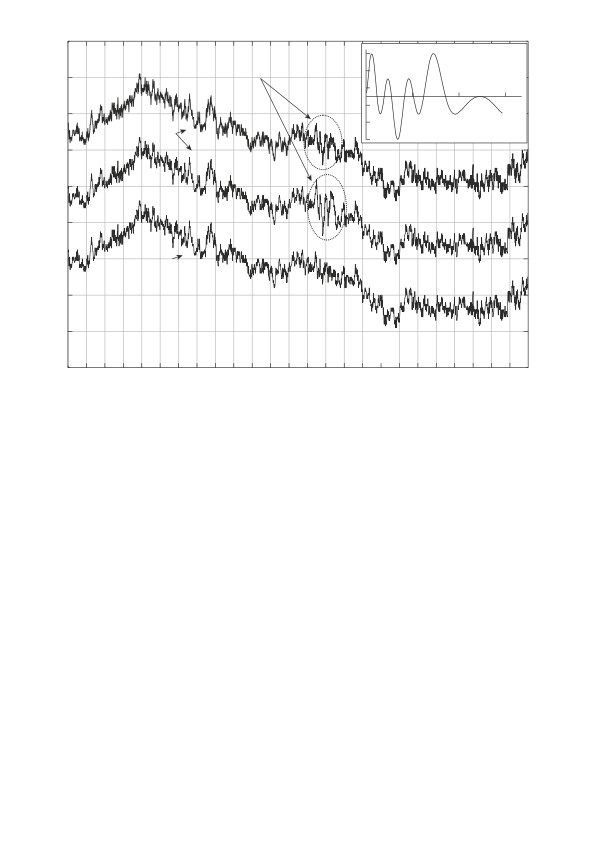
Рис. 1. Графики фоновой ЭГ, двух модельных ЭГ с аддитивным паттерном

при разных его амплитудах, и самого паттерна y_k (вверху справа).

фоновой ЭГ, модельных ЭГ с паттерном и самого паттерна y_k (14) представ-

лены на рис. 1. Ясно, что временная локализация паттерна y_k, инкапсули-

рованного в состав ЭГ на интервале [1100; 1250] отсчетов, представлялась

при моделировании “априорно неизвестной”. Следовательно, в ходе решения

критериальные функции должны были наглядно отображать факты присут-

ствия паттерна в i = 7, 9 и 10 временн ых окнах, охватывавших временн ые

интервалы [896; 1152], [1024; 1280] и [1152; 1408] отсчетов соответственно.

На рис. 2,а представлены графики вейвлет-энтропии H(i) (3) традици-

онного подхода, рассчитанной для модельной ЭГ с паттерном y_k (14) при

K = 10, и вейвлет-энтропии H_S(i) (11), где α = 0,...,(N_α − 1), но рассчи-

танной для фоновой ЭГ до инкапсуляции паттерна. Во-первых, видно, что

критериальная функция H(i) (3) имеет минимумы в i = 5 и 11 временн ых

окнах и, следовательно, не отражает факта наличия в ЭГ искомого паттерна.

Во-вторых, эта функция в большей степени отражает лишь какие-то особен-

ности в составе выборки фоновой ЭГ, что видно из анализа графика функ-

ции H_S (i) (11), рассчитанной для фоновой ЭГ без паттерна, и сопоставления

характеров двух графиков.

На рис. 2,б показаны графики функции H_S (i) (12), найденные для одной

и той же модельной ЭГ с паттерном y_k (K = 10), но отличающиеся тем, что

в одном случае расчет проводился для расширенного априорно известного

129

H(i), H_s(i)

h_S(a )

H(i) для ЭГ с

Для

фоновой

ЭГ

паттерном

H_s(i) для

фоновой

ЭГ

Для модельнойЭГ с паттерном

9 10 11 12 13 14 15

H_s(i)

s(i)

Расчет в расширенном

диапазоне масштабов

К = 5

уточненном

К = 10

диапазоне

9 10 11 12 13 14 15

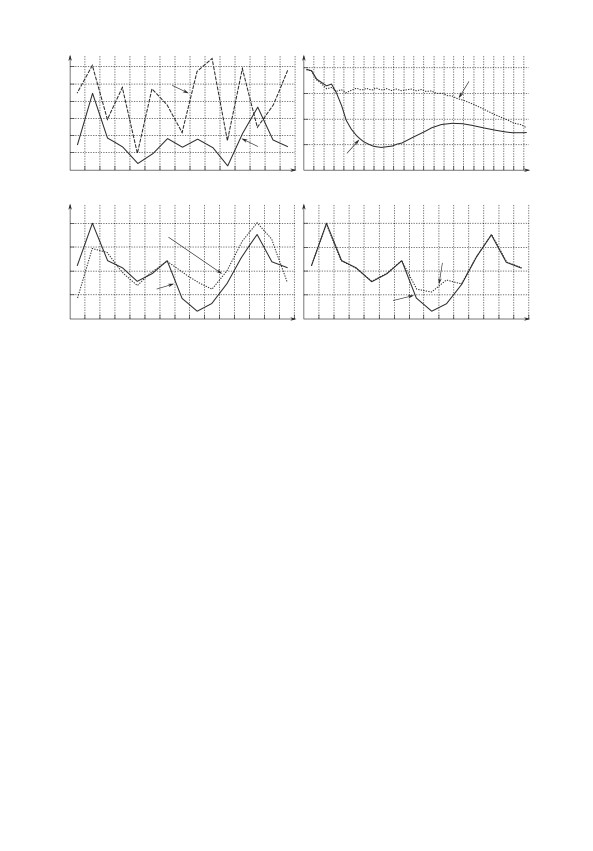
Рис. 2. Графики критериальных функций: а - вейвлет-энтропии (4), рассчи-

танной по ДВП для модельной ЭГ с п аттерном (K = 10), и вейвлет-энтро-

пии (17), рассчитанной по НВП для фоновой ЭГ без паттерна; б - функ-

ций (18), рассчитанных для одной и той же модельной ЭГ с паттерном

(K = 10), но в расширенном или в уточненном диапазонах масштабов (ча-

стот); в - функций (20) для двух ЭГ - фоновой без паттерна и модельной с

паттерном; г - функций (18) для двух модельных ЭГ с паттернами, амплиту-

ды которых отличались в два раза.

диапазона α = α^min, . . . , α^max масштабов a_α, а в другом - для уточненно-

го диапазона α = α^min, . . . , α^max. Расширенный диапазон задавался из зна-

ния того, что искомый паттерн относится к так называемому гамма-ритму

жизненной активности организма, охватывающему диапазон частот от 30

до 170 Гц и выше [8], что для использовавшегося вейвлета ψ соответство-

вало значениям α^max = 30 и α^min = 1. По графику видно, что критериальная

функция (12), рассчитываемая в расширенном локальном диапазоне частот,

также неработоспособна. Уточненный диапазон масштабов (частот), кото-

рый соответствовал максимальному вкладу осцилляций искомого паттерна

в общую вейвлет-энергию сигнала ЭГ, был выбран на основе анализа функ-

ции h_S (α) (13) (рис. 2,в) равным α^max = 23 и α^min = 7. Очевидно, что по

графику критериальной функции (12), рассчитываемой в найденном диапа-

зоне α = α^min, . . . , α^max (рис. 2,б ), можно сделать однозначный вывод о на-

личии в составе наблюдаемых зашумленных сигналов априорно неопреде-

ленных структур неизвестных флуктуаций высокочастотных осцилляторов,

и верно определить их временную локализацию. На рис. 2,в дополнительно

представлен для сравнения вид функции (13) для фоновой ЭГ без паттерна.

130

Был проведен анализ влияния амплитуды искомого паттерна на точ-

ность его поиска. На рис. 2,г представлены графики одной и той же функ-

ции H_S (i) (12), рассчитанной для двух модельных ЭГ с паттернами (14),

амплитуды которых отличались в два раза при K = 5 и K = 10. Хотя по ви-

ду графиков и можно сделать однозначный вывод о наличии в составе ЭГ

высокочастотных паттернов, достаточно точно определить их временную ло-

кализацию в i = 7, 9 и 10 временн ых окнах можно лишь для паттерна с боль-

шой амплитудой. При уменьшении амплитуды в два раза наличие паттерна

в i = 10 окне неочевидно, что неверно. При дальнейшем уменьшении ампли-

туды аддитивного паттерна точность его поиска также ухудшалась.

Следует отметить, что, например, минимальный размах колебаний так

называемых вызванных потенциалов ответной биоэлектрической активности

организма составляет около 10 % от размаха колебаний фоновой ЭГ [8]. В ходе

моделирования при K = 10 в (14) размах колебаний паттерна составлял около

28 % от размаха колебаний ЭГ, а при K = 5 - около 14 %, что соответству-

ет, например, наиболее часто встречающимся в биомедицинских приложени-

ях случаям. В то же время оказалось, что разработанный метод позволяет

обеспечить высокую точность поиска даже при предельно малых амплиту-

дах паттернов, но только тогда, когда существует возможность параллельной

регистрации сигнала в одноименные моменты времени по нескольким измери-

тельным каналам (для ЭГ - отведениям). Здесь для каждой q-й компоненты

{x_q,k}N−1

многомерного сигнала, где q = 1, 2, . . . , Q - количество сенсоров,

k=0

выполняется анализ согласно приведенному за исключением того, что ре-

зультирующие функции стоимости теперь усредняются по каналам:

∑

(15)

H_S (i) =1

H_S (i,q) ; h_S (α) =1

(α, q) ,

Q h^S

q=1

где H_S (i, q), h_S (α, q) - функции (12) и (13) для каждого q-го канала в от-

дельности.

Следует отметить робастность функций (15) к неизбежным относитель-

ным вариациям как форм искомых паттернов, так и времени их проявле-

ния в сигналах по разным измерительным каналам. Например, аналогичное

усреднение по каналам, но одноименных k-х значений многомерного сигна-

ла {x_q,k}N−1

было бы неверным именно вследствие наличия относительных

k=0

смещений как искомых паттернов, так и возможной десинхронизации измере-

ний в разных каналах. Подобные смещения по оси времени могут приводить к

эффекту, в радиосвязи называемому федингом (замиранием) радиосигнала,

обусловленному флуктуациями амплитуд, фаз и углов прибытия паттернов в

каждом канале. Соответственно в некоторых случаях паттерны в разных из-

мерительных каналах могут наблюдаться, например, в противофазе и, таким

образом, усреднение по компонентам многомерного сигнала в отличие от (15)

не приведет к ожидаемому эффекту от увеличения мерности измерений.

В ходе моделирования использовались одноименные эпохи многомерных

фоновых ЭГ {x_q,k }²⁰⁴⁷

k=0 ,записанныхнаQ=12отведениях.Использовалась

та же модель паттерна (14) при K = 5 и при минимальном K = 3, когда

131

H_s(i)

К = 5

К = 3

13 14 15

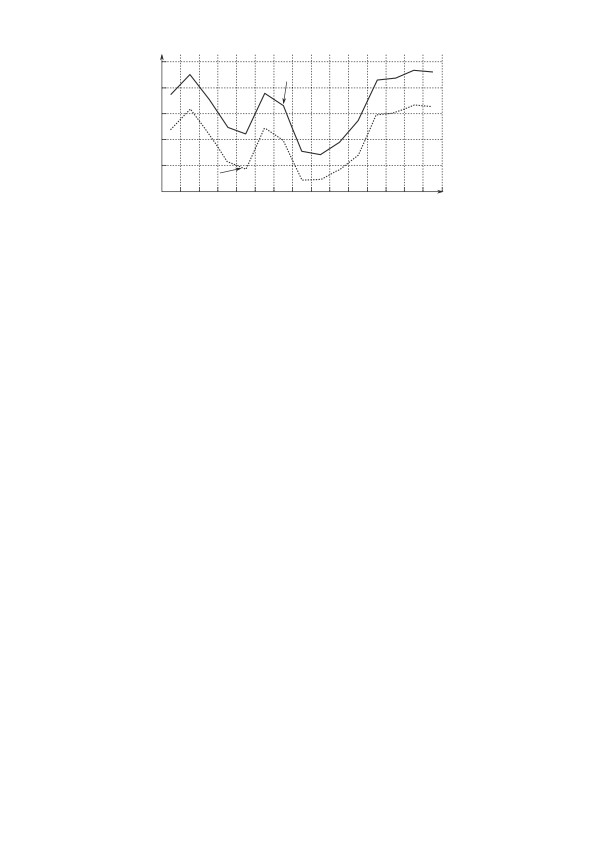
Рис. 3. Графики критериальных функций для модельных ЭГ с паттернами

разной амплитуды, полученные в многомерном случае.

размах составлял уже около 8 % от размаха колебаний ЭГ, и паттерн стано-

вился визуально неразличимым в составе сигнала. В каждом q-м отведении

задавались случайные вариации форм и временн ых параметров модельных

паттернов. Например, максимальное смещение моментов их инкапсуляции

в состав компонент многомерной ЭГ составляло ± 25 отсчетов, а вариации

средней величины значимых колебаний составляли порядка 10 %. Графики

на рис. 3 наглядно отражают факты наличия специфических паттернов в

составе модельных ЭГ и позволяют правильно осуществить их временную

локализацию в i = 7, 9 и 10 временн ых окнах.

5. Заключение

Таким образом, можно сделать окончательный вывод, что разработанный

метод позволяет выявлять слабые вариации высокочастотных структур в со-

ставе зашумленных сигналов и определять их временную локализацию. Это

необходимо, например, при настройке нейросетевых классификаторов, выде-

лении характерных признаков и уточнении их свойств, особенно при ограни-

чениях на объемы обучающих выборок.

СПИСОК ЛИТЕРАТУРЫ

1. Седов А.С., Рачева С.Н. Применение вейвлет-анализа для исследования им-

пульсной активности нейронов головного мозга человека // IX Всеросс. научн.-

технич. конф. “Нейроинформатика-2007”. 2007. Т. 2. № 1. С. 77-87.

2. Basar E., Schurmann M., Demiralp T., Basar-Eroglu C., Ademoglu A. Event-

related Oscillations are

‘Real Brain Responses’- Wavelet-Analysis and New

Strategies // Int. J. Psychophysiol. 2001. V. 39. P. 91-127.

3. Мисриханов А.М. Применение методов вейвлет-преобразования в электроэнер-

гетике // АиТ. 2006. № 5. С. 5-23.

Misrikhanov A.M. Wavelet Transform Methods: Application in Electroenergetics //

Autom. Remote Control. 2006. V. 67. No. 5. P. 682-697.

132

4. Blanco S., Figliola A., Quiroga R.Q., Rosso O.A., Serrano E. Time-Frequency

Analysis of Electroencephalogram Series. III. Wavelet Packets and Information Cost

Function // Phys. Rev. E. 1998. V. 57. P. 932-940.

5. Rosso O.A., Blanco S., Yordanova J., Kolev V., Schurmann M., Figliola A.,

Basar E. Wavelet Entropy: a New Tool for Analysis of Short Duration Brain

Electrical Signals // J. Neurosci. Meth. 2001. V. 105. P. 65-75.

6. Yordanova J., Kolev V., Rosso O.A., Schurmann M., Sakowitz O.W., Ozgoren M.,

Basar E. Wavelet Entropy Analysis of Event-Related Potentials Indicates Modality-

Independent Theta Dominance // J. Neurosci. Meth. 2002. V. 117. Р. 99-109.

7. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB. М.: ДМК

Пресс, 2005.

8. Рангайян Р.М. Анализ биомедицинских сигналов. Практический подход. М.:

Физматлит, 2007.

9. Cek M.E., Ozgoren M., Savaci F.A. Continuous Time Wavelet Entropy of Auditory

Evoked Potentials // Computers Biol. Medici. 2010. V. 40. P. 90-96.

10. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения //

Успехи физ. наук. 1996. Т. 166. № 11. С. 1145-1170.

Статья представлена к публикации членом редколлегии В.И. Васильевым.

Поступила в редакцию 03.02.2017

После доработки 03.01.2019

Принята к публикации 07.02.2019

133