Автоматика и телемеханика, № 7, 2019
© 2019 г. Х.Н. РЗАЕВ, канд.техн.наук (xazail49@mail.ru)
(Азербайджанский государственный университет нефти и промышленности, Баку)
МАТЕМАТИЧЕСКИЕ МОДЕЛИ МОДИФИЦИРОВАННЫХ
КРИПТО-КОДОВЫХ СРЕДСТВ ЗАЩИТЫ
ИНФОРМАЦИИ НА ОСНОВЕ ТКС
Разрабатываются математические модели модифицированных крипто-
кодовых средств защиты информации на основе теоретико-кодовой схемы
Мак-Элиса с использованием алгеброгеометрических блоковых кодов с
укорочением и удлинением информационной посылки, проводится анализ
стойкости и энергетических затрат на их программную реализацию.
Ключевые слова: модифицированные крипто-кодовые системы, теорети-
ко-кодовые схемы, алгеброгеометрические коды, информационная скрыт-
ность.
DOI: 10.1134/S0005231019070080
1. Введение
Современные требования к обеспечению качества обслуживания пользо-
вателей глобальных вычислительных сетей выдвигают новые задачи по ин-
тегрированному решению основных критериев качества обслуживания - на-
дежности и безопасности обслуживания. В эпоху высоких технологий появ-
ление квантовых компьютеров, которые “используют квантово-механические
явления для решения математических задач” [1] ставит под угрозу использо-
вание современных стандартов по симметричной и несимметричной крипто-
графии [1-5]. В отчете специалистов Национального института стандартов и
технологий США (NIST) о состоянии квантовых вычислений и посткванто-
вой криптографии излагается, что если будут построены крупномасштабные
квантовые компьютеры, то они смогут сломать многие криптосистемы с от-
крытым ключом, которые в настоящее время используются. Это серьезно
подорвало бы конфиденциальность и целостность цифровых коммуникаций
в Интернете и в других местах [1].
В отчете специалистами NIST в условиях постквантовой криптографии
(также называемой квантово-устойчивой криптографией) отмечается, что
разработка криптографических систем, защищенных как от квантовых, так
и от классических компьютеров на основе крипто-кодовых систем Мак-Элиса
и Нидеррайтера [1], является одним из перспективных направлений.
Упомянутые крипто-кодовые системы формируют интегрированный меха-
низм обеспечения достоверности и гарантированной криптостойкости в усло-
виях возросшего количества гибридных угроз на составляющие безопасности:
информационную безопасность, кибербезопасность и безопасность информа-
ции [6-9].
155
В [5, 8] авторы используют квазициклические коды четности с низкой
плотностью (QC-LDPC) [10] и коды с максимальным ранговым расстоянием
[5, 8] для построения криптосистем Мак-Элиса и Нидеррайтера соответствен-
но. В [11] рассматривается построение схем Мак-Элиса и Нидеррайтера на
основе альтернантных кодов Гоппы. Однако данные коды являются двоич-
ными, а это существенно увеличивает возможность их взлома на основе пе-
рестановочного декодера за конечное число шагов и не гарантирует защиту
от атаки на основе дробно-линейных преобразований. В [4] авторы предла-
гают использовать коды Рида-Соломона (РС) при построении несимметрич-
ной крипто-кодовой системы (НККС) Мак-Элиса. Однако в [12, 13] показано,
что группа автоморфизмов обобщенного кода РС изоморфна группе дробно-
линейных преобразований. Применяя это свойство, можно эффективно снять
действие используемых маскирующих матриц и восстановить быстрое прави-
ло декодирования алгебраического блокового кода [12, 13]. Этому недостатку
потенциально могут быть подвержены все подкоды обобщенных кодов РС,
включая перечисленные [12, 13].
Предложенные в [14, 15] несимметричные криптосистемы обеспечивают
требуемые показатели оперативности, криптостойкости и достоверности пе-
редаваемых данных и использование одного программно-аппаратного (аппа-
ратного) механизма в обеспечении требуемых показателей основных крите-
риев качества обслуживания.
Проведенный в [15] анализ программной реализации несимметричной
крипто-кодовой системы на теоретико-кодовой системы (ТКС) Нидеррайтера
выявил значительные сложности реализации, что существенно затрудняет ис-
пользование теоретико-кодовых схем для построения криптостойких несим-
метричных систем. Разработка модифицированных крипто-кодовых систем с
использованием модифицированных алгеброгеометрических кодов является
перспективным направлением в решении данной технической задачи.
Цель статьи - разработка формального математического описания мо-
дифицированных крипто-кодовых средств защиты информации на основе
теоретико-кодовой схемы Мак-Элиса с использованием алгеброгеометриче-
ских блоковых кодов на основе укорочения/удлинения информационных сим-
волов, позволяющих обеспечить снижение объема ключевых данных при со-
хранении уровня криптостойкости и оценка криптостойкости и энергетиче-
ских затрат на реализацию таких средств.
Известные способы модификации линейных блоковых кодов наиболее пол-
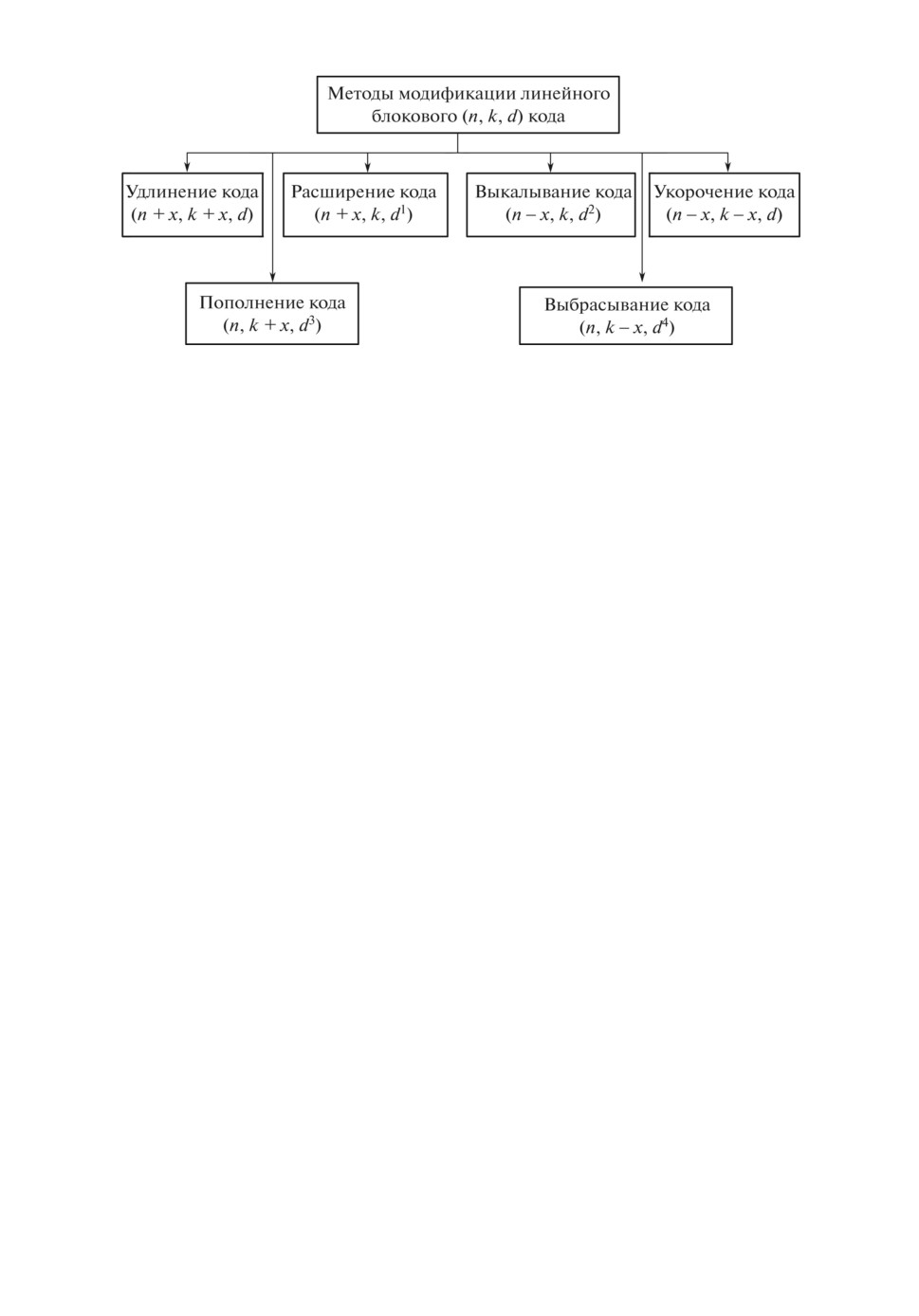
но рассмотрены в [16-20]. На рис. 1 представлены наиболее распространенные
способы модификации.
Удлинение (n, k, d) линейного блокового кода состоит в увеличении длины
n + x путем добавления новых информационных символов k + x. Расширение
(n, k, d) линейного блокового кода состоит в увеличении длины n + x путем
добавления новых проверочных символов r + x. Выкалывание (n, k, d) линей-
ного блокового кода состоит в уменьшении длины n - x путем уменьшения
проверочных символов r - x. Укорочение (n, k, d) линейного блокового ко-
да состоит в уменьшении длины n - x путем уменьшения информационных
символов k - x. Пополнение (n, k, d) линейного блокового кода состоит в уве-
156
Рис. 1. Способы модификации линейных блоковых кодов.
личении длины информационных символов k + x без увеличения длины кода.
Выбрасывание (n, k, d) линейного блокового кода состоит в уменьшении ин-
формационных символов k - x без увеличения длины кода.
Потенциальная стойкость теоретико-кодовых схем определяется сложно-
стью декодирования случайного (n, k, d) блокового кода. Следовательно, для
построения потенциально стойких теоретико-кодовых схем необходимо ис-
пользовать способы модификации, не допускающие снижения минимально-
го кодового расстояния. Маскируя код с быстрым алгоритмом декодирова-
ния (полиномиальной сложности) под произвольный (случайный) блоковый
код, можно представить задачу декодирования для противника как вычис-
лительно сложную задачу (экспоненциальной сложности). Для уполномочен-
ного пользователя системы (имеющего секретный ключ) декодирование -
полиномиально разрешимая задача. Сидельниковым в [12, 13] предложен эф-
фективный способ взлома несимметричных схем Мак-Элиса и Нидеррайтера,
построенных на обобщенных кодах Рида-Соломона. Отмечается, что одним
из перспективных направлений в развитии потенциально стойких теоретико-
кодовых схем являются схемы, построенные с использованием алгеброгеомет-
рических или каскадных кодов [12]. Алгебраические блоковые коды, постро-
енные по алгебраическим кривым (алгеброгеометрические коды), обладают
хорошими асимптотическими характеристиками. Их применение в дискрет-
ных симметричных каналах позволяет получить наибольший энергетический
выигрыш от кодирования (среди алгебраических блоковых кодов) и эффек-
тивно бороться с возникающими пакетами ошибок. Способы удлинения и
укорочения линейных блоковых кодов, не изменяя минимального расстоя-
ния, позволяют строить стойкие к взлому несимметричные крипто-кодовые
системы с меньшим объемом криптограммы и ключевых данных.
В соответствии с формальным математическим описанием несимметрич-
ных крипто-кодовых систем на основе ТКС Мак-Элиса в режиме прямого
исправления ошибок и автоматического переспроса, предложенных в [14],
предлагаются математические модели модифицированных несимметричных
криптосистем на основе ТКС Мак-Элиса, позволяющих снизить энергетиче-
ские затраты на их реализацию.
157
2. Математическая модель модифицированной несимметричной
крипто-кодовой системы защиты информации
2.1. С использованием алгеброгеометрических блоковых кодов на осно-
ве теоретико-кодовой схемы Мак-Элиса на основе укорочения (сокращения
информационных символов) эта модель формально задается совокупностью
следующих элементов [14]:
— множество открытых текстов
{
}
{
}
M =
M1,M2,... ,Mqk
,
где Mi =
I0,Ih1 ,... ,Ihj ,Ik-1
∀Ij ∈ GF (q),
hj - информационные символы, равные нулю, |h| =12k, т.е. Ii = 0 ∀Ii ∈ h;
— множество закрытых текстов (кодограмм)
(
)
{
}
C =
C1,C2,... ,Cqk
,
где Ci = c∗X
,c∗h
,...,c∗h
,c∗
Xn-1
∀c∗
Xj
∈ GF (q);
0
1
j
— множество прямых отображений (на основе использования открытого
ключа - порождающей матрицы)
ϕ = {ϕ1,ϕ2,...,ϕs}, где ϕi : M → Ck-hj, i = 1,2,... ,s;
— множество обратных отображений (на основе использования закрытого
(личного) ключа - матриц маскировки)
{
}
ϕ-1 =
ϕ-11, ϕ-12, . . . , ϕ-1s
,
где ϕ-1i : Ck-h
→ M, i = 1,2,... ,s;
j
— множество ключей, параметризирующих прямые отображения (откры-
тый ключ уполномоченного пользователя),
{
}
s
ai
,
Kai = {K1ai ,K2ai ,... Ksai } = GEC1Xai,GXC2 ai,...,GX
- порождающая (n × k)-матрица замаскированного под слу-
где GECsXai
чайный код алгеброгеометрического блокового (n, k, d) кода с элементами
из GF (q), т.е.
Kia
i
ϕi : M
---→
CK-hj , i = 1,2,... ,s;
ai - набор коэффициентов многочлена кривой a1,... ,a6 ∀ai ∈ GF(q), одно-
значно задающий конкретный набор точек кривой из пространства P2;
— множество ключей, параметризирующих обратные отображения (лич-
ный (закрытый) ключ уполномоченного пользователя),
{
}
K∗ = {K∗1,K∗2,... ,K∗
s
}=
{X, P, D}1, {X, P, D}2, . . . , {X, P, D}s
,
{X, P, D}i = {Xi, Pi, Di},
где Xi - маскирующая невырожденная случайно равновероятно сформиро-
ванная источником ключей (k × k)-матрица с элементами из GF (q); Pi -
158
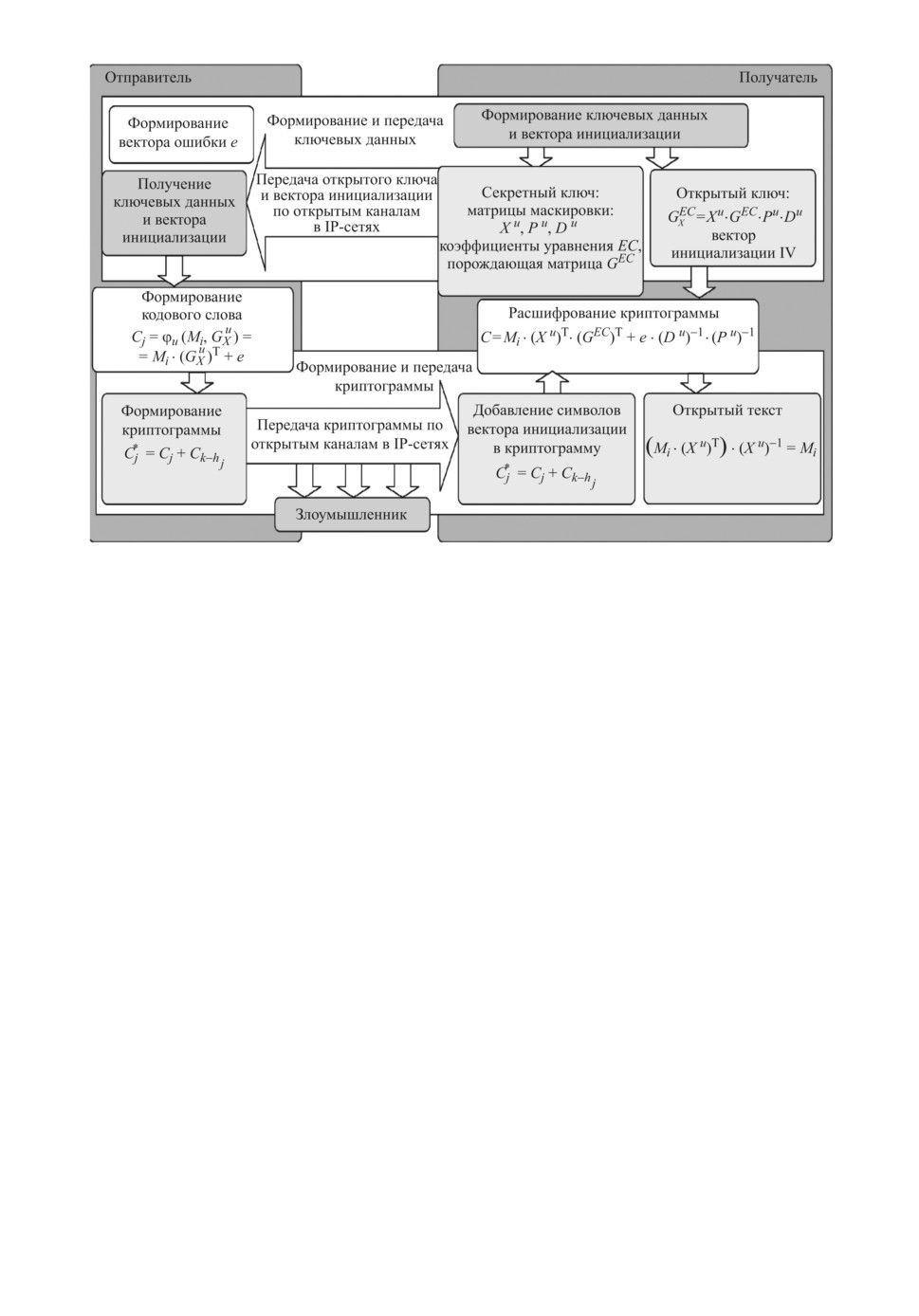
Рис. 2. Протокол обмена информацией в режиме реального времени с исполь-
зованием модифицированной ТКС Мак-Элиса с укороченными ЕС.
перестановочная случайно равновероятно сформированная источником клю-
чей (n × n)-матрица с элементами из GF (q); Di - диагональная сфор-
мированная источником ключей (n × n)-матрица с элементами из GF (q) ,
i
т.е. ϕ-1i : C
-→
M, i = 1,2,...,s, сложность выполнения обратного отобра-
жения ϕ-1i без знания ключа K∗i ∈ K∗ сопряжена с решением теоретико-
сложностной задачи декодирования случайного кода (кода общего положе-
ния). Таким образом, в качестве личного (закрытого) ключа (KR абонента)
в модифицированной крипто-кодовой системе (МККС) Мак-Элиса выступа-
ют матрицы маскировки X, P, D и порождающая матрица G эллиптиче-
ского кода, а в качестве открытого (общедоступного ключа) (KU абонен-
та) используется сформированная путем перемножения матриц маскировки
и порождающей матрицы матрица эллиптического кода GECiXai, вектор ини-
циализации, определяющий места укорочения (удаления символов в кодовом
слове) и вектор ошибки являются сеансовыми ключами отправителя. Струк-
турная схема протокола обмена информацией в режиме реального времени с
использованием модифицированной ТКС Мак-Элиса с укороченными эллип-
тическими кодами (EC) представлена на рис. 2.
Исходными данными при описании рассмотренной несимметричной крип-
то-кодовой системы защиты информации являются:
— алгеброгеометрический блоковый (n, k, d) код Ck-hj над GF (q) , т.е. мно-
жество кодовых слов Ci ∈ Ck-hj таких, что выполняется равенство CiHT = 0,
где H проверочная матрица алгеброгеометрического блокового кода;
159
— ai — набор коэффициентов многочлена кривой a1,...,a6 ∀ai ∈ GF(q),
однозначно задающий конкретный набор точек кривой из пространства P2,
для формирования порождающей матрицы в соответствии с (14);
— hj — информационные символы, равные нулю, |h| = 12k, т.е. Ii = 0
∀Ii ∈ h;
— маскирующие матричные отображения, заданные множеством матриц
{X, P, D}i, где X — невырожденная (k × k)-матрица над GF (q), P — пере-
становочная (n × n)-матрица над GF (q) с одним ненулевым элементом в каж-
дой строке и в каждом столбце матрицы, D — диагональная (n × n)-матрица
над GF (q) с ненулевыми элементами на главной диагонали.
В несимметричной крипто-кодовой системе на основе ТКС Мак-Элиса мо-
дифицированный (укороченный) алгеброгеометрический (n, k, d) код C∗k-hj
с быстрым алгоритмом раскодирования маскируется под случайный (n, k, d)
код Ck-hj посредством умножения порождающей матрицы GEC кода Ck-hj
на хранящиеся в секрете маскирующие матрицы Xu, Pu и Du [14], обеспечи-
вающий формирование открытого ключа уполномоченного пользователя:
GECuX = XuGEC PuDu, u ∈ {1, 2, . . . , s},
где GEC — порождающая (n × k)-матрица алгеброгеометрического блоково-
го (n, k, d) кода с элементами из GF (q), построенная на основе использова-
ния выбранных пользователем коэффициентов многочлена кривой a1, . . . , a6
∀ai GF(q), однозначно задающих конкретный набор точек кривой из про-
странства P2.
Формирование закрытого текста Cj ∈ Ck-hj по введенному открытому
тексту Mi ∈ M и заданному открытому ключу GECuX ai, u ∈ {1, 2, . . . , s}, осу-
ществляется путем формирования кодового слова замаскированного кода с
добавлением к нему случайно сформированного вектора e ∈ (e0, e1, . . . , en-1):
Cj = ϕu (Mi,GuX) = Mi · (GuX)T + e,
причем вес Хемминга (число ненулевых элементов) вектора e не превышает
исправляющей способности используемого алгебраического блокового кода:
⌋
⌊d-1
0 ≤ w(e) ≤ t =
,
2
⌊x⌋- целая часть вещественного числа x.
Для каждого формируемого закрытого текста Cj ∈ Ck-hj соответствую-
щий вектор e ∈ (e0, e1, . . . , en-1) выступает в качестве одноразового сеансово-
го ключа, т.е. для конкретного Ej вектор e формируется случайно, равнове-
роятно и независимо от других закрытых текстов.
В канал связи поступает C∗j = Cj - Ck-hj .
На приемной стороне уполномоченный пользователь, знающий правило
маскировки и количество нулевых информационных символов, может вос-
пользоваться быстрым алгоритмом раскодирования алгеброгеометрического
кода (полиномиальной сложности) для восстановления открытого текста [14]:
(
)
Mi = ϕ-1u
C∗j,{X,P,D}u
160
Для восстановления открытого текста уполномоченный пользователь до-
бавляет нулевые информационные символы
C∗j = Cj + Ck-h
,
j
с восстановленного закрытого текста Cj снимает действие секретных пере-
становочной и диагональной матриц Pu и Du:
(
)
C = C∗j · (Du)-1 · (Pu)-1 = Mi · (GuX)T + e
· (Du)-1 · (Pu)-1 =
(
)
= Mi · (Xu · G · Pu · Du)T + e
· (Du)-1 · (Pu)-1 =
= Mi · (Xu)T · (G)T · (Pu)T · (Du)T · (Du)-1 · (Pu)-1 + e · (Du)-1 · (Pu)-1 =
= Mi · (Xu)T · (G)T + e · (Du)-1 · (Pu)-1
и раскодирует полученный вектор по алгоритму Берлекэмпа-Месси [16, 17]:
(
C = Mi · (Xu)T ·
GEC
)T + e · (Du)-1 · (Pu)-1 ,
т.е. избавляется от второго слагаемого и от сомножителя (G)ECT в пер-
вом слагаемом в правой части равенства, после чего снимает действие мат-
рицы маскирования Xu. Для этого полученный результат раскодирования
Mi · (Xu)T следует умножить на (Xu)-1:
(
)
Mi
· (Xu)T
· (Xu)-1 = Mi.
Полученное решение и есть открытый текст Mi.
2.2. Математическая модель модифицированной несимметричной крипто-
кодовой системы защиты информации с использованием алгеброгеометриче-
ских блоковых кодов на основе теоретико-кодовой схемы Мак-Элиса на основе
удлинения (увеличения информационных символов).
Эта модель формально задается совокупностью следующих элементов:
— множество открытых текстов
{
}
{
}
M =
M1,M2,... ,Mqk
,
где Mi = I0, Ihr1 , . . . Ihrj , Ik-1
∀Ij ∈ GF (q),
hj — информационные символы, равные нулю, |h| =12k, т.е. Ii = 0 ∀Ii ∈ h;
hr — информационные символы удлинения k, |h| =12k;
— множество закрытых текстов (кодограмм)
C = {C1,C2,...,Cqk}, где Ci = (c∗X
,c∗h
,...,c∗h
,c∗X
) ∀c∗
∈ GF (q);
0
n-1
Xj
r1
rj
— множество прямых отображений (на основе использования открытого
ключа - порождающей матрицы)
ϕ = {ϕ1,ϕ2,...,ϕs}, где ϕi : M → Chr, i = 1,2,... ,s;
161
— множество обратных отображений (на основе использования закрытого
(личного) ключа - матриц маскировки)
ϕ-1 = {ϕ-11, ϕ-12, . . . , ϕ-1s}, ϕ-1i : Chr → M, i = 1, 2, . . . , s;
— множество ключей, параметризирующих прямые отображения (откры-
тый ключ уполномоченного пользователя),
{
}
s
ai
,
Kai = {K1ai ,K2ai ,... ,Ksai } = GEC1Xai,GXC2 ai,...,GX
- порождающая (n × k)-матрица замаскированного под слу-
где GECsXai
чайный код алгеброгеометрического блокового (n, k, d) кода с элементами
из GF (q), т.е.
Kia
i
ϕi : M
---→
Chr , i = 1,2,... ,s;
ai - набор коэффициентов многочлена кривой a1,... ,a6 ∀ai ∈ GF(q), одно-
значно задающий конкретный набор точек кривой из пространства P2;
— множество ключей, параметризирующих обратные отображения (лич-
ный (закрытый) ключ уполномоченного пользователя),
{
}
K∗ = {K∗1,K∗2,... ,K∗}=
{X, P, D}1, {X, P, D}2, . . . , {X, P, D}s
,
s
{X, P, D}i = {Xi, Pi, Di},
где Xi - маскирующая невырожденная случайно равновероятно сформиро-
ванная источником ключей (k × k)-матрица с элементами из GF (q); Pi — пе-
рестановочная случайно равновероятно сформированная источником ключей
(n × n)-матрица с элементами из GF (q); Di — диагональная, сформирован-
ная источником ключей (n × n)-матрица с элементами из GF (q), т.е.
i
ϕ-1i : C
--→
M, i = 1,2,... ,s.
Сложность выполнения обратного отображения ϕ-1i без знания ключа
K∗i ∈ K∗ сопряжена с решением теоретико-сложностной задачи декодирова-
ния случайного кода (кода общего положения).
Исходными данными при описании рассмотренной несимметричной
крипто-кодовой системы защиты информации являются параметры, описан-
ные в модели на основе укорочения. Таким образом, отличительной особенно-
стью МККС Мак-Элиса на модифицированных удлиненных эллиптических
кодах от МККС на укороченных ЕС является использование мест укорочения
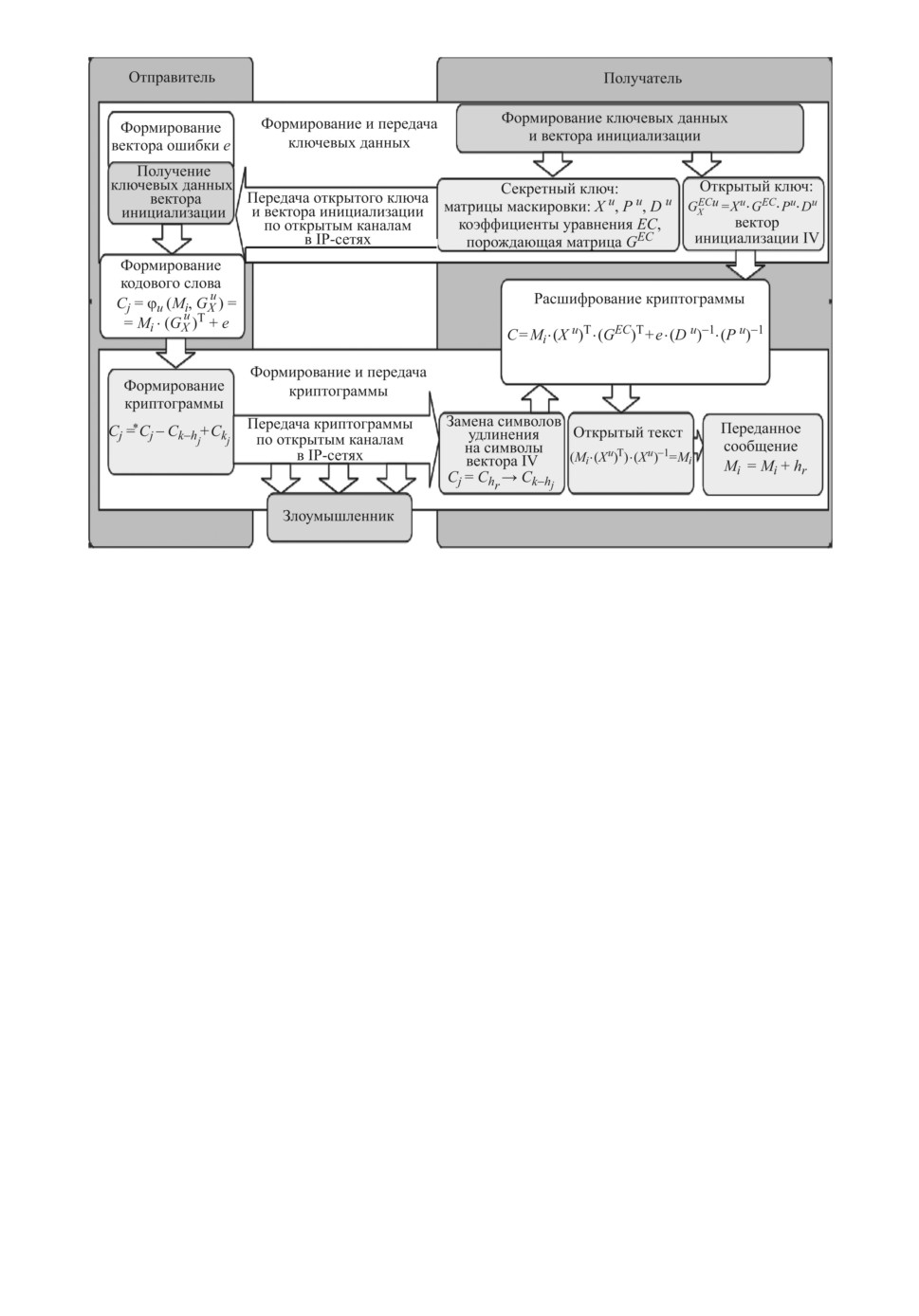
для заполнения символами открытого текста. Протокол обмена с использо-
ванием данной МККС представлен на рис. 3.
В несимметричной крипто-кодовой системе на основе ТКС Мак-Элиса
модифицированный (удлиненный) алгеброгеометрический (n, k, d) код Chr с
быстрым алгоритмом раскодирования маскируется под случайный (n, k, d)
162
Рис. 3. Протокол обмена информацией в режиме реального времени с исполь-
зованием модифицированной ТКС Мак-Элиса с удлиненными ЕС.
код C∗hr посредством умножения порождающей матрицы GEC кода Ck-hj на
хранящиеся в секрете маскирующие матрицы Xu, Pu и Du, обеспечивающий
формирование открытого ключа уполномоченного пользователя:
GECuX = Xu · GEC · Pu · Du, u ∈ {1, 2, . . . , s} ,
где GEC - порождающая (n × k)-матрица алгеброгеометрического блоково-
го (n, k, d) кода с элементами из GF (q), построенная на основе использова-
ния выбранных пользователем коэффициентов многочлена кривой a1, . . . , a6
∀ai ∈ GF(q), однозначно задающих конкретный набор точек кривой из про-
странства P2.
Формирование закрытого текста Cj ∈ Chr по введенному открытому тек-
сту Mi ∈ M и заданному открытому ключу GECuXai,u∈{1,2,...,s},осу-
ществляется путем формирования укороченного кодового слова, а затем
удлинения замаскированного кода с добавлением к нему случайно сформи-
рованного вектора e = (e0, e1, . . . , en-1):
Cj = ϕu (Mi,GuX) = Mi · (GuX)T + e.
Для каждого формируемого закрытого текста Cj ∈ Chr соответствующий
вектор e = (e0, e1, . . . , en-1) выступает в качестве одноразового сеансового
ключа, т.е. для конкретного Ej вектор e формируется случайно, равнове-
роятно и независимо от других закрытых текстов.
163
В канал связи поступает C∗j = Cj - Ck-hj + Chr .
На приемной стороне уполномоченный пользователь, знающий правило
маскировки и количество и места нулевых информационных символов, мо-
жет воспользоваться быстрым алгоритмом раскодирования алгеброгеомет-
рического кода (полиномиальной сложности) для восстановления открытого
текста:
(
)
Mi = ϕ-1u
C∗j,{X,P,D}u
Для восстановления открытого текста уполномоченный пользователь за-
меняет символы удлинения на нулевые информационные символы
C∗j = Chr → Ck-h
,
j
с восстановленного закрытого текста Cj снимает действие секретных пере-
становочной и диагональной матриц Pu и Du:
(
)
C = C∗j · (Du)-1 · (Pu)-1 = Mi · (GuX)T + e
· (Du)-1 · (Pu)-1 =
(
)
= Mi · (Xu · G · Pu · Du)T + e
· (Du)-1 · (Pu)-1 =
= Mi · (Xu)T · (G)T · (Pu)T · (Du)T · (Du)-1 · (Pu)-1 + e · (Du)-1 · (Pu)-1 =
= Mi · (Xu)T · (G)T + e · (Du)-1 · (Pu)-1
и раскодирует полученный вектор по алгоритму Берлекэмпа-Месси [16; 17]:
(
)T
C = Mi · (Xu)T ·
GEC
+ e · (Du)-1 · (Pu)-1 ,
т.е. избавляется от второго слагаемого и от сомножителя (G)ECT в первом
слагаемом в правой части равенства, после чего снимает действие матрицы
маскирования Xu. Для этого полученный результат раскодирования M∗i сле-
дует умножить на (Xu)-1:
M∗i · (Xu)T · (Xu)-1 = Mi.
Полученное решение - открытый текст Mi, к которому добавляются сим-
волы удлинения: Mj = Mi + hr - передаваемое сообщение.
3. Оценка энергетических затрат в предлагаемой модифицированной
несимметричной крипто-кодовой системе Мак-Элиса
Для оценки временных и скоростных показателей принято использовать
единицу измерения cpb, где cpb (cycles per byte) - число тактов процессора,
которое необходимо потратить для обработки одного байта входящей инфор-
мации.
Энергетические затраты на обработку крипто-кодовой системой одного
байта входной информации вычисляем по выражению
P er = Utl ∗ CP U_clock/Rate,
164
Таблица 1. Результаты исследований зависимости длины кодовой последователь-
ности в НККС Мак-Элиса от количества тактов процессора
Mac-Elis
Mac-Elis на
Mac-Elis на
Длина кодовой
укороченных
удлиненных
последовательности
кодах
кодах
10
100
1000
10
100
1000
10
100
1000
11
30
80
10
28
76
33
82
Чтение
1143
018
800
859
294
750
759
460
473
Количество
символа
2131
042
328
933
397
457
874
317
442
вызовов
функций,
3
10
26
3
9
254
3
12
29
Сравнение
реализующих
663
199
364
406
246
78
673
119
469
строк
элементарные
356
898
634
921
748
498
756
867
389
операции
1
5
13
1
5
12
1
6
14
Конкатенация
834
125
415
705
045
379
947
114
456
строк
983
564
329
544
748
422
681
478
729
16
46
120
15
43
114
51
126
Сумма элементарных
1705
516
125
639
406
042
617
694
399
групповых операций
3568
381
790
896
862
953
794
662
560
2
2
2
Чтение
297
831
295
810
300
843
Длительность
183
001
745
символа
487
609
374
478
479
705
выполнения
218
167
148
функций*
1
1
1
Сравнение
197
550
178
531
213
561
в тактах
423
248
739
строк
821
794
814
379
478
754
процессора
690
684
170
1
3
1
3
1
4
Конкатенация
544
544
578
522
984
328
586
647
007
строк
990
990
174
293
353
114
486
638
883
1
2
7
1
2
7
1
3
8
Сумма элементарных
040
904
591
006
749
247
092
053
492
групповых операций
298
696
261
781
548
488
131
097
201
Длительность выполнения**,
0,55
1,53
4
0,52
1,37
3,4
0,56
1,55
4,1
мс
∗длительность 1000 операций в тактах процессора: чтение символа -
27 тактов,
сравнение строк - 54 такта, конкатенация строк - 297 тактов;
∗∗для расчета взят процессор с тактовой частотой 2 ГГц с учетом загрузки опера-
ционной системы 5%.
где Utl - утилизация ядра процессора (%); CP U_clock - время выполнения
одного такта процессора; Rate - пропускная способность алгоритма (байт/с).
В табл. 1 приведены результаты исследований зависимости длины кодовой
последовательности алгеброгеометрического кода в крипто-кодовой системе
Мак-Элиса от количества тактов процессора на выполнение элементарных
операций в программной реализации крипто-кодовых систем.
В табл. 2 приведены результаты исследований оценки временных и ско-
ростных показателей процедур формирования и раскодирования информа-
ции в крипто-кодовых системах на основе НККС и МККС Мак-Элиса.
Анализ табл. 1 и 2 показывает, что использование модифицированных
(укороченных/удлиненных) эллиптических кодов позволяет сохранить объе-
165
Таблица 2. Результаты исследований оценки временных и скоростных показателей
процедур формирования и раскодирования информации
Пропускная
Длина
Утилизация
способность
Сложность
кодовой
ядра
Крипто-кодовые системы
алгоритма,
алгоритма,
последова-
процессора,
Rate,
Per, с/байт
тельности
(%)
(байт/с)
100
46 125 790
56
61,5
НККС Мак-Элиса
1000
120 639 896
56
62,0
МККС Мак-Элиса
100
51 694 662
56
61,7
на удлиненных
эллиптических кодах
1000
126 399 560
56
62,2
МККС Мак-Элиса
100
52 721 778
56
61,5
на укороченных
эллиптических кодах
1000
127 389 928
56
62,1
мы передаваемых данных в несимметричной крипто-кодовой системе Мак-
Элиса, но при этом обеспечить тре(буемый)уровень криптостойкости при ре-
ализации над меньшим полем GF
26 - 28
за счет использования энтропии
вектора инициализации hr.
Исследуем достоверность и информационную скрытность, обеспечиваемые
модифицированными крипто-кодовыми системами на эллиптических кри-
вых. Зафиксируем (n, k, d) эллиптический код над GF (q). Зададим модифи-
цированную крипто-кодовую схему на основе ТКС Мак-Элиса на модифи-
цированных (удлиненных) кодах. Зададим сеансовый ключ e - вектор оши-
бок, который добавляется к кодовому слову при формировании кодограммы.
Пусть w (e) ≤ t, t = [(d - 1) /2]. Обозначим долю веса вектора ошибок e сим-
волом ρ = w (e) /t. Тогда потенциальная стойкость теоретико-кодовой схемы
с эллиптическими кодами будет определяться величиной ρ · t, а помехоустой-
чивость передаваемых кодограмм - величиной (1 - ρ) · t. Сложность взлома
предлагаемых модифицированных систем определим выражением сложности
анализа декодирования случайного кода перестановочным декодером:
IK+ = Nпокрытия · n · r,
где
Ctn
n (n - 1) . . . (n - t - 1)
Nпокрытия ≥
=
Ctn-k
(n - k) (n - k - 1) . . . (n - k - t - 1)
Помехоустойчивость определяется минимальным соотношением сиг-
нал/шум, необходимым для обеспечения требуемой достоверности. Зафикси-
руем соотношение сигнал/шум и вид модуляции. Предположим, что передача
цифровых сообщений осуществляется по дискретному каналу без памяти, т.е.
ошибки в последовательно передаваемых кодовых символах происходят неза-
висимо с вероятностью Po. Тогда вероятность ошибки кратности i на длине
блока n будет равна [16-20]:
Pi = CinPio (1 - Po)n-1 .
166
lg(Ik+)
100
1
2
80
3
60
4
40
5
20
0
0,2
0,4
0,6
0,8
1,0
(
)
Рис. 4. Зависимость сложности взлома Ik+ (ρ) над GF
210
: 1 - R = 0,5; 2 -
R = 0,75; 3 - R = 0,9; 4 - R = 0,25; 5 - R = 0,1.
Если процедура раскодирования позволяет исправить t = [(d - 1) /2] оши-
бок, то вероятность ошибочного раскодирования равна:
∑
∑
Pош =
Pi =
CinPio (1 - Po)n-i .
i=t+1
i=t+1
При интегрированном решении задач достоверности и информационной
скрытности передачи данных модифицированная крипто-кодовая система бу-
дет исправлять (1 - ρ) · t возникших ошибок, следовательно:
∑
∑
Pош =
Pi =
CinPio (1 - Po)n-i .
i=(1-ρ)t+1
i=(1-ρ)t+1
Зафиксируем GF (210) и Po = 10-3. На рис. 4 приведены зависимости
сложности взлома теоретико-кодовой схемы перестановочным декодером
Ik+(ρ) при использовании эллиптических кодов с относительной скоростью R.
На рис. 5 приведены зависимости вероятности ошибки раскодирования
Pош (ρ) при интегрированном решении задач достоверности и информацион-
ной скрытности.
Как видно из зависимостей, приведенных на рис. 4 и 5, модифицирован-
ные крипто-кодовые системы на основе ТКС Мак-Элиса обладают высокими
показателями достоверности и информационной скрытности. Повышение по-
казателя ρ ведет, с одной стороны, к увеличению стойкости (надежности)
схемы, а с другой - к снижению ее помехоустойчивости. Исследуем интегри-
рованное повышение достоверности и информационной скрытности передачи
данных с использованием предлагаемых систем.
На рис. 6 представлены сводные зависимости вероятности ошибки раско-
дирования и сложности взлома теоретико-кодовой схемы с эллиптическими
кодами для различных R при ρ = 0,9.
167
Pош
0,1
0,01
1
0,001
0,0001
2
0,00001
3
0,000001
0,0000001
4
1E 08
5
1E 09
1E 10
1E 11
1E 12
0,75
0,80
0,85
0,90
0,95
1,00
1,05
(
)
Рис. 5. Зависимость вероятности ошибки декодирования Pош (ρ) над GF
210
:
1 - R = 0,1; 2 - R = 0,25; 3 - R = 0,9; 4 - R = 0,75; 5 - R = 0,5.
Pош
0,1
0,01
1
0,001
0,0001
0,00001
2
0,000001
0,0000001
3
1E 08
1E 09
1E 10
4
1E 11
1E 12
10
20
30
40
50
60
70
80
90
100
Ik+
Рис. 6. Сводные зависимости вероятности ошибки раскодирования и сложно-
сти взлома Pош (IK+) для ρ = 0,9: 1 - R = 0,9; 2 - R = 0,75; 3 - R = 0,5; 4 -
R = 0,25.
Как видно из зависимостей, приведенных на рис. 6, предложенные моди-
фицированные крипто-кодовые системы на основе ТКС Мак-Элиса обеспечи-
вают высокие показатели стойкости и достоверности обрабатываемой и пере-
даваемой информации. Их применение позволит использовать открытые ка-
налы IP-сетей для передачи конфиденциальной (коммерческой) информации
в режиме реального времени, обеспечивая требуемые показатели безопасно-
сти и достоверности.
168
4. Заключение
Таким образом, предложено формальное математическое описание моди-
фицированных крипто-кодовых средств защиты информации на основе ТКС
Мак-Элиса с использованием алгеброгеометрических блоковых кодов на ос-
нове укорочения/удлинения информационных символов, позволяющее раз-
работать практические алгоритмы и провести исследование энергетических
затрат их реализации.
Передача ключевой последовательности при использовании модифициро-
ванной НККС Мак-Элиса на основе укороченных кодов позволяет исполь-
зовать открытые каналы связи коммуникационных систем и существенно
снизить объемы ключевых последовательностей, хранящихся у пользовате-
лей данной системы. Оценка сложности программной реализации крипто-
кодовых средств защиты информации на основе ТКС Мак-Элиса подтвер-
ждает предположение о снижении вычислительных затрат на вычисление
криптограммы/кодограммы и необходимости хранения ключевых данных
(открытого ключа) уполномоченным пользователем. Использование удлинен-
ных эллиптических кодов позволяет увеличить объем передаваемых данных
на hr символов, обесп(чивая п)ри этом стойкость криптосистемы при ее фор-
мировании в поле GF
26 - 28
, что существенно снижает энергетические за-
траты на ее реализацию и позволяет ее использование в мобильных прило-
жениях.
Проведенные исследования применения доли веса вектора ошибок позво-
ляют варьированием основных показателей каналов связи коммуникацион-
ной системы усиливать один из показателей интегрированного механизма -
достоверность или безопасность.
СПИСОК ЛИТЕРАТУРЫ
1. NISTIR 8105. Report on Post-Quantum Cryptography. Режим доступа:
2. Dinh H., Moore C., Russell A. McEliece and Niederreiter Cryptosystems That Resist
Quantum Fourier Sampling Attacks. Режим доступа:
3. Simon de Vries. Achieving 128-Bit Security against Quantum Attacks in OpenVPN.
2016. р. 1-16. Режим доступа:
4. Baldi M., Bianchi M., Chiaraluce F., et al. Enhanced Public Key Security for the
5. Rossi M., Hamburg M., Hutter M., Marson M.E. A Side-Channel Assisted
Cryptanalytic Attack Against QcBits. Режим доступа:
6. Грищук Р.В., Даник Ю.Г. Основи кiбербезпеки / За заг. ред. проф. Даника Ю.Г.
Житомир : ЖНАЕУ, 2016.
7. Евсеев С. Методология оценивания безопасности информационных технологий
автоматизированных банковских систем Украины / Науково-nехнiчний журн.
“Безпека iнформацi¨ı”. 2016. Т. 22. № 3. С. 297-309.
169
8.
Zhang G., Cai S., Ma C., Zhang D. Secure Error-Сorrecting (SEC) Schemes for
Network Coding Through McEliece Cryptosystem. Режим доступа:
9.
Zhang G., Cai S., Ma C., Zhang D. Universal Secure Error-Correcting (SEC)
Schemes for Network Coding via McEliece Cryptosystem Based on QC-LDPC Codes.
Режим доступа:
10.
Cho J.Y., Griesser H., Rafique D. A McEliece-Based Key Exchange Protocol for
Optical Communication Systems. Режим доступа:
11.
Morozov K., Roy P.S., Sakurai K. On Unconditionally Binding Code-Based
Commitment Schemes. Режим доступа:
12.
Сидельников В.М. О системе шифрования, построенной на основе обобщенных
кодов Рида-Соломона // Дискретная математика. 1992. Т. 4. № 3. С. 57-63.
13.
Сидельников В.М. Криптография и теория кодирования // Матер. конф. “Мос-
ковский университет и развитие криптографии в России”. МГУ. 2002. С. 1-22.
14.
Рзаев Х.Н. Разработка модифицированной несимметричной крипто-кодовой си-
стемы Мак-Элиса на укороченных эллиптических кодах // Восточно-евр. журн.
передовых технологий. 2016. Т. 4. № 9 (82). С. 18-26.
15.
Рзаев Х.Н., Цыганенко А.С. Анализ программной реализации метода недвоич-
ного равновесного кодирования // Az
rbaycan Texniki Universiteti, Elmi
s
rl
r.
2016. Cild 1. № 1. S
h. 107-112. Issn. 1815-1779.
16.
Блейхут Р. Теория и практика кодов, контролирующих ошибки / Пер. с англ.
М.: Мир, 1986.
17.
Кларк Дж.-Мл., Кейн Дж. Кодирование с исправлением ошибок в системах
цифровой связи / Пер. с англ. под ред. Б.С. Цыбакова. М.: Радио и связь, 1987.
18.
Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки.
М.: Связь, 1979.
19.
Мутер В.М. Основы помехоустойчивой телепередачи информации. Л.: Энерго-
атомиздат. Ленингр. отд-ние, 1990.
20.
Цыбаков Б.С., Гельфанд С.И. Теория кодирования / Пер. с япон. Касами Т.,
Токура Н., Ивадари Е., Инагаки Я. М.: Мир, 1978.
Статья представлена к публикации членом редколлегии О.Н. Граничиным.
Поступила в редакцию 04.05.2016
После доработки 04.02.2017
Принята к публикации 08.11.2018
170