Автоматика и телемеханика, № 8, 2019

Стохастические системы

О.Н. ГРАНИЧИН, д-р физ.-мат. наук (o.granichin@spbu.ru)

(Санкт-Петербургский государственный университет;

Институт проблем машиноведения РАН, Санкт-Петербург)

АЛГОРИТМ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ

С РАНДОМИЗАЦИЕЙ НА ВХОДЕ ДЛЯ ОЦЕНИВАНИЯ

ПАРАМЕТРОВ СМЕСИ ГАУССОВЫХ РАСПРЕДЕЛЕНИЙ

БЕЗ УЧИТЕЛЯ ПРИ РАЗРЕЖЕННЫХ ПАРАМЕТРАХ¹

Рассматриваются возможности применения алгоритмов стохастиче-

ской аппроксимации с рандомизацией на входе в условиях неизвестных,

но ограниченных помех при изучении кластеризации данных, порожден-

ных смесью гауссовых распределений. Предлагаемый алгоритм, устойчи-

вый ко внешним возмущениям, позволяет обрабатывать данные “на ле-

ту” и обладает высокой скоростью сходимости. Работа алгоритма иллю-

стрируется примерами его использования для кластеризации в различных

сложных условиях.

Ключевые слова: кластеризация, обучение без учителя, рандомизация,

стохастическая аппроксимация, смесь гауссовых распределений.

DOI: 10.1134/S0005231019080051

1. Введение

Большинство задач машинного обучения сводятся к многомерной опти-

мизации. В условиях существенно зашумленных данных наблюдений стан-

дартные градиентные алгоритмы оптимизации демонстрируют значительное

ухудшение качества работы. При этом алгоритмы стохастической аппрокси-

мации с рандомизацией на входе во многих случаях остаются работоспособ-

ными.

Основной частью многих методов машинного обучения является решение

задачи многомерной оптимизации [1]. Для этих алгоритмов крайне важны

такие свойства, как точность, скорость работы и устойчивость к внешним

возмущениям. При определении метода оптимизации в теории стандартным

подходом является выбор близкой к реальным процессам математической мо-

дели и включение в нее различных помех, относящихся к грубости математи-

ческой модели и характеризующих неконтролируемые внешние возмущения.

Во многих прикладных задачах (например, при фильтрации спама или в

¹ Работа выполнена при частичной поддержке Российского научного фонда (грант

№ 16-19-00057).

потоковых сервисах) зашумленные данные поступают в систему последова-

тельно, и обрабатывать их и принимать решение необходимо “на лету” (он-

лайн). Для обучения таких систем целесообразно использовать рекуррентные

адаптивные алгоритмы обработки данных, среди которых часто используют

подходы, основанные на стохастической аппроксимации (СА).

Алгоритм СА был впервые предложен Роббинсоном и Монро [2] и был раз-

вит для решения задачи оптимизации Кифером и Вольфовицем [3]. Этот под-

ход, основанный на конечно-разностных аппроксимациях вектора-градиента

функции потерь, был расширен до d-мерного (многомерного d > 1) случая

в [4]. Метод использует 2d наблюдений на каждой итерации, чтобы построить

последовательность оценок: по два наблюдения для аппроксимации каждой

компоненты d-мерного вектора-градиента. Граничиным в [5, 6] и Поляком

с Цыбаковым в [7] были предложены поисковые алгоритмы стохастической

аппроксимации с рандомизацией на входе, которые используют на каждой

итерации всего одно (или два) значение исследуемой функции в точке (или

точках) на линии, проходящей через предшествующую оценку в случайно

выбираемом направлении (как в алгоритме случайного поиска [8]). В англо-

язычной литературе схожие алгоритмы предложил Спал в [9], дав им назва-

ние SPSA (simultaneous perturbation stochastic approximation). Когда в наблю-

даемые данные добавлены неизвестные, но ограниченные помехи, качество

классических методов, основанных на стохастическом градиенте, падает. Од-

нако качество поисковых алгоритмов СА остается высоким [10, 11].

Для задач кластеризации Ллойд в [12] впервые описал классический ме-

тод k-средних (k-means), простота и стабильность которого сделали его по-

пулярным. Однако его основным недостатком является то, что он обрабаты-

вает все данные одновременно, поэтому увеличение объема данных требует

увеличения доступной памяти в компьютере. Кроме того, в худшем случае

временная сложность алгоритма Ллойда экспоненциальна [13]. Чтобы испра-

вить эти недостатки было предложено несколько подходов, основанных на

идее обучения “на лету”. Алгоритм [14] использует мини-батчи (подвыбор-

ки из тренировочных данных) для уменьшения вычислительного времени,

необходимого для сходимости к локальному решению, при этом минимизи-

руя ту же целевую функцию. Полученные таким образом результаты лишь

немногим хуже, чем соответствующие результаты оригинального алгоритма.

Вариант потокового метода k-средних описан в [13]. Он улучшает скорость

сходимости, уменьшает требования к памяти и время работы. Другой метод

онлайн кластеризации, основанный на ансамбле обучаемых агентов, рассмот-

рен в [15]. Более робастным вариантом k-средних является метод k-медоид

(и его реализация Partitioning Around Medoids, PAM) [16]. Рандомизирован-

ный поисковый алгоритм СА, решающий задачу k-средних был предложен и

обоснован в [17].

Смесь гауссовых распределений (СГР) (Gaussian mixture model, GMM) —

это вероятностная модель, которая подразумевает, что все элементы данных

порождены смесью конечного числа гауссовых распределений с неизвестны-

ми параметрами. Будем рассматривать СГР как обобщение кластеризации

с помощью метода k-средних. Хорошо известный EM алгоритм (expectation-

maximization) [18] традиционно используется для нахождения неизвестных

параметров СГР. Он основан на максимизации правдоподобия, когда модель

зависит от скрытых переменных. Алгоритм Variational Bayesian Gaussian

mixture inference является расширением алгоритма EM, которое может опре-

делять количество компонент в смеси (см. [19]). Этот алгоритм включает

регуляризацию с помощью интегрирования информации об априорных рас-

пределениях, что делает его стабильнее, но медленнее, чем EM. Среди онлайн

методов СГР кластеризации отметим потоковый метод, основанный на оцен-

ках плотностей [20].

В настоящей статье рассматривается рандомизированный алгоритм стоха-

стической аппроксимации (РАСА), являющийся расширением и обобщением

для модели СГР подхода из [17], предложенного ранее для случая k-средних.

Предлагаемый алгоритм способен обрабатывать “на лету” потоковые данные

и показывает высокую скорость работы. Сходимость центов кластеров к их

истинным значениям гарантирована, даже если функционалы качества из-

мерены с неизвестными, но ограниченными помехами. В статье дана оценка

временной сложности предложенного метода. Работоспособность представ-

ленного РАСА сравнивается с другими современными алгоритмами класте-

ризации, такими как Affinity Propagation [21] и DBSCAN [22].

Статья организована следующим образом. В разделе 2 формулируется

проблема кластеризации смеси гауссовых распределений как задача много-

мерной оптимизации. В разделе 3 предложен новый алгоритм РАСА для кла-

стеризации и исследованы основные свойства его оценок. Раздел 4 содержит

описания и результаты экспериментов при наличии и в отсутствие различных

типов внешних помех. В разделе 5 описывается использование предложенно-

го алгоритма для кластеризации в случае смеси гауссовых распределений

с разреженными параметрами. В заключении подводится итог проделанной

работы и обсуждаются направления дальнейших исследований.

2. Постановка задачи

Пусть определены натуральное число k > 1, множество входных данных

X = {x¹,x²,...}, являющееся подмножеством Евклидова пространства R^d,

и заданное на X вероятностное распределение P(X). Обозначим через

1, . . . , k множество индексов {1, 2, . . . , k}. Будем считать, что множество вход-

ных данных X разбивается на k неизвестных подмножеств {X⋆1, . . . , X^⋆k}:

X = ∪i∈1,...,kX^⋆i таким образом, что вероятностное распределение P(X) мож-

∑_k

но представить с помощью смеси распределений: P(X) =

p_iP(X^⋆i), где p_i

i=1

(p_i > 0) и P(X^⋆i), i ∈ 1, . . . , k, — соответствующие вероятности и распределе-

ния.

Задача кластеризации заключается в нахождении оптимального разби-

ения X множества входных данных X на k непустых кластеров X (X) =

⋃

= {X₁, . . . , X_k}: X = X_i и X_i ∩ X_j = ∅, i = j. Разбиение X определяется

i=1

функцией γ_X : X → 1 . . . k, которая ставит в соответствие каждой точке X

индекс кластера. Таким образом, X_i = {x ∈ X|γ_X (x) = i}. Задача кластери-

зации заключается в нахождении лучшего из них: X^⋆ = {X⋆1, . . . , X^⋆k}.

Проблему кластеризации можно описать следующим образом: элементы,

принадлежащие одной группе (кластеру), являются более похожими, чем эле-

менты, принадлежащие различным группам (кластерам). Для решения этой

задачи вводится некоторая штрафная функция (функция качества) q_i, опре-

деляющая “близость” к кластеру i, i ∈ 1, . . . , k. Тогда для получения опти-

мальной кластеризации необходимо минимизировать функционал:

(1)

F (X ) = Ef(X , x) → min,

где E — символ математического ожидания и

∑

f (X , x) =

γ_X (x)q_i(X,x).

i=1

Если векторы θ_i, i ∈ 1, . . . , k, интерпретировать как центры кластеров или

центроиды и матрицы Γ_i, i ∈ 1,... ,k, — как ковариационные матрицы, тогда

функционал качества кластеризации (1) принимает вид

∫

∑

(2)

F (X ) =

q_i(θ_i,Γ_i,x)P(dx) → min .

i=1

X_i

Для i ∈ 1, . . . , k и фиксированного x ∈ X каждая функция q_i(·, ·, x) зави-

сит только от θ_i и Γ_i, т.е. q_i(·, ·, ·) : R^d × R^d×d × X → R. Тогда можно выбрать

правило разбиения

{

X_i(Θ,Γ) = x ∈ X : q_i(θ_i,Γ_i,x) < q_j(θ_j,Γ_j,x), j ∈ 1,... ,i - 1;

}

q_i(θ_i,Γ_i,x) ≤ q_j(θ_j,Γ_j,x), j ∈ i + 1... k ,

i ∈ 1,...,k,

которое минимизирует (1). Здесь Θ = (θ₁, θ₂, . . . , θ_k) — (d × k)-матрица, и Γ —

множество, состоящее из k матриц Γ₁, Γ₂, . . . , Γ_k, где Γ_i ∈ R^d×d, i ∈ 1, . . . , k.

Следовательно, (2) можно переписать следующим образом:

∫

(3)

F (Θ, Γ) =

〈 j(Θ,Γ,x),q(Θ,Γ,x)〉 P(dx) → min,

Θ,Γ

где j(Θ, Γ, x) ∈ R^k является вектором, состоящим из нулей и единиц, со-

ответствующих значениям характеристических функций

1Xi(Θ,Γ)(Θ,Γ,x),

i ∈ 1,...,k, и q(Θ,Γ,x) ∈ R^k — вектор значений q_i(θ_i,Γ_i,x), i ∈ 1,...,k.

Важный частный случай соответствует равномерному распределению P(·)

и штрафной функции, представляющей собой квадрат расстояния Маха-

ланобиса

(4)

q_i(θ_i,Γ_i,x) = (x - θ_i)^TΓ-1i(x - θ_i

2.1. Смесь гауссовых распределений

В качестве модели описания данных будем использовать одну из самых

распространенных: Смесь гауссовых распределений (Gaussian Mixture Model)

(СГР, GMM):

∑

(5)

f (X , x) = f(Θ, Γ, x) =

p_iG(x|θ_i,Γ_i

i=1

где G(x|θ_i, Γ_i) — плотность гауссового распределения со средним θ_i ∈ R^d и

ковариационной матрицей Γ_i, i ∈ 1, . . . , k.

Рассмотрим задачу: По последовательности входных данных {x¹, x², . . .}

и заданному значению k найти параметры θ_i ∈ R^d и Γ_i, i ∈ 1, . . . , k, гаус-

совых распределений, смесь которых породила последовательность входных

данных. Такая задача подходит под введенную выше задачу кластеризации.

Существует много возможных разбиений множества X на k подмножеств.

Задача о нахождении неизвестных параметров θ_i ∈ R^d и Γ_i, i ∈ 1 . . . k, тесно

связана с задачей кластеризации, которая согласно (2) заключается в нахож-

дении:

∫

∑

(6)

F (X ) =

(x - θ_i)TΓ-1i(x - θi)P(dx) → min

i=1

X_i

Для последовательности входных данных {x¹, x², . . . xⁿ} функционал (6)

принимает вид

∑

(7)

F (Θ, Γ) =

(x^j - θ_i)^TΓ-1i(x^j - θ_i) → min,

j ∈ 1,...,n.

Θ,Γ

i=1 x^j ∈X_i

Эта связь заключается в том, что при модели данных СГР и при введенной

выше постановке задачи кластеризации нахождение оптимальных парамет-

ров СГР эквивалентно нахождению оптимальных параметров кластеризации

согласно следующей лемме.

Лемма. Пусть последовательность {x¹,x²,... xⁿ} порождена Смесью

гауссовых распределений (5) с параметрами Θ^⋆ и Γ^⋆. Тогда в заданных выше

условиях при n → ∞ функционал (7) стремится к минимуму при Θ^⋆ и Γ^⋆.

Доказательство леммы приводится в Приложении.

Подходы, основанные на максимизации функции правдоподобия, тради-

ционно используются для решения соответствующей задачи кластеризации.

EM алгоритм [18] или Variational Bayesian Gaussian mixture inference алго-

ритм [19] основаны на построении оценки скрытых переменных. Смесь гаус-

совых распределений является обобщением метода кластеризации k-средних,

которое использует предположение о ковариационных структурах данных

так же, как и о центрах скрытых классов.

2.2. Алгоритм k-средних

Рассмотрим один из самых популярных методов кластеризации: алгоритм

k-средних, описанный в [12]. Он ищет такое разбиение X , которое миними-

зирует сумму квадратов внутрикластерных расстояний. Каждый кластер ха-

рактеризуется соответствующим центроидом. Все матрицы Γ будем считать

единичными.

Алгоритм k-средних.

Вход: X, k, максимальное число итераций

Выход: оценка центроидов^Θ, X

1: Иниц(ализация: n )= 0. Случайно выбирается k начальных центроидов

θ0

Θ⁰ =

,θ02,... ,θ0

из элементов X

2: Класс{фикация: i ∈ 1 . . . k

}

Xⁿⁱ = x ∈ X : ∥θni - x∥² ≤ ∥θnj - x∥², j ∈ 1... k

∑

3: Минимизация:θn+1

|Xⁿⁱ|xj ∈Xi x^j

4: Итерация: n := n + 1. Шаги 2 и 3 повторяются, пока центроиды не пе-

рестанут меняться или не будет достигнуто максимальное число ите-

раций.

3. Алгоритм СА с рандомизацией на входе для кластеризации

Пусть x¹, x², . . . , xⁿ, . . . — последовательность входных данных, сгенериро-

ванных в соответствии с вероятностным распределением (5) с параметрами

Θ^⋆ и Γ^⋆. В дальнейшем верхний индекс n будем использовать для обозначения

номера итерации.

Опишем алгоритм стохастической аппроксимации с рандомизацией на вхо-

де для задачи кластеризации со штрафной функцией (3) (квадрат расстояния

Махаланобиса). Покажем, что при такой штрафной функции задача (3) име-

ет решение.

Введем следующие п р е д п о л о ж е н и я:

Предположение 1. Функции q_i(·,·,x) : R^d → R, i ∈ 1,...,k, - диф-

ференцируемы при любом x ∈ X и их градиенты удовлетворяют усло-

вию Липшица, т.е. ∥∇_θq_i(θ₁, Γ_i, x) - ∇_θq_i(θ₂, Γ_i, x)∥ ≤ M∥θ₁ - θ₂∥, с некото-

рой конста

∫

Fi(θi, Γi) =_X

q_i(θ_i,Γ_i,x)P(dx), i ∈ 1,... ,k, имеет единственный минимум в

некоторой точке θ^⋆i и 〈θ - θ^⋆i, ∇F_i(θ)〉 ≥ μ∥θ - θ^⋆i∥², ∀θ ∈ R^d, с некоторой кон-

стантой μ > 0 (условие сильной выпуклости);

Предположение 2. Все матрицы Γ_i, i ∈ 1,...,k, являются симметрич-

ными положительно определенными, и их собственные значения ограничены

λ^ji ≤ C_λ, i ∈ 1,... ,k, j ∈ 1,... ,d;

Предположение 3. Кластеры X_i(Θ^⋆,Γ^⋆), i ∈ 1,...,k, значимо разде-

лены между собой: если для некоторого i ∈ 1, . . . , k, x ∈ X_i(Θ^⋆, Γ^⋆) и для θ_i, Γ_i

неравенство

|q_i(θ_i, Γ_i, x)| ≤ d_max = max

max

|q_i(θ^⋆i, Γ^⋆i, x)|

i∈1...k

x∈X_i(Θ^⋆,Γ^⋆)

выполняется, тогда для ∀j = i, j ∈ 1, . . . , k, следующее неравенство верно:

(8)

|q_i(θ_i, Γ_i, x^′)| > d_max + 2c_v

∀x^′ ∈ X_j(Θ^⋆,Γ^⋆

Для всех точек входных данных xⁿ и для любой выбранной пары Θ, Γ

можем получить зашумленные измерения штрафной функции

(9)

yⁿⁱ(Θ,Γ) = q_i(θ_i,Γ_i,xⁿ) + vⁿⁱ

i ∈ 1,...,k,

где шум vⁿⁱ ограничен: |vⁿⁱ| ≤ c_v, и если шум является случайным, то он не

зависит от выбора Θ, Γ, и E{vⁿⁱ} < ∞, E{vni2} ≤ σn2.

Обозначим k-векторы значений yⁿⁱ(Θ, Γ) и vⁿⁱ через yⁿ(Θ, Γ) и vⁿ соот-

ветственно; jⁿ(Θ, Γ) — k-вектор характеристических функций j(Θ, Γ, x), най-

денных с зашумленными измерениями yⁿ(Θ, Γ), n = 1, 2, . . .;Θn,Γn — оцен-

ки центров и ковариационных матриц кластеров n-го шага алгоритма (т.е.

для xⁿ) соответственно; lⁿ = argmax jⁿ(Θ, Γ) — индекс кластера, к которому

отнесен элемент данных xⁿ.

Пусть Δⁿ ∈ R^d, n = 1, 2, . . . — вектор, состоящий из независимых случай-

ных величин, порожденных распределением Бернулли (стандартно использу-

ется параметр распределения Бернулли 0,5), называемых пробными случай-

ными возмущениями, k — число кластеров,Θ0 ∈ R^d×k — матрица начальных

значений центроидов,Γ0 — набор начальных ковариационных матриц, {αⁿ}

и {βⁿ} — последовательности положительных чисел.

Для оценки ковариационных матриц кластеров будем использовать матри-

цы разброса из оценки по методу максимума правдоподобия [23] и параметри-

зованное кумулятивное скользящее среднее оценок ковариационных матриц

с регуляризацией. Пусть λ — натуральное число (параметр регуляризации);

ωⁿ — последовательность положительных чисел. Тогда алгоритм СА с ран-

домизацией на входе для кластеризации строит следующие оценки:

⎧

(

)

⎨yn

=yⁿ

Θn-1 ± βⁿΔⁿjnT,Γn-1 ,

(10)

⎩̂Θn = Θn-1 - jnTαⁿ y⁺ -y−

ΔⁿjnT,

2βⁿ

⎧

⎨

(θn-1ln - xⁿ)(θn-1ln - xⁿ)^T -Γn-1ln

ωⁿ

n > λ,

Ξ_ln =

^⎩I_d

иначе,

Γn

(11)

=Γn-1ln +Ξ_l

lⁿ

где I_d — единичная (d × d)-матрица.

Теорема. Пусть предположения 1-3 и следующие условия выполнены:

1. Обучающая последовательность x¹, x², . . . , xⁿ, . . . состоит из одинако-

во распределенных независимых случайных векторов, таких что они с нену-

левой вероятностью принимают значения в каждом из k классов в про-

странстве X;

2. ∀n ≥ 1 случайные векторы v¹, v², . . . , vⁿ и x¹, x², . . . , xn-1 не зависят

от xⁿ и Δⁿ, и случайный вектор xⁿ не зависит от Δⁿ;

∑

αⁿ = ∞ и αⁿ → 0, βⁿ → 0, αⁿ(βⁿ)-2 → 0 при n → ∞, ωⁿ → 1 при

n → ∞, λ < C.

Если последовательности оценок {Θn} и {Γn}, полученные с помощью алго-

ритмов (10) и (11), удовлетворяют отношению

(

)

(

(12)

lim

jⁿ

Θn-1,Γn-1 ,q

Θn-1,Γn-1,xⁿ

≤d_max +c_v,

n→∞

тогда последовательность {Θn} сходится в среднеквадратичном смысле:

lim_n→∞ E{∥Θn - Θ^⋆∥²} = 0, и последовательность {Γn} сходится по веро-

∑

→ Γ^⋆. Более того, еслиn αⁿ(βⁿ)² + (αⁿ)²(βⁿ)-2 < ∞, тогда

Θⁿ → Θ^⋆ при n → ∞ с вероятностью единица.

Доказательство теоремы приводится в Приложении.

К основным преимуществам описанного РАСА для кластеризации отно-

сятся:

• Алгоритм является итеративным, т.е. реализует идею онлайн обучения:

• адаптивность, обработка новых данных “на лету”;

• экономия памяти, не нужно хранить весь набор данных в памяти.

• Высокая скорость работы алгоритма.

• Алгоритм сохраняет работоспособность при росте размерности оценивае-

мых параметров (в отличие от, например, метода k-средних).

• Нечувствительность к шуму при измерении штрафной функции в точках

входных данных.

Сравним временную сложность простой базовой версии метода k-средних,

описанного в подразделе (2.2) (как специальной версии EM алгоритма), и

РАСА для кластеризации. В общем случае метод k-средних является NP-

сложной оптимизационной задачей. Обозначим через t число итераций алго-

ритма (максимальное установленное или необходимое для сходимости). Для

одной итерации метода k-средних (классификация, минимизация) необходи-

мо kd операций. Тогда временная сложность равна O(tNkd), так как алго-

ритм использует все N элементов данных на каждой итерации.

Для сравнения с методом k-средних будем считать, что все матрицы Γ_i,

i ∈ 1,...,k, в (4) являются единичными. РАСА для кластеризации необходи-

мо kd операций для вычисления jnT, kd операций для вычисления каждой из

функций y^n- и yn+. Таким образом, временная сложность каждой итерации

РАСА для кластеризации составляет O(3kd). Число итераций равно N. Тогда

оценка временной сложности всего алгоритма равна O(3Nkd).

Из полученных оценок временных сложностей можно сделать вывод, что

в заданных условиях при t > 3 алгоритм СА с рандомизацией на входе для

кластеризации является более быстрым, чем алгоритм k-средних. Отметим,

что в практических задачах t, чаще всего, значительно больше 3.

Метод построения оценок Γ (11) добавляет O((N - λ)d²) к сложности ос-

новного алгоритма.

4. Эксперименты в задаче кластеризации

Представим результаты экспериментов, проведенных для сравнения пред-

ложенного алгоритма с классическими подходами в задаче кластеризации.

Для наглядности в этих экспериментах используются синтетические данные

малой размерности. В качестве метрики качества кластеризации выбран ин-

декс Ранда (Adjusted Rand Index, ARI) [24]. Этот критерий позволяет оценить

качество кластеризации при заранее известном разбиении данных на класте-

ры. ARI отображает влияние как неверных положительных (false positive),

так и неверных отрицательных (false negative) решений, принятых во время

кластеризации. Таким образом, этот критерий позволяет показать, на сколь-

ко построенное разбиение данных X = {X₁, . . . , X_k} близко к эталонному раз-

биению X^⋆ = {X⋆1, . . . , X^⋆k}.

В начале рассмотрим смесь гауссовых ра(пределен)й со сл( ующими п)

-3

-0,7

раметрами: объем данных N = 5000, Θ =

, Γ₁ =

-0,7

(

)

(

)

0,8

Γ₂ =

, Γ₃ =

, вероятности в смеси p = col(0,4, 0,4, 0,2).

0,8

В РАСА для кластеризации были выбраны следующие параметры:

γ = 1/6, αⁿ = 0,25/n^γ, βⁿ = 15/n⁴ и ωⁿ = th(^nλ). Этот выбор основан на ре-

зультатах о быстрейшей сходимости СА из [11].

4.1. k-средние

Рисунок 1 иллюстрирует результаты использования РАСА для кластери-

зации в случае единичных матриц Γ_i, i ∈ 1, . . . , k, (случай k-средних). Он

отображает L₂ расстояния между истинными центроидами и их оценками,

полученными на каждом шаге алгоритма, и движение оценок центроидов в

зависимости от итераций алгоритма.

Для сравнения качества работы был использован метод k-средних с мини-

батчами из [14] с размером мини-батча, равным единице (таким образом, этот

Таблица 1. Средний ARI для эксперимента k-средних

Алгоритм

Среднее ARI

k-средних

0,858

Онлайн k-средних

0,819

PAM

0,84

Affinity Propagation

0,17

DBSCAN

0,41

РАСА для кластеризации

0,857

Центроид 1

Центроид 2

Центроид 3

2,2

6,0

0,7

0,6

2,0

5,5

0,5

5,0

1,8

0,4

4,5

0,3

1,6

4,0

0,2

3,5

0,1

1,4

3,0

1000

2000

3000

4000

5000

0,2

2,0 2,5 3,0 3,5

Итерация

Рис. 1. (Слева) Сходимость L₂-норм оценок центроидов, полученных с помо-

щью РАСА для кластеризации в эксперименте с k-средними. (Справа) Дви-

жение оценок центроидов, полученных с помощью РАСА для кластеризации,

(точки) и истинные значения центров кластеров (квадраты) в эксперименте с

k-средними.

метод можно назвать онлайн k-средних). Таблица 1 показывает средние зна-

чения ARI для каждого алгоритма после 100 запусков. Из этих результатов

видно, что качество работы предложенного в статье метода близко к качеству

работы методов k-средних, онлайн k-средних и Partitioning Around Medoids

(PAM), а также превосходит Affinity Propagation и DBSCAN.

4.2. Смесь гауссовых распределений

Рисунок 2 показывает L₂ расстояния между истинными центроидами и их

оценками, полученными с помощью РАСА для кластеризации с параметром

λ = 1000, и движение оценок центроидов в случае СГР эксперимента.

Центроид 1

Центроид 2

Центроид 3

6,0

2,0

5,5

0,2

1,5

5,0

0,4

1,0

4,5

0,6

0,5

4,0

0,8

3,5

1000

2000

3000

4000

5000

0,2

1,0 1,5 2,0

Итерация

Рис. 2. (Слева) Сходимость L₂-норм оценок центроидов, полученных с помо-

щью РАСА для кластеризации в СГР эксперименте. (Справа) Движение оце-

нок центроидов, полученных с помощью РАСА для кластеризации, (точки) и

истинные значения центров кластеров (квадраты) в СГР эксперименте.

Таблица 2. Средний ARI для СГР эксперимента

Алгоритм

Среднее ARI

0,903

Variational Bayesian Gaussian mixture inference

0,915

Affinity Propagation

0,14

DBSCAN

0,41

РАСА для кластеризации

0,909

В этом случае РАСА для кластеризации сравним с алгоритмами EM и

Variational Bayesian Gaussian mixture inference. Таблица 2 представляет сред-

ние значения ARI для каждого алгоритма после 100 запусков. По этим значе-

ниям видно, что предложенный метод близок к двум классическим подходам

для обучения СГР, но отметим еще раз, что РАСА для кластеризации обла-

дает существенно меньшей временной сложностью. Также представленный

метод превосходит Affinity Propagation и DBSCAN.

4.3. Внешние возмущения

В подразделах 4.1 и 4.2 проведено сравнение предложенного алгоритма с

другими при внешних возмущениях vⁿⁱ в (9), равных нулю. Теперь проведем

эксперименты с разли√ыми видами шума для вс√х i ∈ 1, . . . , k, n = 1, 2, . . .:

vⁿⁱ ∼ N(0,1); vⁿⁱ ∼ N(0,

2); vⁿⁱ ∼ N (1, 1); vⁿⁱ ∼ N (1,

2); случайным: vⁿⁱ = 10×

×(rand( ) · 4 - 2); иррегулярным: vⁿⁱ = 0,1 · sin(n) + 19 · sign(50 - n mod 100);

константным: vⁿⁱ = 20.

В этих условиях были сравнены четыре алгоритма: k-средних (как более

стабильный, чем онлайн версия), предложенный в статье метод с единичны-

ми ковариационными матрицами (обозначим его РАСА единичный), EM ал-

горитм и предложенный в статье метод с оценкой ковариационных матриц с

параметром λ = 3000 (обозначим его РАСА ковариационный). Средние зна-

чения ARI для каждого алгоритма после 10 запусков представлены в табл. 3.

Как видно из этих результатов, РАСА для кластеризации сильно превосхо-

дит метод k-средних почти для всех вариантов помех. Версия предложенного

алгоритма с оценкой ковариационных матриц также почти во всех случаях

превосходит и EM , и версию с единичными матрицами.

Таблица 3. Средний ARI для эксперимента с помехами

Шум

k-средние РАСА единич. EM РАСА ков.

N (0, 1)

0,608

0,768

0,654

0,815

√

N (0,

0,246

0,546

0,463

0,738

N (1, 1)

0,612

0,829

0,657

0,774

√

N (1,

0,246

0,601

0,371

0,612

Случайный

0,418

0,318

0,434

Иррегулярный

0,758

0,854

0,863

0,856

Константный

0,812

0,861

0,807

0,860

5. РАСА при разреженных параметрах смеси гауссовых распределений

В [25] была предложена интересная модель смеси гауссовых распределений

с разреженными (sparse) параметрами (разреженная СГР, sparse GMM). Эта

модель имеет среднее

θ_i ∈ R^d, θ_il ∼ N(0,σ2i), σ_i ∼ C₊(0,1), l ∈ 1... d,

где C₊(0, 1) означает распределение Коши, ограниченное на позитивной оси

(принимает только позитивные значения), с параметрами 0 и 1. Диагональная

ковариационная матрица задается с помощью

(13)

Γ_i = diag(σ²¹,σ²²,... ,σ2d), σ_j ∼ C₊(0; 0,5), j ∈ 1 . . . d.

Веса p_i ∼ D(e₀, . . . , e₀), i ∈ 1 . . . k, предполагаются принадлежащими рас-

пределению Дирихле, где параметр e₀ ∼ G(α_p, kα_p) получен из гамма-

распределения со средним k-1 и дисперсией (α_pk²)-1, α_p = 10.

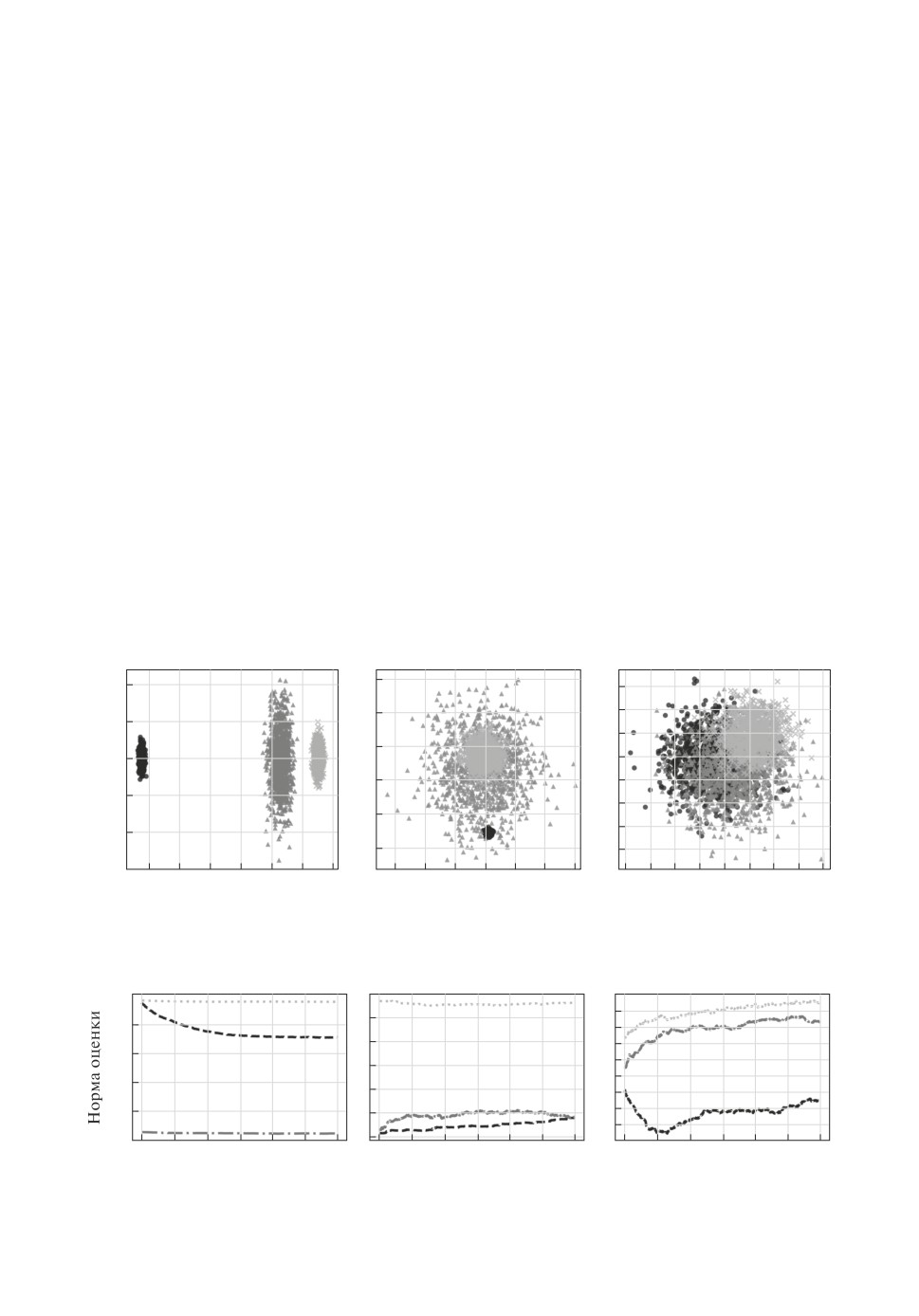
В разреженной СГР можно выделить три основных типа поведения кла-

стеров (рассмотрим случай k = 3, d = 2) (рис. 3). При такой модели данных

часто возникают ситуации, когда данные из одного кластера лежат внутри

другого, что делает процедуру кластеризации сложной.

Авторы [25] использовали этот подход для моделирования множества раз-

личных интересных распределений шума. РАСА для кластеризации, оцени-

вающий только центроиды кластеров Θ (как алгоритм k-средних) показывает

Рис. 3. Типы разреженной СГР: 1, 2, 3.

120

4,5

4,0

100

3,5

3,0

2,5

2,0

1,5

1,0

0,5

0 50010001500200025003000

Итерация

Рис. 4. РАСА k-средних сходимость центроидов: типы 1, 2, 3.

слабые результаты для данных, полученных из модели разреженной СГР (см.

подраздел 5.2). Рисунок 4 демонстрирует графики L₂-норм расстояний меж-

ду истинными центрами кластеров и их оценками, полученными на каждом

этапе алгоритма. Как видно из этих графиков, РАСА k-средних демонстри-

рует слабую сходимость.

5.1. РАСА для кластеризации при разреженной СГР

Рассмотрим подходы для улучшения качества при разреженной СГР. Во-

первых, алгоритмы (10) и (11) позволяют построить более робастные оценки

в случае sparse GMM.

Во-вторых, добавление нового L₂ регуляризатора в функцию потерь (7)

позволяет сделать оценки центроидо

θ_i, i = 1... k, ближе к центрам разре-

женной СГР:

(14)

ψⁿ ∥θ_ln - ξ∥² ,

где lⁿ = argmax jⁿ(Θ, Γ) - индекс кластера, к которому отнесена точка дан-

ных xⁿ; ξ ∈ Rⁿ, ξ_l ∼ N (0, σ²), σ ∼ C₊(0, 1), l ∈ 1, . . . , d; ψⁿ - последователь-

ность возрастающих положительных чисел.

В-третьих, добавление L₁ регуляризатора в функцию потерь (7) по каж-

дой размерности центроидов позволяет сделать их ближе к разреженному

среднему θ_il ∼ N (0, σ2i), σ_i ∼ C₊(0, 1), i ∈ 1 . . . k, j ∈ 1 . . . d:

∑∑

(15)

τⁿ

|Θij

i=1 j=1

где τⁿ - последовательность возрастающих положительных чисел.

5.2. Эксперименты

Для экспериментов были выбраны значения k = 3, d = 2, N = 3000.

Параметры РАСА для кластеризации: γ = 1/6, αⁿ = 0,25/n^γ , βⁿ = 15/n⁴ ,

ωⁿ = th(^nλ ), ψⁿ = 1e-5, τⁿ = 1e-4 th(^nλ). В качестве метрик для сравнения ал-

горитмов были выбраны ARI и среднее L₂-расстояние между центроидами,

полученными с помощью алгоритма, и их истинными значениями.

Сравнение РАСА k-средних и РАСА для кластеризации при разреженной

СГР после 1000 запусков экспериментов представлены в табл. 4.

Для разреженной СГР типа 1 модифицированный РАСА дает: ARI = 1,0,

L₂-расстояние = 0,130 (рис. 5).

Таблица 4. ARI и L₂-расстояние

Алгоритм

Среднее ARI Среднее L₂-расстояние

РАСА k-средних

0,134

1,830

РАСА для разреженной СГР

0,518

1,617

Центроид 1

Центроид 2 Центроид 3

0,2

0,4

0,6

0,8

5,0

5,5

500 1000150020002500 3000

Итерация

Рис. 5. Тип 1: сходимость центроидов, движение оценок центроидов, класте-

ризация РАСА для разреженной СГР.

Центроид 1

Центроид 2

Центроид 3

5,0

4,4

4,5

4,0

4,2

3,5

4,0

3,0

2,5

3,8

2,0

3,6

1,5

0,5

500 1000150020002500 3000

Итерация

Рис. 6. Тип 2: сходимость центроидов, движение оценок центроидов, класте-

ризация РАСА для разреженной СГР.

Центроид 1

Центроид 2 Центроид 3

2,0

2,50

1,5

2,25

1,0

2,00

0,5

1,75

1,50

0,5

1,25

1,0

1,00

1,5

2,5 2,0

0,5

1,5

500 10001500200025003000

Итерация

Рис. 7. Тип 3: сходимость центроидов, движение оценок центроидов, класте-

ризация РАСА для разреженной СГР.

Для разреженной СГР типа 2 модифицированный РАСА дает: ARI =

= 0,521, L₂-расстояние = 0,923 (рис. 6).

Для разреженной СГР типа 3 модифицированный РАСА дает: ARI =

= 0,277, L₂-расстояние = 2,051 (рис. 7).

Также были проведены эксперименты с РАСА-оценкой σ в (13). Результа-

ты были получены многообещающие, но нестабильные.

5.3. Результат

Практический результат заключается в том, что использование (11), (14)

и (15) в РАСА для кластеризации позволяет улучшить результаты для дан-

ных, порожденных смесью гауссовых распределений с разреженными пара-

метрами. Теоретический результат заключается в том, что (11), (14) и (15)

могут ослабить предположение 3 теоремы о значимой разделимости класте-

ров. Причиной для такого предположения является результат, полученный

выше, так как при разреженной СГР кластеры могут лежать друг в друге

(тип 2 и тип 3).

6. Заключение

В статье представлен алгоритм СА с рандомизацией на входе для кла-

стеризации и описано его теоретическое обоснование. Продемонстрирована

робастность этого метода в случае, когда данные измерены с почти произ-

вольными внешними помехами. В дополнение к этому свойству представлен-

ный алгоритм реализует идею обучения “на лету” и обладает высокой ско-

ростью работы. Продемонстрировано применение предложенного метода для

кластеризации смеси гауссовых распределений, в том числе и при разрежен-

ных параметрах этой смеси. В серии экспериментов показаны преимущества

алгоритма перед классическими подходами.

ПРИЛОЖЕНИЕ

Доказательство леммы.

Если последовательность {xⁿ} порождена СГР с параметрами Θ^⋆ и Γ^⋆,

то тогда с этими параметрами(достигается мини)ум минус логарифм функ-

∑

ции правдоподобия -x∈X ln

p_iG(x|θ_i,Γ_i) . По определению плотно-

i=1

сти нормального распределения это выражение может быть переписано как

)

∑∑(

(Π.1)

- ln p_i(2π)-2 |Γ_i|-1 +1(xj - θi)TΓ-1i(xj - θi)

j ∈1,...,n.

i=1 x^j ∈X_i

Обозначим первое слагаемое в (Π.1) через L, а второе - через R, тогда

arg min L = arg min R = (Θ^⋆, Γ^⋆) при n → ∞.

Θ,Γ

Функционал (7) по условию может быть переписан через (2) и (4) как

∑

F (Θ, Γ) =

|X_i|-1

(x^j - θ_i)^TΓ-1i(x^j - θ_i), j ∈ 1, . . . , n.

i=1

x^j∈X_i

Таким образом, arg minΘ,Γ F (Θ, Γ) = arg minΘ,Γ R = (Θ^⋆, Γ^⋆) при n → ∞.

Доказательство леммы закончено.

Доказательство теоремы.

1. На первом шаге доказательства зафиксируем Γ и докажем сходи-

мость {Θn}. Выберем некоторое r из 1, 2, . . . , k и такую подпоследователь-

ность {Θnj }, при построении которой изменениям подверглись только оценки

центра r-го кластера.

Необходимо доказать, что ∃ N_r такое, что xnj ∈ X_r(Θ^⋆, Γ^⋆)

∀j ≥ N_r.

Предположим, что это не так. Тогда ∃ бесконечная возрастающая подпо-

следовательность {njt }, для которой xnjt ∈ X_r(Θ^⋆, Γ^⋆) и xnjt⁺¹ ∈ X_r(Θ^⋆, Γ^⋆).

Сравним значения q(

,Γ_r,xnjt) и q(

,Γ_r,xnjt⁺¹). Сначала оценим

∥

∥. В силу алгоритма (10), теоремы о среднем, компактности

множества Θ и условия предположения 1:



(n_jt -1)



^θ

≤

(



(

))



θnjt-1

≤ αnjt m

2C_v + max

∇_θq

+ sαnjt Δnjt ,Γ_r,xnjt



≤ αnjt C

s∈[-1;1]

с некоторой константой C. Следовательно, для достаточно больших t

разность |q(

,Γ_r,xnjt⁺¹)-q(

,Γ_r,xnjt⁺¹)| < C_v/3. Так как xnjt⁺¹ ∈

∈X_r(Θ^⋆,Γ^⋆), то по (8) |q(

,Γ_r,xnjt⁺¹)| > d_max + 2C_v. Из этих отноше-

ний для достаточно большого t имеем неравенство



(

)



(

)



θ(njt-1)

q

θnjtr , Γr, xnjt+1

≥

q

, Γ_r, xnjt⁺¹

-



(

)

(

)



θ(njt-1)

−

q

θnjtr , Γr, xnjt+1

-q

, Γ_r, xnjt⁺¹

 > d_max + 5/3C_v.

С другой стороны, по условию (12) для достаточно большого t



(

)



θ(njt-1)

q

,Γ_r,xnjt

<d_max +

C_v.

Получили противоречие.

Перенумеруем для удобства последовательность {

} с j = N_r в {θir }.

(

)

По (10) имеем ∥θir - θ^⋆r∥² ≤ ∥

-θ^⋆r -αi

yi+ - y^i-

Δⁱ∥².

2βⁱ

Обозначим через Fn-1r σ-алгебру событий, порождаемых случайными ве-

личинамиθ0r,θ1r, . . . ,

, полученными по алгоритму (10). Тогда получа-

ем, что

(Π.2)

E_Fi-1

∥θir - θ^⋆r∥² ≤ ∥θi-1r - θ^⋆r∥² -

(

)

θ (i-1)

−αⁱ

- θ^⋆r,(βⁱ)-1E_Fi-1

Δⁱ

yir,+ - y^ir,-

(

)₂

(αⁱ)

E_Fi-1

∥Δⁱ∥²

yir,+ - y^ir,-

4(βⁱ)²

Оценим последнее слагаемое в правой части неравенства (Π.2). Функ-

ции q(·, Γ_i, x_i) удовлетворяют условию Липшица, ∥Δⁱ∥² = m, тогда, исполь-

зуя теорему о среднем и неравенство Коши-Буняковского, последовательно

получаем, что

(

)

(

)₂

E_Fi-1

∥Δⁱ∥²

yir,+ - y^ir,-

² = 2m E_Fi-1

vir,+ - v^ir,-

(

)

(

))₂)

θ (i-1)

+ E_Fi-1

+βⁱΔⁱ,Γ_r,xi

-q

-βⁱΔ_i,Γ_r,xⁱ

≤

(

(

)

(

)



θ (i-1)

≤ 2mE_Fi-1(vir)2 + 2mEFi-1

q

+βⁱΔⁱ,Γ_r,xⁱ

-q

θ^⋆r,Γ^⋆r,xⁱ

+



(

)

)₂



(

)

θ (i-1)

+q

-βⁱΔⁱ,Γ_r,xⁱ

-q

θ^⋆r,Γ^⋆r,xⁱ



≤

(

)

(



(i-1)



(i-1)



≤ 2mE_Fi-1

(M + 0,5)

^θ

+Δⁱβⁱ2 +

^θ

-Δⁱβⁱ

)₂



(

)



+∇θq

θ^⋆r,Γ^⋆r,xⁱ



+ 2mE_Fi-1

(v^ir)².

В силу равномерной ограниченности функции ∇_θq(θ^⋆r, Γ^⋆r, ·) получаем нера-

венство

(

)₂

E_Fi-1

∥Δⁱ∥²

yir,+ - y^ir,-

≤ C₁E_Fi-1

(v^ir)² + C₂(βⁱ)²∥θ(i-1)r - θ^⋆r∥² + o((βⁱ)²),

где C_i, i = 1, 2 . . . , — некоторая положительная константа.

Рассмотрим второе слагаемое правой части (Π.2):

(

)

(βⁱ)-1E_Fi-1

Δⁱ

yir,+ - y^ir,-

= (βⁱ)-1E_Fi-1Δivir + (βi)-1EFi-1Δi ×

(

)

(

))

θ (i-1)

(Π.3)

× q

+βⁱΔⁱ,Γ_r,xi

-q

-βⁱΔⁱ,Γ_r,xi

Первое слагаемое в правой части (Π.3) равно нулю в силу свойств Δⁱ и незави-

симости Δⁱ и v^ir,±. Используя теорему о среднем, равномерную ограни-

ченность функции ∇_θq(θ, Γ, ·) и определение F_r(Θ, Γ), преобразуем второе

слагаемое правой части (Π.3) к виду

(

))

(βⁱ)-1E_Fi-1

Δⁱ

yir,+ - y^ir,-

= 2∇F_r(θ(i-1)r) +

(

)

(

),)

θ (i-1)

+ E_Fi-1

Δⁱ Δⁱ,∇_θq θ(i-1)r+,Γ_r

,xⁱ

-∇_θq

,Γ_r,xi

(

)

(

),)

θ (i-1)

+ E_Fi-1

Δⁱ Δⁱ,∇_θq θ(i-1)r-,Γ_r

,xⁱ

-∇_θq

,Γ_r,xi

здесь

[

]

θ(i-1)r± ∈ θ(i-1)r,θ(i-1)r

±βⁱΔⁱ .

Функция q(·, Γ, x) удовлетворяет условию Липшица и функция F_r(·, Γ) стро-

го выпукла, тогда, используя справедливое при любом ε > 0 неравенство

∥

-θ^⋆r∥ ≤ (ε-1βⁱ + ε(βⁱ)-1∥

- θ^⋆r∥²)/2, выводим

(

)

θ (i-1)

-αⁱ

- θ^⋆r,(βⁱ)-1E_Fi-1

Δⁱ

yir,+ - y^ir,-

(

θ (i-1)

= -2αⁱ

- θ^⋆r,∇F_r

,Γ_r

(

)

(

),,

θ (i-1)

-αⁱ

- θ^⋆r, E_Fi-1

Δⁱ Δⁱ,∇_θq θ(i-1)r+,Γ_r

,xi -∇θq

,Γ_r,xi

(

)

(

),,

θ (i-1)

−αⁱ

- θ^⋆r, E_Fi-1

Δⁱ Δⁱ,∇_θq θ(i-1)r-,Γ_r

,xi -∇θq

,Γ_r,xi

≤

(

)



(i-1)



(i-1)



≤ -2μαⁱ

^θ

-θ^⋆r

² + Mm3/2αⁱβⁱ ε-1βⁱ + ε(βⁱ)-1

^θ

-θ^⋆r

Следовательно, имеем



(

)



(i-1)



E_Fi-1

^θ

-θ^⋆r2 ≤

^θ

-θ^⋆r

1 - 2μαⁱ + Mm3/2αⁱε + C₂(αⁱ)²/4 +

(

)

+ Mm3/2αⁱ(βⁱ)²ε-1 + (αⁱ)²/(4(βⁱ)²) C₁E_Fi-1vir2 + o((βi)2)

Выберем ε настолько малым, чтобы Mm3/2ε < 2μ, и пусть i достаточно ве-

лико. По условиям теоремы получаем



)

(i-1)

E_Fi-1

^θ

-θ^⋆r2 ≤

^θ

-θ^⋆r



1-C₃αⁱ

(

)

+C₄

αⁱ(βⁱ)² + (αⁱ)²(βⁱ)-2(1 + E_Fi-1

v^ir)2

Тогда, по лемме Роббинса-Сигмунда [1]θir → θ^⋆r при i → ∞ с вероятностью

единица

{

}

E ∥θir -θ^⋆r∥2

≤

{

}

(

)

≤E ∥θ(i-1)r -θ^⋆r∥2

(1 - C₅αⁿ) + C₆

αⁿ(βⁿ)² + (αⁿ)²(βⁿ)-2(1 + σn2)

Сходимость в среднеквадратичном смысле к точке θ^⋆r последовательности

оценок {θir} следует из [1].

2. Пусть теперь Θ фиксирована. Рассмотрим оценки {Γnl = {ĝ^nij }}, l ∈

∈ 1, . . . , k. Обозначим ŝ^nij = {(θl - xⁿ)(θl - xⁿ)^T}_ij — (i, j)-й элемент l-й мат-

рицы разброса, тогда

(

)

∑

ĝnij = λ +

ω^rŝ^r

n-1.

r=λ+1

По условиям теоремы λn-1 → 0, ω^r → 1, s^rij n-1 → Γ_l при n → ∞. Таким обра-

зом, при n → ∞ оценкаΓn является оценкой по методу максимизации прав-

→Γ^⋆.

Оценки по алгоритмам (10) и (11) строятся итеративно, т.е. на n-м шаге

алгоритма сначала строится оценкаΘn при фиксированномΓn-1, которая

затем фиксируется и строитсяΓn. Таким образом, для каждого из мето-

дов (10) и (11) доказаны в пп. 1 и 2 соответствующие сходимости оценок, а

функция q(Θ, Γ, x) задается с помощью (4), отсюда следует результат теоре-

мы. Это завершает доказательство теоремы.

СПИСОК ЛИТЕРАТУРЫ

Поляк Б.Т. Введение в оптимизацию. М.: Hаука, 1983.

Robbins H., Monro S. A Stochastic Approximation Method // Ann. Math. Stat.

1951. P. 400-407.

Kiefer J., Wolfowitz J. Stochastic Estimation of the Maximum of a Regression

Function // Ann. Math. Stat. 1952. V. 23. No. 3. P. 462-466.

Blum J.R. Multidimensional Stochastic Approximation Methods // Ann. Math. Stat.

1954. V. 25. No. 4. P. 737-744.

Граничин О.Н. Об одной стохастической рекуррентной процедуре при зависи-

мых помехах в наблюдении, использующей на входе пробные возмущения //

Вестн. Ленингр. ун-та. Сер. 1. 1989. №1 (4). С. 19-21.

Granichin O.N. A Stochastic Recursive Procedure with Correlated Noises in the

Observation, that Employs Trial Perturbations at the Input // Vestnik Leningrad

University: Mathematics (Vestnik Leningradskogo Universita. Matematika). 1989.

V. 22. No. 1. P. 27-31.

Граничин О.Н. Процедура стохастической аппроксимации с возмущением на

входе // АиТ. 1992. № 2. C. 97-104.

Granichin O.N. Procedure of Stochastic Approximation with Disturbances at the

Input // Autom. Remote Control. 1992. V. 53. No. 2. P. 232-237.

Поляк Б.Т., Цыбаков А.Б. Оптимальные порядки точности поисковых алгорит-

мов стохастической аппроксимации // Проблемы передачи информации. 1990.

Т. 26. С. 126-133.

Polyak B.T., Tsybakov A.B. Optimal orders of accuracy for search algorithms of

stochastic optimization // Prob. Inform. Transm+. 1990. V. 26. No. 2. P. 126-133.

Растригин Л.А. Статистические методы поиска. М.: Наука, 1968.

Spall J.C. Multivariate Stochastic Aproximation Using a Simultaneous Perturbation

Gradient Aproximation // IEEE Trans. Autom. Control. 1992. V.

37. No. 3.

P. 332-341.

10.

Граничин О.Н. Поисковые алгоритмы стохастической аппроксимации с рандо-

мизацией на входе // АиТ. 2015. № 5. С. 43-59.

Granichin O.N. Stochastic Approximation Search Algorithms with Randomization

at the Input // Autom. Remote Control. 2015. V. 76. No. 5. P. 762-775.

11.

Granichin O., Volkovich Z., Toledano-Kitai D. Randomized Algorithms in Automatic

Control and Data Mining. Springer, 2015.

12.

Lloyd S. Least Squares Quantization in PCM // IEEE Trans. Inform. Theory. 1982.

V. 28. No. 2. P. 129-136.

13.

Shindler M., Wong A., Meyerson A. Fast and Accurate k-means For Large

Datasets // Proc. 24th NIPS Conf. 2011.

14.

Sculley D. Web Scale K-Means clustering // Proc. 19th WWW Conf. 2010.

15. Katselis D., Beck C.L., van der Schaar M. Ensemble Online Clustering through

Decentralized Observations // Proc. 53rd IEEE CDC. 2014. P. 910-915.

16. Kaufman L., Rousseeuw P. Finding Groups in Data: An Introduction to Cluster

Analysis’. N.Y.: John Wiley & Sons Inc., 1990.

17. Граничин О.Н., Измакова О.А. Рандомизированный алгоритм стохастической

аппроксимации в задаче самообучения // АиТ. 2005. № 8. C. 52-63.

Granichin O.N., Izmakova O.A. A Randomized Stochastic Approximation Algorithm

for Self-Learning // Autom. Remote Control. 2005. V. 66. No. 8. P. 1239-1248.

18. Dempster A., Laird N., Rubin D. Maximum Likelihood from Incomplete Data via

the EM Algorithm // J. Royal Stat. Soc. Ser. B. 1977. V. 39. No. 1. P. 1-38.

19. Bishop C.M. Pattern Recognition and Machine Learning. Springer, 2006.

20. Song M., Wang H. Highly Efficient Incremental Estimation of GMM for Online Data

Stream Clust // Proc. SPIE III. 2005. P. 174-184.

21. Frey B.J., Dueck D. Clustering by Passing Messages between Data Points // Science.

2007. No. 315 (5814). P. 972-976.

22. Ester M., Kriegel H.P., Sander J., Xu X. A Density-Based Algorithm for Discovering

Clusters in Large Spatial Databases with Noise // Proc. 2nd Int. Conf. on Knowledge

Discovery and Data Mining. Portland, 1996. P. 226-231.

23. Huber P.J. Robust Statistics. Wiley, 1981.

24. Hubert L., Arabie P. Comparing partitions // J. Classif. 1985. V. 2. No. 1. P. 193-218.

25. Dahlin J., Wills A., Ninness B. Sparse Bayesian ARX Models with Flexible Noise

Distributions // Proc. 18th IFAC Sympos. on System Identification. 2018. P. 25-30.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 01.06.2017

После доработки 19.12.2018

Принята к публикации 07.02.2019