Автоматика и телемеханика, № 8, 2019

Управление в технических системах

Н.В. ДАНИЛОВА, канд. физ.-мат. наук (danilova198686@mail.ru),

И.А. ЗЕМЛЯКОВА (eizzzie@yandex.ru)

(Южный федеральный университет, Ростов-на-Дону;

Институт математики, механики и компьютерных наук

им. И.И. Воровича, Ростов-на-Дону)

НЕКОТОРЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО

УПРАВЛЕНИЯ С РАЗЛАДКОЙ¹

Рассматривается обобщение процессов с разладкой, а именно процессы

с векторной разладкой. Для такого типа задач рассматривается класс за-

дач оптимального управления без обнаружения разладки. Предложен вы-

числительный метод решения задач управления на конечном временном

интервале и с целевым функционалом, определенным на конце интер-

вала, основанный на использовании мартингальной техники. Рассмотрен

вычислительный эксперимент для модели с двумя барьерами и двумя

моментами остановки.

Ключевые слова: процессы с разладкой, векторная разладка, мартингал,

мартингальная мера, винеровский процесс, квантильное хеджирование.

DOI: 10.1134/S0005231019080063

1. Введение

Процессы, о которых пойдет речь, достаточно популярны на протяжении

длительного времени. Эти процессы называются процессами со сменой режи-

мов. Процессы с разладкой являются важным подклассом процессов со сме-

ной режимов. В связи с разладкой основная задача, которая обсуждается в

публикациях, заключается в наиболее быстром обнаружении момента разлад-

ки [1-3]. Рассмотрим обобщение процессов с разладкой, а именно процессы с

векторной разладкой, и важный класс задач оптимального управления тако-

го рода процессами без обнаружения разладки. Будем рассматривать задачи

управления на конечном временном интервале и с целевым функционалом,

определенным на конце интервала. Для этих задач будет предложен вычис-

лительный метод их решения. При этом будет использована мартингальная

техника, применяемая, например, в стохастической финансовой математике

[4, 5]. Статья построена следующим образом. В разделе 2 излагаются основ-

ные понятия, которые используются в остальных разделах, приводится ре-

шаемая задача оптимального управления и описывается метод ее решения.

¹ Работа выполнена при финансовой поддержке Российского научного фонда (проект

№ 17-19-01038).

В разделе 3 рассматривается модель, для которой приводится решение зада-

чи управления. В разделе 4 рассматривается решение задачи квантильного

хеджирования для изучаемой модели. В разделе 5 приводятся результаты

эксперимента. В разделе 6 подводятся итоги статьи и намечается направле-

ние дальнейшего исследования.

2. Основные понятия

Рассмотрим стохастический базис Ω, (F_t)t≥0 , F, P

. Пространство эле-

ментарных случайных событий Ω - это пространство непрерывных на от-

резке [0, T ] траекторий, фильтрация (F_t)t≥0 наделена набором стандартных

)

(⋃

свойств, σ-алгебра F = σt∈[0,T] F_t

= F_T. Основным источником случай-

ности будем считать стандартный винеровский процесс, канонически задан-

ный W_t (ω) = ω (t), более того будем считать, что данный процесс определяет

стохастический базис в следующем смысле: вероятностная мера P является

винеровской мерой, фильтрация F_t = σ (W_s, s ∈ [0, t]

^⋃N), где N - σ-алгебра,

содержащая все множества нулевой меры.

Рассмотрим процесс Ито: dX (ω, t) = α_X (ω, t) dt + β_X (ω, t) dW_t. В следую-

щих далее формулах траектория ω будет опущена там, где это не при-

водит к непониманию. Допустим, что коэффициент β_X (t) = 0 с вероят-

ностью единица, тогда процесс Ито X можно записать в виде dX (t) =

(

)

α_X (t)

= β_X(t)

dt + dW_t . Далее будем интересоватьcя процессом dW =

β_X(t)

= α^X(t)β

dt + dW_t, который будет процессом Ито при выполнении условия су-

X (t)

)

(∫

ществования интеграла P

|χ_X (s)| ds < ∞

= 1, χ_X (t) = αX(t)β

. Для даль-

X(t)

нейшего понадобится одно из утверждений теоремы Гирсанова, см., напри-

мер, [4, c. 833].

Теорема 1. Рассмотрим процесс

⎛

⎞

∫

Z_t = exp^⎝-¹

χ²

(s) ds + χ_X (s) dW_s⎠.

(

)

∫t

Если EZ_t = E exp

-¹

χ²

(s)ds +

χ_X (s)dW_s

= 1, то относительно

меры dP_T = Z_T dP_T процесс Ито dW_t = χ_X (t)dt + dW_t будет стандартным

винеровским процессом, а процесс плотности Z_t будет равномерно интегри-

руемым мартингалом.

Через P_T обозначено сужение меры на σ-алгебру F_T . Достаточным услови-

ем(выполнения раве)ства для математического ожидания является условие

∫

χ²

(s)ds < ∞

= 1. Поскольку Z_T > 0, то новая мера эквивалентна ис-

ходной мере. Относительно этой новой меры процесс X выражается непо-

средственно через стандартный винеровский процесс W_t в виде интеграла

∫t

Ито X (t) = X (0) +

β_X (s)dW_s, для существования которого достаточным

)

(∫

условием является равенство P

β2X (s)ds < ∞

= 1. При выполнении это-

го условия процесс X - мартингал с непрерывной траекторией, причем суще-

ствует единственная мера, относительно которой процесс X будет мартинга-

лом. Далее используем теорему о представлении мартингалов [4, с. 313].

Теорема 2. Пусть Y (t) - мартингал с непрерывной траекторией, то-

гда существует единственный прогрессивно измеримый процесс β_Y (t), при-

)

(∫

∫t

чем P

β2Y (s)ds < ∞

= 1, для которого Y (t) = Y (0) +

β_Y (s)dW_s.

Следствие. При условии, что β_X(t)= 0, мартингал Y может быть вы-

∫t

ражен через мартингал X следующим образом: Y (t) = Y (0)+

β_Y/X(s)dX_s,

где βY/X (t) β_X (t) = β_Y (t). Причем это представление является единствен-

ным.

Рассмотрим задачу оптимального управления на конечном интервале [0, T ]

следующего вида:

min E (Φ (Y_T, ξ))

βY/X,y₀

при ограничениях

∫t

Y (t) = y₀ + βY/X (s) dX_s,

(1)

∫^t

∫

X (t) = x₀ + α_X (s) dX_s + β_X (s) dW_s,

y₀ ≤ a.

Здесь случайная величина ξ измерима относительно σ-алгебры F_T , функция

двух переменных Φ(x, y) - выпуклая функция по первой переменной при

произвольном значении второй переменной.

Далее процесс X будем называть базовым процессом, а процесс β_Y/X -

управлением или стратегией. Для решения этой задачи рассмотрим мартин-

гальную меру P : dP_T = Z_T dP_T . Процесс плотности Z_t был определен ранее.

Относительно этой новой меры процессы X_t и Y_t - мартингалы с непрерыв-

ными траекториями. Предположим, что существует решение задачи

(2)

min

E(Φ(η,ξ)) при условии Eη ≤ a.

Допустим, что η^∗ - решение задачи (2). Рассмотрим процесс

(3)

V (t) = E(η^∗/F_t)

который является равномерно интегрируемым мартингалом относительно

определенной ранее фильтрации и меры P , поэтому процесс (3) выражается

в виде

∫t

(4)

V (t) = Eη^∗ + βV/X (s) dX_s.

Поскольку E [η^∗] < ∞ и V (T ) = η^∗, то процесс β_Y/X = β_V/X и начальное

значение y₀ = Eη^∗ являются решением задачи (1). При получении разложе-

ния (4) применено приведенное ранее следствие. Таким образом, установлено

следующее утверждение.

Теорема 3. Если существует решение задачи (2), то решение зада-

чи (1) строится так:

1. Определяется мартингальная мера P при помощи процесса плотно-

сти Z;

2. Решается задача (2);

3. Вычисляется мартингал V и разложение мартингала (4) по процес-

су X.

На разложении мартингала V остановимся подробнее. Явный способ

вычисления разложения получается при предположении о существова-

нии функции M (x, t) ∈ C2,1 такой, что V (ω, t) = M(X(ω, t), t), и пред-

положении, что интегрант β_X (ω, t) = β_X (X(ω, t), t). При этих предполо-

жениях можно использовать формулу Ито для вычисления разложения.

Действительно, с использованием формулы Ито дифференциал dV (ω, t) =

[

]

∂M

(X(t), t) +¹² β2X (X(t), t)∂2 M(X(t),t)

+ β_X(X(t),t)∂M(X(t),t)∂xdW_t с исполь-

∂t

∂x²

зованием разложения

(4)

- тот же самый дифференциал dV (ω, t) =

= β_V/X (X (ω,t),t)β_X (X (ω,t),t)dW_t. Из сравнения дифференциалов возни-

кает фундаментальное уравнение для функции M

∂M

∂²M

(5)

β²

∂t

^X ∂x²

с начальным условием M (x, 0) = Eη^∗ и выражение для интегранта в разло-

жении (4)

∂M

(6)

β_V/X =

∂x

Поскольку β_Y/X может зависеть от всей предыстории процесса W , то бу-

дем использовать другие соотношения для вычисления разложения (4), на-

пример, если X и Y являются квадратично интегрируемыми мартингалами

с квадратическими характеристиками 〈X〉_t и 〈Y 〉_t. Применение этих харак-

теристик позволяет выразить через них интегрант в разложении (4):

d〈XV 〉_t

(7)

β_V/X (t) =

d〈X〉_t

Рассмотрим два примера.

В примере 1 требуется найти

(8)

min E (ξ - Y_T )²

β_Y/X,y₀

при выполнении ограничений (1). Будем считать, что случайная величина ξ -

квадратично интегрируемая. Следуя предложенной вычислительной схеме,

необходимо решить задачу (2), чтобы найти η^∗. Далее используем результат,

приведенный в [6, гл. 6], из которого следует, что задача (2) эквивалентна

задаче

(

)₂

(9)

minE

ξ-η

при условии, что EZ_T

η = 0.

В (9) ξ = ξ - a. Решение задачи (9) будет иметь вид

EZ_T ξ

(10)

η^∗ = ξ -

Z_T .

EZ²

Используя (10), вычисляем процесс Y_t = a+E (η^∗/F_t) и оптимальное управ-

ление, используя (6) или (7).

В примере 2 требуется найти

(11)

min (ξ - Y_T )⁺

β_Y/X,y₀

при тех же ограничениях. Случайная величина ξ > 0 и ее математиче-

ские ожидания Eξ < ∞ и Eξ < ∞. В (11) использовано обозначение (x)⁺ =

= max(x,0). Согласно предложенной схеме необходимо решить задачу (2),

которая эквивалентна задаче

(12)

max Eξς при ограничениях 0 ≤ ς ≤ 1 и Eξς ≤ a.

Рассмотрим две новые меры:

P =ξEξ и dP =^ξ

dP , относительно которых

Eξ

задача (12) будет иметь вид

(13)

maxEς при ограничениях 0 ≤ ς ≤ 1 и Eς ≤ α, где α =a .

Eξ

Задача (13) является рандомизированной задачей Неймана-Пирсона. Ре-

шение рандомизированной задачи приведено в [7]. Следуя [7], приведем ре-

шение

(14)

ς^∗ = I{d˜

^} + εI^{

^},

P-λ^∗dP>0

P-λ^∗dP=0

В (14) λ^∗

- наименьшее значение λ, при котором EI^{

^} ≤α

P-λ^∗dP>0

α-EI{

P -λ∗dP >0}

и ε=

. Так как 0 ≤ α - EI^{

^} < EI^{

^}, то

P-λ^∗dP>0

P-λ^∗dP=0

EI{

P -λ∗dP =0}

0 ≤ α < 1. После этого находим решение задачи (2) η^∗ = ξς^∗, процесс Y и

оптимальное управление.

3. Основная модель

После описания вычислительной схемы рассмотрим основной класс ис-

следуемых моделей базового процесса X. Процессы α_X и β_X , участвующие в

определении процесса X, задаются последовательностью моментов остановки

0 < τ₁ < ... < τ_n < ..., с вероятностью единица стремящихся к бесконечно-

сти, и двумя детерминированными последовательностями μ и σ с не равными

нулю элементами следующим образом:

∑

(15)

α_X (t) = μ_iI{τi<t≤τ_i}, βX (t) =

σ_iI{τi<t≤τ_i}.

i=1

Поскольку рассматривается конечный отрезок [0, T ], то уместно опреде-

лить случайную величину κ_T = sup {n : τ_n ≤ T } и использовать ее в качестве

верхнего предела сумм в (15):

∑

α_X (t) = μ_iI{τi-1<t≤τ_i} + μκT +1^I{τκT <t≤T},

i=1

(16)

∑

β_X (t) =

σ_iI{τi-1<t≤τ_i} + σκT +1^I{τκT

<t≤T }.

i=1

Очевидно, что P (κ_T < ∞) = 1 и траектории процессов (16) полунепрерыв-

ны слева. Отсюда и из того, что τ_i - моменты остановки, следует утвержде-

ние.

Утверждение 1. Процессы α_X и β_X - прогрессивно измеримы и инте-

)₂

∫_T

∫_T (_α

X (s)

гралы

|α_X (s)| ds,

β2X (s)ds и

ds - конечны с вероятностью

β_X(s)

единица.

Следовательно, существует единственная мартингальная мера, относи-

тельно которой процесс X является мартингалом с плотностью

(

)

√

(17)

Z_T = exp

A_T +

A_T ε

В (17) ε - стандартная нормальная случайная величина. Случайная при-

рода процесса A определяется моментами остановки. Процесс A имеет вид

)₂

∑(μ

(18)

A_t =

(t ∧ τ_i - t ∧ τi-1

σ_i

Относительно мартингальной меры процесс

∑

μ_i

(19)

W_t =

(t ∧ τ_i - t ∧ τi-1) + W_t

σ_i

i=1

является винеровским процессом.

Рассмотрим для данной модели вторую задачу из раздела 2, используя

(17), (18) и (19). Будем считать, что случайная величина ξ = f(X_T ). Причем

функция f такова, что f(x) > 0, Ef (X_T ) < ∞ и Ef (X_T ) < ∞. Относительно

мартингальной меры случайная величина X_T определяется равенством:

√

(20)

X_T = x₀ +

U_T

ε.

∑_∞

В (20) U_t =

σ2i (t ∧ τ_i - t ∧ τi-1). Относительно исходной меры случай-

i=1

ная величина

√

(21)

X_T = x₀ + C_T +

U_T

ε,

∑_∞

где C_t =

μ_i (t ∧ τ_i - t ∧ τi-1). Вычислим математическое ожидание

i=1

Ef (X_T )η (X_T ) по исходной мере. Из (21) следует, что искомое математи-

ческое ожидание вычисляется по формуле

E(f (X_T )ς (X_T )) =

⎛

⎞

∫

∞

(

)

(22)

√

f (x) ς (x) exp

(x - x₀ - C_T)2

dx^⎠ .

2π

U_T

2U_T

-∞

Из (22) получаем, что

P (x) = p(x) dx, где

(

)

E f (x)exp

-12U

(x - x₀ - C_T )²

√

U_T

(23)

(

)

∫

∞

E f (x)ς exp

-12U

(x - x₀ - C_T )²

√

-∞

U_T

Для меры P получаем аналогичный результат:

(

)

E f (x)exp

-2U

(x - x₀)²

√

U_T

(24)

p(x) =

(

)

∫

∞

E f (x)ς (x)exp

-12U

(x - x₀)²

√

-∞

U_T

Из (14), (23) и (24) следует, что оптимальное значение

(25)

ς^∗ (x) = I{˜p(x)-λ∗p(x)>0}+εI{p(x)-λ∗p(x)=0},

где

α - EI{˜p(X

T )-λ^∗p(XT )>0}

ε=

EI{p(XT )-λ^∗p(XT )=0}

Из (25) следует, что случайная величина η^∗ будет функцией от X_T :

(

)

(26)

η^∗

(X_T ) = f (X_T ) I{˜p(X

T )-λ^∗p(XT )>0}+εI{p(XT )-λ^∗p(XT )=0}

Далее, используя (26), рассмотрим вычисление условного математическо-

го ожидания E (η^∗ (X_T ) /F_t) по мартингальной мере. Для этого представим

∫_T

случайную величину X_T следующим образом: X_T = X_t +

σ(s)dW_s. Сле-

довательно, условный закон Law (X_T - X_t/U_T - U_t) = Law

(√U_T - U_tε⁾. Из

измеримости X_t и U_t относительно F_t и выполнения условий регулярности

следует, что условное математическое ожидание является функцией относи-

тельно t, X_t и U_t, т.е.

M (X_t,U_t,t) = E(η^∗ (X_T )/F_t) =

⎛

(

)⎞

∞

∫

(27)

exp

- (x - X_T )² /2 (U_T - U_t)

√

η^∗ (x) E_U

⎝

√

⎠_dx.

T -Ut

2π

U_T - U_t

−∞

Формула (27) существенно упрощается, если разладка затрагивает только

снос процесса X (классический вариант разладки), т.е. σ_i = σ. Соответствую-

щая формула будет иметь вид

⎛

⎞

∞

(

)

∫

(x - X_t)²

(28)

M (X_t, t) =

√

⎝

η^∗ (x) exp

dx^⎠ .

2πσ (T - t)

2σ² (T - t)

−∞

В (28) функция M зависит только от двух аргументов. Далее вычисляем

функцию M (x, t), решая уравнение (5), и вычисляем управление β по фор-

муле (6).

4. Приложение к финансовой математике

Будем рассматривать модель финансового рынка как пары активов: рис-

кового (стоимость акции) S и безрискового (банковский счет) B. Эти активы

представлены своими ценами S (t) и B (t), t ∈ [0, T ] то есть речь идет о (B, S)-

рынке с непрерывным временем.

Активы подчиняются следующим уравнениям:

(29)

dS (t) = S (t) dX (t) , dB (t) = rB (t) dt

c начальными значениями S₀ и B₀. Рассматривается самофинансируе-

мый портфель, капитал которого G(t) удовлетворяет уравнению: dG(t) =

= γ(t)dS(t) + β(t)dB(t). Задача заключается в вычислении

(30)

min (f (S (T )) - G (T ))⁺

γ,β

с учетом (29) при ограничении G₀ ≤ a. В (30) функция f(x) ≥ 0 и огра-

ничена сверху. Сведем задачу (30) к решенной задаче (11), для этого

рассмотрим дисконтированный процесс S (t) =S(t)B(t) , дифференциал которо-

го dS (t) = S (t) ((α_X (t) - r) dt + β_X (t) dW_t). При этом дифференциал дис-

(

)

контированного капитала dG (t) = dG(t)B(t) = γ (t) dS (t). Определим f

S (T)

(

)

S (T ) B (T )

/B (T ), что позволяет рассмотреть эквивалентную и бо-

(

)

)₊

лее простую задачу: min_γ E

S_T

- G(T)

при ограничениях G₀ ≤^a и_B

∫t

G(t) = G₀ +

γ (s) dS (s), которая совпадает с задачей (11), если положить

X (t) = S (t) и Y (t) = G (t). Далее, не нарушая общности, будем считать, что

r = 0.

Для случая, когда разладка затрагивает только снос, а β_X (t) = σ яв-

ляется константой, решениями первого уравнения из (11) являются S (t) =

(

)

(

)

= S0 exp

C (t) - σW_t

и S (t) = S0 exp

-σ2

+ σW_t для исходной меры и

мартингальной меры соответственно. Процесс C (t) = C (t) -σ22t.

5. Пример. “Модель с двумя барьерами и

двумя моментами остановки”

Модель была представлена на московском симпозиуме “Advanced Finance

and Stochastics” [8]. Данная модель поведения стоимости рискового актива

возникает в ситуации, когда “регулятор” желает удержать стоимость в пре-

делах заданного коридора, причем тренд цены в начальный момент времени -

возрастающая функция. На рассматриваемом отрезке [0, T ] регулятор при-

нимает участие в торгах не более двух раз. Первый раз он продает актив,

когда актив достигает верхнего уровня, с целью получить убывающий тренд.

Во второй раз регулятор покупает актив с целью получить возрастающий

тренд, когда цена достигает нижнего уровня.

Таким образом, необходимо рассмотреть векторный момент останов-

ки (τ₁, τ₂), в котором τ_! = inf (t ∈ [0, T ] : S (t) = M₁), где M₁ > S₀ и τ₂ =

= inf (t ∈ (τ₁, T ] : S (t) = M₂), где M₂ < S₀. Определим снос

(

)

(

)

(

)

σ²

C(t) = μ₁ -

(t ∧ τ₁) + μ₂ -

(t ∧ τ₂ - t ∧ τ₁) + μ₃ -

(t - t ∧ τ₂).

< 0,

μ₃ -σ22>0.Найдемплотностьp(x,y)распределения{длявекторногомомен}

остановки (τ₁, τ₂), определенной на множестве D =

(x, y) ∈ R² : 0 ≤ x ≤ y

используя равенство для плотности: p (x, y) = p (y/x) · p (x). Для определения

плотности закона распределения первого момента остановки - p(x) восполь-

(

)

зуемся тем, что τ₁ = inf

t:m₁t+σW_t=M₁

, где m₁ = μ₁ -σ22иM1^=ln

S₀

Для определения плотности p (y/x) условного закона распределения восполь-

зуемся строго марковским свойством винеровского процесса. В соответствии

с этим свойством условное поведение второго момента остановки определяет-

(

)

ся равенством τ₂ = x + inf

t:m₂t+σW_t=M₂

, где m₂ = σ22^-μ2 ^иM2 = ln M1 .₂

Пусть p(m, M, x) - плотность закона распределения момента остановки τ =

= inf(t : mt + σW_t = M), определенная на множестве R⁺ = {x ∈ R : x > 0}.

Параметры плотности m и M

- п(ложитель))е числа. Плотность

(

(_mM )

p(m, M, x) =√

exp

-¹

m²x+M2

, см. [4, с. 265]. Плот-

2π

σ²

x3/2

2σ²

ность совместного закона распределения выражается через плотность

(

)

(

)

p(m, M, x) следующим образом: p (x, y) = p

m₁,M₁,x

m₂,M₂,y - x

. Яв-

ный вид плотности совместного закона распределения позволяет без особого

труда вычислить функцию ς^∗ (x) и решить задачу квантильного хеджирова-

ния для модели с двумя барьерами.

5.1. Вычислительный эксперимент

Функция f (x) = (x - K)⁺. Для расчета выбраны следующие исходные

данные: μ_! = 0,1; μ₂ = -0,1(μ3 = 0,1; σ = 0,05; S0 = K = 6; M)= 7; M2 = 5;

∫

∞

α = 0,35. Функция F (λ) =

- непрерыв-

-∞

p (s) I{˜p(s)-λ∗p(s)>0}(s)ds-α

ная функция, поэтому ε = 0 в (25).

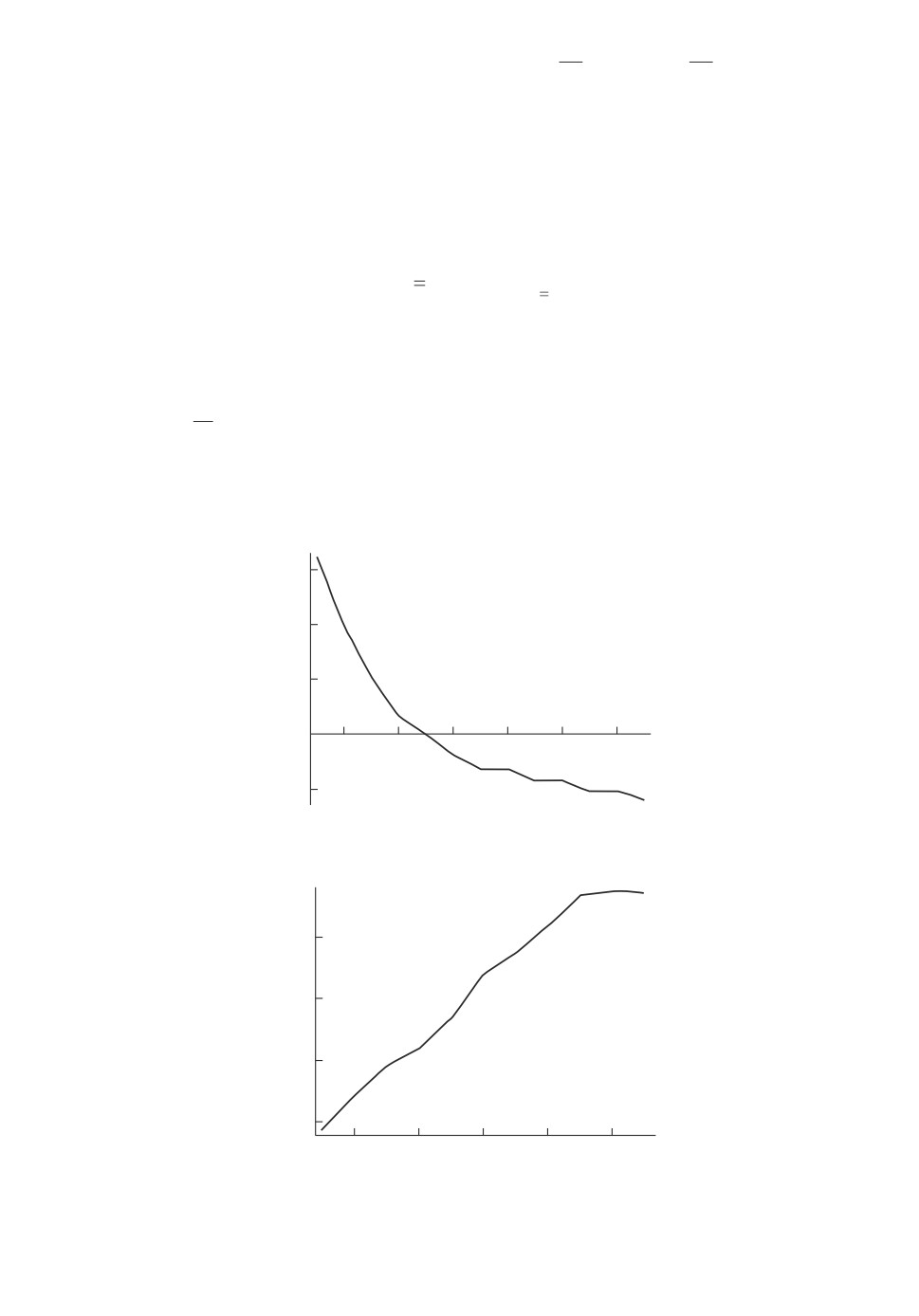
На рис. 1 приведен график F (λ) для значений λ ∈ [0,3; 1,5].

Решение уравнения F (λ) = 0 - λ = 0,7.

Далее √ расчетах использована радемахеровская аппроксимация ΔSn =

=Sn-1σ/

Nδ_n, P (δ_n = 1) = P (δ_n = -1) = 1/2.

Результаты вычислений приведены на рис. 2 и в таблице. При N = 10 и

N = 11 вычисленные значения α совпадают и равны 0,3496. Для N = 10 и

случайной траектории рассчитан портфель, который приведен в таблице.

0,6

0,4

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,2

Рис. 1. График F (λ) для значений λ ∈ [0,3; 1,5].

0,348

0,346

0,344

0,342

Рис. 2. График зависимости вычисленного α от значений N (N = 3, . . . , 11)

(точное значение α = 0,35).

Расчет портфеля

Произвольно

Значения S_n

Значения Y_n

Значения γ_n

Значения β_n

в атомах

n выбранный

путь на дереве

выбранного

(значения ε_n)

пути

0,07966675650

0,4297220522

-2,498665556

6,094868328

0,1204337691

0,5907306195

-3,479991574

6,191236656

0,1773614912

0,7757321767

-4,625379997

-1

6,093344609

0,1014234805

0,5837691069

-3,455682860

-1

5,997000371

0,04518069073

0,3500031905

-2,053788572

-1

5,902179469

0,01199307250

0,1285132911

-0,7465154357

-1

5,808857818

-1

5,717011711

5,807405601

5,899228744

-1

5,805953748

Для радемахеровской аппроксимации является справедливым равенство



E (ΔY_nΔS_n/Fn-1)

ΔY_n



γ_n =

(

) =



ΔS_n

E (ΔS_n)² /Fn-1

δn=1

δn=-1

Вторая составляющая портфеля β_n = Yn-1 - γ_nSn-1.

6. Заключение

Рассмотрена модель с векторной разладкой, для которой предложен алго-

ритм решения широкого класса задач стохастического оптимального управ-

ления. В качестве примера решена задача квантильного хеджирования для

модели с коридором. Приведены результаты применения алгоритма. Даль-

нейшие исследования будут направлены на получение приемлемого вычис-

лительного алгоритма для решения рассмотренных задач стохастического

оптимального управления для других моментов остановки. При этом пред-

полагается аппроксимация винеровкого процесса с использованием принципа

Донскера-Прохорова.

СПИСОК ЛИТЕРАТУРЫ

1. Shiryaev A. Quickest Detection Problems in the Technical Analysis of the Financial

Data / Mathematical finance. Ed. H. Geman, D. Madan, S. Pliska, T. Vorst. Springer,

2000. P. 487-521.

2. Gapeev P.V., Peskir G. The Wiener Disorder Problem With Finite Horizon Stoch //

Proc. Appl. 2006. V. 116. No. 12. P. 1770-1791.

3. Truonga C., Oudrec L., Vayatisa N. A review of change point detection methods //

arXiv:1801.00718v1 [cs.CE] 2 Jan 2018.

4. Ширяев А.Н. Основы стохастической финансовой математики. М.: Фазис, 1998.

5. Фельмер Г., Шид А. Стохастические финансы. М.: МЦНМО, 2008.