Автоматика и телемеханика, № 8, 2019

Интеллектуальные системы управления,

анализ данных

(Научно-конструкторское бюро робототехники и систем управления, Таганрог)

ОБ ОЦЕНКЕ СЛОЖНОСТИ СЦЕНЫ ПО ОДНОМУ

И ДВУМ ЛОКАЛЬНЫМ НАБЛЮДЕНИЯМ¹

Рассматривается задача формальной оценки сложности сцены с много-

численными препятствиями, на которой перемещаются подвижные объ-

екты. Предполагается, что имеется лишь ограниченная информация о

расположении препятствий в небольшой части сцены, получаемая сенсор-

ными системами одного или нескольких объектов. Доказываются верхние

и нижние оценки сложности сцены при одном и двух наблюдениях ло-

кальных областей.

Ключевые слова: подвижный объект, сцена, триангуляция, локальная

сложность, интегральная сложность, оценка сложности.

DOI: 10.1134/S0005231019080105

1. Введение

В настоящее время активно изучаются и разрабатываются методы управ-

ления поведением автономных подвижных объектов в сложных средах с боль-

шим количеством разнородных препятствий [1, 2]. Экспериментально уста-

новлено [3], что выбор стратегий для планирования движения объектов су-

щественно зависит от интуитивно понимаемой сложности среды функциони-

рования. В простых средах можно использовать классические методы плани-

рования. Описание ряда таких методов, основанных на решении задач управ-

ления подвижным объектом по его полной модели по уравнениям динамики и

кинематики и по уравнениям кинематики, можно найти, например, в [4]. Од-

нако в сложных средах эффективными оказываются методы, основанные на

интеллектуальных технологиях, а также комплексное использование разных

методов. Понятие сложности среды на сегодняшний день во многом является

интуитивным, что не позволяет формализовать процедуру выбора того или

иного подхода к планированию движения объектов. В связи с этим необхо-

димо иметь количественно измеримый показатель, характеризующий слож-

ность среды функционирования подвижного объекта, позволяющий обосно-

ванно выбирать наиболее подходящий метод планирования.

В ряде публикаций, например, [5-8] рассматриваются подходы к опреде-

лению сложности сцен с точки зрения визуальной видимости образующих ее

поверхностей, даются оценки сложности полигональных сцен, вводится по-

нятие сложности видимой части трехмерной сцены в зависимости от точки

¹ Работа была выполнена при поддержке Российского научного фонда (грант № 18-19-

00621).

129

наблюдения и разрабатываются методы оценки видимой сложности сцены

при анимации. Однако эти методы порождены задачами машинной графи-

ки и имеют слабое отношение к оценке сложности, которая содержательно

характеризует особенности перемещения в среде подвижных объектов.

В [9] рассмотрена задача формального определения сложности среды

функционирования подвижного объекта, перемещающегося на плоскости. На

основе физически интерпретируемой величины, характеризующей возмож-

ность прохождения среды с препятствиями, построена нормированная ло-

кальная мера сложности в секторе обзора системы технического зрения, за-

висящая от расположения цели, к которой должно осуществляться движение.

Введена интегральная мера сложности сцены, не зависящая от положения

цели, но характеризующая сложность среды при фиксированном положении

подвижного объекта. Представляется, что описанный в [9] подход в доста-

точной степени соответствует физическому смыслу интуитивно понимаемой

сложности среды, в которой происходит выполнение задач автономными по-

движными объектами.

С содержательной точки зрения данная статья посвящена оценке сложно-

сти плоской среды (сцены) на основе данных систем технического зрения со-

вокупности автономных объектов. Неформальная постановка задачи состоит

в следующем. Подвижные объекты независимо перемещаются на плоской по-

верхности, выполняя стоящие перед ними задачи. Объекты обладают сенсор-

ной системой, позволяющей наблюдать некоторый участок сцены; с помощью

специального алгоритма каждый объект может вычислить сложность этого

участка в смысле безопасной проходимости (при наличии препятствий) меж-

ду любыми двумя точками наблюдаемого участка. По совокупности таких

локальных сложностей необходимо провести обоснованные оценки априори

неизвестной сложности всей сцены. Другими словами, возникает задача уточ-

нять сведения о сложности сцены непосредственно в процессе функциониро-

вания группы объектов с помощью средств, имеющихся на борту каждого из

объектов.

Способ вычисления сложности наблюдаемого участка был описан ранее

в [9] и кратко излагается далее. В общем случае сложность можно рассмат-

ривать как функцию множества, определенную на всех возможных подмно-

жествах сцены. Свойства такой функции во многом зависят от ее конкретного

определения. В данной статье сложность интерпретируется как степень сво-

боды, с которой объект может попасть в произвольную целевую точку сцены.

Проходимость при наличии препятствий — нелокальное свойство, что за-

трудняет анализ и построение вычислительно эффективных методов расчета.

Это можно пояснить следующими рассуждениями. Если имеется некоторая

область на сцене, то ее интегральную проходимость нельзя точно вычислить

лишь на основе анализа картины препятствий внутри этой области. Действи-

тельно, может существовать большое количество возможных путей частично

или полностью проходящих за пределами анализируемой области, которые

не будут приняты во внимание. Поэтому для точного вычисления проходи-

мости области необходимо иметь информацию обо всей сцене и проводить

вычисления, учитывая полную картину препятствий.

130

Статья организована следующим образом. В разделе 2 приводятся основ-

ные предположения и допущения, которые используются в данной статье.

В разделе 3 вводится триангуляция Делоне сцены, строится взвешенный то-

пологический граф триангуляции, дается конструктивное определение прохо-

димости на сцене и приводится описание матричной процедуры вычисления

проходимостей. В разделе 4 определяются понятия локальной сложности и

сложностной меры для случая триангулированной сцены. В разделах 5 и 6

доказываются верхние и нижние оценки сложности сцены по известным оцен-

кам сложности локальной области при одном и при двух наблюдениях.

2. Основные предположения и допущения

Будем считать, что сцена S является связной, ограниченной и выпуклой

областью. Предположим также, что на сцене находится конечное количе-

ство препятствий и несколько (в частности, один) подвижных объектов. Все

препятствия и объекты представляют собой круги с известными радиусами.

Если препятствие не является кругом, то будем считать, что оно замеща-

ется минимальным кругом, содержащим это препятствие внутри. Поэтому

размеры препятствий и объекта характеризуются одним числом - радиусом

представляющего их круга. Количество, размеры и положение препятствий

на сцене заранее неизвестны планирующей системе объектов. Будем пред-

полагать также, что размеры препятствий достаточно малы в сравнении с

размерами сцены.

Наблюдаемая каждым подвижным объектом часть сцены тоже является

связной и выпуклой областью. Несмотря на то, что в дальнейшем никаких

особых условий на форму наблюдаемой области не накладывается, можно

для конкретности считать, что она представляет собой некоторый сектор, что

согласуется с современными методами сканирования, например с помощью

лазерных устройств. Представленные далее иллюстрации отражают именно

такое понимание формы наблюдаемой области. Особо подчеркнем, что про-

странство за пределами наблюдаемой объектом области считается полностью

ему неизвестным.

Будем предполагать, что все объекты в значительной степени автономны

и могут обмениваться лишь незначительным объемом информации — коор-

динатами своего положения на сцене и точными сведениями о границах на-

блюдаемой области. Вместе с тем каждый из них имеет полную информацию

о своей зоне наблюдения, в частности о положении всех препятствий и их

геометрических характеристиках.

3. Триангуляция сцены. Топологический граф. Матрица проходимостей

Предположим, что известно положение всех препятствий на сцене. Рас-

смотрим триангуляцию Делоне [10], взяв в качестве точек (узлов) триангу-

ляции центры препятствий. В результате получим разбиение области, лежа-

щей внутри выпуклой оболочки центров препятствий. Триангуляция Делоне

и двойственная к ней диаграмма Вороного многократно использовались и

показали свою эффективность при планировании путей перемещения дви-

жущихся объектов [11-16].

131

Область внутри каждого треугольника, построенного в результате триан-

гуляции, для краткости будем называть треугольником Делоне или просто

треугольником. При этом важно, чтобы триангулированной оказалась вся

сцена, включая области, примыкающие к границе сцены. Один из способов

как это можно сделать, основанный на введении так называемых виртуаль-

ных препятствий, описан в [9].

Пусть s_ПО - точка, задающая текущее положение подвижного объекта на

сцене, а s_Ц - положение цели, в которую должен попасть объект. Тогда любой

путь из s_ПО в s_Ц будет пересекать некоторую последовательность треуголь-

ников Делоне. Введем топологический граф G = (X, U), в котором множество

вершин X соответствует множеству треугольников, а множество ребер U -

границам ненулевой длины, соединяющим треугольники. Из этого определе-

ния следует, что граф имеет петли при каждой вершине, поскольку каждый

треугольник пересекается сам с собой, следовательно, и со своими граница-

ми. В результате s_ПО и s_Ц будут отождествлены с некоторыми вершинами

x_ПО и x_Ц , а соответствующий путь будет соответствовать некоторому пути

на графе.

Движение вдоль каждого ребра в этом пути имеет ограничение, которое

обусловливает возможность физического прохождения объекта между пре-

пятствиями. Это ограничение можно определить следующим образом. Рас-

смотрим два треугольника в триангуляции Делоне, которые соответствуют

смежным вершинам x_i и x_j графа G = (X, U). Поскольку вершины смежные,

то по определению соответствующие треугольники имеют общую границу

ненулевой длины, которая соединяет центры двух препятствий. Предполо-

жим, что положения этих препятствий задаются векторами координат своих

центров, например, Π(1)ij и Π(2)ij.

Если эти препятствия имеют радиусы r_i и r_j , то для подвижного объекта

радиуса ρ условие проходимости имеет вид:



d(x_i,x_j) =

Π⁽

-Π(2)ij

- r_i - r_j - 2ρ ≥ 0,

где ∥∗∥₂ - эвклидово расстояние. Другими словами, свободное расстояние

между препятствиями должно быть больше, чем диаметр подвижного объек-

та. Если же объект и целевая точка окажутся в одном и том же треугольнике

Делоне, т.е. они окажутся отождествленными с одной и той же вершиной гра-

фа, то проходимость объекта к цели ничем не ограничена, и поэтому будем

считать ее символически равной бесконечности. Указанные условия можно

описать с помощью функции на ребрах графа w(u) = w ((x_i, y_i)) = w(u_ij ) =

=w_ij:

^{ d(x_i,x_j)H [d(x_i,x_j)], если i = j,

w_ij =

∞,

если i = j,

где H(∗) - функция Хевисайда. Таким образом, G = (X, U, w), |X| = N, -

взвешенный граф триангуляции Делоне. Значение w_ij будем называть шири-

ной ребра.

132

Пусть P_i = xi1 xi2 . . . xil+1 - некоторый путь на графе G из x_ПО в x_Ц дли-

ны l, т.е. xi1 = x_ПО, xil+1 = x_Ц . Шириной пути будем называть величину

w (P_i) = mink∈{1,...,l} w(uik,ik+1), где ui_k,ik+1 - ребро, соединяющее вершины xi_k

и xik+1. Другими словами, ширина пути равна наименьшей ширине среди всех

ребер, образующих этот путь. Пусть теперь P = {P₁, P₂, . . . , P_L} - множество

путей, соединяющих x_ПО и x_Ц. Тогда под проходимостью к цели будем по-

нимать максимальную ширину среди всех путей

κxПО→x_Ц = max w (Pi) .

i∈{1,...,L}

Существует простая матричная процедура для вычисления проходимости

κxПО→x_Ц. Рассмотрим матрицу смежности R = (rij)Ni,j=1 графа G = (X,U,w),

где

^{ w(u_ij), если x_i и x_j смежные,

r_ij =

в противном случае.

Матрица R имеет размеры N × N, симметрична и отражает не только смеж-

ность вершин, но и определенную на ребрах графа функцию w(u).

Определим максимин(ую)омпозицию R[2] = R ◦ R матрицы R с собой по

(2)

правилу: R^[2] = R ◦ R = r⁽²⁾

, где r_i

= maxk∈{1,...,N} (min (r_ik,r_kj)). Нетруд-

но понять, что r(2)ij равно максимальной ширине среди ширин всех пу-

тей длины 2, соединяющих вершины x_i и x_j . В частности, это означает,

что существует по крайней мере один максимально “безопасный” путь дли-

ны 2 из x_i в x_j , ширина которого равна r(2)ij. Далее индуктивно определя-

(

)

(

)

(n+1)

ем: R^[3] = R^[2] ◦ R = r⁽³⁾

,...,R[n+1] =R[n]

◦R= r_i

,... Значение r(n)ij

равно максимальной ширине среди ширин всех путей длины n, соединяющих

вершины x_i и x_j. Заметим, что для любых i и j все пути из x_i в x_j распада-

ются на непересекающиеся классы путей топологической длины 1, 2, . . . При

этом некоторые из этих классов могут быть пустыми. Поэтому поиск шири-

ны наиболее безопасного пути сводится к выбору наиболее безопасного пути

среди наиболее безопасных путей в каждом классе, т.е. maxk∈{1,2,...} r(k)ij.

Важно подчеркнуть, что, учитывая рефлексивность отношения, задавае-

мого графом G, для всех возможных i и j всегда будут выполняться неравен-

ства r(1)ij ≤ r(2)ij ≤ . . . ≤ r(N-1)ij. Поэтому если, например, x_ПО = x_i, а x_Ц = x_j,

(

. Ввиду этого матрица K = R[N-1] = r(N-1)

то κxПО→x_Ц = κij = r

i,j=1

= (κ_ij )Ni,j=1 содержит ширины наиболее безопасных путей между любой парой

вершин на графе G. Матрицу K будем называть матрицей проходимостей.

Для удобства записи будем обозначать операцию выбора максимума сим-

волом ∨, т.е. a ∨ b = max {a, b}; этот же символ будем использовать и для мат-

ричной поэлементной операции выбора максимальных элементов, т.е. если

A₁ и A₂ - две матрицы одинаковых размеров, то A₁ ∨ A₂ обозначает матрицу

того же размера, каждый элемент которой равен максимальному элементу

среди соответствующих элементов матриц A₁ и A₂.

133

Свойства матриц с операциями ◦ и ∨ аналогичны свойствам обычных мат-

ричных операций [17], но при этом роль единичной матрицы размеров n × n

играет матрица In∞) = diag (∞, ∞, . . . , ∞). Для двух матриц A и B одного

размера будем использовать обозначение A≤B, если элементы в A не пре-

восходят соответствующих элементов в B. Другими словами, символ

≤ уста-

навливает поэлементное отношение на матрицах. Аналогично определяется

отношение A≥B.

4. Мера локальной сложности и сложностная мера

Характеристика сцены в терминах проходимости между любыми двумя

точками неудобна, поскольку она, с одной стороны, выражается в абсолют-

ных единицах расстояния, т.е. зависит от выбранного масштаба измерений,

а с другой - не является нормированной. В [9] предлагается и обосновыва-

ется выражение для меры локальной сложности, связанное с вычисляемы-

ми проходимостями κ_ij и в то же время лишенное указанных недостатков.

Локальной мерой сложности прохождения из s_i в s_j будем называть функ-

цию δ(s_i, s_j) = e-ακij , где κ_ij - проходимость из вершины x_i, соответствую-

щей треугольнику, содержащему точку s_i, в вершину x_j , соответствующую

треугольнику, содержащему точку s_j, α - неотрицательный параметр, воз-

можный способ вычисления которого также описан в [9].

Обозначим через Ξ = {T₁, T₂, . . . , T_N } множество треугольников Делоне,

которые получены в результате триангуляции. Будем обозначать через σ (T_i)

меру (площадь) треугольника T_i, через σ (B) - меру области B = T_i ∪ T_j ∪ . . .,

составленной из нескольких треугольников. Если треугольникам T₁ и T₂ со-

ответствуют вершины x₁ и x₂ в топологическом графе, то это означает, что

локальная мера сложности перемещения из любой точки s₁ ∈ T₁ в любую точ-

ку s₂ ∈ T₂ будет равна δ(s₁, s₂) = e-ακ12 , т.е. функция постоянна на T₁ × T₂.

Тогда если B₁, B₂ ⊆ Ξ, т.е. B₁ и B₂ - некоторые подмножества, составленные

из треугольников Делоне, то сложностная мера перемещения объекта из B₁

в B₂ определяется формулой

∫

δ (B₁, B₂) =

δ(s₁, s₂)ds₁ds₂ =

σ²(S)

B₁ B₂

∫

∑

e^-ακ

ds₁ds₂ =

σ²(S)

T_i ∈B₁ T_j ∈B

T_i T_j

∑

e-ακij σ (T_i)σ (T_j),

σ²(S)

T_i ∈B₁ T_j ∈B₂

где σ (S) - площадь сцены, а сложность - формулой

σ²(S)

Δ (B₁, B₂) =

δ (B₁, B₂) .

σ(B₁)σ(B₂)

134

В частности, если B₁ = B₂ = Ξ, т.е. рассматривается мера на всей сцене, то

∑

δ (S) = δ (Ξ) = δ (Ξ,Ξ) =

e-ακij σ (T_i) σ (T_j) .

σ² (S)

T_i ∈Ξ T_j ∈Ξ

Данное выражение для сложностной меры можно интерпретировать как ма-

тематическое ожидание локальной меры сложности всей сцены. В этом слу-

чае значение сложностной меры совпадает со значением сложности.

Выражение для сложностной меры всей сцены удобно записать в матрич-

ной форме. Для этого введем обозначения

)_T

⁽σ (T₁) σ (T₂)

σ (T_N )

σ=

σ(S) σ(S)

σ(S)

где T обозначает транспонирование, и e-αK = (e-ακij )Ni,j=1. Тогда

δ (S) = σ^Te-αKσ.

Сделаем замечание относительно используемых обозначений. Поскольку

множество треугольников и множество вершин графа находятся во взаимно

однозначном соответствии, то удобно записывать меру множества B ⊆ Ξ как

функцию от множества вершин графа G, соответствующих подмножествам

в B. Другими словами, если B = {T₁,T₂,... ,T_m} - некоторое подмножество

треугольников в разбиении Делоне, а^X = {x₁, x₂, . . . , x_m} - соответствующие

этим треугольникам вершины топологического графа, то будем считать, что

σ(^X) = σ (B).

5. Оценка сложности сцены по одному наблюдению

Выражение для сложности сцены получено в предположении, что имеется

вся необходимая информация о ней, а именно форма и размеры сцены, а

также положение и радиусы всех препятствий. Задача состоит в том, чтобы

получить оценку сложности по отдельным наблюдениям, осуществляемым

группой объектов, когда о самой сцене априори неизвестно ничего, кроме ее

размеров и формы.

Рассмотрим сначала случай, когда имеется одно наблюдение. Наблюдае-

мую область будем называть зоной обзора и обозначать S₁. Предполагаем,

что эта область выпуклая. В зону обзора в общем случае попадает некото-

рое количество препятствий - Π₁, Π₂, . . . , Π_k. Предположим, что произведена

триангуляция Делоне по центрам этих препятствий. Заметим, что требова-

ние выпуклости зоны обзора гарантирует, что триангулированная область

полностью лежит внутри нее. Необходимо сделать два замечания.

1. Полученная триангуляция, рассматриваемая как граф, в общем слу-

чае не будет совпадать с подграфом триангуляции Делоне всей сцены, по-

рожденным этими же препятствиями Π₁, Π₂, . . . , Π_k. Это объясняется тем,

что результат триангуляции наблюдаемых препятствий на всей сцене зави-

сит также от расположения близких препятствий, не попавших в зону обзора

подвижного объекта (например, подобный случай иллюстрируется на рис. 1).

135

ПО

Рис. 1. На среднем рисунке отсутствует ребро (1, 2), а на правом -

оно снова есть.

Поскольку информации о расположении препятствий за пределами зо-

ны обзора нет, то учесть это обстоятельство не представляется возможным.

Можно лишь утверждать, что если препятствия вне зоны обзора находятся

достаточно далеко от наблюдаемой области, то в этом случае триангуляция

наблюдаемых вершин совпадет с соответствующим подграфом на триангу-

ляции всей сцены. По этой причине сложности, вычисленные по графу G₁

триангуляции зоны обзора и подграфу

G₁ триангуляции всей сцены, соот-

ветствующему зоне обзора, вообще говоря, не будут равны. Учет этого раз-

личия и даже обоснование тенденции изменения сложности представляется

трудной задачей. Действительно, с одной стороны, появление в графе G₁ до-

полнительных вершин и ребер увеличивает количество возможных путей, а,

следовательно, может приводить к уменьшению сложности, а с другой - до-

полнительные вершины и ребра увеличивают размер матрицы проходимостей

и, значит, могут приводить к увеличению сложностной меры. Тем не менее

поскольку различия этих графов выражаются лишь в появлении некоторых

граничных вершин, можно предполагать, что отличия в оценке сложности

будут относительно невелики. Поэтому, допуская некоторую неточность, бу-

дем считать, что графы G₁ иG1 структурно изоморфны и имеют одинаковые

ширины соответствующих ребер.

2. Второе замечание относится к области зоны обзора, лежащей вне вы-

пуклой оболочки триангуляции Делоне. Поскольку в данной постановке ре-

шается задача оценки сложности всей сцены по отдельным наблюдениям, а

не планирование маршрута подвижного объекта, то будем игнорировать об-

ласть внутри зоны обзора, лежащую за границами триангуляции.

Если окажется, что количество препятствий, попавших в зону обзора, не

превосходит трех, то сложность данной области будет равна нулю. В этом

случае треугольников либо нет (одно или два препятствия, либо препятствий

нет), либо он один (три препятствия). В последнем случае граф состоит из

одной вершины, следовательно, нетривиальных путей на нем нет. Поэтому

будем считать, что количество препятствий в зоне обзора больше трех, т.е.

k ≥ 4.

Не теряя общности, предполагаем, что на графе всей сцены вершины за-

нумерованы так, что треугольники, попавшие в зону обзора, занумерованы

первыми и в одинаковом порядке. Рассмотрим матрицу смежности графа сце-

ны. Учитывая предположение о нумерации, ее можно представить в блочном

136

виде:

)

⁽ R11 R12

R₂₁

R₂₂

где R₁₁ - матрица смежности подграфа G₁ = (X₁, U₁), соответствующего тре-

угольникам, попавшим в зону обзора.

Будем считать, что число вершин, не попавших в зону обзора, не меньше

трех. Это значит, что размеры подматрицы R₂₂ не меньше 3×3. По индукции

нетрудно доказать следующее утверждение.

Утверждение 1. Для любого k = 1,2,... матрица R[k] может быть

записана в виде

⎛

⎞

[k]

R₁

∨Z(k)11

Z(k)12

R[k] = ⎝

⎠_,

Z(k)21

Z(k)

где Z(k)ij, i = 1, 2, - некоторые неотрицательные матрицы.

В соответствии с матричной процедурой построения проходимостей имеем:

⎛

⎞

[N-1]

R₁

∨Z(N-1)11 Z(N-1)12

⎠_.

K=R[N-1] =⎝

Z(N-1)21

Z(N-1)

Если N₁ - количество вершин в подграфе G₁ = (X₁, U₁) из зоны обзора, т.е.

|X₁| = N₁, то R[N-1]11 = R[N1-^1]11 = KG1 - матрица проходимости для этого под-

графа. Пусть вектор σ также представлен в блочном виде σ = (σ₁σ₂)^T, соот-

ветствующем разбиению на блоки матрицы R. Тогда выражение для слож-

ностной меры принимает вид

(

)

(N-1)

Δ (S) = σ^Te-αKσ = σ^T1

e-αKG1 ∨Z11

σ₁ + σ^T1e-αZ12-1) σ₂ +

(N-1)

N -1)

+ σT2 e^-αZ21 σ₁ + σT2 e-αZ2

σ₂.

(

(N-1)

⁾ .

Поскольку KG1 ∨Z(N-1)11

≥ KG1, то e-αKG1∨Z11

≤e-αKG1 и, следовательно,

получается неравенство

(N-1)

N -1)

Δ (S) ≤ σ^T1e-αKG1 σ₁ + σ^T1e^-αZ12 σ₂ + σ^T2e-αZ2

σ₁ + σ^T2e-αZ22-1) σ₂.

Здесь и иногда далее будем обозначать через J_mn матрицу размеров m × n,

состоящую из единиц. В частности, J1n и Jm1 - матрица-строка и матрица-

столбец соответственно. В тех случаях, когда размеры матрицы J понятны

из контекста, будем опускать индексы.

Поскольку сумма компонент вектора σ равна единице, то J1N σσ^TJN1 =

= σ^TJN1J1Nσ = σ^TJ_NNσ = 1. Представим J_NN в блочном виде:

(

)

N₁N₁

JN1,N-N₁

J_NN =

JN-N1,N₁

JN-N1,N-N₁

137

Тогда

σ^TJ_NN σ = σ^T1JN1N₁ σ1 +σ¹JN₁,N-N₁σ2 +σ²JN-N₁,N₁σ1 +σ²JN-N₁,N-N₁σ2 = 1.

Заметим теперь, что

σ^T1JN1N₁ σ1 = σ² (X1) - мера зоны обзора,

σ^T1JN1,N-N₁σ2 = σ²JN-N₁,N₁ σ1 = σ (X1)σ (X2) - мера области X1 × X2,

наконец,

σ^T2JN-N1,N-N₁σ2 = σ² (X2) - мера внешней области сцены по отношению

к зоне обзора.

∕

Обозначим для удобства σ² (X₁)

σ² (X) = λ. Тогда

(N-1)

N -1)

σ^T1e-αKG1 σ₁

σ^T1e^-αZ12 σ₂ +σ^T2e-αZ2

σ₁ +σ^T2e-αZ22-1)σ₂

Δ(S) = λ

+ (1 - λ)

1-λ

Ноσ1e-αKG1 σ¹λ - это по определению сложность Δ (S1) области, наблюдаемой

в зоне обзора. Таким образом,

(1)

Δ(S) ≤ λΔ(S₁) + (1 - λ)η (S\S₁

Здесь η (S\S₁) - выражение сложностной меры остальных возможных пу-

тей перемещения объекта на сцене S за пределами наблюдаемой области S₁.

С содержательной точки зрения возникновение неравенства в последнем вы-

ражении связано с необходимостью отбросить все возможные пути, ведущие

из S₁ в S₁, но частично или полностью проходящие за пределами зоны обзо-

ра, так как информация о таких путях полностью отсутствует. Из-за этого

значение η (S\S₁), в принципе, может быть любым. Теоретически это поз-

воляет рассмотреть предельные случаи заполнения внешней области S\S₁

препятствиями и на основании этого получить верхние и нижние границы

возможных значений сложности сцены.

Оценим сверху η (S\S₁). Для этого предположим, что препятствий за пре-

делами зоны обзора много и они расположены настолько близко, что про-

ходимость между ними равна нулю. Тогда, как непосредственно следует из

формулы, задающей значения функции w_ij на ребрах топологического графа,

граф, построенный по триангуляции в области S\S₁, имеет матрицу смежно-

сти I(∞) соответствующего размера. Далее потребуется следующее утверж-

дение.

Утверждение 2. Пусть(атрица см)жности графа G сцены S с чис-

R₁₁

R₁₂

лом вершин N имеет вид R =

, где R₁₁ - матрица смежности

R₂₁

I(∞)

графа G₁ с числом вершин N₁, при этом N ≥ N₁ + 2. Тогда матрица прохо-

димостей графа G удовлетворяет неравенству

(

)

KG1

KG1 ◦ R₁₂

≥

R₂₁ ◦ KG1 R₂₁ ◦ KG1 ◦ R₁₂

где KG1 - матрица проходимостей графа G₁.

138

Внутренние вершины

области S\S₁

Внутренние вершины

области S₁

Ребра

разреза

Внешние

граничные

Зона

вершины

обзора

Внутренние

ПО

граничные вершины

Рис. 2. Внутренние и граничные вершины и ребра разреза.

Вершины, соответствующие треугольникам из зоны обзора, которые не

имеют ненулевой границы с внешними треугольниками, будем называть

внутренними, а вершины, которые соответствуют треугольникам, имеющим

общее ребро, - внутренними граничными. Обозначим эти множества Xint1

и X^Γ1 соответственно. Треугольники и соответствующие вершины графа из

внешней области, не имеющие общего ребра с треугольниками из зоны обзо-

ра, тоже будем называть внутренними, а имеющие такие ребра - внешними

граничными (рис. 2). Таким образом, вершины распадаются на непересекаю-

щиеся классы: X₁ = Xint1 ∪ X^Γ1 и X\X₁ = (X\X₁)^int ∪ (X\X₁)^Γ. Ребра топо-

логического графа, соединяющие внешние и внутренние граничные вершины,

образуют разрез графа G [18].

Утверждение 3. При одном наблюдении справедлива следующая верх-

няя оценка сложности сцены:

[

(

)

(

)]

Δ (S) ≤ λΔ (S₁)+ e-αμ

σ²

(X\X₁)int

- σ2 (X₁)

+1-σ²

(X\X₁)int

{

}

где

σ = 1 - σ и μ = min

min K1G1 , min R¹¹²

, K¹

- матрица смежности

G₁

внутренних граничных вершин графа G₁, R¹¹² - подматрица смежности

внутренних и внешних граничных вершин.

Следующее утверждение дает нижнюю оценку сложности.

Утверждение 4. При одном наблюдении справедлива нижняя оценка

сложности сцены: Δ (S) ≥ σ^T1e^-α(KG1^∨νJ)σ₁ + 2e^-αν σ (X₁) σ (X\X₁), где ν =

= max{Ширины ребер разреза}.

139

6. Оценка сложности сцены по двум наблюдениям

Рассмотрим снова задачу оценки сложности всей сцены, но при условии,

что имеются два наблюдения, т.е. две зоны обзора S₁, S₂ ⊆ S. Для общности

будем предполагать, что они пересекаются. Предполагаем также, что извест-

ны границы области пересечения двух зон обзора, следовательно, известны

и препятствия, лежащие в этой области, т.е. “видимые” одновременно двумя

подвижными объектами.

Заметим, что если два наблюдения получены разными объектами, то вы-

числяемые ими сложности зон обзора нельзя использовать в общих вычис-

лениях без предварительного преобразования. Это связано с тем, что в опре-

делении топологического графа весовая функция w(u) зависит от размеров

объекта. Это значит, что сложность одной и той же зоны обзора для разных

объектов будет разная. Для простоты ограничимся предположением, что все

подвижные объекты имеют близкие размеры и их можно считать равными.

Пусть в графе, описывающем триангуляцию всей сцены, сначала зануме-

рованы вершины, попавшие в первую зону обзора и не попавшие во вторую,

затем - вершины, попавшие в пересечение зон обзора, далее оставшиеся вер-

шины из второй зоны обзора и, наконец, остальные вершины графа. Тогда

матрица смежности графа G = (X, U, w) сцены S может быть представлена

в блочном виде:

⎛

⎞

R₁₁

R₁₂

R₁₃

⎜

⎟

R₂₁

R₂₂

R₂₃

R₂₄

⎜

⎟

⎜

⎟

⎝ R31 R32 R33 R34

⎠

R₄₁

R₄₂

R₄₃

R₄₄

(

)

(

)

R₁₁

R₁₂

R₂₂

R₂₃

Здесь подматрицы

будем считать матрицами

R₂₁

R₂₂

R₃₂

R₃₃

смежности подграфов G₁ = (X₁, U₁, w) и G₂ = (X₂, U₂, w), построенных внут-

ри соответственно первой S₁ и второй S₂ зон обзора. Для определенности обо-

значим |X₁| = N₁, |X₂| = N₂, |X₁ ∩ X₂| = N₁₂. Числа N₁, N₁₂, N₂ определяют

размеры квадратных подматриц R₁₁, R₂₂ и R₃₃ соответственно.

Предположим, что первая и вторая зоны объединены в одну S₁ ∪ S₂, кото-

рая описывается графом G₁ ∪ G₂. В этом случае матрицу смежности графа

всей сцены можно рассматривать как матрицу из четырех блоков, показан-

ную в предыдущем абзаце с помощью разделительных линий. Применяя ре-

зультаты, полученные для одного наблюдения, можем записать, что

Δ(S) ≤ λΔ (S₁ ∪ S₂) + (1 - λ)η (S\(S₁ ∪ S₂)) .

Для оценки второго слагаемого η (S\ (S₁ ∪ S₂)) можно воспользоваться ре-

зультатами, полученными для случая одного наблюдения.

Следующее утверждение дает оценку сложности Δ (S₁ ∪ S₂) объединенной

зоны обзора через сложности Δ (S₁) и Δ (S₂) соответственно первой и второй

зон.

140

Утверждение 5.

λ₁ (1 - Δ (S₁)) + λ₂ (1 - Δ (S₂))

Δ (S₁ ∪ S₂) ≤ 1 -

где λ₁ =σ2(X1)

λ₂ =σ2(X2)

σ²(X₁∪X₂)

Следует отметить, что доказанная оценка достигается при S₁ = S₂, т.е.

когда обе зоны обзора совпадают. Если ввести меру “простоты” π (S) =

= 1 - Δ(S), противоположную мере сложности, то из последнего утвержде-

ния следует хорошо интерпретируемое выражение:

λ₁π (S₁) + λ₂π (S₂)

π (S₁ ∪ S₂) ≥

7. Моделирование

Приведем результаты вычисления интегральной сложности сцены, зоны

обзора, а также верхние и нижние оценки сложности сцены, полученные на

основе утверждений 3, 4 и 5. Сцена представляла собой прямоугольник с

размерами 300 × 200 с центром в начале системы координат. Внутри сцены

генерировались препятствия, центры которых распределялись по равномер-

ному закону. При этом радиусы препятствий тоже определялись равномерно

случайным образом в пределах от трех до пяти. Диаметр подвижных объек-

тов равен пяти.

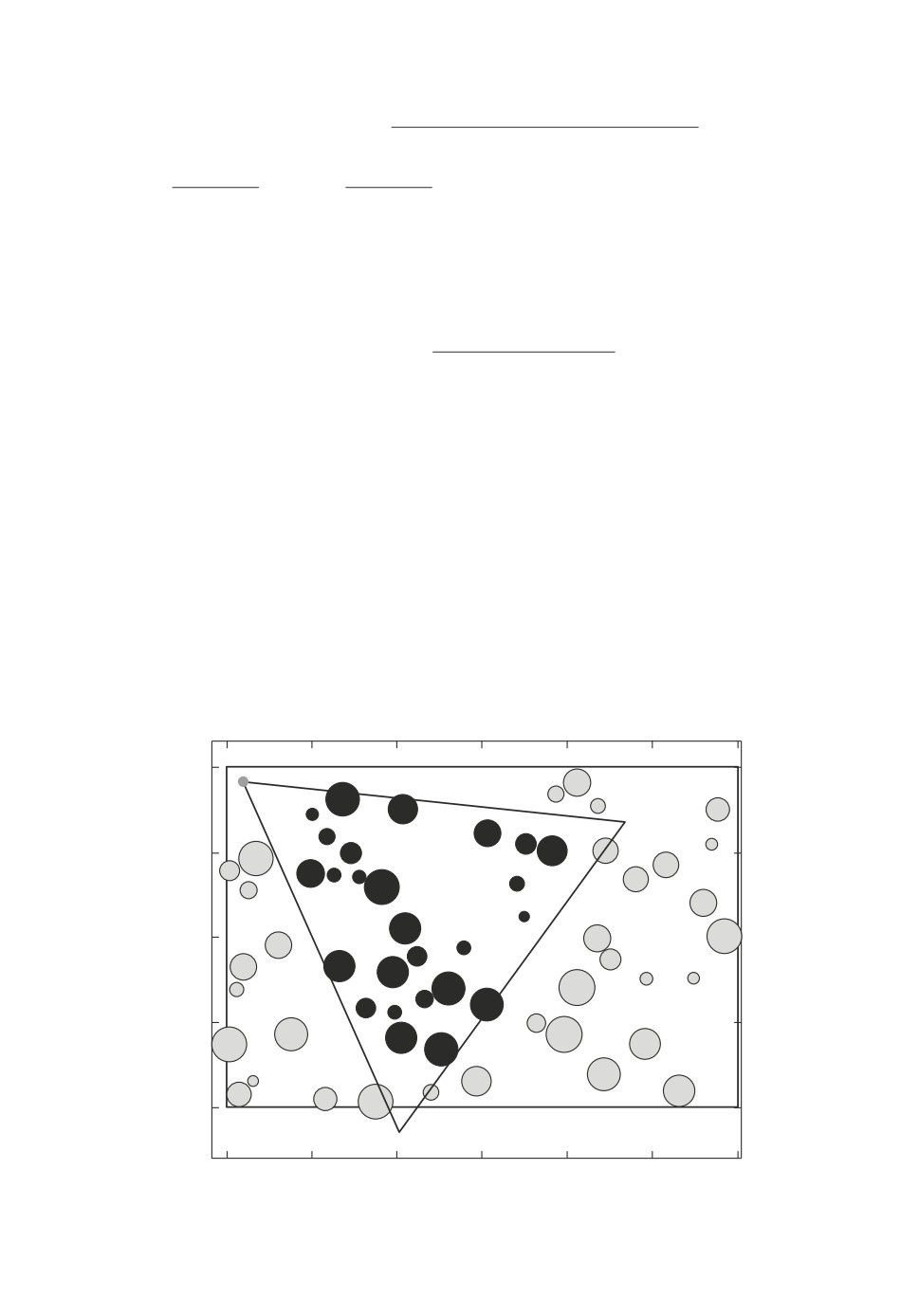
На рис. 3 показана сцена с 60 круговыми препятствиями и одним подвиж-

ным объектом, зона обзора которого ограничена изображенным на рисунке

100

150

100

150

Рис. 3. Моделирование сцены с одной зоной обзора.

141

100

150

100

150

Рис. 4. Моделирование сцены с двумя зонами обзора.

треугольником. Реальная интегральная сложность всей сцены с препятст-

виями равна 0,861, сложность зоны обзора - 0,832. При этом вычисленные в

соответствии с утверждениями 3 и 4 нижняя и верхняя оценки равны соот-

ветственно 0,389 и 0,927.

Как следует из полученных формул, “точность” оценки пропорциональна

отношению (а точнее, квадрату отношения) площади зоны обзора к площади

всей сцены. По этой причине если зона обзора мала относительно всей сцены,

то данные оценки становятся малоинформативными, быстро приближаясь к

своим предельным значениям. Однако современные системы видео и лазер-

ного сканирования позволяют обозревать достаточно большие участки, что

способствует получению достаточно реалистичных оценок сложности.

На рис. 4 приведен случай двух объектов и соответственно двух несколько

отличающихся по размерам зон обзора на сцене тоже с 60 препятствиями. Ре-

альная сложность сцены равна 0,536, сложность первой зоны обзора - 0,569,

второй - 0,568, при этом для этих зон были получены соответственно сле-

дующие нижние и верхние оценки сложности сцены: для первой зоны - 0,296

и 0,936, для второй - 0,207 и 0,946.

Верхняя оценка интегральной сложности объединения двух зон обзора,

вычисленная в соответствии с утверждением 5, оказалась равной 0,706. При

этом за счет объединения двух зон обзора, как и следовало ожидать, заметно

снизилась верхняя оценка, которая оказалась равной 0,781.

8. Заключение

В статье поставлена задача получения количественных оценок для слож-

ности среды функционирования нескольких подвижных объектов. Показа-

142

но, как на основе метрических характеристик триангуляции строится граф,

адекватно в рамках рассматриваемых задач описывающий структуру, порож-

даемую на сцене препятствиями. Введение топологического графа позволяет

ввести локальную меру сложности, которая лежит в основе определения ин-

тегральной меры. Приведена также конструктивная процедура для вычисле-

ния локальных проходимостей и локальных сложностей.

Во второй части статьи приводятся и доказываются верхние и нижние

оценки сложности сцены по одному и двум наблюдениям, осуществляемым

подвижными объектами в тех локальных областях сцены, в которых они на-

ходятся.

Следует отметить, что полученные оценки дают гарантированные грани-

цы сложности сцены по известным наблюдениям, поскольку они получены

при рассмотрении предельных, но, тем не менее, возможных случаев. По

этой причине они могут восприниматься как гарантированные, но чрезмерно

“осторожные”. В реальности, конечно, маловероятно, что такие предельные

случаи расположения препятствий в “невидимой” зоне могут наблюдаться.

Для получения оценок более точных в физическом измерении, но менее точ-

ных в вероятностном смысле следует сделать некоторые реалистичные пред-

положения о распределении препятствий за пределами зон обзора. Поэтому

данная модель для вычисления интегральной сложности сцены может быть

естественным образом развита в данном направлении. Но это требует отдель-

ного исследования.

ПРИЛОЖЕНИЕ

Доказательство утверждения 2. По индукции легко доказать

(

)

[k]

R₁₁

R₁₂

)[k] .

R₁

R[k-1]11 ◦ R₁₂

неравенство R[k] =

≥

, с

R₂₁

I(∞)

R₂₁ ◦ R[k-1]11 R₂₁ ◦ R[k-2]

◦R₁₂

учетом которого можем записать, что

(

)

R₁₂

)[N-1] .

R[N-1]11

R[N-2]11 ◦ R₁₂

≥

R₂₁

I(∞)

R₂₁ ◦ R[N-2]11 R₂₁ ◦ R[N-3]

◦R₁₂

Но для N ≥ N₁ + 2 справедливо R[N-1]11 = R[N-2]11 = R[N-3]11 = KG1 , откуда сле-

дует утверждение.

Доказательство утверждения 3. Рассмотрим неравенство (1) и

уточним выражение для второго слагаемого η. Ввиду утверждения 2 выра-

жение для η (S\S₁) принимает вид:

(

)

η (S\S₁) ≤

σ^T1e-αKG1◦R12 σ₂ + σ^T2e-αR21◦KG1 σ₁ + σ^T2e-αR21◦KG1^◦R12 σ2

1-λ

Рассмотрим более подробно первое слагаемое в скобках. Для этого про-

анализируем структуру подматрицы R₁₂. Подматрица R₁₂ - это матрица,

отражающая смежность вершин из зоны обзора и вершин во внешней обла-

сти S\S₁, при этом строки в R₁₂ соответствуют вершинам в зоне обзора, а

столбцы - вершинам во внешней области.

143

Строки, соответствующие внутренним вершинам из Xint1, будут нулевы-

ми; столбцы, соответствующие внутренним вершинам из внешней области,

т.е. из (X\X₁)^int, тоже будут нулевыми. Ненулевые элементы будут на пе-

ресечении строки, соответствующей вершине из X^Γ1, и столбца, соответст-

вующего вершине из (X\X₁)^Γ. При этом значение этого ненулевого элемента

равно ширине соответствующего ребра. Каждый ненулевой столбец содержит

в точности один ненулевой элемент, в то время как ненулевая строка может

содержать либо один, либо два ненулевых элемента.

Предположим, что граничные вершины в наблюдаемой области занумеро-

ваны первыми, а смежные с ними треугольники во внешней области - с них

начинается нумерация вершин внешней области. Тогда (матрицы K)1 и R12

можно представить в следующем блочном виде: KG1 =

K1G1

K2G1

, R₁₂ =

(

)

R¹¹²

. Здесь R¹¹², вообще говоря, прямоугольная матрица размера



)



^X^Γ×

(X\X₁)^Γ. Следовательно, KG1 ◦ R12 =

⁽K1G

◦R¹¹²

и e-αKG1◦R12 =

(

)

(

)_T

= e-αKG1◦R12 J . Представим вектор σ2 в блочном виде: σ2 =

σ¹² σ²²

, раз-

меры которого согласованы с разбиением матрицы R₁₂. Тогда

σ^T1e-αKG1◦R12 σ₂ = σ^T1e-αKG1◦R12 σ¹² + σ^T1Jσ²².

(

)

Нетрудно видеть, что второе слагаемое равно σ^T1Jσ²² = σ (X₁) σ (X\X₁)int

Рассмотрим теперь σ^T1e-αKG1◦R12 σ¹². Матрица K1G

◦R112 содержит ши-

рины всех путей из каждой вершины в зоне обзора до каждой внешней

{

}

граничной вершины. Тогда, очевидно, K1G1 ◦ R¹¹²

≥ min

min K1G1 , min R¹¹²

где матрица J, очевидно, соразмерна с R₁₂. Обозначим для удобства μ =

{

}

= min

min K1G1 , min R¹¹²

. Следовательно, e-αKG1◦R12

≤e^-αμJ = e^-αμJ. Та-

ким образом,

(

)

σ^T1e-αKG1◦R12 σ₂ ≤ e^-αμσ^T1Jσ¹² + σ (X₁)σ (X\X₁

)^int

(

)

(

)

= e^-αμσ (X₁) σ (X\X₁)Γ

+ σ (X₁)σ (X\X₁)int

Аналогично можно показать, что второе слагаемое в скобках удовлетво-

ряет неравенству

(

)

(

)

σ^T2e-αR21◦KG1 σ₁ ≤ e^-αμσ (X\X₁

)^Γ σ (X₁) + σ (X\X₁)int σ (X1).

Рассмотрим третье слагаемое в скобках. Точно так же представим KG1 =

(

)

K1G1

K2G1

(

)_T

, где K¹

- подматрица проходимостей для внутрен-

G₁

K2G1

K³

G₁

( (

)_T

)

R¹¹²

◦K1G1 ◦R¹¹²

них граничных вершин. Тогда R₂₁ ◦ KG1 ◦ R₁₂ =

144

(

)

e^-α(R12)^T◦KG1◦R12 J

и e-αR21◦KG1◦R12 =

. Используя введенные блочные

представления для вектора σ₂, получаем:

(

)(

)

((

)_T (

)_T)

σ¹²

e^-α(R12)^T◦KG1◦R12 J

σ^T2e-αR12◦KG1◦R12 σ₂ = σ¹²

σ²

(

)_T

(

)_T

σ¹²

e^-α(R12)^T◦KG1◦R12 σ¹² +

σ¹²

Jσ²²

σ((X\X1)^Γ)σ((X\X1)^int)

(

)_T

σ²²

)^T Jσ¹²

σ²²

Jσ²²

σ((X\X1)^int)σ((X\X1)^Γ) σ((X\X1)^int)σ((X\X1)^int)

(

)

(

)

(

)_T

◦K1G

◦R¹¹²

σ¹²

e^-α(R12⁾T

σ¹² + 2σ (X\X₁)^Γ σ (X\X₁)int +

(

)

(

)

+ σ (X\X₁)int σ (X\X1)int

Нетрудно показать, что для композиции справедлива аналогичная оценка:

(

)_T

R¹¹²

◦K1G1 ◦R¹¹²

≥μJ и, значит, e^-α(R12)^T◦KG1◦R12

≤e^-αμJ = e^-αμJ. С уче-

(

)

(

)

(

)_T

◦K1G

◦R¹¹²

том этого

σ¹²

e^-α(R12⁾T

σ¹² ≤ e^-αμσ (X\X₁)Γ σ (X\X1)Γ . Таким

образом,

(

)

σ^T2e-αR12◦KG1◦R12 σ₂ ≤ e^-αμσ² (X\X₁

)^Γ

(

)

(

)

(

)

+ 2σ (X\X₁)Γ σ (X\X1)int

+σ²

(X\X₁)int

Собирая вместе полученные неравенства, после преобразований и упроще-

ний получаем доказываемую в утверждении 3 верхнюю оценку.

Доказательство утверждения 4. Предположим, что за преде-

лами зоны обзора либо нет препятствий, либо их небольшое количество и

расстояния между ними настолько велики, что их(ожно счи)ть условно

R₁₁

R₁₂

равными бесконечности. Пусть, как и раньше, R =

- матрица

R₂₁

R₂₂

смежности топологического графа всей сцены, где R₁₁ - матрица смежности

графа G₁ = (X₁, U₁). Тогда в соответствии с процедурой построения прохо-

димостей можем записать:

⎛

⎞

(N-1)

KG1 ∨ Z₁

Z(N-1)12

⎠_.

K=R[N-1] =⎝

Z(N-1)21

Z(N-1)

Проанализируем подматрицы данной блочной матрицы. Z(N-1)22 содержит

ширины всех возможных путей из внешних вершин во внешние вершины, сле-

довательно, все элементы будут равны ∞, т.е. Z(N-1)22 = (∞). Z(N-1)12 содержит

145

ширины путей, ведущих из зоны обзора S₁ во внешнюю часть сцены S\S₁.

Каждый путь состоит из частей, находящихся в S₁, частей, находящихся

в S\S₁, и, возможно, несколько раз проходящий через ребра разреза. Ширина

ребер в S\S₁ по условию равна ∞, поэтому ширина пути будет определять-

ся ширинами путей, находящихся в G₁, и ширинами ребер разреза. Ширина

каждого такого пути не превосходит ν = max {Ширины ребер разреза}. Та-

ким образом, Z(N-1)12

≤νJ. Аналогично Z(N-1)21

≤νJ^T.

Рассмотрим KG1 ∨ Z(N-1)11. Эта подматрица содержит ширины всех путей

из X₁ в X₁, возможно, проходящих через некоторые ребра в G\G₁ и прохо-

дящих через некоторые ребра разреза. Части путей, лежащие в G\G₁, имеют

по условию бесконечную ширину, поэтому ширина любого полного пути не

будет превосходить ширины частей пути, лежащих в G₁, и ширины проходи-

мых ребер разреза. Понятно, что ширина любого такого пути не может быть

больше ширины любой его части. Поэтому KG1 ∨ Z(N-1)11

≤KG1∨νJ.

(

)

⁽ KG1∨νJ νJ⁾

e^-α(KG1^∨νJ)

e^-ανJ

Таким образом, K≤

и e-αK

≥

(νJ)^T

∞

e^-ανJ^T

Следовательно,

(

)(

)

(

)

σ₁

e^-α(KG1^∨νJ) e^-ανJ

Δ (S) = σ^Te-αKσ≥

σ^T1σ^T

e^-ανJ^T

σ₂

= σT1 e^-α(KG1^∨νJ)σ₁ + 2e^-ανσT1 Jσ₂.

Но σ^T1Jσ₂ = σ (X₁) σ (X\X₁), что и доказывает утверждение 4.

Доказательство утверждения 5. Рассмотрим матрицу смежности

подграфа 〈X₁, X₂〉 графа G, порожденного вершинами графов G₁ и G₂ из

двух зон наблюдения:

⎛

⎞

R₁₁

R₁₂

R₁₃

⎠_.

R〈X1,X₂〉 =^⎝ R21 R22 R23

R₃₁

R₃₂

R₃₃

Подграф 〈X₁, X₂〉, вообще говоря, неизоморфен графу G₁ ∪ G₂, поскольку в

отличие от графа G₁ ∪ G₂ он может содержать ребра, соединяющие вершины

из множеств X₁\X₂ и X₂\X₁. Наличие таких ребер отражено в подматри-

це R₁₃, информации о которой нет, поскольку эти ребра лежат в “ненаблю-

даемой” для обоих подвижных объектов области.

Применим к матрице R〈X1,X₂〉 утв(рждение), считая внедиагональные

KG1

≥

. С учетом этого для слож-

блоки R₁₃ и R₂₃ нулевыми: K〈X1,X₂〉

ностной меры получаем неравенство:

(

)

e-αKG1

JN1,N₂-N₁₂

δ (S₁ ∪ S₂) = σ^Te-αK〈X1^,X2^〉 σ ≤ σ^T

σ.

JN2-N₁₂,N₁ JN₂-N₁₂,N₂-N₁₂

146

(

)_T

Представим теперь вектор σ в блочном виде σ =

σ^T1σ^T2

, где σ₁, σ₂ имеют

размеры, согласованные с размерами матриц e-αKG1 и JN2-N₁₂,N₂-N₁₂ . Тогда

δ (S₁ ∪ S₂) ≤ σT1 e-αKG1 σ₁

+σ^T2JN2-N₁₂,N₁σ1 +

δ(S₁)

+ σT1 JN1,N₂-N₁₂σ2 + σ²JN₂-N₁₂,N₂-N₁₂σ2.

Обозначим через σ (X₁) = J1N1 σ₁ меру области, задаваемой множеством X₁

вершин графа G₁; через σ (X₂\X₁) = J1,N2-N₁₂ σ2 - меру области, задаваемой

вершинами X₂\X₁ графа G₂\G₁. Тогда

δ (S₁ ∪ S₂) ≤ δ (S₁) + 2σ (X₂\X₁)σ (X₁) + σ² (X₂\X₁) .

(

)

Аналогично, получая неравенство K〈X1,X₂〉

≥

, находим:

KG2

δ (S₁ ∪ S₂) ≤ δ (S₁) + 2σ (X₁\X₂)σ (X₂) + σ² (X₁\X₂) .

Складывая оба неравенства и выражая из них δ (S₁ ∪ S₂), после эквива-

лентных преобразований в правой части получаем:

(

)

δ (S₁ ∪ S₂) ≤

(δ (S₁) + δ (S₂)) + σ² (X₁ ∪ X₂) -

σ² (X₁) + σ² (X₂)

Чтобы перейти к сложностям, необходимо нормировать последнее выра-

жение на меру σ² (X₁ ∪ X₂) области, являющейся объединением обеих зон

обзора. Введем обозначения λ₁ =σ2(X1)

и λ₂ =σ2(X2)

, которые име-

σ²(X₁∪X₂)

ют смысл отношений мер первой и второй зон обзора к мере объединенной

области соответственно. В результате получаем:

λ₁Δ (S₁) + λ₂Δ (S₂)

λ₁ + λ₂

Δ (S₁ ∪ S₂) ≤

+1-

откуда и следует доказательство утверждения 5.

СПИСОК ЛИТЕРАТУРЫ

1. Интеллектуальное планирование траекторий подвижных объектов в средах с

препятствиями / Под ред. В.Х. Пшихопова. М.: Физматлит, 2014.

2. Path Planning for Vehicles Operating in Uncertain 2D Environments / Ed. V. Pshi-

khopov. Elsevier Butterworth-Heinemann, 2017.

3. Интеллектуальные технологии планирования перемещений подвижных объек-

тов в трехмерных недетерминированных средах / Под ред. В.Х. Пшихопова.

М.: Наука, 2017.

4. Пшихопов В.Х., Медведев М.Ю. Управление подвижными объектами в опреде-

ленных и неопределенных средах. М.: Наука, 2011.

5. Feixas M., del Acebo E., Bekaert Ph., Sbert M. An information Theory Framework

for the Analysis of Scene Complexity // EUROGRAPHICS ’99. 1999. V. 18. No. 3.

147

Niepel L., Martinka J., Ferko A., Elias P. On Scene Complexity Definition for

Rendering // WSCG’95, Plzen. 1995. P. 209-217.

Plemenos D., Sbert M., Feixas M. On Viewpoint Complexity of 3D Scenes // Int.

Conf. Graphicon. 2004. Moscow, Russia, http://www.graphicon.ru/

Rigau J., Feixas M., Sbert M. Visibility Complexity of a Region in Flatland //

EUROGRAPHICS. 2000.

Каркищенко А.Н., Пшихопов В.Х. К определению сложности среды функцио-

нирования подвижного объекта на плоскости // АиТ. 2019. № 5. С. 136-154.

10.

Скворцов А.В. Триангуляция Делоне и еe применение. Томск: Изд-во Том. ун-та,

2002.

11.

Qu Yaohong, Zhang Yintao, Zhang Youmin. A Global Path Planning Algorithm

for Fixed-wing UAVs // Intell. Robot Syst. Springer Science+Business Media. 2018.

V. 91. P. 691-707.

12.

Kim D., Sugihara K. Voronoi Diagram of a Circle Set from Voronoi Diagram of a

Point Set: I. Topology // Comput. Aided Geom. Des. 2001. V. 18. No. 6. P. 541-562.

13.

Choset H., Burdick J. Sensor-based Exploration: The Hierarchical Generalized

Voronoi Graph // Int. J. Robot. Res. 2000. V. 19. No. 2. P. 96-125.

14.

Merino L., Wiklund J., Caballero F. Vision-based Multi-UAV Position Estimation //

IEEE Robot. Autom. Mag. 2006. V. 13. No. 3. P. 53-62.

15.

Yu X., Zhang Y.M. Sense and Avoid Technologies with Application to Unmanned

Aircraft Systems: Review and Prospects // Progress Aeros. Sci. 2015. V.

74.

P. 152-166.

16.

Borouchaki H., Lo S. Fast Delaunay Triangulation in Three Dimensions // Comput.

Methods Appl. Mech. Eng. 1995. V. 128. P. 153-167.

17.

Нечеткие множества в моделях управления и искусственного интеллекта / Под

ред. Д.А. Поспелова. М.: Наука, 1986.

18.

Харари Ф. Теория графов. М.: Мир, 1973.

Статья представлена к публикации членом редколлегии О.Н. Граничиным.

Поступила в редакцию 24.11.2018

После доработки 12.01.2019

Принята к публикации 25.04.2019

148