Автоматика и телемеханика, № 9, 2019
© 2019 г. Ю.П. ЕМЕЛЬЯНОВА, канд. физ.-мат. наук (emelianovajulia@gmail.com),
П.В. ПАКШИН, д-р физ.-мат. наук (pakshinpv@gmail.com)
(Арзамасский политехнический институт (филиал)
Нижегородского государственного технического
университета им. Р.Е. Алексеева)
СИНТЕЗ УПРАВЛЕНИЯ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ
НА ОСНОВЕ НАБЛЮДАТЕЛЯ СОСТОЯНИЯ1
Рассматриваются линейные системы управления, которые функциони-
руют в режиме с постоянным периодом повторения, возвращаясь всякий
раз в исходное состояние. Ставится задача нахождения такого управле-
ния, которое, используя информацию о выходной переменной на текущем
и предыдущем повторениях и о полученных на основе наблюдателя оце-
нок переменных состояния, обеспечивает сходимость этой переменной к
желаемой траектории при неограниченном увеличении числа повторений.
Управление такого вида известно как управление с итеративным обуче-
нием. Для решения используется подход на основе диссипативности 2D-
моделей и дивергентного метода векторных функций Ляпунова. Конеч-
ные результаты представлены в виде линейных матричных неравенств.
Приводится пример.
Ключевые слова: управление с итеративным обучением, повторяющиеся
процессы, 2D-системы, устойчивость, диссипативность, векторная функ-
ция Ляпунова.
DOI: 10.1134/S0005231019090034
1. Введение
Управление с итеративным обучением эффективно применяется с целью
повышения точности систем, функционирующих в повторяющемся режиме,
который, в частности, характерен для роботов-манипуляторов. Задачам, свя-
занным с таким управлением, посвящено множество публикаций. Для пред-
варительного знакомства с этим важным направлением исследований можно
рекомендовать [1-3]. Процесс итеративного обучения состоит в коррекции за-
кона управления на текущем повторении на основе информации, накопленной
на предыдущем повторении, и текущей информации, т.е. управление с ите-
ративным обучением является простейшей формой управления с памятью.
Пусть на k-м повторении система описывается стандартными линейными
уравнениями состояния:
xk(t) = Axk(t) + Buk(t),
(1.1)
yk(t) = Cxk
(t), t ∈ [0, T ], k = 0, 1, . . . ,
1 Исследование выполнено за счет гранта Российского научного фонда (проект
№ 18-79-00088).
9
где xk ∈ Rnx - вектор состояния, uk ∈ Rnu - вектор управления, yk ∈ Rny -
вектор выходных переменных, k - номер повторения. Цель управления за-
ключается в достижении вектором выходных переменных yk(t) желаемой
траектории yref (t) c заданной точностью. Для достижения этой цели на каж-
дом шаге осуществляется коррекция управления по алгоритму
(1.2)
uk(t) = uk-1(t) + Δuk
(t), k = 1, 2, . . . ,
где Δuk(t) - корректирующая поправка, которая выбирается из условия, что
ошибка обучения
(1.3)
ek(t) = yref(t) - yk
(t)
стремится к нулю при k → ∞ и при этом u∞ = limk→∞ uk(t) остается огра-
ниченным по абсолютной величине.
Наибольшее распространение получил алгоритм коррекции “типа Аримо-
то”
(1.4)
uk(t) = uk-1(t) + Γėk
(t), k = 1, 2, . . . ,
названный так по имени первого автора пионерских работ [4, 5]. В дальней-
шем были предложены различные обобщения (1.4), например алгоритм, на-
поминающий закон ПИД-регулирования
∫t
(1.5)
uk(t) = uk-1(t) + Φek(t) + Γėk(t) + Ψ ek
(τ)dτ, k = 1, 2, . . .
0
В публикациях за (1.2)-(1.5) закрепилось название алгоритмы (законы)
управления с итеративным обучением. Выходная переменная обычно назы-
вается профилем повторения. В этих алгоритмах, как правило, не использу-
ются ни переменные состояния исходной системы (1.1), ни их оценки. В то
же время ясно, что использование этих переменных может обеспечить более
высокое качество управления как в смысле увеличения скорости сходимости
процесса обучения, так и в смысле достижения более высокой точности. Это,
в частности, подтверждает публикация [6], где результаты подтверждены экс-
периментом. Кроме того, когда на объект управления действуют случайные
возмущения и (или) измерения производятся с шумами, фильтрация выход-
ной переменной становится просто необходимой и получающиеся при этом
оценки переменных состояния вполне естественно использовать для построе-
ния алгоритмов коррекции управления. Существенно отметить, что, как это
следует из [7, 8] и [9, 10], в алгоритмах управления с итеративным обучени-
ем стохастическими системами фильтрация либо не использовалась [11] (см.
также другие статьи автора [11] в этой области), либо использовались оценки
только выходных переменных [9, 10]. Лишь в [12], где рассматривается детер-
минированная система с доступным измерению выходом, предложен алго-
ритм управления с итеративным обучением, в котором используются оценки
состояния, получаемые наблюдателем полного порядка.
10
В данной статье рассматриваются детерминированные линейные систе-
мы, которые функционируют в повторяющемся режиме с постоянным перио-
дом повторения, возвращаясь всякий раз в исходное состояние. Измерению
на каждом повторении доступна только выходная переменная. В отличие
от [12] ставится задача нахождения параметризованного множества управ-
лений с итеративным обучением, использующих информацию о выходной
переменной и оценках состояния на текущем и предыдущем повторениях.
Это множество включает подмножество нелинейных управлений, в то время
как в [12] рассматривалось только линейное управление. Для решения ис-
пользуется подход, который сводит нахождение условий сходимости процесса
итеративного обучения к анализу устойчивости частного вида 2D-моделей -
повторяющихся процессов [13]. В свою очередь условия устойчивости выво-
дятся на основе дивергентного метода векторных функций Ляпунова [14, 15].
Это множество включает в себя нелинейные управления. В частном случае
кусочно-линейных управлений конечные соотношения формулируются в тер-
минах линейных матричных неравенств. Приводится пример, показывающий,
что в классе кусочно-линейных управлений можно гибко изменять скорость
сходимости процесса итеративного обучения в зависимости от достигнутой
точности.
2. Постановка задачи
Рассмотрим дискретную систему, функционирующую в повторяющемся
режиме, модель которой на k-м повторении имеет вид:
xk(p + 1) = Axk(p) + Buk(p),
0 ≤ p ≤ N - 1,
(2.1)
yk(p) = Cxk
(p), k = 0, 1, . . . ,
где xk ∈ Rnx - вектор состояния, uk ∈ Rnu - вектор управления, yk ∈ Rny -
вектор выходных переменных, k - номер повторения. Пусть yref (p) - же-
лаемый профиль повторения и на каждом повторении измерению доступен
только вектор профиля yk(p). Введем в рассмотрение ошибку воспроизведе-
ния профиля
(2.2)
ek(p) = yref(p) - yk
(p), k = 0, 1, . . .
Задача состоит в нахождении такой последовательности управлений uk(p),
k = 0,1,..., которая обеспечивает достижение заданной точности воспроиз-
ведения профиля ϵ за конечное число повторений kf и сохранение этой точ-
ности при дальнейших повторениях, т.е.
(2.3)
|ek(p)| ≤ ϵ, k ≥ kf
,
0≤p≤N.
3. Подход к решению
Последовательность uk(p), k = 1, . . . , при заданном граничном усло-
вии u0(p) будем формировать в соответствии с общим алгоритмом управ-
ления с итеративным обучением
(3.1)
uk+1(p) = uk(p) + Δuk+1
(p),
11
задавая корректирующую поправку Δuk+1(p) как функцию ошибки и прира-
щения состояния
(3.2)
Δuk+1(p) = φ(ξk+1(p + 1),ek
(p + 1)), φ(0, 0) = 0,
где ξk+1(p + 1) = xk+1(p) - xk(p).
Замечание 1. В отличие от управления с обратной связью для управле-
ния с итеративным обучением синтезу подлежит корректирующая поправка
Δuk+1(p), которая далее синтезируется как обычное управление с обратной
связью для вводимой далее в рассмотрение вспомогательной системы отно-
сительно приращений переменных. В связи с этим возникает естественный
вопрос о непосредственном построении управления с обратной связью, ре-
шающего поставленную задачу, который детально обсуждался в [1, 16-18].
Управление (3.1) и (3.2) относится к так называемым непричинным управ-
лениям, характерным признаком которых является то, что uk+1(p) зависит
от ek(h), где h > p. Непричинные законы управления с упреждением реа-
гируют на повторяющиеся помехи. Исключая особые случаи, не существует
эквивалентного регулятора с обратной связью, который может обеспечить та-
кое же качество управления, как и непричинное управление с итеративным
обучением, поскольку управление с обратной связью реагирует на текущие
ошибки и не обладает свойством упреждения.
Поскольку вектор состояния недоступен для измерения, будем использо-
вать оценку вектора состояния, полученную на основе измеренных значе-
ний yk(p). Для нахождения этой оценки используем наблюдатель полного
порядка со структурой, аналогичной структуре фильтра Калмана
(3.3)
xk(p + 1) = Axk(p) + Buk(p) + F(yk(p) - Cxk
(p)).
Введем в рассмотрение ошибку оценивания и приращения оценки и ошибки
оценивания
xk(p) = xk(p) - xk(p),
(3.4)
ξk+1(p + 1) = xk+1(p) - xk(p),
ξk+1(p + 1) = xk+1(p) - xk(p),
тогда динамику системы с наблюдателем относительно приращений можно
описать уравнениями:
ξk+1(p + 1) = (A - FC
ξk+1(p),
(3.5)
ξk+1(p + 1) = F
ξk+1(p) +
ξk+1(p) + Bvk+1
(p),
ek+1(p) = -C
ξk+1(p) - C
ξk+1(p) + ek(p) - CBvk+1(p),
где vk+1(p) = Δuk+1(p - 1).
[
]
[
]
A-FC
0
0
Обозначим ηk(p) =
ξk(p)T
ξk(p)T]T, A11 =
, B1 =
,
FC A
B
A12 = 0, A21 = [-CA - CA], A22 = I, B2 = -CB и запишем (3.5) в виде стан-
дартной модели дискретного повторяющегося процесса [13]:
ηk+1(p + 1) = A11ηk+1(p) + A12ek(p) + B1vk+1(p),
(3.6)
ek+1(p) = A12ηk+1(p) + A22ek(p) + B2vk+1
(p).
12
Поскольку xk(p) = xk(p) + xk(p), то корректирующую поправку (3.2) можно
выразить в виде новой функции доступных для формирования управления
переменных
(3.7)
Δuk+1(p - 1) = vk+1(p) = ϕ(ηk+1(p),ek
(p)), ϕ(0, 0) = 0.
Если для всех 0 ≤ p ≤ N ek(p) → 0 при k → ∞, то существует kf , при кото-
ром выполняются условия (2.3). Таким образом, поставленная задача будет
решена, если найдется последовательность vk(p), такая что
(3.8)
lim
ek(p) = 0,
|u∞
(p)| < ∞,
0≤p≤N,
k→∞
при условии, что норма ошибки ограничена сверху монотонно убывающей
функцией, где u∞(p) = limk→∞ uk(p). Ясно, что в этом случае существует kf ,
начиная с которого будет выполнено условие (2.3).
4. Основной результат
Решение будем искать на основе теории устойчивости и диссипативности
повторяющихся процессов [14].
Определение 1
[14]. Система (3.6), (3.7) называется экспоненциаль-
но устойчивой, если существуют числа κ > 0 и 0 < ϱ < 1, такие что
(4.1)
|ηk(p)|2 + |ek(p)|2 ≤ κϱk+p,
где κ и ϱ не зависят от N.
Заметим, в случае выполнения (4.1) гарантируется указанная в разделе 3
ограниченность нормы ошибки монотонно убывающей функцией, что, в свою
очередь, обеспечивает достижение заданной точности.
Система (3.6), (3.7) в общем случае нелинейна. Универсальным методом
анализа устойчивости нелинейных систем является второй метод Ляпуно-
ва. Однако уравнения рассматриваемой системы не разрешены относительно
полных приращений переменных состояния, и применить этот метод непо-
средственно невозможно. Для преодоления этой трудности авторами разра-
ботан так называемый дивергентный метод векторных функций Ляпунова,
в котором, в отличие от классической версии, устойчивость устанавливается
на основе свойств дивергенции (дискретного аналога дивергенции) указанных
векторных функций. В рассматриваемом случае введем векторную функцию
Ляпунова так:
[
]
V
1(ηk+1(p))
(4.2)
V (ηk+1(p), ek(p)) =
,
V2(ek(p))
где V1(xk+1(p)) > 0, xk+1(t) = 0, V2(ek(p)) > 0, yk(p) = 0, V1(0) = 0, V2(0) = 0.
Аналог дивергенции этой функции определим как
(4.3)
DV (ηk+1(p),yk(p)) = ΔpV1(ηk+1(p)) + ΔkV2(ek
(p)),
где ΔpV1(ηk+1(p)) = V1(ηk+1(p + 1)) - V1(ηk+1(p)), ΔkV2(ek(p)) = V2(ek+1(p)) -
- V2(ek(p)).
Справедливо следующее утверждение.
13
Теорема 1
[14]. Система (3.6), (3.7) является экспоненциально устой-
чивой, если существует функция (4.2) и положительные скаляры c1, c2 и
c3, такие что
c1|ηk+1(p)|2 ≤ V1(ηk+1(p)) ≤ c2|ηk+1(p)|2,
c1|ek(p)|2 ≤ V2(ek(p)) ≤ c2|ek(p)|2,
DV (ηk+1(p),ek(p)) ≤ -c3(|ηk+1(p)|2 + |ek(p)|2).
Для получения корректирующей последовательности (3.7), обеспечиваю-
щей экспоненциальную устойчивость, используем подход на основе теории
диссипативности по Виллемсу [19]. Эта теория была эффективно применена
в [20] для синтеза нелинейного стабилизирующего управления с использо-
ванием частного вида диссипативности - пассивности. В русле этой теории
в [21] было введено удобное для решения задач стабилизации понятие экспо-
ненциальной пассивности. В [14, 15] эти результаты были распространены на
2D-системы в форме повторяющихся процессов и разработана соответствую-
щая теория стабилизации.
Введем в рассмотрение вспомогательный вектор
(4.4)
zk+1(p) = C1ηk+1(p) + C2ek(p) + Dvk+1(p),
где C1, C2 и D - постоянные матрицы согласованных размеров.
Определение 2
[14]. Дискретный повторяющийся процесс (3.6) назы-
вается экспоненциально диссипативным относительно входной переменной
vk+1(t) и выходной переменной zk+1(t), определенной в (4.4), если существу-
ют векторная функция (4.2) и положительные скаляры c1, c2 и c3 такие,
что
c1|ηk+1(p)|2 ≤ V1(ηk+1(p)) ≤ c2|ηk+1(p)|2,
c1|ek(p)|2 ≤ V2(ek(p)) ≤ c2|ek(p)|2,
DV (ηk+1(t),ek(t)) ≤ S(zk+1(p),vk+1(p))-
- c3(|ηk+1(t)|2 + |ek(t)|2),
где S - скалярная функция, такая что S(0, 0) = 0.
В теории диссипативности по Виллемсу функции S и V называют-
ся функцией запаса и функцией накопления. Нетрудно видеть, что ес-
ли при некотором выборе z последовательность (3.7) удовлетворяет усло-
вию S(zk+1(p), vk+1(p)) ≤ 0, то система (3.6), (3.7) в соответствии с тео-
ремой 1 будет экспоненциально устойчива. Таким образом, окончатель-
но задача сводится к нахождению стабилизирующей тройки
{V, z, v}.
[
]
[
]
[
]
ηk+1(p)
A11
A12
B1
B=
Обозначим ζk+1(p) =
,
A=
,
. Определим
ek(p)
A21
A22
B2
блочно-диагональную матрицу P = diag[P1 P2] ≻ 0 как решение неравенства
Риккати
(4.5)
AT
A-(1-σ)P
ATPB[BTPB + R]-1 BTPA
+ Q ≼ 0,
14
где 0 < σ < 1 - положительный скаляр, Q ≻ 0 и R ≻ 0 - весовые матрицы.
Нетрудно видеть, что если линейное матричное неравенство
⎡
⎤
(1 - σ)X
XA¯T
X
⎢
⎥
(4.6)
⎣
AX X +BR-1 BT
0
⎦ ≽ 0, X ≻ 0,
X
0
Q-1
разрешимо относительно X = diag[X1 X2] ≻ 0, то P = X-1.
Следующая теорема предлагает одно из возможных множеств стабилизи-
рующих троек.
Теорема 2. Дискретный повторяющийся процесс (3.6) является экспо-
ненциально диссипативным с функцией запаса
S(vk+1(p), zk+1(p)) = zTk+1(p)(BTPB + R)-1zk+1(p) +
(4.7)
+ 2zk+1(p)Tvk+1(p) + vk+1(p)T[ BTP B + R]vk+1(p)
относительно входной переменной vk+1(p) и выходной переменной
(4.8)
zk+1(p) =BT
Aζk+1
(p),
где P = diag[P1 P2] ≻ 0 - решение (4.5). Множество последовательностей
корректирующих поправок (3.7), обеспечивающих экспоненциальную устой-
чивость системы (3.6), (3.7), определяется соотношением
(4.9)
vk+1(p) = -[BTPB + R]-1 BT
AΘ(ζk+1(p))ζk+1
(p),
где Θ(ζ) - симметричная матричная функция, удовлетворяющая соотно-
шению
(4.10)
M - 2MΘ(ζ) + Θ(ζ)MΘ(ζ) - Q - (σ - μ)P ≺ 0
для всех ζ ∈ R2nx+ny , где M
ATPB[BTPB + R]-1 BT
A, 0 < μ < σ.
Доказательство. Выберем компоненты векторной функции накопле-
ния (4.2) в виде квадратичных форм:
V1(ηk+1(p)) = ηk+1(p)TP1ηk+1(p), V2(ek(p)) = ek(p)T(t)P2ek(p),
где P1 ≻ 0 и P2 ≻ 0 - диагональные блоки матрицы P , представляющей собой
решение (4.5). Вычисляя аналог дивергенции (4.2) вдоль траекторий (3.6),
получим, что
(4.11)
DV (ηk+1(p),ek
(p)) =
(
)
[
]
= ζk+1(p)T
AT
A-(1-σ)P
ATPB
BTPB + R
-1 BTPA¯+Qζk+1(p)+
+ζk+1(p)TA¯TPB[BTPB + R]-1 BT
Aζk+1(p) - ζk+1(p)T(Q + σP )ζk+1(p) +
+ 2ζk+1(p)TA¯TP Bvk+1(p) + vk+1(p)T BTP Bvk+1(p) ≤
≤ζk+1(p)TA¯TPB[BTPB + R]-1 BT
Aζk+1(p) + 2ζk+1(p)TA¯TPBvk+1(p) +
+ vk+1(p)T[ BTP B + R]vk+1(p) - ζk+1(p)T(Q + σP)ζk+1(p).
15
Из (4.11) следует, что (3.6) экспоненциально диссипативна относительно вход-
ной переменной vk+1(p) и выходной переменной (4.8) с функцией запаса (4.7).
Из (4.11) также следует, что если последовательность (3.7) определяется со-
отношением (4.9), то
(
)
DV (ηk+1(p),ek(p)) ≤ -μλmin(P)
|ηk+1(p)|2 + |ek(p)|2
и в соответствии с теоремой 1 нелинейная система (4.9), (3.6) является экс-
поненциально устойчивой. Теорема 2 доказана.
Замечание 2. Если Θ выбрать в виде единичной матрицы, то усло-
вие (4.10) заведомо будет выполнено и доказанная теорема 2 дает линейную
последовательность корректирующих поправок. Учитывая то, что эта матри-
ца зависит от изменения ошибки относительно повторений, можно пытаться
уменьшать значения коэффициентов корректирующих поправок после дости-
жения требуемой точности и, наоборот, увеличивать эти коэффициенты, ко-
гда ошибка велика, другими словами, вводить адаптацию к величине ошибки.
Такой подход позволит найти разумный компромисс между скоростью обу-
чения и энергозатратами на управление. Наиболее просто это можно сделать
за счет кусочно-постоянного выбора Θ, см. приведенный далее пример. Более
общие рекомендации здесь сделать затруднительно.
5. Решение в классе дифференциальных моделей
Исходная модель системы для рассматриваемого класса задач обычно за-
дается в виде (1.1). Перейти от нее к дискретной модели (2.1) не составля-
ет труда. С другой стороны, можно искать требуемую последовательность
корректирующих поправок, не переходя к (2.1), а непосредственно исполь-
зуя (1.2). Рассмотрим такой подход подробно. Предположим, что в (1.1) из-
мерению доступен вектор выходных переменных yk(t) и CB = 0. Последнее
ограничение может быть снято, но при этом усложнятся последующие по-
строения. Для получения оценки состояния используем наблюдатель полного
порядка
dxk(t)
(5.1)
= Axk(t) + Buk(t) + F(yk(t) - Cxk
(t))
dt
и введем вспомогательные переменные
∫t
∫
t
(5.2)
ξk+1(t) =
[xk+1(τ) - xk(τ)]dτ,
ξk+1(t) =
[xk+1(τ) - xk
(τ)]dτ,
0
0
где xk(t) = xk(t) - xk(t) - ошибка оценивания. В терминах этих переменных
динамика системы (1.1), (1.2) опишется так:
ξk(t)
= (A - F C
ξ(t),
dt
t
∫
dξk(t)
(5.3)
=
ξ+F
ξ + B Δuk+1(τ)dτ.
dt
0
16
С учетом (5.3) изменение ошибки обучения (1.3) в зависимости от числа по-
вторений опишется уравнением
∫t
(5.4)
ek+1(t) = -C
ξk+1(t) - C
ξk+1(t) + ek(t) - CB Δuk+1(τ)dτ.
0
∫t
Обозначим vk+1(t) =
Δuk+1(τ)dτ и запишем уравнения системы в стан-
0
дартной форме дифференциального повторяющегося процесса:
ηk+1(t) = A11ηk+1(t) + A12ek(t) + B1vk+1(t),
(5.5)
ek+1(t) = A21ηk+1(t) + A22ek(t) + B2vk+1
(t),
где обозначения соответствуют принятым ранее с той разницей, что перемен-
ная ζ и элементы матриц в правой части (5.5) должны выбираться из (1.1),
(5.1) и дискретная переменная p заменяется на непрерывную t. Корректи-
рующую поправку к управлению в (1.3) зададим соотношением
∫t
(5.6)
vk+1(t) = Δuk+1(τ)dτ = ϕ(ηk+1(t),ek
(t)),
0
где ϕ(0, 0) = 0 и при подстановке (5.6) в (5.5) правая часть первого уравнения
в (5.5) удовлетворяет условию Липшица по переменным η и e. Задача состоит
в нахождении такой последовательности управлений uk(t), k = 0, 1, . . . , кото-
рая обеспечивает достижение заданной точности воспроизведения профиля ϵ
за конечное число повторений kf и сохранение этой точности при дальнейших
повторениях, т.е
(5.7)
|ek(t)| ≤ ϵ, k ≥ kf
,
0≤p≤T.
В рамках модели (5.5) эта задача эквивалентна нахождению соответствую-
щей последовательности vk(t), которая в соответствии с (5.6) определяет по-
следовательность корректирующих поправок.
Определение 3
[14]. Система (5.5), (5.6) называется экспоненци-
ально устойчивой, если существуют вещественные числа κ > 0, λ > 0 и
0 < ρ < 1 такие, что
(5.8)
|ηk(t)|2 + |ek(t)|2 ≤ κe-λtρk,
где κ, ρ и λ не зависят от T .
Если система (5.5), (5.6) экспоненциально устойчива, то последователь-
ность (5.5) дает решение поставленной задачи. Такую последовательность
найдем на основе дивергентного метода векторных функций Ляпунова и тео-
рии диссипативности дифференциальных повторяющихся процессов.
Условия устойчивости системы (5.5), (5.6) дает аналог теоремы 1, который
получается заменой переменной p на t и оператора D на
dV1(ηk+1(t))
(5.9)
DcV (ηk+1(t),ek(t)) =
+ ΔkV2(ek
(t)),
dt
17
где ΔkV2(ek(t)) = V2(ek+1(t)) - V2(ek(t)). Для получения аналога определения
диссипативности такие же замены следует провести в определении 2.
Определим матрицу P = diag[P1 P2], P1 ≻ 0, P2 ≻ 0, как решение модифи-
цированного неравенства Риккати
(5.10)
ATPI(1,0) + PI(1,0)A¯
ATPI(0,1)A¯ - (1 - σ)PI(0,1) + γPI(1,0)-
−[P I(1,0) B
ATPI(0,1) B][BTPI(0,1) B+R]-1[BTPI(1,0)+BTPI(0,1)A¯]+Q ≼ 0,
где I(1,0) = diag[I2nx 0], I(0,1) = diag[0 Iny ], 0 < σ < 1 и γ > 0 - скалярные па-
раметры, Q ≻ 0 и R ≻ 0 - весовые матрицы. Следующая теорема определяет
множество последовательностей (5.6), которые обеспечивают экспоненциаль-
ную устойчивость системы (5.5), (5.6)
Теорема 3. Дифференциальный повторяющийся процесс (5.5) является
экспоненциально диссипативным с функцией запаса
(
)-1
(
)
(5.11)
S(v, z) = 2zTv + zT
BTPI(0,1) B + R
z+vT
BTPB + R
v
относительно входа vk+1(t) и выхода
[
]
BT
(5.12)
zk+1(t) =
PI(1,0) +BTPI(0,1)A¯ ζk+1
(t).
1
Множество последовательностей (5.6), которые обеспечивают экспоненци-
альную устойчивость системы (5.5), (5.6), определяется соотношением
vk+1(t) =
(5.13)
[
]-1 [
]
=-
BTPI(0,1) B + R
BTPI(1,0) +BTPI(0,1)A¯ Γ(ζk+1(t))ζk+1(t),
где P - решение неравенства (5.10) и Γ(ζ) - симметричная матричная
функция, удовлетворяющая неравенству
(5.14)
N - 2NΓ(ζ) + Γ(ζ)NΓ(ζ) - Q - (γ - μ1)PI(1,0) - (σ - μ2)PI(0,1)
≺0
для всех ζ ∈ R2nx+ny , где
[
][
]
]-1 [
N = PI(1,0) B
ATPI(0,1) B
BTPI(0,1) B + R
BTPI(1,0) +BTPI(0,1) ,
0 < μ1 < γ, 0 < μ2 < σ и при подстановке (5.13) в (5.5) правая часть первого
уравнения в (5.5) удовлетворяет условию Липшица по переменным η и e.
Доказательство. Выберем компоненты векторной функции (4.2) в ви-
де квадратичных форм
V1(ηk+1(t)) = ηTk+1(t)P1ηk+1(t), V2(ek) = eTk(t)P2ek(t),
18
где P1 ≻ 0 и P2 ≻ 0 - диагональные блоки матрицы P , представляющей собой
решение неравенства (5.10). Вычисляя аналог дивергенции функции (4.2), в
силу (5.5) в результате последовательных оценок получим, что
(5.15)
DcV (ηk+1(t),ek
(t)) =
[
]
= ζk+1(t)T
ATPI(1,0) + PI(1,0)A¯
ATPI(0,1)A¯ - PI(0,1) ζk+1(t) +
[
]
+2ζk+1(t)T P I(1,0) B
ATPI(0,1) B vk+1(t) + vk+1(t)T BTPI(0,1) Bvk+1(t) ≤
[
≤ ζk+1(t)T
ATPI(1,0) + PI(1,0)A¯
ATPI(0,1)A¯ - (1 - σ)PI(0,1) + γPI(1,0) -
(
)(
)-1 (
)
−
ATPI(0,1) B +BTPI(1,0) BTPI(0,1) B + R
BTPI(1,0) +BT
A +
]
[
][
]-1[
+Q ζk+1(t)+ζk+1(t)T P I(1,0) B
ATPI(0,1) B
BTP I(0,1) B + R
BTP I(1,0)+
]
[
]
+BTPI(0,1) ζk+1(t) + 2ζk+1(t)T P I(1,0) B
ATPI(0,1) B vk+1(t) +
[
]
[
+ vk+1(t)T
BTPI(0,1) B + R vk+1(t) - ζk+1(t)T Q + σPI(0,1)+
]
+ γPI(1,0) ζk+1(t) ≤ S(vk+1(t),zk+1(t)) -
- ζk+1(t)T[Q + σPI(0,1) + γPI(1,0)]ζk+1(t) ≤
≤ S(vk+1(t),zk+1(t)) - μλmin(P)|ζk+1(t)|2,
где S(v, z) определяется соотношениями (5.11), (5.12) и μ = min{μ1, μ2}. Из
(5.15) следует, что (5.5) - экспоненциально диссипативна относительно вход-
ной переменной v и выходной переменной (5.12) c функцией запаса (5.11).
Выбирая vk+1(t) из множества (5.13), в силу (5.14) получим, что
DcV (ηk+1(t),ek(t)) ≤ -μλmin(P)|ζk+1(t)|2,
и в соответствии с аналогом теоремы 1 система (5.5), (5.13) экспоненциально
устойчива. Теорема 3 доказана.
Замечание 3. В теореме 3 остается справедливым замечание 1 относи-
тельно выбора матрицы Θ. Существенно отметить, что возникающее в этом
случае модифицированное неравенство Риккати (5.10) и соответствующее
ему уравнение в известных публикациях не изучались, и для их решения
пока можно предложить лишь эвристические итерационные методы.
6. Пример
Рассмотрим модель портального робота из [6]. В [6] траектория движе-
ния исполнительного органа, который схватывает предметы из определенной
области и ставит их на конвейер, разделена на составляющие по трем ортого-
нальным осям, и по каждой из осей экспериментально получена передаточная
функция. Ограничимся построением управления с итеративным обучением
19
0,010
0,009
0,008
0,007
0,006
0,005
0,004
0,003
0,002
0,001
0
20
40
60
80
100
120
140
160
180 200
p
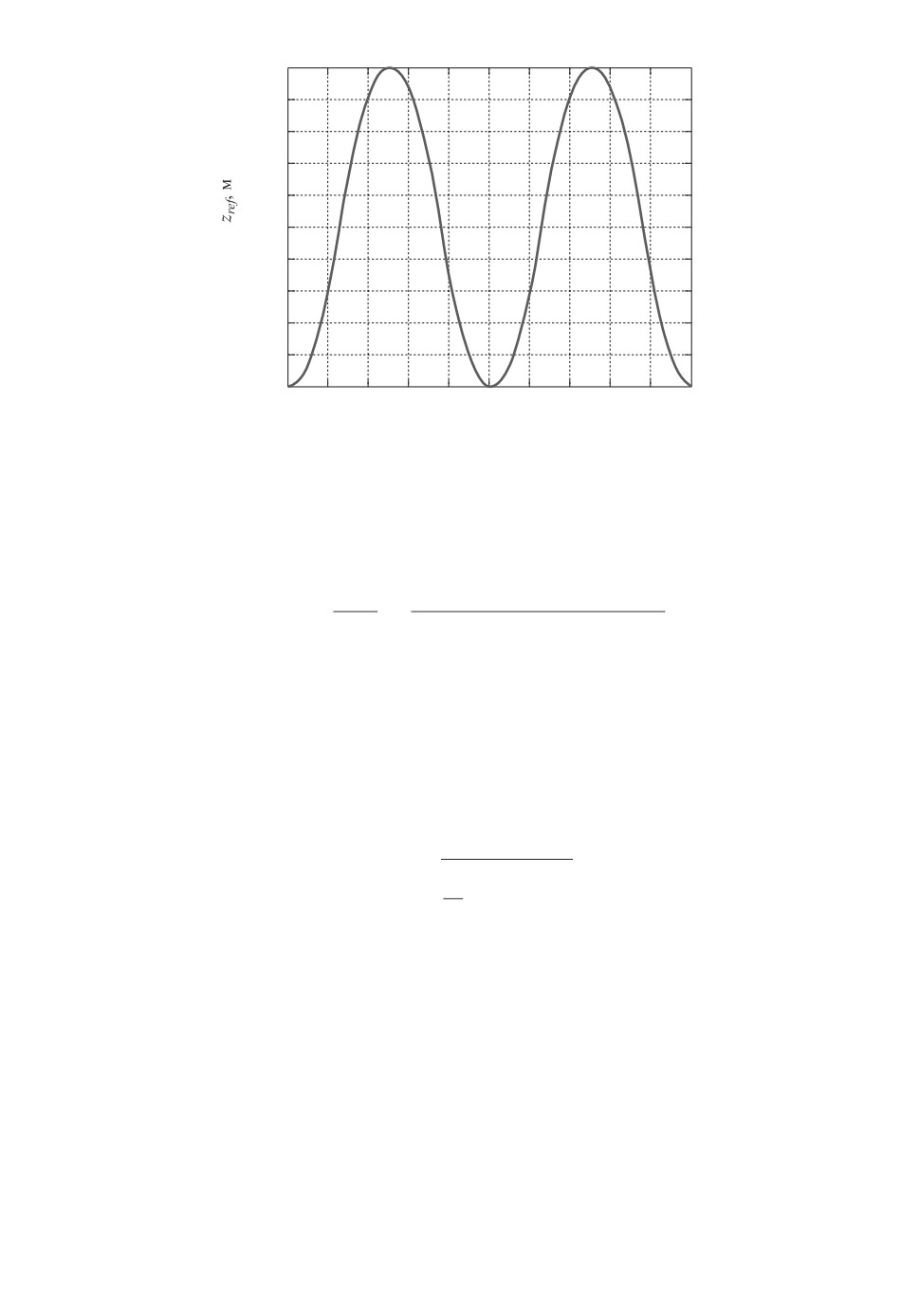
Рис. 1. Желаемая траектория движения по вертикальной оси.
по вертикальной оси. Передаточная функция от управления к вертикально-
му перемещению имеет вид
Y (s)
15,8869(s + 850,3)
(6.1)
Gz(s) =
=
U (s)
s(s2 + 707,6s + 3,377 · 105)
Управление будем строить в рамках дискретной модели состояния. В рас-
сматриваемом случае период дискретности Ts = 0,01 c. Параметры дискрет-
ной модели состояния получим с помощью стандартных функций ss и c2d
пакета MATLAB. Желаемая траектория движения по вертикальной оси пред-
ставлена на рис. 1.
В качестве меры точности воспроизведения желаемой траектории введем
в рассмотрение среднеквадратическую ошибку обучения
∑
(6.2)
E(k) =√1
|êk(p)|2.
N
p=0
Поскольку число повторений велико, целесообразно при соблюдении усло-
вия (4.10) на первых повторениях увеличить коэффициент при ошибке в кор-
ректирующей поправке, чтобы ускорить достижение требуемой точности, а
когда эта точность будет достигнута, уменьшить этот коэффициент. Этого
можно достичь подходящим выбором функции Θ в (4.9). Выбирая эту функ-
цию кусочно-постоянной так, чтобы при каждом ее значении выполнялось
условие (4.10), получим кусочно-линейное управление. Как и в большинстве
методов проектирования, здесь нельзя дать точных рекомендаций по выбору,
он получается методом проб и ошибок. Обозначим
(6.3)
K =-[BTPB+R]-1 BT
A
20
3
10
7
6
5
4
3
2
1
0
5
10
15
20
25
30
35
40
45
50
k
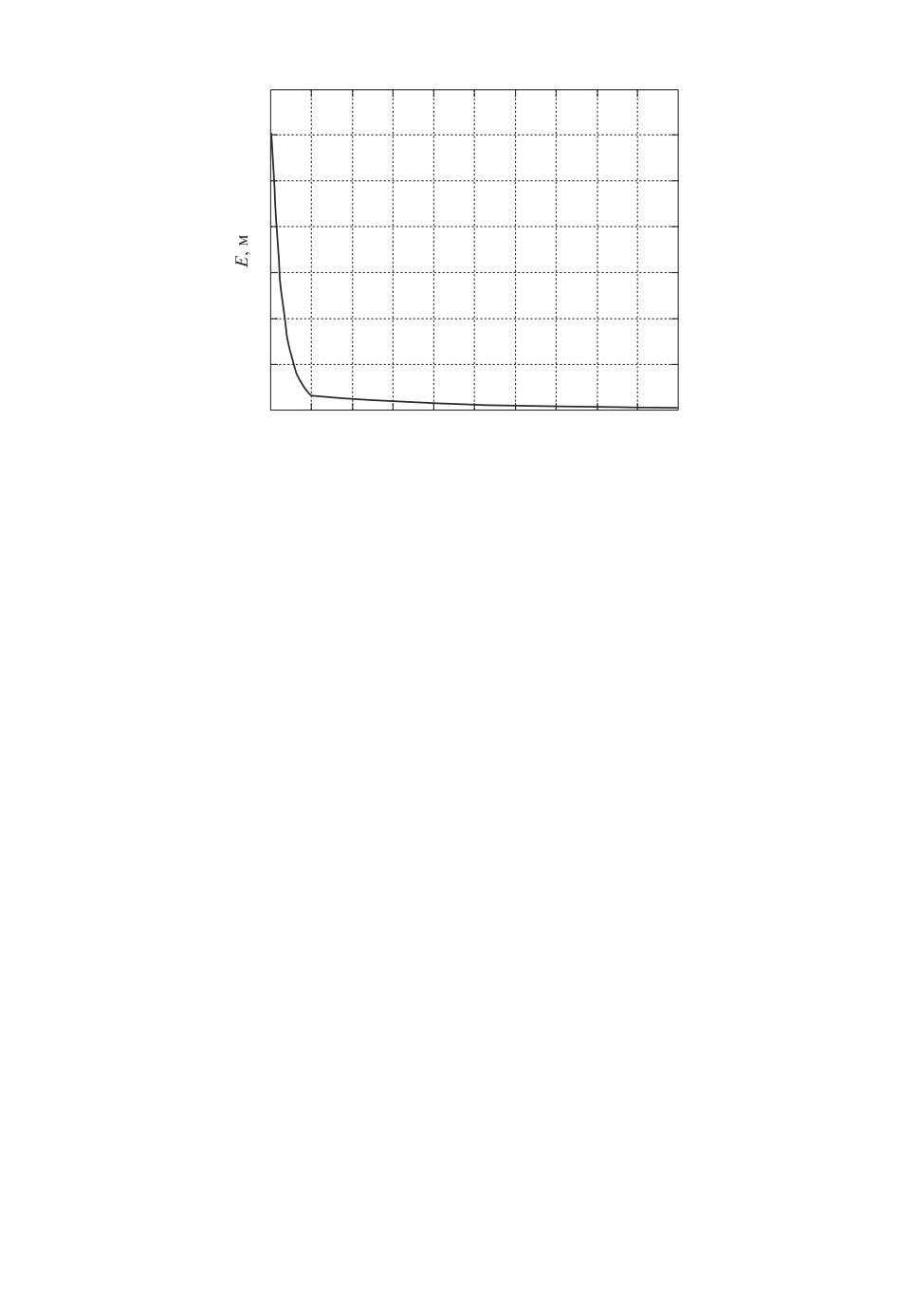
Рис. 2. Изменение среднеквадратической ошибки обучения в зависимости от
числа повторений.
и зададим Θ в виде диагональной матрицы. Тогда в соответствии с теоре-
мой 2 управление с итеративным обучением для рассматриваемой системы
запишется в виде
uk(p) = uk-1(p) + K1Θ1(xk(p) - xk-1(p)) + K2Θ2(xk(p) - xk-1(p))+
(6.4)
+K3Θ3(zref(p + 1) - Cxk-1(p + 1)),
где K1, K2, K3 - соответствующие блоки матрицы (6.3). Пусть требуемая
точность составляет 0,5 · 10-3 м. Поскольку переменная xk(p) недоступна для
измерения, выберем Θ1 в виде нулевой матрицы, Θ2 выберем в виде еди-
ничной матрицы, а Θ3 попытаемся увеличить на начальных повторениях, а
затем уменьшить при достижении указанной точности, не нарушая выполне-
ние неравенства (4.10). Оказывается, что справедливость этого неравенства
сохраняется при увеличении Θ3 в два раза на начальных повторениях и при
последующем уменьшении в 10 раз при достижении требуемой точности. Та-
ким образом, кусочно линейное управление
uk(p) = uk-1(p) + K2(xk(p) - xk-1(p)) +
(6.5)
+ K3Θ3(zref(p + 1) - Cxk-1(p + 1)),
где
{
2,
если |E(k)| > 0,5 · 10-3,
Θ3 =
0, 25,
если |E(k)| ≤ 0,5 · 10-3,
в соответствии с теоремой 2 является стабилизирующим с дополнительной
функцией снижения энергозатрат при достижении требуемой точности. Зави-
симость среднеквадратической ошибки обучения от числа повторений пред-
ставлена на рис. 2. Требуемая точность достигается за пять повторений, после
21
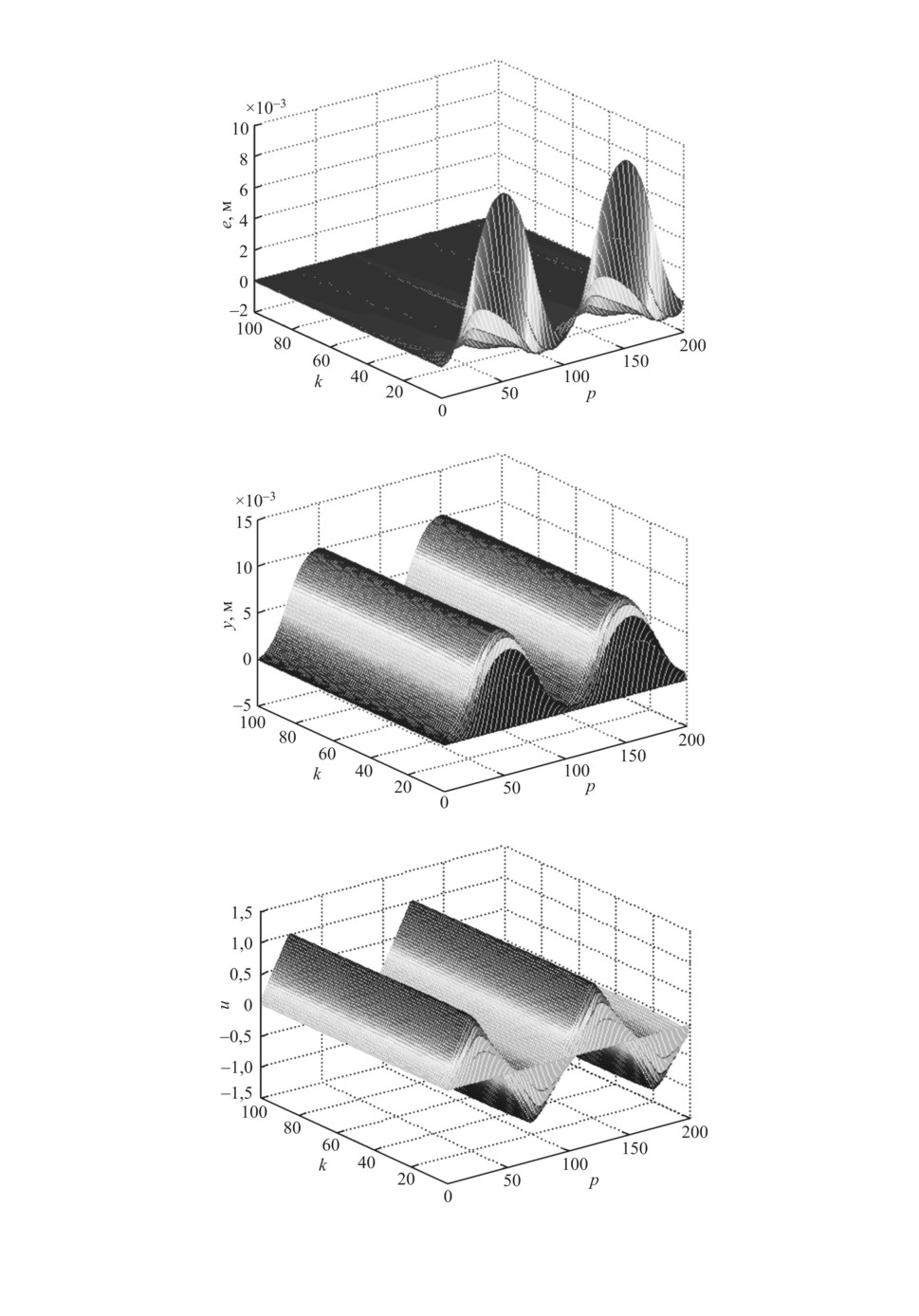
Рис. 3. Изменение ошибки обучения в зависимости от числа повторений.
Рис. 4. Изменение выходной переменной в зависимости от числа повторений.
Рис. 5. Изменение управления в зависимости от числа повторений.
22
чего ошибка продолжает монотонно уменьшаться. На рис. 3-5 для большей
наглядности представлены графики изменения ошибки, выходной перемен-
ной и управления в зависимости от числа повторений.
7. Заключение
Полученные алгоритмы управления с итеративным обучением позволя-
ют гибко изменять скорость сходимости процесса обучения в зависимости
от величины ошибки, но построение регулярной процедуры настройки алго-
ритма это отдельная задача, требующая дальнейших самостоятельных ис-
следований. В данной статье продемонстрирован лишь простейший подход с
элементами эвристики, использующий кусочно-линейное управление. Кроме
того, частный случай линейного управления, который вытекает из теорем 2
и 3, также является новым результатом. Естественным дальнейшим разви-
тием полученных результатов является разработка алгоритмов управления
с итеративным обучением стохастическими системами, в которых на объ-
ект управления действуют случайные возмущения, а измерения проводятся с
шумами. Представляет также интерес изучение свойств модифицированного
неравенства Риккати (5.10) и нахождение эффективного метода его решения.
СПИСОК ЛИТЕРАТУРЫ
1.
Bristow D.A., Tharayil M., Alleyne A.G. A survey of Iterative Learning Control //
IEEE Control Syst. Magazine. 2006. V. 23. No. 3. P. 96-114.
2.
Ahn Hyo-Sung, Chen Yang Quan, Moore K.L. Iterative Learning Control: Brief
Survey and Categorization
// IEEE Trans. Syst., Man, Cybernet. Part C:
Applications and Reviews. 2007. V. 37. No. 6. P 1099-1121.
3.
Ahn Hyo-Sung, Moore K.L., Chen Yang Quan. Iterative Learning Control.
Robustness and Monotonic Convergence for Interval Systems. London: Springer-
Verlag, 2007.
4.
Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Dynamic Systems by
Learning: A New Control Theory for Servomechanism or Mechatronic Systems //
Proc. 23rd Conf. Decision Control. 1984. P. 1064-1069.
5.
Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Robots by
Learning // J. Robot. Syst. 1984. V. 1. No. 2. P. 123-140.
6.
Hladowski L., Galkowski K., Cai Z., Rogers E., Freeman C., Lewin P. Experimentally
Supported 2D Systems Based Iterative Learning Control Law Design for Error
Convergence and Performance // Control Eng. Pract. 2010. V. 18. P. 339-348.
7.
Shen D., Wang Y. Survey on Stochastic Iterative Learning Control // J. Process
Control. 2014. V. 24. P. 64-77.
8.
Shen D. A Technical Overview of Recent Progresses on Stochastic Iterative Learning
Control // Unmanned Syst. 2018. V. 6. No. 3. P. 147-164.
9.
Jayawardhana R.N., Ghosh B.K. Observer Based Iterative Learning Controller
Design for MIMO Systems in Discrete Time // Proc. 2018 Ann. Amer. Control
Conf. (ACC). 2018. P. 6402-6408.
10.
Jayawardhana R.N., Ghosh B.K. Kalman Filter Based Iterative Learning Control
for Discrete Time MIMO Systems // Proc. 30th Chinese Control and Decision Conf.
(2018 CCDC). 2018. P. 2257-2264.
23
11.
Saab S.S. A discrete-Time Stochastic Learning Control Algorithm // IEEE Trans.
Autom. Control. 2001. V. 46. P. 877-887.
12.
Paszke W., Rogers E., Patan K. Observer-Based Iterative Learning Control Design
in the Repetitive Process Setting // IFAC-PapersOnline. 2017. V. 50. No. 1. P. 13390-
13395.
13.
Rogers E., Galkowski K., Owens D.H. Control Systems Theory and Applications for
Linear Repetitive Processes // Lect. Notes Control Inform. Sci. Berlin: Springer-
Verlag, 2007. V. 349.
14.
Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Dissipivity and
Stabilization of Nonlinear Repetitive Processes // Syst. & Control Lett. 2016. V. 91.
P. 14-20.
15.
Галковский К., Емельянов М.А., Пакшин П.В., Роджерс Э. Векторные функ-
ции Ляпунова в задачах устойчивости и стабилизации дифференциальных по-
вторяющихся процессов // Изв. РАН. Теория и системы управления. 2016. № 4.
С. 5-17.
Galkowski K., Emelianov M., Pakshin P., Rogers E. Vector Lyapunov Functions for
Stability and Stabilization of Differential Repetitive Processes // J. Comput. Syst.
Sci. Int. 2016. V. 55. P. 503-514.
16.
Goldsmith P.B. On the Equivalence of Causal LTI Iterative Learning Control and
Feedback Control // Automatica. 2002. V. 38. No. 4. P. 703-708.
17.
Goldsmith P.B. Author’s reply to “On the Equivalence of Causal LTI Iterative
Learning Control and Feedback Control”// Automatica. 2004. V. 40. No.
5.
P. 899-900.
18.
Owens D.H., Rogers E. Comments on “On the Equivalence of Causal LTI Iterative
Learning Control and Feedback Control” // Automatica. 2004. V. 40. No.
5.
P. 895-898.
19.
Willems J.C. Dissipative Dynamical Systems part I: General Theory // Arch. Ration.
Mech. Anal. 1972. V. 45. P. 321-351.
20.
Byrnes C.I., Isidori A., Willems J.C. Passivity, Feedback Equivalence and the Global
Stabilization of Minimun Phase Nonlinear Systems // IEEE Trans. Autom. Control.
1991. V. 36. P. 1228-1240.
21.
Fradkov A.L., Hill D.J. Exponential Feedback Passivity and Stabilizability of
Nonlinear Systems // Automatica. 1998. V. 34. P. 697-703.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 19.07.2018
После доработки 30.08.2018
Принята к публикации 08.11.2018
24