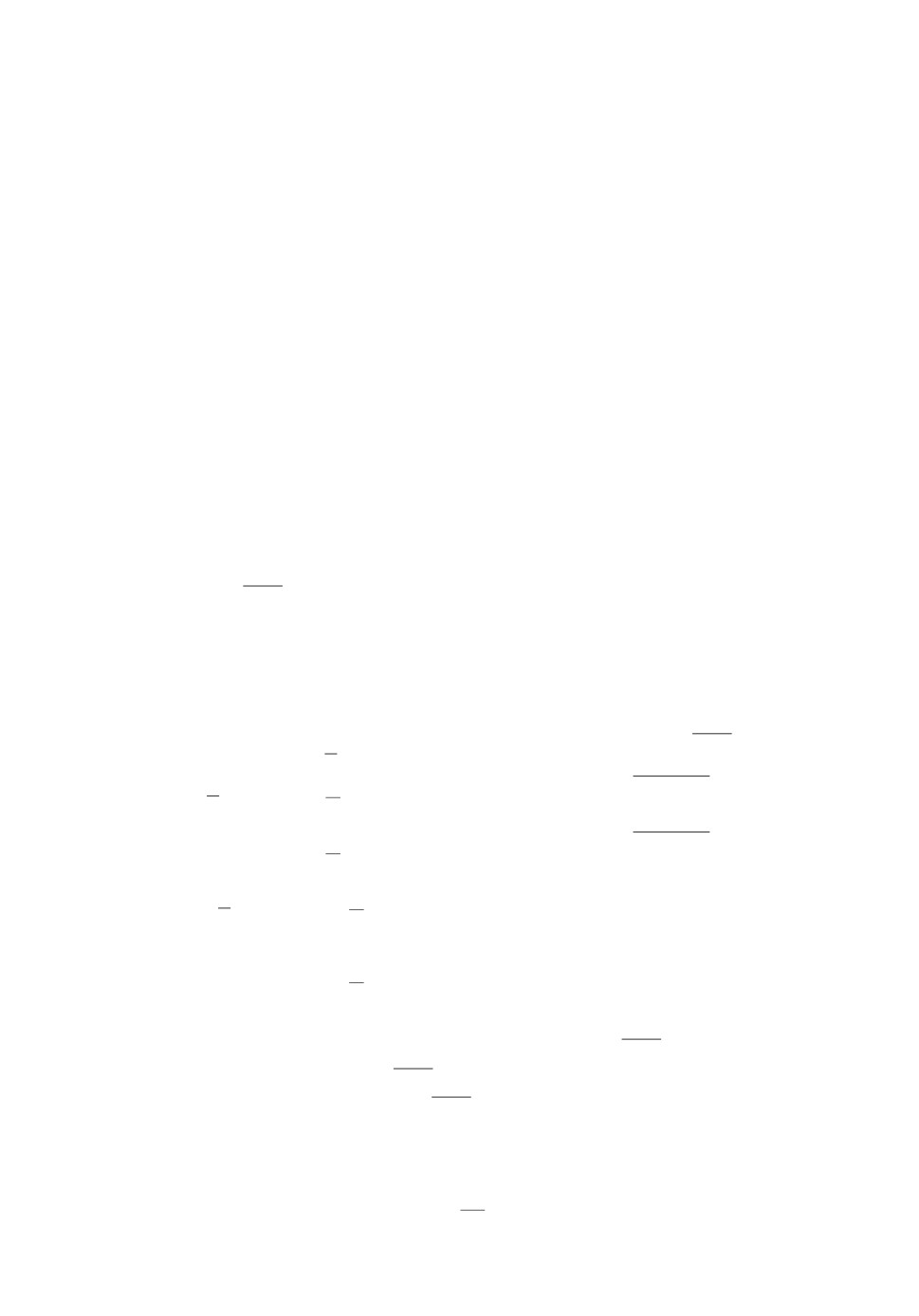Автоматика и телемеханика, № 9, 2019
© 2019 г. В.М. КУНЦЕВИЧ, д-р техн. наук (vsevolod.kuntsevich@gmail.com)
(Институт космических исследований
Национальной академии наук Украины, Киев)
ОЦЕНКИ ВОЗДЕЙСТВИЯ ОГРАНИЧЕННЫХ ВОЗМУЩЕНИЙ
НА НЕЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ
И ИХ МИНИМИЗАЦИЯ1
Получено решение задачи минимизации воздействия ограниченных
возмущений на некоторые классы управляемых нелинейных дискретных
систем. Мерой воздействия возмущений принят радиус инвариантного
множества — аналог дисперсии при вероятностной природе возмущения.
Рассмотрены случаи с двусторонними линейными и нелинейными огра-
ничениями, образующими многозначные отображения, а также случай,
когда для нелинейной функции задана оценка по норме.
Ключевые слова: робастное управление, нелинейные дискретные системы,
ограниченные возмущения.
DOI: 10.1134/S0005231019090046
1. Введение
Проблема анализа воздействия ограниченных возмущений на динамиче-
ские системы интенсивно исследуется в последние несколько десятилетий.
Для класса линейных, как непрерывных, так и дискретных систем с числовы-
ми матрицами, получены существенные результаты по определению оценок
воздействия таких возмущений на эти системы и управлений, минимизирую-
щих меру их воздействия. В [1] подведен определенный итог результатов,
полученных при решении этой проблемы.
Иначе обстоит дело с решением задач определения меры воздействия огра-
ниченных возмущений на нелинейные динамические системы и отысканием
управлений, минимизирующих в том или ином смысле воздействие этих воз-
мущений. В приложениях достаточно часто неизвестен точный вид нелиней-
ных функций математических моделей объекта управления, а известны лишь
те или иные их оценки. Поэтому ниже рассмотрим именно такие случаи.
В имеющихся немногочисленных публикациях, посвященных решению этих
задач (см. [2-4]), используется представление нелинейных функций в ква-
зилинейной форме, что существенно ограничивает класс рассматриваемых
нелинейных систем.
В настоящее время для управления динамическими системами различной
природы и различного назначения используется исключительно цифровая
техника и измерения и управление осуществляются в дискретные моменты
времени, поэтому ниже будут рассмотрены лишь дискретные математические
модели динамических систем.
1 Посвящается 100-летию со дня рождения академика Якова Залмановича Цыпкина.
25
2. Минимизация воздействия возмущений на системы с нелинейными
функциями с двухсторонними линейными ограничениями
Постановка задачи. Задано семейство систем
(2.1)
Xn+1 = AXn + f(Xn)B + SUn + Zn.
Здесь Xn ∈ Rm, A - матрица (m×m), BT = (0, . . . , 0, 1), S - матрица (m × m),
det S = 0, Zn ∈ Rm - возмущение, для которого задана, как это часто бывает
в приложениях, его интервальная оценка
(2.2)
Zn ∈ Z = z1 × z2 × ... × zm,
где zi = {zi : |zi| ≤ σi}, i = 1; m, f(Xn) - нелинейная знакопеременная функция
скалярного аргумента, f(Xn) = f[σ(Xn)], σ(·) = CTXn, ∥C∥ = 0 и f(0) = 0.
Функция f[σ(Xn)] удовлетворяет линейным ограничениям
(2.3)
0 < kσ(·) ≤ f(·) ≤ kσ(·), σ(·) = CTXn
≥ 0,
(2.4)
kσ(·) ≥ f(·) ≥ kσ(·), σ(·) = CTXn
≤ 0.
Нужно определить управление, минимизирующее в оговоренном ниже
смысле воздействие возмущений Zn ∈ Z на семейство систем (2.1)-(2.4).
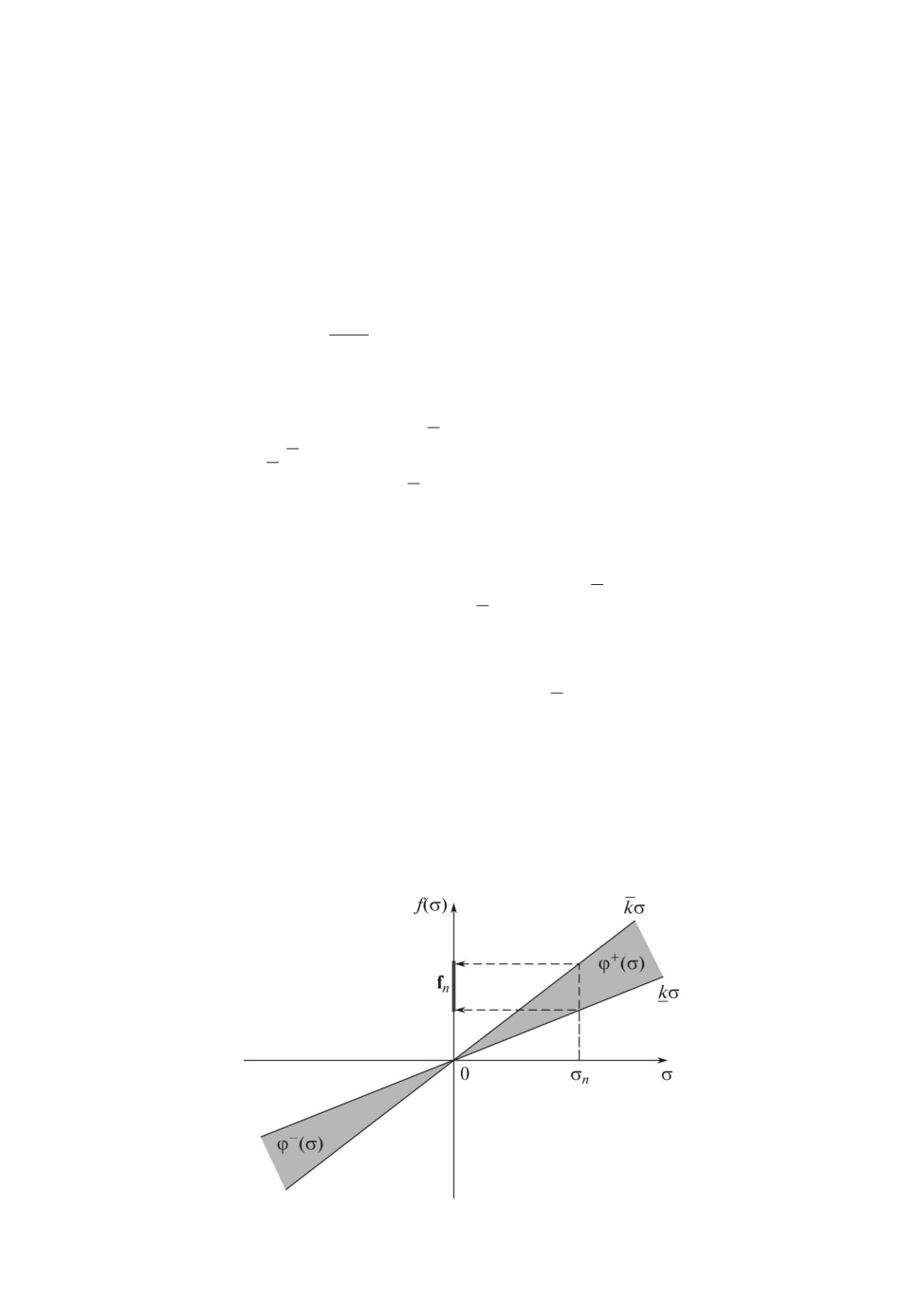
Многозначное отображение (2.3), (2.4) с линейными границами преобра-
зует величины σn в интервалы fn = {f : kσn ≤ fn ≤ kσn}. Размеры (радиусы)
интервалов fn линейно зависят от σn (см. рис. 1). Поэтому система (2.1)-(2.4)
является семейством линейных систем
(2.5)
Xn+1 = (A + kBCT)Xn + SUn + Zn, k ≤ k ≤k, Zn
∈ Z.
Отметим, что класс автономных непрерывных систем
X
= AX + f[σ(X)]B
с нелинейной скалярной функцией, удовлетворяющей ограничениям (2.3),
(2.4), начиная с пионерской работы А.И. Лурье и В.Н. Постникова [5], ак-
Рис. 1.
26
тивно исследовался в работах М.А. Айзермана и Ф.Р. Гантмахера, Е. Джури,
Р. Калмана, В. Пoпова, Я.З. Цыпкина, В.А. Якубовича и др. в рамках проб-
лемы, получившей впоследствии название “исследование абсолютной устой-
чивости”.
Утверждение 1. Исследование нелинейной системы (2.1) с неопреде-
ленностью относительно нелинейной функции, заданной в виде многознач-
ного отображения (2.3), (2.4) с линейными границами, сводится к исследо-
ванию семейства линейных систем (2.5).
Из утверждения 1 следует, что для дискретных систем
Xn+1 = AXn + f[σ(Xn)]B
с ограничениями на нелинейную функцию f(·) в виде (2.3), (2.4) дискретный
аналог гипотезы Айзермана справедлив. Выдвинутая М.А. Айзерманом ги-
потеза [6] для класса непрерывных систем с нелинейной функцией, удовлет-
воряющей ограничениям (2.3), (2.4), в общем случае неверна. Введя до-
полнительное ограничение на величину ∂f(σ)/∂σ, Р. Калман сузил класс
нелинейных функций, для которых гипотеза Айзермана, т.е. уже гипотеза
Айзермана-Калмана, верна (подробнее об этом см. в [7]).
Вернемся к рассмотрению системы (2.5) и введем числовую меру воздей-
ствия возмущений Zn ∈ Z на семейство динамических систем (2.1)-(2.4).
Если ∥A∥, ∥C∥ и радиус (размер) интервала fn таковы, что существует
непустое множество линейных уравнений
Un = HXn,
где H- матрица m × m, то выбором матрицы H можно обеспечить робастную
устойчивость семейства автономных систем
(
)
(2.6)
Xn+1 =
A+kBCT +SH
Xn, k ∈ χ = {k : k ≤ k ≤k}.
При этом семейство систем (2.6) имеет ограниченное инвариантное множе-
⋆
⋆
⋆
ство
X, т.е. такое множество, что если Xn ∈
X, то Xn+1 ∈
X при всех воз-
можных Zn ∈ Z.
В качестве меры воздействия возмущений на семейство систем (2.1)-(2.4),
⋆
⋆
(2.6) примем радиус R(X) множества
X, определяемый как
⋆
(2.7)
R(X) = max∥X∥ .
⋆
X∈X
Тогда целью управления Un примем минимизацию радиуса инвариантно-
⋆
го множества
X. Для этого необходимо, прежде всего, определить величи-
⋆
ну R(X) как функцию параметров системы (2.1)-(2.4).
Примем, что для вектора Xn имеется его интервальная оценка
Xn ∈Xn = x1n × x2n × ... × xmn,
xin = {xi : xin ≤ xi ≤ xin}, i = 1;m.
27
Тогда из (2.1), (2.2), (2.5), (2.6) следует, что это семейство линейных систем
описывается линейным разностным включением
(2.8)
Xn+1 ∈ Xn+1 = X′n+1(Xn,Un
) + Z,
где
⋃
X′n+1(Xn,Un) =
[(A + kBCT)Xn] + SUn.
Xn∈Xn
k ∈χ
Множество X′n+1(·) - неинтервальное множество. Существенные затраты
вычислительного характера, связанные с приближенным определением па-
раметрического множества X′n+1(·) общего вида, и трудности, связанные с
его дальнейшим использованием, оправдывают, как было предложено в [8],
аппроксимацию этого множества интервальным множеством минимального
объема
X′
n+1
(Un) = x′1,n+1(u1n) × . . . × x′m,n+1(umn).
Введем обозначения
(2.9)
Ũn = SUn
и через ũin, i = 1; m, обозначим элементы вектораŨn. Тогда с учетом соот-
ношения (2.9) выражение для множестваX′n+1(Un) перепишем в виде
X′
(2.10)
n+1
(Ũn) = x′1,n+1(ũ1n) × ... × x′m,n+1(ũmn
),
где
{
}
x′i,n+1 =
xi : x′i,n+1(ũin) ≤ xi ≤ x′i,n+1(ũin)
,
i = 1;m,
{
}
(2.11)
x′i,n+1 = min
γi(·) = ATiXn + ũin
,
i = 1;m - 1,
Xn∈Xn
{
}
(2.12)
x′i,n+1 = max
γi(·) = ATiXn + ũin
,
i = 1;m - 1,
Xn∈Xn
{
}
(2.13)
x′m,n+1 = min
γm(·) = (ATm + kCT)Xn + ũmn
,
Xn∈Xn
k∈χ
{
}
(2.14)
x′m,n+1 = max
γm(·) = (ATm + kCT)Xn + ũmn
Xn∈Xn
k∈χ
Отметим, что интервальные множества x′i,n+1, i = 1; m, - проекции мно-
жества X′n+1(·) на оси 0xi, i = 1; m.
Так как функции γi(·), i = 1; m, билинейные, то решения задач
(2.11)-(2.14) принадлежат вершинам Xln множестваXn. Интервальное мно-
жествоXn (2.10) запишем в виде
Xn = conv{Xln},
s=1;L
28
где Xln - l-я вершина многогранникаXn, и перепишем задачи (2.11)-(2.14) в
виде
{
}
x′i,n+1 = min ATiXl
+ũin
,
n
s=1;L
(2.15)
{
}
i = 1;m - 1.
x′i,n+1 = max ATiXl
+ũin
,
n
s=1;L
}
{(
)
x′1,n+1 = min
ATm + kjCT
Xln + ũmn
,
s=1;L
j=1;2
(2.16)
{(
)
}
x′1,n+1 = max
ATm + kjCT
Xln + ũmn
,
s=1;L
j=1;2
где k1 = k и k2 =k.
Экстремумы комбинаторных задач (2.15), (2.16), принимая во внимание
их невысокую размерность, найдем полным перебором всех вариантов. По-
лученные величины x′i,n+1, x′i,n+1, i = 1; m, определяют искомое множество
Xn+1 = Γ[Xn(Ũn)].
Далее рассмотрим эволюцию интервальных множествXn,
(2.17)
Xn+1 = Γ[Xn(Ũn
)] + Z.
∑m
При выборе нормы X в (2.7) в виде ∥Xn∥1 =
|xi| радиус интерваль-
i=1
ного множества (2.17) равен
∑
(2.18)
R(Xn) = r(xi
),
i=1
где r(xi) - радиус одномерного интервального множества xi = {xi : xi ≤ xi ≤
≤ xi}, равный r(xi) = |xi - xi|.
Задача
minR(Xn)
Ũn
в силу (2.18) сводится к решению задач
{
}
(2.19)
min ri
γi[Xn(ũin)]
,
i = 1;m.
ũin
Так как множествоXn центрально-симметрическое, то справедливы ра-
венства
(2.20)
),
i = 1;m.
xi,n+1(ũin) = -xi,n+1(ũin
29
2.1. Решение задачи синтеза управления
Из (2.19), (2.20) следует, что
ri(ũin) = |xin(ũin) - xin(ũin)| = 2|xin(ũin)|
и, следовательно,
{
ri
γi
[Xn(ũin)]} = 2ri [xi,n+1(ũin)], i = 1;m.
Итак, для получения гарантированного результата управления
ũin,
i = 1;m, будем искать как решения задач
(2.21)
min max
ATiXn + zin + ũin
, i = 1;m - 1,
ũin Xn∈Xn
zin∈Zi
AT
(2.22)
min max
+ k(CT)Xn) + zmn + ũmn.
m
ũmn Xn∈Xn
k∈χ
zmn∈zm
В общем случае минимаксные задачи не имеют аналитических решений, и
задачи (2.21), (2.22) не являются исключением из этого правила. Использо-
вание численных методов решения задач (2.21), (2.22) неприемлемо прежде
всего потому, что это не дает возможности провести анализ устойчивости
автономной системы (2.6), а именно, проверки необходимого условия суще-
ствования ограниченного инвариантного множества системы (2.8). Поэтому
ограничимся использованием лишь субоптимального управления. В [9] для
минимаксных задач
min max
ATiXn + ũin,
i = 1;m - 1,
ũin Xn∈Xn
[
]
◦
T
min max
+(k + Δk)CT Xn + ũmn
A
m
,
ũmn Xn∈Xn
Δk∈δχ
◦
где
k = 0,5(k + k), Δk = k + 0,5(k - k), получены их аналитические решения
◦
(2.23)
ũ∗in = -ATiXn, i = 1;m - 1,
ũ∗mn = -(ATm +
kCT)Xn.
Если условие ∥Zn∥1 ≤ ε выполняется для всех n ∈ [0, ∞), где ε - достаточ-
но малая величина, то полученные управления являются субоптимальными.
По определенному соотношениями (2.23) векторуŨ∗n определим искомый
∗
вектор субоптимального управления
Un = S-1 Ũn.
∗
Подставив найденное управление
Un в (2.5), получим уравнение семейства
систем
(2.24)
Xn+1 = (ΔkBCT)Xn + Zn,
◦
где Δk ∈ δχ = χ -
k, Zn ∈ Z.
30
Для оценки вектора Xn из (2.24) получим
⋃
(2.25)
Xn+1 ∈Xn+1 =
(ΔkBCT)Xn
+Z.
Xn∈Xn
Δk∈δχ
Отметим, что множество (2.25) интервальное.
Величины нижних x∗in и верхних
x∗in пределов интервальных мно-
жеств xi,n+1, i = 1; m, в (2.25) получим из решения задач
(2.26)
x∗in = min
CTXn,
x∗in = max CTXn
, i = 1;m - 1,
Xn∈Xn
Xn∈Xn
(2.27)
x∗mn = min
ΔkCTXn,
x∗mn = max
ΔkCTXn.
Xn∈Xn
Xn∈Xn
Δk∈δχ
Δk∈δχ
Решения задач (2.26)-(2.27) с точностью до обозначений совпадают с ре-
шениями задач (2.11)-(2.14). Величины x∗in, x∗in, i = 1; m, определяют интер-
вальное множество
∗
(2.28)
X∗
=
Γ(Xn
).
n+1
Тогда получим уравнение эволюции интервальных множеств
∗
(2.29)
Xn+1 =
Γ(Xn
) + Z.
∗
Приняв в (2.29)Xn+1 = Xn =
X, получим уравнение
∗
∗
∗
X=
Γ(X) + Z,
определяющее искомое интервальное инвариантное множество семейства си-
стем.
Выше было принято, что параметры системы (2.1)-(2.4) таковы, что су-
ществует такое множество управлений Un, которое обеспечивает робастную
устойчивость систем (2.6). Но в общем случае класс систем может быть на-
столько широк (радиус интервала χ настолько велик), что для семейства
систем (2.6) не существует управления, обеспечивающего его устойчивость.
Поэтому необходима проверка устойчивости системы.
Ограничимся здесь лишь требованием выполнения достаточных условий
устойчивости линейных дискретных систем
(2.30)
max
ATi
≤ qi < 1, i = 1;m - 1, max
ATm + kCT≤ qm
< 1.
k≤k≤k
∗
В m-мерном пространстве элементов aij, где j = 1;m, множество
Ai,
удовлетворяющее условиям
(2.30), определяет m-мерный центрально-
31
ai3
1
ai2
1
1
1
ai1
0
1
1
Рис. 2.
симметрический выпуклый многогранник как выпуклую оболочку, натяну-
тую на систему векторов
⎧
1
-1
0
0
0
0
⎫
⎪
⎪
0
⎨
0
0
1
-1
0
⎬
∗
0
0
0
0
Ai = conv
m.
⎪
⎪
⎩
⎭
0
0
0
0
0
0
1
-1
%
&'
(
2m
∗
На рис. 2 при m = 3 показано множество
Ai.
Семейство систем (2.28) устойчиво, если имеют место условия
{
}
(2.31)
Ai ∈ Ai = ATi : ∥ ATi ∥1 < 1
,
i = 1;m,
и тогда система
(2.29) имеет ограниченное инвариантное множество.
Я.З. Цыпкин и Б.Т. Поляк в [10] вывели достаточное условие для включе-
ния (2.31).
Примем, что эти достаточные условия робастной устойчивости (2.30) вы-
полняются и, следовательно, система (2.29) имеет ограниченное инвариант-
∗
ное множество
X.
Определим радиус инвариантного множества системы (2.29).
32
∗
Так как множество
X интервальное, а радиус суммы по Минковскому двух
интервальных множеств равен сумме их радиусов, то
[
(
)
]
[
(
)]
∗
∗
∗
∗
(2.32)
R Γ
X +Z =R
Γ
X
+ R(Z).
∗
∗
Поскольку система (2.28) линейная, то справедливо равенство R[Γ(X )] =
∗
= αR(X).
Так как семейство систем (2.28) асимптотически устойчиво, то α ≤ q < 1.
∗
Тогда из (2.32) получаем оценку снизу радиуса инвариантного множества
X
в виде
∗
R(Z)
R(X) ≤
1-q
∗
Радиус R(X) интервального инвариантного множества — аналог величины
дисперсии при стохастической природе возмущения.
3. Минимизация воздействия возмущений на системы с нелинейными
функциями с двухсторонними нелинейными ограничениями
Постановка задачи: задано семейство систем (2.1), (2.2), а нелинейная
функция f[σ(Xn)] задана с точностью до сомножителя k, о пределах измене-
ния которого известно, что 1 > k ≤ k ≤k, т.е.
∗
(3.1)
k
f [σ(Xn)], σ(Xn) = CTXn.
∗
∗
Функция
f (·)
— монотонная знакопеременная, такая что
f (0) = 0 и
∗
∗
f [-σ(Xn)] = -f [σ(Xn)]. Двухсторонние ограничения (3.1) определяют мно-
гозначное отображение η(σn), поэтому далее будем говорить о системе (2.1),
(2.2) с многозначным отображением
{
}
∗
∗
∗
(3.2)
η(σn) = σn : 0 < kf (σn) ≤
f (σn) ≤kf (σn)
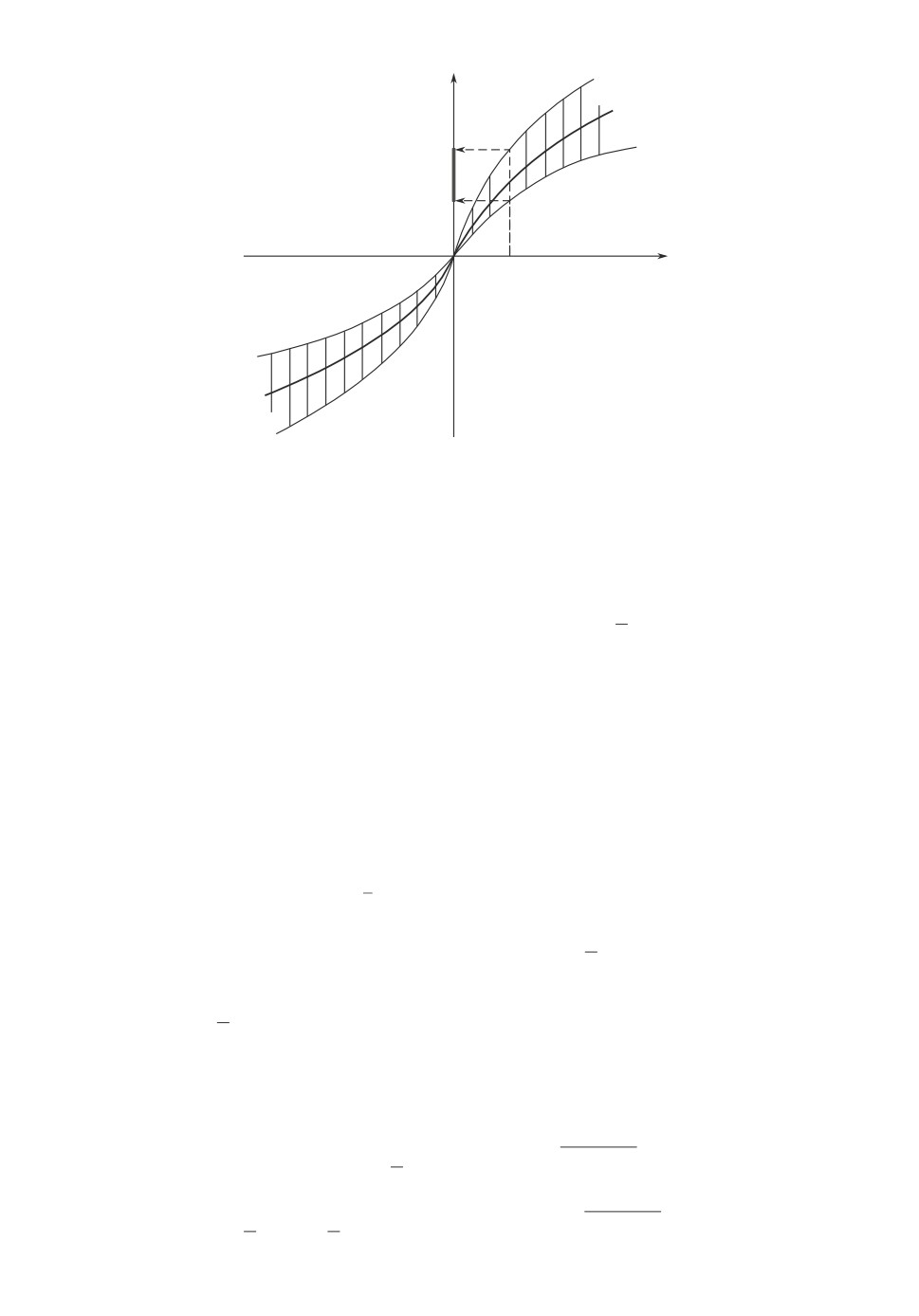
Многозначное отображение η(X) с нелинейными границами преобразует ве-
∗
∗
личины σn в интервалы fn = {f : kf (σn) ≤
f (σn)}, размеры (радиу-
сы) которых нелинейно зависят от σn (см. рис. 3).
Требуется определить управление для семейства систем (2.1), (2.2), (3.2)
(3.3)
Un = Γ(Xn
),
минимизирующее радиус инвариантного множества семейства систем (2.1),
(2.2), (3.2), (3.3) при условии, что параметры этого семейства систем таковы,
33
f
k f (n)
*
f (n)
fn
k f (
n)
0
n
Рис. 3.
что при управлении (3.2) инвариантное множество ограничено. Необходимым
условием этого является робастная устойчивость семейства автономных си-
стем
Xn+1 = AXn + kη(Xn)B + SΓ(Xn),
1<k≤k≤k.
Примем, что требуемое множество управлений (3.2) не пусто. Определим
радиус инвариантного множества как функцию параметров семейства систем
(2.1), (2.2), (3.2), (3.3). Для этого определим уравнение эволюции множества
этого семейства систем. Общая схема решения этой задачи остается такой же,
как и выше, но с внесением необходимых изменений, учитывающих наличие
нелинейных ограничений на нелинейную функцию. Так как множество
[
]
⋃
∗
X′n+1 =
AXn + kf (·)B + SUn
Xn∈Xn
k≤k≤k
неинтервальное, то, как и выше, аппроксимируем его интервальным множе-
ством минимального объема (2.20), где величины x′′m,n+1, x′′m,n+1, в отличие
от (2.11)-(2.14), определяются в виде
{
}
(3.4)
x′′m,n+1 = min
ψm(·) = ATmXn + η(σn) + ũmn
,
Xn∈Xn
ATm∈Am
{
}
(3.5)
x′′m,n+1 = max
ψm(·) = ATmXn + η(σn) + ũmn
,
Xn∈Xn
ATm∈Am
гдеŨn = S-1Un, а для величин x′′i,n+1, x′′i,n+1, i = 1; m - 1, в силу оговоренных
∗
свойств функции
f (·) и центрально-симметричности множествXn справед-
ливы равенства x′′i,n+1 = x′i,n+1, x′′i,n+1 = x′i,n+1, i = 1; m - 1.
34
Экстремумы монотонной функции ψm(·) принадлежат вершинам Xln вы-
пуклого центрально-симметрического множества
Xn и границам k1 = k,
k2 =k интервала значений k. Поэтому задачи (3.4), (3.5) заменим комбина-
торными задачами
{
}
∗
∗
x′′m,n+1 = min
ATmXln + kjf (σln)
,
x′′m,n+1 = max
{ATmXln + kjf (σln)}.
l=1;2m
l=1;2m
j=1;2
j=1;2
Принимая во внимание невысокую размерность этих задач, их реше-
ния найдем полным перебором всех вариантов. Найденные величины x′′i,n+1,
x′′i,n+1, i = 1;m - 1, и величины x′′m,n+1, x′′m,n+1 определяют эволюцию семей-
ства интервальных множеств
(
)
[
Xn+1 = G
Xn(Ũn) , G(·) = gm
γm
(Xn(ũmn))] × ... × gm [γm (Xn(ũmn))].
Радиус множества G(Xn) (2.18) определяется как сумма радиусов ri(·) =
= 2[xi,n+1(ũin)], i = 1; m.
3.1. Решение задачи синтеза управления
Для получения гарантированного результата управления ũin, i = 1; m, бу-
дем искать из решения задач
(3.6)
min max
ATiXn + zin + ũin
,
i = 1;m - 1,
ũin Xn∈Xn
zin∈zi
∗
T
(3.7)
min max
Xn + kf [σ(Xn)] + zmn + ũmn
A
m
.
ũmn Xn ∈Xn
zmn∈zm
k∈χ
Представим множество χ в центрированной форме
◦
◦
χ=
k + δχ,
k = 0,5(k + k), Δk ∈ δχ = {Δk : |Δk| ≤ 0,5(k - k)}
и минимаксные задачи (3.6), (3.7) запишем в виде
(3.8)
min max
ATiXn + zin + ũin
,
i = 1;m - 1,
ũin Xn∈Xn
zin∈zi
◦
∗
T
(3.9)
min max
Xn + (k + Δk)f [σ(Xn)] + zmn + ũmn
A
m
.
ũmn Xn ∈Xn
zmn∈zm
Δk∈δχ
В силу изложенных выше причин, также как и выше, откажемся от чис-
ленного решения задач (3.8), (3.9) и ограничимся полученными в [9] субоп-
тимальными управлениями
(
)
◦
∗
(3.10)
ũ∗in = -AiXn, i = 1;m - 1,
ũ∗mn = - AmXn +
k
f [σ(Xn)]
35
Ũ∗
По определенному вектору
находим искомый вектор управления
n
∗
∗
Un = B-1 Ũ∗n. Подставив найденное управление
Un в уравнение движения се-
мейства систем (2.1), (2.2), (3.2),
◦
∗
[
]
Xn+1 = AXn +(k+Δk)f
σ(Xn) = CTXn
B+SUn+Zn, Zn ∈Z, Δk ∈δχ,
получим
∗
(3.11)
Xn+1 = Δkf [σ(Xn)] BCTXn + Zn, Δk ∈ δχ, Zn
∈ Z.
Если для Xn задана его оценка (2.10), то из (3.11) получим уравнение эволю-
ции множестваXn в виде
(3.12)
Xn+1 = G∗(Xn
) + Z,
где
⋃
∗
G∗(X) =
Δkf (·)BCTXn.
Xn∈Xn
Δk∈δχ
Множество G∗(Xn) определяется величинами нижних и верхних x∗in, x∗in,
i = 1;m, пределов интервальных множеств gi(Xn), i = 1;m. Эти величины
получим из решения задач, аналогичных задачам (2.26), (2.27).
∗
ПринявXn+1 = Xn =
X и подставив эти величины в (3.12), получим урав-
нение
∗
∗
(3.13)
X=G∗(X) + Z,
∗
решение которого определяет инвариантное множество
X.
∗
Система (3.13) имеет ограниченное инвариантное множество
X только то-
гда, когда соответствующая ей автономная система
(3.14)
Xn+1 = G∗(Xn)
асимптотически устойчива в целом или в области, содержащей начало коор-
динат.
Откажемся от избыточного в приложениях требования сохранения устой-
чивости в целом и ограничимся требованием устойчивости в области. Для
анализа устойчивости семейства автономных систем (3.13) воспользуемся ре-
зультатом работы [11], в которой принцип сжатых отображений обобщен на
класс нелинейных разностных включений.
Теорема 1
[11]. Введем функцию Ляпунова в форме
ρ(Xn) = max ∥X∥.
X∈Xn
36
Если ее первая разность, вычисленная вдоль траектории системы (3.14),
отрицательно определенная, т.е.
(3.15)
Δυn = υn+1 - υn = ρ[F(Xn)] - ρ(Xn
)<0
∀n,
то тривиальное решение системы (3.14) асимптотически устойчиво.
Следствие 1. Если начало координат - центр множества Xn, т.е.
центр сферы минимального радиуса, описанной вокруг Xn, является на-
чалом координат, то значение функции ρ(Xn), вычисленной по уравне-
нию (3.14) при использовании нормы ∥X∥1, совпадает с радиусом описан-
ной сферы, и из выполнения неравенства (3.15) следует, что имеет место
включение
(3.16)
Xn+1 ⊂ Xn.
Нетрудно показать, что для интервальных множеств Xn и Xn+1 с цен-
трами в начале координат строгое включение (3.16) имеет место, если
и только если по крайней мере одно из системы нестрогих неравенств
xi,n+1(ũin) ≥ xin(ũin), xi,n+1(ũin) ≤ xin(ũin), i = 1;m, является строгим.
Примем, что многозначное отображение (3.2) таково, что для множества
Xn+1 = G∗(Xn) имеет место включение Xn+1 ⊂ Xn, что является достаточ-
ным условием устойчивости семейства нелинейной системы (3.14) и необхо-
димым условием существования ограниченного инвариантного множества си-
стемы (3.13). В общем случае возможна такая ситуация, когда несмотря на
∗
то, что управление
Un субоптимально в оговоренном смысле, из этого не
следует, что оно гарантирует робастную устойчивость семейства нелинейных
систем (3.14), так как это семейство систем в общем случае может быть на-
столько широким (радиус множества δχ настолько велик), что не существует
управления, обеспечивающего робастную устойчивость всего этого семейства
систем.
Определить в аналитической форме решение нелинейного уравнения (3.13)
∗
относительно искомого множества
X невозможно, и оно может быть найдено
лишь с помощью какой-либо итерационной процедуры. В качестве начального
∗
∗
приближения примем
X0 = Z. Далее на первом шаге определяем G(X1) и
∗
∗
∗
находим величины ri(xi,1), i = 1;m, и Δri = ri(xi,1) - ri(xi,0), i = 1;m. Затем
∗
действуем по правилу деления отрезков Δri,p пополам, а величины ri(xi,p),
i = 1;m, где p - номер итерации, изменяем по алгоритму
∗
∗
ri,p+1(xi,p+1) = ri(xi,p) + 0,5Δri,p, i = 1;m.
Этот итерационный процесс продолжаем до тех пор, пока не будут выпол-
нены неравенства |Δri,p| ≤ ε, i = 1; m, где ε - заданная допустимая погреш-
ность.
Предложенный алгоритм обеспечивает сходимость процесса итераций со
скоростью геометрической прогрессии.
37
4. Минимизация воздействия возмущений на системы
с ограничениями по норме
Постановка задачи: задано семейство систем (2.1), (2.2), но скалярная
нелинейная функция f(Xn) - функция векторного аргумента - имеет вид
∑
(4.1)
f (Xn) = k
|xin|sign(CTXn),
1>k≤k≤k
i=1
Соотношение (4.1) определяет многозначное отображение вектора Xn в
интервал
{
}
(4.2)
fn =
f : k∥Xn∥1 ≤ k∥Xn∥1 ≤ k∥Xn∥1
,
размеры (радиусы) которого нелинейно зависят от ∥Xn∥1, а положение на
оси 0x определяется значением sign(CTXn). Поэтому исследование системы
(2.1), (2.2), (4.1) сводится к исследованию семейства нелинейных систем
(4.3)
Xn+1 = AXn + kf(Xn)B + SUn + Zn,
где 1 > k ≤ k ≤k, Zn ∈ Z.
Требуется определить управление
(4.4)
Un = Φ(Xn
),
минимизирующее радиус инвариантного множества семейства систем (2.1),
(2.2), (4.1)-(4.4) при условии, что параметры системы (2.1), (2.2), (4.1) та-
ковы, что это инвариантное множество ограничено. Необходимым условием
этого является робастная устойчивость семейства автономных систем
∑
(
)
(4.5)
Xn+1 = AXn + k
|xin| sign
CTXn
+ SΦ(Xn
).
i=1
Примем, что множество управлений (4.4) непустое.
Определим сначала радиус инвариантного множества как функцию па-
раметров семейства систем (2.1), (2.2), (4.5). Для этого определим уравне-
ние эволюции множеств этого семейства систем. Общая схема решения этой
задачи остается такой же, как и выше, но с изменениями, учитывающими
особенности рассматриваемой функции f(Xn).
При оценке вектора Xn в виде (2.8) из (2.1) и (4.4)-(4.5) следует, что ди-
намика такой системы описывается нелинейным разностным включением
⋃
∑
Xn+1 ∈ Xn+1 =
AXn + k
|xin|sign(CTXn)B + SUn + Z.
i=1
Xn∈Xn
k∈χ
Также, как и выше, введем обозначение
Ũn = SUn и неинтервальное
множество Xn+1 аппроксимируем интервальным множеством минимального
38
объемаXn+1, для которого границы xi,n+1, xi,n+1, i = 1; m - 1, интервальных
множеств xi,n+1, i = 1; m - 1, определяются соотношениями (2.15), а границы
xm,n+1, xm,n+1 интервального множества xm,n+1 - решения задач
{
}
∑
(4.6) xm,n+1 = min
γ(·) = ATmXn + k
|xi,n|sign(CTXn) + zmn + ũmn
,
Xn∈Xn
i=1
zmn∈zm
k≤k≤k
{
}
∑
(4.7)
xm,n+1 = max
γ(·) = ATmXn + k
|xi,n|sign(CTXn) + zmn + ũmn
Xn∈Xn
i=1
zmn∈zm
k≤k≤k
Экстремумы выпуклой функции γ(·) принадлежат вершинам Xln множе-
стваXn и границам k1 = k, k2 =k интервала значений k. Поэтому задачи
(4.6), (4.7) - комбинаторные задачи
{
}
m
∑
(4.8) xm,n+1(ũmn) = min
ATmXl
+kj
xli,nsign(CTXl
)+zmn +ũmn
,
n
n
l=1;2m
i=1
zmn∈zm
j=1;2
{
}
∑
(4.9)
xm,n+1(ũmn) = max
ATmXln + kj
xli,nsign(CTXl
)+zmn +ũmn
n
l=1;2m
i=1
zmn∈zm
j=1;2
Принимая во внимание невысокую размерность задач (4.8), (4.9), их реше-
∗
ния найдем полным перебором всех вариантов. Так как для функции
f (X)
∗
∗
справедливо равенство
f (-X) = -f (X), то размерность задач (4.8), (4.9)
можно существенно понизить, определяя их решения только для тех вер-
шин Xln, для которых справедливо соотношение CTXln ≥ 0. При этом спра-
ведливо равенство xm,n+1 = -xm,n+1. Поэтому определение величин xi,n+1,
xi,n+1, i = 1;m, требует решения лишь задач
{
}
m
∑
xm,n+1 = max
ATmXl
+kj
xli,n+zmn +ũmn
,
n
j=1;2
i=1
l: CTXln≥0
т.е. только для таких индексов l, для которых справедливо нестрогое нера-
венство CTXln ≥ 0.
Найденные величины xi,n+1, xi,n+1, i = 1; m, определяют семейство интер-
вальных множеств (2.10) и, следовательно, множествXn+1 = Φ[ Xn(Ũn)]. Бу-
дем далее рассматривать эволюцию интервальных множеств
Xn+1 = Φ[Xn(Ũn)] + Z.
39
Радиус R(·) множестваXn+1 в силу (2.18) равен
∑
R[Xn+1] =
ri[φi(·)],
i=1
и задача min
Xn сводится к решению задач minri[φi(·)], i = 1;m.
Un
ũin
Так как ri = 2[xi,n+1(ũin)], i = 1; m, то для получения гарантированного
результата управления ũin, i = 1; m, будем искать как решения задач
(4.10)
min max
ATiXn + zin + ũin
,
i = 1;m - 1,
ũin Xn∈Xn
zin∈zi
∑
(
)
(4.11)
min max
ATmXn + k
|xin|sign
CTXn
+zmn +ũmn
ũmn Xn∈Xn
i=1
zmn∈zm
k∈χ
Так же, как и выше, представим множество χ в центрированной форме и
перепишем минимаксные задачи (4.10), (4.11) в виде
(4.12)
min max
ATiXn + zin + ũin
,
i = 1;m - 1,
ũin Xn∈Xn
zin∈zi
◦
∑
(4.13)
min max
ATmXn + (k + Δk)
|xi,n|sign(CTXn) + zmn + ũmn
ũmn Xn∈Xn
i=1
zmn∈zm
Δk∈δχ
Так как минимаксные задачи (4.12), (4.13) не имеют решений в аналити-
ческой форме, то по изложенным выше причинам откажемся от численных
методов получения их решений и ограничимся использованием субоптималь-
ного управления, полученного с точностью до обозначений в [9] и имеющего
вид
[
(
)
]
◦
∑
ũ∗in = -ATiXn, i = 1;m-1,
ũ∗1n = - ATmXn +k
|xi,n| sign(CTXn)
i=1
∗
По найденному векторуŨ∗n определяем искомый вектор управления
Un =
∗
= B-1 Ũ∗n. Подставив управление
Un в уравнение движения системы (4.3),
получим
∑
(4.14)
Xn+1 = Δk
|xin|sign(CTXn)B + Zn, Δk ∈ δχ, Zn
∈ Z.
i=1
При оценке вектора Xn из (4.16) получим
⋃
∑
(
)
(4.15)
Xn+1 ∈ Xn+1 =
Δk
|xin|sign
CTXn
B + Z.
i=1
Xn∈Xn
Δk∈δχ
40
Отметим, что множество Xn+1, определяемое соотношением (4.15), ин-
тервальное. Воспользовавшись описанной выше методикой, найдем ниж-
ние xi,n+1 и верхние
xi,n+1, i = 1;m, границы множеств xi,n+1 = φi(Xn),
i = 1;m, и запишем соотношение (4.15) в виде
(4.16)
Xn+1 = Φ∗(Xn
) + Z.
∗
Приняв Xn+1 = Xn =
X и подставив эти величины в (4.16), получим урав-
нение
∗
∗
(4.17)
X=Φ∗(X) + Z,
∗
определяющее искомое инвариантное множество
X.
Система (4.17) имеет ограниченное инвариантное множество лишь тогда,
когда соответствующая ей автономная система
Xn+1 = Φ∗(Xn)
устойчива в целом или в заданной области.
В разделе 3 показано, что процесс эволюции множеств Xn, определяемый
уравнением (4.17), устойчив, если имеет место включение (3.16), и там же
была приведена система неравенств, выполнение которых является доста-
точным условием устойчивости нелинейной системы (4.17). Примем, что эти
условия выполняются и, следовательно, система имеет ограниченное инвари-
∗
антное множество
X.
Уравнение (4.16) не имеет аналитического решения, и поэтому для опре-
деления его решения воспользуемся подробно описанной в разделе 3 итера-
ционной процедурой.
5. Заключение
Решена задача минимизации воздействия ограниченных возмущений на
некоторые классы управляемых нелинейных дискретных динамических си-
стем. Мерой оценки воздействия ограниченных возмущений на динамиче-
скую систему принят радиус интервальных инвариантных множеств — ана-
лог величины дисперсии при вероятностной природе возмущений. Рассмот-
рены часто встречающиеся в приложениях случаи, когда для нелинейных
функций заданы лишь те или иные их оценки.
Показано, что для случая, когда ограничения, образующие многозначные
отображения на нелинейную функцию, линейны, исследование таких систем
сводится к исследованию семейств линейных систем, и показано, что дискрет-
ный аналог гипотезы Айзермана для дискретных систем справедлив. Если
ограничения, образующие многозначные отображения, нелинейны, то иссле-
дование таких систем сводится к исследованию семейств нелинейных систем.
Определение управления, обеспечивающего получение гарантированного
результата при минимизации радиуса интервального множества, сводится к
решению минимаксных задач, не имеющих решений в аналитической форме.
41
Для нелинейных систем уравнение, определяющее радиус инвариантно-
го множества, не имеет аналитического решения и искомое решение может
быть определено лишь с помощью итерационной процедуры. Предложено ис-
пользование субоптимального управления, определяемого в аналитической
форме.
Приведен пример, иллюстрирующий предложенный способ определения
инвариантного множества минимального радиуса для семейства нелинейных
систем.
Полученные результаты очевидным образом обобщаются как на случай
систем со многими нелинейностями рассмотренных видов, так и на тот слу-
чай, когда для матрицы линейной части системы задана лишь ее оценка.
ПРИЛОЖЕНИЕ
Иллюстративный пример. Для семейства систем (2.1), (2.2), (3.1) при
m = 2, имеющего вид
∗
[
]
(Π.1)
Xn+1 = AXn + kf
σ(CTXn)
B+SUn +Zn,
где A - матрица 2 × 2, BT = (0, 1), S - единичная матрица, 1 ≤ k ≤ k ≤k,
∗
[
]
(Π.2)
f
σ(CTXn)
= arctg(CTXn
),
при значениях параметров a11 = 0,5, a12 = 0,7, a21 = 0,7, a22 = 0,5, c1 = c2 =
= 1, k = 0,6, k = 1,4, и заданных априори предельных значениях возмущений
|z1| ≤ 1, |z2| ≤ 1, требуется определить субоптимальное управление (3.10) и
∗
размер соответствующего ему интервального множества
X.
Из (3.10) для (Π.1), (Π.2) имеем
(
)
◦
(Π.3)
u∗1n = -AT1Xn, u∗2n = - AT2Xn +
k arctg(CTXn)
,
◦
где AT1 = (a11, a12), AT2 = (a21, a22),
k = 0,5(k + k).
Подставив (Π.3) в (Π.1), получим
0
(Π.4)
Xn+1 =
Zn, Zn
∈ Z,
+
Δk arctg(CTXn)
◦
(Π.5)
Δk ∈ δχ = {k : k ≤ k ≤k} -
k.
∗
Ограниченное инвариантное множество
X семейства систем (Π.4), (2.2),
(Π.5) существует, если автономная система
0
(Π.6)
Xn+1 =
,
Δk ∈ δχ,
Δk arctg(x1n + x2n)
устойчива.
42
Для анализа устойчивости семейства систем (Π.6) введем функцию Ляпу-
нова
∑
(Π.7)
υn = ∥Xn∥1 =
|xin|
i=1
и определим величину Δυn = υn+1-υn вдоль траектории движения семейства
систем (Π.6) как
Δυn = |Δk arctg(x1n + x2n)| - (|x1n| + |x2n|), Δk ∈ δχ.
Нетрудно убедиться в том, что если |Δk| < 1, то Δυn < 0 и, следовательно,
семейство систем (Π.6) устойчиво.
∗
Определим интервальное инвариантное множество
X из решения уравне-
ния
∗
∗
(Π.8)
X = G(X) + Z,
используя описанную в разделе 3 итерационную процедуру. В качестве нуле-
вого приближения выберем множество
{
}
∗
1
1
-1
-1
X0 = conv
1,1
,-1,-1
Примем в качестве критерия останова итерационной процедуры величину
∗
∗
(Xp+1) - R(Xp)
ε=
R
≤0,05,
∗
R(Xp+1)
где p - номер итерации. После четырех итераций достигнем заданной точно-
сти для искомого приближенного решения
{
}
∗
1
-1
-1
1
X = conv
1,47,1.47,-1,47,-1,47
∗
∗
Соответственно, величины радиусов вычисляются как R(x1) = 2 и R(x2) =
= 2,94, а радиус построенного интервального инвариантного множества равен
∗
их сумме, R(X) = 4,94.
СПИСОК ЛИТЕРАТУРЫ
1. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-
ми при внешних возмущениях: техника линейных матричных неравенств. М.:
ЛЕНАНД, 2014.
2. Мазко А.Г. Робастная устойчивость и стабилизация динамических систем. Ме-
тоды матричных и конусных неравенств. Киев: Ин-т матем. НАН Украины,
2016.
43
3. Mazko A.G. Cone inequalities and stability of dynamical systems // Nonlinear
Dynam. Syst. Theory. 2011. V. 11. No. 3. P. 303-318.
4. Vandergraft J.S. Spectral properties of matrices which have invariant cones // SIAM.
J. Appl. Math. 1968. V. 16. P. 1208-1222.
5. Лурье А.И., Постников В.Н. К теории устойчивости регулируемых систем //
Прикл. мат. и механика. 1944. Т. 8. Вып. 3. С. 246-248.
6. Айзерман М.А. Об одной проблеме касающейся устойчивости «в большом» ди-
намических систем // Успехи мат. наук. 1949. Т. 4. Вып. 4. С. 186-188.
7. Леонов Г.А., Кузнецов Н.В. Скрытые колебания в динамических системах:
шестнадцатая проблема Гильберта, гипотезы Айзермана и Кальмана, скрытые
аттракторы в контурах Чуа // Тр. Шестой Междунар. конф. по дифференц. и
функцион.-дифференц. уравнениям (Москва, 14-21 августа, 2011). Ч. 1, СМФН,
45. М.: РУДН, 2012. C. 105-121.
8. Кунцевич В.М., Куржанский А.Б. Области достижимости линейных и некото-
рых классов нелинейных дискретных систем и управление ими // Проблемы
управления и информатики. 2010. № 1. С. 5-21.
9. Кунцевич В.М. Управление семейством нелинейных динамических систем при
измерениях с ограниченными помехами // Тр. ИММ УрО РАН. 2014. Т. 20. № 4.
C. 178-186.
10. Цыпкин Я.З., Поляк Б.Т. Робастная устойчивость линейных систем // Итоги
науки и техники. Сер. Техн. кибернетика. 1991. T. 32. С. 3-31.
11. Кунцевич А.В., Кунцевич В.М. Устойчивость в области нелинейных разностных
включений // Кибернетика и системный анализ. 2010. № 5. С. 11-17.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 13.07.2018
После доработки 04.09.2018
Принята к публикации 08.11.2018
44