Автоматика и телемеханика, № 9, 2019

(Линчёпингский университет, Швеция)

К ОВЫПУКЛЕНИЮ КРИТЕРИЕВ ИДЕНТИФИКАЦИИ СИСТЕМ

Идентификация систем состоит в оценивании моделей динамических

систем на основе измеренных входных и выходных данных. Ее традици-

онная основа — это базовые статистические методы, такие как оценива-

ние максимального правдоподобия, асимптотический анализ смещения и

дисперсии и т.п. Оценка максимального правдоподобия основана на ми-

нимизации функции критерия, которая обычно является невыпуклой и

может приводить к проблемам численного поиска и оценкам, попадав-

шим в локальные минимумы. Недавняя заинтересованность в алгоритмах

идентификации была направлена на методы, которые сосредоточены во-

круг выпуклых формулировок. Это отчасти является результатом разра-

боток в области полуопределенного программирования, машинного обу-

чения и теории статистического обучения. Развитие касается вопросов ре-

гуляризации для разреженности и более совершенных компромиссов сме-

щения/дисперсии. Это также предполагает использование подпростран-

ственных методов, а также ядерных норм в качестве прокси-серверов

для ранговых ограничений. Особый подход — искать разностно-выпуклое

программирование (РВП) в случае, если чистый выпуклый критерий не

найден. Другие методы основаны на лагранжевой теории релаксации и

сжатия. Совершенно другой путь к выпуклости — использовать алгеб-

раические методы для манипулирования параметризацией модели. Эта

статья иллюстрирует все это недавнее развитие.

Ключевые слова: оценка максимального правдоподобия, регуляризация,

овыпукление.

DOI: 10.1134/S0005231019090058

1. Введение

Идентификация систем — это построение математических моделей дина-

мических систем по наблюдаемым входным и выходным сигналам. Существу-

ет обширная литература по этому вопросу со многими учебниками, такими

как [1-3]. Большинство методов идентификации систем имеют свое проис-

хождение в парадигме оценки из математической статистики и такой клас-

сический метод, как метод максимального правдоподобия (ММП), являет-

ся важным элементом в этой области. Однако можно указать на некоторые

проблемы:

• выбор структуры модели (порядка модели) не является тривиальным и

может нарушить свойства оптимальности, в частности, для более короткой

выборки данных,

• типично невыпуклый характер критериев может привести к числовым ар-

тефактам оптимизации (например, завершению не в глобальных, а локаль-

ных минимумах).

Поэтому существует тенденция применять методы оценки, основанные на

выпуклых формулировках. Недавно появились альтернативные методы, в ос-

новном из машинного обучения и области выпуклой оптимизации. Они также

имеют корни в классической статистической (байесовской) теории и построе-

ны на поиске разности выпуклых и вогнутых функций, что позволяет при-

менять методы разностно-выпуклого программирования (РВП). Не всегда

удается эффективно решать проблемы РВП, но опыт (см., например, [4-6])

показывает, что они иногда могут быть решены в разумные сроки.

Другой подход основан на дифференциальной алгебре [7]. Основные эле-

менты его также будут здесь рассмотрены.

Другие новейшие методы овыпукления основаны на лагранжевой теории

релаксации и сжатия [8-10].

2. Оценивание параметрических моделей методом МП (МОП)

Классическая современная теория идентификации основана на концепци-

ях структуры модели, данных и критерии подгонки.

2.1. Структуры модели

Структура модели M является параметризованным набором моделей, опи-

сывающих соотношения между входным и выходным сигналами системы.

Параметры обозначаются через θ, поэтому M(θ) — конкретная модель. Эта

модель дает возможность предсказать (на один шаг вперед) выход в момент

времени t, т.е. y(t), основанный на наблюдениях предыдущих входо-выходных

данных до времени t - 1 (обозначаются через Zt-1):

(1)

ŷ(t|θ) = g(t, θ, Zt-1

2.2. Оценивание: критерий подгонки

Качество модели можно определить путем оценки ее способности прогно-

зировать: определить ошибку прогнозирования в момент времени t как

ε(t, θ) = y(t) - ŷ(t|θ) и взять минимум суммы квадратов ошибок (нормы в

квадрате) по текущим наблюдениям

∑

(2)

θN = argminVN(θ) = argmin

∥ε(t, θ)∥².

t=1

При слабых ограничениях обычно этот метод ошибки предсказания (МОП )

совпадает с методом максимального правдоподобия (МП ).

2.3. Линейные модели

Для линейных систем общая структура модели задается передаточной

функцией G от входа к выходу и передаточной функцией H от источника

белого шума e до выходных аддитивных возмущений:

(3a)

y(t) = G(q, θ)u(t) + H(q, θ)e(t),

(3b)

Ee²

(t) = λ; Ee(t)e(k) = 0, если k = t,

где E означает математическое ожидание. Эта модель строится в дискретном

времени, а q обозначает оператор сдвига вперед qy(t) = y(t + 1). Для про-

стоты предполагаем, что интервал выборки — единовременная единица. Для

нормализации функция H предполагается монарной, т.е. ее разложение на-

чинается с единицы. Разложение G(q, θ) по степеням оператора сдвига назад

дает импульсный отклик (ИО) системы:

∑

(4)

G(q, θ) =

g_k(θ)q^-ku(t) =

g_k

(θ)u(t - k).

k=1

Естественным одноступенчатым предсказателем для (3a) является

H(q, θ) - 1

G(q, θ)

(5)

ŷ(t|θ) =

y(t) +

u(t).

H(q, θ)

Так как разложение H начинается с “1”, числитель в первом члене начинается

с h₁q-1, поэтому есть задержка в y. Теперь вопрос заключается в том, как

параметризовать G и H.

2.3.1. Входо-выходные модели вида черного ящика. Общий черный ящик

(т.е. физическое понимание или интерпретация) параметризации, чтобы G

и H были рациональными при операторе сдвига, описывается уравнениями:

B(q)

C(q)

(6a)

G(q, θ) =

H(q, θ) =

F (q)

D(q)

(6b)

B(q) = b₁q-1 + b₂q-2 + . . . b_nbq^-nb,

(6c)

F (q) = 1 + f₁q-1 + . . . + f_nf q^-nf ,

(6d)

θ = [b₁,b₂,...,f_nf

C и D являются, как F, монарными.

Очень распространенным случаем является то, что F = D = A и C = 1,

что дает ARX-модель:

B(q)

(7a)

y(t) =

u(t) +

e(t), или

A(q)

(7b)

A(q)y(t) = B(q)u(t) + e(t), или

(7c)

y(t) + a₁y(t - 1) + . . . + a_na

y(t - na) =

(7d)

= b₁u(t - 1) + ... + b_nb

u(t - nb) + e(t).

Другими общими структурами черного ящика такого типа являются FIR

(модель конечного импульсного ответа, F = C = D = 1), ARMAX (F = D = A),

OE (C = D = 1) и BJ (Box-Jenkins, все четыре многочлена разные, (6a)).

2.3.2. Модели черного ящика в пространстве состояний. Еще одна возмож-

ность общей структуры черного ящика — использовать модель пространства

состояний n-го порядка

(8a)

x(t + 1) = Ax(t) + Bu(t) + Ke(t),

(8b)

y(t) = Cx(t) + e(t),

где вектор состояний x — вектор-столбец размерности n, а A, B, C, K — мат-

рицы соответствующих размерностей. Параметры θ для оценивания состоят

из всех элементов этой матрицы. Из-за возможных изменений базиса в про-

странстве состояний существует много значений θ, соответствующих тем же

системным свойствам. Легко видеть, что (8) описывает те же модели, что и

модель ARMAX с порядками n для A, B, C-полиномов. Кроме того, если мат-

рица K фиксирована до нуля, (8) описывает те же модели, что и модель OE,

с порядками n для B, F -полиномов (см. главу 4 в [1]).

2.3.3. Модели серого ящика. Если известны какие-то физические факты

о системе, то можно встроить это в модель серого ящика. Это может быть,

например, самолет, для которого уравнения движения известны из законов

Ньютона, но некоторые параметры неизвестны, как аэродинамические произ-

водные. Тогда естественно построить модель пространства состояний в непре-

рывном времени из физических уравнений:

x(t) = A(θ)x(t) + B(θ)u(t),

(9)

y(t) = C(θ)x(t) + D(θ)u(t) + v(t).

Здесь θ соответствует неизвестным физическим параметрам, а другие элемен-

ты матрицы обозначают известное физическое поведение. Эта модель может

быть взята с использованием хорошо известных формул выборки, чтобы дать

x(t + 1) = F(θ)x(t) + G(θ)u(t),

(10)

y(t) = C(θ)x(t) + D(θ)u(t) + w(t).

Модель (10) имеет передаточную функцию от u до y

(11)

G(q, θ) = C(θ)[qI - F(θ)]-1

G(θ) + D(θ),

поэтому определенная параметризация общей линейной модели (3a) достиг-

нута.

3. Овыпукление оценивания модели линейного черного ящика

Очень распространенной задачей идентификации является оценивание ли-

нейной системы без какой-либо конкретной структуры (за исключением зна-

ния/постулирования порядка модели). Затем обычно используется модель-

ная структура, такая как BJ-модель (6a) (или специальный случай ARMAX,

или OE). В качестве альтернативы используется модель пространства состоя-

ний (8), где все матрицы A, B, C, K свободно параметризуются. Во всех этих

случаях хорошо известно, что соответствующая критериальная функция (2)

является невыпуклой и, следовательно, может иметь несколько локальных

минимумов. Это означает, что нужно обратить особое внимание на то, чтобы

найти хорошую начальную оценку параметра, где начинать итерационный

поиск минимизирующего параметра.

В случае с линейным черным ящиком это не очень актуальная проблема,

так как оценивание черного ящика для модели пространства состояний может

быть достигнуто с помощью метода идентификации подпространства, такого

как N4SID или MOESP [11, 12].

3.1. Аппроксимация линейных систем с помощью моделей ARX

Предположим, что истинная линейная система задается формулой

(12)

y(t) = G₀(q)u(t) + H₀

(q)e(t).

Предположим, строится ARX-модель (7) для больших и больших порядков

n = na = nb:

(13)

A_n(q)y(t) = B_n

(q)u(t) + e(t).

Тогда из [13] хорошо известно, что по мере того, как порядки стремятся к

бесконечности одновременно с тем, что число данных N увеличивается еще

быстрее, для оценки ARX имеем

B_n(q)

(14a)

→G₀

(q),

A_n(q)

(14b)

→H₀

(q)

при n → ∞.

A_n(q)

Это весьма полезный результат. ARX-модели легко оценить. Оценки рассчи-

тываются по методам линейных наименьших квадратов, которые являются

выпуклыми и численно надежными. Оценка ARX-модели высокого порядка,

возможно сопровождаемая некоторым уменьшением порядка модели, может

быть жизнеспособной альтернативой более требовательному генератору об-

щего критерия МОП (2).

Единственным недостатком ARX-моделей высокого порядка является то,

что они могут страдать от большой дисперсии. Это проблема, которую рас-

смотрим ниже.

3.2. Регуляризация линейных регрессионных моделей

3.2.1. Линейные регрессии. Задача линейной регрессии имеет вид

(15)

y(t) = ϕ^T

(t)θ + e(t).

Здесь y (выход) и ϕ (вектор регрессии) — наблюденные переменные, e —

возмущающий шум, θ — неизвестный вектор параметров. В общем случае

e(t) предполагается не зависимым от ϕ(t).

В векторной форме удобно переписать (15), уложив все элементы (строки)

в y(t) и ϕ^T(t), чтобы сформировать векторы (матрицы) Y и Φ и получить

(16)

Y = Φθ + E.

(Здесь для простоты Φ рассматривается как детерминированная перемен-

ная. Если она случайная, то все приведенные ниже выражения должны быть

условными относительно Φ.) Оценка наименьших квадратов параметра θ рав-

на

(17a)

θN = argmin |Y - Φθ|²

или

(17b)

θN = R-1NFN , RN = Φ^TΦ, FN = Φ^TY,

где | · | — евклидова норма.

3.2.2. Регуляризованные наименьшие квадраты. Можно показать, что дис-

персия^θ может быть довольно большой, в частности если матрица Φ имеет

много столбцов и/или плохо обусловлена. Поэтому имеет смысл регуляризо-

вать оценку посредством матрицы P , см. [14] по поводу общего подхода к

регуляризации. Это обычно выражается в форме оптимизации как

(18a)

θN = argmin |Y - Φθ|² + θ^TP-1θ или

(18b)

θN = (RN + P-1)-1FN .

Наличие матрицы P улучшает численные свойства оценки и уменьшает ее

дисперсию, в то время как возникает некоторое смещение. Предположим,

что данные были сгенерированы (16) для некоторого “истинного” вектора

θ₀ с дисперсией шума EEE^T = I. Тогда среднеквадратичная ошибка (СКО)

оценки равна

[

]

(θN - θ₀)(θN - θ₀)T = (RN + P-1)-1 ×

(

)(

)-1

(19)

R_N + P-1θ₀θ^T0P-1

R_N + P-1

Рациональный выбор P тот, который делает эту матрицу СКО малой. Как

можно думать о хорошем выборе? Полезно сначала установить следующую

лемму алгебраического характера.

Лемма 1. Рассмотрим матрицу

(20)

M (Q) = (QR + I)-1(QRQ + Z)(RQ + I)-1,

где I — единичная матрица подходящей размерности, Q, R и Z положи-

тельно полуопределенные. Тогда для любой Q

(21)

M (Q) ≥ M(Z),

где неравенство понимается в матричном смысле.

Доказательство состоит из простых вычислений, см., например, [15], где в

обозначениях предполагается, что матрица P обратима. Если это не так, мож-

но разработать эквивалентные выражения, см. (23)-(25) и (54) в [15].

Вопрос о том, какая матрица P дает лучшее СКО регуляризованной оцен-

ки, имеет ясный ответ: используйте

(22)

P =θ₀θ^T0.

Поэтому неудивительно, что лучшая регуляризация зависит от неизвестной

системы.

Можно задать связанный с этим вопрос, но с точки зрения частотного

рассмотрения: при некоторых наборах истинных систем Ω = {θ₀} с Eθ₀θ^T0 =

= Π какая лучше средняя СКО? Среднее значение СКО получается путем

математического ожидания по θ₀ с учетом (19). Это приводит к тому, что

θ₀θ^T0 заменяется на Π, поэтому лемма непосредственно дает следующий ответ.

Наилучшее среднее значение по множеству Ω получается при матрице

регуляризации P = Π.

При этом очень близка байесовская интерпретация, когда θ считается слу-

чайным вектором с предыдущим распределением, как гауссовским (нормаль-

ным), с нулевым средним и ковариационной матрицей P :

(23)

θ ∈ N(0,P).

Тогда среднее по постериорному распределению θ будет определяться фор-

мулой (18a).

3.2.3. Эмпирический байесовский подход. Байесовская интерпретация так-

же дает возможность оценить P из данных: при (23) вектор Y в (16) также

будет гауссовским с нулевым средним и ковариацией

(24)

Z(P ) = ΦP Φ^T

(предполагая, что E является гауссовским с нулевым средним и ковариаци-

онной матрицей I). Минус удвоенный логарифм функции плотности вероят-

ности гауссовского случайного вектора Y будет таковым (без учета аддитив-

ной постоянной):

(25)

W (Y, P ) = Y^TZ(P )-1

Y + logdetZ(P).

Это также будет отрицательной функцией логарифмического правдоподобия

для оценки P из наблюдений Y , поэтому оценка ММП для P будет

(26)

= argmin W (Y, P ).

Это известно как эмпирический метод Байеса [16]. Если P известно с точ-

ностью до (гипер) параметра η, P (η), то этот параметр оценивается соответ-

ствующим образом.

3.3. FIR-модели

Вернемся к импульсной характеристике (4) и предположим, что она ко-

нечна (FIR):

∑

(27)

G(q, θ) =

b_ku(t - k) = ϕTu(t)θ_b,

k=1

где собрано m-элементов u(t - k) в ϕ(t) и m IR-коэффициентов b_k в θ_b. Это

означает, что оценивание FIR-моделей является задачей линейной регрес-

сии. Таким образом, все сказанное выше о линейных регрессиях, регуляриза-

ция и оценка гиперпараметров могут быть применены к оценке FIR-моделей.

В частности, подходящий выбор P должен отражать то, что разумно пред-

положить об импульсной характеристике (ИХ): если система стабильна, ком-

понента b должна затухать экспоненциально, а если ИХ является гладкой,

соседние значения должны иметь положительную корреляцию. Это означа-

ет, что типичной матрицей регуляризации P^b для θ_b будет матрица, у которой

элемент k, j — что-то вроде

(28)

P^bk,j(α) = C min(λ^k,λ^j

α = [C,λ],

где C ≥ 0 и 0 ≤ λ < 1. Это одна из многих возможных параметризаций P

(так называемые ядра). Этот выбор известен как TC-ядро, см. (49c) в [15].

Затем гиперпараметр α может быть настроен на (26):

(29)

α = argminW(Y,P^b

(α)).

Эффективная численная реализация этой задачи минимизации обсуждается

в [17, 18]. Подпрограмма реализуется как Impulseest в версии 2012b [19].

3.4. ARX-модели

Напомним, что модели ARX высокого порядка обеспечивают все более ка-

чественные аппроксимации общих линейных систем. Можно написать ARX-

модель (7) как

y(t) = - a₁y(t - 1) - . . . - a_ny(t - n) + b₁u(t - 1) + . . . +

(30)

+ b_mu(t - m) = ϕTy (t)θ_a + ϕTu(t)θ_b = ϕ^T

(t)θ,

где ϕ_y и θ_a составлены из y и a очевидным образом. Это означает, что так-

же модель ARX представляет собой линейную регрессию, к которой могут

применяться те же идеи регуляризации. Уравнение (30) показывает, что пре-

диктор состоит из двух импульсных характеристик, одна из y и другая из u,

и могут быть использованы подобные идеи о параметризации матрицы регу-

ляризации. Естественно разбить P -матрицу в (18a) вместе с θ_a, θ_b и исполь-

зовать

]

^[P^a(α1)

(31)

P (α₁, α₂) =

P^b(α₂)

с P^a,b(α), как в (28).

3.5. Вопросы выпуклости: множественные выражения ядра

В общем случае проблема настройки гиперпараметров (26) невыпуклая,

поэтому даже если задачу регуляризованной линейной регрессии можно ре-

шить без проблем локальных минимумов, то невыпуклость проявляется при

настройке гиперпараметров. Поскольку α обычно имеет низкую размерность,

проблема локальных минимумов в решении (29) является менее сложной за-

дачей, чем при решении (2) для МОП. Тем не менее интересно рассмотреть

матрицы регуляризации, которые формируются линейно из нескольких из-

вестных ядер P_k:

∑

(32)

P (α) = α_kP_k, α_k

≥ 0.

k=1

Фактически это дает несколько преимуществ, как описано в [20-22]:

• Проблема настройки (26) или (29) становится разностью задач програм-

мирования выпуклых функций, которая решается с помощью метода ми-

нимизации мажорирования в [20, 21].

• Это ядро проявляет полезную гибкость: множественное ядро (32) может

описывать более сложную динамику, например, динамика содержит широ-

ко распространенные постоянные времени, а P_k можно выбрать как кон-

кретные экземпляры ядра TC и также дополнить ядрами ранга 1 вида θ₀θ^T0

(ср. (22)) для набора моделей-кандидатов θ₀.

• Как объясняется в разделе IV [21], минимизация (29) для (32) благопри-

ятствует разреженным решениям, т.е. решениям со многими α_k = 0, что

может быть очень полезно, если P_k соответствует различным гипотетиче-

ским структурным функциям модели. Это означает, что выбор несколь-

ких ядер в идентификации систем может быть применен ко множеству

проблем, требующих разреженных решений.

3.6. Близкие работы

Текст в этом разделе основан на [15]. Важные вклады одного и того же

рода, основанные на идеях машинного обучения, были описаны в [23, 24], см.

также [22, 25, 26].

3.7. Выводы

На самом деле, линейные модели черного ящика не представляют пробле-

мы с точки зрения выпуклости. Даже если модели состояния “черного ящика”

имеют невыпуклый критерий (2), минимизация всегда может быть иниции-

рована близко к глобальному минимуму из оценки подпространства. То же

самое верно для моделей полиномов черного ящика. Кроме того, оценка ли-

нейных моделей с использованием регуляризованных моделей ARX или FIR

является существенно выпуклой задачей и, как правило, приводит к превос-

ходным линейным моделям типа черного ящика.

4. Овыпукление при идентификации модели серого ящика

Ситуация заметно отличается, когда переходим к серым блочным моделям

при произвольных (физических) параметризациях (9)-(11). Критерий (2) по-

прежнему будет невыпуклым, и если параметризация основана на физиче-

ском понимании, то предварительное знание может дать хорошие начальные

значения параметров (внутри области притяжения глобального минимума)

для успешной минимизации критерия. Но как насчет инициализации при слу-

чайно выбранных параметрах?

4.1. Обычны ли локальные минимумы?

4.1.1. Эксперимент. Чтобы исследовать эту проблему, проводился экспе-

римент в [27]: генерировалась случайно выбранная система в пространстве

состояний n-го порядка (9). Фиксировались все параметры, кроме k. Бы-

ли созданы структуры серого ящика, состоящие из данной системы с эти-

ми параметрами k, являющимися свободными параметрами θ. Они оценива-

лись посредством минимизации критерия ММП/МОП (2) при 100 различных

случайных начальных значений. Подсчитывалось, сколько раз минимизация

заканчивается в окрестности истинных значений. Результат изображен на

рис. 1.

4.1.2. Выученный урок. Рисунок показывает, что существует очень ма-

ленький шанс достичь глобального минимума из случайных начальных оце-

нок для задач реалистичных размеров. При оценке десяти параметров будет

только 2% инициализаций, приводящих к глобальному оптимуму. Другими

словами, области притяжения глобального минимума не очень поддающиеся,

поэтому очень важно найти хорошие начальные оценки.

4.2. Аффинная структура серого ящика

Предположим, что модель параметризуется с параметрами физической

значимости/интереса:

x = A(θ)x + B(θ)u + w,

y = C(θ)x + e.

Не трудно предположить, что параметризация аффинная:

∑

(33)

A(θ) = A₀ + A_iθ_i, B(θ) = B₀ + B_iθ_i,

i=1

∑

(34)

C(θ) = C₀ + C_iθ_i.

i=1

Пример. Рассмотрим модель DC-сервомотора (постоянная времени τ и коэф-

фициент усиления β):

[

]

[

]

-1/τ

β/τ

Эта серая модель аффинная при θ₁ = -1/τ и θ₂ = β/τ.

4.3. Начинаем с общей модели

Хотя оценивание отдельных параметров в модели пространства состояний

может быть громоздким, легко оценить полную линейную модель, напри-

мер методы подпространства, такие как N4SID или MOESP, см., например,

раздел 10.6 в [1]. Для моделей с непрерывным временем производим преоб-

разование в непрерывное время после нахождения модели подпространства

с дискретным временем. Таким образом, можно попасть в модель A^∗, B^∗, C^∗,

которая эквивалентна системе с истинными параметрами A(θ₀), B(θ₀), C(θ₀).

(Но реализация в пространстве состояний будет неизвестна.)

Итак, надо решить

(35)

C^∗(sI - A^∗)-1B^∗ = C(θ)(sI - A(θ))-1

B(θ)

для θ. Это, однако, также невыпуклая проблема!

4.4. Альтернативная формулировка — по трансформациям сходства

Как предложено в [28], применим преобразование подобия и решим для θ

иQ

(36)

QA^∗ = A(θ)Q, QB^∗ = B(θ), C^∗

= C(θ)Q

или

(37)

min∥QA∗ - A(θ)Q∥2F + ∥QB∗ - B(θ)∥2F + ∥C∗ - C(θ)Q∥2F ,

θ,Q

где ∥ · ∥_F — норма Фробениуса. Это задача билинейной минимизации в пред-

положении (33). Но все же уравнение имеет много решений, и трудно найти

то, которое соответствует глобальному минимуму.

Возникает вопрос: Это неразрешимая проблема для поиска идентифици-

руемых параметров в случае серого ящика? Ответ на этот вопрос: “Нет, по-

скольку в [27] показано, что билинейная задача (37) может быть переписана

как задача суммы квадратов и, следовательно, может быть решена посред-

ством выпуклых методов.” Цена заключается в том, что размер задачи “сумма

квадратов” быстро возрастает с ростом n и k, поэтому численное решение на

практике может быть невозможным.

Кроме того, из результатов раздела 5 следует, что решение можно найти в

принципе с помощью выпуклых методов, но опять же с возможным взрывом

по размеру задачи. Также из результатов раздела 5 следует, что решение, в

принципе, можно найти, так как любая идентифицируемая проблема может

быть переписана в виде линейной регрессии и, следовательно, разрешима вы-

пуклыми методами, но опять же с возможным взрывом по размеру проблемы.

4.5. Альтернативная формулировка — через матрицу Ганкеля

Опять же проблема состоит в том, чтобы решить (35). Применяя преобра-

зования подобия, можно вычислить ганкелеву матрицу импульсных откликов

для известной (подпространственной оценочной) системы (A^∗, B^∗, C^∗). Это

форма (известной) матрицы

[

]

··· C^∗(A^∗)^kB^∗

···

(38)

Y =H^∗n =

···

Из структуры модели можно затем сформировать то, что является ганкеле-

вой матрицей модели (функция θ):

[

]

··· C(θ)A^k(θ)B(θ) ···

(39)

H_n(θ) =

···

Теперь можно приравнять известную системную ганкелевую матрицу с

модельной, т.е. решить уравнение

(40)

Y =H_n

(θ)

по θ. Это довольно сложные выражения, и не ясно, получено ли что-то по

сравнению с (35). Но можно двигаться дальше.

4.6. Подробнее об уравнении на основе ганкелевой матрицы

Нужно решить

(41)

min∥Y - Hn(θ)∥2F .

Подходим к этой нелинейной задаче путем техники подъема: вводим еще

больше свободных переменных, так что проблема минимизации становится

квадратичной и «отбрасывает» свободу, внося множество линейных ограни-

чений и ранговое ограничение.

Ганкелеву матрицу можно разложить как H_n = OC (матрицы наблюдае-

мости и управляемости). Полагаем^Õ = OA(θ)

C = A(θ)C (сдвинутые мат-

рицы).

4.7. Новая формулировка

С расширенной параметризацией (41) можно перефразировать (см. [29]

для подробных объяснений):

(42a)

min

∥Y - X∥2F

θ,X,C,O,^Õ,C,Ã

при ранговом ограничении

(42b)

rank Z = n

(порядок модели),

где

⎡

⎤

X O

⎢

⎥

(42c)

Z =

⎣C In A(θ)⎦

C A(θ)

при дополнительными ограничениями среди переменных:

O(1 : p, :) = C(θ),

Õ(1 : (n - 1)p, :) = O(p + 1 : np, :),

(42d)

C(:, 1 : m) = B(θ),

C(:, 1 : (n - 1)m) = C(:, m + 1 : nm).

Примечание: Z является линейной по всем переменным минимизации, m

и p — количество входов и выходов соответственно. Обозначение двоеточия

означает столбцы и строки, как в Matlab. Они обеспечивают свойства сдвига

матрицы Ганкеля H_n, выраженные в матрицах наблюдаемости и управляе-

мости O и C [29]. X — (формально) свободная переменная, соответствующая

матрице Ганкеля H_n(θ), которая является произведением OC (в силу верх-

него левого подблока матрицы Z).

4.8. Алгоритм РВП

Пусть f_n(Z) обозначает сумму n наибольших сингулярных значений мат-

рицы Z. Тогда

(43)

rank Z = n ⇐⇒ ∥Z∥_∗ - f_n

(Z) = 0,

∥ · ∥_∗ — ядерная норма.

∥Z∥_∗ и f_n(Z) выпуклые по Z, так что задачу минимизации (42a) с ограниче-

нием (42b) = (43) теперь можно записать с помощью множителя Лагранжа λ

как

(44)

min

∥Y - X∥^2F + λ(∥Z∥_∗ - f_n

(Z)).

θ,X,C,O,^O,C,A

Отметим, что ∥Z∥_∗ и f_n(Z) выпуклые по Z, так что (44) — это минимизация

разницы выпуклого программирования (РВП), которая может быть решена

методом последовательной выпуклой релаксации (с линеаризацией вогнутой

функции -f_n(Z)), см. [29].

4.9. Численные результаты

Повторно проведены эксперименты рис. 1: собраны данные из случайно

созданной системы 5-го порядка. Выделены элементы k как неизвестные в

правильной системной модели. Оценивались эти k элементов посредством

100

n = 5

Рис. 1. Результат случайного теста. Каждая из звезд представляет собой спе-

цифическую систему (5-го порядка). Ось x — это число свободных парамет-

ров k. Ось y — это показатель успеха: как часто достигается глобальный ми-

нимум из случайной начальной точки.

1) минимизации критерия МОП (ММП) (2) из случайно выбранных началь-

ных значений;

2) начальных значений только что описанного метода РВП.

Насколько часто параметры оцениваются правильно, показано в таблице, по-

лученной по более 100 экспериментам.

Таблица

k ММП РВП

22%

88%

20%

Видно, что, хотя алгоритм РВП несовершенен, он является явным улуч-

шением обычного подхода ММП.

4.10. Выводы

• Важной проблемой является поиск начальных оценок параметров при

ММП, чтобы не оказаться в локальных (но неглобальных) экстремальных

точках.

• Это является важной подзадачей для аффинной параметризации!

• Тогда исходная модель, оцененная методами подпространства, может ока-

заться очень полезной. Можно сопоставить соответствие между моделью

этой оценки и структурированной моделью.

• Был показан один метод, основанный на согласовании ганкелевой матрицы

и РВП.

• Это дает определенное улучшение в смысле избежания локальных экстре-

мумов.

• Другие результаты этого характера приведены в [28-31].

5. Овыпукление посредством дифференциальной алгебры

В предыдущем разделе рассмотрены проблемы выпуклости для функции

потерь (2) в линейной модели серого окна. Более серьезная проблема за-

ключается в том, что нелинейные модели серого окна показывают серьезные

нелинейности.

5.1. Общая структура моделирования

Весьма общий способ формирования модели серого ящика можно описать

следующим образом. Собираем все уравнения, которые имеют отношение к

рассматриваемой системе, как дифференциально-алгебраические уравнения

(ДАУ):

(45)

G=g_k

(y(t), u(t), z(t), θ, p); k = 1, . . . , d,

где y, u по-прежнему представляют собой измеренный выход системы и вход-

ной сигнал, z — набор неизмеряемых вспомогательных (скрытых) перемен-

ных, θ содержит все неизвестные параметры для оценки, а p — оператор диф-

ференцирования. Существует несколько методов манипулирования такими

ДАУ. Можно добавлять уравнения, умножать уравнения, дифференцировать

уравнения и добавлять их к множеству G без изменения решения, заданного

уравнениями. Таким образом, можно определить канонические представле-

ния набора уравнений. Алгоритм Ритта [32, 33] — это принятая техника

для поиска такого канонического представления. (Это можно концептуально

рассматривать как метод Гаусса последовательного исключения при манипу-

лировании матрицами.)

В [7] показано, что если набор G является параметрифицируемым (никакие

два разных значения θ не могут дать одно и то же множество решений), то

каноническое представление приводит к линейной регрессии

(46)

Φ(y, u, p) = θ^T

Ψ(y, u, p).

Это явно означает, что множество уравнений модели может быть овыпуклено.

5.2. Пример

Рассмотрим вариант кинетических уравнений роста Михаэлиса—Ментен,

описывающих рост ферментов, см. [34].

Если обозначить через y концентрацию определенного фермента, а через

u — добавление питательного субстрата, то динамика описывается уравне-

нием

(47)

y=θ₁

− y + u.

θ₂ + y

Здесь θ₁ и θ₂ — максимальный темп роста и константа Михаэлиса соответ-

ственно, которые специфичны для определенного фермента. Предположим,

что измеряется концентрация в момент времени t_k с определенной погреш-

ностью измерения e(k):

(48)

y_m(t_k) = y(t_k

) + e(k).

Предиктор (1) и критериальная функция (2) могут быть легко найдены в

виде

∑

(49)

V_N(θ) =

[y_m(t_k) - ŷ(t_k|θ)]²,

k=1

ŷ(t|θ)

(50)

y(t|θ) = θ₁

− ŷ(t|θ) + u(t).

θ₂ + ŷ(t|θ)

Предположим, что u(t) является импульсом в момент времени 0. Обратим

внимание, что форма функции потерь не зависит от уровня шума (размер

дисперсии e). Таким образом, достаточно построить график (49) для e ≡ 0.

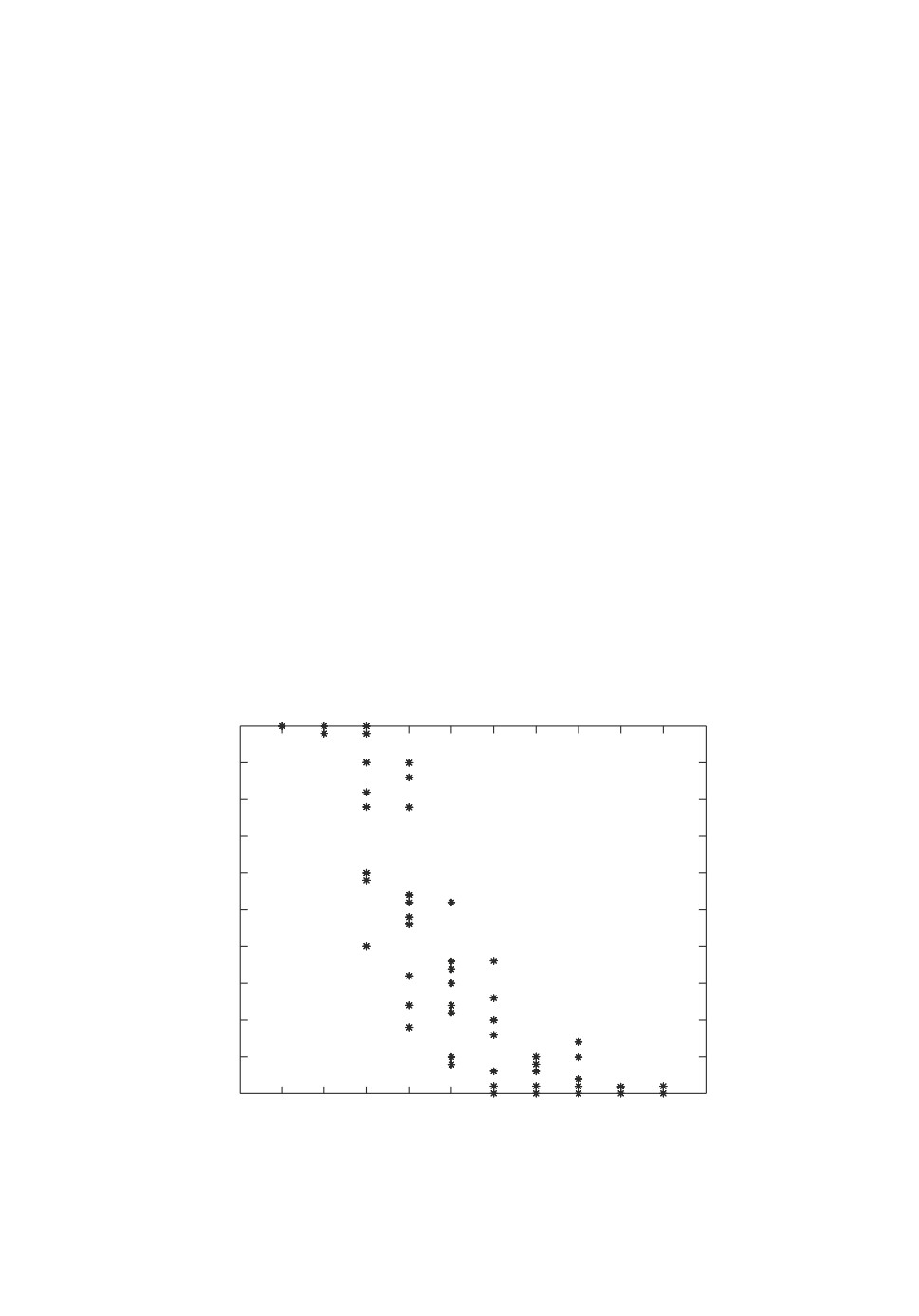
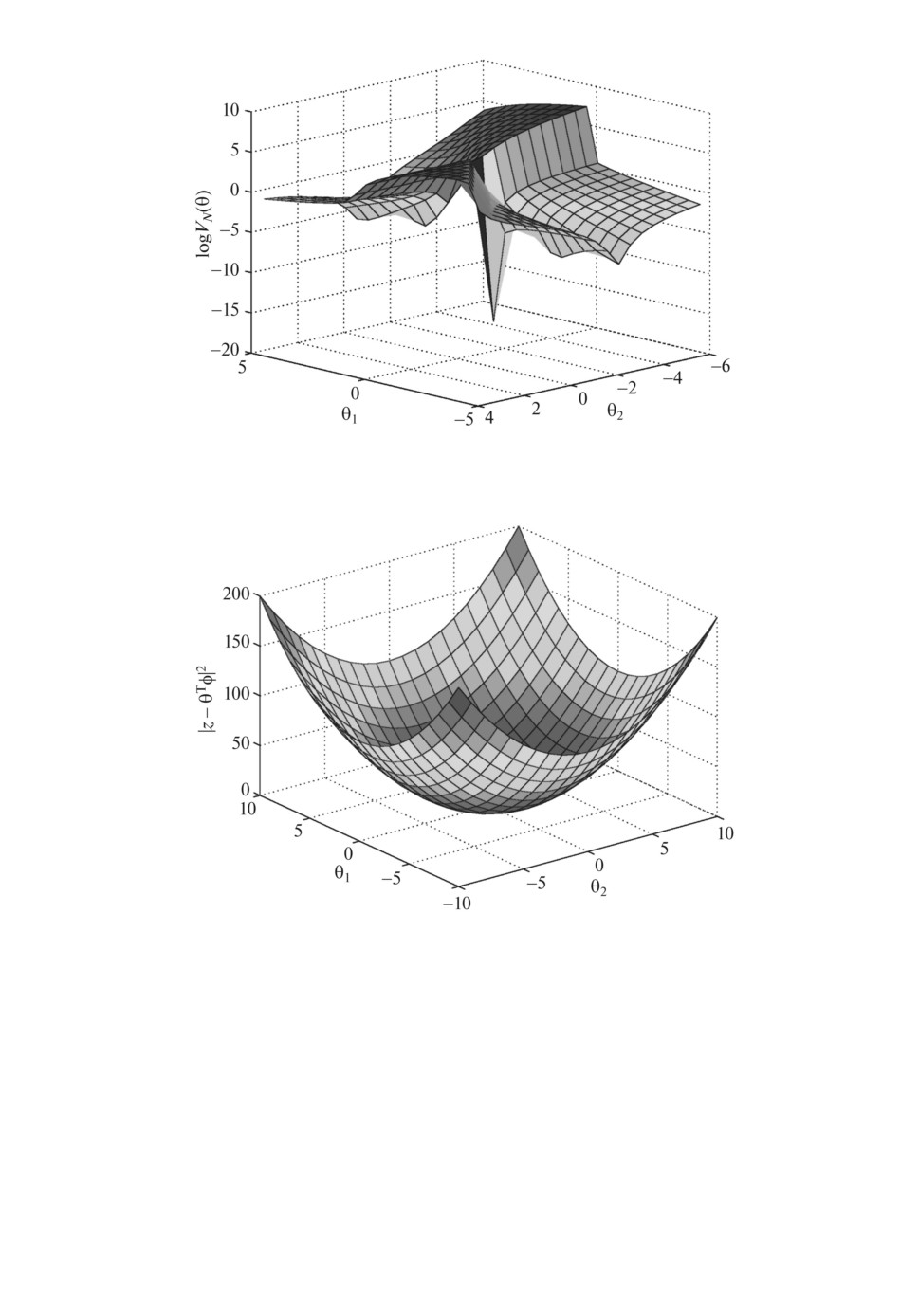
Этот график показан на рис. 2.

Ясно видно, что даже для бесшумных наблюдений довольно сложной за-

дачей является поиск argmin V_N (θ). Необходимы очень хорошие начальные

предположения для успеха при итеративном поиске. Это верно независимо

или

[

]

[

]

(51a)

yy + y² - uy =

θ₁

θ₂

u- y-y

или

(51b)

z =θ^Tφ

с очевидными предположениями для z и φ. Уравнение (51b) представляет со-

бой линейную регрессию, связывающую неизвестные параметры и измеряе-

мые переменные φ и z. Таким образом, можно найти их по простой процедуре

наименьших квадратов, см. рис. 3.

Манипуляции, приводящие к (51a), являются примером алгоритма Ритта

в дифференциальной алгебре.

5.3. Предостережения

Получен в некотором смысле общий результат овыпукления для любой

идентифицируемой задачи оценивания.

Следует сделать ряд предостережений:

• Хотя алгоритм Ритта, как известно, сходится на конечном числе шагов,

из-за сложности вычислений он может быть запрещен для больших задач.

• При зашумленных измерениях следует проявлять осторожность при диф-

ференцировании; кроме того, линейная регрессия может быть вызвана на-

рушениями, которые могут приводить к смещенным оценкам.

Однако факт остается фактом: результат показывает, что сложная, невыпук-

лая форма функции правдоподобия со многими локальными минимумами не

присуща структуре модели.

6. Заключение

Идентификация систем — это область, которая имеет важное значение для

практической работы. В настоящее время она имеет хорошо развитую тео-

рию и является стандартным инструментом в промышленном применении.

Несмотря на то, что область довольно проработанная, со многими связями с

классической теорией, новые интересные и плодотворные идеи продолжают

развиваться. Эта статья представляет некую текущую работу, которая имеет

в качестве главной цели овыпукление. Дальнейшие обсуждения и мнения о

текущем состоянии и будущих перспективах идентификации систем приве-

дены, например, в [35, 36].

СПИСОК ЛИТЕРАТУРЫ

1. Ljung L. System Identification - Theory for the User. Prentice-Hall, Upper Saddle

River, N.J., 2nd edition, 1999.

Льюнг Л. Идентификация систем. Теория для пользователя. М.: Наука, 1991.

432 с.

Söderström T., Stoica P. System Identification. Prentice-Hall Int., London, 1989.

Pintelon R., Schoukens J. System Identification - A Frequency Domain Approach.

Wiley-IEEE Press, New York, 2nd edition, 2012.

Tao P.D., An L.T.H. Convex Analysis Approach to D.C. Programming: Theory,

Algorithms and Applications // ACTA Mathematica Vietnamica. 1997. V. 22. No. 1.

P. 289-355.

Horst R., Thoai N.V. DC Programming: Overview // J. Optim. Theory Appl. 1999.

V. 103. No. 1. P. 1-43.

Thoai R.H.N. DC Programming: an Overview // J. Optim. Theory Appl. 1999.

V. 193(1). P. 1-43.

Ljung L., Glad T. On Global Identifiability of Arbitrary Model Parameterizations //

Automatica. 1994. V. 30. No. 2. P. 265-276.

Tobenkin M.M., Manchester I.R., Megretski A. Convex Paramterizations and

Fidelity Bounds for Nonlinear Identification and Reduced-Order Modelling // IEEE

Trans. Autom. Control. 2017. V. AC-62. No. 7. P. 3679-3686.

Manchester I.R., Tobenkin M.M., Megretski A. Stable Nonliner System Identifiction:

Convexity, Model Class and Consistency // Proc. 16 IFAC Sympos. Syst. Identificat.,

July 2012. P. 328-333. Brussels, Belgium.

10.

Umenberger J., Manchester I.R. Convex Bounds for Equation Error in Stable

Nonlinear Identification // IEEE Control Syst. Lett. 2019. V. 3. No. 1. P. 73-79.

11.

Van Overschee P., De Moor B. N4SID: Subspace Algorithms for the Identification of

Combined Deterministic-Stochastic Systems // Automatica, (Special Issue). 1994.

V. 30. No. 1. P. 75-93.

12.

Verhaegen M., Dewilde P. The Output-Error State-Space Model Identification Class

of Algorithms // Int J. Control. 1992. V. 56. No. 5. P. 1187-1210.

13.

Ljung L., Wahlberg B. Asymptotic Properties of the Least-Squares Method for

Estimating Transfer Functions and Disturbance Spectra // Adv. Appl. Prob. 1992.

V. 24. No. 2. P. 412-440.

14.

Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. 2-е изд. М.:

Наука, 1979.

15.

Chen T., Ohlsson H., Ljung L. On the Estimation of Transfer Functions,

Regularizations and Gaussian Processes - Revisited // Automatica. 2012. V. 48.

No. 8. P. 1525-1535.

16.

Carlin B. P., Lewis T. A. Bayes and Empirical Bayes Methods for Data Analysis.

London, Chapman and Hall, 1996.

17.

Tianshi Chen, Lennart Ljung. Implementation of Algorithms for Tuning Parameters

in Regularized Least Squares Problems in System Identification // Automatica.

2013. V. 49. No. 7. P. 2213-2220.

18.

Carli F.P., Chiuso A., Pillonetto G. Efficient Algorithms for Large Scale Linear

System Identification Using Stable Spline Estimators // Proc. 16 IFAC Sympos.

Syst. Identificat. 2012 (SYSID 2012). P. 119-124.

19.

Ljung L. The System Identification Toolbox: The Manual / The MathWorks Inc.

1st edition 1986, 8th edition 2012, Natick, MA, USA, 2012.

20.

Chen T., Ljung L., Andersen M., Chiuso A., Carli P.F., Pillonetto G. Sparse

Multiple Kernels for Impulse Response Estimation With Majorization Minimization

Algorithms // IEEE Conf. Decision Control. Hawaii, 2012. P. 1500-1505.

21.

Chen T., Andersen M.S., Ljung L., Chiuso A., Pillonetto G.

System

Identification via Sparse Multiple Kernel-Based Regularization Using Sequential

Convex Optimization Techniques // Autom. Control. IEEE Transact. 2014. V. 59.

No. 11. P. 2933-2945.

22.

Dinuzzo F. Kernels for Linear Time Invariant System Identification. Manuscript,

Max Planck Institute for Intelligent Systems, Spemannstrasse 38,72076 Tübingen,

Germany, 2012.

23.

Pillonetto G., De Nicolao G. A New Kernel-Based Approach for Linear System

Identification // Automatica. 2010. V. 46. No. 1. P. 81-93.

24.

Pillonetto G., Chiuso A., De Nicolao G. Prediction Error Identification of Linear

Systems: A Nonparametric Gaussian Regression Approach // Automatica. 2011.

V. 47. No. 2. P. 291-305.

25.

Pillonetto G., Dinuzzo F., Chen T., De Nicolao G., Ljung L. Kernel Methods

in System Identification, Machine Learning and Function Estimation: A Survey //

Automatica. 2014. V. 50. No. 3. P. 657-682.

26.

Mu B., Chen T., Ljung L. On Asymptotic Properties of Hyperparameter Estimators

for Kernel-Based Regularization Methods // Automatica. 2018. V. 94. No. 8.

P. 381-395.

27.

Parrilo P., Ljung L. Initialization of Physical Parameter Estimates / P. van der Hof,

B. Wahlberg, S. Weiland, ed. Proc.

IFAC Sympos. Syst. Identificat.

2003.

P. 1524-1529. Rotterdam, The Netherlands, Aug.

28.

Xie L.L., Ljung L. Estimate Physical Parameters by Black Box Modeling // Proc.

21 Chinese Control Conf., 2002. P. 673-677, Hangzhou, China.

29.

Yu C., Ljung L., Verhaegen M. Identification of Structured State-Space Models //

Automatica. 2018. V. 90. No. 4. P. 54-61.

30.

Yu C., Ljung L., Verhaegen M. Gray Box Identification Using Difference of Convex

Programming // Proc. IFAC World Congress, Toulouse, France, 2017. Elsevier.

31.

Wills A., Yu C., Ljung L., Verhaegen M. Affinely Parametrized State-Space Models:

Ways to Maximize the Likelihood Function // Proc. IFAC Sympos. Syst. Identificat.

SYSID18, Stockholm, July 2018.

32.

Ritt J.F. Differential Algebra // Amer. Math. Soc., Providence, R.I., 1950.

33.

Glad S.T. Implementing Ritt’s Algorithm of Differential Algebra // IFAC Sympos.

Control Systems Design, NOLCOS’92, 1992. P. 398-401, Bordeaux, France.

34.

Ljung L., Chen T. Convexity Issues in System Identification // Proc. 10 IEEE Int.

Conf. Control Automat. (ICCA), 2013. Hangzhou, China.

35.

Ljung L. Pespectives on system identification // IFAC Annual Reviews, Spring

Issue, 2010.

36.

Ljung L., Hjalmarsson H., Ohlsson H. Four Encounters with System Identification //

Eur. J. Control. 2011. V. 17. No. 5-6. P. 449-471.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 25.06.2018

После доработки 27.09.2018

Принята к публикации 08.11.2018