Автоматика и телемеханика, № 9, 2019
© 2019 г. Ю.С. ПОПКОВ, д-р техн. наук (popkov@isa.ru)
(Федеральный исследовательский центр
“Информатика и управление” РАН, Москва;
Институт проблем управления РАН, Москва;
Департамент программной инженерии, ОРТ Брауде Колледж, Кармиель, Израиль;
Югорский научно-исследовательский институт информационных технологий,
Ханты-Мансийск;
Московский физико-технический институт)
ПРОЦЕДУРЫ РАНДОМИЗИРОВАННОГО МАШИННОГО ОБУЧЕНИЯ1
Предлагается новая концепция машинного обучения, основанная на
компьютерной имитации энтропийно-оптимальных рандомизированных
моделей. Рассмотрены процедуры рандомизированного машинного обу-
чения (РМО) с “жесткой” и “мягкой” рандомизацией, которые сводят-
ся либо к точному воспроизведению эмпирических балансов в первом
случае, либо к приближенному в рамках принятого критерия аппрок-
симации. Сформулированы алгоритмы РМО в виде функциональных за-
дач энтропийно-линейного программирования. Приведены примеры при-
менения РМО в задачах классификации текстов и рандомизированного
прогнозирования миграционного взаимодействия региональных систем.
Ключевые слова: рандомизация, жесткие и мягкие процедуры рандоми-
зации, неопределенность, энтропия, матричные нормы, эмпирические ба-
лансы, классификация текстом, динамическая регрессия.
DOI: 10.1134/S0005231019090095
1. Введение
Многие события, явления, процессы, объекты, которые мы пытаемся изу-
чить и использовать, происходят в некой среде, про которую мы что-то не
знаем или знаем не полностью. Другими словами, приходится исследовать,
моделировать или решать проблемы в условиях неопределенности, причем
содержательный смысл этого термина часто оказывается весьма размытым.
Тем не менее, мы оперируем уровнем неопределенности, полагая, что его
можно измерить. Чтобы этот методологический путь не оказался тупиковым,
необходимо как-то имитировать (моделировать) неопределенность. Наиболее
продвинутым и эффективным является подход, основанный на гипотезе о сто-
хастической природе неопределенности. Продвинутым он является потому,
что существуют подходящие инструменты, превращающие гипотезу в при-
кладные технологии, эффективность которых базируется на математических
теориях — вероятности, статистики, оптимизации и др.
Стохастическая природа неопределенности мотивирует ее моделирование
с помощью искусственно генерируемой случайной среды, называемой рандо-
мизированной средой. Разумеется эта среда не произвольная, а отражающая
предположительно существующие особенности неопределенности.
1 Работа поддержана Российским фондом фундаментальных исследований (проект 17-
29-02115).
122
Одним из носителей этих особенностей неопределенности являются дан-
ные. Современные средства вычислительной техники позволяют накапливать
и хранить огромное количество данных как в естественных, так и в оцифро-
ванных форматах. Естественно возникает вопрос: что можно с ними делать,
кроме их сохранения. Весьма привлекательным кажется предложение, попы-
таться извлекать из данных новые знания. По-видимому, первые декларации
на эту тему, в виде концепции Data Mining появились в публикациях [1, 2].
В рамках этой концепции предлагалось интегрировать методы математиче-
ской статистики и теории вероятности, погруженные в дружественную для
пользователя информационно-технологическую среду. Журнал Nature посвя-
тил проблеме извлечения новых знаний из большего объема данных спец-
выпуск [3], в котором были сформулированы так называемые “5V” атрибут,
характеризующие данные, пригодные для указанной цели.
Однако, методологическим ядром многих концепций, связанных с данны-
ми, является параметризованная математическая модель, а физическим яд-
ром является компьютер, на котором обучается указанная модель с помо-
щью соответствующего информационного и алгоритмического обеспечения.
Поэтому процедуры и алгоритмы машинного обучения (МО) являются клю-
чевыми в современных концепциях извлечения знаний. Следует напомнить,
что МО имеет более чем 60-летнюю историю и опыт решения многочислен-
ных задач. Первая публикация из этой области относится к 1957 г., когда
Ф. Розенблатт создал персептрон МАРК I [4]. Понятие эмпирического риска,
ключевое для МО-процедур, было введено в монографии Я.З. Цыпкина [5].
Метод потенциальных функций в задачах классификации и распознавания
был опубликован в 1970 г. в монографии М.А. Айзермана, Э.М. Бравермана,
Л.И. Розоноэра [6]. Основные идеи машинной классификации были опубли-
кованы в монографиях [7, 8], а реализованы они в методе SVM существен-
но позднее [9]. Современный референс-лист работ, посвященных машинно-
му обучению, насчитывает тысячи наименований, обзору и анализу которых
можно посвятить отдельную статью. Но все-таки, некоторые из них следует
упомянуть (исключительно по календарному принципу) [10-18].
Существующие представления о МО базируются на параметризованных
с детерминированным происхождением моделях, параметры которых неиз-
вестны, но, используя данные, можно найти оценки их значений.
Здесь будет развиваться иной, а именно рандомизированный подход к
проблемам машинного обучения (РМО), особенность которого состоит в том,
что в его рамках параметризованная модель имеет случайные параметры, а
данные используются для оценивания не их значений, а функций плотности
распределения вероятностей параметров. Смысл такого подхода состоит в
том, что реальные задачи, для решения которых привлекаются МО-процеду-
ры, как правило, погружены в некоторую неопределенную среду. Если речь
идет о данных, то они получены с ошибками, пропусками, низкой достоверно-
стью. Формирование моделей и их параметризация — процесс неформализуе-
мый и субъективный, зависящий от индивидуальных знаний исследователя.
Поэтому в массовом применении МО-процедур уровень неопределенности до-
статочно высок.
123
В рамках РМО формируются энтропийно-оптимальные оценки функций
плотности распределения вероятностей параметров и шумов, в соответствии
с которыми генерируются ансамбли моделей “наилучших” в условиях макси-
мальной неопределенности. В статье рассмотрены два класса РМО-алгорит-
мов, различающиеся условиями балансировки выхода модели с реальными
данными. В одном из них предполагается так называемая “жесткая” балан-
сировка, когда выход модели в точности должен совпадать с реальными дан-
ными. В другом используется “мягкая” балансировка, когда выход приближен
к реальным данным оптимально в терминах принятого критерия.
В обоих классах РМО обученная модель генерирует ансамбли случайных
векторов или случайных траекторий, соответствующих найденным оптималь-
ным функциям плотности распределения вероятностей (ПРВ) параметров и
шумов. Эти ансамбли используются для решения задач “мягкой” (с вероятно-
стью) классификации и кластеризации, а также для задач рандомизирован-
ного прогнозирования с использованием моделей динамического регрессии.
2. РМО-процедура, структура и классификация
Рандомизация представляется альтернативным подходом к машинно-
му обучению, направленным на повышение достоверности, надежности и
гибкости МО-процедур в условиях неопределенности и функционирова-
ния как при больших, так и при ограниченных объемах данных. Для до-
стижения этих декларируемых целей предлагается комплекс структурных,
информационно-технологических и алгоритмических модификаций стан-
дартных МО-процедур. При этом используется те же коллекции данных для
реализации РМО-процедур. Они состоят из двух массивов данных, которые
будем называть входными X и выходными Y .
Данные в указанных массивах измеряются в дискретные моменты вре-
мени j = 1, . . . , s. Поэтому входные данные характеризуются матрицей X =
= [x(1), . . . , x(s)], а выходные
— матрицей Y = [y(1), . . . , y(s)]. Векторы
x(j) ∈ Rn, y(j) ∈ Rm. Предполагается, что массив входных данных содер-
жит точные данные, а массив выходных данных — с ошибками интер-
вального типа, которые будем характеризовать матрицей случайных шумов
Ξ=
ξ(1),...
ξ(s)]. Случайные вектор
ξ(j) ∈ Rm, j = 1,s, - независимые и
компоненты их также независимые:
ξ(j)i ∈ E(j)i = [ξ-i(j),ξ+i(j)], i = 1,m, j = 1,s;
⋃
(1)
ξ(j) ∈ Ξj =
E(j)i.
i=1
Вероятностные свойства шумов характеризуются функциями плотности
распределения вероятностей (ПРВ) Qj
ξ(j)), j = 1,s. Предполагается, что
ПРВ — непрерывно дифференцируемые функции.
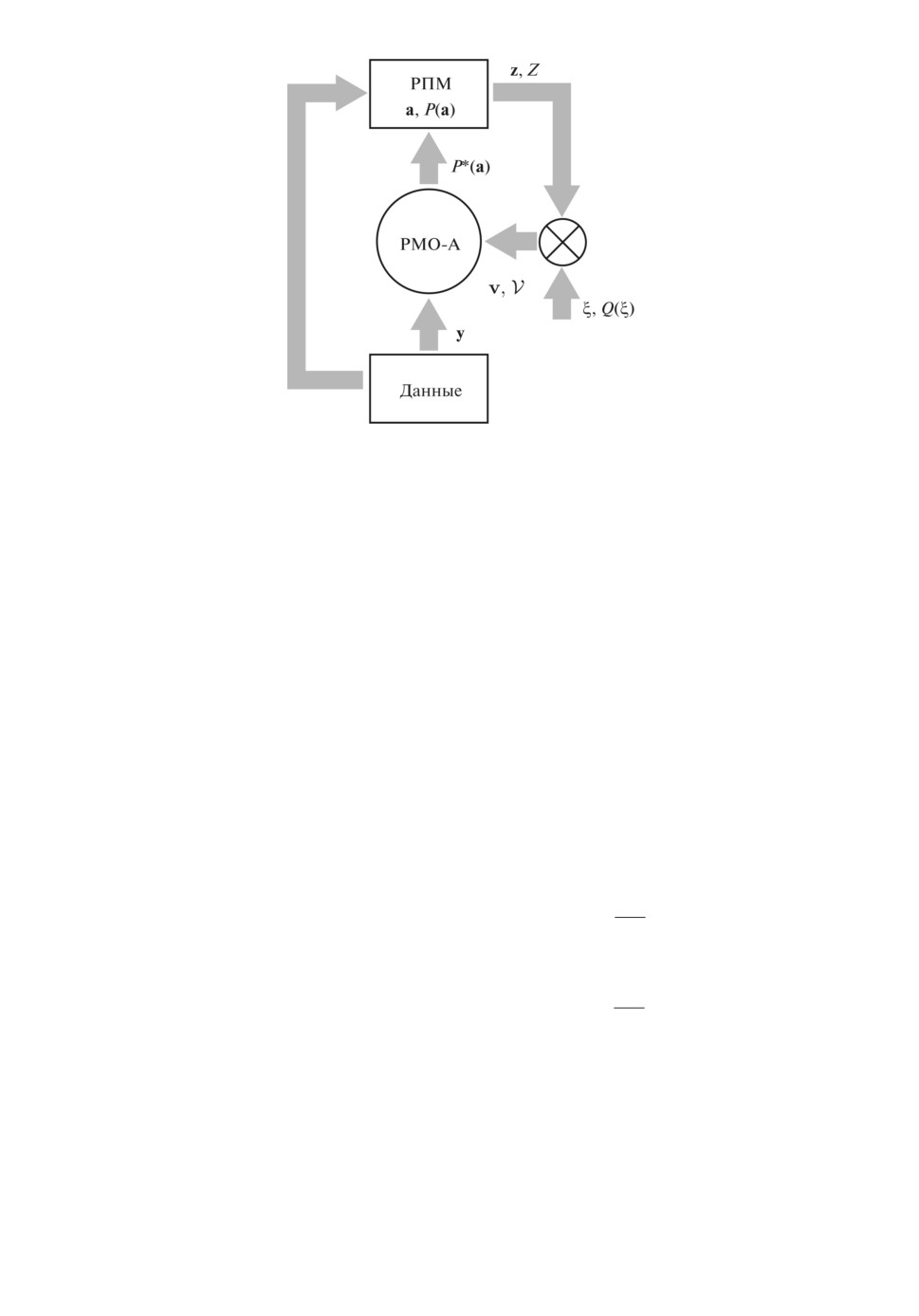
Структура РМО-процедуры представлена на рис. 1. Ее основными эле-
ментами являются рандомизированная параметризованная модель (РПМ) и
алгоритм рандомизированного машинного обучения (РМО-А).
124
Рис. 1. Структура РМО-процедуры.
1. РПМ преобразует массив входных данных X в модельный выход, ха-
рактеризуемый матрицей Z = [z(1), . . . , z(s)], где z(j) ∈ Rm. В общем случае
связь между массивами в обучающей коллекции предполагается динамиче-
ской. Это означает, что модельный выход, наблюдаемый в момент време-
ни j, зависит от входа, наблюдаемого на некотором историческом интервале
j - ϱ,...,j, т.е. от матрицы Xϱ(j) = [x(j-ϱ),...,x(j)]. Математическим обра-
зом этой связи является векторный функционалΩ(Xϱ(j) | a, P (a)) со случай-
ными параметрами a интервального типа
(2)
a ∈ A = [a-,a+
].
Вероятностные свойства параметров характеризуются функцией плотно-
сти распределения вероятностей (ПРВ) P (a), которая предполагается
непрерывно-дифференцируемой.
Выход РПМ в j-й момент времени представляет собой ансамбл
Z(j | P (a))
случайных векторов
(3)
z(j | a) =Ω(Xϱ
(j) | a, P (a)),
j = 1,s.
Для имитации влияния измерительных шумов вводятся случайные векторы
(4)
v(j | a
ξ(j)) = z(j |a)
ξ(j)
,
j = 1,s,
образующие ансамбль V(j | P (a), Qj
ξ(j))). Вероятностные свойства этого ан-
самбля зависят от ПРВ P (a) и Q1
ξ(1)),... ,Qs
ξ(s)). Смысл рандомизирован-
ного обучения состоит в определении таких функций ПРВ, в которых бы
учитывались условия балансирования ансамбля V(j | P (a), Qj
ξ(j))) c выход-
ными обучающими данными Y (эмпирические балансы).
2. РМО-А представляет собой обучающий модуль, в котором формали-
зован принцип оптимальности рандомизированного обучения, который опи-
125
сывается задачей функционального математического программирования, ба-
зовой компонентой которой является функционал информационной энтро-
пии [19, 20], определенный на функциях ПРВ P (a) случайных параметров
РПМ и функциях ПРВ Q1
ξ(1)),... ,Qs
ξ(s)) шумов:
∫
P (a)
H[P (a), Q1
ξ(1)),... ,Qs
ξ(s))] = - P(a) ln
da-
P0(a)
A
∫
∑
Qj
ξ(j))
(5)
-
Qj
ξ(j)) ln
ξ(j),
Q0j
ξ(j))
j=1
Ξj
где P0(a), Q0j
ξ(j)) — априорные ПРВ параметров и шумов.
Eго максимизация гарантирует получение наилучших решений при мак-
симальной неопределенности. Эта логическая цепь была впервые деклари-
рована в [21] (см. также [22-25]). Информационная энтропия характеризует
неопределенность, связанную не только со случайными параметрами, но и с
шумами наблюдений. Поэтому максимум энтропии соответствует наилучшим
оценкам для максимально неопределенных (в единицах энтропии) шумов.
Алгоритмы РМО можно разделить на два класса, в одном из которых
реализуется принцип “жесткой” рандомизации, а в другом — “мягкой” рандо-
мизации. Различие между ними связано с характером выполнения условий
эмпирических балансов — точно или приближенно.
2.1. Под “жесткой” рандомизацией понимаются равенства между число-
выми характеристиками ансамбля V(j | P (a), Qj
ξ(j))) и выходными обучаю-
щими данными Y :
[
]
(6)
m(k) j |P(a),Qj
ξ(j))
= y(j),
j = 1,s.
Здесь m(k)[j | P (a), Qj
ξ(j))] — вектор k-средних с компонентами следующего
вида:
[
]
[
]1/k
(7)
m(k)i j |P(a),Qj
ξ(j)) = MP{zki ((j |a))} + MQj{ξki (j)}
,
где MP , MQj — операторы математического ожидания по ПРВ P , Qj соот-
ветственно. Здесь для характеризации эмпирических балансов при “жесткой”
рандомизации будет использоваться 1-средние, т.е.:
[
]
(8)
m(1) j |P(a),Qj
ξ(j))
= y(j),
j = 1,s.
где
∫
∫
m(1)i(j |P(a),Qj
ξ(j))) =
P (a)zi(j |a)da + Qj
ξ(j))ξ(j)i
ξ(j),
(9)
A
Ξj
i = 1,m, j = 1,s.
126
2.2.
При
“ мягкой” рандомизации балансы между ансамблем
V(j | P (a), Qj
ξ(j))), состоящим из случайных векторов
v(j | a
ξ(j)) (4), и
выходными обучающими данными — (s × m)-матрицей Y = {y(1), . . . , y(s)}
выполняются приближенно в терминах принятого критерия.
Для формирования подходящего критерия обратимся к равенству (4),
определяющему случайные j-векторы, входящие в ансамбль V. Близость век-
торв v(j | a) и y(j) будем оценивать какой-либо гельдеровской векторной нор-
мой [26]:
(10)
N(j)(a
ξ(j),y(j)) = ∥z(j |a) - y(j)
ξ(j)∥H ≤ N(j)z,y(a,y(j)) + NΞ
ξ(j)
),
где
(11)
N(j)z,y(a,y(j)) = ∥z(j |a) - y(j)∥H,
(12)
N(j)ξ
ξ(j)) =
ξ(j)∥H.
Норма (11) характеризует различие между вектором выхода модели и векто-
ром обучающих данных, а норма (12) — “мощность” шумов.
Заметим, что нормы (11) и (12) являются функциями случайных аргумен-
тов: параметров a и шумо
ξ(j). Определим их математические ожидания:
∫
N (j)
z,y
[P (a)] = P (a)N(j)z,y(a, y(j))da,
A
∫
N(j)
(13)
[Qj
ξ(j))] =
Qj
ξ(j))Nξ
ξ(j))
ξ(j).
ξ
Ξj
Качество приближения эмпирических балансов и оценивания “мощности”
шумов в случае мягкой рандомизации будем характеризовать функционала-
ми (13).
3. РМО-алгоритмы с “жесткой” рандомизацией
“Жесткая” рандомизация предусматривает точное выполнение эмпириче-
ских балансов. Поэтому соответствующий ей РМО-А формулируется в сле-
дующем виде:
∫
P (a)
H[P (a), Q
ξ)] = - P (a) ln
da-
P0(a)
A
∫
∑
Qj
ξ(j))
(14)
-
Qj
ξ(j)) ln
ξ(j)
⇒ max
Q0j
ξ(j))
j=1
Ξj
при условиях:
— нормировки функций ПРВ
∫
∫
(15)
P (a)da = 1,
Qj
ξ(j))
ξ(j)
= 1, j = 1, s;
A
Ξj
127
— эмпирические балансы с использованием 1-средних
(16)
m(1)(j |P(a),Qj
ξ(j)
)) = y(j),
j = 1,s.
Здесь P0(a), Q0j
ξ(j)) — априорные ПРВ параметров и шумов; вектор m(k)
имеет компоненты (9). Задача (14) и (16) является функциональной зада-
чей энтропийно-линейного программирования ляпуновского типа [27-31] (все
компоненты задачи описываются интегральными функционалами). Для за-
дач этого типа условия оптимальности могут быть получены с использо-
ванием функционала и множителей Лагранжа. Поскольку функции ПРВ
в РМО-А — непрерывно-дифференцируемые, то вариация функционала
Лагранжа может быть определена с использованием производных Гато [32].
Введем следующие обозначения:
• переменная
∫
(17)
w(P (a)) = 1 -
P (a) da;
A
• вектор q(Q
ξ)) с компонентами
∫
(18)
qj(Qj
ξ(j))) = 1 - Qj
ξ(j))
ξ(j)
,
j = 1,s;
Ξj
• векторы
(19)
e(j)(P(a),Q
ξ)) = y(j) - m(1)(j | P (a), Qj
ξ(j)
)).
• множители Лагранжа μ; ν1, . . . , νs; θ(1), . . . , θ(s).
Здесь Q
ξ) = [Q1
ξ(1)),... ,Qs
ξ(s))]. Используя введенные обозначения, опре-
делим функционал Лагранжа
L[P (A), Q
ξ)] = H[P (a), Q
ξ)] + μw(P (a)) + 〈ν, q(Q
ξ))〉+
∑
(20)
+
〈θ(j),e(j)(P(a),Q(ξ
))〉.
j=1
В этом равенстве 〈•, •〉 — скалярное произведение.
Условия стационарности функционала (20) в терминах производных Гато
имеют вид:
∑
P∗(a)
ln
+1+μ+
〈θ(j),ê(j)〉 = 0,
P0(a)
j=1
Q∗j
ξ(j))
(21)
ln
+1+νj +〈θ(j)
ξ(j)
〉 = 0,
Q0j
ξ(j))
j = 1,s.
128
Отсюда следуют выражения для энтропийно-оптимальных функций ПРВ па-
раметров РПМ и шумов измерений:
⎡
⎤
∑
P∗(a) = P0(a)exp ⎣-1 - μ -
〈θ(j),z(j)〉⎦ ,
j=1
[
]
(22)
Q∗j
ξ(j)) = Q0j
ξ(j))exp
-1 - νj - 〈θ(j)
ξ(j)〉 ,
j = 1,s.
Используя условия нормировки (17) и (18), можно исключить множители
Лагранжа μ и ν. Тогда выражения для энтропийно-оптимальных и нормиро-
ванных функций ПРВ примут вид:
[
]
∑
P0(a)exp -
〈θ(j),z(j)〉
j=1
P∗(a) =
,
P(θ)
[
]
Q0j
ξ(j))exp
-〈θ(j)
ξ(j)〉
(23)
Q∗j
ξ(j)) =
,
Qj(θ(j))
j = 1,s.
В этих равенствах
⎡
⎤
∫
∑
P(θ) = P0(a) exp ⎣-
〈θ(j),z(j)〉⎦ da,
j=1
A
∫
[
]
(24)
Qj(θ(j)) = Q0j
ξ(j))exp
-〈θ(j)
ξ(j)〉
ξ(j)
,
j = 1,s.
Ξj
Здесьθ = {θ(1), . . . ,θ(s)}. Из (23) и (24) следует, что энтропийно-оптимальные
функции ПРВ принадлежат экспоненциальному семейству, параметризован-
ному множителями Лагранжа.
Значения указанных множителей Лагранжа определяются следующими
уравнениями, возникающими из эмпирических балансов (16) при подстановке
в них функций ПРВ из (23) и (24):
⎡
⎤
∫
∑
P-1(θ) P0(a) exp ⎣-
〈θ(j),z(j)〉⎦ da +
j=1
A
∫
[
]
(25)
+Q-1j(θ) Q0j
ξ(j))exp
-〈θ(j)
ξ(j)〉
ξ(j) = y(j),
Ξj
j = 1,s.
129
Уравнения (25) образуют особый класс нелинейных уравнений, в которые
входят интегральные компоненты, определяющие функциональные зависи-
мости левых частей этих уравнений от множителей Лагранжаθ.
4. РМО-алгоритмы с “мягкой” рандомизацией
При “мягкой” рандомизации эмпирические балансы выполняются при-
ближенно в рамках условной минимизации синтетического функционала (5)
и (13):
∑
N (j)
J [P (a), Q
ξ)] = H[P (a), Q
ξ)] -
(P (a)) -
z,y
j=1
(26)
∑
N(j)
-
(Qj
ξ(j))) ⇒ max,
ξ
j=1
при условиях нормировки ПРВ
∫
∫
(27)
P (a)da = 1,
Qj
ξ(j))
ξ(j)
= 1, j = 1, s.
A
Ξj
Эта задача ляпуновского типа, и ее решение может быть найдено с помощью
условий оптимальности в терминах производных Гато [32].
Будем иметь:
[
]
(
)
∑
P0(a)exp -
z,y (a,y(j)) + N(j)ξ
ξ(j))
j=1
P∗(a) =
,
P
[
]
(j)
exp -Nξ
ξ(j))
(28)
Q∗j
ξ(j)) =
,
j = 1,s,
Qj
где
∫
P = P∗(a)da,
A∫
(29)
Qj = Q∗j
ξ(j))
ξ(j)
,
j = 1,s.
Ξj
Отсюда видно, что при “мягкой” рандомизации требуются вычислитель-
ные ресурсы только на вычисление многомерных интегралов (29).
130
5. Некоторые приложения рандомизированного машинного обучения
5.1. РМО с “жесткой” рандомизацией для бинарной вероятностной
классификации текстов
Бинарная вероятностная классификация предполагает определение при-
надлежности объекта соответствующему классу с вероятностью, вычисляе-
мой с учетом имеющейся обучающей коллекции.
Рассмотрим в качестве примера рандомизированный линейный бинарный
классификатор. Пусть имеются две коллекции текстовых документов: обу-
чающая E = {e1, . . . , em} и тестовая T = {t1, . . . , ts}. В обучающей коллекции
документы помечены принадлежностью либо к классу 1, либо к классу 2.
В тестовой коллекции документы никак не помечены.
Документы в обеих коллекциях представлены векторами, компонентами
которых являются веса ключевых слов (термов), встречающихся в докумен-
те. Тем самым формируются наборы векторов, размерность которых равна
количеству n ключевых слов:
E = {e(1),...,e(m)},
e(j) ∈ Rn, j = 1,m,
(30)
T = {t(1),...,t(s)},
t(k) ∈ Rn
,
k = 1,s.
Здесь Rn — пространство признаков, в данном случае — весов ключевых слов.
1. Э т а п о б у ч е н и я. Документы в обучающей коллекции помечены, т.е.
она состоит из пар “номер документа, класс”: O = {(1, 1), (2, 1), . . . , (m, 1)}
длины m. Трансформируем ее в последовательность чисел из интервала [0, 1],
где номеру элемента в коллекции могут соответствовать числа из интервала
[1/2, 1], если документ принадлежит первому классу, и числа из интервала
[0, 1/2), если документ принадлежит второму классу. Таким образом, получа-
ем “обучающий” вектор y с компонентами, значения которых лежат в интер-
вале [0, 1], и размерностью, равной количеству m документов в коллекции,
т.е.
{
}
(31)
y= y(1),...,y(m)
Рандомизированная модель (решающее правило) представляется случайным
вектором z(e(j), a), зависящим от случайных параметров a однослойной ней-
ронной сети
(
)
(32)
z(j)(a) = sigm
〈e(j), a〉
,
j = 1,m.
Здесь
1
(33)
sigm(x) =
,
1 + exp[-α(x - Δ)]
где параметры α и Δ фиксированы. Аргумент этой функции случайный, так
как параметры a рандомизированной модели случайные. Значения функции
131
sigm(x) на интервале [1/2, 1] соответствуют первому классу, и значения в
открытом интервале [0, 1/2) — второму классу.
В рандомизированной модели (32) параметры a = {a1, . . . , an} — незави-
симые, интервального типа:
ak ∈ Ak = [a-k,a+k],
k = 1,n,
⊗
(34)
A= Ak.
k=1
На этих интервальных множествах существует функция ПРВ P (a). Поэтому
для каждого документа с номером j имеет место ансамбл
Z(j) случайных чи-
сел из интервала (0, 1) (32) и (53). Средние значения компонент будут иметь
следующий вид
∫
(
)
(35)
M{zj(a)} = P (a)sigm
〈e(j), a〉
da.
A
Итак, РМО-А классификации с “жесткой” рандомизацией представляются
в следующем виде
∫
(36)
H[P (a)] = -
P (a) ln P (a)da ⇒ max
A
при условиях:
- нормировки
∫
(37)
P (a)da = 1,
A
- эмпирических балансов
∫
(
)
(38)
P (a)sigm
〈e(j), a〉 da = y(j)
,
j = 1,m.
A
Введем множители Лагранжаθ = {θ1, . . . , θm} для ограничений (38). Тогда
решение этой задачи, согласно (22) и адаптированное к модели (53), с точно-
стью до множителей Лагранжа θ1, . . . , θm имеет вид
W∗(a)
(39)
P∗(a) =
P(θ),
где
(
)
(40)
W∗(a) = exp
-〈θ, z(a)〉
,
∫
[
]
(41)
P(θ) = exp
-〈θ, z(a)〉
da.
A
132
Таблица 1
j
e(j)1
e(j)2
e(j)3
e(j)4
1
0,11
0,75
0,08
0,21
2
0,91
0,65
0,11
0,81
3
0,57
0,17
0,31
0,91
Множители Лагранжаθ определяются системой балансовых уравнений (38)
следующего вида
∫
[
]
(42)
P-1(θ) exp
-〈θ, z(a)〉
z(j)(a)da = y(j)
,
j = 1,m.
A
Заметим, что размерность этой системы равна количеству документов в
обучающей коллекции. Поэтому с точки зрения вычислительной трудоем-
кости рандомизированная процедура решения задачи классификации более
эффективна для ограниченных объемов обучающей коллекции. Рассмотрим
два примера, которые демонстрируют основную идею РМО-А с “жесткой”
рандомизацией для бинарной классификации текстов.
Пример
1 — Обучение. Размерность алгоритма равна 4, обучающая
коллекция состоит из трех документов, каждый из которых описывается че-
тырьмя весами, значения которых показаны в табл. 1.
Рандомизированная модель (32) и (53) имеет параметры: α = 1,0 и Δ = 0.
Ответы y = {0,18; 0,81; 0,43} (yi < 0,5 соответствует классу 2, yi ≥ 0,5 со-
ответствует классу 1). Множители Лагранжа для энтропийно-оптимальной
ПРВ (39) и (40) имеют следующие значения:θ = {0,2524; 1,7678; 1,6563}. Па-
раметры ai ∈ [-10, 10], i = 1, 4. Энтропийно-оптимальная для данной обуча-
ющей коллекции функция W∗(a) (39) имеет вид
(
)
∑
W∗(a) = exp
- θizi(a)
,
i=1
(
(
))(-1)
∑
(43)
zi(a) =
1 + exp
- e(j)k, ak
k=1
На рис. 2 показано двумерное сечение функции (39) при a3 = 0,5; a4 = 0,5.
2. Э т а п т е с т и р о в а н и я. На этом этапе используется коллекция T =
= {t1, . . . , ts}, где каждый элемент коллекции характеризуется вектором
t(j) ∈ Rn. Рассмотрим процедуру классификации для произвольного доку-
мента t(j).
Шаг 1. Генерируется ансамбль
Z(i) выхода рандомизированной модели
(решающих правил) (32) и (53) с функцией P∗(a) (39). Ансамбль содержит
N случайных чисел из интервала [0, 1].
Шаг 2. Если случайное число из этого ансамбля больше 1/2, то доку-
мент t(i) относится к классу 1. Если — меньше 1/2, то — к классу 2.
Шаг 3. Пусть N1 чисел оказались в классе 1 и N2 — в классе 2. Посколь-
ку число испытаний N достаточно велико, то можно считать, что величины
133
W(a)
8
6
4
2
0
10
10
5
5
0
0
5
5
a2
10
10
a1
Рис. 2. Двумерное сечение функции
ПРВ для a3 = 0,5, a4 = 0,5,
θ = {3,2807,-3,5127,1,6373}.
a
б
p(i)
Класс 1
p(i)
Класс 2
0,8
0,7
0,7
0,6
0,6
0,5
0,5
0,4
0,4
0,3
0,3
0,2
0,2
0,1
0,1
0
50
100 150 200 250 300 350 400 450 500 0
50
100 150 200 250 300 350 400
450 500
Тестовые документы
Тестовые документы
Рис. 3. Эмпирические вероятности принадлежности классам.
p(i)1
= N1/N и p(i)2 = N2/N есть эмпирические вероятности попадания доку-
мента t(i) в соответствующий класс. Повторяя операции шагов 2, 3 для всей
коллекции T, получим распределения вероятностей попадания документов в
класс 1 или 2.
Пример
1 — Тестирование. Генерируется массив (500 × 4) четырех-
мерных случайных векторов t(i), i = 1, 500, с независимыми компонентами,
равномерно распределенными в интервалах [0, 1]. Для каждого элемента этой
выборки генерируются случайные параметры модели (32) и (53) в соответ-
ствии с ПРВ (39) и (40) (N = 1000) методом исключения [33] и вычисляется
ее выход. Выполняются шаги 2, 3.
На рис. 3a-3б показаны эмпирические вероятности p(i)1, p(i)2 принадлежно-
сти ti-документа классу 1 и 2.
134
5.2. РМО с “мягкой” рандомизацией для прогнозирования миграционного
взаимдействия региональных систем
Взаимовлияние миграционных процессов в региональных системах —
проблема, актуальность которой возрастает в современном мире. Неоднород-
ность социально-экономического статуса регионов возрастает вместе с ростом
политической и военной напряженности. Все это приводит к резкому пере-
распределению миграционных потоков и, как следствие, к изменению числен-
ности регионального населения и росту затрат на его обеспечение. Поэтому
важными оказываются инструментальные средства (математические модели,
алгоритмы, программное обеспечение), позволяющие в режиме адаптации к
динамике миграции прогнозировать ее распределение с учетом имеющихся
обеспечивающих ресурсов.
Рассмотрим динамическую модель миграционного взаимодействия с огра-
ничением на общий ресурс и дискретным временем, изложенную в [34]. Она
состоит из двух блоков. Первый блок моделирует миграционные потоки внут-
ри системы S1 и описывается уравнением динамической регрессии:
(44)
K[(s + 1)h] = (A - E)K[sh] + F(z[sh]),
(K, F) ∈ RN
, s = 0,K - 1,
где A — матрица пространственных передвижек, E — диагональная матрица
мобильности, K[sh] — распределение населения в региональной системе S1 в
момент времени sh.
Локально-стационарное распределение в момент времени sh иммиграци-
онных потоков из региональной системы S2 в систему S1, характеризуемое
энтропийным оператором, моделирует второй блок, допускающий описание
вектор-функцией F(z[sh]) с компонентами
∑
(45)
fn[sh] = h
bjn(z[sh])cjn
,
n = 1,N, s = 0,K - 1.
j=1
Переменная z — экспоненциальный множитель Лагранжа в задаче энтро-
пийно-оптимального распределения иммиграционных потоков определяется
решением уравнения
∑
(46)
cknbkn(z[sh])ckn
= T[sh],
k=1 n=1
где T [sh] — объем общего для регионов системы S1 ресурса, который исполь-
зуется для поддержки иммигрантов.
Входными данными для модели являются объемы T [0], T [h],
...,T[(K - 1)h] и выходными
— распределения регионального населе-
ния K[0], K[h], . . . , K[(K - 1)h] в системе S1.
Рассмотрим применение “мягкой” рандомизации для оценивания и прогно-
зирования иммиграционных потоков из Сирии (1) и Ливии (2) (система S2)
в Германию (1), Францию (2) и Италию (3) (система S1).
135
Таблица 2
mn
0,43
0,50
0,40
h1n
0
0,3
0,3
h2n
0,3
0
0,3
h3n
0,5
0,4
0
b1n
0,4
0,3
0,3
b2n
0,3
0,1
0,4
c1n
0,4
0,4
0,3
c2n
0,4
0,4
0,3
1. Рандомизированная модель, параметры, ошибки измерений, временные
интервалы и коллекции реальных данных. Воспользуемся рандомизирован-
ной математической моделью (44)-(46), применив в ней нормализованные
переменные
Kn[sh]
(47)
pn[sh] =
,
n = 1,3.
Kmax
Получим:
∑
pn[(s + 1)h] = (1 - b1mn)pn[sh] + hb1b2
mihinpi[sh] + hfn[sh],
i=1,i=n
∑
(48)
fn[sh] =
,
n = 1,3,
binbcin3
i=1
∑∑
T [sh] =
cinbinbcin3.
n=1 i=1
В этих уравнениях переменные состояния системы S1 и иммиграционнные
потоки из системы S2 нормализованы, т.е.
(49)
0 ≤ pn[sh] ≤ 1,
0≤fn
[sh] ≤ 1,
n = 1,N.
Переменная z∗ есть характеристика энтропийного оператора иммиграцион-
ного процесса, которая определяется решением последнего уравнения в (48).
Значения параметров mi, hin, bin и cin указаны в табл. 2.
Согласно этой таблице mmax = 0,5; hmax = 0,5; bmin = 0,3; bmax = 0,4;
cmax = cmin = c = 0,5. Ошибки измерений численности (в нормализованных
единицах
ξ[sh] ∈ R3 интервального типа
(50)
ξ[sh] ∈ Ξ =
ξ-
ξ+],
ξ±n
= 0,01,
причем границы интервалов предполагаются одинаковыми для моментов вре-
мени sh.
Нормализованный наблюдаемый выход модели имеет вид
(51)
v[sh] = p[sh] +ξ
[sh].
136
Таблица 3. Входные и выходные коллекции данных
год
2009
2010
2011
2012
2013
s
0
1
2
3
4
Y1[s]
81,90
81,77
80,27
80,42
80,64
y1[s]
1,00
0,998
0,980
0,982
0,985
Y2[s]
62,47
62,80
63,11
63,41
63,70
y2[s]
0,762
0,767
0,771
0,774
0,778
Y3[s]
59,39
59,53
59,63
59,71
59,75
y3[s]
0,725
0,727
0,728
0,729
0,726
T [s] (млрд)
0,093
0,094
0,095
0,096
0,097
Модель (48) со случайными параметрами будет использоваться для оце-
нивания их характеристик и тестирования на соответствующих временных
интервалах с шагом h = 1 год:
• интервал оценивания Test = 2009 - 2013 годы;
• интервал тестирования Ttst = 2014 - 2018 годы.
2. Энтропийное оценивание ПРВ параметров и шумов (интервал Test).
Для решения этой задачи используются данные о распределении населения
в Германии n = 1, Франции n = 2 и Италии n = 3 и об общих затратах на
обустройство иммигрантов в интервале оценивания, которые приведены в
табл. 3, (UNDATA a world information, data.un.org).
В этой модели параметры b1, b2, b3 — случайные со значениями из интер-
валов:
(52)
b1 ∈ B1 = [1,0;2,5]; b2 ∈ B2 = [0,5;1,8], b3 ∈ B3
= [0,3; 1,5].
Cогласно (4)
(53)
U1 = 0,5; U2 = 00,5; U3 = 1,2, U4
= 0,986.
Тогда метод “мягкого” РМО дает следующие оптимальные ПРВ парамет-
ров и шумов:
(
)
0,5
exp
-0,5b1 - 0,5b1b2 - 1,2b
- 0,986
3
W∗(b) =
,
W
(
)
∑
3
2
exp
-
ξ
n=1
n
(54)
Q∗
ξ) =
,
Q
где
∫
∫
∫
(
)
W =
exp
-0,5b1 - 0,5b1b2 - 1,2b0,53 - 0,986 db1db2db3,
B1 B2 B3
∫
∏
(55)
Q=
exp(-ξ2
)dξ.
n=1-0,01
137
а
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0
0
2,0
1
1,5
1,0
x3
0,5
2
x2
0
б
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
5
1
4
x3
3
2
x2
1
2
0
в
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0
0
5
1
4
3
x2
2
1
2
x1
0
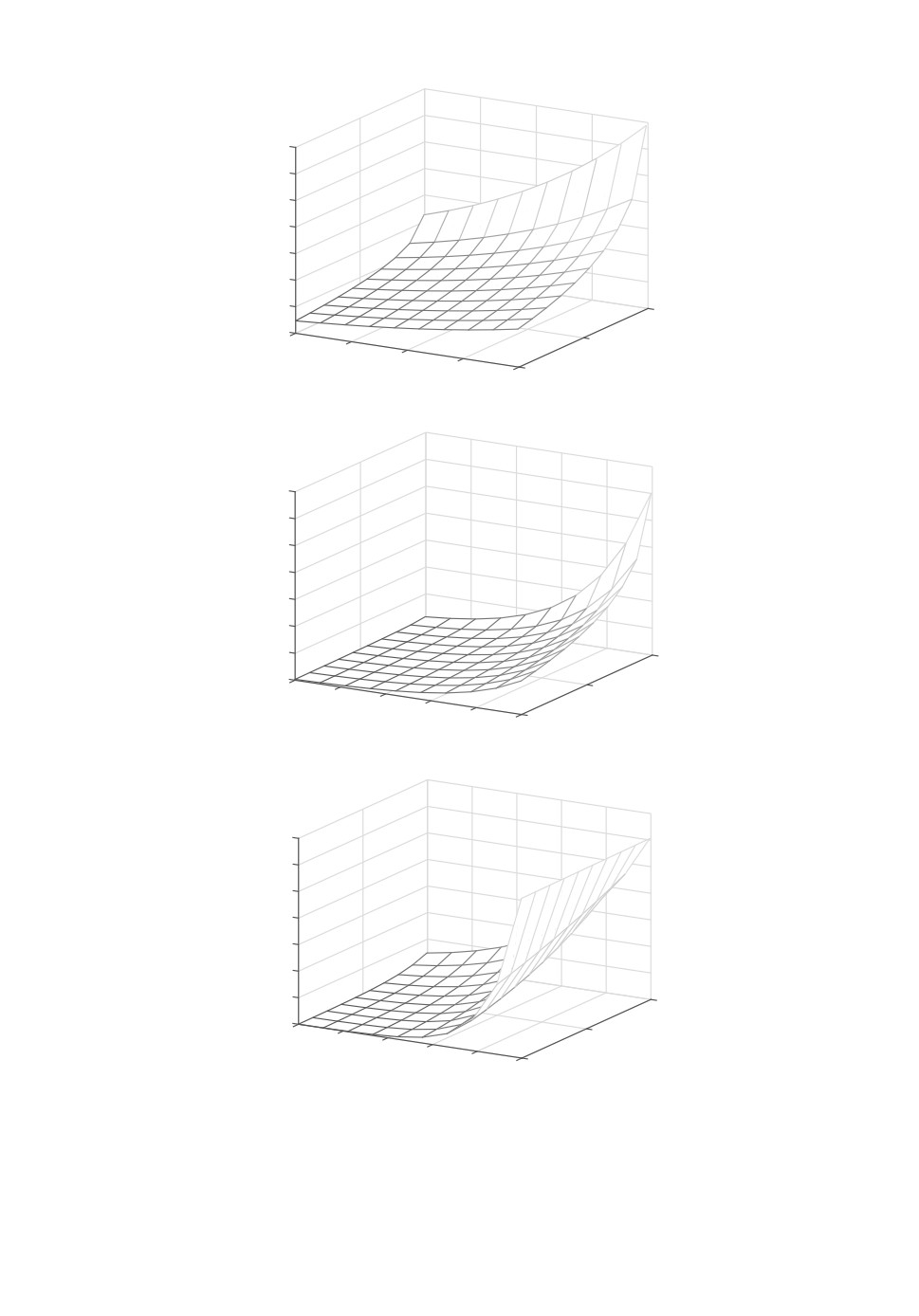
Рис. 4. a — Двумерное сечение функции ПРВ параметров W∗(x1, x2, x3),
x1 = 1,1189, I = 0,54562. б — Двумерное сечение функции ПРВ параметров
W∗(x1, x2, x3), x2 = 0,45222, I = 0,54562. в — Двумерное сечение функции
ПРВ параметров W∗(x1, x2, x3), x3 = 0,45222, I = 0,54562.
138
105
1,25000
1,24995
1,24990
1,24985
1,24980
1,24975
0,010
0,005
0,010
0,005
0
0
2
0,005
1
0,005
0,010
0,010
Рис. 5. Двумерное сечение функции ПРВ шума Q∗(ξ1, ξ2, ξ3), ξ3 = 0,01, I =
= 7,9992E - 06.
На рис. 4,a-4,в приведены графики двумерных сечений 3-мерных функции
ПРВ параметров, и на рис. 5 — функции ПРВ шума.
3. Тестирование модели. Для тестироваия рандомизированной модели (50)
с оптимальными ПРВ (54) и (55) используются тестовые данные о числен-
ности населения в исследуемых странах из UNDATA a world information
(data.un.org), приведенные в табл. 4. Там же приведены результаты тести-
рования в терминах средних по ансамблю траекторий p1[sh], p2[sh], p3[sh].
Тестирование производится путем сэмлирования значений рандомизиро-
ванных интервальных параметров, имеющих функции ПРВ (54) и (55),
и построения соответствующих траекторий согласно уравнениям (50). На
рис. 6,a-6,в показаны ансамбли таких траекторий v1[sh], v2[sh], v[sh]. На этих
же рисунках нанесены средние v1[sh], v2[sh], v3[sh] по ансамблям траектории
(штриховая линия) и траектории y1[sh], y2[sh], y3[sh] реальных изменений ре-
гиональных численностей (сплошная линия), а также указаны границы дис-
персионных трубок p∗1[sh] ± σ1, p∗2[sh] ± σ2, p∗3[sh] ± σ3 (пунктирная линия).
Таблица 4. Входные и выходные коллекции данных
год
2014
2015
2016
2017
2018
s
0
1
2
3
4
Y1[s]
81,489
81,707
82,063
82,386
82,674
y1[s]
0,985
0,988
0,993
0,996
1,000
p1[sh]
0,986
0,615
0,743
0,639
0,999
Y2[s]
64,190
64,457
64,791
65,134
65,484
y2[s]
0,721
0,472
0,564
0,529
0,708
p2[sh]
0,722
0,695
0,707
0,691
0,715
Y3[s]
59,585
59,504
59,504
59,509
59,516
y3[s]
0,775
0,609
0,562
0,699
0,650
p3[sh]
0,776
0,617
0,607
0,705
0,628
T [s] (млрд)
0,097
0,097
0,097
0,098
0,098
139
Рис. 6. a — Ансамбль траекторий v1[4] = 0,96678. б — Ансамбль траекторий
v2[4] = 0,69204. в — Ансамбль траекторий v3[4] = 0,62205.
140
Погрешность при тестировании оценивалась относительной среднеквадра-
тичной ошибкой
√
4
(pn[sh] - yn[sh])2
s=0
(56)
δn
=
√
√
∑
∑
(pn[sh])2 +
(yn[sh])2
s=0
s=0
В данном примере она составила: по региону 1 — 4,6 %, по региону 2 — 3,5 %,
по региону 3 — 2,6 %.
6. Заключение
Рандомизированное машинное обучение является эффективным инстру-
ментом решения задач оценивания, классификации, распознавания и прогно-
зирования в условиях неопределенности. Математическое описание алгорит-
мов РМО формализуется в терминах функциональных задач оптимизации.
Рассмотрены задачи с “жесткой” и “мягкой” рандомизацией и получены соот-
ветствующие алгоритмы их решения. Приведены примеры задач классифика-
ции текстов и оценивания (тестирования) моделей динамической регрессии.
СПИСОК ЛИТЕРАТУРЫ
1.
Piatetsky-Shapiro G., Frawley W. Knowledge Discovery in Databases. AAAI/MIT
Press, 1991.
2.
Witten I.H., Frank E. Data Mining: Practical Learning Tools and Techniques (2nd
Ed.). Morgan Kaufmann, 2005.
3.
Editorial Community cleverness required // Nature. 2008. V. 455. No. 1.
4.
Rosenblatt M. The Perceptron — perceiving and recognizing automaton. Report 85-
460-1, 1957.
5.
Цыпкин Я.З. Основы теории обучающихся систем. М.: Наука, 1970.
6.
Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций
в теории обучения машан. М.: Наука, 1970.
7.
Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М.: Наука, 1974.
8.
Вапник В.Н., Червоненкис А.Я. Восстановление зависимостей по эмпиричеким
данным. М.: Наука, 1979.
9.
Bishop C.M. Pattern Recognition and Machine Learning. Serise: Information Theory
and Statistics. Springer. 2006.
10.
Dempster A.P., Laird N.M., Rubin D.B. Maximum Likelihood from incomplete data
via the EM algorithm // J. Royal Statistical Society. Ser. B. 1977. No. 34. P. 1-38.
11.
Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Новосибирск:
Наука, 1998.
12.
Jain A., Murty M., Flunn P. Data clastering: A review. ASM Computing Surveys,
1999. V. 31. No. 3. P. 264-323.
13.
Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. Springer,
14.
Воронцов К.В. Математические методы обучения по прецендентам. Курс лекций
МФТИ, 2006.
141
15.
Мерков А.Б. Распознавание образов. Введение в методы статистического обуче-
ния. М.: Едиториал УРСС, 2010.
16.
Золотых Н.Ю. Машинное обучение и анализ данных. 2013.
17.
Флах П. Машинное обучение. М.: ДМК Пресс, 2015.
18.
Abellan J., Castellano J.G. Improving the Naive Bayes Classifier via a Quick Variable
Selection Method Using Maximumu of Entropy // Entropy. 2017. V. 19. No. 6.
P. 246-254.
19.
Kullback S., Leibler R.A. On Information and Sufficiency // Ann. Math. Stat. 1951.
V. 22 (1). P. 79-86.
20.
Kapur J.N. Maximum entropy models in science and engineering. John Wiley &
Sons, Inc., 1989.
21.
Jaynes E.T. Information Theory and Statistical Mechanics // Physics Review Notes.
1957. V. 106. P. 620-630.
22.
The maximum entropy formalism / Eds. R.D. Levin, M. Tribus. MIT Press, 1979.
23.
Jaynes E.T. Papers on Probability, Statistics and Statistical Physics. Dordrecht:
Kluwer Acad. Publisher, 1989.
24.
Jaynes E.T. Probability Theory. The logic and science. Cambrige Univ. Press, 2003.
25.
Racine J., Maasoumi E. A Versatile and Robust Metric Entropy Test of Time-
Reversibility, and Other Hypotheses // J. Econometrics. 2007. V. 138. P. 547-567.
26.
Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
27.
Kaashoek M.A., Seatzu S., van der Mee C. Recent Advances in Operator Theory
and its Applications. Springer, 2006.
28.
Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.
29.
Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Нау-
ка, 1979.
30.
Darkhovskii B.S., Popkov Y.S., Popkov A.Y. Monte Carlo Method of Batch
Iterations: Probabilistic Characteristics // Autom. Remote Control. 2015. V. 76.
No. 5. P. 776-785.
Дарховский Б.С., Попков Ю.С., Попков А.Ю. Метод пакетных итераций Монте-
Карло: вероятностные характеристики // АиТ. 2015. № 5. С. 60-71.
31.
Попков Ю.С., Попков А.Ю., Дарховский Б.С. Параллельный Монте-Карло для
построения энтропийно-робастных оценок // Метематическое моделирование.
2015. Т. 27. № 6. С. 14-32.
32.
Kolmogorov F.N., Fomin S.V. Elements of the Theory of Functions and Functional
Analysis. Duver Books of Mathematics, 1999.
33.
Rubinstein R.Y., Kroese D.P. Simulation and the Monte Carlo Method, John Wiley
& Sons, 2008.
34.
Попков Ю.С. Динамическая модель миграционного взаимодействия региональ-
ных систем с энтропийным оператором // Тр. ИСА РАН. 2018. Т. 68. № 3.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 06.06.2018
После доработки 13.09.2018
Принята к публикации 08.11.2018
142