Автоматика и телемеханика, № 9, 2019

(The Ohio State University, Коламбус, США),

Ю.В. ОРЛОВ, д-р физ.-мат. наук (yorlov@cicese.mx)

(CICESE, Энсенада, Мексика,

Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СИСТЕМЫ УПРАВЛЕНИЯ С ВЕКТОРНЫМИ РЕЛЕ

Статья посвящена вопросам эволюции разрывных систем управления

начиная от реле с двумя постоянными выходными значениями. Методы

анализа и синтеза управления для них были развиты Я.З. Цыпкиным и

обсуждены в его монографии “Теория релейных систем автоматического

регулирования”, опубликованной в 1955 г. Было показано, как модифи-

цируется релейная функция в так называемых системах с переменной

структурой, в которых релейный выход может быть равен одной из двух

непрерывных функций состояния. Следующий шаг был сделан в рамках

систем с переменной структурой с векторным управлением. Процедура

синтеза для систем с векторным релейным управлением основывается

на выборе разрывной поверхности для каждой компоненты управления.

Высокая эффективность так сконструированных систем объясняется воз-

никновением скользящих режимов. Наконец, было предложено векторное

релейное единичное управление. Этот метод не связан с покомпонентным

синтезом и применим для бесконечномерных систем.

Ключевые слова: скользящий режим, поверхность разрыва, регуляриза-

ция, выпуклое множество.

DOI: 10.1134/S0005231019090101

1. Введение

Системы с разрывным, в частности релейным, управлением издавна широ-

ко используются в практике автоматического управления. Тому есть две при-

чины: легкость реализации и использование всего ресурса управления. Так

называемое вибрационное управление [1], предложенное В.С. Кулебакиным в

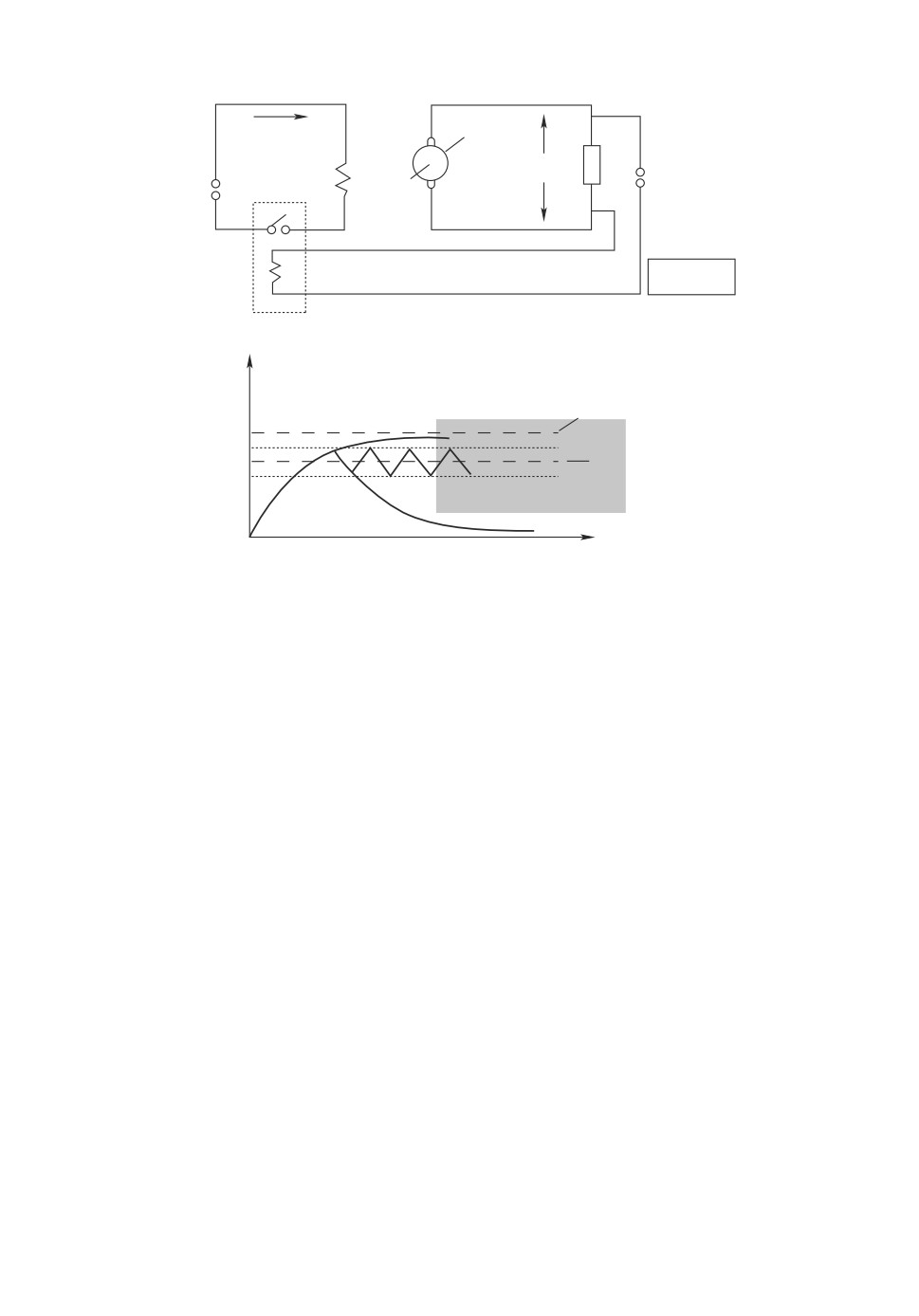
1932 г., является примером одной из первых релейных систем (см. рис. 1).

Обмотка возбуждения включалась или выключалась в зависимости от

несоответствия между задающим воздействием и выходным напряжением ге-

нератора. Как результат, разность между ними есть высокочастотная функ-

ция с малой амплитудой, зависящей от несовершенства реле (запаздывание,

зона нечувствительности, гистерезис и т.д.).

Интересно заметить, что две монографии по теории релейных систем

управления — И. Флюгге-Лотц [2] и Я.З. Цыпкина [3] — были опубликованы

ранее первых учебников по теории управления.

143

Обмотка

возбуждения

u₀

u_ex

L, r

Задание

u ki

Реле

Ku_ex

u₀

Рис. 1. Вибрационное управление генератором постоянного тока (В.С. Куле-

бакин, 1932 г.).

2. Историческая перспектива

Системы со скалярным управлением изучались авторами множества пуб-

ликаций по релейным системам. Выходы регулятора и объекта скалярны, а

управление представляет собой функцию

(1)

u = -Msgn(s),

где M — константа, а s — скалярная функция всех имеющихся переменных

(фазовые состояния объекта и динамического регулятора, внешние входы).

Монография [3] охватывает вопросы устойчивости релейных систем, ме-

тоды синтеза управления, анализ различных типов поведения: предельные

циклы, скользящие режимы, бифуркации. В силу разрывности управления

скользящий режим является одним из типов поведения релейных систем. Он

не может иметь места в системах, описываемых дифференциальными уравне-

ниями с липшицевой правой частью. Это поведение также изучалось в ранних

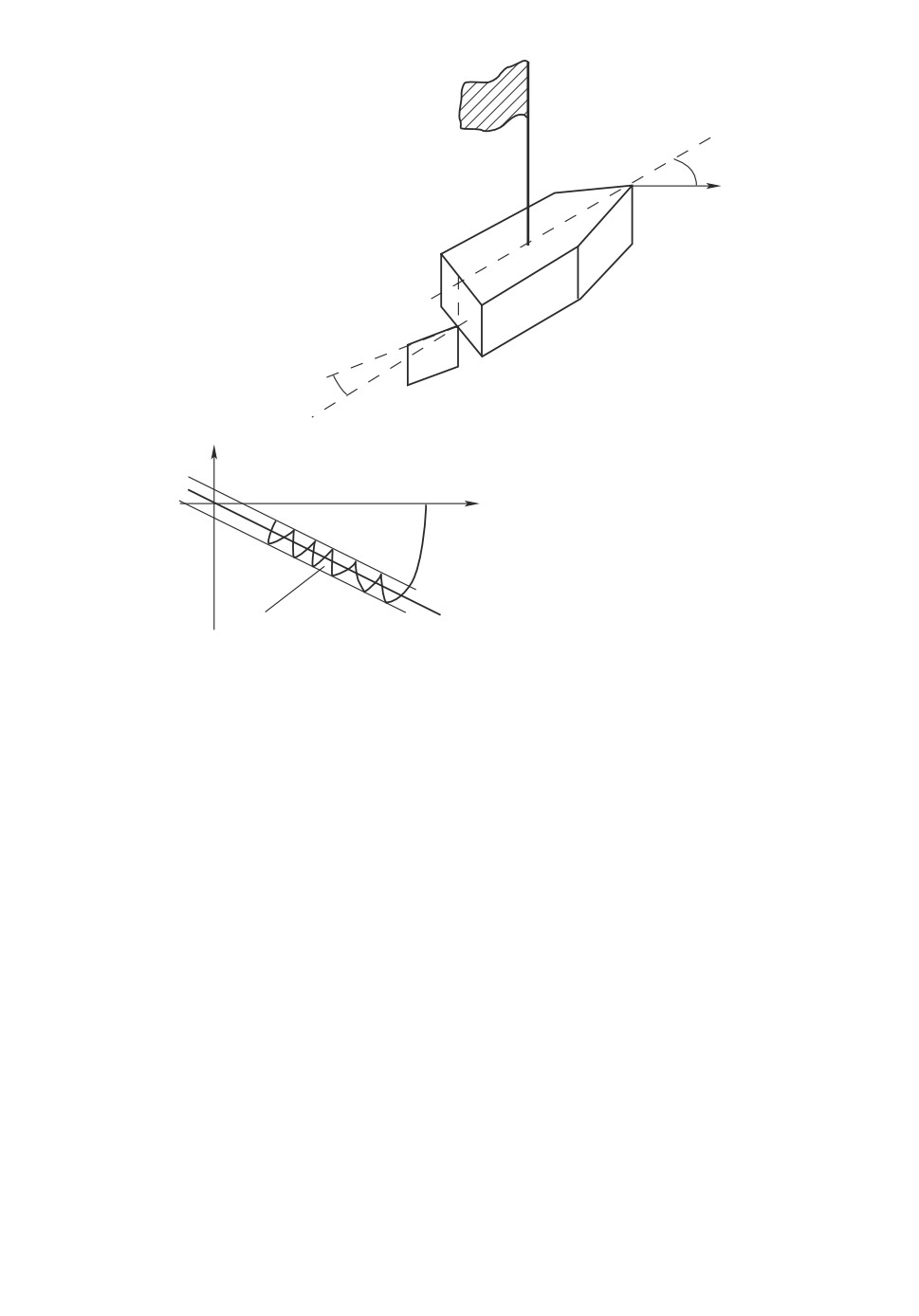
публикациях; термин “скользящий режим” (см. рис. 2) может быть найден в

монографии [4], опубликованной в 1934 г.

Заметим, что скользящий режим исследовался методом фазовой плоско-

сти за много лет то того, как метод пространства состояний стал основным.

Вибрационное управление (рис. 1) есть ни что иное, как управление со сколь-

зящим режимом в современной терминологии.

Формально уравнения релейных систем не удовлетворяют теореме су-

ществования и единственности из классической теории дифференциальных

144

- курс корабля

- положение руля

u - релейное управление

Заданный

курс

Корабль

Руль

Фазовая плоскость

Линия переключения

s = 0

Скользящий

режим

Рис. 2. Об автоматической устойчивости корабля на заданном курсе (Г.Н.

Никольский, 1934 г.).

уравнений. Что представляют собой уравнения, описывающие скользящий

режим? Это вопрос был предметом дискуссии в течение многих лет, см. тру-

ды Второй всесоюзной конференции 1953 г. [5] и труды Первого конгресса

ИФАК 1960 г. [6]. Я.З. Цыпкин ответил на этот вопрос для аффинных систем

в [3]. Уравнения скользящего режима совпадают с уравнениями медленного

движения, если элемент реле заменить на линейный усилитель с коэффици-

ентом усиления, стремящимся к бесконечности. Это выглядит разумно, так

как вход релейного элемента равен нулю в скользящем режиме, в то время

как средняя величина выхода принимает конечные значения. Цель публи-

каций до 1960-х гг. была в обнаружении скользящих режимов и в анализе

поведения систем при их возникновении. Один из участников вышеупомяну-

той дискуссии в 1953 г. рекомендовал избегать скользящих режимов, так как

контакты электромеханических реле подгорали при таком поведении систе-

мы. Достижения силовой электроники в течение последних двух десятилетий

позволили реализовать релейные функции на бесконтактных устройствах с

частотой и мощностью многих кГц и кВт.

Позже исследователи обратили внимание на важное свойство скользящего

режима: понижение размерности и низкую чувствительность по отношению

145

к неопределенностям. Эти свойства являются общими для систем с большим

коэффициентом усиления, но они присущи и релейным системам со скользя-

щим режимом, использующим конечные управляющие воздействия. Первые

попытки их использования относятся к так называемым системам с пере-

менной структурой [7, 8]. Дальнейшее развитие этого подхода приводит к

системам с разрывным векторным управлением. В настоящей работе концеп-

ция “реле” обобщается на векторный случай и обсуждаются методы синтеза

управления.

3. Конечномерные системы с векторным управлением

Авторы упомянутых выше монографий [2, 3] изучали лишь системы со

скалярным управлением (1). Подобным образом модифицированное скаляр-

ное управление

(2)

u = -M(x)sgn(s),

где M(x) > 0 — функция, зависящая от состояния, изучалось в рамках теории

систем с переменной структурой ранее 1970-х гг. Формально управление в

системах с переменной структурой выбиралось в форме

{

F⁺, s(x) > 0,

F^-, s(x) < 0,

но оно легко сводится к форме (2):

F⁺ + F

F⁺ - F^-

sgn(s).

Множество современных технологических процессов описываются аффин-

ными дифференциальными уравнениями и управляются несколькими входа-

ми, т.е. векторным управлением

(3)

x = f(x,t) + B(x,t)u,

где x ∈ Rⁿ, u ∈ R^m, а f и B — дифференцируемые функции состояния и

времени, rank B = m.

Каждая компонента вектора управления имеет разрывную поверхность

s_i(x)=0, i = 1,... ,m:

(4)

u_i = M_i(x,t)sgn[s_i

(x)],

i = 1,...,m.

Управление может быть представлено в виде

u = M(x,t)sgn[s(x)],

где

M (x) = diag [M_i(x)],

s^T = [s₁,... ,s_m],

[

]_T

sgn[s(x)] =

sgn[s₁(x)], . . . , sgn[s_m(x)]

и будет называться векторным релейным управлением.

146

Скользящий режим на многообразии s(x) = 0 становится типичным. Вы-

шеупомянутые свойства, редукция размерности и низкая чувствительность

к неопределенностям (включая подавление возмущений) могут быть легко

продемонстрированы для систем в регулярной форме [9]. Регулярная форма

влечет декомпозицию исходной системы на две подсистемы меньших поряд-

ков. Первая из них не содержит управления, а размерность второй совпадает

с размерностью управления:

x₁ = f₁(x₁,x₂,t), x₁ ∈ R^n-m,

(5)

x₂ = f₂(x₁,x₂,t) + B₂(x₁,x₂,t)u, x₂ ∈ R^m,

|det B₂| > d₀ > 0.

Синтез скользящего режима состоит из двух шагов. На первом шаге фазо-

вая переменная x₂ рассматривается как фиктивное управление и выбирается

как функция состояния первой подсистемы x₂ = -s₀(x₁) так, что синтезиро-

ванная система

(6)

x₁ = f₁[x₁,-s₀(x₁

), t]

(n - m)-го порядка будет обладать желаемыми свойствами. Управление u

должно быть выбрано на втором шаге так, чтобы скользящий режим реали-

зовался на многообразии s(x₁, x₂) = x₂ + s₀(x₁) = 0. Это эквивалентно задаче

сходимости в начало координат за конечное время в пространстве s для си-

стемы m-го порядка

}

^{∂s₀

(7)

s = f₂(x₁,x₂,t) +

f₁(x₁,x₂,t) + B₂(x₁,x₂

,t)u,

∂x₁

где ∂s₀/∂x₁ — матрица размера m × (n - m).

Условия сходимости вектора состояния в начало координат, или устой-

чивость системы (7) с управлением (2), зависят от матрицы B₂. Исследо-

ватели этого вопроса старались найти необходимые и достаточные условия

устойчивости в течение последних 20 лет для простейшего случая (2), (7),

M = const, B₂ = const, f₁ = 0, f₂ = 0, но без особого успеха. Поэтому интерес-

но постараться найти достаточные условия; они легко находятся, если B₂ —

диагональная матрица с диагональными элементами |b_i| > bi0 > 0. Тогда для

sgn(s_i) = sgn(b_i) вычислим производную по времени функции Ляпунова V =

= (s^Ts)/2 = ∥s∥²/2:



}



^{∂s₀



(8)

≤ |s|

2(x1, x2, t) +

f₁(x₁,x₂,t)

|M(x)B₂

(x)s|,

^f

^-

∂x₁

где для произвольного вектора a полагаем |a| =

^∑ |a_i|.

Очевидно, что существует функция M(x, t), такая чтоV < 0, это и озна-

чает асимптотическую устойчивость. Неравенство (8) может быть записано в

√

форме^V ≤ -r∥s∥, где r — положительное число, или^V ≤ -r

V . Сходимость

за конечное время следует из решения этого уравнения:

(

√

)₂

√

(9)

V (t) ≤

V₀

V (t) = s(t) ≡ 0 для t ≥

V₀.

Заметим, что время сходимости убывает с ростом M и, как результат, с ро-

стом r.

147

Этот результат может быть легко обобщен, если B₂

— матрица с

доминирующей диагональю. Сходимость за конечное время может быть до-

стигнута для системы (2), (7) для положительно определенной матрицы

B₂ + B^T2 > 0 [8].

Если условия устойчивости для системы (2), (7) неизвестны, управление

должно быть модифицировано. Например, если u = B-12[-M(x)sgn(s)], то

релейное управление умножается на единичную матрицу. Это случай, ко-

гда решение известно; этот метод не применим в приложениях, связанных

с силовыми преобразователями, где каждая компонента управления может

принимать только два значения.

Теперь продемонстрируем еще один метод, когда сходимость за конечное

время может быть достигнута для произвольной матрицы B₂ и управление

может принимать только два значения. Вновь вычислим производную функ-

ции Ляпунова V = (s^Ts)/2 = ∥s∥²/2 вдоль траекторий системы (7):

[

]

^{∂s₀}

(10)

≤ s^T f₂(x₁,x₂,t) +

f₁(x₁,x₂,t)

+ s^TB₂(x₁,x₂

,t)u.

∂x₁

Введем новые разрывные поверхности s^∗ = 0, (s^∗)^T = s^TB₂(x₁, x₂, t). Сколь-

зящий режим на s^∗ = 0 означает скользящий режим на s = 0. Для управления

u = -M(x)sgn(s^∗)



}



^{∂s₀



≤ |B-12s^∗|

2(x1, x2, t) +

f₁(x₁,x₂,t)

|M(x)B₂s^∗|,

^f

^-

∂x₁

где функция M(x) может быть найдена так, что сходимость за конечное вре-

мя в начало координат пространства s будет иметь место.

Во всех методах задача синтеза управления распадается на две независи-

мые подзадачи меньшей размерности (n - m и m) и уравнения скользящего

режима не зависят от функций f₂(x₁, x₂, t) и B₂(x₁, x₂, t).

4. Конечномерные системы с векторным релейным единичным управлением

Каждая компонента векторного управления в (3) есть скалярная релей-

ная функция (4). Установление условий устойчивости системы (7) является

непростой задачей ввиду многочисленных переключений релейных функций

и того факта, что в ходе движения к началу координат может возникать

скользящий режим. Анализ устойчивости может быть существенно упрощен,

если уравнения движения всюду непрерывны за исключением многообразия

s = 0, как это имеет место в системах со скалярным управлением.

Представление скалярной функции переключения sgn(s) в виде sgn(s) =

= s/∥s∥ дает указание на то, как может быть записана аналогичная функция

векторного аргумента:

(11)

u=M

∥s∥

148

где M — скалярная постоянная или функция, зависящая от состояния. В от-

личие от управления (4) управление (11) становится непрерывной функци-

ей состояния, даже если произвольный компонент вектора s поменяет знак.

Поскольку норма s/∥s∥ равна единице, такое управление назовем вектор-

ным релейным единичным управлением или, короче, единичным управлени-

ем. Управление в форме (11) было предложено в 1970-х гг. С. Гутманом [10]

и Г. Лейтманом [11]. Аффинная система (3) с “согласованным” с управлени-

ем [12] ограниченным возмущением ∥h(x, t)∥ ≤ h₀

(12)

x = f(x,t) + B(x,t)[u + h(x,t)]

была изучена в предположении, что номинальная система

x = f(x,t)

асимптотически устойчива с известной функцией Ляпунова V (x) > 0,

= (grad V )^Tf(x, t) = -W < 0. Управление выбирается аналогично (11):

B^Tgrad V

(13)

u = -M

∥B^Tgrad V ∥

Тогда производная функции Ляпунова вдоль траекторий системы (12)

= -W - M∥B^Tgrad V ∥ + (grad V )^TBh(x,t) ≤

≤ -W - M∥B^Tgrad V ∥ + ∥B^Tgrad V ∥h₀

отрицательно определена для M > h₀. Это означает, что точка равно-

весия глобально асимптотически устойчива, если функция W радиально

не ограничена [13]. Норма функции (11), (13) при M = 1 равна едини-

це. Правая часть (12) должна быть равна нулю для x ≡ 0, следователь-

но, u = -(B^TB)-1f - h. Если B^Tgrad V = 0, то норма управления (13) рав-

на M. Вообще говоря, норма -(B^TB)-1f - h отличается от M. Единственно

возможное поведение системы — это скользящий режим на многообразии

B^Tgrad V = 0, где управление становится разрывным.

Единичное управление — это эффективное средство обеспечения скользя-

щего режима в системе (12) на заранее выбранном многообразии s(x) = 0,

s(x) ∈ R^m.

}

^{∂s₀

^{∂s₀}

(14)

(f + h) + Du, D =

∂x₁

Выберем единичное управление аналогично (13):

D^Ts(x)

(15)

u = -M(x,t)

∥D^Ts(x)∥

и вычислим производную функции Ляпунова V = (s^Ts)/2 = ∥s∥²/2 вдоль

траекторий (14) при управлении (15):

}

^{∂s₀

D^Ts(x)

=s^T

(f + h) - Ms^T

∂x₁

∥D^Ts(x)∥

[

}



]



^{∂s₀



< ∥D^Ts(x)∥^D-1

(f + h)

M (x, t)

^-

∂x₁

149

Она отрицательна при



}



^{∂s₀



M (x, t) >^D-1

(f + h)

.

∂x₁

С учетом неравенства ∥D^Ts(x)∥ ≤

√λ_max∥s(x)∥ (где λ_max — максимальное

собственное значение DD^T) M(x, t) может быть выбрана так, что

(

)₂

√

(16)

≤ -q∥s(x)∥, q > 0 или

≤ -q

2V и V (t) ≤

-√ t+

V (0)

Это означает√что многообразие s = 0 достигается за конечный интервал

времени t_r ≤

2V (0)/q. В отличие от покомпонентного синтеза управление

непрерывно, и, следовательно, в течение этого временного интервала пере-

ключения отсутствуют.

Как показано в предыдущем разделе, условия достижимости эквивалент-

ны устойчивости в подпространстве s со сходимостью за конечное время

и достаточные условия были получены лишь в некоторых случаях. Дока-

жем применимость предназначенного для линейных стационарных систем

критерия Гурвица для анализа устойчивости систем с единичным управ-

лением. Начнем со случая, когда B — константа, многообразие s = 0 ли-

нейно, s = Cx, C — константа, а D = CB — гурвицева матрица. Пусть

V = s^TPs — функция Ляпунова, где P > 0 является решением уравнения

Ляпунова D^TP + P D = -Q, Q > 0. Вычислим ее производную для системы

с управлением u = -M(x,t)s/∥s∥:

s^TQs

(17)

= 2(Cf + Dh)^TP s - M

≤ 2(Cf + Dh)^TP s - Mλ_min

∥s∥,

∥s∥

где λ_min — минимальное собственное значение Q. Как и ранее, функция

M (x, t) может быть найдена так, чтобы имела место сходимость за конеч-

ное время к многообразию s.

Критерий Гурвица не применим для линейных нестационарных систем,

но единичное управление может быть применено для нахождения области

притяжения нелинейных нестационарных систем. Предположим, что матри-

ца D(x, t) удовлетворяет условию Гурвица для всех x и t. Тогда решение

уравнения Ляпунова P (x, t) > 0 есть также функция от x и t, и правая часть

неравенства (16) должна быть дополнена еще одним членом:

≤ 2(Cf + Dh)^TP s - Mλ_min∥s∥ + s^T P˙ s

или аналогично (16)

≤ -q∥s(x)∥ + s^TP˙ s.

Последний член есть квадратичная форма, следовательно, знак производ-

ной по времени определяется первым членом для малых значений ∥s(x)∥ в

предположении, что

ограничена. Это означает, что скользящий режим су-

ществует в любой точке многообразия s = 0 и потому существует область

притяжения.

150

5. Релейное управление в бесконечномерной постановке

С начала 1980-х гг. релейные алгоритмы управления и, в частности, алго-

ритмы на скользящих режимах в значительной степени обобщены на беско-

нечномерную постановку. Впервые бесконечномерные обобщения подобных

алгоритмов были получены в [14, 15] для некоторых параболических и ги-

перболических дифференциальных уравнений в частных производных, что

не только подтвердило их полезность, но и обозначило проблемы для даль-

нейшего исследования.

Существенные моменты, возникающие в бесконечномерной постановке,

можно проиллюстрировать тестовым примером, связанным с распростране-

нием тепла вдоль однородного одномерного стержня с изолированными кон-

цами. Этот процесс описывается линейным параболическим дифференциаль-

ным уравнением в частных производных

(18)

x_t(r,t) = x_rr

(r, t) + f(r, t) + u(r, t)

с краевыми условиями Неймана

(19)

x_r(0,t) = 0, x_r

(1, t) = 0,

где x(·, t) — распределение температуры вдоль стержня в момент t > 0, а

управление u и внешнее возмущение f воздействуют на температуру стерж-

ня в каждой точке r ∈ (0, 1). В дальнейшем x_t(r, t) =∂x(r,t)∂t , x_rr(r, t) =∂2x(r,t)

∂r²

обозначают соответствующие частные производные по времени и простран-

√∫₁

ству, символ ∥x(·, t)∥₂ означает L₂-норму

x²(r,t)dr.

Рассмотрим распределенный единичный сигнал

x(r, t)

(20)

u(r, t) = -M

∥x(·, t)∥₂

с коэффициентом усиления M > 0, который, возможно, генерирует скользя-

щий режим в системе вдоль множества разрыва x = 0. Заметим, что L₂-норма

единичного сигнала x(r, t)∥x(·, t)∥-12 равна единице всюду, кроме начала ко-

ординат x ≡ 0. При этом возникает ряд фундаментальных вопросов:

• при каких условиях возникает скользящий режим на множестве разрыва?

• какая эквивалентная величина единичного сигнала x(r, t)∥x(·, t)∥-12 долж-

на быть использована в замкнутой системе (18)-(20), чтобы корректно

описать скользящий режим на множестве разрыва x = 0?

По аналогии с конечномерным случаем условия

limxt(r,t) = lim[xrr(r, t) + f(r, t) + u(r, t)] > 0,

x↑0

(21)

limxt(r,t) = lim[xrr(r, t) + f(r, t) + u(r, t)] < 0

x↓0

локального существования скользящего режима на множестве разрыва

x(·, t) = 0 потребовали бы, чтобы величина регулятора M локально превы-

шала не только равномерную норму ∥f(·, t)∥C(0,1) внешних возмущений, но

151

также и равномерную норму ∥x_rr(·, t)∥C(0,1) пространственной частной произ-

водной второго порядка x_rr. Последнее требование, однако, невозможно удо-

влетворить ввиду того, что оператор двойного дифференцирования A =∂2

∂r²

неограничен (для этого достаточно заметить, что ∥A sin πnr∥C(0,1) → ∞ при

n → ∞). Таким образом, условия (21) существования скользящего режима

должны быть пересмотрены в бесконечномерной постановке.

Подход Ляпунова - Красовского в настоящее время широко применим для

изучения скользящих режимов в системах, описываемых дифференциальны-

ми уравнениями в частных производных [16]. В случае замкнутой системы

(18)-(20) функционал Ляпунова - Красовского может быть выбран в виде

∫

(22)

V (x) =

x²

(r, t)dr.

В самом деле, дифференцируя (22) вдоль решений (18)-(20), получаем

∫1

[x_rr + u + f]xdr ≤ -(M - ∥f(·, t)∥L2 )∥x(·, t)∥L2 =

(23)

√

= -(M - ∥f(·,t)∥L2 )

2V (t).

Таким образом, при условии M > ∥f(·, t)∥L2 попадание замкнутой системы

(18)-(20) в начало координат за конечное время устанавливается так же, как

и в (9), и существование скользящих режимов на множестве разрыва x = 0

√

гарантируется за конечное время T =

2(M - ∥f(·, t)∥L2 )-1

V (0).

Следует отметить, что распространение методов анализа скользящих ре-

жимов на бесконечномерную постановку весьма нетривиально. Хотя сходи-

мость за конечное время в бесконечномерном случае была изучена для эво-

люционных уравнений (в частности, для линейных), см. [17] и ссылки там,

анализ скользящих режимов остается открытой проблемой для бесконечно-

мерных систем. Функционал Ляпунова (22), обеспечивающий попадание за

конечное время в начало координат для замкнутой системы (18), (19), по-

рожденный единичным распределенным управлением (20), пока что остается

единственным в рамках систем, описываемых дифференциальными уравне-

ниями в частных производных.

Обобщение синтеза единичного управления для произвольных систем в

гильбертовом пространстве может быть осуществлено следующим образом.

Для бесконечномерной динамики

x = Ax + Bu + f(t,x)

в гильбертовом пространстве при воздействии неизвестных возмущений ти-

пичной целью управления является асимптотическая стабилизация. Пусть

состояния и управления являются элементами гильбертова пространства:

x ∈ X, u ∈ U; f : R × X → X — возмущение; A : D(A) ⊂ X → X — замкну-

тый линейный оператор с D(A) в X; B : U → X — линейный ограниченный

152

оператор. Неизвестное возмущение f(t, x) предполагается ограниченным в

некоторой заранее заданной норме. Конечно, эта проблема может быть ре-

шена при выполнении условия принадлежности возмущений пространству

управления:

f (t, x) = Bγ(t, x),

∥γ(t, x)∥ ≤ γ₀, γ : R × X → U.

Не углубляясь в детали (интересующегося читателя отошлем, например,

к [16, 18]), выберем процедуру синтеза, следуя методологии раздела 4. Такая

процедура применима, если номинальная система x = Ax экспоненциально

устойчива с непрерывным положительно определенным функционалом Ля-

пунова

(24)

v : X → R, v(0) = 0, v(x) > 0 для x = 0.

Иными словами, пусть существует непрерывный функционал (24) такой что

v = ∇_x{v}Ax < 0 для всех x ∈ D(A), где ∇_x{v} : X → R — линейный функ-

ционал (он может быть интерпретирован как аналог конечномерного опера-

тора ∇^TV : Rⁿ → R), обладающий свойством

v(x + Δx) - v(x) - ∇_x{v}(Δx)

lim

= 0, Δx ∈ X.

∥Δx∥→0

∥Δx∥

Вычисляя производную v(x) вдоль траекторий исходной системы, получаем

v = ∇_x{v}Ax + ∇_x{v}B(u + γ).

Пусть (∇_x{v}B)^∗ ∈ U — сопряженный оператор к ∇_x{v}B [19]. По свойству

сопряженного оператора [20] ∇_x{v}B(∇_x{v}B)^∗ = ∥∇_x{v}B∥², поэтому еди-

ничный закон управления

∗

(∇_x{v}B)

(25)

u = -ρ

ρ>γ₀

∥∇_x{v}B∥

приводит к тому, что

v ≤ ∇_x{v}Ax + ∥∇_x{v}B∥(-ρ + γ₀) < 0.

Следовательно, состояние x = 0 асимптотически устойчиво.

Как показано ранее, подход, основанный на единичном управлении, успеш-

но проиллюстрирован в бесконечномерной постановке для параболической

краевой задачи (18), (19). Заметим, что вместе с единичным управлением (20)

распределенное релейное управление

(26)

u = -ρsgnx(r,t)

диффузионным процессом также приводит к асимптотической стабилизации,

но верхняя оценка скорости убывания x(r, t) до сих пор не получена.

Еще одним препятствием для распределенного релейного управления (26)

является разрывность во всех точках r, где x(r, t) = 0. В этом состоит отли-

чие от единичного управления (25), которое остается непрерывным на протя-

жении переходного процесса и становится разрывным, только когда процесс

завершен и x(r, t) становится равным нулю при любом значении простран-

ственной переменной r.

153

6. Заключение

Широко используемые системы с разрывным управлением восходят к пер-

вым исследованиям релейных систем второй половины прошлого века. Ста-

тья демонстрирует развитие этой области исследований, модификацию тер-

мина “релейное управление”, причины, почему эти модификации необходимы,

а также новые проблемы и их решения. Применения релейного управления

обсуждаются в контексте одномерных, многомерных и бесконечномерных си-

стем.

СПИСОК ЛИТЕРАТУРЫ

Кулебакин В.С. К теории автоматических вибрационных регуляторов для элек-

трических машин // Теоретическая и экспериментальная электроника. 1932.

№ 4. С. 3-21.

Flugge-Lotz I. Discontinuous Automatic Control. N.J.: Princeton Univers. Press,

1953.

Цыпкин Я.З. Теория релейных систем автоматического регулирования. М.: Гос-

техиздат, 1955.

Никольский Г.Н. К вопросу об автоматической устойчивости корабля на задан-

ном курсе // Тр. центр. лаб. проводной связи. 1934. № 1. С. 34-75.

Труды второго всесоюзного совещания по теории автоматического регулирова-

ния. 1955. Дискуссия. С. 460-462.

Neymark Yu.I. Note on A. Filippov’s Paper // Proc. 1st IFAC Сongr. London:

Butterworth, 1961.

Теория систем с переменной структурой / Под ред. С.В. Емельянова. М.: Наука,

1970.

Уткин В.И. Скользящие режимы и их применение в системах с переменной

структурой. М.: Наука, 1974.

Лукьянов А.Г., Уткин В.И. Методы сведения уравнений динамических систем

к регулярной форме // АиТ. 1981. № 3. C. 5-13.

Luk’yanov A.G., Utkin V.I. Methods for Reduction of Equations of Dynamic

Systems to a Regular Form // Autom. Remote Control. 1981. V. 42. No. 4.

P. 413-420.

10.

Gutman S. Uncertain Dynamic Systems — a Lyapunov Min-Max Approach // IEEE

Trans. Autom. Control. 1979. V. AC-24. P. 437-449.

11.

Gutman S., Leitmann G. Stabilizing feedback control for dynamic systems with

bounded uncertainties // Proc. 1976 IEEE Conf. Decision Control. P. 94-99.

12.

Drazenovic B. The Invariance Conditions in Variable Structure Systems //

Automatica. 1969. V. 5. No. 3. P. 287-295.

13.

Барбашин Е.А. Введение в теорию устойчивости. М.: Наука, 1967.

14.

Орлов Ю.В., Уткин В.И. Применение скользящих режимов в задачах управ-

ления распределенными системами // АиТ. 1982. № 9. С. 36-46.

Orlov Y.V., Utkin V.I. Use of Sliding Modes in Distributed System Control

Problems // Autom. Remote Control. 1982. V. 43. No. 9. P. 1127-1135.

15.

Орлов Ю.В. Применение метода Ляпунова в распределенных системах // АиТ.

1983. № 4. С. 22-28.

Orlov Y.V. Application of Lyapunov Method in Distributed Systems // Autom.

Remote Control. 1983. No. 4. V. 44. P. 426-430.

154

16. Orlov Y.V. Discontinuous Systems: Lyapunov Analysis and Robust Synthesis under

Uncertainty Conditions. Communications and Control Engineering Series. Berlin:

Springer Verlag, 2009.

17. Perrollaz V., Rosier L. Finite-Time Stabilization of 2x2 Hyperbolic Systems on

Tree-Shaped Networks // SIAM J. Control Optim. 2014. V. 52. No. 1. P. 143-163.

18. Curtain R., Zwart H. An Introduction to Infinite-Dimensional Linear Systems

Theory. Texts in applied mathematics. Springer, 1995.

19. Orlov Y., Utkin V. Unit sliding mode control in infinite-dimensional systems //

J. Appl. Math. Comput. Sci. 1998. V. 8. P. 7-20.

20. Rudin W. Functional Analysis (2nd ed.). N.Y.: McGraw-Hill, 1991.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 20.07.2018

После доработки 01.10.2018

Принята к публикации 08.11.2018

155