Автоматика и телемеханика, № 9, 2019

(Научно-производственный центр автоматики и приборостроения

им. акад. Н.А. Пилюгина;

Институт проблем управления им. В.А. Трапезникова РАН, Москва),

В.Н. ТИМИН, канд. техн. наук (timin.victor@rambler.ru),

А.П. КУРДЮКОВ , д-р техн. наук

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СИНТЕЗ АНИЗОТРОПИЙНОГО СУБОПТИМАЛЬНОГО

ПИД РЕГУЛЯТОРА ДЛЯ ДИСКРЕТНОЙ ЛИНЕЙНОЙ

СТАЦИОНАРНОЙ СИСТЕМЫ: ОДНОМЕРНЫЙ СЛУЧАЙ¹

Рассматривается задача синтеза пропорционально-интегрально-диф-

ференциального закона управления (ПИД регулятора) для дискретной

линейной стационарной системы с одномерными входом управления и из-

меряемым выходом, работающей под воздействием стохастических воз-

мущений, неопределенность которых описывается в терминах средней

анизотропии. Возможности замкнутой системы по подавлению возмуще-

ний количественно характеризуются анизотропийной нормой. Получены

достаточные условия существования анизотропийного субоптимального

ПИД регулятора, стабилизирующего замкнутую систему и гарантирую-

щего, что ее анизотропийная норма строго ограничена заданным порого-

вым значением.

Ключевые слова: ПИД регулятор, средняя анизотропия, норма, субопти-

мальное управление, выпуклая оптимизация.

DOI: 10.1134/S0005231019090113

1. Введение

Имя Якова Залмановича Цыпкина, академика РАН, выдающегося совет-

ского и российского ученого в области автоматического управления, столет-

нему юбилею которого посвящен этот номер журнала, широко известно в

нашей стране и за рубежом. Его классические статьи о системах с запазды-

вающей обратной связью, об импульсном регулировании и релейных системах

управления являются основополагающими в теории автоматического управ-

ления. Невозможно переоценить роль Якова Залмановича в теории адаптив-

ных и обучающихся систем управления. Работы В.Л. Харитонова о робаст-

ной устойчивости в свое время вызвали всплеск научной активности в этой

области. Я.З. Цыпкин вместе с Б.Т. Поляком, основываясь на результатах

А.В. Михайлова, положил начало новому методу в исследованиях по робаст-

ному управлению. Один из авторов этой статьи хорошо помнит круглый стол,

¹ Работа выполнена при частичной финансовой поддержке Программы № 15 ОЭММПУ

РАН и Российского фонда фундаментальных исследований (проект 17-08-00185).

156

который вел Яков Залманович на 11-м Всемирном конгрессе ИФАК в Тал-

лине в 1990 г., на котором Яков Залманович провозгласил эру робастности в

теории управления.

Предлагаемая читателям статья посвящена дальнейшему развитию ани-

зотропийной (стохастической робастной) теории управления, предложенной

в 1990-е гг. И.Г. Владимировым, в которой идеи H_∞ теории управления со-

четались с теоретико-информационными критериями качества (см., напри-

мер, [1-4]).

Зная живой интерес Якова Залмановича к этой области исследований, ав-

торы первой в российской печати работы по анизотропийной теории [1] при-

шли к нему и попросили дать отзыв в журнал “Доклады Академии наук”.

Яков Залманович просмотрел работу и попросил принести отзывы от спе-

циалистов. Авторы статьи [1] показали работу М.С. Пинскеру и А.Ю. Вере-

тенникову и получили достаточно лестные отзывы. Яков Залманович, озна-

комившись с отзывами, написал рекомендацию в ДАН. Эта статья вышла

в 1995 г. Таким образом он благословил анизотропийную теорию, которой

сейчас посвящено около сотни публикаций (книг, статей в ведущих научных

журналах у нас в стране и за рубежом) на право занять достойное место в

теории управления.

Анизотропийная теория стохастического робастного управления, основы

которой были заложены в [1-3], направлена на синтез управления, обладаю-

щего большей робастностью по отношению к статистически неопределенным

коррелированным возмущениям, чем гауссовское линейно-квадратичное и H₂

управление, и в то же время меньшей консервативностью, чем H_∞ управле-

ние. В анизотропийной теории статистическая неопределенность многомерно-

го сигнала — последовательности случайных векторов — описывается в тер-

минах анизотропии (для конечной последовательности) или средней анизо-

тропии (для бесконечной последовательности), представляющих собой меру

отклонения данного сигнала от центрированного гауссовского белого шума с

единичной ковариационной матрицей, а возможности системы по подавлению

неопределенных стохастических возмущений количественно характеризуют-

ся ее анизотропийной нормой [1, 2, 4].

Изначально анизотропийный оптимальный регулятор, задача синтеза ко-

торого была решена в [3], представлял собой регулятор в форме наблюдате-

ля. Критерий ограниченности анизотропийной нормы заданным значением,

сформулированный в [5] в терминах матричных неравенств, позволил приме-

нить методы выпуклой оптимизации и технику линейных матричных нера-

венств (ЛМН) к решению задач анизотропийного субоптимального управле-

ния, что привело к дальнейшему развитию анизотропийной теории. Приме-

нение новой техники дало возможность строить анизотропийные регуляторы

не только в форме наблюдателя, но и в форме динамических компенсаторов

заданного или полного порядка, а также в виде статических обратных связей

по состоянию и измеряемому выходу. В настоящей статье впервые рассматри-

вается задача анизотропийного субоптимального управления — подавления

неопределенных стохастических возмущений с ограниченной средней анизо-

тропией — с помощью регулятора не только заданного порядка, но и заданной

структуры.

157

Пропорционально-интегрально-дифференциальный (ПИД) регулятор от-

носится к наиболее распространенному типу регуляторов. Более 90 % регу-

ляторов, применяющихся в промышленности, используют ПИД алгоритм [6].

Причиной столь высокой популярности является простота построения и про-

мышленного использования, ясность функционирования, пригодность для

решения большинства практических задач и низкая стоимость. Усилия мно-

гих и многих исследователей на протяжении десятилетий и в настоящее время

сосредоточены на создании и разработке новых методов синтеза и настройки

параметров ПИД регуляторов на основе новых современных теорий и с при-

менением различных критериев качества. Методам синтеза и настройки ПИД

регуляторов посвящено огромное количество публикаций, которое невозмож-

но даже обзорно охватить в рамках этой статьи.

Структура статьи следующая. В разделе 2 излагается постановка задачи.

В разделе 3 представлено решение задачи синтеза анизотропийного субоп-

тимального ПИД регулятора. В разделе 4 рассматривается вычислительный

пример. Заключительные замечания даны в разделе 5.

В статье используются следующие обозначения: Rⁿ - множество веще-

ственных n-мерных векторов, R^n×m - множество вещественных (n × m)-мат-

риц. Для вещественной матрицы M = [m_ij ] M^T - транспонированная мат-

рица, M^T := [m_ji]. Для вещественных симметричных матриц M = M^T и

N = N^T M ≻ N (или M ≽ N) означает, что матрица M - N положительно

(или неотрицательно) определена. В блочно-симметричных матрицах сим-

вол ∗ заменяет блоки, вид которых определяется симметрией. Единичная

матрица размерности n × n обозначается через I_n, нулевая матрица размер-

ности n × m обозначается 0_n×m. Размерности нулевых матриц в тех случаях,

когда их нетрудно понять из контекста, указываться не будут. Определитель

матрицы M = [m_ij ] обозначается через det M, след этой матрицы обозначает-

ся через tr M. Евклидова норма вектора обозначаются через | · |. Символом E

обозначено математическое ожидание случайной величины.

2. Постановка задачи синтеза анизотропийного субоптимального

ПИД регулятора

Рассмотрим объект управления, представленный в пространстве состоя-

ний дискретной линейной стационарной моделью P (z) с n_x-мерным состояни-

ем X = (x_k), m_w-мерным входом возмущения W = (w_k), одномерным входом

управления U = (u_k), u_k ∈ R¹, p_z-мерным регулируемым выходом Z = (z_k) и

одномерным измеряемым выходом Y = (y_k), y_k ∈ R¹ :

⎡

⎤

⎡

⎤⎡

⎤

xk+1

A B_w B_u

x_k

⎦₌ ⎣

⎦⎣

⎦,x0

(2.1)

P (z) : ⎣ zk

C_z D_zw

w_k

= 0,

y_k

C_y D_yw

u_k

где размерности всех матриц согласованы, p_z ≤ m_w, пара матриц (A, B_u) яв-

ляется стабилизируемой, а пара (A, C_y) — детектируемой.

158

Предполагается, что средняя анизотропия последовательности возмуще-

ния W не превосходит известного положительного уровня a, т.е.

{

}

W ∈ W_a := W ∈ ℓmwP^:A(W) ≤ a,a > 0,

где

∫

)

⁽m_wS(ω)

A(W ) = -

ln det

dω

4π

∥W ∥²

-π

— функционал средней анизотропии [3, 4];

{

}

(2.2)

ℓmwP:=W=(wk⁾

: w_k ∈ Lmw2 и∥W∥P < +∞

−∞<k<+∞

— пространство стационарных в узком смысле последовательностей случай-

ных векторов, интегрируемых с квадратом;

(

)1/2

(2.3)

∥W ∥_P := lim

E|w_k|2

M→∞ 2M + 1

k=-M

— мощностная норма последовательности случайных векторов W [7], которая

может быть вычислена через спектральную плотность S(ω) этой последова-

тельности:

⎛

⎞

1/2

∫

∥W ∥_P =⎝1

tr S(ω)dω^⎠

2π

−π

Рассматриваемая в данной статье задача управления заключается в ста-

билизации замкнутой системы и обеспечении некоторого желаемого качества

подавления случайных возмущений. Для решения этой задачи будет исполь-

зоваться пропорционально-интегрально-дифференциальный закон управле-

ния — ПИД регулятор. Известно достаточно много структур ПИД регулято-

ров [6]. Модель идеального (теоретического) ПИД регулятора как системы с

непрерывным временем описывается передаточной функцией

(2.4)

K(s) = K_p + K_i

+K_d

где s — переменная преобразования Лапласа, K_p, K_i и K_d — коэффициенты

усиления пропорциональной, интегрирующей и дифференцирующей состав-

ляющих регулятора соответственно. При переходе к дискретному времени с

постоянным шагом Δt = T с заменой операции дифференцирования взятием

левой конечной разности, что в комплексной области соответствует замене

159

переменной преобразования Лапласа s :=z-1Tz , передаточная функция иде-

ального ПИД регулятора примет вид

K_d z - 1

(2.5)

K(z) = K_p + K_iT

z-1

T z

Передаточная функция идеального ПИД регулятора (2.4) не является пра-

вильной (порядок числителя превышает порядок знаменателя), а идеальное

дифференцирующее звено невозможно реализовать, поэтому в практических

приложениях используется ПИД регулятор с передаточной функцией

(2.6)

K(s) = K_p + K_i

+K_d

αs + 1

где α — заданный малый постоянный параметр фильтра, заменяющего диф-

ференцирующее звено. При переходе к дискретному времени с использова-

нием замены s :=z-1Tz передаточная функция ПИД регулятора (2.6) примет

вид

z-1

b₂z² + b₁z + b₀

(2.7)

K(z) = K_p + K_iT

+K_d

z-1

α(z - 1) + T z

a₂z² + a₁z + a₀

где

b₂ := K_p(α - T) + K_d,

b₁ := -K_p(2α + T) - K_iT(α + T) - K_d,

(2.8)

b₀ := K_pα - K_iTα + K_d,

a₂ := α + T,

a₁ := -2α - T,

a₀ = α.

Реализация передаточной функции (2.7) дискретного ПИД регулятора в

пространстве состояний в канонической управляемой форме имеет вид

[

]

[

][

]

xck+1

A_c B_c

xck

(2.9)

K(z) :

, x^c0

= 0,

u_k

C_c D_c

y_k

где xck ∈ R², u_k ∈ R¹, y_k ∈ R¹, а матрицы реализации определяются выраже-

ниями

⎡

⎤

⎡

⎤

⎦_,

A_c =^⎣

a₀

a₁

⎦,Bc = ⎣

(2.10)

a₂

[

]

a₀

a₁

b₂

C_c = b0 -

b₂

b₁ -

b₂

D_c =

a₂

Следует отметить, что в силу (2.8) элементы матриц ПИД регулятора A_c

и B_c не зависят от коэффициентов усиления K_p, K_i и K_d, а зависят лишь от

известных заданного параметра α и шага дискретного времени T.

160

Пусть T_zw(z) обозначает матричную передаточную функцию от внешнего

входа W к регулируемому выходу Z замкнутой системы с ПИД регулятором:

K(z)

(2.11)

T_zw(z) = P_zw(z) + P_zu(z)

P_yw

(z),

1 - P_yu(z)K(z)

где

P_zw(z) = C_z(zInx - A)-1B_w + D_zw, P_zu(z) = C_z(zInx - A)-1B_u,

P_yw(z) = C_y(zInx - A)-1B_w + D_yw, P_yu(z) = C_y(zInx - A)-1B_u,

а передаточная функция ПИД регулятора имеет вид (2.7).

Возможности замкнутой системы по подавлению стохастических возмуще-

ний W с уровнем средней анизотропии, не превышающим известного значе-

ния a, количественно характеризуются анизотропийной нормой передаточной

функции (2.11), определяемой как наибольшее отношение мощностной нормы

выхода этой системы к мощностной норме входа:

∥Z∥_P

(2.12)

|||T_zw|||_a := sup

W ∈Wa ∥W∥P

Постановка задачи синтеза анизотропийного субоптимального ПИД регуля-

тора для стабилизации объекта управления под воздействием стохастических

возмущений формулируется следующим образом.

Задача управления. Для заданных объекта управления c передаточ-

ной функцией

[

]

Pzw(z) Pzu(z)

(2.13)

P (z) =

P_yw(z) P_yu(z)

и моделью в пространстве состояний (2.1), уровня средней анизотропии

a > 0 стохастического возмущения W и некоторого желаемого порогово-

го значения γ > 0 найти коэффициенты усиления K_p, K_i и K_d ПИД регу-

лятора с передаточной функцией (2.7) и моделью в пространстве состоя-

ний (2.9), (2.10), такие чтобы замкнутая система (2.11) была асимптоти-

чески устойчива, а ее анизотропийная норма была строго ограничена поро-

говым значением γ, т.е. чтобы выполнялось условие

(2.14)

|||T_zw|||_a

< γ.

3. Решение задачи синтеза анизотропийного субоптимального

ПИД регулятора

Для решения поставленной задачи управления воспользуемся тем, что

от искомых неизвестных коэффициентов усиления ПИД регулятора K_p, K_i

и K_d зависят лишь матрицы C_c и D_c его реализации в пространстве состоя-

ний (2.9). Это позволяет дополнить вектор состояния системы (2.1) состоя-

ниями регулятора (2.9) и в дальнейшем рассматривать в качестве объекта

161

управления расширенную модель с матрицами реализации

⎡

⎤

B_w B_u

⎡

⎤

⎢

⎥

B_cC_y A_c B_cD_yw

⎢

⎥

A B_w B_u

⎢

⎥

⎢

⎥

(3.1)

⎣ C_z D_zw

⎦ :=

C_z

D_zw

⎢

⎥^,

C_y D_yw

⎢

⎥

⎣

I₂

⎦

C_y

D_yw

а в качестве синтезируемого закона управления — статическую обратную

связь по выходу расширенной системы с коэффициентом усиления

[

]

[

]

(3.2)

K :=

C_c D_c

k₀

k₁

k₂

представляющим собой матрицу-строку K ∈ R1×3. Нетрудно убедиться, что

матрицы реализации замкнутой системы T_zw в этом случае имеют вид

[

]

[

]

[

]

A B

A B_w

B_u

[

]

(3.3)

C_y D_yw

C D

C_z D_zw

[

]

A+B_uKC_y B_w +B_uKD_yw

C_z

D_zw

⎡

⎤

A+B_uD_cC_y B_uC_c B_w +B_uD_cD_yw

⎢

⎥

⎣ BcCy

A_c

B_cD_yw

⎦.

C_z

D_zw

Далее отметим, что матрица-столбец B_u ∈ R(nx+2)×1, очевидно, имеет

полный ранг по столбцам, и следовательно существует невырожденная

матрица преобразования координат состояния расширенной системы T_u ∈

∈ R(nx+2)×(nx+2), такая что

[

]

(3.4)

B_u := T_uB_u =

0(nx+1)×1

В частности, эта матрица может быть выбрана в виде

[

]-1

(3.5)

T_u = B_u N

BTu

где столбцы матрицы N_BT

образуют базис нуль-пространства матрицы BTu.

В новых координатах матрицы реализации расширенного объекта управле-

ния (3.1) имеют вид

(3.6)

A := T_uAT-1u,

B_w := T_uB_w,

C_z := C_zT-1u,

C_y := C_yT-1u.

162

Решение поставленной задачи управления дано в следующей теореме,

устанавливающей достаточные условия существования ПИД регулятора, ста-

билизирующего замкнутую систему (2.11) и гарантирующего выполнение

условия (2.14).

Теорема. Для заданных a > 0 и γ > 0 ПИД регулятор (2.9), (2.10), ста-

билизирующий замкнутую систему (2.11) и гарантирующий выполнение

условия (2.14), существует, если система неравенств

(3.7)

η - (e-2a detΨ)1/mw < γ²,

⎡

⎤

Ψ-ηImw

∗

⎢

⎥

(3.8)

⎣

B_w + LD_yw

^Φ

S^T

∗

⎦ ≺ 0,

D_zw

-Ipz

⎡

⎤

-^Φ

∗

⎢

⎥

⎢

-ηImw

∗

⎥

(3.9)

⎢

⎥

≺ 0,

⎣

SA¯+

C_y

B_w + LD_yw

^Φ

S^T

∗

⎦

D_zw

-Ipz

(3.10)

Ψ ≻ 0,

Φ_≻ 0, η > γ², η ≤

1 - e-2a/mw

где

B_w

C_z

C_y определяются выражениями (3.6), разрешима относитель-

но скалярной переменной η, вещественных симметричных (m_w × m_w)-мат-

рицы Ψ, ((n_x + 2) × (n_x + 2))-матрицы^Φ и двух структурированных мат-

ричных переменных

[

]

[

]

s₁

01×(nx+1)

L₁

(3.11)

S :=

L :=

S₂

0(nx+1)×1

0(nx+1)×3

Если система неравенств (3.7)-(3.10) разрешима и неизвестные переменные

найдены, то матрица

[

]

(3.12)

K = k₀ k₁ k₂

L₁,

s₁

а искомые коэффициенты усиления ПИД регулятора K_p, K_i и K_d вычисля-

ются как

⎡

⎤

⎡

⎤

⎤-1^⎡

K_p

-Tα

k₀ + k₂α

⎢

⎥

⎢

⎥

⎢

⎥

(3.13)

⎣ Ki

⎦=

⎣ -2α - T

-Tα - T² -1

⎦

⎣ k1 - k2(2α + T )

⎦,

K_d

α-T

k₂(α + T)

где α — заданный малый постоянный параметр передаточной функции ПИД

регулятора (2.7), T — шаг дискретного времени.

163

Доказательство приводится в Приложении.

Следствие. Условия теоремы позволяют минимизировать γ := γ² из

решения задачи выпуклой оптимизации

γ → inf

(3.14)

на множестве Ψ,^Φ

S,L,η,γ,

удовлетворяющих ограничениям γ > 0 и (3.7)-(3.10).

Таким образом, решение задачи синтеза анизотропийного субоптимально-

го ПИД регулятора (задача вычисления его коэффициентов усиления) сво-

дится к задаче выпуклой оптимизации: минимизировать положительную пе-

ременную при ограничениях в виде системы неравенств, включающей нера-

венство относительно среднего геометрического собственных значений поло-

жительно определенной матрицы и двух линейных матричных неравенств.

4. Вычислительный пример

Рассмотрим простой вычислительный пример, в котором объектом управ-

ления является модель линейного осциллятора — математического маятника

[

]

][

]

[

]

[

]

x₁(t)

(4.1)

w₁(t) +

u(t)

x₂(t)

-ω²

-2ξ

x₂(t)

с частотой собственных колебаний ω = 8 и коэффициентом демпфирования

ξ = 0,01. Колебания линейного осциллятора (4.1) возбуждаются стохастиче-

ским внешним возмущением w₁(t). Система (4.1) является устойчивой, но

переходные процессы в ней являются сильно колебательными и затухают

слишком медленно. Управление u(t) служит для стабилизации угла отклоне-

ния маятника x₁(t) под воздействием возмущения w₁(t).

Для синтеза закона управления (2.6) регулируемый выход непрерывной

модели линейного осциллятора (4.1) был выбран в виде z(t) = x₂(t), а изме-

ряемый выход — в виде y(t) = x₂(t) + 0,5w₂(t), где w₂(t) — шум измерений.

Непрерывная модель (4.1) была дискретизована с шагом дискретного време-

ни Δt = T = 10-3 секунды и приведена к виду (2.1), полученные матрицы

реализации дискретной модели объекта управления в пространстве состоя-

ний имеют вид

[

]

[

]

-3

0,999968

0,999979 · 10

0,999988 · 10-6

B_w =

−0,063999

0,999948

0,199996 · 10-2

[

]

−5

0,499994 · 10

[

]

B_u =

C_z = C_y =

0,999979 · 10-2

[

]

D_zw = 0, D_yw =

0,5

Малый постоянный параметр α фильтра передаточной функции ПИД ре-

гулятора (2.6) был выбран равным 0,005. Передаточная функция K(s) была

164

дискретизована с шагом Δt = T = 10-3 секунды и приведена к виду (2.7), для

нее была получена реализация в пространстве состояний (2.9) с матрицами

[

]

[

]

A_c =

B_c =

−0,833333

1,833333

-166,666667

Модель объекта управления была расширена согласно (3.1), и для нее по

формуле (3.5) была построена невырожденная матрица преобразования ко-

ординат

⎡

⎤

0,500015 · 10-1

100,002042

⎢

⎥

⎢

−0,500004 · 10-3

0,250004 · 10-6

⎥

T_u =

⎢

⎥

⎣

⎦

Матрицы реализации расширенной модели объекта управления в простран-

стве состояний A, B_w, C_z и C_y были преобразованы по формулам (3.6).

Для ряда значений средней анизотропии возмущения a, перечисленных

в таблице, из решения задачи выпуклой оптимизации (3.14) по форму-

лам (3.12), (3.13) были рассчитаны коэффициенты усиления K_p, K_i и K_d

анизотропийного субоптимального ПИД регулятора. Расчеты при a → +∞

(H_∞ субоптимальный ПИД регулятор) были выполнены из решения задачи

выпуклой оптимизации

(4.2)

γ → inf

на множестве

^Φ

S,L, γ, удовлетворяющих ограничениям

⎡

⎤

∗

⎢

⎥

⎢

-γImw

∗

⎥

⎢

⎥

(4.3)

⎢

⎥ ≺ 0,

≻ 0,

γ > 0.

⎢

⎥

SA¯+

C_y

B_w + LD_yw

^Φ

S^T

∗

⎣

⎦

D_zw

-Ipz

Все расчеты выполнялись в системе Matlab с использованием интерфейса

YALMIP и программы-решателя SDPT3 [8]. Результаты расчетов коэффи-

циентов усиления ПИД регулятора для различных значений a и сравнение

замкнутых систем с этими регуляторами сведены в таблицу.

Из анализа результатов решений оптимизационных задач для различных

значений уровня средней анизотропии возмущения a, приведенных в таблице,

можно заключить, что с ростом параметра a

• минимальное значение γ_min, полученное при решении задачи выпуклой

оптимизации, увеличивается;

• вычисленное значение анизотропийной нормы замкнутой системы с со-

ответствующим ПИД регулятором увеличивается и не привышает значе-

ния γ_min, полученного для того же уровня средней анизотропии возмуще-

ния a, т.е. все рассчитанные анизотропийные ПИД регуляторы являются

субоптимальными;

165

Сравнение замкнутых систем и параметров ПИД регуляторов, рассчитанных для

различных значений a

0,02

0,05

0,1

0,4

1,6

6,4

→ +∞

Результаты решения:

γ_min

0,0841

0,1223

0,1647

0,2943

0,4496

0,49974

0,6585

|||T_zw|||_a

0,0838

0,122

0,1643

0,2938

0,4493

0,49968

0,5

∥T_zw∥_∞

0,5266

0,5154

0,5098

0,5035

0,5008

0,50001

0,5

Коэффициенты усиления ПИД регулятора:

K_p

-0,55125

-0,72652

-0,90904

-1,49915

-3,01166

-17,1849

-46,3446

K_i

-348,171

-458,875

-574,157

-946,886

-1902,03

-10854,1

-29267,6

K_d

-0,00493

-0,0065

-0,00813

-0,01341

-0,02695

-0,15376

-0,41463

Результаты моделирования для системы с анизотропийным ПИД регулятором:

max_k |u_k|

4,41

5,88

6,325

8,997

14,318

10,44

22,09

max_k |x1,k|

0,339

0,323

0,33

0,326

0,344

1,39

2,17

max_k |x2,k|

2,28

1,98

1,66

1,25

1,602

1,49

1,97

Результаты моделирования для системы с H_∞ ПИД регулятором:

max_k |u_k|

302,63

320,92

290,95

214,993

116,92

34,2

22,09

max_k |x1,k|

0,0701

0,0944

0,128

0,0989

0,635

3,68

2,17

max_k |x2,k|

2,68

2,72

2,87

2,5

2,48

2,32

1,97

• вычисленное значение H_∞ нормы замкнутой системы с соответствующим

анизотропийным ПИД регулятором уменьшается и стремится к H_∞ норме

системы, замкнутой H_∞ субоптимальным ПИД регулятором;

• коэффициенты усиления K_p, K_i и K_d анизотропийного субоптимального

ПИД регулятора увеличиваются и принимают наибольшие значения при

a → +∞, что соответствует H_∞ субоптимальному ПИД регулятору.

Некоторые результаты моделирования движения замкнутых систем с ПИД

регуляторами, построенными для различных уровней средней анизотропии

возмущения a, также отражены в таблице, где для сравнения приводятся

аналогичные величины для системы, замкнутой H_∞ субоптимальным ПИД

регулятором, на вход которой воздействуют возмущения с теми же уровнями

средней анизотропии. Из анализа данных таблицы можно заключить, что

• с ростом параметра a максимальные абсолютные амплитуды сигналов

управления, вырабатываемых соответствующими анизотропийными ПИД

регуляторами, также возрастают;

• при этом для всех значений a < +∞ амплитуды управляющих воздействий

анизотропийных регуляторов значительно меньше (для малых значений

средней анизотропии — в десятки раз) аналогичных показателей для за-

мкнутой системы с H_∞ регулятором при тех же возмущениях;

• максимальные абсолютные значения регулируемой переменной — угловой

скорости математического маятника x₂ — в замкнутых системах с анизо-

тропийными ПИД регуляторами для всех значений a < +∞ меньше ана-

логичных значений в замкнутой системе с H_∞ регулятором при тех же

возмущениях;

166

w1 0

w₁

t, c

w₂

t, c

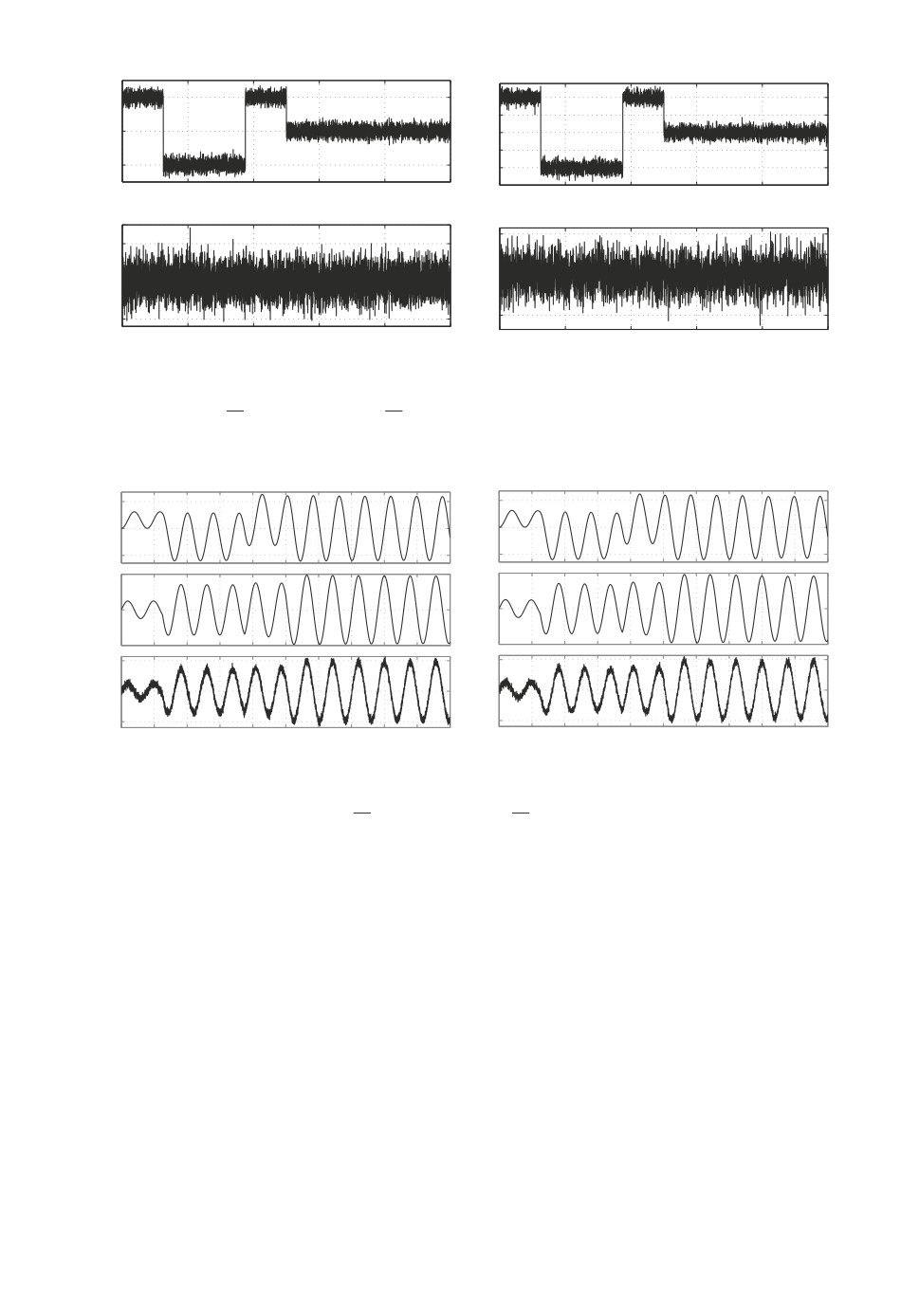
Рис. 1. Стохастические возмущения с различными уровнями средней анизо-

тропии: а — A(W ) = 0,1; б — A(W ) = 0,4.

x₁

x₂

t, c

Рис. 2. Реакция разомкнутой системы на возмущения с различными уровнями

средней анизотропии: а — A(W ) = 0,1; б — A(W ) = 0,4.

• несмотря на то что замкнутая система с H_∞ регулятором демонстрирует

меньшие максимальные абсолютные значения угла отклонения математи-

ческого маятника — переменной x₁ — для ряда возмущений с невысоким

уровнем средней анизотропии a, это достигается за счет совершенно несо-

поставимых энергетических затрат на управление по сравнению с анизо-

тропийными субоптимальными ПИД регуляторами.

Результаты моделирования для двух уровней средней анизотропии возмуще-

ния (a = 0,1 и a = 0,4) проиллюстрированы на рис. 1-4, на которых пред-

ставлены графики сигналов возмущений с данными уровнями средней ани-

зотропии, временные диаграммы переменных состояния и измеряемого вы-

хода разомкнутой системы при подаче на ее вход данных возмущений (при

нулевом входе управления), а также временные диаграммы переменных со-

стояния и сигналов управления в замкнутых системах с соответствующими

анизотропийными ПИД регуляторами и с H_∞ регулятором.

167

0.2

x₁

0.2

x₂

t, c

Рис. 3. Реакция замкнутых систем с анизотропийными ПИД регуляторами,

построенными для различных a, на возмущения с соответствующими уровня-

ми средней анизотропии: а — A(W ) = 0,1; б — A(W ) = 0,4.

0.10

0.05

x₁

0.05

x₂

200

t, c

Рис. 4. Реакция замкнутой системы с H_∞ ПИД регулятором на возмущения

с различными уровнями средней анизотропии: а — A(W ) = 0,1; б — A(W ) =

= 0,4.

5. Заключение

Поставлена и решена задача синтеза анизотропийного субоптимального

пропорционально-интегрально-дифференциального (ПИД) закона управле-

ния для дискретной линейной стационарной системы с одномерными входом

управления и измеряемым выходом, подверженной воздействию неопреде-

ленного стохастического возмущения с ограниченной средней анизотропией.

Задача заключалась в нахождении трех коэффициентов усиления ПИД ре-

гулятора, таких чтобы замкнутая система была асимптотически устойчива и

анизотропийная норма ее передаточной функции от входа возмущения к регу-

лируемому выходу была строго ограничена заданным пороговым значением,

обеспечивая заданное качество подавление возмущения. При дискретизации

передаточной функции непрерывной модели выбранной формы ПИД регуля-

168

тора и при последующем переходе при его описании к модели в пространстве

состояний две матрицы реализации регулятора являются полностью извест-

ными и лишь две другие зависят от искомых неизвестных коэффициентов

усиления. Этот факт используется для решения поставленной задачи. Ис-

ходная модель объекта управления в пространстве состояний дополняется

известным вектором состояния ПИД регулятора, известные матрицы реали-

зации регулятора включаются в расширенную модель объекта, и для нее за-

дача нахождения неизвестных коэффициентов усиления становится задачей

синтеза закона управления в виде статической обратной связи по измеряе-

мому выходу. Последняя задача решается методами выпуклой оптимизации

и линейных матричных неравенств. Получены достаточные условия суще-

ствования анизотропийного субоптимального ПИД регулятора, а процедура

его синтеза сводится к решению системы неравенств, включающей неравен-

ство относительно среднего геометрического собственных значений положи-

тельно определенной матрицы и двух линейных матричных неравенств. При

этом возможна минимизация порогового значения, ограничивающего анизо-

тропийную норму передаточной функции системы, замкнутой ПИД регуля-

тором.

ПРИЛОЖЕНИЕ

Приведем лемму, применяемую в доказательстве теоремы.

Лемма. Для заданных a > 0 и γ > 0 передаточная функция замкнутой

системы T_zw с реализацией (3.3) устойчива и удовлетворяет условию (2.14),

если система неравенств

(Π.1)

η - (e-2a detΨ)1/mw < γ²,

⎡

⎤

⎡

⎤

-Φ

∗

Ψ-ηImw

∗

⎢

⎥

⎢

⎥

⎢

-ηImw

∗

⎥

(Π.2)

⎣ B

-Φ-1

∗

⎦ ≺ 0,

⎢

⎥

≺ 0,

⎣ A B

-Φ-1

∗

⎦

-Ipz

(Π.3)

Ψ ≻ 0, Φ ≻ 0, η > γ², η ≤

1 - e-2a/mw

разрешима относительно скалярной переменной η и вещественных симмет-

ричных (m_w × m_w)-матрицы Ψ и (n × n)-матрицы Φ, где n — порядок за-

мкнутой системы.

Доказательство леммы следует из теоремы 4 в [5].

Доказательство теоремы. Пусть решение системы неравенств

(3.7)-(3.10) существует, найдено и данные неравенства выполняются. Кон-

груэнтное преобразование неравенств (3.8), (3.9) с матрицами

blockdiag (Imw , TTu, Ipz ), blockdiag (TTu, Imw , TTu, Ipz )

169

соответственно приводит к линейным матричным неравенствам

⎡

⎤

Ψ-ηImw

∗

⎢

⎥

⎣

ST_uB_w + TTuLD_yw TTu(Φ

S^T)T_u

∗

⎦ ≺ 0,

D_zw

-Ipz

⎡

⎤

-TTu ΦT_u

∗

⎢

⎥

⎢

-ηImw

∗

⎥

⎢

⎥

≺ 0.

⎣ T

ST_uA + TTuLC_y T

ST_uB_w + TTuLD_yw TTu(Φ

S^T)T_u

∗

⎦

C_z

D_zw

-Ipz

Обозначим S := TTu

ST_u, Φ := TTuΦT_u. Из выражений (3.4) и (3.12) следу-

ет, что B_u = T-1uB¯_u, L₁ = s₁K. С учетом определения блочных матриц (3.11)

получаем

]

[

]

L₁

s₁K

(Π.4) TTuL = TTu

=TTu

0(nx+1)×3

[

][

]

01×(nx+1)

=T^T

K =T

B_uK = SB_uK,

S₂

0(nx+1)×1

и предыдущие ЛМН можно переписать в виде

⎡

⎤

Ψ-ηImw

∗

⎢

⎥

⎣ S(Bw + BuKDyw) Φ - S - S^T

∗

⎦ ≺ 0,

D_zw

-Ipz

⎡

⎤

-Φ

∗

⎢

⎥

⎢

-ηImw

∗

⎥

⎢

⎥

≺ 0,

⎣ S(A + B_uKC_y) S(B_w + B_uKD_yw) Φ - S - S^T

∗

⎦

C_z

D_zw

-Ipz

или в терминах матриц реализации замкнутой системы (3.3) — в виде

⎡

⎤

Ψ-ηImw

∗

⎢

⎥

⎣ SB Φ - S - S^T

∗

⎦ ≺ 0,

-Ipz

⎡

⎤

-Φ

∗

⎢

⎥

⎢

-ηImw

∗

⎥

⎢

⎥

≺ 0.

⎣ SA SB Φ - S - S^T

∗

⎦

-Ipz

Конгруэнтное преобразование этих неравенств с матрицами

blockdiag (Imw , S-1, Ipz ), blockdiag (Inx , Imw , S-1, Ipz )

170

соответственно приводит к неравенствам

⎡

⎤

Ψ-ηImw

∗

⎢

⎥

(Π.5)

⎣ B

S-1ΦS-T - S-1 - S-T

∗

⎦ ≺ 0,

-Ipz

⎡

⎤

-Φ

∗

⎢

⎥

-ηImw

∗

⎢

⎥

(Π.6)

⎢

⎥

≺ 0.

⎣ A B S-1ΦS-T - S-1 - S-T

∗

⎦

-Ipz

Поскольку Φ ≻ 0, то для любой обратимой матрицы S всегда выполняется

неравенство

(S-1 - Φ-1)(-Φ)(S-1 - Φ-1)^T ≼ 0

(-S-1Φ + Inx+2)(S-1 - Φ-1)^T = -S-1ΦS-T + S-T + S-1 - Φ-1 ≼ 0,

откуда следует, что

-Φ-1 ≼ S-1ΦS-T - S-1 - S-T,

т.е. при выполнении неравенств (3.7), (Π.5), (Π.6) и (3.10) выполняются нера-

венства (Π.1)-(Π.3), и в силу леммы передаточная функция замкнутой си-

стемы T_zw с реализацией (3.3) устойчива и удовлетворяет условию (2.14) по-

ставленной задачи управления. Выражения (3.13) для вычисления искомых

коэффициентов усиления ПИД регулятора K_p, K_i и K_d следуют из (2.8),

(2.10) и проверяются непосредственной подстановкой. Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Владимиров И.Г., Курдюков А.П., Семенов А.В. Анизотропия сигналов и эн-

тропия линейных стационарных систем // ДАН. 1995. № 3. C. 583-585.

Vladimirov I.G., Kurdyukov A.P., Semenov A.V. Anisotropy of Signals and Entropy

of Linear Stationary Systems // Doklady Math. 1995. V. 82. No. 3. P. 386-390.

2. Владимиров И.Г., Курдюков А.П., Семенов А.В. Стохастическая проблема H_∞-

оптимизации // ДАН. 1995. Т. 343. № 5. C. 607-609.

Vladimirov I., Kurdyukov A., Semyonov A. The Stochastic Problem of H-infinity

Optimization // Doklady Math. 1995. V. 52. P. 155-157.

3. Vladimirov I.G., Kurdjukov A.P., Semyonov A.V. State-Space Solution to Anisotro-

py-Based Stochastic H_∞-optimization Problem // Proc. 13th IFAC World Congr.,

San-Francisco, USA. 1996. P. 427-432.

4. Diamond P., Vladimirov I.G., Kurdyukov A.P., et al. Anisotropy-Based Performance

Analysis of Linear Discrete Time Invariant Control Systems // Int. J. Contr. 2001.

No. 74. P. 28-42.

171

5. Чайковский М.М., Курдюков А.П. Критерий строгой ограниченности анизотро-

пийной нормы заданным значением в терминах матричных неравенств // ДАН.

2011. Т. 441. № 3. C. 318-321.

Tchaikovsky M.M., Kurdyukov A.P. Strict Anisotropic Norm Bounded Real Lemma

in Terms of Matrix Inequalities // Doklady Math. 2011. V. 84. No. 3. P. 895-898.

6. Aström K.J., Hägglund T. Advanced PID control. Instrumentation, Systems, and

Automation Society: Research Triangle Park, NC, 2006.

7. Zhou K., Glover K., Bodenheimer B.A., et al. Mixed H₂2 and H_∞ Performance

Objectives I: Robust Performance Analysis, II: Optimal Control // IEEE Trans.

AC. 1994. V. 39. P. 1564-1574, 1575-1587.

8. Löfberg J. YALMIP: A Toolbox for Modeling and Optimization in Matlab // Proc.

CACSD Conf. Taipei, Taiwan, 2004.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 28.06.2018

После доработки 09.09.2018

Принята к публикации 08.11.2018

172