Автоматика и телемеханика, № 1, 2020

Линейные системы

(Московский авиационный институт

(национальный исследовательский университет))

СТРУКТУРНО-ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ

ЛИНЕЙНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ

С ПОСТОЯННЫМИ ПАРАМЕТРАМИ

Рассматривается задача структурно-параметрической идентификации

стационарных линейных динамических систем. Предложен новый метод

структурно-параметрической идентификации динамической системы, ос-

нованный на построении множества слабоэквивалентных систем возрас-

тающей сложности. Под структурно-параметрической идентификацией

понимается оценка порядка дифференциальных уравнений, всех коэф-

фициентов, удовлетворяющих некоторым ограничениям, неизвестных на-

чальных условий и смещения измерителя. Решение задачи структурно-

параметрической идентификации получается за конечное число шагов.

На тестовом примере показано, что предложенный метод имеет высокую

чувствительность в условиях интенсивных измерительных ошибок.

Ключевые слова: структурная идентификация, параметрическая иденти-

фикация, линейные динамические системы.

DOI: 10.31857/S0005231020010018

1. Введение

Большое количество работ по структурной идентификации математиче-

ских моделей, появившихся в трудах различных конференций, семинаров,

монографиях и журналах указывает на значительный интерес специалистов

к этой проблеме и актуальность самой проблемы. Необходимость решения

проблемы структурной идентификации обусловлена различными причинами,

которые встречаются в процессе создания сложных технических систем [1].

Одной из таких причин является повышение точности вычисления оценок

неизвестных параметров по результатам ограниченного числа эксперимен-

тов. Вычисленные оценки параметров сравниваются с их априорными зна-

чениями, полученными либо расчетным путем, либо в полунатурных экспе-

риментах в полностью контролируемых условиях их проведения. Неприемле-

мые ошибки оценок неизвестных параметров, существенное отличие оценок

от их априорных значений указывают на несоответствие экспериментальных

данных структуре математической модели, принятой на этапе обработки ре-

зультатов эксперимента. Причиной несоответствия экспериментальных дан-

ных структуре математической модели могут быть скрытые, ненаблюдае-

мые переменные, влияющие на отклик динамической системы. Ненаблюдае-

мые переменные могут быть обусловлены изменением условий эксперимента

и их присутствие в каждом эксперименте не обязательно. Таким образом,

возникает проблема совместного определения параметров и структуры ма-

тематической модели по результатам натурного эксперимента, т.е. проблема

структурно-параметрической идентификации.

Л. Заде [2] связывает структурную идентификацию с понятием эквива-

лентности систем из выбранного класса систем. Одной из первых моногра-

фий, посвященных структурной идентификации линейных динамических си-

стем, была, по-видимому, [3], в которой был разработан метод типовой таб-

личной идентификации устойчивых динамических систем. Основой метода

является анализ оценок корреляционных функций пары вход — выход. Этот

метод давал решение задачи структурной идентификации для динамических

систем до третьего порядка включительно. Эквивалентность структур ди-

намических систем рассматривалась в терминах корреляционных функций

пары вход — выход. В [4, 5] с общих позиций рассматривается анализ проб-

лемы структурной идентификации и установлено, что ее успешное решение

сводится к разработке и обоснованию соответствующих критериев и алгорит-

мов. В монографии [6] предлагается метод оценки порядка линейной динами-

ческой системы, основанный на расширении входного пространства системы

введением вспомогательных переменных. В [7] анализируется структура мо-

дели в целях дальнейшего решения задачи параметрической идентификации.

Решение задачи параметрической идентификации динамических систем,

заданных дифференциальными уравнениями, традиционно проводится во

временной области и связано с необходимостью численного интегрирования

дифференциальных уравнений. Это может привести к дополнительным труд-

ностям решения задачи параметрической идентификации, обусловленным

динамическими характеристиками объекта и информационно-измерительной

системы. Поэтому иногда задачу параметрической идентификации целесооб-

разно решать частотными методами [8]. Частотные методы идентификации

были одними из первых методов идентификации математических моделей ди-

намических систем. Свойства стационарной линейной динамической системы

можно описать в терминах отношения амплитуд и сдвига фаз гармонических

сигналов на входе и выходе изучаемого объекта. К особенностям частот-

ных методов относятся: а) простота вычислений частотных характеристик

наблюдаемых переменных в присутствии измерительных шумов; б) возмож-

ность непараметрической идентификации структуры математической модели

в виде частотных характеристик; в) возможность независимого выбора то-

чек частотного диапазона для каждой пары входного и выходного сигналов;

г) возможность идентификации временных запаздываний в эксперименталь-

ных данных; д) возможность обобщения вычислительных алгоритмов иден-

тификации на многоканальные системы вход — выход и на нелинейные ди-

намические системы; е) возможность применения к идентификации неустой-

чивых динамических систем.

В [9-11] предложен частотно-временной метод параметрической иденти-

фикации, сочетающий в себе вычисления в частотной и во временной области

и позволяющий применить его к решению задачи структурно-параметриче-

ской идентификации линейных систем с постоянными коэффициентами. Но-

вый метод структурно-параметрической идентификации основан на сквозном

применении частотно-временного метода как для решения задачи параметри-

ческой идентификации, так и для решения проблемы структурной идентифи-

кации. В данной статье предложен новый метод структурной идентификации,

основанный на анализе свойств слабой эквивалентности линейных систем [12]

различной структуры. Проведенный анализ позволил предложить алгоритм

определения порядка системы дифференциальных уравнений на множестве

слабоэквивалентных динамических систем по наблюдаемой паре вход — вы-

ход на ограниченном интервале времени в присутствии измерительных помех.

Порядок динамической системы определяется за конечное число шагов.

На иллюстративном примере показано, что предложенный метод имеет

высокую чувствительность и позволяет выявить скрытые ненаблюдаемые

входные сигналы в условиях интенсивных инструментальных помех.

2. Постановка задачи структурно-параметрической идентификации

Рассмотрим устойчивую линейную стационарную непрерывную систему,

заданную дифференциальным уравнением n-го порядка на интервале време-

ни t ∈ [0, T ]

x(n) + an-1x(n-1) + an-2x(n-2) + ... + a₁x⁽¹⁾ + a₀x =

(1)

= bn-1u(n-1) + bn-2u(n-2) + ... + b₁u⁽¹⁾ + b₀u,

где x — скалярный выходной сигнал; u — скалярный входной сигнал, та-

кой что u(t) = const; x(k), u(k) — k-е производные; начальные условия x(k)0;

k = 0,1,...,n - 1 известны полностью или частично.

Наблюдается скалярная функция времени y(t), линейно связанная с про-

цессом x(t):

(2)

y(t) = x(t) + b_y

+ η(t),

где η(t) — стационарный случайный процесс с нулевым средним, описыва-

ет измерительный шум; b_y — неизвестное смещение измерителя на интерва-

ле [0, T ], обусловленное смещением нуля измерителя и/или конечным времен-

ным интервалом измерений (на этом интервале измеритель “шумит” несим-

метрично).

Обозначим через α = (an-1, . . . , a₀), β = (bn-1, . . . , b₀), χ = (x(n-1)0, . . . , x₀) -

n-мерные векторы параметров и начальных условий уравнения (1). На вход-

ном сигнале u(t) наблюдается выход y(t) = y(t; α, β, χ), зависящий от век-

торов параметров, начальных условий и смещения, т.е. наблюдаемый вы-

ход y(t) является траекторией в (3n + 1)-мерном параметрическом простран-

стве. В общем случае на входной сигнал и параметры наложены ограничения

u ∈ U, (α,β) ∈ Θ.

Под структурно-параметрической идентификацией будем понимать реше-

ние следующей задачи.

Задача 1. На интервале [0,T] выполняется одиночный эксперимент.

Требуется по наблюдениям пары вход — выход (u(t),y(t)), t ∈ [0,T] опреде-

лить порядок n; все коэффициенты (α, β) ∈ Θ; неизвестные начальные усло-

вия χ системы (1) и смещение b_y в (2).

Дальнейший анализ ограничен системами конечного порядка.

3. Принцип оценки порядка динамической системы

Рассмотрим уравнения (1) и (2) при условиях b_y = 0, η(t) ≡ 0, а в каче-

стве пары вход — выход — (u, x). Принцип оценки порядка динамической

системы (1) по результатам единственного эксперимента на интервале [0, T ]

основан на фундаментальных свойствах линейных систем, к которым отно-

сится свойство эквивалентности двух и более систем [12]. Обозначим через S_n

линейную динамическую систему (1) порядка n; векторы α, β, χ имеют раз-

мерности, согласованные с порядком системы.

Определение 1. Система S_n является следствием системы S_m на ин-

тервале [0,T] (вложением в систему S_m), или S_n ⊂ S_m, если каждая пара

вход — выход (u, x) системы S_n является также парой вход — выход (u, x)

системы S_m.

Определение 2. Если система S_n является следствием системы S_m

на интервале [0,T], а система S_m является следствием системы S_n на том

же интервале, то системы S_n и S_m слабоэквивалентны S_n ≡ S_m (в условиях

одиночного эксперимента) на интервале [0,T].

Определение 3. Системы слабоэквивалентны S_n ≡ S_m (в условиях

одиночного эксперимента) на интервале [0,T] тогда и только тогда, ко-

гда для каждого входа u(t) и (3n + 1)-мерного параметрического состояния

γ_n = (α,β,χ)_n системы S_n найдется (3m + 1)-мерное параметрическое со-

стояние γ_m = (α,β,χ)_m (зависящее от u(t) и γ_n) системы S_m такое, что

реакция на u(t) системы S_n, находящейся в состоянии γ_n, совпадает с ре-

акцией на u(t) системы S_m, находящейся в состоянии γ_m, и наоборот.

В символической записи

{S_n ≡ S_m} ⇔ {∀γ_n∀u∃γ_m

S_n(γ_n;u)

S_m(γ_m;u)]};

{S_m ≡ S_n} ⇔ {∀γ_m∀u∃γ_n

S_m(γ_m;u)

S_n(γ_n;u)]}.

Здесь порядок кванторов указывает на зависимость начального состояния од-

ной системы от начального состояния другой системы

S_n(γ_n;u)

S_m(γ_m;u) —

реакции систем S_n, S_m на входной сигнал u(t) и параметры γ_n, γ_m (различной

размерности) соответственно.

Теорема 1. Пусть наблюдаемая на интервале [0,T] пара вход — выход

(u, x) порождена динамической системой S_n порядка n. Тогда не существует

динамической системы (S_k,k < n) меньшего порядка, слабоэквивалентной

системе S_n.

Доказательство теоремы 1. Действительно, выход x(t) системы S_n

порядка n определяется (3n + 1)-мерным вектором параметров γ_n, тогда как

реакция системы (S_k, k < n) порядка k для всех входных сигналов u(t) опре-

деляется (3k +1)-мерным вектором параметров γ_k меньшей размерности. По-

этому любой отклик системы S_k порядка k является проекцией выхода x(t) на

пространство параметров меньшей размерности. Следовательно, система S_k

не может быть вложением в систему S_n.

□

Пусть на интервале [0, T ] в единичном эксперименте с динамической систе-

мой Sn0 порядка n₀ получена пара вход — выход (u, x). Предположим, что для

∀k,m таких, что n₀ < k < m, можно построить слабоэквивалентные системы

S_n ⊂ S_k и S_k ⊂ S_m и выполняется свойство транзитивности S_n ⊂ S_m. Тогда су-

ществует последовательность вложений Sn0 ⊂ Sn0+1 ⊂ · · · ⊂ Sm ⊂ · · ·. Отсюда

следует, что для данной пары вход — выход (u, x) в условиях единичного

эксперимента n₀ — наименьший порядок, начиная с которого существуют

слабоэквивалентные системы большего порядка.

Порядок n динамической системы (1) определяется размерностью векто-

ров параметров α и β и не зависит от вектора начальных условий χ. По-

этому необходимо рассмотреть некоторые общие свойства вложенных систем

Sn0 ⊂ Sn0+1 ⊂ ··· ⊂ Sm ⊂ ··· на наборах эквивалентных начальных условий.

Определение 4. Динамические системы S_n и S_m слабоэквивалентны

на интервале [0,T] при нулевых начальных условиях (в единичном экспери-

менте), если каждому нулевому начальному состоянию системы S_n соот-

ветствует эквивалентное нулевое начальное состояние системы S_m.

Теорема 2. Пусть слабоэквивалентные системы S_n ≡ S_m,n = m так-

же слабоэквивалентные при нулевом входном сигнале u(t) ≡ 0 на интерва-

ле [0, T ]

x(t, γ_n; u = 0) = x(t, γ_m; u = 0).

Тогда динамические системы S_n и S_m слабоэквивалентны при нулевых на-

чальных условиях

x(t; α_n, β_n, χ_n = 0; u) = x(t; α_m, β_m, χ_m = 0; u),

а их передаточные функции равны W_n(p) = W_m(p).

Доказательство теоремы 2 следует из свойства разложения реак-

ции линейной динамической системы на сумму свободного и вынужденного

движений.

□

Таким образом, анализ вложений динамической системы сводится к ана-

лизу передаточных функций и их частотных характеристик в условиях еди-

ничного эксперимента.

Следствие 1. Пусть n₀ — наименьший порядок, начиная с которого су-

ществуют слабоэквивалентные системы большего порядка при нулевых на-

чальных условиях. Тогда для вложений Sn0 ⊂ Sn0+1 ⊂ · · · ⊂ Sm ⊂ · · · последо-

вательные отношения частотных характеристик слабоэквивалентных ди-

намических систем возрастающего порядка не зависят от частоты

Wn0+1(jω)

Wn0+2(jω)

Wn0+k(jω)

(3)

=···=

= ··· = 1.

Wn0(jω)

Wn0+1(jω)

Wn0+k-1(jω)

Доказательство следствия вытекает из теоремы 2 путем очевидных по-

следовательных подстановок частотных характеристик динамических систем

возрастающего порядка. Амплитудно-фазовые частотные характеристики (3)

имеют значения (1, ±2πk, k = 0, 1, . . .) для всех частот, согласованных с ин-

тервалом [0, T ] (см. далее раздел 4).

□

Полученные результаты приводят к следующему принципу оценки поряд-

ка динамической системы: по наблюдениям на интервале [0, T ] пары вход —

выход (u, x) вычисляются последовательность оценок передаточных функций

возрастающего порядка и отношение их частотных характеристик (3); наи-

меньшее значение n₀, для которого выполняются условия (3), принимается за

оценку порядка динамической системы (1); оценка порядка n₀ динамической

системы выполняется за (n₀ + 1) шагов.

Рассмотрим условия слабой эквивалентности динамических систем в при-

сутствии измерительного шума η(t) = 0, t ∈ [0, T ]. Этот случай сводится к

предыдущему, если принять

y(t) = x(t),

где x(t) = x(t) + η(t) — оценка выходного сигнала системы (1). Вычисляя ма-

тематическое ожидание оценки x(t), получим

M[x(t)] = x(t),

т.е. необходимо потребовать выполнение условия несмещенности x(t). Если

условие несмещенности оценки x(t) выполняется, то свойства слабой эквива-

лентности динамических систем следует записать относительно математиче-

ского ожидания оценки выходного сигнала M[x(t)]. Кроме того, из свойства

несмещенности оценки выхода x(t) следует несмещенность оценки частотной

характеристики

M[^W(jω)] = W(jω)

и выражение (3) принимает вид

M[Wn0+1(jω)]

M[Wn0+2(jω)]

M[Wn0+k(jω)]

=···=

= ··· = 1.

M[Wn0(jω)]

M[Wn0+1(jω)]

M[Wn0+k-1(jω)]

Необходимо отметить следующие особенности применения принципа оцен-

ки порядка к данным натурного эксперимента:

1) амплитудно-фазовые частотные характеристики отношений (3) имеют

значения (1, ±2πk), k = 0, 1, . . . для всех n > n₀ и на всех частотах;

2) если условия (3) выполняются начиная с некоторого (n₀ + 1) для всех

практически важных частот, то это указывает на линейную динамическую

систему;

3) если условия (3) выполняются в ограниченном частотном диапазоне, то

это указывает на исходную нелинейную систему, но которая проявляет

себя как линейная система в этом частотном интервале;

4) частотный диапазон для проверки условий (3) должен быть согласован

с частотным спектром входного сигнала и не пересекаться с частотным

спектром измерительного шума.

4. Параметрическая идентификация динамической системы

Идентификация частотных характеристик пары вход — выход (u, x) для

систем возрастающего порядка по наблюдениям системы (1), (2) на интерва-

ле [0, T ] является нетривиальной задачей. Трудности ее решения обусловлены

влиянием на оценки частотных характеристик измерительного шума, неиз-

вестного смещения и неизвестных начальных условий как функций неизвест-

ного порядка динамической системы. Поэтому в настоящей работе предлага-

ется сначала определить все неизвестные параметры (α, β) ∈ Θ, χ, b_y динами-

ческой системы (1), (2) для различных возрастающих порядков, а затем на

оценках параметров при нулевых начальных условиях χ = 0 вычислить ча-

стотные характеристики. Для решения этой задачи запишем динамическую

систему (1), (2) в форме Фробениуса:

(4)

Ż = A(α)z + B(β)u,

где

⎡

⎤

⎡

⎤

-an-1

···

bn-1

⎡

⎤

⎢−an-2

···

0⎥

⎢bn-2⎥

⎢

⎥

⎢

⎥

⎢

z₁

⎥

⎢

⎥

⎢

⎥

A(α) =^⎢⎢

;

B(β) =

;

⎥

⎢

⎥

⎣

⎦^;

⎣

⎦

⎣

⎦

-a₁

b₁

zn-1

−a₀

b₀

(z₁, . . . , zn-1)^T — вектор ненаблюдаемых вспомогательных переменных.

Наблюдаемая скалярная функция (2) примет вид

(5)

y(t) = Hz + b_y

+ η(t),

где H = [1, 0, · · · 0] — матрица размера 1 × n.

Математические модели динамической системы, записанные уравнениями

(1), (2) и в форме Фробениуса (4), (5), эквивалентны по параметрам (α, β)

на паре вход — выход (u, x) и не эквивалентны по вектору начальных усло-

вий (x(n-1)0, . . . , x₀) = (x₀, z₁₀, . . . , z(n-1)0). Неэквивалентность по вектору на-

чальных условий не оказывает влияния на оценку частотных характеристик,

которые вычисляются на оценках параметров (α, β).

Задача 2. Пусть задан порядок n динамической системы (4), (5). Тре-

буется по наблюдениям пары вход — выход (u,y) на интервале [0,T] вы-

числить оценки неизвестных параметров (α, β) ∈ Θ, начальных условий

χ = (x₀,z₁₀,...,z(n-1)0) и смещения b_y.

Для решения этой задачи применим частотно-временной метод иденти-

фикации [9-11], который имеет ряд следующих достоинств: 1) переход в ча-

стотную область выполняется с помощью финитного преобразования Фурье,

которое вычисляется только один раз; 2) общая задача идентификации раз-

деляется на задачу оценки параметров (α, β) ∈ Θ (решается в частотной об-

ласти) и задачу оценки начальных условий (решается во временной области

на оценках параметров); 3) если ограничиться только вычислением частот-

ных характеристик системы (1), то необходимость решения второй задачи

отсутствует.

Определим дискретное множество частот

{

}

2π

(6)

Ω= ω_k :ω_k =

k,k = 1,... ,K

где K ≤ T f_N ; f_N = 1/h — частота Найквиста; h — шаг измерений, и вычислим

на Ω финитное преобразования Фурье уравнений (4), (5):

jω_kZ_T(jω_k) - z(0) + z(T) = A(α)Z_T(jω_k) + B(β)U_T(jω_k);

Y_T (jω_k) = HZ_T (jω_k) + η_T (jω_k).

Здесь (U_T (jω_k), Z_T (jω_k), Y_T (jω_k), η_T (jω_k)) — финитные преобразования Фу-

рье функций (u(t), z(t), y(t), η(t)):

(U_T (jω_k), Z_T (jω_k), Y_T (jω_k), η_T (jω_k), 0) =

∫T

√

= (u(t), z(t), y(t), η(t), b_y )e-jωktdt; j =

-1.

Выполняя элементарные алгебраические преобразования, получим

(7)

Y_T (jω_k) = H[jω_kE_n - A(α)]-1[Δz + B(β)U_T (jω_k)] + η_T (jω_k

где E_n — единичная матрица порядка n; Δz = z(0) - z(T ). Отсюда видно, что

Y_T (jω_k) зависит от параметров (α,β) и от разности граничных условий Δz,

которые не наблюдаются и нуждаются в оценке.

Запишем критерий метода наименьших квадратов на дискретном множе-

стве частот (6) в виде

∑

(8)

J (α, β, Δz) =

ε(-jω_k)ε(jω_k

k=1

где ε(jω_k) = Y_T (jω_k) - H[jω_kE_n - A(α)]-1[Δz + B(β)U_T (jω_k)].

Оценки параметров (α

β) ∈ Θ и разности граничных условий Δz вычис-

ляются минимизацией критерия (8) численными методами нелинейного про-

граммирования:

(9)

( α

β,Δz) = arg min

J (α, β, Δz).

(α

β)∈Θ,Δz

Вычисление интегралов Фурье целесообразно выполнять по формуле Фи-

лона [11, 13], так как в этом случае точность вычислений не зависит от частот-

ного спектра измеренных данных. Оценки (α

β) ∈ Θ вычисляются алгебраи-

ческими методами. Необходимость численного интегрирования уравнений (4)

отсутствует. Поэтому требование устойчивости систем (1) и (4) учитывается

неявно через множество допустимых значений неизвестных параметров Θ.

Оценки вектора начальных условий χ и смещенияby определяются на

оценках параметров (α

β) во временной области методом наименьших квад-

ратов

∫

(10)

(χ,by) = arg min

e²(t, α

β;χ,b_y

)dt,

(χ,by)

где e(t, α

β;χ,b_y) = y(t) - x(t, α

β;χ) - b_y;

x — оценка выходного сигнала

системы (1) или (4), вычисляется на входном сигнале u(t) многократным

интегрированием уравнений n-го порядка системы (4) на оценках парамет-

ров (α

β) и начальных условиях χ.

Результаты, полученные решением задач (9) и (10), дают полное решение

задачи 2 параметрической идентификации системы (1) в частотно-временной

области.

5. Алгоритм идентификации порядка системы (1)

Рассмотрим алгоритм определения порядка системы (1), если измеритель-

ные шумы отсутствуют η(t) ≡ 0.

1. Задают начальное приближение частотной характеристики W₀(jω) и по-

лагают n := 0.

2. Увеличивают порядок системы на единицу n := n + 1 и решают задачу 2

параметрической идентификации.

3. На оценках параметров (α

β) ∈ Θ вычисляют частотные характеристики

системы (1)

bn-1(jωk)n-1 +^bn-2(jωk)n-2 + . . . +^b1(jωk) +^b0

W_n(jω_k) =

(jω_k)ⁿ + ân-1(jω_k)n-1 + ân-2(jω_k)n-2 + . . . + â₁(jω_k) + â₀

4. Вычисляют отношение частотных характеристик (3) Wn+1(jω)/W_n(jω).

5. Строят диаграммы Боде отношений (3) на множестве частот Ω и запоми-

нают W_n(jω), найденную на шаге 3.

6. Переходят к шагу 2 и повторяют все вычисления.

7. За оценку порядка динамической системы n₀ принимается наименьшее n,

начиная с которого диаграммы Боде отношений (3) на всех частотах Ω

принимают значения (0, ±2πk, k = 0, 1, . . .). На этом процесс решения за-

дачи структурно-параметрической идентификации заканчивается.

Алгоритм оценивания порядка системы (1) в присутствии измерительных

шумов η(t) = 0, t ∈ [0, T ] состоит из аналогичной последовательности шагов.

Однако отношение частотных характеристик на шаге 4 вычисляется на оцен-

ках частотных характеристик возрастающего порядка

Wn+1(jω)/Wn(jω).

Очевидно, что в этом случае условие (3) будет выполняться только в среднем

и шаг 7 формулируется в следующем виде

8. За оценку порядка динамической системы n₀ принимается наименьшее n,

начиная с которого диаграммы Боде отношений (3) на всех частотах Ω

принимают средние по частоте значения (0, ±2πk, k = 0, 1, . . .).

Следует отметить высокую вычислительную эффективность метода

частотно-временной идентификации по сравнению с методами идентифика-

ции динамических систем только во временной области.

6. Пример

Рассмотрим пример решения задачи структурно-параметрической иденти-

фикации двух динамических систем.

Первая динамическая система описывается системой дифференциальных

уравнений второго порядка

x = a₁x + z₁ + b₁u;

(11)

Ż₁ = a₀x + b₀u.

Вторая динамическая система описывается системой дифференциальных

уравнений третьего порядка

x = ã₂x + z₁ +b2u;

(12)

Ż₁ = ã₁x + z₂ +b1u;

Ż₂ = ã₀x +b0u.

Рассмотрим динамические системы (11), (12) такие, что (a₀ = ã₁, a₁ = ã₂,

b₀ =b1, b₁ =b2). Входной сигнал u(t) в системах (11), (12) является одним

и тем же. В этих условиях систему (12) можно рассматривать как систе-

му (11), в которой переменная z₁(t) возбуждается дополнительным ненаблю-

даемым сигналом z₂(t), зависящим от наблюдаемой пары (u, x). Множество

допустимых значений параметров определяется условиями устойчивости си-

стем (11), (12) Θ = {(a₀, a₁, ã₀, ã₁, ã₂) < 0}.

Отклик систем (11), (12) наблюдается одним и тем же измерителем

y(t) = x(t) + b_y + η(t),

где η(t) ∈ [-1, 1] — случайная последовательность с нулевым средним, рас-

пределенная по равномерному закону; b_y = 1 — смещение измерителя. Здесь

уровень измерительных шумов и величина смещения приняты нереально

большими.

Можно ли в экспериментах над динамическими системами (11) и (12),

выполненными в одинаковых условиях, различить структуры этих систем?

Данные одиночного “эксперимента” получены численным решением систе-

мы (11) с параметрами (a₀ = -4, a₁ = -1, b₀ = 10, b₁ = 0) и системы (12) с па-

раметрами (ã₀ = -4, ã₁ = -1, ã₂ = -1,b2 = 0,b1 = 10,b0 = -1). Начальные

значения для первых двух переменных систем (11) и (12) приняты равны-

ми x(0) = 1, z₁(0) = -1, z₂(0) = 0. Эксперимент выполняется на интервале

времени t ∈ [0, T ], T = 30 и на одном и том же входном сигнале переменной

частоты

2-ω₀

2π

u(t) = 1 + 2 sin((ω₀ + ωt)t),

ω=

;

ω₀ =

Уравнения (11) и (12) интегрировались с шагом h = 0,001. Псевдослучайная

последовательность η(t) получена генератором случайных чисел RANDOM

пакета MATLAB.

3,0

2,5

2,0

1,5

1,0

0,5

1,0

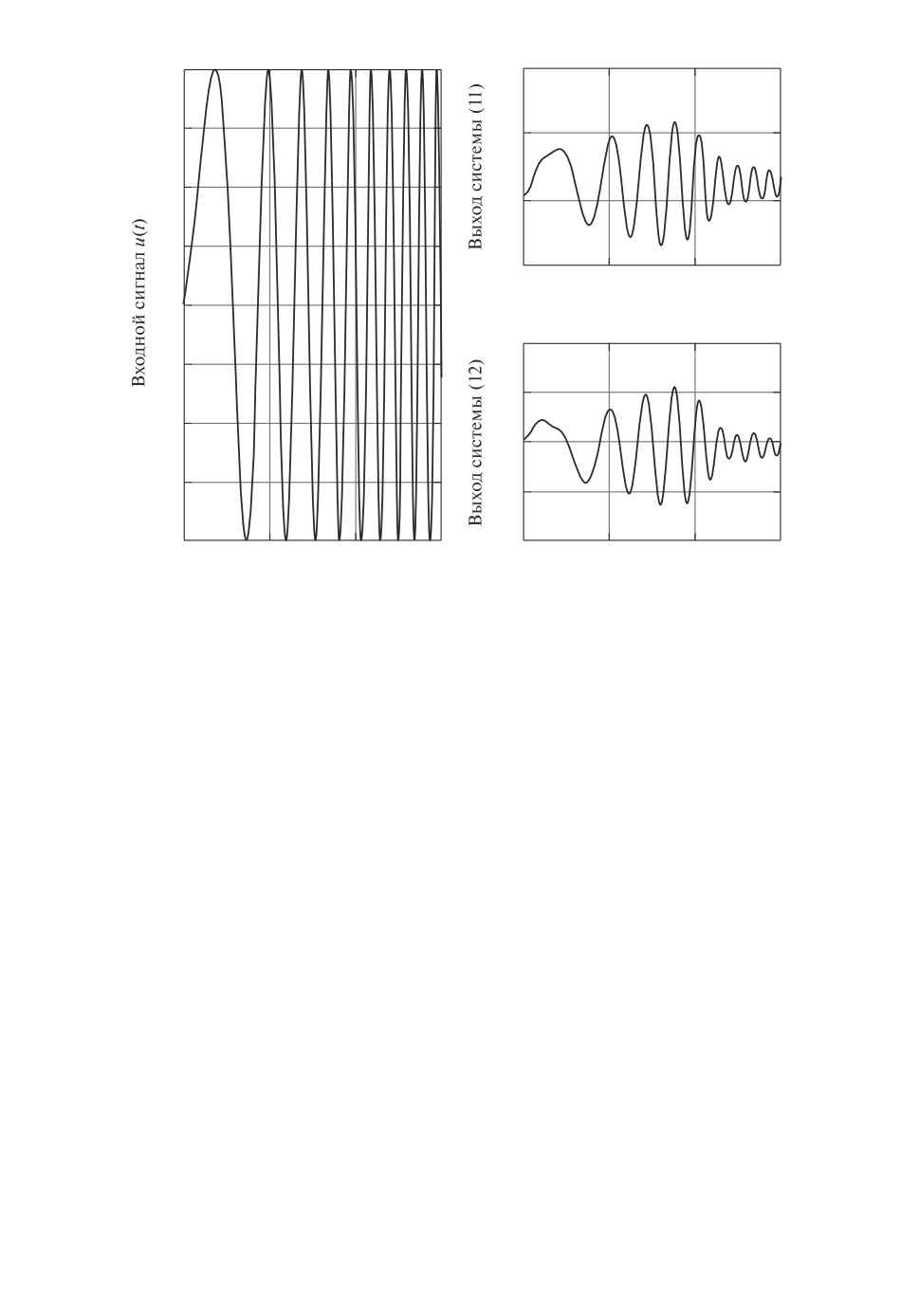
Рис. 1. Входной и выходные сигналы систем (11) и (12).

На рис. 1 показаны входной сигнал и выходные сигналы систем (11)

и (12) (для удобства восприятия графики приведены без измерительного шу-

ма η(t) ≡ 0). Видно, что выходы систем (11) и (12) почти не отличаются друг

от друга.

Задача параметрической идентификации решалась частотно-временным

методом на множестве частот Ω = {ω_k : ω_k = kω₀, k = 1, . . . , 50}. В задаче

идентификации порядка начальное приближение частотной характеристи-

ки было принято W₀(jω) = 1. В процессе решения задачи структурно-па-

раметрической идентификации порядок динамических систем возрастал

от n = 1 до n = 5. Полученные результаты показаны на рис. 2 и 3. Вид-

но, что для системы (11) слабоэквивалентные системы появляются начи-

ная с n = 2, а для системы (12) — начиная с порядка n = 3, т.е. поряд-

ки систем (11) и (12) вычислены правильно. Получены следующие оцен-

ки параметров систем (11) и (12), оценки начальных условий и оцен-

ка смещения: для системы

(11)

â₁ = -1;

â₀ = -3,99;

b₁ = 10;

b₀ = 0,01;

x(0) = 0,996; z₁(0) = -1,036;by = 0,993; для системы (12) â₂ = -1; â₁ = -4;

â₀ = -1;b2 = -0,005;b1 = 9,987;b0 = -1,017;

x(0) = 1,039;

z₁(0) = -0,941;

z₂(0) = 0,123;by = 1,011. Очевидна близость этих оценок и априорных зна-

чений. Для сравнения приведем значения оценок параметров системы (11),

тогда как “экспериментальные” данные были получены интегрированием

системы (12): â₁ = -0,643; â₀ = -3,714;b1 = 1,141;b0 = 8,833; x(0) = 0,959;

z₁(0) = 3,076;by = -2,451. Эти результаты получены на некоторой реализа-

ции измерительного шума и являются типичными и для других реализаций.

Численное решение примера получено в пакете компьютерной математи-

ки MATLAB с применением программ: LSIM для решения систем (11) и (12);

FMINCON для решения задач (9) и (10); BODE для вычисления частотных

характеристик. Финитные интегралы Фурье вычислялись по формуле Фило-

на программой, приведенной в [11].

Таким образом, предложенный метод корректно решает задачу струк-

турно-параметрической идентификации (в условиях смещения нуля измери-

теля и большой интенсивности измерительного шума).

7. Заключение

Предложен новый метод структурно-параметрической идентификации ди-

намической системы, заданной линейными дифференциальными уравнения-

ми с постоянными коэффициентами. Под структурно-параметрической иден-

тификацией понимаются: оценка порядка дифференциальных уравнений;

всех коэффициентов, удовлетворяющих некоторым ограничениям (например,

по условиям устойчивости); неизвестных начальных условий и смещения из-

мерителя. Метод основан на свойстве слабой эквивалентности двух и более

систем. Решение задачи структурной идентификации ищется на множестве

слабоэквивалентных систем. Для рассматриваемого класса динамических си-

стем определение порядка линейных дифференциальных уравнений сводит-

ся к анализу отношений частотных характеристик последовательно услож-

няемых структур. За оценку порядка динамической системы принимается

наименьший порядок динамической системы, начиная с которого усложне-

ние структуры динамической системы приводит только к последовательности

новых слабоэквивалентных систем. Оценка порядка динамической системы

определяется за конечное число шагов. Учет влияния измерительного шума

на решение задачи структурной идентификации приводит к замене частот-

ных характеристик динамических систем на математическое ожидание этих

частотных характеристик. Однако в условиях одиночного эксперимента (или

с малым числом реализаций) это не приводит к изменению алгоритма струк-

турной идентификации.

Решению задачи структурной идентификации предшествует необходи-

мость решения задачи параметрической идентификации, которое ищется

частотно-временным методом. В процессе решения задачи параметрической

идентификации вычисляются оценки параметров динамической системы в

частотной области, а затем во временной области определяются оценки на-

чальных условий и смещение измерителя. На оценках параметров вычисля-

ются частотные характеристики динамической системы. В результате реше-

ния задачи структурно-параметрической идентификации получают оценки

порядка динамической системы, оценки параметров и оценку смещения из-

мерителя.

На иллюстративном примере (рис. 2 и 3) показано, что предложенный но-

вый метод структурно-параметрической идентификации имеет высокую чув-

ствительность и позволяет разделить две динамические системы различной

структуры в условиях одиночного эксперимента и больших измерительных

ошибок, переходные процессы которых визуально близки.

Разработанный метод полностью решает задачу структурно-параметриче-

ской идентификации стационарной линейной системы по наблюдениям пары

вход — выход на ограниченном временном интервале в условиях измеритель-

ных ошибок.

СПИСОК ЛИТЕРАТУРЫ

Труды XII Всероссийского совещания по проблемам управления. М.: ИПУ, 2014.

Эйкхофф П. Основы идентификации систем управления. М.: Мир, 1975.

Типовые линейные модели объектов управления / Под ред. Н.С. Райбмана.

М.: Энергоатомиздат, 1983. 264 с.

Гинсберг К.С. Новый подход к проблеме структурной идентификации. II // АиТ.

2002. № 6. С. 85-98.

Ginsberg K.S. A New Approach to the Problem of Structural Identification. II //

Autom. Remote Control. 2002. V. 63. No. 6. C. 946-959.

Гинсберг К.С. К основам методологии структурной идентификации для цели

проектирования технических систем // Тр. XIII Всерос. сов. по проблемам

управления. М.: ИПУ, 2019.

Карабутов Н.Н. Структурная идентификация систем: анализ информационных

структур. М.: Книжный дом “ЛИБРОКОМ”, 2009. 176с.

Novara C., Vincent T., Hsu K., Milanese M., Poolla K. Parametric identification of

structured nonlinear systems // Automatica. 2011. № 47. C. 711-721.

Корсун O.H. Алгоритм идентификации динамических систем с функционалом

в частотной области // АиТ. 2003. № 5. С. 111-121.

Korsun O.N. An Identification Algorithm for Dynamic Systems with a Functional

in the Frequency Domain // Autom. Remote Control. 2003. Т. 64. № 5. С. 772-781.

Овчаренко В.Н. Идентификация аэродинамических характеристик воздушных

судов по полетным данным. М.: Изд-во МАИ, 2017.

10.

Danilevich E.V., Evstratov A.R., Kukharenko N.I., Ovcharenko V.N., Poplavs-

kii B.K. Identification of Constant Parameters of Dynamic Systems by a Time-

Frequency Method // J. Comput. Syst. Sci. Int. 2018. V. 57. No. 4. P. 3-13.

11.

Овчаренко В.Н. Аэродинамические характеристики летательных аппаратов:

идентификация по полетным данным. М.: ЛЕНАНД, 2019. 236 с.

12.

Заде Л., Дезоер Ч. Теория линейных систем. М.: Наука, ГРФ.-М; Л., 1970.

13.

Бахвалов Н.С. Численные методы. М.: Наука, 1973.

Статья представлена к публикации членом редколлегии Н.Н. Бахтадзе.

Поступила в редакцию 20.03.2019

После доработки 25.06.2019

Принята к публикации 18.07.2019