Автоматика и телемеханика, № 1, 2020

(Государственный морской технический университет, Санкт-Петербург),

Б.П. ЛЯМПЕ , д-р инженерии,

В. ДРЕВЕЛОВ, д-р инженерии (wolfgang.drewelow@uni-rostok.de),

Т. ЯЙНШ, д-р инженерии (torsten.jeinsch@uni-rostok.de)

(Университет Росток, ФРГ)

СТАНДАРТИЗИРУЕМОСТЬ И H₂-ОПТИМИЗАЦИЯ

ОДНОКОНТУРНОЙ МНОГОМЕРНОЙ ИМПУЛЬСНОЙ СИСТЕМЫ

С МНОЖЕСТВЕННЫМИ ЗАПАЗДЫВАНИЯМИ

Изучается одноконтурная многомерная система с тремя звеньями чис-

того запаздывания. Приводятся достаточные условия стандартизируемо-

сти системы S₀, при выполнении которых задача H₂-оптимизации си-

стемы S₀ сводится к более простой задаче H₂-оптимизации некоторой

эквивалентной импульсной системы с одним звеном чистого запаздыва-

ния. Строится множество фиксированных полюсов H₂-оптимальной си-

стемы S₀.

Ключевые слова: одноконтурная многомерная импульсная система с

запаздыванием, стандартизируемость, H₂-оптимизация, фиксированные

полюса.

DOI: 10.31857/S000523102001002X

1. Введение

Проблема учета запаздывания играет важную роль при решении задач

анализа и синтеза импульcных систем. Различным аспектам этой пробле-

мы посвящена значительная литература. Разнообразные подходы к решению

указанной проблемы содержатся в публикациях [1-20] и цитированных там

источниках. Анализ существующей литературы показывает, что теоретиче-

ские и вычислительные трудности, связанные с исследованием импусльных

систем с запаздыванием, существенно возрастают с увеличением количества

элементов чистого запаздывания в структуре изучаемой системы. В связи с

этим несомненный теоретический и практический интерес представляет за-

дача построения для заданной импульсной системы с множественными за-

паздываниями эквивалентной системы с меньшим числом элементов чистого

запаздывания.

В [20] на основе концепции параметрической передаточной матрицы

(ППМ) сформирован класс многомерных импульсных систем с множествен-

ными запаздываниями, которые названы стандартизируемыми. При этом по-

казано, что задача H₂-оптимизации стандартизируемой системы сводится к

решению аналогичной задачи для эквивалентной стандартной импульсной

системы S_τ , содержащей только один элемент чистого запаздывания. По-

этому решение задачи H₂-оптимизации для стандартизируемой импульсной

системы может быть получено с помощью алгоритма, описанного в [19]. В на-

стоящей статье, которая является непосредственным продолжением [20], об-

щие результаты [20] применяются к практически важному типу импульсных

систем: многомерной одноконтурной импульсной системе S₀ с несколькими

запаздываниями. Для конкретности рассматривается ситуация, когда число

элементов чистого запаздывания в контуре управления равно трем, а чис-

ло составляющих наблюдаемого вектора выхода, имеющих различные вре-

менные сдвиги, равно двум. Однако предлагаемый подход без существенных

изменений распространяется на общий случай. В статье приведены доста-

точные условия стандартизируемости системы S₀, обычно выполняющиеся в

приложениях, и построена соответствующая стандартная система S_τ . Кроме

того, определена совокупность стационарных элементов, которые порождают

полюса замкнутой H₂-оптимальной системы, не зависящие от вида исполь-

зуемого преобразователя «цифра-аналог».

2. Обобщенная стандартная импульсная система

с множественными запаздываниями

Приведем используемые в последующем изложении общие свойства обоб-

щенной стандартной импульсной системы с запаздыванием S_g, установлен-

ные в [20]. В определении обобщенной стандартной импульсной системы пред-

полагается, что управляемый стационарный объект описывается уравнения-

ми состояния:

dv(t)

= Av(t) + B₁x(t - τ₁) + Bu(t - τ₂),

(2.1)

y(t) = Cv(t),

где v(t) - вектор состояния объекта, y(t) - вектор управляемого выхода, x(t) -

вектор входа, u(t) - вектор управления и A, B, B₁, C - постоянные матрицы

соответствующих размеров. Предполагается, что пара A, B полностью управ-

ляема и пара A, C полностью наблюдаема. Кроме того, в (2.1) τ₁ и τ₂ - неот-

рицательные постоянные.

Предполагается, что объект (2.1) управляется импульсным регулятором

(ИР), который имеет период квантования T и описывается системой уравне-

ний (2.2)-(2.4)

(2.2)

ξ_k

= y(kT), k = 0,±,1,... ,

α₀ψ_k + α₁ψk-1 + ... + α_ρψ_k-ρ =

(2.3)

= β₀ξ_k + β₁ξk-1 + ... + β_ρξ_k-ρ, detα₀ = 0,

(2.4)

u(t) = h(t - kT )ψ_k

kT < t < (k + 1)T,

где α_i, β_i - постоянные матрицы соответствующих размеров и h(t) - матрица,

элементы которой имеют ограниченную вариацию на интервале 0 ≤ t ≤ T ,

а условие det α₀ = 0 является условием каузальности дискретного регулятора.

Используя оператор обратного сдвига ζ [3], уравнение алгоритма управле-

ния (2.3) можно записать в полиномиальной форме

(2.5)

α(ζ)ψ_k = β(ζ)ξ_k,

где α(ζ) и β(ζ) - полиномиальные матрицы вида

α(ζ) = α₀ + α₁ζ + . . . + α_ρζ^ρ,

(2.6)

β(ζ) = β₀ + β₁ζ + . . . + β_ρζ^ρ.

Далее рациональную матрицу

(2.7)

=α-1

(ζ)β(ζ)

будем называть передаточной матрицей алгоритма управления.

Кроме того, в определении системы S_g предполагается, что для любой

пары различных собственных чисел матрицы A p₁ и p₂ выполняется условие

непатологичности периода квантования [3]

(2.8)

ep1T = ep2T .

В качестве наблюдаемого выхода системы S_g рассматривается вектор

[

]

(2.9)

z′(t) =

z′1(t) ... z^′γ(t)

где штрих - оператор транспонирования и z_i(t) - наблюдаемые парциальные

векторы, заданные соотношениями

(2.10)

z_i(t) = C_iv(t - τ3i) + D_iu(t - τ₂ - τ3i

где τ3i, i = 1, . . . , γ, - вещественные постоянные, которые могут иметь значе-

ния произвольного знака.

В совокупности соотношения (2.1)-(2.10) определяют систему дифферен-

циально разностных уравнений, которую, при выполнении всех указанных

выше условий, назвали в [20] обобщенной стандартной системой с множе-

ственными запаздываниями S_g. Частный случай системы S_g, соответствую-

щий значению γ = 1, рассмотрен в [19] и назван там стандартной импульсной

системой S_τ .

По отношению к парциальному выходу z_i(t) система S_g сводится к стан-

дартной системе S_τi, которой в соответствии с [19] может быть сопоставлена

параметрическая передаточная матрица (ППМ) W_i(s, t), определяемая фор-

мулой

(2.11)

W_i(p,t) = φLτiμ(T,p,t)^RN (p)Mτ (p) + Kτi(p), i = 1, . . . , γ.

Здесь

∑

2π

φLτiμ(T,p,t) =

L_τi(p + kjω)μ(p + kjω)e^kjωt, ω =

k=-∞

∫T

μ(p) = h(t)e^-ptdt,

(2.12)

[

]

R_N(p) =Wd(p) I -DNμ(T,p,-τ₂)Wd(p)

-1,

∑

D_Nμ(T,p,-τ₂) =1

N (p + kjω)μ(p + kjω)e-(p+kjω)τ2 ,

k=-∞



W_d(p) = W_d(ζ)

ζ=e^-pT .

В (2.11) и (2.12) использованы обозначения

(2.13)

K_τi(p) = K_i(p)e-pτKi , L_τi(p) = L_i(p)e-pτLi ,

где K_i(p), L_i(p) - рациональные матрицы вида:

(2.14)

K_i(p) = C_i(pI - A)-1 B₁, L_i(p) = C_i(pI - A)-1 B + D_i.

Помимо этого, в (2.11) и далее

(2.15)

M_τ (p) = M(p)e-pτM , N_τ (p) = N(p)e-pτN ,

где

(2.16)

M (p) = C(pI - A)-1B₁, N(p) = C(pI - A)-1

Фигурирующие в (2.13), (2.15) постоянные τ_Ki, τ_Li, τ_M , τ_N определяются

формулами:

τ_Ki = τ_M + τ3i, τ_Li = τ_N + τ3i,

(2.17)

τ_M = τ₁, τ_N = τ₂.

Из (2.9) следует, что при входе x(t) и наблюдаемом выходе z(t) ППМ си-

стемы S_g имеет вид

⎡

⎤

W₁(p,t)

⎦_,

(2.18)

W_zx(p,t) =^⎣ ...

W_γ(p,t)

что с учетом (2.11) приводит к соотношению

(2.19)

W_zx(p,t) = φL_τμ(T,p,t)^RN (p)Mτ (p) +^Kτ(p),

где

[

]

[

]

K′

L′

(2.20)

(p) =

K′τ1(p) ... K^′τγ(p)

(p) =

L′τ1(p) ... L^′τγ(p)

∑

(2.21)

φL_τμ(T,p,t) =

L_τ (p + kjω)μ(p + kjω)e^kjωt.

k=-∞

Далее правую часть формулы (2.19) будем называть стандартной формой

ППМ для импульсной системы с множественными запаздываниями.

3. Стандартизируемость одноконтурной импульсной системы

с множественными запаздываниями

Определение 1. Далее импульсную систему S⁰ произвольной струк-

туры со входом x(t) и выходом z(t), состоящую из линейных стационар-

ных элементов и импульсного регулятора вида (2.2)-(2.4), будем называть

структурно стандартизируемой, если у нее существует ППМ W0¯zx(p,t) от

входа x(t) к выходу z(t), имеющая стандартную форму (2.19).

Определение 2. Структурно стандартизируемую систему S⁰ с ППМ

W0¯zx(p,t) будем называть стандартизируемой, если существует обобщен-

W_¯

ная стандартная систем

S_g, ППМ которой

zx(p,t) совпадает с ППМ

W0¯zx(p,t).

Далее обобщенную стандартную систем

S_g будем называть порождаю-

щей для стандартизируемой системы S⁰. Ниже систем

S_g и S⁰ считаются

эквивалентными. При этом на систему S⁰ переносятся все качественные осо-

бенности систем

S_g, установленные в [20].

В данном разделе изучается вопрос стандартизируемости многомерной од-

ноконтурной системы S₀ с тремя запаздываниями, структура которой изоб-

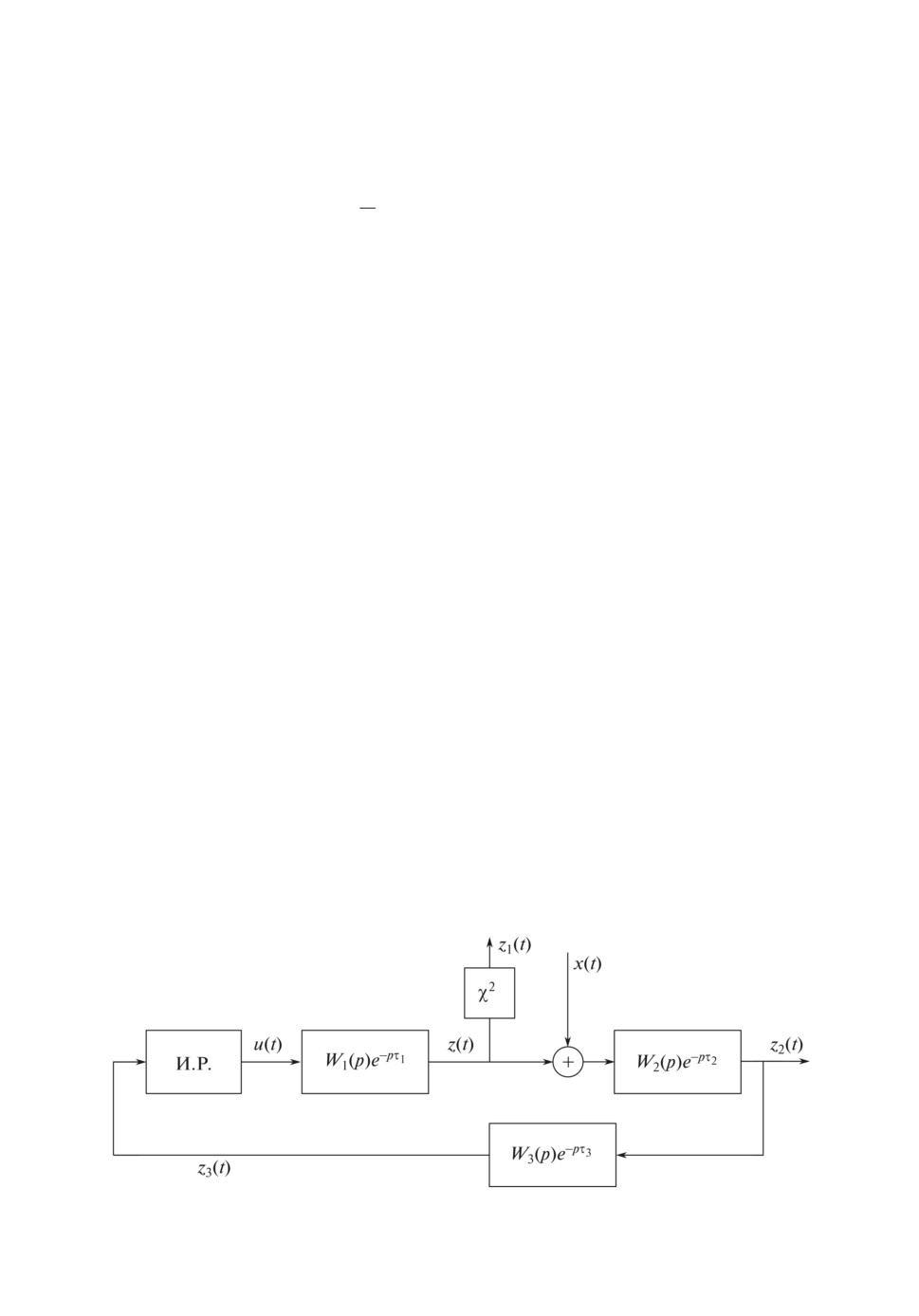
ражена на рис. 1.

На рис. 1 И.Р. - импульсный регулятор (2.2)-(2.4), W_i(p), i = 1, 2, 3, - ра-

циональные матрицы, свойства которых будут оговорены далее, χ² - положи-

тельная постоянная, τ_i, i = 1, 2, 3, - неотрицательные постоянные. В качестве

Рис. 1.

вектора наблюдаемого выхода будем рассматривать вектор

[

]

[

]

χ²z(t)

z₁(t)

(3.1)

z(t) =

z₂(t)

Теорема 1. Для стандартизируемости системы S⁰ при выборе наблю-

даемого выхода в виде (3.1) достаточно выполнения следующих условий:

1) рациональные матрицы

=W₃(p)W₂(p)W₁(p), M(p) = W₃(p)W₂(p),

[

]

(3.2)

W₂(p)

- строго правильные;

2) рациональная матрица

[

]

χ²W₁(p)

(3.3)

W₂(p)W₁(p)

- по меньшей мере правильная;

3) выполнено условие

(3.4)

MdegN(p) = MdegW₁(p) + MdegW₂(p) + MdegW₃

(p),

где M deg - обозначение степени Мак-Миллана [20, 21];

4) для всех различных полюсов матрицы N(p) выполнены условия вида

(2.8).

Доказательства теоремы 1 и последующих теорем 2 и 3 приведены в При-

ложении.

Замечание 1. Условие (3.4) означает отсутствие внутренних сокраще-

ний в произведении W₃(p)W₂(p)W₁(p). В скалярном случае условие (3.4) рав-

носильно несократимости этого произведения.

Замечание 2. Условия теоремы 1 не зависят от величин запаздыва-

ний τ_i, i = 1, 2, 3.

Если для системы S₀ не выполняется хотя бы одно из условий 1-3 теоре-

мы 1, то она не является стандартизируемой.

4. H₂-оптимизация и фиксирующие полюса стандартизируемой системы S₀

Теорема 2. Пусть для системы S₀ выполнены условия теоремы 1. То-

гда передаточная матрица W0d(ζ) H₂-оптимального алгоритма управления

совпадает с передаточной матрицей H₂-оптимального алгоритма управле-

ния для одноконтурной систем

S₀, изображенной на рис. 2, где выполнено

условие

(4.1)

τ =τ₁ +τ₂ +τ₃

Рис. 2.

и вектор наблюдаемого выхода z(t) выбран в виде

[

]

[

]

χ²z(t)

z₁(t)

(4.2)

z(t) =

z₂(t)

При выполнении условий теоремы 2 задача H₂-оптимизации систем

S₀

сводится к решению аналогичной задачи для соответствующей порождающей

расширенной стандартной систем

S_τ, что может быть выполнено на основе

результатов [19].

В соответствии с указанным в [20] на системы S₀

S₀ распространяются

все качественные особенности H₂-оптимальной порождающей системы

S_τ.

В частности, системы S₀

S₀ имеют совпадающие множества фиксирующих

полюсов.

Теорема 3. Пусть для системы S₀ выполнены условия теоремы 1. Обо-

значим через M₀ объединение множеств полюсов матриц W₁(p) и W₃(p).

Также обозначим через M₁ множество различных полюсов из множе-

ства M₀. Пусть p₁,... ,p_λ — элементы множества M₁. Тогда при Rep_i < 0

число ζ_i = e-piT является полюсом H₂-оптимальной системы S₀, а при

Rep_i > 0 аналогичным свойством обладает число ζ_i = epiT .

В соответствии с терминологией [21] M₁ - это множество фиксирующих

полюсов системы S₀, а множество чисел ζ_i - это множество фиксирован-

ных полюсов H₂-оптимальной системы. Из теоремы 3 следует практически

важный вывод о том, что при проектировании системы S₀ на основе мето-

дов H₂-оптимизации необходимо накладывать определенные ограничения на

свойства полюсов матриц W₁(p) и W₃(p). Если среди этих полюсов имеют-

ся полюса, лежащие вблизи мнимой оси, то степень устойчивости процессов

в H₂-оптимальной системе может оказаться неудовлетворительной. Если же

среди полюсов матриц W₁(p) и W₃(p) имеются полюса, лежащие на мни-

мой оси, то проектирование на основе методов H₂-оптимизации оказывается

невозможным, поскольку H₂-оптимальная система оказывается на границе

области устойчивости.

5. Заключение

В статье описан подход к решению задач стандартизируемости и H₂-оп-

тимизации многомерных одноконтурных импульсных систем с несколькими

запаздываниями, основанный на переходе к эквивалентной системе с одним

запаздыванием. Рассмотрен способ построения множества фиксированных

полюсов для H₂-оптимальной системы.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Доказательство проводится в несколь-

ко этапов.

Покажем, прежде всего, что при выполнении условий теоремы 1 для си-

стемы S₀ существует ППМ W₀(p, t), которая имеет стандартную формулу.

Это означает, что система S₀ структурно стандартизируема. Для этого в со-

ответствии с общим подходом [16-21] предполагаем, что на вход системы S₀

поступает матричный экспоненциальный сигнал

(Π.1)

x(t) = e^pt

и находим режим функционирования системы S₀, в котором

(Π.2)

z_i(p,t) = e^ptW_i

(p, t), i = 1, 2, 3,

где матрицы

(Π.3)

W_i(p,t) = W_i

(p, t + T ), i = 1, 2, 3,

— это ППМ от входа x(t) к выходам z_i(t), i = 1, 2, 3. В условиях тео-

ремы 1 элементы матрицы W₃(p, t) непрерывны относительно t. Поэто-

му, используя стробоскопическое свойство аналого-цифрового преобразова-

теля (АЦП) (2.2), можно перейти к рассмотрению разомкнутой системы на

рис. 3.

Рис. 3.

Используя (Π.1)-(Π.3), из рис. 3 можно получить после сокращения на e^pt

W₃(p,t) = φNτ μ(T,p,t)^Wd(p)W3(p,0) + W3(p)W2(p)e-p(τ2+τ3),

(Π.4)

где

∑

(Π.5)

φNτ μ(T,p,t) =

N (p + kjω)μ(p + kjω)e-(p+kjω)τ e^kjωt.

k=-∞

Кроме того,

(Π.6)

N_τ (p) = N(p)e^-pτ ,

где, как и ранее,

(Π.7)

τ =τ₁ +τ₂ +τ₃.

Поскольку матрица (Π.5) при всех p, не являющихся ее полюсами, непре-

рывна относительно t, то в левой и правой частях (Π.4) можно положить

t = 0. В результате приходим к равенству

(Π.8)

W₃(p,0) = φNτ μ(T,p,0)^Wd(p)W3(p,0) + W3(p)W2(p)e-p(τ2+τ3).

Если учесть, что

φNτ μ(T,p,0) =

∑

(Π.9)

N (p + kjω)M(p + kjω)e-(p+kjω)τ =DNμ (T, p, -τ),

k=-∞

то от (Π.8) приходим к равенству

[

]-1

(Π.10)

W₃(p,0) = I -DNμ(T,p,-τ)Wd(p) W₃(p)W₂(p)e-p(τ3+τ2).

Возвращаясь к рис. 3, с учетом (Π.10) получаем

W₁(p,t) = χ²φW1τ μ(T,p,t)^RN (p)W3(p)W2(p)e-p(τ3+τ2),

W₂(p,t) = φW2τ W1τ μ(T,p,t)^RN (p)W3(p)W2(p)e-p(τ2+τ3) + W2(p)e-pτ2 ,

(Π.11)

[

]-1

R_N(p) =Wd(p) I -DNμ(T,β,-τ)Wd(p)

Используя (Π.11) и (2.18), после несложных преобразований можно уста-

новить, что ППМ системы S₀ от входа x(t) к выходу (3.1) имеет стандартную

форму (2.19) с матрицами^K(p),^L(p), M(p), N(p), которые определены фор-

мулами (3.2), (3.3), а постоянные τ_N , τ_M , τ_Li, τ_Ki равны

τ_N = τ₁ + τ₂ + τ₃ = τ, τ_M = τ₂ + τ₃,

(Π.12)

τL1 = τ₁, τL2 = τ₁ + τ₂,

τK1 = 0, τK2 = τ₂.

Из доказанного следует, что система S₀ структурно стандартизируема.

Для доказательства стандартизируемости системы S₀ покажем, что при

выполнении условий теоремы 1 выполнены общие необходимые и достаточ-

ные условия стандартизируемости, приведенные в теореме 1 из [20]. Усло-

вия а) и б) этой теоремы выполняются очевидным образом. Выполнение усло-

вий (2.17) сразу следует из (Π.12).

Условие 1 выполнено по определению. Остается доказать, что условие в)

теоремы 1 из [20] также выполняется, т.е. что из условия (3.4) вытекает ра-

венство

[

]

^K(p)

^L(p)

(Π.13)

MdegN(p) = Mdeg

=MdegW₀

(p).

M (p) N(p)

Для этого отметим, что с учетом (3.2) и (3.3) имеем

⎡

⎤

[

]

χ²W₁(p)

^K(p)

^L(p)

⎢

⎥

⎢

⎥

(Π.14) W₀(p) =

2(p)

W₂(p)W₁(p)

⎣ W

⎦^.

M (p) N(p)

W₃(p)W₂(p) W₃(p)W₂(p)W₁(p)

Ведем обозначения:

(Π.15)

=ψ_i, i = 1,2,3, ψ₁ + ψ₂ + ψ₃=

ψ.

Из свойств степени Мак-Миллана, (Π.14) и (3.4) сразу следует, что

MdegW₀(p) ≥ MdegN(p) =

(Π.16)

= MdegW₁(p) + MdegW₂(p) + MdegW₃(p) = ψ.

С другой стороны, матрицу W₀(p) можно представить в виде произведения

(Π.17)

W₀(p) =W3(p)W2(p)W1

(p),

где

⎡

⎤

⎡

⎤

χ²I

⎥

W₃(p) =^⎣ 0 I

⎦,

W₂(p) =^⎣ W₂(p) W₂(p)

⎦,

(Π.18)

W₃(p)

W₂(p) W₂(p)

[

]

W₁(p) =

W₁(p)

Покажем, что справедливы равенства

(Π.19)

MdegWi(p) = ψ_i

i = 1,2,3.

Для этого отметим, что из (Π.18) имеем

(Π.20)

MdegWi(p) ≥ ψ_i

i = 1,2,3.

С другой стороны, из (Π.15) вытекает существование представлений MFD

(Matrix fraction description) [22]

(Π.21)

W_i(p) = a-1i(p)bi(p), i = 1, 2, 3,

где

(Π.22)

deg det a_i(p) = ψ_i

i = 1,2,3.

С помощью (Π.21) и (Π.18) при i = 3 находим MFD

(Π.23)

W₃(p) = a-13(p)^b3(p),

где

⎡

⎤

⎡

⎤

⎢

⎥

(Π.24)

a₃(p) =

⎣ 0 I

⎦,

b₃(p) =^⎣ 0 I

⎦.

a₃(p)

b₃(p)

Поскольку

(Π.25)

deg det a₃(p) = deg det a₃(p) = ψ₃,

то из свойств непонижаемых MFD [22] следует, что

(Π.26)

MdegW3(p) ≤ ψ₃.

Сопоставляя (Π.26) и (Π.20), приходим к равенству (Π.19) при i = 3. Для

случая i = 1 доказательство (Π.20) проводится аналогично.

Остается рас-

смотреть случай i = 2. Очевидно, что имеем

⎡

⎤

⎥

(Π.27)

W₂(p) =^⎣ 0 I I

⎦ W

(p),

где

⎡

⎤

χ²I

⎥

(Π.28)

W₄(p) =^⎣

⎦.

W₂(p) W₂(p)

Из (Π.27) следует, что

(Π.29)

MdegW2(p) = MdegW₄

(p),

так как первый сомножитель в (Π.27) - постоянная несингулярная матрица.

Используя MFD (Π.21) при i = 2, можно получить MFD

(Π.30)

(p),

W₂(p) = a-12^b2

где

(Π.31)

deg det a₂(p) = ψ₂.

Из (Π.31), (Π.30) следует, что

(Π.32)

MdegW2(p) ≤ ψ₂.

Сопоставляя (Π.32) и (Π.20), получаем, что

(Π.33)

MdegW2(p) = ψ₂,

что завершает доказательство формул (Π.19). Из (Π.19) и (Π.17) вытекает,

что

(Π.34)

MdegW₀(p) ≤ ψ₁ + ψ₂ + ψ₃

= ψ.

С другой стороны, из (Π.14), (Π.15) находим, что

(Π.35)

MdegW₀(p) ≥ MdegN(p) = ψ₁ + ψ₂ + ψ₃

= ψ.

Сопоставление (Π.34) и (Π.35) приводит к равенству

(Π.36)

MdegW₀

(p) = M degN(p) = ψ,

что завершает доказательство теоремы 1.

Доказательство теоремы 2. С помощью выкладок, аналогичных

использованным при доказательстве теоремы 1, устанавливается, что ППМ

систем

S₀ от входа x(t) к выходам z_i(t) имеют вид:

Wz1x(p,t) = χ²ψW1τ μ(T,p,t)^RN (p)W3(p)W2(p),

(Π.37)

Wz2x(p,t) = χ²ψW21τ μ(T,p,t)^RN (p)W3(p)W2(p) + W2(p),

где использованы обозначения:

W1τ (p) = W₁(p)e^-pτ , W21τ (p) = W₂(p)W₁(p)e^-pτ ,

(Π.38)

[

]-1

R_N(p) =Wd(p) I -DNμ(T,p,-τ)Wd(p)

Поэтому ППМ W_zx(p, t) от входа x(t) к выходу z(t) (4.2) имеет стандарт-

ную форму

(Π.39)

(p).

W_zx(p,t) = φL_τ μ(T,p,t)RN (p)M(p) +K

Здесь

(Π.40)

L_τ (p) =^L(p)e^-pτ

и аналогично предыдущему

[

]

[

]

K₁(p)

L₁(p)

(Π.41)

^K(p) =

^L(p) =

K₂(p)

L₂(p)

где

K₁(p) = 0, K₂(p) = W₂(p),

(Π.42)

L₁(p) = χ²W₁(p), L₂(p) = W₂(p)W₁(p),

M (p) = W₃(p)W₂(p), N(p) = W₃(p)W₂(p)W₁(p).

Из приведенных соотношений и теоремы 4 из [20] следует, что системы S₀

S₀ - H₂-эквивалетны в смысле [20] и им соответствует единая порождающая

расширенная стандартная систем

S_τ .

Доказательство теоремы 3. Пусть имеем непонижаемые левые и

правые MFD (ILMFD и IRMFD) [22]

(Π.43)

(p), i = 1, 2, 3,

где в силу (Π.15)

(Π.44)

deg det a_ℓi(p) = deg det a_ri(p) = ψ_i.

Из (Π.42) и (Π.43) следует

(Π.45)

(p)bℓ2

(p).

ℓ2

Из (3.4) вытекает

MdegM(p) = ψ₂ + ψ₃.

Поэтому существует ILMFD

(Π.46)

(p)bℓ4

(p),

ℓ4

в котором

(Π.47)

det aℓ4(p) ∼ det aℓ2

(p),

где символ ∼ означает эквивалентность полиномиальных матриц [22, 23] и, в

частности, скалярных полиномов. Поэтому справедливо равенство

(Π.48)

deg det aℓ4(p) = deg det aℓ2(p) = ψ₂.

С помощью (Π.46) получаем MFD

(Π.49)

(p),

M (p) = a-1M(p)BM

где

(Π.50)

a_M (p) = aℓ4(p)aℓ3(p), b_M (p) = bℓ4(p)bℓ2

(p),

причем

(Π.51)

deg det a_M (p) = ψ₂ + ψ₃

= MdegM(p).

Равенство (Π.51) означает, что правая часть (Π.49) - это ILMFD. Продол-

жая вычисления, используем равенство

(Π.52)

N (p) = W₃(p)W₂(p)W₁(p) = M(p)W₁

(p).

С помощью (Π.43) при i = 1 и (Π.49) получаем, что

(Π.53)

(p)b₁

(p).

При выполнении (3.4) существует ILMFD

(Π.54)

(p)bℓ5

(p),

ℓ5

где

det aℓ5(p) ∼ det aℓ1(p),

(Π.55)

deg det aℓ5(p) = deg det aℓ1(p) = ψ₁.

С учетом (Π.54) из (Π.52) получается ILMFD

(Π.56)

(p)b_ℓN

(p),

где

(Π.57)

a_ℓN(p) = aℓ5(p)a_M (p), b_ℓN (p) = bℓ5(p)b_M

(p),

причем по построению

(Π.58)

deg det a_ℓN (p) = ψ₁ + ψ₂ + ψ₃

= MdegN(p).

Из (Π.55) и (Π.57) в силу доказанного в [21] следует, что полюса матри-

цы W₁(p) являются фиксирующими.

Для доказательства утверждения, относящегося к матрице W₃(p), исполь-

зуем (3.3) в виде

[

]

χ²I

(Π.59)

^L(p) =

W₁

(p).

W₂(p)

Аналогично предыдущему с помощью (Π.59) устанавливается, что

(Π.60)

Mdeg^L(p) ≤ ψ₂ + ψ₁.

В то же время из (3.3) имеем

(Π.61)

Mdeg^L(p) ≥ ψ₁ + ψ₂.

Сопоставляя (Π.60) и (Π.61), находим, что

(Π.62)

Mdeg^L(p) = ψ₁ + ψ₂.

Из (Π.62) вытекает существование IRMFD

(Π.63)

(p),

где

(Π.64)

deg det a_r L(p) = ψ1 + ψ2.

Из (Π.63) следует, что произведение

[

]

χ²W₁(p)

(Π.65)

^L(p)a_r ¯_L(p) =

arL

(p)

W₂(p)W₁(p)

— п олиномиальная матрица. Следовательно, произведение

(Π.66)

=b_L

(p)

— тоже полиномиальная матрица. Из (Π.66) находим правое MFD

(Π.67)

(p),

которое в силу (3.4) непонижаемо. С помощью (Π.43) и (Π.67) находим

(Π.68)

(p).

При выполнении (3.4) имеем

(Π.69)

(p),

где правая часть - IRMFD. Подставляя (Π.69) в (Π.68), приходим к IRMFD

(Π.70)

(p),

где

(Π.71)

a_rN(p) = arL(p)ar4(p), brN(p) = bL(p)br4(p).

Сопоставляя IRMFD (Π.66) и (Π.70) на основании результатов [21] полу-

чаем, что полюса матрицы W₃(p) являются фиксирующими.

СПИСОК ЛИТЕРАТУРЫ

Kwakernaak H., Sivan R. Linear Optimal Control Systems. N.Y.: Wiley-Interscience,

a Division of John Wiley & Sons, Inc., 1972.

Ackermann J. Abtastregelung. Berlin: Springer-Verlag, 3 ed., 1988.

Astrom K.J.,Wittenmark B. Computer Controlled Systems: Theory and Design.

Englewood Cliffs, NJ: Prentice-Hall, 3rd ed., 1997.

Chen T., Francis B.A. Optimal sampled-data control systems. Berlin-Heidelberg-

N.Y.: Springer-Verlag, 1995.

Fridman E., Shaked U. Sampled-Data H_∞ State Feedback Control of Systems with

State Delays // Int. J. Control. 2000. V. 73. No. 12. P. 1115-1128.

Khargonekar P.P., Yamamoto J. Delayed Signal Reconstruction Using Sampled-

Data Control

// Proc.

35th IEEE Conf. on Decision Contr. Kyoto.

1996.

P. 1259-1263.

Yamamoto Y., Hara S. Performance Lower Bound for a Sampled-Data Signal

Reconstruction / V. Blondel, E. Sontag, M. Vidyasagar, J. Willems eds. Open

Problems in Mathematical Systems and Control Theory. London: Springer-Verlag,

1998. P. 277-279.

Lennartson B. Sampled-Data Control for Time-Delayed Plants // Int. J. Control.

1989. V. 49. P. 1601-1614.

Hara S., Fujioka H., Kabamba P.T. A Hybrid State-Space Approach to Sampled-

Data Feedback Control // Linear Algebra Appl. 1994. P. 679-712.

10.

Wittenmark B. Sampling of a System with Time Delay // IEEE Trans. Autom.

Control. May 1985. V. AC-30. P. 507-510.

11.

Jugo J. Discretization of Continuous Time-Delay Systems // Proc. 15th IFAC

Triennial World Congr. V. Linear systems/Time-delay systems. P. REG1450,

Barcelona, 2002.

12.

Polyakov K.Yu. H₂-optimal Sampled-Data Control of Plants with Multiple Input

and Output Delays // Asian J. Control. June 2006. V. 8. No. 2. P. 107-116.

13.

Emilia Fridman Introduction to Time-Delay Systems. Analysis and Control //

Cham-Heidelberg-N.Y.-Dordrecht-London: Springer, 2014.

14.

Mirkin L., Shima T., Tadmor G. Analog Loop Shifting in H₂ Optimization of

Input-Delay Sampled-Data Systems // 52nd IEEE Conf. on Decision and Control.

December 10-13, 2013, Florence, Italy.

15.

Mirkin L., Shima T., Tadmor G. Sampled-Data H₂ Optimization of Systems with

I/O Delays via Analog Loop Shifting // IEEE Trans. Autom. Control. March 2014.

V. 59. No. 3. P. 787-791.

16.

Розенвассер Е.Н. Линейная теория цифрового управления в непрерывном вре-

мени. М.: Наука, 1994.

17.

Rosenwasser E.N., Lampe B.P. Digitale Regelung in kontinuierlicher Zeit - Analyse

und Entwurf im Frequenzbereich. B.G. Teubner, Stuttgart, 1997.

18.

Rosenwasser E.N., Lampe B.P. Computer Controlled Systems - Analysis and Design

with Process-orientated Models. London-Berlin-Heidelberg: Springer-Verlag, 2000.

19.

Лямпе Б.П., Розенвассер Е.Н. H₂-оптимизация импульсных систем с запазды-

ванием на основе метода параметрической передаточной матрицы // АиТ. 2010.

№ 1. С. 49-69.

Lampe B.P., Rosenwasser E.N. H₂-optimization of Time-Delayed Sampled-Data

Systems on the Basis of the Parametric Transfer Matrix Method // Autom. Remote

Control. 2010. V. 71. No. 1. P. 49-69.

20. Розенвассер Е.Н., Лямпе Б.П., Древело В., Яйнш Т. Стандартизируемость и H₂-

оптимизация импульсных систем с множественными запаздываниями // АиТ.

2019. № 3. С. 26-44.

Rosenwasser E.N., Lampe B.P., Drewelow W., Jeinsch T. Standardizability and H₂-

Optimization of Sampled-Data Systems with Multiple Delays // Autom. Remote

Control. 2019. V. 80. No. 3. P. 413-428.

21. Rosenwasser E.N., Lampe B.P. Multivariable Computer-Controlled Systems —

A Transfer Function Approach. London: Springer, 2006.

22. Kailath T. Linear Systems. Englewood Cliffs, NJ: Prentice Hall, 1980.

23. Гантмахер Ф.Р. Теория матриц. М.: ГИТТЛ, 1954.

Статья представлена к публикации членом редколлегии А.А. Бобцовым.

Поступила в редакцию 01.03.2019

После доработки 29.04.2019

Принята к публикации 18.07.2019