Автоматика и телемеханика, № 1, 2020

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

УСОВЕРШЕНСТВОВАННЫЙ ГЕНЕРАТОР 3-КНФ ФОРМУЛ

Рассматривается задача выполнимости (SAT-problem) булевых фор-

мул, заданных в конъюнктивной нормальной форме с ограничением,

что каждый дизъюнкт содержит по три литерала переменных (3-КНФ).

В эмпирических исследованиях широко используется генерация случай-

ных формул с фиксированной длиной дизъюнкта. Феноменом этого ме-

тода является многократно подтвержденная линейная зависимость числа

дизъюнктов формулы от числа булевых переменных в точке «фазового

перехода» - от статуса выполнимых к статусу невыполнимых (когда доля

невыполнимых формул становится превалирующей). Предложен и иссле-

дован метод генерации случайных формул, имеющий меньший коэффи-

циент (3,49) пропорциональности между числом дизъюнктов и числом

переменных в точке «фазового перехода» (для известного метода генера-

ции этот коэффициент равен 4,23).

Ключевые слова: задача выполнимости (SAT-problem), конъюнктивная

нормальная форма (КНФ), дизъюнкт, литерал, булевы переменные.

DOI: 10.31857/S0005231020010110

1. Введение

В работе исследуется генерация сложных примеров для задачи выпол-

нимости логических формул (SAT-problem). Задача выполнимости являет-

ся опорной для обширного класса NP-complete. Многие практически важ-

ные задачи несложными преобразованиями могут быть приведены к задаче

выполнимости. Таковыми, например, являются задачи верификации аппара-

туры и программного обеспечения, планирования, составления расписаний,

комбинаторного анализа [1]. Важнейшим применением задачи выполнимо-

сти является автоматическое доказательство теорем - основа искусственного

интеллекта.

Задача выполнимости относится к труднорешаемым задачам, при этом

вопрос о возможности существования решения, алгоритмическая сложность

которого ограничена некоторым полиномом от длины записи логической фор-

мулы, остается открытым.

Многие из встречающихся частных примеров в действительности оказы-

ваются достаточно простыми. Как правило, достаточно простыми являются

и взятые из практики (индустриальные) примеры.

Поиск путей построения сложных примеров важен как для понима-

ния природы сложности задачи, так и для построения тестовых примеров

(benchmarks) с целью экспериментальной оценки алгоритмов [2]. Сложные

161

примеры активно способствуют выявлению недостатков в разработанных ал-

горитмах и тем самым указывают пути их дальнейшего совершенствования.

Считается, что относительно сложные примеры удается строить с помо-

щью случайных чисел. Генерируемые при помощи случайных чисел формулы

широко изучаются, поскольку это достаточно естественная модель, которая

проливает свет на фундаментальные структурные свойства задачи выполни-

мости. Такие формулы хорошо отражают специфику задач в системах логи-

ческих доказательств [3].

Первое известное значимое исследование было выполнено на формулах со

случайной длиной дизъюнктов. Было продемонстрировано [4], что при неко-

торых параметрах генератора таких формул задача выполнимости для них

может быть решена в среднем за O(MN²) шагов. Последующие исследова-

ния [2-6] показали, что семейство формул, со случайной длиной дизъюнктов,

должно рассматриваться как простое. Простота анализа формул со случай-

ной длиной дизъюнктов объясняется тем, что они часто содержат пустые

дизъюнкты, дизъюнкты из единственного литерала (юниты) и тривиальные

дизъюнкты. В настоящее время эмпирические исследования смещены к ме-

тодам построения формул, в которых генерация таких простых дизъюнктов

исключена [7, 8]. Подробное изложение результатов по рассматриваемой те-

матике содержится в [1].

Подавляющее большинство исследователей используют вариации генера-

тора с фиксированной длиной дизъюнкта. Для 3-КНФ длина дизъюнкта

равна трем. Литералы переменных, включенные в дизъюнкт, выбираются

c использованием последовательности случайных чисел. Такой генератор хо-

рош тем, что если подать на его вход нужную последовательность чисел, он

способен породить любую формулу. Он очень удобен для теоретических ис-

следований: его простота позволила аналитически доказать, что (в пределе)

при увеличении количества переменных при R ≤ 3,52 (R - отношение числа

дизъюнктов к числу переменных) генератор порождает пренебрежимо малое

число невыполнимых формул, а при 4,51 ≤ R алгоритм порождает пренебре-

жимо малое число выполнимых формул [9, 10].

Известна интересная гипотеза [5] о том, что нетривиальные формулы, яв-

ляющиеся невыполнимыми при меньшем числе ограничений (дизъюнктов),

как правило являются более сложными для доказательства невыполнимо-

сти - анализа. Поэтому для построения сложных примеров представляет ин-

терес поиск способов генерации формул, значительный процент которых яв-

ляется невыполнимыми при R ≤ 3,52.

2. Генераторы случайных формул

Будем использовать следующие обозначения. X - множество из N буле-

вых переменных X_ı, X = {X₁, . . . , X_N }. Литералами переменной X_ı назовем

термы x0i и x1i, где x0i = X_i и x1i = ¬X_i.

Рассматриваются формулы F (M) = C³¹ ∧ C³² ∧ . . . ∧ C3M , представленные в

конъюнктивной нормальной форме 3-КНФ, являющиеся конъюнкцией набо-

ра из M трехлитеральных дизъюнктов C3j. Исследуется их выполнимость, т.е.

162

возможность отыскания набора значений булевых переменных, на которых

формула принимает значение «истина».

Трехлитеральным дизъюнктом C3j(x^pk, x^qℓ, x^rm) является дизъюнкция трех

литералов переменных X_ı из множества X. Пример дизъюнкта с конкретны-

ми значениями верхних индексов литералов: C3j(x0k, x1ℓ, x0m) = x0k ∨ x1ℓ ∨ x0m =

= X_k ∨ ¬X_ℓ ∨ X_m.

Большое число публикаций, связанных с задачей выполнимости булевых

формул, заданных в 3-КНФ, представляют результаты эмпирических иссле-

дований. Основным инструментом таких исследований является генератор

случайных формул. Обычно для заданного числа N переменных желательно

строить набор из V невыполнимых формул F_v (v = 1, . . . , V ).

Формула, не имеющая дизъюнктов, выполнима. Искомая невыполнимая

формула строится так, что, пока она остается выполнимой, к ранее построен-

ным дизъюнктам добавляется новый. При получении невыполнимого набора

дизъюнктов процесс генерации формулы заканчивается. После того, как фор-

мула стала невыполнимой, добавление новых дизъюнктов не может сделать

ее выполнимой.

Формулу F_v удобно продуцировать на основе потока дизъюнктов. Принад-

лежащие такому потоку дизъюнкты строятся на основе одной последователь-

ности S_v случайных натуральных чисел ξ_ν , предположительно равномерно

распределенных в диапазоне от 1 до 2N(N - 1)(N - 2).

Разные формулы строятся на основе отличающихся друг от друга после-

довательностей случайных чисел.

Первый генератор с независимым выбором литералов (далее НВЛ-генера-

тор).

Для построения очередного дизъюнкта Cj+1 формулы F_v (в предположе-

нии, что при построении предшествующих дизъюнктов использованы ω чи-

сел из S_v) выбираются три последовательных случайных числа ξω+1, ξω+2,

ξω+3. В произвольным образом упорядоченном множестве A, состоящем

из 2N литералов от N, переменных выбираем элементы, имеющие номе-

ра ξω+1 (mod 2N), ξω+2 (mod 2N) и ξω+3 (mod 2N). Пусть этими элемен-

тами являются литералы x^pk, x^qℓ и x^rm, из них строим очередной дизъюнкт

Cj+1(x^pk,x^qℓ,x^rm).

После построения невыполнимого набора дизъюнктов процесс генерации

формулы F_v заканчивается.

При использовании такого генератора с небольшой вероятностью (поряд-

ка 1/N²) продуцируется дизъюнкт, содержащий более одного литерала од-

ной переменной. В этом случае дизъюнкт будет тавтологией, если верхние

индексы литералов, представляющих одну переменную, различны, либо бу-

дет дизъюнктом, в котором число различных литералов меньше трех. Такая

ситуация уменьшает сложность анализа формулы, поэтому следует предпо-

честь следующий генератор.

Второй генератор формул без простых дизъюнктов (далее БПД-генера-

тор) исключает возможность построения дизъюнкта, содержащего более од-

ного литерала одной переменной.

163

Для построения очередного дизъюнкта C3j+1 формулы F_v из S_v выбирают-

ся три последовательных случайных числа ξω+1, ξω+2, ξω+3. Затем в упорядо-

ченном множестве A выбирается элемент x^pk с номером ξω+1 (mod 2N). Этот

элемент полагается первым литералом дизъюнкта. Второй литерал назнача-

ется из множества A - {x0k, x1k}, содержащего 2N - 2 элементов. Выбирается

элемент x^qℓ с номером ξω+2 (mod 2N - 2). Третий литерал дизъюнкта выби-

рается из множества A - {x0k, x1k, x0ℓ, x1ℓ}, содержащего 2N - 4 элементов. Это

элемент с номером ξω+2 (mod 2N - 4). Выбранный элемент x^rm становится

третьим литералом дизъюнкта C3j+1(x^pk, x^qℓ, x^rm).

После построения невыполнимого набора дизъюнктов процесс генерации

формулы F_v заканчивается.

Поскольку при больших N вероятность того, что дизъюнкт формулы, по-

строенной первым генератором, содержит литералы одной переменной, неве-

лика (порядка 1/N²), то результаты эмпирических исследований с этими ге-

нераторами близки.

Отметим, что существенная разница в частоте использования различ-

ных переменных обычно является одним их факторов упрощения анализа

формул и часто используется алгоритмами решения задачи выполнимости

(SAT-solver). С целью получения более сложных для анализа формул в на-

стоящей публикации предлагается третий генератор, особенностью которого

является выравнивание частоты использования в формуле литералов различ-

ных переменных.

Третий генератор, выравнивающий нагрузку на литералы (далее ВНЛ-ге-

нератор), использует статистическую информацию о количестве использова-

ния литералов переменных в построенных дизъюнктах.

Для построения очередного дизъюнкта C3j+1 формулы F_v выбираем ли-

терал, который минимальное число T раз встречается в ранее построенных

дизъюнктах. Пусть это литерал x^tf переменной X_f . Его полагаем первым ли-

тералом генерируемого дизъюнкта.

В отличие от первых двух, третий генератор при задании первого лите-

рала очередного дизъюнкта не использует элементы последовательности S_v

случайных чисел.

Для выбора второго и третьего литералов дизъюнкта используются числа

ξη+1 и ξη+2 из S_v (η чисел использованы при построении предшествующих

дизъюнктов формулы F_v).

Для генерации второго литерала дизъюнкта строится множество B лите-

ралов (переменных, отличных от переменной X_f ), входящих в построенные

дизъюнкты формулы не более чем T + 2 раз. Если множество оказалось пу-

стым, повторяем построение множества B с новым увеличенным на единицу

значением T (T = T + 1). Если множество не пусто, фиксируем число его эле-

ментов B и порядок элементов в множестве B. Вторым литералом назначаем

элемент x^qℓ, имеющий номер ξη+1 (mod B) в множестве B.

При построении третьего литерала дизъюнкта снова строится множе-

ство B литералов (переменных, отличных от переменных X_f и X_ℓ), входящих

в построенные дизъюнкты формулы не более чем T + 2 раз. Если множество

оказалось пустым, повторяем построение множества B с новым увеличенным

164

Распределение литералов в невыполнимой формуле, постоенной вторым генератором

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₈

X₉

X₁₀

X₁₁

X₁₂

X₁₃

X₁₄

X₁₅

X₁₆

Распределение литералов в невыполнимой формуле, постоенной третьим генератором

Рис. 1. Иллюстрация неравномерности использования литералов в 3-КНФ

формулах, построенных БПД- и ВНЛ-генераторами.

на единицу значением T (T = T + 1). Если множество не пусто, фиксируем

число его элементов B и порядок элементов в множестве B. Третьим лите-

ралом назначаем элемент x^rm, имеющий номер ξη+2 (mod B) в множестве B.

Построение дизъюнкта C3j+1(x^tf , x^qℓ, x^rm) завершено.

После построения невыполнимого набора дизъюнктов процесс генерации

формулы F_v заканчивается.

На рис. 1 представлены две гистограммы, иллюстрирующие количествен-

ное присутствие литералов 16 переменных в двух невыполнимых формулах,

построенных ВНЛ-генератором (внизу) и БПД-генератором (вверху). Лите-

ралы, представляющие переменные без инверсии, обозначены нулем по зна-

чению верхнего индекса, а литералы, представляющие инвертированные пе-

ременные, обозначены единицей. В формуле от 16 переменных, построенной

третьим генератором, число использованных литералов каждого типа отли-

чается не более чем на два. В формуле от 16 переменных, построенной вторым

генератором, 15-я переменная без инверсии используется трижды, а, напри-

мер, 10-я переменная - одиннадцать раз.

165

Отметим, что все три описанных генератора могут породить формулу,

дизъюнкты которой имеют одинаковые наборы литералов. Вероятность то-

го, что в формуле из M = kN дизъюнктов два будут содержать одинако-

вые наборы литералов, будет порядка 1/N². Присутствие в формуле таких

дизъюнктов не приводит к существенному упрощению ее анализа. Поэтому

усложнение генераторов, направленное на исключение возможности генера-

ции формул с дизъюнктами, содержащими идентичные наборы литералов,

считается нецелесообразным.

3. Эмпирическое исследование генератора

Замечательным свойством второго БПД-генератора является соблюдае-

мая с высокой точностью линейная зависимость M₂ от N.

Если генерировать формулы содержащие по ⌊M(N)⌋ дизъюнктов от

N переменных, математическое ожидание вероятности выполнимости фор-

мул будет больше либо равно 0,5. Если генерировать формулы содержащие

по ⌈M(N)⌉ дизъюнктов от N переменных, математическим ожиданием веро-

ятности невыполнимости будет величина большая, либо равная 0,5.

100

N = 16

N = 32

N = 48

N = 64

3,4

3,6

3,8

4,0

4,2

4,4

4,6

4,8

5,0

5,2

Отношение числа дизъюнктов к числу переменных

Рис. 2. Иллюстрация статистики перехода от статуса выполнимости к статусу

невыполнимости для 3-КНФ формул, порожденных БПД-генератором.

166

Этот удивительный результат [6] до сих пор не нашел удовлетворительного

объяснения.

Феномен линейной зависимости от N точки «фазового перехода» 3-КНФ

формул (порожденных БПД-генератором) от статуса выполнимых к статусу

невыполнимых был многократно подтвержден последующими публикация-

ми, например [7, 8], и его статистическая достоверность не вызывает сомне-

ния.

Для большей наглядности график процентной доли формул, ставших

невыполнимыми после включения в их состав M дизъюнктов, строят отно-

сительно величины R = M/N, являющейся отношением числа дизъюнктов к

числу переменных. На рис. 2 совместно представлены такие зависимости для

формул с числом переменных 16, 32, 48, 64, построенных БПД-генератором.

Результированы данные по 2000, 4000, 16000 и 32000 формулам для N = 64,

N = 48, N = 32 и N = 16. В выбранных координатах на графике «фазовый

переход» становится все более крутым с увеличением числа переменных.

Проведенные исследования [6-8] показали колоколообразную зависимость

медианной сложности анализа формул от числа дизъюнктов. При этом мак-

симальная медианная сложность имела место в непосредственной близости

от точки «фазового перехода».

Медианная сложность в определенном смысле является усредненной слож-

ностью анализа формул, содержащих фиксированное число дизъюнктов.

В одной из пионерских работ [5], ориентированных на построение сложных

для анализа формул, отмечено, что самыми сложными, как правило, ока-

зываются формулы, являющиеся невыполнимыми при минимальном числе

дизъюнктов.

Этот эмпирический результат объяснен [5] тем, что задача выполнимо-

сти, как и большинство других NP-comlete задач, может рассматриваться

как поиск решения, удовлетворяющего определенным ограничениям. Интуи-

тивно ясно, что если ограничений мало, то решение найти легко, так как при

этом обычно имеет место множество возможных решений. Аналогично, если

ограничений слишком много, достаточно интеллектуальный алгоритм обыч-

но способен быстро отбрасывать большинство тупиковых ветвлений в дереве

поиска. Таким образом, разумно ожидать, что самые сложные задачи - это

задачи, которые, с одной стороны, не перегружены ограничениями, с другой

стороны, имеющиеся ограничения оставляют возможность лишь для неболь-

шого числа решений [6]. Эмпирическими исследованиями подтверждено, что

это действительно имеет место [6-8].

Приведенные рассуждения являются мотивацией для поиска алгоритмов

построения 3-КНФ формул, являющихся невыполнимыми при меньшем чис-

ле дизъюнктов, чем в невыполнимых формулах, построенных ставшими клас-

сическими НВЛ- и БПД-генераторами.

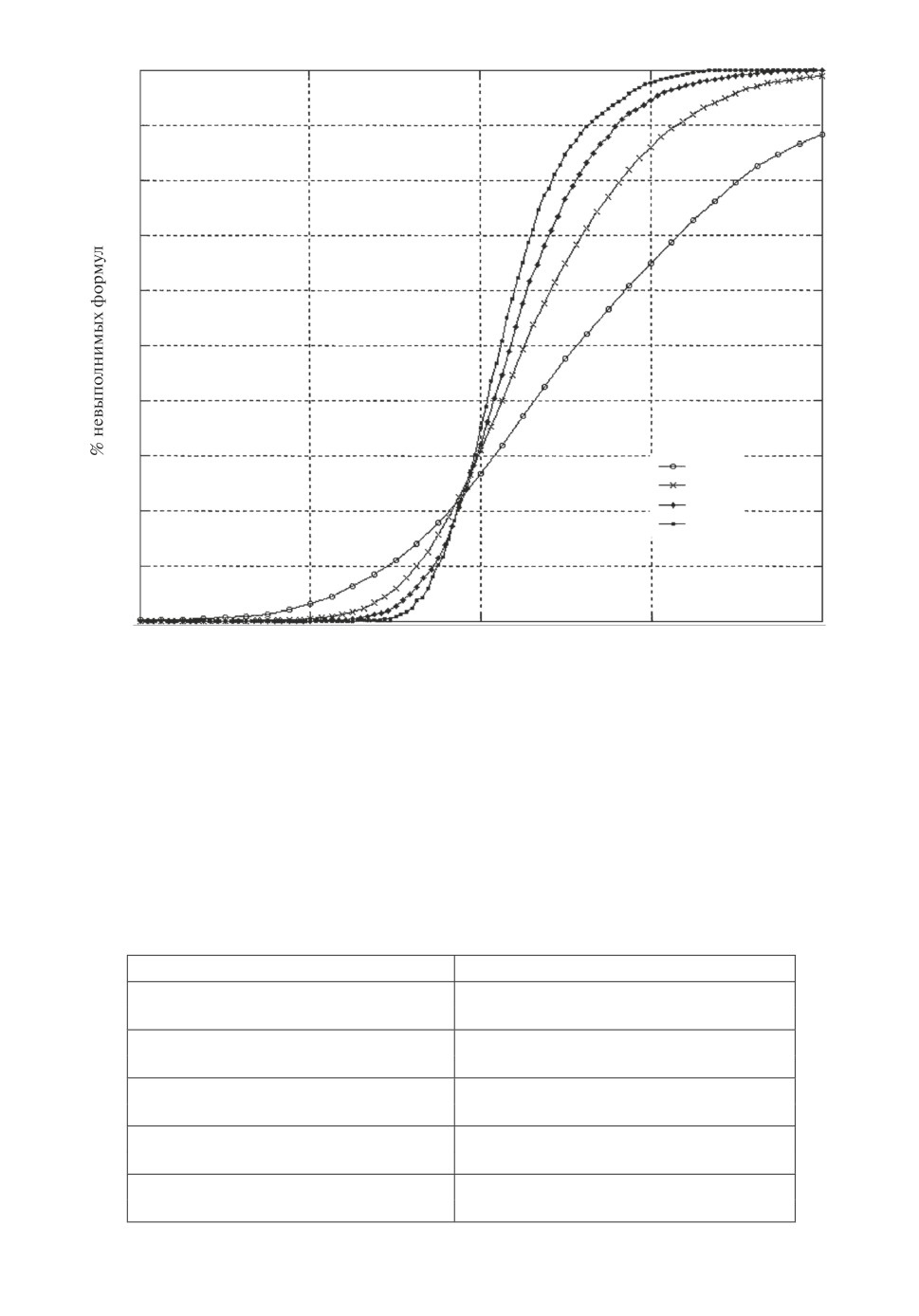
На рис. 3 представлены результаты исследований, для формул с числом пе-

ременных 16, 32, 48, 64, построенных ВНЛ-генератором. Для N = 64, N = 48,

N = 32 и N = 16 построено 2000, 4000, 16000 и 32000 формул соответственно.

Как и для второго БПД-генератора, «фазовый переход» на графике рис. 3

становится все более крутым с увеличением числа переменных. Заметно,

167

100

N = 16

N = 32

N = 48

N = 64

2,5

3,0

3,5

4,0

4,5

Отношение числа дизъюнктов к числу переменных

Рис. 3. Иллюстрация статистики перехода от статуса выполнимости к статусу

невыполнимости для 3-КНФ формул, порожденных ВНЛ-генератором.

что при одинаковом числе переменных для формул, порожденных третьим

ВНЛ-генератором, «фазовый переход» более крутой, чем для формул, порож-

денных БПД-генератором (см. рис. 2). Важно, что при заданном числе пе-

ременных «фазовый переход» для формул, построенных ВНЛ-генератором,

Таблица 1. Связь эмпирических вероятностей невыполнимости формулы

со значениями ⌊M(N)⌋ и ⌈M(N)⌉

Второй генератор

Третий генератор

⌊M₂(3)⌋ = 19 (47,835)

⌊M₃(3)⌋ = 14 (44,160)

⌈M₂(3)⌉ = 20 (53,056)

⌈M₃(3)⌉ = 15 (51,900)

⌊M₂(16)⌋ = 75 (48,919)

⌊M₃(16)⌋ = 60 (47,503)

⌈M₂(16)⌉ = 76 (52,366)

⌈M₃(16)⌉ = 61 (52,031)

⌊M₂(32)⌋ = 143 (48,756)

⌊M₃(32)⌋ = 116 (47,503)

⌈M₂(32)⌉ = 144 (52,419)

⌈M₃(32)⌉ = 117 (53,656)

⌊M₂(48)⌋ = 209 (49,000)

⌊M₃(48)⌋ = 172 (48,825)

⌈M₂(48)⌉ = 210 (51,500)

⌈M₃(48)⌉ = 173 (53,350)

⌊M₂(64)⌋ = 278 (49,850)

⌊M₃(64)⌋ = 227 (46,800)

⌈M₂(64)⌉ = 279 (52,700)

⌈M₃(64)⌉ = 228 (50,700)

168

происходит при существенно меньшем соотношении числа дизъюнктов к чис-

лу переменных, чем для формул, построенных БПД-генератором.

Процент невыполнимых формул построенных БПД- и ВНЛ-генераторами

при заданном числе переменных и заданном числе дизъюнктов, представлен

в табл. 1.

При N = 3 вероятность того, что содержащая M дизъюнктов формула, по-

рожденная БПД-генератором, будет невыполнимой, может быть вычислена

аналитически. Если переменных всего три, то для получения невыполнимой

формулы необходимо и достаточно, чтобы среди дизъюнктов формулы при-

сутствовали восемь различных дизъюнктов, каждый из которых содержит

литералы различных переменных. Если общее число дизъюнктов в формуле

меньше восьми, формула выполнима.

Вероятность того, что формула, содержащая восемь случайных дизъюнк-

тов, будет невыполнимой, равна

7!/8⁷ = 0,0024. При увеличении числа

дизъюнктов в формуле вероятность того, что формула невыполнима, будет

возрастать, стремясь к единице.

Как указано в [6], вероятность генерирования невыполнимой формулы,

составленной из M дизъюнктов, соответствует вероятности того, что за M

обращений к генератору случайных чисел с диапазоном (1:8) будут сгенери-

рованы все восемь возможных чисел (т.е. в полученной последовательности

будет представлено каждое из восьми чисел).

Обозначим через P^kM вероятность того, что среди M дизъюнктов k будут

различными. Вероятности P^kM (1 ≤ k ≤ 8) связаны рекуррентными соотноше-

ниями:

P^kM = (k/8)PkM-1 + ((9 - k)/8)Pk-1M-1

при начальных условиях P⁰⁰ = 1, Pj0 = 0, j = 1, 8 и граничных условиях P0M =

= 0.

Вычисления по этим формулам дают P⁸¹⁹ = 0,478348, а P⁸²⁰ = 0,530558. Та-

ким образом, для трех переменных точка «фазового перехода» находится

между 19 и 20 дизъюнктами.

В ячейках табл. 1 в круглых скобках приведены процентные доли невы-

полнимых формул.

Аппроксимация методом наименьших квадратов данных, представленных

в табл. 1, подтверждает хорошо известную для БПД-генератора линейную

зависимость числа M₂ от числа переменных N.

M₂(N) = 4,23N + 7,18.

Аппроксимация представленных в табл. 1 эмпирических данных выявляет

линейную зависимость M₃ от числа переменных N и для ВНЛ-генератора.

M₃(N) = 3,49N + 4,46.

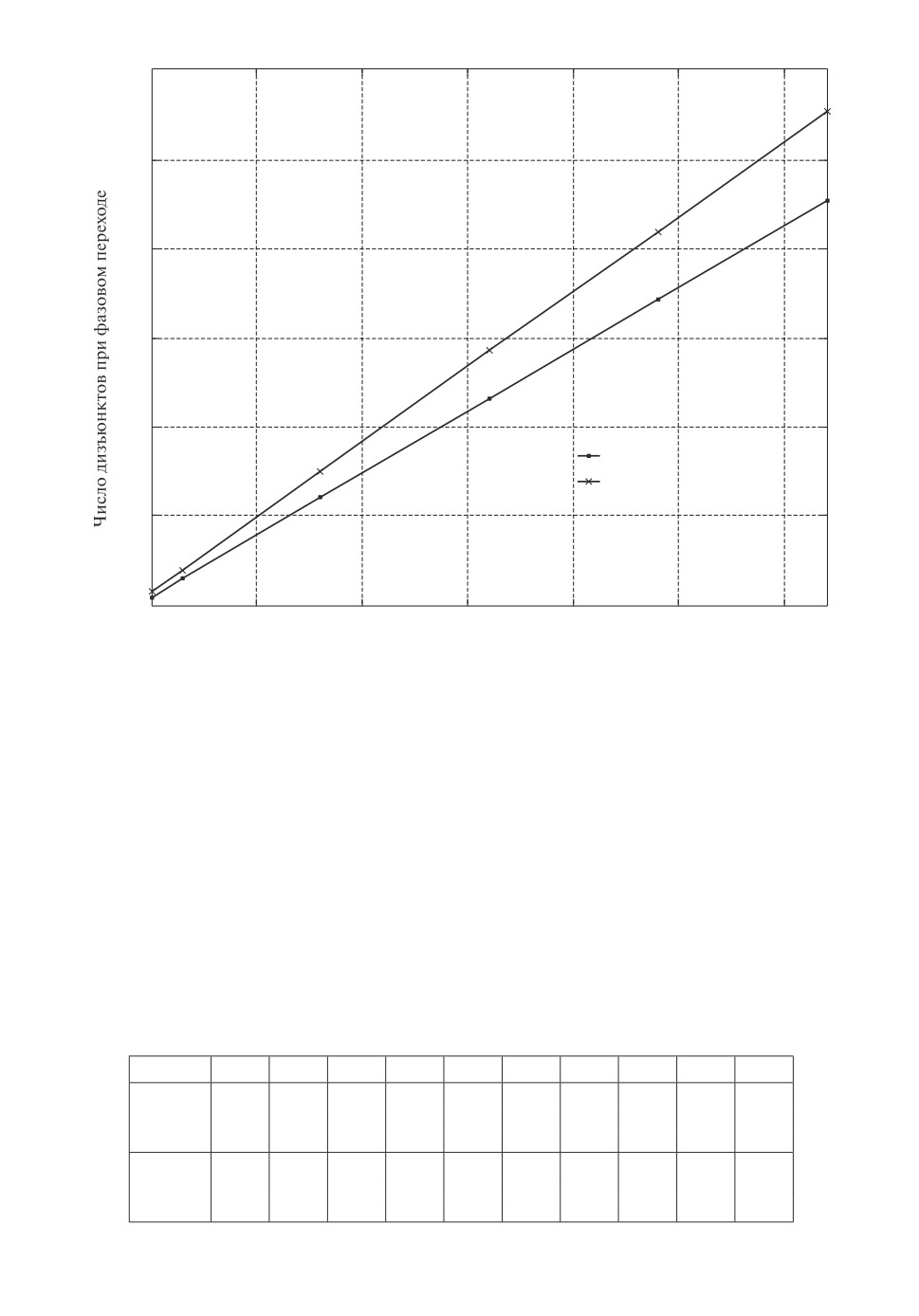
Обе эти зависимости представлены на рис. 4. Полученные зависимости

позволяют предположить, что величины 4,23 и 3,49, возможно, являются

169

300

250

200

150

100

GEN 3

GEN 2

Число переменных

Рис. 4. Иллюстрация эмпирической линейной зависимости M₂ и M₃ от N.

асимптотами (при N → ∞) для отношения числа дизъюнктов к числу пе-

ременных в точке «фазового перехода» для БПД- и ВНЛ-генераторов соот-

ветственно.

В табл. 2 представлены экспериментальные данные для зависимостей

M₂(N) = α₂(N)N + 7,18 и M₃(N) = α₃(N)N + 4,46 при числах переменных,

превышающих 64. Приведенные результаты позволяют оценить стабильность

коэффициентов пропорциональности α₂(N) и α₃(N) при увеличении числа

булевых переменных. Каждое из представленных значений получено на ос-

нове анализа 200 формул.

Значение коэффициента пропорциональности с вероятностью 0,99 нахо-

дится в доверительном интервале (α_i(N) - δ_i(N), α_i(N) + Δ_i(N)), i = 2, 3.

Таблица 2. Зависимость коэффициентов пропорциональности от N

112

128

160

192

224

256

288

320

α₂(N)

4,23

4,20

4,24

4,22

4,23

4,21

4,23

δ₂(N)

0,04

0,05

0,04

0,03

0,04

0,02

Δ₂(N)

0,09

0,05

0,03

0,06

0,05

0,04

0,03

α₃(N)

3,52

3,49

3,51

3,50

3,51

3,50

3,49

δ₃(N)

0,03

0,02

0,01

0,02

0,01

Δ₃(N)

0,04

0,02

0,01

0,02

0,01

0,02

0,01

170

Невыполнимые формулы полученные ВНЛ-генератором, в среднем су-

щественно сложнее для анализа, чем невыполнимые формулы, полученные

БПД-генератором. Анализ формул от 256 переменных, построенных ВНЛ-

генератором, длится в среднем в 20 раз дольше, чем для формул, построен-

ных БПД-генератором.

4. Заключение

Предложен и исследован ВНЛ-генератор (выравнивающий нагрузку на

литералы) случайных формул 3-КНФ. Этот генератор продуцирует форму-

лы, являющиеся невыполнимыми, при меньшем числе дизъюнктов, чем у ши-

роко используемого в настоящее время БПД-генератора (формул без простых

дизъюнктов), для которого асимптотическое значение R в точке «фазового

перехода» оценивается как 4,23.

Для предложенного в настоящей работе ВНЛ-генератора асимптотическое

значение R (при N → ∞) в точке «фазового перехода» оценивается как 3,49.

Характерная для НВЛ,- БПД- и ВНЛ-генераторов линейная зависимость

числа дизъюнктов от числа переменных в точке «фазового перехода» удоб-

на при построении тестовых примеров для испытания алгоритмов решения

задачи выполнимости (SAT-problem). По заданному числу переменных легко

вычисляется количество дизъюнктов, при котором больше половины из гене-

рируемых случайных 3-КНФ формул будут выполнимыми, а при добавлении

по одному дизъюнкту в каждую формулу больше половины формул станут

невыполнимыми.

Проведенные исследования свидетельствуют в пользу выдвинутой в ли-

тературе [5-8] гипотезы о том, что анализ невыполнимых формул, имеющих

меньшее число дизъюнктов, как правило, сложнее, чем анализ формул, со-

держащих больше дизъюнктов. Представляет интерес разработка способов

построения формул, невыполнимых при еще меньшем числе дизъюнктов.

Представляет также интерес поиск зависимости количества дизъюнктов,

минимально необходимого для невыполнимости нетривиальной 3-КНФ фор-

мулы, от числа булевых переменных.

СПИСОК ЛИТЕРАТУРЫ

1. Biere A., Heule M., Maaren H., Walsh T. Handbook of Satisfiability // IOS Press,

2009. P. 1-966.

2. Cook S., Mitchell D. Finding hard instances of the satisfiability problem: a survey //

DIMACS Ser. Discret Math. Theoret. Comput. Sci., Amer. Math. Sos. 1997. V. 35.

P. 1-17.

3. Beame P., Karp R., Pitassi T., Saks M. On the Complexity of Unsatisfiability Proofs

for Random k-CNF Formulas // 30thSTOC, Dallas, TX. May 1998. P. 561-571.

4. Goldberg A. On the complexity of the satisfiability problem // Appl. Math. Comput.

J. Amer. Math. Sos. 1997. V. 35. No. 1. P. 1-17.

5. Mitchell D., Selman B., Levesque H. Hard and easy distribution of SAT problem //

Proc. Tenth National Conf. Artific. Intelligence (AAAI-92), San Jose, CA. 1997.

P. 459-465.

171