Автоматика и телемеханика, № 10, 2020
Стохастические системы
© 2020 г. В.М. АЗАНОВ, канд. физ.-мат. наук (azanov59@gmail.com),
А.Н. ТАРАСОВ (tarrapid@gmail.com)
(Московский авиационный институт)
ДВУСТОРОННЯЯ ОЦЕНКА ФУНКЦИИ БЕЛЛМАНА
В ЗАДАЧЕ ОПТИМАЛЬНОГО УДЕРЖАНИЯ
ТРАЕКТОРИЙ ДИСКРЕТНОЙ СТОХАСТИЧЕСКОЙ СИСТЕМЫ
В ТРУБКЕ ПО КРИТЕРИЮ ВЕРОЯТНОСТИ1
Исследуется задача оптимального управления дискретной стохастиче-
ской системой с критерием вероятности удержания траекторий системы
на заранее заданных множествах. С помощью метода динамического про-
граммирования и поверхностей уровня 1 и 0 функции Беллмана нахо-
дятся двусторонние оценки функции правой части соотношения динами-
ческого программирования, двусторонние оценки функции Беллмана и
функции оптимального значения вероятностного критерия. С помощью
этих результатов выводятся выражения для приближенного определения
оптимального управления. В качестве примера рассматривается задача
удержания перевернутого маятника в окрестности неустойчивого поло-
жения равновесия.
Ключевые слова: дискретные системы, стохастическое оптимальное
управление, вероятностный критерий, метод динамического программи-
рования, функция Беллмана, перевернутый маятник.
DOI: 10.31857/S0005231020100037
1. Введение
Задачи оптимального управления дискретными стохастическими систе-
мами с вероятностным критерием представляют интерес в аэрокосмических
[1-3], экономических [4-6] и робототехнических [7-9] приложениях. К настоя-
щему моменту качественная теория этих задач проработана в плоскости во-
просов существования оптимальных стратегий [1, 10]. В этих работах для
случая, когда критерий представляет собой вероятность попадания терми-
нального состояния на некоторое множество, получены достаточные условия
оптимальности в форме метода динамического программирования. В [11] по-
добные условия получены для случая, когда критерий задан в виде вероят-
ности пребывания траекторий стохастической системы в трубке. В [11] также
показано, что указанные случаи являются взаимно приводимыми.
1 Работа, за исключением раздела 4, выполнена при поддержке Российского научного
фонда (проект № 16-11-00062). Результаты раздела 4 получены при поддержке Российского
фонда фундаментальных исследований (проект № 18-08-00595).
93
Менее проработанной является методологическая и алгоритмическая сто-
рона вопроса. Метод динамического программирования [1, 10] вычислительно
связан с “проклятьем размерности”, а в случае его аналитического примене-
ния даже для относительно “простых” малоразмерных задач известны резуль-
таты в основном для одношаговых [12, 13] и двухшаговых постановок [2, 5, 14].
Впоследствии данное направление получило развитие в [15, 16], где были най-
дены двусторонние границы функции Беллмана, на основе которых был пред-
ложен алгоритм поиска субоптимального управления. В [7-9] для широкого
класса систем, точностных функционалов и случайных возмущений предло-
жен численный метод поиска оптимального управления в классе полиномов.
Данный результат не связан с методом динамического программирования и
основан на сведении исходной задачи к задаче стохастического программиро-
вания большой размерности. В [17] этот метод был применен для решения за-
дачи оптимального управления полиномиальной дискретной стохастической
системой с критерием вероятности пребывания вектора состояния на задан-
ных множествах, имеющих выпуклую структуру, в каждый момент времени.
В настоящей статье исследуется задача оптимального управления дис-
кретной стохастической системой с критерием вероятности пребывания ее
траекторий в трубке. С помощью метода динамического программирования
находятся соотношения для поверхностей уровня 1 и 0 функции Беллма-
на, двусторонние границы функции правой части уравнения динамическо-
го программирования, двусторонние границы функции Беллмана и функции
оптимального значения вероятностного критерия. С помощью нижней гра-
ницы функции Беллмана находятся выражения для поиска субоптимального
управления. Предлагается оценка точности субоптимального управления, ис-
следуются его свойства. В качестве примера рассматривается задача управ-
ления простейшей маятниковой системой.
2. Постановка задачи
Рассмотрим стохастическую управляемую систему с дискретным време-
нем
{
xk+1 = fk (xk,uk,ξk) ,
(1)
k = 0,N,
x0 = X,
где xk ∈ Rn - вектор состояния, uk ∈ Uk ⊂ Rm - вектор управления, Uk - мно-
жество ограничений на управление, ξk - вектор случайных возмущений с зна-
чениями на Rs и известным распределением Pk, fk : Rn × Rm × Rs → Rn -
функция перехода (функция системы), N ∈ {0} ∪ N - горизонт управления.
В отношении системы (1) введем предположения:
1) известна полная информация о векторе состояния xk (данный факт позво-
ляет строить управление в классе функций uk = γk (xk), где γk (·) - некото-
рая измеримая функция. В данном случае говорят, что “управление ищет-
ся в классе полной обратной связи по состоянию”;
2) начальное состояние x0 = X является в общем случае случайным вектором
с значениями в Rn и с известным распределением PX ;
94
3) функция системы fk (xk, uk, ξk) непрерывна для всех k;
4) вектор управления uk формируется следующим образом: uk = γk (xk), где
γk : Rn → Rm - измеримая функция с ограниченными значениями uk ∈ Uk,
причем Uk - компактное множество;
5) вектор состояния xk+1 формируется следующим образом: на шаге k реа-
лизуется вектор xk, далее формируется вектор управления uk = γk (xk) и
в последнюю очередь реализуется случайное возмущение ξk;
6) управлением называется набор функций u (·) = (γ0 (·) , . . . , γN (·)) ∈ U,
классом допустимых управлений называется множество U = U0 × . . . × UN ,
где Uk - множество борелевских функций γk (·) с ограниченными на Uk
значениями;
7) случайный вектор ξk является непрерывным с значениями в Rs и извест-
ным распределением Pk, причем компоненты вектора ζ = (X, ξ0, . . . , ξN )
независимы.
Заметим, что система (1) является марковской, т.е. ее поведение в будущем
не зависит от прошлого и полностью определяется текущим состоянием.
На траекториях системы (1) определим функционал вероятности
(
)
⋂
Pϕ (u(·)) = P
{xk+1 ∈ Fk+1}
,
k=0
множества Fk имеют вид
{
Fk = {x ∈ Rn : Φk (x) ≤ ϕ} , k = 1,N + 1,
F0 = Rn,
где ϕ ∈ R
известный скаляр, Φk : Rn → R
непрерывные функции,
k = 1,...,N + 1, причем ΦN+1 (x) ограничена снизу.
Рассматривается задача
(2)
Pϕ (u(·)) → max ,
u(·)∈U
где U = U0 × . . . × UN .
Сформулируем достаточные условия оптимальности для задачи (2), дока-
занные в [11], имеющие форму метода динамического программирования.
3. Условия оптимальности в форме уравнения Беллмана
Определим функцию Беллмана Bk : Rn → [0, 1] в задаче (2) как
(
(
(
Bk (x) =
sup
P max Φi+1
xi+1
xk,γk (·) ,...
γk(·)∈Uk,...,γN (·)∈UN
i=k,N
)
))
...,γi (·),ξk,...,ξi
≤ϕxk = x
Принимая во внимание сделанные в разделе 2 предположения, cформулируем
теорему об уравнении Беллмана для задачи (2) в пространстве состояний
размерности n.
95
Теорема 1
[11]. Пусть выполнены условия:
1) функции fk (xk, uk, ξk) непрерывны для всех k = 0, N;
2) функции Φk (xk) непрерывны для всех k = 1, N + 1;
3) функция ΦN+1 (xN+1) ограничена снизу;
4) случайные векторы X, ξ0, . . . , ξN независимы в совокупности;
5) множества U0, . . . , UN компактны.
Тогда оптимальная стратегия в задаче (2) существует в классе изме-
римых функций u∗ (·) ∈ U и определяется в результате решения следующих
задач:
[
]
(3)
u∗k = arg max Mk IF
(xk) Bk+1 (fk (xk,uk,ξk))xk ,
k
uk∈Uk
[
]
(4)
Bk (x) = max Mk IFk (xk)Bk+1 (fk (xk,uk,ξk))xk = x
,
k = 0,N,
uk∈Uk
(5)
BN+1 (x) = IFN+1
(x) .
В формулах (3), (4) Mk [·] означает оператор математического ожидания
по распределению Pk. Отличием уравнений (3)-(5) от уравнения Беллмана
для задачи с вероятностным терминальным критерием является наличие в
правой части сомножителя в виде индикаторной функции IFk (xk) множе-
ства Fk.
Отметим, что поиск оптимальной стратегии в соответствии с методом ди-
намического программирования (3)-(5) даже для относительно простых при-
меров, например для задачи оптимальной импульсной коррекции траектории
движения искусственного спутника Земли [18], затруднен. Причем трудности
вычисления функции Беллмана распространяются как на численный, так и
на аналитический пути решения задач. Как правило, удается найти управле-
ние, оптимальное лишь на последнем k = N шаге по времени [2, 12, 13], и в
более редких случаях так называемое двухшаговое управление k = N - 1, N
[4, 5, 14]. В [15, 16] для задачи оптимального управления дискретной системой
с вероятностным терминальным критерием общего вида с помощью поверхно-
стей уровня 1 и 0 функции Беллмана найдены двусторонние оценки функции
правой части уравнения метода динамического программирования, функции
Беллмана и функции оптимального значения вероятностного критерия. На
этом фундаменте предложен алгоритм приближенного поиска оптимально-
го управления, который при определенных условиях дает точное решение.
В следующем разделе аналогичные результаты распространяются на настоя-
щую задачу (2).
4. Двусторонние оценки функции Беллмана
Введем в рассмотрение поверхности уровней 1 и 0 функции Беллмана
Ik = {x ∈ Rn : Bk (x) = 1} , Ok = {x ∈ Rn : Bk (x) = 0}
и множество Bk = Rn \ {Ik ∪ Ok}. Для удобства введем обозначение Fk =
= Rn \ Fk. Нетрудно видеть, что из определения введенных множеств вы-
96
текает, что
Bk (x) = 1,
x∈Ik,
Ik ∪ Bk ∪ Ok = Rn,
Bk (x) ∈ (0,1) ,
x∈Bk,
Bk (x) = 0,
x∈Ok.
Теорема 2. Справедливы утверждения:
1. Множества Ik, k = 0, N удовлетворяют рекуррентным соотношени-
ям в обратном времени
{
}
Ik = Fk ∩ x ∈ Rn :
∃u ∈ Uk : Pk (fk (x,u,ξk) ∈ Ik+1) = 1 ,
k = 0,N,
IN+1 = FN+1;
2. Множества Ok, k = 0, N удовлетворяют рекуррентным соотношени-
ям в обратном времени
{
}
Ok = Fk ∪ x ∈ Rn :
∀u ∈ Uk : Pk (fk (x,u,ξk) ∈ Ok+1) = 1 ,
k = 0,N,
ON+1 = FN+1;
3. Для xk ∈ Ik оптимальным управлением на шаге k является любой эле-
мент из множества UIk (xk)
{
}
(6)
UIk (xk) = u ∈ Uk : Pk (fk (xk,u,ξk) ∈ Ik+1) = 1 ;
4. Для xk ∈ Ok оптимальным управлением на шаге k является любой
элемент из множества Uk;
5. Уравнение Беллмана в области x ∈ Bk допускает представление
{
(7) Bk (x) = max Pk (fk (x, uk, ξk) ∈ Ik+1) +
uk∈Uk
[
]}
+ Pk (fk (x,uk,ξk) ∈ Bk+1)Mk Bk+1 (fk (x,uk,ξk))
fk (x,uk,ξk) ∈ Bk+1
;
6. Для x ∈ Bk и uk ∈ Uk справедлива система неравенств
Mk [Bk+1 (fk (x,uk,ξk))] ≥ Pk (fk (x,uk,ξk) ∈ Ik+1),
(8)
Mk [Bk+1 (fk (x,uk,ξk))] ≤ Pk (fk (x,uk,ξk) ∈ Fk+1),
Mk [Bk+1 (fk (x,uk,ξk))] ≤ 1 - Pk (fk (x,uk,ξk) ∈ Ok+1) ,
причем
(9)
1 - Pk (fk (x,uk,ξk) ∈ Ok+1) ≤ Pk (fk (x,uk,ξk) ∈ Fk+1
);
7. Для x ∈ Bk функция Беллмана удовлетворяет двустороннему неравен-
ству
(10)
Bk (x) ≤ Bk (x) ≤ Bk (x) ≤ Fk
(x) ,
97
где
(11)
Fk (x) = sup Pk (fk (x, uk, ξk) ∈ Fk+1),
uk∈Uk
Bk(x)-нижняя,аBk(x)-верхняяоценкифункцииБеллмана:
Bk (x) = sup Pk (fk (x,uk,ξk) ∈ Ik+1) ,
uk∈Uk
Bk (x) = sup {1 - Pk (fk (x, uk, ξk) ∈ Ok+1)} ,
uk∈Uk
причем BN (x) = BN (x) = BN (x).
Доказательство теоремы 2 вынесено в Приложение.
Отличием правой части соотношений п. 1 теоремы 2 от соотношений для
поверхности уровня 1 функции Беллмана в задаче с терминальным вероят-
ностным критерием [15] является наличие операции пересечения с множе-
ством Fk. Для поверхности уровня 0 функции Беллмана отличие заключа-
ется в наличии операции объединения с множеством Fk. Пп. 3 и 4 устанав-
ливают простейшие (относительно (3)) выражения для определения опти-
мального управления при xk ∈ Ik ∪ Ok, которые с точностью до конструкций
множеств Ik совпадают с аналогичными в задаче с терминальным вероят-
ностным критерием. Пп. 6 и 7 теоремы 2 устанавливают двусторонние оценки
функции правой части уравнения динамического программирования и функ-
ции Беллмана соответственно. При этом выражения для нижних и верхних
границ с точностью до конструкций множеств Ik и Ok совпадают с анало-
гичными в задаче с терминальным критерием [15, 16]. Отличием же являет-
ся наличие дополнительного неравенства (9) и, как следствие, неравенства
Bk (x) ≤ Fk (x), которые усиливают верхние границы функции правой части
уравнения метода динамического программирования и функции Беллмана.
Отметим также, что из теоремы 1 и пп. 1 и 2 теоремы 2 следует важное
геометрическое свойство множеств Ik, Bk и Fk, сформулированное в виде
следствия.
Следствие. Для всех k = 0,N выполнено включение Ik ∪ Bk ⊆ Fk.
В [15, 16, 18] предложена идея поиска управления, которое максимизирует
нижнюю границу функции правой части уравнения динамического програм-
мирования. В [18] получены условия, при которых такое управление является
оптимальным, однако данные условия достаточно трудно проверить. В слу-
чае, когда такие условия не выполняются, ставится вопрос о том, насколько
“хороша” предлагаемая стратегия и какое значение критерия она обеспечи-
вает. В следующем разделе разъясняются некоторые из этих вопросов.
5. Субоптимальная стратегия и оценка точности
(
)
Рассмотрим стратегию u (·) = γ
(·) , . . . , γ
(·)
, где uk = γ
(xk), которая
0
N
k
на каждом шаге k максимизирует нижнюю оценку функции правой части
98
уравнения динамического программирования
(12)
uk = γk (xk) = arg max Pk (fk (xk,u,ξk) ∈ Ik+1),
k = 0,N.
u∈Uk
Ввиду громоздкости выкладок и отсутствия общности опустим важнейшие
вопросы существования такой стратегии и далее будем предполагать, что она
существует в классе измеримых функций. Отметим, что необходимым усло-
вием существования, дополняющим условия 1-5 теоремы 1, является непу-
стота множеств Ik, k = 0, N . Исследования вопросов существования решения
задач стохастического программирования с вероятностным критерием мож-
но найти в монографии [19]. Получение таких условий является предметом
дальнейших исследований.
Заметим, что из теоремы 1 и пп. 3 и 4 теоремы 2 следует, что такая стра-
тегия является оптимальной при xk ∈ Ik ∪ Ok, k = 0, N и оптимальной для
любых xk ∈ Rn при k = N. В случае xk ∈ Bk, k = 0, N , как было сказано ра-
нее, эта стратегия максимизирует нижнюю границу функции правой части
уравнения динамического программирования. В настоящем разделе исследу-
ются вопросы нижней границы значений вероятностного критерия на субоп-
тимальной стратегии Pϕ (u (·)).
Теорема 3. Пусть стратегия u(·), определяющаяся в результате ре-
шений задач (12), существует в классе U. Тогда справедливы утверждения:
1. Справедливо представление
Pϕ (u(·)) = F (ϕ,N) +
(
) (
)
∑
⋃
⋂
{
}
⋃
+ P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
+
(13)
l=1
k=0
k=0
k=0
(
) (
)
⋃
⋂
{
}
⋃
+P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
,
k=0
k=0
k=0
где xk - вектор состояния системы (1), замкнутой управлением (12),
{
xk+1 = fk (xk,uk,ξk) ,
k = 0,N;
x0 = X,
2. Справедливо представление
F (ϕ, N) = F (ϕ, N) +
(
) (
)
∑
⋃
⋂
⋃
{
}
+ P
{x∗k ∈ Ik} P
x∗k+1 ∈ Ik+1
{x∗k ∈ Ik}
+
(14)
l=1
k=0
k=0
k=0
(
) (
)
⋃
⋂
⋃
{
}
+P
{x∗k ∈ Ik} P
x∗k+1 ∈ Fk+1
{x∗k ∈ Ik}
,
k=0
k=0
k=0
99
где x∗k - вектор состояния системы (1), замкнутой оптимальным управле-
нием,
{
x∗k+1 = fk (x∗k,u∗k,ξk) ,
k = 0,N;
x∗0 = X,
3. Выполнена система неравенств
(15)
F (ϕ, N) ≤ Pϕ (u (·)) ≤ F (ϕ, N) ≤ F (ϕ, N) ≤ MX [F0
(X)] ,
где F0 : Rn → [0, 1] определяется в соответствии с (11) и
F (ϕ, N) = sup Pϕ(u (·)), F (ϕ, N) = MX [B0 (X)] , F (ϕ, N) = MX [B0 (X)].
u(·)∈U
Выше MX [·] - оператор математического ожидания по распределению PX .
Доказательство теоремы 3 вынесено в Приложение.
Из теоремы 3 видно, для субоптимальной стратегии u (·) справедлива оцен-
ка точности
(16)
F (ϕ, N) - Pϕ
(u(·)) ≤ Δ (ϕ,N) ,
где
Δ (ϕ, N) = F (ϕ, N) - F (ϕ, N) -
(
) (
)
∑
⋃
⋂
⋃
{
}
− P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
-
(17)
l=1
k=0
k=0
k=0
(
) (
)
⋃
⋂
{
}
⋃
−P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
,
k=0
k=0
k=0
причем Δ (ϕ, N) ∈ [0, 1]. Следует отметить вычислительную простоту полу-
чения оценки точности (17) субоптимальной стратегии. А именно, если най-
дена стратегия u (·) и найдены нижняя F (ϕ, N) и верхняя F (ϕ, N) грани-
цы функции оптимальных значений вероятностного критерия, то достаточно
воспользоваться методом Монте-Карло для оценки неизвестных вероятностей
в правой части (17).
Применим полученные результаты в задаче оптимального управления пе-
ревернутым маятником.
6. Пример
Рассмотрим простейшую модель управления математическим маятником
в окрестности неустойчивого положения равновесия. Динамика системы опи-
сывается разностным уравнением
θk+1 = θk + Δtk
θk,
θk+1 =θk + (-γΔtkθk + uk)ξk,
(18)
k = 0,N,
θ0 = Θ,
θ0 = Θ,
100
где θk - угол отклонения маятника,θk - угловая скорость отклонения маят-
ника, uk - управляющее воздействие, ξk - непрерывная случайная величи-
на, распределение которой конкретизируется ниже, Δtk - параметр дискре-
(изац)и непрерывной системы, γ - детерминированный параметр системы,
Θ,Θ
- начальные условия.
Пусть на траекториях системы (18) задан функционал вероятности.
(
)
{
}
(19)
Pϕ (u(·)) = P max max ω |θk+1|, ω
θk+1
≤ϕ
,
k=0,N
где ω, ω, ϕ > 0 - известные параметры. Ставится задача (2). Ее физиче-
ский смысл в том, чтобы найти управление, которое удерживает маятник
в окрестности не[стойчивого ]ол[жения равно]есия, являющейся прямо-
угольником Fk =
-ϕω-1, ϕω-1
×
-ϕ ˙ω-1,ϕ ω-1
в пространстве состояний,
с максимальной вероятностью. Введем обозначения
(
)
(
)
θ
k
(1 Δtk)
0
0
xk =
,
Ak =
,
Aξk =
,
θk
0
1
-γΔtk
0
)
(0
(ω 0)
Bk =
,
Ω=
1
0
ω
и запишем систему (18) и функционал вероятности (19) в векторном виде
{
(
)
xk+1 = Akxk + Aξxk + Bkuk ξk,
k
k = 0,N,
x0 = X,
(
)
Pϕ (u(·)) = P max
∥Ωxk+1∥∞ ≤ ϕ
k=0,N
Во введенных в статье обозначениях имеем n = 2, m = 1, s = 1, fk(xk, uk, ξk) =(
)
{
}
=Akxk + Aξxk + Bkuk ξk, Uk = R, Fk =
x ∈ R2 : ∥Ωx∥∞ ≤ ϕ
, Φk (x) =
k
= ∥Ωx∥∞, где ∥x∥∞ = max
xi
- Гельдерова норма вектора. Заметим так-
i=1,n
же, что несмотря на то, что Uk не является компактом (что является одним
из условий теоремы 1), теорема 1 не будет использована непосредственно в
данном примере и, более того, условия теоремы 1 являются достаточными.
Последнее означает, что если все-таки удается найти стратегию u∗ (·) исполь-
зуя соотношения динамического программирования (3)-(5), то она является
оптимальной [1].
Воспользуемся теоремой 2 и найдем поверхности уровней 1 и 0 функции
Беллмана и оптимальное управление при xk ∈ Ik.
Пусть
1
∏
(1)
(0)
∑
e1 =
,
e2 =
,
βk = AT
j
e1 =
.
0
1
Δtj
j=k
j=k
101
Лемма 1. Справедливы утверждения:
1. Поверхность уровня 1 функции Беллмана имеет вид
{
{
}
}
Ik = x ∈ R2 : max
∥Ωx∥∞, max ω
βTl
x
≤ϕ
,
k = 0,N;
l=k,N
2. Поверхность уровня 0 функции Беллмана имеет вид
{
}
Ok = Fk = x ∈ R2 :
∥Ωx∥∞ > ϕ , k = 0, N ;
3. Оптимальное управление при xk ∈ Ik единственно и имеет вид
u∗k = -BTkAξkxk = γΔtkθk, xk ∈ Ik, k = 0,N.
Доказательство леммы 1 вынесено в Приложение.
Из леммы 1 видно, что поверхность уровня 0 не меняется со временем,
в то время как поверхность уровня 1 “уменьшается” с уменьшением k, т.е.
I0 ⊂ I1 ⊂ ... ⊂ IN. Следует также отметить, что в данном примере выполнено
Ik ∪ Bk = Fk.
Выпишем выражения для нижней и верхней границ функции Беллмана
при x ∈ Bk, k = 0, N - 1
(
{
(
(
)
)
(20) Bk (x) = maxP max
ω
eT
2
Akx + Aξkx + Bku ξk
,
u
}
)
(
(
)
)
max
ω
βTl+1
Akx + Aξkx + Bku ξk
≤ϕ ,
l=k,N
(
(
(
)
)
)
(21)
P ˙ω
eT
Akx + Aξkx + Bku ξk
≤ϕ
Bk (x) = Fk (x) = max
2
u
Поскольку поиск решений задач (20) и (21) при любом распределении слу-
чайного возмущения ξk затруднен, рассмотрим случай гауссовского распре-
деления.
(
)
Лемма 2. Пусть ξk ∼ N mξ,σ2
, где mξ > 0. Тогда справедливы
ξ
утверждения:
1. Решения задач стохастического программирования (20) при xk ∈ Bk,
k = 0,N - 1 имеют вид
v
-1
u
)
u
2σ2ξ
( |ck (xk)| + rk (xk)
(22) uk = -2ck (xk)1 +
√1 +
ln
-BTkAξkxk,
m2ξ
|ck (xk)| - rk (xk)
где функции ϕk : R2 → R, ϕk : R2 → R, ck : R2 → R, ck : R2 → R имеют вид
{
}
-ϕ ˙ω-1 - eT2Akx
-ϕω-1 - βTl+1Ak
x
, max
,
ϕk(x)=max
mξ
l=k,N
mξeT2βl+1
102
{
}
ϕω-1 -eT2Akx
ϕω-1 - βTl+1Akx
ϕ
k
(x) = min
, min
,
mξ
l=k,N
mξeT2βl+1
(
)
)
1
1(
ck (x) = -
ϕk (x) + ϕk (x)
,
rk (x) =
;
ϕk (x) - ϕk (x)
2
2
2. Нижняя граница функции Беллмана при x ∈ Bk имеет вид
rk (x) + |ck (x)|
mξ
(
)
-
-
Bk(x)=Φ
σξ
σξm-1ξ
eT
Aξkx + Bkuk
2
(23)
-rk (x) + |ck (x)|
mξ
-Φ
(
)
-
;
σξ
σξm-1ξ
eT
Aξkx + Bkuk
2
3. Решения задач стохастического программирования (21) при xk ∈ Bk,
k = 0,N - 1 имеют вид
-BTkAξkxk,
eT2Akxk≤ ϕ ω-1,
v
u
(
)-1
(24) uk =
2eT2Akxk
u
2σ2ξ
eT2Akxk+ ϕ ω-1
1+
-BT
−
√1 +
ln
Aξkxk,
k
mξ
m2ξ
|eT2Akxk| - ϕ ω-1
eT2Akxk> ϕ ω-1;
4. Верхняя граница функции Беллмана при x ∈ Bk имеет вид
(25) Bk(x) =
1,
eT2Akx≤ ϕ ω-1,
ϕω-1 +
eT2Akx
mξ
-ϕ ˙ω-1 +
eT2Akx
mξ
Φ
(
)
-
-Φ
(
)
-
,
=
σξ
σξ
σξ
eT
Aξkx + Bkuk
σξ
eT
Aξkx + Bkuk
2
2
eT2Akx>ϕ ω-1.
Доказательство леммы 2 вынесено в Приложение.
В лемме 2 введено обозначение Φ (x) - функция Лапласса
∫x
Φ (x) = et2/2dt.
-∞
103
Шаг k = 0
Шаг k = 1
15
15
10
10
5
5
0
0
-5
-5
-10
-10
-15
-15
-1,5
-1,0
-0,5
0
0,5
1,0
1,5
-1,5
-1,0
-0,5
0
0,5
1,0
1,5
x1
x1
Шаг k = 11
Шаг k = 12
15
15
10
10
5
5
0
0
-5
-5
-10
-10
-15
-15
-1,5
-1,0
-0,5
0
0,5
1,0
1,5
-1,5
-1,0
-0,5
0
0,5
1,0
1,5
x1
x1
Рис. 1. Множества Ok (черная область), Bk (темно-серая область), Ik (светло-
серая область), k = 0, 1, 11, 12.
Итого получаем следующее выражение субоптимального управления для
всех k = 0, N .
-BTkAξkxk,
xk ∈ Ik,
(
√
−1
2σ2ξ
−2ck (xk)
1+
1+
ln
-BTkAξkxk,
(26) uk =
m2ξ
|ck (xk)| - rk (xk)
xk ∈ Bk,
любое,
xk ∈ Ok,
104
1,0
Нижняя, на шаге k = 0
Верхняя, на шаге k = 0
Нижняя, на шаге k = 1
0,8
Верхняя, на шаге k = 1
Нижняя, на шаге k = 11
0,6
Верхняя, на шаге k = 11
Нижняя, на шаге k = 12
0,4
Верхняя, на шаге k = 12
0,2
0
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
x1
1,0
Нижняя, на шаге k = 0
Верхняя, на шаге k = 0
Нижняя, на шаге k = 1
0,8
Верхняя, на шаге k = 1
Нижняя, на шаге k = 11
0,6
Верхняя, на шаге k = 11
Нижняя, на шаге k = 12
0,4
Верхняя, на шаге k = 12
0,2
0
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
8
10
12
14
16
x2
Рис. 2. Нижняя Bk(x) и верхняя Bk(x) границы функции Беллмана при k =
= 0, 1, 11, 12.
1,0
0,8
0,6
0,4
0,2
0
0,70
0,75
0,80
0,85
0,90
0,95
j
Рис. 3. Значение критериальной функции в зависимости от ϕ.
а замкнутая система принимает вид
Akxk,
xk ∈ Ik,
(
)
xk+1 =
Akxk + Aξxk + Bkuk ξk, xk ∈ Bk ∪ Ok.
k
Отметим интересное свойство найденного управления. При xk ∈ Ik в силу
включения Ik ⊆ Fk (см. следствие к теореме 2) система уже находится в
окрестности неустойчивого положения равновесия Fk. Причем режим управ-
ления, соответствующий первой ветви (26), “зануляет” стохастическое сла-
105
Значения параметров системы
N
tk
ϕ
γ
ω
ω
mξ
dξ
x0
15
0,05
1,1
0,8
1
0,1
0,9
0.1
[0,65, 2,5]
гаемое в системе, и она таким образом становится детерминированной при
xk ∈ Ik.
Проведем численный эксперимент для системы (18), замкнутой управле-
нием (26). Значения параметров системы занесены в таблицу.
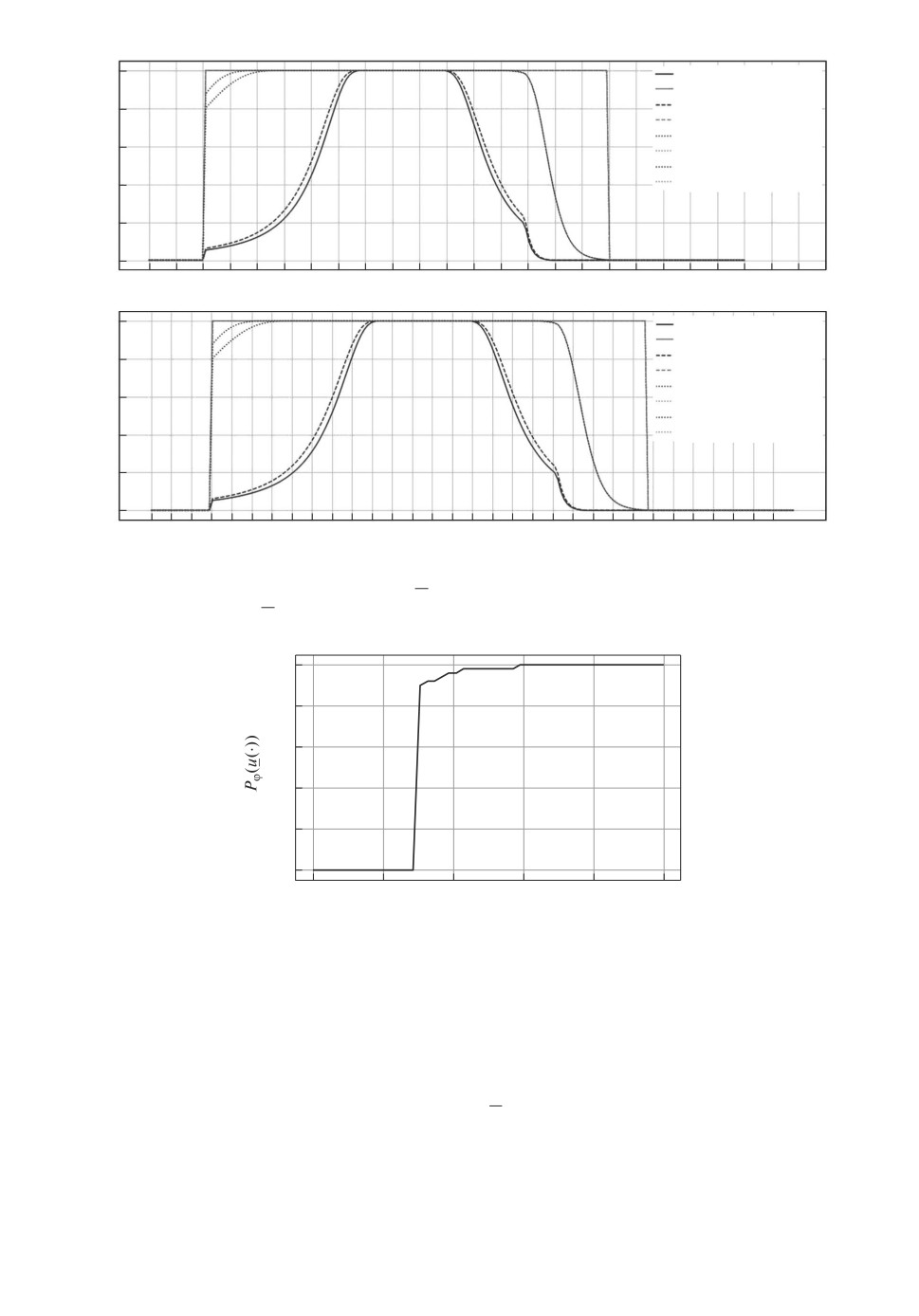
На рис. 1 изображены поверхности уровней 1 и 0 функции Беллмана в про-
странстве состояний на разных шагах дискретного времени. На рис. 2 изоб-
ражены нижняя и верхняя границы функции Беллмана. На рис. 3 приведен
график значений вероятностного критерия при субоптимальном управлении.
Оценка точности (17) субоптимального управления равна 0,059, что демон-
стрирует его близость к оптимальному и обоснованность предлагаемого в
статье подхода.
7. Заключение
В статье рассмотрена задача оптимального управления дискретной сто-
хастической системой с критерием вероятности пребывания вектора состоя-
ния в каждый момент времени на заданных множествах. С помощью по-
верхностей уровня 1 и 0 функции Беллмана получены двусторонние оценки
функции правой части уравнения динамического программирования, двусто-
ронние оценки функции Беллмана и функции оптимального значения веро-
ятностного критерия. Найдены выражения для приближенного поиска оп-
тимального управления. В качестве примера рассмотрена модельная задача
удержания перевернутого маятника в неустойчивом положении равновесия.
Для данной модели субоптимальное управление найдено в явном виде.
ПРИЛОЖЕНИЕ
Доказательство теоремы 2. Из определения множеств Ik и Ok и
соотношений динамического программирования (3)-(5) имеем:
{
}
[
]
(Π.1)
Ik = x ∈ Rn : max Mk
IFk (xk) Bk+1 (fk (xk,uk,ξk))xk = x
=1
,
uk∈Uk
{
}
[
]
(Π.2)
Ok = x ∈ Rn : max Mk
IFk (xk)Bk+1 (fk (xk,uk,ξk))xk = x
=0
uk∈Uk
Рассмотрим некоторый шаг k алгоритма динамического программирования
(3)-(5). С учетом базовых свойств множеств Ik, Bk, Ok выполнено тождество
Bk+1 (x) = IIk (x)Bk+1 (x) + IBk (x) Bk+1 (x) + IOk (x) Bk+1 (x) =
= IIk (x)Bk+1 (x) + IBk (x)Bk+1 (x).
Введем в рассмотрение систему гипотез, образующих полную группу несов-
местных событий,
{fk (xk, uk, ξk) ∈ Ik+1} ,
{fk (xk, uk, ξk) ∈ Ik+1} .
106
Преобразуем выражение (4) с использованием формулы полного математи-
ческого ожидания
[
]
(Π.3)
Bk (x) = max Mk
IFk (xk) Bk+1 (fk (xk,uk,ξk))xk = x
=
uk∈Uk
= max Mk [IFk (x) Bk+1 (fk (x,uk,ξk))] =
uk∈Uk
= max IFk (x)Mk [Bk+1 (fk (x,uk,ξk))] =
uk∈Uk
(
= max IFk (x) P(fk (x,uk,ξk) ∈ Ik+1)×
uk∈Uk
[
]
× Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ik+1 +
)
[
]
+ P(fk (x,uk,ξk) ∈ Ik+1)Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ik+1
С учетом равенства
[
]
Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ik+1
=1
выражение (П.3) принимает вид
(
(Π.4) Bk (x) = max IFk (x) P (fk (x, uk, ξk) ∈ Ik+1) +
uk∈Uk
[
])
+ P(fk(x, uk, ξk) ∈ Ik+1)Mk Bk+1(fk(x, uk, ξk))fk(x,uk,ξk) ∈ Ik+1
=
(
= max IFk(x) P(fk(x,uk,ξk) ∈ Ik+1) + (1 - P(fk(x,uk,ξk) ∈ Ik+1)) ×
uk∈Uk
[
])
× Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Ik+1
Поскольку выполнено
[
]
Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Ik+1
∈ [0, 1) ,
то правая часть (П.4) принимает значение 1 тогда и только тогда, когда
max IFk (x) P (fk (x, uk, ξk) ∈ Ik+1) = 1.
uk∈Uk
Отсюда видно, что (П.1) принимает вид
{
}
[
]
Ik = x ∈ Rn : max Mk
IFk (xk) Bk+1 (fk (xk,uk,ξk))xk = x
=1
=
uk∈Uk
{
}
= x ∈ Rn : max IF
(x) P (fk (x, uk, ξk) ∈ Ik+1) = 1
=
k
uk∈Uk
(Π.5)
{
}
= Fk ∩ x ∈ Rn : max P(fk (x,uk,ξk) ∈ Ik+1) = 1
=
uk∈Uk
{
}
=Fk ∩ x∈Rn :
∃uk ∈ Uk : P(fk (x,uk,ξk) ∈ Ik+1) = 1
107
Из (П.5) получаем, что при xk ∈ Ik оптимальным управлением является лю-
бой элемент из множества
(Π.6)
UIk (xk) = {u ∈ Uk : P(fk (xk,u,ξk) ∈ Ik+1
) = 1}.
Пп. 1, 3 и 5 теоремы 2 доказаны.
Введем в рассмотрение систему гипотез, образующих полную группу
несовместных событий,
{fk (xk,uk,ξk) ∈ Ik+1} ,
{fk (xk,uk,ξk) ∈ Bk+1} ,
{fk (xk,uk,ξk) ∈ Ok+1}.
Преобразуем выражение (4) с использованием формулы полного математи-
ческого ожидания
[
]
(Π.7)
Bk (x) = max Mk
IFk (xk) Bk+1 (fk (xk,uk,ξk))xk = x
=
uk∈Uk
= max Mk [IFk (x) Bk+1 (fk (x,uk,ξk))] =
uk∈Uk
= max IFk (x)Mk [Bk+1 (fk (x,uk,ξk))] =
uk∈Uk
(
= max IFk (x) P(fk (x,uk,ξk) ∈ Ik+1) ×
uk∈Uk
[
]
× Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ik+1 +
[
]
+ P(fk (x,uk,ξk) ∈ Bk+1)Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Bk+1 +
)
[
]
+ P(fk (x,uk,ξk) ∈ Ok+1)Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ok+1
С учетом справедливости равенств
[
]
Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Ik+1
= 1,
[
]
Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Ok+1
=0
выражение (П.1) принимает вид
(
(Π.8) Bk (x) = max IFk (x) P (fk (x, uk, ξk) ∈ Ik+1) +
uk∈Uk
[
])
+ P(fk (x,uk,ξk) ∈ Bk+1)Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Bk+1
Поскольку выполнено
[
]
Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Bk+1
∈ (0, 1) ,
то правая часть выражения (П.8) равна 0, если
max IFk (x) P(fk (x,uk,ξk) ∈ Ik+1) = 0,
uk∈Uk
max IFk (x) P(fk (x,uk,ξk) ∈ Bk+1) = 0
uk∈Uk
108
или, что то же самое,
{
IFk (x)P(fk(x,uk,ξk) ∈ Ik+1) = 0,
∀uk ∈Uk :
IFk (x)(1 - P(fk(x,uk,ξk)∈ Ik+1) - P(fk(x,uk,ξk)∈ Ok+1)) = 0.
Отсюда с учетом (П.2) получаем
{
}
[
]
Ok = x ∈ Rn : max Mk
IFk (xk)Bk+1 (fk (xk,uk,ξk))xk = x
=0
=
uk∈Uk
{
}
= x ∈ Rn : max IF
(x) P (fk (x, uk, ξk) ∈ Ok+1) = 1
=
k
uk∈Uk
(Π.9)
{
}
= Fk ∪ x ∈ Rn : max (x)P(fk (x,uk,ξk) ∈ Ok+1) = 1
=
uk∈Uk
= Fk ∪ {x ∈ Rn :
∀uk ∈ Uk : (x) P(fk (x,uk,ξk) ∈ Ok+1) = 1} .
Из (П.9) видно, что при xk ∈ Ok любое допустимое управление uk ∈ Uk явля-
ется оптимальным.
Пп. 2 и 4 теоремы 2 доказаны.
Рассмотрим уравнение Беллмана в форме (П.8). Пусть x ∈ Bk, тогда
{
Bk (x) = max P(fk (x,uk,ξk) ∈ Ik+1) + P(fk (x,uk,ξk) ∈ Bk+1) ×
uk∈Uk
[
]}
× Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Bk+1
=
{
= max P(fk (x,uk,ξk) ∈ Ik+1) +
uk∈Uk
(
)
+ 1 - P(fk (x,uk,ξk) ∈ Ik+1) - P(fk (x,uk,ξk) ∈ Ok+1)
×
[
]}
(Π.10)
× Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Bk+1
=
{
= max P(fk (x,uk,ξk) ∈ Ik+1)×
uk∈Uk
(
[
])
× 1 - Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Bk+1
+
+ (1 - P (fk (x, uk, ξk) ∈ Ok+1)) ×
[
]}
× Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Bk+1
Воспользуемся известным неравенством
∑
∑
min zi ≤
aizi ≤ max zi, a1,... ,an ≥ 0,
ai = 1.
i=1,n
i=1,n
i=1
i=1
109
Если формально принять, что
[
]
a1 = Mk Bk+1 (fk (x,uk,ξk))fk (x, uk, ξk) ∈ Bk+1 ,
[
]
a2 = 1 - Mk Bk+1 (fk (x,uk,ξk))fk (x,uk,ξk) ∈ Bk+1 ,
z1 = P(fk (x,uk,ξk) ∈ Ik+1), z2 = 1 - P(fk (x,uk,ξk) ∈ Ok+1),
то справедлива двусторонняя оценка для функции правой части уравнения
Беллмана при x ∈ Bk
min
zi ≤ Mk [Bk+1 (fk (x,uk,ξk))] ≤ maxzi.
i=1,2
i=1,2
В силу равенства
P(fk(x, uk, ξk) ∈ Ik+1) + P(fk(x, uk, ξk) ∈ Bk+1) + P(fk(x, uk, ξk) ∈ Ok+1) = 1
для z2 справедливо другое представление
z2 = P(fk (x,uk,ξk) ∈ Ik+1) + P(fk (x,uk,ξk) ∈ Bk+1) .
Cледовательно z2 ≥ z1 и выполнено
z1 ≤ Mk [Bk+1 (fk (x,uk,ξk))] ≤ z2.
Из пп. 1 и 2 теоремы 2 видно, что для всех k = 0, N выполнено Ik ⊆ Fk и
Fk ⊆ Ok, откуда получаем Ik ∪ Bk ⊆ Fk. Следовательно, справедливо нера-
венство
P(fk (x,uk,ξk) ∈ Ik+1) + P(fk (x,uk,ξk) ∈ Bk+1) ≤ P(fk (x,uk,ξk) ∈ Fk+1) ,
и, следовательно,
Mk [Bk+1 (fk (x,uk,ξk))] ≤ P(fk (x,uk,ξk) ∈ Fk+1).
Таким образом, справедлива система неравенств (8). Если взять супремум
по uk ∈ Uk во всех частях неравенств, то получаем (10). Пп. 6 и 7 теоремы 2
доказаны.
Теорема доказана.
Доказательство теоремы 3. Введем систему гипотез, образующих
полную группу несовместных событий:
{
}
{
}
⋂
⋃
{xk ∈ Ik}
,
{xk ∈ Ik}
k=0
k=0
Тогда с учетом формулы полной вероятности справедлива цепочка равенств
(
)
⋂
{
}
Pϕ (u(·)) = P
xk+1 ∈ Fk+1
=
k=0
(
) (
)
⋂
⋂
⋂
{
}
(Π.11)
=P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
+
k=0
k=0
k=0
(
) (
)
⋃
⋂
{
}
⋃
+P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
k=0
k=0
k=0
110
Заметим, что из определения стратегии u (·), а также из свойств множества Ik
(п. 1 теоремы 2) следует, что
(
)
(Π.12)
P
xk+1 ∈ Ik+1
=1
при xk ∈ Ik
,
k = 0,N.
Тогда с учетом включения Ik ⊆ Fk для всех k = 1, N + 1 выполнено равенство
(
)
P
xk+1 ∈ Fk+1
=1
при xk ∈ Ik, k = 0, N ,
и, следовательно,
(
)
⋂
{
}
⋂
P
xk+1 ∈ Fk+1
{xk ∈ Ik}
= 1.
k=0
k=0
С учетом последнего равенства выражение (П.11) принимает вид
(
)
⋂
Pϕ (u(·)) = P
{xk ∈ Ik}
+
k=0
(Π.13)
(
) (
)
⋃
⋂
⋃
{
}
+P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
k=0
k=0
k=0
Введем в рассмотрение систему гипотез, образующих полную группу несов-
местных событий:
{
}
{
}
⋂
⋃
{xk ∈ Ik}
,
{xk ∈ Ik}
k=0
k=0
Воспользуемся формулой полной вероятности для первого слагаемого в пра-
вой части (П.13)
(
)
⋂
P
{xk ∈ Ik}
=
k=0
(
) (
)
⋂
⋂
{
}
⋂
(Π.14)
=P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
+
k=0
k=0
k=0
(
) (
)
⋃
⋂
⋃
{
}
+P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
k=0
k=0
k=0
С учетом (П.12) преобразуем правую часть (П.14), откуда получим
(
) (
)
⋂
⋂
P
{xk ∈ Ik}
=P
{xk ∈ Ik}
+
k=0
k=0
(Π.15)
(
) (
)
⋃
⋂
{
}
⋃
+P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
k=0
k=0
k=0
111
Выполним подстановку (П.15) в (П.13)
(
)
⋂
Pϕ (u(·)) = P
{xk ∈ Ik}
+
k=0
(
) (
)
⋃
⋂
⋃
{
}
(Π.16)
+P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
+
k=0
k=0
k=0
(
) (
)
⋃
⋂
{
}
⋃
+P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
k=0
k=0
k=0
Проводя аналогичные преобразования в отношении первого слагаемого в
(П.16), вводя системы гипотез
{
}
{
}
⋂
⋃
{xk ∈ Ik}
,
{xk ∈ Ik}
,
l = 1,...,N - 2,
k=0
k=0
получаем следующее выражение для значения вероятностного критерия на
стратегии u (·):
Pϕ (u(·)) = P(x1 ∈ I1) +
(
) (
)
∑
⋃
⋂
{
}
⋃
+ P
{xk ∈ Ik} P
xk+1 ∈ Ik+1
{xk ∈ Ik}
+
(Π.17)
l=1
k=0
k=0
k=0
(
) (
)
⋃
⋂
⋃
{
}
+P
{xk ∈ Ik} P
xk+1 ∈ Fk+1
{xk ∈ Ik}
k=0
k=0
k=0
Заметим теперь, что для первого слагаемого (П.17) справедлива цепочка ра-
венств
P(x1 ∈ I1) = P(f0 (X,u0,ξ0) ∈ I1) = B0 (X) ,
откуда следует выражение (14).
Первый пункт теоремы 3 доказан.
Для доказательства второго пункта теоремы 3 достаточно заметить, что
при xk ∈ Ik выполнено u∗k = uk для всех k = 0, N , откуда аналогичным спо-
собом можно получить выражение (14) для функции оптимального значения
вероятностного критерия на траекториях системы {x∗k}N+1k=1, замкнутой опти-
мальным управлением u∗ (·).
Второй пункт теоремы 3 доказан.
Третий пункт теоремы 3 непосредственно следует из п. 7 теоремы 2 и п. 1
теоремы 3.
Теорема доказана.
Доказательство леммы 1. Воспользуемся п. 1 теоремы 2 и запишем
выражение для поверхности уровня 1 функции Беллмана при k = N
{
(
(
(
)
)
)
}
IN = FN ∩ x ∈ R2 : ∃u ∈ UN : P
Ω AN x+ Aξ
x+BNu ξN
≤ϕ =1 .
N
∞
112
С учетом того, что случайная величина ξN имеет неограниченный носитель,
оптимальное управление при k = N и xN-1 ∈ IN единственно и имеет вид
u∗N = -BTNAξNxN-1, а поверхность уровня 1 функции Беллмана имеет вид
{
}
IN = FN ∩ x ∈ R2 : ∥ΩANx∥∞ ≤ ϕ
=
{
}
{
}
= x ∈ R2 : max
∥Ωx∥∞ ,
βTNx
≤ϕ .
Из п. 2 теоремы 2 получаем поверхность уровня 0 функции Беллмана при
k=N
{
}
(
(
(
)
)
)
ON = FN ∪ x ∈ R2 : ∀u ∈ UN : P
Ω AN x + Aξ
x+BNu ξN
>ϕ =1
=
N
∞
{
}
= FN ∪ ∅ = x ∈ R2 : ∥Ωx∥∞ > ϕ .
Аналогично шагу k = N при k = N - 1 получаем поверхность уровня 1
{
IN-1 = FN-1 ∩ x ∈ R2 : ∃u ∈ UN-1 :
(
{ (
(
)
)
P max
Ω AN-1x + Aξ
x+BN-1u ξN-1
,
N-1
∞
}
)
}
(
(
)
)
ΩAN AN-1x + Aξ
x+BN-1u ξN-1
≤ϕ
=1
=
N-1
∞
{
{
}
}
= x ∈ R2 : max
∥Ωx∥∞
,
max
βTjx
≤ϕ
,
j=N-1,N
причем, как и при k = N, если xN-1 ∈ IN-1, то выполнено
u∗N-1 = -BTN-1AξN-1xN-1,
и поверхность уровня 0 функции Беллмана равна
{
ON-1 = FN-1 ∪ x ∈ R2 : ∀u ∈ UN-1 :
}
(
(
(
)
)
)
P
Ω AN-1x + Aξ
x+BN-1u ξN-1
>ϕ =1
=
N-1
∞
{
}
= FN-1 ∪ ∅ = x ∈ R2 : ∥Ωx∥∞ > ϕ .
Продолжая аналогичные размышления по индукции, завершаем доказатель-
ство леммы 1.
Лемма 1 доказана.
113
Доказательство леммы 2. Проведем серию преобразований правой
части выражения (20):
(
{
(
(
)
)
Bk (x) = maxP max
ω
eT
Akx + Aξx+Bkuk ξk
,
2
k
u
}
)
(
(
)
)
max
ω
βTl+1
Akx + Aξx+Bkuk ξk
≤ϕ
=
k
l=k,N
(
{
(
(
)
)
}
⋂
ξ
=P
ω
βT
Akx + A
x+Bkuk ξk
≤ϕ
∩
l+1
k
l=k
)
{
(
(
)
)
}
ξ
∩
ω
eT
Akx + A
x+Bkuk ξk
≤ϕ
=
2
k
(
{
}
⋂
(
)
-ϕω-1 - βTl+1Akx
-ϕω-1 - βTl+1Akx
=P
≤eT
Aξx+Bkuk ξk ≤
∩
2
k
eT2βl+1
eT2βl+1
l=k
)
{
(
)
}
∩ -ϕ ˙ω-1 - eT2Akx ≤ eT
Aξx+Bkuk ξk ≤ϕω-1 -eT2Akx
2
k
(
)
Введем замену переменных для управления ũk = eT2 Aξx + Bkuk и обозна-
k
◦
чение для центрированной случайной величины
ξk = ξk - mξ. Продолжим
преобразования функции правой части выражения (20):
(
{
}
⋂
-ϕω-1 - βTl+1Akx
-ϕω-1 - βTl+1Akx
P
≤ ũkξk ≤
∩
eT2βl+1
eT2βl+1
l=k
)
{
}
∩
-ϕω-1 -eT2Akx≤ ũkξk ≤ϕω-1 -eT2Akx
=
(
{
}
(
)
⋂
-ϕω-1 - βTl+1Akx
◦
-ϕω-1 - βTl+1Akx
=P
≤ ũk
ξk + mξ
≤
∩
eT2βl+1
eT2βl+1
l=k
{
(
)
})
◦
∩
-ϕ ˙ω-1 - eT2Akx ≤ ũk
ξk + mξ
≤ϕω-1 -eT2Akx
=
(
{
}
(
)
⋂
-ϕω-1 - βTl+1Akx
◦
-ϕω-1 - βTl+1Akx
=P
≤ũk m-1ξξk +1
≤
∩
mξeT2βl+1
mξeT2βl+1
l=k
(
)
})
◦
{-ϕ ˙ω-1 - eT2Akx
ϕω-1 -eT2Akx
∩
≤ ũk m-1ξξk + 1
≤
=
mξ
mξ
114
(
{
}
(
)
-ϕ ˙ω-1 -eT2Akx
-ϕω-1 - βTl+1Ak
x
◦
=P
max
, max
≤ũk m-1ξξk +1 ≤
mξ
l=k,N
mξeT2βl+1
{
})
ϕω-1 -eT2Akx
ϕω-1 - βTl+1Ak
x
≤ min
, min
=
mξ
l=k,N
mξeT2βl+1
(
(
)
)
◦
= P ϕk (x) ≤ ũk m-1ξξk + 1
≤ ϕk (x)
=
(
(
)
(x)
◦
ϕk (x) - ϕk
ϕk (x) + ϕk (x)
=P
-
+
≤ ũk m-1ξξk + 1
≤
2
2
)
ϕk (x) - ϕ
(x)
ϕk (x) + ϕk (x)
k
≤
+
=
2
2
(
(
)
)
◦
= P -rk (x) - ck (x) ≤ ũk m-1ξξk + 1
≤ rk (x) - ck (x)
◦
(
)
Для удобства обозначим: ηk = m-1ξξk, ηk ∼ N
0, σ2η
, σ2η = σ2ξm-2ξ. Нетрудно
видеть, что выражение (20) с учетом сделанных преобразований и введенных
функций можно представить в следующем виде
(
)
(Π.18)
Bk (x) = maxP
|ck (x) + ũk (1 + ηk)| ≤ rk (x)
ũk
Решение задачи стохастического программирования в правой части (П.18) с
точностью до параметров ck (x), rk (x) известно [2, 15]. При условии x ∈ Bk
это решение имеет вид
(
√
( |ck (x)| + rk (x)))-1
(Π.19)
ũ∗k = -2ck (x)
1+
1 + 2σ2η ln
,
|ck (x)| - rk (x)
откуда с учетом замены переменных для u окончательно получаем (22).
Пп. 1 и 2 леммы 2 доказаны.
Для доказательства пп. 3 и 4 леммы 2 достаточно заметить, что по анало-
гии со сделанными преобразованиями при доказательстве пп. 1 и 2 настоящей
леммы можно получить следующее выражение для верхней оценки функции
Беллмана (21):
(
(
(
)
)
)
ω
eT
Akx + Aξx+Bkuk ξk
≤ϕ
=
Bk (x) = max P
2
k
uk
(
(
)
)
◦
T
(Π.20)
= maxP
Akm-1x+ũk m-1ξ
ξk + 1
ϕω-1m-1
=
e
2
ξ
≤
ξ
ũk
(
)
= maxP
eT2Akm-1ξx + ũk (1 + ηk)≤ϕω-1m-1ξ
ũk
115
Задача стохастического программирования в правой части (П.20) с точно-
стью до параметров совпадает с задачей стохастического программирования
в правой части (П.18), откуда по аналогии с доказательствами пп. 1 и 2 лем-
мы 2 получаем (24) и (25).
Лемма 2 доказана.
СПИСОК ЛИТЕРАТУРЫ
1.
Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления лета-
тельными аппаратами. М.: Машиностроение, 1987.
2.
Кан Ю.С. Оптимизация управления по квантильному критерию // АиТ. 2001.
№ 5. С. 77-88.
Kan Yu.S. Control Optimization by the Quantile Criterion // Autom. Remote Con-
trol. 2001. V. 62. Nо. 5. P. 746-757.
3.
Охоцимский Д.Е., Рясин В.А., Ченцов Н.Н. Оптимальная стратегия при кор-
ректировании // Докл. АН СССР. 1967. Т. 175. № 1. С. 47-50.
4.
Григорьев П.В., Кан Ю.С. Оптимальное управление по квантильному критерию
портфелем ценных бумаг // АиТ. 2004. № 2. С. 179-197.
Grigor’ev P.V., Kan Yu.S. Optimal Control of the Investment Portfolio with Respect
to the Quantile Criterion // Autom. Remote Control. 2004. V. 65. Nо. 2. P. 319-336.
5.
Бунто Т.В., Кан Ю.С. Оптимальное управление по квантильному критерию
портфелем ценных бумаг с ненулевой вероятностью разорения // АиТ. 2013.
№ 5. С. 114-136.
Bunto T.V., Kan Yu.S. Quantile Criterion-based control of the Securities Portfolio
with a nonzero ruin Probability // Autom. Remote Control. 2013. V. 74. Nо. 5.
P. 811-828.
6.
Кибзун А.И., Игнатов А.Н. Двухшаговая задача формирования портфеля цен-
ных бумаг из двух рисковых активов по вероятностному критерию // АиТ. 2015.
№ 7. С. 78-100.
Kibzun A.I., Ignatov A.N. The Two-Step Problem of Investment Portfolio Selection
from two Risk Assets via the Probability Criterion // Autom. Remote Control. 2015.
V. 76. No. 7. P. 1201-1220.
7.
Jasour A.M., Aybat N.S., Lagoa C.M. Semidefinite Programming For Chance Con-
strained Optimization Over Semialgebraic Sets // SIAM J. Optim. 2015. Nо. 25 (3).
P. 1411-1440.
8.
Jasour A.M., Lagoa C.M. Convex Chance Constrained Model Predictive Control //
2016. arXiv preprint arXiv:1603.07413.
9.
Jasour A.M., Lagoa C.M. Convex Relaxations of a Probabilistically Robust Control
Design Problem // 52nd IEEE Conf. on Decision and Control. 2013. P. 1892-1897.
10.
Кибзун А.И., Игнатов А.Н. О существовании оптимальных стратегий в задаче
управления стохастической системой с дискретным временем по вероятностному
критерию // АиТ. 2017. № 10. С. 139-154.
Kibzun A.I., Ignatov A.N. On the Existence of Optimal Strategies in the Control
Problem for a Stochastic Discrete Time System with Respect to the Probability
Criterion // Autom. Remote Control. 2017. V. 78. No. 10. P. 1845-1856.
11.
Азанов В.М., Кан Ю.С. Об оптимальном удержании траектории дискретной
стохастической системы в трубке // АиТ. 2019. № 1. С. 38-53.
Azanov V.M., Kan Yu.S. On Optimal Retention of the Trajectory of Discrete
Stochastic System in Tube // Autom. Remote Control. 2019. V. 80. Nо. 1. P. 30-42.
116
12.
Кибзун А.И., Кузнецов Е.А. Оптимальное управление портфелем ценных бу-
маг // АиТ. 2001. № 9. C. 101-113.
Kibzun A.I., Kuznetsov E.A. Optimal Control of the Portfolio // Autom. Remote
Control. 2001. V. 62. Nо. 9. P. 1489-1501.
13.
Кибзун А.И., Кузнецов Е.А. Позиционная стратегия формирования портфеля
ценных бумаг // АиТ. 2003. № 1. C. 151-166.
Kibzun A.I., Kuznetsov E.A. Positional Strategy of Forming the Investment Portfo-
lio // Autom. Remote Control. 2003. V. 64. Nо. 1. P. 138-152.
14.
Азанов В.М., Кан Ю.С. Оптимизация коррекции околокруговой орбиты искус-
ственного спутника Земли по вероятностному критерию // Тр. ИСА РАН. 2015.
№ 2. С. 18-26.
15.
Азанов В.М., Кан Ю.С. Синтез оптимальных стратегий в задачах управле-
ния стохастическими дискретными системами по критерию вероятности // АиТ.
2017. № 6. C. 57-83.
Azanov V.M., Kan Yu.S. Design of Optimal Strategies in the Problems of Discrete
System Control by the Probabilistic Criterion // Autom. Remote Control. 2017.
V. 78. No. 6. P. 1006-1027.
16.
Азанов В.М., Кан Ю.С. Двухсторонняя оценка функции Беллмана в задачах
стохастического оптимального управления дискретными системами по вероят-
ностному критерию качества // АиТ. 2018. № 2. С. 3-18.
Azanov V.M., Kan Yu.S. Bilateral Estimation of the Bellman Function in the Prob-
lems of Optimal Stochastic Control of Discrete Systems by the Probabilistic Perfor-
mance Criterion // Autom. Remote Control. 2018. V. 79. No. 2. P. 203-215.
17.
Jasour A.M., Lagoa C.M. Convex constrained semialgebraic volume optimization:
Application in systems and control, arXiv:1701.08910, 2017.
18.
Азанов В.М., Кан Ю.С. Однопараметрчиеская задача оптимальной коррек-
ции траектории летательного аппарата по критерию вероятности // Изв. РАН.
ТиСУ. 2016. № 2. С. 1-13.
19.
Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероят-
ностными критериями. М.: ФИЗМАТЛИТ, 2009.
Статья представлена к публикации членом редколлегии А.В.Назиным.
Поступила в редакцию 24.12.2019
После доработки 20.05.2020
Принята к публикации 09.07.2020
117