Автоматика и телемеханика, № 11, 2020

(Институт проблем информатики ФИЦ ИУ РАН, Москва;

Московский авиационный институт;

Центр фундаментальной и прикладной математики МГУ)

L₁-ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ МАРКОВСКИХ

СКАЧКООБРАЗНЫХ ПРОЦЕССОВ I: ТОЧНОЕ РЕШЕНИЕ

И ЧИСЛЕННЫЕ СХЕМЫ РЕАЛИЗАЦИИ¹

Первая часть статьи посвящена разработке класса алгоритмов числен-

ного решения задачи фильтрации состояний марковских скачкообразных

процессов по косвенным непрерывным наблюдениям в присутствии ви-

неровских шумов. В качестве критерия оптимальности выступает сред-

няя L₁-норма ошибки оценки. Интенсивность шумов в наблюдениях мо-

жет зависеть от оцениваемого состояния. Алгоритмы численного реше-

ния используют не исходные непрерывные, а дискретизованные по време-

ни наблюдения. Особенностью предлагаемых алгоритмов является учет

вероятности появления нескольких скачков оцениваемого состояния на

интервале дискретизации наблюдений. Основным результатом являют-

ся утверждения о точности приближенного решения задачи фильтрации

в зависимости от числа учитываемых скачков оцениваемого состояния,

размера шага дискретизации по времени и применяемой схемы числен-

ного интегрирования. Они служат теоретической основой последующего

анализа конкретных численных схем реализации решения задачи филь-

трации.

Ключевые слова: марковский скачкообразный процесс, устойчивый алго-

ритм численного решения, локальная и глобальная точность аппрокси-

мации.

DOI: 10.31857/S0005231020110021

1. Введение

Фильтр Вонэма [1] является одной из наиболее распространенных проце-

дур обработки сигналов, используемых в технике, телекоммуникациях, эко-

номике и финансах, биологии, медицине и в других областях [2-5]. Уравне-

ния данного фильтра описывают решение задачи оптимального оценивания

состояний марковского скачкообразного процесса (МСП) по его косвенным

наблюдениям в присутствии аддитивных винеровских шумов. Оценки филь-

трации представляют собой условное распределение состояния МСП относи-

тельно имеющихся наблюдений, обладающее очевидными свойствами поком-

понентной неотрицательности и нормировки. Несмотря на элегантный вид

¹ Работа выполнена при частичной поддержке Российского фонда фундаментальных

исследований, проект № 19-07-00187 А.

уравнений фильтра, его численная реализация сталкивается со значитель-

ными проблемами. Например, явные численные методы решения систем сто-

хастических дифференциальных уравнений, основанные на разложении Ито-

Тейлора [6], примененные к системе уравнений фильтра Вонэма, проявляют

свойства неустойчивости и ¾разваливаются¿: вычисленные с его помощью

аппроксимации перестают удовлетворять условиям неотрицательности и нор-

мировки и со временем достигают произвольно больших по модулю значений.

Далее в статье будем называть устойчивыми алгоритмы численного реше-

ния уравнений фильтра Вонэма, сохраняющие свойства неотрицательности и

нормировки для получаемых оценок, которые также будем называть устой-

чивыми. Для оценок - приближений условного распределения МСП сохране-

ние введенного выше определения устойчивости представляется ключевым,

так как этим свойством обладает и само приближаемое условное распреде-

ление. В данной работе термин ¾устойчивость¿ не используется как сино-

ним слова ¾робастность¿, но близок по смыслу к устойчивости численных

алгоритмов решения нелинейных дифференциальных уравнений [7, 8] и мно-

гошаговых нелинейных дискретных схем [9]. Устойчивость гарантирует, что

L₁-норма ошибки аппроксимации всегда ограничена сверху одной и той же

константой.

Уравнения фильтра Вонэма являются частным случаем нелинейных сто-

хастических уравнений типа Кушнера-Стратоновича. Для этого класса раз-

работаны различные алгоритмы решения, обладающие свойством устойчиво-

сти:

- процедуры, основанные на слабой аппроксимации исходных процессов

марковскими цепями [10, 11],

- варианты схемы дробных шагов [12],

- робастные процедуры, основанные на преобразовании Кларка [13, 14],

- схемы, связанные с представлением распределений через их логарифм [15],

и др. Все эти алгоритмы созданы для систем аддитивных винеровских шумов

в наблюдениях и базируются на гирсановской замене вероятностной меры.

Различные алгоритмы численного решения стохастических дифференциаль-

ных уравнений со скачками изложены в [16], а в приложении к решению за-

дач оценивания и управления для систем с мультипликативными шумами -

в [17-19].

Последние исследования заставляют вернуться к данной теме. В [20] пред-

ставлено обобщение результата Вонэма на случай мультипликативных шу-

мов в наблюдениях. Известно [24], что задачи фильтрации по наблюдениям с

мультипликативными шумами сводятся к оцениванию по косвенным наблю-

дениям с вырожденными шумами: в их качестве выступают квадратические

характеристики шумов в наблюдениях - процессы, не доступные прямому на-

блюдению, которые сами являются результатом некоторого предельного пе-

рехода. В заметке [25] предложена идея аппроксимации обобщенного фильтра

Вонэма с помощью дискретизации наблюдений и их последующего оптималь-

ного использования, однако численно реализуемый алгоритм, равно как и его

точностные характеристики, не представлены.

На проблему численной реализации алгоритма оптимальной фильтрации

стохастической системы с непрерывным временем можно взглянуть с другой

точки зрения. При решении современными средствами вычислительной тех-

ники задач фильтрации по имеющимся непрерывным наблюдениям на первом

этапе их дискретизуют, либо они изначально поступают уже в дискретизо-

ванном виде со средств наблюдения. На следующем этапе обработки обычно

подбираются численные методы, обеспечивающие при уменьшении шага дис-

кретизации по времени сильную или слабую сходимость получаемых аппрок-

симаций к решению задачи оптимальной фильтрации по непрерывным на-

блюдениям. За редким исключением (см. [26, 27]) авторы не предпринимают

попыток оптимизировать процесс обработки дискретизованных наблюдений.

А ведь решение задачи оптимальной фильтрации состояний МСП по наблю-

дениям, дискретизованным по времени, во-первых, дало бы наилучшее при-

ближение точного решения уравнений фильтра Вонэма и, во-вторых, гаран-

тировало бы устойчивость этой аппроксимации. Более того, решение задачи

оптимальной фильтрации по дискретизованным наблюдениям без дополни-

тельных предположений о малости шага по времени имеет самостоятельную

практическую ценность. Отказ от такого подхода объясняется узостью клас-

са стохастических дифференциальных систем наблюдения, которые можно

точно дискретизовать по времени так, чтобы итоговая система являлась ре-

куррентной системой с дискретным временем и некоторым белым шумом в

правой части. Помимо этого, в ряде реальных задач шаг дискретизации на-

блюдений не может быть уменьшен в связи с техническими ограничениями

используемых измерительных средств или из-за необходимости проведения

некоторой предобработки (осреднения, сглаживания и т.д.) ¾сырых¿ наблю-

дений.

Целью первой части работы является представление решения задач L₁-оп-

тимальной фильтрации состояния МСП по непрерывным и дискретизован-

ным наблюдениям с аддитивными и/или мультипликативными шумами, а

также устойчивых аппроксимаций данного решения. Статья имеет следую-

щую структуру. Раздел 2 содержит постановку задач фильтрации МСП.

В разделе 3 представлены решения этих задач: L₁-оптимальные оценки филь-

трации совпадают с оценками максимума апостериорной вероятности. Это

значит, что для их определения нужно знать условное распределение МСП

относительно имеющихся наблюдений. Условное распределение вычисляется

рекуррентно в виде некоторой дроби, представляющей собой формулу Байе-

са. Числитель и знаменатель в ней содержат интегралы - дисперсионно-сдви-

говые смеси гауссовских распределений. Смешивающим в них является рас-

пределение времени пребывания МСП в том или ином состоянии на времен-

ном отрезке дискретизации наблюдений. Так как смешивающее распределе-

ние имеет громоздкий вид, оптимальную оценку предлагается приближать

сходящейся последовательностью устойчивых аппроксимаций, ограничиваю-

щих возможное число скачков МСП на интервале дискретизации. Для этих

аппроксимаций получены локальная и глобальная характеристики точности.

Данные сведения изложены в разделе 4. В числителе и знаменателе анали-

тических аппроксимаций присутствуют слагаемые - интегралы, не вычис-

ляемые аналитически. Выбор той или иной схемы их численной реализации

влияет на итоговую точность полученных оценок. В разделе 5 представлены

локальная и глобальная характеристики влияния ошибок численного инте-

грирования на отклонение приближенного решения от оптимального. Анализ

полученных результатов и их обсуждение представлены в разделе 6.

2. Постановка задачи L₁-оптимальной фильтрации

На полном вероятностном пространстве с фильтрацией (Ω, F, P, {F_t}_t≥0)

рассматривается стохастическая динамическая система

∫t

(2.1)

X_t = X₀ + Λ^⊤X_sds + µ_s,

∫^t

∫

∑

(2.2)

Y_t = fX_sds +

X^nsg^1/2ndW_s,

n=1

где

X_t ≜ col(X^1t,... ,X^Nt ) ∈ SN - ненаблюдаемое состояние системы, яв-

ляющееся однородным МСП с конечным множеством состояний S^N ≜

≜ {e₁, . . . , e_N } (SN - множество единичных векторов евклидова простран-

ства R^N ), матрицей интенсивностей переходов Λ и начальным распределе-

нием π;

µ_t ≜ col (µ^1t,... ,µ^Nt ) ∈ R^N

F_t-согласованный мартингал;

Y_t ≜ col (Y^1t,... ,Y^Mt ) ∈ R^M

косвенные наблюдения, зашумленные

F_t-согласованным стандартным винеровским процессом W_t ≜ col (W^1t,

...,W^Mt)∈R^M; f

(M × N)-мерная матрица плана наблюдений, а набор

симметричных матриц {g_n}_n=1,N характеризует интенсивности шумов в за-

висимости от текущего состояния X_t.

Возможны два варианта статистической информации для последующего

оценивания состояния МСП.

1. Наблюдению полностью доступен процесс Y ; поток σ-алгебр, им порож-

денный, обозначен следующим образом: O_t ≜ σ {Y_s : 0 ≤ s ≤ t}.

2. Наблюдению доступны приращения исходного непрерывного процесса Y

при равномерной дискретизации времени с шагом h > 0:

∫tr

∫

∑

(2.3)

Y_r =

fX_sds +

X^nsg^1/2ndW_s

r ∈ N,

n=1

tr-1

где t_r ≜ rh - точки полученной сетки. Неубывающее семейство σ-алгебр, по-

рожденное последовательностью {Y_r}_r∈N, обозначено следующим образом:

O_r ≜ σ{Y_ℓ : 0 ≤ ℓ ≤ r}, O₀ ≜ {∅, Ω}.

Расстояние между точками α = col (α¹, . . . , α^N ) и β = col (β¹, . . . , β^N ) в

∑

пространстве R^N определяется с помощью L₁-нормы: ∥α-β∥₁ ≜

|αⁿ -βⁿ|.

n=1

Задача L₁-оптимальной фильтрации состояния X по непрерывным на-

блюдениям Y заключается в нахождении такой оценкиXt, t ≥ 0, что

{

}

(2.4)

X_t ∈ Argmin E

∥Xt - X_t∥1 ,

X_t∈Xt

где X_t - множество всех таких O_t-согласованных процессовXt с конечным

∑

первым моментом, что

≡ 1 с вероятностью 1.

n=1

Задача L₁-оптимальной фильтрации состояния X по дискретным на-

блюдениям Y заключается в нахождении такой оценкиXr, r ∈ N состояния

МСП X_rh, что

{

}

(2.5)

X_r ∈ Argmin E

∥Xr - X_rh∥1 ,

X_r∈Xr

где X_r - множество всех таких O_r-согласованных последовательностей {Xr}

∑

с конечным первым моментом, что

≡ 1 с вероятностью 1.

n=1

В дальнейшем изложении, если какой-либо вектор-столбец α удовлетворя-

ет условию нормировки, то это условие будет записываться в форме 1α = 1,

где 1 - вектор-строка подходящей размерности, состоящая из единиц.

Исследуемая частично наблюдаемая динамическая система и поставлен-

ные задачи фильтрации имеют некоторые особенности.

Во-первых, процесс непрерывных наблюдений Y_t может быть преобразован

к виду

∫t

(

)

∑

Y_t =

Xⁿ

fe_nds + g^1/2

dW_s

n=1

Из него следует, что полезный сигнал X_t наблюдается в присутствии мульти-

пликативного шума - процесса броуновского движения с известными неслу-

чайными сносом и диффузией. В то же время в частном случае g_n ≡ g,

n = 1,N процесс Y_t может быть преобразован к виду

∫t

Y_t = fX_sds + g^1/2W_t

и рассматриваться как полезный сигнал, аддитивно зашумленный процессом

броуновского движения с нулевым сносом и известной неслучайной диффу-

зией. Поэтому в общем случае Y_t можно назвать наблюдениями с аддитив-

ными/мультипликативными шумами.

Во-вторых, дополнительное требование выполнения условия нормировки

для допустимых оценок представляется достаточно естественным, ведь все

возможные значения оцениваемого состояния X_t, образующие множество S^N

координатных ортов пространства R^N , также удовлетворяют этому свойству.

3. Решение задач L₁-оптимальной фильтрации

Решать задачи фильтрации будем в предположении, что для (2.1) и (2.2)

выполняются следующие условия.

а. Исследуемое вероятностное пространство с фильтрацией имеет вид

(

)

{

}

Ω^X × Ω^W , F^X × F^W , P^X × P^W ,

F^Xt × F^W

t≥0

и процессы X_t(ω^X ) и W_t(ω^W ) независимы.

б. Шумы в наблюдениях равномерно невырожденные, т.е. g_n > 0 для всех

n = 1,N.

Приведенные выше условия являются естественными для задач фильтрации

и не обременительными.

Пусть x_t ≜ E {X_t|O_t} и x_r ≜ E {Xtr |O_r} - векторы условных математи-

ческих ожиданий (УМО) состояния МСП X_t относительно непрерывных и

дискретизованных наблюдений, которые в силу того, что X_t ∈ S^N , совпадают

с условными распределениями. Построим по этим условным распределениям

xt и xr оценки максимума апостериорной вероятности:

X_t = e_n∗, где n^∗ ∈ Argmaxx^nt

n=1,N

оценка максимума апостериорной вероятности по непрерывным наблюде-

ниям,

X_r = e_n∗ , где n^∗ ∈ Argmax x^nr

n=1,N

оценка максимума апостериорной вероятности по дискретизованным на-

блюдениям.

Лемма 1. Решение задач L₁-оптимальной фильтрации по непрерывным

и дискретизованным наблюдениям доставляется оценками максимальной

апостериорной вероятности.

Доказательство леммы 1 дано в [21, с. 125].

Результат леммы нуждается в некоторых комментариях. Во-первых,

L₁-оптимальная оценка не единственна. В качестве нее может выступать

любой орт с номером, соответствующим максимальной условной вероят-

ности, в случае, если таких компонент несколько. Более того, в качестве

L₁-оптимальной оценки может выступать любая выпуклая комбинация по-

добных ортов. Однако представляется, что практического значения такая

неединственность не имеет. Ниже будет получен явный вид условного рас-

пределения как относительно непрерывных, так и дискретизованных наблю-

дений. Анализируя вид последних, можно сделать вывод: условные распреде-

ления получаются путем рекуррентного нелинейного преобразования невы-

рожденных гауссовских случайных векторов, поэтому вероятность появления

двух или более условных мод равна нулю. Поиск условий, при которых услов-

ные моды не единственны с положительной вероятностью, не входит в цели

данной работы.

Во-вторых, факт, что L₁-оптимальной оказалась оценка максимума апо-

стериорной вероятности, является не вполне очевидным. Например, в класси-

ческой статистической задаче оценивания скалярного параметра относитель-

но L₁-критерия [22] оптимальной оказывается выборочная медиана. Согласно

классической монографии [23, Sect. 2.3, Problem 3.3] медиана апостериорного

распределения также является L₁-оптимальной оценкой случайного скаляр-

ного параметра. Кстати, к этому же случаю сведется L₁-оптимальная филь-

трация состояния МСП в случае, если его фазовым пространством высту-

пит некоторое конечное подмножество числовой оси, например {1, 2, . . . , N}.

Результат леммы 1 базируется именно на том, что фазовым пространством

для X_t выступает множество единичных ортов S^N . Выбор такого фазового

пространства вполне распространен (см., например, [5]) и весьма эффективен

при математических выводах.

Стохастическая дифференциальная система, определяющая УМО x_t отно-

сительно непрерывных наблюдений, представлена в [20]. Рекуррентная схема

вычисления УМО x_t относительно дискретных наблюдений представлена в

заметке [25]. Схема является основой построения алгоритмов численного ре-

шения задач фильтрации, представленных в данной работе, поэтому ниже

приведен ее корректный вывод.

Воспользуемся подходом из [28]. Применим метод математической индук-

ции. При r = 0

(3.1)

x₀ = E {X₀|O₀} = E {x₀

}=π.

П{сть для н}которого r ∈ N известно условное распределение

xr-1 =

Xtr-1 |O_r-1

. Определим УМО x_r на следующем шаге. Для этого необхо-

димо найти совместное распределение (Xtr , Y_r) относительно O_r-1. Из моде-

ли наблюдений и леммы 7.5 [29] следует, что распределение Y_r относительно

σ-алгебры F^Xt

∨ O_r-1 является гауссовским с параметрами

{

}

∑

(3.2)

Y_r|F^Xt

=fτ_r,

cov(Y_r, Y_r|F^Xt)= τnrgn,

n=1

∫ tr

где τ_r = col (τ^1r, . . . , τ^Nr ) ≜

X_sds - случайный вектор, n-я компонента ко-

tr-1

торого равна случайному времени пребывания процесса X в состоянии e_n на

отрезке [t_r-1, t_r]. Ниже в изложении будем использовать следующие обозна-

чения:{

}

∑

D ≜ u = col(u¹,...,u^N) : u_n ≥ 0,

uⁿ = h

- (N -1)-мерный симплекс

n=1

в пространстве R^M - носитель распределения τ_r;

{

}

∑

Π ≜ π = col(π¹,...,π^N) : π_n ≥ 0,

πⁿ = 1

¾вероятностный сим-

n=1

плекс¿, множество возможных начальных распределений π;

N^Xr - случайное число скачков состояния X_t, произошедших на отрезке

времени [t_r-1, t_r],

{

}

∏_r

a^sr ≜

ω ∈ Ω : NXr (ω) ≤ s

, A^sr ≜

a^sq;

q=1

ρ^k,ℓ,q(du) - распределение вектора Xℓtr I_{q}(N^Xr)τ_r при условии Xtr-1 = e_k,

т.е. для любого G ∈ B(R^M ) верно равенство

∫

{

}

E I_G(τ_r)I_{q}(N^Xr)X^ℓ

|Xtr-1 = e_k

= ρ^k,ℓ,q(du);

{

}

N(y, m, K) ≜ (2π)^-M/2det^-1/2K exp

-¹²∥y - m∥2K-1

M -мерная плот-

ность гауссовского распределения с математическим ожиданием m и невы-

рожденной ковариационной матрицей K;

∥α∥^2K ≜ α^⊤Kα,

〈α, β〉_K ≜ α^⊤Kβ.

В силу марковского свойства {(Xtr , Y_r)}_r≥0, формулы полной вероятно-

сти и теоремы Фубини для любого множества A ∈ B(R^M ) верна следующая

цепочка равенств:

{

}

{



}



}

Xtr I_A(Y_r)

O_r-1

= E E XtrI_A(Y_r)

F^Xt

∨O_r-1

O_r-1











∫





∑



g_p dyOr-1

=EXtr Ny,fτr,τr



p=1









∫



∑









g_p dyXtr-1 ∨ Or-1

O_r-1

=EEXtr Ny,fτr,τr



p=1









∫





∑∑

∑



e^⊤

Xtr-1

Ny,fu, u^pgp dyρk,ℓ,q(du)Or-1

=Eeℓ



ℓ=1

q=0 k=1

p=1

D A









∫

∑ ∫

∑

= e_ℓ



Ny,fu, u^pgpρk,ℓ,q(du) dy

r-1

ℓ=1

q=0D

p=1

A k=1

из чего следует, что интегранд в квадратных скобках в последнем выражении

определяет искомое совместное распределение (Xtr , Y_r) относительно O_r-1.

Тогда условное распределение x_r покомпонентно определяется с помощью

обобщенного варианта формулы Байеса [29]

(

)

∑

∫

∑

N Y_r,fu,

u^pg_p ρ^k,j,q(du)

r-1

q=0 D

p=1

(3.3)

xjr =^k=1

(

)

j = 1,N.

∑

∫

∑

N Y_r,fv,

vⁿg_n ρ^i,ℓ,c(dv)

r-1

i,ℓ=1

c=0 D

n=1

Таким образом, доказана следующая

Лемма 2. Если для системы наблюдения (2.1), (2.3) верны условия а и б,

то условное распределение x_r определяется формулой (3.1) при r = 0 и ре-

куррентным соотношением (3.3) в моменты t_r получения наблюдений Y_r.

В [30] в качестве иллюстративного примера рассматривалась задача

СК-оптимальной фильтрации состояний МСП по дискретизованным наблю-

дениям, полученным в некоторые неслучайные моменты времени. В этой ра-

боте оценка фильтрации определяется также с помощью некоторой рекур-

рентной процедуры. Однако в [30] эта процедура записана в абстрактной

форме: интегранды в ее числителе и знаменателе содержат условные мате-

матические ожидания без указания, как их можно вычислить. В данной же

работе все интегранды в числителе и знаменателе (3.3) явным образом опре-

делены и могут быть вычислены аналитически или численно сколь угодно

точно.

4. Аналитическая аппроксимация условного распределения и ее точность

Рекурсия (3.3) не может быть непосредственно реализована в виде некото-

рой численной схемы: суммы бесконечных рядов из интегралов в числителе

и знаменателе не могут быть вычислены аналитически. Поэтому их предла-

гается заменить конечными рядами, а векторную последовательность x_r(s),

вычисляемую покомпонентно с помощью рекурсии

(

)

∑∫

∑

^N x^kr-1(s)

N Y_r,fu, u^pg_p ρ^k,j,q(du)

q=0D

p=1

(4.1)

x^jr(s) =^k=1

(

)

j = 1,N

∑

∫

∑

x^ir-1(s)

N Y_r,fv, vⁿg_n ρ^i,ℓ,c(dv)

i,ℓ=1

c=0D

n=1

назовем аналитической аппроксимацией s-го порядка условного распределе-

ния. Легко видеть, что аппроксимация x_r(s) обладает свойством устойчиво-

сти.

Так как искомая L₁-оптимальная оценкаXr является функцией условно-

го распределения x_r, которое может быть вычислено только приближенно в

форме аппроксимации x_r(s), то важным представляется определить степень

близости x_r и x_r(s).

Введем следующие обозначения для неотрицательных случайных величин

и матриц из них:





∫

∑

ξ^kjq ≜

NY_q,fu, u^pgp ρk,j,m(du),

m=0D

p=1





∫

(4.2)

∑

θ^kjq ≜

NY_q,fu, u^pgp ρk,j,m(du),

m=0D

p=1

ξ_q ≜ ∥ξ^kjq∥_k,j=1,N,

θ_q ≜ ∥θ^kjq∥_k,j=1,N.

Оценки x_r (3.3) и x_r(s) (4.1) могут быть записаны в рекуррентной форме:

(

)_-1

(4.3)

xr =

1θ^⊤rx_r-1

θ^⊤rx_r-1,

(

)_-1

(4.4)

x_r(s) =

1ξ^⊤rx_r-1(s)

ξ^⊤rx_r-1

(s).

Определим характеристики близости оценок {x_r(s)} и {x_r}. Так как система

(2.1), (2.3) является автономной, то в качестве локальной характеристики

точности аппроксимации {x_r(s)} может быть выбрана величина

∑

{

}

(4.5)

σ(s) ≜ supE {∥x1 - x1(s)∥1} = sup

|x^j1 - x^j1(s)|

π∈Π

π∈Π j=1

определяющая, насколько сильно рекурсии (3.3) и (4.1) разойдутся за один

шаг, стартуя из одной точки π.

Обе схемы, примененные r раз, позволяют вычислить и оценки x_r и x_r(s)

в точке t_r. В качестве глобальной характеристики точности аппроксимации

в этом случае естественно рассмотреть величину

∑

{

}

(4.6)

Σ_r(s) ≜ supE {∥xr - xr(s)∥1} = sup

|x^jr - x^jr(s)|

π∈Π

π∈Π j=1

определяющую, насколько сильно рекурсии (3.3) и (4.1) разойдутся за r ша-

гов, стартуя из единой точки π.

В отличие от традиционных показателей точности [6], представляющих

собой L₂-норму ошибок аппроксимации, предлагаемые характеристики свя-

заны с L₁-нормой.

Следующее утверждение определяет верхние оценки величин σ(s) и Σ_r(s).

Теорема 1. В условиях леммы 2 верны неравенства

(λh)^s+1

(4.7)

σ(s) ≤ 2C₁

(s + 1)!

(

(λh)^s+1

(4.8)

Σ_r(s) ≤ 2 - 2

1-C₁

(s + 1)!

где λ ≜ max_1≤n≤N |λ_nn|, а C₁ = C₁(h, λ) ∈ (0, 1) - параметр

∑

(s + 1)!

(λh)^k

(4.9)

C₁ ≜ e^-λh

(λh)^s+1

k=s+1

При этом верно неравенство

(λh)^s+1

C₁ (s + 1)!<1.

Доказательство теоремы 1 приведено в Приложении.

Неравенства (4.7) и (4.8) имеют следующую интерпретацию. Для произ-

вольной устойчивой оценки x_r ее отклонение от оптимальной x_r не превосхо-

дит 2:

maxE {∥xr - xr∥1} = 2.

x,r,π

Аппроксимация x₁(s) построена в предположении, что на интервале дискре-

тизации наблюдений длиной h состояние МСП совершит не более s скач-

(λh)^s+1

ков. При этом величина C₁

ограничивает сверху вероятность того, что

(s+1)!

число скачков превзойдет порог s. Правая часть неравенства (4.7) является

произведением максимально возможного промаха на вероятность превыше-

ния порога s числом скачков. Глобальная оценка (4.8) построена аналогично:

предполагается, что максимальное расхождение x_r(s) и x_r может произойти

в том случае, если хотя бы на одном из r отрезков длины h МСП X совершит

более s скачков.

Утверждения теоремы 1 имеют практическую пользу. В них нет требова-

ний асимптотики по параметрам s и h: представленные оценки точности носят

универсальный характер. В подавляющем большинстве современных цифро-

вых систем управления частота съема измерений фиксирована или ограниче-

на сверху. В некоторых случаях имеются дополнительные алгоритмические

ограничения на интервал дискретизации: исходные ¾сырые¿ данные должны

быть подвергнуты предварительной обработке типа сглаживания, осредне-

ния и т.п. Например, использование диффузионной аппроксимации процессов

восстановления [31] правомерно лишь при значительных интервалах осред-

нения, длина которых зависит от моментных характеристик времени между

скачками.

Неравенство (4.8) позволяет также получить следующие асимптотические

результаты. При фиксированных (h, s) и r → +∞ глобальная ошибка Σ_r(s)

экспоненциально стремится к своему максимально возможному значению 2,

причем делает это тем медленнее, чем меньше показатель локальной ошибки

(λh)^s+1

C_1(s+1)! .

Рассмотрим глобальный показатель точности аппроксимации в фиксиро-

ванный момент времени T при асимптотике h → 0. В этом случае r =^Th ,

и из (4.8) следует цепочка неравенств

(

)_r

(λh)^s+1

Σ_r(s) ≤ 2 - 2

(s + 1)!

[

(

))]

(λT )^s+1

= 2 1 - exp rln

≜ S_r(s).

(s + 1)!r^s+1

При достаточно больших r имеет место эквивалентность

(

)

(λT )^s+1

∼-

(s + 1)!r^s+1

т.е.



 (

)_s



[

(

)]

λT

(λT )^s+1

S_r(s) ∼ 2 1 - exp

-r

= 21 - exp -λT^r

.

(s + 1)!r^s+1

(s + 1)!

В то же время, чтобы сохранить свойство оценки сверху, можно воспользо-

ваться неравенством ln(1 - x) > -x - x², верным для любых x ∈ (0,¹² ): как

200

400

600

800

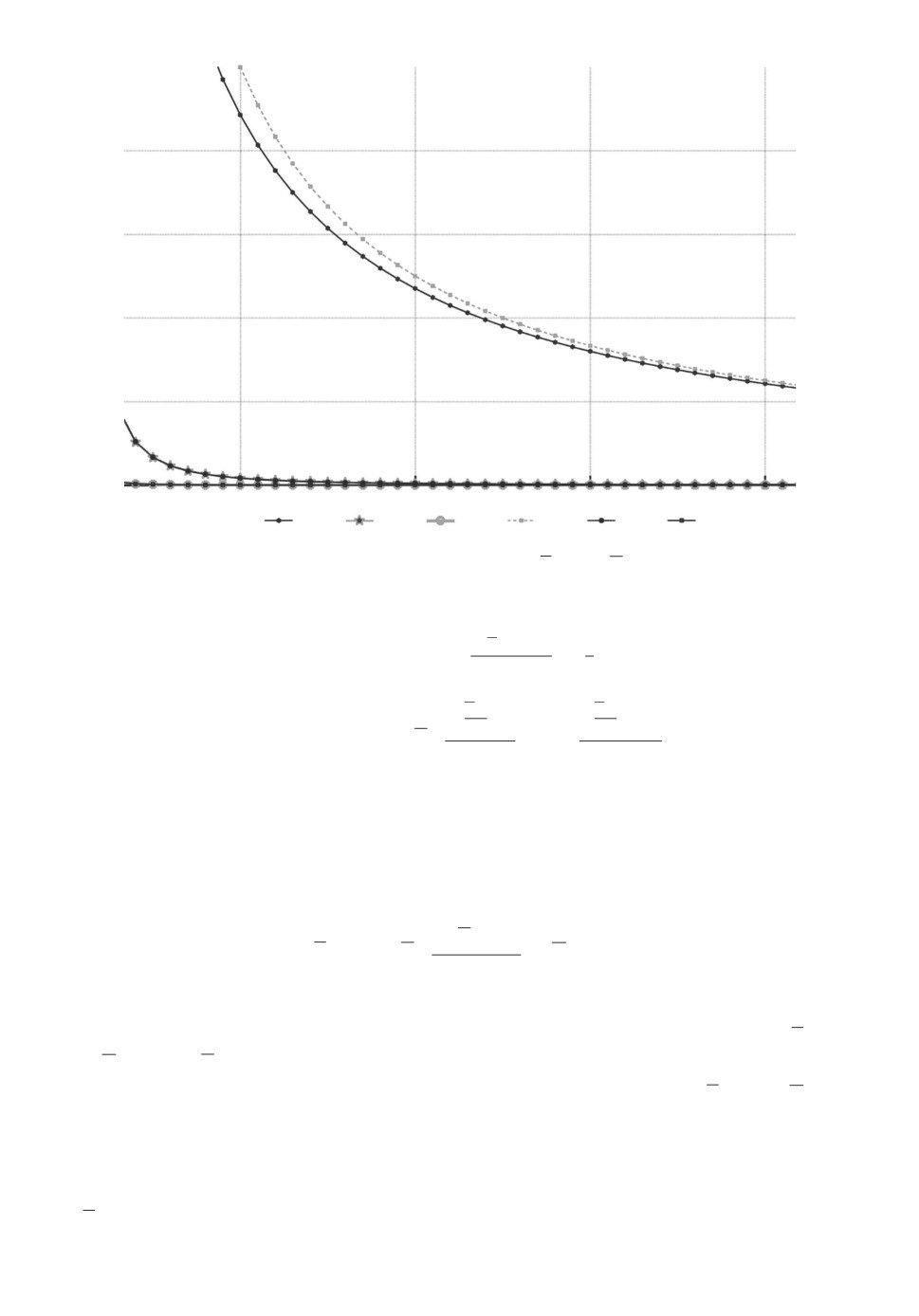
S_r(1)

S_r(2)

S_r(3)

S_r(1)

S_r(2)

S_r(3)

Сравнение показателей глобальной точности S_r(s) и S_r(s) аналитических

аппроксимаций порядков s = 1, 2, 3.

только r станет настолько велико, что(λT)s+1

<¹², то

(s+1)!r^s+1





(

)_s

 (

)_s+1



λT









Σ_r(s) ≤ 2

1 - exp−λT

1+





(s + 1)!



Для определения порядка точности более предпочтительна верхняя оценка

точности Σ_r(s) в виде степенной функции шага дискретизации h. Используя

неравенство (1 - x)^r > 1 - rx, верного для любого x ∈ (0, 1) и r > 1, можно

получить следующую оценку сверху

(λT )

S_r(s) ≤ 2λT

≜ S_r(s).

(s + 1)!r^s

Для иллюстрации влияния порядка аппроксимации s на показатель гло-

бальной точности на рисунке приведены зависимости от r величины S_r(s)

и S_r(s) для λ = 10, T = 1 и s = 1,2,3.

Из рисунка следуют два вывода. Во-первых, показатели S_r(s) и S_r(s)

очень близки друг к другу за исключением случая s = 1. Во-вторых, уве-

личение степени аппроксимации значительно повышает ее точность, напри-

мер, при s = 2 и r = 100 (т.е. h = 0,1) показатель точности составляет 0,33,

что для порядка s = 1 не достигается даже при r = 1000 (т.е. при h = 0,01):

S₁₀₀₀(1) = 0,1.

5. Численная аппроксимация условного распределения и ее точность

В рекуррентной схеме (4.4) требуется вычисление интегралов ξ^rj , что

невозможно сделать аналитически. Использование численного интегрирова-

ния вносит дополнительные ошибки. Исследуем их влияние на общую точ-

ность аппроксимации условного распределения.

Значения интегралов ξ^ij(y) аппроксимируются суммами





∑

ξ^ij(y) ≈ ψ^ij(y) ≜

Ny,fw_ℓ, w^pgp̺ijℓ,

ℓ

(5.1)

ℓ=1

p=1

ψ(y) ≜ ∥ψ^ij (y)∥_i,j=1,N ,

определяемыми множеством пар {(w_ℓ, ̺^ijℓ )}_ℓ=1,L. Здесь ̺^ijℓ ≥ 0 (ℓ = 1, L) - ве-

∑

са,

∑ ̺^ijℓ ≤ W ≤ 1, а w_ℓ ≜ col(w^1ℓ,...,wNℓ ) ∈ D - точки. Аналогично мат-

j=1 ℓ=1

рицам ξ_q строятся их аппроксимации ψ_q ≜ ∥ψ^ij (Y_q)∥_i,j=1,N .

По построению элементы матрицы ψ_q являются положительными случай-

ными величинами, поэтому приближенная оценка x_r, вычисляемая рекур-

рентно по формуле

(

)_-1

(5.2)

xr ≜

1ψ^⊤r x_r-1

ψ^⊤rx_r-1,

обладает свойством устойчивости.

Обозначим



(5.3)

γ^kj ≜ ψ^kj - ξ^kj,

γ_r ≜

γ^kj(Y_r)

k,j=1,N



(5.4)

γ^kj ≜ |γ^kj|,

γ_r ≜

|γ^kj (Y_r)|

k,j=1,N

ошибки аппроксимации интегралов и их абсолютные значения.

Рекуррентная схема вычисления x_r (4.4) заменяется на схему (5.2), при

этом обе рекурсии стартуют из одного и того же начального условия π.

Схемы (4.4) и (5.2) строились в расчете на выполнение события A^sr, т.е.

на непревышение числом скачков порога s на всех интервалах [t_q-1, t_q], при-

надлежащих отрезку [0, t_r]. Поэтому показатель близости x_r и x_r(s) нужно

выбирать с учетом этого ограничения. В качестве локальной характеристики

будем рассматривать псевдометрику

{

}

{

}

∑

(5.5)

ε(s) ≜ supE

I_as

(ω)∥x₁ - x₁(s)∥₁

= sup E I_as(ω)|xj1 - xj1(x)|

π∈Π

π∈Π j=1

Глобальный показатель близости определяется аналогично:

{

}

∑

{

}

(5.6) E_r(s) ≜ supE

I_As

(ω)∥x_r - x₁(x)∥₁

= sup E

I_As

(ω)|x^nr - x^nr(x)|

π∈Π

π∈Πn=1

Эти величины характеризуют разницу применения алгоритмов (4.4) и (5.2)

за один и r шагов при выполнении ограничений на число скачков состояния,

описанных выше.

Теорема 2. Если для схемы (5.1) приближенного вычисления интеграла

(4.2) выполняется неравенство

∫

∑

(5.7)

max

|ψ^ij (y) - ξ^ij

(y)|dy < δ,

i=1,N j=1

R^M

то для локального и глобального показателей близости верны оценки сверху

(5.8)

ε(s) ≤ 2δ,

E_r(s) ≤ 2rW^r-1

δ.

Доказательство теоремы 2 приведено в Приложении.

Возможность характеризации точности численного решения задачи филь-

трации, стохастической по своей природе, с помощью условия (5.7), относя-

щегося к чистому математическому анализу, представляется замечательной.

∑

Далее, если сумма весов W =_ℓ,j ̺^ijℓ отделена от единицы, т.е. W < 1, гло-

бальный показатель ошибки численного интегрировния E_r(s) растет с увели-

чением r сублинейно, так же как и глобальный показатель ошибки аналити-

ческой аппроксимации Σ_r(s). При этом следует отметить, что в классических

численных методах решения стохастических дифференциальных уравнений

глобальная ошибка растет линейно с ростом времени интегрирования [6].

Характеристики точности аналитической аппроксимации и ее численной

реализации должны быть объединены в единый показатель. Если выполня-

ются условия теорем 1 и 2, то

{

}

τ (s) ≜ sup E

∥x₁ - x₁∥₁

≤

π∈Π

{

}

≤ sup

E I_as(ω)∥x1 - x1(s) + x1(s) - x1∥1 + Ias(ω)∥x1 - x1(s)∥1

≤

π∈Π

(5.9)

{

}

{

}

≤ 2P {a^s1} + supE

∥x₁(s) - x₁∥₁

+ sup

E I_as(ω)∥x1 - x1(s)∥1

π∈Π

s+1

(λh)

= 2P {a^s1} + σ(s) + ε(s) ≤ 4

+ 2δ.

(s + 1)!

Итоговый глобальный показатель близости условного распределения x_r ≜

≜ E {X_r|O_r} и его приближения x_r может быть ограничен сверху аналогич-

ным образом:

[

(

)r^]

s+1

(λh)

(5.10)

T(s) ≜ supE {∥xr - xr∥1} ≤ 4

+ 2rW^r-1

δ.

π∈Π

(s + 1)!

Вообще говоря, параметры аналитической аппроксимации (h, s) и числен-

ного интегрирования δ могут выбираться независимо друг от друга. Однако

наличие ограничений по доступным вычислительным ресурсам и требований

к точности аппроксимации ведут к совместной оптимизации данных пара-

метров.

Тем не менее при разработке эффективных алгоритмов численного ре-

шения задачи фильтрации состояний МСП по непрерывным наблюдениям

эти параметры нуждаются в совместном оптимальном выборе. Зафиксиру-

ем некоторый горизонт T и порядок аналитической аппроксимации s. Бу-

дем увеличивать число шагов r → ∞, а значит уменьшать шаг дискретиза-

ции h =^Tr → 0. В этом случае в силу неравенства Бернулли и неравенства

0<W≤1

[

(

)_r]

{



}

(λh)^s+1



supE

x_T/h - x_T/h

≤4 1-

+ 2rW^r-1δ ≤

π∈Π

(s + 1)!

s+1

(λh)

(λh)^s

(5.11)

≤ 4r

+ 2rW^r-1δ = 4λT

+ 2rW^r-1δ ≤

(s + 1)!

(

)

(λh)^s

≤ 2T

2λ

(s + 1)!

Первое слагаемое в скобках соответствует вкладу в суммарную ошибку, опре-

деляемую аналитической аппроксимацией, второе - вкладу ошибки числен-

ного интегрирования. Ясно, что оптимальным будет выбор параметров, обес-

печивающий обоим слагаемым одинаковый порядок малости, который дости-

гается при δ ∼(λh)s+1

6. Заключение

Решение задачи L₁-оптимальной фильтрации состояний МСП по непре-

рывным или дискретизованным наблюдениям не может быть получено в яв-

ной аналитической форме. Для реализации решения средствами вычисли-

тельной техники требуются классы специальных алгоритмов приближенного

решения. Основным результатом данной статьи являются теоремы 1, 2 и фор-

мула (5.11), описывающие влияние выбранных аналитической аппроксима-

ции и схемы численного интегрирования на итоговую точность приближения

условного распределения. Сравнительный численный анализ конкретных ал-

горитмов, используемых для фильтрации состояний МСП по наблюдениям с

аддитивными и мультипликативными шумами, будет представлен во второй

части работы.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Используя обозначения Ξ_r ≜ ξ₁ξ2 ...ξ_r

и Θ_r ≜ θ₁θ2 ...θ_r для матриц со случайными элементами, оценки x_r и x_r(s)

можно выписать в явной форме:

(

)_-1

(

)_-1

xr =

1Θ^⊤rπ

Θ^⊤rπ,

xr(s) =

1Ξ^⊤rπ

Ξ^⊤rπ.

Из определения (4.2) следует, что ξ^qj ≤ θ^qj, поэтому матрица Θ_r - Ξ_r со-

держит только неотрицательные элементы. Для краткости запись зависимо-

сти от r в обозначениях Ξ_r и Θ_r будет опущена. Верна следующая цепочка

неравенств

{



}



E {∥x_r - x_r(s)∥₁} = E

^⊤π -

Ξ^⊤π



 1Θ^⊤πΘ

1Ξ^⊤π

{

}



1Ξ^⊤π(Θ - Ξ)^⊤π - 1(Θ - Ξ)^⊤πΞ^⊤π

≤

1Θ^⊤π1Ξ^⊤π

(Π.1)

{

(

)}

≤E

1Ξ^⊤π∥(Θ - Ξ)^⊤π∥₁ + 1(Θ - Ξ)^⊤π∥Ξ^⊤π∥1

1Θ^⊤π1Ξ^⊤π

{

}

= 2E

1(Θ - Ξ)^⊤π

1Θ^⊤π

Рассмотрим вспомогательную оценку

{

}

x_r ≜ E

Xtr I_As

(ω)|O_r

Из абстрактного варианта формулы Байеса следует, что x_r =

Ξ^⊤π и

1Θ^⊤π

{

}

(Π.2)

(Θ - Ξ)^⊤

π.

xr - xr = E Xtr IA^sr (ω)|Or

1Θ^⊤π

Из (Π.1) и (Π.2) следует, что для r = 1 и ∀ π ∈ Π

{

}

{

{

}



∥x₁ - x₁(s)∥₁

≤ 2E

E

Xt1 I_as

(ω)|O₁

{

}

(Π.3)

∑{

}

{

}}

= 2E

E Xⁿ

t₁

I_as

(ω)|O₁

= 2E E

I_as

(ω)|O₁

= 2P {a^s1} .

n=1

Процесс N^Xt общего числа скачков состояния X_t является считающим, и его

квадратическая характеристика равна

∫t

∑

〈N^X , N^X 〉_t = -

λ_nnX^nsds,

n=1

поэтому искомую вероятность можно оценить сверху следующим образом

∑

(λh)^k

(λh)^s+1

(Π.4)

P {a^s1} ≤ e^-λh

=C₁

(s + 1)!

k=s+1

Из последнего неравенства и (Π.3) следует истинность неравенства σ(s) ≤

(λh)^s+1

≤ 2C₁

, т.е. оценка локальной точности (4.7) верна.

(s+1)!

) и (Π.4) можно оценить

)_r

{

(λh)^s+1

сверху и вероятность P

A^sr}: P{A^sr}

≤1- 1-C₁

, из чего следует

(s+1)!

истинность оценки глобальной точности (4.8). Теорема 1 доказана.

Доказательство теоремы

Итак,

x₁ = (1ψ^⊤1π)^-1ψ^⊤1π, x₁ =

= (1ξ⊤1 π)^-1ξ⊤1 π и Δ₁ = x₁ - x₁. Используя свойства матричных операций,

легко показать, что [γ^⊤π1 - 1γ^⊤πI]γ^⊤π = 0. Обе оценки обладают свойством

устойчивости, поэтому ∥x₁∥₁ = ∥x₁∥₁ = 1. Верна следующая цепочка нера-

венств:



∥Δ₁∥₁ =

1ξ^⊤1πψ^⊤1π - 1ψ^⊤1πξ^⊤1π

1ψ^⊤1π1ξ^⊤1π



1ξ^⊤1πγ^⊤1π - 1γ^⊤1πξ^⊤1π

1ψ^⊤1π1ξ^⊤1π

[

]



 γ^⊤1π1 - 1γ^⊤1πI ξ^⊤1π

1ψ^⊤1π1ξ^⊤1π

[

][

]



 γ^⊤1π1 - 1γ^⊤1πI ξ^⊤1π + γ^⊤1π



1ψ^⊤1π1ξ^⊤1π

[

]



 γ^⊤1π1 - 1γ^⊤1πI

X₁

≤

1ξ^⊤1π

[

]



≤

 γ^⊤1π1 - 1γ^⊤1πI



X



≤

1ξ^⊤1π

∑

γ^ij1

∑

1γ^⊤1π

j=1

≤2

π_i

1ξ^⊤π

∑

i=1

ξ^kℓ1π_k

k,ℓ=1

Используя последнее неравенство, (5.7) и (Π.7), можно показать, что

∫

{

}

∑

I_as

(ω)∥Δ₁∥₁

≤2

π_i

γ^ij(y)dy ≤ 2δ.

i=1

R^M

Истинность первого неравенства (5.8) следует из того, что неравенство вверху

выполняется для любого π ∈ Π.

Определим матрицы со случайными элементами - функции от ξ_r и ψ_r:

{ ξqξq+1 ... ξr, если q ≤ r,

Ξ_q,r ≜

в противном случае,

{ ψ_qξq+1 ...ψ_r, если q ≤ r,

Ψ_q,r ≜

в противном случае,

Γ_q,r ≜ Ψ_q,r - Ξ_q,r.

Для доказательства теоремы 2 потребуется вспомогательная

Лемма 3. Если φ_r ≜ φ_r(Y₁,...,Y_r) - неотрицательная Or-измеримая

случайная величина и Φ_r ≜φr

, то

1Ξ^⊤1,rπ

∫

{

}

(Π.5)

I_As

(ω)Φ_r

= ... φ_r(y₁,...,y_r)dyr ...dy₁.

R^M R^M

Доказательство леммы

3. Рассмотрим неотрицательную интег-

рируемую функцию φ₁ = φ₁(y) : R^M → R₊ и O₁-измеримую случайную ве-

личину

φ₁(Y₁)

(Π.6)

Φ₁ ≜

(

)

1ξ^⊤1(Y₁)π

∑ s∑ ∫

∑

N Y₁,fu, u^pg_p ρ^i,j,m(du)π_i

i,j=1 m=0 D

p=1

{

}

Найдем E

I_as

(ω)Φ₁

{

}

I_as

(ω)Φ₁

(

)

∑

N y,fv, v^qg_q ρ^k,ℓ,n(dv)π_k

∫

∫ φ1^(y)

k,ℓ=1 n=0

q=1

(

)

dy =

∑

∑ ∫

∑

R^M D

N y,fu, u^pg_p ρ^i,j,m(du)π_i

i,j=1 m=0 D

p=1

(

)

(Π.7)

∑

∑ ∫

∑

N y,fv, v^qg_q ρ^k,ℓ,n(dv)π_k

∫

k,ℓ=1 n=0D

q=1

= φ₁

(y)

(

)

dy =

∑

∑ ∫

∑

R^M

N y,fu, u^pg_p ρ^i,j,m(du)π_i

i,j=1 m=0 D

p=1

∫

= φ₁(y)dy.

R^M

Рассмотрим неотрицательную интегрируемую функцию φ₂ = φ₁(y₁, y₂) :

R^2M → R₊ и O₂-измеримую случайную величину

φ₁(Y₁,Y₂)

Φ₂ ≜

1Ξ^⊤1,2(Y₁, Y₂)π

φ₂(Y₁,Y₂)

(

) (

)

∑

∫ ∫

∑

N Y1,fu1,

up1

gp₁

N Y2,fu2, up2

gp₂

ρi,i2,m1 (du1)ρi2,j,m2 (du2)πi

i,i₂,j=1 m₁,m₂=0D D

p₁=1

p₂=1

{

}

и найдем E

I_As

(ω)Φ₂

∫

{

}

I_As

(ω)Φ₂

φ₂(y₁,y₂) ×

R^M R^M

(

) (

)

∑

∫ ∫

∑

N y1,fv1,

vq1

gq₁

N y2, fv2, vq2

gq₂

ρk,k2,n1 (dv1)ρk2,ℓ,n2 (dv2)πk

k,k₂,ℓ=1 n1,n2=0D D

q₁=1

q₂=1

(

) (

)

∑

∫ ∫

∑

N y1,fu1,

u^p

1gp₁

N y2,fu2, u^p

2gp₂

ρ^i,i2^,m1 (du1)ρi2,j,m2 (du2)πi

i,i₂,j=1 m₁,m₂=0D D

p₁=1

p₂=1

∫

× dy₂dy₁ =

φ₂(y₁,y₂)dy₂dy₁.

R^M R^M

{

}

Справедливость утверждения леммы в общем случае E

I_As

(ω)Φ_r

проверя-

ется аналогично. Лемма 3 доказана.

Оценим сверху норму ошибки Δ_r = x_r - x_r. Из определения матриц Ξ, Ψ

и Γ следует, что

∑

(Π.8)

Γ_1,r ≜ Ψ_1,r - Ξ_1,r =

Ψ_1,t-1γ_tΨ_t+1,r.

t=1

Проводя преобразования, аналогичные выкладкам для Δ₁, получаем, что

[

]



∥Δ_r∥₁ ≤

 Γ^⊤1,rπ1 - 1Γ^⊤1,rπI



≤

1Ξ^⊤1,rπ

(Π.9)

∑

≤2

1Ψ^⊤t+1,rγ^⊤tΨ^⊤1,t-1π.

1Ξ^⊤1,rπ

t=1

Для оценки вклада каждого слагаемого в (Π.9) используем (Π.5). Для

простоты изложения рассмотрим случай r = 3, функцию φ(y₁, y₂, y₃) : R^3M →

→R₊

φ(y₁, y₂, y₃) = 1ψ^⊤(y₃)γ^⊤(y₂)ψ^⊤(y₁)π

и O₃-измеримую случайную величину Φ ≜φ(Y1,Y2,Y3)

. Оценим сверху сле-

1Ξ^⊤1,3(Y₁,Y₂,Y₃)π

дующее математическое ожидание:

∫

{

}

∑

I_As (ω)Φ

π_iψ^ij(y₁)γ^jk(y₂)ψ^km(y₃)dy₃dy₂dy₁ =

i,j,k,m=1

R^M R^M R^M

∫

∑ L∑

∑

π_i

̺^ij

γ^jk(y2)dy2

̺^kmn =

ℓ

i,j,k=1

ℓ=1

m=1 n=1

R^M

∫

∑ L∑

∑

∑∑

=W π_i

̺^ij

γ^jk(y2)dy2 ≤ Wδ

π_i

̺^ijℓ ≤ W²δ.

ℓ

i,j=1

ℓ=1

k=1

i=1

j=1 ℓ=1

R^M

Действуя аналогичным образом, можно показать, что для произвольного

r≥2

{

}

1Ψ^⊤t+1,rγ^⊤tΨ^⊤1,t-1

E I_As(ω)

≤ W^r-1δ.

1Ξ^⊤1,rπ

{

}

Тогда окончательно E I_As(ω)∥Δr∥1

≤ 2rW^r-1δ, и истинность второго нера-

венства (5.8) следует из того, что неравенство вверху выполняется для любого

π ∈ Π.

Теорема 2 доказана.

СПИСОК ЛИТЕРАТУРЫ

Wonham W. Some applications of stochastic differential equations to optimal non-

linear filtering // SIAM J. Contr. Optim. 1964. P. 347-369.

Rabiner L.R. A tutorial on hidden Markov models and selected applications in speech

recognition // Proc. IEEE. 1989. V. 77. P. 257-286.

Ephraim Y., Merhav N. Hidden Markov processes // IEEE Transactions on Infor-

mation Theory. 2002. V. 48. No. 6. P. 1518-1569.

Cappé O., Moulines E., Ryden T. Inference in Hidden Markov Models. Berlin:

Springer, 2005.

Elliott R.J., Aggoun L., Moore J.B. Hidden Markov Models: Estimation and Control.

New York: Springer, 2008.

Kloeden P., Platen E. Numerical Solution of Stochastic Differential Equations.

Berlin: Springer, 1992.

Kahaner D., Moler C., Nash S. Numerical Methods and Software. New Jersey: Pren-

tice Hill, 1989.

Isaacson E., Keller H. Analysis of Numerical Methods. New York: Dover Publica-

tions, 1994.

Stoer J., Bulirsch R. Introduction to Numerical Analysis. New York: Springer, 1993.

10.

Кушнер Г. Вероятностные методы аппроксимации в стохастических задачах

управления и теории эллиптических уравнений. М.: Физматлит, 1985.

11.

Kushner H., Dupuis P. Numerical Methods for Stochastic Control Problems in Con-

tinuous Time. New York: Springer, 2001.

12.

Ito K., Rozovskii B. Approximation of the Kushner Equation for Nonlinear Filter-

ing // SIAM J. Contr. Optim. 2000. V. 38. No. 3. P. 893-915.

13.

Clark J. The design of robust approximations to the stochastic differential equations

of nonlinear filtering / J.K. Skwirzynski (ed.), Communication systems and random

process theory. Amsterdam. Sijthoff and Noordhoff, 1978.

14.

Malcolm V., Elliott R., van der Hoek J. On the numerical stability of time-discretized

state estimation via Clark transformations // Proc. 42nd IEEE Conf. Decis. Contr.

2003. Maui. P. 1406-1412.

15.

Yin G., Zhang Q., Liu Y. Discrete-time approximation of Wonham filters // J. Con-

trol Theory Appl. 2004. No. 2. P. 1-10.

16.

Platen E., Bruti-Liberati N. Numerical Solution of Stochastic Differential Equations

with Jumps in Finance. Berlin: Springer, 2010.

17.

Crisan D., Kouritzin M., Xiong J. Nonlinear filtering with signal dependent obser-

vation noise // Electron. J. Probab. 2009. No. 14. P. 1863-1883.

18.

Dragan V., Morozan T., Stoica A. Mathematical Methods in Robust Control of

Discrete-Time Linear Stochastic Systems. New York: Springer, 2010.

19.

Dragan V., Aberkane S. H₂-Optimal Filtering for Continuous-Time Periodic Linear

Stochastic Systems with State-Dependent Noise // Syst. Control Lett. 2014. No. 66.

P. 35-42.

20.

Борисов А.В. Фильтрация Вонэма по наблюдениям с мультипликативными шу-

мами // АиТ. 2018. № 1. C. 52-65.

Borisov A.V. Wonham Filtering by Observations with Multiplicative Noises // Au-

tom. Remote Control. 2018. V. 79. No. 1. P. 39-50.

21.

Борисов А.В. Применение методов оптимальной фильтрации для оперативно-

го оценивания состояний сетей массового обслуживания // АиТ. 2016. № 2.

C. 115-141.

Borisov A.V. Application of Optimal Filtering Methods for On-Line of Queueing

Network States // Autom. Remote Control. 2016. V. 77. No. 2. P. 277-296.

22.

Хубер П. Робастность в статистике. М.: Мир, 1984.

23.

Anderson B., Moore J. Optimal Filtering. New Jersey: Prentice Hill, 1979.

24.

Takeuchi Y., Akashi H. Least-squares state estimation of systems with state-

dependent observation noise // Automatica. 1985. V. 21. No. 3. P. 303-313.

25.

Борисов А.В. Фильтрация состояний марковских скачкообразных процессов по

дискретизованным наблюдениям // Информатика и ее применения. 2018. Т. 12.

№. 3. C. 115-121.

26.

Bäuerle N., Gilitschenski I., Hanebeck U. Exact and Approximate Hidden Markov

Chain Filters Based on Discrete Observations // Statistics & Risk Modeling. 2016.

V. 32. No. 3-4. P. 159-176.

27.

James M., Krishnamurthy V., Le Gland F. Time Discretization of Continuous-Time

Filters and Smoothers for HMM Parameter Estimation // IEEE Trans. Autom.

Contr. 1996. V. 42. No. 2. P. 593-605.

28.

Бертсекас Д., Шрив С. Стохастическое оптимальное управление. Случай дис-

кретного времени. М.: Физматлит, 1985.

29.

Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.: Наука, 1974.

30.

Cvitanić J., Liptser R., Rozovskii B. A filtering approach to tracking volatility

from prices observed at random times //Annals Appl. Probab. 2006. V. 16. No. 3.

P. 1633-1652.

31.

Боровков А.А. Асимптотические методы в теории массового обслуживания. М.:

Физматлит, 1995.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 02.03.2020

После доработки 20.05.2020

Принята к публикации 09.07.2020