Автоматика и телемеханика, № 11, 2020

(Институт проблем передачи информации РАН, Москва;

Казанский федеральный университет),

К.С. КОЛОСОВ (kirill.kolosov.com@mail.ru)

(Институт проблем передачи информации РАН, Москва)

РОБАСТНОЕ ОЦЕНИВАНИЕ НА ОСНОВЕ МЕТОДА

НАИМЕНЬШИХ МОДУЛЕЙ И ФИЛЬТРА КАЛМАНА¹

Предлагается новый подход для решения задачи фильтрации в линей-

ных системах по неполным измерениям, где характеристики динамиче-

ского шума точно неизвестны, а в измерениях могут присутствовать ано-

мальные негауссовские ошибки. В основе предлагаемого алгоритма лежит

идея совместного использования адаптивного фильтра Калмана и обоб-

щенного метода наименьших модулей. На примерах численного модели-

рования показано, что в сравнении с классическим методом оптимальной

линейной фильтрации решение обладает меньшей чувствительностью к

кратковременным выбросам в измерениях и обеспечивает быструю на-

стройку параметров динамики системы. Предлагаемый алгоритм может

быть использован для решения навигационной задачи на борту летатель-

ных аппаратов или для решения задачи сопровождения цели. Для реали-

зации метода наименьших модулей используется эффективный алгоритм

L₁-оптимизации.

Ключевые слова: фильтр Калмана, метод наименьших модулей, L₁-оп-

тимизация, адаптивная фильтрация, робастная фильтрация, навигация,

отказоустойчивость, негауссовские шумы.

DOI: 10.31857/S0005231020110057

1. Введение

Методы фильтрации широко используются в задачах, где необходимо по-

лучать оценку состояния системы в реальном времени на основе выборки из-

мерений нарастающего объема. Более точно, предположим, что на момент t_i,

i ∈ N, имеется выборка наблюдений Y_i = y(t₀),...,y(t_i), каждое наблюдение

является реализацией случайной величины с условной плотностью распре-

деления f(y(t_i) | x(t_i), Y_i-1), где x(t_i) ∈ X, а X - пространство состояний

системы. Динамика системы описывается марковским процессом, в котором

состояние системы x(t_i) в момент времени t_i связано с состоянием систе-

мы x(t_i-1) в момент времени t_i-1 через условную плотность распределения

φ(x(t_i) | x(t_i-1)). При решении задачи фильтрации основной интерес пред-

ставляет апостериорная плотность распределения p(x(t_i) | Y_i). Известно, что

¹ Работа выполнена частично за счет средств субсидии, выделенной в рамках Госу-

дарственной поддержки Казанского (Приволжского) федерального университета в целях

повышения его конкурентоспособности среди ведущих мировых научно-образовательных

центров.

когда наблюдения и динамика системы описываются линейными уравнения-

ми, а f и φ представляют собой гауссовские распределения, искомая плот-

ность p(x(t_i) | Y_i) также является гауссовской и задача имеет аналитическое

решение. В этом случае уравнения динамики и наблюдений имеют вид:

x(t_i) = F (t_i-1, t_i)x(t_i-1) + n(t_i-1, t_i),

(1)

y(t_i) = Hx(t_i) + ξ(t_i),

где F (t_i-1, t_i) - матрица прогноза состояния; H - постоянная матрица наблю-

дений; n(t_i) и ξ(t_i) - векторы нормально распределенных случайных величин,

таких что

cov(n(t_i-1, t_i), n(t_i-1, t_i)) = Q(t_i-1, t_i),

(2)

cov(ξ(t_i), ξ(t_i)) = R(t_i).

Параметры апостериорной плотности распределения p(x(t) | Y_t) - вектор ма-

тематических ожиданий и ковариационная матрица - рассчитываются в со-

ответствии с рекуррентным алгоритмом Калмана, который состоит из двух

шагов:

• Прогнозирование:

x(t_i) = F (t_i-1, t_i)x(t_i-1),

(3)

P (t_i) = F (t_i-1, t_i

P (t_i-1)F^T(t_i-1, t_i) + Q(t_i-1, t_i);

• Коррекция оценки состояния по текущим измерениям:

P (t_i)H^T(

P (t_i)H^T + R)^-1,

(4)

x(t_i) = x(t_i) + K(y(t_i) - H x(t_i)),

P (t_i) = (I - KH

P (t_i).

Такая оценка является оптимальной по критерию минимума дисперсии ошиб-

ки оценивания [1, 2]. Фильтр Калмана нашел широчайшее применение в за-

дачах навигации [3-5]. Но предположение о нормальности распределений не

всегда является адекватным. Например, в навигационных системах ЛА для

коррекции инерциальных датчиков нужно использовать радионавигацион-

ные системы, измерения которых могут быть подвержены помехам. Под воз-

действием помех вид распределения ошибок измерений f(y(t) | x(t), Y_t-1) мо-

жет существенно отличаться от нормального. В таких условиях применение

фильтра Калмана в оригинальном виде в системах с избыточными измере-

ниями снижает надежность решения в целом, так как наличие аномальных

ошибок хотя бы в одном измерении приводит к аномальным ошибкам в оцен-

ке всех компонент вектора состояния. Для повышения устойчивости оценки

к аномальным ошибкам измерений необходимо использовать робастные ме-

тоды фильтрации.

Модель динамики системы также может стать источником аномальных

ошибок оценки. Такая проблема возникает, например, в задаче сопровожде-

ния маневрирующей цели, где модель динамики системы может существен-

но изменяться во времени. В работах [2, 6] приводится описание адаптив-

ных алгоритмов, нацеленных на решение задачи оптимальной фильтрации в

условиях неопределенности модели динамики системы и модели измерений.

Фильтры Лайниотиса-Калмана хорошо решают задачу идентификации си-

стем с гауссовскими шумами, но применение этих алгоритмов в системах,

где ошибки измерений могут быть существенно негауссовскими, мало изуче-

но. Существуют адаптивные алгоритмы, которые основаны на сопоставлении

теоретических значений ковариационных матриц ошибок измерений и оши-

бок оценки с фактическими, рассчитанными по выборке измерений. Такие

алгоритмы рассматриваются в публикациях [4, 7-9]. В [10] рассматривается

алгоритм робастной фильтрации с использованием квадратичного критерия.

В [11-13] предлагается робастная форма фильтра Калмана, где используется

М-оценка для обнаружения и устранения аномальных измерений. Отмечает-

ся, что использование L₁-нормы ошибок в штрафной функции для М-оценки

существенно повышает устойчивость решения по отношению к аномальным

ошибкам негауссовского типа [14].

В [14] также отмечается, что одновременное достижение свойств робастно-

сти и адаптивности в общем случае не представляется возможным: свойство

адаптивности обычно рассматривается в контексте повышения эффективно-

сти оценки при условии симметричных распределений ошибок, а свойство

робастности рассматривается в контексте повышения стабильности решения

в случае асимметричных распределений. При этом рассматривать адаптив-

ность в контексте асимметричных распределений не имеет смысла. Цель дан-

ной статьи - разработка такого метода фильтрации, который в один момент

времени будет обладать либо свойством адаптивности, либо свойством ро-

бастности, но выполняться это переключение должно автоматически.

Предлагается новый подход, в котором для обнаружения и устранения

аномальных измерений на каждой итерации используется метод наименьших

модулей. Одновременно с этим используется метод сопоставления ковариаци-

онных матриц для настройки параметров динамики системы и метод филь-

трации Калмана для получения оценки текущего состояния. На численных

примерах будет показано, что предлагаемый алгоритм повышает устойчи-

вость решения к асимметричным помехам в измерениях и повышает эффек-

тивность решения в некоторых случаях симметричных негауссовских помех.

Используемый в алгоритме метод наименьших модулей минимизирует

L₁-норму ошибок в избыточной системе линейных уравнений. Эта процедура

требует применения специальных методов оптимизации, так как рекурсив-

ный метод наименьших квадратов, применяемый в [11-13], не дает точного

решения и обладает численной нестабильностью, которая приводит к пробле-

ме выбора критерия сходимости [15]. Поэтому в статье уделяется внимание

численным методам, которые могут быть использованы для эффективной

реализации алгоритма на ЭВМ (см. подраздел 3.1).

В разделе 2 рассматриваются основные соотношения адаптивных алгорит-

мов, основанных на принципе сопоставления ковариационных матриц. В раз-

деле 3 дается описание предлагаемого алгоритма, который основан на методе

наименьших модулей. В разделе 4 представлены результаты моделирования

и сравнение характеристик предлагаемого алгоритма с методом оптимальной

фильтрации Калмана.

2. Адаптивный фильтр Калмана, основанный на сопоставлении

ковариационных матриц

Адаптивные алгоритмы разделяются на две категории. К первой относят-

ся алгоритмы, в которых оцениваются элементы матриц F и H в уравнени-

ях (1). Эти алгоритмы разрабатываются в контексте задач идентификации

системы. Ко второй категории относятся алгоритмы, где оцениваемыми па-

раметрами являются элементы матриц Q и R, т.е. предполагается, что харак-

теристики динамического шума и шума измерений точно неизвестны. Будем

рассматривать алгоритмы, относящиеся ко второй категории.

Предположим, что в модели

(1)-(2) в матрицах Q и R содержит-

ся p неизвестных элементов a_i, i = 1, . . . , p. Расположим их в векторе a =

= [a₁, a₂, . . . , a_p]^T размерности p. С учетом (3)-(4) и в соответствии с [16] оцен-

ка вектора a по критерию максимума правдоподобия может быть получена

на основе уравнения:

{

∑

∂P(t_i)

∂ x(t_i)^T

tr P (t_i)^-1

-2

H^TP_r(t_i)^-1r(t_i) +

∂a_k

i=1

(5)

}

∑

{[

]∂P_r(t_i)



P_r(t_i)^-1 - P_r(t_i)^-1r(t_i)r(t_i)^TP_r(t_i)^-1



∂a_k



i=1

a=a^∗(t_i)

для k = 1, 2, . . . , p, где

r(t_i) = y(t_i) - H x(t_i),

(6)

P_r(t_i) =

P (t_i)H^T + R.

Но решения уравнения (5) в замкнутой форме не существует. В [16] приво-

дится упрощенное уравнение для субоптимальной оценки матриц Q и R с

осреднением на скользящем окне фиксированной ширины N:

∑

[

]

R (t_i) =

r (t_j ) r (t_j )^T -

P (t_j)H^T

j=i-N+1

(7)

∑

r(t_j )r(t_j)^T -

P (t_i)H^T,

j=i-N+1

∑

[

Q (t_i) =

K (t_j) r (t_j)r (t_j)^T K (t_j)^T +

(8)

j=i-N+1

]

+ P (t_j) - F (t_j-1,t_j)P (t_j-1)F (t_j-1,t_j

)^T

В уравнении (7) предполагается, что матрица Q известна. В уравнении (8),

наоборот, полагается, что матрица R известна. Осреднение (7) и (8) справед-

ливо для установившегося режима, ширина окна N в этом случае выбирается

такой, что дальнейшее увеличение ширины не приводит к существенному уве-

личению эффективности оценки. Чтобы использовать адаптивный фильтр

в нестационарной задаче, ширина окна должна подбираться эмпирически -

большие значения N будут приводить к инерционности оценки, а малень-

кие значения увеличат шум оценки. В нестационарной задаче осреднение на

скользящем окне можно заменить простым α-фильтром:

(

)

(9)

R(t_i) = (1 - α)R(t_i-1) + α r(t_j)r(t_j )^T -

P (t_i)HT

Q(t_i) = (1 - α)Q(t_i-1) +

(

)

(10)

+ α K(t_i)r(t_i)r(t_i)^TK(t_i)^T + P(t_i) - F(t_i-1,t_i)P(t_i-1)F(t_i-1,t_i)T ,

где 0 < α < 1 - настраиваемый коэффициент. Так как на момент t_i для рас-

четаQ(t_i) необходимо знать P (t_i), оценка находится в две итерации: снача-

ла осуществляется оценка в соответствии с (3)-(4), где матрица Q задана в

соответствии с априорной моделью (2), затем рассчитывается оценка

Q(t_i),

после чего вновь применяется алгоритм (3)-(4), где матрица Q уже заменена

наQ(t_i).

Алгоритмы, основанные на оценке (7) и (8) в различных вариациях ис-

пользуются в публикациях [7-9]. Необходимо иметь в виду, что при попытке

одновременной оценки R и Q могут возникнуть проблемы, так как в этом

случае ошибки вR будут неотличимы от ошибок вQ и оценка может быть

смещенной.

3. Робастный фильтр Калмана с идентификацией отказов

на основе метода наименьших модулей

Предлагаемый в настоящей статье метод отличается от адаптивного ал-

горитма (6)-(10) публикации [16] тем, что для оценки дисперсии измерений

вместо (9) используется апостериорная невязка измерений, полученная после

применения метода наименьших модулей (МНМ).

Рассмотрим линейную систему (1). На каждом шаге фильтрации известен

вектор измерений y(t_i), прогнозное значение вектора состояния x(t_i), кова-

риационные матрицы R(t_i)

P (t_i). Робастный алгоритм состоит из следую-

щих шагов:

1. Прогноз состояния в соответствии с (1)-(2);

2. Используя измерения на текущем шаге y(t_i) и прогноз состояния x(t_i),

находим оценку вектора состояния x_L1(t_i) по методу наименьших модулей;

3. Обнаружение и идентификация отказов. Для обнаружения отказа

используем критерий Неймана-Пирсона и в случае обнаружения вычисляем

оценку ковариационной матрицы измеренийR(t_i) в зависимости от величины

невязок y(t_i) - H x_L1(t_i);

4. Используя оценку ковариационной матрицы измеренийR(t_i), находим

значение ковариационной матрицы динамического шумаQ(t_i) в соответствии

c (10);

5. Вычисляем оценку текущего состояния системы в соответствии с (3)-(4),

заменив Q(t_i-1, t_i) и R на их оценкиQ иR соответственно.

Пункт 1 эквивалентен оптимальному алгоритму фильтрации Калмана.

Далее рассмотрим пп. 2-5 более подробно. Точное описание шагов представ-

лено в алгоритме 1.

3.1. Оценка состояния по методу наименьших модулей

Целью метода наименьших модулей является минимизация L₁-нормы век-

тора ошибок. L₁-норма вектора рассчитывается как сумма модулей его эле-

ментов, и для одномерного случая решением задачи минимизации будет ме-

дианное значение

(11)

θL₁ = Median(z) = arg min [L1(z - θ)] ,

∑_N

где z - вектор, θ - скаляр и L₁(z - θ) =

|z_(i) - θ|.

i=1

Если элементы вектора z - независимые случайные величины, распреде-

ленные по закону Лапласа с одинаковыми параметрами

(

√

)

z_(i) ∼ Laplace(y;µ,σ) =

√

exp

|y - µ|

i = 1,...,N,

то медиана (11) является оценкой максимума правдоподобия центрального

параметра распределения. В [14, 17] отмечается свойство робастности стати-

стик, основанных на L₁-метрике, которые оказываются более устойчивыми к

выбросам в больших выборках. Несмотря на то, что для случая нормального

распределения вектора z оценка (11) является менее эффективной по сравне-

нию со средним арифметическим, именно свойство робастности делает (11)

предпочтительной в задачах, где в выборке могут присутствовать аномаль-

ные ошибки.

Рассмотрим применение L₁-метрики на примере системы линейных урав-

нений

(12)

z = Hx + ǫ,

где H - матрица наблюдений, x - вектор оцениваемых параметров, ǫ - ошиб-

ки измерений, z - вектор измерений (размерность z ≥ размерности x). Оцен-

кой x_L1 вектора x по методу наименьших модулей будем называть оценку

(13)

x_L1 = arg min [L₁

(z - Hx)]

при условии, что ошибки измерений независимые и с единичной дисперсией

[

]

C =E

ǫǫ^T

= I.

В общем случае, когда ковариационная матрица ошибок измерений C = I,

задача может быть сведена к (12)-(13) через процедуру декорреляции из-

мерений. Так как ковариационная матрица положительно определенная и

симметричная, она допускает разложение

(14)

LDL^T

= C,

где D - диагональная матрица со строго положительными диагональными

элементами. Это означает, что матрицу D можно представить в виде произ-

ведения D = D^1/2D^1/2. Тогда справедливо:

ǫ_d = D^-1/2L^-1ǫ,

[

]

(

ǫ_dǫ^Td

=D^-1/2L^-1C

L^-1

)^T D^-1/2 =

(

)(

)

(

)_-1

= D^-1/2L^-1LD^1/2 D^1/2L^T

L^T

D^-1/2

= I.

Таким образом, для произвольной ковариационной матрицы C можно све-

сти задачу к (12)-(13), заменив z, H, ǫ на z_d, H_d, ǫ_d соответственно:

z_d = D^-1/2L^-1z,

H_d = D^-1/2L^-1H.

Разложение (14) может быть получено также через разложение Холецкого

L = chol(C), LL^T = C,

где матрица L - нижняя треугольная со строго положительными элемента-

ми на диагонали. Самым простым подходом к решению задачи минимиза-

ции является итерационный метод наименьших квадратов, который предла-

галось использовать в [11-13] для получения M-оценки. Но при решении за-

дачи L₁-оптимизации итерационный метод наименьших квадратов обладает

численной нестабильностью, которая приводит к проблеме выбора критерия

сходимости [15]. В [18, 19] показано, что задача (12)-(13) сводится к задаче

линейного программирования, решение которой может быть получено более

эффективными алгоритмами, чем итерационный метод наименьших квадра-

тов. Минимизируемая функция представляется в виде

(

)

∑



∑

=

(15)

ǫ_d(i)

ǫ_1(i) +

ǫ_2(i)

→ min

i=1

с ограничениями





[

]

H_d,I_(n×n),-I_(n×n)

· ǫ₁

=zd,

(16)

ǫ₂

ǫ_1(i) ≥ 0, ǫ_2(i) ≥ 0, i = 1,... ,n.

Для повышения эффективности алгоритма в [20] осуществляется переход к

двойственной форме задачи (15)-(16)

(

)

∑

(17)

z_d(i) (b_i - 1)

→ max

i=1

для системы





∑



H_d(i,1)











H^Tdb =



ⁱ⁼¹ . . .





,

(18)



∑







H_d(i,m)

i=1

0 ≤ b_(i) ≤ 2, i = 1,...,n.

Далее, для решения задачи (17)-(18) можно применить симплекс-метод.

Чтобы повысить скорость сходимости в [20] предложена специальная моди-

фикация симплекс-метода. Подробное описание алгоритма L₁-оптимизации

можно найти в [20].

Теперь рассмотрим применение метода наименьших модулей в задаче

фильтрации. На каждом шаге имеется вектор измерений y(t_i) и прогноз век-

тора состояния x(t_i), а также их ковариационные матрицы R(t_i)

P (t_i) со-

ответственно. Составим из этих векторов один и назовем его расширенным

вектором измерений:

[

]_T

z_e(t_i) =

y(t_i)^T, x(t_i)^T

[

]

(19)

R(t_i)

0_(m×n)

C_e(t_i) =

0_(n×m)

P (t_i)

где C_e - ковариационная матрица расширенного вектора измерений z_e. С уче-

том (1)

z_e(t_i) = H_ex(t_i) + ǫ(t_i),

(20)

[

]

H_e(t_i) =

H(t_i)^T, I_(n×n)

^T,

где ǫ(t_i)

- вектор случайных величин с ковариационной матрицей

cov(ǫ(t_i), ǫ(t_i)) = C_e(t_i).

Используя разложение Холецкого LL^T = chol(C_e(t_i)) для ковариацион-

ной матрицы расширенного вектора измерений, осуществим декоррелирую-

щее преобразование:

z_d (t_i) = H_d (t_i) x(t_i) + ǫ_d (t_i) = L^-1z_e (t_i),

H_d (t_i) = L^-1H_e (t_i) ,

ǫ_d (t_i) = L^-1ǫ(t_i) ,

причем

(

)

(

)

cov ǫ_d (t_i) , ǫ_d (t_i)T

= L-1 cov ǫ(t_i),ǫ(t_i)T L-T =

(21)

= L^-1C_eL^-T = L^-1LL^TL^-T = I.

Таким образом, задача сведена к задаче (15)-(16), и теперь, применив ме-

тод L₁-оптимизации, можно получить оценку вектора состояния x(t_i) по ме-

тоду наименьших модулей

x_L1(t_i) = arg min(L1(zd(ti) - Hd(ti)x)) .

(22)

Для реализации разложения Холецкого на ЭВМ рекомендуется использовать

алгоритм, приведенный в [21].

3.2. Обнаружение отказов и расчет ковариационной матрицы измерений

При нормальном функционировании системы распределение ошибок изме-

рений и ошибок прогноза состояния предполагается гауссовским с нулевым

математическим ожиданием. В случае отклонений от модели будем полагать,

что ошибка соответствующего измерения имеет ненулевое математическое

ожидание. Рассмотрим две конкурирующие гипотезы

H₀ : E [z_d(t_i)] = H_dx(t_i),

H₁ : E [z_d(t_i)] = H_dx(t_i) + AΔ,

где A - матрица коэффициентов (модель отклонений), Δ - параметры модели

отклонений. Учитывая, что cov(ǫ_d(t_i), ǫ_d(t_i)^T) = I, подходящая для проверки

гипотез статистика может быть получена в виде [22]

(23)

T = zTd B_k(BTk B_k)^-1BTk z_d,

где rank(B_k) = (m + n) - n = m, m - размерность вектора измерений, n -

размерность вектора состояния, (m + n) - размерность расширенного век-

тора измерений и B^TkH_d = 0. Матрица B_k может быть получена через QR-

разложение матрицы H_d:

[

]

[Q_k, B_k]

= qr(H_d).

0_(m-n×n)

Для реализации QR-разложения рекомендуется использовать алгоритм, при-

веденный в [21]. В зависимости от принятой гипотезы статистика (23) будет

иметь нецентральное распределение хи-квадрат с m степенями свободы и

различным значением параметра нецентральности [22, 23]:

H₀ : T ∼ χ²(m,0);

H₁ : T ∼ χ²(m,λ).

Здесь λ - параметр нецентральности, рассчитываемый в зависимости от при-

нятой модели отказа. В соответствии с леммой Неймана-Пирсона наиболее

мощным критерием выбора гипотез является критерий вида

H₀ : T ≤ c(m);

(24)

H₁ : T > c(m);

где пороговое значение c(m) рассчитывается как значение аргумента функ-

ции распределения χ²(m, 0), при котором эта функция равна заданному зна-

чению вероятности ошибок первого рода η:

(25)

c(m) = F^-1(m, η, 0).

χ²

Вероятность ошибок второго рода рассчитывается как

β = F_χ2(c(m),m,λ),

где F_χ2 (c(m), m, λ) - значение функции вероятности нецентрального χ²-рас-

пределения с m степенями свободы и параметром нецентральности λ в точ-

ке c(m). Значение параметра нецентральности с учетом (21) рассчитывается

в соответствии [22]:

(

)_-1

λ=z^TdB^TkA

A^TB_kB^TkA

A^TB_kz_d.

Для обнаружения отказа используется единичная матрица A = I. Тогда при-

менение критерия (24) решает задачу обнаружения отказа с минимальным

значением вероятности ошибок второго рода при λ = c(m):

β_min = F_χ2 (c(m),m,c(m)).

На практике эта вероятность ограничивается сверху значением β_TH в со-

ответствии с требованиями, предъявляемыми к системе. Случай когда

β_min > β_TH, означает, что конфигурация системы в принципе не может обес-

печить достаточно низкий уровень ошибок второго рода.

В зависимости от того, обнаружен ли отказ (принята гипотеза H₁) или

не обнаружен (принята гипотеза H₀), вычисляется оценка ковариационной

матрицы измерений

(26)

R(t_i) = (LDL^T)_(1:m,1:m),

где LL^T = chol(C_e(t_i)) (см. (19)), D - диагональная матрица, элементы кото-

рой рассчитываются по невязкам измерений по методу наименьших модулей:

{ ρ(Δ_(j)), если H₁,

D_(j,j) =

иначе

для j = 1, . . . , m и Δ = z_d - H_d x_L1(t_i). Вид функции ρ нужно подобрать так,

чтобы условие ρ(x) > 1 выполнялось только с вероятностью ложной трево-

ги α при условии выбора H₀. Аналитическое решение такой задачи выходит

за рамки данного исследования, поэтому использовалась эмпирическая ку-

сочно гладкая функция:





если |x| < 5,

(27)

ρ(x) =

(1 + (|x| - 5)),

если 10 > |x| ≥ 5,



√

(1 + (|x| - 5)) · (1 + 4

|x| - 10), если |x| ≥ 10.

3.3. Оценка ковариационной матрицы динамического шума

и оценка текущего состояния

Для получения оценки

Q сначала нужно рассчитать коэффициент уси-

ления калмановского фильтра K и апостериорную ковариационную матри-

цу P . Для их вычисления используется априорно заданная ковариационная

матрица динамического шума Q и рассчитанная с использованием (26)-(27)

ковариационная матрица измерений R:

P =F(t_i-1,t_i

P (t_i-1) F^T (t_i-1, t_i) + Q (t_i-1, t_i) ,

(

)_-1

PH^T

PH^T +R(t_i)

(

)

P (t_i) = I - KH

Введем обозначения:

dx =Kr(t_i),

(28)

Q_dx = dx · dx^T,

Q_p = P(t_i) - F(t_i-1,t_i)P(t_i-1)F(t_i-1,t_i)^T,

где r(t_i) - априорная невязка измерений, вычисляемая в соответствии с (6).

Тогда соотношение (10) можно записать в виде

(29)

Q(t_i) = (1 - α)Q(t_i-1) + α (Q_dx + Q_p

Вычисление оценки

Q(t_i) через соотношение (29) может привести к про-

граммным ошибкам, так как оно не гарантирует положительной определенно-

сти результирующей матрицы. Чтобы избежать этих проблем, будем искать

оценку в следующей форме:

Q(t_i) = V Q(t_i-1, t_i)V^T,

V_(l,l) > 0,

V_(l,j) = 0 при l = j,

где l = 1, . . . , n, j = 1, . . . , n, V - диагональная матрица со строго положитель-

ными элементами на диагонали. Обозначим через γ_j отношение j-го диаго-

нального элемента матрицы в правой части (29) к j-му диагональному эле-

менту номинальной матрицы динамического шума:

(

)

(1 - α)Q(t_i-1)_(j,j) + α

dx,(j,j) + Qp,(j,j)

γ_j

Q(t_i-1, t_i)_(j,j)

Если значения элементов матрицы V рассчитывать по правилу

{ 1,

если γ_j < 1,

(30)

V_(j,j) =

√γ_j иначе,

то, в случае когда γ_j > 1 для всех j = 1, . . . , n, выполняется условие

{

}

{

}

(31)

trace V Q(t_i-1, t_i)VT

= trace

(1 - α)Q(t_i-1) + α (Q_dx + Q_p)

В остальных случаях диагональные элементы матрицы

Q ограничиваются

снизу соответствующими значениями диагональных элементов матрицы Q.

В соответствии с (31) необходимо вычислять приближенное значение дис-

персий элементов вектора dx. Чтобы сделать оценку более робастной, вос-

пользуемся известным фактом, что для нормального распределения отноше-

ние среднеквадратического отклонения (RMS) к среднему абсолютному от-

√

клонению (MAD) является постоянной величиной RMS/MAD =

(π/2). Это

нетрудно доказать:

∫∞

(

)

(a - µ)²

E[|x - µ|] =

|a - µ|

√

exp

da =

2π

2σ²

−∞

∫∞

(

)

√

∫

∞

√

a-µ

(a - µ)²

√

exp

da = 2

σ bexp(-b²)db =

σ.

2π

2σ²

В то же время MAD является более робастной статистикой, когда в вы-

борке присутствуют выбросы. Для применения робастной статистики при вы-

численииQ перепишем (29) в виде:



G(t_i)_(j,j) = (1 - α) G(t_i-1)_(j,j) + α ·

dx_(j)

,

j = 1,...,n,

Q_p (t_i) = (1 - α)Qp (t_i-1) + αQ_p,

(32)

(

)₂

G(t_i)_(j,j)

+ Qp (t_i)

(j,j)

γ_j

Q (t_i-1, t_i)_(j,j)

Далее выполняем основной шаг фильтрации:

Q(t_i) = V Q(t_i-1, t_i)V^T;

P_a = F(t_i-1,t_i

P (t_i-1)F^T(t_i-1, t_i) +Q(t_i);

(33)

K = P_aH^T(HP_aH^T + R(t_i))^-1;

x(t_i) = x(t_i) + Kr(t_i);

P (t_i) = (I - KH)P_a.

Здесь V вычисляется в соответствии с (30) и (32), аR вычисляется в соответ-

ствии с (26). На основе приведенных выше соотношений строится алгоритм 1,

который обеспечивает рекуррентную оценку состояния системы, идентифика-

цию отказов в измерениях и адаптивную настройку коэффициента обратной

связи.

Алгоритм 1 (одна итерация робастного фильтра).

Входные данные:

текущее время t_i;

оценка состояния с предыдущего шага x(t_i-1)

P (t_i-1);

оценка составляющих ковариационной матрицы прогноза с предыдущего

шагаQp(t_i-1), G(t_i-1);

матрица наблюдений H и матрица прогноза F (t_i-1, t_i);

номинальная ковариационная матрица динамического шума Q(t_i-1, t_i);

вектор измерений y(t_i) и его номинальная ковариационная матрица R(t_i).

Выходные данные:

оценка состояния x(t_i)

P (t_i);

оценка составляющих ковариационной матрицы прогнозаQp(t_i), G(t_i).

1. Прогноз состояния на текущий момент.

x = F(t_i-1,t_i)x(t_i-1);

P =F(t_i-1,t_i

P (t_i-1)F^T(t_i-1, t_i) + Q(t_i-1, t_i).

2. Составить расширенный вектор измерений z_e(t_i) и его ковариационную

матрицу C_e(t_i) в соответствии с (19).

3. Составить матрицу наблюдений H_e для расширенного вектора измере-

ний в соответствии с (20).

4. Осуществить разложение Холецкого матрицы C_e:

C_e = chol(C_e) = LL^T.

5. Осуществить декорреляцию вектора псевдоизмерений:

z_d = L^-1z_e; H_d = L^-1H_e.

6. С использованием симплекс-метода L₁-оптимизации (см. [20]) решить

задачу:

x_L1(t_i) = arg min (L₁(z_d(t_i) - H_d(t_i)x)).

7. Осуществить QR разло[ение матр]цы Hd:

R_k

H_d = qr(H_d) = [Q_k,B_k]

0_(m-n×n)

8. Рассчитать тестовую статистику:

T = zTd B_k(BTk B_k)^-1BTk z_d.

9. Рассчитать пороговое значение c(r) для заданного значения вероятности

ложной тревоги α в соответствии с (25) (в данном случае число степеней

свободы равно числу измерений, т.е. размерности вектора y).

10. Если (T ≥ c(r)), то принимается гипотеза H₁, ковариационная матрица

измеренийR(t_i) рассчитывается в соответствии с (26) для Δ = z_d -H_d x_L1(t_i).

11. Иначе принимается гипотеза H₀, ковариационная матрица измерений

остается номинальной:R(t_i) = R(t_i);

12. Осуществить шаг фильтрации с использованием номинального значе-

ния ковариационной матрицы динамического шума:

P =F(t_i-1,t_i

P (t_i-1)F^T(t_i-1, t_i) + Q(t_i-1, t_i);

PH^T(

PH^T +R(t_i))^-1;

P (t_i) = (I -KH

13. Рассчитать адаптивные параметры:

dx =K(y(t_i) - H x);

Q_p = P(t_i) - F(t_i-1,t_i

P (t_i-1)F^T(t_i-1, t_i).

14. Рассчитать G(t_i),Qp(t_i) и γ в соответствии с (32).

15. Рассчитать V в соответствии с (30).

16. Рассчитать оценку ковариационной матрицы динамического шума:

Q(t_i) = V Q(t_i-1, t_i)V^T.

17. Рассчитать оценку текущего состояния и его ковариационной матрицы

(33):

P_a = F(t_i-1,t_i

P (t_i-1)F^T(t_i-1, t_i)+Q(t_i); K = P_aH^T(HP_aH^T +R(t_i))^-1;

x(t_i) = x + K(y(t_i) - H x)

P (t_i) = (I - KH)P_a.

18. Конец.

4. Результаты тестирования

Для проверки рабочих характеристик алгоритма моделировалось движе-

ние цели в одномерном пространстве. Задача состояла в оценке текущей коор-

динаты цели, а также ее скорости и ускорения по зашумленным измерениям

координаты, т.е. решалась задача фильтрации по неполным измерениям. Ис-

пользовалась следующая модель динамики системы в непрерывном времени:





dh(t)





dx(t) =

 dv(t)

 = Ax(t)dt + Bdw(t);

da(t)

















 0 0 1

; B=

 0

.

√s

Здесь h(t) - координата цели, v(t) - скорость цели, a(t) - ускорение цели,

w(t) - винеровский случайный процесс, s > 0 - интенсивность динамического

шума. В дискретном времени модель динамики принимает вид:

x(t_i) = F (t_i-1, t_i)x(t_i-1) + n_i;





Δt Δt²/2





F (0, Δt) =

 0

Δt

;

∫Δt

Q(0, Δt) = cov(n_i, n_i) = F (0, t)BB^TF^T(0, t)dt =





(Δt⁵)/20 (Δt4)/8 (Δt3)/6





=s·

 (Δt⁴)/8 (Δt³)/3 (Δt²)/2

.

(Δt³)/6

(Δt²)/2

Δt

Для проверки отказоустойчивости алгоритма использовалась модель систе-

мы с двукратным резервированием (два датчика с одинаковыми номиналь-

ными характеристиками синхронно измеряют координату цели):

y(t_i) = Hx(t_i) + ξ_i;

[

]

H =

;

[

]

R = cov(ξ_i,ξ_i) =

Использовались следующие значения параметров: вероятность ложной тре-

воги η = 5 · 10^-4, параметр сглаживания α = 0,01 (см. (32)), параметр дина-

мики системы s = 0,1. Частота измерений 10 Гц (t_i - t_i-1 = 0,1). В ходе те-

стирования истинная траектория и фактические наблюдения формировались

в соответствии с соотношениями:

dx_true(t) = Ax_true(t)dt + Bdw(t) + u(t),

y(t_i) = Hx(t_i) + ξ_i + δ_i.

Здесь u(t) и δ_i имитировали неучтенные ошибки.

Для демонстрации адаптивных и робастных свойств фильтра были разра-

ботаны различные сценарии моделирования:

Сценарий 1. Маневр цели в виде полета по кругу с постоянным цен-

тростремительным ускорением a_max = 20 ед/c² и угловой скоростью ω =

= 2π/10 рад/c. В этом случае проекция траектории на одну из осей декар-

товой системы координат представляет собой гармонические колебания во

времени (u(t) = a_max · sin(ωt)).

Сценарий 2. В одном из измерений присутствует аддитивный гауссовский

шум δ_i,(1) ∼ N(0,100) (первый параметр - математическое ожидание, вто-

рой - среднеквадратическое отклонение (СКО)), δ_i,(2) = 0.

Сценарий 3. Оба измерения содержат аддитивный некоррелированный

гауссовский шум: δ_i,(1) ∼ N (0, 100), δ_i,(2) ∼ N (0, 100).

Сценарий 4. Ошибки измерений δ_i представляют собой независимые слу-

чайные величины (с.в.), распределенные по закону Коши. Для такого распре-

деления дисперсия и математическое ожидание не определены, но определена

медиана.

Сценарий 5. Для одного из измерений добавочная ошибка представляет

собой кусочно линейную функцию δ_i,(1) = 0 для t_i < t_s и δ_i,(1) = k(t_i - t_s) для

t_i ≥ t_s, t_s = 50, k = 0,4.

Сценарий 6. В измерениях с заданной вероятностью присутствует смещен-

ная гауссовская ошибка: δ_i = Λψ_i, где Λ - диагональная матрица, на диагона-

ли которой располагаются независимые дискретные с.в. принимающие зна-

чения либо 0, либо 1 с заданной вероятностью P_j ; ψ - вектор независимых

гауссовских с.в. ψ_i ∼ N (100, 3).

В задаче навигации в качестве датчиков, измеряющих положение объекта,

могут выступать приемники сигналов глобальных навигационных спутнико-

Оценка для маневрирующей цели

-20

-40

100

150

200

250

300

CКО ошибка оценки (осреднение по времени)

100

150

200

250

300

Время, с

Рис. 1. Имитация маневра цели по сценарию 1. Показана проекция на одну ось

декартовой системы координат. 1 - робастный фильтр, 2 - фильтр Калмана.

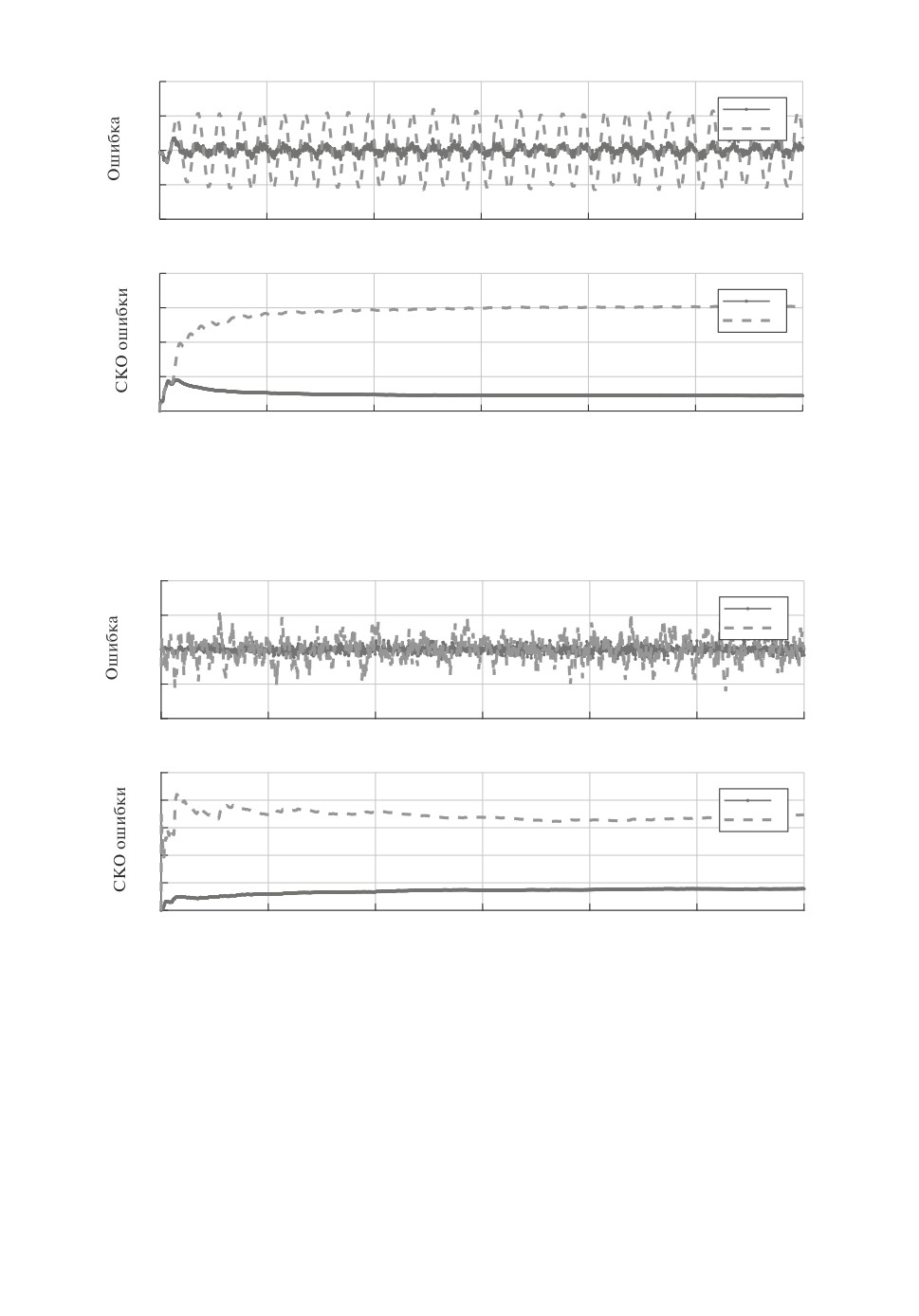
Оценка по измерениям с гауссовским загрязнением в одном источнике

100

-50

-100

100

150

200

250

300

CКО ошибка оценки (осреднение по времени)

100

150

200

250

300

Время, с

Рис. 2. Моделирование по сценарию 2 с загрязнением измерений одного из ис-

точников аддитивным гауссовским шумом. 1 - робастный фильтр, 2 - фильтр

Калмана.

вых систем. Известно, что сигналы спутниковых навигационных систем об-

ладают низкой помехозащищенностью. В последнее время ведутся активные

исследования в направлении борьбы с так называемым “спуфингом”

- ти-

пом помех, которые имитируют ложный сигнал (в качестве примера можно

привести публикацию [24]). Сценарии 5 и 6 моделируют именно такой тип

ошибок.

Оценка по измерениям с гауссовским загрязнением

400

200

-200

-400

100

150

200

250

300

CКО ошибка оценки (осреднение по времени)

100

150

200

250

300

Время, с

Рис. 3. Моделирование по сценарию 3 с загрязнением всех измерений адди-

тивным гауссовским шумом. 1 - робастный фильтр, 2 - фильтр Калмана.

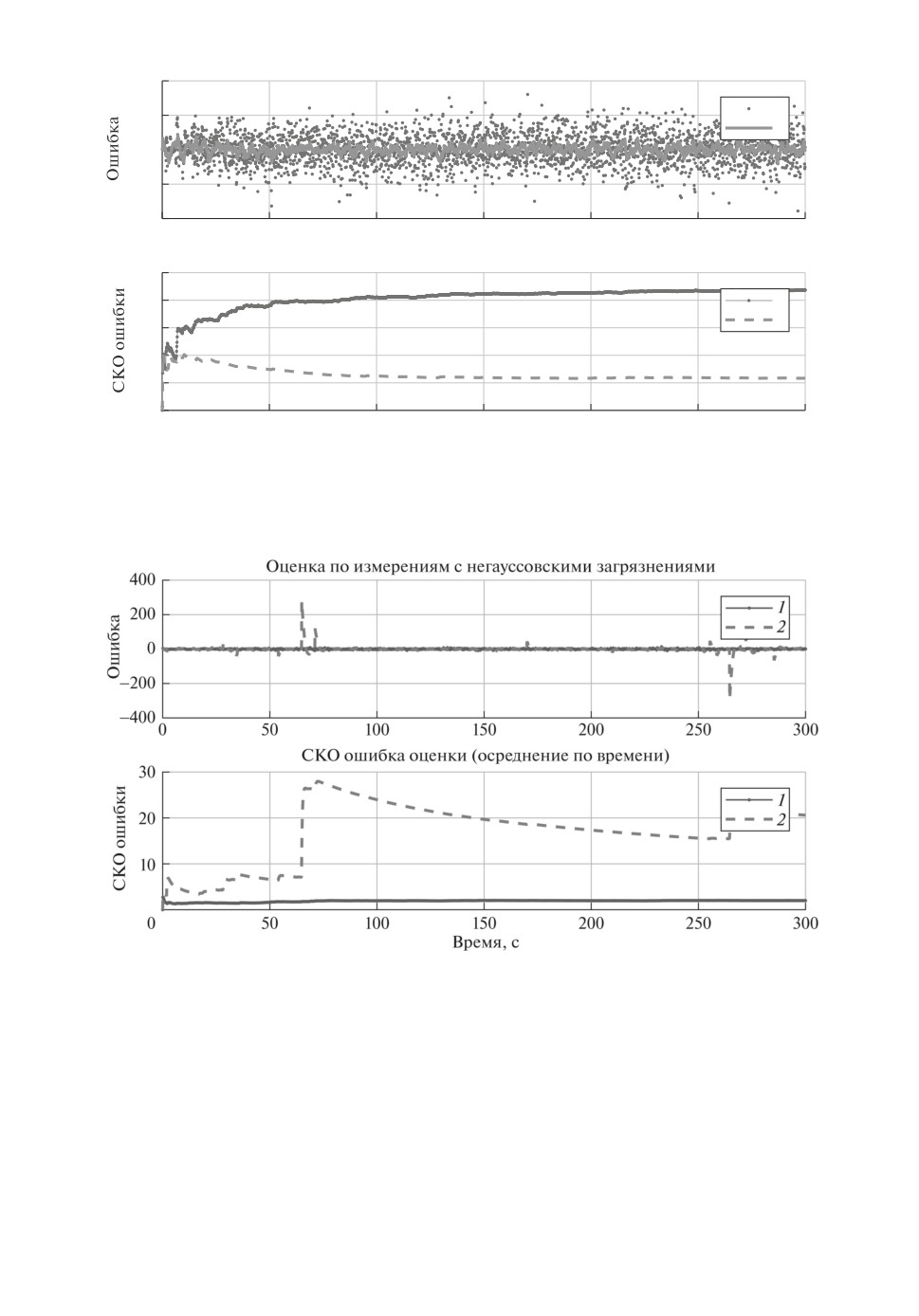
Рис. 4. Моделирование по сценарию 4 с загрязнением измерений ошибками,

распределенными по закону Коши. 1 - робастный фильтр, 2 - фильтр Кал-

мана.

Результаты моделирования по сценариям 1-5 показаны на рисунках 1-5

соответственно. Робастный фильтр обладает адаптивными свойствами и су-

щественно повышает эффективность в смысле уменьшения дисперсии оши-

бок оценки в сценариях 1, 2 и 4. Моделирование по сценарию 3 показывает,

что эффективность робастного фильтра снижается по сравнению с фильтром

Калмана. Такой результат объясняется тем, что алгоритм со временем спи-

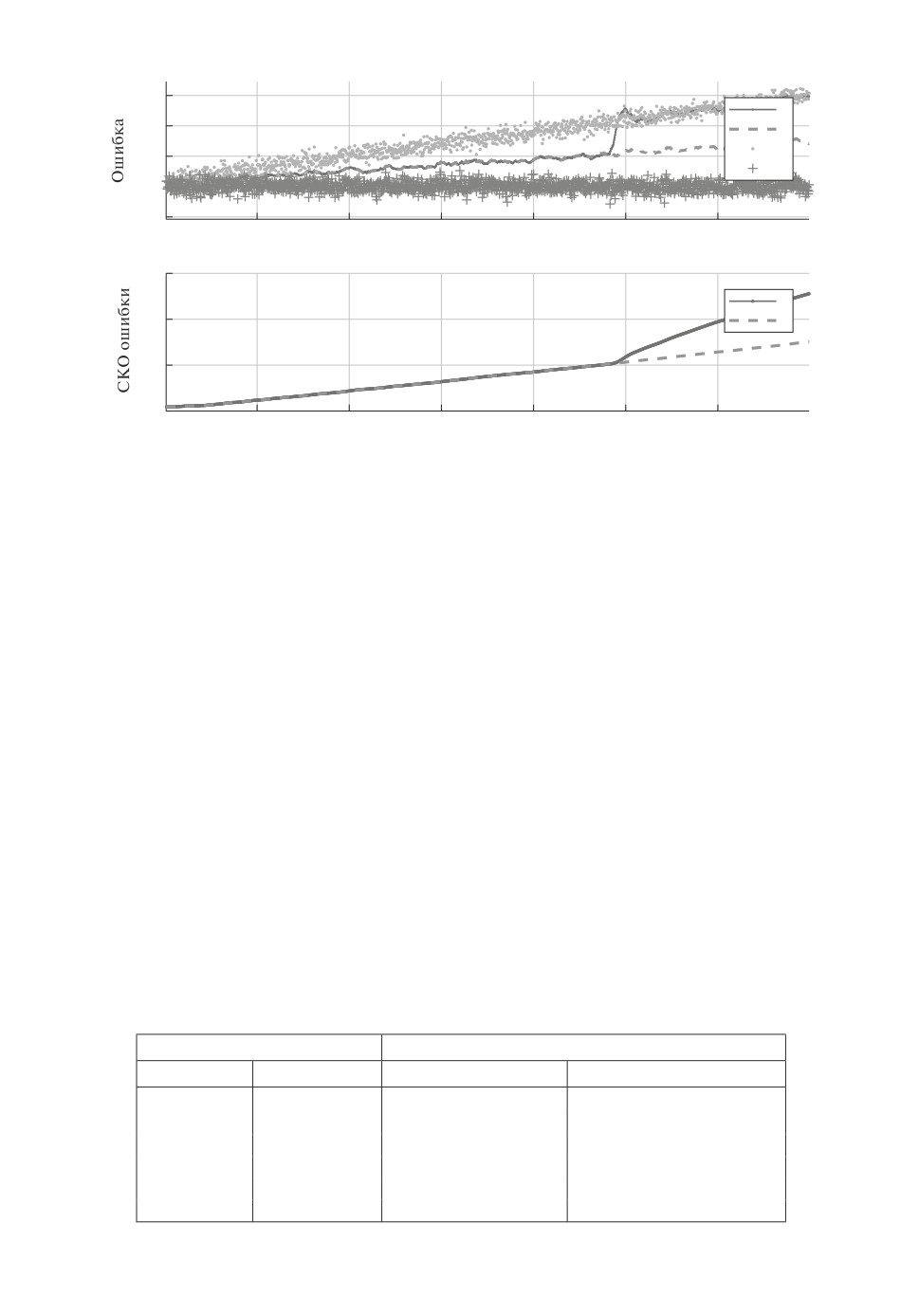
Оценка по измерениям с линейным увеличением ошибки

-20

100

120

140

160

180

CКО ошибка оценки (осреднение по времени)

100

120

140

160

180

Время, с

Рис. 5. Моделирование по сценарию 5 с нарастающим математическим ожида-

нием ошибки в одном источнике измерений. 1 - робастный фильтр, 2 - фильтр

Калмана, 3 - измерения первого источника, 4 - измерения второго источника.

сывает большие невязки измерений на ошибки модели, что приводит к увели-

чению коэффициента обратной связи. Интересно, что результаты моделиро-

вания по сценарию 4 существенно отличаются от результатов моделирования

по сценарию 3, хотя и в том и в другом случае моделируется симметричное

распределение неучтенных ошибок. Возможно, различия связаны с тем, что

для распределения Коши не определены математическое ожидание и диспер-

сия, и поэтому неустойчивость оценки калмановского фильтра объясняется

применением квадратичного критерия. В разработанном алгоритме робаст-

ной фильтрации применяется метод наименьших модулей, который в одно-

мерном случае дает оценку медианы (о связи метода наименьших модулей

с медианой говорилось в подразделе 3.1). Можно предположить, что именно

это свойство делает робастный фильтр более устойчивым к распределению

Коши.

Моделирование по сценарию 5 продемонстрировало специфику работы

фильтра в условиях медленного увеличения систематической ошибки в одном

Сравнения СКО оценок h(t) робастного фильтра и фильтра Калмана

при обработке загрязненных измерений по сценарию 6

Вероятность загрязнения

СКО оценки

источник 1 источник 2 робастный фильтр фильтра Калмана

1,02

45,7

1,04

45,6

0,1

0,7

11,5

0,3

0,9

28,9

0,5

60,8

47,7

0,7

83,7

65,9

измерении. Робастный фильтр равновероятно выбирает один из источников

и отслеживает его измерения как достоверные, снижая вес измерений дру-

гого источника. На рис. 5 показан пример, когда алгоритмом был выбран

источник, содержащий ошибку.

По результатам моделирования сценария 6 составлена таблица. Данные

таблицы показывают, что устойчивость робастного фильтра к моделируемым

помехам зависит от вероятности, с которой помехи появляются в измерениях.

Если помехи присутствуют только в одном источнике измерений, то робаст-

ный фильтр существенно повышает точность оценки. Если же помехи при-

сутствуют во всех источниках с вероятностью больше 0,5, точность оценки

резко ухудшается.

5. Заключение

Разработан алгоритм робастной фильтрации, который обладает свойством

отказоустойчивости по отношению к аномальным ошибкам в измерениях и

адаптивными свойствами по отношению к изменяющимся параметрам моде-

ли динамического шума системы. Было проведено численное моделирование

решения задачи сопровождения цели в линейной системе с двукратным ре-

зервированием измерений.

Результаты моделирования показывают, что робастный фильтр повышает

эффективность оценки по сравнению с классическим фильтром Калмана,

когда цель выполняет неучтенные в модели маневры. Одновременно с этим

обеспечивается устойчивость оценки к систематическим ошибкам в одном из

источников измерений, а также к симметричным помехам, распределенным

по закону Коши. Разработанный алгоритм устойчив к импульсным помехам

в более чем 30 % измерений.

В другой ситуации, когда в модели не учитывается увеличение диспер-

сии нормального шума по всем измерениям, эффективность оценки робаст-

ного фильтра снижается. В случае когда ошибки по всем источникам изме-

рений содержат смещенную составляющую, отказоустойчивость обеспечива-

ется только условно: существует пороговое значение вероятности появления

смещенной ошибки в измерениях, для которой эффективность оценки резко

снижается. Разработанный алгоритм неустойчив к медленному увеличению

математического ожидания ошибки в одном из источников измерений.

Для компенсации указанных недостатков может потребоваться исполь-

зование дополнительных источников измерений, что является предметом

дальнейших исследований. Другим направлением дальнейших исследова-

ний является использование разработанного метода в нелинейных системах.

Так как разработанный алгоритм относится к классу алгоритмов “прогноз-

коррекция”, для работы с нелинейными системами можно попробовать заме-

нить шаги прогноза и коррекции на соответствующие процедуры, например

метода псевдоизмерений [3] или сигма-точечного фильтра [25].

СПИСОК ЛИТЕРАТУРЫ

1. Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.: Наука, 1974.

2. Синицын И.Н. Фильтры Калмана и Пугачева. М.: Логос, 2006.

Miller A.B., Miller B.M. Tracking of the UAV trajectory on the basis of bearing-only

observations // 53rd IEEE Conf. on Decision and Control. Los Angeles, CA. 2014.

P. 4178-4184.

Salychev O.S. Mems-based Inertial Navigation: Expectations and Reality. M.: Bau-

man Moscow State Technical University, 2012.

Времеенко К.К., Желтов С.Ю., Ким Н.В., Козорез Д.А., Красильщиков М.Н.,

Себряков Г.Г., Сыпало К.И., Черноморский А.И. Современные информацион-

ные технологии в задачах навигации и наведения беспилотных маневренных

летательных аппаратов. М.: Физматлит, 2009.

Lainiotis D. Optimal adaptive estimation: Structure and parameter adaption //

IEEE T. Autom. Contr. 1971. No. 16. P. 160-170.

Yang Y., Gao W. An Optimal Adaptive Kalman Filter // J. Geodesy. 2006. No. 80.

P. 177-183.

Mohamed A.H., Schwarz K.P. Adaptive Kalman Filtering for INS/GPS

J. Geodesy. 1999. No. 73. P. 193-203.

Reina G., Vargas A., Nagatani K., Yoshida K. Adaptive Kalman Filtering for GPS-

based Mobile Robot Localization // Int. Workshop on Safety, Security and Rescue

Robotics. Rome, Italy, September 2007.

10.

Босов А.В., Панков А.Р. Робастное рекуррентное оценивание процессов в сто-

хастических системах // АиТ. 1992. № 9. C. 102-110.

Bosov A.V., Pankov A.R. Robust Recurrent Estimations of Processes in Stochastic

Systems // Autom. Remote Control. 1992. V. 53. No. 9. P. 1395-1402

11.

Koch K.R., Yang Y. Robust Kalman Filter for Rank Deficient Observation Models //

J. Geodesy. 1998. No. 72. P. 436-441.

12.

Chang Guobin, Liu Ming. M-estimator-based Robust Kalman Filter for Systems

with Process Modeling Errors and Rank Deficient Measurement Models // Nonlinear

Dynam. 2015. No. 80. P. 1431-1449.

13.

Cao L., Qiao D., Chen X. Laplace L1 Huber Based Cubature Kalman Filter for

Attitude Estimation of Small Satellite // Acta Astronaut. 2018. V. 148.

http://10.1016/j.actaastro.2018.04.020.

14.

Huber P.J. Robust statistics. Wiley series in probability and mathematical statistics.

1981.

15.

Armstrong R.D., Frome E.L. A Comparison of Two Algorithms for Absolute Devi-

ation Curve Fitting // J. Amer. Statist. Association. 1976. V. 71:354. P. 328-330

16.

Maybeck P.S. Stochastic Models, Estimation, and Control. Academic Press. 1982.

V. 2. P. 70-129.

17.

Kotz Samuel, Kozubowski Tomasz J., Podgorski Krzysztof. The Laplace Distribution

and Generalizations. Springer, 2001.

18.

Barrodale Ian, Roberts F. An Improved Algorithm for Discrete L1 Linear Approxi-

mation // Siam J. Numer. Anal. 1973. No. 10. P. 839-848.

19.

Abdelmalek Nabih N. On the Discrete Linear L1 Approximation and L1 Solutions of

Overdetermined Linear Equations // J. Approx. Theory. 1974. No. 11. P. 38-53.

20.

Abdelmalek Nabih N. An Efficient Method for the Discrete Linear L1 Approximation

Problem // Math. Comput. 1975. V. 29. No. 131. P. 844-850.

21.

Hogben L. Handbook of Linear Algebra. Second Edition. CRC Press, 2013.

22.

Teunissen P.J.G. Distributional Theory for the DIA Method // J. Geodesy. 2018.

V. 92. P. 59-80.