Автоматика и телемеханика, № 11, 2020

Ю.П. ЕМЕЛЬЯНОВА, канд. физ.-мат. наук (emelianovajulia@gmail.com)

(Арзамасский политехнический институт (филиал)

Нижегородского государственного технического

университета им. Р.Е. Алексеева)

УПРАВЛЕНИЕ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ ДИСКРЕТНЫМИ

СТОХАСТИЧЕСКИМИ СИСТЕМАМИ С ПЕРЕКЛЮЧЕНИЯМИ¹

Рассматриваются дискретные линейные системы с переключениями в

повторяющемся режиме. Системы находятся под действием случайных

внешних возмущений, и в измерениях присутствуют аддитивные шумы.

Предлагаются два метода синтеза управления с итеративным обучени-

ем. Оба метода основаны на построении вспомогательной 2D-модели в

форме дискретного повторяющегося процесса. Первый метод основан на

установлении условий диссипативности указанной модели при специаль-

ном выборе функций запаса и накопления. Такой выбор позволяет за-

тем найти управление, в общем случае нелинейное, которое гарантирует

сходимость процесса обучения. Второй метод использует линейный за-

кон коррекции управления с итеративным обучением заданного вида, при

этом сходимость процесса обучения гарантируется условиями устойчиво-

сти вспомогательной 2D-модели. Оба предложенных закона управления

используют в своей структуре стационарный фильтр Калмана. Для полу-

чения условий устойчивости используется дивергентный метод векторных

функций Ляпунова. Приводится пример, демонстрирующий возможности

и особенности нового метода.

Ключевые слова: управление с итеративным обучением, стохастические

системы, системы с переключениями, повторяющиеся процессы, 2D-си-

стемы, устойчивость, диссипативность, векторная функция Ляпунова.

DOI: 10.31857/S0005231020110069

1. Введение

Управление с итеративным обучением играет важную роль в повышении

точности систем, функционирующих в повторяющемся режиме, в частности

в разработке высокоточных роботов-манипуляторов. В связи с высокой эф-

фективностью и относительно простой формой такого управления оно при-

влекает широкий интерес как теоретиков, так и практиков. Начиная с конца

80-х гг. XX в. на крупнейших международных конференциях регулярно ор-

ганизуются сессии, посвященные проблемам управления с итеративным обу-

чением.

Реальные системы находятся под действием случайных возмущений, и в

системах всегда присутствуют как систематические, так и случайные погреш-

ности измерений. Эти факторы снижают точность управления, к тому же

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 19-08-00528_а).

следует учесть, что одним из условий эффективности итеративного обуче-

ния является то, что для каждого повторения процесса начальные условия

должны быть одинаковыми. Таким образом, учет упомянутых случайных

факторов имеет существенное значение.

Впервые идея управления с итеративным обучением была предложена в

патенте США [1] с приоритетом от 1967 г., затем концепция такого управ-

ления была сформулирована в [2] на японском языке. Эти результаты не

были востребованы, пока не появилась серия публикаций [3-6], вызвавшая

широкий интерес как теоретиков, так и практиков. В дальнейшем, по раз-

личным вопросам управления с итеративным обучением было опубликова-

но большое количество работ, в том числе монографии [7, 8], обзорные ста-

тьи [9, 10] и специальные выпуски журналов (Int. J. Control. 2000, 2011; Asian

J. Control. 2002, 2011). В настоящее время управление с итеративным обуче-

нием стало важным направлением интеллектуального управления, и оно ши-

роко используется во многих практических приложениях, в первую очередь

в робототехнике.

Обзор результатов по стохастическому управлению с итеративным обу-

чением представлен в [11, 12]. Эти обзоры и самостоятельный анализ пуб-

ликаций в базе SCOPUS показывают, что решению задачи стохастического

управления с итеративным обучением в классической постановке (измерения

содержат шумы и на объект управления действуют случайные возмущения)

посвящено небольшое число работ, основное внимание уделяется учету слу-

чайных потерь информационных пакетов в канале связи между измеряемым

выходом и входом (random packet losses, data dropouts). Исследование этих

вопросов, безусловно, важно, но оно не заменяет и не исключает исследова-

ний упомянутых классических задач.

Анализ упомянутых публикаций показывает, что конструктивные методы

синтеза стохастического управления с итеративным обучением в рамках клас-

сической постановки предложены в [13-18] для линейных систем с дискрет-

ным временем, другие работы учитывают только дополнительные к класси-

ческой постановке случайные факторы. В этих работах предложены алго-

ритмы двух типов. В [13, 14] предложен так называемый алгоритм D-типа,

использующий для построения алгоритма управления с итеративным обуче-

нием аналог производной ошибки обучения, в [15], дополнительно предложен

алгоритм P-типа, непосредственно использующий ошибку обучения, этот ал-

горитм затем был расширен и усовершенствован в [16], в [17, 18] рассмотрены

некоторые специальные вопросы, связанные со сходимостью и оптимизацией

этих алгоритмов.

В [19-21] задача управления с итеративным обучением решается на основе

предложенного авторами дивергентного метода векторных функций Ляпу-

нова в сочетании с использованием фильтра Калмана. Сравнительный ана-

лиз показал, что полученные результаты позволяют во много раз увеличить

скорость сходимости ошибки обучения по сравнению с [13-16], кроме того,

за счет применения фильтра Калмана существенно уменьшается дисперсия

ошибки.

В [22] для дискретных линейных систем с постоянными параметрами пред-

ложен алгоритм управления с итеративным обучением на основе совместно-

го применения метода супервектора [8] и фильтра Калмана. В силу того что

в [22] решается специальная задача, связанная с вариациями эталонной тра-

ектории, сравнить результаты этой работы c [13-16] и [19-21] не представ-

ляется возможным. По-видимому, по этой причине в [22] публикации [13-16]

даже не упоминаются.

В данной статье результаты [19, 20] распространяются на системы с пе-

реключениями. В современной теории управления под системами с переклю-

чениями обычно понимают класс моделей динамических систем, состоящих

из конечного числа подсистем, из которых в текущий момент времени функ-

ционирует лишь одна, называемая активной подсистемой, при этом выбор

активной подсистемы определяется некоторым логическим правилом. Про-

стейшим примером может служить многорежимная система, в которой под-

системы интерпретируются как отдельные режимы этой системы. Обычно

подсистемы описываются индексированным множеством дифференциальных

или разностных уравнений. Для первоначального знакомства с результатами

теории систем с переключениями можно рекомендовать [23-27]. При управ-

лении с итеративным обучением переключения возникают естественным об-

разом при начальной настройке системы. Например, в случае манипулятора,

перемещающего грузы на конвейер, целесообразно делать несколько повто-

рений без нагрузки и запускать рабочий режим при достижении требуемой

точности.

2. Постановка задачи

Рассмотрим дискретную стохастическую систему в повторяющемся режи-

ме, описываемую линейной моделью c переключениями

x_k(p + 1) = A(k)x_k(p) + B(k)u_k(p) + v_k(p), (A(k),B(k)) ∈ F,

(2.1)

y_k(p) = Cx_k(p),

y_wk(p) = Cx_k(p) + w_k(p), p ∈ [0,T - 1], k = 0,1,... ,

где x_k(p) ∈ Rnx - вектор состояния, y_k(p) ∈ Rny - вектор выходных пере-

менных, y_wk(p) ∈ Rny - вектор измеряемых переменных, u_k(p) ∈ Rnu - век-

тор управления, v_k(p) ∈ Rnv - вектор возмущений, действующих на объект,

w_k(p)∈Rnw - вектор шумов измерений, F={(A₁,B₁),(A₂,B₂),... ,(A_N ,B_N )} -

множество пар матриц согласованных размеров. Предполагается, что v_k(p) и

w_k(p) - независимые гауссовские белые шумы с ковариационными матрицами

E[v_k(p)v^Tk (p)] = S_v, E[w_k(p)w^Tk (p)] = S_w.

Следуя понятиям, принятым в теории систем с переключениями [23], рас-

смотрим кусочно постоянное отображение множества неотрицательных це-

лых чисел Z⁺ → F. Такое отображение задается кусочно постоянной функ-

цией σ : Z⁺ → N = {1, . . . , N} так, что A(k) = A_σ(k) и B(k) = B_σ(k), k =

= 0, 1, 2, . . .

Функцию σ можно рассматривать как сигнал переключения относитель-

но повторений. Предположим, что переключения происходят в начале каж-

дого повторения, и определим моменты переключения k₁, k₂, . . . как номера

повторений, на которых в системе (2.1) происходят переключения. Таким

образом, сигнал переключения определяет на каждом повторении k индекс

i = σ(k) ∈ N активной подсистемы, динамика которой описывается уравне-

ниями

x_k(p + 1) = A_ix_k(p) + B_iu_k(p) + v_k(p), i ∈ N,

(2.2)

y_k(p) = Cx_k(p),

y_wk(p) = Cx_k(p) + w_k(p), p ∈ [0,T - 1], k = 0,1,...

Выходная переменная системы (2.1) на каждом повторении должна вос-

производить желаемую траекторию y_ref (p), 0 ≤ p ≤ N - 1. Для достижения

этой цели можно использовать управление с обратной связью. Обозначим че-

рез e_k(p) ошибку воспроизведения желаемой траектории на k-м повторении:

(2.3)

e_k(p) = y_ref(p) - y_k

(p),

0 ≤ p ≤ T - 1.

Если начальные условия на каждом повторении одинаковы, такое управление

будет обеспечивать одинаковую ошибку воспроизведения желаемой траекто-

рии на всех шагах, причем может оказаться, что величина этой ошибки не

соответствует требованиям по точности. Поставим задачу найти такое управ-

ление, которое последовательно уменьшает ошибку с увеличением числа по-

вторений. Такую задачу может решить управление с итеративным обучением,

которое на очередном повторении определяется соотношением

(2.4)

u_k+1(p) = u_k(p) + Δu_k+1

(p),

где Δu_k+1(p) - корректирующая поправка, формируемая на основе инфор-

мации с предыдущего повторения. Эту поправку будем находить из условия

выполнения соотношений

(2.5)

lim

E[||e_k(p)||] = E||e_∞(p)||, E[||e_k+1(p)||] ≤ E[||e_k(p)||]

∀ k,

k→∞

lim

E[||u_k(p)||] = E[||u_∞(p)||],

0 ≤ p ≤ T - 1,

k→∞

при этом lim_k→∞ E [ || e_k(p) ||² ] и lim_k→∞ E [ || u_k(p) || ] = E [ || u_∞(p) ||² ] долж-

ны оставаться ограниченными для всех 0 ≤ p ≤ T - 1. Соотношение (2.4) мо-

жет рассматриваться как алгоритм итеративного обучения, а значение u_∞(p)

называется обученным управлением.

Замечание 1. В приложениях процесс обучения считается завершен-

ным, когда достигнута требуемая точность. В рассматриваемом случае, когда

система находится под воздействием шумов, адекватной мерой точности мо-

жет служить среднее или среднеквадратичное значение ошибки на интервале

изменения выходной переменной и условие (2.5) является необходимым для

достижения требуемой точности.

Таким образом, задача состоит в нахождении корректирующей по-

правки Δu_k+1(p), обеспечивающей выполнение (2.5) при ограниченности

lim_k→∞ E [ || e_k(p) ||² ] и lim_k→∞ E [ || u_k(p) ||² ] = E [ || u_∞(p) ||² ] для всех 0 ≤

≤ p ≤ T - 1.

Будем предполагать, что моменты переключений наблюдаемы. Поскольку

вектор выходных переменных измеряется с шумами, для его предварительной

обработки используем фильтр Калмана

x_k(p + 1) = A_ix_k(p) + B_iu_k(p) + F_i(y_wk(p) - Cx_k(p)),

(2.6)

x_k(0) = F_iy_wk(0), i ∈ N,

где x_k(p) - оценка вектора состояния и ŷ_k(p) = C x_k(p),

Fi = AiSiC^T[CSiC^T + Sw]^-1

и S_i - решение алгебраического уравнения Риккати

(2.7)

S_i = A_iS_iA^Ti - A_iS_iC^T[CS_iC^T + S_w]^-1CS_iA^Ti + S_w.

Введем в рассмотрение ошибку оценивания x_k(p) = x_k(p) - x_k(p) и вспомога-

тельные векторы приращений по переменной k оценки вектора состояния и

ошибки оценивания,

(2.8)

ηk+1(p + 1) = xk+1(p) - xk(p),

ηk+1(p + 1) = xk+1(p) - xk(p).

Поскольку y_k(p) недоступен для наблюдения, ошибка обучения

e_k(p) = y_ref(p) - y_k(p)

не может быть непосредственно использована для управления. Вместо нее

будем далее использовать оценку

êk(p) = yref (p) - C xk(p).

Запишем уравнения относительно приращений:

ηk+1(p + 1) = Ai11 ηk+1(p) + Ai12 êk(p) + Bi1νk+1(p) + Di1 wk+1(p),

(2.9)

êk+1(p) = Ai21 ηk+1(p) + Ai22 êk(p) + Bi2νk+1(p) + Di2 wk+1(p), i ∈ N ,

где

[

]_T

ηk+1(p) =

ηk+1(p)^T ηk+1(p)^T

ν_k+1(p) = Δu_k+1(p - 1),

[

]_T

w_k+1(p) =

Δv_k+1(p - 1)^T Δw_k+1(p - 1)

Δv_k+1(p - 1) = v_k+1(p - 1) - v_k(p - 1),

Δw_k+1(p - 1) = w_k+1(p - 1) - w_k(p - 1),

[

]

[

]

[

]

A_i - F_iC

-F_i

A_i11 =

B_i1 =

D_i1 =

FiC

A_i

B_i

A_i12 = 0, A_i22 = I, A_i21 = [-CF_iC - CA],

B_i2 = -CB_i, D_i2 = [0 - CF_i].

Система (2.9) относится к классу дискретных повторяющихся процес-

сов, представляющих собой одну из разновидностей так называемых 2D-си-

стем [28]. Особенность таких систем состоит в том, что они разрешены отно-

сительно частных приращений переменных состояния, в случае дискретного

времени, или относительно частных производных переменных состояния, в

случае непрерывного времени, по каждому из независимых аргументов, и

стандартные методы классической и современной теории управления стано-

вятся неприменимыми для их исследования. В последние годы авторы систе-

матически развивали теорию устойчивости, диссипативности и стабилизации

таких систем на основе свойств дивергенции векторных функций Ляпуно-

ва [20, 21, 29-32]. Этот подход, названный дивергентным методом векторных

функций Ляпунова, далее используется для решения поставленной задачи.

3. Устойчивость и диссипативность

Корректирующую поправку будем строить как управление с обратной свя-

зью для системы (2.9) относительно приращений. Развиваемый далее подход

открывает возможность искать это управление в достаточно общем виде

(3.1)

ν_k+1(p) = ϕ(η_k+1(p), ê_k

(p)), ϕ(0, 0) = 0.

В частности, как показано в [19, 20], такая форма корректирующей поправки

расширяет возможности синтеза в случае линейных систем без переключе-

ний.

Определение 1. Дискретный повторяющийся процесс (2.9), (3.1) на-

зывается устойчивым вдоль повторений по второму моменту, если

(3.2)

lim

E[||η_k(p)||² + ||ê_k(p)||²

] ≤ Γ < ∞,

k+p→∞

где Γ не зависит от T .

Дальнейший анализ основан на векторной функции Ляпунова

[

]

V1(ξ)

(3.3)

V_i(ξ,ǫ) =

ξ∈R2nx, ǫ∈Rny

i∈N,

V_2i(ǫ)

где

V₁(ξ) > 0, ξ = 0, V_2i(ǫ) > 0, ǫ = 0, V₁(0) = 0, V_2i(0) = 0, i ∈ N.

Стохастический аналог дивергенции этой функции вдоль траекторий си-

стемы (2.9), (3.1) определяется выражением

DV_i(ξ,ǫ) = E[V₁(η_k+1(p + 1))| η_k+1(p) = ξ, ê_k(t) = ǫ] - V₁(ξ) +

(3.4)

+ E[V_2i(ê_k+1(p))| η_k+1(p) = ξ, ê_k(p) = ǫ] - V_2i

(ǫ), i ∈ N .

Этот оператор представляет сумму средних частных приращений по пере-

менным k и p функции V_i при условии, что аргументы на предыдущем шаге

принимают фиксированные значения ξ и ǫ, и, таким образом, является есте-

ственным обобщением дивергенции на рассматриваемый случай стохастиче-

ской системы.

Обозначим число переключений сигнала σ на интервале (k_s, k_f ) че-

рез N_σ(k_f , k_s) и, следуя общим принципам теории систем с переключени-

ем [23-25], введем в рассмотрение среднее время ожидания в соответствии со

следующим определением.

Определение 2. Положительное число κ_a ∈ Z⁺ называется средним

временем ожидания для сигнала переключения относительно повторений σ,

если для некоторого N₀ ≥ 0

k_f - k_s

(3.5)

N_σ(k_f ,k_s) ≤ N₀ +

k_f ≥ k_s

≥ 0.

κ_a

Неравенство (3.5) означает, что в среднем число шагов между любыми дву-

мя последовательными переключениями на рассматриваемом интервале не

меньше κ_a.

Теорема 1. Eсли существует векторная функция (3.3) и положитель-

ные скаляры c₁, c₂, c₃ и γ, такие что

(3.6)

c₁||ξ||² ≤ V₁(ξ) ≤ c₂||ξ||²,

(3.7)

c₁||ǫ||² ≤ V_2i(ǫ) ≤ c₂||ǫ||²,

(3.8)

DV_i(ξ,ǫ) ≤ γ - c₃(||ξ||² + ||ǫ||²

i∈N,

то дискретный повторяющийся процесс (2.9), (3.1) является устойчивым

вдоль повторений по второму моменту для любого сигнала переключения

относительно повторений σ со средним временем ожидания

)(

(

))_-1

(c₁

c₃

(3.9)

κ_a > ln

c₂

c₁

и произвольным N₀.

Доказательство. Рассмотрим интервал (0,k_f) и обозначим через N_σ =

= N_σ(k_f,0) число переключений на этом интервале. Обозначим

V₁(η_k+1(p)) = E[V₁(η_k+1(p))],

V_2i(ê_k(p)) = E[V_2i(ê_k(p))].

Применяя к обеим частям (3.8) оператор математического ожидания и учи-

тывая (3.4), получим, что

V₁(η_k+1(p + 1))

V_2σ(k+1)(ê_k+1(p)) ≤

(

)

(3.10)

c₃

≤

V₁(η_k+1(p)

V_2σ(k)(ê_k(p)) + γ.

c₂

Левая часть (3.10) является положительно определенной и поскольку c₂ > 0

и c₃ > 0, из (3.10) следует, что 0 < 1 - c3c₂ < 1. Обозначим λ = 1 - c3 и пере-2

пишем (3.10) в виде

V₁(η_k+1(p + 1)) ≤

(3.11)

≤

V₁(η_k+1(p)) +

V_2σ(k)(ê_k(p))

V_2σ(k+1)(ê_k+1(p)) + γ.

Решая неравенство (3.11) относительн

V₁(η_k+1(p)), имеем

V₁(η_k+1(p))

V₁(η_k+1(0))λ^p +

∑[

]

V_2σ(k)(ê_k(h))

V_2σ(k+1)(ê_k+1(h)) λ^p-1-h +

(3.12)

h=0

∑

+γ λ^p-1-q.

q=0

Обозначим

∑

H_k(p) =

V_2,σ(k)(ê_k(p))λ^p-1-q,

q=0

тогда из (3.12) следует, что

H_k+1(p) ≤ λH_k,σ(k)(p) + λ^p

V₁(η_k+1(0)) -

(3.13)

∑

V₁(η_k+1(p)) + γ

λ^p-1-q.

q=0

Пусть на повторении k_n происходит переключение с активной системы i на

активную систему j. Тогда в соответствии с (3.7)

(3.14)

V_2j(y) ≤ µV_2i

(y), i, j ∈ N ,

где

c₂

µ=

≥ 1.

c₁

Решая неравенство (3.13) и учитывая (3.14), получим

H_k(t) ≤ µNσ λ^kH_0,σ(0)(p) +

∑

[

]

+ λ^k-1-n λ

V₁(η_n+1(0))

V₁(η_n+1(p))

n=0





∑



+γ

λ^p-1-q λ^k-1-n,

n=0

q=0

100

откуда

∑

λ^k-1-n

V₁(η_n+1(p)) +

λ^p-1-h

V_2σ(k)(ê_k(h)) ≤

n=0

h=0

∑

≤µNσ λ^k-1-nV₁(η_n+1(p))+ λ^p-1-

V_2σ(k)(ê_k(h)) ≤

n=0

h=0

(3.15)

(

)

∑

≤µNσ λ^p λ^k-1-

V₁(η_n+1

(0)) + λ^k

λ^p-1-h

V_2,σ(0)(ê₀(h))

n=0

h=0





∑



+γ

λ^p-1-qλ^k-1-n.

n=0

q=0

Из неравенства (3.15) с учетом (3.6), (3.7) и того, что η_n+1(0)) = 0, следует,

что





Nσ

∑

(3.16)

E[|η_k(p))|2] ≤

λk

λ^p-1-q

V₂(ê₀(q)) +

c₁

c₁(1 - λ)²

q=0





Nσ

∑

(3.17)

E[|ê_k(p - 1))|2] ≤

λ^k

λ^p-1-q

V₂(ê₀(q)) +

c₁

c₁(1 - λ)²

q=0

Поскольку величина ê₀(p) = y_ref (p) - C x₀(p) ограничена для всех 0 ≤ p ≤

≤ T - 1, то правые части (3.16) и (3.17) будут ограничены тогда и только

тогда, когда µNσ λ^k < 1. Отсюда с учетом (3.5) следует (3.9). Это означает,

что повторяющийся процесс (2.9), (3.1) является устойчивым вдоль повто-

рений по второму моменту для любого сигнала переключения относительно

повторений σ со средним временем ожидания, удовлетворяющим (3.9), и про-

извольным N₀. Теорема 1 доказана.

Из доказательства теоремы вытекает следующий результат.

Следствие. Дискретный повторяющийся процесс (2.9), (3.1) являет-

ся устойчивым вдоль повторений по второму моменту для произвольного

сигнала переключения относительно повторений σ, если существует век-

торная функция

(3.18)

V (ξ, ǫ) = [V₁(ξ) V₂(ǫ)]^T

и положительные скаляры c₁, c₂, c₃, и γ, такие что

c₁||ξ||² ≤ V₁(ξ) ≤ c₂||ξ||²,

(3.19)

c₁||ǫ||² ≤ V₂(ǫ) ≤ c₂||ǫ||²,

DV (ξ,ǫ) ≤ γ - c₃(||ξ||² + ||ǫ||²).

101

Сформируем для системы (2.9) дополнительный вектор выхода z_k+1(p) ∈

∈ Rnz, определяемый выражением

(3.20)

z_k+1(p) = C₁η_k+1(p) + C₂ê_k(p) + C₃v_k+1

(p),

где C₁, C₂ и C₃ - постоянные матрицы согласованных размеров. Следуя [20],

введем определение диссипативности вдоль повторений.

Определение 3. Дискретный повторяющий процесс (2.9) называет-

ся диссипативным вдоль повторений по второму моменту относитель-

но входной переменной ν_k+1(t) и выходной переменной z_k+1(t), определенной

в (3.20), если существуют векторная функция вида (3.3), скалярная функ-

ция S_i(ν_k+1(p), z_k+1(p)), i ∈ N , положительные скаляры c₁, c₂, c₃ и γ, удовле-

творяющие условиям (3.6), (3.7) и

(3.21)

DV_i(ξ,ǫ) ≤ S_i(ν_k+1(p),z_k+1(p)) + γ - c₃(||ξ||² + ||ǫ||²

i∈N.

4. Синтез управления

4.1. Синтез нелинейного управления с переключениями

В теории диссипативности по Виллемсу функции S_i и V_i называются функ-

цией запаса и функцией накопления. Нетрудно видеть, что если при некото-

ром выборе z корректирущая поправка (3.1) удовлетворяет условию

S_i(z_k+1(p),ν_k+1(p)) ≤ 0, i ∈ N,

то система (2.9), (3.1) в соответствии с теоремой 1 будет устойчивой вдоль

повторений по второму моменту для любого сигнала переключения относи-

тельно повторений σ со средним временем ожидания, удовлетворяющим (3.9)

и произвольным N₀. Таким образом, задача сводится к нахождению стаби-

лизирующей тройки {V, z, ν}.

Обозначим

[

]

[

]

[

]

ηk+1(p)

A_i11

A_i12

B_i1

ζ_k+1(p) =

A_i =

B_i =

i∈N,

êk(p)

A_i21

A_i22

B_i2

и определим блочно-диагональную матрицу P_i = diag[P₁ P_2i] ≻ 0 как решение

неравенства Риккати

(4.1)

A^TiP_iA¯ - (1 - σ)P_i

A^TiP_i B_i[BTiP_i B_i + R]^-1 B^TiP_iA¯_i

+ Q ≼ 0, i ∈ N,

где 0 < δ < 1 - положительный скаляр, Q ≻ 0 и R ≻ 0 - весовые матрицы.

Нетрудно видеть, что если система линейных матричных неравенств





(1 - δ)X_i

XA¯^T

X_i





(4.2)



A_iX_i X_i +BiR^-1 B^Ti

 ≽ 0, Xi ≻ 0, i ∈ N,

X_i

Q^-1

102

разрешима относительно

X_i = diag[X₁ X_2i] ≻ 0,

то

P_i = X^-1i, i ∈ N.

Следующая теорема 2 предлагает одно из возможных множеств стабили-

зирующих троек.

Теорема 2. Дискретный повторяющийся процесс (2.9) является дисси-

пативным вдоль повторений по второму моменту с функцией запаса

S_i(ν_k+1(p),z_k+1(p)) = z^Tk+1(p)(BTiP_i B_i + R)^-1z_k+1(p) +

(4.3)

+ 2z_k+1(p)^Tν_k+1(p) + ν_k+1(p)^T[ BTi P_i B_i + R]ν_k+1(p), i ∈ N ,

относительно входной переменной ν_k+1(t) и выходной переменной

(4.4)

z_k+1(p) =BTiP_iA¯_iζ_k+1

(p), i ∈ N ,

где P_i = X^-1i, a X_i = diag[X₁ X₂i] ≻ 0, i ∈ N , является решением (4.1). Мно-

жество корректирующих поправок (3.1), обеспечивающих устойчивость

вдоль повторений по второму моменту системы (2.9), (3.1), определяет-

ся соотношением

(4.5)

ν_k+1(p) = -[BTiP_i B_i + R]^-1 B^Ti

A_iΘ_i(ζ_k+1(p))ζ_k+1

(p), i ∈ N ,

где Θ(ζ) - симметричная матричная функция, удовлетворяющая соотно-

шению

M_i -M_iΘ_i(ζ)-Θ_i(ζ)M_i -Θ_i(ζ)M_i +Θ_i(ζ)M_iΘ_i(ζ)-Q-(δ-µ)P_i ≼0,

(4.6)

i∈N,

для всех ζ ∈ R2nx+ny , где M_i

A^TiP_i B_i[BTiP_i B_i +R]^-1 B^TiP_iA¯_i, 0<µ<σ, i∈N.

Доказательство. Выберем компоненты функции (3.3) в виде квадра-

тичных форм

V₁(ξ) = ξ^TP₁ξ, V₂(ǫ) = ǫ^T P_2iǫ,

где P₁ ≻ 0 и P_2i ≻ 0 - соответствующие диагональные блоки матрицы P_i,

являющейся решением (4.1). Обозначи

ξ = [ξ^T ǫ^T]^T. Последовательно оце-

нивая дивергенцию (3.3) вдоль траекторий (2.9), получим

DV_i(ξ,ǫ) =

(

)

[

]_-1

ξ^T

A^TiP_iA¯_i - (1 - δ)P_i

A^TiP_i B_i

P_i B_i + R

P_iA¯_i + Q

ξ+

[

]^-1 BT

ξ^TA¯^TiP_i B_i

P_i B_i + R

P_iA¯_i

ξ-

(4.7)

ξ^T (Q + δP_i

ξ+

ξ^TA¯^TiP_i B_iν_k+1(p) +

[

]

+ ν_k+1(p)^T BTi P_i B_iν_k+1(p) + 2 tr[P₁S_1i] + tr[P_2iS_2i] ≤

≤

ξ^TA¯^TiP_i B_i[BTiP_i B_i + R]^-1 B^TiP_iA

ξ+

ξ^TA¯^TiP_i Bν_k+1(p) +

[

]

+ν_k+1(p)^T B^TiP_i B_iν_k+1(p)

ξ^T(Q + δP_i

ξ + 2 tr[P₁S_1i] + tr[P_2iS_2i] ,

103

где

[

]

v +FiSw

-F_iS_wF^Ti

S_1i =

S_2i = CF_iS_wF^TiC^T.

−F_iS_wF^Ti

FiSwFiT

Из (4.7) следует, что система (2.9) является диссипативной вдоль повторений

по второму моменту относительно входа ν_k+1(p) и выхода (4.4) с функцией

запаса (4.3) и

{

}

γ = max

2[tr[P₁S_1i] + tr[P₂iS_2i]] ,

c₃ = µ min{λmin(Pi)}.

i∈N

Для корректирующей поправки в виде (4.5) из (4.7) с учетом (4.6) и принятых

обозначений следует, что

(

)

DV_i(η, ê) ≤ -c₃

||ξ||² + ||ǫ||²

+ γ.

Следовательно, в соответствии с теоремой 1, система (4.5), (2.9) устойчива

вдоль повторений по второму моменту для любого сигнала переключения

относительно повторений σ со средним временем ожидания, удовлетворяю-

щим (3.9) и произвольным N₀. Постоянные c₁ и c₂ в (3.9) определятся выра-

жениями

{

}

{

}

c₁ = min λ_min(P₁),min{λmin(P2i)}

c₂ = max λ_max(P₁),max{λmax(P2i)}

i∈N

Теорема 2 доказана.

Замечание 2. Посколькуприращениеошибкиоценивани

ξ_k+1(p) недо-

ступно для формирования корректирующей поправки, матрица Θ_i всегда

должна иметь вид Θ_i(ζ) = diag[0nx Θ_i1(ζ)]. В простейшем случае матрица Θ_i1

может быть выбрана не зависящей от ζ, и тогда, после нахождения матри-

цы P_i, условие (4.6) сводится к системе линейных матричных неравенств,

при этом теорема 1 дает линейную корректирующую поправку. В общем слу-

чае Θ_i(ζ) зависит от изменения ошибки относительно повторений и можно

пытаться уменьшать значения коэффициентов корректирующих поправок

после достижения требуемой точности и, наоборот, увеличивать эти коэф-

фициенты, когда ошибка велика, другими словами, вводить адаптацию к ве-

личине ошибки. Такой подход позволит найти разумный компромисс между

скоростью обучения и энергозатратами на управление. Наиболее просто это

можно сделать за счет кусочно-постоянного изменения Θ в зависимости от

достигнутой точности. Такое решение для систем без переключений рассмот-

рено в [20].

4.2. Синтез линейного управления без переключений

В ряде случаев представляет интерес построить управление без переклю-

чений. Здесь более эффективным представляется другой подход к реше-

нию. Рассмотрим функцию Ляпунова (3.18) с компонентами V₁(ξ) = ξ^TP₁ξ,

104

V₂(ǫ) = ǫ^TP₂ǫ, где P₁ ≻ 0 и P₂ ≻ 0 - постоянные матрицы. Закон коррекции

будем искать в виде линейной обратной связи по приращениям доступных

для измерения переменных и по ошибке:

(4.8)

v_k+1(p) = K₁

ξ_k+1(p) + K₂ê_k(p) = KHζ_k+1(p),

где K = [K₁ K₂], H = [0 Inx+ny ]. Вычисляя дивергенцию (3.18) вдоль траек-

торий (2.9), (4.8), получим

(4.9)

ξ^T

A^Tci

A_ci - P

ξ + 2[tr[P₁S_1i] + tr[P₂S_2i

]],

i∈N,

где

P = diag[P₁ P₂],





A_i - F_iC





A_ci =

 FiC

A_i + B_iK₁

B_iK₂

, i ∈ N.

−CF_iC

-C(A_i + B_iK₁) I - CB_iK₂

Предположим, что матрицы P ≻ 0 и K удовлетворяют системе неравенств

(4.10)

A_i +BiKH)^TP

A_i

B_iKH) - P_i + Q + H^TK^T

RKH ≼ 0, i ∈ N,

где Q ≻ 0 и R ≻ 0 - матрицы, аналогичные весовым матрицам в теории

линейно-квадратичного регулятора. Поскольку выполняется (4.10), то вы-

полняются условия следствия теоремы 1 с параметрами

{

[

]}

(

)

γ = max

tr[P₁S_1i] + tr[P₂S_2i]

c₃ = λ_min

Q+H^TK^TRKH

i∈N

и, таким образом, система (2.9), (4.8) является устойчивой вдоль повторений

по второму моменту для произвольного сигнала переключения относительно

повторений σ. Неравенства (4.10) с помощью известной леммы о дополнении

Шура сводятся к линейным матричным неравенствам и уравнению относи-

тельно переменных X = diag[P^-11 P^-12] , Y , и Z:





A_iX +BiY H)^T X (Y H)^T







A_iX +BiY H







≽ 0,

(4.11)



Q^-1



R^-1

X ≻ 0, HX = ZH, i ∈ N.

Если неравенства и уравнение (4.11) совместны, то K = [K₁ K₂] = Y Z^-1, по-

скольку в силу структуры матрицы H матрица Z является невырожденной.

105

5. Пример

Рассмотрим модель манипулятора c одним гибким звеном [33], функцио-

нирующего в повторяющемся режиме с постоянным периодом повторения в

условиях действия внешних возмущений и шумов измерений. Динамика дви-

жения манипулятора в пространстве состояний описывается уравнениями

x_k(t) = A₀x_k(t) + B₀(u_k(t) + µ_k(t)),

0≤t≤T_f,

(5.1)

y_k(t) = Cx_k(t) + ω_k(t), k = 0,1,2,... ,

[

]_T

где на k-м повторении x_k(t) = θ_k(t) α_k(t)

θ_k(t)

α(t)_k

, θ_k(t) - угол пово-

рота сервопривода, α_k(t) - угол отклонения гибкого звена,



















K_s

B_eq







A₀ =



J_eq













K_s(J_l + J_eq)

B_eq



J_lJ_eq

J_eq





















B₀ =



,

C = [1

0] ,



J_eq











J_eq

B_eq - коэффициент вязкого трения сервопривода, K_s - жесткость гибкого

звена, J_l - момент инерции гибкого звена относительно центра масс, J_eq -

момент инерции сервопривода, µ_k(t) и ω_k(t) - независимые последователь-

ности непрерывных гауссовских шумов с постоянными интенсивностями Q_n

и R_n. Движение гибкого звена происходит в горизонтальной плоскости. Для

построения и анализа управления с итеративным обучением перейдем к эк-

вивалентной дискретной модели с постоянным периодом T_s

(5.2)

x_k(p + 1) = Ax_k(p) + Bu_k(p) + v_k

(p),

y_wk(p) = Cx_k(p) + w_k(p), p = 0,1,... ,NTf , k = 0,1,2,... ,

∫Ts

где A = exp(A₀T_s), B =

exp(A₀τ)B₀dτ, p - номер периода дискретности,

NTf - число периодов дискретности на отрезке [0, T_f], v_k(p) и w_k(p) - незави-

симые последовательности гауссовских дискретных белых шумов с ковариа-

циями

∫Ts

(5.3)

S_v = exp(A₀τ)B₀Q_nB^T0 exp(A^T0 τ)dτ, S_w = R_n/T_s.

106

y_ref, рад

1,6

1,4

1,2

1,0

0,8

0,6

0,4

0,2

100

150

200

250

300

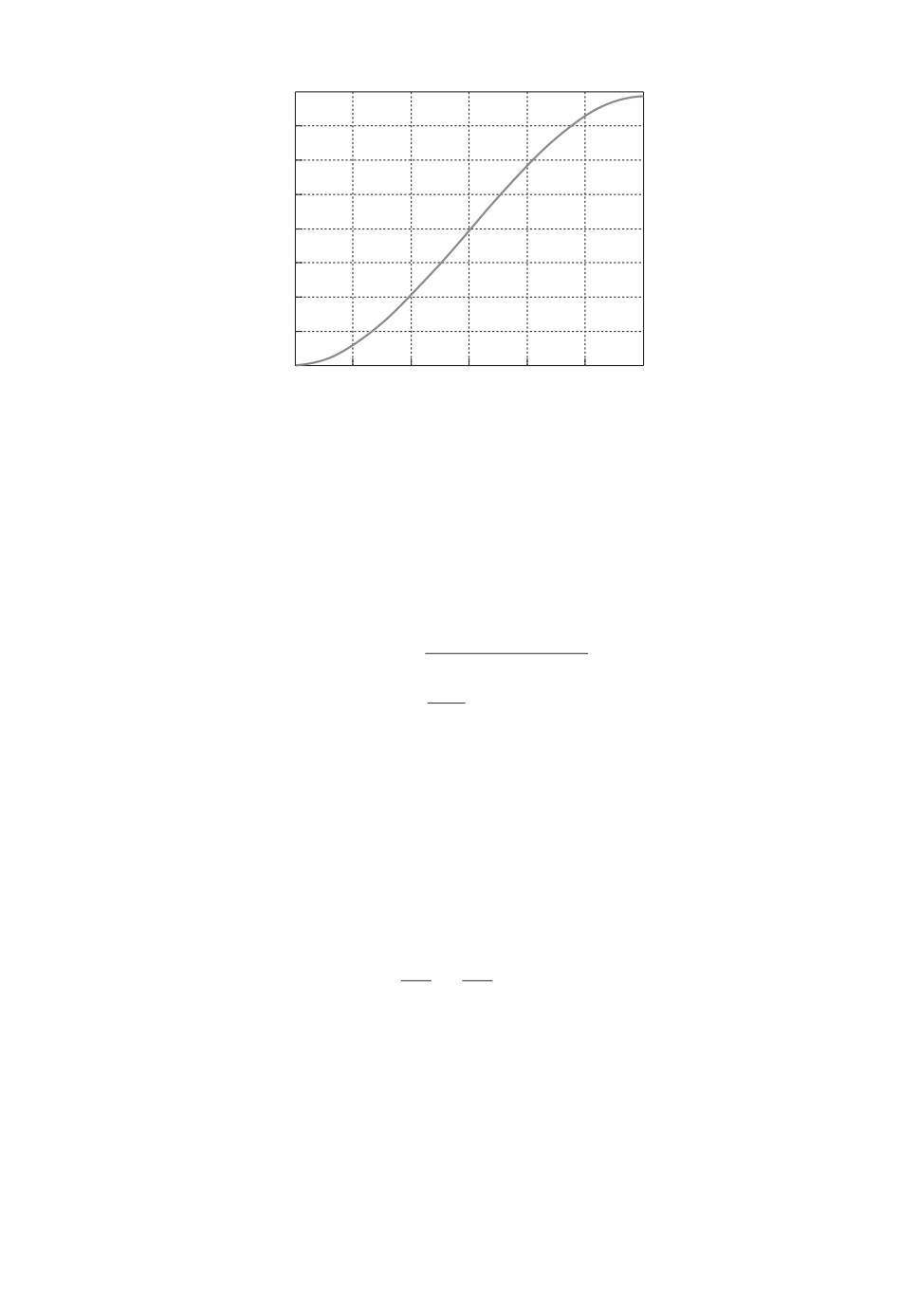
Рис. 1. Желаемая траектория изменения угла поворота вала сервомотора.

Задача состоит в нахождении алгоритма управления с итеративным обу-

чением, при котором выходная переменная y_k(p) = θ_k(p) воспроизводила бы

желаемую траекторию y_ref (t) с заданной точностью e^∗. Для формирования

управления доступен только угол θ_k(p), который в соответствии с (5.2) изме-

ряется с шумами. Точность будем оценивать по выборочному среднеквадра-

тическому отклонению

∑

(5.4)

E(k) =

√

||ê_k(p)||².

NTf

p=0

Для расчетов и моделирования были приняты следующие номинальные

значения параметров из [33]: B_eq = 0,004 Н·м/(рад/с), K_s = 1,3 Н·м/рад, J_l =

= 0,0038 кг·м², J_eq = 2,08 · 10^-3 кг·м². Продолжительность цикла повторе-

ния T_f составляет 3 c, требуемая точность e^∗ = 1град. = 0,0175 рад., постоян-

ные интенсивности шумов имеют величины Q_n = 0,16 · 10^-4 и R_n = 0,2 · 10^-5.

Желаемая траектория изменения выходной переменной описывается урав-

нением

πt

πt³

y_ref(t) =

t ∈ [0;T],

и представлена на рис. 1

При начале работы манипулятора несколько первых повторений прохо-

дят без нагрузки для предварительной настройки, при этом значения па-

раметров соответствуют номинальным. После трех повторений манипулятор

нагружается, при этом изменяется значение J_l, которое становится равным

0,1038кг · м². Исходя из физического смысла переменных состояния зададим

весовые матрицы

Q = diag[10^-4

10^-3

10^-2

10^-4

10^-3

10^-2

10^-4

10⁶], R = 1

107

Е, рад

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

X: 3

0,1

Y: 0,01656

Рис. 2. Изменение среднеквадратической ошибки в зависимости от числа по-

вторений для управления с переключением.

Е, рад

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

X: 6

0,1

Y: 0,01572

Рис. 3. Изменение среднеквадратической ошибки в зависимости от числа по-

вторений для управления без переключения.

и примем T_s = 0,01 c. Рассматривая скачкообразное изменение нагрузки на

манипулятор как переключение, воспользуется результатами подраздела 4.2,

которые удобны для сравнительного анализа. Обозначим матрицы ненагру-

женного манипулятора через A₁, B₁ и матрицы нагруженного манипулято-

ра A₂, B₂. Переключаемый алгоритм управления с итеративным обучени-

ем имеет вид

x_k (p) = A_ix_k (p - 1) + B_iu_k (p - 1) + F_i (y_k (p - 1) - Cx_k (p - 1)),

{

1, если k < 3,

2, если k ≥ 3,

108

{

F₁ = [0,4321

- 0,2936

6,1515

- 4,0246]^T, если k < 3,

Fi =

F₂ = [0,3950

- 0,3667

4,5955

- 4,4811]^T, если k ≥ 3,

u_k (p) = u_k-1 (p) + K₁ (x_k (p) - x_k-1 (p)) + K_2i (y_ref (p) - y_k-1 (p + 1)) ,

K₁ = [-29,5324

6,1375

- 1,1415

- 0,7588],

{

27,8263, если k < 3,

K_2i =

26,6316, если k ≥ 3.

При использовании алгоритма без переключений

u_k(p) = u_k-1(p) + K₁(x_k(p) - x_k-1(p)) + K₂(y_ref(p) - y_k-1(p + 1)),

K₁ = [-21,1783

14,6783

- 2,0471

- 1,6679], K₂ = 20,8358.

На рис. 2, 3 показано изменение среднеквадратической ошибки в зависи-

мости от числа повторений для управления с переключением и без переклю-

чения соответственно.

Анализ полученных зависимостей показывает, что в случае управления с

переключением требуемая точность достигается сразу же после настроечных

повторений, в то время как в случае управления без переключений для дости-

жения нужной точности требуются дополнительные шаги в рабочем режиме,

что, очевидно, нежелательно.

6. Заключение

В данной статье предложены методы синтеза управления с итеративным

обучением для стохастических систем с переключениями на основе теории

2D-систем в форме дискретных повторяющихся процессов. Приведенный при-

мер показывает, что когда переключения наблюдаемы, управление с пере-

ключением поволяет ускорить сходимость процесса обучения. Дальнейшего

исследования требует вопрос выбора нелинейной функции Θ_i(ζ) в методе син-

теза на основе диссипативности (теорема 2 и замечание 2). Открытым остал-

ся вопрос о влиянии динамики фильтра Калмана на скорость сходимости

процесса обучения и точность. Значительный интерес представляют сетевые

задачи управления с итеративным обучением, где переключения являются

естественной моделью изменений информационной структуры сети. Комби-

нация управления с итеративным обучением и управления с обратной связью

также представляет интересную задачу для дальнейших исследований.

СПИСОК ЛИТЕРАТУРЫ

1. Garden M. Learning Сontrol of Actuators in Control Systems. U.S. Patent 3555252,

1971.

2. Uchiyama M. Formulation of High-Speed Motion Pattern of a Mechanical Arm by

Trial // Trans. SICE (Soc. Instrum. Contr. Eng.). 1978. V. 14. No. 6. P. 706-712.

3. Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Robots by Learn-

ing // J. Robot. Syst. 1984. V. 1. P. 123-140.

109

Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Dynamic Systems by

Learning: A New Control Theory for Servomechanism or Mechatronic Systems //

Proc. 23rd Conf. Decicion Control. Las Vegas. 1984. P. 1064-1069.

Craig J.J. Adaptive Control of Manipulators through Repeated Trials // Proc. Amer.

Control Conf. 1984. P. 1566-1573.

Casalino G., Bartolini G. A Learning Procedure for the Control of Movements of

Robotic Manipulators // Proc. IASTED Symp. Robot. Autom. 1984. P. 108-111.

Xu J.-X., Tan Y. Linear and Nonlinear Iterative Learning Control. Lecture Notes in

Control and Information Sciences. N.Y.: Springer, 2003.

Ahn H.-S., Moore K.L., Chen Y.Q. Iterative Learning Control. Robustness and

Monotonic Convergence for Interval Systems. London: Springer-Verlag, 2007.

Bristow D.A., Tharayil M., Alleyne A.G. A Survey of Iterative Learning Control //

IEEE Control Syst. Mag. 2006. V. 23. No. 3. P. 96-114.

10.

Ahn H.-S., Chen Y.Q., Moore K.L. Iterative Learning Control: Brief Survey and Cat-

egorization // IEEE Trans. Syst. Man. Cybernet. Part C: Applications and Reviews.

2007. V. 37. No. 6. P. 1099-1121.

11.

Shen D., Wang Y. Survey on Stochastic Iterative Learning Control // J. Process

Control. 2014. V. 24. P. 64-77.

12.

Shen D. A Technical Overview of Recent Progresses on Stochastic Iterative Learning

Control // UST. 2018. V. 6. No. 3. P. 147-164.

13.

Saab S.S. A Discrete-Time Stochastic Learning Control Algorithm // IEEE Trans.

Autom. Control. 2001. V. 46. No. 6. P. 877-887.

14.

Saab S.S. On a Discrete-Time Stochastic Learning Control Algorithm // IEEE Trans.

Autom. Control. 2001. V. 46. No. 8. P. 1333-1336.

15.

Saab S.S. Stochastic P-type/D-type Iterative Learning Control Algorithms // Int.

J. Control. 2003. V. 76. No. 2. P. 139-148.

16.

Saab S.S. A Stochastic Iterative Learning Control Algorithm with Application to an

Induction Motor // Int. J. Control. 2004. V. 77. No. 2. P. 144-163.

17.

Saab S.S. Optimal Selection of the Forgetting Matrix into an Iterative Learning Con-

trol Algorithm // IEEE Trans. Autom. Control. 2005. V. 50. No. 12. P. 2039-2043.

18.

Saab S.S. Optimality of First-Order ILC among Higher Order ILC // IEEE Trans.

Autom. Control. 2006. V. 51. No. 8. P. 1332-1336.

19.

Pakshin P., Emelianova J., Galkowski K., Rogers E. Iterative Learning Control De-

sign for Discrete Stochastic Linear Systems // Proc. 18th Eur. Control Conf. Napoli,

Italy. 2019. P. 3776-3771.

20.

Pakshin P., Emelianova J., Rogers E., Galkowski K. Repetitive Process Based

Stochastic Iterative Learning Control Design for Linear Dynamics // Syst. Control

Lett. 2020. V. 137. https://doi.org/10.1016/j.sysconle.2020.104625

21.

Пакшин П.В., Копосов А.С., Емельянова Ю.П. Управление с итеративным обу-

чением мультиагентной системой в условиях случайных возмущений // АиТ.

2020. № 3. С. 132-156.

Pakshin P.V., Koposov A.S., Emelianova J.P. Iterative Learning Control of a Multi-

agent System under Random Perturbations // Autom. Remote Control. 2020. V. 81.

No. 3. P. 483-502.

22.

Oh S-K, Lee J.M. Stochastic Iterative Learning Control for Discrete Linear Time-

Invariant System with Batch-Varying Reference Trajectories // J. Process Control.

2015. V. 36. P. 64-78.

23.

Liberzon D. Switching in Systems and Control. Boston, MA: Birkhäuser, 2003.

110

24.

Shorten R., Wirth F., Mason O., Wulff K., King C. Stability Criteria for Switched

and Hybrid Systems // SIAM Rev. 2007. V. 49. P. 545-592.

25.

Lin H., Antsaklis P.J. Stability and Stabilizability of Switched Linear Systems: A

Survey of Recent Results // IEEE Trans. Autom. Control. 2009. V. 54. P. 308-321.

26.

Sun Z., Ge S.S. Stability Theory of Switched Dynamical Systems. London: Springer-

Verlag, 2011.

27.

Alwan M.S, Liu X. Theory of Hybrid Systems:Deterministic and Stochastic. Beijing:

Springer Nature Singapore Pte Ltd. and Higher Education Press, 2018.

28.

Rogers E., Galkowski K., Owens D.H. Control Systems Theory and Applications

for Linear Repetitive Processes / Lect. Notes Control Inform. Sci. Berlin: Springer-

Verlag, 2007. V. 349.

29.

Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Dissipivity and

Stabilization of Nonlinear Repetitive Processes // Syst. Control Lett. 2016. V. 91.

P. 14-20.

30.

Пакшин П.В., Емельянова Ю.П., Емельянов М.А., Галковский К., Роджерс Э.

Стохастическая устойчивость некоторых классов 2D-систем // АиТ. 2018. № 1.

С. 113-129.

Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Stochastic Sta-

bility of Some Classes of Nonlinear 2D Systems // Autom. Remote Control. 2018.

V. 79. No. 1. P. 89-102.

31.

Pakshin P., Emelianova J., Galkowski K., Rogers E. Stabilization of Two-

Dimensional Nonlinear Systems Described by Fornasini-Marchesini and Roesser

models //SIAM J. Control Optim. 2018. V. 56. P. 3848-3866.

32.

Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Passivity Based

Stabilization of Repetitive Processes and Iterative Learning Control Design // Syst.

Control Lett. 2018. V. 122. P. 101-108.

33.

Apkarian J., Karam P., Levis M. Workbook on Flexible Link Experiment for Mat-

lab/Simulink Users. Quanser, 2011.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 02.03.2020

После доработки 27.05.2020

Принята к публикации 09.07.2020

111