Автоматика и телемеханика, № 11, 2020

А.В. ЛОБАНОВ (lobbsasha@mail.ru)

(Московский авиационный институт)

МИНИПАКЕТНЫЙ МЕТОД АДАПТИВНОГО СЛУЧАЙНОГО ПОИСКА

ДЛЯ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ

ДИНАМИЧЕСКИХ СИСТЕМ

Рассматривается один из возможных способов решения задачи

оценки неизвестных параметров динамических моделей, описываемых

дифференциально-алгебраическими уравнениями. Оценка параметров

производится по результатам наблюдений за поведением математической

модели. Значения параметров находятся в результате минимизации кри-

терия, описывающего суммарное квадратическое отклонение значений

координат вектора состояния от полученных при измерениях точных зна-

чений в различные моменты времени. На значения параметров наложены

ограничения параллелепипедного типа. Для решения задачи оптимиза-

ции предлагается пакетный метод адаптивного случайного поиска, разви-

вающий идеи методов оптимизации, применяемых в машинном обучении.

Предложенный метод применен при решении трех модельных задач, их

результаты сравнивались с полученными при помощи градиентных ме-

тодов оптимизации, используемых в процедурах машинного обучения, и

метаэвристических алгоритмов.

Ключевые слова: параметрическая идентификация, динамическая систе-

ма, градиентные методы оптимизации, минипакетный метод, адаптивный

случайный поиск.

DOI: 10.31857/S0005231020110070

1. Введение

В статье рассматривается математическая модель динамической систе-

мы с неизвестными параметрами, описываемая системой дифференциально-

алгебраических уравнений. На каждый параметр могут быть наложены огра-

ничения в виде отрезка возможных значений с фиксированными концами.

Известны результаты наблюдения за состоянием системы в определенные

моменты времени функционирования системы. Целевая функция представ-

ляется в виде суммы квадратов отклонений значений всех компонент реше-

ния системы дифференциальных уравнений в заданные моменты времени

от полученных в результате точных измерений значений координат векто-

ра состояния модели. Ставится задача минимизации целевой функции на

множестве возможных значений параметров, удовлетворяющих заданным

ограничениям.

Большинство публикаций в области идентификации параметров основано

на вероятностном подходе (метод максимального правдоподобия, построение

доверительных интервалов и т.д.) [1, 2]. Другим направлением исследований

112

является применение методов оптимизации [3, 4]. Применяются метод кол-

локаций совместно с линеаризацией и последовательным квадратичным про-

граммированием, методы Гаусса-Ньютона, генетические алгоритмы с уточне-

нием на основе алгоритма Левенберга-Марквардта, метод ветвей и границ,

метод Лууса и др. [5-14]. Могут быть использованы классические методы

нулевого, первого и второго порядков, однако их реализация при больших

объемах измерений может быть затруднительной. Альтернативой является

применение метаэвристических алгоритмов [15-17], которые при отсутствии

теоретического доказательства сходимости позволяют получить решение до-

статочно хорошего качества за приемлемое время. Однако с ростом числа пе-

ременных их эффективное применение требует значительных вычислитель-

ных ресурсов.

Поскольку в решаемой задаче целевая функция представляется суммой

некоторых функций, то задача параметрической идентификации может быть

решена с помощью алгоритмов оптимизации, применяемых в машинном обу-

чении, в частности градиентных методов оптимизации, таких как: метод сто-

хастического градиентного спуска (Stochastic Gradient Descent, SGD), мини-

пакетный метод градиентного спуска (Mini-batch Gradient Descent), классиче-

ский метод моментов (Classical Momentum), ускоренный градиентный метод

Нестерова (Nesterov Accelerated Gradient, NAG), метод адаптивного гради-

ента (Adaptive Gradient, AdaGrad), метод скользящего среднего (Root Mean

Square Propagation, RMSProp), метод адаптивной оценки моментов (Adaptive

Moment Estimation, Adam), модификация метода Adam (Adamax), ускорен-

ный по Нестерову метод адаптивной оценки моментов (Nesterov-accelerated

Adaptive Moment Estimation, Nadam) [18-21]. В градиентных методах, при-

меняемых в машинном обучении, упрощается процедура поиска за счет вы-

числения градиента по одной (SGD) или нескольким реализациям (минипа-

кетный метод градиентного спуска), накапливания информации о величине

составляющей градиента или ее квадрате по соответствующей координате

вектора неизвестных параметров, покоординатной организации вычислений

за счет применения операций поэлементного деления и умножения векторов

(по Адамару).

Предлагается распространить идею методов стохастического и минипакет-

ного градиентного спуска на методы нулевого порядка, использующие при по-

иске информацию только о величине функции. Среди методов этой группы

выбран адаптивный метод случайного поиска [22], хорошо зарекомендовав-

ший себя при решении классических задач оптимизации. При подсчете значе-

ния целевой функции предлагается выбирать случайным образом одну, две,

три и т.д. реализации, образующие минипакет. За счет этого вычислительные

затраты могут существенно сокращаться, однако с уменьшением числа реа-

лизаций может убывать точность решения задачи и ухудшаться сходимость.

Кроме изменения способа вычисления целевой функции в методе должны

учитываться ограничения параллелепипедного типа, накладываемые на мно-

жество возможных значений оцениваемых параметров. По сравнению с гра-

диентными процедурами и методами второго порядка (Ньютона, Левенберга-

Марквардта, Ньютона-Гаусса) нет необходимости приближенно вычислять

градиент и аппроксимацию матрицы Гессе. Статья посвящена исследованию

113

предложенной минипакетной модификации адаптивного метода случайного

поиска в приложении к задачам идентификации параметров динамических

систем, описываемых дифференциально-алгебраическими уравнениями.

2. Постановка задачи

Сформулируем задачу параметрической идентификации параметров нели-

нейных динамических систем по результатам измерений.

Пусть заданы:

целевая функция

∑∑

(1)

E(θ) =

(x_i(t_j) - x_i(θ,t_j))² →min,

θ∈Θ

j=1 i=1

и ограничения

{

x(t) = f(t, x(t), θ),

(2)

x(t₀) = x₀,

{

}

(3)

θ ∈ Θ = θ ∈ R^p|a_i ≤ θ_i ≤ b_i, i = 1,...,p

где x ∈ Rⁿ - вектор состояния системы, x₀ ∈ Rⁿ - вектор начального состоя-

ния; θ - вектор неизвестных параметров системы, Θ ⊆ R^p - множество воз-

можных значений параметров, определяемое параллелепипедными ограниче-

ниями (3); t ∈ [t₀, t_T ] - время функционирования системы, f(t, x, θ) - извест-

ная непрерывно-дифференцируемая вектор-функция. На промежутке време-

ни [t₀, t_T ] известны наблюдения x(t) за вектором состояния системы в момен-

ты времени t = t_j ∈ [t₀, t_T ], j = 1, . . . , T ; T - заданное число реализаций. При

фиксированном векторе параметров θ можно найти решение x(θ, t) системы

дифференциальных уравнений аналитически или численным методом.

Требуется найти оценкуθ вектора неизвестных параметров θ, при которой

x(θ, t) наилучшим образом согласуется с наблюдениями, т.е. обеспечивается

минимальное значение целевой функции E(θ).

3. Минипакетный адаптивный метод случайного поиска

3.1. Стратегия поиска

Задается объем минипакета d(1 ≤ d ≤ T ), определяющий способ вычисле-

ния целевой функции E_d(θ) (при d = T справедливо E_d(θ) = E(θ)). Минипа-

кет образуют попарно несовпадающие моменты времени tqj ∈ [t₀, t_T ] со слу-

чайными номерами. Случайный номер q_j (j = 1, 2, . . . , T ) выбирается из мно-

жества возможных номеров q_j ∈ {1, . . . , T } с равной вероятностью, затем он

исключается из множества, и процесс выбора продолжается, т.е. q₁ = q₂ =

...=q_d:

∑∑(

)₂

(4)

E_d(θ) =

x_i(tqj ) - x_i(θ,tqj )

→min,

θ∈Θ

j=1 i=1

114

где x_i(θ, tqj ) - значение соответствующей координаты решения задачи Ко-

ши (2), определяемое одним из известных численных методов в случае систе-

мы нелинейных дифференциальных уравнений или аналитически (если воз-

можно) в случае линейных систем. Выражение (4) используется вместо (1) в

ходе поиска вектора наилучших оценокθd.

При решении задачи идентификации параметров возможны следующие

варианты задания минипакета:

• фиксировать число d;

• последовательно увеличивать число d, т.е. d = 1, 2, . . . , T (этот способ при-

меняется в описанной далее методике для проведения сравнения работо-

способности метода при различных объемах минипакета);

• изменять объем пакета динамически в зависимости от достижения задан-

ной точности оценивания, определяемой величиной критерия (1).

Если объем минипакета и суммарное число итераций применяемого алго-

ритма оптимизации фиксированы, то результат применения алгоритма может

изменяться при каждом его новом запуске в силу случайного характера вы-

бора моментов tqj , входящих в минипакет. Поэтому предлагается выполнить

заданное число запусков метода S_max, найти наилучшую оценкуθd по всем

запускам, а с целью анализа процесса поиска найти оценку среднего значения

критерия (4) по всем запускам и оценку среднеквадратического отклонения:

∑

[

]₂

√

(5)

E_d

= s=1

σEd =

E^sd - E_d

S_max

S_max - 1

s=1

гдеθsd и E^sd = E^sd(θsd) - вектор оценок и значение целевой функции (4), по-

лученные в результате s-го запуска (s = 1, . . . , S_max). По завершении S_max

запусков алгоритма завершается проход.

Поскольку численные значения показателей E_d и σEd меняются при реали-

зации независимых проходов, для проведения более детального анализа влия-

ния объема минипакета предлагается провести повторное осреднение по за-

данному числу проходов B_max и найти оценку математического ожидания и

оценку среднеквадратического отклонения оценок средних значений крите-

рия (4):

∑

[

]₂

√

(6)

E_d

= b=1

σ_E

E^bd - E_d

B_max

B_max - 1

b=1

где E^bd - значение E_d после b-го прохода (b = 1, . . . , B_max). В итоге можно

найти наилучшую оценкуθ∗d после B_max проходов, в каждом из которых реа-

лизуется S_max запусков алгоритма минимизации, и ее рассматривать в каче-

стве финального результата поиска. Для анализа результирующей точности

оценивания находится значение E(θ∗d) целевой функции (1).

115

Для решения задачи (4) применяется известный метод адаптивного слу-

чайного поиска [22], относящийся к методам минимизации нулевого порядка

(без использования информации о производных), модифицированный про-

веркой, процедурами обеспечения выполнения ограничений и минипакетным

способом вычисления значений целевой функции. При выполнении одного

s-го запуска алгоритма выполняются следующие операции.

Задается начальная точка θ^s,0d. Каждая последующая точка находится по

формуле

θ^s,k+1d = θ^s,kd + t_kξ^k,

где t_k > 0 - величина шага; ξ^k - случайный вектор единичной длины, опреде-

ляющий направление поиска; k - номер итерации. На текущей итерации при

помощи генерирования случайных векторов ξ^k получаются точки, лежащие

на гиперсфере радиуса t_k с центром в точке θ^s,kd. Полученная точка прове-

ряется на принадлежность множеству допустимых решений, определяемому

параллелепипедными ограничениями (3). Если по какой-либо i-й координа-

те ограничения не выполняются, то возможны несколько последовательных

вариантов: генерировать решение заново, взять в качестве координаты по-

ложение ближайшей границы отрезка [a_i, b_i], генерировать случайную точку

согласно равномерному распределению на отрезке [a_i, b_i]. Значение функции

находится по формуле (4).

Если значение функции в полученной точке θ^s,k+1d не меньше, чем в цен-

тре, шаг считается неудачным. Если число неудачных шагов из текущей точ-

ки достигает некоторого числа M, дальнейший поиск продолжается из той

же точки, но с меньшим шагом до тех пор, пока он не станет меньше за-

ранее заданной величины R. Если же значение функции в полученной точке

меньше, чем в центре, шаг считается удачным и в найденном направлении де-

лается увеличенный шаг, играющий роль ускоряющего шага (как при поиске

по образцу в известном методе конфигураций [22]). Если при этом значе-

ние функции снова меньше, чем в центре, направление считается удачным, и

дальнейший поиск продолжается из этой точки. Если же значение функции

стало не меньше, чем в центре, направление считается неудачным, и поиск

продолжается из старого центра.

Процедура завершается либо при достижении заданного максимального

числа итераций N, либо в случае, если радиус окрестности текущего реше-

ния станет меньше величины R. В результате запуска находятся наилучшее

решениеθsd и соответствующее значение E^sd = E^sd(θsd) целевой функции (4).

3.2. Методика решения задачи

Обозначим: E^sd - минимальное значение функции после s-го запуска;θsd -

наилучший вектор параметров после запуска.

Шаг 0. Задать:

d = 1 - начальное число реализаций (в общем случае можно начать с лю-

бого значения 1 ≤ d ≤ T );

S_max - максимальное число запусков;

116

B_max - максимальное число проходов;

α ≥ 1 - коэффициент расширения;

0 < β < 1 - коэффициент сжатия;

M - максимальное число неудачно выполненных испытаний на текущей

итерации;

t₀ = 1 - начальную величину шага (можно задать любую величину t₀ > R);

R - минимальную величину шага;

N - максимальное число итераций в процедуре запуска.

Шаг 1. Положить:

b = 1 (счетчик числа проходов);

P_d = 0 (начальная величина суммы средних значений целевой функции).

Шаг 2. Положить:

s = 1 (счетчик числа запусков);

E^1d = 10⁸ ÷ 10¹⁰ (начальное значение критерия);

S_d = 0 (начальная величина суммы значений целевой функции).

Шаг 3. Задать начальную точку θ^s,0d, удовлетворяющую параллелепипед-

ным ограничениям (3). Положить k = 0, j = 1.

(

)_T

Шаг 4. Получить случайный вектор ξ^j =

ξ_1j,... ,ξ_nj

, где ξ_ij - случай-

ная величина, равномерно распределенная на промежутке [-1, 1].

Шаг 5. Вычислить y^j = θ^s,k

+t_k

∥ξ^j ∥

Проверить принадлежность решения y^j множеству допустимых решений Θ.

При негативном результате возможны следующие варианты действий:

а) выбрать в качестве нового положения ближайшую граничную точку

множества допустимых решений;

б) генерировать новое положение заново, так как в расчетных формулах

используются случайные величины и есть вероятность, что при других их

реализациях новое решение будет принадлежать множеству допустимых ре-

шений;

в) если вне множества Θ оказывается i-я компонента вектора y^j, т.е. y^ji,

в качестве нового положения выбрать точку на отрезке, соединяющем y^ji и a_i,

если y^ji > b_i (y^ji и b_i, если y^ji < a_i):

(

)

y^j,Newi = a_i + γ y^j

- a_i , если y^ji > b_i;

(

)

y^j,Newi = b_i - γ b_i - y^j

, если y^ji < a_i;

параметр γ можно задать, например, случайным образом на основе закона

равномерного распределения, γ ∼ R[0, 1];

г) комбинировать описанные выше способы, например несколько раз про-

бовать сгенерировать положение заново и если после определенного количе-

ства попыток новое решение все равно оказывается вне множества Θ, поло-

жить y^ji = a_i, если y^ji < a_i (y^ji = b_i, если y^ji > b_i).

117

Шаг 6. Генерировать минипакет (tq1,...,tqd) объема d, где tq1,...,tqd -

попарно несовпадающие моменты времени из множества (t₁, . . . , t_T ). Подсчи-

тать величину E_d(y^j ) по формуле (4).

Проверить выполнение условий:

(

)

а) если E_d(y^j) < E_d(θ^s,kd), шаг удачный. Положить z^j = θ^s,kd +α y^j - θ^s,k

Определить, является ли текущее направление y^j - θ^s,kd удачным:

• если E_d(z^j ) < E_d(θ^s,kd), направление поиска удачное.

Положить θ^s,k+1d = z^j , t_k+1 = αt_k, k = k + 1 и проверить условие оконча-

ния. Если k < N, положить j = 1 и перейти к шагу 4. Если k = N, поиск

завершить:θsd = θ^s,kd, перейти к шагу 8;

• если E_d(z^j ) ≥ E_d(θ^s,kd), направление поиска неудачное, перейти к шагу 7;

б) если E_d(y^j) ≥ E_d(θ^s,kd), шаг неудачный и перейти к шагу 7.

Шаг 7. Оценить число неудачных шагов из текущей точки:

а) если j < M, следует положить j = j + 1 и перейти к шагу 4;

б) если j = M, проверить условие окончания:

• если t_k ≤ R, процесс закончить:θsd = θ^s,kd, E^sd = E_d(θ^s,kd), перейти к шагу 8;

• если t_k > R, положить t_k = βt_k, j = 1 и перейти к шагу 4.

Шаг 8. Проверить улучшение значения целевой функции в результате s-го

запуска:

• если E_d(θ^s,kd) < E^sd, следует положить E^sd = E_d(θ^s,kd),θsd = θ^s,kd и перейти

к шагу 9;

• если E_d(θ^s,kd) ≥ E^sd, перейти к шагу 9;

Шаг 9. Вычислить S_d = S_d + E^sd и проверить выполнение условий окон-

чания числа запусков:

а) если s < S_max, следует положить s = s + 1 и перейти к шагу 3;

б) если s = S_max, то положитьθd =θsd - наилучшее решение в течение b-го

прохода при заданном d; вычислить

∑[

]₂

S^sd

√

E_d =

σEd =

E^sd - E_d

S_max

S_max - 1

s=1

и перейти к шагу 10.

Шаг 10. Положить P_d = P_d+E_d, E^bd = E_d и проверить условие завершения

заданного числа проходов:

а) если b < B_max, следует положить b = b + 1 и перейти к шагу 2;

б) если b = B_max, вычислить:

∑

[

]₂

P_d

√

E_d =

σ_E

E^bd - E_d

B_max

B_max - 1

b=1

118

Шаг 11. Проверить условие завершения исследований влияния объема

минипакета:

• если d < T , положить d = d + 1, s = 1 и перейти к шагу 1;

• если d = T , перейти к шагу 12.

Шаг 12. В результате найти наилучшую оценкуθ∗d после B_max проходов

и показатели E_d, σ при каждом значении объема минипакета d. Для ана-_E

лиза результирующей точности оценивания найти значение E(θ∗d) критерия

точности оценивания (1):

∑∑(

)₂

E(θ∗d) =

x_i(t_j) - x_i(θ∗d,t_j)

j=1 i=1

Шаги 10 и 11 выполняются при необходимости.

Рекомендации по выбору параметров метода. Величина ξ_ij , равномерно

распределенная на отрезке [-1, 1], генерируется обычно с помощью датчиков

псевдослучайных чисел. Вырабатывается случайная величина η^ji , равномерно

распределенная на [0, 1], а затем используется линейное преобразование: ξ^ji =

= 2η^ji -1. Параметры алгоритма: коэффициент расширения α ≥ 1: α = 1,618;

коэффициент сжатия 0 < β < 1: β = 0,618; максимальное число неудачно вы-

полненных испытаний на текущей итерации M = 3n; начальный шаг t₀ > R

можно задавать произвольно.

4. Модельные примеры

Пример 1. Математическая модель описывает необратимую реакцию

первого порядка, в которой измеряются концентрации x₁, x₂ компонент ве-

ществ, а θ₁, θ₂ - коэффициенты скоростей реакций соответственно [7, 8]:

{

x₁(t) = -θ₁x₁(t),

x₁(0) = 1,

(7)

x₂(t) = θ₁x₁(t) - θ₂x₂(t), x₂(0) = 0.

Целевая функция имеет вид:

∑∑

(8)

E(θ) =

[x_i(t_j) - x_i(θ,t_j)]² → min ,

θ ∈ Θ

j=1 i=1

где T = 10, n = 2. Ограничения на параметры: 0 ≤ θ₁ ≤ 10, 0 ≤ θ₂ ≤ 10.

В табл. 1 представлены результаты наблюдений за реакцией.

Таблица 1. Наблюдения

t_j

0,100

0,200

0,300

0,400

0,500

0,600

0,700

0,800

0,900

x₁

0,606

0,368

0,223

0,135

0,082

0,050

0,030

0,018

0,011

0,007

x₂

0,373

0,564

0,647

0,669

0,656

0,624

0,583

0,539

0,494

0,451

119

Результат метода МАМСП

0,6

0,5

0,4

0,3

0,2

0,1

2,5

5,0

7,5 10,0 12,5

15,0

17,5

2,5

5,0

7,5 10,0 12,5

15,0

17,5

Количество итераций

Результат метода МАМСП

0,6

0,5

0,4

0,3

0,2

0,1

2,5

5,0

7,5 10,0 12,5

15,0

17,5

2,5

5,0

7,5 10,0 12,5

15,0

17,5

Количество итераций

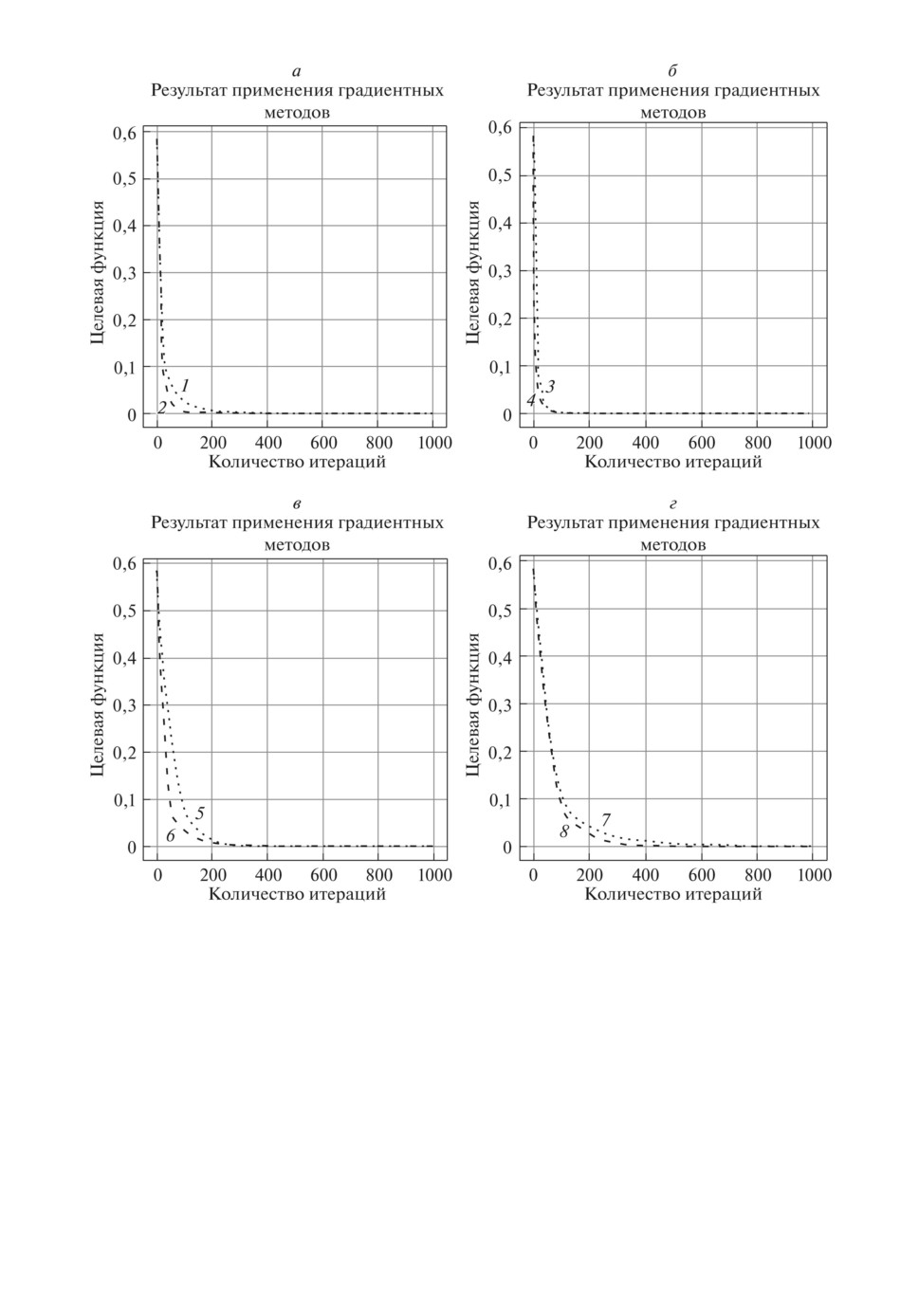
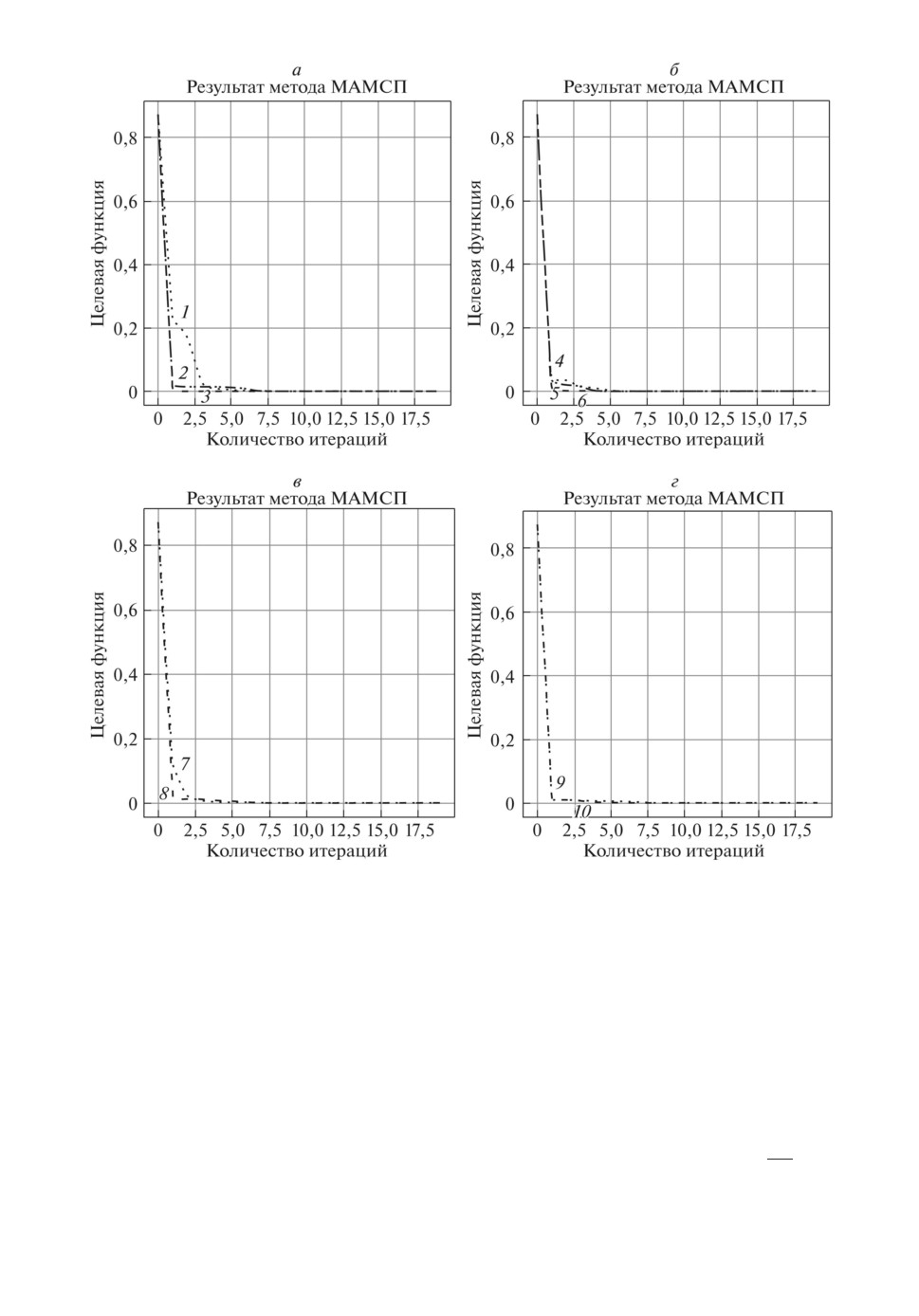
Рис. 1. Результат работы минипакетного адаптивного метода случайного по-

иска в зависимости от объема минипакета: 1 - [d = 1], 2 - [d = 2], 3 - [d = 3],

4 - [d = 4], 5 - [d = 5], 6 - [d = 6], 7 - [d = 7], 8 - [d = 8], 9 - [d = 9], 10 - [d = 10].

Наилучшее известное решение

[7, 8]: значение целевой функции

(1)

1,18584 · 10^-6; вектор параметров: θ = (5,0035; 1,0000)^T. Сравнимые резуль-

таты, полученные с помощью метаэвристических алгоритмов без использо-

вания минипакетов: методом фейерверков, методом большого взрыва - боль-

шого сжатия и методом гранат, приведены в [17].

Результаты решения минипакетным адаптивным методом случайного по-

иска представлены на рис. 1 и в табл. 2. На рис. 1 приведены решения в за-

висимости от объема минипакета. В табл. 2 показаны лучшие результаты в

зависимости от объема минипакета. Во всех тестах N = 150 - максимальное

число итераций, M = 10 - максимальное число неудачно выполненных ис-

120

Таблица 2. Результат решения минипакетным адаптивным методом

случайного поиска (МАМСП)

θ^∗1d

θ^∗2d

E(θ∗d)

E_d

σEd

5,00486

1,00006

1,24600 · 10^-6

0,02034

0,25643

5,00269

0,99998

1,20612 · 10^-6

0,00513

0,15234

5,00343

0,99999

1,18608 · 10^-6

0,00149

0,09354

5,00323

0,99997

1,18844 · 10^-6

0,00034

0,04729

5,00365

1,00001

1,18673 · 10^-6

0,00025

0,03888

5,00342

1,00003

1,18663 · 10^-6

1,30989 · 10^-6

0,00115

5,00350

1,00000

1,18595 · 10^-6

1,25257 · 10^-6

0,00112

5,00346

1,00002

1,18623 · 10^-6

1,22674 · 10^-6

0,00111

5,00341

1,00001

1,18624 · 10^-6

1,20433 · 10^-6

0,00110

5,00349

1,00000

1,18595 · 10^-6

0,00109

Таблица 3. Результаты сравнения МАМСП (E(θ∗10) = 1, 18595 · 10^-6)

с градиентными методами по наилучшей достигнутой величине кри-

терия (1) (наилучшее известное решение E(θ) = 1, 18584 · 10^-6)

SGD

ClassMom

NAG

AdaGrad

1,37131 · 10^-6

1,05923 · 10^-6

9,32474 · 10^-7

1,82699 · 10^-6

RMSProp

ADAM

AdaMax

Nadam

7,13530 · 10^-5

9,83579 · 10^-7

1,18653 · 10^-6

1,33935 · 10^-6

пытаний на текущей итерации, R = 8 · 10^-10 - минимальная величина шага,

S_max = 100 - максимальное число запусков, B_max = 100 - максимальное чис-

ло проходов, α = 1,618 - коэффициент расширения, β = 0,618 - коэффициент

сжатия, E_d и σ

- оценка математического ожидания и оценка среднеквадра-

E_d

тического отклонения оценок средних значений критерия (4), θ^s,0d = (2, 3)^T -

начальная точка.

В табл. 2 представлены результаты решения примера 1 минипакетным

адаптивным методом случайного поиска при различных объемах минипакета

1 ≤ d ≤ 10 (суммарное время работы алгоритма составило 57 c (процессор

intel CORE i5 2.10 GHz)).

Анализ табл. 2 позволяет сделать вывод о том, что сходимость к извест-

ному результату достигается при всех объемах минипакета, точность оценок

возрастает с увеличением d, при d = 10 ответ практически совпадает с извест-

ным. Следует отметить, что зависимость величины паказателя E_d от объема

минипакета, как правило, является монотонной, а показателя E_d может быть

не монотонной в силу случайности генерации минипакета.

Так как система дифференциальных уравнений (7) линейная, то удает-

ся найти ее аналитическое решение, что позволяет находить производные

целевой функции по параметру θ и пользоваться градиентными методами

оптимизации процедур машинного обучения. В табл. 3 представлены резуль-

таты сравнения решений, полученных предложенным методом и известными

градиентными методами машинного обучения.

121

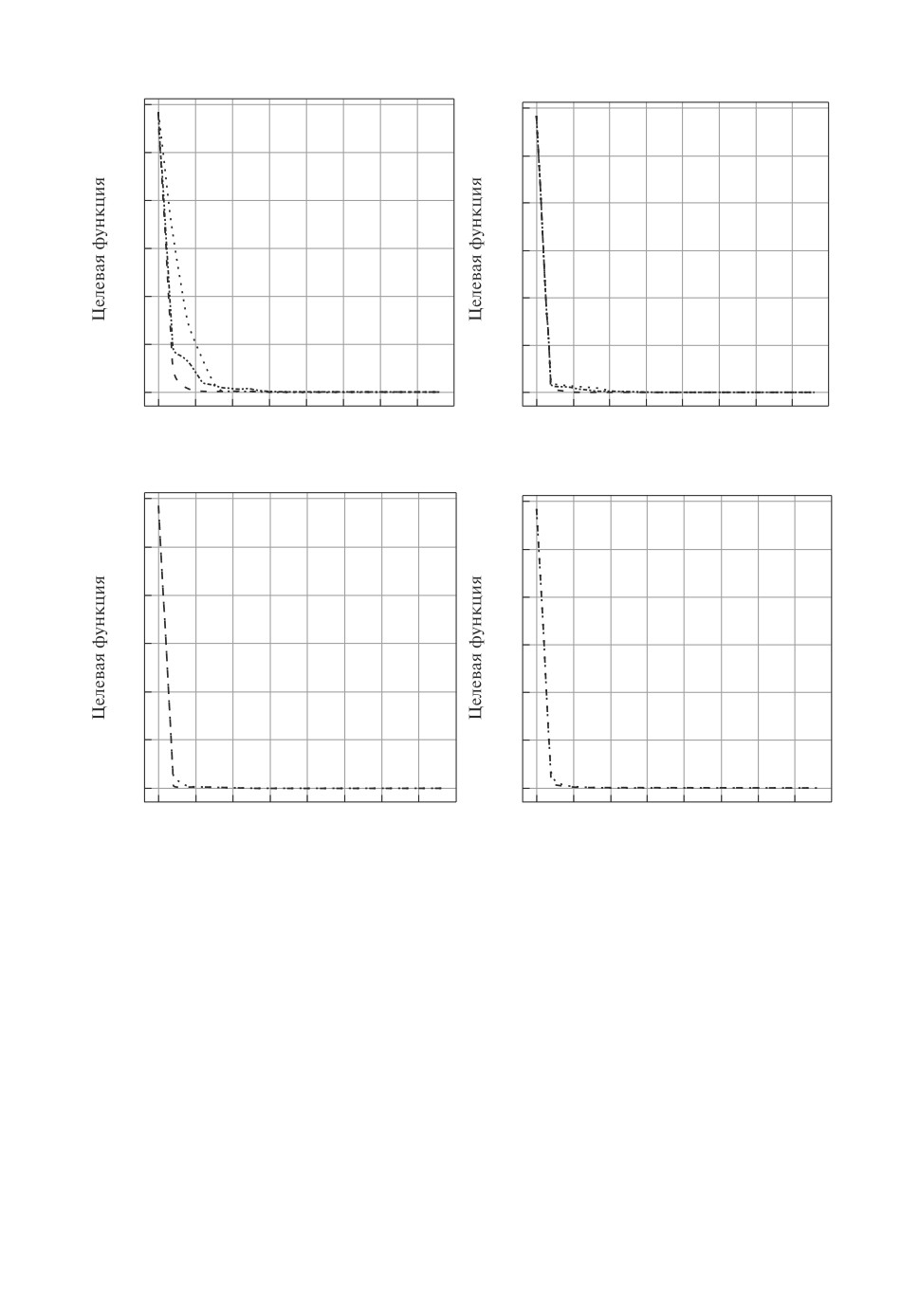
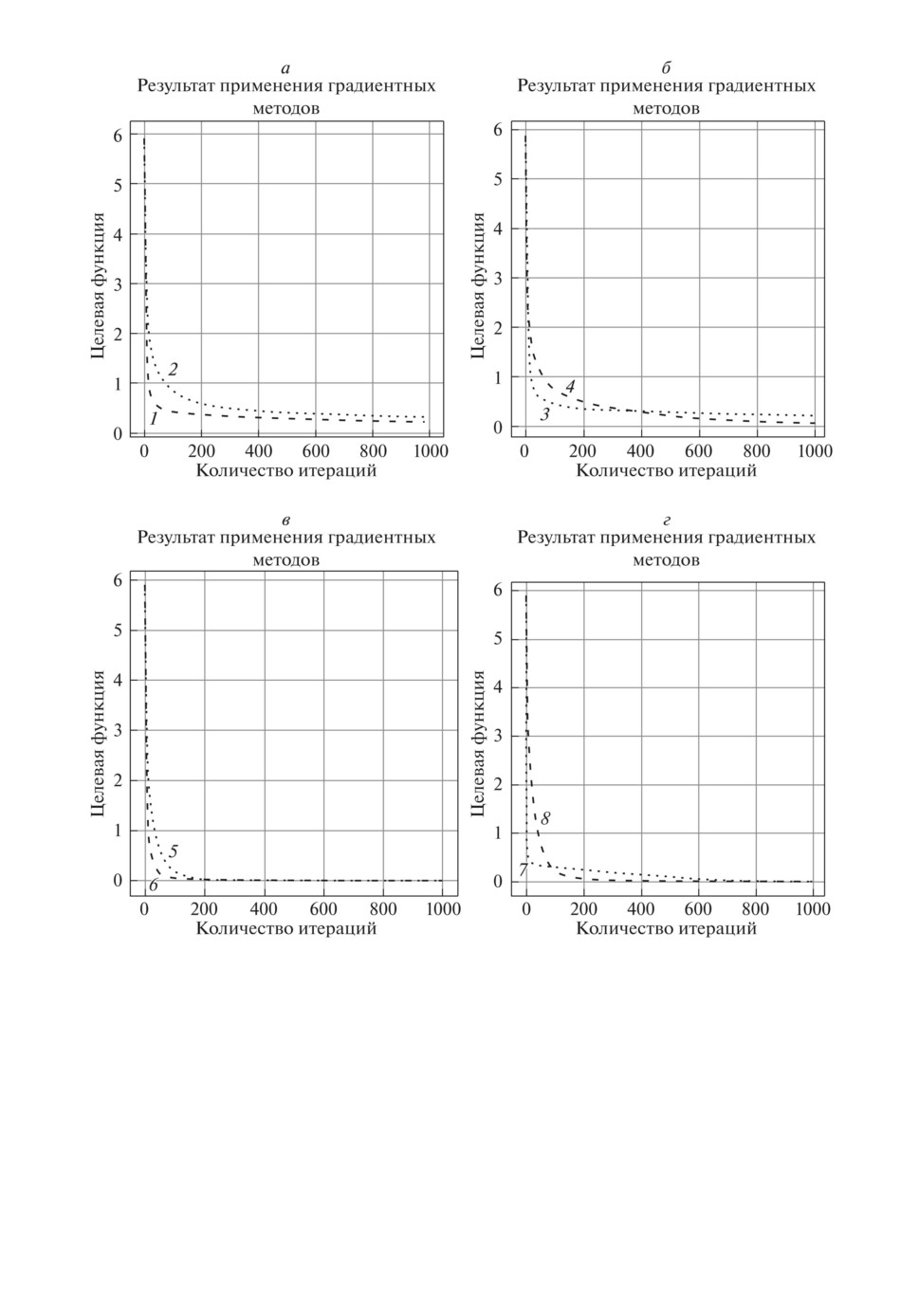
Рис. 2. Результаты применения градиентных методов оптимизации: 1 - SGD,

2 - ClasMom, 3 - NAG, 4 - AdaGrad, 5 - RMSProp, 6 - ADAM, 7 - AdaMax,

8 - Nadam.

На рис. 2 приведены результаты решения примера 1 (изменение целевой

функции с ростом числа итераций) при выбранных для обеспечения сходимо-

сти значениях шага градиентных методов машинного обучения. Рисунок 2 со-

ответствует начальной точке θ^s,0d = (2, 3)^T, значениям шага SGD - 0,2; Class-

Mom - 0,2; NAG - 0,2; AdaGrad - 0,3; RMSProp - 0,02; ADAM - 0,02; AdaMax -

0,02; Nadam - 0,02 (краткое описание методов приведено в Приложении).

Пример 2. Модель описывает каталитический крекинг для превращения

газойля в бензин. x₁, x₂ - концентрации компонент, θ₁, θ₂, θ₃ - коэффициенты

122

Таблица 4. Наблюдения

t_j

0,0250

0,0500

0,0750

0,1000

0,1250

0,1500

0,1750

0,2000

0,2250

0,2500

x₁

0,7307

0,5982

0,4678

0,4276

0,3436

0,3126

0,2808

0,2692

0,2210

0,2122

x₂

0,1954

0,2808

0,3175

0,3047

0,2991

0,2619

0,2391

0,2210

0,1898

0,1801

t_j

0,3000

0,3500

0,4000

0,4500

0,5000

0,5500

0,6500

0,7500

0,8500

0,9500

x₁

0,1903

0,1735

0,1615

0,1240

0,1190

0,1109

0,0890

0,0820

0,0745

0,0639

x₂

0,1503

0,1030

0,0964

0,0581

0,0417

0,0413

0,0367

0,0219

0,0124

0,0089

Таблица 5. Результат решения минипакетным адаптивным методом

случайного поиска

θ^∗1d

θ^∗2d

θ^∗3d

E(θ∗d)

E_d

σEd

12,71954

8,62194

1,94031

3,87373 · 10^-3

0,09323

0,24901

12,19646

8,30268

2,10194

3,15674 · 10^-3

0,02092

0,07256

12,31779

8,13561

2,04472

2,77824 · 10^-3

0,01287

0,04473

12,41866

8,13885

2,03050

2,78531 · 10^-3

0,00421

0,00457

12,13970

7,97463

2,15734

2,81254 · 10^-3

0,00391

0,00408

12,26164

8,07087

2,17864

2,76099 · 10^-3

0,00352

0,00361

12,21603

8,01094

2,10274

2,79811 · 10^-3

0,00327

0,00330

12,26468

8,03486

2,25584

2,78409 · 10^-3

0,00312

0,00314

12,27566

8,05249

2,12116

2,75432 · 10^-3

0,00309

0,00312

12,20370

8,03736

2,15236

2,76500 · 10^-3

0,00305

0,00311

12,23648

8,01906

2,19338

2,74747 · 10^-3

0,00300

0,00310

12,17853

7,97887

2,21586

2,75452 · 10^-3

0,00294

0,00300

12,21782

8,01541

2,20164

2,74887 · 10^-3

0,00291

0,00295

100

12,22653

8,01777

2,19107

2,74819 · 10^-3

0,00287

0,00292

100

12,18114

7,97683

2,21814

2,75350 · 10^-3

0,00283

0,00287

100

12,23149

7,99277

2,21086

2,74755 · 10^-3

0,00282

100

12,22948

7,98994

2,21324

2,74755 · 10^-3

0,00279

100

12,22944

8,00584

2,19629

2,74727 · 10^-3

0,00277

100

12,23437

8,00666

2,19891

2,74701 · 10^-3

0,00276

100

12,23645

8,00809

2,19849

2,74699 · 10^-3

0,00274

100

скоростей реакций [7, 8]:

{

x₁(t) = -(θ₁ + θ₃)x²¹(t), x₁(0) = 1,

(9)

x₂(t) = θ₁x²¹(t) - θ₂x₂(t), x₂(0) = 0.

Целевая функция имеет вид:

∑∑

(10)

E(θ) =

[x_i(t_j) - x_i(θ,t_j)]² → min,

θ∈Θ

j=1 i=1

где T = 20, n = 2. Ограничения на параметры: 0 ≤ θ1 ≤ 20, 0 ≤ θ2 ≤ 20,

0 ≤ θ₃ ≤ 20.

В табл. 4 представлены результаты наблюдений за реакцией.

123

Результат метода МАМСП

2,5 5,0

7,5 10,0 12,5

15,0

17,5

2,5 5,0

7,5 10,0 12,5

15,0

17,5

Количество итераций

Результат метода МАМСП

2,5

5,0

7,5 10,0 12,5

15,0 17,5

2,5

5,0

7,5 10,0 12,5

15,0

17,5

Количество итераций

Рис. 3. Результат работы минипакетного адаптивного метода случайного по-

иска в зависимости от объема минипакета: 1 - [d = 1], 2 - [d = 2], 3 - [d = 3],

4 - [d = 4], 5 - [d = 5], 6 - [d = 6], 7 - [d = 7], 8 - [d = 8], 9 - [d = 9], 10 - [d = 10].

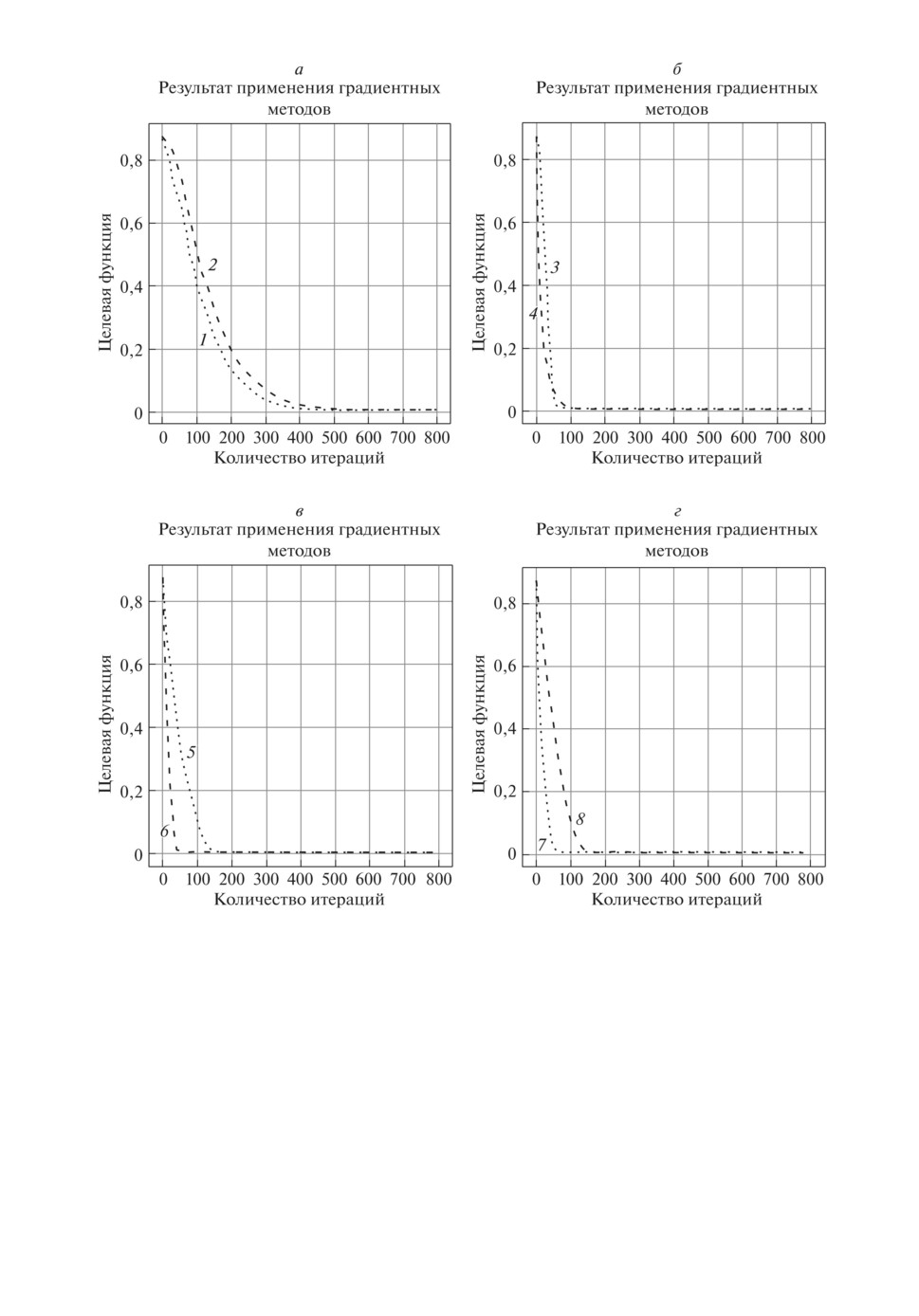
Наилучшее известное решение [7, 8]: значение целевой функции: 2,65567×

×10^-3, вектор параметров: θ = (12,214; 7,9798; 2,2216)^T.

Сравнимые результаты, полученные с помощью метаэвристических алго-

ритмов без использования минипакетов: методом фейерверков, методом боль-

шого взрыва - большого сжатия и методом гранат, приведены в [17].

Результат решения минипакетным адаптивным методом случайного поис-

ка представлены в табл. 5 и на рис. 3. На рис. 3 приведены решения в за-

висимости от объема минипакета. В табл. 5 показаны лучшие результаты в

зависимости от объема минипакета. Во всех тестах N = 150 - максимальное

124

Таблица 6. Результаты сравнения МАМСП (E(θ∗20) = 2,74699 · 10^-3)

с градиентными методами по наилучшей достигнутой величине кри-

терия (1) (наилучшее известное решение E(θ) = 2,65567 · 10^-3)

SGD

ClassMom

NAG

AdaGrad

8,60908 · 10^-3

3,06110 · 10^-3

3,51929 · 10^-3

7,01255 · 10^-3

RMSProp

ADAM

AdaMax

Nadam

4,11410 · 10^-3

2,95625 · 10^-3

5,81047 · 10^-3

3,01257 · 10^-3

число итераций, M = 20 - максимальное число неудачно выполненных ис-

пытаний на текущей итерации, R = 8 · 10^-10 - минимальная величина шага,

S_max = 100 - максимальное число запусков, α = 1,618 - коэффициент рас-

ширения, β = 0,618 - коэффициент сжатия, E_d - оценка математического

ожидания, σEd - оценка среднеквадратического отклонения, L - количество

попаданий (значение E(θ) попало в ε-окрестность известного значения целе-

вой функции, где ε = 0,001), θ^s,0d = (1, 20, 0)^T - начальная точка.

В табл. 5 представлены результаты решения примера 2 минипакетным

адаптивным методом случайного поиска при различных объемах минипакета

1 ≤ d ≤ 20 (суммарное время работы алгоритма составило 18 мин (процессор

intel CORE i5 2.10 GHz)).

На рис. 3 представлены результаты решения задачи с применением ми-

нипакетного адаптивного метода случайного поиска при объеме минипакета

1≤ d ≤ 10. При 10 ≤ d ≤ 20 характер изменения такой же, как на рис. 3,г.

При этом с увеличением объема минипакета характеристика отклонения от

наилучшего известного решения уменьшается.

Так как система дифференциальных уравнений (9) нелинейная, то для

нахождения градиента функции будем использовать конечно-разностные ап-

проксимации, а решение системы дифференциальных уравнений находим

численным методом Рунге-Кутты 4-го порядка (с шагом 0,005). В данном

случае градиент целевой функции имеет вид:





∂E(θ)

= E(θ1^+Δ;θ2^;θ3^)-E(θ1^;θ2^;θ3⁾



∂θ₁



∂θ₁











∂E(θ)



∂E(θ)

= E(θ1^;θ2^+Δ;θ3^)-E(θ1^;θ2^;θ3⁾

∇_θE(θ) =



,



∂θ₂



∂θ₂







 ∂E(θ)

∂E(θ)

= E(θ1^;θ2^;θ3^+Δ)-E(θ1^;θ2^;θ3⁾

∂θ₃

где Δ = 0,01.

В табл. 6 представлены результаты сравнения решений, полученных пред-

ложенным методом и известными градиентными методами машинного обу-

чения.

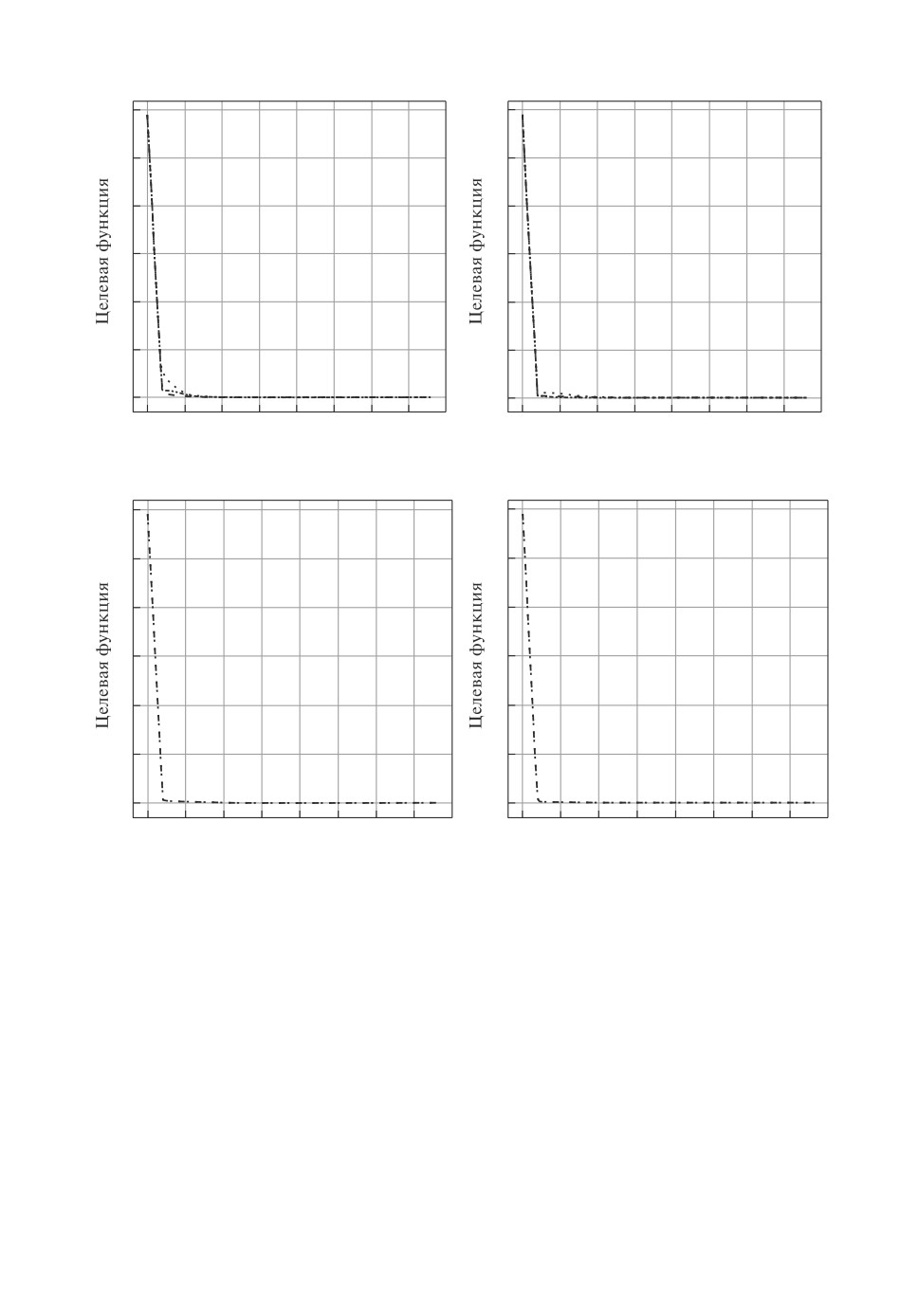
На рис. 4 приведены результаты решения примера (изменение целевой

функции с ростом числа итераций) при разных значениях шага. Рисунок 3

соответствует начальной точке θ^s,0d = (1, 20, 0)^T и значениям шага SGD - 1;

125

Таблица 7. Наблюдения

t_j

1,0000 2,0000 3,0000 4,0000 5,0000 6,0000 7,0000 8,0000 9,0000 10,0000

x1 0,7990 0,8731 1,2487 1,0362 0,7483 1,0024 1,2816 0,8944 0,7852

1,1527

x2 1,0758 0,8711 0,9393 1,1468 1,0027 0,8577 1,0274 1,1369 0,9325

0,9074

Таблица 8. Результат решения минипакетным адаптивным методом

случайного поиска

θ^∗1d

θ^∗2d

E(θ∗d)

E(θ)

E_d

σEd

3,15622

0,95191

0,001501

1,24924 · 10^-3

0,64113

0,78286

3,27374

0,91270

0,001268

1,24924 · 10^-3

0,74766

0,85022

3,24234

0,92115

0,001250

1,24924 · 10^-3

0,67812

0,74912

3,22817

0,92447

0,001276

1,24924 · 10^-3

0,64793

0,71009

3,25294

0,91882

0,001255

1,24924 · 10^-3

0,58970

0,68599

3,26656

0,91384

0,001256

1,24924 · 10^-3

0,66807

0,71758

3,26416

0,91397

0,001264

1,24924 · 10^-3

0,61353

0,67164

3,24321

0,92107

0,001249

1,24924 · 10^-3

0,45911

0,54942

3,24711

0,91979

0,001250

1,24924 · 10^-3

0,36868

0,42101

3,24444

0,92080

0,001249

1,24924 · 10^-3

0,30586

0,34670

Модель описывает взаимодействие двух биологических видов: “хищник”-

“жертва”. x₁ - число особей “жертва”, x₂ - число особей “хищник”. θ₁ - ко-

эффициент роста и истребления популяции вида “жертва”, θ₂ - коэффициент

роста и смертности популяции вида “хищник”. Различные методы решения

задач анализа и фильтрации в вольтерровских системах изложены в [23, 24].

Целевая функция имеет вид:

∑∑

(12)

E(θ) =

[x_i(t_j) - x_i(θ,t_j)]² → min ,

θ ∈ Θ

j=1 i=1

где T = 10, n = 2. Ограничения на параметры: 0 ≤ θ₁ ≤ 10, 0 ≤ θ₂ ≤ 10.

В табл. 7 представлены результаты наблюдений за реакцией.

Наилучшее известное решение [7, 8]: значение целевой функции: 1,24924×

×10^-3, вектор параметров: θ = (3,2434; 0,9209)^T.

Сравнимые результаты, полученные с помощью метаэвристических алго-

ритмов без использования минипакетов: методом фейерверков, методом боль-

шого взрыва - большого сжатия и методом гранат, приведены в [17].

Результат решения минипакетным адаптивным методом случайного поис-

ка представлены в табл. 8 и на рис. 5. В табл. 8 показаны лучшие результаты

в зависимости от объема минипакета. На рис. 5 приведены решения в за-

висимости от объема минипакета. Во всех тестах N = 150 - максимальное

число итераций, M = 15 - максимальное число неудачно выполненных ис-

пытаний на текущей итерации, R = 8 · 10^-10 - минимальная величина шага,

S_max = 100 - максимальное число запусков, α = 1,618 - коэффициент рас-

ширения, β = 0,618 - коэффициент сжатия, E_d - оценка математического

127

Рис. 5. Результат работы минипакетного адаптивного метода случайного по-

иска в зависимости от объема минипакета: 1 - [d = 1], 2 - [d = 2], 3 - [d = 3],

4 - [d = 4], 5 - [d = 5], 6 - [d = 6], 7 - [d = 7], 8 - [d = 8], 9 - [d = 9], 10 - [d = 10].

ожидания, σEd - оценка среднеквадратического отклонения, θ^s,0d = (4, 1)^T -

начальная точка.

В табл. 8 представлены результаты решения примера 3 минипакетным

адаптивным методом случайного поиска при различных объемах минипакета

1 ≤ d ≤ 10 (суммарное время работы алгоритма составило 20 минут (процес-

сор intel CORE i5 2.10 GHz)).

Анализ данных табл. 8 показывает, что значения характеристики E_d зна-

чительно отличаются от наилучших значений критерия E(θ∗d) при всех рас-

сматриваемых объемах минипакета. Это свидетельствует о том, что для по-

128

Таблица 9. Результаты сравнения МАМСП (E(θ∗10) = 1, 24924 · 10^-3)

с градиентными методами по наилучшей достигнутой величине кри-

терия (1) (наилучшее известное решение E(θ) = 1, 24924 · 10^-3)

SGD

ClassMom

NAG

AdaGrad

7,05873 · 10^-3

7,03563 · 10^-3

6,85268 · 10^-3

4,39537 · 10^-3

RMSProp

ADAM

AdaMax

Nadam

4,55656 · 10^-3

3,28811 · 10^-3

6,85572 · 10^-3

4,51559 · 10^-3

с ростом числа итераций) при разных значениях шага. Рисунок 6 соответ-

ствует начальной точке θ^s,0d = (4, 1)^T, значениям шага SGD - 0,002; Class-

Mom - 0,0002; NAG - 0,002; AdaGrad - 0,02; RMSProp - 0,002; ADAM - 0,002;

AdaMax - 0,02; Nadam - 0,002.

В табл. 9 представлены результаты сравнения решений, полученных пред-

ложенным методом и известными градиентными методами машинного обу-

чения.

Как следует из сравнительного анализа рис. 1, 3, 5 и рис. 2, 4, 6, метод

МАМСП не только не уступает известным градиентным методам, но и превос-

ходит большинство методов при достаточном объеме минипакета d. Характер

сходимости алгоритма МАМСП к наилучшему известному результату срав-

ним с поведением метода ADAM - наилучшего из приведенных градиентных

методов.

5. Заключение

Предложен минипакетный алгоритм адаптивного случайного поиска для

решения задачи оценивания параметров динамических систем, использую-

щий идеи популярных методов оптимизации, применяемых в машинном обу-

чении. Приведены результаты сравнения эффективности его применения по

сравнению с известными градиентными методами оптимизации: SGD, Clas-

sical Momentum, NAG, AdaGrad, RMSProp, Adam, Adamax, Nadam на трех

модельных примерах. На данный момент представляется возможным его при-

менение в задачах параметрического синтеза субоптимального управления

пучками траекторий детерминированных систем, а также управления стоха-

стическими системами при неполной информации о состоянии, в том числе

систем совместного оценивания и управления, в которых критерий качества

управления может быть приближенно представлен в виде суммы некоторых

функций.

ПРИЛОЖЕНИЕ

А. Метод стохастического градиентного спуска (Stochastic Gradient De-

scent, SGD):

θ^k+1 = θ^k - α_k∇_θ L(θ^k, x(t_j),t_j) =

[

]

∑

=θ^k -α_k∇_θ

(x_i(t_j) - x_i(θ,t_j))2

i=1

}

L(θ^k ,x(t_j ),t_j )

130

где α_k > 0, k = 0, 1, . . . , - величина шага, t_j - случайный момент времени на

множестве T , выбираемый на каждой k-й итерации заново; ∇_θ - градиент по

вектору параметров.

Б. Классический метод моментов (Classical Momentum, ClassMom):

θ^k+1 = θ^k - α_kv^k,

v^k+1 = βv^k + (1 - β)∇_θL(θ^k, x(t_j),t_j),

где v⁰ = o - нулевой вектор-столбец, β = 0,9.

В. Ускоренный градиентный метод Нестерова (Nesterov Accelerated Gradi-

ent, NAG) для решения задачи f(x^∗) = min_x∈Rn f(x).

Шаг 1. Задать параметры: γ, γ ∈ (0,1), - коэффициент сохранения

(γ = 0,9); η - коэффициент влияния новой информации; x⁰ ∈ Rⁿ - началь-

ная точка; v⁰ = o; ε₁ > 0.

Положить k = 0.

Шаг 2. Положить k = k + 1 и выполнить:

y^k = x^k - γv^k-1, g^k = ∇f^k(y^k), v^k = γv^k-1 + ηg^k.

Шаг 3. Вычислить x^k = x^k-1 - v^k.



Шаг 4. Проверить выполнение условия

x^k - x^k-1< ε1.

Если условие выполнено, то x^∗ = x^k. Иначе перейти к шагу 2.

Г. Метод адаптивного градиента (Adaptive Gradient, AdaGrad) для реше-

ния задачи f(x^∗) = min_x∈Rn f(x).

Шаг 1. Задать параметры: γ, γ ∈ (0,1), - коэффициент сохранения (γ =

= 0,9); η - скорость обучения (обычно η = 0,01); x⁰ ∈ Rⁿ - начальная точка;

ε = 10^-6 ÷ 10^-8 - сглаживающий параметр; ε₁ > 0; G^-1 = o.

Положить k = 0.

Шаг 2. Положить

g^k = ∇f^k(x^k); G^k = G^k-1 + g^k ⊙ g^k,

где ⊙ - поэлементное произведение матриц по Адамару.

Шаг 3. Вычислить

√

x^k+1 = x^k - ηg^k ⊘ G^k + ε,

где ⊘ - операция поэлементного деления матриц.



Шаг 4. Проверить выполнение условия

x^k+1 - x^k< ε1.

Если условие выполнено, то x^∗ = x^k+1. Иначе положить k = k + 1 и перей-

ти к шагу 2.

Д. Метод скользящего среднего (Root Mean Square Propagation, RMSProp)

для решения задачи f(x^∗) = min_x∈Rn f(x).

131

Шаг 1. Задать параметры: γ, γ ∈ (0,1), - коэффициент сохранения

(γ = 0,9); x⁰ ∈ Rⁿ - начальная точка; ε = 10^-6 ÷ 10^-8 - сглаживающий па-

раметр; ε₁ > 0; η - величина шага (обычно η = 0,001); M^-1 = o.

Положить k = 0.

Шаг 2. Положить g^k = ∇f^k(x^k); G^k = g^k ⊙ g^k; M^k = γM^k-1 + (1 - γ)G^k.

√

Шаг 3. Вычислить x^k+1 = x^k - ηg^k ⊘

M^k + ε.



Шаг 4. Проверить выполнение условия

x^k+1 - x^k< ε1.

Если условие выполнено, то x^∗ = x^k+1. Иначе положить k = k+1 и перейти

к шагу 2.

Е. Метод адаптивной оценки моментов (Adaptive Moment Estimation,

Adam) для решения задачи M[f(x)] → min, в которой имеются случайные

реализации f¹(x), f²(x), . . . , f^K (x).

Шаг 1. Задать параметры: α = 0,001 - величина шага; β₁ = 0,9; β₂ =

= 0,999 - параметры оценки моментов, x⁰ ∈ Rⁿ - начальная точка; ε = 10^-8 -

сглаживающий параметр; ε₁ > 0; m⁰ = o - начальное значение первого век-

тора моментов M[∇f(x)]; v⁰ = o - начальное значение второго вектора мо-

ментов M[∇f(x) ⊙ ∇f(x)].

Положить k = 0.

Шаг 2. Положить k = k + 1,

g^k = ∇f^k(x^k-1); m^k = β₁m^k-1 + (1 - β₁)g^k;

Gk = g^k ⊙ g^k; v^k = β₂v^k-1 + (1 - β₂)G^k;

v^k

m^k =

;

vk =

1-β_1k

1-β₂

√

Шаг 3. Вычислить x^k = x^k-1 - α m^k ⊘

vk + ε.



xk+1_-xk

Шаг 4. Проверить выполнение условия

<ε1.

Если условие выполнено, то x^∗ = x^k. Иначе перейти к шагу 2.

Ж. Модификация метода Adam (Adamax) для решения задачи M[f(x)] →

→ min, где f(x)∈C¹. Имеются случайные реализации f¹(x),f²(x),... ,f^K(x).

Шаг 1. Задать параметры: α = 0,002 - величина шага; β₁ = 0,9; β₂ =

= 0,999 - параметры оценки моментов, β₂ ∈ [0, 1); x⁰ ∈ Rⁿ - начальная точ-

ка; ε = 10^-8 - сглаживающий параметр; ε₁ > 0, m⁰ = o - начальное значение

первого вектора моментов M[∇f(x)]; u⁰ = o.

Положить k = 0.

Шаг 2. Положить k = k + 1,

g^k = ∇f^k(x^k-1); m^k = β₁m^k-1 + (1 - β₁)g^k,

{

}



u^k = max β₂u^k-1,gk

(операция max выполняется поэлементно).

Шаг 3. Вычислить x^k = x^k-1 -

m^k ⊘ u^k.

1-β₁

132



Шаг 4. Проверить выполнение условия

x^k+1 - x^k< ε1.

Если условие выполнено, то x^∗ = x^k. Иначе перейти к шагу 2.

З. Ускоренный по Нестерову метод адаптивной оценки моментов (Neste-

rov-accelerated Adaptive Moment Estimation, Nadam).

Шаг 1. Задать параметры: α = 0,002 - величина шага; β₁ = 0,975; β₂ =

= 0,999 - параметры оценки моментов, x⁰ ∈ Rⁿ - начальная точка; ε = 10^-8 -

сглаживающий параметр; m⁰ = o - начальное значение первого вектора мо-

ментов M[∇f(x)]; v⁰ = o - начальное значение второго вектора моментов

M [∇f(x) ⊙ ∇f(x)]. Положить k = 0.

Шаг 2. Положить k = k + 1,

g^k = ∇f^k(x^k-1); m^k = β₁m^k-1 + (1 - β₁)g^k;

Gk = g^k ⊙ g^k; v^k = β₂v^k-1 + (1 - β₂)G^k;

β₁m

(1 - β₁)g^k

β₂v^k

m^k =

;

vk =

1-β_1k+1

1-β_1k

1-β₂

√

Шаг 3. Вычислить x^k = x^k-1 - α m^k ⊘

vk + ε.



Шаг 4. Проверить выполнение условия

x^k+1 - x^k< ε1.

Если условие выполнено, то x^∗ = x^k. Иначе перейти к шагу 2.

И. Минипакетный метод градиентного спуска (Mini-batch Gradient De-

scent):

θ^k+1 = θ^k - α_k∇_θ Q(θ^k), α_k > 0, k = 0,1,... ,

где α_k - величина шага (learning rate),





∑

Q(θ) =



θ_jf_j(x_i) - y_i

L(θ, x_i, y_i),

i∈Jm j=1

i∈Jm

}

L(θ,x_i,y_i)

где J_m - набор из m номеров произвольных элементов (x_i, y_i) ∈ X^l обучаю-

щей выборки (можно взять m подряд идущих элементов). Чтобы реализовать

одно улучшение параметров, требуется использовать не весь набор данных

(dataset), а его небольшую часть (в прикладных задачах обычно от 50 до

256 элементов).

СПИСОК ЛИТЕРАТУРЫ

1. Bard Y. Nonlinear parameter estimation. N.Y.: Acad. Press, 1974.

2. Ивченко Г.И., Медведев Ю.И. Введение в математическую статистику. М.:

Книжный дом “ЛИБРОКОМ”, 2014.

3. Stewart W.E., Caracotsios M., Sorensen J.P. Parameter Estimation from Multire-

sponse Data // AIChE J. 1992. 38 (5). P. 641-650.

133

Biegler L.T. Optimization Algorithms for Parameter Estimation and Data Reconcil-

iation. Carnegie Mellon Center.

http://numero.cheme.cmu.edu/content/06606/Parestnotes.pdf

Csendes T. Nonlinear Parameter Estimation by Global Opitmization - Efficiency

and reliability // Acta Cybernetica, 1988. 8 (4). P. 361-372.

Arora N., Bieglera L.T. Trust Region SQP Algorithm for Equality Constrained Pa-

rameter Estimation with Simple Parameter Bounds // Comput. Optim. Appl. 2004.

No. 28. P. 51-86.

Floudas C.A., Pardalos P.M., Adjimann C.S., Esposito W.R., Gumus Z.H., Hard-

ing S.T., Schweiger C.A. Handbook of test problems in local and global optimization,

1999. V. 67. Springer US. https://titan.princeton.edu/TestProblems

Tjoa I.B., Biegler L.T. Simultaneous Solution and Optimization Strategies for Pa-

rameter Estimation of Differential-algebraic Equation Systems // Industrial & En-

gineering Chemistry Research. 1991. V. 30. No. 2. P. 376-385.

https://doi.org/10.1021/ie00050a015

Bock H.G. Recent Advances in Parameter Identification Techniques in ODE / Deu-

flhard P., Hairer E. (eds.). Numerical treatment of inverse problems in differential

and integral equations. P. 95-121. Birkhauser, 1983.

10.

Panteleev A.V., Letova T.A., Pomazueva E.A. Parametric Design of Optimal in Av-

erage Fractional-Order PID Controller in Flight Control Problem // Autom. Remote

Control. 2018. V. 79. № 1. P. 153-166.

Пантелеев А.В., Летова Т.А., Помазуева Е.А. Параметрический синтез опти-

мального в среднем дробного ПИД-регулятора в задаче управления полетом //

Управление большими системами. 2015. Вып. 56. С. 176-200.

11.

Esposito W.R., Floudas C.A. Global Optimization for the Parameter Estimation of

Differential-Algebraic Systems // Ind. Eng. Chem. Res. 2000. V. 39. P. 1291-1310.

12.

Osborne M.R. On Estimation Algorithms for Ordinary Differential Equations //

ANZIAM J. 2008. No. 50. P. 107-120.

13.

Adjiman C.S., Androulakis I.P., Floudas C.A., Neumaier A.A. Global Optimization

Method for General Twice-Differentiable NLPs, II. Implementation and Computa-

tional Results // Comput. Chem. Eng. 1998. No. 22 (9). P. 1159.

14.

Cizniar M., Podmajersky M., Hirmajer T., Fikar M. Global Optimization for Pa-

rameter Estimation of Differential-algebraic Systems // CHEM PAP. 2009. V. 63 (3).

P. 274-283.

15.

Floudas C.A., Pardalos P.M. (eds.) Encyclopedia of optimization. Springer, 2009.

16.

Glover F.W., Kochenberger G.A. Handbook of methaheuristics. Boston, MA: Kluwer

Acad. Publishers, 2003.

17.

Пантелеев А.В., Крючков А.Ю. Метаэвристические методы оптимизации в за-

дачах оценки параметров динамических систем // Науч. вестн. Моск. гос. тех-

нического ун-та гражданской авиации. 2017. T. 20. № 2. С. 37-45.

18.

Ruder S. An Overview of Gradient Descent Optimization Algorithms.

arXiv:1609.04747v2 [cs.LG] 15 Jun 2017.

19.

Karpathy Andrej (2017). A Peek at Trends in Machine Learning.

https://medium.com/@karpathy/a-peek-at-trends-in-machine-learning-

ab8a1085a106

20.

Sra Suvrit, Nowozin Sebastian, Wright Stephen J. Optimization for machine learning.

MIT Press, 2012.

134

21. Пантелеев А.В., Лобанов А.В. Градиентные методы оптимизации в машинном

обучении идентификации параметров динамических систем // Моделирование

и анализ данных. 2019. № 4. С. 88-99.

22. Пантелеев А.В. Методы оптимизации. Уч. пос. / А.В. Пантелеев, Т.А. Летова.

М.: Логос, 2011.

23. Синицын И.Н., Синицын В.И. Условно-оптимальное линейное оценивание нор-

мальных процессов в вольтерровских стохастических системах // Системы и

средства информатики. 2019. Т. 29. № 3. С. 16-28.

24. Синицын И.Н., Синицын В.И. Аналитическое моделирование процессов в воль-

терровских стохастических системах методом канонических разложений // Си-

стемы и средства информатики. 2019. Т. 29. № 1. С. 109-127.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 02.03.2020

После доработки 21.05.2020

Принята к публикации 09.07.2020

135