Автоматика и телемеханика, № 11, 2020
© 2020 г. И.Н. СИНИЦЫН, д-р техн. наук (sinitsin@dol.ru),
В.И. СИНИЦЫН, д-р физ.-мат. наук (sinitsin_vi@mail.ru)
(Федеральное государственное учреждение
“Федеральный исследовательский центр
“Информатика и управление” РАН” (ФИЦ ИУ РАН), Москва;
Московский авиационный институт
(национальный исследовательский университет)),
Э.Р. КОРЕПАНОВ, канд. техн. наук (ekorepanov@ipiran.ru),
Т.Д. КОНАШЕНКОВА (tkonashenkova64@mail.ru)
(Федеральное государственное учреждение
“Федеральный исследовательский центр
“Информатика и управление” РАН” (ФИЦ ИУ РАН), Москва)
ОПТИМИЗАЦИЯ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ
НА ОСНОВЕ ВЕЙВЛЕТ КАНОНИЧЕСКИХ РАЗЛОЖЕНИЙ
На основе вейвлет канонических разложений (ВЛКР) рассматриваются
задачи синтеза линейных оптимальных в среднем квадратическом (с.к.)
фильтров. Для моделирования существенно нестационарных стохастиче-
ских процессов (СтП), в том числе описывающих ударные воздействия,
предлагается использовать ВЛКР, построенные на основе коэффициентов
разложения его ковариационной функции по ортогональному двумерно-
му вейвлет базису. Для оценки наблюдаемого процесса, представленного
в виде ВЛКР, построен с.к. оптимальный линейный оператор в виде на-
бора формальных правил, описывающих реакцию оператора на базисные
вейвлет функции. Получены формулы для вычисления с.к. оптимальной
оценки сигнала и с.к. оптимальной оценки качества построенного с.к. оп-
тимального линейного оператора. Дано описание инструментального про-
граммного обеспечения “Синтез-ВЛ”, разработанного в среде MATLAB.
Приводится тестовый пример с дельта-функцией.
Ключевые слова: вейвлет каноническое разложение, нестационарный ли-
нейный с.к. оптимальный фильтр, ортогональные вейвлеты с конечным
носителем, вейвлеты Хаара.
DOI: 10.31857/S0005231020110082
1. Введение
В [1] приведен обстоятельный обзор современных подходов решения за-
дачи синтеза линейных оптимальных в среднем квадратическом фильтров.
В [2] дан краткий обзор известного алгоритмического и программного обеспе-
чения для решения задач нелинейного анализа стохастических систем (СтС)
на основе канонических разложений (КР). Приводятся примеры с результата-
ми работы инструментального программного обеспечения в среде MATLAB.
Изложенные в [3] материалы входят в состав разработанного инструменталь-
ного программного обеспечения в среде MATLAB и позволяют решать ши-
рокий круг задач, связанных со спектрально-корреляционным анализом и с
136
моделированием стационарных и нестационарных стохастических процессов
(СтП). С помощью данных алгоритмов можно проводить анализ линейных
и нелинейных преобразований случайных величин и функций. Проведенные
вычислительные эксперименты показали, что для большинства типовых ин-
женерных задач достаточно ограничиваться небольшим числом членов КР.
Описанное методическое и алгоритмическое обеспечение нашло применение
в задачах моделирования и оценки параметров вибровозмущений и синтеза
средств виброзащиты, вибронадежности компьютерного и коммуникацион-
ного оборудования.
Для моделирования существенно нестационарных СтП в условиях, напри-
мер, ударных воздействий успешно применяются вейвлет методы. Методы
моделирования СтП в линейных СтС и линейных СтС с параметрическими
шумами на основе вейвлет канонических разложений (ВЛКР) разработаны
в [3-8]. Вопросы синтеза с.к. оптимальных линейных фильтров посредством
вейвлет канонических разложений в регулярных случаях рассмотрены в [9].
В настоящей статье на основе ВЛКР рассматриваются задачи синтеза опти-
мальных с.к. фильтров.
2. Теорема о вейвлет с.к. оптимальном линейном операторе
Пусть наблюдаемый сигнал Z(t) и сигнал W (s), подлежащий воспроизве-
дению, можно представить в виде суммы линейной комбинации известных
функций со случайными коэффициентами и помехи в виде некоторой слу-
чайной функции [10]:
∑
(2.1)
Z(t) =
Urξr
(t) + X(t), t ∈ T,
r=1
∑
(2.2)
W (s) = Urζr
(s) + Y (s), s ∈ S,
r=1
где X(t), Y (s) - случайные функции с нулевыми математическими ожида-
ниями; ξ1, . . . , ξN , ζ1, . . . , ζN - заданные структурные функции; U1, . . . , UN -
случайные величины (СВ) с нулевыми математическими ожиданиями и не
коррелированные со случайными функциями X(t) и Y (s). Требуется найти
такой оператор At, чтобы случайная функция
W∗(s) = AtZ(t)
была с.к. оптимальной оценкой сигнала W (s). Согласно [10] для этого необ-
ходимо и достаточно, чтобы линейный оператор At был с.к. оптимальным,
т.е. удовлетворял уравнению
∑
(2.3)
At[KX(t,τ)] = KYX(s,τ) +
γpq (ζp(s) - At[ξp(t)]) ξq
(τ).
p,q=1
137
При этом для определения с.к. оптимального линейного оператора при-
годны только такие решения уравнения (2.3), которые преобразуют X(t)
в случайные функции, обладающие конечными дисперсиями. Тогда уравне-
ние (2.3) имеет общий вид
(2.4)
At[KX
(t, τ)] = f(s, τ) (t, τ ∈ T ; s ∈ S),
где f(s, τ) - известная функция. В [9] доказана теорема о вейвлет с.к. опти-
мальном линейном операторе.
Теорема 1. Пусть выполнены следующие условия:
1) в пространстве L2(T ), где T = [t0, t1] - некоторый промежуток, задан
ортонормированный вейвлет базис, порожденный вейвлетами с конечными
носителями, вида
(
)
(2.5)
ϕt00(t), ψtjk(t) ,
√
где ϕt00(t) = ϕt(t) - масштабирующая функция ϕtjk =
2j ϕt(2j t - k); ψt00(t) =
√
= ψt(t) - материнский вейвлет; ψtjk(t) =
2j ψt(2j t - k); j = 1, 2, . . . , Jt; k =
= 0, 1, . . . , 2j - 1; Jt - максимальный уровень разрешения;
2) в пространстве L2(S), где S = [s0, s1] - некоторый промежуток, задан
ортонормированный вейвлет базис вида, порожденный вейвлетами с конеч-
ными носителями, вида
(
)
(2.6)
ϕs00(s), ψsjk(s) ,
√
(
)
где ϕs00 (s) = ϕs (s)
масштабирующая функция ϕsjk =
2j ϕs
2j s - k
;
√
ψs00(s) = ψs(s) - материнский вейвлет; ψsjk(s) =
2j ψs(2j s - k); j = 1, 2, . . .
...,Js; k = 0,1,...,2j - 1; Js - максимальный уровень разрешения;
3) в пространстве L2(T ×T ) определен двумерный ортонормированный ба-
зис путем тензорного произведения двух одномерных вейвлет базисов (2.5)
в случае, когда масштабирование по обеим переменным происходит одина-
ково:
(2.7)
ΦtA00(t1,t2) = ϕt00(t1)ϕt00(t2
),
(2.8)
ΨtHjkn(t1,t2) = ϕtjk(t1)ψtjn(t2
),
(2.9)
ΨtBjkn(t1,t2) = ψtjk(t1)ϕtjn(t2
),
(2.10)
ΨtDjkn(t1,t2) = ψtjk(t1)ψtjn(t2
),
где j = 1, . . . , Jt; k, n = 0, 1, . . . , 2j - 1;
4) в пространстве L2(S×T ) определен двумерный ортонормированный ба-
зис вида путем тензорного произведения двух одномерных вейвлет базисов
(2.5) и (2.6) в случае, когда масштабирование по обеим переменным проис-
ходит по-разному:
(2.11)
ΦsA00(s,t) = ϕs00(s)ϕt00
(t),
138
(2.12)
ΨsHj
(s, t) = ϕs00(s)ψtj
(t),
2n
2n
(2.13)
ΨsBj
(s, t) = ψsj
(s)ϕt00
(t),
1k
1k
(2.14)
ΨsDj
(s, t) = ψtj
(s)ψtj
(t),
1kj2n
1k
2n
где j1 = 0, 1, . . . , Js; k = 0, 1, . . . , 2j1 - 1; j2 = 0, 1, . . . , Jt; n = 0, 1, . . . , 2j2 - 1;
5) функция f(s, t) ∈ L2(S×T ) имеет сходящееся вейвлет разложение
(ВЛР) согласно
[11-13]:
∑
∑
∑
∑
f (s, τ) = af ΦsA00(s, τ) +
hfjkΨsHjk(s,τ) +
bfjkΨsBjk(s,τ) +
j=0 k=0
j=0 k=0
∑
∑
+
dfj
ψsDj
(s, τ),
1kj2n
1kj2n
j1=0 k=0 j2=0 n=0
где
∫
∫
af =
f (s, τ)ΦsA00(s, τ)dtds,
S T∫
∫
hfjk =
f (s, τ)ΨsHjk (s, τ)dtds,
S T
∫
∫
bfjk =
f (s, τ)ΨsBjk(s, τ)dtds,
S T
∫
∫
dfj
=
f (s, τ)ΨsDj
(s, τ)dtds;
1kj2
n
1kj2n
S T
6) функция KX (t, τ) ∈ L2(T ×T ) допускает сходящееся ВЛР согласно
[11-13]:
KX(t,τ) = atΦtA00(t,τ) +
(2.15)
∑
∑(
)
+
htjknΨtHjkn(t,τ) + btjknΨtBjkn(t,τ) + dtjknΨtjknD(t,τ)
,
j=0 k=0 n=0
где
∫
∫
at =
KX(t1,t2)ΦtA00(t1,t2)dt1dt2,
T T∫
∫
htjkn =
KX(t1,t2)ΨtHjkn(t1,t2)dt1dt2,
T T
139
∫
∫
bt
jkn
=
KX(t1,t2)ΨtBjkn(t1,t2)dt1dt2,
T T
∫
∫
dtjkn =
KX(t1,t2)ΨtDjkn(t1,t2)dt1dt2;
T T
7) результат воздействия неизвестного линейного оператора At на ба-
зисные вейвлет функции вида (2.5) представляют собой функции, принад-
лежащие пространству L2(S).
Тогда линейный оператор At, который является решением уравнения
(2.4), определяется посредством набора формальных правил:
At[ϕtjk(t)] = ujk(s) (j = 0,1,... ,Jt;k = 0,1,... ,2j - 1),
(2.16)
At[ψt00(t)] = v00(s),
At[ψtjk(t)] = 0 (j = 1,... ,Jt;k = 0,1,... ,2j - 1),
где
∑
∑
u00(s) = au00ϕs00(s) +
du00inψsin(s);
i=0 n=0
∑
∑
v00(s) = av00ϕs00(s) +
dv00inψsin(s);
i=0 n=0
∑
∑
ujk(s) = aujkϕs00(s) +
dujkinψsin(s) (j = 1,... ,Jt;k = 0,1,... ,2j - 1);
i=0 n=0
параметры au00 , du00in, av00 , dv00in, aujk, dujkin (i = 0, . . . , Js; n = 0, 1, . . . , 2i - 1;
j = 1, . . . , Jt; k = 0, 1, . . . , 2j - 1) являются решением системы линейных
алгебраических уравнений (СЛАУ ):
atau00 + bt000av00 = af ,
ht000au00 + dt000av00 = hf00,
∑
htjknaujk = hfjn (j = 1,... ,Jt;k = 0,1,... ,2j - 1),
k=0
(2.17)
f
atdu00il + bt000dv00il = b
(i = 0, . . . , Js; l = 0, 1, . . . , 2i - 1),
il
ht000du00il + dt000dv00il = dfil00 (i = 0,... ,Js;l = 0,1,... ,2i - 1),
∑
htjkndujkil = dfiljn
k=0
(i = 1, . . . , Js; l = 0, 1, . . . , 2i - 1; j = 1, . . . , Jt; n = 0, 1, . . . , 2j - 1).
140
3. Вейвлет канонические разложения
Примем, что случайная функция (СФ) X(t) в (2.1) допускает каноническое
разложение (КР) вида
∑
(3.1)
X(t) =
Vνxν
(t),
ν=1
где Vν - некоррелированные СВ с нулевыми математическими ожидания-
ми и дисперсиями Dν ; xν (t) - детерминированные координатные функции,
представленные в виде линейной комбинации базисных вейвлет функций ви-
да (2.5).
Для удобства представим одномерный ортонормированный вейвлет базис
(2.5) в виде:
(3.2)
f1(t) = ϕt00(t); f2(t) = ψt00(t); fν(t) = ψtjk
(t)
для ν = 3, 4 . . . , Lt; ν = l + k + 1; l = 2j ; j = 1, 2, . . . , Jt; k = 0, 1, . . . , l - 1;
Lt = 2 · 2Jt .
Последовательный алгоритм построения вейвлет канонического разложе-
ния СФ X(t) определяется известными формулами [10] декорреляции СВ:
∫
Aν = fνX(t)dt (ν = 1,2,... ,Lt).
T
Определим ковариационные моменты СВ Aν :
∫
∫
kνµ = M[A◦ν A¯◦µ] =
fν(t1)fµ(t2)KX(t1,t2)dt1dt2 (ν,µ = 1,2,... ,Lt).
T T
На основании (2.15) имеем:
k11 = at; k12 = ht; k21 = bt; k22 = dt000; kνµ = dtjn
(3.3)
1n2
для ν = l + n1 + 1; µ = l + n2 + 1; l = 2j ; j = 1, 2, . . . , Jt; n1, n2 = 0, 1,
...,l - 1. Остальные kνµ = 0.
Для удобства введем функции
∫
(3.4)
zν(t) = fν(τ)KX(t,τ)dτ (ν = 1,2,... ,Lt
).
T
Тогда в силу (2.15) имеем:
z1(t) = atϕt00(t) + bt000ψt00(t); z2(t) = ht000ϕt00(t) + dt000ψt00(t);
∑
(
)
zν(t) =
htjknϕtjk(t) + dtjknψtjk(t)
k=0
для ν = 3, . . . , Lt; ν = l + n + 1; l = 2j ; j = 1, 2, . . . , Jt; n = 0, 1, . . . , l - 1.
141
При этом некоррелированные СВ Vν удовлетворяют соотношениям:
∑
A◦1 = V1; A◦r = - crνVν + Vr (r = 2,3,... ,Lt);
ν=1
где
kν1
cν1 = -
(ν = 2, 3, . . . , Lt);
D1
(
)
(3.5)
∑
1
cνµ = -
kνµ -
Dλcµλcνλ
(µ = 2, 3, . . . , ν - 1; ν = 3, 4, . . . , Lt);
D
µ
λ=1
∑
(3.6)
D1 = D[V1] = k11; Dν = D[Vν] = kνν - Dν|cνλ|2 (ν = 2,3,... ,Lt
).
λ=1
Координатные функции xν (t) в силу [10] определяются последовательно фор-
мулами:
1
x1(t) =
z1(t);
D1
(
)
∑
1
xν(t) =
dνλzλ(t) + zν(t)
(ν = 2, 3, . . . , Lt);
D
ν
λ=1
∑
dνλ = cνλ +
cνµdµλ (λ = 1,2,... ,ν - 2); dν,ν-1 = cν,ν-1.
µ=λ+1
Далее представим координатные функции xν (t) в виде линейных комби-
наций базисных вейвлет функций вида (2.5):
(
)
1
(3.7)
x1(t) =
atϕt00(t) + bt000ψt00(t) ;
D1
)
1
((
)
(
)
(3.8)
x2(t) =
d21at + ht000
ϕt00(t) +
d21bt000 + dt000
ψt00(t) ;
D2
1
((
)
(
)
x3(t) =
d31at + d32ht000
ϕt00(t) +
d31bt000 + d32dt000
ψt00(t) +
D3
(3.9)
)
+ ht100ϕt10(t) + ht110ϕt11(t) + dt100ψt10(t) + dt110ψt11(t) ;
(
1
(
)
(
)
x4(t) =
d41at + d42ht000
ϕt00(t) +
d41bt000 + d42dt000
ψt00(t) +
D4
(3.10)
)
∑(
)
∑(
)
+
d43ht1k0 + ht1k1
ϕt1k(t) +
d43dt1k0 + dt1k1
ψt1k(t)
k=0
k=0
142
Для следующих координатных функций для удобства введем обозначения
(3.11)
xν(t) = x∗jn(t)
(ν = 5, 6, . . . , Lt; ν = 2j + n + 1; j = 2, 3, . . . , Jt; n = 0, 1, . . . , 2j - 1).
Если n = 0, то ν = 2j + 1 для j = 2, 3, . . . , Jt и
(3.12)
xν(t) = x∗j0
(t) =
1
=
(dν1at + dν2ht000)ϕt00(t) + (dν1bt000 + dν2dt000)ϕt00(t) +
Dν
∑
∑
∑
+
dνλ(htikn
ϕtik(t) + dtikn
ψtik(t)) +
(htjk0ϕtjk(t) + dtjk0ψtjk(t))
1
1
i=0 k=0 n1=0
k=0
для λ = 2i + n1 + 1.
Если n = 0, то ν = 2j + n + 1 для j = 2, 3, . . . , Jt; n = 0, 1, . . . , 2j - 1 и
xν(t) = x∗jn(t) =
1
(
)
(
)
=
dν1at + dν2ht000
ϕt00(t) +
dν1bt000 + dν2dt000
ψt00(t) +
Dν
∑
∑
(
)
+
dνλ
htikn
ϕtik(t) + dtikn
ψtik(t)
+
1
1
(3.13)
i=0 k=0 n1=0
∑
∑
(
)
+
dνλ1
htikn
ϕtik(t) + dtikn
ψtik(t)
+
1
1
k=0 n1=0
∑
(
+
htjknϕtjk(t) + dtjknψtjk(t)
)
k=0
для λ = 2i + n1 + 1, λ1 = 2j + n1 + 1 .
Наконец, можно убедиться, что выражения (3.7)-(3.13) можно записать в
общем виде:
∑
∑(
)
(3.14)
xν(t) =
axνjkϕtjk(t) + dxjkψtjk(t)
(ν = 1, 2, . . . , Lt
).
j=0 k=0
4. Синтез вейвлет с.к. оптимальной оценки сигнала
Для решения операторного уравнения (2.3) применим теорему 1. Будем
считать, что выполнены все условия теоремы 1, а также дополнительные
условия:
143
1) функции ξ1, . . . , ξN ∈ L2(T ) и представимы в виде сходящихся вейвлет
разложений (ВЛР) на промежутке T :
∑
∑
(4.1)
ξp(t) = aξpϕt00(t) +
dξpjkψtjk
(t) (p = 1, . . . , N),
j=0 k=0
где
∫
aξp = ξp(t)ϕt00(t)dt,
T∫
dξpjk = ξp(t)ψtjk(t)dt;
T
2) функции ζ1, . . . , ζN (s) ∈ L2(S) и представимы в виде сходящихся ВЛР
на промежутке S:
∑
∑
(4.2)
ζp(t) = aζpϕs00(s) +
dζpjkψsjk
(s) (p = 1, . . . , N),
j=0 k=0
где
∫
aζp = ζp(t)ϕs00(s)ds,
S∫
dζpjk = ζp(s)ψsjk(s)ds;
S
3) функция KYX (s, τ) ∈ L2(S ×T ) и представима в виде сходящегося ВЛР:
∑
∑
KYX(s,τ) = asΦsA00(s,τ) +
hsjkΨsHjk(s,τ) +
j=0 k=0
(4.3)
∑
∑
∑
∑
+
bsjkΨsBjk(s,τ) +
dsj
ΨsDj
(s, τ),
1kj2n
1kj2n
j=0 k=0
j1=0 k=0 j2=0 n=0
где
∫
∫
as =
KYX(s,τ)ΦsA00(s,τ)dτds,
S T∫
∫
hsjk =
KYX(s,τ)ΨsHjk(s,τ)dτds,
S T
144
∫
∫
bs
jk
=
KYX(s,τ)ΨsBjk(s,τ)dτds,
S T
∫
∫
dsj
=
KYX(s,τ)ΨsDj
(s, τ)dτds.
1kj2
n
1kj2n
S T
Тогда с.к. оптимальный линейный оператор At задается набором формаль-
ных правил теоремы 1. Коэффициенты ВЛР функций u00(s), v00(s), ujk(s)
(j = 1, . . . , Jt; k = 0, 1, . . . , 2j - 1) по базису вида (2.6) удовлетворяют систе-
ме линейных алгебраических уравнений (СЛАУ) вида (2.17):
∑
(
)
(4.4)
atau00 + bt000av00 = as
+ γpq aζp -aξpau00 -dξp00av
00
aξq,
p,q=1
∑
(
)
(4.5)
dt000av00 + ht000au00 = hs
+ γpq aζp -aξpau00 -dξp00av
dξq00,
00
00
p,q=1
∑
∑
(
)
(4.6)
htjknaujk = hs
+ γpq aζp -aξpau00 -dξp00av
dξqjn
jn
00
k=0
p,q=1
(i = 0, 1, . . . , Js; l = 0, 1, . . . , 2i - 1),
∑
(
)
(4.7)
atdu00il + bt000dv000il = bs
+ γpq aζp -aξpau00 -dξp00av
aξq
il
00
p,q=1
(i = 0, 1, . . . , Js; l = 0, 1, . . . , 2i - 1),
∑
(
)
(4.8)
dt000dv000il + ht000du00il = ds
+ γpq dζpil -aξpdu00il -dξp00dv
dξq00
il00
000il
p,q=1
(i = 0, 1, . . . , Js; l = 0, 1, . . . , 2i - 1),
∑
∑
(
)
(4.9)
htjkndujkil = ds
iljn
+ γpq dζpil -aξpdu00il -dξp00dv
000il
dξqjn
k=0
p,q=1
(j = 1, . . . , Jt; n = 0, 1, . . . , 2j - 1; i = 0, 1, . . . , Js; l = 0, 1, . . . , 2i - 1) .
Качество оптимального с.к. оператора определяется с.к. оценкой [10]:
[
]
[
]
[
]
η(s) = M |δW |2
= M |W(s) - W∗(s)|2
= M |W(s) - AtZ(t)|2
=
= ΓW(s,s) - AtΓWZ(s,t) = ΓW(s,s) - AtΓWZ(s,t),
145
так как ΓWZ (s, t) - действительная функция. Согласно (2.1), (2.2):
∑
ΓW (s,s) =
γpqζp(s)ζq(s) + KY (s,s),
p,q=1
∑
ΓWZ(s,t) =
γpqζp(s)ξq(t) + KYX(s,t).
p,q=1
Отсюда находим
∑
η (s) =
γpqζp (s)ζq (s) + KY (s,s) -
p,q=1
∑
−At
γpqζp (s) ξq (t) + KYX (s,t) =
p,q=1
∑
(
)
= γpqζp(s) ζq(s) - aξqu00(s) - dξq00v00(s)
+ KY (s,s) -
p,q=1
∑
∑
-asϕs00 +
bsjkϕsjk(s) u00(s) + hs00ϕs00(s)v00(s) .
j=0 k=0
В итоге получено следующее утверждение.
Теорема 2. Пусть выполнены условия теоремы 1, а также:
1) наблюдаемый сигнал Z(t) имеет вид (2.1), сигнал, подлежащий вос-
произведению, W(s) имеет вид (2.2);
2) ξ1, . . . , ξN ∈ L2(T );
ζ1,... ,ζN ∈ L2(S);
KYX(s,t) = M[Y (s)X(t)] ∈
∈ L2(S×R).
Тогда справедливы следующие утверждения:
1) с.к. оптимальный линейный оператор At, определяемый уравнени-
ем (2.3), задается набором формальных правил (2.16), а параметры aujk,
dujkin, au00, du00in, av00, dv00in (i = 0,... ,Js; n = 0,1,... ,2i - 1; j = 1,... ,Jt;
k = 0,1,...,2j - 1) определяются СЛАУ (4.4)-(4.9);
2) качество с.к. оптимального линейного оператора At определяется с.к.
оценкой:
∑
(
)
η(s) =
γpqζp(s) ζq(s) - aξqu00(s) - dξq00v00(s)
+ KY (s,s) -
p,q=1
(4.10)
∑
∑
-asϕs00 +
bsjkϕsjk(s) u00(s) + hs00ϕs00(s)v00(s) .
j=0 k=0
146
Следствие. Пусть выполнены все условия теоремы 2. Тогда с.к. опти-
мальная оценка W∗(s) сигнала W (s) определяется формулой:
∑
(
)
W∗(s) = AtZ(t) =
Ur aξru00(s) + dξr00v00(s)
+
r=1
(4.11)
(
)
∑
∑
∑
+ Vν dxν00v00(s) +
axνjkujk(s)
ν=1
j=0 k=0
Следствием теоремы 2 являются два алгоритма: построение с.к. оптималь-
ного линейного оператора At и построение с.к. оптимальной оценки W∗(s)
сигнала W (s).
Алгоритм 1.
1. Задание вейвлет базисов (2.5), (2.6), (2.7)-(2.10), (2.11)-(2.14).
2. Вейвлет разложение функций ξ1, . . . , ξN ∈ L2(T ) по базису (2.5), функ-
ций ζ1, . . . , ζN (s) ∈ L2(S) по базису (2.6), функции KX (t, τ) ∈ L2(T ×T ) по
базису (2.7)-(2.10), KYX (s, τ) ∈ L2(S×T ) по базису (2.11)-(2.14).
3. Составление и решение СЛАУ (4.4)-(4.9) относительно aujk, dujkil, au00,
du00in, av00, dv00in (i = 0,... ,Js; n = 0,1,... ,2i - 1; j = 1,... ,Jt; k = 0,1,
...,2j - 1).
4. Задание набора формальных правил (2.16), которыми определяется с.к.
оптимальный линейный оператор At.
5. Вычисление с.к. оптимальной оценки η по формуле (4.10) для опреде-
ления качества с.к. оптимального линейного оператора At.
Алгоритм 2.
1. Вейвлет разложение функций ξ1, . . . , ξN ∈ L2(T ) по базису (2.5) в виде
(4.1).
2. Вейвлет каноническое разложение случайной функции (СФ) X(t) в виде
(3.1):
определение kνµ по формулам (3.3), остальные kνµ = 0;
определение Dν = D[Vν ] по формулам (3.5), (3.6);
определение координатных функции xν (t) в виде линейных комбинаций
базисных вейвлет функций вида (2.5) по формулам (3.7)-(3.14).
3. Построение с.к. оптимальной оценки W∗(s) сигнала W (s) в виде (4.11).
5. Инструментальное программное обеспечение “Синтез-ВЛ”
На основе методических результатов разделов 3 и 4 в ФИЦ ИУ РАН раз-
работано инструментальное программное обеспечение (ИПО) “Синтез-ВЛ” в
среде MATLAB, которое реализует алгоритмы построения вейвлет с.к. оп-
тимального линейного оператора в случае линейной зависимости сигнала от
параметров и аддитивной помехи и осуществляет:
1) ввод исходных данных: набор подпрограмм-функций, задающих струк-
турные функции ξ1, . . . , ξN , ζ1, . . . , ζN и ковариационные функции KX (t, τ),
KYX(s,τ); промежуток наблюдения [t0,t1] СтП Z(t); промежуток оценки
[s0, s1] СтП W (t); максимальные уровни вейвлет разложения Jt и JS ;
147
2) одномерное вейвлет разложение структурных функций ξ1, . . . , ξN ,
ζ1,... ,ζN по вейвлет базису Хаара с применением стандартной функции
wavedec;
3) двумерное вейвлет разложение ковариационных функций KX (t, τ) и
KYX(s,τ) по вейвлет базису Хаара с применением стандартной функции
wavedec2;
4) автоматическое составление и решение СЛАУ для вычисления пара-
метров: aujk, dujkil, av00, dv00in (i = 1, . . . , Js; n = 0, 1, . . . , 2i - 1; j = 1, . . . , Jt;
k = 0,1,...,2j - 1);
5) построение ВЛКР процесса X(t) на основе двумерного вейвлет разло-
жения ковариационной функции KX (t, τ) по вейвлетам Хаара;
6) вывод результатов в числовом виде.
Исходные данные для ИПО “Синтез-ВЛ”, задаваемые в числовом виде:
1) начальный момент времени наблюдения сигнала T 0 = t0;
2) конечный момент времени наблюдения сигнала T = t1;
3) начальный момент времени оценки сигнала S0 = s0;
4) конечный момент времени оценки сигнала SS = s1;
5) максимальные уровни вейвлет разложения Jt = Jt, Js = Js;
6) количество базисных вейвлет функций Nt = 2 · 2Jt , Ns = 2 · 2Js .
Исходные данные для ИПО “Синтез-ВЛ” в аналитическом виде, задаваемые
в виде пользовательских функций-подпрограмм:
1) набор функций-подпрограмм fksi1, . . . , fksiN для задания структур-
ных функций ξ1, . . . , ξN ;
2) набор функций-подпрограмм fdzet1, . . . , fdzetN для задания структур-
ных функций ζ1, . . . , ζN ;
3) подпрограмма-функция fcov для задания ковариационной функции
KX(t,τ);
4) подпрограмма-функция fcovY X для задания ковариационной функции
KYX(s,τ).
Подпрограммы-функции имеют синтаксис вызова: cov = fcov(t1, t2);
covY X = fcovY X(s, t); ksi = fksii(t) (i = 1, . . . , N); dzet = fdzeti(s) (i =
= 1, . . . , N).
Все вычисления осуществляются в подпрограмме-функции SYNTHESISWL1,
которая имеет синтаксис вызова:
[W Ot, nett] = SYNTHESISWL1(Jt, Nt, T 0, T, Js, Ns, S0, SS).
Выходные данные выдаются в матричном виде:
1) W Ot(Ns) вектор значений с.к. оптимальной оценки W∗(s) сигна-
ла W (s) в точках sj = S0 + (j - 1) для j = 1, 2, . . . , Ns;
2) nett(Ns)
вектор значений с.к. оптимальной оценки η качества с.к.
оптимального линейного оператора At в точках sj = S0 + (j - 1) для j =
= 1, 2, . . . , Ns.
При вычислениях используется подпрограмма-функция KRWL1 для по-
строения ВЛКР процесса X(t), заданного на промежутке [0, T ], на основе дву-
мерного вейвлет разложения ковариационной функции KX (t, τ) по вейвлетам
Хаара и для реализации алгоритма, изложенного в разделе 3. Подпрограмма-
148
функция KRWL1 имеет синтаксис вызова:
[Xnu, Dnu, DispX, XKRW ] = KRWL1(J, NJ, T ),
где J - максимальный уровень вейвлет разложения; NJ = 2 · 2J . При вычис-
лениях используется стандартная функция wavedec2 для получения коэффи-
циентов двумерного вейвлет разложения ковариационной функции одномер-
ного СтП X(t), заданной с помощью подпрограммы-функции fcov. Выходные
данные выдаются в матричном виде:
1) Xnu(NJ, NJ) матрица значений координатных функций ВЛКР:
(T(j - 0,5))
Xnu(i,j) = xi
для i, j = 1, 2, . . . , NJ;
N
2) Dnu(NJ) вектор значений дисперсий Dν (ν = 1, 2, . . . , NJ) некор-
релированных СВ V1, . . . , VNJ ;
3) DispX(NJ)
вектор значений дисперсии СтП X(t) в точках tj =
= T(j-0,5)NJ для j = 1,2,... ,NJ;
4) XKRW (NJ) вектор значений реализации СтП X(t) в точках tj =
= T(j-0,5)NJ для j = 1,2,... ,NJ.
6. Применения
Найти с.к. оптимальный линейный фильтр, предназначенный для воспро-
изведения сигнала
(6.1)
W (s) = U1 + U2δ(s - s∗)
по результатам наблюдения суммы этого сигнала и некоррелированной поме-
хи, т.е.
(6.2)
Z(t) = U1 + U2δ(t - t∗
) + X(t).
Наблюдение производится в течение интервала времени длительностью T ,
предшествующего данному моменту s (s ≥ T ). Случайная функция X(t) за-
дана математическим ожиданием, равным нулю, и ковариационной функцией
KX(t,τ) = Dexp(-α|t - τ|). U1,U2 - СВ с нулевыми математическими ожи-
даниями, не коррелированные с X(t), M[UpUq] = γpq(p, q = 1, 2).
Применим алгоритм 1 для построения с.к. оптимального линейного опе-
ратора At для воспроизведения сигнала W (s), заданного формулой (6.1), по
результатам наблюдения сигнала Z(t), заданного формулой (6.2), и для опре-
деления с.к. оптимальной оценки η качества оператора At . При вычислениях
будем использовать ортонормированный базис Хаара вида (2.5), где
{
0, если t ∈ [0, 1),
масштабирующая функция ϕt00(t) = ϕt(t) =
1, если t ∈ [0, 1),
1,
если t ∈ [0,12 ),
материнский вейвлет ψt00(t) = ψt(t) =
−1,
если t ∈ [12 , 1),
0,
если t ∈ [0, 1).
149
Перейдем от переменной t ∈ [s - T, s] к переменной t ∈ [0, 1] с помощью
замены переменной t=t-(s-T)s-(s-T) =t-(s-T)T . Тогда
KX(t,τ) = KX(t, τ) = Dexp(-αT(|t- τ|)),
Z(t) = Z(t) = U1 + U2((s - T ) + T t) + X((s - T ) + T t).
Далее в примере для простоты записи будем считать, что t = t, τ = τ.
Уравнение (2.3) в данном случае имеет вид:
(
)
∑
At[KX(t,τ)] =
γpq ζp(s) - At[ξp(t)] ξq(τ),
p,q=1
так как Y (s) = 0 и как следствие KYX (s, τ) = 0.
Тогда СЛАУ для определения неизвестных функций u00(s), v00(s), ujk(s)
(j = 1, 2, . . . , Jt; k = 0, 1, . . . , 2j - 1) для заданного значения переменной s
имеет вид:
∑
atu00(s) + bt000v00(s) =
γpqλpaξq,
p,q=1
∑
dt000v00(s) + ht000u00(s) =
γpqλpdξq00,
p,q=1
∑
∑
htjknujk(s) =
γpqλpdξqjn
k=0
p,q=1
(j = 1, 2, . . . , Jt; k = 0, 1, . . . , 2j - 1),
λ1 = ζ1(s) - aξ1u00(s) - dξ100v00(s),
λ2 = ζ2(s) - aξ2u00(s) - dξ200v00(s).
Здесь для удобства введены переменные
λp = ζp(s) - aξpu00(s) - dξp00v00(s) (p = 1,2).
Для заданного значения переменной s набор формальных правил, которы-
ми определяется с.к. оптимальный линейный оператор At при t ∈ [0, 1], имеет
вид (2.16). При этом с.к. оптимальная оценка η для определения качества с.к.
оптимального линейного оператора At вычисляется по формуле:
∑
(
)
η(s) =
γpqζp(s) ζq(s) - aξqu00(s) - dξq00v00(s)
p,q=1
C.к. оптимальная оценка η качества с.к. оптимального линейного опера-
тора At зависит только от функций u00(s), v00(s). Для построения с.к. оп-
тимальной оценки W∗(s) сигнала W (s) необходимо выполнить алгоритм 2.
150
1,06
1,05
1
1,04
1,03
1,02
1,01
2
1,00
0,99
0,98
0,99
14,5
15,5
16,5
17,5
18,5
19,5
20,5
21,5
Рис. 1. Графики дисперсии СФ X(t): график 1 - точные значения, график 2 -
приближенные значения.
В результате имеем
∑
(
)
W∗(s) =
Ur aξru00(s) + dξr00v00(s)
+
r=1
(
)
∑
∑
∑
+ Vnu dxν00v00(s) +
axνjkujk(s)
ν=1
j=0 k=0
Вычисления осуществлялись на основе ИПО “Синтез-ВЛ”. Использовались
следующие исходные данные: α = 1; s = 11, 12, . . . , 18; T = 8; t∗ = (s - T )+
+3T
; s∗ = s; γ11 = γ22 = 1; γ12 = γ21 = 0.
2∗2Jt
Как показали вычислительные эксперименты, уже при Jt = 2 относитель-
ная точность аппроксимации дисперсии X(t) оказывается менее 5 %. Был
использован вейвлет базис Хаара для Jt = 2. В табл. 1 и на рис. 1 приведены
точные значения дисперсии DT (ti) для X(t) в точках ti ∈ [10, 18] и прибли-
женные значения дисперсии Da(ti), полученные методом ВЛКР.
Величина с.к. ошибки аппроксимации дисперсии в этом случае равна
v
u
(
)2
u
∑
√1
σDn =
Da(ti) - DT (ti)
= 0,0374.
n
i=1
Значения дисперсий Dν независимых нормально распределенных СВ Vν ,
вычисленные по формулам (3.5), (3.6), приведены в табл. 2.
Таблица 1
n
1
2
3
4
5
6
7
8
ti
10,5
11,5
12,5
13,5
14,5
15,5
16,5
17,5
Da(ti)
1,0499
1,0185
1,0387
1,0383
1,0383
1,0387
1,0185
1,0499
DT (ti)
1
1
1
1
1
1
1
1
Таблица 2
ν
1
2
3
4
5
6
7
8
Dν
0,2206
0,1785
0,1302
0,1302
0,0851
0,0851
0,0851
0,0851
151
2,0
1,5
1,0
0,5
0
-0,5
-1,0
-1,5
-2,0
10
11
12
13
14
15
16
17
18
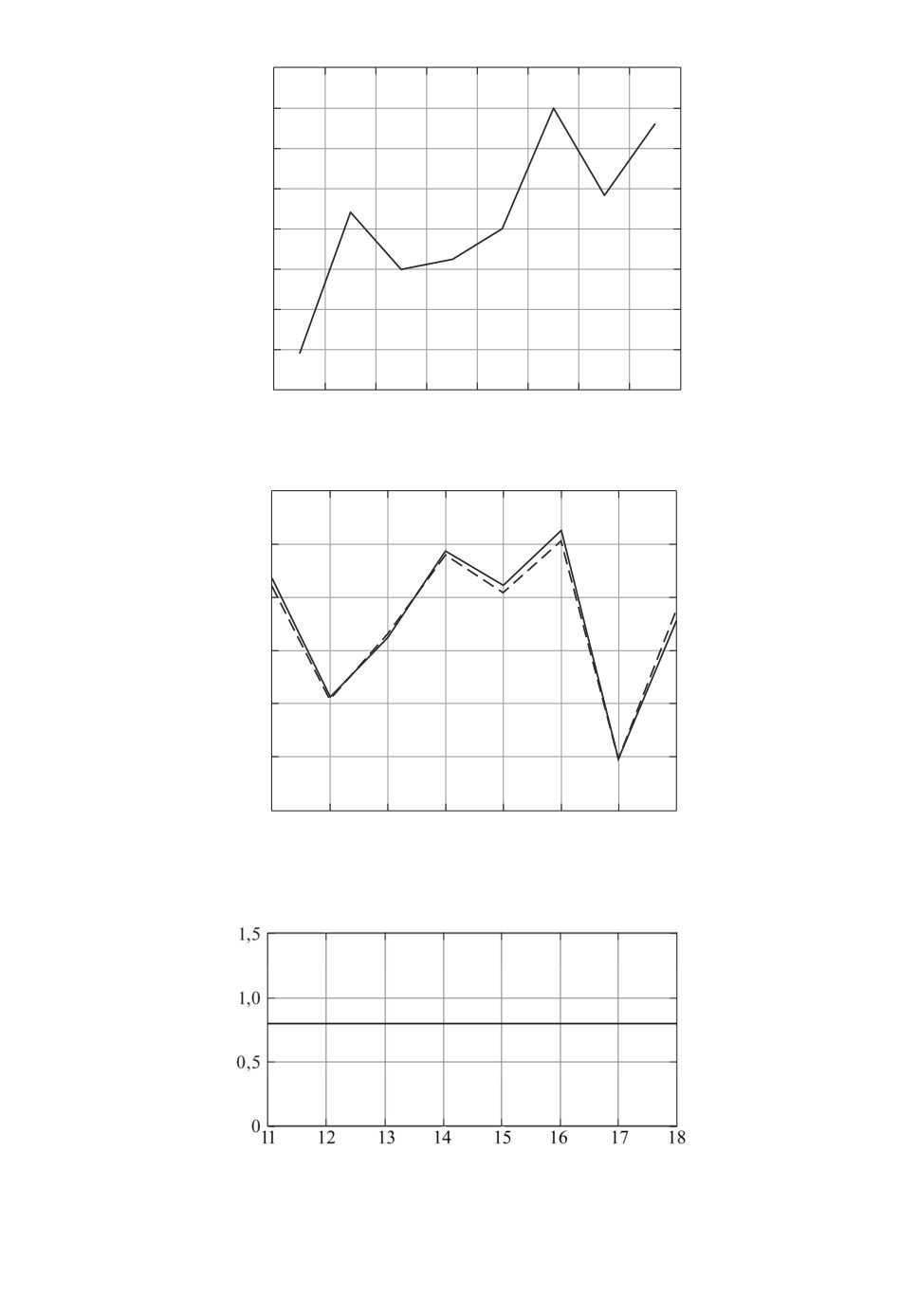
Рис. 2. График реализации СФ X(t).
10
5
0
-5
-10
-15
-20
11
12
13
14
15
16
17
18
Рис.
3. Графики
реализации сигнала W (s) и его оценки
W∗(s) (s =
= 11, 12, . . ., 18): сплошная линия сигнал, штриховая линия
его оценка.
Рис. 4. График с.к. оптимальной оценки η точности оператора At.
152
На рис. 2 изображена одна из реализаций X(t), смоделированная на основе
ее ВЛКР (3.1).
На рис. 3 и 4 представлены результаты вычислительного эксперимента для
s ∈ [11,18].
Значение η зависит от того, насколько значения ζq(s) отличаются от значе-
ний выражений ζ∗q(s) = aqu00(s) - dξq00v00(s) (q = 1, 2). Вычислительные экс-
перименты показали, что с.к. оптимальная оценка η точности с.к. оптималь-
ного линейного оператора At равна 0,7973 при значениях сигнала W (s) ∈
∈ [-15,2122; 6,2199].
7. Заключение
Разработано вейвлет методическое и инструментальное программное обес-
печение для с.к. оптимального синтеза существенно нестационарных линей-
ных фильтров на основе вейвлет канонических разложений в среде MATLAB.
Для стохастических систем в условиях стохастических одно- и многократ-
ных ударных воздействий, описываемых КР, ВЛР и ВЛКР разработано спе-
циальное инструментальное обеспечение для оптимизации фильтров, оценки
и идентификации ударных воздействий. Эти результаты нашли применения
в задачах анализа и моделирования, оценки и идентификации ударных воз-
действий в прецизионных информационно-управляющих системах.
Аналогично [13, 14] рассматриваются сложные виброударные одно- и мно-
гомерные виброударные воздействия, представимые КР, ВЛР и ВЛКР.
СПИСОК ЛИТЕРАТУРЫ
1. Карпенко А.П. Современные алгоритмы поисковой оптимизации. М.: Изд-во
МГТУ им. Н.Э. Баумана, 2017.
2. Синицын И.Н., Синицын В.И., Корепанов Э.Р., Белоусов В.В., Сергеев И.В.
Развитие алгоритмического обеспечения анализа стохастических систем, осно-
ванного на канонических разложениях случайных функций // АиТ. 2011. № 2.
С. 195-206.
Sinitsyn I.N., Sinitsyn V.I., Korepanov E.R., Belousov V.V., Sergeev I.V. Devel-
opment of Algorithmic Support for the Analysis of Stochastic Systems Based on
Canonical Expansions of Random Functions // Autom. Remote Control. 2011. V. 72.
No. 2. P. 405-415.
3. Синицын И.Н., Сергеев И.В., Корепанов Э.Р., Конашенкова Т.Д. Инструмен-
тальное программное обеспечение анализа и синтеза стохастических систем
высокой доступности. IV // Системы высокой доступности. 2017. Т. 13. № 3.
С. 55-69.
4. Синицын И.Н., Сергеев И.В., Корепанов Э.Р., Конашенкова Т.Д. Инструмен-
тальное программное обеспечение анализа и синтеза стохастических систем
высокой доступности. V // Системы высокой доступности. 2018. Т. 14. № 1.
С. 59-70.
5. Синицын И.Н., Сергеев И.В., Корепанов Э.Р., Конашенкова Т.Д. Инструмен-
тальное программное обеспечение анализа и синтеза стохастических систем
высокой доступности. VI // Системы высокой доступности. 2018. Т. 14. № 2.
С. 40-56.
153
6.
Синицын И.Н., Жуков Д.В., Корепанов Э.Р., Конашенкова Т.Д. Инструмен-
тальное программное обеспечение анализа и синтеза стохастических систем вы-
сокой доступности. VII // Системы высокой доступности. 2019. Т. 15. № 1.
С. 47-61.
7.
Синицын И.Н., Жуков Д.В., Корепанов Э.Р., Конашенкова Т.Д. Инструмен-
тальное программное обеспечение анализа и синтеза стохастических систем вы-
сокой доступности. VIII // Системы высокой доступности. 2019. Т. 15. № 1.
С. 62-69.
8.
Синицын И.Н., Жуков Д.В., Корепанов Э.Р., Конашенкова Т.Д. Развитие пря-
мых методов аналитического интерполяционного моделирования распределений
в стохастических системах // Системы компьютерной математики и их прило-
жения. Матер. XX Междунар. науч. конф. Смоленск: Изд-во СмолГУ, 2019.
Вып. 20.4.1. С. 256-260.
9.
Синицын И.Н., Жуков Д.В., Корепанов Э.Р., Конашенкова Т.Д. Метод линей-
ной оптимальной обработки информации посредством вейвлет разложений //
Системы компьютерной математики и их приложения. Матер. XXI Междунар.
науч. конф. Смоленск: Изд-во СмолГУ, 2020. Вып. 21. С. 213-220.
10.
Синицын И.Н. Канонические представления случайных функций и их приме-
нение в задачах компьютерной поддержки научных исследования. М.: ТОРУС
ПРЕСС, 2009.
11.
Добеши И. Десять лекций по вейвлетам. Москва-Ижевск: НИЦ “Регулярная и
хаотическая динамика”, 2004.
12.
Новиков И.Я., Стечкин С.Б. Основы теории всплесков // Успехи математиче-
ских наук. 1998. Т. 53. № 6 (324). С. 53-126.
13.
Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование //
УФН. 2001. Т. 171. № 5. С. 465-501.
14.
Синицын И.Н., Сергеев И.В. Применение канонических представлений случай-
ных функций в задачах расчета виброзащитных систем для компьютерного обо-
рудования // Тр. XI Междунар. науч. конф., посвящ. 70-летию проф. В.П. Дья-
конова. Смоленск: Изд-во СмолГУ, 2010. ISBN 978-5-88018-445-3. С. 239-241.
15.
Синицын И.Н., Синицын В.И., Корепанов Э.Р., Белоусов В.В., Сергеев И.В.
Компьютерное моделирование стохастических систем на базе канонических раз-
ложений // Тр. ХI Междунар. конф. “Кибернетика и высокие технологии ХХI в.
(C&T 2010)”. Воронеж: НПФ “Саквоее” ООО, 2010. ISBN 978-5-904259-05-1.
С. 798-809.
Статья представлена к публикации членом редколлегии А.И. Кибзуном.
Поступила в редакцию 02.03.2020
После доработки 25.05.2020
Принята к публикации 09.07.2020
154