Автоматика и телемеханика, № 11, 2020
© 2020 г. М.М. ХРУСТАЛЕВ, д-р физ.-мат. наук (mmkhrustalev@mail.ru),
К.А. ЦАРЬКОВ, канд. физ.-мат. наук (k6472@mail.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ДОСТАТОЧНЫЕ УСЛОВИЯ ТЕРМИНАЛЬНОЙ
ИНВАРИАНТНОСТИ СТОХАСТИЧЕСКИХ СИСТЕМ
ДИФФУЗИОННО-СКАЧКООБРАЗНОГО ТИПА1
Сформулированы и доказаны достаточные условия терминальной ин-
вариантности нелинейных динамических стохастических управляемых
систем диффузионно-скачкообразного типа. Скачкообразная компонента
имеет вид интеграла по случайной мере Пуассона. Предполагается, что
параметры меры (интенсивность и распределение величин скачков) ме-
няются со временем. Предлагаются как условия инвариантности по воз-
мущениям при заданном начальном состоянии, так и условия абсолют-
ной инвариантности, обеспечивающие постоянство значения терминаль-
ного критерия при любых начальных данных. Применимость результатов
продемонстрирована на ряде модельных примеров, включающих в себя
результаты численного моделирования и аналитическое исследование по-
строенных терминально инвариантных динамических систем.
Ключевые слова: достаточные условия терминальной инвариантности,
нелинейные стохастические системы, диффузионно-скачкообразные про-
цессы, системы с импульсными воздействиями.
DOI: 10.31857/S0005231020110094
1. Введение
Исследования в области теории терминальной инвариантности динами-
ческих управляемых систем начались в 1963 г. [1]. После этого в 1968 г.
в [2] были получены глобальные необходимые и достаточные условия инвари-
антности по возмущениям (или слабой инвариантности, в терминологии [1])
и условия абсолютной инвариантности как по возмущениям, так и по началь-
ным данным для детерминированных систем управления. Затем, в 1987 г. эти
условия были собраны и структурированы в монографии [3], где также была
подробно описана обширная база практических приложений теории, которые
остаются актуальными и по сей день. Более подробную информацию о при-
мерах решения конкретных прикладных задач динамики полета методами
теории инвариантности можно также найти в [4] и по ссылкам из [3].
Исследования продолжились в 2017 г. в [5, 6], когда условия терминальной
инвариантности удалось обобщить на случай стохастических управляемых
систем диффузионного типа. Наконец, в 2018 г. вышла статья [7], в которой
1 Работа выполнена при частичной финансовой поддержке Российского фонда фунда-
ментальных исследований (проект № 20-08-00400).
155
теоретические результаты приобрели более строгую и точную математиче-
скую формулировку, а возможность их использования для решения конкрет-
ных прикладных задач была показана на нескольких нетривиальных при-
мерах. Исследования условий терминальной инвариантности для различных
значимых частных случаев управляемых диффузионных процессов продол-
жаются и в настоящее время [8].
В данной работе авторы намерены положить начало новому витку разви-
тия теории терминальной инвариантности и рассмотреть обобщение управ-
ляемых систем диффузионного типа в виде стохастических систем, содер-
жащих не только непрерывную гауссовскую часть, но и разрывную пуассо-
новскую компоненту [9]. Такие системы (и соответствующие им процессы)
в различных источниках называют системами с импульсными воздействия-
ми, со случайным периодом квантования или диффузионно-скачкообразными
процессами. Авторы считают последнее наименование наиболее удачным в
рамках рассматриваемой теории и ориентируются, в частности, на рабо-
ты [10, 11], где оно также использовано. В сравнении с исследованиями этих
процессов и систем в [10], здесь пуассоновская компонента дополнительно
предполагается неоднородной по времени [11-13].
Необходимость подобного обобщения продиктована в том числе интереса-
ми практики, так как в настоящее время для более эффективного математи-
ческого моделирования реальных управляемых процессов все чаще исполь-
зуются ¾событийные¿ стохастические модели [14, 15]. В различных областях
приложений в роли независимых друг от друга однотипных случайных со-
бытий могут выступать скачки напряжения, обрывы связи, порывы ветра,
малые метеоритные воздействия, поломки, чрезвычайные происшествия на
производстве, корпоративные дефолты, страховые случаи и т.п. Одной из
наиболее распространенных моделей подобного рода является рассматривае-
мая в данной работе диффузионно-скачкообразная модель.
Несмотря на то, что исследования различных свойств стохастических си-
стем диффузионно-скачкообразного типа в последние годы по всему миру ве-
дутся весьма активно, свойство терминальной инвариантности для них фак-
тически не изучено. Последнее может быть связано в первую очередь с тем,
что широкую известность приобрели различные приближенные и численные
методы, позволяющие конструировать некоторые аппроксимации терминаль-
но инвариантных систем. Для этого могут быть использованы disturbance at-
tenuation approach, model predictive control (MPC), теория робастного управ-
ления. В то же время точное аналитическое построение терминально инвари-
антных систем имеет ряд существенных преимуществ. Так, например, в ре-
зультате применения точного аналитического решения методическая ошибка
(равная в этом случае нулю) не прибавляется к ошибкам измерений и реа-
лизации управляющих воздействий, имеющих место на практике. Еще од-
ним преимуществом методов теории инвариантности является существенная
неединственность решений, что дает возможность получения результатов в
том числе и для нелинейных задач (см. статью [4] или академический при-
мер в [7]). В силу этих причин, авторы считают оправданным продолжение
развития теории терминальной инвариантности несмотря на то, что других
подобных результатов для сколь-нибудь общей ситуации им не известно.
156
Основная идея теории терминальной инвариантности достаточно близка к
понятию первого интеграла рассматриваемой динамической системы. Соот-
ветствующее понятие для систем диффузионно-скачкообразного типа сфор-
мулировано, например, в [16].
2. Постановка задачи
Будем считать, что управляемая динамическая система описывается сто-
хастическим дифференциальным уравнением [9]
dx (t) = f (t, x (t), u (t, γ (x (t), v (t))), v (t)) dt +
+ g (t,x(t),u(t,γ (x(t),v (t))),v (t))dw(t)+
(1)
∫
(
(
)
(
(
(
)
))
)
+ h
t,x
t-
,u
t,γ
x
t-
,v
,v
µ(dt × dv), x(t0) = x0,
Rr
где t ∈ [t0; tF ] ⊂ [tS ; tF ] ⊂ R - время, моменты tS и tF фиксированы, tF совпа-
дает с конечным моментом времени функционирования системы; начальное
условие (t0, x0) ∈ B0, t0 ≥ tS , заранее не задано, но определено множество
B0 ⊂ [tS;tF ) × Rn всех возможных начальных условий; x(t) - n-мерный век-
тор, характеризующий состояние системы в момент времени t; отображение
t → v(t) - r-мерный случайный процесс с заданным (одномерным) распреде-
лением ν(t, ·) (вероятностной мерой при каждом t), имеющий смысл случай-
ного внешнего возмущения, мгновенные значения которого могут частично
измеряться в процессе наблюдений; отображение t → w(t) - q-мерный стан-
дартный винеровский процесс, стартующий в момент времени t0 из точки
w(t0) = 0, который описывает полностью ненаблюдаемую часть непрерывных
возмущений;
{ µ(dt × dv) - Π(t,dv)dt, если dv ⊂ Θ,
(2)
µ(dt × dv) :=
µ(dt × dv),
если dv ⊂ Rr \ Θ,
µ(·) - l-мерная неоднородная случайная пуассоновская мера на [tS ; tF ] × Rr
с интенсивностью Π(·), в каждый момент времени t значение Π(t, ·) - заданная
l-мерная неслучайная ненормированная мера на Rr с условием 0 < Π(t, Rr) <
< +∞ такая, что выполнено равенство Π(t,·) = Π(t,Rr)ν(t,·), Θ - заданное
измеримое подмножество Rr; (x, v) → γ(x, v) - заданная измеримая p-мер-
ная функция, описывающая процесс наблюдений; (t, γ) → u(t, γ) - m-мерная
неслучайная измеримая стратегия управления (заранее не задана, но может
быть выбрана произвольно в целях, формулируемых далее); f(·), g(·), h(·) -
заданные измеримые матричные функции соответствующих размеров; здесь
и далее в работе используется обозначение x(t-) := lims→t-0 x(s), t ∈ (t0; tF ],
x(t-0) := x0, а под измеримостью (подмножеств действительного простран-
ства и действительнозначных функций на нем) понимается измеримость
по Борелю. Предполагается, что процессы v(t), w(t) и мера µ(·) независи-
мы в совокупности.
157
Отдельных разъяснений требует конструкция последнего слагаемого в
правой части системы (1), включающая в себя случайную меру µ(·). Предпо-
лагается, что на управляемый процесс оказывают влияние некоторые пото-
ки событий произвольной природы, происходящих независимо друг от друга
(внутри одного потока и между ними), с известными неслучайными неод-
нородными по времени интенсивностями Πj (t, Rr), j = 1, l. Если в момент
времени s ∈ [t0; tF ] произошло одно из таких событий, то вектор состояния
системы получает мгновенное (скачкообразное) приращение на величину, за-
висящую от момента времени s, текущего состояния x(s-) и значения слу-
чайного вектора внешних возмущений v(s) с распределением ν(s, ·). Эта ве-
личина также зависит от вида функции h(·) и выбранной стратегии управ-
ления (t, γ) → u(t, γ). Конструкция (2) со множеством Θ определяет общий
характер данных воздействий. А именно, если Θ = ∅, то на состояние систе-
мы также влияет дополнительная непрерывная компонента, в среднем пол-
ностью компенсирующая влияние скачков. Если же Θ = Rr, то со временем
влияние скачков в среднем только нарастает. Промежуточные варианты уста-
навливают некоторую (линейную) комбинацию указанных эффектов.
Замечание 1. В [2-8] не использовалась p-мерная функция наблюде-
ний γ(·). Вместо этого предполагалось, что γ(x, v) = (xT, vT)T, p = n + r. Од-
нако вполне естественно предположить, что вектор возмущений v(t) может
быть не доступен для прямых измерений в процессе управления, точно так-
же, как и вектор состояния x(t). Таким образом, введение в рассмотрение
функции γ(·) отвечает практическим требованиям и в то же время не сильно
затрагивает конструкцию условий терминальной инвариантности.
Определение 1. Стратегию управления (t,γ) → u(t,γ) будем назы-
вать B0-допустимой, если уравнение (1) имеет хотя бы одно слабое реше-
ние
[9, с. 519] на интервале [t0; tF ] для любого фиксированного начального
условия (t0, x0) ∈ B0.
Еще до непосредственной постановки задачи терминально инвариантно-
го управления и до формулировки достаточных условий терминальной ин-
вариантности подчеркнем, что определение 1 не предусматривает проверки
каких-либо условий существования слабого решения (например, [9, с. 519,
теорема 2]) на первых этапах исследования каждой конкретной задачи. Под-
ход, который пропагандируют авторы, состоит в том, чтобы попытаться фор-
мально удовлетворить достаточные условия инвариантности с помощью неко-
торой стратегии управления. После этого ее следует подставить в систему, и
в том случае, если для замкнутой таким образом системы удастся проверить
выполнение тех или иных достаточных условий существования слабого (или,
тем более, единственного сильного) решения, задача будет решена. Если же
никаких условий проверить не удастся, то результат тем не менее можно бу-
дет использовать как эвристическое средство решения задачи, хотя послед-
ний вариант и не будет гарантировать получение искомого результата.
Тем не менее со строго математической точки зрения все дальнейшие след-
ствия и формулировки справедливы только в том случае, когда существует
хотя бы одна B0-допустимая стратегия, которую удается найти. Для каждой
такой стратегии уравнение (1) допускает [13, 17] представление в интеграль-
158
ной форме
(3)
∫t
x(t) = x0 + f(s, x(s), u(s, γ(x(s), v(s))), v(s))ds +
t0
∫t
+ g(s,x(s),u(s,γ(x(s),v(s))),v(s))dw(s) +
t0
∑
Pj(t0,t)∑
(
(
)
(
( (
) (
))) (
))
+
h(j) t(j)k,x t(j)-
,u t(j)k,γ x t(j)-
,v t(j)
,v t(j)
-
k
k
k
k
j=1
k=1
∫t
∫
-
h(s, x(s-), u(s, γ(x(s-), v)), v)Π(s, dv)ds,
t0
Θ
где h(j)(·) - j-й столбец матрицы h(·);
Pj(t0,t) := Pj(t - tS) - Pj(t0 - tS),
Pj(t) - неоднородный считающий процесс (процесс Пуассона при t ≥ 0), со-
гласованный с j-м пуассоновским потоком событий с мгновенной интенсив-
ностью Πj (t + tS , Rr); t(j)1, t(j)2, . . . - моменты наступления событий потока,
t0 ≤ t(j)k ≤ t ≤ tF , k = 1,2,3,... , j = 1,l. Третье и пятое слагаемые в правой
части (3) определены в смысле интегралов Ито и Лебега соответственно. Дан-
ное представление может быть эффективно использовано для численного мо-
делирования процесса управления. В некоторых случаях оно также более
удобно для аналитического исследования.
Замечание 2. Необходимость использования предела суммирования
Pj(t0,t) в представлении (3) связана с тем, что t0 ≥ tS и, в отличие от класси-
ческого определения меры Пуассона [9], мера µ(·) предполагается заданной
на множестве [tS ; tF ] × Rr, где интервал [tS ; tF ] вовсе не обязательно явля-
ется подмножеством R+. Данные допущения удобны с точки зрения теории
терминальной инвариантности [7].
Пусть (B0-допустимая) стратегия (t, γ) → u(t, γ) фиксирована. Рассмот-
рим некоторое начальное условие (t0, x0) ∈ B0. В соответствии с определени-
ем 1 существует слабое решение S уравнения (1), включающее в себя вероят-
ностное пространство (Ω, F, P) с фильтрацией {Ft ⊂ F, t ∈ [t0; tF ]}, на кото-
ром найдутся процесс v(t) с распределением ν(t, ·), винеровский процесс w(t),
пуассоновская мера µ(·) интенсивности Π(·) и процесс x(t), все согласован-
ные с Ft и P-п.н. (почти наверное) связанные соотношениями (1) и (3) при
t ∈ [t0;tF]. Через D(t0,x0) обозначим множество всех таких решений S и вве-
дем также множество
⋃
D(B0) :=
D(t0, x0).
(t0,x0)∈B0
159
Определение 2. Будем говорить, что некоторое свойство относи-
тельно процессов v(t), w(t), x(t) и меры µ(·) выполняется на D(B0) (или на
D(t0, x0)) с вероятностью 1 или почти наверное, если при любом S ∈ D(B0)
(или S ∈ D(t0, x0)) оно P-п.н. выполнено.
В частности, если задана (B0-допустимая) стратегия управления, то мож-
но сказать, что процессы v(t), w(t), x(t) и мера µ(·) почти наверное связаны
соотношениями (1) и (3) на D(B0).
На множестве D(B0) определим терминальный критерий, который каж-
дому элементу S ∈ D(B0) ставит в соответствие случайную величину
(4)
J (S) = F (x(tF )), F (·) ∈ C2(Rn
).
Замечание 3. Терминальный критерий (4) представляет собой парамет-
ризованное семейство отображений, так как для каждого слабого решения
S ∈ D(B0) случайная величина F(x(tF)) определена на своем соответствую-
щем S вероятностном пространстве (Ω, F, P).
Определение 3. Систему (1) при фиксированной стратегии (t,γ) →
→ u(t, γ) будем называть инвариантной по возмущениям, если для любого
фиксированного начального условия (t0, x0) ∈ B0 случайная величина (4) с
вероятностью 1 на D(t0, x0) совпадает с некоторым числом Jc(t0, x0).
Определение 4. Систему (1) при фиксированной стратегии (t,γ) →
→ u(t, γ) будем называть абсолютно инвариантной, если случайная величи-
на (4) с вероятностью 1 на D(B0) совпадает с одним и тем же числом JAc.
В условиях задачи, сформулированных в настоящем разделе, требуется
определить стратегию управления, обеспечивающую терминальную инвари-
антность динамической системы (1) в смысле определения 3 или определе-
ния 4.
3. Достаточные условия терминальной инвариантности
В данном разделе дадим обобщение достаточных условий инвариантности
[7] на класс систем диффузионно-скачкообразного типа. Действуя в полном
соответствии с [7], введем в рассмотрение множество Φ := C1,2([tS ; tF ] × Rn)
функций (t, x) → ϕ(t, x) : [tS ; tF ] × Rn → R, имеющих непрерывные производ-
ные ϕt, ϕx, ϕxx. Для краткости обозначим
(5)
σ(t, x, u, v) = g(t, x, u, v)gT
(t, x, u, v),
1
(6)
K(t, x, u, v) = ϕt(t, x) + ϕTx(t, x)f(t, x, u, v) +
tr[σ(t, x, u, v)ϕxx
(t, x)],
2
(7)
S(t, x, u, v) = ϕTx
(t, x)g(t, x, u, v),
(8)
Γ(j)(t,x,u,v) = ϕ(t,x + h(j)(t,x,u,v)) - ϕ(t,x), Γ = (Γ(1),... ,Γ(l)
),
(9)
Λ(t, x, u, v) = Γ(t, x, u, v) - ϕTx
(t, x)h(t, x, u, v),
∫
(10)
L(t, x, u, v) = K(t, x, u, v) +
Λ(t, x, u, v)Π(t, dv).
Θ
160
Теорема 1. Если при фиксированной стратегии (t,γ) → u(t,γ) суще-
ствуют измеримая ограниченная функция t → η(t) : [tS;tF ] → R и функция
ϕ(·) ∈ Φ такие, что для всех x ∈ Rn, v ∈ Rr выполнены условия
(i) ϕ(tF , x) = F (x),
(ii) L(t, x, u(t, γ(x, v)), v) = η(t) почти всюду на [tS ; tF ],
(iii) S(t, x, u(t, γ(x, v)), v) = 0 почти всюду на [tS ; tF ],
(iv) Γ(t, x, u(t, γ(x, v)), v) = 0 всюду на [tS ; tF ],
то система (1) инвариантна по возмущениям, а значение критерия п.н.
равно
tF
∫
(11)
Jc(t0,x0) = ϕ(t0,x0) +
η(t)dt.
t0
Теорема 2. Если при фиксированной стратегии (t,γ) → u(t,γ) суще-
ствуют измеримая ограниченная функция t → η(t) : [tS;tF ] → R, функция
ϕ(·) ∈ Φ и постоянная A > 0 такие, что для всех x ∈ Rn, v ∈ Rr выполнены
условия
(i) η(t-F) = η(tF ),
(ii) ϕ(tF , x) = F (x),
(iii) L(t, x, u(t, γ(x, v)), v) = (η(t) - Aϕ(t, x))(tF - t)-1 почти всюду на
[tS ; tF ],
(iv) S(t, x, u(t, γ(x, v)), v) = 0 почти всюду на [tS ; tF ],
(v) Γ(t, x, u(t, γ(x, v)), v) = 0 всюду на [tS ; tF ],
то система (1) абсолютно инвариантна, а значение критерия п.н. равно
η(tF )
(12)
JAc =
A
Структура полученных результатов практически не отличается от соответ-
ствующих утверждений из [7]. Это связано с тем, что доказательства теорем 1
и 2 (см. Приложение), как и в случае работы [7], основаны на применении
формулы Ито, принимающей в контексте рассматриваемой задачи некоторый
обобщенный вид [9, 10, 16]. Поэтому также остаются справедливыми следую-
щие два утверждения.
Замечание 4
[7]. Если условия теоремы 2 оказываются выполнены для
функции η(t) ≡ 0 и A > 1, то функция
t → L(t) := L(t,x(t),u(t,γ(x(t),v(t))),v(t))
вида (10), несмотря на условие (iii), является ограниченной п.н. на D(B0)
и п.в. на [tS ; tF ] и, более того, L(t-F) = 0.
Замечание 5
[8]. Из определения абсолютной инвариантности 4 следу-
ет, что для наличия этого свойства у системы (1) достаточно, чтобы условия
теоремы 2 выполнялись п.н. на D(B0) лишь для моментов времени мало-
го интервала [tF - ε; tF ]. Величина числа ε > 0 может быть, вообще говоря,
различной для каждого S ∈ D(B0).
161
Замечание 6. Если Θ = ∅, то все условия теорем 1, 2 и формулы (11)
и (12) не зависят от интенсивности Π(·) пуассоновской меры µ(·). В этом
случае из терминальной инвариантности системы (1) для некоторой интен-
сивности Π(·) следует ее терминальная инвариантность и для любой другой
интенсивности Π′(·).
4. Примеры
В [7] было изучено несколько модельных примеров терминальной инва-
риантности стохастических систем диффузионного типа. В данной работе
в силу новизны скачкообразной компоненты с точки зрения теории терми-
нального управления, а также с целью более наглядной демонстрации новых
результатов, сконцентрируем внимание в основном на системах чисто скачко-
образного типа (т.е. без диффузионного слагаемого). При решении общей за-
дачи терминальной инвариантности диффузионно-скачкообразной системы
можно объединить исследования примеров настоящей работы и статьи [7].
Пример 1. Рассмотрим систему
{ dx1(t) = x2(t)dt + x2(t-)µ(dt × R),
dx2(t) = -x1(t)dt + u(t, x(t-))µ(dt × R),
где t ∈ [t0; 0] ⊂ [-1; 0]; интенсивность пуассоновской меры Π(t, R) ≡ 5; размер-
ности векторов n = 2, m = l = 1; отсутствуют возмущения, связанные со слу-
чайными процессами v(t) и w(t) (поэтому интеграл в уравнении (1) устраняет-
ся с введением обозначения µ(·, R) и можно считать, что r = q = 1); p = n = 2,
γ(x, v) = x; множество Θ = ∅, так что µ(·) ≡ µ(·).
Требуется обеспечить инвариантность системы по возмущениям относи-
тельно величины J = x2(0) для множества B0 = [-1; 0) × R2.
Функции ϕ(·) и η(·) построим в форме
ϕ(t, x) = ψ1(t)x1 + ψ2(t)x2, η(t) ≡ 0,
тогда условия теоремы 1 с учетом обозначений (5)-(10) примут вид
(i) ψ1(0)x1 + ψ2(0)x2 = x2,
(ii)
ψ1(t)x1 +ψ2(t)x2 + ψ1(t)x2 - ψ2(t)x1 = 0 п.в. на [-1;0],
(iii) заведомо выполнено,
(iv) ψ1(t)x2 + ψ2(t)u(t, x) = 0 всюду на [-1; 0].
Из условия (iv) сразу получаем структуру инвариантного управления
ψ1(t)
u(t, x) = -
x2,
ψ2(t)
а коэффициенты ψ1(t), ψ2(t) найдем из условий (i), (ii). В силу произвольно-
сти значений x1, x2 получаем задачу Коши
dψ1(t)
= ψ2(t), ψ1(0) = 0,
dt
dψ2(t)
= -ψ1(t), ψ2(0) = 1,
dt
162
x2(t)
x1(t)
18
50
16
14
40
12
30
10
8
20
6
4
10
2
-1,0
-0,8
-0,6
-0,4
-0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
t
Рис. 1. Три реализации состояния x(t).
u(t)
16
14
12
10
8
6
4
2
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
Рис. 2. Три реализации управления u(t, x(t)).
которая имеет решение ψ1(t) = sin(t), ψ2(t) = cos(t). Таким образом,
u(t, x) = -tg(t)x2.
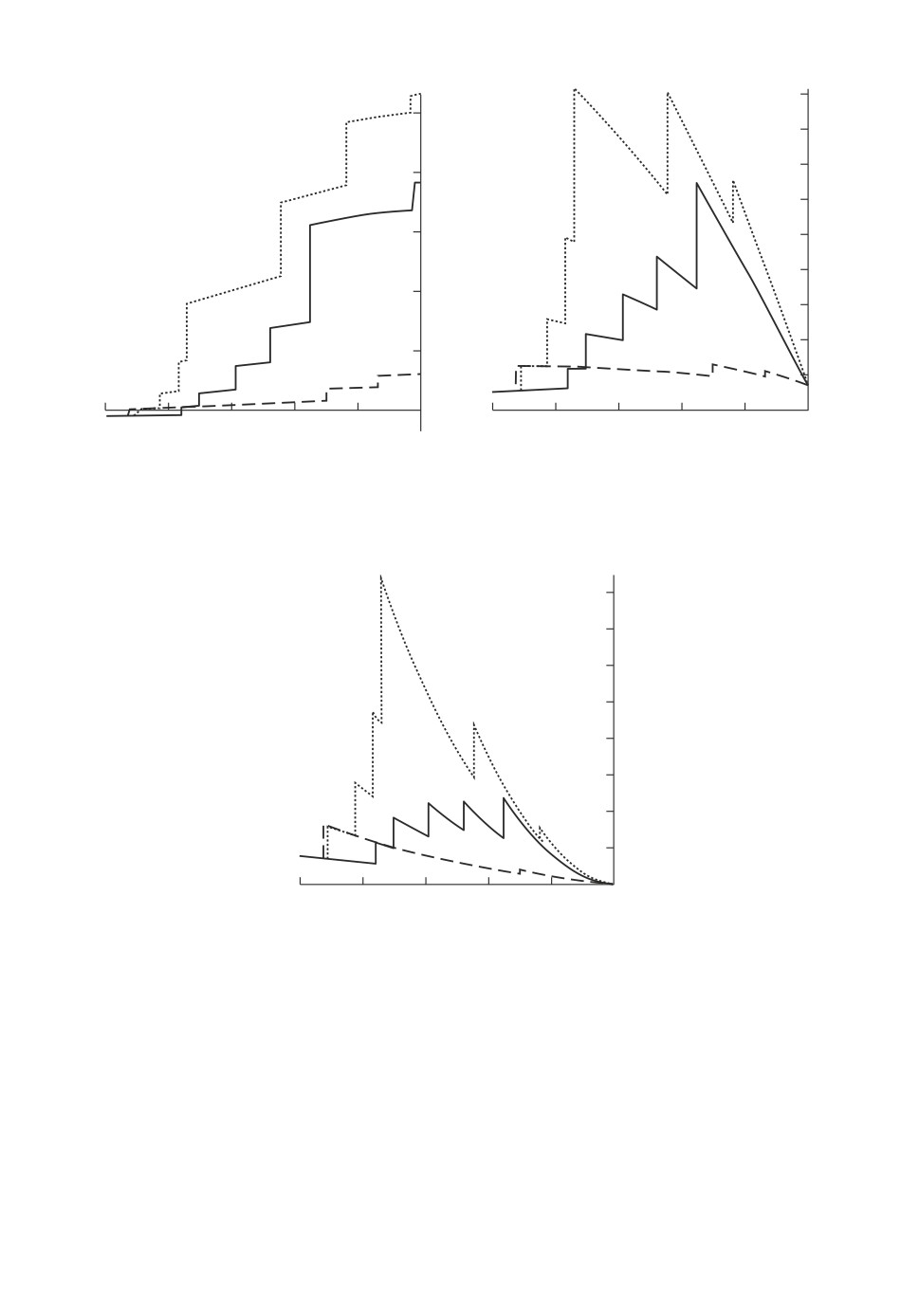
На рис. 1-2 представлены результаты простейшего численного модели-
рования методом Эйлера для нескольких реализаций траекторий компо-
нент вектора состояния x(t) и управления u(t, x(t)) с начальным условием
(t0, x(t0)) = (-1, (-1, 1)T).
Значения величины J = x2(0) отличаются друг от друга в пределах по-
грешности численного счета и равны 1,386, 1,382, 1,387 соответственно для
163
полученных реализаций. Точное терминальное значение критерия по форму-
ле (11) п.н. равно Jc(t0, x0) = sin(1) + cos(1) ≈ 1,381.
Пример 2. В условиях примера 1 покажем явно, что найденное (инва-
риантное по возмущениям) управление не обеспечивает абсолютную инвари-
антность системы относительно величины J = x2(0) для произвольного на-
чального условия (t0, x(t0)) ∈ B0.
Положим u(t, x) = -tg(t)x2 и перепишем исходную систему стохастиче-
ских уравнений в матричной форме:
dx(t) = F x(t)dt + H(t)x(t-)µ(dt × R),
где
(
)
(
)
0
1
0
1
F =
,
H(t) =
-1 0
0
- tg(t)
Получаем линейное по x(t) стохастическое уравнение скачкообразного ти-
па, для которого выполнены достаточные условия существования и един-
ственности сильного решения [9, с. 528, теорема 1] на интервале [-1; 0]. Это
решение может быть записано явно в виде [10]
∫
t
x(t) = exp
Ft + ln[I + H(s)]µ(ds,R)
x(t0),
t0
I - единичная матрица.
Переходя к представлению типа (3), получаем
∑
x(t) = exp
Ft+
ln[I + H(tk)]
x(t0),
k=1
а значит,
∏
x(0) =
[I + H(tk)]x(t0) =: Hx(t0),
-1 ≤ t0 < 0.
k=1
В силу структуры матрицы H(t) справедливо равенство
x2(0) = H22x2(t0),
где H22 - второй диагональный элемент случайной матрицы H. Последнее
равенство означает, что абсолютная инвариантность возможна, только если
случайная величина H22 равна нулю п.н. на D(B0). В то же время нетрудно
проверить, что
P (1)-P (t0+1)∏
H22 =
(1 - tg(tk)),
k=1
164
а условие tg(t) = 1 верно лишь для счетного числа значений t < 0 и не выпол-
нено ни в одной точке интервала [-1; 0], поэтому событие {H22 = 0} заведомо
имеет нулевую вероятность на D(B0).
Таким образом, полученная в примере 1 инвариантная по возмущениям
динамическая система не является абсолютно инвариантной.
Трудность построения абсолютно инвариантной системы связана с тем,
что правая часть условия (iii) теоремы 2 содержит сингулярность (tF - t)-1.
Тем не менее, как отмечено в замечании 4, если такую систему построить все
же удается, то эта сингулярность некоторым образом устраняется. Реализуем
данный процесс, дополнив систему еще одной компонентой управления.
Пример 3. Запишем систему с дополнительным управлением
{ dx1(t) = [x2(t) + u1(t, x(t))]dt + x2(t-)µ(dt × R),
dx2(t) = -x1(t)dt + u2(t, x(t-))µ(dt × R).
При тех же значениях параметров, что и в примере 1, требуется обеспечить
абсолютную инвариантность системы относительно величины J = x2(0) для
произвольного начального условия (t0, x(t0)) ∈ B0.
Зафиксируем снова
ϕ(t, x) = ψ1(t)x1 + ψ2(t)x2, η(t) ≡ 0,
тогда условия теоремы 2 примут вид
(i) заведомо выполнено,
(ii) ψ1(0)x1 + ψ2(0)x2 = x2,
(iii)
ψ1(t)x1 +ψ2(t)x2 + ψ1(t)x2 + ψ1(t)u1(t,x) - ψ2(t)x1 = t-1A(ψ1(t)x1+
+ ψ2(t)x2) п.в. на [-1;0], A > 0,
(iv) заведомо выполнено,
(v) ψ1(t)x2 + ψ2(t)u2(t, x) = 0 всюду на [-1; 0].
Условие (v) определяет аналогичную примеру 1 структуру для второй ком-
поненты вектора управления
ψ1(t)
u2(t,x) = -
x2,
ψ2(t)
а чтобы выполнить условие (iii), положим
(
)
A
ψ2(t)
u1(t,x) =
x1 +
x2
t
ψ1(t)
После этого условия (iii) и (ii) принимают вид задачи Коши из примера 1,
так что ψ1(t) = sin(t), ψ2(t) = cos(t) и
A
u1(t,x) =
(x1 + ctg(t)x2) ,
t
u2(t,x) = - tg(t)x2.
165
x1(t)
x2(t)
20
6
5
15
4
10
3
2
5
1
-1,0
-0,8
-0,6
-0,4
-0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
t
Рис. 3. Три реализации состояния x(t) с начальными условиями: t0 = -1,
x(t0) = (-1, 1)T; t0 = -1/2, x(t0) = (-2, 2)T; t0 = -1/3, x(t0) = (-3, 3)T.
u1(t)
u2(t)
140
2,0
120
1,5
100
80
1,0
60
40
0,5
20
-1,0
-0,8
-0,6
-0,4
-0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
t
Рис. 4. Три реализации управления u(t, x(t)).
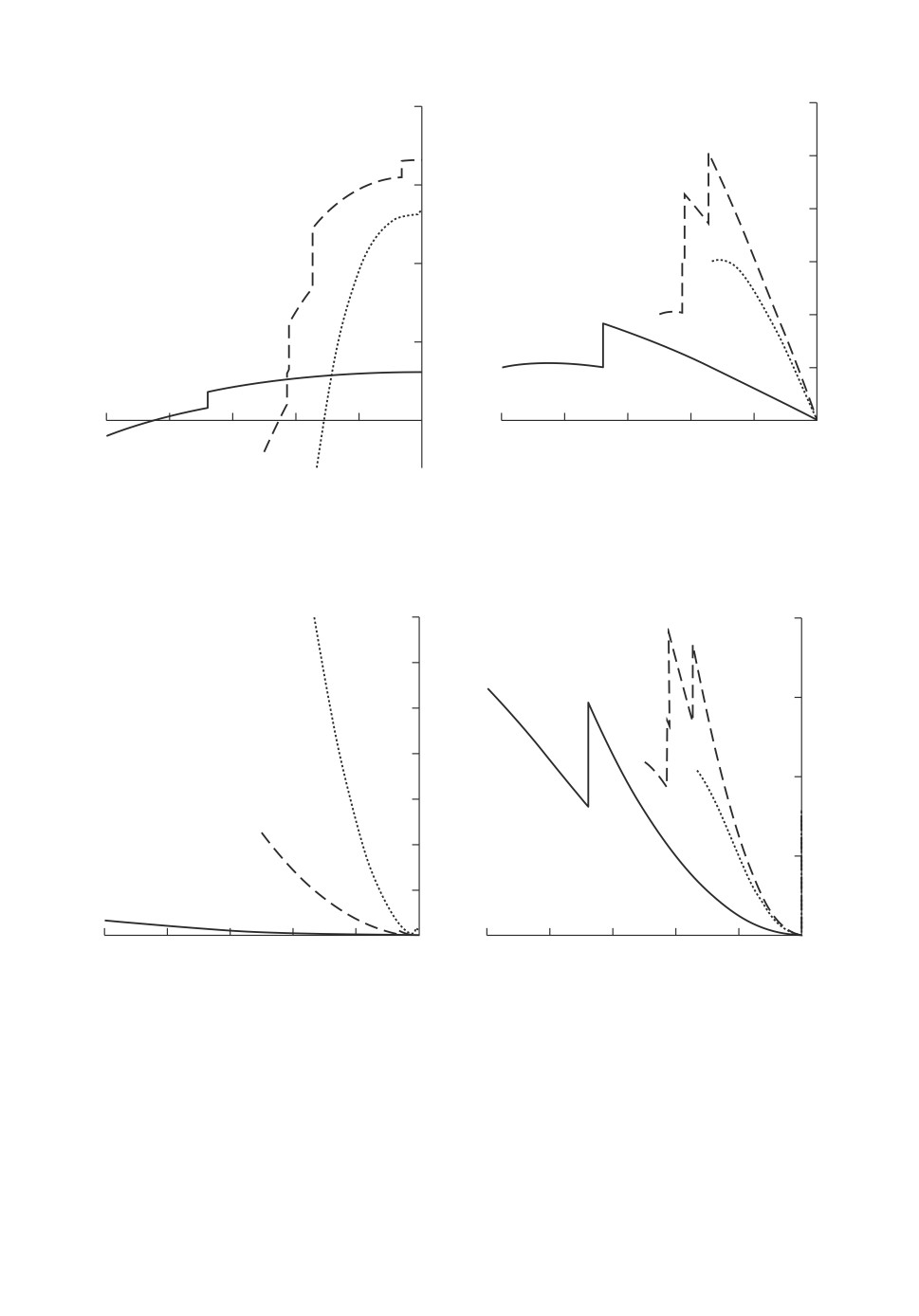
На рис. 3-4 представлены реализации траекторий компонент x(t) и
u(t, x(t)) для различных начальных условий при A = 4.
Значения величины J = x2(0) оказались равными 10-9, 10-8, 0,0044, т.е.
они с достаточной точностью совпадают со значением (12) JAc = η(0)/A = 0.
Необходимо отметить следующие важные детали приведенного выше по-
строения.
166
Во-первых, введение дополнительной компоненты управления действи-
тельно дает значительно больше возможностей для выполнения условий тео-
ремы 2. Его основной функцией является устранение ¾неприятной¿ правой
части условия (iii), которая оказывает серьезное влияние на возможности
решения задачи. Тем не менее полученная за счет этой дополнительной ком-
поненты свобода действий, на самом деле, является несколько избыточной.
Так, например, можно было бы выполнить условия (ii) и (iii), положив
(
)
A
ψ2(t)
u1(t,x) = -x2 +
x1 +
x2
,
t
ψ1(t)
тогда ψ1(t) = t, ψ2(t) ≡ 1 и соответственно
(
)
A
A
u1(t,x) =
x1 +
-1
x2, u2(t,x) = -tx2.
t
t2
Результат моделирования системы, замкнутой таким управлением, при том
же значении A = 4 отличается незначительно от результатов, показанных
на рис. 3 и 4. Последнее объясняется соотношением
lim tg(t)/t = 1.
t→0
Во-вторых, для систем вида (1) само дополнительное управление, влияю-
щее на условие (iii), можно ввести различными способами. В частности,
запись [x2(t) + u1(t, x(t))]dt в правой части уравнения для dx1(t) мож-
но получить, положив в (1) f1(t, x, u, v) = x2 + u1 либо f1(t, x, u, v) = x2,
h1(t,x,u,v) = u1/Π(t,R), Θ = R, но тогда это скажется не только на усло-
вии (iii), но и на условии (v). Наконец, аналогичным образом повлиять на
условие (iii) можно и за счет введения управляемой диффузионной части
(разумеется, при этом условие (iv) уже не будет заведомо выполнено).
В-третьих, выбор значения постоянной A = 4 основан на замечании 4.
В условиях данного примера следствием этого является ограниченность с ве-
роятностью 1 на D(B0) и п.в. на [-1; 0] функции u(t, x(t)), что вполне можно
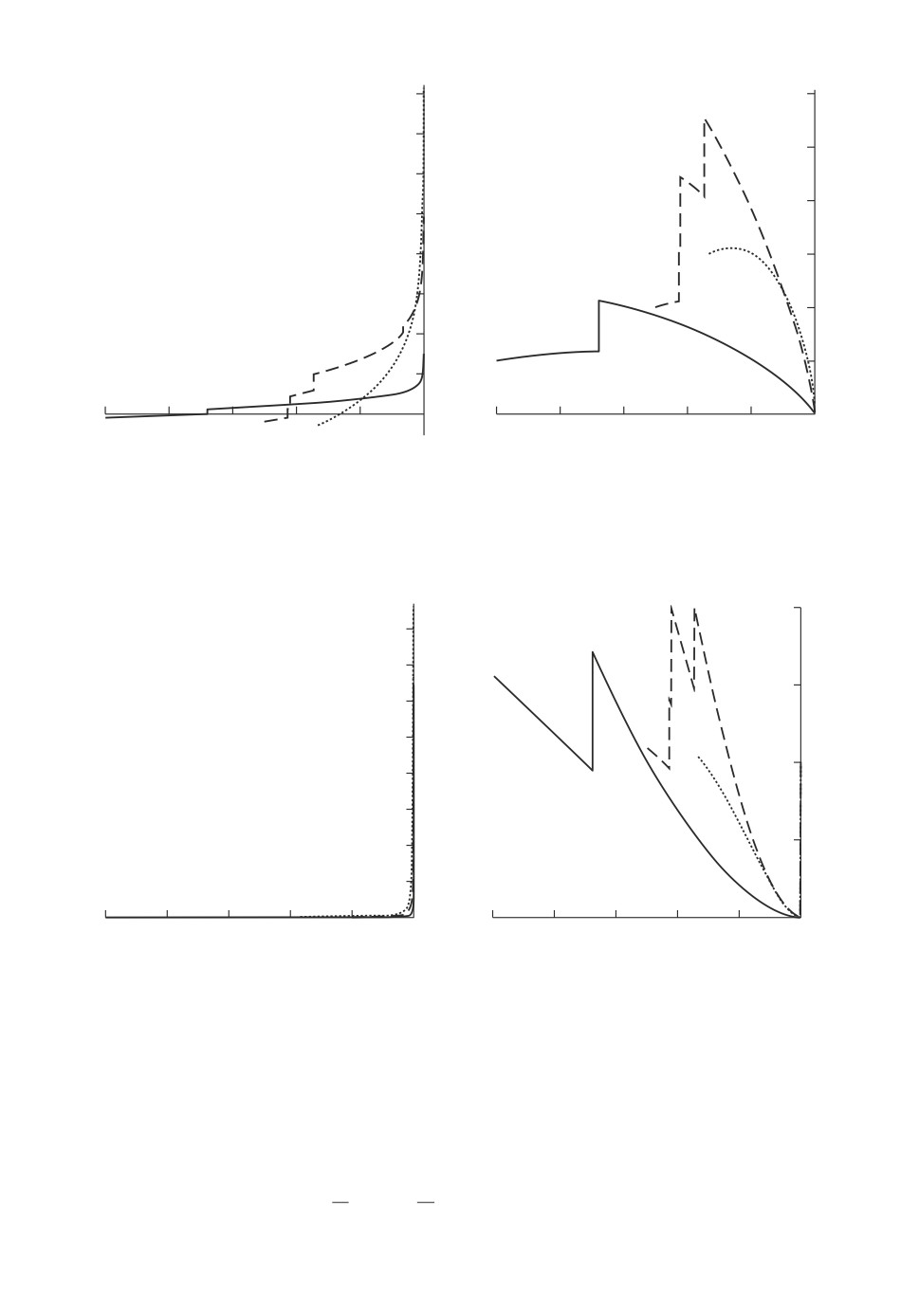
наблюдать на рис. 4. На рис. 5-6 представлены результаты аналогичного мо-
делирования для случая A = 1. Видно, что в конечный момент времени tF = 0
значения x1(t) и u1(t, x(t)) начинают неограниченно возрастать, так как коэф-
фициент ψ1(0) = 0, а функция L(t) вида (10) (см. замечание 4) из условия (iii)
уже не обладает свойством L(t-F) = 0. Однако даже при этом система остается
абсолютно инвариантной по критерию J = x2(0).
Данный пример отлично демонстрирует все отмеченные ранее свойства
абсолютно инвариантных систем. В следующем, заключительном, примере
докажем абсолютную инвариантность полученной системы с помощью пря-
мого решения (по аналогии с примером 2).
Пример 4. В условиях примера 3 покажем явно, что найденное (абсо-
лютно инвариантное) управление действительно обеспечивает абсолютную
инвариантность системы относительно величины J = x2(0) для произвольно-
го начального условия (t0, x(t0)) ∈ B0.
167
x1(t)
x2(t)
80
6
70
5
60
4
50
40
3
30
2
20
1
10
-1,0
-0,8
-0,6
-0,4
-0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
t
Рис. 5. Три реализации состояния x(t) с теми же начальными условиями при
A = 1.
u2(t)
u1(t)
2,0
16 000
14 000
1,5
12 000
10 000
1,0
8000
6000
0,5
4000
2000
-1,0
-0,8
-0,6
-0,4
-0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
t
t
Рис. 6. Три реализации управления u(t, x(t)) при A = 1.
В примере 3 было записано два, вообще говоря, различных варианта аб-
солютно инвариантного управления при разных значениях A. Для простоты
возьмем A > 1, вариант
(
)
A
A
u1(t,x) =
x1 +
-1
x2, u2(t,x) = -tx2
t
t2
168
и подставим его в исходную систему из примера 3, переписав ее в форме (3)
∫
t
(
)
P (t0,t)∑
A
x2(s)
x1(t) = x1(t0) +
x1(s) +
ds +
x2(t-k),
s
s
k=1
t0
∫
t
∑
tkx2(t-k).
x
2(t) = x2(t0) - x1(s)ds -
k=1
t0
Введем обозначения
P (t0,t)∑
x3(t) =
x2(t-k),
x1(t) = x1(t) - x3(t),
x2(t) = x2(t) + tx3(t),
k=1
так что x3(t0) = 0 п.н. на D(B0), тогда в силу равенства
∫
t
P (t0,t)∑
P (t0,t)∑
x3(s)ds =
(t - tk)x2(t-k) = tx3(t) -
tkx2(t-k)
k=1
k=1
t0
систему можно записать в виде
∫
t
(
)
A
x2(s)
x1(t) = x1(t0) +
x1(s) +
ds,
s
s
t0
t
∫
x2(t) = x2(t0) -
x1(s)ds
t0
или, возвращаясь к дифференциальной форме,
(
)
dx1(t)
A
x2(t)
=
x1(t) +
,
x1(t0) = x1(t0),
dt
t
t
dx2(t)
= -x1(t),
x2(t0) = x2(t0).
dt
Таким образом, подстановка управления u2(t, x), выбранного из усло-
вия (v) теоремы 2, фактически позволяет убрать из рассмотрения случайную
скачкообразную составляющую системы и сводит задачу к проверке абсолют-
ной инвариантности только ее детерминированной части.
Решение полученной детерминированной системы на интервале [t0; 0)
единственно и при A > 1 имеет вид
{
x1(t) = -C1(t0,x(t0)) - C2(t0,x(t0))AtA-1,
x2(t) = C1(t0,x(t0))t + C2(t0,x(t0))tA,
169
где
tx1 - Ax2
tx1 - x2
C1(t,x) =
,
C2(t,x) =
t(A - 1)
tA(1 - A)
Отсюда для любых начальных условий (t0, x(t0)) ∈ B0 имеем
lim
x2(s) = x2(0) = x2(0) = 0,
s→0
что означает абсолютную инвариантность детерминированной, а значит, и ис-
ходной стохастической системы при использовании управления u1(t, x), вы-
бранного из условия (iii). Непосредственно подставляя полученные соотно-
шения в формулы для x1,2(t), а затем и для u1,2(t, x(t)), легко убедиться в
ограниченности всех этих функций на [-1; 0].
5. Заключение
Теоретические исследования инвариантных по терминальному критерию
систем далеки от завершения. Полученные в данной работе общие достаточ-
ные условия инвариантности нелинейных стохастических систем в ряде част-
ных случаев приобретают весьма интересные и неочевидные свойства. Одно-
значно подлежат внимательному исследованию линейные системы, а также
системы с линейными по состоянию коэффициентами как в непрерывном слу-
чае, так и при наличии скачков, для которых условия в общем виде могут
быть доведены до простых регулярных выражений.
Еще больше предстоит сделать в практическом плане. Многие математи-
ческие модели реальных физических процессов в настоящее время содержат
случайные параметры, зачастую имеющие вид диффузионных или скачкооб-
разных компонент стохастического уравнения. Условия терминальной инва-
риантности позволяют не приближенно, а точно решать на основе таких мо-
делей множество актуальных прикладных проблем управления. Достаточно
сказать, что модели, рассмотренные в учебном пособии [3] и статье [4], могут
быть уточнены за счет введения в рассмотрение параметров, учитывающих
случайные внешние воздействия непрерывной и дискретной (¾событийной¿)
природы.
Тем не менее следует отметить, что решение конкретных прикладных про-
блем с помощью изложенных в данной работе подходов в силу специфики до-
статочных условий каждый раз представляет собой отдельную (порой нетри-
виальную) исследовательскую задачу, что непосредственно наблюдается уже
на модельных примерах. В силу этих причин авторы считают оправданным
отделение непосредственных приложений от теоретических разработок и на-
деются охватить, по крайней мере, часть из указанных вопросов в своих даль-
нейших исследованиях.
ПРИЛОЖЕНИЕ
Прежде чем перейти к обоснованию полученных в работе результатов,
приведем без доказательства следующее утверждение.
170
Утверждение 1. С учетом определений 1, 2 и обозначений (5)-(10) для
любых начального условия (t0, x0) ∈ B0, функции ϕ(·) ∈ Φ и момента време-
ни t ∈ [t0;tF ] верна формула Ито [9, 10, 13, 18]
dϕ(t, x(t)) = L(t, x(t), u(t, γ(x(t), v(t))), v(t))dt +
+ S(t,x(t),u(t,γ(x(t),v(t))),v(t))dw(t) +
(Π.1)
∫
+ Γ(t,x(t-),u(t,γ(x(t-),v)),v)µ(dt × dv)
Rr
или, что то же самое,
∫t
(Π.2)
ϕ(t, x(t)) = ϕ(t0, x0) +
L(s, x(s), u(s, γ(x(s), v(s))), v(s))ds +
t0
∫t
+ S(s,x(s),u(s,γ(x(s),v(s))),v(s))dw(s) +
t0
∑
Pj(t0,t)∑
(
(
)
(
( (
) (
))) (
))
+
Γ(j) t(j)k,x t(j)-
,u t(j)k,γ x t(j)-
,v t(j)
,v t(j)
-
k
k
k
k
j=1
k=1
∫t
∫
-
Γ(s, x(s-), u(s, γ(x(s-), v)), v)Π(s, dv)ds
t0
Θ
с вероятностью 1 на множестве D(t0, x0).
Обоснование утверждения 1 можно найти в [10, 13], а строгое доказатель-
ство - в [18]. Нижеследующие доказательства основаны на данном утверж-
дении и в остальных своих частях практически повторяют доказательства
из [7], поэтому здесь они приведены в достаточно краткой форме.
Доказательство теоремы 1. Пусть точка (t0,x0) ∈ B0 фиксирована.
Из формулы Ито (Π.2) в силу условий (ii)-(iv) теоремы следует справедли-
вость п.н. на D(t0, x0) равенства
∫t
ϕ(t, x(t)) = ϕ(t0, x0) + η(s)ds,
t0
и, в частности, при t = tF , из условия (i) вытекает соотношение (11), что по
определению 3 означает инвариантность системы (1) по возмущениям.
Доказательство теоремы 2. Пусть точка (t0,x0) ∈ B0 произвольна.
Из формулы Ито (Π.1) в силу условий (iii)-(v) теоремы следует справедли-
вость п.н. на D(B0) и п.в. на [tS ; tF ] равенства
η(t) - Aϕ(t, x(t))
dϕ(t, x(t)) =
dt,
tF - t
171
представляющего собой обыкновенное дифференциальное уравнение для
функции ϕ∗(t) := ϕ(t, x(t)) с произвольным начальным условием ϕ∗(t0) =
= ϕ(t0, x0) в произвольной точке t0. Данное уравнение имеет на интервале
[t0; tF ) решение [7]
∫
t
η(s)
ϕ∗(t) = (tF - t)A ϕ(t0,x0)
+
ds ,
(tF - t0)A
(tF
- s)A+1
t0
и можно показать [7, лемма 1], что при t = tF в силу условия (i) теоремы
это решение допускает непрерывное продолжение
η(tF )
ϕ(tF , x(tF )) = ϕ∗(t-F) =
,
A
а значит, из условия (ii) вытекает соотношение (12), что по определению 4
означает абсолютную инвариантность системы (1).
СПИСОК ЛИТЕРАТУРЫ
1.
Розоноэр Л.И. Вариационный подход к проблеме инвариантности // АиТ. 1963.
№ 6. С. 744-756; № 7. С. 17-22.
Rozonoer L.I. A Variational Approach to the Problem of Invariance of Automation
Control Systems // Autom. Remote Control. 1963. V. 24. No. 6. P. 680-743; No. 7.
P. 793-800.
2.
Хрусталев М.М. Необходимые и достаточные условия слабой инвариантно-
сти // АиТ. 1968. № 4. С. 17-22.
Khrustalev M.M. Necessary and sufficient conditions of invariance // Autom. Remote
Control. 1968. V. 29. No. 4. P. 540-544.
3.
Хрусталев М.М. Методы теории инвариантности в задачах синтеза законов тер-
минального управления летательными аппаратами. Учебное пособие. М: МАИ,
1987.
4.
Khrustalev M.M., Plotnikov Ju.P., Belov V.A. The invariant control of vehicle de-
scent into the atmosphere // Acta Astronautica. 1976. No. 5-6. P. 357-367.
5.
Хрусталев М.М. Слабая инвариантность стохастических систем диффузион-
ного типа // Тр. XI Международной Четаевской конф. Аналитическая меха-
ника, устойчивость и управление. Т. 3. Часть III. Казань: КНИТУ-КАИ, 2017.
С. 171-177.
6.
Хрусталев М.М. Инвариантность стохастических систем диффузионного ти-
па // ДАН. 2017. Т. 476. № 2. С. 148-150.
Khrustalev M.M. Invariance of Stochastic Diffusion Systems // Doklady Mathema-
tics. 2017. V. 96. № 2. P. 535-537.
7.
Хрусталев М.М. Терминальная инвариантность стохастических систем диффу-
зионного типа // АиТ. 2018. № 8. С. 81-100.
Khrustalev M.M. Terminal Invariance of Stochastic Diffusion Systems // Autom.
Remote Control. 2018. V. 79. No. 8. P. 1434-1449.
8.
Хрусталев М.М. Терминальная инвариантность линейных стохастических си-
стем диффузионного типа // Тр. Всерос. сов. по пробл. управления (ВСПУ-2019,
Москва). М.: ИПУ РАН, 2019. С. 1305-1309.
172
9. Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по тео-
рии вероятностей и математической статистике. М.: Наука, 1985.
10. Øksendal B., Sulem A. Applied Stochastic Control of Jump Diffusions. Berlin Hei-
delberg, Germany: Springer, 2005.
11. Рыбаков К.А. Достаточные условия оптимальности в задаче управления систе-
мами диффузионно-скачкообразного типа // Тр. Всерос. сов. по пробл. управ-
ления (ВСПУ-2014, Москва). М.: ИПУ РАН, 2014. С. 734-744.
12. Аверина Т.А., Рыбаков К.А. Два метода анализа стохастических систем с пуас-
соновской составляющей // Дифференциальные уравнения и процессы управ-
ления. 2013. № 3. С. 85-116.
13. Параев Ю.И. Введение в статистическую динамику процессов управления
и фильтрации. М.: Сов. радио, 1976.
14. Platen E., Bruti-Liberati N. Numerical Solution of Stochastic Differential Equations
with Jumps in Finance. Berlin Heidelberg, Germany: Springer, 2010.
15. Yin G., Zhu C. Hybrid Switching Diffusions. New York, USA: Springer, 2010.
16. Карачанская Е.В. Обобщенная формула Ито-Вентцеля для случая нецентриро-
ванной пуассоновской меры, стохастический первый интеграл и первый инте-
грал // Матем. тр. 2014. Т. 17. № 1. С. 99-122.
17. Миллер Б.М., Панков А.Р. Теория случайных процессов в примерах и задачах.
М.: ФИЗМАТЛИТ, 2002.
18. Гихман И.И., Скороход А.В. Стохастические дифференциальные уравнения.
Киев: Наукова думка, 1968.
Статья представлена к публикации членом редколлегии А.И. Кибзуном.
Поступила в редакцию 02.03.2020
После доработки 18.05.2020
Принята к публикации 09.07.2020
173