Автоматика и телемеханика, № 12, 2020

(Институт проблем информатики ФИЦ ИУ РАН, Москва;

Московский авиационный институт;

Центр фундаментальной и прикладной математики МГУ)

L₁-ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ МАРКОВСКИХ

СКАЧКООБРАЗНЫХ ПРОЦЕССОВ II:

ЧИСЛЕННЫЙ АНАЛИЗ КОНКРЕТНЫХ СХЕМ¹

Вторая часть статьи посвящена определению порядка точности раз-

личных численных схем реализации алгоритма фильтрации состояний

марковских скачкообразных процессов по косвенным наблюдениям в при-

сутствии винеровских шумов. Отдельно исследованы случаи аддитивных

и мультипликативных шумов в наблюдениях: показано, что одни и те же

схемы в этих случаях обеспечивают разную точность. Для наблюдений

с аддитивными шумами предложены схемы реализации порядка ¹² , 1 и 2,

а для наблюдений с мультипликативными шумами порядка 1 и 2. Пред-

ставленные теоретические результаты проиллюстрированы численными

примерами.

Ключевые слова: марковский скачкообразный процесс, устойчивая оцен-

ка, оценка максимума апостериорной вероятности, схема численного ин-

тегрирования.

DOI: 10.31857/S0005231020120028

1. Введение

Данная статья является продолжением [1]. В первой части поставлена и

решена задача L₁-оптимальной фильтрации состояний марковских скачко-

образных процессов (МСП) по непрерывным косвенным наблюдениям в при-

сутствии винеровских шумов. Представлены точное решение этой задачи,

а также класс алгоритмов его численной реализации. Точность вычисляе-

мых оценок зависит от порядка выбранной аналитической аппроксимации

и численной схемы ее реализации. В [1] представлены показатели точности

численных реализаций оценок и доказаны утверждения, их описывающие.

Целью второй части статьи является вычисление показателей точности

для аналитических аппроксимаций различного порядка и численных схем

их реализации. Показатели точности анализируются отдельно для случаев

наблюдений с аддитивными и мультипликативными шумами: в этих двух

случаях они различны.

Статья организована следующим образом. В разделе 2 сформулирована

задача L₁-оптимальной фильтрации, ее теоретическое решение, представле-

ны аналитические аппроксимации и их численные реализации. Для точного

¹ Работа выполнена при частичной поддержке Российского фонда фундаментальных

исследований, проект № 19-07-00187 А.

и приближенного решения предложены показатели близости и сформулиро-

ваны утверждения, их характеризующие.

В разделе 3 для случая наблюдений с аддитивными шумами рассмотрены

различные схемы численной реализации. В качестве численных реализаций

использовалась прямая дискретизация системы наблюдения, схемы ¾левых¿

и ¾средних¿ прямоугольников, а также квадратуры Гаусса. Использование

простых (несоставных) схем численного интегрирования позволило получить

аппроксимации оценок фильтрации порядка точности¹² , 1 и 2.

Раздел 4 посвящен исследованию точности приближенных схем при филь-

трации состояний МСП по наблюдениям с мультипликативными шумами.

В качестве численных реализаций вновь выступали схема ¾средних¿ прямо-

угольников и схема средних 2-го порядка. Показано, что простые схемы не

могут быть использованы для построения аппроксимаций и следует исполь-

зовать соответствующие составные схемы с дополнительным дроблением об-

ласти интегрирования. В итоге получены численные алгоритмы фильтрации

общего порядка точности 1 и 2.

Раздел 5 содержит иллюстративные примеры применения различных чис-

ленных схем для фильтрации состояний МСП по наблюдениям с аддитивны-

ми и мультипликативными шумами. В разделе 6 представлены заключитель-

ные выводы и направления дальнейших исследований.

2. Необходимые сведения об аналитическом и

приближенном решении задачи фильтрации

На полном вероятностном пространстве с фильтрацией (Ω^X × Ω^W, F^X × F^W,

P^X× P^W , {F^Xt× F^Wt }_t≥0) рассматривается стохастическая динамическая си-

стема

∫t

(2.1)

X_t = X₀ + Λ^⊤X_sds + µ_s,

∫tr

∫

∑

(2.2)

Y_r =

fX_sds +

X^nsg^1/2ndW_s

r ∈ N,

n=1

tr-1

где

(

)

X_t ≜ col

X^1t,... ,X^Nt

∈ S^N - ненаблюдаемое состояние системы, яв-

ляющееся однородным МСП с конечным множеством состояний S^N ≜

≜ {e₁, . . . , e_N } (SN - множество единичных векторов евклидова простран-

ства R^N ), матрицей интенсивностей переходов Λ и начальным распределе-

нием π;

µ_t ≜ col (µ^1t,... ,µ^Nt ) ∈ R^N - F^Xt-согласованный мартингал;

Y_r ≜ col (Y^1r,... ,Y^Mr ) ∈ R^M - косвенные наблюдения, зашумленные F_t-со-

гласованным стандартным винеровским процессом W_t ≜ col (W^1t, . . . , W^Mt ) ∈

∈ R^M; f - матрица плана наблюдений, а набор невырожденных симметрич-

ных матриц {g_n}_n=1,N характеризует интенсивности шумов в зависимости от

текущего состояния X_t; наблюдения {Y_r}_r получены путем дискретизации по

времени с постоянным шагом h соответствующих непрерывных наблюдений.

Неубывающее семейство σ-алгебр, порожденное последовательностью

{Y_r}_r∈N, обозначено как O_r ≜ σ{Y_ℓ : 0 ≤ ℓ ≤ r}, O₀ ≜ {∅, Ω}.

Задача L₁-оптимальной фильтрации состояния X по дискретным на-

блюдениям Y заключается в нахождении такой оценкиXr, r ∈ N состояния

МСП X_rh, что

{

}

(2.3)

X_r ∈ Argmin E

∥Xr - X_rh∥1 ,

X_r∈Xr

где X_r - множество всех таких O_r-согласованных последовательностей {Xr}

с конечным первым моментом, что

∑̂Xn

≡1

с вероятностью 1.

n=1

Ниже в изложении будем использовать следующие обозначения:

{

}

∑

D ≜ u = col(u¹,...,u^N) : u_n ≥ 0,

uⁿ = h

- (N - 1)-мерный сим-

n=1

плекс в пространстве R^M ;

{

}

∑

Π ≜ π = col(π¹,...,π^N) : π_n ≥ 0,

πⁿ = 1

- ¾вероятностный сим-

n=1

плекс¿, множество возможных начальных распределений МСП π;

N^Xr - случайное число скачков состояния X_t, произошедшее на отрезке

времени [t_r-1, t_r],

ρ^r,ℓ,q(du) - распределение вектора X^ℓt

I_{q}(N^Xr)τ_r при условии Xtr-1 =

= e_k, т.е. для любого G ∈ B(R^M) верно равенство

∫

{

}

E I_G(τ_r)I_{q}(N^Xr)X^ℓ

|Xtr-1 = e_k

= ρ^k,ℓ,qr(du);

{

}

N(y, m, K) ≜ (2π)^-M/2det^-1/2K exp

-¹²∥y - m∥2K-1

- M-мерная плот-

ность гауссовского распределения с математическим ожиданием m и невы-

рожденной ковариационной матрицей K;

∥α∥^2K ≜ α^⊤Kα, 〈α, β〉_K ≜ α^⊤Kβ.

Решение задачи фильтрации выражается через условное распределе-

ние состояния МСП относительно доступных наблюдений x_r ≜ E {Xtr |O_r} и

совпадает с оценкой максимума апостериорной вероятности:

X_r = e_n∗ , где

n^∗ ∈ Argmax_n=1,N x^nr.

Условное распределение определяется рекуррентной процедурой

(

)

∑

∫

∑

N Y_r,fu,

u^pg_p ρ^k,j,q(du)

r-1

q=0D

p=1

(2.4)

xjr =^k=1

(

)

j = 1,N,

x₀

= π.

∑

∫

∑

N Y_r,fv,

vⁿg_n ρ^i,ℓ,c(dv)

r-1

i,ℓ=1

c=0D

n=1

Дробь в (2.4) содержит в числителе и знаменателе бесконечные суммы инте-

гралов, не вычисляемые аналитически. Для компьютерной реализации дан-

ная рекурсия должна быть преобразована. На первом шаге преобразования

оценка x_r заменяется аналитической аппроксимацией порядка s: бесконеч-

ные суммы в числителе и знаменателе заменяются конечными, содержащими

только s + 1 слагаемых:

(

)

∑∫

∑

^N x^kr-1(s)

N Y_r,fu, u^pg_p ρ^k,j,q(du)

q=0D

p=1

(2.5)

x^jr(s) =^k=1

(

)

, j =1,N, x₀

= π.

∑

∫

∑

xir-1

(s)

N Y_r,fv, vⁿg_n ρ^i,ℓ,c(dv)

i,ℓ=1

c=0D

n=1

Ограничение числа слагаемых означает, что в аппроксимации учитывается

возможность не более чем s скачков оцениваемого состояния X на интервале

дискретизации [t_r-1, t_r]. Рекурсия (2.5) представима в матричной форме

(

)_-1

(2.6)

x_r(s) =

1ξ^⊤rx_r-1(s)

ξ^⊤rx_r-1

(s),

где





∫

∑

(2.7)

ξ^kjq ≜

NY_q,fu, u^pgp ρk,j,m(du), ξq ≜ ∥ξkjq∥k,j=1,N.

m=0D

p=1

На втором шаге преобразования интегралы ξ^ij (2.7) заменяются суммами





∑

(2.8) ξ^ij (y) ≈ ψ^ij (y) ≜

Ny,fw_ℓ, w^pgp̺ijℓ,

ψ(y) ≜ ∥ψ^ij (y)∥_i,j=1,N ,

ℓ

ℓ=1

p=1

{

}

определяемыми множеством пар (w_ℓ, ̺^ijℓ )

. Здесь ̺^ijℓ ≥ 0 (ℓ = 1, L) -

ℓ=1,L

веса:

∑∑

(2.9)

W≜

̺^ijℓ

≤ 1,

j=1 ℓ=1

а w_ℓ ≜ col(w^1ℓ,...,wNℓ ) ∈ D - точки. Аналогично матрицам ξ_q строятся их

аппроксимации ψ_q ≜ ∥ψ^ij (Y_q)∥_i,j=1,N . В результате условное распределение x_r

приближенно вычисляется с помощью рекуррентной процедуры

(

)_-1

(2.10)

xr ≜

1ψ^⊤r x_r-1

ψ^⊤rx_r-1, r ≥ 1,

x₀

= π.

Оценка x_r называется численной реализацией аналитической аппроксима-

ции x_r, соответствующей той или иной схеме численного интегрирования.

Оценки x_r, x_r и x_r обладают свойством устойчивости [1]: их компоненты

почти наверное неотрицательны и нормированы.

Если λ ≜ max_n=1,N |λ_nn| и для схемы численного интегрирования верно

неравенство

∫

∑

(2.11)

max

|ψ^ij (y) - ξ^ij

(y)|dy ≤ δ,

i=1,N

j=1

R^M

то расхождение x_r и x_r характеризуется неравенством

{

}

[ (

)r^]

(λh)^s+1

(2.12)

supE

∥x_r - x_r∥₁

≤4 1-

+ 2rW^r-1

δ.

π∈Π

(s + 1)!

При фиксированном горизонте T и уменьшении шага дискретизации h → 0

это же неравенство приобретает асимптотический вид

(

)

{

}

(λh)^s

(2.13)

supE

∥x_T/h - x_T/h∥₁

≤ 2T

2λ

π∈Π

(s + 1)!

Ниже исследуются аппроксимации порядка s = 1 и s = 2. Для них с помо-

щью обобщенной формулы полной вероятности легко получить вид интегра-

лов (2.7), используемых в дальнейшем изложении:





∫

∑

(

)

(2.14)

NY_r,fu, u^pgpρk,j,0(du) = δkjeλkkhN Yr,hfk, hgk

p=1





∫

∑

(2.15)

NY_r,fu, u^p

g_p ρ^k,j,1

(du) =

p=1

∫

(

)

= (1 - δ_kj )λ_kjeλjj h e(λkk -λjj )uN Y_r, uf^k + (h - u)f^j

, ug_k + (h - u)g_j du,





∫

∑

NY_r,fu, u^pgp ρk,j,2(du) =

p=1

∫

(2.16)

∑

λ_kiλ_ijeλjjh

e(λkk-λii)u+(λii-λjj)v×

i:i=k,

i=j

(

)

× N Y_r,uf^k + vfⁱ + (h - u - v)f^j, ugk + vgi + (h - u - v)gj dvdu,

где f^j - j-й столбец матрицы f.

В следующих разделах представлено исследование влияния точности раз-

личных схем вычисления интегралов в (2.15) и (2.16) на точность аппрокси-

мации решений задач фильтрации состояний МСП с аддитивными и мульти-

пликативными шумами в наблюдениях. Доказательства всех утверждений,

сформулированных ниже, характеризующих это влияние, базируются на ис-

пользовании неравенств (2.11), (2.13) и построены по единой схеме. На первом

шаге доказательства величина |ψ^ij (y) - ξ^ij (y)| оценивается сверху с исполь-

зованием известных границ ошибок численного интегрирования [2]. Обыч-

но эта оценка выражается через производные интеграндов. На втором шаге

строится оценка сверху для интеграла в левой части (2.11). Эта операция яв-

ляется нетривиальной, так как выполняется в предположении малости ша-

га h. Дело в том, что с уменьшением h как масштаба области интегрирова-

ния синхронно изменяется масштаб интеграндов, которые становятся близ-

ки к δ-функции Дирака. Данный факт соответствующим образом влияет и

на производные интеграндов. В итоге порядок малости интеграла в правой

части (2.11) оказывается ниже, чем порядок численной схемы [2] без усло-

вия асимптотической малости h. Основная проблема доказательств утверж-

дений ниже заключается в определении, насколько изменится этот порядок

малости.

3. Численные схемы фильтрации по наблюдениям

с аддитивными шумами

3.1. Случай s = 1: дискретизация стохастической дифференциальной

системы наблюдения и схема ¾левых прямоугольников¿

В данном подразделе демонстрируется связь алгоритма (2.10) приближен-

ной фильтрации состояния МСП по дискретизованным наблюдениям для слу-

чая s = 1 и алгоритма фильтрации состояний марковских цепей - процессов

с дискретным временем - по дискретным наблюдениям.

На (Ω^x × Ω^w, F^x × F^w, P^x × P^w, {F^xr × F^wr}r∈Z+ ) рассмотрим стохастиче-

скую систему наблюдения с дискретным временем



 xr=P⊤xr-1 + mr, r ∈ N, x0 ∼ π,

(3.1)

∑

 y_r =Fx_r + x^nrG^1/2nw_n.

n=1

Здесь

x_r ≜ col(x^1r,... ,x^Nr) - ненаблюдаемая однородная марковская цепь со

значениями в S^N , с матрицей P переходных вероятностей на одном шаге и

начальным распределением π; {m_r}_r∈N - F^xr-согласованная мартингал-раз-

ность;

y_r ≜ col (y^1r,... ,y^Mr ) - наблюдаемая последовательность, F - матрица

плана наблюдения, а {G_n}_n=1,N являются условными матрицами ковариаций

шумов в наблюдениях относительно текущего значения марковской цепи;

w_r ≜ col(w^1r,... ,w^Mr ) - F^wr-согласованный стандартный гауссовский дис-

кретный белый шум, не зависимый от {x_r}, представляющий ошибки наблю-

дений.

Задача фильтрации цепи x по наблюдениям y заключается в вычислении

условного распределения x_r ≜ E {x_r|y₁, . . . , y_r}. Решение ее известно [3]: оно

определяется следующей рекуррентной схемой вида ¾прогноз-коррекция¿:

(3.2)

x₀

= π - начальное условие,

(3.3)

x_r = P^⊤x_r-1

– прогноз,

(3.4)

xr =

κ_r x_r

– коррекция,

1κ_r x_r

где

κ_r ≜ diag (N(y₁,Fe₁,G₁),... ,N(y_N ,Fe_N ,G_N )) .

Вернемся к системе наблюдения (2.1), (2.2) на сетке с шагом h < λ^-1 и

покажем, что на ней система может быть приближена некоторой системой с

дискретным временем (3.1). Уравнение динамики (2.1) может быть дискре-

тизовано точно: cогласно разложению Ито-Тейлора [4]

(3.5)

Xtr = exp(hΛ^⊤)Xtr-1 + (µtr - µtr-1

где

exp(hΛ^⊤) = I + hΛ^⊤ + O(h²).

Из (2.2) также следует, что

∑

(3.6)

Ytr = hfXtr +

X^nt

g^1/2n(Wtr - Wtr-1 ) + ϑ_r,

n=1

где стохастическая последовательность {ϑ_r} такова, что E {∥ϑ_r∥₂} ≤ Ch^3/2

для любого r ∈ N и некоторой константы C > 0. Формулы (3.5) и (3.6) пред-

ставляют схему временной дискретизации системы (2.1), (2.2), и к ней может

быть применим алгоритм фильтрации (3.2)-(3.4) со следующими значениями

параметров:

P = I + hΛ, F = hf, G_n = hg_n, j = 1,N.

При этом рекурсия (3.3), (3.4) для данной системы записывается в форме

(3.7)

xr =

κ_r(I + hΛ^⊤)x_r-1,

1κ_r(I + hΛ^⊤)x_r-1

и ее можно рассматривать как один из видов численной схемы реализации

аппроксимации порядка s = 1: элементы матрицы ξ имеют вид

∫

(

)

(3.8)

ξ^kj(y) = δ_kjeλjjhN

y,hf^j,hg_j

+ (1 - δ_kj )λ_kjeλjj h Q^kj

(y, u)du,

где

(

)

(3.9)

Q^kj(y,u) ≜ e(λkk-λjj)uN y,uf^k + (h - u)f^j, ugk + (h - u)gj

В рекуррентной процедуре (3.7) элементы ξ^kj аппроксимированы функциями

(

)

(3.10)

ψ^kj(y) = (δ_kj + hλ_kj)N

y,hf^j,hg_j

Следующее утверждение определяет показатель точности численной схе-

мы (3.7).

Лемма 1. В случае фильтрации состояний МСП по наблюдениям с ад-

дитивными шумами схема (3.7) обеспечивает глобальный порядок точно-

сти¹², т.е. для любого T > 0 при достаточно малом шаге h > 0

{

}

(3.11)

sup E

∥x_T/h - x_T/h∥₁

≤CTh²

π∈Π

для некоторой константы C > 0.

Доказательство леммы 1 дано в Приложении. Предложенная реализация ал-

горитма фильтрации при выбранном порядке аналитической аппроксимации

s = 1 имеет результирующий порядок точности ¹² из-за неэффективного вы-

бора схемы численного интегрирования. Лемма 1 также позволяет получить

следствие, согласно которому использование схемы ¾левых¿ прямоугольни-

ков для численного интегрирования сохранит результирующий порядок точ-

ности на уровне¹² .

Аппроксимируем интеграл (2.15) по отрезку [0, h] одноточечной схемой

(2.8), используя значение интегранда N(·) в левой точке, беря его с весом ̺^kj

(k = j):



 eλjjh -eλkkh

λ_kj

, если λ_jj = λ_kk,

(3.12)

̺^kj ≜

λ_jj - λ_kk



hλ_kj eλjj h,

если λ_jj = λ_kk.

При этом схема ¾левых¿ прямоугольников вычисления интегралов в рекур-

сии (2.10) примет вид

(

)

(

)

(3.13)

ψ^kj(y) = δ_kjeλjjhN

y,hf^j,hg_j

+ (1 - δ_kj )̺^kjN

y,hf^j,hg_j

Следствие 1. В случае фильтрации состояний МСП по наблюдениям

с аддитивными шумами схема ¾левых¿ прямоугольников в рекурсии (2.10)

обеспечивает глобальный порядок точности¹².

Доказательство следствия 1 приведено в Приложении.

3.2. Случай s = 1: простая схема ¾средних¿ прямоугольников

Вычислим ψ^kj (y) по формуле ¾средних¿ прямоугольников:

(

)

ψ^kj(y) = δ_kjeλjjhN

y,hf^j,hg_j

(

)

(3.14)

)

(λkk+λjj

+ (1 - δ_kj)λ_kjhe

N y,

f^k + f^j

(g_k + g_j )

Лемма 2. В случае фильтрации состояний МСП по наблюдениям с адди-

тивными шумами схема (3.14) в рекурсии (2.10) обеспечивает глобальный

порядок точности 1, т.е. для любого T > 0 при достаточно малом шаге

h>0

{

}

(3.15)

sup E

∥x_T/h - x_T/h∥₁

≤CTh¹

π∈Π

для некоторой константы C > 0.

Доказательство леммы 2 дано в Приложении.

Таким образом, заменой схемы численного интегрирования без увеличе-

ния вычислительных затрат возможно повысить общий порядок точности до

первого. Дальнейшая фиксация порядка s = 1 и использование более точных

методов численного интегрирования не приведет к значительному уточне-

нию оценок, так как в суммарной погрешности основную роль будет играть

ошибка аналитической аппроксимации, а не численного интегрирования. Для

увеличения общей точности следует увеличить порядок аналитической ап-

проксимации до второго.

3.3. Случай s = 2: квадратуры Гаусса

Формулы (2.14)-(2.16) для s = 2 позволяют получить вид функций ξ^kj:

∫

(

)

ξ^kj(y) = δ_kjeλjj hN

y,hf^j,hg_j

+ (1 - δ_kj)λ_kj eλjj h Q^kj(y, u)du +

(3.16)

∫

∑

λ_kiλ_ijeλjj h

R^kij(y,u,v)dvdu,

i:i=k, i=j

где функция Q^kj(y, u) определена формулой (3.9) и

R^kij(y, u, v) ≜ e(λkk-λii)u+(λii-λjj)v ×

(3.17)

(

)

× N y,uf^k + vfⁱ + (h-u-v)f^j, ugk + vgi +(h - u - v)gj

Для вычисления одномерного интеграла в (3.16) будем использовать двухто-

чечную квадратуру Гаусса

∫

(

)

e(λkk-λjj)uN y,uf^k + (h - u)f^j,y,ugk + (h - u)gj du =

[

√

(

√

)

√

3-1)h

(

3 - 1)h

(

3 + 1)h

(

3 - 1)h

(

3 + 1)h

e(λkk-λjj)(

N y,

√

f^k +

√

f^j,

√

g_k +

√

(

√

)]

(

√

3+1)h

(

3+1)h

(

3-1)h

(

3+1)h

(

3-1)h

+e(λkk-λjj)

N y,

√

f^k +

√

f^j,

√

g_k +

√

+ ǫ1(y),

для повторного интеграла - трехточечную:

∫

(

)

e(λkk-λii)u+(λii-λjj)vN y, uf^k +vfⁱ +(h-u-v)f^j, ugk + vgi + (h - u - v)gj dvdu =

[

(

)

+(λ_ii-λ_jj )^h

e(λkk-λii)

6N y,

f^k +

fⁱ +

f^j,

g_k +

g_i +

g_j

(

)

+(λ_ii-λ_jj )^h

+e(λkk-λii)

6N y,

f^k +

fⁱ +

f^j,

g_k +

g_i +

g_j

(

)]

+e(λkk-λii)⁶+(λii-λjj)

3 N y,

f^k +

fⁱ +

f^j,

g_k +

g_i +

g_j

+ ǫ₂(y),

где ǫ₁(y) и ǫ₂(y) - ошибки интегрирования. Таким образом, интегралы в ре-

курсии (2.10)) вычисляются с помощью следующей схемы:

(

)

λ_jjh

λ_kjhe

(3.18)

ψ^kj(y) = δ_kjeλjjhN

y,hf^j,hg_j

+ (1 - δ_kj)

[

(

√

)

√

(

√

3-1)h

(

3-1)h

(

3+1)h

(

3-1)h

(

3+1)h

× e(λkk-λjj)

N y,

√

f^k +

√

f^j,

√

g_k +

√

g_j

(

√

)]

√

(

√

3+1)h

(

3+1)h

(

3-1)h

(

3+1)h

(

3-1)h

+e(λkk-λjj)

N y,

√

f^k +

√

f^j,

√

g_k +

√

g_j

[

(

)

∑

λ_kiλijh²eλjjh

2h h

e(λkk-λii)6+(λii-λjj)6 N y,

f^k +

fⁱ +

f^j,

g_k +

gi +

i:i=k, i=j

(

)

+(λ_ii-λ_jj )^h

+e(λkk-λii)

6N y,

f^k +

fⁱ +

f^j,

g_k +

g_i +

g_j

(

)]

+e(λkk-λii)⁶+(λii-λjj)

3 N y,

f^k +

fⁱ +

f^j,

g_k +

g_i +

g_j

Лемма 3. В случае фильтрации состояний МСП по наблюдениям с адди-

тивными шумами cхема (3.18) в рекурсии (2.10) обеспечивает глобальный

порядок точности 2, т.е. для любого T > 0 при достаточно малом шаге

h>0

{

}

(3.19)

sup E

∥x_T/h - x_T/h∥₁

≤CTh²

π∈Π

для некоторой константы C > 0.

Доказательство леммы 3 дано в Приложении. Сравнивая схемы (3.14) и (3.18)

можно сделать вывод, что увеличивая число операций в схеме примерно в

N (N - 1) раз удается повысить общий порядок точности аппроксимации до

второго.

4. Численные схемы фильтрации по наблюдениям

с мультипликативными шумами

Для простоты сравнения точности различных численных схем будем счи-

тать, что в (2.1), (2.2) f = 0, т.е. аддитивный полезный сигнал полностью

отсутствует, и все матрицы {g_n}_n=1,N различны. Будет исследована точность

тех же численных реализаций алгоритма фильтрации, которые исследова-

лись в предыдущем разделе. Поэтому выполнение условия (2.9) ниже в дан-

ном разделе уже не проверяется.

Если все матрицы интенсивности шумов в наблюдениях различны, то

оценка оптимальной фильтрации почти наверное совпадает с оцениваемым

состоянием [6]. Несмотря на это многообещающее свойство, в разделе будет

показано, что системы наблюдения с мультипликативными шумами обладают

худшими свойствами для численной реализации, нежели системы с аддитив-

ными шумами. Это означает, что одна и та же численная схема, примененная

для фильтрации состояний по наблюдениям с мультипликативными шумами,

позволяет получить менее точные оценки, чем при фильтрации состояний по

наблюдениям с аддитивными шумами.

4.1. Случай s = 1: составная схема ¾средних¿ прямоугольников

Рассмотрим аналитическую аппроксимацию x_r(1), определенную (3.8), и

ее аппроксимацию составной схемой ¾средних¿ прямоугольников с шагом

дискретизации h^1+α, α ≥ 0:

(

)

ψ^kj(y) = δ_kjeλjj hN

y,hf^j,hg_j

(4.1)

[h^-α]∑

(

))

+ (1 - δ_kj )λ_kjh1+α

Q^kj y,h^1+α i -

i=1

Легко проверить, что при α = 1 последняя формула представляет простую

схему ¾средних¿ прямоугольников.

Лемма 4. В случае фильтрации состояний МСП по наблюдениям с

мультипликативными шумами схема (4.1) в рекурсии (2.10) обеспечива-

ет глобальный порядок точности p = min(1,2α), т.е. для любого T > 0 при

достаточно малом шаге h > 0

{

}

(4.2)

sup E

∥x_T/h - x_T/h∥₁

≤CTh^p

π∈Π

для некоторой константы C > 0.

Доказательство леммы 4 дано в Приложении. Из него следует, что точности

простого метода ¾средних¿ прямоугольников недостаточно для построения

численного алгоритма фильтрации любого положительного порядка точно-

сти. Какая-либо замена этой схемы на другую несоставную (например, на

схему Симпсона, квадратуры Гаусса и пр.) к улучшению не приведут. При-

чиной этому является алгебраическая связь между порядком производной и

степенью h в оценке ошибки интеграла по остатку ряда Тейлора. Из лем-

мы также можно заключить, что при s = 1 рациональным выбором порядка

шага дробления является α =¹² .

4.2. Случай s = 2: составная схема средних

Результаты леммы 4 позволяют построить аппроксимацию элементов ξ^kj

(3.16) порядка s = 2, вычисляя как одномерные, так и двумерные интегралы

с помощью составной схемы средних с шагом h²:

(

)

ψ^kj(y) = δ_kjeλjjhN

y,hf^j,hg_j

[h^-1]∑

(

)

+ (1 - δ_kj)λ_kjh2

Q^kj y,h²(i -

)

(4.3)

i=1

[h^-1]∑[h-1]-n∑

( (

)

(

))

∑

λ_jjh

λ_kiλ_ij

R^kij y,h² n -

,h²

i:i=k,

n=1

m=1

i=j

Следствие 2. В случае фильтрации состояний МСП по наблюдениям

с мультипликативными шумами схема (4.3) в рекурсии (2.10) обеспечива-

ет глобальный порядок точности 2, т.е. для любого T > 0 при достаточно

малом шаге h > 0

{

}

(4.4)

sup E

∥x_T/h - x_T/h∥₁

≤CTh²

π∈Π

для некоторой константы C > 0.

Доказательство следствия 2 приведено в Приложении.

5. Численные примеры

Численное сравнение точности представленных выше методов являет-

ся нетривиальной задачей из-за сложности подбора подходящего примера.

Во-первых, разница в точности, обеспечиваемой различными схемами, будет

мала в случае, когда столбцы fⁿ или матрицы g_n для разных значений n

близки по значению между собой. Во-вторых, доказанные в [1] утвержде-

ния о порядке точности носят асимптотический характер при h → 0: выбор

слишком малого шага дискретизации может привести к тому, что вероят-

ность превышения числом скачков состояния на отрезке дискретизации еди-

ницы окажется столь незначительной, что численные реализации высокого

порядка будут практически не отличимы по точности от численных реализа-

ций первого порядка. Наконец, в-третьих, характеристики точности того или

иного метода приходится вычислять методом Монте-Карло, что приводит к

необходимости моделирования пучков траекторий и оценок очень большого

объема для визуального ¾разделения¿ этих характеристик.

5.1. Сравнительный анализ схем фильтрации по наблюдениям

с аддитивными шумами

Для сравнительного анализа различных численных реализаций алгоритма

фильтрации использовалась система наблюдения (2.1), (2.2) со следующими

характеристиками: t ∈ [0, 1], N = 3, h = 0,01,









-10,0

2,0

8,0

0,333

Λ=

8,0

-10,0

2,0

,π= 0,333

,

2,0

8,0

-10,0

0,334





0,0

f = -50,0

,g1 = g₂ = g₃ = 1,

50,0

объем пучка траекторий для метода Монте-Карло S = 100000.

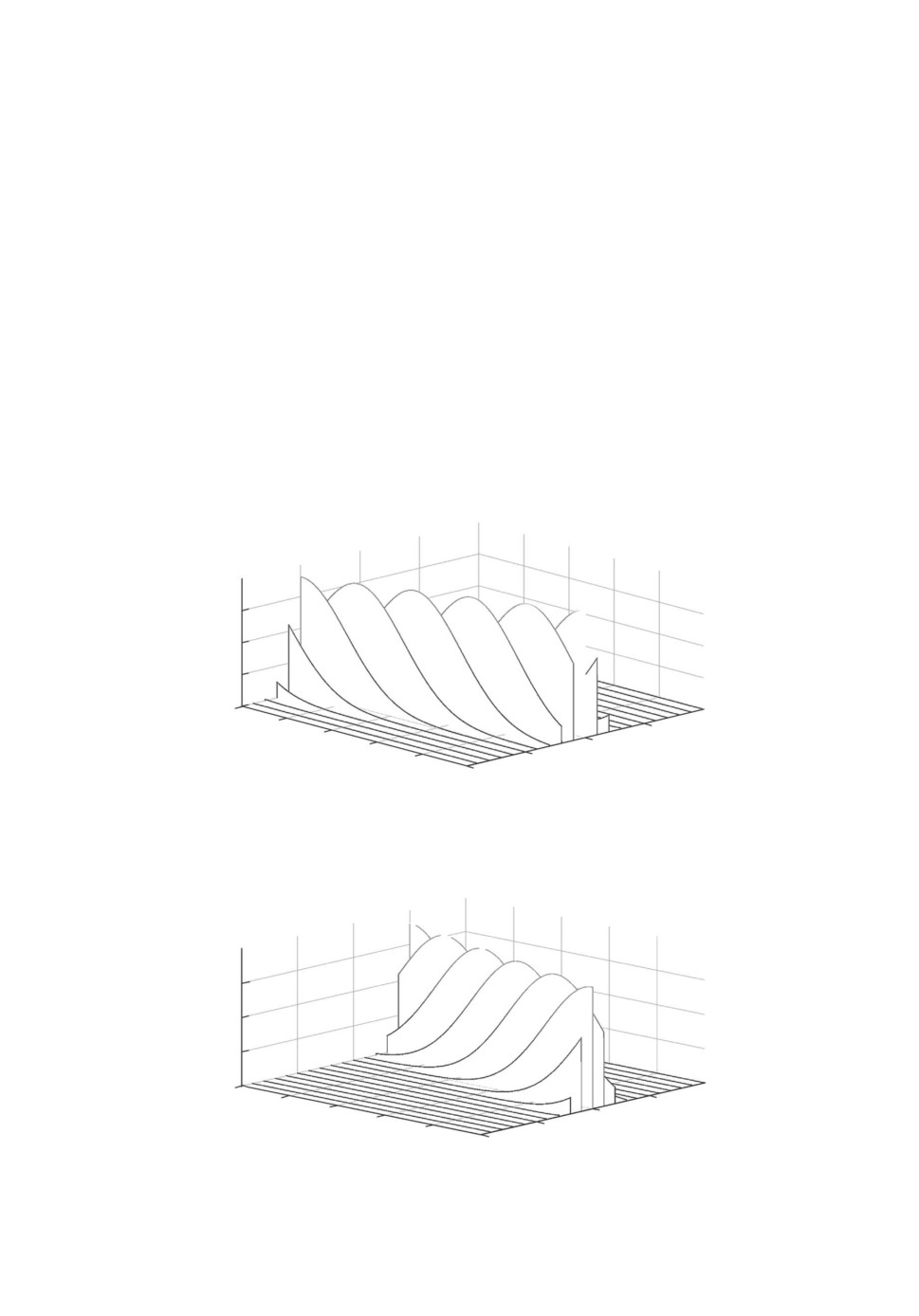
На рис. 1 и 2 представлены графики Q^1,2(y, u) и Q^1,3(y, u) интеграндов

в (2.15) как функций аргумента u для некоторых фиксированных значений y.

´10^-4

Q^1,2(y, u)

1,5

1,0

0,5

0,002

0,5

0,004

0,006

0,008

-0,5

-1,0

Рис. 1. Графики функции Q^1,2(y, u) при некоторых фиксированных y: адди-

тивные шумы в наблюдениях.

´10^-4

Q^1,3(y, u)

1,5

1,0

0,5

0,002

0,5

0,004

0,006

0,008

-0,5

-1,0

Рис. 2. Графики функции Q^1,3(y, u) при некоторых фиксированных y: адди-

тивные шумы в наблюдениях.

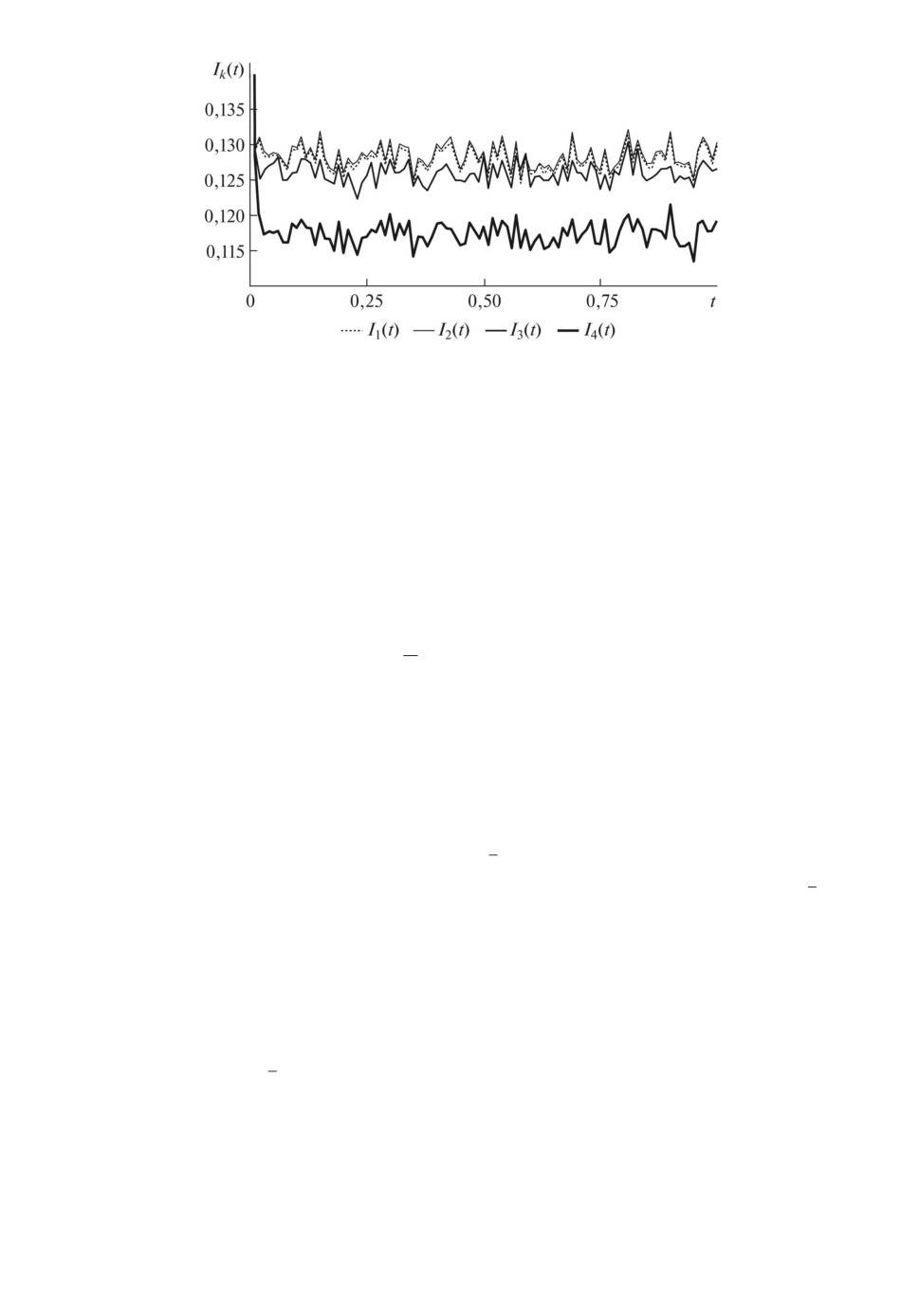
Рис. 3. Критерий точности при использовании различных схем численной ре-

ализации: аддитивные шумы в наблюдениях.

С помощью метода имитационного моделирования по пучку траекторий

были вычислены выборочные значения критерия качества

{

}

I(t) ≜ E

∥Xt - X_t∥₁

для различных численных реализаций аналитических аппроксимаций:

∑

I_k(t) ≜

∥Xs,kt - X^st∥₁,

s=1

где X^st - значение s-й траектории состояния в момент времени t,Xs,kt - значе-

ние s-й траектории аппроксимации оценки, полученной применением k-й схе-

мы реализации, в момент времени t. В данном эксперименте были вычислены

характеристики точности следующих схем:

I₁(t) - простая схема дискретизации стохастической дифференциальной

системы наблюдения (порядок точности¹² ),

I₂(t) - простая схема ¾левых¿ прямоугольников (порядок точности¹²),

I₃(t) - простая схема ¾средних¿ прямоугольников (порядок точности 1),

I₄(t) - простая схема квадратур Гаусса (порядок точности 2).

Их графики представлены на рис. 3. Полученные результаты вполне соответ-

ствуют теоретическим выкладкам. Характеристики I₁(t) и I₂(t) сопоставимы

между собой, так как соответствуют численным реализациям одного поряд-

ка точности. Характеристика I₃(t) меньше I₁(t) и I₂(t), так как порядок ее

точности выше на¹² . Характеристика I₄(t) значительно меньше I₃(t), так как

порядок ее точности выше на 1.

Примечательно, что для порядка s = 1 был проведен дополнительный рас-

чет с использованием схемы адаптивного вычисления интеграла (2.15). Ре-

зультат ее использования оказался визуально не отличимым от результата

метода ¾средних¿ прямоугольников. При этом время вычисления оценок с

использованием схемы адаптивного интегрирования значительно возросло.

5.2. Сравнительный анализ схем фильтрации по наблюдениям

с мультипликативными шумами

Для сравнительного анализа различных численных реализаций алгоритма

фильтрации использовалась система наблюдения (2.1), (2.2) со следующими

характеристиками:





-10,0

2,0

8,0

t ∈ [0,1], N = 3, h = 0,05, Λ = 

8,0

-10,0

2,0

,

2,0

8,0

-10,0









0,333

0,0

g₁ = 1,0,

π =  0,333

,f= 0,0

,

g₂ = 2,0,

0,334

0,0

g₃ = 3,0,

объем пучка траекторий для метода Монте-Карло 100000.

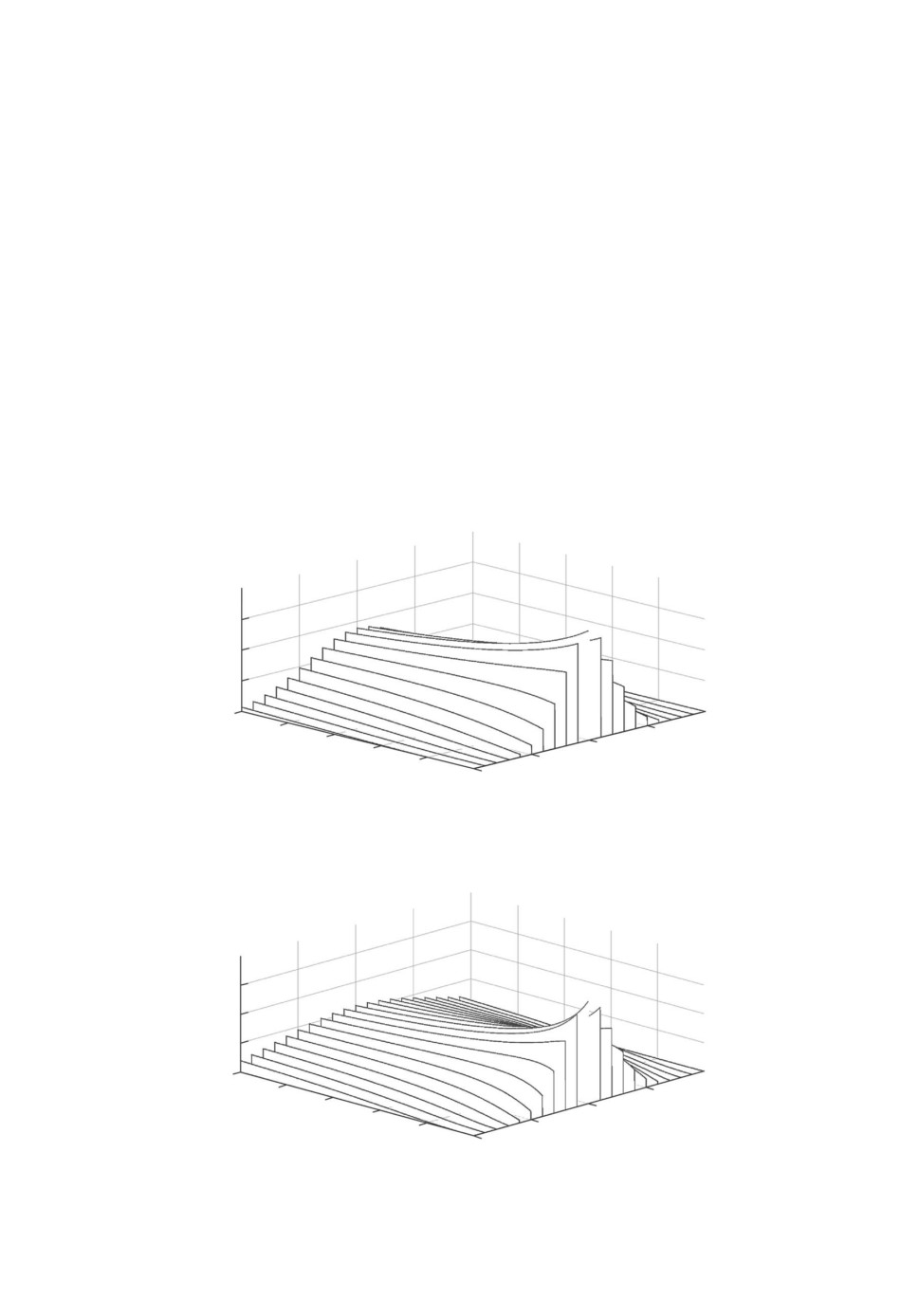
На рис. 4 и 5 представлены графики Q^1,2(y, u) и Q^1,3(y, u) интеграндов в

(2.15) как функций аргумента u для некоторых фиксированных значений y.

Q¹²(y, u)

1,5

1,0

0,5

0,01

0,5

0,02

0,03

0,04

-0,5

-1,0

Рис. 4. Графики функции Q^1,2(y, u) при некоторых фиксированных y: муль-

типликативные шумы в наблюдениях.

Q¹³(y, u)

1,5

1,0

0,5

0,01

0,5

0,02

0,03

-0,5

0,04

-1,0

Рис. 5. Графики функции Q^1,3(y, u) при некоторых фиксированных y муль-

типликативные шумы в наблюдениях.

I_k(t)

I₅(t)

I₆(t)

1,065

1,060

1,055

0,25

0,50

0,75

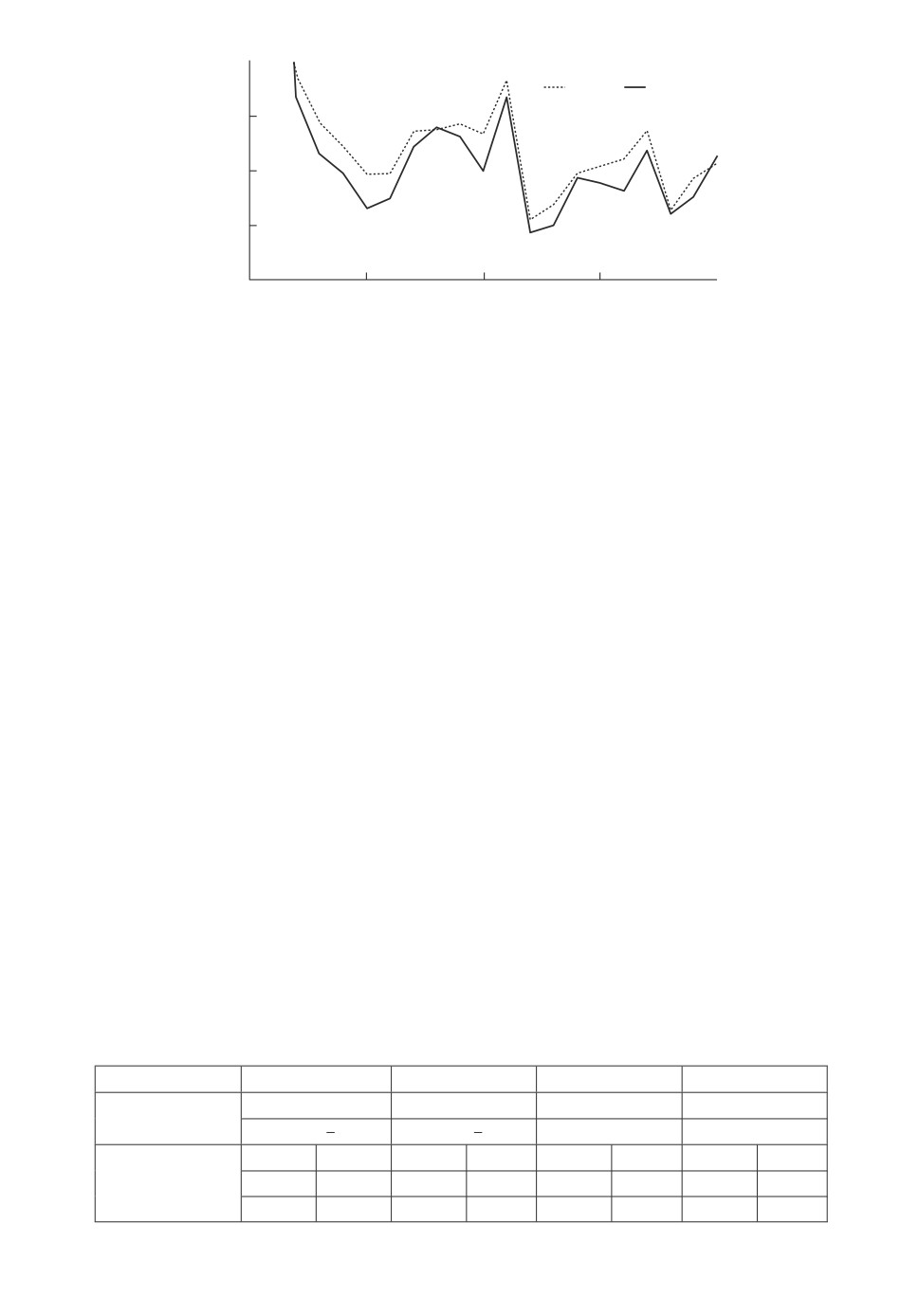
Рис. 6. Критерий точности при использовании различных схем численной реа-

лизации: мультипликативные шумы в наблюдениях.

Методом Монте-Карло были вычислены выборочные значения критерия

качества I(t) для следующих численных схем:

I₅(t) - составная схема ¾средних¿ прямоугольников (порядок точно-

сти 1),

I₆(t) - составная схема средних (порядок точности 2).

Их графики приведены на рис. 6. Полученные результаты соответствуют тео-

ретическим выкладкам. Величина I₆(t) меньше I₅(t), так как порядок ее точ-

ности выше.

6. Заключение

Таблица содержит сводную информацию о порядке точности различных

схем численных реализаций оценок фильтрации в зависимости от вида шу-

ма в наблюдениях: аддитивного или мультипликативного. Первое значение в

ячейке означает порядок аналитической аппроксимации, второе - итоговый

порядок точности, обеспечиваемый выбранной схемой численной реализации.

Значение, взятое в скобки, означает, что детальный вывод итогового порядка

в данной работе не приведен.

Анализируя данные в таблице, можно прийти к следующим заключениям.

В случае фильтрации с наблюдениями общего вида (снос в наблюдени-

ях - ненулевой, матрицы интенсивности шумов - неодинаковы для разных

состояний МСП) следует применять составные схемы вычисления интегра-

лов. При этом схема должна быть наиболее экономичной с вычислительной

Порядок точности различных схем реализации

Вид шума Диск-ция сист.

¾Лев.¿ пр-ки

¾Сред.¿ пр-ки Кв. Гаусса

Прост.

Аддитив. шум

1|¹²

1 |¹²

1| 1

2| 2

Прост. Сост. Прост. Сост. Прост. Сост. Прост. Сост.

Мультиплик.

1| 0

1 | (1)

1 | (0)

1 | (1)

1 |0

1 |1

1 | (0)

1 | (2)

шум

–

1 | (0)

2 |2

точки зрения, а требуемая точность должна достигаться путем выбора под-

ходящего дробного шага интегрирования, меньшего, чем шаг дискретизации

по времени. В качестве такой схемы предлагается выбрать метод ¾средних¿

прямоугольников.

Судя по результатам численных экспериментов, при малых шагах дис-

кретизации по времени, когда полученные асимптотические оценки порядка

точности имеют место, разница в применении аналитической аппроксима-

ции того или иного порядка незначительна. Поэтому выбор пары ¾порядок

аналитической аппроксимации-численная схема¿ должен проводиться инди-

видуально для каждой конкретной задачи. В итоге должен быть достигнут

компромисс между требованиями к точности получаемых оценок и к ограни-

чениям на имеющиеся вычислительные ресурсы.

Построение алгоритмов численного решения задачи фильтрации марков-

ских процессов по непрерывным наблюдениям с аддитивными/мультипли-

кативными шумами нельзя считать законченным. Во-первых, при выводе по-

рядка точности численных реализаций использовались достаточно консерва-

тивные неравенства - оценки сверху. Именно они привели к пессимистиче-

скому выводу о невозможности использования простых (несоставных) схем

численного интегрирования для обработки наблюдений с мультипликативны-

ми шумами. Использование более ¾тонких¿ неравенств, возможно, позволит

уточнить порядки точности тех или иных схем интегрирования. Во-вторых,

полученные результаты делают возможным разработку численных методов

решения задач фильтрации по непрерывным наблюдениям состояний марков-

ских процессов более общего вида: общих МСП, диффузионных процессов и

пр. В-третьих, открытым остается вопрос о величине расхождения оценок

фильтрации по непрерывным и по дискретизованным наблюдениям. Все эти

проблемы представляются перспективными для дальнейших исследований.

ПРИЛОЖЕНИЕ

Доказательство леммы 1. Первый сомножитель в (3.10) представ-

ляет собой вес ̺^kj, при этом число точек в интегральной сумме L = 1. Из

∑_N

свойств матрицы интенсивности следует, что W =

̺^kj = 1. Далее в изло-

j=1

жении будем использовать следующие обозначения: γ^kj(y) ≜ ψ^kj(y) - ξ^kj(y),

γ(y) ≜ ∥γ^kj (y)∥_k,j=1,N . Разность γ^kj(y) с учетом того, что g_k ≡ g, может быть

записана в виде

(

)

γ^kj(y) = δ_kj

1+λ_jjh - eλjjh N(y,hfj,hg) +

(

)

+ (1 - δ_kj)λ_kjh

1 - eλjjh N(y,hf^j,hg) +





∫

+ (1 - δ_kj )λ_kj eλjj hhN(y, hf^j , hg) - e(λkk -λjj )uN(y, uf^k + (h - u)f^j, hg)du

}

≜I^kj(y)

Оценим сверху интеграл в правой части (2.11) с использованием формулы

Тейлора первого и второго порядков:

∫

(

)

(

)

|γ^kj(y)|dy ≤ δkj

1+λ_jjh-eλjjh

+ (1 - δ_kj )λ_kjh

1-eλjjh

R^M

∫

+ (1 - δ_kj)λ_kj

eλjj h

|I^kj (y)|dy ≤

(Π.1)

R^M

∫

≤ K₁h² + (1 - δ_kj)λ_kjeλjjh

|I^kj (y)|dy

R^M

для некоторой константы K₁ > 0. Разность I^kj(y) представляет собой ошиб-

ку численного интегрирования при использовании простой схемы ¾левых¿

прямоугольников и определяется следующим образом [2]:

(

)]

d [



I^kj(y) =

e(λkk-λjj)uN y,uf^k + (h - u)f^j,hg



2 du

u=z

(

)

e(λkk-λjj)zN y,zf^k + (h - z)f^j,hg ζ₀(y,z),

где z = z(y) ∈ [0, h] - некоторый параметр, зависящий от y, и

(Π.2)

ζ₀(z) ≜ λ_kk -λ_jj +〈f^j,f^k -f^j〉_g-1 -

∥f^k - f^j∥2g-1 +

〈y, f^k - f^j〉_g

−1 .

Непосре

∫

так какRM |I^kj(y)|dy =RM |I^kj (y, z^kj (y))|dy, а зависимость z^kj (y) в общем

случае неизвестна. Поэтому предварительно оценим |I^kj| сверху. Прежде все-

го, можно непосредственно проверить истинность неравенства



(

)

₂



y - z^kjf^k - h - z^kj f^j

≥

(hg)^-1

(Π.3)



(

)

₂



≥ ∥y∥2(2hg)-1 -

z^kj f^k + h - z^kj f^j

(hg)^-1

Отсюда следует, что

(

)

h²

(Π.4)

e(λkk-λjj)zN y,z^kjf^k + h - z^kj f^j,hg

(

)



(

)

₂



e(λkk-λjj)z(2π)^-M/2|hg|^-1/2 exp -

y -z^kjf^k - h-z^kj f^j

≤

(hg)^-1

(

)

≤

e(λkk-λjj)z(2π)^-M/2|hg|^-1/2 exp

∥y∥²

(2hg)^-1

)



(

)

₂



× exp

z^kjf^k + h - z^kj f^j

≤ h²K₂N(y,0,2hg),

(hg)^-1

где K₂ > 0 - некоторая константа. Тогда

∫

(Π.5)

|I^kj(y)|dy ≤ K₂h2

N(y, 0, 2hg)|ζ₀

(y, z)|dy ≤

R^M

∫





₂







≤K₂h2

kk - λjj + 〈f^j,f^k - f^j〉g-1 -

f^k - f^j

(y, 0, 2hg)dy +

λ

N

g^-1

R^M

∫



1



+K₂h2



y,f^k - f^j〉_g-1



(y, 0, 2hg)dy =

N

h〈

R^M

∫





₂







=K₂h2

kk - λjj + 〈f^j,f^k - f^j〉g-1 -

f^k - f^j

(y, 0, 2hg)dy +

λ

N

g^-1

R^M

∫



√

1



2K₂h²



,g-2(f^k - f^j)



(y, 0, I)dy = K₃h² + K₄h²

N

hy

R^M

для некоторых неотрицательных констант K₃ и K₄. Подставим эти неравен-

ства в оценку интеграла абсолютной величины γ^kj:

∫



(

)



γ^kj(y) dy ≤ K1h2 + (1 - δkj )λkjeλjjh K3h2 + K4h2

≤K₅h²

R^M

с некоторой константой K₅ > 0. Условие (2.11) в этом случае приобретает

форму

∫

∑

max

|γ^kj(y)|dy ≤ NK₅h² ,

k=1,N

j=1

R^M

а неравенство (2.13), характеризующее разницу условного распределения

xT/h и его аппроксимации первого порядка, реализованной с помощью дис-

кретизации дифференциальной системы наблюдения, имеет вид

{

}

(

)

(Π.6)

sup E

∥XT/h -XT/h∥₁

≤ 2T λ²h + NK₅h²

≤Ch²

π∈Π

для некоторой константы C > 0.

Лемма 1 доказана.

Доказательство следствия 1. Оценим сначала величину W, пред-

полагая для простоты, что λ_jj = λ_kk:

∑

W=eλkkh +

̺^kj ≤

j:j=k

λ^2jjh

∑

λ²

λ_jjh +

- λ_kkh - λkkh²2 + K7h³

≤1+λ_kkh+

+K₆h³ +

λ_kj

≤

λ_jj - λ_kk

j:j=k

λ^2kkh²

∑

λ^2jj - λ^2kk

≤1+

λ_kjh²

+K₈h³ =

2(λ_jj - λ_kk)

j:j=k

∑

λ²

h²λ_kj(λ_jj + λ_kk)

=1+

+K₈h³ =

j:j=k

∑

h²λ_kjλ_jj

=1+

+K₈h³ ≤ 1

j:j=k

для достаточно малых h и некоторых положительных констант K₆, K₇, и K₈.

Аналогичным образом можно показать, что W ≤ 1 и при λ_kk = λ_jj. Далее,

определим отклонение схемы (3.13) от эталона (3.8), учитывая, что g_j ≡ g:

γ^kj(y) = ψ^kj(y) - ξ^kj(y) =





∫

(

)

= (1 - δ_kj )̺^kj N(y, hf^j , hg) - λ_kj

eλjj h e(λkk-λjj )uN

y, uf^k +(h-u)f^j, hg

du =

(

)

= (1 - δ_kj )

̺^kj - λ_kjheλjj h N(y, hfj , hg) +





∫

(

)

+ (1 - δ_kj )λ_kjeλjjhhN(y, hf^j, hg)- e(λkk-λjj)uN y, uf^k + (h - u)f^j, hg du =

(

)

= (1 - δ_kj)

̺^kj - λ_kjheλjj h N(y, hfj , hg) +

(

)]

λ_kjh

d [



+ (1 - δ_kj )

eλjjh

e(λkk-λjj)uN y,uf^k + (h - u)f^j,hg



u=z

где z = z(y) ∈ [0, h] - некоторый параметр, зависящий от y, и ζ₀(z) опре-

делено (Π.2). Полностью повторяя выкладки (Π.3)-(Π.5), можно убедить-

ся в справедливости неравенства (Π.8) для схемы ¾левых¿ прямоугольни-

ков, которая также имеет порядок глобальной точности

. Следствие

доказано.

Доказательство леммы 2. Проверим для (3.14) выполнение усло-

вия (2.9), используя формулу Тейлора второго порядка и свойства матрицы

интенсивности переходов Λ:

∑

(λkk+λjj)h

̺^kjℓ =

δ_kjeλkkh + (1 - δ_kj)λ_kjhe

j,ℓ

j=1

(

)

∑

λ^2kjh²

λ²

=1+λ_kkh+

+C_kk(h)h3 +

λ_kjh

1+λ_kjh+

+C_kj(h)h3

j:j=k

∑

=1+

λ_kjλ_jj + C(h)h³.

j:j=k

Здесь все функции {C_kj}_k,j ограничены сверху константойmaxk |λkk|³6^.Так

∑_N

как

λ_kjλ_jj ≤ 0, то при достаточно малых h условие (2.9) выполнено:

j:j=k

W ≤ 1.

]

λ_kjh

d² [



γ^kj(y) = (1-δ_kj)

eλjjh

e(λkk-λjj)uN(y,uf^k +(h-u)f^j,hg)



du²

u=z

(

)

λ_kjh

= (1 - δ_kj)

eλjjhe(λkk-λjj)zN y,zf^k + (h - z)f^j,hg

[ζ²⁰(y, z) - ζ₁],

где вновь z = z(y) ∈ [0, h] - некоторый параметр, зависящий от y, а

∂

(Π.7)

ζ₁(z) ≜

ζ₀(z) =

∥f^j - f^k∥2g-1 .

∂z

Выполняя выкладки, аналогичные (Π.3)-(Π.5), можно получить вариант

∑_N ∫

условия (2.11) maxk=1,Nj=1RM |γ^kj (y)|dy ≤ NK₉h² и неравенства (2.13)

{

}

(

)

(Π.8)

sup E

∥x_T/h - x_T/h∥₁

≤ 2T λ²h + NK₁₀h

≤CTh

π∈Π

для схемы интегрирования простых ¾средних¿ прямоугольников. В двух по-

следних неравенствах K₉, K₁₀ и C - некоторые положительные константы.

Лемма 2 доказана.

Доказательство леммы 3. Выполнение условия (2.9) доказывается

аналогично, как и в леммах 1 и 2. Согласно [2] и с учетом того, что g_n ≡ g,

абсолютные значения ошибок ограничены следующим образом:



[

(

)]

 ∂⁴



(Π.9)

|ǫ₁(y)| ≤ h⁵K₁₁ max

e(λkk-λjj)uN y,uf^k + (h - u)f^j,hg

,

u∈[0,h]

∂u⁴

(Π.10)

|ǫ₂

(y)| ≤



[

(

)]

∂³



≤h⁵K₁₂

max

(λ_kk-λii)u+(λii-λjj )vN y, uf^k + vfⁱ + (h - u - v)f^j, hg

(u,v)∈D,

,

∂u^k∂v^3-k e

k=0,3

где K₁₁ и K₁₂ - некоторые положительные константы.

Производная в (Π.9) имеет вид

[

(

)]

∂⁴

e(λkk-λjj)uN y,uf^k + (h - u)f^j,hg

∂u⁴

(Π.11)

(

)(

)

= e(λkk-λjj)uN y,ufk +(h-u)f^j,hg

ζ⁴⁰(u)+6ζ²⁰(u)ζ₁(u)+3ζ²¹(u)

где ζ₀ и ζ₁ определены (Π.2) и (Π.7). Строя оценки сверху интеграла от

абсолютного значения e₁(y) подобно (Π.5), можно получить неравенство

∫

|e₁(y)|dy ≤ K₁₃h³, и аналогичная оценка для |e₂(y)| имеет вид

|e₂(y)|dy ≤

R^M

≤ K₁₄h³ для некоторых неотрицательных констант K₁₃ и K₁₄. В этом случае

{

}

неравенство (2.13) принимает вид sup_π∈Π E

∥x_T/h - x_T/h∥₁

≤ CTh² для неко-

торой константы C > 0 и достаточно малого шага h. Лемма 3 доказана.

Доказательство леммы 4. Сначала исследуем характеристики точ-

ности интегрирования простой схемы

¾средних¿ прямоугольников (т.е.

α = 0), а затем сделаем выводы на случай составного варианта данной схемы.

Итак, с учетом того, что f^j ≡ 0,

(

)

ψ^kj(y) = δ_kjeλjjhN(y,0,hg_j) + (1 - δ_kj)λ_kjhQ^kj y,

При этом разность γ^kj(y) = ψ^kj (y) - ξ^kj(y) представима в виде





(

) ∫h

γ^kj(y) = (1 - δ_kj)λ_kjeλjjh Qkj y,h

- Q^kj(y,u)du,

и согласно [2] для нее верно следующее равенство

λ_jjh



λ_kjh³e

∂²



γ^kj(y) = (1 - δ_kj)

Q^kj(y,u)

∂u²

u=z

λ_jjh

[

]

λ_kjh³e

= (1 - δ_kj)

Q^kj(y,z)

η²⁰(y,z) - η₁(y,z)

где z = z(y) ∈ [0, h] - параметр, зависящий от y,

|zg_k + (h - z)g_j |

η₀(y,z) ≜ λ_kk - λ_jj -^dz

2|zg_k + (h - z)g_j |

(Π.12)

y^⊤[zg_k + (h - z)g_j]^-1(g_k - g_j)[zg_k + (h - z)g_j]^-1y

(Π.13)

η₁

(y, z) ≜

d²

|zg_k + (h - z)g_j |_d

|zg_k + (h - z)g_j | - (^ddz |zg_k + (h - z)g_j |)²

z²

≜

2|zg_k + (h - z)g_j |²

+ y^⊤[zg_k + (h - z)g_j]^-1(g_k - g_j)[zg_k + (h - z)g_j]^-1(g_k - g_j)[zg_k + (h - z)g_j]-1y.

Предварительно оценим |γ^kj | сверху. Свойства системы (2.2) гарантируют,

что существуют такие симметрические матрицы g и G, что 0 < g ≤ g_n ≤ G

для всех n = 1, N . Поэтому выполняется неравенство

(Π.14)

Q^kj(y,u) ≤ K₁₅

N(y, 0, hg),

где

|G|

K₁₅ =

max

e(λkk-λjj)u.

|g|

k,j=1,N:k=j

u∈[0,h]

Из свойства определителей [5] следует, что

∑

(Π.15)

|zg_k + (h - z)g_j | = |z(g_k - g_j ) + hg_j | =

zⁿh^N-nG_kjn,

n=0

где G_kjn - сумма всех определителей матриц, полученных из u(g_k - g_j ) путем

замены n столбцов соответствующими столбцами hg_j . Отсюда следует, что

∑

(Π.16)

|zg_k + (h - z)g_j | =

nz^n-1h^N-nG_kjn.

n=1

Поэтому верно неравенство



∑

(_u)n-1



Gkjn



|zg_k + (h - z)g_j |



K₁₆

n=1



=h^-1



≤

 2|zg_k + (h - z)g_j |



∑

(_u)m



Gkjm



m=0

∑N

n=1

n|Gkjn|

для K₁₆ = max_k,j=1,N:

∑_N

. Таким образом, для |η₀| верна

k=j

2 min_w∈[0,1]|_m=0 Gkjmw^m|

следующая оценка сверху:

K₁₆

K₁₈

(Π.17)

|η₀| ≤ K₁₇ +

∥y∥^2I,

h²

где K₁₇ = max_k,j=1,N: |λ_kk - λ_jj|, K₁₈ = ∥g^-1Gg^-1∥²² - квадрат спектральной

k=j

∫

нормы матрицы. Заметим также, чтоRM ∥y∥^2IN(y, 0, hg)dy = htr (g).

Из (Π.17) следует оценка сверху для квадрата ζ₀:

K₂₂

(

)

K₂₃

K₂₄

(Π.18)

η²⁰(y,u) ≤ K₂₁ +

1 + ∥y∥^2I

∥y∥^2I +

∥y∥^4I

h²

h³

h⁴

с некоторыми положительными константами K₂₁, K₂₂, K₂₃ и K₂₄. Исполь-

зуя (Π.15) и (Π.16), можно получить оценку абсолютного значения первого

слагаемого в ζ₁(y, u):



)₂



|zgk + (h - z)gj|^d

|zg_k + (h - z)g_j | -

|zg_k + (h - z)g_j |



dz²



2|zg_k + (h - z)g_j |²



(

)₂



∑



z^sh^N-nG_kjn

m(m - 1)z^m-2h^N-mG_kjm -

ℓz^ℓ-1h^N-ℓG_kjℓ



n=0

m=2

ℓ=1



(

)₂



∑



z^sh^N-sG_kjs



s=0



(

)₂



∑ (

∑

(_z)

∑

(_z



)ℓ-1



m(m - 1)

^m-2 G_kjm -

ℓ



Gkjn

kjℓ



n=0

m=2

ℓ=1



K₂₅



(

)₂

≤

h²



h²

∑

(_z)s



Gkjs



s=0

∑_N

∑N

|G_kjn|

m(m-1)|G_kjm |+(

ℓ|G_kjℓ|)²

n=0

m=2

ℓ=1

где K₂₅ = max_k,j=1,N:

∑_N

. Абсолютное

2 min_w∈[0,1](_s=0 w^sG_kjs)²

k=j

значение второго слагаемого в ζ₁(y, u) также оценивается сверху:

y^⊤[zg_k +(h-z)g_j]^-1(g_k -g_j)[zg_k +(h-z)g_j]^-1(g_k -g_j)[zg_k +(h-z)g_j]^-1y ≤

K₂₆

≤

∥y∥^2I,

h³

где K₂₆ = 4∥g^-1Gg^-1Gg^-1∥²².

Используя все эти неравенства и связь между моментами 2-го и 4-го поряд-

ков гауссовского распределения, получаем следующий вариант неравенства

(2.11):

∑∫

|γ^kj (y)|dy ≤ K₂₇h + K₂₈h² + K₂₉h³

j=1

R^M

∫ля некоторых положительных констант K₂₇, {28 и K29. Это }начит, что

|γ^kj (y)|dy = O(h), и согласно (2.13) sup_π∈Π E

∥x_T/h - x_T/h∥₁

= O(h⁰).

R^M

Используем для приближенного вычисления ξ^kj составную схему ¾сред-

них¿ прямоугольников, разбив отрезок интегрирования [0, h] с шагом h^1+α.

В этом случае

λ_jj h



λ_kjh^3+2αe

∂²



γ^kj(y) = (1 - δ_kj)

Q_kj(y,u)

∂u²

u=z

Повторяя все предыдущие выводы этого доказательства для составной схемы

¾средних¿ прямоугольников, можно проверить, что она обеспечивает поря-

док точности 1 + 2α:

∑∫

|γ^kj(y)|dy ≤ NCh^1+2α,

j=1

R^M

и согласно (2.13) глобальный показатель точности имеет порядок p

= min(1,2α):

{

}

sup E

∥XT/h -XT/h∥₁

≤CTh^p.

π∈Π

Лемма 4 доказана.

Доказательство следствия 2. Согласно (2.13) для сохранения вто-

рого порядка точности аналитической аппроксимации необходимо, чтобы ло-

кальная ошибка численного интегрирования на каждом шаге имела порядок

не более O(h³). Составная схема ¾средних¿ прямоугольников, представлен-

ная в лемме 4, обеспечивает эту точность для вычисления одномерного ин-

теграла - второго слагаемого в (3.16) - при выборе α = 1.

Выберем подходящую схему вычисления двойных интегралов по треуголь-

нику, входящих в третье слагаемое (3.16). Прежде всего, определим величину

ошибки приближения интеграла в (2.16) простым методом средних:

∫

(

)

h²

λ_kiλ_ijeλjj h

R^kij(y,u,v)dvdu =

λ_kiλ_ijeλjjhRkij y,

∫

+λ_kiλ_ijeλjjh

χ^kij2(y,u,v)dvdu,

где функция χ^kij2(y, u, v) имеет вид



((

)

(

)

)₂



∂



χ^kij2(y,u,v) ≜1

+ w-

R^kij(y,z,w)

∂z

∂w



(z(y,u),w(y,v))

Согласно [2] для некоторой положительной константы K₃₀ верно неравенство

∫



∂²



kij

λ_kiλ_ijeλjjh

χ^kij2(y,u,v)dvdu ≤ h⁴K₃₀ max



(y, z, w)

ℓ=0,1,2;

.

∂z^ℓ∂w^2-ℓχ

(z,w)∈D

В лемме 4 также оценивалась вторая производная, однако, от другой функ-

ции, Q^kj. Она содержала h² в знаменателе. Сравнивая Q^kj и R^kij, можно

заключить, что вторая производная от R^kij также будет содержать h² в зна-

∫_h ∫_h-u

менателе, т.е. λ_kiλ_ijeλjj h

χ^kij2(y,u,v)dvdu ≤ h²K₃₁ для некоторой по-

ложительной константы K₃₁. Так как требуемый порядок точности - третий,

то последнее равенство позволяет сделать вывод о том, что простой метод

средних в данном случае нужной точности не обеспечивает.

Используем для вычисления двойного интеграла составной метод средних,

разбив область интегрирования, прямоугольный треугольник с катетами дли-

ны h, на подобные треугольники с катетами h². В этом случае

∫h

∫

λ_kiλ_ijeλjjh

χ^kij2(y,u,v)dvdu ≤ h⁴K₃₂

для некоторой положительной константы K₃₂, и отсюда согласно (2.13) сле-

дует выполнение неравенства

{

}

sup E

∥XT/h -XT/h∥₁

≤CTh²,

π∈Π

т.е. для численной реализации аппроксимации порядка s = 2 достаточно ис-

пользования составных схем средних при вычислении одномерных и двойных

интегралов с шагом дискретизации h².

Следствие 2 доказано.

СПИСОК ЛИТЕРАТУРЫ

1. Борисов А.В. L₁-оптимальная фильтрация марковских скачкообразных про-

цессов I: точное решение и численные схемы реализации // АиТ. 2020. № 11.

C. 12-34.

Borisov A.V. L₁-Optimal Filtering of Markov Jump Processes I: Exact Solution and

Numerical Realization Schemes // Autom. Remote Control. 2020. V. 81. No. 11.

2. Isaacson E., Keller H. Analysis of Numerical Methods. N.Y.: Dover Publications,

1994.

3. Elliott R.J., Aggoun L., Moore J.B. Hidden Markov Models: Estimation and Control.

N.Y.: Springer, 2008.

4. Kloeden P., Platen E. Numerical solution of stochastic differential equations. Berlin:

Springer, 1992.

5. Magnus J., Neudecker H. Matrix Differential Calculus with Applications in Statistics

and Econometrics. N.Y.: Wiley, 2019.

6. Борисов А.В. Фильтрация Вонэма по наблюдениям с мультипликативными шу-

мами // АиТ. 2018. № 1. C. 52-65.

Borisov A.V. Wonham filtering by observations with multiplicative noises // Autom.

Remote Control. 2018. V. 79. No. 1. P. 39-50.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 02.03.2020

После доработки 25.05.2020

Принята к публикации 09.07.2020