Автоматика и телемеханика, № 12, 2020

(Московский авиационный институт)

О ФОРМИРОВАНИИ ПОЗИЦИОННОГО УПРАВЛЕНИЯ

В МНОГОШАГОВОЙ ЗАДАЧЕ ПОРТФЕЛЬНОЙ ОПТИМИЗАЦИИ

С ВЕРОЯТНОСТНЫМ КРИТЕРИЕМ¹

Исследуется многошаговая задача портфельной оптимизации. Рассмат-

ривается возможность вложения капитала на каждом шаге в безрисковый

актив с фиксированной доходностью и рисковый актив со случайной до-

ходностью с финитной плотностью. Критерием оптимальности выступает

вероятность достижения или превышения капитала инвестора в терми-

нальный момент времени некоторого заранее заданного уровня. На ос-

нове использования кусочно-постоянного управления предлагается пози-

ционное управление, которое на обширном наборе примеров превосходит

по значению вероятностного критерия ранее известные универсальные

управления, применяющиеся в задачах портфельной оптимизации.

Ключевые слова: многошаговая задача, портфельная оптимизация, веро-

ятностный критерий, позиционное управление.

DOI: 10.31857/S000523102012003X

1. Введение

Исторически исследование задач портфельной оптимизации началось в

1950-х гг. с конструирования различных критериев и мер риска в одноша-

говой постановке, когда портфель ценных бумаг не предполагается к реба-

лансировке в течение инвестиционного горизонта. Хотя в настоящее время

также продолжаются поиски новых мер риска и постановок задач, позволяю-

щих сформировать тот или иной портфель ценных бумаг, особый интерес ис-

следователей привлекают многошаговые задачи портфельной оптимизации,

в которых в течение инвестиционного горизонта предполагается несколько

ребалансировок.

За рубежом исследования многошаговых задач портфельной оптимиза-

ции проводятся, как правило, с использованием математического ожидания

от некоторой целевой функции в качестве критерия. Так, в [1] в качестве

критерия использовалась взвешенная дисперсия, а именно сумма дисперсий

капиталов, вкладываемых в произвольное число активов, в каждый момент

времени инвестиционного горизонта с некоторыми заданными весами; сред-

ний капитал в терминальный момент времени должен быть выше некото-

рой заданной отметки. Априорно выбранные управления, зависящие от мо-

мента времени, корректировались линейно в зависимости от того, насколько

реализация доходностей в прошлый момент времени отличается от средних

¹ Работа выполнена при поддержке Российского фонда фундаментальных исследований

(проект № 20-37-70022 Стабильность).

доходностей. В [2] было найдено оптимальное аналитическое решение при

использовании экспоненциальной функции полезности, а доходности подчи-

нялись авторегрессии первого порядка с гауссовским белым шумом. А в [3]

предлагались процедуры поиска оптимального управления для различных

функций полезности, в том числе логарифмической и степенной. В [4] рас-

сматривалась многошаговая задача с критерием в виде суммы сверток сред-

него дохода, дисперсии дохода, а также транзакционных издержек в каждый

момент ребалансировки с управлениями, выбираемыми в классе программ-

ных стратегий: для некоторых частных случаев транзакционных издержек

находились оптимальные стратегии или устанавливались их свойства.

В России авторы фокусируются, как правило, на вероятностном или кван-

тильном критериях для формирования портфеля ценных бумаг. Для нахож-

дения оптимального позиционного управления в таких задачах используют

соотношения метода динамического программирования [5]. В силу трудоем-

кости нахождения аналитических выражений функций Беллмана получение

оптимального решения возможно лишь в очень ограниченном числе случа-

ев: в [6] рассматривалась двухшаговая задача с вероятностным критерием,

в которой на каждом шаге был один актив, имеющий нулевую дисперсию

доходности, так называемый безрисковый, и один рисковый актив, имеющий

равномерное на отрезке [-1, A] распределение доходности; в [7] рассматрива-

лась двухшаговая задача с вероятностным критерием, в которой на каждом

шаге был один рисковый актив с равномерным распределением на отрезке

[-1, A] доходности, а другой рисковый актив имел доходность, равномерно

распределенную на отрезке [-1, B]. В связи с ограниченностью в возможно-

сти получения оптимального управления найден целый спектр приближен-

ных к оптимальным управлений в задачах с различной постановкой. В [8] на

основе доверительного метода было найдено приближенное решение в двух-

шаговой задаче с квантильным критерием, одним безрисковым активом и

одним рисковым, имеющим усеченное нормальное распределение доходности

активом на каждом шаге. В [9] также на основе доверительного метода был

предложен алгоритм получения приближенного управления в многошаговой

задаче с квантильным критерием, одним безрисковым и одним рисковым ак-

тивом, имеющим плотность доходности с носителем [-1, A] со специальными

ограничениями на форму плотности, на каждом шаге. В [10] на основе ис-

пользования кусочно-постоянного управления был предложен алгоритм на-

хождения приближенного управления в двухшаговой задаче с вероятностным

критерием и произвольным количеством рисковых активов с произвольным

финитным распределением на каждом шаге. С использованием полученных

в [11] оценок функций Беллмана в [12] обосновывалось использование так

называемый рисковой стратегии, оказавшейся асимптотически оптимальной

в многошаговой задаче с вероятностным критерием. В [13] предлагалось по-

строенное на основе оптимального решения из [6] приближенное управление

в многошаговой задаче с вероятностным критерием, одним безрисковым ак-

тивом и одним рисковым активом, имеющим равномерное на отрезке [-1, A]

распределение доходности. Таким образом, разработка универсального ал-

горитма поиска приближенного к оптимальному решения в многошаговой

задаче с вероятностным критерием является крайне актуальной задачей и

составляет предмет настоящей статьи.

В настоящей работе исследуется многошаговая задача портфельной опти-

мизации с одним безрисковым активом и одним рисковым активом, имею-

щим финитную плотность доходности, на каждом шаге. Для формирова-

ния управления используется вероятностный критерий. С использовани-

ем формулы полной вероятности и выбора управления в классе кусочно-

постоянных управлений предлагается приближенное к оптимальному пози-

ционному управление. Рассматривается содержательный пример, в котором

проводится исследование различных стратегий и демонстрируется преиму-

щество предлагаемого управления над известными универсальными управ-

лениями.

2. Постановка задачи

Рассмотрим многошаговую задачу портфельной оптимизации с безриско-

вым активом, имеющим детерминированную доходность b₀, и одним риско-

вым активом (например, некоторой акцией или фондовым индексом в целом),

имеющим на t-м шаге случайную доходность X_t, t = 1, T , где T - количество

шагов, причем T ∈ {3, 4, . . .}. Будем предполагать, что случайные величины

X₁,X₂,... ,X_T являются независимыми в совокупности. Будем рассматри-

вать абсолютно непрерывные случайные величины X₁, X₂, . . . , X_T , имеющие

финитный носитель, т.е.

{

}

inf

x ∈ R¹ : FXt(x) > 0

= a_t, t = 1,T,

{

}

sup

x ∈ R¹ : FXt(x) < 1

= b_t, t = 1,T,

где a_t и b_t - некоторые числа. При этом ∀t ∈ {1, . . . , T } должно выполняться

-1 ≤ a_t < b₀ < b_t. Неравенства -1 ≤ a_t должны быть выполнены, поскольку

цена продажи актива не может быть отрицательной, нарушение неравенств

a_t < b₀ приведет к тому, что на каком-то шаге/каких-то шагах использование

безрискового актива бессмысленно в силу того, что минимальная доходность

рискового актива будет выше. Нарушение неравенств b₀ < b_t приведет к то-

му, что на каком-то шаге/каких-то шагах использование рискового актива

бесполезно, так как его максимальная доходность не превышает доходность

безрискового актива. Пусть начальный капитал инвестора известен и состав-

ляет C₁. Пусть u_0t - доля капитала инвестора, вкладываемого в безрисковый

актив на t-м шаге, а u_1t - доля капитала инвестора, вкладываемого в рис-

ковый актив на t-м шаге. Будем предполагать, что операции ¾short-sales¿

невозможны, т.е. нельзя брать деньги в долг. С учетом данного ограничения

= col(u_0t, u_1t) выбираются из множества

{

}

U =

(x, y)^T : x + y = 1, x ≥ 0, y ≥ 0

А динамика капитала инвестора описывается соотношением

(1)

C_t+1 = C_t(1 + u_0tb₀ + u_1tX_t

t = 1,T,

где C_t+1 - капитал по окончании t-го шага. Отметим, по постановке задачи

капитал не может оказаться отрицательным.

Пусть ϕ - желаемый инвестором уровень капитала в терминальный мо-

мент времени. Очевидно, что в зависимости от выбранного управления -

структуры инвестиционного портфеля - на каждом шаге вероятность дости-

жения или превышения порога ϕ различна. Будем выбирать управление в

классе позиционных стратегий, т.е. u_t = u_t(C_t), t = 2, T . Управление на пер-

вом шаге в силу известности C₁ является программным. Целью управления

портфелем ценных бумаг является максимизация вероятности достижения

или превышения капиталом инвестора желаемого порога ϕ. Для этой цели

зададим функционал вероятности

(2)

P_ϕ(u(·)) = P (C_T+1

(u(·), X) ≥ ϕ) ,

где

X = col(X₁,X₂,...,X_T), а u(·) = col(u₁,u₂(·),...,u_T(·)).

Поставим задачу

(3)

P_ϕ(u(·)) →

max

u₁∈U,u₂(·)∈U₂,...,u_T (·)∈U_T

где U_t - множество измеримых функций u_t(·), имеющих значения на множе-

стве U. В силу того, что для непосредственного решения задачи (3) требу-

ется проводить поиск в функциональном пространстве, задачу (3) решают с

использованием метода динамического программирования Беллмана, пред-

варительно проверяя измеримость и оптимальность получаемых стратегий

с помощью ряда условий из [14]. Данные условия для рассматриваемой по-

становки задачи выполнены. Однако использование соотношений метода ди-

намического программирования для вероятностного критерия практически

невозможно в силу трудностей, возникающих в получении аналитического

вида функций Беллмана. В этой связи в [10, 15] было предложено сузить

класс допустимых управлений до класса кусочно-постоянных управлений.

Воспользуемся этим подходом и здесь.

Вначале введем разбиение множества значений состояния системы (капи-

тала инвестора) C_t к началу t-го шага, t = 2, T :

s_t = s^1t ∪ s^2t ∪ ... ∪ sntt,

где

s^1t = [s_t1,s_t2) , s^2t = [s_t2,s_t3) , ... , snt-1t = [stnt-1,stnt ), stt = [stnt,stnt+1] ,

где

∏

s_t1 = C₁

(1 + a_k), stnt+1 = C1

(1 + b_k),

k=1

stnt+1 - st1

s_ti = s_t1 + (i - 1)

i = 2,n_t.

n_t

Отметим, что разбиение s_t может быть и другим, а равномерная длина

промежутков s^it выбрана для простоты, t = 2, T , i = 1, n_t.

Управление на каждом шаге за исключением первого, являющегося про-

граммным из-за известности C₁, будет иметь вид



(u10t, u11t)T, Ct ∈ s1t,



(u^20t, u^21t)^T, C_t ∈ s^2t,

u_t(C_t,s_t) =



..,

.

)^T, C_t ∈ sntt.

Введя обозначение

= col(u₁, u₂(·, s₂), . . . , u_T (·, s_T )),

сформулируем задачу поиска оптимального кусочно-постоянного управления

(

)

(4)

u^ϕ1,u^ϕ2(·,s₂),... ,u^ϕT(·,s_T )

= arg

max

P_ϕ(u_s

(·)).

u₁∈U,u₂(·,s₂)∈U,...,u_T (·,s_T )∈U

3. Нахождение приближенного решения

Уже при T = 2 поиск аналитического решения в задаче (4) затрудните-

лен. Приходится строить [10, 15] нижнюю оценку функционала вероятно-

сти P_ϕ(u_s(·)) (функционала (2) в классе кусочно-постоянных управлений).

Однако согласно [16] имеется сходимость максимального значения конструи-

руемой в [10, 15] нижней оценки к значению вероятностного критерия на оп-

тимальной позиционной стратегии при устремлении мелкости разбиения s₂

к нулю. В этой связи воспользуемся аналогичным подходом и при решении

многошаговой задачи.

На последнем шаге, следуя [15], имеем

∑

(

)

P_ϕ(u_s(·)) =

C_T+1 ≥ ϕ,C_T ∈ s^iT

≥

i=1

(5)

∑

(

)

(

)

≥ P

s_Ti(1 + u^i0T b₀ + u^i1T X_T ) ≥ ϕ

C_T ∈ s^iT

i=1

Так как задача

(4)

- задача максимизации функционала вероятности

P_ϕ(u_s(·)), то полученную в (5) оцен)у также нужно максимизировать. По

определению вероятности P

C_T ∈ s^iT

≥ 0, поэтому нужно решить задачи

(

)

(6)

P^∗Ti =

max

s_Ti(1 + u^i0T b₀ + u^i1T X_T ) ≥ ϕ

(u^i0T ,u^i1T )^T∈U

(

)

(7)

(ũ^i∗0T, ũ^i∗1T)^T = arg

max

s_Ti(1 + u^i0T b₀ + u^i1T X_T ) ≥ ϕ

(u^i0T ,u^i1T )^T∈U

i = 1,n_T. Решение в задачах (6) и (7) найдено в [17] и имеет вид



1,

s_Ti(1 + b₀) ≥ ϕ,

(

)

P^∗

1 - FXT

-1

s_Ti(1 + b₀) < ϕ,

s_Ti

{

0, s_Ti(1 + b₀) ≥ ϕ,

ũ^i∗1T =

1, s_Ti(1 + b₀) < ϕ,

ũ^i∗0T = 1 - ũ^i∗1T , i = 1,n_T . Составив вектор-функцию





(ũ^1∗0T,ũ^1∗1T)^T,

C_T ∈ s^1T ,



(ũ^2∗0T,ũ^2∗1T)^T,

C_T ∈ s^2T ,

(8)

ũ^ϕT(C_T ,s_T ) =



..,

...,

.

(ũnT∗0T, ũnT∗1T)^T, C_T ∈ snTT^,

будем использовать ее как приближенное решение задачи (4) на последнем

шаге, т.е. как приближение функции u^ϕT (·, s_T ). С использованием коэффи-

циентов P^∗Ti получим следующую нижнюю оценку максимального значения

функционала вероятности P_ϕ(u_s(·))

∑

(

)

(9)

= P^∗TiP

C_T ∈ s^iT

i=1

Принимая в расчет формулу полной вероятности, получаем

P^T-1ϕ(u₁,u₂(·,s₂),... ,u_T-1(·,s_T-1)) =

∑

n_T-1∑

(

)

P^∗TiP C_T ∈ s^iT , C_T-1 ∈ s^k

T-1

i=1 k=1

∑

n_T-1∑

(

)

P^∗TiP C_T-1(1 + u^k0T-1b₀ + u^k1T-1X_T-1) ∈ s^iT , C_T-1 ∈ s^k

T-1

i=1 k=1

К сожалению, получение нижней оценки последнего выражения приводит впо-

следствии к решению минимаксной задачи с нелинейной целевой функцией,

поэтому ограничимся построением нового функционал

P^T-1ϕ(u₁,u₂(·, s₂),...

...,u_T-1(·, s_T-1)), приближенно равного по значениям функционалу

P^T-1ϕ(u₁,u₂(·, s₂),... ,u_T-1(·, s_T-1)), т.е.

P^T-1ϕ(u₁,u₂(·,s₂),... ,u_T-1(·,s_T-1)) ≈

∑

n_T-1∑

(

)

^def=

P^∗TiP s_T-1k(1 + u^k0T-1b₀ + u^k1T-1X_T-1) ∈ s^iT ,C_T-1 ∈ s^k

T-1

i=1 k=1

Учтя, что случайные величины X₁, X₂, . . . , X_T-1 независимы, и поменяв по-

рядок суммирования в последнем выражении, получим

P^T-1ϕ(u₁,u₂(·,s₂),... ,u_T-1(·,s_T-1)) =

∑

n_T-1∑

(

) (

)

P^∗TiP s_T-1k(1 + u^k0T-1b₀ + u^k1T-1X_T-1) ∈ sⁱ

P C_T-1 ∈s^k

T-1

i=1 k=1

n_T-1∑

(

∑

(

)

= P C_T-1 ∈s^k

P^∗TiP s_T-1k(1 + u^k0T-1b₀ + u^k1T-1X_T-1) ∈ sⁱ

T-1

k=1

i=1

Для нахождения приближенного решения задачи на предпоследнем шаге (4)

максимизируем функционал

(

)

P^T-1ϕ u₁,u₂(·, s₂),... ,u_T-1(·, s_T-1)

Так как управления на различных шагах не зависят друг от друга, в силу

конструкции множества U необходимо решить задачи

∑

(

( (

)

= P^∗

P s_T-1k

1-u^k

1T -1

b₀ +

i=1

)

+u^k

X_T-1

∈sⁱ

→ max

1T -1

0≤u^k1T-1≤1

k = 1,n_T-1. Имеет место равенство



∑

(

)



P^∗TiP

s_T-1k (1 + b₀) ∈ s^iT

u^k1T-1 = 0,



i=1



Gk,sT-1(u^k1T-1) =

(

( (

)

∑



P^∗

P s_T-1k

1+ 1-u^k

b₀ + u^k

X_T-1

∈sⁱ

1T -1



ⁱ

u^k1T-1 > 0.

Поскольку последняя функция задается кусочно, на открытом множестве,

то будем искать приближенное решение в задаче (10), сравнивая значение

последней функции в точке u^k1T-1 = 0 и максимальное значение последней

функции на отрезке ε ≤ u^k1T-1 ≤ 1, где ε > 0 - некоторое малое число. Таким

образом, обозначив

∑

(

)

= P^∗TiP

s_T-1k(1 + b₀) ∈ s^iT

i=1

∑

(

( (

)

= max

P^∗

P s_T-1k

1-u^k

b₀ + u^k

X_T-1

∈s

1T -1

ε≤u^k

≤1

1T -1

i=1

в качестве приближенного решения в задаче (4), т.е. управления u^ϕT-1(·, s_T-1),

выберем





(ũ^1∗0T-1, ũ^1∗1T-1)^T,

C_T-1 ∈ s^1T-1,



(ũ^2∗0T-1, ũ^2∗1T-1)^T,

C_T-1 ∈ s^2T-1,

ũ^ϕT-1(C_T-1,s_T-1) =



..,

.

−1

где



0,

P^kT-1

PkT-1 и

P^kT-1 = 0,



(

)



∑

arg max

P^∗

P s_T-1k

1 + b0 + uk1T-1 (XT-1 - b₀)

∈sⁱ

ũ^k∗1T-1 =

ε≤u^k

≤1

1T -1

i=1



P^kT-1

P^kT-1,



1,

P^kT-1

PkT-1 и

P^kT-1 = 0,

k = 1,n_T-1. Прокомментируем наличие единицы в ũ^k∗1T-1: равенство величин

P^kT-1

P^kT-1 нулю означает, что функция G^k,sT-1(u^k1T-1) на множестве {0} ∪ [ε,1]

тождественно равна нулю, так как по определению вероятности функция

Gk,sT-1(u^k1T-1) неотрицательна. Это означает, что все управления одинаково

плохи, а значит, можно выбрать наиболее рискованное.

= max

P^kT-1

P^kT-1}, получим следующую оцен-

ку максимального значения функционала вероятности P_ϕ(u_s(·))

n_T-1∑

(

)

(11)

= P^∗T-1kP C_T-1 ∈s^k

T-1

k=1

Отметим, что структура функционалов (9) и (11) идентична. А значит,

если двигаться в обратном времени, аналогично для шагов t = T - 1, . . . , 2

получаются следующие приближенные к оптимальным u^ϕt(·, s_t) стратегии





(ũ^1∗0t, ũ^1∗1t)^T,

C_t ∈ s^1t,



(ũ^2∗0t, ũ^2∗1t)^T,

C_t ∈ s^2t,

(12)

ũ^ϕt(C_t,s_t) =



..,

.

(ũnt∗0t, ũnt∗1t)^T, C_t ∈ sntt,

где



0,

P^kt

P^kt = 0,





∑

(

)

ũ^k∗1t =

arg max

P^∗

P s_tk

1+b₀-u^k1tb₀+u^k

X_t ∈ sⁱ

P^kt

P^kt,

t+1i

t+1



ε≤u^k

≤1



i=1



P^kt

P^kt = 0,

ũ^k∗0t = 1 - ũ^k∗1t

и где, в свою очередь,

∑

(

)

= P^∗t+1iP

s_tk (1 + b₀) ∈ s^it+1

i=1

n_t+1∑

(

)

= max

P^∗

P s_tk

1+b₀ -u^k1tb₀ +u^k

X_t

∈s

t+1i

t+1

ε≤u^k

≤1

i=1

{

}

= max

P^kt

P^k

а k = 1,n_t. Отметим, что при 0 < ε ≤ u^k1t ≤ 1 в силу непрерывности случайной

величины X_t имеет место

(13)

( (

)

P s_tk

1+b₀ -u^k1tb₀ +u^k

X_t

∈sⁱ

t+1

(

)

=P s_t+1i ≤s_tk

1+b₀ -u^k1tb₀ +u^k

X_t

≤s_t+1i+1

)

(s_t+1i+1/s_tk - 1 - b₀ + u^k1tb₀

(s_t+1i/s_tk - 1 - b₀ + u^k1tb₀

=FXt

-FXt

u^k1t

u^k

когда s_tk > 0, k = 1, n_t, i = 1, n_t+1. Когда s_tk = 0, а s_t+1i = 0, то выражение (13)

равно нулю, в случае s_tk = s_t+1i = 0 выражение (13) равно единице, k = 1, n_t,

i = 1,n_t+1.

Для отыскания стратегии первого шага нужно решить задачу

∑

(

)

(14)

P^∗2iP

C₂ ∈ sⁱ²

→

max

01≥0,u11≥0,u01+u11=1

i=1

Поскольку критериальная функции в последней задаче

∑

(

)

P^∗2iP

C₂ ∈ sⁱ²

i=1

∑

(

)

= P^∗2iP

C₁ (1 + u₀₁b₀ + u₁₁X₁) ∈ sⁱ²

i=1



∑

(

)



P^∗2iP

C₁(1 + b₀) ∈ sⁱ²

u₁₁ = 0,



i=1

=∑

(

)



C₁ (1 + b₀ - u₁₁b₀ + u₁₁X₁) ∈ sⁱ²

u₁₁ > 0



i=1

задается кусочно, на открытом множестве, то найдем приближенное решение

задачи (14). Для этого введем

∑

(

)

P₁ = P^∗2iP

C₁(1 + b₀) ∈ sⁱ

i=1

и найдем

∑

(

)

P₁ = max

P^∗2iP

C₁ (1 + b₀ - u₁₁b₀ + u₁₁X₁) ∈ sⁱ²

ε≤u₁₁≤1

i=1

Используя величин

P₁

P₁, доопределим приближенное к оптимальному

управление, получаемое с использованием соотношений (8) и (12), в задаче (4)

на первом шаге:

(15)

ũ^ϕ1 = (ũ^∗01, ũ^∗11)^T,

где



0,

P₁

P₁,



ũ^∗11 =

∑

(

)



rg max

P^∗2iP

C₁ (1 + b₀ - u₁₁b₀ + u₁₁X₁) ∈ sⁱ²

P₁

P₁,

a

ε≤u₁₁≤1

i=1

ũ^∗01 = 1 - ũ^∗11.

При u₁₁ ≥ ε > 0 имеет место равенство

∑

(

)

P^∗2iP

C₁ (1 + b₀ - u₁₁b₀ + u₁₁X₁) ∈ sⁱ²

i=1

∑

= P^∗2iP (s_2i ≤ C1 (1 + b₀ - u₁₁b₀ + u₁₁X₁) ≤ s_2i+1) =

i=1

( (

)

))

∑

s_2i+1/C₁ -1-b₀ +u₁₁b₀

(s_2i/C1 -1-b0 +u₁₁b₀

P^∗

FX₁

-FX1

u₁₁

i=1

В этой связи заключаем, что для поиска предлагаемого по формулам (8),

(12), (15) приближенного к оптимальному управления, называемого в даль-

нейшем вероятностным, не нужно проводить оптимизацию в функциональ-

ном пространстве или вычислять функцию Беллмана на каждом шаге, необ-

ходимо лишь решить ряд одномерных задач условной нелинейной оптими-

зации. При этом оценкой вероятности превышения капиталом инвестора за-

планированного порога ϕ при использовании такой стратегии выступает ве-

личина P^∗1 = max

P₁

P₁}, которая является оценкой максимального значе-

ния функционала P_ϕ(u_s(·)). Данную величину можно уточнить, используя

статистическую оценку исследуемой вероятности.

Отметим, что исследование сходимости предлагаемого управления к точ-

ному позиционному при уменьшении мелкости разбиений s_t, t = 2, T , пред-

ставляет отдельный интерес, однако затруднительно ввиду разрывности

функций Беллмана для данной постановки задачи.

4. Пример

Пусть C₁ = 1, ϕ = 1,5, b₀ = 0,03, ε = 10^-6, n₁ = n₂ = . . . = n_T = N, где N -

некоторое число, а T = 10. Предположим также, что инвестиционный порт-

фель ребалансируется каждый год. Сравним предлагаемую многошаговую

вероятностную стратегию (8), (12), (15) с известными: рисковой стратегией

{

(1, 0)^T, ϕ ≤ Ct(1 + b0)T-t+1,

u^Rt(C_t) =

(0, 1)^T, ϕ > C_t(1 + b₀)^T-t+1

из [17], достоинства которой обсуждались в [12], и логарифмической стра-

тегией (стратегией Келли) [18-20], обеспечивающей максимальную среднюю

скорость роста капитала [17], являющейся решением задачи

u^Lt = (u^L0t,u^L1t)^T = arg

max

M [ln(1 + u_0tb₀ + u_1tX_t)] ,

u_0t+u_1t=1,u_0t≥0,u_1t≥0

t = 1,...,T. Будем предполагать, что случайные величины X₁,X₂,...,X_T

одинаково распределены. Рассмотрим несколько случаев: когда X_t ∼ R[a, b],

т.е. когда плотность случайной величины X_t имеет вид



1

a ≤ x ≤ b,

fXt(x) =

b-a

0

иначе,

и когда X_t ∼ N (m, σ²), т.е. когда плотность случайной величины X_t имеет

вид



{

}



(x - m)²

√

exp

m - 5σ ≤ x ≤ m + 5σ,

(16)

fXt(x) =

2πσ²

2σ²



иначе,

где константа c = 1/0,9999994 определяется из условия нормировки плот-

ности, а m - 5σ ≥ -1 для соответствия постановке задачи. Плотность (16)

является плотностью усеченного нормального распределения, t = 1, T . Выбор

именно такого усечения связан с тем фактом, что для случайной величины

Y ∼ N(m,σ²) с любыми значениями параметров m и σ² имеет место равен-

ство P{m - 5σ ≤ Y ≤ m + 5σ} = 0,9999994. А это значит, что построенное

таким образом усечение оставляет плотность симметричной и ¾отбрасывает¿

диапазоны значений исходной неусеченной случайной величины, вероятность

попадания в которые ничтожно мала. В силу введенного в примере предпо-

ложения об одинаковой распределенности случайных величин X₁, X₂, . . . , X_T

далее для краткости будем говорить только о распределении случайной вели-

чины X₁, опуская, что случайные величины X₂, . . . , X_T распределены по тому

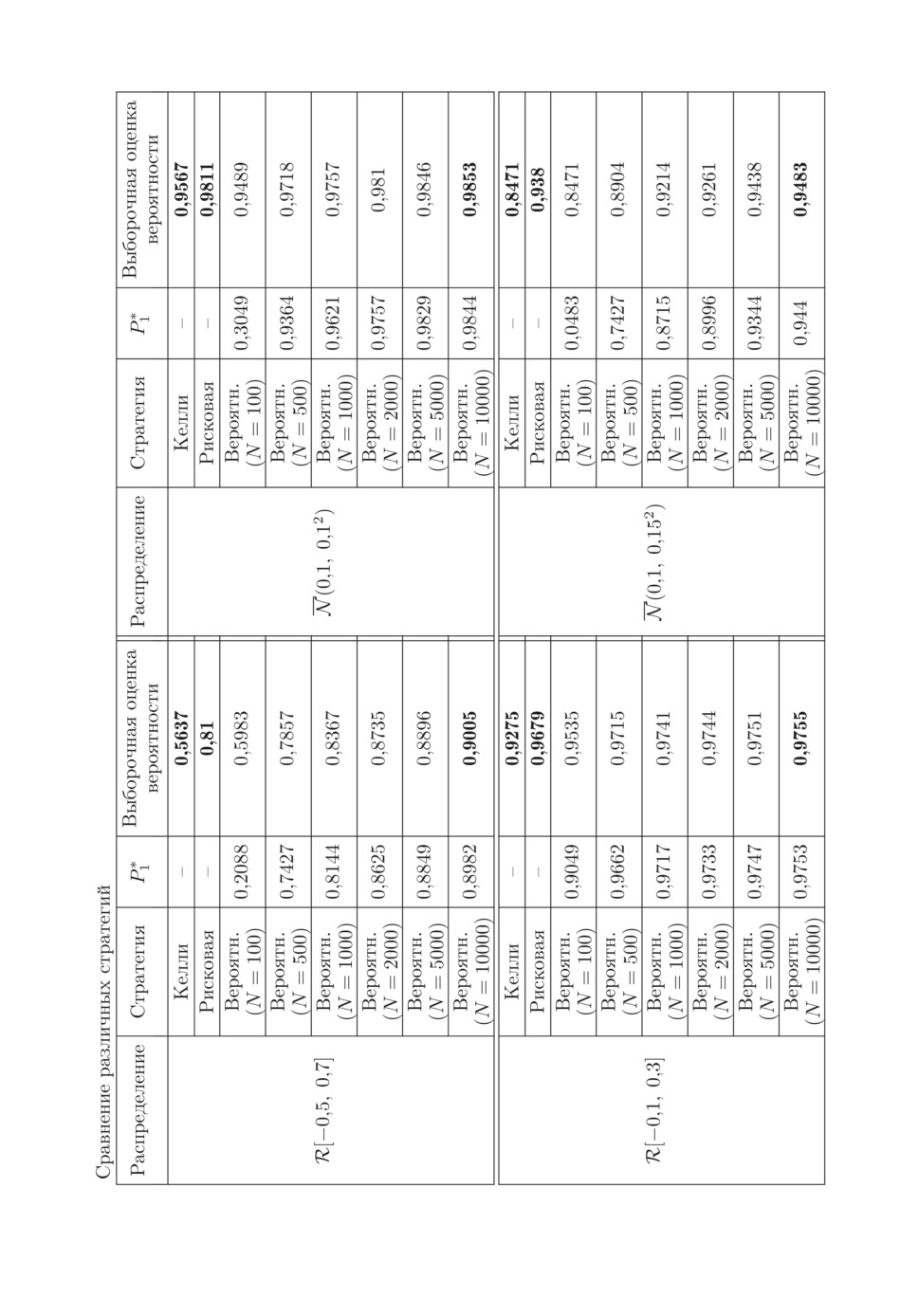
же закону. Для сравнения указанных стратегий в каждом из рассматривае-

мых случаев найдем 5 · 10⁶ реализаций случайного вектора X и с помощью

выборочной оценки вероятности оценим вероятность события P{C_T+1 ≥ ϕ}

на этих стратегиях.

Во всех рассмотренных случаях математическое ожидание случайной ве-

личины X₁ составляет 0,1, что примерно соответствует средней годовой

доходности индекса S & P 500, оцененной по данным за последние 30 лет,

и предлагается в качестве примера годовой доходности в [21]. Отличием

же рассмотренных случаев друг от друга выступает форма плотности рас-

пределения случайной величины X₁, а также их дисперсия и, как след-

ствие, коэффициент вариации, т.е. отношение среднеквадратического откло-

нения к математическому ожиданию. Отметим также, что среднеквадра-

тичное отклонение доходности индекса S & P 500, оцененной по данным за

последние 30 лет, составляет порядка 0,15. Таким образом, ¾естественное¿

значение коэффициента вариации на основе данных по индексу S & P 500

составляет 1,5.

Как следует из таблицы, стратегия Келли существенно уступает риско-

вой и вероятностной (при больших значениях N) в терминах выборочной

оценки вероятности P{C_T+1 ≥ ϕ}. C ростом величины N во всех рассмот-

ренных случаях растет величина P^∗1, при этом растет и выборочная оценка

вероятности P{C_T+1 ≥ ϕ} при использовании вероятностной стратегии. При

увеличении N наблюдается сближение P^∗1 и выборочной оценки вероятно-

сти P{C_T+1 ≥ ϕ}. В этой связи по значениям P^∗1 и выборочной оценки веро-

ятности P{C_T+1 ≥ ϕ} можно сделать вывод, что дальнейшее увеличение N

для случаев X₁ ∼ R[-0,1, 0,3] и X₁ ∼ N (0,1, 0,1²) не приведет к существен-

ному увеличению P^∗1 и оценки вероятности P{C_T+1 ≥ ϕ} на вероятностной

стратегии. В то же время увеличение N для случаев X₁ ∼ R[-0,5, 0,7] и

X₁ ∼ N(0,1, 0,15²) позволит сформировать еще более качественное управле-

ние в терминах оценки вероятности P{C_T+1 ≥ ϕ}. Во всех рассмотренных

случаях (уже при N = 5000) вероятностная стратегия лучше рисковой в тер-

минах оценки вероятности P{C_T+1 ≥ ϕ}. При этом с увеличением коэффи-

циента вариации разница между выборочной оценкой вероятности на веро-

ятностной и рисковой стратегиях растет, достигая практически 0,1 в случае

X₁ ∼ R[-0,5, 0,7].

В статьях [6, 7, 22], связанных или посвященных отысканию оптималь-

ной инвестиционной стратегии в задаче с вероятностным и логарифмическим

критерием использовалось равномерное распределение доходности с носите-

лем [-1, A]. Отметим, что хотя такой случай и малореален на практике, но

получаемое с учетом такого распределения управление полезно, когда досто-

верно известна только средняя доходность. Заметим, что использование тако-

го носителя учитывает случай возможного банкротства компании-эмитента

рискового актива. Более того, как отмечено в [17, 23], равномерное распреде-

ление при минимальных предположениях о законе распределения случайных

величин в целевой функции оказывается наихудшим с точки зрения величи-

ны вероятностного критерия. Таким образом, получаемое управление при та-

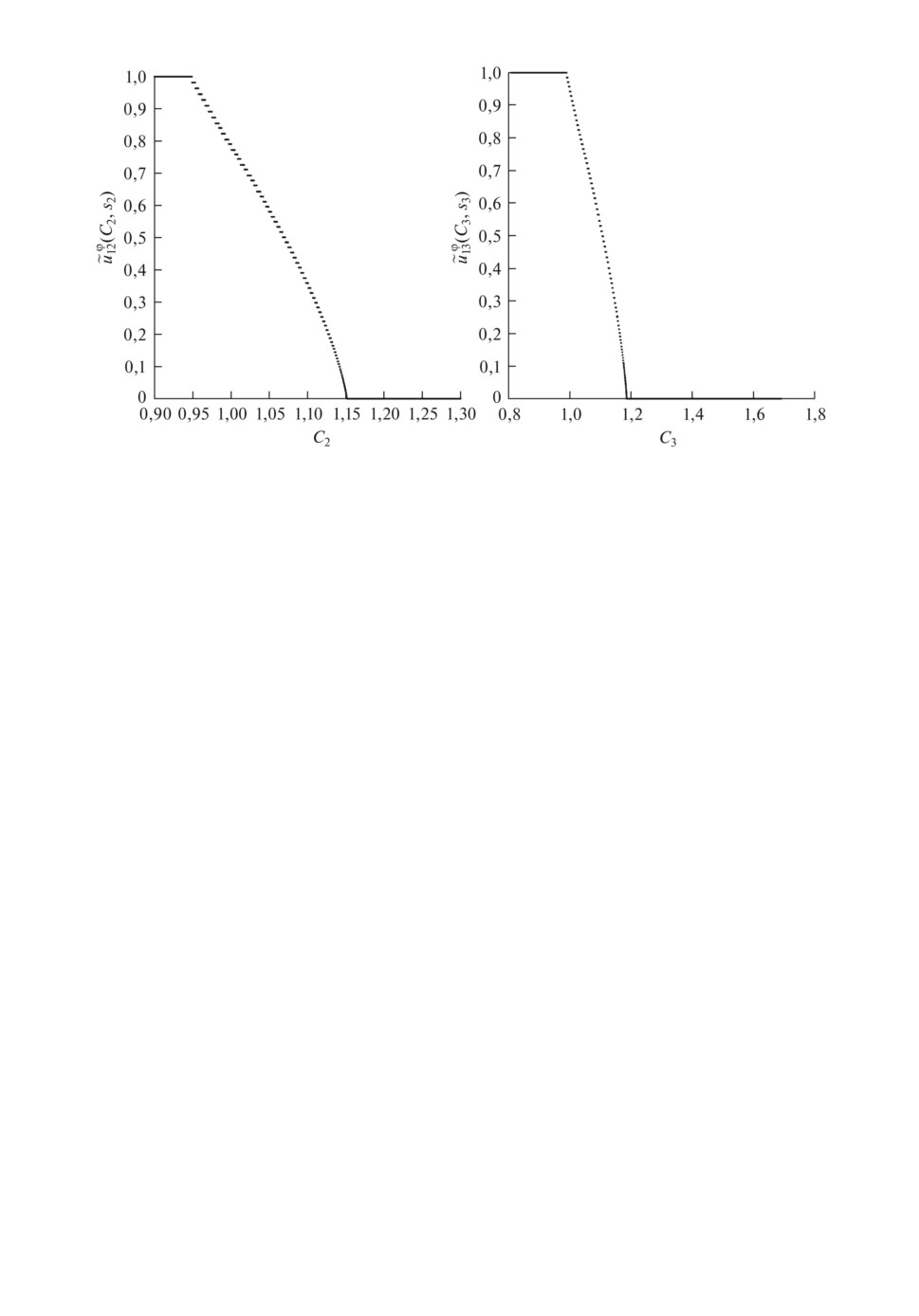
Вид второй компоненты вероятностной стратегии на втором и третьем шагах

для случая X₁ ∼ R[-0,1, 0,3], . . . , X_T ∼ R[-0,1, 0,3].

ком носителе интересно не только с теоретической точки зрения, но и полезно

с точки зрения получения наилучшей стратегии при недостатке информации.

При A = 1,2 оказалось, что выборочная оценка вероятности P{C_T+1 ≥ ϕ} на

5 · 10⁶ реализациях случайного вектора X для предлагаемой вероятностной

стратегии при N = 10000 составляет 0,8253 (при P^∗1 = 0,8165), что существен-

но выше выборочной оценки вероятности для рисковой стратегии, составляю-

щей в этом случае 0,6953.

Таким образом, в условиях ¾естественной¿ неопределенности (коэффици-

ента вариации, примерно равного или меньшего 1,5) вероятностная страте-

гия несколько лучше рисковой по значению выборочной оценки вероятности

P{C_T+1 ≥ ϕ}, в случае же существенной неопределенности предлагаемая ве-

роятностная стратегия значительно превосходит рисковую.

Теперь рассмотрим вид второй компоненты вероятностной стратегии, т.е.

доли капитала инвестора, вкладываемого в рисковой актив, при N = 10000

на некоторых шагах для случая X₁ ∼ R[-0,1, 0,3].

Как видно из рисунка вторая компонента вероятностной стратегии далека

от релейного типа управления, доставляемого рисковой стратегией. Имеется

¾нелинейный¿ участок, описание которого простыми функциями (линейной,

параболической, логарифмической) вряд ли возможно, что еще раз доказы-

вает полезность предлагаемой вероятностной стратегии.

Результаты получены на персональном компьютере (Intel Core i5 4690,

3.5 GHz, 8 GB DDR3 RAM). Время вычислений для N = 10000 составило от

одного до трех часов в зависимости от используемого распределения доходно-

стей, что доказывает применимость на практике разработанного алгоритма.

При этом было задействовано только одно ядро компьютера, распараллели-

вание не применялось, а значит, процесс вычислений может быть еще суще-

ственно ускорен.

5. Заключение

В работе было предложено новое позиционное управление, приближенное

к оптимальному в многошаговой задаче портфельной оптимизации с веро-

ятностным критерием. Соотношения, на основе которых построено предла-

гаемое управление, получены на основе полной вероятности и формирова-

ния управления в классе кусочно-постоянных управлений. На каждом шаге

предлагаемое управление получается исходя из решения ряда задач одномер-

ной условной нелинейной оптимизации. В рассмотренном примере продемон-

стрировано преимущество предлагаемого управления над известными уни-

версальными управлениями. Рассмотренный подход и предлагаемое управ-

ление можно обобщить на случай произвольного количества рисковых ак-

тивов на каждом шаге, не отыскивая при поиске вероятностной стратегии

на каждом шаге детерминированный эквивалент, как в настоящей статье, а,

например, используя дискретизацию вероятностной меры, что является пред-

метом дальнейших исследований, как и исследование статистических свойств

предлагаемого управления.

СПИСОК ЛИТЕРАТУРЫ

Calafiore G. Multi-period Portfolio Optimization with Linear Control Policies //

Automatica. 2008. V. 44. No. 10. P. 2463-2473.

Bodnar T., Parolya N., Schmid W. On the Exact Solution of the Multi-period Port-

folio Choice Problem for an Exponential Utility under Return Predictability // Eur.

J. Oper. Res. 2015. V. 246. No. 2. P. 528-542.

Canakoglu E., Ozekici S. Portfolio Selection in Stochastic Markets with HARA Util-

ity Functions // Eur. J. Oper. Res. 2010. V. 201. No. 2. P. 520-536.

Mei X., DeMiguel V., Nogales F.J. Multiperiod Portfolio Optimization with Mul-

tiple Risky Assets and General Transaction Costs // J. Bank. & Fin. 2016. V. 69.

P. 108-120.

Кан Ю.С. Оптимизация управления по квантильному критерию // АиТ. 2001.

№ 5. С. 77-88.

Kan Yu.S. Control Optimization by the Quantile Criterion // Autom. Remote Con-

trol. 2001. V. 62. No. 5. P. 746-757.

Григорьев П.В., Кан Ю.С. Оптимальное управление по квантильному критерию

портфелем ценных бумаг // АиТ. 2004. № 2. С. 179-197.

Grigor’ev V.P., Kan Yu.S. Optimal Control of the Investment Portfolio with Respect

to the Quantile Criterion // Autom. Remote Control. 2004. V. 65. No. 2. P. 319-336.

Кибзун А.И., Игнатов А.Н. Двухшаговая задача формирования портфеля цен-

ных бумаг из двух рисковых активов по вероятностному критерию // АиТ. 2015.

№ 7. С. 78-100.

Kibzun A.I., Ignatov A.N. The Two-step Problem of Investment Portfolio Selection

from Two Risk Assets via the Probability Criterion // Autom. Remote Control. 2015.

V. 76. No. 7. P. 1201-1220.

Кибзун А.И., Кузнецов Е.А. Оптимальное управление по квантильному крите-

рию портфелем ценных бумаг // АиТ. 2001. № 9. С. 101-113.

Kibzun A.I., Kuznetsov E.A. Optimal Control of Discretionary Portfolio // Autom.

Remote Control. 2001. V. 64. No. 9. P. 1489-1501.

Кибзун А.И., Кузнецов Е.А. Позиционная стратегия формирования портфеля

ценных бумаг // АиТ. 2003. № 1. С. 151-166.

Kibzun A.I., Kuznetsov E.A. Positional Strategy of Forming the Investment Portfo-

lio // Autom. Remote Control. 2003. V. 64. No. 1. P. 138-152.

10.

Кибзун А.И., Игнатов А.Н. Сведение двухшаговой задачи стохастического про-

граммирования с билинейной функцией дохода к задаче смешанного целочис-

ленного линейного программирования // АиТ. 2016. № 12. C. 89-111.

Kibzun A.I., Ignatov A.N. Reduction of the Two-step Problem of Stochastic Optimal

Control with Bilinear Model to the Problem of Mixed Integer Linear Programming //

Autom. Remote Control. 2016. V. 77. No. 12. P. 2175-2192.

11.

Азанов В.М., Кан Ю.С. Синтез оптимальных стратегий в задачах управления

дискретными системами по вероятностному критерию // АиТ. 2017. № 6. 57-83.

Azanov V.M., Kan Yu.S. Design of Optimal Strategies in the Problems of Discrete

System Control by the Probabilistic Criterion // Autom. Remote Control. 2017.

V. 78. No. 6. P. 1006-1027.

12.

Азанов В.М., Кан Ю.С. Двухсторонняя оценка функции Беллмана в задачах

стохастического оптимального управления дискретными системами по вероят-

ностному критерию качества // АиТ. 2018. № 2. C. 3-18.

Azanov V.M., Kan Yu.S. Bilateral Estimation of the Bellman Function in the Prob-

lems of Optimal Stochastic Control of Discrete Systems by the Probabilistic Perfor-

mance Criterion // Autom. Remote Control. 2018. V. 79. No. 2. P. 203-215.

13.

Азанов В.М., Кан Ю.С. Усиленная оценка функции Беллмана в задачах стоха-

стического оптимального управления с вероятностным критерием качества //

АиТ. 2019. № 4. С. 53-69.

Azanov V.M., Kan Yu.S. Refined Estimation of the Bellman Function for Stochas-

tic Optimal Control Problems with Probabilistic Performance Criterion // Autom.

Remote Control. 2019. V. 80. No. 4. P. 634-647.

14.

Кибзун А.И., Игнатов А.Н. О существовании оптимальных стратегий в задаче

управления стохастической системой с дискретным временем по вероятностному

критерию. // АиТ. 2017. № 10. С. 139-154.

Kibzun A.I., Ignatov A.N. On the Existence of Optimal Strategies in the Control

Problem for a Stochastic Discrete Time System with Respect to the Probability

Criterion // Autom. Remote Control. 2017. V. 78. No. 10. P. 1845-1856.

15.

Ignatov A.N. The Structure of an Investment Portfolio in Two-step Problem of Opti-

mal Investment with One Risky Asset Via the Probability Criterion // Sup. Proc. 5th

Int. Conf. Analysis of Images, Soc, Networks and Texts (AIST’2016). Yekaterinburg,

Russia, April 7-9, 2016. P. 42-50.

16.

Игнатов А.Н. Синтез оптимальных стратегий в двухшаговых задачах стохасти-

ческого оптимального управления билинейной моделью с вероятностным кри-

терием // Дисс

канд. физ.-мат. наук. МАИ, Москва, 2016. 135 с.

17.

Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероят-

ностными критериями. М.: Физматлит, 2009.

18.

Kelly J.L. A New Interpretation of Information Rate // Bell Sys. Tech. J. 1956.

No. 35. P. 917-926.

19.

MacLean L.C., Thorp E.O., Zhao Y., Ziemba W.T. How Does the Fortune’s Formula

Kelly Capital Growth Model Perform? // J. Port. Man. Sum. 2011. V. 37. No. 4.

P. 96-111.

20.

Ziemba W.T., Wickson R.G. Stochastic Optimization Models in Finance. World

Scientific, 2006.