Автоматика и телемеханика, № 12, 2020
© 2020 г. Ю.С. КАН, д-р физ.-мат. наук (yu_kan@mail.ru)
(Московский авиационный институт
(национальный исследовательский университет))
РАСШИРЕНИЕ ЗАДАЧИ КВАНТИЛЬНОЙ ОПТИМИЗАЦИИ
С ЛИНЕЙНОЙ ПО СЛУЧАЙНЫМ ПАРАМЕТРАМ
ФУНКЦИЕЙ ПОТЕРЬ1
Задача стохастического программирования с квантильным критерием
исследуется в классической одноэтапной постановке в предположении,
что функция потерь линейна по случайным параметрам. Расширением
данной задачи является минимаксная задача, в которой внутренний мак-
симум берется от функции потерь по реализациям вектора случайных па-
раметров на ядре вероятностного распределения этого вектора, а внешний
минимум по оптимизируемой стратегии на заданном множестве допус-
тимых стратегий. На основе принципа расширения оптимизационных за-
дач устанавливается, что достаточным условием оптимальности решения
этой минимаксной задачи в исходной задаче с квантильным критерием
является выполнение некоторого вероятностного ограничения.
Ключевые слова: стохастическое программирование, функция квантили,
принцип расширения, ядро вероятностного распределения, вероятностное
ограничение.
DOI: 10.31857/S0005231020120041
1. Введение
Конечномерные задачи оптимизации квантильного критерия являются
частными случаями более общих оптимизационных моделей, изучаемых в
теории стохастического программирования с вероятностными ограничения-
ми. Сам квантильный критерий определяется как квантиль заданного уров-
ня вероятностного распределения некоторой функции потерь, зависящей от
оптимизируемой стратегии и вектора случайных параметров. Видимо, впер-
вые такой критерий введен в рассмотрение в [1] для учета инвестиционно-
го риска в задаче оптимизации портфеля ценных бумаг, но в [1] он не был
назван квантильным. В этой статье приведена лишь математическая фор-
мула для определения квантильного критерия и подчеркнуто, что это дове-
рительная граница для дохода портфеля. Впервые термин функция (функ-
ционал) квантили использован Райком [2], который заложил основы каче-
ственной теории стохастических оптимизационных задач с вероятностными
критериями, к числу которых относится и квантильный. Бурное развитие
теории в области оптимизационных задач с квантильным критерием связа-
но с публикацией [3], в которой было установлено, что задача минимизации
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 18-08-00595).
67
квантильного критерия эквивалентна обобщенной минимаксной задаче, в ко-
торой внутренний максимум (на самом деле точная верхняя грань) функ-
ции потерь ищется по реализациям случайных параметров на доверитель-
ном множестве, а внешний минимум по оптимизируемой стратегии и по
доверительным множествам. Таким образом, в обобщенной минимаксной за-
даче требуется подобрать множество неопределенности. Этот результат по-
лучил название “обобщенный минимаксный подход” и сразу зарекомендовал
себя как методологическая основа для решения прикладных задач, модель-
ных примеров и разработки численных методов минимизации квантильного
критерия. Важное свойство, фактически аналитическое представление опти-
мального доверительного множества, установлено в [4]. Подробнее об этом
речь пойдет далее. Многочисленные примеры и некоторые прикладные за-
дачи были решены сравнительно в короткое время, что нашло отражение
в [5]. Можно отметить, что использование обобщенного минимаксного под-
хода для разработки приближенных методов в течение длительного времени
шло в основном по пути сужения класса доверительных множеств, который
используется в обобщенной минимаксной задаче. Такое сужение подбиралось
в каждом конкретном случае с использованием специфики решаемой задачи.
Некоторые результаты в этом направлении собраны в [6], но общих рекомен-
даций по построению таких сужений к настоящему времени практически не
сформулировано.
Отметим, что для случая, когда вектор случайных параметров является
дискретным с конечным числом реализаций, существует лишь конечное чис-
ло доверительных множеств. В этом случае обобщенная минимаксная задача
может быть решена простым перебором этих множеств. Такая идея реализо-
вана в [7] для случая, когда функция потерь имеет полиэдральную структуру.
В общем случае реализация этой идеи затруднена ввиду того, что возникаю-
щие на этом пути оптимизационные модели могут иметь ярко выраженную
многоэкстремальную структуру, примером является минимум конечного чис-
ла выпуклых функций.
Структура статьи следующая. В разделе 2 формулируется задача мини-
мизации квантильного критерия, которая часто называется также задачей
квантильной оптимизации. Рассматривается частный случай, когда функция
потерь линейна по случайным параметрам. Важность именно такой струк-
туры подкрепляется методом линеаризации [8]. В разделе 3 формулируют-
ся результаты, составляющие теоретическую основу доверительного мето-
да: обобщенная минимаксная задача, свойство оптимального доверительного
множества, понятие и свойства α-ядра вероятностного распределения. С ис-
пользованием α-ядра формулируется вспомогательная минимаксная задача,
в которой внутренний максимум функции потерь берется по реализациям
случайных параметров на α-ядре, а внешний минимум по оптимизируе-
мой стратегии. Эта минимаксная задача является нижней аппроксимацией
обобщенной минимаксной, а следовательно и исходной задачи квантильной
оптимизации. В разделе 4 приводится формулировка известного принципа
расширения (название ввел В.И. Гурман в [9]), позволяющего конструиро-
вать достаточные условия оптимальности решений нижних аппроксимаций
абстрактных задач минимизации. С помощью этого принципа в разделе 5 вы-
68
водится достаточное условие оптимальности решения указанной выше вспо-
могательной минимаксной задачи для исходной задачи квантильной опти-
мизации. Это условие имеет вид некоторого вероятностного неравенства и
составляет основной результат настоящей статьи. Различные аспекты этого
результата иллюстрируются в разделе 6 тремя примерами. В разделе 7 приво-
дится обобщение предлагаемого достаточного условия для минимизирующих
последовательностей.
2. Постановка задачи
Рассмотрим функцию вероятности:
Pϕ(u) = P(f(u,ξ) ≤ ϕ) ,
где u ∈ U ⊂ IRm - вектор стратегии (на самом деле можно считать, что U -
множество элементов u произвольной природы, не обязательно векторов), ϕ -
скалярный параметр, ξ - n-мерный случайный вектор с распределением P,
т.е. P - вероятностная мера, определенная на борелевских подмножествах
пространства IRn и определяющая вероятность принадлежности вектора ξ
этим подмножествам. Функция f(u, ξ) называется далее функцией потерь и
предполагается линейной по ξ:
(1)
f (u, ξ) = aT
(u)ξ + b(u),
где a(u) и b(u) - некоторые векторная и скалярная функции, (·)T - операция
транспонирования.
Введем в рассмотрение функцию квантили (квантильный критерий):
(2)
ϕα(u) = [f(u, ξ)]α = min {ϕ : Pϕ(u) ≥ α} ,
где α ∈ (0, 1) - доверительная вероятность.
Предметом исследования настоящей статьи является задача квантильной
оптимизации:
(3)
ϕ0α = ϕα (uα) = min
ϕα
(u).
u∈U
Цель статьи - вывод достаточных условий оптимальности. По этой причине
вопрос существования решения uα задачи (3) здесь не затрагивается.
3. Обобщенные минимаксные задачи и α-ядра
Отправной точкой исследования задачи квантильной оптимизации (3) яв-
ляется следующий результат, составляющий основу доверительного мето-
да [6]:
Теорема 1. Справедливо обобщенное минимаксное соотношение:
(4)
ϕ0α = min sup
f (u, x),
u∈U,E∈Eαx∈E
69
где Eα - семейство всех доверительных борелевских множеств E в IRn (т.е.
P(E) ≥ α). Если пара uα, Eα доставляет минимум в (4), то uα - оптималь-
ная стратегия в задаче (3). При этом минимум по E ∈ Eα в (4) достигается
на множестве
{
}
(5)
Eα =
x : f (uα,x) ≤ ϕ0α
Впервые идея доверительного метода была сформулирована в [3], затем
развита и уточнена в [4]. Как отмечено в [5], теорема 1 устанавливает взаи-
мосвязь между стохастическими и игровыми (минимаксными) оптимизаци-
онными моделями. Но сложность задачи (4) долгое время не позволяла полу-
чать на ее основе способы точного решения задач квантильной оптимизации.
Эта сложность обусловлена неконструктивностью операции оптимизации до-
верительного множества. В частном случае, когда доверительных множеств
конечное число и их можно просто перебрать, задача (4) распадается на ко-
нечное число обычных минимаксных задач, в которых операция оптимизации
множества отсутствует. Это обстоятельство использовано в [7] для сведения
задачи квантильной оптимизации с полиэдральной функцией потерь и дис-
кретным вектором случайных параметров к задаче смешанного целочислен-
ного линейного программирования.
В [5] впервые сформулирована идея сужения задачи (4): несмотря на то
что оптимальное доверительное множество (5) невозможно использовать для
решения задачи (4), так как оно зависит от искомых параметров uα и ϕ0α,
свойства функции потерь f(u, x) делают априори известными геометрические
свойства этого множества. В частности, из линейности функции потерь (1)
следует, что оптимальное доверительное множество Eα является замкнутым
полупространством, т.е. выпуклым замкнутым множеством. Поэтому в [10]
предложено сузить задачу (4) следующим образом:
(6)
ϕ0α = min sup
f (u, x),
u∈U,E∈Ecα x∈E
где Ecα - семейство всех выпуклых, замкнутых, доверительных множеств
в IRn. Задача (6) оказывается более конструктивной по сравнению с (4) вви-
ду того, что пересечение всех множеств семейства Ecα может оказаться не
пустым в отличие от семейства Eα. В [5] это пересечение Kα, как понятие, ис-
пользовано, видимо, впервые и названо ядром вероятностной меры уровня α.
Но поскольку, как указано выше в постановке задачи, вероятностная мера P
есть распределение случайного вектора ξ, в этом частном случае удобнее на-
зывать Kα α-ядром распределения случайного вектора ξ. Итак,
⋂
⋂
{
[
]
}
(7)
Kα =
E=
x: cTx≤
cT
,
ξ α
E∈Ecα
c: ∥c∥=1
где ∥ · ∥ - любая векторная норма. Непустота α-ядра обоснована в [8] следую-
щей теоремой.
Теорема 2. Kα не пусто, если α >nn+1.
70
Отметим, что этот результат справедлив для любого распределения P. Пред-
положим далее, что Kα не пусто. Очевидно, что оно является выпуклым и
компактным множеством. Введем в рассмотрение функцию максимума на
ядре:
(8)
ψα(u) = max
f (u, x).
x∈Kα
В [5] установлено, что
(9)
ψα(u) ≤ ϕα
(u)
для любой непрерывной и квазивыпуклой по x функции потерь f(u, x). По-
скольку в соответствии с (1) рассматриваемая функция потерь линейна по x,
то она выпукла по x и неравенство (9) для нее справедливо, т.е. функция
максимума на ядре нижняя граница квантильного критерия.
Определение
[10]. Ядро Kα регулярно, если любое замкнутое полу-
пространство, его содержащее, является доверительным.
В [10] доказано, что для регулярного α-ядра Kα в неравенстве (9) дости-
гается равенство:
(10)
ψα(u) = ϕα
(u)
∀u ∈ U.
В этом случае задача (3) оказывается эквивалентной минимаксной задаче
(11)
ψ∗α = ψα (u∗α) = minψα
(u)
u∈U
(если, конечно, оптимальная стратегия u∗α существует), т.е. uα = u∗α, ϕ0α = ψ∗α.
В отличие от (4) в минимаксной задаче (11) отсутствует операция оптимиза-
ции доверительного множества. В связи с этим проблема регулярности α-яд-
ра представляется важной.
Теорема 3. Ядро Kα регулярно, если его граница является гладкой по-
верхностью в IRn, а ξ имеет плотность вероятности.
Эта теорема впервые сформулирована и доказана в [10], где на ее основе
установлено, что регулярность имеет место при α ≥ 1/2 для эллиптически
симметричных распределений с плотностями
(
)
p(x) = h (x - m)TQ-1(x - m) ,
где h(·) - некоторая функция скалярного аргумента, m ∈ IRn - детермини-
рованный вектор (центр симметрии), Q - симметричная положительно опре-
деленная матрица. Примером такого распределения, помимо многомерного
нормального и равномерного на эллипсоиде, является равномерное распре-
деление на эллиптическом кольце
{
}
(12)
x : r21 ≤ (x - m)TQ-1(x - m) ≤ r2
,
2
71
где r1 < r2. Тогда ядро является эллипсоидом
{
}
Kα = x : (x - m)TK-1(x - m) ≤ r2
,
α
где параметр rα зависит от α, функции h(·) и матрицы K. При α, близком
к 1/2, может получиться rα < r1, т.е. α-ядро для равномерного распределения
на эллиптическом кольце (12) может оказаться внутри эллипсоида
{
}
x : (x - m)TQ-1(x - m) ≤ r2
1
и будет иметь пустое пересечение с данным кольцом.
В [11] регулярное α-ядро в случае абсолютно непрерывного распределения
случайного вектора ξ названо плавающим телом. При этом понятие α-ядра
не использовалось. Под плавающим телом понималось выпуклое тело, для
которого любая опорная гиперплоскость отсекает вероятностную меру, в точ-
ности равную 1 - α. Основной результат статьи [11] заключается в том, что
существование плавающего тела, т.е. регулярность α-ядра, доказано для аб-
солютно непрерывных распределений с логарифмически вогнутыми и сим-
метричными плотностями p(x). Отметим, что указанное выше равномерное
распределение на эллиптическом кольце (12) не обладает свойством лога-
рифмической вогнутости. Поэтому классы симметричных эллиптических и
логарифмически вогнутых плотностей дополняют друг друга.
В [12, 13] предложены алгоритмы построения сколь угодно точных, внеш-
них, полиэдральных аппроксимаций α-ядра. Эти алгоритмы хорошо зареко-
мендовали себя для n = 2, т.е. для плоского случая. Но они имеют один мето-
дологический недостаток: указанные аппроксимации всегда имеют кусочно-
гладкую границу и поэтому с их помощью невозможно проверить условие
гладкости в теореме 3 при исследовании вопроса о регулярности α-ядра.
Это обстоятельство затрудняет использование вспомогательной задачи (11)
для решения исходной задачи (3). Ведь при отсутствии свойства регулярно-
сти или при отсутствии обоснования, что регулярность имеет место, можно
лишь гарантировать выполнение неравенства (9), т.е. что функция максиму-
ма ψα(u) на α-ядре является нижней оценкой квантильного критерия. Ма-
тематический аппарат, обосновывающий использование нижних оценок оп-
тимизируемого критерия в задачах минимизации для вывода достаточных
условий оптимальности, впервые предложен в [14]. В настоящее время он
известен как принцип расширения [9].
4. Замечание о принципе расширения
Принцип расширения выражает следующее свойство абстрактных опти-
мизационных задач. Рассмотрим множество M элементов m произвольной
природы.
Лемма 1. Пусть имеются функционалы I,L : M → IR1 и множества
D,E ⊂ M, удовлетворяющие условиям:
1) L(m) ≤ I(m) ∀m ∈ D,
72
2) D ⊂ E,
3) m∗ = arg min L(m) ∈ D,
m∈E
4) I (m∗) = L (m∗) .
Тогда m∗ = arg min I(m).
m∈D
Эта лемма в такой редакции опубликована в [15]. Ее обоснование дано
в [14, 16], а в книге [9] она получила название “принцип расширения”. Прин-
цип позволяет получить достаточные условия оптимальности решения m∗
вспомогательной оптимизационной задачи L(m) → minm∈E в исходной задаче
I(m) → minm∈D. Эти достаточные условия получаются в результате приме-
нения третьего и четвертого условий леммы с учетом конкретики исходной
задачи оптимизации. При этом четвертое условие имеет форму равенства,
которое при конкретизации приводит к некоторому достаточному условию в
форме алгебраического соотношения типа равенства. Однако можно указать
одну интересную альтернативную возможность. Заменим четвертое условие
леммы неравенством
(13)
I (m∗) ≤ L (m∗
).
Это неравенство равносильно четвертому условию леммы 1. Действитель-
но, из выполнения четвертого условия следует выполнение неравенства (13),
так как это неравенство нестрогое. С другой стороны, если справедливо нера-
венство (13), то из первого и третьего условий леммы 1 следует, что в этом
неравенстве строгое неравенство невозможно. Однако применение леммы 1 к
синтезу достаточных условий оптимальности с заменой четвертого условия
неравенством (13) приводит к формулировке некоторого достаточного усло-
вия в виде неравенства, что открывает дополнительные возможности, как
демонстрируется, например, в разделе 5.
5. Достаточные условия оптимальности в задаче
квантильной минимизации
Из (9) и леммы 1 очевидно вытекает истинность следующего утверждения.
Лемма 2. Пусть существует решение вспомогательной минимаксной
задачи (11), причем
(14)
ϕα (uα) ≤ ψα.
Тогда оно оптимально в задаче (3), т.е. ϕ0α = ψ∗α, uα = u∗α.
Неравенство (14) является конкретизацией четвертого условия леммы 1.
Именно оно и гарантирует, что решение минимаксной задачи (11) оптималь-
но в исходной задаче квантильной минимизации. Заметим, что проверка (14)
требует вычисления квантильного критерия на стратегии u∗α, которая подо-
зревается на оптимальность в задаче (3). Этого можно избежать, поскольку,
как доказано в [17], неравенство (14) равносильно следующему:
(15)
Pϕ (u∗α)|
≥ α.
ϕ=ψ∗α
73
Это неравенство как достаточное условие оптимальности стратегии u∗α для
исходной задачи квантильной оптимизации и составляет основной результат
данной статьи, который оформим в виде следующей теоремы.
Теорема 4. Пусть существует решение вспомогательной минимакс-
ной задачи (11), удовлетворяющее вероятностному ограничению (15). Тогда
оно оптимально в задаче (3), т.е. ϕ0α = ψ∗α, uα = u∗α.
Обсудим смысл этого утверждения. Пусть
(16)
ψ∗α = max f (u∗α,x) = f (u∗α,xα
),
x∈Kα
где xα - граничная точка Kα. Тогда неравенство (15) можно записать в виде
{
}
(17)
P x : f (u∗α,x) ≤ f (u∗α,xα)
≥ α.
Это неравенство, по существу, означает регулярность α-ядра в локальном
смысле, в граничной точке xα. В [18] доказана следующая лемма.
Лемма 3. Для любой граничной точки α-ядра существует замкнутое,
доверительное полупространство, для которого эта точка также являет-
ся граничной.
Поэтому если некоторая граничная точка α-ядра является точкой гладко-
сти его границы, то существует единственное замкнутое полупространство,
содержащее в себе α-ядро, для которого эта точка является граничной. Это
опорное полупространство в данной граничной точке. По лемме 3 оно дове-
рительное из-за того, что единственное. Поэтому неравенство (17) оказывает-
ся выполненным, если xα - точка гладкости границы α-ядра. Многочислен-
ные аналитические и численные примеры построения плоских α-ядер, при-
веденные в [12, 13, 18], свидетельствуют о том, что граница α-ядра является
кусочно-гладкой. В указанных примерах число точек негладкости границы
не превышает четырех.
6. Примеры
Пример 1. Рассмотрим задачу квантильной оптимизации с билинейной
функцией потерь
(18)
f (u, ξ) = u1ξ1 + u2ξ2,
где u = (u1, u2)T - двумерный вектор стратегии со значениями из множества
допустимых стратегий
{
}
(19)
U = (u1,u2)T : u1 ≥ 0, u2 ≥ 0, u1 + u2 = 1
Случайные величины ξ1, ξ2 независимы, причем ξ1 распределена равномерно
на отрезке [-1/2, 1/2], а ξ2 распределена равномерно в граничных точках
этого отрезка, т.е.
1
P (ξ2 = -1/2) = P (ξ2 = 1/2) =
2
74
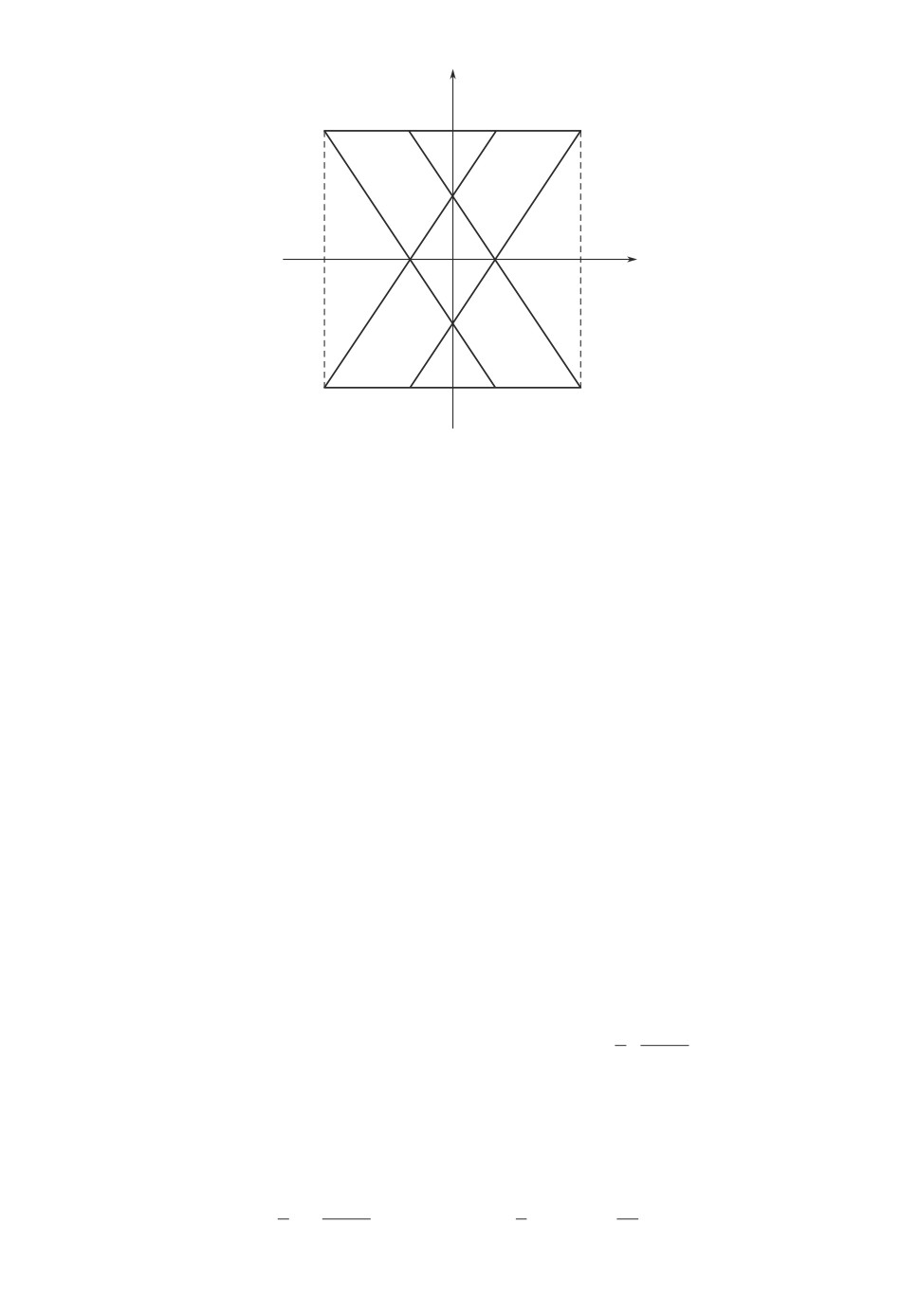
y
B
E
0,5
F
C
L
K
M
-0,5
0,5
x
N
H
A
G
-0,5
D
Рис. 1. Нерегулярное ядро KLMN. xM = 1/6. yL = 1/4.
Поэтому двумерный случайный вектор (ξ1, ξ2)T распределен равномерно на
противоположных сторонах AD и BC квадрата ABCD, см. рис. 1. Уровень
доверительной вероятности примем равным α = 2/3.
В [10] показано, что ядро Kα в рассматриваемом случае не регулярно и
представляет собой ромб KLMN. Нерегулярность обусловлена тем, что полу-
плоскость, задаваемая неравенством y ≤ 3/8, содержит целиком отрезок AD
и не пересекается с BC. Поэтому она имеет вероятностную меру 1/2, что
меньше 2/3. На рис. 1 точки E, F, G и H делят каждый из отрезков AD
и BC на три равные части, имеющие вероятностную меру 1/6.
С учетом (19) можно ввести в рассмотрение скалярную переменную
v ∈ [0,1], с помощью которой можно параметризовать все допустимые стра-
тегии: u1 = v, u2 = 1 - v.
Задача на максимум функции потерь на ядре
ψα(v) = max vx + (1 - v)y
(x,y)∈Kα
является задачей линейного программирования на многоугольнике (ромбе
KLMN). Из-за того что вектор (v,1 - v)T лежит на числовой плоскости в
неотрицательном квадранте, этот максимум может достигаться лишь в вер-
шинах M и L. Поэтому
}
{v
1-v
ψα(v) = max{v · xM ,(1 - v) · yL} = max
,
6
4
Минимум этой функции по v легко находится путем приравнивания двух ли-
нейных функций, из которых берется максимум в последнем соотношении.
Поэтому решение минимаксной задачи (11) в рассматриваемом примере име-
ет вид:
v
1-v
3
1
=
=⇒ v∗α =
,
ψ∗α =
6
4
5
10
75
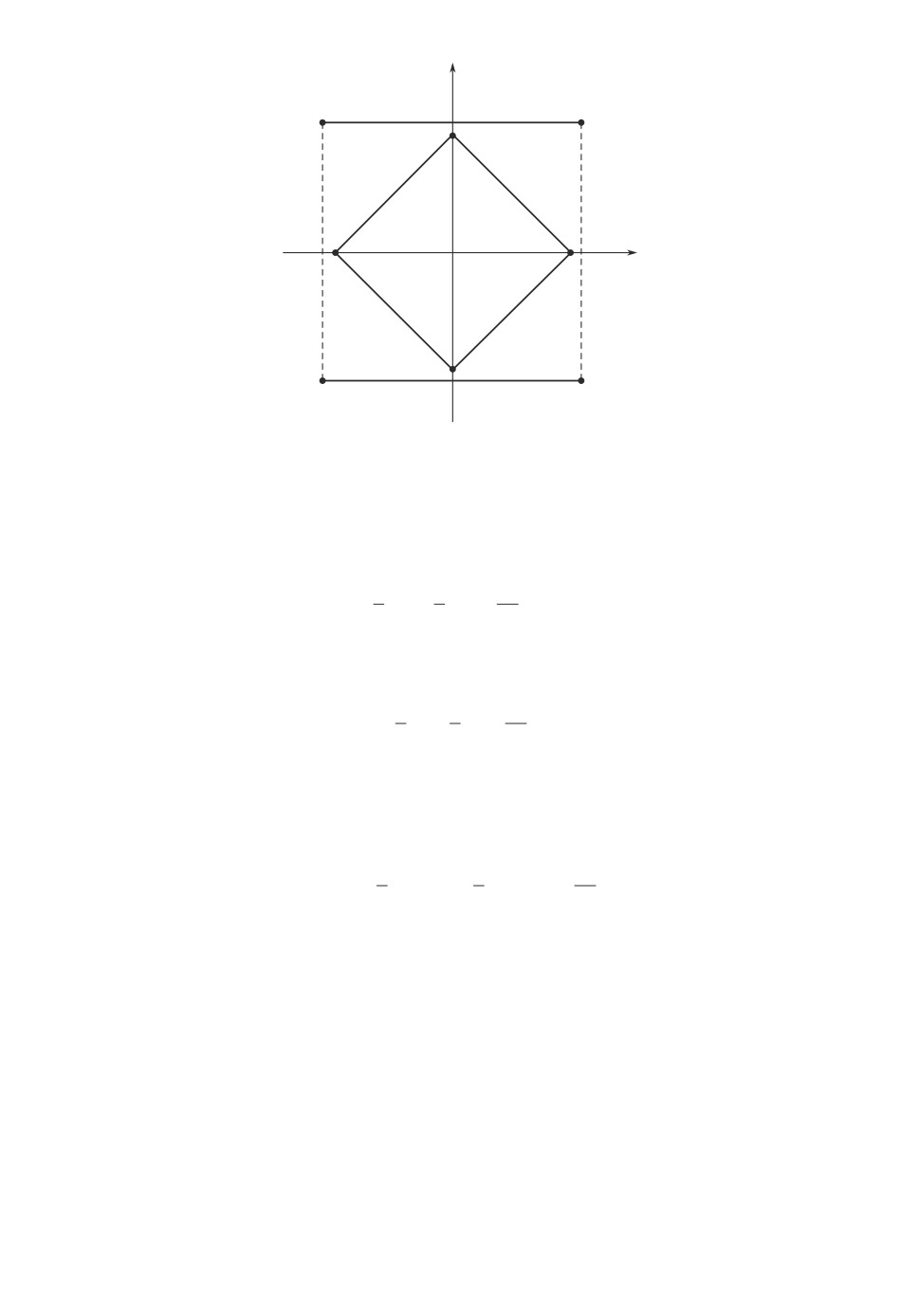
y
B
1,1
A
1
L
K
M 1,1
x
1
N
С
D
Рис. 2. Нерегулярное ядро KLMN для дискретного распределения.
Проверим достаточное условие оптимальности (15). В данном случае оно при-
водит к неравенству
}
{3
2
1
(20)
P
ξ1 +
ξ2 ≤
≥ α.
5
5
10
Неравенство
3
2
1
x+
y≤
5
5
10
определяет доверительную полуплоскость с границей, содержащей M и L.
Поэтому (20) справедливо, и, следовательно, найденное решение минимакс-
ной задачи
3
2
1
u∗1 =
,
u∗2 =
,
ψ∗α =
5
5
10
есть решение задачи квантильной оптимизации: u1α = u∗1, u2α = u∗2 и ϕ0α = ψ∗α.
Пример 2. Рассмотрим задачу примера 1 с другим законом распределе-
ния случайного вектора ξ. А именно: функция потерь определена соотноше-
нием (18), множество допустимых стратегий - формулой (19), а двумерный
случайный вектор ξ имеет дискретное распределение с восемью реализация-
ми в вершинах квадратов KLMN и ABCD, изображенных на рис. 2. Верши-
ны внутреннего квадрата KLMN имеют одинаковые вероятностные веса 0,2,
а вершины внешнего квадрата ABCD - одинаковые вероятностные веса 0,05.
Рассмотрим задачу квантильной оптимизации с α = 0,95.
Целью данного примера является иллюстрация того обстоятельства, что
предложенный подход может успешно применяться и для дискретных рас-
пределений случайных параметров.
76
Нетрудно видеть, что ядро Kα совпадает с внутренним квадратом KLMN
и не является регулярным. Действительно, каждая из четырех полуплоско-
стей, задаваемых неравенствами x ≥ -1,05, x ≤ 1,05, y ≥ -1,05 и y ≤ 1,05,
содержит α-ядро, но имеет меру 0,9, что меньше, чем α = 0,95. Так же как и
в примере 1, введем в рассмотрение скалярную переменную v. С ее помощью
легко находим
ψα(v) = max{v · xM ,(1 - v) · yL} = max {v,1 - v} ,
откуда v∗ = 1/2, ψ∗α = 1/2. Достаточное условие оптимальности (15) приводит
к неравенству
x + y ≤ 1,
которое определяет доверительную полуплоскость с границей, содержащей
M и L. Следовательно, найденное решение минимаксной задачи
1
1
1
u∗1 = v∗ =
,
u∗2 = 1 - v∗ =
,
ψ∗α =
2
2
2
есть решение задачи квантильной оптимизации: u1α = u∗1, u2α = u∗2 и ϕ0α = ψ∗α.
Пример 3. Покажем, что в условии (15) на оптимальном решении мо-
жет иметь место строгое неравенство. С этой целью расширим пример 1 сле-
дующим образом. Рассмотрим функцию потерь, характерную для портфеля
ценных бумаг:
(21)
f (u, ξ) = u0b + u1ξ1 + u2ξ2,
где u = (u0, u1, u2)T - трехмерный вектор стратегии со значениями из мно-
жества допустимых стратегий
{
}
(22)
U = (u0,u1,u2)T : u0 ≥ 0, u1 ≥ 0, u2 ≥ 0, u0 + u1 + u2 = 1 ,
b - детерминированная константа. В портфельной проблематике величи-
на (-b) имеет смысл доходности безрисковой ценной бумаги, поэтому типич-
ными для b являются отрицательные значения. Случайный вектор (ξ1, ξ2)T
тот же, что и в примере 1. Т.е. его α-ядро для α = 2/3 - тот же самый ромб
KLMN, как в примере 1.
С целью решения вспомогательной минимаксной задачи (11), как и выше,
введем скалярную переменную v ∈ [0, 1 - u0]: u1 = v, u2 = 1 - u0 - v. Тогда
}
{v
1-u0 -v
ψα (u0,v) = u0b + max
,
6
4
Приравнивая линейные функции под знаком максимума, находим, что мини-
мум этой функции по v достигается в точке
3
v∗ =
(1 - u0) ∈ [0, 1 - u0] .
5
77
Поэтому
(
)
1
1
minψα (u0,v) = ψα (u0,v∗) =
+u0
b-
v
10
10
Минимум этой функции по u0 ∈ [0, 1] легко находится. Если b ≥ 1/10, то
u∗0 = 0, и решением рассматриваемой задачи квантильной оптимизации явля-
ется решение примера 1. А вот если b < 1/10, то u∗0 = 1, откуда v∗ = u∗1 = u∗2.
В этом случае
1
1
ψ∗α =
+b-
= b.
10
10
Проверим достаточное условие оптимальности (15). В данном случае из-за
того что f (u∗, ξ) ≡ b, оно имеет вид
P{b ≤ b} = 1 > α,
т.е. выполняется как строгое неравенство. Таким образом, в случае b < 1/10
решением рассматриваемой задачи квантильной оптимизации является “без-
рисковая” стратегия u0α = 1, u1α = u2α = 0, ϕ0α = b.
Если же b ≥ 1/10, то как установлено в примере 1, решением является:
u0α = 0, u1α = 3/5, u2α = 2/5, ϕ0α = 1/10.
7. Обобщение для минимизирующих последовательностей
Минимаксная задача (11) в общем случае является сложной главным обра-
зом ввиду того, что α-ядро Kα сложно задать в простой аналитической фор-
ме. Следствием этого является то, что оптимальную стратегию для указанной
задачи приходится определять с помощью некоторой численной процедуры,
приводящей не к нахождению оптимальной стратегии u∗α, а к построению
некоторой минимизирующей последовательности uNα . Такую последователь-
ность можно получить, например, следующим образом.
В [12] предложен алгоритм аппроксимации α-ядра последовательностью
содержащих его полиэдров KNα :
{
}
⋂
[
]
(23)
KNα =
x: cTjx≤
cTξ
,
j
α
j∈J(N)
где cj, j ∈ J(N), - конечный, сгущающийся набор векторов на единичной сфе-[]
ре. Предположим, что величины cTjξ вычисляются точно, см. по данному
α
вопросу примеры в [12]. Ситуация, когда эти величины определяются с ошиб-
ками, возможно случайными, требует специального исследования, выходяще-
го за рамки настоящей статьи. В [18] доказано, что последовательность (23)
сходится к Kα в метрике Хаусдорфа. В указанном алгоритме предусмотре-
на возможность строить сгущающийся набор векторов таким образом, что
J (N) ⊂ J(N + 1). Будем считать, что именно такая возможность реализова-
на. Это приводит к тому, что (23) сходится к Kα монотонно, т.е. KN+1α ⊂ KNα .
78
Определим последовательность функций максимума
ψNα (u) = max f(u,x).
x∈KNα
Пусть
(24)
uNα = argminψNα
(u).
u∈U
Если U - компактное подмножество пространства IRm и функции a(u) и b(u)
в (1) непрерывны, то согласно [19, с. 29] uNα cуществует и является миними-
зирующей для задачи (11), т.е.
(
)
lim
ψα
uNα
=ψ∗α.
N→∞
Для формулировки достаточных условий оптимальности последователь-
ности uNα в исходной задаче квантильной оптимизации воспользуемся сле-
дующей версией принципа расширения [9].
Лемма 4. Пусть имеются функционалы I,L : M → IR1 и множества
D,E ⊂ M и последовательность mN ∈ D, удовлетворяющие условиям:
1) L(m) ≤ I(m) ∀m ∈ D,
2) D ⊂ E,
3) l ≤ inf L(m),
m∈E
(
)
4) I
mN
→ l.
Тогда mN минимизирует функционал I на D.
Рассуждая по аналогии с замечанием раздела 4, можно легко установить,
что четвертое условие этой леммы равносильно существованию числовой по-
следовательности aN со свойствами:
(
)
(25)
I
mN
≤l+aN,
aN ≥ 0, aN → 0 при N → ∞. Роль функционала I, как и выше, играет кван-
тильный критерий, роль функционала L - функция максимума ψα(u). Роль
константы l в квантильной проблематике играет ψ∗α. Тогда
(
)
aN = ψNα
uNα
-ψ∗α,
где uNα определяется согласно (24) (если, конечно, U - компакт). Таким об-
разом, конкретизация четвертого условия леммы 4 приводит к неравенству:
(
)
(
)
ϕα
uNα
≤ψNα
uNα
,
которое по лемме Розенблатта [17] равносильно условию
(
)
(26)
Pϕ
uNα
≥ α,
(
)
где ϕ = ψNα
uNα
. Именно это условие и гарантирует, что последователь-
ность uNα минимизирует квантильный критерий качества.
79
8. Заключение
Можно констатировать, что в статье предложен новый метод оптимиза-
ции квантильного критерия для линейной по случайным параметрам функ-
ции потерь. Метод сводит задачу квантильной оптимизации к вспомогатель-
ной минимаксной, в которой в роли множества неопределенности выступа-
ет α-ядро распределения вектора случайных параметров. Эта минимаксная
задача получена путем сужения и расширения обобщенной минимаксной за-
дачи, составляющей основу доверительного метода решения задач квантиль-
ной оптимизации. Предложено достаточное условие оптимальности решения
вспомогательной задачи для исходной задачи с квантильным критерием в
форме некоторого вероятностного ограничения. В отличие от известных ра-
нее результатов метод применим без предположения о регулярности α-ядра.
На примерах показано, что он работает и в случаях, когда α-ядро не регу-
лярно, в частности для дискретных и непрерывно-дискретных распределений
вектора случайных параметров.
СПИСОК ЛИТЕРАТУРЫ
1.
Kataoka S. On a Stochastic Programming Model // Econometrica. 1963. V. 31.
P. 181-196.
2.
Райк Э. О функции квантиля в стохастическом нелинейном программирова-
нии // Изв. АН ЭССР. Физ.-мат. 1971. Т. 20. № 2. С. 229-231.
3.
Кибзун А.И., Малышев В.В. Обобщенный минимаксный подход к решению за-
дач с вероятностными ограничениями // Изв. АН СССР. Техн. киберн. 1984.
№ 1. С. 20-29.
4.
Кибзун А.И., Лебедев А.А., Малышев В.В. О сведении задачи с вероятностными
ограничениями к эквивалентной минимаксной // Изв. АН СССР. Техн. киберн.
1984. № 4. С. 73-80.
5.
Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления лета-
тельными аппаратами. М.: Машиностроение, 1987.
6.
Кибзун А.И., Кан Ю.С. Задачи стохастического программирования с вероят-
ностными критериями. М.: Физматлит, 2009.
7.
Иванов С.В., Наумов А.В. Алгоритм оптимизации квантильного критерия для
полиэдральной функции потерь и дискретного распределения случайных пара-
метров // АиТ. 2012. № 1. С. 116-129.
Ivanov S.V., Naumov A.V. Algorithm to Optimize the Quantile Criterion for the
Polyhedral Loss Function and Discrete Distribution of Random Parameters // Au-
tom. Remote Control. 2012. V. 73. No. 1. P. 105-117.
8.
Васильева С.Н., Кан Ю.С. Метод линеаризации для решения задачи квантиль-
ной оптимизации с функцией потерь, зависящей от вектора малых случайных
параметров // АиТ. 2017. № 7. С. 95-109.
Vasil’eva S.N., Kan Yu.S. Linearization Method for Solving Quantile Optimization
Problems with Loss Function Depending on a Vector of Small Random Parameters //
Autom. Remote Control. 2017. V. 78. No. 7. P. 1251-1263.
9.
Гурман В.И. Принцип расширения в задачах управления. М.: Наука, 1985.
10.
Kan Yu.S. Application of the Quantile Optimization to Bond Portfolio Selection //
Stochastic Optimization Techniques. Numerical Methods and Technical Applica-
tions. Lecture Notes in Economics and Mathematical Systems. V. 513. K. Marti,
ed. Berlin: Springer, 2002. P. 145-153.
80
11.
Meyer M., Reisner S. Characterizations of affinely-rotation-invariant log-concave
measures by section-centroid location // Geometric Aspects of Functional Analy-
sis. Lecture Notes in Math. 1989-1990. V. 1469. Berlin: Springer, 1991. P. 145-152.
12.
Васильева С.Н., Кан Ю.С. Метод решения задачи квантильной оптимизации с
билинейной функцией потерь // АиТ. 2015. № 9. С. 83-101.
Vasil’eva S.N., Kan Yu.S. A Method for Solving Quantile Optimization Problems
with a Bilinear Loss Function // Autom. Remote Control. 2015. V. 76. No. 9.
P. 1582-1597.
13.
Васильева С.Н., Кан Ю.С. Алгоритм визуализации плоского ядра вероятност-
ной меры // Информатика и ее применения. 2018. № 12. Вып. 2. С. 60-68.
14.
Кротов В.Ф. Методы решения вариационных задач на основе достаточных усло-
вий абсолютного минимума. I // АиТ. 1962. Т. 23. Вып. 12. С. 1571-1583.
Krotov V.F. Methods for the Solution of Variational Problems Using Sufficient Con-
ditions for an Absolute Minimum. I // Autom. Remote Control. 1962. V. 23. No. 12.
P. 1473-1484.
15.
Гурман В.И., Хрусталев М.М. Анормальность в теории необходимых условий
оптимальности // Изв. Иркутского гос. ун-та. Сер. Математика. 2017. № 19.
С. 44-61.
16.
Хрусталев М.М. О достаточных условиях оптимальности в задачах с ограниче-
ниями на фазовые координаты // АиТ. 1967. Вып. 4. С. 18-29.
Khrustalev M.M. On Sufficient Optimality Conditions in the Problems with Phase
Coordinates Constraints // Autom. Remote Control. 1967. No. 4. P. 544-554.
17.
Rosenblatt-Roth. M. Quantiles and Medians // The Annals of Mathematical Statis-
tics. 1965. V. 36. P. 921-925.
18.
Васильева С.Н., Кан Ю.С. Аппроксимация вероятностных ограничений в зада-
чах стохастического программирования с использованием ядра вероятностной
меры // АиТ. 2019. № 11. С. 93-107.
Vasil’eva S.N., Kan Yu.S. Approximation of Probabilistic Constraints in Stochas-
tic Programming Problems with a Probability Measure Kernel // Autom. Remote
Control. 2019. V. 80. No. 11. P. 2005-2016.
19.
Федоров В.В. Численные методы максимина. М.: Наука, 1979.
Статья представлена к публикации членом редколлегии А.И. Кибзуном.
Поступила в редакцию 02.03.2020
После доработки 29.05.2020
Принята к публикации 09.07.2020
81